Linguistic Multiple-Attribute Decision Making Based on Regret Theory and Minimax-DEA

Abstract

Given that most current linguistic multiattribute decision-making methods do not consider the optimal efficiency of decision-making units and the psychological behavior of decision makers, a linguistic multiattribute decision-making method based on regret theory, data envelopment analysis, and the minimax reference point method is proposed. First, based on the decision-maker psychology of regret and avoidance, the perceived utility value of each decision-making unit was calculated using the language regret–joy value function. The subjective and optimal efficiency values of each decision-making unit were obtained using the subjective weighting and data envelopment analysis methods, respectively. Next, we considered the best efficiency as the reference point and the subjective efficiency as the decision preference to establish a minimax reference point model. By solving the model, a set of public weights that minimizes the difference between the efficiency values of all decision-making units and their optimal efficiency values can be obtained to sort the decision-making units and select the best. The feasibility of the method was verified using an example of employee evaluation and selection; the effectiveness of the method was demonstrated through comparative analysis with other methods.

1. Introduction

Multiattribute decision making refers to the ranking or selection of limited schemes that consider several attributes. In recent years, multiattribute decision making has been widely used in enterprise development and social decision making. However, owing to the complexity of objective things and the ambiguity of human thinking, it is difficult to fully express the decision-maker cognition of objective things only with precise numbers. For some attributes, it is difficult for decision makers to express quantitative values; qualitative language information is preferred to describe them [1,2]. For example, when evaluating and selecting employees, decision makers may say, “the employee’s work style is good, but the expression ability is poor” or other language-evaluation information. The solution of linguistic multiattribute decision-making problems is a worthwhile topic.

In language-based multiattribute decision-making problems, researchers have obtained fruitful results. From the literature on language-based multiattribute decision-making methods, research focuses mainly on three areas: (1) Measurement research based on linguistic information, where researchers have discussed the expression form of linguistic information in depth. Zadeh [3] defined language set S, which was used to qualitatively describe evaluation information. Xu [4] proposed a subscription-symmetric additivity set for language terms. (2) The second area involves integrated research based on language information. Lin et al. [5] applied TOPSIS and VIKOR to the Probabilistic Linguistic Term Set (PLTS) to enhance applicability. Cheng et al. [6] improved the linguistic intuition fuzzy-set distance measure and proposed a new similarity measure defined by a nonlinear Gaussian diffusion model. Zhu et al. [7] argued that decision makers have their confidence values in the decision-making process and proposed a model of group decision making with confident linguistic preferences. (3) The third area is application research based on language information. Researchers have widely used language-based multiattribute decision-making methods in project management [8], elderly care institution evaluation [9], and technology financing [10].

Taken together, the research provides a theoretical reference and design ideas for solving the linguistic multiattribute decision-making problem; however, the research has some deficiencies. First, most studies are based on the expected utility theory, which assumes that decision makers are perfectly rational. The influence of decision-maker psychological behavior on decision-making results has received considerable attention. Among the many methods based on bounded rationality, prospect and regret theories are the most widely used. Regret theory is better than prospect theory for describing and explaining the reflection effect, preference reversal, and other phenomena in actual behavior, and it also assumes fewer constraints; thus, it is increasingly used in multiattribute decision-making problems [11,12].

Second, the construction of weighted composite indicators is not sufficiently comprehensive in the calculation of weights. It is known that a reasonable distribution of weights is key to multiattribute decision-making problems. Currently, the methods for determining weights include subjective, objective, and combined weighting methods [13]. The subjective weighting method is a method of weighting according to the subjective judgment of decision-making experts and can better reflect the subjective wishes of decision makers. Representative methods include the AHP [14] and Delphi methods [15]. The objective weighting rule determines the weight according to actual information reflected by the attribute, generally ignoring the subjective intention of the decision maker. When the data change, the weight also changes; thus, the stability of the objective weight is poor. Data envelopment analysis [16], entropy value [17], and principal component analysis [18] methods are used. Given the limitations of these methods, many researchers have begun to focus on subjective and objective combination weighting methods [19,20,21]. After synthesizing subjective and objective approaches, Alexei et al. proposed a participatory goal-based weighting scheme that constructed a composite indicator more relevant to the conceptual meaning of the multidimensional phenomenon to ensure its external validity, they and determined the weights of the subindicators while respecting expert opinions [22]. The combined weighting method was significantly improved compared to the single weighting method.

The aggregation is also not sufficiently comprehensive; the weights assigned to a variable are not directly interpreted as a measure of the importance of that variable, but they also consider the way in which aggregation is performed [23]. Three types of aggregation methods are commonly used: linear, geometric, and multicriteria. As there is no perfect weighting scheme, there is no perfect case for aggregation; each method has advantages and disadvantages in different applications [24]. Thus, a specific analysis of the problem is required, and the effect of aggregation on the weighting of comprehensive indicators cannot be ignored.

The data envelopment analysis method proposed by Charnes et al. [25] can obtain the optimal efficiency value of each decision-making unit, which is an important means for solving multiattribute decision-making problems. Wang et al. [26] used the DEA-TOPSISI method for multiattribute decision making to improve the recycling efficiency of end-of-life vehicles. The attribute weights obtained by the traditional data envelopment analysis method are not uniform, resulting in a lack of basis for a horizontal comparison of decision-making results. Moreover, in actual decision making, it is sometimes necessary to incorporate subjective expert preferences in the decision-making process. At this point, the general DEA model is no longer applicable. As a method for solving multiobjective programming, the minimax reference point approach [27] can assign subjective preferences of decision-making experts to the objective function in the form of preference coefficients and minimize the gap between each objective function and its optimal value. Thus, it is widely used in many fields, such as supplier selection [28] and quality risk assessment [29].

Based on this analysis, this study proposes a language-based multiattribute decision-making method based on regret theory and minimax DEA. The main contributions of our method are presented as follows:

(1)

We considered the influence of decision-maker psychological factors on decision making and incorporated decision-maker attitudes toward regret and avoidance into the language-based multiattribute decision-making method, making the decision-making results more realistic.

(2)

Compared to general combinatorial assignment methods, the method in this study simultaneously considers both the subjective tendency of the decision maker and the best intention of each decision unit. We used the minimal–extremely large reference point method to aggregate subjective and objective information to find the most eclectic solution as the public weight of the attributes recommended by all decision units, fairly and simultaneously considering the interests of all decision units.

The remainder of this paper is organized as follows: Section 2 introduces the basic concepts of language assessment scales and regret theory. Section 3 introduces the data envelopment analysis and minimax reference point methods. Section 4 proposes a language-based multiattribute decision-making method based on regret theory and minimax DEA and details the specific decision-making steps. Section 5 verifies the feasibility of the proposed method through an example and compares it with other methods. Section 6 summarizes the proposed approach and provides an outlook for future research.

2. Relevant Theoretical Basis

2.1. Language Assessment Scale

When decision makers use language terms for evaluation, they must generally choose an appropriate language evaluation scale. Compared to the uniform language scale, the non-uniform language evaluation scale is more in line with human thinking habits, and the consistency of the conclusions is higher [30]. Based on the analysis, this study used a non-uniform language evaluation scale.

$$S=\left\{S_{\alpha }|\alpha =-(\tau -1),-\frac{2}{3}(\tau -2),\cdots ,\frac{2}{3}(\tau -2),(\tau -1)\right\}$$

(1)

In Equation (1), $S_{\alpha }$ represents the language term, and $\tau$ is a positive integer. When $\alpha >0$, the language term set is

$$S^{+}=\left\{S_{\alpha }|\alpha =\frac{2(i-1)}{\tau +2-i},i=2,\cdots ,\tau -1,\tau \right\}$$

(2)

When $\alpha <0$, the language term set is

$$S^{-}=\left\{S_{\alpha }|\alpha =-\frac{2(i-1)}{\tau +2-i},i=2,\cdots ,\tau -1,\tau \right\}$$

(3)

For example, when $\tau =4$, the granularity of the linguistic term set is 7.

$$S=\left\{{\mathrm{S}}_{-3}={\mathrm{extremely} \mathrm{poor},\mathrm{S}}_{-\frac{4}{3}}={\mathrm{very} \mathrm{poor},\mathrm{S}}_{-\frac{1}{2}}=\mathrm{poor},{\mathrm{S}}_0=\mathrm{medium},{\mathrm{S}}_{\frac{1}{2}}=\mathrm{good},{\mathrm{S}}_{\frac{4}{3}}={\mathrm{very} \mathrm{good},\mathrm{S}}_3=\mathrm{extremely} \mathrm{good}\right\}$$

(4)

Regret Theory

The core idea of regret theory is that decision makers consider the outcome of their choice and compare it with the outcomes of other options. If the other options are better, there is regret. Regret theory was first proposed by Bell [31] and Loomes and Sugden [32]. Initially, it was used to solve a selection problem with two schemes. It was later extended to solve selection problems with multiple schemes [33]. Bleichrodt et al. [34] proposed a calculation method for the regret–joy value based on the decision information of exact numbers. Based on regret theory, Tang et al. [35] and Wang et al. [36] used interval and fuzzy numbers, respectively, to characterize the uncertainty of decision-making information. However, in an actual decision-making process, the attribute values of the DMUs are more likely to be presented in the form of language terms. Thus, it is particularly important to calculate regret–joy values based on linguistic information.

Definition 1.

Let $S_{\alpha }\in S$ be the language evaluation term and $I(S_{\alpha })=\alpha$ be the subscript conversion function of the language term [37]. Using this function, any language term can be converted to an exact number.

Definition 2.

Let $I(S_{\alpha })$ be the subscript conversion function of the language term $S_{\alpha }$. The language utility function of the language term $S_{\alpha }$ is

$$LV(S_{\alpha })=V(\frac{I(S_{\alpha })+\tau -1}{2(\tau -1)})=V(\frac{\alpha +\tau -1}{2(\tau -1)})$$

(5)

where $\tau -1$ is the potential of the language evaluation scale S, satisfying $\frac{\alpha +\tau -1}{2(\tau -1)}\in (0, 1)$. $V(x)$ is the classical utility function of the exact number $x$ that satisfies $V^{\prime }(x)>0,V^{″}(x)<0$. The degree of the risk aversion of decision makers is inversely proportional to the value of $\epsilon$.

Definition 3.

Let $s_{\alpha }, s_{{\alpha }^{*}}\in S$ be the decision-maker linguistic judgment values for the currently selected option $A_i$ and ideal option $A^{*}$, respectively, and $R(y)$ be the classical regret–joy function of the exact number $y$. $R(0)=0$, $R^{\prime }(y)>0$, and $R^{″}(y)<0$. $L{R}_i$ is said to be the linguistic regret–joy function of the decision-maker selection of option $A_i$ and the abandonment of ideal option $A^{*}$.

$$\begin{gathered} L{R}_i=R(LV(s_{\alpha })-LV(s_{{\alpha }^{*}})) \\ =R(V(\frac{\alpha +\tau -1}{2(\tau -1)})-V(\frac{{\alpha }^{*}+\tau -1}{2(\tau -1)})) \end{gathered}$$

(6)

In Equation (6), when $s_{{\alpha }^{*}}=s_{{\alpha }^{+}}$, the value of the linguistic judgment of the positive ideal scheme $A^{+}$ can be calculated; the result computed by the function $LR$ is the regret value.

$$L{R}_{\mathrm{i}}^{+}=R(V(\frac{\alpha +\tau -1}{2(\tau -1)})-V(\frac{{\alpha }^{+}+\tau -1}{2(\tau -1)}))$$

(7)

when $s_{{\alpha }^{*}}=s_{{\alpha }^{-}}$, the value of the linguistic judgment of the positive ideal scheme $A^{-}$ can be calculated; the result computed by the function $LR$ is the regret value.

$$L{R}_{\mathrm{i}}^{-}=R(V(\frac{\alpha +\tau -1}{2(\tau -1)})-V(\frac{{\alpha }^{-}+\tau -1}{2(\tau -1)}))$$

(8)

Definition 4.

When the decision maker chooses option $A_i$, the language-aware utility value is

$$L{U}_{\mathrm{i}}=LV(S_{\alpha })+L{R}_i^{+}+L{R}_i^{-}$$

$$\begin{array}{l}=V(\frac{\alpha +\tau -1}{2(\tau -1)})+R(V(\frac{\alpha +\tau -1}{2(\tau -1)})-V(\frac{{\alpha }^{+}+\tau -1}{2(\tau -1)}))\\ +R(V(\frac{\alpha +\tau -1}{2(\tau -1)})-V(\frac{{\alpha }^{-}+\tau -1}{2(\tau -1)}))\end{array}$$

(9)

Equation (9) can be used to calculate the language-perceived utility value of any scheme, which also means that any language evaluation term can be converted into an exact number using the formula for effective decision making.

3. Methodology

3.1. Data Envelopment Analysis

Data envelopment analysis is used to evaluate the relative efficiency of decision-making units. From the perspective of inputs and outputs, efficiency is maximized by flexibly assigning weights to each decision-making unit. In the DEA model, decision-making efficiency is defined as the ratio of the weighted output index to the weighted input index. An effective way to identify whether the evaluation index is an input or output is described as follows: if the index value of an attribute is as small as possible, it is the output of the input index and is an output indicator.

However, in practical applications, there are many multiattribute decision-making problems that do not require a consideration of input indicators, such as evaluating the scientific research strength of EU countries [38] and evaluating and selecting employees and cadres. At this point, traditional data envelopment analysis methods are no longer applicable. Adolphson et al. [39] first proposed the input-free DEA model. Liu et al. [40] systematically studied this type of model and referred to it as the data envelopment analysis model without explicit input (DEA-WEI model). Yang et al. [41] studied a DEA-WEI model with quadratic terms from the perspective of extended utility. In general, DEA-WEI does not reflect the technical efficiency of the decision unit input–output system as a classical DEA does. They investigated the link between the DEA-WEI model and multiattribute utility theory. The form of the objective function is similar to that of a classical utility function. Unlike the classic utility theory, only the functional form of the objective function is determined by decision-makers to reflect a subjective emphasis on evaluation. In turn, the decision unit determines the coefficients of the function through deal-style programming to ensure that it receives the most favorable evaluation.

Suppose that there are $n$ decision-making units, $DM{U}_{\mathrm{i}}(i=1,2,\cdots n)$. Each decision-making unit has $\mathrm{m}$ attributes, $\mathrm{m}=p+q$, among which $p$ attributes are input indicators and $q$ attributes are output indicators. $x_{ai}(a=1,2,\cdots p)$ represents the measured value of the $a$ input indicator for the $i$ decision-making unit. $y_{bi}(b=1,2,\cdots ,q)$ represents the measured value of the $b$ output indicator for the $i$ decision-making unit. ${\mathrm{u}}_a(a=1,2,\cdots ,p)$ represents the weight assigned to the $a$ input indicator. ${\mathrm{v}}_b(b=1,2,\cdots ,q)$ represents the weight assigned to the $b$ output.

Based on the analysis, for a multiattribute decision-making problem with input and output indicators, the traditional CCR model can be expressed as

$$\max {\displaystyle \sum _{b=1}^q{y}_{bi}{v}_b}$$

$$\mathrm{s}.\mathrm{t}.\left\{\begin{array}{c}{\displaystyle \sum _{b=1}^q{y}_{bi}{v}_b-{\displaystyle \sum _{a=1}^p{x}_{ai}{u}_a\le 0,i=1,2,\cdots ,n}}\\ {\displaystyle \sum _{a=1}^p{x}_{a0}{u}_a=1,v_b\ge 0,b=1,2,\cdots n}\\ u_a,v_b\ge 0,a=1,2,\cdots p;b=1,2,\cdots q\end{array}\right.$$

(10)

For multiattribute decision-making problems without input indicators, the DEA-WEI model proposed by Yang et al. [38] was used

$$\max {\displaystyle \sum _{b=1}^q{y}_{b0}{v}_b}$$

$$\mathrm{s}.\mathrm{t}.\left\{\begin{array}{c}{\displaystyle \sum _{b=1}^q{y}_{bi}{v}_b\le 1,i=1,2,\cdots ,n}\\ v_b\ge 0,b=1,2,\cdots q\end{array}\right.$$

(11)

where the subscript “0” refers to the DMU of interest.

Minimax Reference Point Approach

In management and engineering, most decision-making problems involve potentially conflicting goals; research has focused on the effective coordination of these goals. Yang [27] proposed the minimax reference point method. The basic idea of this method is that it assumes that all objective functions have their optimal values; with the existing constraints, it is not possible to make all objective functions reach optimal values at the same time. Thus, a set of solutions must be found such that all combined deviations between the objective function value and its optimal value are the smallest. In other words, the optimal solution should be obtained when all objective function values are closest to their optimal values. The specific solutions are described as follows:

Suppose a multiobjective programming problem can be expressed as

$$\max f(x)=\left\{f_1(x),f_2(x),\cdots ,f_k(x)\right\}$$

$$s.t.\left\{\begin{array}{c}{x}_j\in \Omega ,j=1,2\cdots ,n\\ \Omega =\left\{x|g_z(x)\le 0,h_r(x)=0;z=1,\cdots ,m_1,r=1,\cdots m_2\right\}\end{array}\right.$$

(12)

$f_i(x)$ refers to the $i$ objective function; $x_j$ represents the $j$ decision variable; $\Omega$ represents the constraints of the decision variable $x$, and $g_z(x)$ and $h_r(x)$ represent the inequality and equality constraints of the decision variable $x$, respectively.

Before solving this multiobjective programming problem, each objective function was solved separately, and the optimal value of $f_i^{\ast }(x)$ was obtained. The mini-maximization method was used to make all objective functions as close as possible to their optimal values. Thus, the multiobjective programming problem can be transformed into a single-objective programming problem.

$$\min d$$

$$s.t.\left\{\begin{array}{c}\left|f_i^{\ast }(x)-f_i(x)\right|\le d,i=1,2,\cdots ,n\\ x\in \Omega \end{array}\right.$$

(13)

The solution to the multiobjective programming problem can be obtained by solving Equation (13).

4. Linguistic Multiple-Attribute Decision Making Based on Regret Theory and Minmax-DEA

4.1. Determination of Attribute Weights

A reasonable distribution of weights is key to multiattribute decision-making problems. To consider the decision-maker psychology of regret and avoidance and reflect the best intentions of each decision-making unit and the decision-maker subjective tendency, this study proposes a weight determination method for linguistic multiattribute decision-making problems. The specific steps are presented as follows:

Suppose there are $n$ candidates for the linguistic multiattribute decision-making problem $A_i(1\le i\le n)$, where $A_i$ represents the $i$ solution, and $m$ attributes $Y_j(1\le j\le m)$, where $Y_j$ represents the $j$ attribute, linguistic multiattribute evaluation matrix $X={(x_{ij})}_{n\times m}$, where $x_{ij}$ represents the decision-maker linguistic evaluation of option $A_i$ with respect to attribute $Y_j$.

Step 1: According to the rich knowledge and experience of decision-making experts and using the language evaluation scale in Equation (4), the language-type multiattribute evaluation matrix $X={(x_{ij})}_{n\times m}$ is obtained.

Step 2: The language term subscript conversion function $I$ I of Definition 1 is used to convert the linguistic evaluation matrix $X$ x in Step 1 into an exact number-based evaluation matrix $X^{\prime }$. Considering decision-maker regret avoidance, Equations (5)–(9) are used to process the matrix $X^{\prime }$ to obtain the perceived utility matrix $P=(p_{ij}{)}_{m\times n}$.

Step 3: Based on the perceived utility matrix $P=(p_{ij}{)}_{m\times n}$, Equations (10) and (11) are used to calculate the optimal efficiency value ${\theta }^{\ast }$ for each decision-making unit. The data envelopment analysis method can flexibly assign weights to each decision-making unit to maximize its efficiency; thus, the efficiency value represents the best of each decision-making unit.

Step 4: In Step 3, an optimal efficiency value is obtained for each decision-making unit. However, the weights are not uniform, and the decision-making results lack a basis for horizontal comparison. Thus, it is particularly important to determine a set of public weights that satisfies all decision-making units. Thus, we constructed a minimax-DEA model based on the data envelopment analysis method and minimax reference point methods. By solving the model, a set of common weights can be found that minimizes the gap between the efficiency values of all decision-making units and their optimal values.

It is assumed that not all decision-making units contain input indicators; thus, the following model is established based on

$$\min d=\max \left\{\begin{array}{c}{t}_1={\theta }_1^{\ast }-{\displaystyle \sum _{b=1}^q{y}_{b1}{v}_b}\\ t_2={\theta }_2^{\ast }-{\displaystyle \sum _{b=1}^q{y}_{b2}{v}_b}\\ \cdots \\ t_{\mathrm{n}}={\theta }_n^{\ast }-{\displaystyle \sum _{b=1}^q{y}_{bn}{v}_b}\end{array}\right.$$

$$s.t.\left\{\begin{array}{c}{\displaystyle \sum _{b=1}^q{y}_{bi}{v}_b\le 1,i=1,2,\cdots n}\\ v_b\ge 0,b=1,2,\cdots ,q\end{array}\right.$$

(14)

In Equation (14), ${\theta }^{\ast }=({\theta }_1^{\ast },{\theta }_2^{\ast },\cdots ,{\theta }_n^{\ast })$ represents the optimal efficiency value of each decision-making unit. $t=(t_1,t_2,\cdots t_n)$ represents the difference between the efficiency value of each decision-making unit and its optimal efficiency value with weight $v_b$.

A set of common weights is obtained by solving the model. However, these weights only consider the optimal efficiency value of each decision-making unit at the objective level and not at the subjective level. It is known that a reasonable weight distribution should reflect the actual data and the subjective intentions of decision makers. To consider the best intentions of each decision-making unit and the subjective inclinations of decision makers, a new variable $g_i$ is introduced based on multiobjective planning. It represents the “speak” of each decision-making unit.

$$g_i=\frac{o_i}{{\displaystyle \sum _{i=1}^n{o}_i}},i=1,2,\cdots ,n$$

(15)

$${\mathrm{o}}_i={\displaystyle \sum _{b=1}^q{w}_b{y}_{ib}},i=1,2,\cdots ,n$$

(16)

${\mathrm{w}}_j$ represents the subjective weight of each decision-making unit; ${\mathrm{o}}_i$ represents the subjective efficiency value of each decision-making unit. The subjective weight and subjective efficiency value of each attribute can be calculated using any subjective weighting method. Here, the analytic hierarchy process from the literature [14] is used to calculate. Li et al. [21] showed that the order of the size of each attribute in the subjective weight can better reflect the importance of the attribute itself and is the expression of the intention of the decision maker. Thus, to ensure that the order of the combined weights is consistent with the order of the subjective weights, it is necessary to add a constraint set $\Omega$ based on the model. For example, if the subjective weight $\mathrm{w}=(w_1,w_2,w_3)=(0.3,0.5,0.2)$ has three attributes, then $\Omega = \left\{{\mathrm{v}}_1|v_2>v_1>v_3\right\}$. Thus, the final weighting model is

$$\min d=\max \left\{\begin{array}{c}{t}_1=g_1({\theta }_1^{\ast }-{\displaystyle \sum _{b=1}^q{y}_{b1}{v}_b})\\ t_2=g_2({\theta }_2^{\ast }-{\displaystyle \sum _{b=1}^q{y}_{b2}{v}_b})\\ \cdots \\ t_n=g_n({\theta }_n^{\ast }-{\displaystyle \sum _{b=1}^q{y}_{bn}{v}_b})\end{array}\right.$$

$$s.t.\left\{\begin{array}{c}{\displaystyle \sum _{b=1}^q{y}_{bi}{v}_b\le 1,i=1,2,\cdots n}\\ v_b\in \Omega ,b=1,2,\cdots q\end{array}\right.$$

(17)

According to the model, if the subjective efficiency value of a certain decision-making unit is larger, then $g_i$ is larger. In multiobjective planning, more consideration is given to the gap between the decision-making unit and its optimal efficiency value, which also means that it has more “speak” than other decision-making units. Thus, when using a multiobjective programming model for weight allocation, the willingness of the decision-making unit to assign weights increases.

It is clear that model (17) is equivalent to model (18).

$$\min \mathrm{d}$$

$$s.t.\left\{\begin{array}{c}{g}_i({\theta }_i^{\ast }-{\displaystyle \sum _{b=1}^q{y}_{bi}{v}_b})\le d,i=1,2,\cdots ,n\\ {\displaystyle \sum _{b=1}^q{y}_{bi}{v}_b\le 1,i=1,2,\cdots ,n}\\ v_b\in \Omega ,b=1,2,\cdots q\end{array}\right.$$

(18)

Step 5: However, the weight at this time does not necessarily satisfy ${\displaystyle {\sum }_{b=1}^q{v}_b^{\ast }=1}$. Thus, after normalization, the final public weight is obtained as

$${\mathrm{w}}_b^{\ast }=\frac{v_b^{\ast }}{{\displaystyle \sum _{b=1}^q{v}_b^{\ast }}},b=1,2,\cdots ,q$$

(19)

4.2. Decision Steps and Processes

The steps of the linguistic multiattribute decision-making method based on regret theory and minimax DEA are presented as follows:

Step 1: Considering decision-maker regret avoidance, the linguistic multiattribute evaluation matrix $X{=(\mathrm{x}}_{ij}{)}_{m\times n}$ is processed according to Equations (5)–(9) and the perceived utility matrix $P{=(p}_{ij}{)}_{m\times n}$ is obtained.

Step 2: The optimal efficiency value ${\theta }^{\ast }$ of each decision-making unit according to Equations (10) and (11) are calculated. The analytic hierarchy process is used to perform subjective weighting to obtain the subjective weight ${\mathrm{w}}_b$ and subjective efficiency value ${\mathrm{o}}_i$.

Step 3: Using LINGO software, the public weight ${\mathrm{w}}_b^{\ast }$ of each attribute is calculated according to Equations (15)–(19).

Step 4: The comprehensive perceptual utility value $p_i^{\ast }$ of each decision-making unit is calculated through the perceptual utility matrix $p$ and the public weight ${\mathrm{w}}_b^{\ast }$; the ranking is based on this.

5. Case Analysis

When a unit was evaluating and selecting cadres, experts evaluated 15 candidates according to work responsibility ability $(C_1)$, scientific research assistance ability $(C_2)$, project completion ability $(C_3)$, thesis writing ability $(C_4)$, awards $(C_5)$, and academic communication ability $(C_6)$. The chosen language evaluation scale was

$$S=\left\{{\mathrm{S}}_{-3}={\mathrm{extremely} \mathrm{poor},\mathrm{S}}_{-\frac{4}{3}}={\mathrm{very} \mathrm{poor},\mathrm{S}}_{-\frac{1}{2}}=\mathrm{poor},{\mathrm{S}}_0=\mathrm{medium},{\mathrm{S}}_{\frac{1}{2}}=\mathrm{good},{\mathrm{S}}_{\frac{4}{3}}={\mathrm{very} \mathrm{good},\mathrm{S}}_3=\mathrm{extremely} \mathrm{good}\right\}$$

The corresponding decision information is shown in Table 1.

Table 1. Linguistic multiattribute evaluation matrix.

Personnel	Evaluation Metrics
	C1	C2	C3	C4	C5	C6
DMU1	S4/3	S4/3	S−1/2	S−1/2	S−1/2	S1/2
DMU2	S4/3	S1/2	S1/2	S4/3	S−4/3	S−1/2
DMU3	S0	S1/2	S−4/3	S−4/3	S1/2	S−4/3
DMU4	S4/3	S1/2	S4/3	S1/2	S−1/2	S−1/2
DMU5	S4/3	S4/3	S1/2	S−4/3	S1/2	S0
DMU6	S4/3	S−1/2	S0	S0	S1/2	S−4/3
DMU7	S4/3	S0	S−1/2	S0	S0	S−1/2
DMU8	S4/3	S4/3	S1/2	S−1/2	S−1/2	S4/3
DMU9	S1/2	S0	S4/3	S−4/3	S−4/3	S−1/2
DMU10	S4/3	S1/2	S0	S−1/2	S−1/2	S−1/2
DMU11	S4/3	S1/2	S0	S−4/3	S−4/3	S0
DMU12	S4/3	S0	S4/3	S−4/3	S−4/3	S0
DMU13	S4/3	S−1/2	S−1/2	S−4/3	S−1/2	S−1/2
DMU14	S4/3	S−1/2	S0	S−4/3	S−1/2	S0
DMU15	S4/3	S0	S1/2	S−4/3	S−4/3	S0

5.1. Decision Step

Step 1: According to Equations (5)–(8), the language-type multiattribute evaluation matrix $X$ is processed, and the perceptual utility matrix $P$ is obtained, as shown in Table 2, where $\epsilon =0.88, \delta =0.3$ [42].

Table 2. Perceived utility matrix P.

Personnel	Evaluation Metrics
	C1	C2	C3	C4	C5	C6
DMU1	0.811	0.834	0.413	0.413	0.455	0.669
DMU2	0.811	0.630	0.669	0.871	0.230	0.413
DMU3	0.479	0.630	0.187	0.187	0.708	0.187
DMU4	0.811	0.630	0.871	0.669	0.455	0.413
DMU5	0.811	0.834	0.669	0.187	0.708	0.543
DMU6	0.811	0.373	0.543	0.543	0.708	0.187
DMU7	0.811	0.503	0.413	0.543	0.583	0.413
DMU8	0.811	0.834	0.669	0.413	0.455	0.871
DMU9	0.606	0.503	0.871	0.187	0.230	0.413
DMU10	0.811	0.630	0.543	0.413	0.455	0.413
DMU11	0.811	0.630	0.543	0.187	0.230	0.543
DMU12	0.811	0.503	0.871	0.187	0.230	0.543
DMU13	0.811	0.373	0.413	0.187	0.455	0.413
DMU14	0.811	0.373	0.543	0.187	0.455	0.543
DMU15	0.811	0.503	0.669	0.187	0.230	0.543

Step 2: Because the multiattribute decision-making problem does not contain input indicators, Lingo software was used to solve it according to Equation (10), and the optimal efficiency value ${\theta }^{\ast }$ of each decision-making unit was obtained. Using the analytic hierarchy process, the subjective weight of each decision-making unit was calculated as

$${\mathrm{w}}_b={(0.1592,0.0416,0.3854,0.2474,0.0649,0.1015)}^T$$

Step 3: According to Equations (14)–(19), Lingo software was used to solve the problem, and the optimal public weight of each attribute was obtained as

$${\mathrm{w}}^{\ast }={(0.1592,0.0808,0.2824,0.1592,0.1592,0.1592)}^T$$

Step 4: According to the perceptual utility matrix $P$ and public weight ${\mathrm{w}}^{\ast }$, the comprehensive perceptual utility value $P^{\ast }$ of each decision-making unit and its ranking can be obtained, as is presented in Table 3. The comprehensive perceived utility value of DMU4 was the largest, and the comprehensive perceived utility value of DMU3 was the smallest. Thus, considering decision-maker regret and avoidance psychology, the minimax-DEA model proposed in this study was used to determine DMU4 as the optimal solution.

Table 3. Comprehensive perceived utility value and ranking results.

Personnel	Subjective Efficiency Value	Voice	Comprehensive Utility Value	Rank
	Oi	gi	P *
DMU1	0.523	0.064	0.558	6
DMU2	0.686	0.084	0.610	4
DMU3	0.286	0.035	0.352	15
DMU4	0.728	0.090	0.671	1
DMU5	0.569	0.070	0.614	3
DMU6	0.553	0.068	0.542	7
DMU7	0.524	0.065	0.532	9
DMU8	0.642	0.079	0.662	2
DMU9	0.557	0.069	0.516	10
DMU10	0.538	0.066	0.537	8
DMU11	0.481	0.059	0.486	13
DMU12	0.602	0.074	0.569	5
DMU13	0.422	0.052	0.444	14
DMU14	0.485	0.060	0.501	12
DMU15	0.524	0.065	0.512	11

5.2. Comparison of Methods

To further illustrate the effectiveness of the method, it was compared with methods used in other studies. The decision-making methods in the literature can be divided into two categories. Without considering the psychological factors of the decision-makers, the hesitant fuzzy language TOPSIS decision method proposed by Wu et al. [43] was used to analyze the examples in this study. The method proposed by Li et al. [21] was used to analyze the examples in this study using AHP and subjective and objective combination weighting.

The sorting results of the method used in this study were compared with those of Wu et al. [43]. The sorting results are shown in Figure 1. Although the overall ranking results of the two methods slightly differed, the ranking of each decision did not significantly change. This is because Wu et al. [43] assumed that the decision maker was completely rational in the decision-making process, unlike the reality of decision-making to a certain extent. The method in this study considers the psychology of decision-maker regret and avoidance and simulates decision-making judgments based on the subjective psychological characteristics and objective preference information of decision makers in an actual environment for more realistic decision-making results.

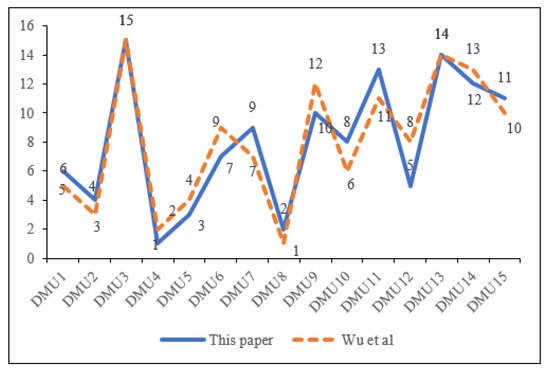
Figure 1. The sorting results of both methods [43].

Considering decision-maker regret avoidance, a comparative analysis was carried out according to the determination methods of different attribute weights. The final ranking results for the different decision-making methods are presented in Table 4.

Table 4. The sorting results of both methods.

Personnel	This Study	Li et al. [21]	AHP
DMU1	6	6	11
DMU2	4	2	2
DMU3	15	15	15
DMU4	1	1	1
DMU5	3	4	5
DMU6	7	5	7
DMU7	9	8	9
DMU8	2	3	3
DMU9	10	10	6
DMU10	8	9	8
DMU11	13	12	13
DMU12	5	7	4
DMU13	14	14	14
DMU14	12	13	12
DMU15	11	11	10

It is observed from the table that the overall ranking results of the three methods are slightly different, but the optimal and least optimal schemes are consistent. We refer to a change in the ordering of more than three as a large change. Compared with the AHP, the decision-making units that underwent large changes were DMU1 and DMU9. The main reason for this is that AHP has strong subjective randomness and ignores the objective information of attributes, which leads to the ranking of DMU9 at the top and the low ranking of DMU6. The method used in this study was consistent with the ranking results of the subjective and objective combination weighting methods proposed by Li et al. [21]. Subjective arbitrariness was reduced, and decision-making preferences were considered; thus, the ranking results are more reasonable. In addition, the method used in this study considers the best intentions of each decision-making unit in the decision-making process, which makes the decision-making results more realistic.

In summary, the method proposed in this study incorporates decision-maker regret and avoidance psychology into the decision-making process, considers decision-maker subjective tendencies and the best intentions of each decision-making unit, and ensures weight calculation rationality, making the decision-making results more reliable.

6. Conclusions

For a multiattribute decision-making problem whose attribute value is language evaluation information, this study proposes a language-based multiattribute decision-making method based on regret theory and minimax-DEA. First, based on the decision-maker psychology of regret and avoidance, the perceived utility value of each decision-making unit was calculated using the language regret–joy value function. The subjective weighting and data envelopment analysis methods were used to calculate the subjective and optimal efficiency values of each decision-making unit, respectively. We considered the best efficiency as the reference point and the subjective efficiency as the decision preference to establish a minimax reference point model. By solving the model, a set of public weights that minimizes the difference between the efficiency values of all DMUs and their optimal efficiency values can be obtained, and the decision-making units can be sorted and selected.

The main features of the method are as follows: (1) the regret avoidance of the decision maker is incorporated into the linguistic multiattribute decision-making method, which considers the influence of decision-maker psychological factors on decision making and, to a certain extent, makes the decision-making results more realistic. (2) Regret theory is effectively cross-fertilized using the data envelopment analysis method and the minimal–extremely large reference point method, and a new type of linguistic multiattribute decision-making method is proposed that provides a new path for weight determination in multiattribute decision-making problems. (3) A new goal-planning model is constructed based on the data envelopment analysis method and the minimal–extremely large reference point method, considering the subjective tendency of the decision maker and the best intentions of all decision units, ensuring the rationality of the weight calculation and producing more reliable decision results.

This study only considered a single-person decision-making problem with attribute values in linguistic terms. Multiattribute group decision-making problems with uncertain data including attribute values, fuzzy numbers, and interval numbers will be our next research focus.