Linguistic Multiple-Attribute Decision Making Based on Regret Theory and Minimax-DEA
Abstract
1. Introduction
- (1)
- We considered the influence of decision-maker psychological factors on decision making and incorporated decision-maker attitudes toward regret and avoidance into the language-based multiattribute decision-making method, making the decision-making results more realistic.
- (2)
- Compared to general combinatorial assignment methods, the method in this study simultaneously considers both the subjective tendency of the decision maker and the best intention of each decision unit. We used the minimal–extremely large reference point method to aggregate subjective and objective information to find the most eclectic solution as the public weight of the attributes recommended by all decision units, fairly and simultaneously considering the interests of all decision units.
2. Relevant Theoretical Basis
2.1. Language Assessment Scale
Regret Theory
3. Methodology
3.1. Data Envelopment Analysis
Minimax Reference Point Approach
4. Linguistic Multiple-Attribute Decision Making Based on Regret Theory and Minmax-DEA
4.1. Determination of Attribute Weights
4.2. Decision Steps and Processes
5. Case Analysis
5.1. Decision Step
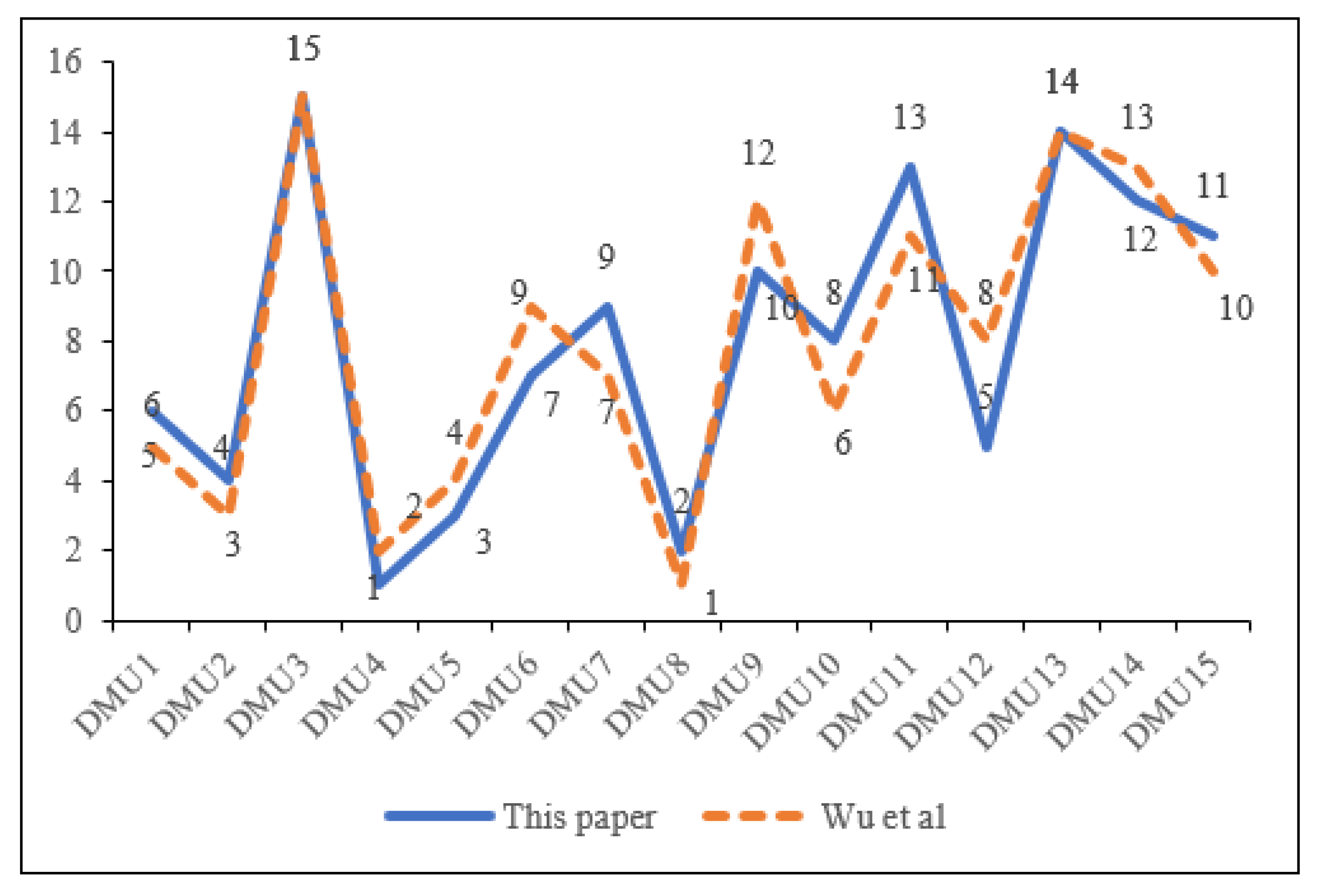
5.2. Comparison of Methods
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, T.; Zhang, L. Multiple-attribute group decision-making method based on intuitionistic multiplicative linguistic information. Comput. Appl. Math. 2022, 41, 209. [Google Scholar] [CrossRef]
- Xue, W.; Xu, Z.; Mi, X. Solving hesitant fuzzy linguistic matrix game problems for multiple attribute decision making with prospect theory. Comput. Ind. Eng. 2021, 161, 107619. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Xu, Z. Uncertain linguistic aggregation operators based approach to multiple attribute group decision making under uncertain linguistic environment. Inf. Sci. 2004, 168, 171–184. [Google Scholar] [CrossRef]
- Lin, M.; Chen, Z.; Xu, Z.; Gou, X.; Herrera, F. Score function based on concentration degree for probabilistic linguistic term sets: An application to TOPSIS and VIKOR. Inf. Sci. 2021, 551, 270–290. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, Y.; Yang, J. Multi-attribute decision-making method based on a novel distance measure of linguistic intuitionistic fuzzy sets. J. Intell. Fuzzy Syst. 2021, 40, 1147–1160. [Google Scholar] [CrossRef]
- Zhu, S.; Huang, J.; Xu, Y. A consensus model for group decision making with self-confident linguistic preference relations. Int. J. Intell. Syst. 2021, 36, 6360–6386. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, H.; Cheng, Y.; Qin, L. Project evaluation method using non-formatted text information based on multi-granular linguistic labels. Inf. Fusion 2015, 24, 93–107. [Google Scholar] [CrossRef]
- Li, P.; Peng, H. A Novel IVPLTS Decision Method Based on Regret Theory and Cobweb Area Model. Math. Probl. Eng. 2020, 2020, 5649525. [Google Scholar] [CrossRef]
- Mao, X.; Wu, M.; Dong, J.; Wan, S.; Jin, Z. A new method for probabilistic linguistic multi-attribute group decision making: Application to the selection of financial technologies. Appl. Soft Comput. 2019, 77, 155–175. [Google Scholar] [CrossRef]
- Somasundaram, J.; Diecidue, E. Regret theory and risk attitudes. J. Risk Uncertain. 2018, 55, 147–175. [Google Scholar] [CrossRef]
- Wang, H.; Pan, X.; Yan, J.; Yao, J.; He, S. A projection-based regret theory method for multi-attribute decision making under interval type-2 fuzzy sets environment. Inf. Sci. 2020, 512, 108–122. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, Y.; Zhang, J.; Lv, X. Improved TOPSIS Model and its Application in the Evaluation of NCAA Basketball Coaches. Mod. Appl. Sci. 2015, 9, 259. [Google Scholar] [CrossRef][Green Version]
- Solangi, Y.; Cheng, L.; Shah, S. Assessing and overcoming the renewable energy barriers for sustainable development in Pakistan: An integrated AHP and fuzzy TOPSIS approach. Renew. Energy 2021, 173, 209–222. [Google Scholar] [CrossRef]
- Belton, I.; MacDonald, A.; Wright, G.; Hamlin, I. Improving the practical application of the Delphi method in group-based judgment: A six-step prescription for a well-founded and defensible process. Technol. Forecast. Soc. Change 2019, 147, 72–82. [Google Scholar] [CrossRef]
- Omrani, H.; Alizadeh, A.; Naghizadeh, F. Incorporating decision makers’ preferences into DEA and common weight DEA models based on the best-worst method (BWM). Soft Comput. 2020, 24, 3989–4002. [Google Scholar] [CrossRef]
- Duo, T.; Guo, J.; Wu, F.; Zhai, R. Application of entropy-based multi-attribute decision-making method to structured selection of settlement. J. Vis. Commun. Image Represent. 2019, 58, 220–232. [Google Scholar]
- Dettmar, B.; Peltier, C.; Schlich, P. Beyond principal component analysis (PCA) of product means: Toward a psychometric view on sensory profiling data. J. Sens. Stud. 2019, 35, e12555. [Google Scholar] [CrossRef]
- Shuang, Y.; Ding, Y. Combination Weighting Method of Engineering Disciplines Evaluation Index Based on Soft Computing. IETE J. Res. 2022. [Google Scholar] [CrossRef]
- Merigo, J.; Palacios-Marques, D.; Zeng, S. Subjective and objective information in linguistic multi-criteria group decision making. Eur. J. Oper. Res. 2016, 248, 522–531. [Google Scholar] [CrossRef]
- Li, G.; Li, J.; Sun, X.; Wu, D. Research on a combined method of subjective-objective weighting based on the ordered information and intensity information. Chin. J. Manag. Sci. 2017, 25, 179–187. [Google Scholar]
- Correa Machado, A.M.; Ekel, P.I.; Libório, M.P. Goal-based participatory weighting scheme: Balancing objectivity and subjectivity in the construction of composite indicators. Qual. Quant. 2022, 57, 4387–4407. [Google Scholar] [CrossRef]
- Becker, W.; Saisana, M.; Paruolo, P.; Vandecasteele, I. Weights and importance in composite indicators: Closing the gap. Ecol. Indic. 2017, 80, 12–22. [Google Scholar] [CrossRef] [PubMed]
- Greco, S.; Ishizaka, A.; Tasiou, M.; Torrisi, G. On the Methodological Framework of Composite Indices: A Review of the Issues of Weighting, Aggregation, and Robustness. Soc. Indic. Res. 2019, 141, 61–94. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Wang, Z.; Hao, H.; Gao, F.; Zhang, Q.; Zhang, J.; Zhou, Y. Multi-attribute decision making on reverse logistics based on DEA-TOPSIS: A study of the Shanghai End-of-life vehicles industry. J. Clean. Prod. 2019, 214, 730–737. [Google Scholar] [CrossRef]
- Yang, J. Minimax reference point approach and its application for multiobjective optimisation. Eur. J. Oper. Res. 2000, 126, 541–556. [Google Scholar] [CrossRef]
- Memon, M.; Lee, Y.; Mari, S. Group multi-criteria supplier selection using combined grey systems theory and uncertainty theory. Expert Syst. Appl. 2015, 42, 7951–7959. [Google Scholar] [CrossRef]
- Song, W.; Zhu, J. Three-reference-point decision-making method with incomplete weight information considering independent and interactive characteristics. Inf. Sci. 2019, 503, 148–168. [Google Scholar] [CrossRef]
- Zhou, W.; Xu, Z. Generalized asymmetric linguistic term set and its application to qualitative decision making involving risk appetites. Eur. J. Oper. Res. 2016, 254, 610–621. [Google Scholar] [CrossRef]
- Bell, D. Regret in decision making under uncertainty. Oper. Res. 1982, 30, 961–981. [Google Scholar] [CrossRef]
- Loomes, G.; Sugden, R. Regret theory: An alternative theory of rational choice under uncertainty. Econ. J. 1982, 125, 513–532. [Google Scholar] [CrossRef]
- Quiggin, J. Regret theory with general choice sets. J. Risk Uncertainy 1994, 8, 153–165. [Google Scholar] [CrossRef]
- Bleichrodt, H.; Cillo, A.; Diecidue, E. A Quantitative Measurement of Regret Theory. Manag. Sci. 2010, 56, 161–175. [Google Scholar] [CrossRef]
- Tang, G.; Long, J.; Gu, X.; Chiclana, F.; Liu, P.; Wang, F. Interval type-2 fuzzy programming method for risky multicriteria decision-making with heterogeneous relationship. Inf. Sci. 2021, 584, 184–211. [Google Scholar] [CrossRef]
- Wang, W.; Tian, G.; Zhang, T.; Jabarullah, N.; Li, F.; Fathollahi-Fard, A. Scheme selection of design for disassembly (DFD) based on sustainability: A novel hybrid of interval 2-tuple linguistic intuitionistic fuzzy numbers and regret theory. J. Clean. Prod. 2021, 281, 124724. [Google Scholar] [CrossRef]
- Xu, Z. Linguistic Decision Making: Theory and Methods; Science Press: Beijing, China, 2012. [Google Scholar]
- Yang, G.; Yang, J.; Xu, D. A three-stage hybrid approach for weight assignment in MADM. Omega-Int. J. Manag. Sci. 2017, 71, 93–105. [Google Scholar] [CrossRef]
- Adolphson, D.; Cornia, G.; Walters, L. A United Frame Work for Classifying DEA Models; Pergamon Press: New York, NY, USA, 1991. [Google Scholar]
- Liu, W.; Zhang, D.; Meng, W.; Li, X.; Xu, F. A study of DEA models without explicit inputs. Omega-Int. J. Manag. Sci. 2011, 39, 472–480. [Google Scholar] [CrossRef]
- Yang, J.; Xu, D. Interactive minimax optimisation for integrated performance analysis and resource planning. Comput. Oper. Res. 2014, 46, 78–90. [Google Scholar] [CrossRef]
- Liao, H.; Zhang, Z.; Xu, Z.; Banaitis, A. A Heterogeneous Regret-Theory-Based Method with Choquet Integral to Multiattribute Reverse Auction. IEEE Trans. Eng. Manag. 2022, 69, 2248–2259. [Google Scholar] [CrossRef]
- Wu, P.; Wu, Q.; Zhou, L. Hesitant fuzzy linguistic TOPSIS decision making method based on multi-objective attribute weight optimization. Oper. Res. Manag. Sci. 2021, 30, 42–47. [Google Scholar]
| Personnel | Evaluation Metrics | |||||
|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | |
| DMU1 | S4/3 | S4/3 | S−1/2 | S−1/2 | S−1/2 | S1/2 |
| DMU2 | S4/3 | S1/2 | S1/2 | S4/3 | S−4/3 | S−1/2 |
| DMU3 | S0 | S1/2 | S−4/3 | S−4/3 | S1/2 | S−4/3 |
| DMU4 | S4/3 | S1/2 | S4/3 | S1/2 | S−1/2 | S−1/2 |
| DMU5 | S4/3 | S4/3 | S1/2 | S−4/3 | S1/2 | S0 |
| DMU6 | S4/3 | S−1/2 | S0 | S0 | S1/2 | S−4/3 |
| DMU7 | S4/3 | S0 | S−1/2 | S0 | S0 | S−1/2 |
| DMU8 | S4/3 | S4/3 | S1/2 | S−1/2 | S−1/2 | S4/3 |
| DMU9 | S1/2 | S0 | S4/3 | S−4/3 | S−4/3 | S−1/2 |
| DMU10 | S4/3 | S1/2 | S0 | S−1/2 | S−1/2 | S−1/2 |
| DMU11 | S4/3 | S1/2 | S0 | S−4/3 | S−4/3 | S0 |
| DMU12 | S4/3 | S0 | S4/3 | S−4/3 | S−4/3 | S0 |
| DMU13 | S4/3 | S−1/2 | S−1/2 | S−4/3 | S−1/2 | S−1/2 |
| DMU14 | S4/3 | S−1/2 | S0 | S−4/3 | S−1/2 | S0 |
| DMU15 | S4/3 | S0 | S1/2 | S−4/3 | S−4/3 | S0 |
| Personnel | Evaluation Metrics | |||||
|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | |
| DMU1 | 0.811 | 0.834 | 0.413 | 0.413 | 0.455 | 0.669 |
| DMU2 | 0.811 | 0.630 | 0.669 | 0.871 | 0.230 | 0.413 |
| DMU3 | 0.479 | 0.630 | 0.187 | 0.187 | 0.708 | 0.187 |
| DMU4 | 0.811 | 0.630 | 0.871 | 0.669 | 0.455 | 0.413 |
| DMU5 | 0.811 | 0.834 | 0.669 | 0.187 | 0.708 | 0.543 |
| DMU6 | 0.811 | 0.373 | 0.543 | 0.543 | 0.708 | 0.187 |
| DMU7 | 0.811 | 0.503 | 0.413 | 0.543 | 0.583 | 0.413 |
| DMU8 | 0.811 | 0.834 | 0.669 | 0.413 | 0.455 | 0.871 |
| DMU9 | 0.606 | 0.503 | 0.871 | 0.187 | 0.230 | 0.413 |
| DMU10 | 0.811 | 0.630 | 0.543 | 0.413 | 0.455 | 0.413 |
| DMU11 | 0.811 | 0.630 | 0.543 | 0.187 | 0.230 | 0.543 |
| DMU12 | 0.811 | 0.503 | 0.871 | 0.187 | 0.230 | 0.543 |
| DMU13 | 0.811 | 0.373 | 0.413 | 0.187 | 0.455 | 0.413 |
| DMU14 | 0.811 | 0.373 | 0.543 | 0.187 | 0.455 | 0.543 |
| DMU15 | 0.811 | 0.503 | 0.669 | 0.187 | 0.230 | 0.543 |
| Personnel | Subjective Efficiency Value | Voice | Comprehensive Utility Value | Rank |
|---|---|---|---|---|
| Oi | gi | P * | ||
| DMU1 | 0.523 | 0.064 | 0.558 | 6 |
| DMU2 | 0.686 | 0.084 | 0.610 | 4 |
| DMU3 | 0.286 | 0.035 | 0.352 | 15 |
| DMU4 | 0.728 | 0.090 | 0.671 | 1 |
| DMU5 | 0.569 | 0.070 | 0.614 | 3 |
| DMU6 | 0.553 | 0.068 | 0.542 | 7 |
| DMU7 | 0.524 | 0.065 | 0.532 | 9 |
| DMU8 | 0.642 | 0.079 | 0.662 | 2 |
| DMU9 | 0.557 | 0.069 | 0.516 | 10 |
| DMU10 | 0.538 | 0.066 | 0.537 | 8 |
| DMU11 | 0.481 | 0.059 | 0.486 | 13 |
| DMU12 | 0.602 | 0.074 | 0.569 | 5 |
| DMU13 | 0.422 | 0.052 | 0.444 | 14 |
| DMU14 | 0.485 | 0.060 | 0.501 | 12 |
| DMU15 | 0.524 | 0.065 | 0.512 | 11 |
| Personnel | This Study | Li et al. [21] | AHP |
|---|---|---|---|
| DMU1 | 6 | 6 | 11 |
| DMU2 | 4 | 2 | 2 |
| DMU3 | 15 | 15 | 15 |
| DMU4 | 1 | 1 | 1 |
| DMU5 | 3 | 4 | 5 |
| DMU6 | 7 | 5 | 7 |
| DMU7 | 9 | 8 | 9 |
| DMU8 | 2 | 3 | 3 |
| DMU9 | 10 | 10 | 6 |
| DMU10 | 8 | 9 | 8 |
| DMU11 | 13 | 12 | 13 |
| DMU12 | 5 | 7 | 4 |
| DMU13 | 14 | 14 | 14 |
| DMU14 | 12 | 13 | 12 |
| DMU15 | 11 | 11 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J. Linguistic Multiple-Attribute Decision Making Based on Regret Theory and Minimax-DEA. Mathematics 2023, 11, 4259. https://doi.org/10.3390/math11204259
Hu J. Linguistic Multiple-Attribute Decision Making Based on Regret Theory and Minimax-DEA. Mathematics. 2023; 11(20):4259. https://doi.org/10.3390/math11204259
Chicago/Turabian StyleHu, Jinyi. 2023. "Linguistic Multiple-Attribute Decision Making Based on Regret Theory and Minimax-DEA" Mathematics 11, no. 20: 4259. https://doi.org/10.3390/math11204259
APA StyleHu, J. (2023). Linguistic Multiple-Attribute Decision Making Based on Regret Theory and Minimax-DEA. Mathematics, 11(20), 4259. https://doi.org/10.3390/math11204259





