Ad-Hoc Lanzhou Index

Abstract

This paper initiates the study of the mathematical aspects of the ad-hoc Lanzhou index. If G is a graph with the vertex set $\{x_1,\dots ,x_n\}$, then the ad-hoc Lanzhou index of G is defined by $\widetilde{Lz}\left(G\right)={\sum }_{i=1}^n{d}_i{(n-1-d_i)}^2$, where $d_i$ represents the degree of the vertex $x_i$. Several identities for the ad-hoc Lanzhou index, involving some existing topological indices, are established. The problems of finding graphs with the extremum values of the ad-hoc Lanzhou index from the following sets of graphs are also attacked: (i) the set of all connected $\xi$-cyclic graphs of a fixed order, (ii) the set of all connected molecular $\xi$-cyclic graphs of a fixed order, (iii) the set of all graphs of a fixed order, and (iv) the set of all connected molecular graphs of a fixed order.

1. Introduction

Graph invariants are regarded as the properties of a graph that the graph isomorphism preserves [1]. Real-valued graph invariants are often known as topological indices [2]. We mention [2,3,4,5] as sources for terminology and notations related to (chemical) graph theory.

One of the most extensively researched topological indices is the first Zagreb index, which originally appeared in [6]. For a graph G, its first Zagreb index is often represented by $M_1\left(G\right)$ and is defined (for example see [7]) as

$$M_1\left(G\right)=\sum _{t\in V\left(G\right)}{\left(d_t\right)}^2=\sum _{rs\in E\left(G\right)}\left(d_r+d_s\right),$$

where $d_t$ represents the degree of the vertex t in G and $E\left(G\right)$ is the set of edges of G. The forgotten topological index [8] (which is sometimes referred to as the F-index, see also [9]) is another index that first appeared in [6]. The F-index of a graph G is represented by $F\left(G\right)$ and is defined [8] as follows:

$$F\left(G\right)=\sum _{t\in V\left(G\right)}{\left(d_t\right)}^3=\sum _{rs\in E\left(G\right)}\left({\left(d_r\right)}^2+{\left(d_s\right)}^2\right).$$

Vukičević et al. [10] studied (chemically as well as mathematically) the following linear combination of the indices $M_1\left(G\right)$ and $F\left(G\right)$ for a graph of order n and referred it to as the Lanzhou index:

$$Lz\left(G\right)=(n-1)M_1\left(G\right)-F\left(G\right).$$

(1)

The Lanzhou index can be rewritten as

$$Lz\left(G\right)=\sum _{t\in V\left(G\right)}{\left(d_t\right)}^2\overline{d_t},$$

where $\overline{G}$ is the complement of G and $\overline{d_t}$ represent the degree of t in $\overline{G}$. The refs. [11,12,13,14,15] provide some recent extremal results regarding the Lanzhou index.

If $TI\left(G\right)$ is a topological index of a graph G, then $TI\left(L\right(G\left)\right)$ is known as its reformulated version [16,17]. Here, $L\left(G\right)$ means the line graph of G. Motivated by the concept of reformulated topological indices [16,17], we consider ad-hoc topological indices as follows: if $TI\left(G\right)$ is a topological index of a graph G, then we call $TI\left(\overline{G}\right)$ as the ad-hoc version of $TI\left(G\right)$. Thus, applying the idea of ad-hoc topological indices to the Lanzhou index gives the ad-hoc Lanzhou index, represented by $\widetilde{Lz}$. The ad-hoc Lanzhou index [10], for a graph G, is defined as

$$\widetilde{Lz}\left(G\right)=\sum _{t\in V\left(G\right)}{d}_t{\left(\overline{d_t}\right)}^2=Lz\left(\overline{G}\right).$$

Here, we mention that the Lanzhou index of the complement of G was also studied in [18]. If $\left|V\right(G\left)\right|=n$, then $\overline{d_t}=n-d_t-1$ and thus

$$Lz\left(G\right)=\sum _{t\in V\left(G\right)}{\left(d_t\right)}^2\left(n-d_t-1\right)\mathrm{and}\widetilde{Lz}\left(G\right)=\sum _{t\in V\left(G\right)}{d}_t{\left(n-d_t-1\right)}^2.$$

The ad-hoc Lanzhou index was examined in [10] for predicting the octanol–water partition coefficient of nonane isomers, and it was found that this index performs better than both the well-known first Zagreb index and the F-index.

A graph with n vertices is called an n-order graph. Molecular graphs are those with a maximum degree of at most 4. A connected $\xi$-cyclic graph of order n is a connected n-order graph with $\xi +n-1$ edges. For $\xi =0,1,2$, and 3, a connected $\xi$-cyclic graph is also known as a tree, connected unicyclic graph, connected bicyclic graph, and connected tricyclic graph, respectively.

In this paper, several identities for the ad-hoc Lanzhou index, involving some existing topological indices, are established. The problems of finding graphs with the extremum values of the ad-hoc Lanzhou index from the following sets of graphs are also attacked: (i) the set of all n-order connected $\xi$-cyclic graphs (with a particular emphasis on unicyclic graphs, trees, and bicyclic as well as tricyclic graphs), (ii) the set of all n-order connected molecular $\xi$-cyclic graphs, (iii) the set of all n-order graphs, and (iv) the set of all n-order connected molecular graphs.

2. Identities

For a graph G, its forgotten topological coindex (or simply the F-coindex) is represented by $\overline{F}$ and is defined [19,20] by

$$\overline{F}\left(G\right)=\sum _{st\notin E\left(G\right)}\left({\left(d_s\right)}^2+{\left(d_t\right)}^2\right).$$

Actually, the F-coindex is equal to the Lanzhou index for every graph; see, for example, [21]. Generally, if ${\sum }_{st\in E\left(G\right)}f(g\left(s\right),g\left(t\right))$ is a topological index of a graph G then the corresponding coindex is defined as ${\sum }_{st\notin E\left(G\right)}f(g\left(s\right),g\left(t\right))$, where g may be the degree, the eccentricity, or any other (real-valued) parameter defined on the vertices of G and where f is a real-valued symmetric function. Note that the Lanzhou index can be rewritten as

$$Lz\left(G\right)=\sum _{st\in E\left(G\right)}\left(d_s\left(G\right)d_s\left(\overline{G}\right)+d_t\left(G\right)d_t\left(\overline{G}\right)\right),$$

where $d_s\left(G\right)$ and $d_s\left(\overline{G}\right)$ indicate the degrees of the vertex $s\in V\left(G\right)$ in G and $\overline{G}$, respectively. When there is no chance of confusion, we drop “$\left(G\right)$” from the notation $d_s\left(G\right)$. Applying the definition of a coindex to the Lanzhou index yields the Lanzhou coindex $\overline{Lz}$:

$$\begin{array}{cc}\hfill \overline{Lz}\left(G\right)& ={\displaystyle \sum _{st\notin E\left(G\right)}}\left(d_s\left(G\right)d_s\left(\overline{G}\right)+d_t\left(G\right)d_t\left(\overline{G}\right)\right).\hfill \end{array}$$

Consequently, we have

$$\overline{Lz}\left(G\right)=\sum _{st\in E\left(\overline{G}\right)}\left(d_s\left(\overline{G}\right)d_s\left(G\right)+d_t\left(\overline{G}\right)d_t\left(G\right)\right)=Lz\left(\overline{G}\right).$$

The following result is immediate from the above.

Observation 1.

For every graph G, its Lanzhou coindex is equal to the Lanzhou index of $\overline{G}$ (which is termed as the ad-hoc Lanzhou index of G), which is equal to the F-coindex of $\overline{G}$; that is,

$$\overline{Lz}\left(G\right)=Lz\left(\overline{G}\right)=\widetilde{Lz}\left(G\right)=\overline{F}\left(\overline{G}\right).$$

(2)

Because of (2), the identity given in the following proposition is already known (see Equation (3.6) in [20]); however, here we provide its more simple proof.

Proposition 1.

For any graph G with size m and order n, the following identity holds:

$$\widetilde{Lz}\left(G\right)=2{(n-1)}^{2}m+F\left(G\right)-2(n-1)M_1\left(G\right).$$

Proof. 

Note that the formula for $\widetilde{Lz}$ can be rewritten as

$$\widetilde{Lz}\left(G\right)=\sum _{rs\in E\left(G\right)}\left({\left(n-d_r-1\right)}^2+{\left(n-d_s-1\right)}^2\right).$$

(3)

Expanding the squared terms in (3) and then making use of the definitions of F and $M_1$, we obtain the desired identity. □

By Proposition 1, every upper bound on $M_1$ provides a lower bound on $\widetilde{Lz}$ and every lower bound on $M_1$ gives an upper bound on $\widetilde{Lz}$; many bounds on $M_1$ can be found in [7]. Also, from the aforementioned proposition, it is concluded that every lower/upper bound on F provides a(n) lower/upper bound on $\widetilde{Lz}$, respectively; several bounds on F-index can be found in [22].

Proposition 2.

For any graph G with size m and order n, the following identity holds:

$$\widetilde{Lz}\left(G\right)=2{(n-1)}^{2}m-Lz\left(G\right)-(n-1)M_1\left(G\right).$$

Proof. 

The identity given in Proposition 1 gives the desired result after utilizing Identity (1). □

By Proposition 2, every upper bound on $Lz$ provides a lower bound on $\widetilde{Lz}$ and every lower bound on $Lz$ gives an upper bound on $\widetilde{Lz}$; a considerable number of bounds on $Lz$ can be found in [22].

3. Extremal Results Concerning $\mathit{\xi }$-Cyclic Graphs

If $st\in E\left(G\right)$ and $rt\notin E\left(G\right)$, then let $G-st+rt$ denote the graph formed from G by removing the edge $st$ and adding the edge $rt$. We begin this section by providing the following simple but useful lemma that will be used frequently in the remaining part of this paper:

Lemma 1.

Suppose that G is an n-order graph containing $r,s,t,$ such that $rt\notin E\left(G\right)$ and $st\in E\left(G\right)$. If $G^{*}=G-st+rt$, then

$$\widetilde{Lz}\left(G\right)-\widetilde{Lz}\left(G^{*}\right)=\left((n-4)+3(n-d_r-d_s)\right)(d_r-d_s+1),$$

where $d_r=d_r\left(G\right)$ and $d_s=d_s\left(G\right)$.

Proof. 

Utilizing the definition of $\widetilde{Lz}$, we obtain

$$\begin{array}{cc}\hfill \widetilde{Lz}\left(G\right)-\widetilde{Lz}\left(G^{*}\right)=& d_r{(n-d_r-1)}^2+d_s{(n-d_s-1)}^2\hfill \\ \hfill & -(d_r+1){(n-d_r-2)}^2-(d_s-1){(n-d_s)}^2\hfill \\ \hfill =& \left((n-4)+3(n-d_r-d_s)\right)(d_r-d_s+1).\hfill \end{array}$$

□

Lemma 2.

Let G be an n-order graph containing a path $rst$ such that $rt\notin E\left(G\right)$ and the edge $rs$ does not lie on any cycle of length 3, where $d_r\left(G\right)\ge d_s\left(G\right)$ and $n\ge 5$. If $G^{*}=G-st+rt$; then,

$$\widetilde{Lz}\left(G\right)>\widetilde{Lz}\left(G^{*}\right).$$

Proof. 

By Lemma 1, we obtain

$$\widetilde{Lz}\left(G\right)-\widetilde{Lz}\left(G^{*}\right)=\left((n-4)+3(n-d_r-d_s)\right)(d_r-d_s+1),$$

(4)

where $d_r=d_r\left(G\right)$ and $d_s=d_s\left(G\right)$. Since the edge $rs$ does not lie on any cycle of length 3, we have $n-d_r-d_s\ge 0$; thus, under the given constraints, Equation (4) gives

$$\begin{array}{c}\hfill \widetilde{Lz}\left(G\right)-\widetilde{Lz}\left(G^{*}\right)>0.\end{array}$$

□

Now, we provide the first extremal result involving the minimum possible value of $\widetilde{Lz}$ for trees.

Theorem 1.

In the set of all n-order trees, with $n\ge 5$, only the star graph $S_n$ possesses the lowest value of $\widetilde{Lz}$; the mentioned lowest value is $(n-1){(n-2)}^2$.

Proof. 

Let T be a tree possessing the lowest value of $\widetilde{Lz}$ in the set of all n-order trees. Suppose on the contrary that $T\ne S_n$. Then, $\Delta \left(T\right)\ne n-1$. Consider a path $rst$ of T such that $d_r\left(T\right)\ge d_s\left(T\right)$. If $T^{*}$ is the graph deduced from T by dropping $st$ and inserting $rt$, then by Lemma 2 we have

$$\widetilde{Lz}\left(T\right)>\widetilde{Lz}\left(T^{*}\right),$$

a contradiction. Also, by elementary computations, one has

$$\widetilde{Lz}\left(S_n\right)=(n-1){(n-2)}^2.$$

□

Next, we pay attention to deriving extremal results involving the minimum possible value of $\widetilde{Lz}$ for connected $\xi$-cyclic graphs. For this, we require the next two results.

Lemma 3.

If G is an n-order connected ξ-cyclic graph, $rs$ is an edge of G, and γ is the number of common neighbors of s and r, then $d_r+d_s\le n+\gamma \le n+\xi$.

Proof. 

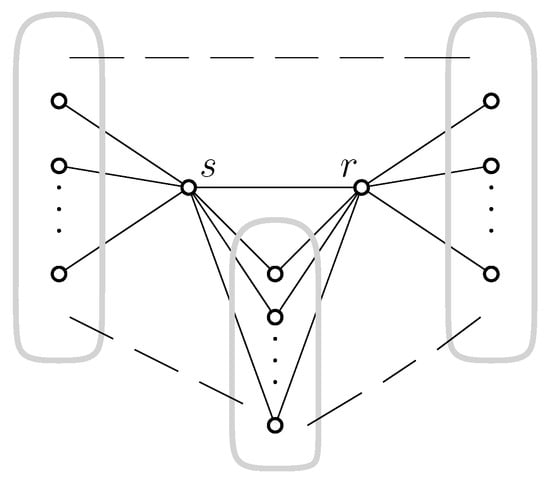
Let $\alpha$ be the number of those neighbors of r that are neither adjacent to s nor equal to s; see Figure 1. Let $\beta$ be the number of those neighbors of s that are neither adjacent to r nor equal to r. Then, $d_r=\alpha +\gamma +1$ and $d_s=\beta +\gamma +1$. Note that $\alpha +\beta +\gamma \le n-2$ and $\gamma \le \xi$. Thus,

$$d_r+d_s=\alpha +\beta +2\gamma +2\le n+\gamma \le n+\xi .$$

□

Figure 1. The structure of the graph G used in Lemma 3.

Lemma 4.

Suppose that G is a connected ξ-cyclic graph of order n containing a path $rst$ such that $rt\notin E\left(G\right)$, where $d_r\left(G\right)\ge d_s\left(G\right)$ and $n\ge 3\xi +5$. If $G^{*}=G-st+rt$, then

$$\widetilde{Lz}\left(G\right)>\widetilde{Lz}\left(G^{*}\right).$$

Proof. 

In the following, we take $d_r=d_r\left(G\right)$ and $d_s=d_s\left(G\right)$. By Lemma 3, the inequality $n-d_r-d_s\ge -\xi$ holds, and thus under the given constraints, Lemma 1 yields

$$\begin{array}{cc}\hfill \widetilde{Lz}\left(G\right)-\widetilde{Lz}\left(G^{*}\right)=& \left((n-4)+3(n-d_r-d_s)\right)(d_r-d_s+1)>0.\hfill \end{array}$$

□

Corollary 1.

Let G be a graph possessing the lowest value of $\widetilde{Lz}$ in the set of all n-order connected ξ-cyclic graphs, with $n\ge 3\xi +5$. Then, $\Delta \left(G\right)=n-1$.

Proof. 

Contrarily, assume that $\Delta \left(G\right)\ne n-1$. Take a vertex $r\in V\left(G\right)$ satisfying $d_r\left(G\right)=\Delta \left(G\right)$. Then, G has a path $rst$ such that $rt\notin E\left(G\right)$. Take $G^{*}=G-st+rt$. By Lemma 4, it holds that $\widetilde{Lz}\left(G\right)>\widetilde{Lz}\left(G^{*}\right)$, which is not possible because of the definition of G. Thus, $\Delta \left(G\right)=n-1$. □

Next, we provide extremal results involving the minimum possible values of $\widetilde{Lz}$ for connected $\xi$-cyclic graphs when $\xi =1,2,3$.

Note that there are only two (non-isomorphic) 4-order connected unicyclic graphs, and both of them have the same value of $\widetilde{Lz}$. Thus, in the next theorem, we find the extremal graphs of the order of at least 5.

Theorem 2.

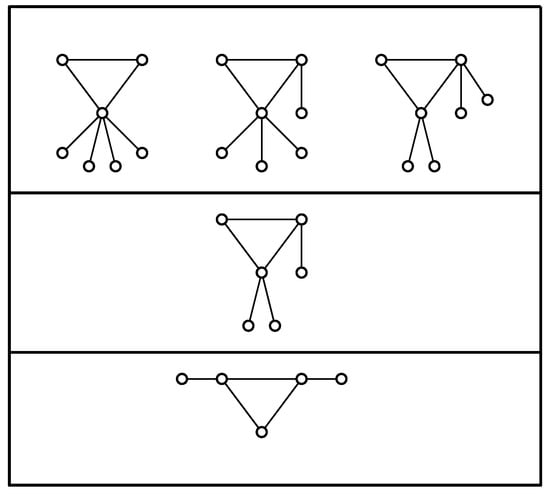
The graph generated from the n-order start graph $S_n$ by inserting an edge solely possesses the lowest value of $\widetilde{Lz}$ in the set of all n-order connected unicyclic graphs, for every $n\ge 8$. For $n=7,6,5$, the extremal graphs are depicted in the first row, second row, and third row of Figure 2, respectively.

Figure 2. The graphs possessing the lowest value of $\widetilde{Lz}$ in the set of all n-order connected unicyclic graphs, for $n=5,6,7$.

Proof. 

Since there is only one n-order unicyclic graph of maximum degree $n-1$ for every $n\ge 8$, the desired conclusion follows from Corollary 1 for $n\ge 8$. Lemma 2 implies that if G is a graph possessing the least value of $\widetilde{Lz}$ in the set of all n-order connected unicyclic graphs, with $n\ge 5$, then the number of pendent vertices in G becomes $n-3$. Simple calculations yield the desired conclusion for $n=5,6,7$. □

For $n\ge 5$, denote by $B_n^{\left(1\right)}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4)$ the n-order bicyclic graph shown in Figure 3, where ${\eta }_1+{\eta }_2+{\eta }_3+{\eta }_4=n-4$ with ${\eta }_1\ge {\eta }_4\ge 0$ and ${\eta }_2\ge {\eta }_3\ge 0$. Also, for $n\ge 5$, denote by $B_n^{\left(2\right)}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4,{\eta }_5)$ the n-order bicyclic graph shown in Figure 4, where ${\eta }_1+{\eta }_2+{\eta }_3+{\eta }_4+{\eta }_5=n-5$ with ${\eta }_1\ge max\{{\eta }_2,{\eta }_3,{\eta }_4\}$ and ${\eta }_i\ge 0$ for every $i\in \{1,2,\dots ,5\}$.

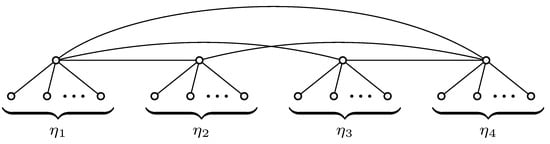
Figure 3. The n-order bicyclic graph $B_n^{\left(1\right)}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4)$, where ${\eta }_1+{\eta }_2+{\eta }_3+{\eta }_4=n-4\ge 1$ with ${\eta }_1\ge {\eta }_4\ge 0$ and ${\eta }_2\ge {\eta }_3\ge 0$.

Figure 4. The n-order bicyclic graph $B_n^{\left(2\right)}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4,{\eta }_5)$, where ${\eta }_1+{\eta }_2+{\eta }_3+{\eta }_4+{\eta }_5=n-5\ge 0$ with ${\eta }_1\ge max\{{\eta }_2,{\eta }_3,{\eta }_4\}$ and ${\eta }_i\ge 0$ for every $i\in \{1,2,\dots ,5\}$.

Theorem 3.

Considering the family of all n-order bicyclic connected graphs having $n\ge 11$, only the graph $B_n^{\left(1\right)}(n-4,0,0,0)$ possesses the lowest value of $\widetilde{Lz}$.

Proof. 

Let $B_n$ be an n-order connected bicyclic graph, with $n\ge 11$. If $\Delta \left(B_n\right)\ne n-1$, then Corollary 1 implies that $B_n$ cannot possess the lowest value of $\widetilde{Lz}$ in the set of all n-order connected bicyclic graphs. If $\Delta \left(B_n\right)=n-1$, then

$$B_n\in \{B_n^{\left(1\right)}(n-4,0,0,0),B_n^{\left(2\right)}(0,0,0,0,n-5)\}.$$

By elementary calculations, we verify that the inequality

$$\widetilde{Lz}\left(B_n^{\left(1\right)}(n-4,0,0,0)\right)<\widetilde{Lz}\left(B_n^{\left(2\right)}(0,0,0,0,n-5)\right)$$

holds for $n\ge 11$. Hence, for every $n\ge 11$, it holds that

$$\widetilde{Lz}\left(B_n\right)>\widetilde{Lz}\left(B_n^{\left(1\right)}(n-4,0,0,0)\right)\mathrm{whenever}{B}_n\ne B_n^{\left(1\right)}(n-4,0,0,0).$$

□

Next, we characterize the graphs possessing the lowest value of $\widetilde{Lz}$ from the set of graphs mentioned in Theorem 3 for $5\le n\le 10$.

Theorem 4.

Let $B_n$ be an n-order connected bicyclic graph with $n\ge 8$ such that the cycles of $B_n$ do not share any edge and $\Delta \left(B_n\right)\ne n-1$. Then, $B_n$ does not possess the lowest value of $\widetilde{Lz}$ in the set of all n-order connected bicyclic graphs for every $n\ge 8$.

Proof. 

Take a vertex $r\in V\left(B_n\right)$ satisfying $d_r\left(B_n\right)=\Delta \left(B_n\right)$. Since $\Delta \left(B_n\right)\ne n-1$, the graph $B_n$ has a path $rst$ such that $rt\notin E\left(B_n\right)$. Form a new graph $B_n^{*}$ from $B_n$ by dropping $st$ and inserting $rt$. By Lemma 3, the inequality $n-d_r\left(B_n\right)-d_s\left(B_n\right)\ge -1$ holds, and thus by bearing in mind the given assumptions and Lemma 1, we obtain

$$\begin{array}{cc}\hfill & \widetilde{Lz}\left(B_n\right)-\widetilde{Lz}\left(B_n^{*}\right)\hfill \\ \hfill =& \left((n-4)+3\left(n-d_r\left(B_n\right)-d_s\left(B_n\right)\right)\right)\left(d_r\left(B_n\right)-d_s\left(B_n\right)+1\right)>0,\hfill \end{array}$$

which implies that $B_n$ cannot possess the lowest value of $\widetilde{Lz}$ in the set of all n-order connected bicyclic graphs for every $n\ge 8$. □

Lemma 2 implies the next corollary.

Corollary 2.

If G is a graph possessing the least value of $\widetilde{Lz}$ in the set of all n-order connected bicyclic graphs, with $n\ge 5$, then G is isomorphic to either $B_n^{\left(1\right)}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4)$ or $B_n^{\left(2\right)}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4,{\eta }_5)$ (see Figure 3 and Figure 4).

Lemma 5.

For the n-order bicyclic graph $B_n^{\left(1\right)}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4)$ (depicted in Figure 3) with ${\eta }_2\ge {\eta }_3\ge 1$ and $n\ge 6$, the following inequality holds:

$$\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1,{\eta }_2+1,{\eta }_3-1,{\eta }_4)\right)<\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4)\right).$$

Proof. 

Since ${\eta }_1+{\eta }_2+{\eta }_3+{\eta }_4=n-4$ with ${\eta }_1\ge {\eta }_4\ge 0$, it holds that ${\eta }_2+{\eta }_3\le n-4$. Therefore, by bearing in mind the given assumptions and Lemma 1, we obtain

$$\begin{array}{cc}\hfill & \widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4)\right)-\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1,{\eta }_2+1,{\eta }_3-1,{\eta }_4)\right)\hfill \\ \hfill =& \left((n-4)+3(n-{\eta }_2-{\eta }_3-4)\right)({\eta }_2-{\eta }_3+1)>0.\hfill \end{array}$$

□

Lemma 6.

For the n-order bicyclic graph $B_n^{\left(1\right)}({\eta }_1,{\eta }_2,0,{\eta }_4)$ (depicted in Figure 3) with ${\eta }_1\ge {\eta }_4\ge 1$ and $6\le n\le 10$, it holds that

$$\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1+1,{\eta }_2,0,{\eta }_4-1)\right)\left\{\begin{array}{cc}=\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1,{\eta }_2,0,{\eta }_4)\right)\hfill & \mathit{if}\mathit{either}{\eta }_2=1\mathit{and}n=7,\hfill \\ & \mathit{or}{\eta }_2=0\mathit{and}n=10,\hfill \\ <\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1,{\eta }_2,0,{\eta }_4)\right)\hfill & \mathit{if}{\eta }_2\ge 1\mathit{and}8\le n\le 10,\hfill \\ >\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1,{\eta }_2,0,{\eta }_4)\right)\hfill & \mathit{if}{\eta }_2=0\mathit{and}6\le n\le 9.\hfill \end{array}\right.$$

Proof. 

By Lemma 1, we obtain

$$\begin{array}{cc}\hfill & \widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1,{\eta }_2,0,{\eta }_4)\right)-\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1+1,{\eta }_2,0,{\eta }_4-1)\right)\hfill \\ \hfill =& \left((n-4)+3(n-{\eta }_1-{\eta }_4-6)\right)({\eta }_1-{\eta }_4+1).\hfill \end{array}$$

(5)

If ${\eta }_2\ge 1$, then the equation ${\eta }_1+{\eta }_2+{\eta }_4=n-4$ gives ${\eta }_1+{\eta }_4\le n-5$ (and hence $n\ge 7$; if $n=7$ then ${\eta }_1={\eta }_2={\eta }_4=1$) and thus under the given constraints Equation (5) yields

$$\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1,{\eta }_2,0,{\eta }_4)\right)-\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1+1,{\eta }_2,0,{\eta }_4-1)\right)\left\{\begin{array}{cc}=0\hfill & \mathrm{if}n=7,\hfill \\ >0\hfill & \mathrm{if}8\le n\le 10.\hfill \end{array}\right.$$

If ${\eta }_2=0$, then ${\eta }_1+{\eta }_4=n-4$ and thus Equation (5) yields the desired conclusion. □

Lemma 7.

For the n-order bicyclic graph $B_n^{\left(1\right)}({\eta }_1,{\eta }_2,0,0)$ with $n\ge 6$, the following relations hold:

$$\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1+1,{\eta }_2-1,0,0)\right)\left\{\begin{array}{cc}<\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1,{\eta }_2,0,0)\right)\hfill & \mathit{if}{\eta }_1\ge {\eta }_2-1\ge 0\mathit{and}n\ge 8,\hfill \\ =\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1,{\eta }_2,0,0)\right)\hfill & \mathit{if}\mathit{either}n=7\mathit{and}{\eta }_2\ge 1,\hfill \\ & \mathit{or}{\eta }_1={\eta }_2-2\mathit{and}{\eta }_2\ge 1,\hfill \\ >\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1,{\eta }_2,0,0)\right)\hfill & \mathit{if}\mathit{either}{\eta }_2={\eta }_1=1\mathit{and}n=6,\hfill \\ & \mathit{or}{\eta }_1<{\eta }_2-2\mathit{and}n\ge 8.\hfill \end{array}\right.$$

and

$$\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1-1,{\eta }_2+1,0,0)\right)\left\{\begin{array}{cc}& \\ <\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1,{\eta }_2,0,0)\right)\hfill & \mathit{if}\mathit{either}{\eta }_2-1\ge {\eta }_1\ge 1\mathit{and}n\ge 8,\hfill \\ & \mathit{or}{\eta }_2=0,{\eta }_1=2\mathit{and}n=6,\hfill \\ =\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1,{\eta }_2,0,0)\right)\hfill & \mathit{if}\mathit{either}n=7\mathit{and}{\eta }_1\ge 1,\hfill \\ & \mathit{or}{\eta }_2={\eta }_1\ge 1,\hfill \\ >\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1,{\eta }_2,0,0)\right)\hfill & \mathit{if}{\eta }_2<{\eta }_1\mathit{and}n\ge 8.\hfill \end{array}\right.$$

Proof. 

Since ${\eta }_1+{\eta }_2=n-4$, we have

$$\begin{array}{cc}\hfill \widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1,{\eta }_2,0,0)\right)-\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1+1,{\eta }_2-1,0,0)\right)=& (n-7)({\eta }_1-{\eta }_2+2)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1,{\eta }_2,0,0)\right)-\widetilde{Lz}\left(B_n^{\left(1\right)}({\eta }_1-1,{\eta }_2+1,0,0)\right)=& (n-7)({\eta }_2-{\eta }_1),\hfill \end{array}$$

which yield the desired relations. □

Lemma 8.

For the n-order bicyclic graph $B_n^{\left(2\right)}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4,{\eta }_5)$ (depicted in Figure 4) with $n\ge 7$, the following inequalities hold:

$$\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1+1,{\eta }_2,{\eta }_3,{\eta }_4-1,{\eta }_5)\right)<\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4,{\eta }_5)\right)\mathit{when}{\eta }_4\ge 1,$$

$$\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1+1,{\eta }_2,{\eta }_3-1,{\eta }_4,{\eta }_5)\right)<\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4,{\eta }_5)\right)\mathit{when}{\eta }_3\ge 1,$$

$$\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1+1,{\eta }_2-1,{\eta }_3,{\eta }_4,{\eta }_5)\right)<\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4,{\eta }_5)\right)\mathit{when}{\eta }_2\ge 1,$$

Proof. 

Since ${\eta }_1+{\eta }_2+{\eta }_3+{\eta }_4+{\eta }_5=n-5$ with ${\eta }_i\ge 0$ for $i\in \{1,2,\dots ,5\}$, it holds that ${\eta }_1+{\eta }_j\le n-5$ for every $j\in \{2,\dots ,5\}$. Also, we recall that ${\eta }_1\ge max\{{\eta }_2,{\eta }_3,{\eta }_4\}$. Therefore, by using the given constraints, we have

$$\begin{array}{cc}\hfill & \widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4,{\eta }_5)\right)-\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1+1,{\eta }_2-1,{\eta }_3,{\eta }_4,{\eta }_5)\right)\hfill \\ \hfill =& \left((n-4)+3(n-{\eta }_1-{\eta }_2-4)\right)({\eta }_1-{\eta }_2+1)>0,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4,{\eta }_5)\right)-\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1+1,{\eta }_2,{\eta }_3-1,{\eta }_4,{\eta }_5)\right)\hfill \\ \hfill =& \left((n-4)+3(n-{\eta }_1-{\eta }_3-4)\right)({\eta }_1-{\eta }_3+1)>0,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4,{\eta }_5)\right)-\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1+1,{\eta }_2,{\eta }_3,{\eta }_4-1,{\eta }_5)\right)\hfill \\ \hfill =& \left((n-4)+3(n-{\eta }_1-{\eta }_4-4)\right)({\eta }_1-{\eta }_4+1)>0.\hfill \end{array}$$

□

Lemma 9.

For the n-order bicyclic graph $B_n^{\left(2\right)}({\eta }_1,0,0,0,{\eta }_5)$, the following relations hold:

$$\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1-1,0,0,0,{\eta }_5+1)\right)\left\{\begin{array}{cc}<\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1,0,0,0,{\eta }_5)\right)\hfill & \mathit{if}1\le {\eta }_1\le {\eta }_5+2\mathit{and}n\ge 8,\hfill \\ =\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1,0,0,0,{\eta }_5)\right)\hfill & \mathit{if}\mathit{either}n=7\mathit{and}{\eta }_1\ge 1,\hfill \\ & \mathit{or}{\eta }_5+3={\eta }_1\ge 1,\hfill \\ >\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1,0,0,0,{\eta }_5)\right)\hfill & \mathit{if}{\eta }_1=1,{\eta }_5=0\mathit{and}n=6,\hfill \\ & \mathit{or}{\eta }_5+3<{\eta }_1\mathit{and}n\ge 8.\hfill \end{array}\right.$$

and

$$\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1+1,0,0,0,{\eta }_5-1)\right)\left\{\begin{array}{cc}& \\ <\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1,0,0,0,{\eta }_5)\right)\hfill & \mathit{if}{\eta }_1-2\ge {\eta }_5\ge 1\mathit{and}n\ge 8,\hfill \\ & \mathit{or}{\eta }_1=0,{\eta }_5=1\mathit{and}n=6,\hfill \\ =\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1,0,0,0,{\eta }_5)\right)\hfill & \mathit{if}\mathit{either}n=7\mathit{and}{\eta }_5\ge 1,\hfill \\ & \mathit{or}{\eta }_1-1={\eta }_5\ge 1,\hfill \\ >\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1,0,0,0,{\eta }_5)\right)\hfill & \mathit{if}{\eta }_5\ge 1,{\eta }_1-1<{\eta }_5\mathit{and}n\ge 8.\hfill \\ \end{array}\right.$$

Proof. 

Since ${\eta }_1+{\eta }_5=n-5$, we have

$$\begin{array}{cc}\hfill \widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1,0,0,0,{\eta }_5)\right)-\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1-1,0,0,0,{\eta }_5+1)\right)=& (n-7)({\eta }_5-{\eta }_1+3)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1,0,0,0,{\eta }_5)\right)-\widetilde{Lz}\left(B_n^{\left(2\right)}({\eta }_1+1,0,0,0,{\eta }_5-1)\right)=& (n-7)({\eta }_1-{\eta }_5-1),\hfill \end{array}$$

from which the required relations follow. □

Denote by $K_4-e$ the graph deduced from the 4-order complete graph $K_4$ by dropping an edge. Let $B_{n;\alpha }$ be the n-order graph formed from $K_4-e$ by connecting $\alpha$ pendent vertices with one vertex having degree 3 and the rest $n-4-\alpha$ pendent vertices with the other vertex having degree 3 (see the graph placed on the left-hand side in Figure 5), where $0\le \alpha \le \lfloor (n-4)/2\rfloor$. Let $B_n^{*}$ denote the graph generated from $K_4-e$ by attaching $n-4$ pendent vertices to a vertex of degree 2 (see the graph placed on the right-hand side in Figure 5). Certainly, $B_{n;0}=B_n^{\left(1\right)}(n-4,0,0,0)$.

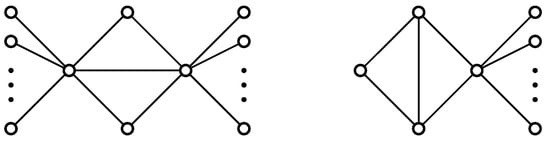
Figure 5. The n-order bicyclic graphs $B_{n;\alpha }$ (on the left side) and $B_n^{*}$ (on the right side), where $0\le \alpha \le \lfloor (n-4)/2\rfloor$.

Now, we are in the position to characterize the graphs possessing the lowest value of $\widetilde{Lz}$ from the set of graphs mentioned in Theorem 3 for $5\le n\le 10$.

Theorem 5.

Among all n-order connected bicyclic graphs,

(i) 

only the graph $B_n^{\left(1\right)}(0,n-4,0,0)$ has the minimum value of $\widetilde{Lz}$ for $n=5$,

(ii) 

only the graph $B_{n;1}$ has the minimum value of $\widetilde{Lz}$ for each $n\in \{6,7\}$,

(iii) 

only the graph $B_{n;2}$ has the minimum value of $\widetilde{Lz}$ for each $n\in \{8,9\}$,

(iv) 

only the graphs $B_{n;0},B_{n;1},B_{n;2},B_{n;3}$ have the minimum value of $\widetilde{Lz}$ for $n=10$.

Proof. 

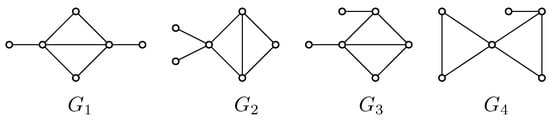
By Corollary 2, it is enough to investigate the values of $\widetilde{Lz}$ for the graphs:

$$B_n^{\left(1\right)}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4)\mathit{and}{B}_n^{\left(2\right)}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4,{\eta }_5).$$

For $n=5$, there are only three such graphs; namely, $B_n^{\left(1\right)}(n-4,0,0,0)$, $B_n^{\left(1\right)}(0,n-4,0,0)$, and $B_n^{\left(2\right)}(0,0,0,0,n-5)$. Certainly, for $n=5$, it holds that

$$\widetilde{Lz}\left(B_n^{\left(1\right)}(0,n-4,0,0)\right)<\widetilde{Lz}\left(B_n^{\left(1\right)}(n-4,0,0,0)\right)<\widetilde{Lz}\left(B_n^{\left(2\right)}(0,0,0,0,n-5)\right),$$

which confirms Part (i) of the theorem.

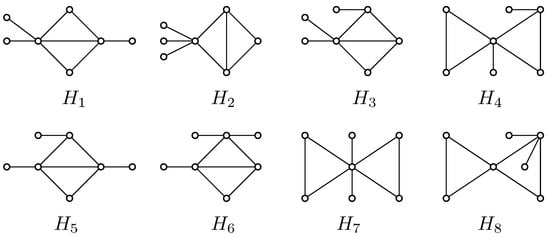
If G is a graph possessing the least value of $\widetilde{Lz}$ in the set of all 6-order connected bicyclic graphs, then from Corollary 2 and Lemmas 5–9, it follows that $G\in \{G_1,G_2,G_3,G_4\}$ where the graphs $G_1,G_2,G_3,G_4$ are depicted in Figure 6. It holds that

$$\widetilde{Lz}\left(G_1\right)<\widetilde{Lz}\left(G_2\right)=\widetilde{Lz}\left(G_3\right)<\widetilde{Lz}\left(G_4\right).$$

Figure 6. The 6-order connected bicyclic graphs $G_1$, $G_2$, $G_3$, and $G_4$.

If G is a graph possessing the least value of $\widetilde{Lz}$ in the set of all 7-order connected bicyclic graphs, then from Corollary 2 and Lemmas 5–9, it follows that $G\in \{H_1,H_2,\dots ,H_8\}$ where the graphs $H_1,H_2,\dots ,H_8$ are depicted in Figure 7. It holds that

$$\widetilde{Lz}\left(H_1\right)<\widetilde{Lz}\left(H_2\right)=\widetilde{Lz}\left(H_3\right)=\widetilde{Lz}\left(H_5\right)=\widetilde{Lz}\left(H_6\right)$$

and

$$\widetilde{Lz}\left(H_1\right)<\widetilde{Lz}\left(H_4\right)=\widetilde{Lz}\left(H_7\right)=\widetilde{Lz}\left(H_8\right).$$

Since $G_1=B_{6;1}$ and $H_1=B_{7;1}$, the proof of Part (ii) is completed.

Figure 7. The 7-order connected bicyclic graphs $H_1,H_2,\dots ,H_8$.

Theorem 4 states that if $B_n$ is an n-order connected bicyclic graph with $n\ge 8$ such that the cycles of $B_n$ do not share any edge and $\Delta \left(B_n\right)\ne n-1$; then, $B_n$ does not possess the lowest value of $\widetilde{Lz}$ in the family of all n-order bicyclic connected graphs having $n\ge 8$. Thus, if G is a graph possessing the least value of $\widetilde{Lz}$ in the set of all n-order connected bicyclic graphs for $n\in \{8,9,10\}$, then from Corollary 2 and Lemmas 5–7 it follows that

$$\left\{\begin{array}{cc}G\in \{B_{n;0},B_{n;2},B_n^{*},B_n^{†}\}\hfill & \mathrm{when}n\in \{8,9\},\hfill \\ G\in \{B_{n;\alpha },B_n^{*},B_n^{†}\}\hfill & \mathrm{when}n=10.\hfill \end{array}\right.$$

where $B_n^{†}=B_n^{\left(2\right)}(0,0,0,0,n-5)$. For $n\in \{8,9,10\}$, the following relations hold:

$$\begin{array}{cc}\hfill \widetilde{Lz}\left(B_{n;0}\right)& =n^3-n^2-28n+68\hfill \\ & <\widetilde{Lz}\left(B_n^{*}\right)=n^3-39n+96\hfill \\ \hfill & <\widetilde{Lz}\left(B_n^{†}\right)=n^3-n^2-24n+52.\hfill \end{array}$$

Also, the inequality $\widetilde{Lz}\left(B_{n;2}\right)<\widetilde{Lz}\left(B_{n;0}\right)$ holds for each $n\in \{8,9\}$. Moreover, the equation $\widetilde{Lz}\left(B_{10;\alpha }\right)=688$ holds for every $\alpha \in \{0,1,2,3\}$. Thus, Parts (iii) and (iv) also hold. □

Theorem 6.

Considering the family of all n-order tricyclic connected graphs with $n\ge 14$, only the right-most graph in Figure 8 possesses the lowest value of $\widetilde{Lz}$.

Figure 8. The graphs $J_1,J_2,\dots ,J_5,$ (from left to right, respectively) used in Theorem 6.

Proof. 

Let G be an n-order connected tricyclic graph, with $n\ge 14$. If $\Delta \left(G\right)\ne n-1$, then Corollary 1 implies that G cannot possess the lowest value of $\widetilde{Lz}$ in the set of all n-order connected tricyclic graphs. If $\Delta \left(G\right)=n-1$, then G is one of the graphs $J_1,J_2,\dots ,J_5$ (from left to right, respectively) shown in Figure 8. We have

$$\begin{array}{cc}\hfill & \widetilde{Lz}\left(J_1\right)=(n-7){(n-2)}^2+12{(n-3)}^2,\hfill \\ \hfill & \widetilde{Lz}\left(J_2\right)=(n-6){(n-2)}^2+8{(n-3)}^2+3{(n-4)}^2,\hfill \\ \hfill & \widetilde{Lz}\left(J_3\right)=(n-5){(n-2)}^2+4{(n-3)}^2+6{(n-4)}^2,\hfill \\ \hfill & \widetilde{Lz}\left(J_4\right)=(n-5){(n-2)}^2+6{(n-3)}^2+4{(n-5)}^2,\hfill \\ \hfill & \widetilde{Lz}\left(J_5\right)=(n-4){(n-2)}^2+9{(n-4)}^2.\hfill \end{array}$$

But, $\widetilde{Lz}\left(J_i\right)>\widetilde{Lz}\left(J_5\right)$ for every $i\in \{1,2,3,4\}$ because $n\ge 14$. Hence, $\widetilde{Lz}\left(G\right)\ge \widetilde{Lz}\left(J_5\right)$ with equality if and only if $G=J_5$. □

A non-trivial path $P:r_1\dots r_p$ of a graph G is said to be a pendent path if

$$max\{d_{r_1}\left(G\right),d_{r_p}\left(G\right)\}\ge 3\mathrm{and}min\{d_{r_1}\left(G\right),d_{r_p}\left(G\right)\}=1,$$

provided that $d_{r_i}\left(G\right)=2$ when $2\le i\le p-1$. By adjacent pendent paths in a graph G, we mean the pendent paths of G having a common vertex.

Lemma 10.

For $n\ge 5$, if G is a connected n-order graph possessing adjacent pendent paths, then there a connected n-order graph $G^{*}$ exists that has no adjacent pendent paths satisfying $\left|E\left(G\right)\right|=|E\left(G^{*}\right)|$ and

$$\widetilde{Lz}\left(G\right)<\widetilde{Lz}\left(G^{*}\right).$$

Proof. 

Let s be the common vertex of two adjacent pendent paths $P_1$ and $P_2$ in G. Assume that the edge $st$ belongs to the path $P_1$. Let $r\in V\left(G\right)$ be the vertex of $P_2$ satisfying $d_r\left(G\right)=1$. Take $G^{\prime }=G-st+rt$. Evidently, $\left|E\left(G\right)\right|=|E\left(G^{\prime }\right)|$. Since $n-4>0$ and $n-1\ge d_s\left(G\right)\ge 3$, by Lemma 1 we obtain

$$\begin{array}{cc}\hfill \widetilde{Lz}\left(G\right)-\widetilde{Lz}\left(G^{\prime }\right)=& -[n-4+3(n-1-d_s\left(G\right))](d_s\left(G\right)-2)<0.\hfill \end{array}$$

If $G^{\prime }$ contains no adjacent pendent paths, the lemma holds true. If $G^{\prime }$ does contain such paths, we can again perform the above-mentioned transformation successively until we obtain the desired graph $G^{*}$ satisfying $\widetilde{Lz}\left(G\right)<\widetilde{Lz}\left(G^{\prime }\right)<\cdots <\widetilde{Lz}\left(G^{*}\right)$. □

The next result is one of the direct outcomes of Lemma 10.

Theorem 7.

In the set of all n-order trees, with $n\ge 5$, only the path graph $P_n$ possesses the highest value of $\widetilde{Lz}$; the mentioned highest value is

$$2(n-2)(n^2-5n+7).$$

Lemma 11.

If G is a graph possessing the highest value of $\widetilde{Lz}$ among the family of all n-order connected ξ-cyclic graphs admitting $n\ge 5$ and $\xi \ge 1$, then $\delta \left(G\right)>1$.

Proof. 

Contrary, let $\delta \left(G\right)=1$. Because of the constraint $\xi \ge 1$, the graph G must contain at least one pendent path, say P. Let r and s be the terminal vertices of the path P; particularly, assume that $d_s\left(G\right)\ge 3$ and $d_r\left(G\right)=1$. Let $st\in E\left(G\right)$, where t does not belong to the path P. Take $G^{*}=G-st+rt$. After the same calculations as made in the proof of Lemma 10, we arrive at $\widetilde{Lz}\left(G\right)<\widetilde{Lz}\left(G^{*}\right)$; this contradicts the definition of G. Thereby, $\delta \left(G\right)>1$. □

The next result is one of the direct outcomes of Lemma 11.

Theorem 8.

Considering the family of all n-order unicyclic connected graphs having $n\ge 5$, only the cycle graph $C_n$ possesses the highest value of $\widetilde{Lz}$; the mentioned highest value is $2n{(n-3)}^2.$

Lemma 12.

If G is a graph possessing the highest value of $\widetilde{Lz}$ in the family of all n-order connected ξ-cyclic graphs admitting $n\ge 2(\xi -1)\ge 2$ and $n\ge 8$, then $\Delta \left(G\right)=3$.

Proof. 

The connectedness of G and the constraint $\xi \ge 2$ guarantee that $\Delta \left(G\right)\ge 3$. Contrarily, let $\Delta \left(G\right)\ge 4$. By Lemma 11, the inequality $\delta \left(G\right)\ge 2$ holds.

Suppose that G has m edges. Represent by $N_i$ the number of members of $\{r\in V\left(G\right):d_r\left(G\right)=i\}$. Since $\xi =m-n+1$, the inequality $n\ge 2(\xi -1)$ yields $n\ge 2(m-n)$, which further implies that

$$\sum _{i=2}^{\Delta \left(G\right)}{N}_i\ge 2\left(\sum _{i=2}^{\Delta \left(G\right)}\frac{i{N}_i}{2}-\sum _{i=2}^{\Delta \left(G\right)}{N}_i\right)=2\left(\sum _{i=3}^{\Delta \left(G\right)}\frac{i{N}_i}{2}-\sum _{i=3}^{\Delta \left(G\right)}{N}_i\right),$$

which guaranties that

$$N_2\ge \sum _{i=4}^{\Delta \left(G\right)}(i-3)N_i;$$

that is, G possess at least one vertex with degree 2.

Consider a vertex $s\in V\left(G\right)$ such that $d_s\left(G\right)=\Delta \left(G\right)$ (then, we certainly have $4\le d_s\left(G\right)\le n-1$). Also consider a vertex $r\in V\left(G\right)$ having degree 2. The inequality $d_s\left(G\right)\ge 4$ confirms the existence of no less than two neighbors of s that are not adjacent to r. We pick from these neighbors of s a vertex t such that the graph $G^{*}=G-st+rt$ is connected. First, by using Lemma 1 and then by using the inequalities $4\le d_s\left(G\right)\le n-1$ and $n\ge 8$, we obtain

$$\begin{array}{cc}\hfill \widetilde{Lz}\left(G\right)-\widetilde{Lz}\left(G^{*}\right)=& -[n-7+3(n-1-d_s\left(G\right))](d_s\left(G\right)-3)<0,\hfill \end{array}$$

which is at odds with the definition of G. Therefore, we derive that $\Delta \left(G\right)=3$, as desired. □

Theorem 9.

Consider the set ${\mathbb{G}}_{n,\xi }$ of all n-order connected ξ-cyclic graphs with $n\ge 2(\xi -1)\ge 2$ and $n\ge 8$.

(i). 

If $n=2(\xi -1)$, then only (the) 3-regular graph(s) possess(es) the highest value of $\widetilde{Lz}$ in ${\mathbb{G}}_{n,\xi }$.

(ii). 

If $n>2(\xi -1)$, then only the graphs with $(\Delta ,\delta )=(3,2)$ possess the highest value of $\widetilde{Lz}$ in ${\mathbb{G}}_{n,\xi }$.

Proof. 

Assume that G is a graph possessing the highest value of $\widetilde{Lz}$ in ${\mathbb{G}}_{n,\xi }$. Then, by Lemmas 11 and 12, it holds that $\delta \left(G\right)\ge 2$ and $\Delta \left(G\right)=3$. Thus, we have

$$N_2+N_3=n$$

(6)

and

$$2N_2+3N_3=2(n+\xi -1),$$

(7)

where $N_i$ is defined in the proof of Lemma 12.

(i)

If $n=2(\xi -1)$, then Equations (6) and (7) yield $N_2=0$ and thus G is 3-regular.

(ii)

If $n>2(\xi -1)$, then Equations (6) and (7) imply that $N_2>0$ and $N_3>0$, as desired.

□

One of the implications of Theorem 9 is the following result.

Theorem 10.

Only the graphs with $(\Delta ,\delta )=(3,2)$ possess the highest value of $\widetilde{Lz}$ in the family of all n-order bicyclic connected graphs admitting $n\ge 6$. For $n=5$, such an extremal graph can be constructed from the star graph through inserting two non-adjacent edges.

Proof. 

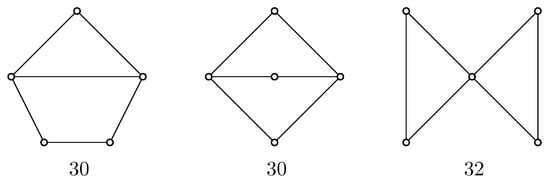
If $n\ge 8$, then the desired conclusion follows from Theorem 9. If $n\ge 5$, then by Lemma 11, the minimum degree of a graph possessing the highest value of $\widetilde{Lz}$ in the set of all n-order connected bicyclic graphs must be at least 2. If $n=5$, then there are only three n-order connected bicyclic graphs with minimum degree of at least 2; Figure 9 shows all these three graphs together with the values of $\widetilde{Lz}$. Now, in the following, assume that $n\in \{6,7\}$.

Figure 9. All connected bicyclic graphs of order 5 and minimum degree at least 2, together with the values of $\widetilde{Lz}$.

Assume that G is a graph possessing the highest value of $\widetilde{Lz}$ in the family of all n-order connected bicyclic graphs. Then, by Lemma 11, it holds that $\delta \left(G\right)\ge 2$. We claim that $\Delta \left(G\right)=3$. We note that there is no bicyclic graph with $\Delta =n-1$ and $\delta \ge 2$ (because $n\ge 6$). Thus, from the proof of Lemma 12 it follows that $\Delta \left(G\right)=3$. Since $n>2(\xi -1)=2$, from the proof of Theorem 9(ii) it follows that $\delta \left(G\right)=2$. □

Another implication of Theorem 9 is the following theorem.

Theorem 11.

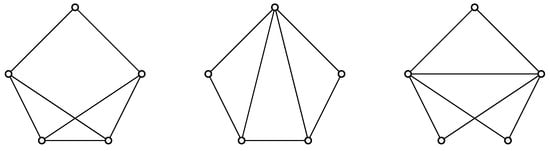
Only the graphs with $(\Delta ,\delta )=(3,2)$ possess the highest value of $\widetilde{Lz}$ in the family of all n-order tricyclic connected graphs admitting $n\ge 7$. For $n=5$, such an extremal graph can be constructed from the star graph through inserting three edges between one fixed pendent vertex and three other pendent vertices (see the right-most graph in Figure 10). For $n=6$, the set of such extremal graphs consists of the graphs for which $(\Delta ,\delta )\in \left\{\right(3,2),(5,2\left)\right\}$.

Figure 10. All connected tricyclic graphs of order 5 and minimum degree at least 2. The first, second, and third graphs (from left to right) have the following values of $\widetilde{Lz}$, respectively: 20, 22, and 24.

Proof. 

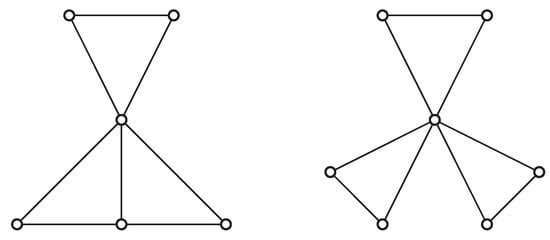
If $n\ge 8$, then the desired conclusion follows from Theorem 9. If $n\ge 5$, then by Lemma 11 the minimum degree of a graph possessing the highest value of $\widetilde{Lz}$ in the set of all n-order connected tricyclic graphs must be at least 2. If $n=5$, then there are only three n-order connected tricyclic graphs with a minimum degree at least 2; Figure 10 shows all these three graphs, and its caption gives the values of $\widetilde{Lz}$ for the mentioned three graphs. Now, in the following, assume that $n\in \{6,7\}$.

Assume that G is a graph possessing the highest value of $\widetilde{Lz}$ in the family of all n-order tricyclic connected graphs. Then, by Lemma 11, it holds that $\delta \left(G\right)\ge 2$. First, let $\Delta \left(G\right)<n-1$. Then, from the proof of Lemma 12, it follows that $\Delta \left(G\right)=3$. Since $n>2(\xi -1)=4$, from the proof of Theorem 9(ii) it follows that $\delta \left(G\right)=2$. Equations (6) and (7) yield $N_2=n-4$ and $N_3=4$. Thus, we have

$$\widetilde{Lz}\left(G\right)=2(n-4)(n^2-15).$$

On the other hand, if $\Delta \left(G\right)=n-1$ then $G\cong G^{★}$, where $G^{★}$ is the n-order connected tricyclic graph with maximum degree $n-1$ and minimum degree at least 2 (see Figure 11). Here,

$$\widetilde{Lz}\left(G^{★}\right)\left\{\begin{array}{cc}=2(n-4)(n^2-15)\hfill & \mathrm{if}n=6,\hfill \\ <2(n-4)(n^2-15)\hfill & \mathrm{if}n=7.\hfill \end{array}\right.$$

This completes the proof. □

Figure 11. The n-order connected tricyclic graphs $G^{★}$ of maximum degree $n-1$ and minimum degree no less than 2, for $n=6,7$.

4. Extremal Results Concerning Molecular $\mathit{\xi }$-Cyclic Graphs

Note that the extremal graphs specified in Theorems 9–11 are molecular ones, except for $n=6$ in Theorem 11. Thus, these graphs remain extremal if one puts the following additional constraint on the graphs considered in these theorems: the maximum degree is at most 4. Also, from Theorem 11 we deduce that the graphs with $(\Delta ,\delta )=(3,2)$ are the only graphs possessing the highest ad-hoc Lanzhou index in the set of all n-order molecular connected tricyclic graphs for $n=6$. Next, we turn our attention to the results concerning the minimum ad-hoc Lanzhou index of molecular $(n,m)$-graphs (or, equivalently n-order $\xi$-cyclic graphs). An $(n,m)$-graph is an n-order graph of size m. For a graph G, define

$$H_f\left(G\right)=\sum _{s\in V\left(G\right)}f\left(d_s\right).$$

(8)

where f is a real-valued function. Some initial studies, recent developments, and a survey on the indices of the form (8) can be found in [23,24,25,26,27,28,29], respectively.

Lemma 13

([30]). Consider a molecular $(n,m)$-graph G, where $n\ge 5$. Take

$${\psi }_1=-\frac{2}{3}f\left(1\right)+f\left(2\right)-\frac{1}{3}f\left(4\right)\mathit{and}{\psi }_2=-\frac{1}{3}f\left(1\right)+f\left(3\right)-\frac{2}{3}f\left(4\right).$$

If $min\{{\psi }_1,{\psi }_2\}>0$ and ${\psi }_2/2<{\psi }_1<2{\psi }_2$, then

$$\begin{array}{cc}\hfill H_f\left(G\right)& \ge \frac{1}{3}\left(4f\left(1\right)-f\left(4\right)\right)n+\frac{2}{3}\left(f\left(4\right)-f\left(1\right)\right)m\hfill \\ \hfill & +\left\{\begin{array}{cc}f\left(2\right)-\frac{2}{3}f\left(1\right)-\frac{1}{3}f\left(4\right)\hfill & \mathit{if}2m-n\equiv 1(mod3)\hfill \\ f\left(3\right)-\frac{1}{3}f\left(1\right)-\frac{2}{3}f\left(4\right)\hfill & \mathit{if}2m-n\equiv 2(mod3)\hfill \\ 0\hfill & \mathit{if}2m-n\equiv 0(mod3)\hfill \end{array}\right.\hfill \end{array}$$

where the equality holds if and only if the degree set of G is

• •$\{1,2,4\}$ and G admits exactly one vertex of degree 2 whenever $2m-n\equiv 1(mod3)$;
• •$\{1,3,4\}$ and G admits exactly one vertex of degree 3 whenever $2m-n\equiv 2(mod3)$;
• •$\{1,4\}$ whenever $2m-n\equiv 0(mod3)$.

Theorem 12.

For a molecular $(n,m)$-graph G, with $n\ge 8$, the following holds:

$$\begin{array}{cc}\hfill \widetilde{Lz}\left(G\right)& \ge 2m(n-8)(n-4)+4n(2n-7)\hfill \\ \hfill & +\left\{\begin{array}{cc}2(2n-9)\hfill & \mathit{if}2m-n\equiv 1(mod3)\hfill \\ 4(n-5)\hfill & \mathit{if}2m-n\equiv 2(mod3)\hfill \\ 0\hfill & \mathit{if}2m-n\equiv 0(mod3)\hfill \end{array}\right.\hfill \end{array}$$

where the equality characterization is the same as mentioned in Lemma 13.

Proof. 

Consider $f\left(x\right)=x{(n-1-x)}^2$ with $n\ge 8$. Then, we have

$$-\frac{2}{3}f\left(1\right)+f\left(2\right)-\frac{1}{3}f\left(4\right)>0,$$

$$-\frac{1}{3}f\left(1\right)+f\left(3\right)-\frac{2}{3}f\left(4\right)>0,$$

and

$$\frac{1}{2}\left(-\frac{1}{3}f\left(1\right)+f\left(3\right)-\frac{2}{3}f\left(4\right)\right)<-\frac{2}{3}f\left(1\right)+f\left(2\right)-\frac{1}{3}f\left(4\right)<2\left(-\frac{1}{3}f\left(1\right)+f\left(3\right)-\frac{2}{3}f\left(4\right)\right).$$

Thus, by Lemma 13, the desired result follows. □

One of the simple but noticeable consequences of Theorem 12 is the following extremal result involving molecular trees.

Corollary 3.

For every $n\ge 8$, in the family of all n-order molecular trees, only the trees having the degree set

(i) 

$\{1,2,4\}$ and admitting exactly one vertex of degree 2 possess the least value of $\widetilde{Lz}$, when $n\equiv 0(mod3)$;

(ii) 

$\{1,3,4\}$ and admitting exactly one vertex of degree 3 possess the least value of $\widetilde{Lz}$, when $n\equiv 1(mod3)$;

(iii) 

$\{1,4\}$ possess the least value of $\widetilde{Lz}$, when $n\equiv 2(mod3)$.

5. Extremal Results for $\mathit{n}$-Order Graphs

To prove the first extremal result involving $\widetilde{Lz}$ for n-order graphs, we require the following known result:

Lemma 14

([10]). If G is an n-order graph, then

$$0\le Lz\left(G\right)\le \frac{4n{(n-1)}^3}{27}.$$

Here, the left equality is true if and only if $G\in \{K_n,{\overline{K}}_n\}$, and the right equality is true if and only if $n\equiv 1(mod3)$ and G is a $\frac{2(n-1)}{3}$ - regular graph.

Proposition 3.

In the set of all n-order graphs, only the edgeless graph ${\overline{K}}_n$ and the complete graph $K_n$ possess the least value of $\widetilde{Lz}$; the mentioned least value is 0. Also, in the same set with the constraint $n\equiv 1(mod3)$, only the $\frac{(n-1)}{3}$-regular graph possesses the highest value of $\widetilde{Lz}$; the mentioned highest value is

$$\frac{4n{(n-1)}^3}{27}.$$

Proof. 

Since $Lz\left(\overline{G}\right)=\widetilde{Lz}\left(G\right)$, by Lemma 14 it is enough to show the existence of at least one $\frac{(n-1)}{3}$-regular graph with n vertices satisfying the congruence $n\equiv 1(mod3)$. Since $n\equiv 1(mod3)$, we have $n-1=3k$ for some integer k. Thus, if $n-1$ is even then k must be even, and thereby $\frac{n-1}{3}$ remains even. Eventually, whether $n-1$ is even or odd, in either case, we conclude that $\frac{n(n-1)}{3}$ is even. Also, it is a well-known observation that at least one t-regular graph with order n exists whenever $tn$ is even; this fact implies that at least one $\frac{(n-1)}{3}$-regular graph with order n exists for every n satisfying $n\equiv 1(mod3)$. □

Next, we pay our attention to the extremum values of $\widetilde{Lz}$ for n-order molecular graphs.

Theorem 13.

In the set of all n-order molecular graphs, with the constraint $n\ge 14$, only 4-regular graphs possess the highest value of $\widetilde{Lz}$.

Proof. 

Consider an n-order molecular graph G. For every $s\in V\left(G\right)$ and $n\ge 14$, it holds that $d_s{(n-1-d_s)}^2\le 4{(n-5)}^2$ with equality if and only if $d_s=4$. Consequently, we have

$$\widetilde{Lz}\left(G\right)\le 4n{(n-5)}^2,$$

(9)

where the equality is true if and only if G is 4-regular. Since at least one 4-regular graph exists for every $n\ge 14$, the desired result follows from (9). □

For the minimal version of Theorem 13, we require the following:

Lemma 15.

If G is an n-order molecular graph, with $n\ge 14$, and $st\in E\left(G\right)$, then

$$\widetilde{Lz}\left(G\right)>\widetilde{Lz}(G-st).$$

Proof. 

Since the function $f\left(x\right)=x{(n-1-x)}^2$, with $n\ge 14$, is strictly increasing for $0\le x\le 4$, we obtain

$$\begin{array}{cc}\hfill \widetilde{Lz}\left(G\right)-\widetilde{Lz}(G-st)& =d_s{(n-1-d_s)}^2+d_t{(n-1-d_t)}^2\hfill \\ \hfill & -(d_s-1){(n-2-d_s)}^2+(d_t-1){(n-2-d_t)}^2>0,\hfill \end{array}$$

where $d_s=d_s\left(G\right)$ and $d_t=d_t\left(G\right)$. □

Theorem 14.

For every $n\ge 14$, in the set of all n-order connected molecular graphs, only the trees having the degree set

(i) 

$\{1,2,4\}$ and admitting exactly one vertex of degree 2 possess the least value of $\widetilde{Lz}$, when $n\equiv 0(mod3)$;

(ii) 

$\{1,3,4\}$ and admitting exactly one vertex of degree 3 possess the least value of $\widetilde{Lz}$, when $n\equiv 1(mod3)$;

(iii) 

$\{1,4\}$ possess the least value of $\widetilde{Lz}$, when $n\equiv 2(mod3)$.

Proof. 

Consider an n-order connected molecular graph G containing at least one cycle, where $n\ge 14$. By Lemma 15, it holds that $\widetilde{Lz}\left(G\right)>\widetilde{Lz}(G-st)$, where $st$ is an edge lying on a cycle of G. Thus, for every $n\ge 14$, a graph possessing the least value of $\widetilde{Lz}$ in the set of all n-order connected molecular graphs must be a tree. Consequently, the desired conclusion follows from Corollary 3. □