Prediction of Infectious Disease to Reduce the Computation Stress on Medical and Health Care Facilitators

Abstract

Prediction of the infectious disease is a potential research area from the decades. With the progress in medical science, early anticipation of the disease spread becomes more meaningful when the resources are limited. Also spread prediction with limited data pose a deadly challenge to the practitioners. Hence, the paper presents a case study of the Corona virus (COVID-19). COVID-19 has hit the major parts of the world and implications of this virus, is life threatening. Research community has contributed significantly to understand the spread of virus with time, along with meteorological conditions and other parameters. Several forecasting techniques have already been deployed for this. Considering the fact, the paper presents a proposal of two Rolling horizon based Cubic Grey Models (RCGMs). First, the mathematical details of Cubic Polynomial based simple grey model is presented than two models based on time series rolling are proposed. The models are developed with the time series data of different locations, considering diverse overlap period and rolling values. It is observed that the proposed models yield satisfactory results as compared with the conventional and advanced grey models. The comparison of the performance has been carried out with calculation of standard error indices. At the end, some recommendations are also framed for the authorities, that can be helpful for decision making in tough time.

1. Introduction

COVID-19 or coronavirus is rapidly spreading all over the world since its first case in December 2019 at Wuhan city, China. The initial symptoms are similar to viral pneumonia, which can be further converted into severe respiratory disease or even lungs failure. The virus named as SAES-CoV-2 is very infectious and easily transmissible [1] and thus became a threat to society. Due to its exponential infectious rate, it is challenging task to treat infected persons [2] and stop the spread further. Despite all types of safety measures like social distancing, washing hands regularly, proper sanitization, and use of mask to cover nose and mouth, a large number of cases are reported worldwide creating panic among people. Under these severe conditions, it has been declared a global pandemic by world Health Organization [3].

In India, the first infection of coronavirus has came in light on 30 January 2020 and after that, it spread in almost every city although rural areas remain safe. Later-on, the spread became hazardous as till 28 May 2021, there are 2,343,152 active cases recorded out of which 318,895 have lost their lives. This create a lot of stress and pressure on health officials and administration as they are doing multitasking works. To treat the infected, proper vaccination, arrangement of various safety measures at work places and common places and prepare policies for future are among top priorities. Scientist community did not left behind this crucial time and many researcher use forecasting techniques as a powerful boon to predict the future conditions [4,5].

Forecasting, became a new research tool in recent years and widely used in almost all areas of social sciences like economics, energy prediction and energy demand, engineering, air pollution, recommendation systems, control systems, retail fashion etc. Refs. [6,7,8,9,10,11,12,13,14] are some fine examples of application of different methods in forecasting. There exists traditional forecasting methods like LR (Linear Regression), ARIMA (Auto Regressive Integrated Moving Average), ANN (Artificial Neural Network), SVR (Support Vector Machine) etc., which need ample amount of data. In case of disease, it is not easy to collect the data of large sample size following a, specific distribution model at early stages. It has became more difficult, when facing the pandemic like COVID-19. A time series based prediction has been conducted for Canada. The research employed Long short-term memory (LSTM) network for carrying out the prediction [15]. Auto Regressive Integrated Moving Average (ARIMA) based models are employed for prediction of the COVID-19 in five countries namely US, Brazil, India, Russia and Spain [16]. A rich review of forecasting model pertaining to COVID-19 has been presented in paper [17]. A comparative analysis of strength and weakness of different forecasting models has been presented in the paper. The analysis conducted in the paper inherent problems pertaining to limited data availability (Deep learning algorithms), stability of the ARIMA models and black box characteristics of Artificial Neural Networks.

Grey prediction theory proposed by Prof. J. Deng [18], is the best tool to approach problems having limited data with uncertainty. It can be said that grey model employs local information and act as a local predictor. Grey theory works as a transform model as it transform the unknown data into consistent data. This transformation has done through Accumulation Generation Operator known as AGO. The main objective of Grey theory is to provide a real time based non-functional model which can replace the regression and stochastic models while dealing with poor and hidden data. Recently some authors approached Grey models for forecasting due to their accurate prediction and practical approach. Halis Bilgil [19] proposed an exponential Grey model to forecast the prediction no of new cases, recovered cases and no. of deaths from COVID-19 in Turkey. In [20] authors developed a grey forecasting model enabled with quadratic terms to predict about the COVID-19 impact at early stages in China. A. Saxena [21] used optimized Grey prediction model for forecasting about the pandemic using the data of four different states of India. Similarly Particle Swarm Optimization is used in [22] to optimized the results provided by GM(1,1) and others.

GM(1,1) [23] model has considered as the classical grey model due to its accuracy and practical approach. Cui and others [24] proposed NGM having a linear function of time in the whitening equation. This model is further improved as NGM(1,1,k,c) [25] by adding a constant term in RHS component of whitening equation. A kernel based model is introduced in [26] to increase the accuracy and application areas of NGM. A novel discrete Grey forecasting model known as DGM has been developed for further improvisation in existing grey models in [27,28]. Some multivariable grey models are also proposed as an extensions of earlier grey models in [29,30,31]. However, GM(1,1) model provide very good results with homogeneous data set only. Some models which can deal with non-homogeneous terms also provide large amount of errors with some specific sequences. Some very useful experimentation for the prediction of market clearing price is showcased in references [32,33]. Further the rich review of forecasting methods has been presented in reference [34]. Also come of the approaches used grey model in financial transactions [35].

The parameter of grey action term is also an important factor which fluctuate the accuracy of prediction using grey models. Some recent approaches also employed, advance meta heuristic approaches for tuning the parameters of grey model. In [36] cuckoo search algorithm is used to select the optimal value of grey parameter. Similarly Whale Optimization Algorithm has been applied in [37] to find the best suitable value of nonlinear parameter.

Hence, to overcome these weaknesses, we proposed a grey model (RCGM), which has a negative term in its whitening equation and act as a corrector while dealing with specific data sequence. This literature review clearly indicates that scope of improvement is always available.

Hence, the research directions of developing the new grey models can be identified as follows:

• Change in accumulation operator
• Change in back ground value information
• Transformation of the series into a new one in order to deal with negative data.

Hence, It is pragmatic to state that a new model that possess better matching quality (or mechanisms discussed above) of limited data availability can be potential area of investigation. On the basis of the critical review, we framed the following research objectives for this work

1.

To develop a rolling horizon based grey model for identification of Novel Corona virus cases in a span of week.

2.

To establish mathematical framework of Cubic polynomial driven grey model by analysing the response and mathematical induction.

3.

To present a comparative analysis of developed models with some known grey models and evaluate the performance with the calculation of various error indices.

4.

To frame the recommendations on the basis of forecasting results for authorities to take preventive steps for combating Corona effectively.

Paper Structure

Remaining part of this paper is organized as follows: in Section 2, development of grey models is explained. In Section 3, results of the proposed models are exhibited and last but not the least some future directions along with conclusions of the study are presented in conclusion section. Figure 1, shows the basic philosophy adopted in this research work.

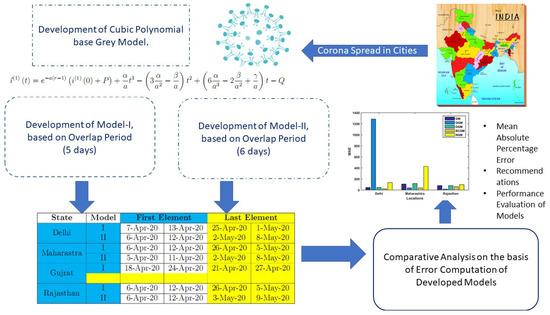
Figure 1. Paper structure.

2. Development of Rolling Horizon Grey Model Comprises with Cubic Polynomial (RCGM)

2.1. Details of Conventional Grey Models

This subsection provides a general outlook of some well known Grey models and their mathematical equations, which will be used further in this paper

1.

GM(1,1) model: The classical GM(1,1) model is also known as the basic foundation model of grey theory and widely used in the forecasting of data with uncertainty. This model comprises of differential equation varying with time for variance of parameters. The basic equation of this model is

$$\frac{d{y}^{\left(1\right)}\left(t\right)}{dt}+a{y}^{\left(1\right)}\left(t\right)=b$$

(1)

The sequence based on time series is given by

$${\widehat{y}}^{\left(1\right)}\left(k+1\right)=e^{-a\left(k\right)}\left(y^{\left(1\right)}\left(0\right)-\frac{b}{a}\right)+\frac{b}{a}$$

(2)

$${\widehat{y}}^{\left(0\right)}\left(k\right)=e^{-a\left(k-2\right)}\left(y^{\left(1\right)}\left(0\right)-\frac{b}{a}\right)\left(e^a-1\right)$$

(3)

2.

DGM(1,1) model: The mathematical terms of discrete grey model (DGM) proposed in [27,38] are given by

$$y^{\left(1\right)}\left(k+1\right)=a{y}^{\left(1\right)}\left(k\right)+b$$

(4)

$${\widehat{y}}^{\left(1\right)}\left(k+1\right)=a^k{y}^{\left(0\right)}\left(1\right)+\left(\frac{1-a^k}{1-a}\right)b$$

(5)

3.

NGM(1,1) model: The grey differential equation of NGM [25] is

$$y^{\left(0\right)}\left(k\right)+a{z}^{\left(1\right)}\left(k\right)=kb+c$$

(6)

The time response equation is given by

$${\widehat{y}}^{\left(1\right)}\left(k\right)=\left(y^{\left(1\right)}\left(1\right)-\frac{b}{a}+\frac{b}{a^2}-\frac{c}{a}\right)e^{-ak}+\frac{b}{a}k-\frac{b}{a^2}+\frac{c}{a}$$

(7)

and the restored value is given mathematically as

$${\widehat{y}}^{\left(0\right)}\left(k\right)=\left(y^{\left(1\right)}\left(1\right)-\frac{b}{a}+\frac{b}{a^2}-\frac{c}{a}\right)\left(1-e^a\right)e^{-ak}+\frac{b}{a}$$

(8)

4.

QGM model: This nonlinear grey model was first proposed by [20] and provide higher prediction accuracy than previously proposed model. The whitenization differential equation of QGM model is represented by

$$\frac{d{y}^{\left(1\right)}\left(t\right)}{dt}+a{y}^{\left(1\right)}\left(t\right)=b{t}^2+ct+d$$

(9)

The time response term and restored values can be given as

$$\begin{array}{c}\hfill {\widehat{y}}^{\left(1\right)}\left(k+1\right)=\left(y^{\left(1\right)}\left(0\right)-\frac{b}{a}+2\frac{b}{a^2}-2\frac{b}{a^3}-\frac{c}{a}+\frac{c}{a^2}-\frac{d}{a}\right)e^{-ak}+\frac{b}{a}{\left(k+1\right)}^2\\ \hfill -\left(2\frac{b}{a^2}-\frac{c}{a}\right)\left(k+1\right)+2\frac{b}{a^3}-\frac{c}{a^2}+\frac{d}{a}\end{array}$$

(10)

$$\begin{array}{c}\hfill {\widehat{y}}^{\left(0\right)}\left(k+1\right)=\left(y^{\left(1\right)}\left(0\right)-\frac{b}{a}+2\frac{b}{a^2}-2\frac{b}{a^3}-\frac{c}{a}+\frac{c}{a^2}-\frac{d}{a}\right)e^{-a\left(k-1\right)}\left(e^a-1\right)\\ \hfill +2\frac{b}{a}\left(k+1\right)-\frac{b}{a}-2\frac{b}{a^2}+\frac{c}{a}\end{array}$$

(11)

In recent years, grey models have been developed on several theories such as change in accumulation operators, transformation of the series to some other hyper space and incorporation of different background value modification techniques. In this work, we first explain some terms.

Definition 1.

Let us assume initial sequence as

$$I_{(W,\mu )}^{\left(0\right)}=i^{\left(0\right)}\left(1\right),i^{\left(0\right)}\left(2\right),\cdots i^{\left(0\right)}\left(r\right)$$

(12)

where all terms of the sequence are taken non-negative.

The one time accumulated generating term is given by

$$I_{(W,\mu )}^{\left(1\right)}=i^{\left(1\right)}\left(1\right),i^{\left(1\right)}\left(2\right),\cdots i^{\left(1\right)}\left(r\right)$$

(13)

$$I_{(W,\mu )}^{\left(r\right)}=\sum _{j=1}^r{i}^{\left(0\right)}\left(j\right),r=1,\cdots n$$

(14)

Definition 2.

The inverse process of finding the accumulated generation sequence can be given as

The sequence mean of $I_{W,\mu }^{\left(0\right)}$ can be given as

$$Z^{\left(1\right)}=z^{\left(1\right)}\left(1\right),z^{\left(1\right)}\left(2\right),\cdots z^{\left(1\right)}\left(r\right)$$

(15)

where

$$Z^{\left(1\right)}\left(k\right)=\frac{i^{\left(1\right)}\left(k\right)+i^{\left(1\right)}(k-1)}{2}\mathrm{for}k=2,\cdots r$$

(16)

2.2. Rolling Horizon Based Cubic Grey Model (RCGM)

The first order linear differential equation known as whitening equation of proposed model GMCP is given by

$$\frac{d{i}^{\left(1\right)}\left(t\right)}{dt}+a{i}^{\left(1\right)}\left(t\right)=\alpha t^3+\beta t^2+\gamma t+\delta$$

(17)

where a is the development coefficients and right hand side term is known as grey action quantity of grey model.

It can be easily observed that when $\alpha =0$, the GMCP model reduced to QGM model. When $\alpha =0,\beta =0$, it reduced to NGM(1,1,k,c) model. On putting $\alpha =0,\beta =0,\gamma =0$, one can find the classical GM(1,1) model.

Theorem 1.

If $y^{\left(0\right)}\left(r\right)$ is a term of the non-negative sequence and $z^{\left(1\right)}\left(r\right)$ is the $rth$ term of mean sequence $Z^{\left(1\right)}\left(r\right)$ defined by (16) then

$$i^{\left(0\right)}\left(r\right)+a{z}^{\left(1\right)}\left(r\right)=\alpha \left(r^3-\frac{3}{2}{r}^2+r-\frac{1}{4}\right)+\beta \left(r^2+r-\frac{1}{3}\right)+\gamma \left(r-\frac{1}{2}\right)+\delta$$

(18)

Proof. 

Integrating the whitening equation defined in (17) both sides w. r. to t between the interval $[r-1,r]$

$${\int }_{r-1}^r\left[\frac{d{i}^{\left(1\right)}\left(t\right)}{dt}+a{y}^{\left(1\right)}\left(t\right)\right]dt=\alpha {\int }_{r-1}^r{t}^{3}dt+\beta {\int }_{r-1}^r{t}^{2}dt+\gamma {\int }_{r-1}^{r}tdt+\delta {\int }_{r-1}^{r}dt$$

(19)

which gives us

$$i^{\left(0\right)}\left(r\right)+a{\int }_{r-1}^r+i^{\left(1\right)}\left(t\right)dt=$$

$$\alpha \frac{\left(r^4-{(r-1)}^4\right)}{4}+\beta \frac{\left(r^3-{(r-1)}^3\right)}{3}+\gamma \frac{\left(r^2-{(r-1)}^2\right)}{3}+\delta$$

(20)

using Trapezoidal formula ${\int }_{r-1}^r{i}^{\left(1\right)}\left(t\right)dt=\frac{i^{\left(1\right)}\left(r\right)+i^{\left(1\right)}(r-1)}{2}=z^{\left(1\right)}\left(r\right)$ and after some simplification, we have the RHS of Theorem 1. □

Theorem 2.

If the initial sequence and its inverse accumulated sequence is given by Definitions 1 and 2 and the mean sequence is represented by (16) then the values of parameters $a,\alpha ,\beta ,\gamma$ and δ in terms of matrix A and X are given by

$${\left(a,\alpha ,\beta ,\gamma ,\delta \right)}^T={\left(A^{T}A\right)}^{-1}{A}^{T}X$$

(21)

where

$$A=\left[\begin{array}{ccccc}-z^1\left(2\right)& \frac{15}{4}& \frac{7}{3}& \frac{3}{2}& 1\\ -z^{1}3& \frac{77}{4}& \frac{19}{3}& \frac{5}{2}& 1\\ ⋮& ⋮& ⋮& ⋮\\ -z^1\left(r\right)& \left(r^3-\frac{3}{2}{r}^2+r-\frac{1}{4}\right)& \left(r^2-r+\frac{1}{3}\right)& \left(r-\frac{1}{2}\right)& 1\end{array}\right]$$

(22)

and

$$X=\left[\begin{array}{c}{i}^0\left(2\right)\\ i^0\left(3\right)\\ ⋮\\ i^0\left(r\right)\end{array}\right]$$

(23)

Proof. 

Using the concept of mathematical induction on taking $r=2,3,\cdots n$ in Theorem 1, we find

$$\left\{\begin{array}{c}{i}^0\left(2\right)=-a{z}^{\left(2\right)}+\frac{15}{4}\alpha +\frac{7}{3}\beta +\frac{3}{2}\gamma t+\delta \hfill \\ i^0\left(3\right)=-a{z}^{\left(3\right)}+\frac{77}{4}\alpha +\frac{19}{3}\beta +\frac{5}{2}\gamma t+\delta \hfill \\ ⋮\hfill \\ i^0\left(n\right)=-a{z}^{\left(n\right)}+\left(n^3-\frac{3}{2}{n}^2+n-\frac{1}{4}\right)\alpha +\left(n^2-n+\frac{1}{3}\right)\beta +\left(n-\frac{1}{2}\right)\gamma t+\delta \hfill \end{array}\right.$$

(24)

On expressing the above system of linear equations in matrix form we obtain

$$\left[\begin{array}{ccccc}-z^1\left(2\right)& \frac{15}{4}& \frac{7}{3}& \frac{3}{2}& 1\\ -z^{1}3& \frac{77}{4}& \frac{19}{3}& \frac{5}{2}& 1\\ ⋮& ⋮& ⋮& ⋮\\ -z^1\left(r\right)& \left(r^3-\frac{3}{2}{r}^2+r-\frac{1}{4}\right)& \left(r^2-r+\frac{1}{3}\right)& \left(r-\frac{1}{2}\right)& 1\end{array}\right]\left[\begin{array}{c}a\\ \alpha \\ \beta \\ \gamma \\ \delta \end{array}\right]=\left[\begin{array}{c}{i}^0\left(2\right)\\ i^0\left(3\right)\\ ⋮\\ i^0\left(n\right)\end{array}\right]$$

(25)

□

Theorem 3.

The time response sequence of proposed model GMCP is given by

$${\widehat{i}}^{\left(1\right)}\left(r\right)=e^{-a\left(r-1\right)}\left(i^{\left(1\right)}\left(0\right)+P\right)+\frac{\alpha }{a}{r}^3-\left(3\frac{\alpha }{a^2}-\frac{\beta }{a}\right)r^2+\left(6\frac{\alpha }{a^3}-2\frac{\beta }{a^2}+\frac{\gamma }{a}\right)r-Q$$

(26)

and its restored value is

$${\widehat{i}}^{\left(0\right)}\left(r\right)=e^{-a\left(r-2\right)}\left(i^{\left(1\right)}\left(0\right)+P\right)+\frac{\alpha }{a}\left(3r^2-3r-1\right)-\left(\frac{3\alpha }{a}-\frac{\beta }{a}\right)\left(2r-1\right)+Q$$

(27)

where

$$P=-\frac{\alpha }{a}+\frac{3\alpha }{a^2}-\frac{6\alpha }{a^3}+\frac{6\alpha }{a^4}+\frac{\beta }{a}-\frac{2\beta }{a^2}+\frac{2\beta }{a^3}+\frac{\gamma }{a}-\frac{\gamma }{a^2}+\frac{\delta }{a}$$

(28)

$$Q=\frac{6\alpha }{a^3}-\frac{2\beta }{a^2}+\frac{\gamma }{a}-\frac{\delta }{a}$$

(29)

Proof. 

The general solution of whitening equation can be obtained easily from the theory of first order ordinary differential equation and given by

$$i^1\left(t\right)=i^1\left(0\right)e^{-{\int }_1^{t}adu}+{\int }_1^t\left(\alpha s^3+\beta s^2+\gamma s+\delta \right)e^{{\int }_t^{s}adu}ds$$

(30)

Now using the formula of simple integration, we can easily get

$${\widehat{i}}^{\left(1\right)}\left(t\right)=e^{-a\left(r-1\right)}\left(i^{\left(1\right)}\left(0\right)+P\right)+\frac{\alpha }{a}{t}^3-\left(3\frac{\alpha }{a^2}-\frac{\beta }{a}\right)t^2+\left(6\frac{\alpha }{a^3}-2\frac{\beta }{a^2}+\frac{\gamma }{a}\right)t-Q$$

(31)

we can easily obtained its restore value by using the relation $i^{\left(0\right)}\left(r\right)=i^{10)}\left(r\right)-i^{\left(1\right)}(r-1)$.

To examine our proposed model we have used Mean Absolute Percentage Error (MAPE), Absolute Percentage error (APE) and Mean Absolute Error (MAE) defined as

• Mean Absolute Percentage Error

$$\mathrm{MAPE}=\frac{1}{n}\sum _{r=1}^n\left|\frac{{\widehat{y}}^{\left(0\right)}\left(r\right)-y^{\left(0\right)}\left(r\right)}{y^{\left(0\right)}\left(r\right)}\right|\times 100$$

• Absolute Percentage Error

$$\mathrm{APE}=\left|\frac{y^{\left(0\right)}\left(r\right)-{\widehat{y}}^{\left(0\right)}\left(r\right)}{y^{\left(0\right)}\left(r\right)}\right|\times 100r=2,3\cdots n$$

• Mean Absolute Error

$$\mathrm{MAE}=\frac{1}{n-l+1}\sum _{r=l}^n\left|{\widehat{y}}^{\left(0\right)}\left(r\right)-y^{\left(0\right)}\left(r\right)\right|$$

• Mean Square Error

$$\mathrm{MSE}=\frac{1}{n}\sum _{r=l}^n{\left(y^{\left(0\right)}\left(r\right)-{\widehat{y}}^{\left(0\right)}\left(r\right)\right)}^2$$

Here $n=$ total no of data points, $y^{\left(0\right)}\left(r\right)=$ actual value and ${\widehat{y}}^{\left(0\right)}\left(r\right)=$ predicted value.

□

2.3. Development of Rolling Cubic Grey Model (RCGM)

In this section, we explain the development of the rolling horizon based cubic grey model for prediction of covid cases at different locations of India. For constructing these models infected case values of a week are chosen and the mean values of the infected cases of this duration are considered as the element of time series. For obtaining second element of the time series, the values of infected cases are rolled to two places for model-I and one place for Model-II as shown in Figure 2. In the figure, the yellow boxes show the rolled values of infected cases. Further, the construction of the time series data can be understood by reading the values from Table 1. The data presented in this work has been taken from reference [21]. The time series constructed on the basis of rolling horizon of a week data of infected cases at different locations of India [39,40].

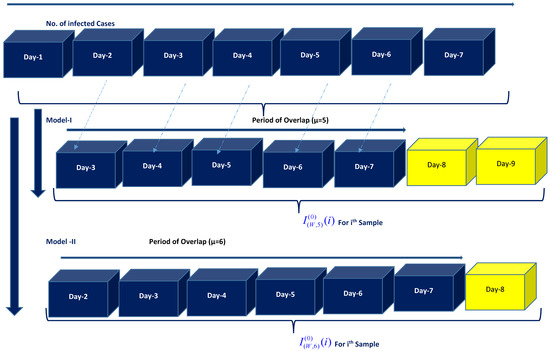
Figure 2. Proposed Rolling horizon based Grey Forecasting Models.

Table 1. Construction of Rolling Grey Models-I and II [21].

State	Model	First Element		Last Element
Delhi	I	7-April-20	13-April-20	25-April-20	1-May-20
	II	6-April-20	12-April-20	2-May-20	8-May-20
Maharastra	I	6-April-20	12-April-20	26-April-20	5-May-20
	II	5-April-20	11-April-20	2-May-20	8-May-20
Gujrat		-	-	-	-
	II	18-April-20	24-April-20	21-April-20	27-April-20
Rajasthan	I	6-April-20	12-April-20	26-April-20	5-May-20
	II	6-April-20	12-April-20	3-May-20	9-May-20

This table shows the relevant statistics for construction of the time series data for three different states and Capital. The column entries under first element shows the mean values of infected cases during the mentioned time period for different states. Like wise, last entry of the time series is shown under last element. For example, for state of Maharashtra the first element of the time series of the model-I mean values of 6 April 2020 to 12 April 2020 and the mean values of infected cases between 26 the April-2020 to 5 May 2020 will be the last value for time series. The data presented in this work has been taken from reference [21]. The time series constructed on the basis of rolling horizon of a week data of infected cases at different locations of India [39,40].

2.4. Discussion

Normally grey models are employed for the forecasting of the variable that contains exponential component. Corona spread between the duration mentioned in Table 1, observed an exponential increment during the period of time. Hence, application of rolling models on this particular duration for dealing with non-linearity is very helpful in prediction on the other hand exponential trend makes the model more compatible for prediction the spread. From the reference [21], it has been observed that the presence of monotonically increasing exponential component in the data pattern , the grey models are applicable on these data sets. Hence, the mechanisms that can improve the internal prediction capability of grey structure can substantially enhance the prediction.

Motivation of the two models has been taken from the reference paper of COVID-19, where the article showcases the impact of different windowing and overlap period. Further, we directly implement our algorithm from the results and discussions from the paper. We also argue whether the same results are obtained with the philosophy. Hence, the two models by considering the same overlap period are proposed in the work with optimized cubic grey model.

3. Results

On the basis of framework developed in previous section, in this section we present a comparative analysis of the proposed model with some contemporary models such as GM(1,1) and NGM model. Following are the salient features of this analysis: a. Establishment of the efficient architecture on the basis of calculation of error indices. Calculation of the mean values of infected cases in the state of Rajasthan, Gujarat and Maharashtra and Capital of India (Delhi).

3.1. Model I

Results of model-I are shown in Table 2, Table 3 and Table 4. From the results shown in tables following points can be concluded:

Table 2. Predicted values from Delhi data Model I.

Index	Initial Value	GM	NGM	DGM	QGM	RCGM
1	355.5714	355.5714	355.5714	355.5714	355.5714	355.5714
2	503.8571	694.262	332.871	697.5088	491.9806	497.5609
3	685	799.4657	553.1245	803.0879	686.1868	661.824
4	871.8571	920.6112	770.0057	924.6481	883.4866	841.5746
5	1061.429	1060.114	983.5661	1064.608	1083.353	1034.188
6	1256.143	1220.757	1193.857	1225.754	1285.349	1235.844
7	1493.714	1405.742	1400.927	1411.291	1489.112	1440.973
8	1727.714	1618.758	1604.827	1624.913	1694.341	1641.468
9	1933.286	1864.053	1805.605	1870.87	1900.786	1825.52
10	2111.714	2146.519	2003.309	2154.056	2108.24	1975.927
11	2278.571	2471.788	2197.985	2480.107	2316.531	2067.639

Table 3. Predicted values from Maharashtra data Model I.

Index	Initial Value	GM	NGM	DGM	QGM	RCGM
1	1028.143	1028.143	1028.143	1028.143	1028.143	1028.143
2	1386.429	1662.276	778.5358	1669.154	1424.073	1371.877
3	1834.714	2006.884	1309.287	2016.133	1806.895	1796.358
4	2352.571	2422.934	1893.203	2435.242	2285.809	2273.47
5	2872.429	2925.236	2535.608	2941.473	2865.265	2837.874
6	3522.429	3531.67	3242.362	3552.939	3549.919	3509.077
7	4274.857	4263.826	4019.911	4291.514	4344.643	4298.055
8	5234.714	5147.765	4875.345	5183.623	5254.533	5210.985
9	6355	6214.956	5816.466	6261.181	6284.923	6251.342
10	7500.429	7503.386	6851.859	7562.738	7441.394	7421.084
11	8690.571	9058.924	7990.964	9134.86	8729.784	8721.31

Table 4. Predicted values from Rajasthan data Model I.

Index	Initial value	GM	NGM	DGM	QGM	RCGM
1	355.5714	355.5714	355.5714	355.5714	355.5714	355.5714
2	503.8571	694.262	332.871	697.5088	491.9806	497.5609
3	685	799.4657	553.1245	803.0879	686.1868	661.824
4	871.8571	920.6112	770.0057	924.6481	883.4866	841.5746
5	1061.429	1060.114	983.5661	1064.608	1083.353	1034.188
6	1256.143	1220.757	1193.857	1225.754	1285.349	1235.844
7	1493.714	1405.742	1400.927	1411.291	1489.112	1440.973
8	1727.714	1618.758	1604.827	1624.913	1694.341	1641.468
9	1933.286	1864.053	1805.605	1870.87	1900.786	1825.52
10	2111.714	2146.519	2003.309	2154.056	2108.24	1975.927
11	2278.571	2471.788	2197.985	2480.107	2316.531	2067.639

1.

For obtaining the results of Model-I, the time series is constructed with overlap period of five days and a rolling model is developed by rolling the mean values of a week by two days. The prediction of this series is evaluated with proposed RCGM and four other models such as (GM [23], NGM [24], DGM [38] and QGM [20]).

2.

The prediction results of the states of Maharashtra, Rajasthan and Delhi are shown in tables. These prediction results show that pandemic spread is exponentially increasing in these locations and an acute requirement or advisory is necessary along with the medical help.

3.

Inspecting the results of Delhi, we observed that the values of infected cases in the Capital is accurately predicted by RCGM as the value of MAPE is optimal as compared to others. Also, it is observed that the values of MAPE are optimal for state of Maharashtra and Rajasthan. The analysis of the MAPE values are depicted in Figure 3. Addition to that analysis MAE is for these places are also depicted in Figure 4.

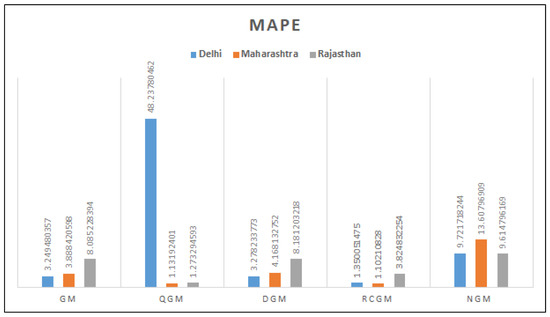Figure 3. Forecasting Results-MAPE for Model-I.

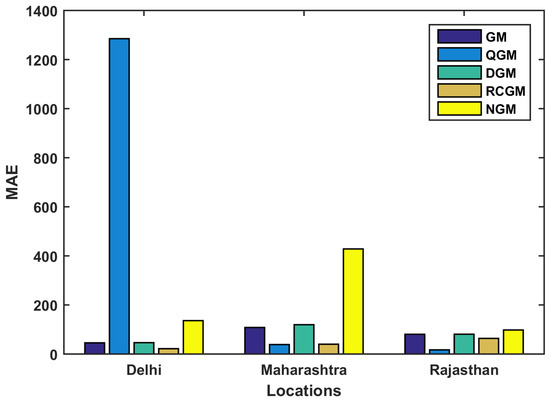Figure 4. Forecasting Results-MAE.

3.2. Model II

Table 5, Table 6, Table 7 and Table 8 showcase the results of model II. After inspecting the results the following points can be framed:

Table 5. Predicted values from Delhi data Model II.

Index	Initial Value	GM	NGM	DGM	QGM	RCGM
1	664	664	664	664	664	664
2	744.8571	974.7736	236.7698	975.3504	800.5598	757.1481
3	835	1036.207	395.2235	1036.827	905.0348	903.6271
4	968.4286	1101.511	553.189	1102.179	1010.093	1039.558
5	1109.143	1170.932	710.6676	1171.65	1115.872	1166.29
6	1239	1244.727	867.661	1245.5	1222.545	1285.185
7	1345	1323.173	1024.171	1324.004	1330.323	1397.62
8	1459.857	1406.564	1180.198	1407.457	1439.469	1504.988
9	1577.571	1495.209	1335.744	1496.17	1550.308	1608.692
10	1698.857	1589.442	1490.811	1590.474	1663.242	1710.156
11	1780.429	1689.613	1645.4	1690.723	1778.77	1810.813
12	1865.429	1796.097	1799.513	1797.29	1897.508	1912.114
13	1961.143	1909.292	1953.151	1910.574	2020.218	2015.526
14	2066.286	2029.621	2106.316	2030.998	2147.845	2122.529
15	2181.571	2157.534	2259.008	2159.013	2281.557	2234.62
16	2286.143	2293.508	2411.23	2295.097	2422.8	2353.311
17	2416.857	2438.052	2562.983	2439.758	2573.364	2480.131
18	2563.571	2591.705	2714.268	2593.538	2735.465	2616.623
19	2729	2755.041	2865.087	2757.01	2911.844	2764.348
20	2899.143	2928.672	3015.441	2930.786	3105.894	2924.882
21	3061.857	3113.245	3165.332	3115.515	3321.814	3099.819
22	3236.714	3309.451	3314.761	3311.887	3564.804	3290.768
23	3450.571	3518.022	3463.729	3520.637	3841.294	3499.356
24	3683.571	3739.738	3612.238	3742.545	4159.248	3727.227
25	3939.286	3975.427	3760.29	3978.44	4528.52	3976.041
26	4195	4225.969	3907.885	4229.203	4961.304	4247.477
27	4494	4492.302	4055.026	4495.772	5472.695	4543.231

Table 6. Predicted values from Maharashtra data Model II.

Index	Initial Value	GM	NGM	DGM	QGM	RCGM
1	1028.143	1028.143	1028.143	1028.143	1028.143	1028.143
2	1209.714	1764.746	411.5523	1767.215	1235.981	1234.322
3	1386.429	1920.443	673.441	1923.175	1404.138	1399.326
4	1596.286	2089.876	947.8645	2092.897	1593.681	1586.744
5	1834.714	2274.258	1235.423	2277.598	1805.163	1796.955
6	2089.571	2474.908	1536.744	2478.599	2039.156	2030.362
7	2352.571	2693.259	1852.488	2697.339	2296.242	2287.388
8	2602.429	2930.875	2183.344	2935.383	2577.021	2568.485
9	2872.429	3189.455	2530.036	3194.434	2882.108	2874.129
10	3189.286	3470.849	2893.322	3476.347	3212.134	3204.827
11	3522.429	3777.069	3273.996	3783.14	3567.746	3561.114
12	3884.429	4110.305	3672.89	4117.007	3949.608	3943.556
13	4274.857	4472.942	4090.876	4480.338	4358.402	4352.756
14	4735.571	4867.572	4528.868	4875.734	4794.825	4789.348
15	5234.714	5297.02	4987.824	5306.024	5259.596	5254.008
16	5802.857	5764.356	5468.747	5774.288	5753.449	5747.45
17	6355	6272.923	5972.688	6283.876	6277.141	6270.43
18	6915.143	6826.359	6500.75	6838.437	6831.444	6823.749
19	7500.429	7428.623	7054.086	7441.938	7417.153	7408.257
20	8109.429	8084.022	7633.906	8098.699	8035.084	8024.853
21	8690.571	8797.245	8241.479	8813.42	8686.072	8674.489
22	9360.429	9573.392	8878.131	9591.216	9370.976	9358.174
23	10,027.29	10,418.02	9545.256	10,437.65	10,090.68	10,076.98
24	10,728.14	11,337.16	10,244.31	11,358.79	10,846.07	10,832.03
25	11,578.29	12,337.39	10,976.83	12,361.22	11,638.1	11,624.54
26	12,465	13,425.87	11,744.4	13,452.11	12,467.7	12,455.76
27	13,442.57	14,610.39	12,548.71	14,639.28	13,335.85	13,327.05

Table 7. Predicted values from Gujarat data Model II.

Index	Initial	GM	NGM	DGM	QGM	RCGM
1	1784.714	1784.714	1784.714	1784.714	1784.714	1784.714
2	2013.714	2112.806	834.7846	2113.869	2027.652	2012.995
3	2234.143	2274.534	1427.203	2275.746	2224.325	2231.876
4	2443.714	2448.642	1951.999	2450.021	2427.026	2438.733
5	2650.857	2636.077	2416.892	2637.641	2636.678	2644.116
6	2862.571	2837.859	2828.72	2839.629	2854.346	2855.155
7	3077.143	3055.088	3193.54	3057.085	3081.256	3076.672
8	3316.429	3288.944	3516.717	3291.193	3318.824	3311.925
9	3569.429	3540.702	3803.006	3543.229	3568.682	3563.115
10	3841.714	3811.73	4056.615	3814.566	3832.711	3831.734
11	4125.143	4103.505	4281.277	4106.682	4113.081	4118.786
12	4429	4417.614	4480.294	4421.167	4412.294	4424.953
13	4751.286	4755.767	4656.595	4759.736	4733.235	4750.694
14	5104.286	5119.805	4812.772	5124.232	5079.231	5096.32
15	5467.571	5511.708	4951.122	5516.64	5454.118	5462.041

Table 8. Predicted values from Rajasthan data Model II.

Index	Initial	GM	NGM	DGM	QGM	RCGM
1	355.5714	355.5714	355.5714	355.5714	355.5714	355.5714
2	427	742.8266	187.9169	744.2623	388.3991	421.3425
3	503.8571	787.6736	313.8585	789.1484	488.5277	503.6302
4	588.2857	835.2282	437.8058	836.7415	588.6708	590.8635
5	685	885.6538	559.7903	887.2049	688.8283	682.2075
6	776.4286	939.1237	679.8431	940.7118	789.0003	776.9297
7	871.8571	995.8218	797.9947	997.4456	889.1866	874.3874
8	968.4286	1055.943	914.2754	1057.601	989.3873	974.0169
9	1061.429	1119.694	1028.715	1121.384	1089.602	1075.324
10	1156.571	1187.294	1141.342	1189.014	1189.832	1177.874
11	1256.143	1258.975	1252.185	1260.723	1290.075	1281.286
12	1369.857	1334.983	1361.274	1336.757	1390.333	1385.228
13	1493.714	1415.581	1468.634	1417.376	1490.605	1489.405
14	1612.714	1501.044	1574.295	1502.857	1590.891	1593.561
15	1727.714	1591.668	1678.282	1593.494	1691.191	1697.471
16	1832.286	1687.762	1780.623	1689.596	1791.505	1800.936
17	1933.286	1789.658	1881.343	1791.495	1891.834	1903.784
18	2031.286	1897.706	1980.468	1899.539	1992.176	2005.861
19	2111.714	2012.277	2078.024	2014.099	2092.533	2107.035
20	2190	2133.765	2174.034	2135.568	2192.903	2207.188
21	2278.571	2262.587	2268.525	2264.363	2293.287	2306.218
22	2368.857	2399.188	2361.519	2400.926	2393.686	2404.034
23	2467.286	2544.035	2453.04	2545.725	2494.098	2500.557
24	2567.429	2697.627	2543.112	2699.256	2594.524	2595.719
25	2681.571	2860.492	2631.757	2862.046	2694.963	2689.457
26	2795	3033.19	2718.999	3034.655	2795.417	2781.72
27	2920.571	3216.314	2804.86	3217.673	2895.884	2872.458

1.

For obtaining the results of Model-II, the time series is constructed with overlap period of six days and a rolling model is developed again. The prediction of this series is evaluated with proposed RCGM and four other grey models.

2.

The prediction results in terms of MAPE are depicted through Figure 5, from the figure, it is empirical to state that the MAPE values are optimal for proposed model. This fact affirms the applicability of of this RCGM model.

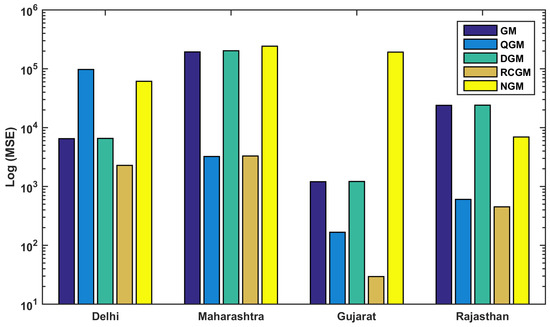Figure 5. Forecasting Results-MSE for Model-II.

3.

In case of all states along with Delhi, the values of MAPE are optimal. Addition to that, Mean absolute errors are also calculated for this model. Inspecting these values, it is concluded that these values are also quite optimal for RCGM. The analysis of MAE and MSE are shown in Figure 4 and Figure 5.

3.3. Discussion

Further, with the help of error indices, we can conclude that developed forecast is meaningful as the MAPE calculated for different models are meaningful. In reference [33] criterion has been employed to judge the quality of forecast. We conclude that the forecasting performance of the Model-I and II falls in the range of good and excellent as MAPE values are less than 10%.

3.4. Recommendations

On the basis of forecasting performance of the RCGM, it is concluded that proposed model yields satisfactory performance for obtaining the infected cases at the major hot spots of India. Based on the forecasts following recommendations can be given to the authorities:

• It is empirical to state that the no. of infected cases can be increased in due course of time, hence an acute arrangement of medical facilities and health care related facilities can be appended.
• An awareness program can be initiated for imparting the education to the rural areas about the disease and its implications. Addition to that, an online alert can be issued to major spots and guidelines for travel and other social gatherings can be changed according to the situation.
• Adequate arrangements can be done for converting the unused buildings/schools and colleges for conversion in major relief centres of the corona. Also, the awareness programs can be arranged by the people who have successfully defeated this disease. This can be broadcast on social media and local channels of televisions and radio.

4. Conclusions

Forecasting of a pandemic is a challenging task due to various reasons such as unavailability of the data, effect of unexpected influence of policy decisions, public fear and scant facility of the medical resources. During last two years, the world is fighting hand in hand with corona virus. The work presented in the paper describes development of Rolling horizon forecast model based on Cubic polynomial realization. First the mathematical aspects of the cubic model are explained and then the development of the optimized models is carried out for identifying the corona infected cases at different location of India.

• Two time series models based on diverse overlapping periods and rolling horizon are presented. Mathematical representation of these models is presented. Further, the analysis of these models is conducted with the help of COVID-19 case studies at different states of India.
• It has been observed that proposed models produce accurate results as compared to previous reported approaches on the same data. Comparison of the performance of the models has been done on the basis of different error indices evaluation. Further, we argue that due to lack of abundant data, we employ grey model with rolling horizon and also analyses are conducted with the calculation of many indices.
• It is concluded that the proposed approach is effective and yields accurate results and further can be implemented for improving medical facilities and other life supporting resources.

It would be interesting to observe the performance of RCGM on forecasting of energy price and market clearing price for the energy markets along with other existing problems that suffers from limited data availability.