A Relaxed Inertial Tseng’s Extragradient Method for Solving Split Variational Inequalities with Multiple Output Sets

Abstract

Recently, the split inverse problem has received great research attention due to its several applications in diverse fields. In this paper, we study a new class of split inverse problems called the split variational inequality problem with multiple output sets. We propose a new Tseng extragradient method, which uses self-adaptive step sizes for approximating the solution to the problem when the cost operators are pseudomonotone and non-Lipschitz in the framework of Hilbert spaces. We point out that while the cost operators are non-Lipschitz, our proposed method does not involve any linesearch procedure for its implementation. Instead, we employ a more efficient self-adaptive step size technique with known parameters. In addition, we employ the relaxation method and the inertial technique to improve the convergence properties of the algorithm. Moreover, under some mild conditions on the control parameters and without the knowledge of the operators’ norm, we prove that the sequence generated by our proposed method converges strongly to a minimum-norm solution to the problem. Finally, we apply our result to study certain classes of optimization problems, and we present several numerical experiments to demonstrate the applicability of our proposed method. Several of the existing results in the literature in this direction could be viewed as special cases of our results in this study.

1. Introduction

Let H be a real Hilbert space endowed with inner product $⟨·,·⟩$ and induced norm $\left|\right|·\left|\right|.$ Let C be a nonempty, closed and convex subset of $H,$ and let $A:H\to H$ be an operator. Recall that the variational inequality problem (VIP) is formulated as finding an element $p\in C$ such that

$$⟨x-p,Ap⟩\ge 0,\forall x\in C.$$

(1)

The solution set of the VIP (1) is denoted by $VI(C,A).$ Fichera [1] and Stampacchia [2] were the first to introduce and initiate a study independently on variational inequality theory. The variational inequality model is known to provide a general and useful framework for solving several problems in engineering, optimal control, data sciences, mathematical programming, economics, etc. (see [3,4,5,6,7,8] and the references therein). In recent times, the VIP has received great research attention owing to its several applications in diverse fields, such as economics, operations research, optimization theory, structural analysis, sciences and engineering (see [9,10,11,12,13,14] and the references therein). Several methods have been proposed and analyzed by authors for solving the VIP (see [15,16,17,18,19] and references therein).

One of the well-known and highly efficient methods is the Tseng extragradient method [20] (which is also known as the forward–backward–forward algorithm). The method is a two-step projection iterative method, which only requires single computation of the projection onto the feasible set per iteration. Several authors have modified and improved on the Tseng extragradient method to approximate the solution of the VIP (1) (for instance, see [19,21,22,23] and the references therein).

Another active area of research interest in recent years is the split inverse problem (SIP). The SIP finds applications in various fields, such as in medical image reconstruction, intensity-modulated radiation therapy, signal processing, phase retrieval, data compression, etc. (for instance, see [24,25,26,27]). The SIP model is presented as follows:

$$\mathrm{Find}\widehat{x}\in H_1\mathrm{that}\mathrm{solves}{\mathrm{IP}}_1$$

(2)

such that

$$\widehat{y}:=T\widehat{x}\in H_2\mathrm{solves}{\mathrm{IP}}_2,$$

(3)

where $H_1$ and $H_2$ are real Hilbert spaces, IP${}_1$ denotes an inverse problem formulated in $H_1$, and IP${}_2$ denotes an inverse problem formulated in $H_2,$ and $T:H_1\to H_2$ is a bounded linear operator.

The first instance of the SIP, called the split feasibility problem (SFP), was introduced in 1994 by Censor and Elfving [26] for modeling inverse problems that arise from medical image reconstruction. The SFP has numerous areas of applications, for instance, in signal processing, biomedical engineering, control theory, approximation theory, geophysics, communications, etc. [25,27,28]. The SFP is formulated as follows:

$$\mathrm{Find}\widehat{x}\in C\mathrm{such}\mathrm{that}\widehat{y}=T\widehat{x}\in Q,$$

(4)

where C and Q are nonempty, closed and convex subsets of Hilbert spaces $H_1$ and $H_2,$ respectively, and $T:H_1\to H_2$ is a bounded linear operator.

A well-known method for solving the SFP is the CQ method proposed by Byrne [29]. The CQ method has been improved and extended by several researchers. Moreover, many authors have proposed and analyzed several other iterative methods for approximating the solution of SFP (4) both in the framework of Hilbert and Banach spaces (for instance, see [25,27,28,30,31]).

Censor et al. [32] introduced an important generalization of the SFP called the split variational inequality problem (SVIP). The SVIP is defined as follows:

$$\mathrm{Find}\widehat{x}\in C\mathrm{that}\mathrm{solves}⟨A_1\widehat{x},x-\widehat{x}⟩\ge 0,\forall x\in C$$

(5)

such that

$$\widehat{y}=T\widehat{x}\in H_2\mathrm{solves}⟨A_2\widehat{y},y-\widehat{y}⟩\ge 0,\forall y\in Q,$$

(6)

where $A_1:H_1\to H_1,A_2:H_2\to H_2$ are single-valued operators. Many authors have proposed and analyzed several iterative techniques for solving the SVIP (e.g., see [33,34,35,36]).

Very recently, Reich and Tuyen [37] introduced and studied a new split inverse problem called the split feasibility problem with multiple output sets (SFPMOS) in the framework of Hilbert spaces. Let C and $Q_i$ be nonempty, closed and convex subsets of Hilbert spaces H and $H_i,i=1,2,\dots ,N,$ respectively. Let $T_i:H\to H_i,i=1,2,\dots ,N$ be bounded linear operators. The SFPMOS is formulated as follows: find an element $u^{†}\in H$ such that

$$u^{†}\in \mathsf{\Gamma }:=C\cap \left({\cap }_{i=1}^N{T}_i^{-1}\left(Q_i\right)\right)\ne \varnothing .$$

(7)

Reich and Tuyen [38] proposed and analyzed two iterative methods for solving the SFPMOS (7) in the framework of Hilbert spaces. The proposed algorithms are presented as follows:

$$x_{n+1}=P_C\left[x_n-{\gamma }_n{\displaystyle {\displaystyle \sum _{i=1}^N}}{T}_i^{*}(I-P_{Q_i})T_i{x}_n\right],$$

(8)

and

$$x_{n+1}={\alpha }_{n}f\left(x_n\right)+(1-{\alpha }_n)P_C\left[x_n-{\gamma }_n{\displaystyle {\displaystyle \sum _{i=1}^N}}{T}_i^{*}(I-P_{Q_i})T_i{x}_n)\right],$$

(9)

where $f:C\to C$ is a strict contraction, $\left\{{\gamma }_n\right\}\subset (0,+\infty )$ and $\left\{{\alpha }_n\right\}\subset (0,1).$ The authors obtained weak and strong convergence results for Algorithm (8) and Algorithm (9), respectively.

Motivated by the importance and several applications of the split inverse problems, in this paper, we examine a new class of split inverse problems called the split variational inequality problem with multiple output sets. Let $H,H_i,i=1,2,\dots ,N,$ be real Hilbert spaces and let $C,C_i$ be nonempty, closed and convex subsets of real Hilbert spaces H and $H_i,i=1,2,\dots ,N,$ respectively. Let $T_i:H\to H_i,i=1,2,\dots ,N,$ be bounded linear operators and let $A:H\to H,A_i:H_i\to H_i,i=1,2,\dots ,N,$ be mappings. The split variational inequality problem with multiple output sets (SVIPMOS) is formulated as finding a point $x^{*}\in C$ such that

$$x^{*}\in \mathsf{\Omega }:=VI(C,A)\cap \left({\cap }_{i=1}^N{T}_i^{-1}VI(C_i,A_i)\right)\ne \varnothing .$$

(10)

Observe that the SVIPMOS (10) is a more general problem than the SFPMOS (7).

In recent times, developing algorithms with high rates of convergence for solving optimization problems has become of great interest to researchers. There are two important techniques that are generally employed by researchers to improve the rate of convergence of iterative methods. These techniques include the inertial technique and the relaxation technique. The inertial technique first introduced by Polyak [39] originates from an implicit time discretization method (the heavy ball method) of second-order dynamical systems. The main feature of the inertial-algorithm is that the method uses the previous two iterates to generate the next iterate. We note that this small change can significantly improve the speed of convergence of an iterative method (for instance, see [21,23,40,41,42,43,44,45]). The relaxation method is another well-known technique employed by authors to improve the rate of convergence of iterative methods (see, e.g., [46,47,48]). The influence of these two techniques on the convergence properties of iterative methods was investigated in [46].

In this study, we introduce and analyze the convergence of a relaxed inertial Tseng extragradient method for solving the SVIPMOS (10) in the framework of Hilbert spaces when the cost operators are pseudomonotone and non-Lipschitz. Our proposed algorithm has the following key features:

• The proposed method does not require the Lipschitz continuity condition often imposed by the cost operator in the literature when solving variational inequality problems. In addition, while the cost operators are non-Lipschitz, the design of our algorithm does not involve any linesearch procedure, which could be time-consuming and too expensive to implement.
• Our proposed method does not require knowledge of the operators’ norm for its implementation. Rather, we employ a very efficient self-adaptive step size technique with known parameters. Moreover, some of the control parameters are relaxed to enlarge the range of values of the step sizes of the algorithm.
• Our algorithm combines the relaxation method and the inertial techniques to improve its convergence properties.
• The sequence generated by our proposed method converges strongly to a minimum-norm solution to the SVIPMOS (10). Finding the minimum-norm solution to a problem is very important and useful in several practical problems.

Finally, we apply our result to study certain classes of optimization problems, and we carry out several numerical experiments to illustrate the applicability of our proposed method.

This paper is organized as follows: In Section 2, we present some definitions and lemmas needed to analyze the convergence of the proposed algorithm, while in Section 3, we present the proposed method. In Section 4, we discuss the convergence of the proposed method, and in Section 5, we apply our result to study certain classes of optimization problems. In Section 6, we present several numerical experiments with graphical illustrations. Finally, in Section 7, we give a concluding remark.

2. Preliminaries

Definition 1

([21,22]). An operator $A:H\to H$ is said to be

(i) 

α-strongly monotone, if there exists $\alpha >0$ such that

$$\begin{array}{c}\hfill ⟨x-y,Ax-Ay⟩\ge {\alpha \parallel x-y\parallel }^2,\forall x,y\in H;\end{array}$$

(ii) 

monotone, if

$$⟨x-y,Ax-Ay⟩\ge 0,\forall x,y\in H;$$

(iii) 

pseudomonotone, if

$$⟨Ay,x-y⟩\ge 0\Rightarrow ⟨Ax,x-y⟩\ge 0,\forall x,y\in H,$$

(iv) 

L-Lipschitz continuous, if there exists a constant $L>0$ such that

$$\left|\right|Ax-Ay\left|\right|\le L\left|\right|x-y\left|\right|,\forall x,y\in H;$$

(v) 

uniformly continuous, if for every $ϵ>0,$ there exists $\delta =\delta \left(ϵ\right)>0,$ such that

$$\parallel Ax-Ay\parallel <ϵwhenever\parallel x-y\parallel <\delta ,\forall x,y\in H;$$

(vi) 

sequentially weakly continuous, if for each sequence $\left\{x_n\right\},$ we have $x_n\rightharpoonup x\in H$ implies that $A{x}_n\rightharpoonup Ax\in H.$

Remark 1.

It is known that the following implications hold: $\left(i\right)\Rightarrow \left(ii\right)\Rightarrow \left(iii\right)$ but the converses are not generally true. We also note that uniform continuity is a weaker notion than Lipschitz continuity.

It is well-known that if D is a convex subset of $H,$ then $A:D\to H$ is uniformly continuous if and only if, for every $ϵ>0,$ there exists a constant $K<+\infty$ such that

$$\parallel Ax-Ay\parallel \le K\parallel x-y\parallel +ϵ\forall x,y\in D.$$

(11)

Lemma 1

([49]).Suppose $\left\{a_n\right\}$ is a sequence of nonnegative real numbers, $\left\{{\alpha }_n\right\}$ is a sequence in $(0,1)$ with ${\sum }_{n=1}^{\infty }{\alpha }_n=+\infty$ and $\left\{b_n\right\}$ is a sequence of real numbers. Assume that

$$a_{n+1}\le (1-{\alpha }_n)a_n+{\alpha }_n{b}_{n}foralln\ge 1.$$

If ${\displaystyle \underset{k\to \infty }{lim\; sup}}{b}_{n_k}\le 0$ for every subsequence $\left\{a_{n_k}\right\}$ of $\left\{a_n\right\}$ satisfying ${\displaystyle \underset{k\to \infty }{lim\; inf}}(a_{n_{k+1}}-a_{n_k})\ge 0,$ then ${\displaystyle \underset{n\to \infty }{lim}}{a}_n=0.$

Lemma 2

([50]).Suppose $\left\{{\lambda }_n\right\}$ and $\left\{{\theta }_n\right\}$ are two nonnegative real sequences such that

$${\lambda }_{n+1}\le {\lambda }_n+{\varphi }_n,\forall n\ge 1.$$

If ${\sum }_{n=1}^{\infty }{\varphi }_n<+\infty ,$ then ${\displaystyle \underset{n\to \infty }{lim}}{\lambda }_n$ exists.

Lemma 3

([51]).Let H be a real Hilbert space. Then, the following results hold for all $x,y\in H$ and $\delta \in (0,1):$

(i) 

$\left|\right|x+{y\left|\right|}^2\le {\left|\right|x\left|\right|}^2+2⟨y,x+y⟩;$

(ii) 

$\left|\right|x+{y\left|\right|}^2={\left|\right|x\left|\right|}^2+2⟨x,y⟩+{\left|\right|y\left|\right|}^2;$

(iii) 

$\left|\right|\delta x+{(1-\delta )y\left|\right|}^2={\delta \left|\right|x\left|\right|}^2+{(1-\delta )\left|\right|y\left|\right|}^2-\delta (1-\delta )\left|\right|x-{y\left|\right|}^2.$

Lemma 4

([52]).Consider the $VIP$ (1) with C being a nonempty, closed, convex subset of a real Hilbert space H and $A:C\to H$ being pseudomonotone and continuous. Then p is a solution of $VIP$ (1) if and only if

$$⟨Ax,x-p⟩\ge 0,\forall x\in C$$

3. Main Results

In this section, we present our proposed iterative method for solving the SVIPMOS (10). We establish our convergence result for the proposed method under the following conditions:

Let $C,C_i$ be nonempty, closed and convex subsets of real Hilbert spaces $H,H_i,i=1,2,\dots ,N,$ respectively, and let $T_i:H\to H_i,i=1,2,\dots ,N$ be bounded linear operators with adjoints $T_i^{*}.$ Let $A:H\to H,A_i:H_i\to H_i,i=1,2,\dots ,N,$ be uniformly continuous pseudomonotone operators satisfying the following property:

$$\mathrm{whenever}\left\{T_i{x}_n\right\}\subset C_i,T_i{x}_n\rightharpoonup T_{i}z,\mathrm{then}\parallel A_i{T}_{i}z\parallel \le {\displaystyle \underset{n\to \infty }{lim\; inf}}\parallel A_i{T}_i{x}_n\parallel ,i=0,1,2\dots ,N,C_0=C,A_0=A,T_0=I^H.$$

(12)

Moreover, we assume that the solution set $\mathsf{\Omega }\ne \varnothing$ and the control parameters satisfy the following conditions:

Assumption B:

(A1)

$\left\{{\alpha }_n\right\}\subset (0,1),{\displaystyle \underset{n\to \infty }{lim}}{\alpha }_n=0,{\sum }_{n=1}^{\infty }{\alpha }_n=+\infty ,{\displaystyle \underset{n\to \infty }{lim}}\frac{{ϵ}_n}{{\alpha }_n}=0,\left\{{\xi }_n\right\}\subset [a,b]\subset (0,1),\theta >0;$

(A2)

$0<c_i<c_i^{\prime }<1,0<{\varphi }_i<{\varphi }_i^{\prime }<1,{\displaystyle \underset{n\to \infty }{lim}}{c}_{n,i}={\displaystyle \underset{n\to \infty }{lim}}{\varphi }_{n,i}=0,{\lambda }_{1,i}>0,\forall i=0,1,2,\dots ,N;$

(A3)

$\left\{{\rho }_{n,i}\right\}\subset {\mathbb{R}}_{+},{\sum }_{n=1}^{\infty }{\rho }_{n,i}<+\infty ,0<a_i\le {\delta }_{n,i}\le b_i<1,{\sum }_{i=0}^N{\delta }_{n,i}=1$ for each $n\ge 1.$

Now, the Algorithm 1 is presented as follows:

Algorithm 1. A Relaxed Inertial Tseng’s Extragradient Method for Solving SVIPMOS (10).

Step 0. Select initial points $x_0,x_1\in H.$ Let $C_0=C,T_0=I^H,A_0=A$ and set $n=1.$ Step 1. Given the $(n-1)th$ and $nth$ iterates, choose ${\theta }_n$ such that $0\le {\theta }_n\le {\widehat{\theta }}_n$ with ${\widehat{\theta }}_n$ defined by $${\widehat{\theta }}_n=\left\{\begin{array}{c}min\left\{\theta ,\frac{{ϵ}_n}{\parallel x_n-x_{n-1}\parallel }\right\},\mathrm{if}{x}_n\ne x_{n-1},\hfill \\ \theta ,\mathrm{otherwise}.\hfill \end{array}\right.$$ (13) Step 2. Compute $$w_n=(1-{\alpha }_n)(x_n+{\theta }_n(x_n-x_{n-1})).$$ Step 3. Compute $$y_{n,i}=P_{C_i}(T_i{w}_n-{\lambda }_{n,i}{A}_i{T}_i{w}_n).$$ Step 4. Compute $$u_{n,i}=y_{n,i}-{\lambda }_{n,i}(A_i{y}_{n,i}-A_i{T}_i{w}_n),$$ $${\lambda }_{n+1,i}=\left\{\begin{array}{cc}min\{\frac{(c_{n,i}+c_i)\parallel T_i{w}_n-y_{n,i}\parallel }{\parallel A_i{T}_i{w}_n-A_i{y}_{n,i}\parallel },{\lambda }_{n,i}+{\rho }_{n,i}\},\hfill & \mathrm{if}{A}_i{T}_i{w}_n-A_i{y}_{n,i}\ne 0,\hfill \\ {\lambda }_{n,i}+{\rho }_{n,i},\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$ Step 5. Compute $$v_n={\displaystyle \sum _{i=0}^N}{\delta }_{n,i}\left(w_n+{\eta }_{n,i}{T}_i^{*}(u_{n,i}-T_i{w}_n)\right),$$ where $${\eta }_{n,i}=\left\{\begin{array}{cc}\frac{({\varphi }_{n,i}+{\varphi }_i){\parallel T_i{w}_n-u_{n,i}\parallel }^2}{\parallel T_i^{*}(T_i{w}_n-u_{n,i}){\parallel }^2},\hfill & \mathrm{if}\parallel T_i^{*}(T_i{w}_n-u_{n,i})\parallel \ne 0,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$ (14) Step 6. Compute $$x_{n+1}={\xi }_n{w}_n+(1-{\xi }_n)v_n.$$

Set $n:=n+1$ and return to Step 1.

Remark 2.

Observe that by conditions (C1) and (C2) together with (13), we have that

$${\displaystyle \underset{n\to \infty }{lim}}{\theta }_n\left|\right|x_n-x_{n-1}\left|\right|=0and{\displaystyle \underset{n\to \infty }{lim}}\frac{{\theta }_n}{{\alpha }_n}\left|\right|x_n-x_{n-1}\left|\right|=0.$$

Remark 3.

We also note that while the cost operators $A_i,i=0,1,2,\dots ,N$ are non-Lipschitz, our method does not require any linesearch procedure, which could be computationally very expensive to implement. Rather, we employ self-adaptive step size techniques that only require simple computations of known parameters per iteration. Moreover, some of the parameters are relaxed to accommodate larger intervals for the step sizes.

Remark 4.

We remark that condition (12) is a weaker assumption than the sequentially weakly continuity condition. We present the following example satisfying condition (12), which also illustrates that the condition is a weaker assumption than the sequentially weakly continuity condition.

Let $A:{\ell }_2\left(\mathbb{R}\right)\to {\ell }_2\left(\mathbb{R}\right)$ be an operator defined by

$$Ax=x\parallel x\parallel ,\forall x\in {\ell }_2\left(\mathbb{R}\right).$$

Suppose $\left\{z_n\right\}\subset {\ell }_2\left(\mathbb{R}\right)$ such that $z_n\rightharpoonup z.$ Then, by the weakly lower semi-continuity of the norm we obtain

$$\parallel z\parallel \le {\displaystyle \underset{n\to +\infty }{lim\; inf}}\parallel z_n\parallel .$$

Thus, we have

$$\parallel Az\parallel ={\parallel z\parallel }^2\le ({\displaystyle \underset{n\to +\infty }{lim\; inf}}\parallel z_n{\parallel )}^2\le {\displaystyle \underset{n\to +\infty }{lim\; inf}}\parallel z_n{\parallel }^2={\displaystyle \underset{n\to +\infty }{lim\; inf}}\parallel A{z}_n\parallel .$$

Therefore, A satisfies condition (12).

On the other hand, to establish that A is not sequentially weakly continuous, choose $z_n=e_n+e_1,$ where $\left\{e_n\right\}$ is a standard basis of ${\ell }_2\left(\mathbb{R}\right),$ that is, $e_n=(0,0,\dots ,1,\dots )$ with 1 at the n-th position. It is clear that $z_n\rightharpoonup e_1$ and $A{z}_n=A(e_n+e_1)=(e_n+e_1)\parallel e_n+e_1\parallel \rightharpoonup \sqrt{2}{e}_1,$ but $A{e}_1=e_1\parallel e_1\parallel =e_1.$ Consequently, A is not sequentially weakly continuous. Therefore, condition (12) is strictly weaker than the sequentially weakly continuity condition.

4. Convergence Analysis

First, we prove some lemmas needed for our strong convergence theorem.

Lemma 5.

Let $\left\{{\lambda }_{n,i}\right\}$ be the sequence generated by Algorithm 1 such that Assumption B holds. Then $\left\{{\lambda }_{n,i}\right\}$ is well-defined for each $i=0,1,2,\dots ,N$ and ${\displaystyle \underset{n\to \infty }{lim}}{\lambda }_{n,i}={\lambda }_{1,i}\in [min\{\frac{c_i}{M_i},{\lambda }_{1,i}\},{\lambda }_{1,i}+{\mathsf{\Phi }}_i],$ where ${\mathsf{\Phi }}_i={\sum }_{n=1}^{\infty }{\rho }_{n,i}.$

Proof. 

Observe that since $A_i$ is uniformly continuous for each $i=0,1,2,\dots ,N,$ it follows from (11) that for any given ${ϵ}_i>0,$ there exists $K_i<+\infty$ such that $\parallel A_i{T}_i{w}_n-A_i{y}_{n,i}\parallel \le K_i\parallel T_i{w}_n-y_{n,i}\parallel +{ϵ}_i.$ Thus, for the case $A_i{T}_i{w}_n-A_i{y}_{n,i}\ne 0$ for all $n\ge 1$, we obtain

$$\frac{(c_{n,i}+c_i)\parallel T_i{w}_n-y_{n,i}\parallel }{\parallel A_i{T}_i{w}_n-A_i{y}_{n,i}\parallel }\ge \frac{(c_{n,i}+c_i)\parallel T_i{w}_n-y_{n,i}\parallel }{K_i\parallel T_i{w}_n-y_{n,i}\parallel +{ϵ}_i}=\frac{(c_{n,i}+c_i)\parallel T_i{w}_n-y_{n,i}\parallel }{(K_i+{\zeta }_i)\parallel T_i{w}_n-y_{n,i}\parallel }=\frac{(c_{n,i}+c_i)}{M_i}\ge \frac{c_i}{M_i},$$

where ${ϵ}_i={\zeta }_i\parallel T_i{w}_n-y_{n,i}\parallel$ for some ${\zeta }_i\in (0,1)$ and $M_i=K_i+{\zeta }_i.$ Therefore, by the definition of ${\lambda }_{n+1,i},$ the sequence $\left\{{\lambda }_{n,i}\right\}$ has lower bound $min\{\frac{c_i}{M_i},{\lambda }_{1,i}\}$ and has upper bound ${\lambda }_{1,i}+{\mathsf{\Phi }}_i.$ By Lemma 2, the limit ${\displaystyle \underset{n\to \infty }{lim}}{\lambda }_{n,i}$ exists and is denoted by ${\lambda }_i={\displaystyle \underset{n\to \infty }{lim}}{\lambda }_{n,i}.$ Clearly, ${\lambda }_i\in \left[min\{\frac{c_i}{M_i},{\lambda }_{1,i}\},{\lambda }_{1,i}+{\mathsf{\Phi }}_i\right]$ for each $i=0,1,2\dots ,N.$ □

Lemma 6.

If $\parallel T_i^{*}(T_i{w}_n-u_{n,i})\parallel \ne 0,$ then the sequence $\left\{{\eta }_{n,i}\right\}$ defined by (14) has a positive lower bounded for each $i=0,1,2,\dots ,N.$

Proof. 

If $\parallel T_i^{*}(T_i{w}_n-u_{n,i})\parallel \ne 0,$ it follows that for each $i=0,1,2,\dots ,N$

$${\eta }_{n,i}=\frac{({\varphi }_{n,i}+{\varphi }_i){\parallel T_i{w}_n-u_{n,i}\parallel }^2}{\parallel T_i^{*}(T_i{w}_n-u_{n,i}){\parallel }^2}.$$

Since $T_i$ is a bounded linear operator and ${\displaystyle \underset{n\to \infty }{lim}}{\varphi }_{n,i}=0$ for each $i=0,1,2,\dots ,N,$ we have

$$\frac{({\varphi }_{n,i}+{\varphi }_i){\parallel T_i{w}_n-u_{n,i}\parallel }^2}{\parallel T_i^{*}(T_i{w}_n-u_{n,i}){\parallel }^2}\ge \frac{({\varphi }_{n,i}+{\varphi }_i){\parallel T_i{w}_n-u_{n,i}\parallel }^2}{\parallel T_i{\parallel }^2\parallel T_i{w}_n-u_{n,i}{\parallel \parallel }^2}\ge \frac{{\varphi }_i}{\parallel T_i{\parallel }^2},$$

which implies that $\frac{{\varphi }_i}{\parallel T_i{\parallel }^2}$ is a lower bound of $\left\{{\eta }_{n,i}\right\}$ for each $i=0,1,2,\dots ,N.$ □

Lemma 7.

Suppose Assumption B of Algorithm 1 holds. Then, there exists a positive integer N such that

$${\varphi }_i+{\varphi }_{n,i}\in (0,1),and\frac{{\lambda }_{n,i}(c_{n,i}+ci)}{{\lambda }_{n+1,i}}\in (0,1),\forall n\ge N.$$

Proof. 

Since $0<{\varphi }_i<{\varphi }_i^{\prime }<1$ and ${\displaystyle \underset{n\to \infty }{lim}}{\varphi }_{n,i}=0$ for each $i=0,1,2,\dots ,N,$ there exists a positive integer $N_{1,i}$ such that

$$0<{\varphi }_i+{\varphi }_{n,i}\le {\varphi }_i^{\prime }<1,\forall n\ge N_{1,i}.$$

Similarly, since $0<c_i<c_i^{\prime }<1,{\displaystyle \underset{n\to \infty }{lim}}{c}_{n,i}=0$ and ${\displaystyle \underset{n\to \infty }{lim}}{\lambda }_{n,i}={\lambda }_i$ for each $i=0,1,2,\dots ,N,$ we have

$${\displaystyle \underset{n\to \infty }{lim}}\left(1-\frac{{\lambda }_{n,i}(c_{n,i}+c_i)}{{\lambda }_{n+1,i}}\right)=1-c_i>1-c_i^{\prime }>0.$$

Thus, for each $i=0,1,2,\dots ,N,$ there exists a positive integer $N_{2,i}$ such that

$$1-\frac{{\lambda }_{n,i}(c_{n,i}+c_i)}{{\lambda }_{n+1,i}}>0,\forall n\ge N_{2,i}.$$

Now, setting $N=max\{N_{1,i},N_{2,i}:i=0,1,2,\dots ,N\},$ we have the required result. □

Lemma 8.

Let $\left\{x_n\right\}$ be a sequence generated by Algorithm 1 under Assumption B. Then the following inequality holds for all $p\in \mathsf{\Omega }:$

$$\begin{array}{cc}\hfill \parallel u_{n,i}-T_i{p\parallel }^2& \le \parallel T_i{w}_n-T_i{p\parallel }^2-\left(1-\frac{{\lambda }_{n,i}^2}{{\lambda }_{n+1,i}^2}{(c_{n,i}+c_i)}^2\right){\parallel T_i{w}_n-y_{n,i}\parallel }^2.\hfill \end{array}$$

Proof. 

From the definition of ${\lambda }_{n+1,i},$ we have

$$\parallel A_i{T}_i{w}_n-A_i{y}_{n,i}\parallel \le \frac{(c_{n,i}+c_i)}{{\lambda }_{n+1,i}}\parallel T_i{w}_n-y_{n,i}\parallel ,\forall n\in \mathbb{N},i=0,1,\dots ,N.$$

(15)

Observe that (15) holds both for $A_i{T}_i{w}_n-A_i{y}_{n,i}=0$ and $A_i{T}_i{w}_n-A_i{y}_{n,i}\ne 0.$ Let $p\in \mathsf{\Omega }.$ Then, it follows that $T_{i}p\in VI(C_i,A_i),i=0,1,2,\dots ,N.$ Using the definition of $u_{n,i}$ and applying Lemma 3, we have

$$\begin{array}{cc}\hfill \parallel u_{n,i}-T_i{p\parallel }^2& =\parallel y_{n,i}-{\lambda }_{n,i}(A_i{y}_{n,i}-A_i{T}_i{w}_n)-T_i{p\parallel }^2\hfill \\ \hfill & =\parallel y_{n,i}-T_i{p\parallel }^2+{\lambda }_{n,i}^2{\parallel A_i{y}_{n,i}-A_i{T}_i{w}_n\parallel }^2-2{\lambda }_{n,i}⟨y_{n,i}-T_{i}p,A_i{y}_{n,i}-A_i{T}_i{w}_n⟩\hfill \\ \hfill & =\parallel T_i{w}_n-T_i{p\parallel }^2+\parallel y_{n,i}-T_i{w}_n{\parallel }^2+2⟨y_{n,i}-T_i{w}_n,T_i{w}_n-T_{i}p⟩+{\lambda }_{n,i}^2{\parallel A_i{y}_{n,i}-A_i{T}_i{w}_n\parallel }^2\hfill \\ \hfill & -2{\lambda }_{n,i}⟨y_{n,i}-T_{i}p,A_i{y}_{n,i}-A_i{T}_i{w}_n⟩\hfill \\ \hfill & =\parallel T_i{w}_n-T_i{p\parallel }^2+{\parallel y_{n,i}-T_i{w}_n\parallel }^2-2⟨y_{n,i}-T_i{w}_n,y_{n,i}-T_i{w}_n⟩+2⟨y_{n,i}-T_i{w}_n,y_{n,i}-T_{i}p⟩\hfill \\ \hfill & +{\lambda }_{n,i}^2{\parallel A_i{y}_{n,i}-A_i{T}_i{w}_n\parallel }^2-2{\lambda }_{n,i}⟨y_{n,i}-T_{i}p,A_i{y}_{n,i}-A_i{T}_i{w}_n⟩\hfill \\ \hfill & =\parallel T_i{w}_n-T_i{p\parallel }^2-\parallel y_{n,i}-T_i{w}_n{\parallel }^2+2⟨y_{n,i}-T_i{w}_n,y_{n,i}-T_{i}p⟩+{\lambda }_{n,i}^2{\parallel A_i{y}_{n,i}-A_i{T}_i{w}_n\parallel }^2\hfill \\ \hfill & -2{\lambda }_{n,i}⟨y_{n,i}-T_{i}p,A_i{y}_{n,i}-A_i{T}_i{w}_n⟩.\hfill \end{array}$$

(16)

Since $y_{n,i}=P_{C_i}(T_i{w}_n-{\lambda }_{n,i}{A}_i{T}_i{w}_n)$ and $T_{i}p\in VI(C_i,A_i),i=0,1,2,\dots ,N,$ by the property of the projection map we have

$$⟨y_{n,i}-T_i{w}_n+{\lambda }_{n,i}{A}_i{T}_i{w}_n,y_{n,i}-T_{i}p⟩\le 0,$$

which is equivalent to

$$⟨y_{n,i}-T_i{w}_n,y_{n,i}-T_{i}p⟩\le -{\lambda }_{n,i}⟨A_i{T}_i{w}_n,y_{n,i}-T_{i}p⟩.$$

(17)

Furthermore, since $y_{n,i}\in C_i,i=0,1,2,\dots ,N,$ we have

$$⟨A_i{T}_{i}p,y_{n,i}-T_{i}p⟩\ge 0,$$

By the pseudomonotonicity of $A_i,$ it follows that $⟨A_i{y}_{n,i},y_{n,i}-T_{i}p⟩\ge 0.$ Since ${\lambda }_{n,i}>0,i=0,1,2,\dots ,N,$ we obtain

$${\lambda }_{n,i}⟨A_i{y}_{n,i},y_{n,i}-T_{i}p⟩\ge 0.$$

(18)

Next, by applying (15), (17) and (18) in (16), we obtain

$$\begin{array}{cc}\hfill \parallel u_{n,i}-T_i{p\parallel }^2& \le \parallel T_i{w}_n-T_i{p\parallel }^2-\parallel y_{n,i}-T_i{w}_n{\parallel }^2-2{\lambda }_{n,i}⟨A_i{T}_i{w}_n,y_{n,i}-T_{i}p⟩+{(c_{n,i}+c_i)}^2\frac{{\lambda }_{n,i}^2}{{\lambda }_{n+1,i}^2}{\parallel T_i{w}_n-y_{n,i}\parallel }^2\hfill \\ \hfill & -2{\lambda }_{n,i}⟨y_{n,i}-T_{i}p,A_i{y}_{n,i}-A_i{T}_i{w}_n⟩\hfill \\ \hfill & =\parallel T_i{w}_n-T_i{p\parallel }^2-\left(1-\frac{{\lambda }_{n,i}^2}{{\lambda }_{n+1,i}^2}{(c_{n,i}+c_i)}^2\right){\parallel T_i{w}_n-y_{n,i}\parallel }^2-2{\lambda }_{n,i}⟨y_{n,i}-T_{i}p,A_i{y}_{n,i}⟩\hfill \\ \hfill & \le \parallel T_i{w}_n-T_i{p\parallel }^2-\left(1-\frac{{\lambda }_{n,i}^2}{{\lambda }_{n+1,i}^2}{(c_{n,i}+c_i)}^2\right){\parallel T_i{w}_n-y_{n,i}\parallel }^2,\hfill \end{array}$$

(19)

which is the required inequality. □

Lemma 9.

Suppose $\left\{x_n\right\}$ is a sequence generated by Algorithm 1 such that Assumption B holds. Then $\left\{x_n\right\}$ is bounded.

Proof. 

Let $p\in \mathsf{\Omega }.$ By the definition of $w_n$ and applying the triangular inequality, we have

$$\begin{array}{cc}\hfill \parallel w_n-p\parallel & =\parallel (1-{\alpha }_n)(x_n+{\theta }_n(x_n-x_{n-1}))-p\parallel \hfill \\ \hfill & =\parallel (1-{\alpha }_n)(x_n-p)+(1-{\alpha }_n){\theta }_n(x_n-x_{n-1})-{\alpha }_{n}p\parallel \hfill \\ \hfill & \le (1-{\alpha }_n)\parallel x_n-p\parallel +(1-{\alpha }_n){\theta }_n\parallel x_n-x_{n-1}\parallel +{\alpha }_n\parallel p\parallel \hfill \\ \hfill & =(1-{\alpha }_n)\parallel x_n-p\parallel +{\alpha }_n\left[(1-{\alpha }_n)\frac{{\theta }_n}{{\alpha }_n}\parallel x_n-x_{n-1}\parallel +\parallel p\parallel \right].\hfill \end{array}$$

By Remark (2), we obtain

$${\displaystyle \underset{n\to \infty }{lim}}\left[(1-{\alpha }_n)\frac{{\theta }_n}{{\alpha }_n}\parallel x_n-x_{n-1}\parallel +\parallel p\parallel \right]=\parallel p\parallel .$$

Thus, there exists $M_1>0$ such that $(1-{\alpha }_n)\frac{{\theta }_n}{{\alpha }_n}\parallel x_n-x_{n-1}\parallel +\parallel p\parallel \le M_1$ for all $n\in \mathbb{N}.$ It follows that

$$\begin{array}{c}\hfill \parallel w_n-p\parallel \le (1-{\alpha }_n)\parallel x_n-p\parallel +{\alpha }_n{M}_1.\end{array}$$

(20)

By Lemma 7, there exists a positive integer N such that $1-\frac{{\lambda }_{n_k,i}}{{\lambda }_{n_k+1,i}}(c_{n_k,i}+c_i)>0,\forall n\ge N,i=0,1,2,\dots ,N.$ Consequently, it follows from (19) that for all $n\ge N$ and $i=0,1,2,\dots ,N$

$$\le \parallel u_{n,i}-T_i{p\parallel }^2\le {\parallel T_i{w}_n-T_{i}p\parallel }^2.$$

(21)

Next, since the function ${\parallel ·\parallel }^2$ is convex, we have

$$\begin{array}{cc}\hfill \parallel v_n{-p\parallel }^2& =\parallel {\displaystyle \sum _{i=0}^N}{\delta }_{n,i}\left(w_n+{\eta }_{n,i}{T}_i^{*}(u_{n,i}-T_i{w}_n)\right){-p\parallel }^2\hfill \\ \hfill & \le {\displaystyle \sum _{i=0}^N}{\delta }_{n,i}{\parallel w_n+{\eta }_{n,i}{T}_i^{*}(u_{n,i}-T_i{w}_n)-p\parallel }^2.\hfill \end{array}$$

(22)

By Lemma 7, there exists a positive integer N such that $0<{\varphi }_{n,i}+{\varphi }_i<1,i=0,1,2,\dots ,N$ for all $n\ge N.$ From (22) and by applying Lemma 3 and (21), we obtain

$$\begin{array}{cc}\hfill \parallel w_n+{\eta }_{n,i}{T}_i^{*}(u_{n,i}-T_i{w}_n){-p\parallel }^2& =\parallel w_n{-p\parallel }^2+{\eta }_{n,i}^2{\parallel T_i^{*}(u_{n,i}-T_i{w}_n)\parallel }^2+2{\eta }_{n,i}⟨w_n-p,T_i^{*}(u_{n,i}-T_i{w}_n)⟩\hfill \\ \hfill & =\parallel w_n{-p\parallel }^2+{\eta }_{n,i}^2{\parallel T_i^{*}(u_{n,i}-T_i{w}_n)\parallel }^2+2{\eta }_{n,i}⟨T_i{w}_n-T_{i}p,u_{n,i}-T_i{w}_n⟩\hfill \\ \hfill & =\parallel w_n{-p\parallel }^2+{\eta }_{n,i}^2\parallel T_i^{*}(u_{n,i}-T_i{w}_n){\parallel }^2+{\eta }_{n,i}[\parallel u_{n,i}-T_i{p\parallel }^2-{\parallel T_i{w}_n-T_{i}p\parallel }^2\hfill \\ \hfill & -\parallel u_{n,i}-T_i{w}_n{\parallel }^2]\hfill \\ \hfill & \le \parallel w_n{-p\parallel }^2+{\eta }_{n,i}^2\parallel T_i^{*}(u_{n,i}-T_i{w}_n){\parallel }^2-{\eta }_{n,i}{\parallel u_{n,i}-T_i{w}_n\parallel }^2\hfill \\ \hfill & =\parallel w_n{-p\parallel }^2-{\eta }_{n,i}[\parallel u_{n,i}-T_i{w}_n{\parallel }^2-{\eta }_{n,i}\parallel T_i^{*}(u_{n,i}-T_i{w}_n){\parallel }^2].\hfill \end{array}$$

(23)

If $\parallel T_i^{*}(u_{n,i}-T_i{w}_n)\parallel \ne 0,$ then by the definition of ${\eta }_{n,i}$, we have

$$\parallel u_{n,i}-T_i{w}_n{\parallel }^2-{\eta }_{n,i}\parallel T_i^{*}(u_{n,i}-T_i{w}_n){\parallel }^2=[1-({\varphi }_{n,i}+{\varphi }_i)]{\parallel T_i{w}_n-u_{n,i}\parallel }^2\ge 0.$$

(24)

Now, applying (24) in (23) and substituting in (22), we have

$$\begin{array}{cc}\hfill \parallel v_n{-p\parallel }^2& \le \parallel w_n{-p\parallel }^2-{\displaystyle \sum _{i=0}^N}{\delta }_{n,i}{\eta }_{n,i}[1-({\varphi }_{n,i}+{\varphi }_i)]{\parallel T_i{w}_n-u_{n,i}\parallel }^2\hfill \\ \hfill & \le \parallel w_n{-p\parallel }^2.\hfill \end{array}$$

(25)

Observe that if $\parallel T_i^{*}(u_{n,i}-T_i{w}_n)\parallel =0,$ (25) still holds from (23).

Next, using the definition of $x_{n+1},$ and applying (20) and (25), we have

$$\begin{array}{cc}\hfill \parallel x_{n+1}-p\parallel & =\parallel {\xi }_n{w}_n+(1-{\xi }_n)v_n-p\parallel \hfill \\ \hfill & \le {\xi }_n\parallel w_n-p\parallel +(1-{\xi }_n)\parallel v_n-p\parallel \hfill \\ \hfill & \le {\xi }_n\parallel w_n-p\parallel +(1-{\xi }_n)\parallel w_n-p\parallel \hfill \\ \hfill & =\parallel w_n-p\parallel \hfill \\ \hfill & \le (1-{\alpha }_n)\parallel x_n-p\parallel +{\alpha }_n{M}_1\hfill \\ \hfill & \le max\{\parallel x_n-p\parallel ,M_1\}\hfill \\ \hfill & ⋮\hfill \\ \hfill & \le max\{\parallel x_N-p\parallel ,M_1\},\hfill \end{array}$$

which implies that $\left\{x_n\right\}$ is bounded. Hence, $\left\{w_n\right\},\left\{y_{n,i}\right\},\left\{u_{n,i}\right\}$ and $\left\{v_n\right\}$ are all bounded. □

Lemma 10.

Let $\left\{w_n\right\}$ and $\left\{v_n\right\}$ be two sequences generated by Algorithm 1 with subsequences $\left\{w_{n_k}\right\}$ and $\left\{v_{n_k}\right\},$ respectively, such that ${\displaystyle \underset{k\to \infty }{lim}}\parallel w_{n_k}-v_{n_k}\parallel =0.$ Suppose $w_{n_k}\rightharpoonup z\in H,$ then $z\in \mathsf{\Omega }.$

Proof. 

From (25), we have

$$\begin{array}{cc}\hfill \parallel v_{n_k}{-p\parallel }^2& \le \parallel w_{n_k}{-p\parallel }^2-{\displaystyle \sum _{i=0}^N}{\delta }_{n_k,i}{\eta }_{n_k,i}[1-({\varphi }_{n_k,i}+{\varphi }_i)]{\parallel T_i{w}_{n_k}-u_{n_k,i}\parallel }^2.\hfill \end{array}$$

(26)

From the last inequality, we obtain

$$\begin{array}{cc}\hfill {\displaystyle \sum _{i=0}^N}{\delta }_{n_k,i}{\eta }_{n_k,i}[1-({\varphi }_{n_k,i}+{\varphi }_i)]{\parallel T_i{w}_{n_k}-u_{n_k,i}\parallel }^2& \le \parallel w_{n_k}{-p\parallel }^2-{\parallel v_{n_k}-p\parallel }^2\hfill \\ \hfill & \le \parallel w_{n_k}-v_{n_k}{\parallel }^2+2\parallel w_{n_k}-v_{n_k}\parallel \parallel v_{n_k}-p\parallel \hfill \end{array}$$

(27)

Since by the hypothesis of the lemma ${\displaystyle \underset{k\to \infty }{lim}}\parallel w_{n_k}-v_{n_k}\parallel =0,$ it follows from (27) that

$${\displaystyle \sum _{i=0}^N}{\delta }_{n_k,i}{\eta }_{n_k,i}[1-({\varphi }_{n_k,i}+{\varphi }_i)]{\parallel T_i{w}_{n_k}-u_{n_k,i}\parallel }^2\to 0,k\to \infty ,$$

which implies that

$${\delta }_{n_k,i}{\eta }_{n_k,i}[1-({\varphi }_{n_k,i}+{\varphi }_i)]{\parallel T_i{w}_{n_k}-u_{n_k,i}\parallel }^2\to 0,k\to \infty ,\forall i=0,1,2,\dots ,N.$$

By the definition of ${\eta }_{n,i},$ we have

$${\delta }_{n_k,i}({\varphi }_{n_k,i}+{\varphi }_i)[1-({\varphi }_{n_k,i}+{\varphi }_i)]\frac{\parallel T_i{w}_{n_k}-u_{n_k,i}{\parallel }^4}{\parallel T_i^{*}(T_i{w}_{n_k}-u_{n_k,i}){\parallel }^2}\to 0,k\to \infty ,\forall i=0,1,2,\dots ,N.$$

From this, we obtain

$$\frac{\parallel T_i{w}_{n_k}-u_{n_k,i}{\parallel }^2}{\parallel T_i^{*}(T_i{w}_{n_k}-u_{n_k,i})\parallel }\to 0,k\to \infty ,\forall i=0,1,2,\dots ,N,$$

Since $\{\parallel T_i^{*}(T_i{w}_{n_k}-u_{n_k,i})\parallel \}$ is bounded, it follows that

$$\parallel T_i{w}_{n_k}-u_{n_k,i}\parallel \to 0,k\to \infty ,\forall i=0,1,2,\dots ,N.$$

(28)

Hence, we have

$$\parallel T_i^{*}(T_i{w}_{n_k}-u_{n_k,i})\parallel \le \parallel T_i^{*}\parallel \parallel (T_i{w}_{n_k}-u_{n_k,i})\parallel =\parallel T_i\parallel \parallel (T_i{w}_{n_k}-u_{n_k,i})\parallel \to 0,k\to \infty ,\forall i=0,1,2,\dots ,N.$$

(29)

From (19), we obtain

$$\begin{array}{c}\hfill \left(1-\frac{{\lambda }_{n_k,i}^2}{{\lambda }_{n_k+1,i}^2}{(c_{n_k,i}+c_i)}^2\right)\parallel T_i{w}_{n_k}-y_{n_k,i}{\parallel }^2\le \parallel T_i{w}_{n_k}-T_i{p\parallel }^2-{\parallel u_{n_k,i}-T_{i}p\parallel }^2\\ \hfill \le \parallel T_i{w}_{n_k}-u_{n_k,i}\parallel \left(\parallel T_i{w}_{n_k}-T_{i}p\parallel +\parallel u_{n_k,i}-T_{i}p\parallel \right).\end{array}$$

(30)

By applying (28), it follows from (30) that

$$\left(1-\frac{{\lambda }_{n_k,i}^2}{{\lambda }_{n_k+1,i}^2}{(c_{n_k,i}+c_i)}^2\right){\parallel T_i{w}_{n_k}-y_{n_k,i}\parallel }^2\to 0,k\to \infty ,i=0,1,\dots ,N.$$

Consequently, we have

$$\parallel T_i{w}_{n_k}-y_{n_k,i}\parallel \to 0,k\to \infty ,i=0,1,\dots ,N.$$

(31)

Since $y_{n,i}=P_{C_i}(T_i{w}_n-{\lambda }_{n,i}{A}_i{T}_i{w}_n),$ by the property of the projection map, we obtain

$$\begin{array}{cc}\hfill & ⟨T_i{w}_{n_k}-{\lambda }_{n_k,i}{A}_i{T}_i{w}_{n_k}-y_{n_k,i},T_{i}x-y_{n_k,i}⟩\le 0,\forall T_{i}x\in C_i,i=0,1,2,\dots ,N,\hfill \end{array}$$

which implies that

$$\frac{1}{{\lambda }_{n_k,i}}⟨T_i{w}_{n_k}-y_{n_k,i},T_{i}x-y_{n_k,i}⟩\le ⟨A_i{T}_i{w}_{n_k},T_{i}x-y_{n_k,i}⟩,\forall T_{i}x\in C_i,i=0,1,2,\dots ,N.$$

From the last inequality, it follows that

$$\frac{1}{{\lambda }_{n_k,i}}⟨T_i{w}_{n_k}-y_{n_k,i},T_{i}x-y_{n_k,i}⟩+⟨A_i{T}_i{w}_{n_k},y_{n_k,i}-T_i{w}_{n_k}⟩\le ⟨A_i{T}_i{w}_{n_k},T_{i}x-T_i{w}_{n_k}⟩,\forall T_{i}x\in C_i,i=0,1,2,\dots ,N.$$

(32)

By applying (31) and the fact that ${\displaystyle \underset{k\to \infty }{lim}}{\lambda }_{n_k,i}={\lambda }_i>0,$ from (32) we obtain

$${\displaystyle \underset{k\to \infty }{lim\; inf}}⟨A_i{T}_i{w}_{n_k},T_{i}x-T_i{w}_{n_k}⟩\ge 0,\forall T_{i}x\in C_i,i=0,1,2,\dots ,N.$$

(33)

Observe that

$$⟨A_i{y}_{n_k,i},T_{i}x-y_{n_k,i}⟩=⟨A_i{y}_{n_k,i}-A_i{T}_i{w}_{n_k},T_{i}x-T_i{w}_{n_k}⟩+⟨A_i{T}_i{w}_{n_k},T_{i}x-T_i{w}_{n_k}⟩+⟨A_i{y}_{n_k,i},T_i{w}_{n_k}-y_{n_k,i}⟩.$$

(34)

By the continuity of $A_i,$ from (31) we obtain

$$\parallel A_i{T}_i{w}_{n_k}-A_i{y}_{n_k,i}\parallel \to 0,k\to \infty ,\forall i=0,1,2,\dots ,N.$$

(35)

Using (31) and (35), it follows from (33) and (34) that

$${\displaystyle \underset{k\to \infty }{lim\; inf}}⟨A_i{y}_{n_k,i},T_{i}x-y_{n_k,i}⟩\ge 0,\forall T_{i}x\in C_i,i=0,1,2,\dots ,N.$$

(36)

Next, let $\left\{{\vartheta }_{k,i}\right\}$ be a decreasing sequence of positive numbers such that ${\vartheta }_{k,i}\to 0$ as $k\to \infty ,i=0,1,2,\dots ,N.$ For each $k,$ let $N_k$ denote the smallest positive integer such that

$$⟨A_i{y}_{n_j,i},T_{i}x-y_{n_j,i}⟩+{\vartheta }_{k,i}\ge 0,\forall j\ge N_k,T_{i}x\in C_i,i=0,1,2,\dots ,N,$$

(37)

where the existence of $N_k$ follows from (36). Since $\left\{{\vartheta }_{k,i}\right\}$ is decreasing, then $\left\{N_k\right\}$ is increasing. Moreover, since $\left\{y_{N_k,i}\right\}\subset C_i$ for each $k,$ we can suppose $A_i{y}_{N_k,i}\ne 0$ (otherwise, $y_{N_k,i}\in VI(C_i,A_i),i=0,1,2\dots ,N$) and let

$$z_{N_k,i}=\frac{A_i{y}_{N_k,i}}{\parallel A_i{y}_{N_k,i}{\parallel }^2}$$

Then, $⟨A_i{y}_{N_k,i},z_{N_k,i}⟩=1$ for each $k,i=0,1,2,\dots ,N.$ From (37), we have

$$⟨A_i{y}_{N_k,i},T_{i}x+{\vartheta }_{k,i}{z}_{N_k,i}-y_{N_k,i}⟩\ge 0,\forall T_{i}x\in C_i,i=0,1,2,\dots ,N.$$

It follows from the pseudomonotonicity of $A_i$ that

$$⟨A_i(T_{i}x+{\vartheta }_{k,i}{z}_{N_k,i}),T_{i}x+{\vartheta }_{k,i}{z}_{N_k,i}-y_{N_k,i}⟩\ge 0,\forall T_{i}x\in C_i,i=0,1,2,\dots ,N,$$

which is equivalent to

$$⟨A_i{T}_{i}x,T_{i}x-y_{N_k,i}⟩\ge ⟨A_i{T}_{i}x-A_i(T_{i}x+{\vartheta }_{k,i}{z}_{N_k,i}),T_{i}x+{\vartheta }_{k,i}{z}_{N_k,i}-y_{N_k,i}⟩-{\vartheta }_{k,i}⟨A_i{T}_{i}x,z_{N_k,i}⟩,\forall T_{i}x\in C_i,i=0,1,\dots ,N.$$

(38)

In order to complete the proof, we need to establish that ${\displaystyle \underset{k\to \infty }{lim}}{\vartheta }_{k,i}{z}_{N_k,i}=0.$ Since $w_{n_k}\rightharpoonup z$ and $T_i$ is a bounded linear operator for each $i=0,1,2,\dots ,N,$ we have $T_i{w}_{n_k}\rightharpoonup T_{i}z,\forall i=0,1,2,\dots ,N.$ Thus, from (31), we obtain $y_{n_k,i}\rightharpoonup T_{i}z,\forall i=0,1,2,\dots ,N.$ Since $\left\{y_{n_k,i}\right\}\subset C_i,i=0,1,2,\dots ,N,$ we have $T_{i}z\in C_i.$ If $A_i{T}_{i}z=0,\forall i=0,1,2,\dots ,N,$ then $T_{i}z\in VI(C_i,A_i)\forall i=0,1,2,\dots ,N,$ which implies that $z\in \mathsf{\Omega }.$ On the contrary, we suppose $A_i{T}_{i}z\ne 0,\forall i=0,1,2,\dots ,N.$ Since $A_i$ satisfies condition (12), we have for all $i=0,1,2,\dots ,N$

$$0<\parallel A_i{T}_{i}z\parallel \le {\displaystyle \underset{k\to \infty }{liminf}}\parallel A_i{y}_{n_k,i}\parallel .$$

Applying the facts that $\left\{y_{N_k,i}\right\}\subset \left\{y_{n_k,i}\right\}$ and ${\vartheta }_{k,i}\to 0$ as $k\to \infty ,i=0,1,2\dots ,N,$ we have

$$0\le {\displaystyle \underset{k\to \infty }{lim\; sup}}\parallel {\vartheta }_{k,i}{z}_{N_k,i}\parallel ={\displaystyle {\displaystyle \underset{k\to \infty }{lim\; sup}}}\left(\frac{{\vartheta }_{k,i}}{\parallel A_i{y}_{n_k,i}\parallel }\right)\le \frac{{\displaystyle \underset{k\to \infty }{lim\; sup}}{\vartheta }_{k,i}}{{\displaystyle \underset{k\to \infty }{lim\; inf}}\parallel A_i{y}_{n_k,i}\parallel }=0,$$

which implies that ${\displaystyle \underset{k\to \infty }{lim\; sup}}{\vartheta }_{k,i}{z}_{N_k,i}=0.$ Applying the facts that $A_i$ is continuous, $\left\{y_{N_k,i}\right\}$ and $\left\{z_{N_k,i}\right\}$ are bounded and ${\displaystyle \underset{k\to \infty }{lim}}{\vartheta }_{k,i}{z}_{N_k,i}=0,$ from (38) we get

$${\displaystyle \underset{k\to \infty }{liminf}}⟨A_i{T}_{i}x,T_{i}x-y_{N_k,i}⟩\ge 0,\forall T_{i}x\in C_i,i=0,1,2,\dots ,N.$$

From the last inequality, we have

$$⟨A_i{T}_{i}x,T_{i}x-T_{i}z⟩={\displaystyle \underset{{}_{k\to \infty }}{lim}}⟨A_i{T}_{i}x,T_{i}x-y_{N_k,i}⟩={\displaystyle \underset{k\to \infty }{liminf}}⟨A_i{T}_{i}x,T_{i}x-y_{N_k,i}⟩\ge 0,\forall T_{i}x\in C_i,i=0,1,2,\dots ,N.$$

By Lemma 4, we obtain

$$T_{i}z\in VI(C_i,A_i),i=0,1,2,\dots ,N,$$

which implies that

$$z\in T_i^{-1}\left(VI(C_i,A_i)\right),i=0,1,2,\dots ,N,$$

Consequently, we have $z\in {\bigcap }_{i=0}^N{T}_i^{-1}\left(VI(C_i,A_i)\right),$ which implies that $z\in \mathsf{\Omega }$ as desired. □

Lemma 11.

Suppose $\left\{x_n\right\}$ is a sequence generated by Algorithm 1 under Assumption B. Then, the following inequality holds for all $p\in \mathsf{\Omega }:$

$$\begin{array}{cc}\hfill \parallel x_{n+1}{-p\parallel }^2& \le (1-{\alpha }_n)\parallel x_n{-p\parallel }^2+{\alpha }_n{d}_n-(1-{\xi }_n){\displaystyle \sum _{i=0}^N}{\delta }_{n,i}{\eta }_{n,i}[1-({\varphi }_{n,i}+{\varphi }_i)]\parallel T_i{w}_n-u_{n,i}{\parallel }^2-{\xi }_n(1-{\xi }_n){\parallel w_n-v_n\parallel }^2.\hfill \end{array}$$

Proof. 

Let $p\in \mathsf{\Omega }.$ By applying Lemma 3 together with the definition of $w_n$, we obtain

$$\begin{array}{cc}\hfill \parallel w_n{-p\parallel }^2& =\parallel (1-{\alpha }_n)(x_n-p)+(1-{\alpha }_n){\theta }_n(x_n-x_{n-1})-{\alpha }_n{p\parallel }^2\hfill \\ \hfill & \le \parallel (1-{\alpha }_n)(x_n-p)+(1-{\alpha }_n){\theta }_n(x_n-x_{n-1}){\parallel }^2+2{\alpha }_n⟨-p,w_n-p⟩\hfill \\ \hfill & \le {(1-{\alpha }_n)}^2\parallel x_n{-p\parallel }^2+2(1-{\alpha }_n){\theta }_n\parallel x_n-p\parallel \parallel x_n-x_{n-1}\parallel +{(1-{\alpha }_n)}^2{\theta }_n^2{\parallel x_n-x_{n-1}\parallel }^2\hfill \\ \hfill & +2{\alpha }_n⟨-p,w_n-x_{n+1}⟩+2{\alpha }_n⟨-p,x_{n+1}-p⟩\hfill \\ \hfill & \le (1-{\alpha }_n)\parallel x_n{-p\parallel }^2+2{\theta }_n\parallel x_n-p\parallel \parallel x_n-x_{n-1}\parallel +{\theta }_n^2\parallel x_n-x_{n-1}{\parallel }^2+2{\alpha }_n\parallel p\parallel \parallel w_n-x_{n+1}\parallel \hfill \\ \hfill & +2{\alpha }_n⟨p,p-x_{n+1}⟩.\hfill \end{array}$$

(39)

Now, using the definition of $x_{n+1},$ (25), (39) and applying Lemma 3, we obtain

$$\begin{array}{cc}\hfill \parallel x_{n+1}{-p\parallel }^2& =\parallel {\xi }_n{w}_n+(1-{\xi }_n)v_n{-p\parallel }^2\hfill \\ \hfill & ={\xi }_n\parallel w_n{-p\parallel }^2+(1-{\xi }_n)\parallel v_n{-p\parallel }^2-{\xi }_n(1-{\xi }_n){\parallel w_n-v_n\parallel }^2\hfill \\ \hfill & \le {\xi }_n{\parallel w_n-p\parallel }^2+(1-{\xi }_n)\left[\parallel w_n{-p\parallel }^2-{\displaystyle \sum _{i=0}^N}{\delta }_{n,i}{\eta }_{n,i}[1-({\varphi }_{n,i}+{\varphi }_i)]{\parallel T_i{w}_n-u_{n,i}\parallel }^2\right]\hfill \\ \hfill & -{\xi }_n(1-{\xi }_n){\parallel w_n-v_n\parallel }^2\hfill \\ \hfill & =\parallel w_n{-p\parallel }^2-(1-{\xi }_n){\displaystyle \sum _{i=0}^N}{\delta }_{n,i}{\eta }_{n,i}[1-({\varphi }_{n,i}+{\varphi }_i)]\parallel T_i{w}_n-u_{n,i}{\parallel }^2-{\xi }_n(1-{\xi }_n){\parallel w_n-v_n\parallel }^2\hfill \\ \hfill & \le (1-{\alpha }_n)\parallel x_n{-p\parallel }^2+2{\theta }_n\parallel x_n-p\parallel \parallel x_n-x_{n-1}\parallel +{\theta }_n^2\parallel x_n-x_{n-1}{\parallel }^2+2{\alpha }_n\parallel p\parallel \parallel w_n-x_{n+1}\parallel \hfill \\ \hfill & +2{\alpha }_n⟨p,p-x_{n+1}⟩-(1-{\xi }_n){\displaystyle \sum _{i=0}^N}{\delta }_{n,i}{\eta }_{n,i}[1-({\varphi }_{n,i}+{\varphi }_i)]\parallel T_i{w}_n-u_{n,i}{\parallel }^2-{\xi }_n(1-{\xi }_n){\parallel w_n-v_n\parallel }^2\hfill \\ \hfill & =(1-{\alpha }_n)\parallel x_n{-p\parallel }^2+{\alpha }_n[2\parallel x_n-p\parallel \frac{{\theta }_n}{{\alpha }_n}\parallel x_n-x_{n-1}\parallel +{\theta }_n\parallel x_n-x_{n-1}\parallel \frac{{\theta }_n}{{\alpha }_n}\parallel x_n-x_{n-1}\parallel \hfill \\ \hfill & +2\parallel p\parallel \parallel w_n-x_{n+1}\parallel +2⟨p,p-x_{n+1}⟩]-(1-{\xi }_n){\displaystyle \sum _{i=0}^N}{\delta }_{n,i}{\eta }_{n,i}[1-({\varphi }_{n,i}+{\varphi }_i)]{\parallel T_i{w}_n-u_{n,i}\parallel }^2\hfill \\ & -{\xi }_n(1-{\xi }_n){\parallel w_n-v_n\parallel }^2\hfill \\ \hfill & =(1-{\alpha }_n)\parallel x_n{-p\parallel }^2+{\alpha }_n{d}_n-(1-{\xi }_n){\displaystyle \sum _{i=0}^N}{\delta }_{n,i}{\eta }_{n,i}[1-({\varphi }_{n,i}+{\varphi }_i)]\parallel T_i{w}_n-u_{n,i}{\parallel }^2-{\xi }_n(1-{\xi }_n){\parallel w_n-v_n\parallel }^2,\hfill \end{array}$$

where $d_n=2\parallel x_n-p\parallel \frac{{\theta }_n}{{\alpha }_n}\parallel x_n-x_{n-1}\parallel +{\theta }_n\parallel x_n-x_{n-1}\parallel \frac{{\theta }_n}{{\alpha }_n}\parallel x_n-x_{n-1}\parallel +2\parallel p\parallel \parallel w_n-x_{n+1}\parallel +2⟨p,p-x_{n+1}⟩,$ which is the required inequality. □

Theorem 1.

Let $\left\{x_n\right\}$ be a sequence generated by Algorithm 1 under Assumption B. Then, $\left\{x_n\right\}$ converges strongly to $\widehat{x}\in \mathsf{\Omega },$ where $\parallel \widehat{x}\parallel =min\{\parallel p\parallel :p\in \mathsf{\Omega }\}.$

Proof. 

Let $\parallel \widehat{x}\parallel =min\{\parallel p\parallel :p\in \mathsf{\Omega }\},$ that is, $\widehat{x}=P_{\mathsf{\Omega }}\left(0\right).$ Then, from Lemma 11, we obtain

$$\parallel x_{n+1}-\widehat{x}{\parallel }^2\le (1-{\alpha }_n){\parallel x_n-\widehat{x}\parallel }^2+{\alpha }_n{\widehat{d}}_n,$$

(40)

where ${\widehat{d}}_n=2\parallel x_n-\widehat{x}\parallel \frac{{\theta }_n}{{\alpha }_n}\parallel x_n-x_{n-1}\parallel +{\theta }_n\parallel x_n-x_{n-1}\parallel \frac{{\theta }_n}{{\alpha }_n}\parallel x_n-x_{n-1}\parallel +2\parallel \widehat{x}\parallel \parallel w_n-x_{n+1}\parallel +2⟨\widehat{x},\widehat{x}-x_{n+1}⟩.$

Next, we claim that the sequence $\{\parallel x_n-\widehat{x}\parallel \}$ converges to zero. To do this, in view of Lemma 1 it suffices to show that ${\displaystyle \underset{k\to \infty }{lim\; sup}}{\widehat{d}}_{n_k}\le 0$ for every subsequence $\{\parallel x_{n_k}-\widehat{x}\parallel \}$ of $\{\parallel x_n-\widehat{x}\parallel \}$ satisfying

$$\begin{array}{c}\hfill {\displaystyle \underset{k\to \infty }{lim\; inf}}\left(\parallel x_{n_k+1}-\widehat{x}\parallel -\parallel x_{n_k}-\widehat{x}\parallel \right)\ge 0.\end{array}$$

(41)

Suppose that $\{\parallel x_{n_k}-\widehat{x}\parallel \}$ is a subsequence of $\{\parallel x_n-\widehat{x}\parallel \}$ such that (41) holds. Again, from Lemma 11, we obtain

$$\begin{array}{cc}\hfill (1-{\xi }_{n_k}){\displaystyle \sum _{i=0}^N}{\delta }_{n_k,i}{\eta }_{n_k,i}[1-({\varphi }_{n_k,i}+{\varphi }_i)]{\parallel T_i{w}_{n_k}-u_{n_k,i}\parallel }^2& +{\xi }_{n_k}(1-{\xi }_{n_k}){\parallel w_{n_k}-v_{n_k}\parallel }^2\hfill \\ \hfill & \le (1-{\alpha }_{n_k})\parallel x_{n_k}-\widehat{x}{\parallel }^2-{\parallel x_{n_k+1}-\widehat{x}\parallel }^2+{\alpha }_{n_k}{\widehat{d}}_{n_k}.\hfill \end{array}$$

By (41), Remark 2 and the fact that ${\displaystyle \underset{k\to \infty }{lim}}{\alpha }_{n_k}=0,$ we obtain

$$\begin{array}{c}\hfill (1-{\xi }_{n_k}){\displaystyle \sum _{i=0}^N}{\delta }_{n_k,i}{\eta }_{n_k,i}[1-({\varphi }_{n_k,i}+{\varphi }_i)]\parallel T_i{w}_{n_k}-u_{n_k,i}{\parallel }^2+{\xi }_{n_k}(1-{\xi }_{n_k}){\parallel w_{n_k}-v_{n_k}\parallel }^2\to 0,k\to \infty .\end{array}$$

Consequently, we obtain

$$\begin{array}{c}\hfill {\displaystyle \underset{k\to \infty }{lim}}\parallel w_{n_k}-v_{n_k}\parallel =0;{\displaystyle \underset{k\to \infty }{lim}}\parallel T_i{w}_{n_k}-u_{n_k,i}\parallel =0,\forall i=0,1,2,\dots ,N.\end{array}$$

(42)

From the definition of $w_n$ and by Remark 2, we have

$$\begin{array}{cc}\hfill \parallel w_{n_k}-x_{n_k}\parallel & =\parallel (1-{\alpha }_{n_k})(x_{n_k}+{\theta }_{n_k}(x_{n_k}-x_{n_k-1}))-x_{n_k}\parallel \hfill \\ \hfill & =\parallel (1-{\alpha }_{n_k})(x_{n_k}-x_{n_k})+(1-{\alpha }_{n_k}){\theta }_{n_k}(x_{n_k}-x_{n_k-1})-{\alpha }_{n_k}{x}_{n_k}\parallel \hfill \\ \hfill & \le (1-{\alpha }_{n_k})\parallel x_{n_k}-x_{n_k}\parallel +(1-{\alpha }_{n_k}){\theta }_{n_k}\parallel x_{n_k}-x_{n_k-1}\parallel +{\alpha }_{n_k}\parallel x_{n_k}\parallel \to 0,k\to \infty .\hfill \end{array}$$

(43)

Using (42) and (43), we obtain

$$\parallel v_{n_k}-x_{n_k}\parallel \to 0,k\to \infty .$$

(44)

From the definition of $x_{n+1}$ and by applying (43) and (44), we obtain

$$\begin{array}{cc}\hfill \parallel x_{n_k+1}-x_{n_k}\parallel & =\parallel {\xi }_{n_k}{w}_{n_k}+(1-{\xi }_{n_k})v_{n_k}-x_{n_k}\parallel \hfill \\ \hfill & \le {\xi }_{n_k}\parallel w_{n_k}-x_{n_k}\parallel +(1-{\xi }_{n_k})\parallel v_{n_k}-x_{n_k}\parallel \to 0,k\to \infty .\hfill \end{array}$$

(45)

Next, by combining (43) and (45), we obtain

$$\parallel w_{n_k}-x_{n_k+1}\parallel \to 0,k\to \infty .$$

(46)

Since $\left\{x_n\right\}$ is bounded, $w_{\omega }\left(x_n\right)\ne \varnothing .$ We choose an element $x^{*}\in w_{\omega }\left(x_n\right)$ arbitrarily. Then, there exists a subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$ such that $x_{n_k}\rightharpoonup x^{*}.$ From (42), it follows that $w_{n_k}\rightharpoonup x^{*}.$ Now, by invoking Lemma 10 and applying (42), we obtain $x^{*}\in \mathsf{\Omega }.$ Since $x^{*}\in w_{\omega }\left(x_n\right)$ was selected arbitrarily, it follows that $w_{\omega }\left(x_n\right)\subset \mathsf{\Omega }.$

Next, by the boundedness of $\left\{x_{n_k}\right\},$ there exists a subsequence $\left\{x_{n_{k_j}}\right\}$ of $\left\{x_{n_k}\right\}$ such that $x_{n_{k_j}}\rightharpoonup q$ and

$$\begin{array}{c}\hfill {\displaystyle \underset{k\to \infty }{lim\; sup}}⟨\widehat{x},\widehat{x}-x_{n_k}⟩={\displaystyle \underset{j\to \infty }{lim}}⟨\widehat{x},\widehat{x}-x_{n_{k_j}}⟩.\end{array}$$

Since $\widehat{x}=P_{\mathsf{\Omega }}\left(0\right),$ it follows from the property of the metric projection map that

$$\begin{array}{c}\hfill {\displaystyle \underset{k\to \infty }{lim\; sup}}⟨\widehat{x},\widehat{x}-x_{n_k}⟩={\displaystyle \underset{j\to \infty }{lim}}⟨\widehat{x},\widehat{x}-x_{n_{k_j}}⟩=⟨\widehat{x},\widehat{x}-q⟩\le 0,\end{array}$$

(47)

Thus, from (45) and (47), we obtain

$$\begin{array}{c}\hfill {\displaystyle \underset{k\to \infty }{lim\; sup}}⟨\widehat{x},\widehat{x}-x_{n_{k+1}}⟩\le 0.\end{array}$$

(48)

Next, by Remark 2, (46) and (48) we have ${\displaystyle \underset{k\to \infty }{lim\; sup}}{\widehat{d}}_{n_k}\le 0.$ Therefore, by invoking Lemma 1, it follows from (40) that $\{\parallel x_n-\widehat{x}\parallel \}$ converges to zero as required. □

5. Applications

In this section, we apply our result to study related optimization problems.

5.1. Generalized Split Variational Inequality Problem

First, we apply our result to study and approximate the solution of the generalized split variational inequality problem (see [37]). Let $D_i$ be nonempty, closed and convex subsets of real Hilbert spaces $H_i,i=1,2,\dots ,N,$ and let $S_i:H_i\to H_{i+1},i=1,2,\dots ,N-1,$ be bounded linear operators, such that $S_i\ne 0.$ Let $B_i:H_i\to H_i,i=1,2,\dots ,N,$ be single-valued operators. The generalized split variational inequality problem (GSVIP) is formulated as finding a point $x^{*}\in D_1$ such that

$$x^{*}\in \mathsf{\Gamma }:=VI(D_1,B_1)\cap S_1^{-1}\left(VI(D_2,B_2)\right)\cap \dots S_1^{-1}(S_2^{-1}\dots \left(S_{N-1}^{-1}\left(VI(D_N,B_N)\right)\right))\ne \varnothing ;$$

(49)

that is, $x^{*}\in D_1$ such that

$$x^{*}\in VI(D_1,B_1),S_1{x}^{*}\in VI(D_2,B_2),\dots ,S_{N-1}(S_{N-2}\dots S_1{x}^{*})\in VI(D_N,B_N).$$

We note that by setting $C=D_1,C_i=D_{i+1},A=B_1,A_i=B_{i+1},1\le i\le N-1,T_1=S_1,T_2=S_2{S}_1,\dots ,$ and $T_{N-1}=S_{N-1}{S}_{N-2}\dots S_1,$ then the SVIPMOS (10) becomes the GSVIP (49). Consequently, we obtain the following strong convergence theorem for finding the solution of GSVIP (49) in Hilbert spaces when the cost operators are pseudomonotone and uniformly continuous.

Theorem 2.

Let $D_i$ be nonempty, closed and convex subsets of real Hilbert spaces $H_i,i=1,2,\dots ,N,$ and suppose $S_i:H_i\to H_{i+1},i=1,2,\dots ,N-1,$ are bounded linear operators with adjoints $S_i^{*}$ such that $S_i\ne 0.$ Let $B_i:H_i\to H_i,1,2,\dots ,N$ be uniformly continuous pseudomonotone operators that satisfy condition (12), and suppose Assumption B of Theorem 1 holds and the solution set $\mathsf{\Gamma }\ne \varnothing .$ Then, the sequence $\left\{x_n\right\}$ generated by the following Algorithm 2 converges in norm to $\widehat{x}\in \mathsf{\Gamma },$ where $\parallel \widehat{x}\parallel =min\{\parallel p\parallel :p\in \mathsf{\Gamma }\}.$

Algorithm 2. A Relaxed Inertial Tseng’s Extragradient Method for Solving GSVIP (49).

Step 0. Select initial points $x_0,x_1\in H_1.$ Let $S_0=I^{H_1},{\widehat{S}}_{i-1}=S_{1-1}{S}_{i-2}\dots S_0,{\widehat{S}}_{i-1}^{*}=S_0^{*}{S}_1^{*}\dots S_{i-1}^{*},i=1,2,\dots ,N$ and set $n=1.$ Step 1. Given the $(n-1)th$ and $nth$ iterates, choose ${\theta }_n$ such that $0\le {\theta }_n\le {\widehat{\theta }}_n$ with ${\widehat{\theta }}_n$ defined by $${\widehat{\theta }}_n=\left\{\begin{array}{c}min\left\{\theta ,\frac{{ϵ}_n}{\parallel x_n-x_{n-1}\parallel }\right\},\mathrm{if}{x}_n\ne x_{n-1},\hfill \\ \theta ,\mathrm{otherwise}.\hfill \end{array}\right.$$ Step 2. Compute $$w_n=(1-{\alpha }_n)(x_n+{\theta }_n(x_n-x_{n-1})).$$ Step 3. Compute $$y_{n,i}=P_{D_i}({\widehat{S}}_{i-1}{w}_n-{\lambda }_{n,i}{B}_i{\widehat{S}}_{i-1}{w}_n).$$ Step 4. Compute $$u_{n,i}=y_{n,i}-{\lambda }_{n,i}(B_i{y}_{n,i}-B_i{\widehat{S}}_{i-1}{w}_n),$$ $${\lambda }_{n+1,i}=\left\{\begin{array}{cc}min\{\frac{(c_{n,i}+c_i)\parallel {\widehat{S}}_{i-1}{w}_n-y_{n,i}\parallel }{\parallel B_i{\widehat{S}}_{i-1}{w}_n-B_i{y}_{n,i}\parallel },{\lambda }_{n,i}+{\rho }_{n,i}\},\hfill & \mathrm{if}{B}_i{\widehat{S}}_{i-1}{w}_n-B_i{y}_{n,i}\ne 0,\hfill \\ {\lambda }_{n,i}+{\rho }_{n,i},\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$ Step 5. Compute $$v_n={\displaystyle \sum _{i=1}^N}{\delta }_{n,i}\left(w_n+{\eta }_{n,i}{\widehat{S}}_{i-1}^{*}(u_{n,i}-{\widehat{S}}_{i-1}{w}_n)\right),$$ where $${\eta }_{n,i}=\left\{\begin{array}{cc}\frac{({\varphi }_{n,i}+{\varphi }_i){\parallel {\widehat{S}}_{i-1}{w}_n-u_{n,i}\parallel }^2}{\parallel {\widehat{S}}_{i-1}^{*}({\widehat{S}}_{i-1}{w}_n-u_{n,i}){\parallel }^2},\hfill & \mathrm{if}\parallel {\widehat{S}}_{i-1}^{*}({\widehat{S}}_{i-1}{w}_n-u_{n,i})\parallel \ne 0,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$ Step 6. Compute $$x_{n+1}={\xi }_n{w}_n+(1-{\xi }_n)v_n.$$

Set $n:=n+1$ and return to Step 1.

5.2. Split Convex Minimization Problem with Multiple Output Sets

Let C be a nonempty, closed and convex subset of a real Hilbert space $H.$ The convex minimization problem is defined as finding a point $x^{*}\in C$, such that

$$g\left(x^{*}\right)={\displaystyle \underset{x\in C}{min}}g\left(x\right),$$

(50)

where g is a real-valued convex function. The solution set of Problem (50) is denoted by $argming.$

Let $C,C_i$ be nonempty, closed and convex subsets of real Hilbert spaces $H,H_i,i=1,2,\dots ,N,$ respectively, and let $T_i:H\to H_i,i=1,2,\dots ,N,$ be bounded linear operators with adjoints $T_i^{*}.$ Let $g:H\to \mathbb{R},g_i:H_i\to \mathbb{R}$ be convex and differentiable functions. In this subsection, we apply our result to find the solution of the following split convex minimization problem with multiple output sets (SCMPMOS): Find $x^{*}\in C$ such that

$$x^{*}\in \mathsf{\Psi }:=argming\cap \left({\cap }_{i=1}^N{T}_i^{-1}\left(argmin{g}_i\right)\right)\ne \varnothing .$$

(51)

The following lemma is required to establish our next result.

Lemma 12

([53]).Suppose C is a nonempty, closed and convex subset of a real Banach space $E,$ and let g be a convex function of E into $\mathbb{R}.$ If g is Fréchet differentiable, then x is a solution of Problem (50) if and only if $x\in VI(C,▿g),$ where $▿g$ is the gradient of $g.$

Applying Theorem 1 and Lemma 12, we obtain the following strong convergence theorem for finding the solution of the SCMPMOS (51) in the framework of Hilbert spaces.

Theorem 3.

Let $C,C_i$ be nonempty, closed and convex subsets of real Hilbert spaces $H,H_i,i=1,2,\dots ,N,$ respectively, and suppose $T_i:H\to H_i,i=1,2,\dots ,N,$ are bounded linear operators with adjoints $T_i^{*}.$ Let $g:H\to \mathbb{R},g_i:H_i\to \mathbb{R}$ be fréchet differentiable convex functions such that $▿g,▿g_i$ are uniformly continuous. Suppose that Assumption B of Theorem 1 holds and the solution set $\mathsf{\Psi }\ne \varnothing .$ Then, the sequence $\left\{x_n\right\}$ generated by the following Algorithm 3 converges strongly to $\widehat{x}\in \mathsf{\Psi },$ where $\parallel \widehat{x}\parallel =min\{\parallel p\parallel :p\in \mathsf{\Psi }\}.$

Algorithm 3. A Relaxed Inertial Tseng’s Extragradient Method for Solving SCMPMOS (51).

Step 0. Select initial points $x_0,x_1\in H.$ Let $C_0=C,T_0=I^H,▿g_0=▿g$ and set $n=1.$ Step 1. Given the $(n-1)th$ and $nth$ iterates, choose ${\theta }_n$ such that $0\le {\theta }_n\le {\widehat{\theta }}_n$ with ${\widehat{\theta }}_n$ defined by $${\widehat{\theta }}_n=\left\{\begin{array}{c}min\left\{\theta ,\frac{{ϵ}_n}{\parallel x_n-x_{n-1}\parallel }\right\},\mathrm{if}{x}_n\ne x_{n-1},\hfill \\ \theta ,\mathrm{otherwise}.\hfill \end{array}\right.$$ Step 2. Compute $$w_n=(1-{\alpha }_n)(x_n+{\theta }_n(x_n-x_{n-1})).$$ Step 3. Compute $$y_{n,i}=P_{C_i}(T_i{w}_n-{\lambda }_{n,i}▿g_i{T}_i{w}_n).$$ Step 4. Compute $$u_{n,i}=y_{n,i}-{\lambda }_{n,i}(▿g_i{y}_{n,i}-▿g_i{T}_i{w}_n),$$ $${\lambda }_{n+1,i}=\left\{\begin{array}{cc}min\{\frac{(c_{n,i}+c_i)\parallel T_i{w}_n-y_{n,i}\parallel }{\parallel ▿g_i{T}_i{w}_n-▿g_i{y}_{n,i}\parallel },{\lambda }_{n,i}+{\rho }_{n,i}\},\hfill & \mathrm{if}▿g_i{T}_i{w}_n-▿g_i{y}_{n,i}\ne 0,\hfill \\ {\lambda }_{n,i}+{\rho }_{n,i},\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$ Step 5. Compute $$v_n={\displaystyle \sum _{i=0}^N}{\delta }_{n,i}\left(w_n+{\eta }_{n,i}{T}_i^{*}(u_{n,i}-T_i{w}_n)\right),$$ where $${\eta }_{n,i}=\left\{\begin{array}{cc}\frac{({\varphi }_{n,i}+{\varphi }_i){\parallel T_i{w}_n-u_{n,i}\parallel }^2}{\parallel T_i^{*}(T_i{w}_n-u_{n,i}){\parallel }^2},\hfill & \mathrm{if}\parallel T_i^{*}(T_i{w}_n-u_{n,i})\parallel \ne 0,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$ Step 6. Compute $$x_{n+1}={\xi }_n{w}_n+(1-{\xi }_n)v_n.$$

Set $n:=n+1$ and return to Step 1.

Proof. 

We know that since $g_i,i=0,1,2,\dots ,N$ are convex, then $▿g_i$ are monotone [53] and, hence, pseudomonotone. Therefore, the required result follows by applying Lemma 12 and taking $A_i=▿g_i$ in Theorem 1. □

6. Numerical Experiments

Here, we carry out some numerical experiments to demonstrate the applicability of our proposed method (Proposed Algorithm 1). For simplicity, in all the experiments, we consider the case when $N=5.$ All numerical computations were carried out using Matlab version R2021(b).

In all the computations, we choose ${\alpha }_n=\frac{1}{3n+2},{ϵ}_n=\frac{5}{{(3n+2)}^3},{\xi }_n=\frac{n+1}{2n+1},\theta =1.50,{\lambda }_{1,i}=i+1.25,c_i=0.10,{\varphi }_i=0.20,{\rho }_{n,i}=\frac{50}{n^2},{\delta }_{n,i}=\frac{1}{6}.$

Now, we consider the following numerical examples both in finite and infinite dimensional Hilbert spaces for the proposed algorithm.

Example 1.

For each $i=0,1,\dots ,5,$ we define the feasible set $C_i={\mathbb{R}}^m,$$T_{i}x=\frac{3x}{i+3}$ and $A_i\left(x\right)=Mx,$ where M is a square $m\times m$ matrix given by

$$a_{j,k}=\left\{\begin{array}{cc}-1,\hfill & ifk=m+1-jandk>j,\hfill \\ 1\hfill & ifk=m+1-jandk\le j,\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

We note that M is a Hankel-type matrix with a nonzero reverse diagonal.

Example 2.

Let $H_i={\mathbb{R}}^2$ and $C_i={[-2-i,2+i]}^2,i=0,1,\dots ,5.$ We define $T_{i}x=\frac{2x}{i+2}$, and the cost operator $A_i:{\mathbb{R}}^2\to {\mathbb{R}}^2$ is defined by

$$A_i(x,y)=(i+1)(-x{e}^y,y),(i=0,1,\dots ,5).$$

Finally, we consider the last example in infinite dimensional Hilbert spaces.

Example 3.

Let $H_i={\ell }_2:=\{x=(x_1,x_2,\dots ,x_i,\dots ):{\displaystyle {\displaystyle \sum _{j=1}^{\infty }}}|x_j{|}^2<+\infty \},i=0,1,\dots ,5.$ Let $r_i,R_i\in {\mathbb{R}}^{+}$ be such that $\frac{R_i}{k_i+1}<\frac{r_i}{k_i}<r_i<R_i$ for some $k_i>1.$ The feasible sets are defined as follows for each $i=0,1,\dots ,5:$

$$C_i=\{x\in H_i:\parallel x\parallel \le r_i\}.$$

The cost operators $A_i:H_i\to H_i$ are defined by

$$A_i\left(x\right)=(R_i-\parallel x\parallel )x.$$

Then $A_i$ are pseudomonotone and uniformly continuous. We choose $R_i=1.4+i,r_i=0.8+i,k_i=1.2+i,$ and we define $T_{i}x=\frac{4x}{i+4}.$

We test Examples 1–3 under the following experiments:

Experiment 1.

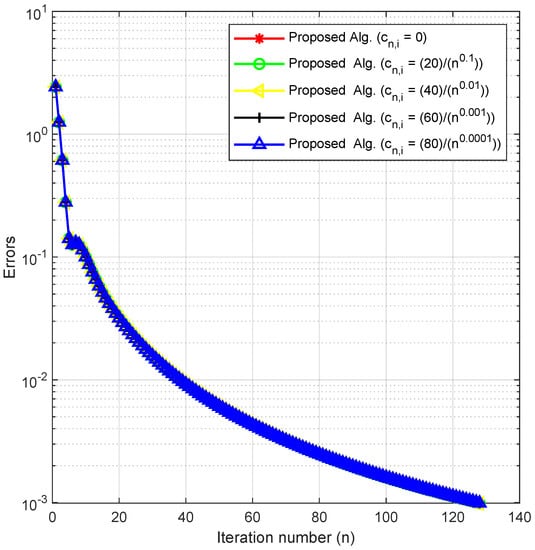
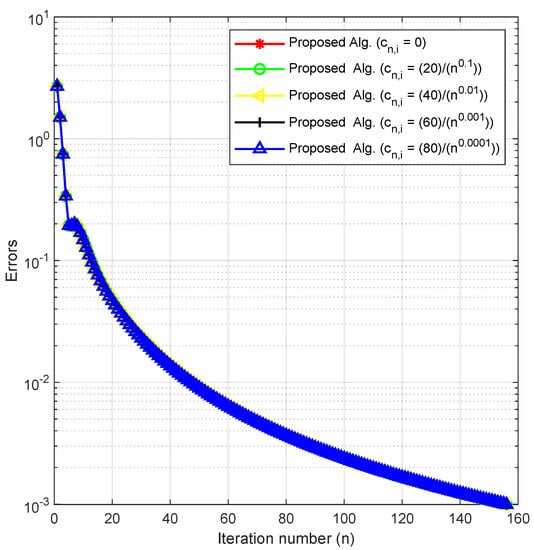
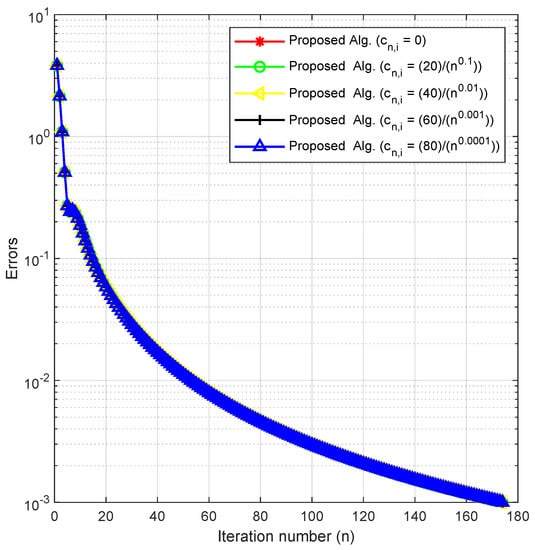
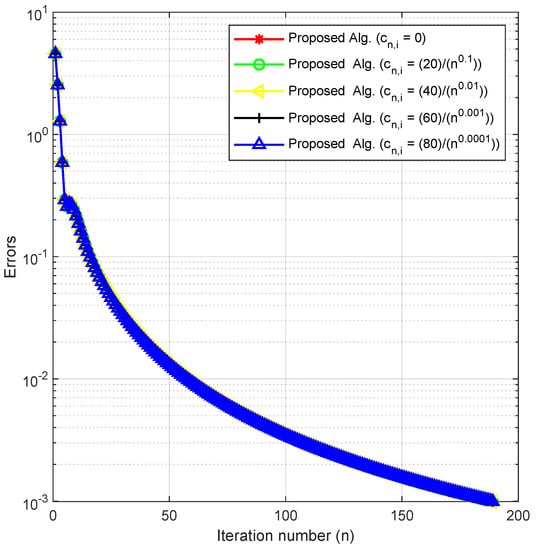
In this experiment, we check the behavior of our method by fixing the other parameters and varying $c_{n,i}$ in Example 1. We do this to check the effects of this parameter and the sensitivity of our method on it.

We consider $c_{n,i}\in \{0,\frac{20}{n^{0.1}},\frac{40}{n^{0.01}},\frac{60}{n^{0.001}},\frac{80}{n^{0.0001}}\}$ with $m=20,$$m=40,$$m=60$ and $m=80.$

Using $\parallel x_{n+1}-x_n\parallel <{10}^{-3}$ as the stopping criterion, we plot the graphs of $\parallel x_{n+1}-x_n\parallel$ against the number of iterations for each $m.$ The numerical results are reported in Figure 1, Figure 2, Figure 3 and Figure 4 and Table 1.

Figure 1. Experiment 1: $m=20$.

Figure 2. Experiment 1: $m=40$.

Figure 3. Experiment 1: $m=60$.

Figure 4. Experiment 1: $m=80$.

Table 1. Numerical results for Experiment 1.

	$m=20$		$m=40$		$m=60$		$m=80$
Proposed Algorithm 1	Iter.	CPU Time	Iter.	CPU Time	Iter.	CPU Time	Iter.	CPU Time
$c_{n,i}=0$	128	$0.0889$	156	$0.1235$	174	$0.2028$	189	$0.2412$
$c_{n,i}=\frac{20}{n^{0.1}}$	128	$0.0652$	156	$0.1241$	174	$0.2664$	189	$0.2930$
$c_{n,i}=\frac{40}{n^{0.01}}$	128	$0.0719$	156	$0.1495$	174	$0.3013$	189	$0.3220$
$c_{n,i}=\frac{60}{n^{0.001}}$	128	$0.0695$	156	$0.1549$	174	$0.2959$	189	$0.3342$
$c_{n,i}=\frac{80}{n^{0.0001}}$	128	$0.0701$	156	$0.1678$	174	$0.2877$	189	$0.3129$

Experiment 2.

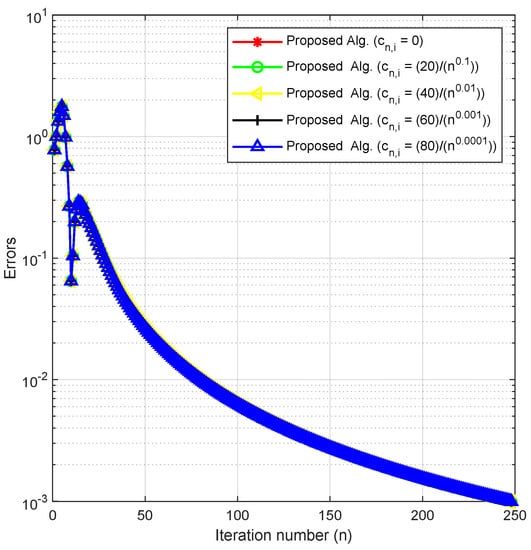
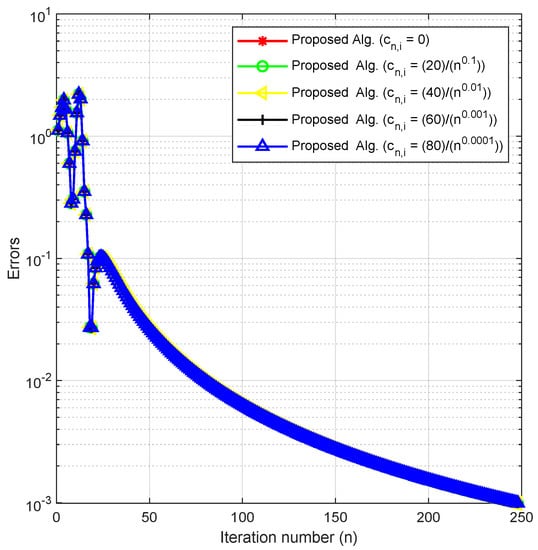
In this experiment, we check the behavior of our method by fixing the other parameters and varying $c_{n,i}$ in Example 2. We do this to check the effects of this parameter and the sensitivity of our method to it.

We consider $c_{n,i}\in \{0,\frac{20}{n^{0.1}},\frac{40}{n^{0.01}},\frac{60}{n^{0.001}},\frac{80}{n^{0.0001}}\}$ with the following two cases of initial values $x_0$ and $x_1:$

Case I:

$x_0=(2,1);$$x_1=(0,3);$

Case II:

$x_0=(3,2);$$x_1=(1,1).$

Using $\parallel x_{n+1}-x_n\parallel <{10}^{-3}$ as the stopping criterion, we plot the graphs of $\parallel x_{n+1}-x_n\parallel$ against the number of iterations in each case. The numerical results are reported in Figure 5 and Figure 6 and Table 2.

Figure 5. Experiment 2: Case 1.

Figure 6. Experiment 2: Case 2.

Table 2. Numerical results for Experiment 2.

	Case I		Case II
Proposed Algorithm 1	Iter.	CPU Time	Iter.	CPU Time
$c_{n,i}=0$	248	$0.0916$	248	$4.0980$
$c_{n,i}=\frac{20}{n^{0.1}}$	248	$0.0778$	248	$0.0816$
$c_{n,i}=\frac{40}{n^{0.01}}$	248	$0.0852$	248	$0.0818$
$c_{n,i}=\frac{60}{n^{0.001}}$	248	$0.0875$	248	$0.0753$
$c_{n,i}=\frac{80}{n^{0.0001}}$	248	$0.0817$	248	$0.0811$

Finally, we test Example 3 under the following experiment:

Experiment 3.

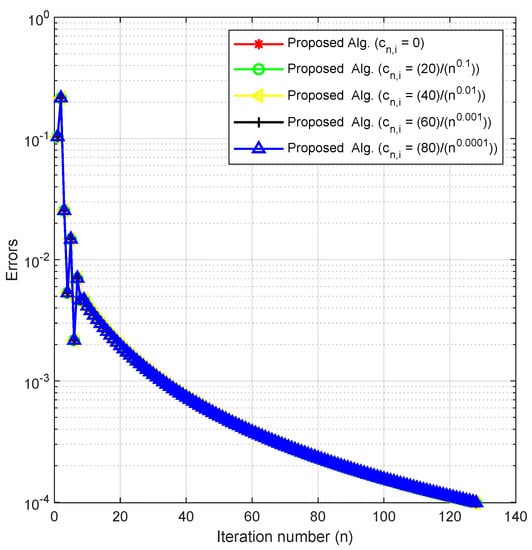
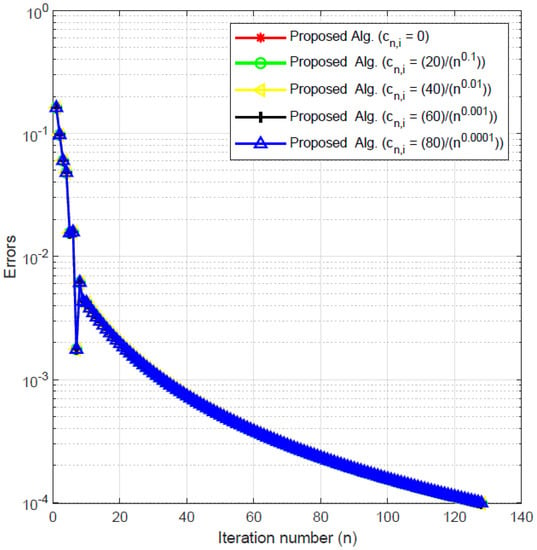
In this experiment, we check the behavior of our method by fixing the other parameters and varying $c_{n,i}$ in Example 3. We do this to check the effects of these parameters and the sensitivity of our method to it.

We consider $c_{n,i}\in \{0,\frac{20}{n^{0.1}},\frac{40}{n^{0.01}},\frac{60}{n^{0.001}},\frac{80}{n^{0.0001}}\}$ with the following two cases of initial values $x_0$ and $x_1:$

Case I:

$x_0=(\frac{1}{10},\frac{1}{100},\frac{1}{1000},\cdots );$$x_1=(\frac{1}{2},\frac{1}{4},\frac{1}{8},\cdots );$

Case II:

$x_0=(\frac{3}{10},\frac{3}{100},\frac{3}{100},\cdots );$$x_1=(\frac{1}{3},\frac{1}{9},\frac{1}{27},\cdots ).$

Using $\parallel x_{n+1}-x_n\parallel <{10}^{-4}$ as the stopping criterion, we plot the graphs of $\parallel x_{n+1}-x_n\parallel$ against the number of iterations in each case. The numerical results are reported in Figure 7 and Figure 8 and Table 3.

Figure 7. Experiment 3: Case 1.

Figure 8. Experiment 3: Case 2.

Table 3. Numerical results for Experiment 3.

	Case I		Case II
Proposed Algorithm 1	Iter.	CPU Time	Iter.	CPU Time
$c_{n,i}=0$	128	$0.0682$	128	$0.0620$
$c_{n,i}=\frac{20}{n^{0.1}}$	128	$0.0434$	128	$0.0422$
$c_{n,i}=\frac{40}{n^{0.01}}$	128	$0.0446$	128	$0.0474$
$c_{n,i}=\frac{60}{n^{0.001}}$	128	$0.0423$	128	$0.0414$
$c_{n,i}=\frac{80}{n^{0.0001}}$	128	$0.0416$	128	$0.0424$

Remark 5.

By using different initial values, cases of m and varying the key parameter in Experiments 1–3, we obtained the numerical results displayed in Table 1, Table 2 and Table 3 and Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. In Figure 1, Figure 2, Figure 3 and Figure 4, we considered different initial values and cases of m with varying values of the key parameter $c_{n,i}$ for Experiment 1 in ${\mathbb{R}}^m.$ As observed from the figures, these varying choices do not have a significant effect on the behavior of the algorithm. Similarly, Figure 5 and Figure 6 show that the behavior of our algorithm is consistent under varying initial starting points and different values of the key parameter $c_{n,i}$ for Experiment 2 in ${\mathbb{R}}^2.$ Likewise, Figure 7 and Figure 8 reveal that the behavior of the algorithm is not affected by varying starting points and values of $c_{n,i}$ for Experiment 3 in ${\ell }_2.$ From these results, we can conclude that our method is well-behaved since the choice of the key parameter and initial starting points do not affect the number of iterations or the CPU time in all the experiments.

7. Conclusions

In this article, we studied a new class of split inverse problems called the split variational inequality problem with multiple output sets. We introduced a relaxed inertial Tseng extragradient method with self-adaptive step sizes for finding the solution to the problem when the cost operators are pseudomonotone and non-Lipschitz in the framework of Hilbert spaces. Moreover, we proved a strong convergence theorem for the proposed method under some mild conditions. Finally, we applied our result to study and approximate the solutions of certain classes of optimization problems, and we presented several numerical experiments to demonstrate the applicability of our proposed algorithm. The results of this study open up several opportunities for future research. As part of our future research, we would like to extend the results in this paper to a more general space, such as the reflexive Banach space. Furthermore, we would consider extending the results to a larger class of operators, such as the classes of quasimonotone and non-monotone operators. Moreover, in our future research, we would be interested in investigating the stochastic variant of our results in this study.