On the Existence and Stability of Solutions for a Class of Fractional Riemann–Liouville Initial Value Problems

Abstract

This article deals with a class of nonlinear fractional differential equations, with initial conditions, involving the Riemann–Liouville fractional derivative of order $\alpha \in (1,2)$. The main objectives are to obtain conditions for the existence and uniqueness of solutions (within appropriate spaces), and to analyze the stabilities of Ulam–Hyers and Ulam–Hyers–Rassias types. In fact, different conditions for the existence and uniqueness of solutions are obtained based on the analysis of an associated class of fractional integral equations and distinct fixed-point arguments. Additionally, using a Bielecki-type metric and some additional contractive arguments, conditions are also obtained to guarantee Ulam–Hyers and Ulam–Hyers–Rassias stabilities for the problems under analysis. Examples are also included to illustrate the theory.

1. Introduction

Given the importance that fractional derivatives and integrals [1,2,3,4,5,6,7] have shown to have in the optimization and improvement of mathematical models of real events or even of those associated with other areas of knowledge (namely through making these models more accurate when compared to what they effectively model), we have recently witnessed a large development in the mathematical analysis of classes of fractional order differential and integral equations.

In this context, it is essential to know about the possible existence of several solutions to the problems in question, possible sufficient conditions to obtain a unique solution and even conditions that eventually guarantee distinct forms of stability of the solutions (this being a crucial aspect, in particular, for the study of approximate solutions to the problems in analysis). The most used techniques in these problems involve the consideration and identification of operators that (in a sense) represent the problem (in some “equivalent” way) and usually involve different principles of contraction, as well as different estimates, usually framed, or dependent, on norms (or metrics), within the spaces framework most suited to the problems under study.

For this type of problem, the analysis of their eventual stability is also a study of significant importance. Namely, through the Ulam–Hyers and Ulam–Hyers–Rassias stabilities [1,8,9,10,11,12,13,14,15,16,17] which, with their specific characteristics, make it possible to identify forms of a slight disturbance in the system (that defines the problem) does not have a too disturbing effect on that system.

Having this general framework in mind, we would like to start by emphasizing that in [18], Chai studied the existence of solutions to the boundary value problem

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}^C{\mathcal{D}}_{0+}^{\alpha }x\left(t\right)+r{}^C{\mathcal{D}}_{0+}^{\alpha -1}x\left(t\right)=f(t,x\left(t\right)),t\in (0,1),\\ x\left(0\right)=x\left(1\right),x\left(\xi \right)=\eta ,\xi \in (0,1),\end{array}\right.\end{array}$$

where ${}^C{\mathcal{D}}_{a+}^{\alpha }$ and ${}^C{\mathcal{D}}_{a+}^{\alpha -1}$ denote the standard Caputo derivatives of order $\alpha$ and $\alpha -1$, respectively, in this case with $1<\alpha \le 2$, and $r\ne 0$. Additionally, more recently, Xu et al. [19] considered the existence of solutions and the Ulam–Hyers stability for the fractional boundary value problem

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\lambda {\mathcal{D}}_{0+}^{\alpha }x\left(t\right)+{\mathcal{D}}_{0+}^{\beta }x\left(t\right)=f(t,x\left(t\right)),t\in (0,T),\\ x\left(0\right)=0,\mu {\mathcal{D}}_{0+}^{{\gamma }_1}x\left(T\right)+I_{0+}^{{\gamma }_2}x\left(\eta \right)={\gamma }_3,\end{array}\right.\end{array}$$

where ${\mathcal{D}}_{0+}^{\vartheta }$ denotes the Riemann–Liouville fractional derivative operator of order $\vartheta$, $1<\alpha \le 2$, $1\le \beta <\alpha$, $0<\lambda \le 1$, $0<\mu \le 1$, $0\le {\gamma }_1\le \alpha -\beta$, ${\gamma }_2\ge 0$, $I_{0+}^{{\gamma }_2}$ denotes the Riemann–Liouville fractional integral operator of order ${\gamma }_2$, and $0<\eta <T$. Moreover, in [20], Ahmad et al. investigated the existence of solutions and the Ulam–Hyers stability for a fractional initial value problem given by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}({}^C{\mathcal{D}}_{a+}^{\alpha }x\left(t\right)+{\lambda }_1{}^C{\mathcal{D}}_{a+}^{\alpha -1}x\left(t\right)+{\lambda }_2{}^C{\mathcal{D}}_{a+}^{\alpha -2}x\left(t\right)=f(t,x\left(t\right)),t\in [a,T],\\ x^{\left(k\right)}\left(a\right)=b_k,k=0,1,2,\end{array}\right.\end{array}$$

where ${}^C{\mathcal{D}}_{a+}^{\alpha }$ is again the Caputo fractional derivative of order $\alpha \in (2,3)$, and ${\lambda }_1$ and ${\lambda }_2$ are nonzero constants. In [21], Alvan et al. investigated the existence of solutions for the fractional boundary value problem

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}^C{\mathcal{D}}_{0+}^{\alpha }x\left(t\right)+2r{}^C{\mathcal{D}}_{0+}^{\alpha -1}x\left(t\right)+r^2{}^C{\mathcal{D}}_{0+}^{\alpha -2}x\left(t\right)=f(t,x\left(t\right),{\mathcal{D}}_{0+}^{\sigma -1}),r>0,t\in (0,1),\\ x\left(0\right)=x\left(1\right),x^{\prime }\left(0\right)=x^{\prime }\left(1\right),x^{\prime }\left(\xi \right)+rx\left(\xi \right)=\eta ,\xi \in (0,1),\end{array}\right.\end{array}$$

where $2\le \alpha <3$ and $\eta$ is a positive real number. Bilgici and Şan [22] considered the existence and uniqueness of solutions to the problem

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\lambda {\mathcal{D}}_{0+}^{\alpha }x\left(t\right)=f(t,x\left(t\right),{\mathcal{D}}_{0+}^{\alpha -1}x\left(t\right)),t>0,\\ x\left(0\right)=0,{\mathcal{D}}_{0+}^{\alpha -1}{x\left(t\right)|}_{t=0}=b,\end{array}\right.\end{array}$$

where $\alpha \in (1,2)$ and $b\ne 0$.

Motivated by the analysis and the results already achieved for the above-mentioned problems (included in the works [18,19,20,21,22]), we investigate in this paper the stabilities of Ulam–Hyers and Ulam–Hyers–Rassias types [1,8,9,10,11,14,16], and the existence and uniqueness of solutions to the following initial value problem of fractional order (IVPFO)

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{D}}_{a+}^{\alpha }x\left(t\right)+\lambda \left({\mathcal{D}}_{a+}^{\alpha -1}x\right)\left(t\right)=f(t,x\left(t\right)),t\in [a,b],\\ x\left(a\right)=x^{\prime }\left(a\right)=0,\end{array}\right.\end{array}$$

(1)

where $1<\alpha <2$, $\lambda$ is a nonzero constant, $a,b\in \mathbb{R}$ (with $a<b$) and $f:[a,b]\times \mathbb{R}\to \mathbb{R}$ is a continuous function. Thus, this problem can also be viewed as a class of problems depending on the parameter $\lambda$, and with the form of a single-point boundary problem “a” of a two-term fractional differential equation.

The remaining part of the work is organized as follows: Section 2 contains the necessary definitions and the fundamental tools that are used in the sections that follow; in Section 3, we derive different conditions for the existence and uniqueness of solutions for the IVPFO (1); in Section 4, we discuss the Ulam–Hyers and the Ulam–Hyers–Rassias stabilities and obtain conditions for their existence. Finally, some examples are included to describe the obtained results in a more concrete way.

2. Preliminaries and Background Material

We start this section by presenting the known basic definitions of the main objects that we will use.

Definition 1.

The Riemann–Liouville fractional integral of order $\alpha \in {\mathbb{R}}^{+}$ of a function x (on $[a,b]$) is defined by

$$I_{a+}^{\alpha }x\left(t\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_a^t{(t-s)}^{\alpha -1}x\left(s\right)\mathrm{d}s(a\le t\le b)$$

provided the right-hand side is pointwise defined and where $\Gamma$ denotes the Euler Gamma function (given by $\Gamma \left(\alpha \right)={\int }_0^{\infty }{t}^{\alpha -1}{e}^{-t}\mathrm{d}t,\alpha >0$).

Definition 2.

The Riemann–Liouville fractional derivative of order $\alpha >0$ of a function x (on $[a,b]$) is defined by

$${\mathcal{D}}_{a+}^{\alpha }x\left(t\right)=\frac{1}{\Gamma (n-\alpha )}\frac{d^n}{d{t}^n}{\int }_a^t{(t-s)}^{n-\alpha -1}x\left(s\right)ds,$$

with $n=\left[\alpha \right]+1$.

In what follows, we denote by $L^1\left([a,b]\right)$ the Banach space of Lebesgue integrable functions from $[a,b]$ into $\mathbb{R}$ with the norm ${\parallel x\parallel }_{L^1}={\int }_a^b\left|x\left(t\right)\right|\mathrm{d}t$ and by $C\left(\right[a,b\left]\right)$ the Banach space of all continuous functions $g:[a,b]\to \mathbb{R}$ endowed with the norm $\parallel g\parallel ={sup}_{t\in [a,b]}\left|g\left(t\right)\right|$.

Lemma 1

([3]). Assume that $x\in C\left([a,b]\right)\cap L^1\left([a,b]\right)$ with a fractional derivative of order $\alpha >0$. Then

$${\mathcal{D}}_{a+}^{\alpha }{I}_{a+}^{\alpha }x\left(t\right)=x\left(t\right)$$

and

$$I_{a+}^{\alpha }{\mathcal{D}}_{a+}^{\alpha }x\left(t\right)=x\left(t\right)+c_1{(t-a)}^{\alpha -1}+c_2{(t-a)}^{\alpha -2}+\cdots +c_n{(t-a)}^{\alpha -n},$$

for some $c_i\in \mathbb{R}$, $i=1,2,\dots ,n$, where n is the smallest integer greater than or equal to α.

For the reader’s convenience, let us recall some classic principles of contraction and inequalities that we will use later.

Theorem 1

(Banach contraction principle). Let $(X,d)$ be a generalized complete metric space, and consider a mapping $T:X\to X$ which is a strictly contractive operator, that is

$$d(Tx,Ty)\le Ld(x,y),\forall x,y\in X,$$

for some constant $0\le L<1$. Then:

(a) 

the mapping T has a unique fixed point $x^{*}=T{x}^{*}$;

(b) 

the fixed point $x^{*}$ is globally attractive, namely, for any starting point $x\in X$, the following identity holds:

$$\underset{n\to \infty }{lim}{T}^{n}x=x^{*};$$

(c) 

we have the following inequalities:

$$\begin{array}{ccc}\hfill d(T^{n}x,x^{*})& \le & L^{n}d(x,x^{*}),n\ge 0,x\in X;\hfill \\ \hfill d(T^{n}x,x^{*})& \le & \frac{1}{1-L}d(T^{n}x,T^{n+1}x),n\ge 0,x\in X;\hfill \\ \hfill d(x,x^{*})& \le & \frac{1}{1-L}d(x,Tx),x\in X.\hfill \end{array}$$

Theorem 2

(Schauder’s fixed point theorem). If$\Omega$ is a closed, bounded, convex subset of a Banach space X and the mapping $T:\Omega \to \Omega$ is completely continuous, then T has a fixed point in $\Omega$.

Keeping in mind some parts of the proofs of the next results, let us recall an important integral inequality that we will actually use later.

Theorem 3

([23], [Theorem 11.2]). Let $u\left(t\right),b\left(t\right),\sigma \left(t\right)$ and $k(t,s)$ be nonnegative continuous functions for $a\le s\le t\le b$ and suppose that

$$u\left(t\right)\le c_1+\sigma \left(t\right)\left(c_2+{\int }_a^{t}b\left(s\right)u\left(s\right)\mathrm{d}s+{\int }_a^t{\int }_a^{s}k(s,\tau )u\left(\tau \right)\mathrm{d}\tau \mathrm{d}s)\right),$$

for $t\in [a,b]$, where $c_1,c_2\ge 0$ are constants. Then,

$$u\left(t\right)\le c_2{e}^{{\int }_a^{t}B\left(s\right)\sigma \left(s\right)\mathrm{d}s}+{\int }_a^t{c}_{1}B\left(s\right)e^{{\int }_s^{t}B\left(\tau \right)\sigma \left(\tau \right)\mathrm{d}\tau }\mathrm{d}s,$$

where $B\left(s\right)=b\left(s\right)+{\int }_a^{s}k(s,\tau )\mathrm{d}\tau$.

We denote by $C^2\left([a,b]\right)$ the space of functions x which are 2-times continuously differentiable on $[a,b]$ endowed with the norm

$${\parallel x\parallel }_{C^2}=\sum _{k=0}^2\underset{t\in [a,b]}{sup}\left|x^{\left(k\right)}\left(t\right)\right|.$$

It is well-known that $(C^2\left([a,b]\right),\parallel ·{\parallel }_{C^2})$ is a Banach space.

In our next analysis of the existence and uniqueness of solutions for the IVPFO (1), we will make use of the following auxiliary property (which may be considered as a very natural and expectable property; cf., e.g., [24]).

Lemma 2

(See also [24]). Let $\alpha \in (1,2)$ and $x\in C^2\left([a,b]\right)$ with $x\left(a\right)=x^{\prime }\left(a\right)=0$. Then ${\mathcal{D}}_{a+}^{\alpha }x\in C\left([a,b]\right)$ and

$$\left({\mathcal{D}}_{a+}^{\alpha }x\right)\left(t\right)=\frac{1}{\Gamma (2-\alpha )}{\int }_a^t{(t-s)}^{1-\alpha }{x}^{″}\left(s\right)\mathrm{d}s.$$

Moreover,

$$\left({\mathcal{D}}_{a+}^{\alpha }x\right)\left(t\right)=\left({\mathcal{D}}_{a+}^{\alpha -1}{x}^{\prime }\right)\left(t\right).$$

(2)

Proof. 

For the reader’s convenience, we have chosen to include here a proof of this lemma. Within the stated conditions, we simply have to use integration by parts to obtain

$$\begin{array}{ccc}\hfill {\int }_a^t{(t-s)}^{1-\alpha }x\left(s\right)\mathrm{d}s& =& \frac{1}{2-\alpha }{\int }_a^t{(t-s)}^{2-\alpha }{x}^{\prime }\left(s\right)\mathrm{d}s,\hfill \\ \hfill {\int }_a^t{(t-s)}^{2-\alpha }{x}^{\prime }\left(s\right)\mathrm{d}s& =& \frac{1}{3-\alpha }{\int }_a^t{(t-s)}^{3-\alpha }{x}^{″}\left(s\right)\mathrm{d}s.\hfill \end{array}$$

And so, it follows

$$\begin{array}{ccc}\hfill \left({\mathcal{D}}_{a+}^{\alpha }x\right)\left(t\right)& =& \frac{1}{\Gamma (2-\alpha )}{\left(\frac{d}{dt}\right)}^2{\int }_a^t{(t-s)}^{1-\alpha }x\left(s\right)\mathrm{d}s\hfill \\ & =& \frac{1}{\Gamma (3-\alpha )}{\left(\frac{d}{dt}\right)}^2{\int }_a^t{(t-s)}^{2-\alpha }{x}^{\prime }\left(s\right)\mathrm{d}s\hfill \\ & =& \frac{1}{\Gamma (4-\alpha )}{\left(\frac{d}{dt}\right)}^2{\int }_a^t{(t-s)}^{3-\alpha }{x}^{″}\left(s\right)\mathrm{d}s\hfill \\ & =& \frac{1}{\Gamma (2-\alpha )}{\int }_a^t{(t-s)}^{1-\alpha }{x}^{″}\left(s\right)\mathrm{d}s.\hfill \end{array}$$

Since under the present conditions ${\int }_a^t{(t-s)}^{1-\alpha }{x}^{″}\left(s\right)\mathrm{d}s$ is continuous on $[a,b]$, we conclude that ${\mathcal{D}}_{a+}^{\alpha }x$ is continuous on $[a,b]$.

Moreover,

$$\begin{array}{ccc}\hfill \left({\mathcal{D}}_{a+}^{\alpha }x\right)\left(t\right)& =& \frac{1}{\Gamma (2-\alpha )}{\left(\frac{d}{dt}\right)}^2{\int }_a^t{(t-s)}^{1-\alpha }x\left(s\right)\mathrm{d}s\hfill \\ & =& \frac{1-\alpha }{\Gamma (2-\alpha )}\frac{d}{dt}{\int }_a^t{(t-s)}^{-\alpha }x\left(s\right)\mathrm{d}s.\hfill \end{array}$$

Integrating by parts, and using the circumstance that $x\left(a\right)=0$, we obtain

$$\left({\mathcal{D}}_{a+}^{\alpha }x\right)\left(t\right)=\frac{1}{\Gamma (2-\alpha )}\frac{d}{dt}{\int }_a^t{(t-s)}^{1-\alpha }{x}^{\prime }\left(s\right)\mathrm{d}s=\left({\mathcal{D}}_{a+}^{\alpha -1}{x}^{\prime }\right)\left(t\right),$$

which concludes the proof. □

Remark 1.

Proceeding in a similar way as in the previous lemma, for $\alpha \in (1,2)$, $x\in C^2\left([a,b]\right)$ and $x\left(a\right)=x^{\prime }\left(a\right)=0$, it follows that ${\mathcal{D}}_{a+}^{\alpha -1}x\in C\left([a,b]\right)$ and

$$\left({\mathcal{D}}_{a+}^{\alpha -1}x\right)\left(t\right)=\frac{1}{\Gamma (3-\alpha )}{\int }_a^t{(t-s)}^{2-\alpha }{x}^{″}\left(s\right)\mathrm{d}s.$$

3. Different Conditions for the Existence and Uniqueness of Solutions

In the present section, we will analyse conditions to ensure the existence of solutions to the IVPFO (1) and also conditions to guarantee the uniqueness of the solution. In view of this, let us first start to “translate” the IVPFO (1) through a fractional integral equation.

Proposition 1.

As before, let $\alpha \in (1,2)$, $f:[a,b]\times \mathbb{R}\to \mathbb{R}$ be a continuous function and $\lambda \ne 0$. A function $x\in C^2\left([a,b]\right)$ is a solution of the IVPFO (1) if and only if x satisfies the integral equation

$$x\left(t\right)=\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}f(s,x\left(s\right))\mathrm{d}s\mathrm{d}u.$$

(3)

Proof. 

Let $x\in C^2\left([a,b]\right)$ be the solution of IVPFO (1). By Lemma 2, we have that ${\mathcal{D}}_{a+}^{\alpha }x,{\mathcal{D}}_{a+}^{\alpha -1}x\in C\left([a,b]\right)$ and ${\mathcal{D}}_{a+}^{\alpha }x={\mathcal{D}}_{a+}^{\alpha -1}{x}^{\prime }$. Thus, we can rewrite our main equation in (1),

$$\left({\mathcal{D}}_{a+}^{\alpha }x\right)\left(t\right)+\lambda \left({\mathcal{D}}_{a+}^{\alpha -1}x\right)\left(t\right)=f(t,x\left(t\right)),$$

in the form

$$\left({\mathcal{D}}_{a+}^{\alpha -1}{x}^{\prime }\right)\left(t\right)+\lambda \left({\mathcal{D}}_{a+}^{\alpha -1}x\right)\left(t\right)=f(t,x\left(t\right)).$$

(4)

In view of Lemma 1, one has

$$\begin{array}{ccc}\hfill \left(I_{a+}^{\alpha -1}{\mathcal{D}}_{a+}^{\alpha -1}x\right)\left(t\right)& =& x\left(t\right)+c_1{(t-a)}^{\alpha -2},\hfill \\ \hfill \left(I_{a+}^{\alpha -1}{\mathcal{D}}_{a+}^{\alpha -1}{x}^{\prime }\right)\left(t\right)& =& x^{\prime }\left(t\right)+d_1{(t-a)}^{\alpha -2},t\in [a,b].\hfill \end{array}$$

Thus, applying $I_{a+}^{\alpha -1}$ to both members of Equation (4), we obtain

$$x^{\prime }\left(t\right)+\lambda x\left(t\right)+(\lambda c_1+d_1){(t-a)}^{\alpha -2}=\left[I_{a+}^{\alpha -1}f(·,x(·))\right]\left(t\right).$$

(5)

Since $x\left(a\right)=x^{\prime }\left(a\right)=0$, we conclude that

$$\lambda c_1+d_1=0,$$

and so it follows

$$x^{\prime }\left(t\right)+\lambda x\left(t\right)=\left[I_{a+}^{\alpha -1}f(·,x(·))\right]\left(t\right).$$

(6)

Let $y\left(t\right)=e^{\lambda t}x\left(t\right)$. One has that

$$x^{\prime }\left(t\right)=-\lambda e^{-\lambda t}y\left(t\right)+e^{-\lambda t}{y}^{\prime }\left(t\right).$$

Substituting the last two identities in (6), we obtain

$$y^{\prime }\left(t\right)=e^{\lambda t}\left[I_{a+}^{\alpha -1}f(·,e^{-\lambda ·}y(·))\right]\left(t\right).$$

(7)

Since $x\in C^2\left([a,b]\right)$, we have that $y^{\prime }\in C^1\left([a,b]\right)$. Moreover, $I_{a+}^{\alpha -1}f$ is a continuously differentiable function. Thus, integrating Equation (7) from a to t, we obtain

$$y\left(t\right)=y\left(a\right)+\frac{1}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}f(s,e^{-\lambda s}y\left(s\right))\mathrm{d}s\mathrm{d}u.$$

Taking into account that $y\left(t\right)=e^{\lambda t}x\left(t\right)$, it follows that

$$x\left(t\right)=e^{-\lambda (t-a)}x\left(a\right)+\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}f(s,x\left(s\right))\mathrm{d}s\mathrm{d}u,$$

and using the initial conditions, we conclude that

$$x\left(t\right)=\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}f(s,x\left(s\right))\mathrm{d}s\mathrm{d}u.$$

Conversely, assume that x is given by (3), and thus

$$e^{\lambda t}x\left(t\right)=\frac{1}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}f(s,x\left(s\right))\mathrm{d}s\mathrm{d}u.$$

(8)

It is clear that $x\left(a\right)=0$ and since x is continuously differentiable on $[a,b]$, differentiating both sides of (8), we get

$$\begin{array}{ccc}\hfill e^{\lambda t}{x}^{\prime }\left(t\right)+\lambda e^{\lambda t}x\left(t\right)& =& \frac{e^{\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{(t-s)}^{\alpha -2}f(s,x\left(s\right))\mathrm{d}s,\hfill \end{array}$$

which is equivalent to

$$x^{\prime }\left(t\right)+\lambda x\left(t\right)=\frac{1}{\Gamma (\alpha -1)}{\int }_a^t{(t-s)}^{\alpha -2}f(s,x\left(s\right))\mathrm{d}s.$$

(9)

Thus $x^{\prime }\left(a\right)=0$ and since $x\in C^2\left([a,b]\right)$, accordingly to Lemma 2, we have that ${\mathcal{D}}_{a+}^{\alpha }x$ and ${\mathcal{D}}_{a+}^{\alpha -1}x$ exist. Applying ${\mathcal{D}}_{a+}^{\alpha -1}$ to both sides of Equation (9), using Lemma 1 and (2), we also obtain

$$\left({\mathcal{D}}_{a+}^{\alpha }x\right)\left(t\right)+\lambda \left({\mathcal{D}}_{a+}^{\alpha -1}x\right)\left(t\right)=f(t,x\left(t\right)),$$

which completes the proof. □

Having in mind Proposition 1, we realize that studying the solutions of IVPFO (1) is the same as studying the solutions of

$$x=Tx,$$

where T is the fractional integral operator given by

$$\left(Tx\right)\left(t\right)=\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}f(s,x\left(s\right))\mathrm{d}s\mathrm{d}u,$$

(10)

for $x\in C^2\left([a,b]\right)$ and $\lambda \in \mathbb{R}\setminus \left\{0\right\}$.

Remark 2.

Another way to discover an integral form of $x\left(t\right)$ is to consider the integral equation

$$x\left(t\right)=-\lambda {\int }_a^{t}x\left(s\right)\mathrm{d}s+\frac{1}{\Gamma \left(\alpha \right)}{\int }_a^t{(t-s)}^{\alpha -1}f(s,x\left(s\right))\mathrm{d}s.$$

(11)

In fact, applying $I_{a+}^{\alpha }$ to both members of equation $\left({\mathcal{D}}_{a+}^{\alpha }x\right)\left(t\right)+\lambda \left({\mathcal{D}}_{a+}^{\alpha -1}x\right)\left(t\right)=f(t,x\left(t\right))$, and using Lemma 1, we obtain

$$\begin{array}{c}\hfill x\left(t\right)+a_1{(t-a)}^{\alpha -1}+a_2{(t-a)}^{\alpha -2}+\lambda {\int }_a^t\left(x\left(s\right)+b_1{(s-a)}^{\alpha -2}\right)\mathrm{d}s=\left[I_{a+}^{\alpha }f(·,x(·))\right]\left(t\right)\end{array}$$

($a_1,a_2,b_1\in \mathbb{R}$), which is equivalent to

$$\begin{array}{c}\hfill x\left(t\right)=-\left(a_1+\lambda \frac{b_1}{\alpha -1}\right){(t-a)}^{\alpha -1}-a_2{(t-a)}^{\alpha -2}-\lambda {\int }_a^{t}x\left(s\right)\mathrm{d}s+\left[I_{a+}^{\alpha }f(·,x(·))\right]\left(t\right).\end{array}$$

Since $x\left(a\right)=0$, it follows that $a_2=0$. Observing that

$$x^{\prime }\left(t\right)=-\left((\alpha -1)a_1+\lambda b_1\right){(t-a)}^{\alpha -2}-\lambda x\left(t\right)+\left[I_{a+}^{\alpha -1}f(·,x(·))\right]\left(t\right),$$

and using the initial condition $x^{\prime }\left(a\right)=0$, we also conclude that $a_1+\lambda \frac{b_1}{\alpha -1}=0$, and thus, Equation (11) is obtained.

Let us fix the following notation

$$\begin{array}{ccc}\hfill k_{-}& =& \frac{{(b-a)}^{\alpha -1}}{\lambda \Gamma \left(\alpha \right)}\left[1-(1-\lambda +{\lambda }^2)e^{-\lambda (b-a)}\right],\hfill \\ \hfill k_{+}& =& \frac{{(b-a)}^{\alpha -1}}{\lambda \Gamma \left(\alpha \right)}\left[1+2\lambda +2{\lambda }^2-(1+\lambda +{\lambda }^2)e^{-\lambda (b-a)}\right],\hfill \end{array}$$

and

$$\begin{array}{c}\hfill K=K\left(\lambda \right):=\left\{\begin{array}{c}{k}_{-},\lambda <0\\ k_{+},\lambda >0\end{array}\right..\end{array}$$

(12)

Theorem 4.

If $f:[a,b]\times \mathbb{R}\to \mathbb{R}$ is continuously differentiable, then the IVPFO (1) has at least one solution in $C^2\left([a,b]\right)$.

Proof. 

We will use the Schauder fixed point theorem for the fractional integral operator T, defined in (10). The continuity of $Tx$ follows from the continuity of f. Moreover, we have that

$$\begin{array}{ccc}\hfill {\left(Tx\right)}^{\prime }\left(t\right)& =& \frac{-\lambda e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{e}^{\lambda u}{(u-s)}^{\alpha -2}f(s,x\left(s\right))\mathrm{d}s\mathrm{d}u\hfill \\ & & +\frac{1}{\Gamma (\alpha -1)}{\int }_a^t{(t-s)}^{\alpha -2}f(s,x\left(s\right))\mathrm{d}s\hfill \\ & =& \frac{-\lambda e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{e}^{\lambda u}{(u-s)}^{\alpha -2}f(s,x\left(s\right))\mathrm{d}s\mathrm{d}u\hfill \\ & +& \frac{1}{\Gamma \left(\alpha \right)}\left({(t-a)}^{\alpha -1}f(a,0)+{\int }_a^t{(t-s)}^{\alpha -1}{f}^{\prime }(s,x\left(s\right))\mathrm{d}s\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\left(Tx\right)}^{″}\left(t\right)& =& \frac{{\lambda }^2{e}^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{e}^{\lambda u}{(u-s)}^{\alpha -2}f(s,x\left(s\right))\mathrm{d}s\mathrm{d}u\hfill \\ & & -\frac{\lambda }{\Gamma (\alpha -1)}{\int }_a^t{(t-s)}^{\alpha -2}f(s,x\left(s\right))\mathrm{d}s\hfill \\ & & +\frac{1}{\Gamma (\alpha -1)}\left({(t-a)}^{\alpha -2}f(a,0)+{\int }_a^t{(t-s)}^{\alpha -2}{f}^{\prime }(s,x\left(s\right))\mathrm{d}s\right).\hfill \end{array}$$

Since f is continuously differentiable, there exist positive constants A and B such that $\left|f\right(t,x\left(t\right)|\le A$ and $|f^{\prime }(t,x\left(t\right))|\le B$, $t\in [a,b]$. Define $\Omega =\{x\in C^2\left([a,b]\right):\parallel x{\parallel }_{C^2}\le R\}$ with R being a positive real number satisfying

$$R\ge KA+\frac{{(b-a)}^{\alpha -2}}{\Gamma (\alpha -1)}f(a,0)+\frac{{(b-a)}^{\alpha -1}}{\Gamma \left(\alpha \right)}B.$$

It is clear that $\Omega$ is a closed, bounded and convex subset of $C^2\left([a,b]\right)$. Moreover, we have that

$$\begin{array}{ccc}\hfill \left|\right(Tx\left)\right(t\left)\right|& =& \left|\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}f(s,x\left(s\right))\mathrm{d}s\mathrm{d}u\right|\hfill \\ & \le & \frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{e}^{\lambda u}{\int }_a^u{(u-s)}^{\alpha -2}\left|f(s,x\left(s\right))\right|\mathrm{d}s\mathrm{d}u\hfill \\ & \le & \frac{e^{-\lambda t}A}{\Gamma (\alpha -1)}{\int }_a^t{e}^{\lambda u}{\int }_a^u{(u-s)}^{\alpha -2}\mathrm{d}s\mathrm{d}u\hfill \\ & \le & \frac{e^{-\lambda t}}{\Gamma \left(\alpha \right)}A{(b-a)}^{\alpha -1}{\int }_a^t{e}^{\lambda u}\mathrm{d}u\hfill \\ & =& \frac{{(b-a)}^{\alpha -1}}{\lambda \Gamma \left(\alpha \right)}(1-e^{-\lambda (t-a)})A,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {|\left(Tx\right)}^{\prime }\left(t\right)|& \le & \left|\frac{-\lambda e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}f(s,x\left(s\right))\mathrm{d}s\mathrm{d}u\right|\hfill \\ & & +\left|\frac{1}{\Gamma (\alpha -1)}{\int }_a^t{(t-s)}^{\alpha -2}f(s,x\left(s\right))\mathrm{d}s\right|\hfill \\ & \le & \frac{{(b-a)}^{\alpha -1}}{\lambda \Gamma \left(\alpha \right)}\left(\left|\lambda \right|(1-e^{-\lambda (t-a)})+\lambda \right)A,\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {|\left(Tx\right)}^{″}\left(t\right)|& \le & \left|\frac{{\lambda }^2{e}^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{e}^{\lambda u}{(u-s)}^{\alpha -2}f(s,x\left(s\right))\mathrm{d}s\mathrm{d}u\right|\hfill \\ & & +\left|\frac{\lambda }{\Gamma (\alpha -1)}{\int }_a^t{(t-s)}^{\alpha -2}f(s,x\left(s\right))\mathrm{d}s\right|\hfill \\ & & +\left|\frac{1}{\Gamma (\alpha -1)}\left({(t-a)}^{\alpha -2}f(a,0)+{\int }_a^t{(t-s)}^{\alpha -2}{f}^{\prime }(s,x\left(s\right))\mathrm{d}s\right)\right|\hfill \\ & \le & \frac{{(b-a)}^{\alpha -1}}{\lambda \Gamma \left(\alpha \right)}\left({\lambda }^2(1-e^{-\lambda (t-a)})\lambda \left|\lambda \right|\right)A+\frac{{(b-a)}^{\alpha -2}}{\Gamma (\alpha -1)}f(a,0)+\frac{{(b-a)}^{\alpha -1}}{\Gamma \left(\alpha \right)}B.\hfill \end{array}$$

Thus, we have that

$$\begin{array}{ccc}\hfill {\parallel Tx\parallel }_{C^2}& \le & \underset{t\in [a,b]}{sup}\left\{\frac{{(b-a)}^{\alpha -1}}{\lambda \Gamma \left(\alpha \right)}(1-e^{-\lambda (t-a)})A\right\}\hfill \\ & & +\underset{t\in [a,b]}{sup}\left\{\frac{{(b-a)}^{\alpha -1}}{\lambda \Gamma \left(\alpha \right)}\left(\left|\lambda \right|(1-e^{-\lambda (t-a)})+\lambda \right)A\right\}\hfill \\ & & +\underset{t\in [a,b]}{sup}\left\{\frac{{(b-a)}^{\alpha -1}}{\lambda \Gamma \left(\alpha \right)}\left({\lambda }^2(1-e^{-\lambda (t-a)})+\lambda \left|\lambda \right|\right)A\right.\hfill \\ & & \left.+\frac{{(b-a)}^{\alpha -2}f(a,0)}{\Gamma (\alpha -1)}+\frac{{(b-a)}^{\alpha -1}}{\Gamma \left(\alpha \right)}B\right\}.\hfill \end{array}$$

Thus, if $\lambda <0$, we have that

$$\begin{array}{ccc}\hfill {\parallel Tx\parallel }_{C^2}& \le & \frac{{(b-a)}^{\alpha -1}}{\lambda \Gamma \left(\alpha \right)}\left[1-\lambda +{\lambda }^2-(1-\lambda +{\lambda }^2)e^{-\lambda (b-a)}+\lambda -{\lambda }^2\right]A\hfill \\ & & +\frac{{(b-a)}^{\alpha -2}}{\Gamma (\alpha -1)}f(a,0)+\frac{{(b-a)}^{\alpha -1}}{\Gamma \left(\alpha \right)}B\hfill \\ & =& k_{-}A+\frac{{(b-a)}^{\alpha -2}}{\Gamma (\alpha -1)}f(a,0)+\frac{{(b-a)}^{\alpha -1}}{\Gamma \left(\alpha \right)}B\le R,\hfill \end{array}$$

and if $\lambda >0$, we have

$$\begin{array}{ccc}\hfill {\parallel Tx\parallel }_{C^2}& \le & \frac{{(b-a)}^{\alpha -1}}{\lambda \Gamma \left(\alpha \right)}\left[1+\lambda +{\lambda }^2-(1+\lambda +{\lambda }^2)e^{-\lambda (b-a)}+\lambda +{\lambda }^2\right]A\hfill \\ & & +\frac{{(b-a)}^{\alpha -2}}{\Gamma (\alpha -1)}f(a,0)+\frac{{(b-a)}^{\alpha -1}}{\Gamma \left(\alpha \right)}B\hfill \\ & =& k_{+}A+\frac{{(b-a)}^{\alpha -2}}{\Gamma (\alpha -1)}f(a,0)+\frac{{(b-a)}^{\alpha -1}}{\Gamma \left(\alpha \right)}B\le R.\hfill \end{array}$$

Consequently, we conclude that T is a bounded operator on $\Omega \subset C^2\left([a,b]\right)$.

Let us prove that operator $T:\Omega \to \Omega$ is completely continuous. For $t_1,t_2\in [a,b]$, $t_1<t_2$, one has

$$\begin{array}{ccc}\hfill |\left(Tx\right)\left(t_2\right)-\left(Tx\right)\left(t_1\right)|& =& \left|\frac{e^{-\lambda t_2}}{\Gamma (\alpha -1)}{\int }_a^{t_2}{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}f(s,x\left(s\right))\mathrm{d}s\mathrm{d}u\right.\hfill \\ & & \left.-\frac{e^{-\lambda t_1}}{\Gamma (\alpha -1)}{\int }_a^{t_1}{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}f(s,x\left(s\right))\mathrm{d}s\mathrm{d}u\right|\hfill \\ & \le & \frac{e^{-\lambda t_2}}{\Gamma (\alpha -1)}{\int }_{t_1}^{t_2}{\int }_a^u\left|{(u-s)}^{\alpha -2}{e}^{\lambda u}f(s,x\left(s\right))\right|\mathrm{d}s\mathrm{d}u\hfill \\ & & +\frac{|e^{-\lambda t_2}-e^{-\lambda t_1}|}{\Gamma (\alpha -1)}{\int }_a^{t_1}{\int }_a^u\left|{(u-s)}^{\alpha -2}{e}^{\lambda u}f(s,x\left(s\right))\right|\mathrm{d}s\mathrm{d}u,\hfill \end{array}$$

which tends to zero as $t_2\to t_1$ (independently of x and $\lambda$). In the same way, we get

$$\begin{array}{ccc}& & {|\left(Tx\right)}^{\prime }\left(t_2\right)-{\left(Tx\right)}^{\prime }\left(t_1\right)|\hfill \\ & =& \left|\lambda \right||\left(Tx\right)\left(t_2\right)-\left(Tx\right)\left(t_1\right)|+\frac{1}{\Gamma (\alpha -1)}{\int }_{t_1}^{t_2}{(t_2-s)}^{\alpha -2}\left|f(s,x\left(s\right))\right|\mathrm{d}s+\hfill \\ & & +\frac{1}{\Gamma (\alpha -1)}{\int }_a^{t_1}[{(t_2-s)}^{\alpha -2}-{(t_1-s)}^{\alpha -2}]\left|f(s,x\left(s\right))\right|\mathrm{d}s,\hfill \end{array}$$

which tends to zero as $t_2\to t_1$. Finally, we observe that

$$\begin{array}{ccc}& & {|\left(Tx\right)}^{″}\left(t_2\right)-{\left(Tx\right)}^{″}\left(t_1\right)|\hfill \\ & =& {\left|\lambda \right||\left(Tx\right)}^{\prime }\left(t_2\right)-{\left(Tx\right)}^{\prime }\left(t_1\right)|+\frac{1}{\Gamma (\alpha -1)}{\int }_{t_1}^{t_2}{(t_2-s)}^{\alpha -2}\left|f^{\prime }(s,x\left(s\right))\right|\mathrm{d}s+\hfill \\ & & +\frac{1}{\Gamma (\alpha -1)}{\int }_a^{t_1}[{(t_2-s)}^{\alpha -2}-{(t_1-s)}^{\alpha -2}]\left|f^{\prime }(s,x\left(s\right))\right|\mathrm{d}s\hfill \\ & & +\frac{{(t_2-a)}^{\alpha -2}-{(t_1-a)}^{\alpha -2}}{\Gamma (\alpha -1)}f(a,0)\hfill \end{array}$$

tends to zero as $t_2\to t_1$. Thus, we conclude that $T\Omega$ is equicontinuous. Following Arzelà-Ascoli Theorem, we obtain that T is completely continuous. Applying Schauder’s fixed point theorem (cf. Theorem 2), we conclude that the operator T has at least one fixed point, which means that the IVPFO (1) has at least one solution and the proof is completed. □

We will now exhibit other conditions under which, besides the existence of solutions, we will also guarantee the uniqueness of the solution to the IVPFO (1).

Theorem 5.

Let $f:[a,b]\times \mathbb{R}\to \mathbb{R}$ be a continuously differentiable function and suppose that there are $L_1$ and $L_2\ge 0$ such that, for $t\in [a,b]$,

$$\begin{array}{ccc}\hfill \left|f\right(t,x\left(t\right))-f(t,y\left(t\right)\left)\right|& \le & L_1|x\left(t\right)-y\left(t\right)|,\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill |f^{\prime }(t,x\left(t\right))-f^{\prime }(t,y\left(t\right))|& \le & L_2\left(|x\left(t\right)-y\left(t\right)|+|x^{\prime }\left(t\right)-y^{\prime }\left(t\right)|\right).\hfill \end{array}$$

(14)

If

$$K{L}_1+L_2\frac{{(b-a)}^{\alpha -1}}{\Gamma \left(\alpha \right)}<1,$$

then the problem (1) has a unique solution on $C^2\left([a,b]\right)$.

Proof. 

Since f is a continuously differentiable function, according to Theorem 4, the IVPFO (1) admits at least one solution. Let us assume that conditions (13)–(14) hold. Thus, we can obtain that, for $x,y\in C^2\left([a,b]\right)$,

$$\begin{array}{ccc}\hfill \left|\right(Tx\left)\right(t)-(Ty\left)\right(t\left)\right|& \le & \frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{e}^{\lambda u}{\int }_a^u{(u-s)}^{\alpha -2}|f(s,x\left(s\right))-f(s,y\left(s\right))|\mathrm{d}s\mathrm{d}u\hfill \\ & \le & \frac{L_1{e}^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{e}^{\lambda u}{\int }_a^u{(u-s)}^{\alpha -2}|x\left(s\right)-y\left(s\right)|\mathrm{d}s\mathrm{d}u\hfill \\ & \le & L_1{\parallel x-y\parallel }_{C^2}\frac{{(b-a)}^{\alpha -1}(1-e^{-\lambda (t-a)})}{\lambda \Gamma \left(\alpha \right)},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {|\left(Tx\right)}^{\prime }\left(t\right)-{\left(Ty\right)}^{\prime }\left(t\right)|& \le & \frac{1}{\Gamma (\alpha -1)}{\int }_a^t{(t-s)}^{\alpha -2}|f(s,x\left(s\right))-f(s,y\left(s\right))|\mathrm{d}s\hfill \\ & & +\frac{\left|\lambda \right|e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{e}^{\lambda u}{\int }_a^u{(u-s)}^{\alpha -2}|f(s,x\left(s\right))-f(s,y\left(s\right))|\mathrm{d}s\mathrm{d}u\hfill \\ & \le & \frac{L_1}{\Gamma (\alpha -1)}{\int }_a^t{(t-s)}^{\alpha -2}|x\left(s\right)-y\left(s\right)|\mathrm{d}s\hfill \\ & & +\frac{L_1\left|\lambda \right|e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{e}^{\lambda u}{\int }_a^u{(u-s)}^{\alpha -2}|x\left(s\right)-y\left(s\right)|\mathrm{d}s\mathrm{d}u\hfill \\ & \le & L_1{\parallel x-y\parallel }_{C^2}\frac{{(b-a)}^{\alpha -1}\left(\lambda +\left|\lambda \right|(1-e^{-\lambda (t-a)})\right)}{\lambda \Gamma \left(\alpha \right)},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {|\left(Tx\right)}^{″}\left(t\right)-{\left(Ty\right)}^{″}\left(t\right)|& \le & \frac{{\lambda }^2{e}^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{e}^{\lambda u}{(u-s)}^{\alpha -2}|f(s,x\left(s\right))-f(s,y\left(s\right))|\mathrm{d}s\mathrm{d}u\hfill \\ & & +\frac{\left|\lambda \right|}{\Gamma (\alpha -1)}{\int }_a^t{(t-s)}^{\alpha -2}|f(s,x\left(s\right))-f(s,y\left(s\right))|\mathrm{d}s\hfill \\ & & +\frac{1}{\Gamma (\alpha -1)}{\int }_a^t{(t-s)}^{\alpha -2}|f^{\prime }(s,x\left(s\right))-f^{\prime }(s,y\left(s\right))|\mathrm{d}s\hfill \\ & \le & \frac{L_1{\lambda }^2{e}^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{e}^{\lambda u}{(u-s)}^{\alpha -2}|x\left(s\right)-y\left(s\right)|\mathrm{d}s\mathrm{d}u\hfill \\ & & +\frac{\left|\lambda \right|L_1}{\Gamma (\alpha -1)}{\int }_a^t{(t-s)}^{\alpha -2}|x\left(s\right)-y\left(s\right)|\mathrm{d}s\hfill \\ & & +\frac{L_2}{\Gamma (\alpha -1)}{\int }_a^t{(t-s)}^{\alpha -2}\left(|x\left(s\right)-y\left(s\right)|+|x^{\prime }\left(s\right)-y^{\prime }\left(s\right)|\right)\mathrm{d}s\hfill \\ & \le & L_1{\parallel x-y\parallel }_{C^2}\frac{{(b-a)}^{\alpha -1}\left({\lambda }^2(1-e^{-\lambda (t-a)})+\lambda \left|\lambda \right|\right)}{\lambda \Gamma \left(\alpha \right)}\hfill \\ & & +L_2{\parallel x-y\parallel }_{C^2}\frac{{(b-a)}^{\alpha -1}}{\Gamma \left(\alpha \right)}.\hfill \end{array}$$

Thus, we conclude that, for $\lambda >0$

$$\begin{array}{ccc}& & {\parallel Tx-Ty\parallel }_{C^2}\hfill \\ & =& \underset{t\in [a,b]}{sup}|\left(Tx\right)\left(t\right)-\left(Ty\right)\left(t\right)|+\underset{t\in [a,b]}{sup}{|\left(Tx\right)}^{\prime }\left(t\right)-{\left(Ty\right)}^{\prime }\left(t\right)|+\underset{t\in [a,b]}{sup}|{\left(Tx\right)}^{″}\left(t\right)-{\left(Ty\right)}^{″}\left(t\right)|\hfill \\ & \le & {\parallel x-y\parallel }_{C^2}\left[L_1\frac{{(b-a)}^{\alpha -1}[1+2\lambda +2{\lambda }^2-(1+\lambda +{\lambda }^2)e^{-\lambda (b-a)}]}{\lambda \Gamma \left(\alpha \right)}+L_2\frac{{(b-a)}^{\alpha -1}}{\Gamma \left(\alpha \right)}\right]\hfill \\ & =& \left(k_{+}{L}_1+L_2\frac{{(b-a)}^{\alpha -1}}{\Gamma \left(\alpha \right)}\right){\parallel x-y\parallel }_{C^2},\hfill \end{array}$$

and for $\lambda <0$,

$$\begin{array}{ccc}& & {\parallel Tx-Ty\parallel }_{C^2}\hfill \\ & \le & {\parallel x-y\parallel }_{C^2}\left[L_1\frac{{(b-a)}^{\alpha -1}[1-e^{-\lambda (b-a)}+\lambda e^{-\lambda (b-a)}-{\lambda }^2{e}^{-\lambda (b-a)}]}{\lambda \Gamma \left(\alpha \right)}+L_2\frac{{(b-a)}^{\alpha -1}}{\Gamma \left(\alpha \right)}\right]\hfill \\ & =& \left(k_{-}{L}_1+L_2\frac{{(b-a)}^{\alpha -1}}{\Gamma \left(\alpha \right)}\right){\parallel x-y\parallel }_{C^2}.\hfill \end{array}$$

Since $K{L}_1+L_2\frac{{(b-a)}^{\alpha -1}}{\Gamma \left(\alpha \right)}<1$, we have that T is a contractive operator. Thus, by Banach contraction principle (cf. Theorem 1), we conclude that T has a unique fixed point, which from Proposition 1 means that the IVPFO (1) has a unique solution on $C^2\left([a,b]\right)$. □

4. Ulam–Hyers and Ulam–Hyers–Rassias Stabilities

In this section, we analyse the Ulam–Hyers and the Ulam–Hyers–Rassias stabilities of the above class of problems. In fact, since from Proposition 1 we have a new Equation (3) to describe the IVPFO (1) equivalently, we may choose to discuss the stabilities of (1) or (3). Thus, in here, we choose to exhibit, in detail, conditions for the Ulam–Hyers stability of (1) and the Ulam–Hyers–Rassias stability of (3). To this purpose, let us first point out what are the definitions of such stabilities in each of those cases.

Definition 3.

The IVPFO (1) is Ulam–Hyers stable if there exists a real constant $k>0$ such that, for each $ϵ>0$ and for each solution $y\in C^2\left([a,b]\right)$ of the inequality problem

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\left|{\mathcal{D}}_{a+}^{\alpha }y\left(t\right)+\lambda \left({\mathcal{D}}_{a+}^{\alpha -1}y\right)\left(t\right)-f(t,y\left(t\right))\right|\le ϵ,t\in [a,b],\\ y\left(a\right)=y^{\prime }\left(a\right)=0,\end{array}\right.\end{array}$$

(15)

there exists a solution $x\in C^2\left([a,b]\right)$ of the problem (1) (or, equivalently, of (3)) such that

$$\left|y\right(t)-x(t\left)\right|\le kϵ,t\in [a,b].$$

Remark 3.

If we look at what is inside the modulus function in (15) as a single “new” function h, it directly follows that a function $y\in C^2\left([a,b]\right)$ is a solution of the inequality in (15) if and only if there exists a function $h\in C\left(\right[a,b\left]\right)$ (which depends on y) such that

(i) 

$\left|h\right(t\left)\right|\le ϵ$, $t\in [a,b]$,

(ii) 

$y\left(a\right)=y^{\prime }\left(a\right)=0$,

(iii) 

${\mathcal{D}}_{a+}^{\alpha }y\left(t\right)+\lambda \left({\mathcal{D}}_{a+}^{\alpha -1}y\right)\left(t\right)-f(t,y\left(t\right))=h\left(t\right)$, $t\in [a,b]$.

Definition 4.

The fractional integral Equation (3) is Ulam–Hyers–Rassias stable with respect to $\phi :[a,b]\to {\mathbb{R}}^{+}$ if there exists a real constant $k_{\phi }>0$ such that, for each $ϵ>0$ and for each solution y of

$$\left|y\left(t\right)-\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}f(s,y\left(s\right))\mathrm{d}s\mathrm{d}u\right|\le ϵ\phi \left(t\right),t\in [a,b],$$

(16)

there exists a solution x of the problem (3) with

$$|y\left(t\right)-x\left(t\right)|\le k_{\phi }ϵ\phi \left(t\right),t\in [a,b].$$

4.1. Ulam–Hyers Stability

As indicated above, we will start by identifying conditions that guarantee the Ulam–Hyers of the IVPFO (1).

Theorem 6.

Let the continuously differentiable function f satisfy the Lipschitz conditions (13)–(14), for all $t\in [a,b]$, and assume that

$$K{L}_1+L_2\frac{{(b-a)}^{\alpha -1}}{\Gamma \left(\alpha \right)}<1.$$

(17)

If $y\in C^2\left([a,b]\right)$ satisfies the inequality and initial conditions (15) (with $ϵ>0$), for all $t\in [a,b]$, then there exists a unique solution $x\in C^2\left([a,b]\right)$ of the IVPFO (1) such that

$$\left|y\right(t)-x(t\left)\right|\le kϵ,t\in [a,b],$$

for

$$k=\frac{{(b-a)}^{\alpha -1}}{\alpha -1}{e}^{L_1\frac{\left(1-e^{-\lambda (b-a)}\right){(b-a)}^{\alpha -1}}{\lambda \Gamma \left(\alpha \right)}}$$

(18)

which, in particular, means that the IVPFO (1) is Ulam–Hyers stable.

Proof. 

According to the hypothesis, there exists a unique solution of the IVPFO (1).

Let $y\in C^2\left([a,b]\right)$ be any solution of the inequality of (15). By Remark 3, following the procedure of Proposition 1, one has that

$$\begin{array}{ccc}\hfill y\left(t\right)& =& \frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}f(s,y\left(s\right))\mathrm{d}s\mathrm{d}u\hfill \\ & & +\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}h\left(s\right)\mathrm{d}s\mathrm{d}u,\hfill \end{array}$$

with $\left|h\right(t\left)\right|<ϵ$. Thus, we have that

$$\begin{array}{ccc}\hfill \left|x\right(t)-y(t\left)\right|& =& \left|\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}(f(s,x\left(s\right))-f(s,y\left(s\right)))\mathrm{d}s\mathrm{d}u\right.\hfill \\ & & \left.-\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}h\left(s\right)\mathrm{d}s\mathrm{d}u\right|\hfill \\ & \le & \frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}|f(s,x\left(s\right))-f(s,y\left(s\right))|\mathrm{d}s\mathrm{d}u\hfill \\ & & +\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}\left|h\left(s\right)\right|\mathrm{d}s\mathrm{d}u\hfill \\ & \le & L_1\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{e}^{\lambda u}{\int }_a^u{(u-s)}^{\alpha -2}|x\left(s\right)-y\left(s\right)|\mathrm{d}s\mathrm{d}u\hfill \\ & & +ϵ\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{e}^{\lambda u}{\int }_a^u{(u-s)}^{\alpha -2}\mathrm{d}s\mathrm{d}u\hfill \\ & \le & L_1\frac{1-e^{-\lambda (t-a)}}{\lambda \Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}|x\left(s\right)-y\left(s\right)|\mathrm{d}s\mathrm{d}u\hfill \\ & & +ϵ\frac{(1-e^{-\lambda (t-a)}){(b-a)}^{\alpha -1}}{\lambda \Gamma \left(\alpha \right)}\hfill \\ & \le & \frac{1-e^{-\lambda (t-a)}}{\lambda \Gamma (\alpha -1)}\left(ϵ\frac{{(b-a)}^{\alpha -1}}{\alpha -1}+{\int }_a^t{\int }_a^u{L}_1{(u-s)}^{\alpha -2}|x\left(s\right)-y\left(s\right)|\mathrm{d}s\mathrm{d}u\right)\hfill \\ & \le & \frac{1-e^{-\lambda (b-a)}}{\lambda \Gamma (\alpha -1)}\left(ϵ\frac{{(b-a)}^{\alpha -1}}{\alpha -1}+{\int }_a^t{\int }_a^u{L}_1{(u-s)}^{\alpha -2}|x\left(s\right)-y\left(s\right)|\mathrm{d}s\mathrm{d}u\right).\hfill \end{array}$$

Thus, according to Theorem 3, we have that

$$\begin{array}{ccc}\hfill \left|x\right(t)-y(t\left)\right|& \le & ϵ\frac{{(b-a)}^{\alpha -1}}{\alpha -1}{e}^{\frac{1-e^{-\lambda (b-a)}}{\lambda \Gamma (\alpha -1)}{L}_1\frac{{(t-a)}^{\alpha -1}}{\alpha -1}}\hfill \\ & \le & ϵ\frac{{(b-a)}^{\alpha -1}}{\alpha -1}{e}^{L_1\frac{\left(1-e^{-\lambda (b-a)}\right){(b-a)}^{\alpha -1}}{\lambda \Gamma \left(\alpha \right)}},\hfill \end{array}$$

and we conclude the above claimed inequality and that the IVPFO (1) is Ulam–Hyers stable. □

4.2. Ulam–Hyers–Rassias Stability

We will now consider the Ulam–Hyers–Rassias stability. For that purpose, we consider the space $C\left(\right[a,b\left]\right)$ equipped with the Bielecki type metric

$$d(x,y)=\underset{t\in [a,b]}{sup}\frac{\left|x\right(t)-y(t\left)\right|}{\sigma \left(t\right)},$$

where $\sigma$ is a non-decreasing continuous function $\sigma :[a,b]\to {\mathbb{R}}^{+}$. It is known that $\left(C\right([a,b]),d)$ is a complete metric space (cf. [25]).

Theorem 7.

Let $f:[a,b]\times \mathbb{R}\to \mathbb{R}$ be a continuous function satisfying the Lipschitz condition

$$|f(t,{\rho }_1)-f(t,{\rho }_2)|\le L|{\rho }_1-{\rho }_2|,{\rho }_1,{\rho }_2\in \mathbb{R},t\in [a,b],$$

with $L>0$. Additionally, let $\sigma :[a,b]\to {\mathbb{R}}^{+}$ be a nondecreasing function and suppose that exist a constant $\xi \in [0,1)$ such that

$$\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}\sigma \left(s\right)\mathrm{d}s\mathrm{d}u\le \xi \sigma \left(t\right),t\in [a,b].$$

If y satisfies

$$\left|y\left(t\right)-\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}f(s,y\left(s\right))\mathrm{d}s\mathrm{d}u\right|\le ϵ\sigma \left(t\right),t\in [a,b],$$

and $L\xi <1$, then there exist a solution x of the fractional integral Equation (3) such that

$$|x\left(t\right)-y\left(t\right)|\le \frac{ϵ\sigma \left(t\right)}{1-L\xi },t\in [a,b],$$

i.e., under the present conditions, the fractional integral Equation (3) has the Ulam–Hyers– Rassias stability.

Proof. 

Having in mind the fractional integral Equation (3), we will consider (in the framework of the above presented Bielecki type metric) the operator $T:C\left(\right[a,b],d)\to C\left(\right[a,b],d)$ defined by

$$\left(Ty\right)\left(t\right)=\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}f(s,y\left(s\right))\mathrm{d}s\mathrm{d}u.$$

Let us first prove that T is strictly contractive in $C\left(\right[a,b],d)$. For any $v,w\in C\left(\right[a,b],d)$, we have

$$\begin{array}{ccc}\hfill d(Tv,Tw)& =& \underset{t\in [a,b]}{sup}\frac{\left|\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}(f(s,v\left(s\right))-f(s,w\left(s\right))\mathrm{d}s\mathrm{d}u\right|}{\sigma \left(t\right)}\hfill \\ & \le & L\underset{t\in [a,b]}{sup}\frac{\left|\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}\sigma \left(s\right)\frac{\left|v\left(s\right)-w\left(s\right)\right|}{\sigma \left(s\right)}\mathrm{d}s\mathrm{d}u\right|}{\sigma \left(t\right)}\hfill \\ & \le & L\xi d(v,w).\hfill \end{array}$$

Consequently, for $L\xi <1$, we have that T is strictly contractive in the present framework, and we have a unique solution x to the equation $Ty=y$.

Let us now identify $ϵ$ as an upper bound for $d(Ty,y)$, and use this knowledge. Indeed, from the hypothesis, we have

$$|y\left(t\right)-Ty\left(t\right)|=\left|y\left(t\right)-\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}f(s,y\left(s\right))\mathrm{d}s\mathrm{d}u\right|<ϵ\sigma \left(t\right),$$

which allows us to conclude that

$$d(x,y)\le \frac{1}{1-L\xi }d(y,Ty)\le \frac{ϵ}{1-L\xi },$$

and so

$$|x\left(t\right)-y\left(t\right)|\le \frac{ϵ}{1-L\xi }\sigma \left(t\right),t\in [a,b].$$

□

The Ulam–Hyers stability is a particular case of the Ulam–Hyers–Rassias stability in the sense that instead of having a function $\phi$ controlling the differences in the last stability, we simply have a constant k in the first one. Thus, attending that

$$\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}\mathrm{d}s\mathrm{d}u\le \frac{{(b-a)}^{\alpha -1}}{\lambda \Gamma \left(\alpha \right)}(1-e^{-\lambda (b-a)}),t\in [a,b],$$

and proceeding in an identical way to the proof of Theorem 7, we would pass from an upper bound that depends on a function (of the variable t) to an upper bound in the form of a constant, which is here directly concluded (following the proof of Theorem 7) in the next result:

Corollary 1.

Let $f:[a,b]\times \mathbb{R}\to \mathbb{R}$ be a continuous function satisfying the Lipschitz condition

$$|f(t,{\rho }_1)-f(t,{\rho }_2)|\le L|{\rho }_1-{\rho }_2|,{\rho }_1,{\rho }_2\in \mathbb{R},t\in [a,b],$$

with $L>0$. Let

$$\eta =\frac{{(b-a)}^{\alpha -1}}{\lambda \Gamma \left(\alpha \right)}(1-e^{-\lambda (b-a)}).$$

(19)

If $L\eta <1$ and y satisfies

$$\left|y\left(t\right)-\frac{e^{-\lambda t}}{\Gamma (\alpha -1)}{\int }_a^t{\int }_a^u{(u-s)}^{\alpha -2}{e}^{\lambda u}f(s,y\left(s\right))\mathrm{d}s\mathrm{d}u\right|\le ϵ,t\in [a,b],$$

then there exist a solution x of the fractional integral Equation (3) such that

$$|x\left(t\right)-y\left(t\right)|\le \frac{ϵ}{1-L\eta },t\in [a,b],$$

(20)

i.e., under the above conditions, the fractional integral Equation (3) has the Ulam–Hyers stability.

Remark 4.

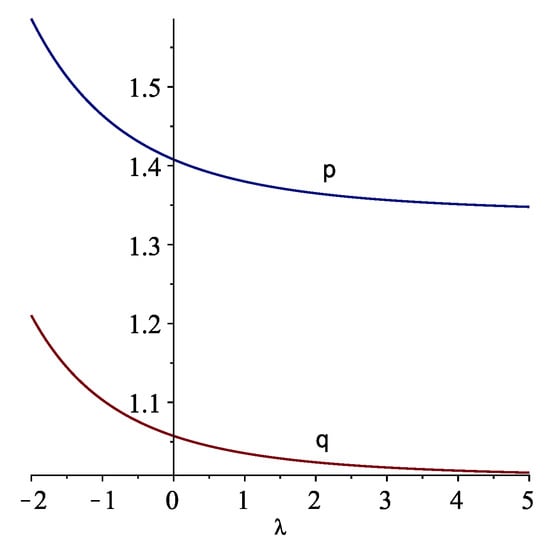
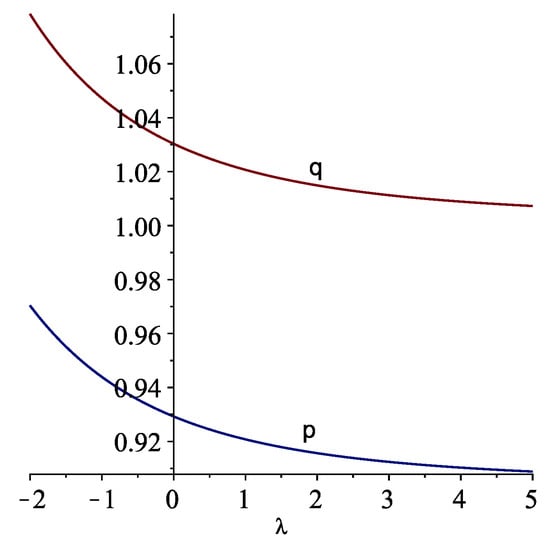
Please, note that the constants k in (18) and $\frac{1}{1-L\eta }$ in (20) cannot be compared for all the values of the parameters. Consider, for example, the following cases. Admit that $L=L_1=L_2=\frac{1}{20}$, $\alpha =\frac{7}{4}$ and consider two intervals, one of amplitude equal 1 and another one with amplitude $0.8$. With these values, we have that, for $\lambda \in ]-2,0[\cup ]0,5[$ condition (17) is verified and also, $L\eta <1$ for η as defined in (19). For the case $b-a=1$, it is possible to observe that $k>\frac{1}{1-L\eta }$ (cf. Figure 1, where $p\left(\lambda \right)>q\left(\lambda \right)$). For the case $b-a=0.8$, we verify that $k<\frac{1}{1-L\eta }$ (cf. Figure 2, where $p\left(\lambda \right)<q\left(\lambda \right)$).

Figure 1. The graphs of $p\left(\lambda \right)=k\left(\lambda \right)$ and $q\left(\lambda \right)=\frac{1}{1-L\eta \left(\lambda \right)}$ for $\lambda \in [-2,0]\cup [0,5]$: case $b-a=1$.

Figure 2. The graphs of $p\left(\lambda \right)=k\left(\lambda \right)$ and $q\left(\lambda \right)=\frac{1}{1-L\eta \left(\lambda \right)}$ for $\lambda \in [-2,0]\cup [0,5]$: case $b-a=0.8$.

4.3. Concrete Examples

Let us now consider some concrete examples to illustrate the above theory.

We start by considering the following IVPFO

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\left({\mathcal{D}}^{\frac{3}{2}}x\right)\left(t\right)+\lambda \left({\mathcal{D}}^{\frac{1}{2}}x\right)\left(t\right)=\frac{t}{75}(x\left(t\right)+sin\left(t\right)),\\ x\left(2\right)=x^{\prime }\left(2\right)=0,\end{array}\right.\end{array}$$

(21)

for $t\in [2,3]$. Thus, in the previous notation, we have in here $\alpha =\frac{3}{2}$, $a=2$, $b=3$ and

$$f(t,\rho )=\frac{t}{75}(\rho +sin\left(t\right)),$$

being clear that f is a continuously differentiable function.

According to Theorem 4, there exists, at least, one solution of the IVPFO (21). In addition, having in mind that $f^{\prime }(t,x\left(t\right))=\frac{1}{75}\left(x\left(t\right)+t{x}^{\prime }\left(t\right)+sin\left(t\right)+tcos\left(t\right)\right)$, for $t\in [2,3]$, one has that

$$\begin{array}{ccc}\hfill \left|f\right(t,x\left(t\right))-f(t,y\left(t\right)\left)\right|& \le & \frac{1}{25}|x\left(t\right)-y\left(t\right)|,\hfill \\ \hfill |f^{\prime }(t,x\left(t\right))-f^{\prime }(t,y\left(t\right))|& \le & \frac{1}{25}\left(|x^{\prime }\left(t\right)-y^{\prime }\left(t\right)|+|x\left(t\right)-y\left(t\right)|\right).\hfill \end{array}$$

Following Theorem 5 and its notation, we have in here $L_1=L_2=\frac{1}{25}$. Thus, for $a=2$ and $b=3$, we obtain that

$$K{L}_1+L_2\frac{{(b-a)}^{\alpha -1}}{\Gamma \left(\alpha \right)}<1,$$

for $\lambda \in [-1,0]\cup [0,9]$ (cf. (12) and Figure 3). Thus, for these cases of $\lambda$, the IVPFO (21) admits a unique solution in $C^2\left([2,3]\right)$. Moreover, from Theorem 6, we also know that for those $\lambda$ the IVPFO (21) is Ulam–Hyers stable.

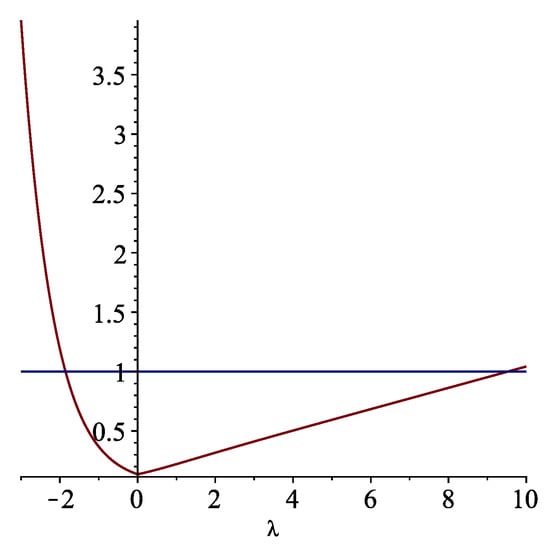
Figure 3. The graphs of $z_1\left(\lambda \right)=K\left(\lambda \right)L_1+\frac{L_2}{\Gamma \left(\frac{3}{2}\right)}$ and $z_2=1$.

The example we have just analyzed allows us to see that there really are classes of problems, dependent on $\lambda$, in which the conditions required in Theorem 5 are met, and there are still other cases (for different parameters $\lambda$) in which this is not the case. In view of this, and keeping in mind that the conditions of Theorem 5 are just sufficient conditions, an open analysis eventually involves obtaining other weaker conditions according to which the uniqueness of solution for those classes of problems can still be guaranteed. The same can be envisaged for Theorem 6 and its sufficient conditions to guarantee the stability of the Ulam–Hyers type.

Let us now investigate the Ulam–Hyers–Rassias stability of

$$x\left(t\right)=\frac{e^{-\lambda t}}{\Gamma (\frac{3}{2}-1)}{\int }_2^t{\int }_2^u{(u-s)}^{\frac{3}{2}-2}{e}^{\lambda u}\frac{t}{75}(y\left(s\right)+sin\left(s\right))\mathrm{d}s\mathrm{d}u,$$

(22)

for $t\in [2,3]$ and $\lambda =3$.

Letting $\sigma \left(t\right)=e^t$, we have that $\sigma$ is a non-decreasing function and

$$\frac{e^{-3t}}{\Gamma \left(\frac{1}{2}\right)}{\int }_2^t{\int }_2^u{(u-s)}^{\frac{3}{2}-2}{e}^{3u}\sigma \left(s\right)\mathrm{d}s\mathrm{d}u\le \frac{1}{5}\sigma \left(t\right),t\in [2,3]$$

(cf. Figure 4). Thus, for the notation of Theorem 7, we have $L=\frac{1}{25}$, $\xi =\frac{1}{5}$ and so $L\xi =\frac{1}{125}<1$.

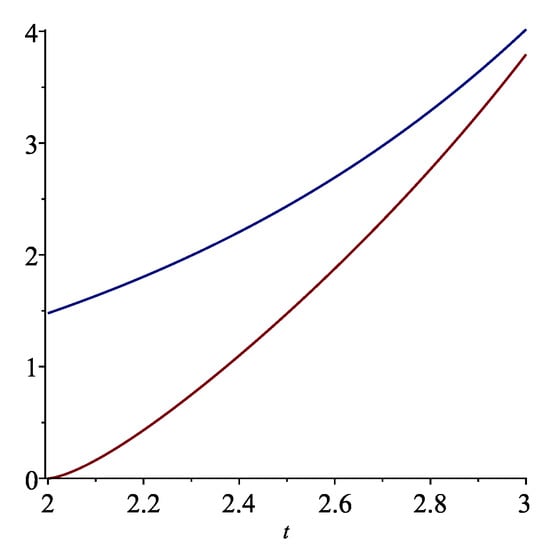
Figure 4. The graphs of $p_1\left(t\right)=\frac{1}{5}\sigma \left(t\right)=\frac{1}{5}{e}^t$ (the upper one), and $p_2\left(t\right)=\frac{e^{-3t}}{\Gamma \left(\frac{1}{2}\right)}{\int }_2^t{\int }_2^u{(u-s)}^{\frac{3}{2}-2}{e}^{3u}\sigma \left(s\right)\mathrm{d}s\mathrm{d}u,t\in [2,3]$.

Take $y\left(t\right)=\frac{1}{10}{(t-2)}^2$. We have that $y\in C^2\left([2,3]\right)$ and $y\left(2\right)=y^{\prime }\left(2\right)=0$. We have that (cf. Figure 5)

$$\left|y\left(t\right)-\frac{e^{-3t}}{\Gamma \left(\frac{3}{2}\right)}{\int }_2^t{\int }_2^u{(u-s)}^{-\frac{1}{2}}{e}^{3u}\frac{s}{75}(y\left(s\right)+sin\left(s\right))\mathrm{d}s\mathrm{d}u\right|\le \frac{1}{200}\sigma \left(t\right),t\in [2,3].$$

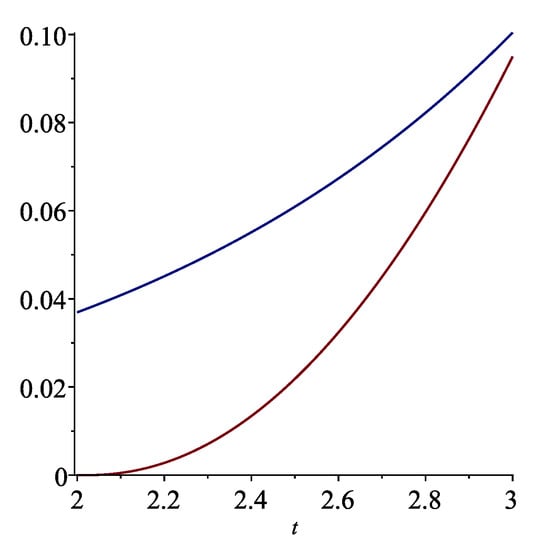
Figure 5. The graphs of $q_1\left(t\right)=\frac{1}{200}\sigma \left(t\right)$ (the upper one) and $q_2\left(t\right)=\left|y\left(t\right)-\frac{e^{-3t}}{\Gamma \left(\frac{3}{2}\right)}{\int }_2^t{\int }_2^u{(u-s)}^{-\frac{1}{2}}{e}^{3u}\frac{s}{75}(y\left(s\right)+sin\left(s\right))\mathrm{d}s\mathrm{d}u\right|$, $t\in [2,3]$.

Thus, according to Theorem 7, the problem (22) is Ulam–Hyers–Rassias stable with respect to $\sigma \left(t\right)=e^t$ and

$$|y\left(t\right)-x\left(t\right)|\le \frac{5e^t}{992},t\in [2,3].$$

Moreover, we can also observe that

$$\left|y\left(t\right)-\frac{e^{-3t}}{\Gamma \left(\frac{3}{2}\right)}{\int }_2^t{\int }_2^u{(u-s)}^{-\frac{1}{2}}{e}^{3u}\frac{s}{75}(y\left(s\right)+sin\left(s\right))\mathrm{d}s\mathrm{d}u\right|\le \frac{1}{10},t\in [2,3].$$

Thus, applying Corollary 1 and the respective notation, we have that $ϵ=\frac{1}{10}$. Additionally, $\eta =\frac{1-e^{-3}}{3\Gamma \left(\frac{3}{2}\right)}\approx 0.36$ and we conclude that

$$\left|x\right(t)-y(t\left)\right|\le 0.1.$$

In this last example, it is relevant to emphasize the importance of the function $\sigma$ in the whole process, with special predominance, from the outset, in the determination of the exhibited upper bounds. In this case, we chose to work with the exponential function, and this had expected consequences given the growth that the function presents. Incidentally, the importance of the choice and the impact that the $\sigma$ function has is well evidenced by the fact that the same problem can be Ulam–Hyers–Rassias stable for a given ${\sigma }_1$ function and not Ulam–Hyers–Rassias stable for another ${\sigma }_2$ function. Thus, it is precisely for this reason that the Ulam–Hyers–Rassias stability is determined depending on the chosen $\sigma$ function (and it is also for this reason that this is explicitly mentioned in the name of this type of stability).

Let us now consider the following different IVPFO

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\left({\mathcal{D}}^{\frac{6}{5}}x\right)\left(t\right)+\lambda \left({\mathcal{D}}^{\frac{1}{5}}x\right)\left(t\right)=\frac{t}{10}x\left(t\right)-e^{-t},t\in [0,1],\\ x\left(0\right)=x^{\prime }\left(0\right)=0.\end{array}\right.\end{array}$$

(23)

Accordingly to the previous notations, we have now $\alpha =\frac{6}{5}$, $a=0$, $b=1$ and $f(t,x\left(t\right))=\frac{t}{10}x\left(t\right)-e^{-t}$. It is clear that f is a continuously differentiable function in $[0,1]\times \mathbb{R}$. Thus there exists, at least, one solution of the IVPFO (23) (cf. Theorem 4). Moreover, one has that

$$\begin{array}{ccc}\hfill \left|f\right(t,x\left(t\right))-f(t,y\left(t\right)\left)\right|& \le & \frac{1}{10}|x\left(t\right)-y\left(t\right)|,\hfill \\ \hfill |f^{\prime }(t,x\left(t\right))-f^{\prime }(t,y\left(t\right))|& \le & \frac{1}{10}\left(|x^{\prime }\left(t\right)-y^{\prime }\left(t\right)|+|x\left(t\right)-y\left(t\right)|\right).\hfill \end{array}$$

Following Theorem 5, we have $L_1=L_2=\frac{1}{10}$. Since $a=0$ and $b=1$, we obtain that for $\lambda \in ]-1,0[\cup \left]0,\frac{5}{2}\right[$, the condition

$$K{L}_1+L_2\frac{{(b-a)}^{\alpha -1}}{\Gamma \left(\alpha \right)}<1$$

is verified (cf. Figure 6), which means that the IVPFO (23) admits a unique solution in $C^2\left([0,1]\right)$ when considering those values of $\lambda$ (cf. Theorem 5).

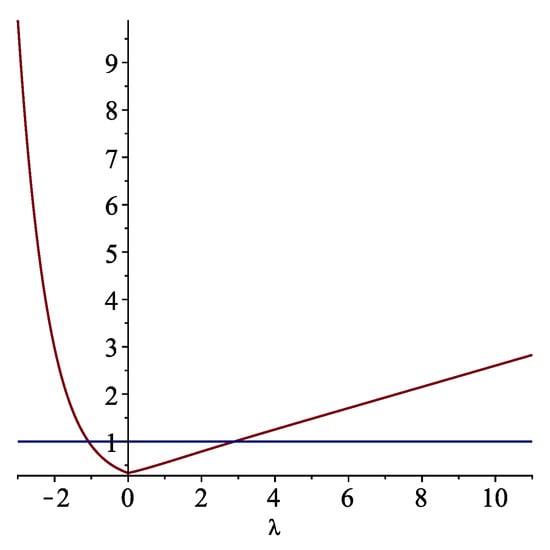
Figure 6. The graphs of $h_1\left(\lambda \right)=K\left(\lambda \right)L_1+\frac{L_2}{\Gamma \left(\frac{6}{5}\right)}$ and $h_2=1$.

Thus, for these cases of $\lambda$, the IVPFO (23) admits a unique solution in $C^2\left([0,1]\right)$. Moreover, from Theorem 6, we also know that for those $\lambda$ the IVPFO (23) is Ulam–Hyers stable.

Let us now analyse the Ulam–Hyers–Rassias stability of

$$x\left(t\right)=\frac{e^{-\lambda t}}{\Gamma (\frac{6}{5}-1)}{\int }_0^t{\int }_0^u{(u-s)}^{\frac{6}{5}-2}{e}^{\lambda u}\left(\frac{s}{10}x\left(s\right)-e^{-s}\right)\mathrm{d}s\mathrm{d}u,$$

(24)

for $t\in [0,1]$, $\lambda =2$, and with respect to $\sigma \left(t\right)=t$. Let $x\in C^2\left([0,1]\right)$ be the exact solution of the IVPFO (23), and let us consider $y\left(t\right)=sin\left(t\right)-t$. It follows that $y\in C^2\left([0,1]\right)$ and $y\left(0\right)=y^{\prime }\left(0\right)=0$. We have that $\sigma$ is a nondecreasing function and

$$\frac{e^{-2t}}{\Gamma \left(\frac{1}{5}\right)}{\int }_0^t{\int }_0^u{(u-s)}^{-\frac{4}{5}}{e}^{2u}\sigma \left(s\right)\mathrm{d}s\mathrm{d}u\le \frac{1}{4}\sigma \left(t\right),t\in [0,1]$$

(cf. Figure 7).

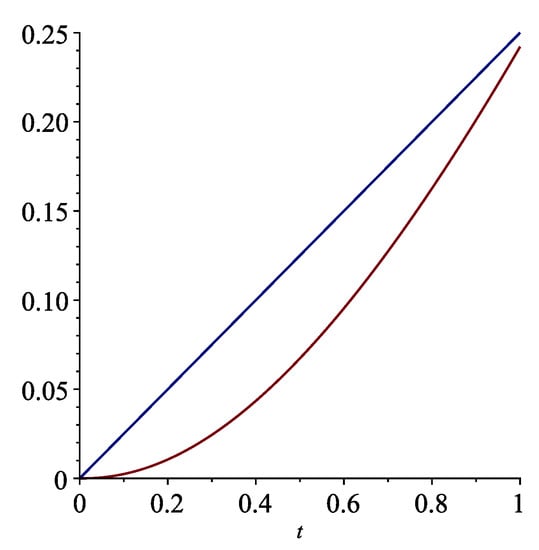
Figure 7. The graphs of $m_1\left(t\right)=\frac{e^{-2t}}{\Gamma \left(\frac{1}{5}\right)}{\int }_0^t{\int }_0^u{(u-s)}^{-\frac{4}{5}}{e}^{2}u\sigma \left(s\right)\mathrm{d}s\mathrm{d}u$ and $m_2\left(t\right)=\frac{1}{4}\sigma \left(t\right)=\frac{t}{4},t\in [0,1]$.

For the notation of Theorem 7, we have $L=\frac{1}{25}$ and $\xi =\frac{1}{4}$, and so $L\xi =\frac{1}{100}<1$. Thus,

$$\left|y\left(t\right)-\frac{e^{-2t}}{\Gamma \left(\frac{1}{5}\right)}{\int }_0^t{\int }_0^u{(u-s)}^{-\frac{4}{5}}{e}^{2u}\left(\frac{s}{10}y\left(s\right)-e^{-s}\right)\mathrm{d}s\mathrm{d}u\right|\le \frac{7}{50}\sigma \left(t\right),t\in [0,1]$$

(cf. Figure 8).

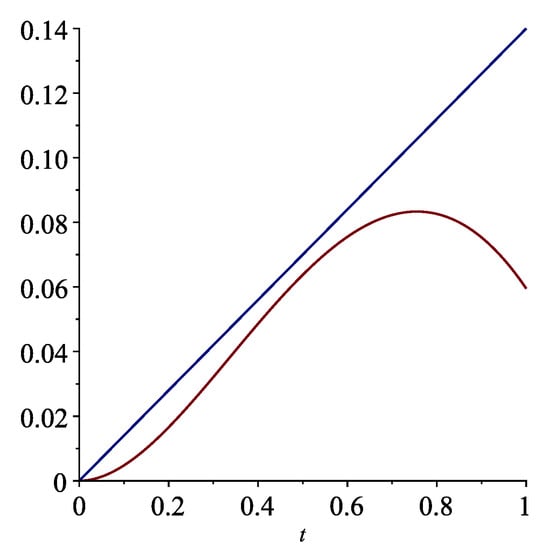
Figure 8. The graphs of $w_1\left(t\right)=\left|y\left(t\right)-\frac{e^{-2t}}{\Gamma \left(\frac{1}{5}\right)}{\int }_0^t{\int }_0^u{(u-s)}^{-\frac{4}{5}}{e}^{2u}\left(\frac{s}{10}y\left(s\right)-e^{-s}\right)\mathrm{d}s\mathrm{d}u\right|$ (the lower one) and $w_2\left(t\right)=\frac{7}{50}\sigma \left(t\right),t\in [0,1]$.

Therefore, according to Theorem 7, the problem (24) is Ulam–Hyers–Rassias stable with respect to $\sigma \left(t\right)=t$ and

$$|y\left(t\right)-x\left(t\right)|\le \frac{14}{99}\sigma \left(t\right),t\in [0,1].$$

In this last example, we deliberately chose $\sigma \left(t\right)=t$ to work with $y\left(t\right)=sin\left(t\right)-t$, which can be considered not the most ideal choice (which, by the way, can be easily noticed when we look at Figure 8 and see, on the right, the “greatest” distance between the two functions represented there). Anyway, we consider this example important because it emphasizes that the theoretical conditions obtained earlier are robust enough to guarantee stability in less favorable or obvious choices.

Moreover, according to Corollary 1, we can also conclude the Ulam–Hyers stability. Using the respective notation of the Corollary, we have that $ϵ=\frac{7}{50}$, $\eta =\frac{1-e^{-2}}{2\Gamma \left(\frac{6}{5}\right)}\approx 0.47$ and $L=\frac{1}{25}$. Thus, we conclude that $|x\left(t\right)-y\left(t\right)|\le \frac{7}{50}.$

5. Conclusions

We conclude this article by summarizing the results obtained. We analyze a class of nonlinear fractional differential equations, with initial conditions, characterized by having the Riemann–Liouville fractional derivative of order $\alpha \in (1,2)$. Having made use of distinct fixed-point arguments, we were able to deduce conditions that guarantee the existence and uniqueness of solutions in a frame of adequate spaces, and we also obtained sufficient conditions to have the Ulam–Hyers and Ulam–Hyers–Rassias stabilities of the problems in the analysis (where the use of a Bielecki-type metric and some additional contractive arguments were of crucial importance). In the last section, some examples were included mainly to illustrate that the conditions obtained in the theoretical part really exist and can be considered in particular cases.