Some Common Fixed Point Results in Modular Ultrametric Space Using Various Contractions and Their Application to Well-Posedness

Abstract

The aim of this study is to prove the existence and uniqueness of fixed point and common fixed point theorems for self-mappings in modular ultrametric spaces. These theorems are proved under varying contractive circumstances and without the property of spherical completeness. As a consequence, the examples of fixed point and common fixed point problems are correctly formulated. As an application, the well-posedness of a common fixed point problem is proved. This study expands on prior research in modular ultrametric space to provide a more comprehensive understanding of such spaces using generalized contraction.

1. Introduction

Fixed point theory is a branch of mathematics that deals with the existence and uniqueness of fixed points for various functions. During the late 19th century, fixed point theory solved challenging problems and significantly contributed to real-world problems. A fixed point of a function is a point in the domain that maps to itself. In particular, if we have a function f and an element x in the domain, then x is a fixed point (FP) of f if $f\left(x\right)=x$. The concept of fixed points has wide ranging applications in mathematics, physics, economics, computer science, and other disciplines. Fixed point theory provides powerful tools and techniques to analyze and understand the behavior of functions and mappings, particularly in situations where immediate solutions may be challenging. If a function does have a fixed point, then we are interested in determining its properties such as uniqueness, stability, or sensitivity to perturbations. In addition, fixed point theory investigates the existence of multiple fixed points and the structure of fixed point sets. One of the most famous fixed point theorems is the Banach fixed point theorem. The Banach contraction principle [1] states that when a complete metric space is equipped with a contractive mapping, then a fixed point exists, which leads to the solutions of a wide range of mathematical problems for proving the existence and uniqueness of solutions. Furthermore, many authors have made significant contributions, including improvements, extensions, and generalizations of these theorems over different spaces, such as quasi-metric, cone metric, partial metric, G-metric, ultrametric, F-metric, and modular ultrametric spaces [2,3,4,5,6,7].

Various modular structures, which are viewed as alternatives to classical normed or metric spaces, have been intensely studied in connection with fixed point theory. Many research papers related to modularity have adopted the setting of a modular vector space; Nakano [8] first introduced the concept of modular space in 1950. Subsequently, many authors have made various observations around modular spaces (see [9,10]). The notion of a metric modular, together with its stronger convex version, was first introduced and studied by Chistyakov [11], who establishede a more general form of a metric space as a modular metric space. In addition, he made a significant contribution to developing the theory of modular metric spaces (see [12,13]). Khamsi [14] demonstrated the solution for the existence and uniqueness of fixed points via quasi-contractive maps in modular metric space. Azadifar et al. [15] showed that a common and unique fixed point exists for compatible mappings of the integral type in the above spaces. Hussain and Salimi [16] conducted a study on fixed points using generalized alpha-admissible contractive mappings in modular metric spaces. Many studies have been conducted in the above spaces; see [17,18,19,20,21]. The new modular proves to be a parameterized family of classical metrics; therefore, for each parameter value, the triangle inequality or the continuity is ensured. This makes the newly defined object an excellent instrument for analyzing various contractive conditions or using non-standard iterative procedures.

In the late 19th century, fixed point theory was shown to be successful in challenging problems, and has significantly contributed to many real-world problems. Various strong fixed-point results have been proven under strong assumptions. Several of these assumptions can lead to induced norms, particularly in modular spaces. For example, certain assumptions only sometimes hold in practice, or can lead to reformulation as particular problems in normed vector spaces. A recent research trend has been dedicated to studying the fundamentals of fixed point theorems and relaxing the assumptions used to prove these results in order to further relax the convexity of the modular spaces. Modular ultrametric spaces are closely linked to non-Archimedean analysis, which focuses on spaces that satisfy the ultrametric triangle inequality. These spaces offer solutions to functional equations that arise in mathematics and various sciences. Modular ultrametric spaces are beneficial in studying fixed point problems associated with functional equations. These equations are commonly found in number theory, functional analysis, and p-adic analysis.

In a series of papers published in 1943, Monna founded non-Archimedean functional analysis as a distinct field. Van Rooij’s book on the analysis of non-Archimedean Banach spaces influenced many researchers to obtain results in this field (see [22,23,24]). Recently, Gajic [25] used generalized contractive conditions to establish fixed-point results in an ultrametric space. The authors of [26] presented sufficient conditions for coincidence points for three and four self-maps using generalized contractive conditions; for more details, refer to the articles [27,28], and references therein. Alaca et al. (2016) established fixed point results for modular ultrametric spaces (see [29]). In modular ultrametric spaces, theorems may possess distinct characteristics that are irrelevant in other metric spaces or general modular spaces. The ultrametric inequality in ultrametric spaces creates exceptional geometric and topological properties, which can produce dissimilar outcomes compared to standard metric spaces. Theorems proved in modular ultrametric spaces may be more specific and tailored towards these exceptional properties. Later, in 2017, Hamid Mamghaderi [30] proved several fixed point theorems in partially-ordered ultrametric and non-Archimedean normed spaces, in which he considered single-valued and strongly contractive mappings. In addition, Ramesh Kumar and Pitchaimani [23] analyzed set-valued contractions and precis-Reich types of mappings in ultrametric spaces. Quite recently, Balaanandhan and Uma [31] established new fixed point theorems on partially ordered ultrametric space using the p-adic distance.

In 1976, Bogin [32] proved the following statement in complete metric spaces.

Theorem 1.

Let $(E,d)$ be a complete metric space and let T be a self-map on E fulfilling the following:

$$\begin{array}{c}\hfill d(Ta,Tb)\le \alpha d(a,b)+\beta \left[d\right(a,Ta)+d(b,Tb\left)\right]+\gamma \left[d\right(a,Tb)+d(b,Ta\left)\right],\forall a,b,c\in X,\end{array}$$

where $\alpha ,\beta ,\gamma \ge 0$ with $\alpha +2\beta +2\gamma <1$. Then, T has precisely one fixed point.

In 2017, Pitchaimani and Ramesh Kumar [33] proved the following fixed point theorem in complete ultrametric spaces using the contraction.

Theorem 2.

Let $(E,d)$ be a complete ultrametric space and let T be a self-map on X that fulfills the following:

$$\begin{array}{c}\hfill d(Ta,Tb)\le \alpha d(a,b)+\beta \left[d\right(a,Ta)+d(b,Tb\left)\right]+\gamma \left[d\right(a,Tb)+d(b,Ta\left)\right],\forall \mathsf{a},\mathsf{b},\mathsf{c}\in X\end{array}$$

where $\alpha ,\beta ,\gamma \ge 0$ with $\alpha +2\beta +2\gamma <1$. Then, T has a unique fixed point in E.

Based on the above motivation, in this paper we explore various fixed point results in modular ultrametric spaces under different contractive conditions. The main framework of our study is as follows:

• First, we check for the existence and uniqueness of common fixed points in a modular ultrametric space using various contractions.
• The same is then investigated for fixed points in the above spaces.
• Finally, our main results utilize the application of well-posedness.

In 2014, Sarwar et al. [34] established common fixed point results using the following contractive condition in dislocated quasi-metric space. For two continuous self-maps $S,T:E\to E$, we have

$$\begin{array}{cc}\hfill d(Sa,Tb)& \le \alpha d(a,b)+\beta d(a,Sa)+\gamma d(b,Tb)\hfill \\ \hfill & +\delta \left[d\right(a,Sa)+d(b,Tb\left)\right]+\lambda \left[d\right(a,Tb)+d(b,Sa\left)\right].\hfill \end{array}$$

(1)

In 2017, Li et al. [35] investigated the same using the following contraction:

$$\begin{array}{cc}\hfill d(Sa,Tb)\le \alpha d(a,b)& +\beta d(a,Sa)+\gamma d(b,Tb)+\delta \left[d\right(a,Sa)+d(b,Tb\left)\right]\hfill \\ \hfill & +\lambda \left[d\right(a,Tb)+d(b,Sa\left)\right]+\eta \left[d\right(a,Sa)+d(a,b\left)\right].\hfill \end{array}$$

(2)

In Section 3.1, we prove several Common Fixed Point (CFP) theorems using the above Contractions (1) and (2) in modular ultrametric spaces. In 1974, Ćirić discussed the following contraction in metric spaces, in which he considered a continuous self-map $T:E\to E$ with the condition

$$\begin{array}{c}\hfill d(Ta,Tb)\le \alpha d(a,b)+\beta d(a,Ta)+\gamma d(b,Tb)+\delta \left[d\right(a,Tb)+d(b,Ta\left)\right].\end{array}$$

(3)

In 2013, Patel et al. [36] investigated fixed point theorems on dislocated quasi-metric spaces using the following contraction:

$$\begin{array}{cc}\hfill d(Ta,Tb)\le \alpha d(a,b)+\beta d(a,Ta)& +\gamma d(b,Ta)+\delta \left[d\right(a,Ta)+d(b,Tb\left)\right]\hfill \\ \hfill & +\lambda \left[d\right(a,Tb)+d(b,Ta\left)\right].\hfill \end{array}$$

(4)

In Section 3.2, we derive fixed point results using the aforementioned Contractions (3) and (4) in modular ultrametric spaces.

The objective of this study is to analyze the results of fixed points and common fixed points for existence and uniqueness in modular ultrametric spaces by employing a more generalized form of contraction.

2. Preliminaries

In this paper, E is a non-void set, $\eta >0$, and the function $\omega :(0,\infty )\times E\times E\to {\mathbb{R}}^{+}$ is written as ${\omega }_{\eta }(a,b)=\omega (\eta ,a,b)$ for all $\eta >0$ and $a,b\in E$.

We next recall a number of basic definitions needed to achieve our desired results.

Definition 1

([37]). Let $(E,d)$ be a metric space. If the metric d fulfills the stronger triangle inequality, that is, for all $a,b,c\in E$,

$$\begin{array}{c}\hfill d(a,c)\le max\left\{d\right(a,b),d(b,c\left)\right\},\end{array}$$

then the pair $(E,d)$ is said to be an ultrametric space.

Example 1.

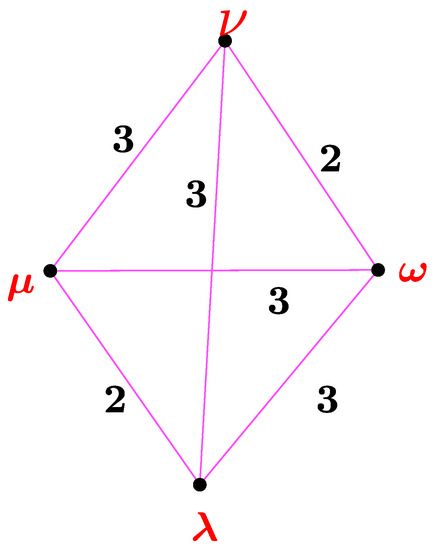
Consider $E=\{\mu ,\upsilon ,\omega ,\lambda \}$ and $d(\upsilon ,\omega )=d(\mu ,\lambda )=2,d(\mu ,\upsilon )=d(\upsilon ,\lambda )=d(\mu ,\omega )=d(\omega ,\lambda )=3$. Then, $(E,d)$ is an ultrametric space. The graphical representation is shown in Figure 1.

Figure 1. Graphical representation of Example 1.

Definition 2

([29]). Let E be a non-void set. A modular ultrametric is a function $\omega :{\mathbb{R}}^{+}\times E\times E\to {\mathbb{R}}^{+}\cup \infty$ satisfying the following conditions:

(i) 

${\omega }_{\eta }(a,b)=0$$\forall \eta >0$ iff $a=b$,

(ii) 

${\omega }_{\eta }(a,b)={\omega }_{\eta }(b,a)$$\forall \eta >0$,

(iii) 

${\omega }_{\eta }(a,c)\le max\{{\omega }_{\eta }(a,b),{\omega }_{\eta }(b,c)\}$, for every $a,b,c\in E$.

In this case, ($E_{\omega },\omega )$ is called a modular ultrametric space.

A modular $\omega$ on E is said to be regular if the following weaker version of (i) is satisfied:

$$\begin{array}{c}\hfill a=b\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}{\omega }_{\eta }(a,b)=0\mathrm{for}\mathrm{some}\lambda >0.\end{array}$$

This condition plays a significant role in ensuring the existence of fixed points for contractive-type mappings in the setting of modular metric spaces.

Example 2

([38]). Let $E=\mathbb{R}$ and ω be defined by ${\omega }_{\eta }(a,b)=\infty$ if $\eta <1$, and let ${\omega }_{\eta }(a,b)=\frac{1}{\eta }|a-b|$ if $\eta \ge 1$. It is easy to verify that ω is regular and is not modular on E.

Definition 3.

Let $E_{\omega }$ be a modular ultrametric space and let $\left\{a_n\right\}$ be a sequence in $E_{\omega }$.

• A point $a\in E_{\omega }$ is called a limit of $\left\{a_n\right\}$ if for each $\eta ,ϵ>0$ there exists $n_0\in \mathbb{N}$ such that ${\omega }_{\eta }(a_n,a)<ϵ$ for all $n\ge n_0$. A sequence that has a limit is said to be convergent (or to converge to a), which is written as $\underset{n\to \infty }{lim}{a}_n=a$.
• A sequence $\left\{a_n\right\}$ in $E_{\omega }$ is said to be a Cauchy sequence if for each $\eta ,ϵ>0$ there exists $n_0\in \mathbb{N}$ such that ${\omega }_{\eta }(a_n,a_{n+1})<ϵ$ for all $n\le n_0$.
• If every Cauchy sequence in E converges, E is said to be complete.

Definition 4

([11]). Let $(E,\omega )$ be a modular ultrametric space. Then, fix $a_0\in E$ and set $E_{\omega }=E_{\omega }\left(a_0\right)=\{a\in E:{\omega }_{\eta }(a,a_0)=0as\eta \to \infty \}$ and $E_{\omega }^{*}=E_{\omega }^{*}\left(a_0\right)=\{a\in E:{\omega }_{\eta }(a,a_0)<\infty for\eta >0\}$, where $E_{\omega }$ and $E_{\omega }^{*}$ are said to be modular spaces centered at $a_0$.

3. Main Results

3.1. Common Fixed Point Theorems in a Complete Modular Ultrametric Space

In this subsection, we prove a number of common fixed point (CFP) results in modular ultrametric spaces.

Theorem 3.

Let $(E_{\omega },\omega )$ be a complete modular ultra-metric space and let $T,S:E_{\omega }\to E_{\omega }$ be continuous self-maps satisfying the following contraction:

$$\begin{array}{cc}\hfill {\omega }_{\eta }(Sa,Tb)\le \alpha {\omega }_{\eta }(a,b)& +\beta {\omega }_{\eta }(a,Sa)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Sa)]\hfill \\ \hfill & +\lambda [{\omega }_{\eta }(a,Sa)+{\omega }_{\eta }(b,Tb)]+\eta [{\omega }_{\eta }(a,Sa)+{\omega }_{\eta }(a,b)]\hfill \end{array}$$

(5)

with $\alpha +\beta +\gamma +2\delta +2\lambda +2\eta <1$, where $\alpha ,\beta ,\gamma ,\delta ,\lambda ,\eta \in [0,1)$. Then, T and S have a unique CFP.

Proof. 

Let $a_0$ be chosen arbitrarily in $E_{\omega }$ with an arbitrary point $a_0$. Further, define a sequence $\left\{a_n\right\}$ with $a_{n+1}=S{a}_n$ and $a_{n+2}=T{a}_{n+1}$ for every $\mathfrak{n}\in \mathbb{N}$.

Now, our aim is to show that $\left\{a_n\right\}$ is a Cauchy sequence in $E_{\omega }$. For this, we take

$$\begin{array}{ccc}\hfill {\omega }_{\eta }(a_{n+1},a_n)& =& {\omega }_{\eta }(S{a}_n,T{a}_{n-1})\hfill \\ \hfill {\omega }_{\eta }(a_{n+1},a_n)& \le & \alpha {\omega }_{\eta }(a_n,a_{n-1})+\beta {\omega }_{\eta }(a_n,S{a}_n)\hfill \\ & & +\gamma {\omega }_{\eta }(a_{n-1},T{a}_{n-1})\hfill \\ & & +\delta [{\omega }_{\eta }(a_n,T{a}_{n-1})+{\omega }_{\eta }(a_{n-1},S{a}_n)]\hfill \\ & & +\lambda [{\omega }_{\eta }(a_n,S{a}_n)+{\omega }_{\eta }(a_{n-1},T{a}_{n-1})]\hfill \\ & & +\eta [{\omega }_{\eta }(a_n,S{a}_n)+{\omega }_{\eta }(a_n,a_{n-1})]\hfill \\ & \le & \alpha {\omega }_{\eta }(a_n,a_{n-1})+\beta {\omega }_{\eta }(a_n,a_{n+1})\hfill \\ & & +\gamma {\omega }_{\eta }(a_{n-1},a_n)\hfill \\ & & +\delta [{\omega }_{\eta }(a_n,a_n)+{\omega }_{\eta }(a_{n-1},a_{n+1})]\hfill \\ & & +\lambda [{\omega }_{\eta }(a_n,a_{n+1})+{\omega }_{\eta }(a_{n-1},a_n)]\hfill \\ & & +\eta [{\omega }_{\eta }(a_n,a_{n+1})+{\omega }_{\eta }(a_n,a_{n-1})]\hfill \\ & \le & \alpha {\omega }_{\eta }(a_n,a_{n-1})+\beta {\omega }_{\eta }(a_n,a_{n+1})\hfill \\ & & +\gamma {\omega }_{\eta }(a_{n-1},a_n)\hfill \\ \hfill & & +\delta max[{\omega }_{\eta }(a_{n-1},a_n),{\omega }_{\eta }(a_n,a_{n+1})]\hfill \\ & & +\lambda [{\omega }_{\eta }(a_n,a_{n+1})+{\omega }_{\eta }(a_{n-1},a_n)]\hfill \\ & & +\eta [{\omega }_{\eta }(a_n,a_{n+1})+{\omega }_{\eta }(a_n,a_{n-1})]\hfill \end{array}$$

(6)

Case 1: If $max\left\{{\omega }_{\eta }(a_{n-1},a_n),{\omega }_{\eta }(a_n,a_{n+1})\right\}={\omega }_{\eta }(a_{n-1},a_n)$, then we have

$$\begin{array}{ccc}\hfill {\omega }_{\eta }(a_{n+1},a_n)& \le & \alpha {\omega }_{\eta }(a_n,a_{n-1})+\beta {\omega }_{\eta }(a_n,a_{n+1})+\gamma {\omega }_{\eta }(a_{n-1},a_n)+\delta {\omega }_{\eta }(a_{n-1},a_n)\hfill \\ & & +\lambda [{\omega }_{\eta }(a_n,a_{n+1})+{\omega }_{\eta }(a_{n-1},a_n)]+\eta [{\omega }_{\eta }(a_n,a_{n+1})+{\omega }_{\eta }(a_n,a_{n-1})],\hfill \end{array}$$

which implies that

$$\begin{array}{cc}\hfill {\omega }_{\eta }(a_{n+1},a_n)& \le {\mathsf{k}}_1{\omega }_{\eta }(a_{n-1},a_n),\hfill \end{array}$$

where ${\mathsf{k}}_1=\frac{\alpha +\gamma +\delta +\lambda +\eta }{1-(\beta +\lambda +\eta )}<1$. Thus,

$$\begin{array}{cc}\hfill {\omega }_{\eta }(a_{n+1},a_n)& \le {\mathsf{k}}_1^n{\omega }_{\eta }(a_{n-1},a_n).\hfill \end{array}$$

(7)

Case 2: If $max\left\{{\omega }_{\eta }(a_{n-1},a_n),{\omega }_{\eta }(a_n,a_{n+1})\right\}={\omega }_{\eta }(a_n,a_{n+1})$, then we have

$$\begin{array}{ccc}\hfill {\omega }_{\eta }(a_{n+1},a_n)& \le & \alpha {\omega }_{\eta }(a_n,a_{n-1})+\beta {\omega }_{\eta }(a_n,a_{n+1})+\gamma {\omega }_{\eta }(a_{n-1},a_n)+\delta {\omega }_{\eta }(a_n,a_{n+1})\hfill \\ & & +\lambda [{\omega }_{\eta }(a_n,a_{n+1})+{\omega }_{\eta }(a_{n-1},a_n)]+\eta [{\omega }_{\eta }(a_n,a_{n+1})+{\omega }_{\eta }(a_n,a_{n-1})],\hfill \end{array}$$

which implies that

$$\begin{array}{cc}\hfill {\omega }_{\eta }(a_{n+1},a_n)& \le {\mathsf{h}}_1{\omega }_{\eta }(a_{n-1},a_n),\hfill \end{array}$$

where ${\mathsf{h}}_1=\frac{\alpha +\gamma +\lambda +\eta }{1-(\beta +\delta +\lambda +\eta )}<1$. Thus,

$$\begin{array}{cc}\hfill {\omega }_{\eta }(a_{n+1},a_n)& \le {\mathsf{h}}_1^n{\omega }_{\eta }(a_{n-1},a_n).\hfill \end{array}$$

(8)

Because ${\mathsf{k}}_1,{\mathsf{h}}_1<1$, we have $\underset{n\to \infty }{lim}{\mathsf{k}}_1^n=\underset{n\to \infty }{lim}{\mathsf{h}}_1^n=0$ in both cases, and can conclude that $\left\{a_n\right\}$ is a Cauchy sequence in $E_{\omega }$. Because $E_{\omega }$ is complete, there exists a point $\upsilon \in E_{\omega }$ such that $\underset{n\to \infty }{lim}{a}_n=\upsilon$. Now, applying Condition (5), we have

$$\begin{array}{ccc}\hfill {\omega }_{\eta }(\upsilon ,T\upsilon )& \le & max\{{\omega }_{\eta }(\upsilon ,a_{n+1}),{\omega }_{\eta }(a_{n+1},T\upsilon )\}\hfill \\ & \le & max\{{\omega }_{\eta }(\upsilon ,a_{n+1}),{\omega }_{\eta }(S{a}_n,T\upsilon )\}\hfill \\ & \le & max\{{\omega }_{\eta }(\upsilon ,a_{n+1}),\alpha {\omega }_{\eta }(a_n,\upsilon )+\beta {\omega }_{\eta }(a_n,S{a}_n)+\gamma {\omega }_{\eta }(\upsilon ,T\upsilon )\hfill \\ & & +\delta [{\omega }_{\eta }(a_n,T\upsilon )+{\omega }_{\eta }(\upsilon ,S{a}_n)]+\lambda [{\omega }_{\eta }(a_n,S{a}_n)+{\omega }_{\eta }(\upsilon ,T\upsilon )]\hfill \\ & & +\eta [{\omega }_{\eta }(a_n,S{a}_n)+{\omega }_{\eta }(a_n,\upsilon )]\}.\hfill \end{array}$$

Taking the limit $n\to \infty$, we obtain

$$\begin{array}{c}\hfill {\omega }_{\eta }(\upsilon ,T\upsilon )\le (\gamma +\delta +\lambda ){\omega }_{\eta }(\upsilon ,T\upsilon ).\end{array}$$

As $\gamma +\delta +\lambda <1$, it can easily be seen that $\upsilon$ is a fixed point of T and a CFP of S and T, as indicated by $\upsilon =T\upsilon$ and $\upsilon =S\upsilon$. To prove the uniqueness, suppose that T and S have an another CFP with $\mathsf{w}\ne \upsilon$. Then, we have

$$\begin{array}{ccc}\hfill {\omega }_{\eta }(\upsilon ,\mathsf{w})& =& {\omega }_{\eta }(S\upsilon ,T\mathsf{w})\hfill \\ & \le & \alpha {\omega }_{\eta }(\upsilon ,\mathsf{w})+\beta {\omega }_{\eta }(\upsilon ,S\upsilon )+\gamma {\omega }_{\eta }(\mathsf{w},T\mathsf{w})\hfill \\ & & +\delta [{\omega }_{\eta }(\upsilon ,T\mathsf{w})+{\omega }_{\eta }(\omega ,S\upsilon )]\hfill \\ & & +\lambda [{\omega }_{\eta }(\upsilon ,S\upsilon )+{\omega }_{\eta }(\mathsf{w},T\mathsf{w})]\hfill \\ & & +\eta [{\omega }_{\eta }(\upsilon ,S\upsilon )+{\omega }_{\eta }(\upsilon ,\mathsf{w})]\hfill \\ & \le & (\alpha +2\delta +\eta ){\omega }_{\eta }(\upsilon ,\mathsf{w}),\hfill \end{array}$$

and because $\alpha +2\delta +\eta <1$, we can conclude that $\mathsf{w}=\upsilon$. Therefore, T and S have a unique CFP in $E_{\omega }$. □

If we set $\eta =0$ in Theorem 3, we obtain the following result.

Theorem 4.

Let $(E_{\omega },\omega )$ be a complete modular ultra-metric space and let $T,S:E_{\omega }\to E_{\omega }$ be continuous self-maps satisfying the following contraction:

$$\begin{array}{ccc}\hfill {\omega }_{\eta }(Sa,Tb)& \le & \alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Sa)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Sa)+{\omega }_{\eta }(b,Tb)]\hfill \\ & & +\lambda [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Sa)],\hfill \end{array}$$

(9)

with $\alpha +\beta +\gamma +2\delta +2\lambda <1$ and $\alpha ,\beta ,\gamma ,\delta ,\lambda \in [0,1)$. Then, T and S have a unique CFP.

By setting $\lambda =0$ in Theorem 4, we can derive the following outcome.

Theorem 5.

Let $(E_{\omega },\omega )$ be a complete modular ultra-metric space and let $T,S:E_{\omega }\to E_{\omega }$ be continuous self-mappings fulfilling the following contraction:

$$\begin{array}{c}\hfill {\omega }_{\eta }(Sa,Tb)\le \alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Sa)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Sa)],\end{array}$$

(10)

with $\alpha +\beta +\gamma +2\delta <1$ and $\alpha ,\beta ,\gamma ,\delta \in [0,1)$. Then, T and S have a unique CFP.

Example 3.

Let $E_{\omega }=[0,1]$ be equipped with modular ultrametric

$$\begin{array}{c}\hfill {\omega }_{\eta }(a,b)=\left\{\begin{array}{ccc}\hfill \frac{a+b}{\eta }& for& a\ne b;\hfill \\ \hfill 0& for& otherwise,\hfill \end{array}\right.\end{array}$$

for all $a,b\in E_{\omega }$ and let $\eta >0$. Moreover, define the mappings $S,T:E_{\omega }\to E_{\omega }$ by $Ta=\frac{a^2}{4}$ and $Sa=\frac{a}{2}$ for all $a\in E_{\omega }$ and take $\alpha =\beta =\gamma =\delta =\frac{1}{6}$. Then, we have $\alpha +\beta +\gamma +2\delta <1$. Further, we obtain

$$\begin{array}{cc}\hfill {\omega }_{\eta }(Sa,Tb)& =\frac{Sa+Tb}{\eta }\hfill \\ \hfill & =\frac{2a+b^2}{4\eta }\hfill \\ \hfill & \le \frac{1}{6}\left(\frac{32a+20b+3b^2}{4\eta }\right)\hfill \\ \hfill & \le \alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Sa)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Sa)]\hfill \\ \hfill & +\lambda [{\omega }_{\eta }(a,Sa)+{\omega }_{\eta }(b,Tb)]+\eta [{\omega }_{\eta }(a,Sa)+{\omega }_{\eta }(a,b)].\hfill \end{array}$$

From the above inequality, it is clear that Condition (5) holds for S and T, that there is a fixed point in common, and that this point is $a=0$.

From Figure 2, it is clear that S and T have a common fixed point.

Figure 2. Common fixed point.

Remark 1.

In the above examples, when $\lambda =0$ and $\eta =0$ we obtain the results shown below.

Consider $E_{\omega }=[0,1]$ to be equipped with the modular ultrametric

$$\begin{array}{c}\hfill {\omega }_{\eta }(a,b)=\left\{\begin{array}{ccc}\hfill \frac{a+b}{\eta }& for& a\ne b;\hfill \\ \hfill 0& for& otherwise,\hfill \end{array}\right.\end{array}$$

for all $a,b\in E_{\omega }$ and $\eta >0$. Moreover, define the mappings $S,T:E_{\omega }\to E_{\omega }$ by $Ta=\frac{a^2}{4}$ and $Sa=\frac{a}{2}$ for all $a\in E_{\omega }$, and take $\alpha =\beta =\gamma =\delta =\frac{1}{6}$. Then, we have $\alpha +\beta +\gamma +2\delta <1$. Further, we obtain

$$\begin{array}{cc}\hfill {\omega }_{\eta }(Sa,Tb)& =\frac{Sa+Tb}{\eta }\hfill \\ \hfill & =\frac{2a+b^2}{4\eta }\hfill \\ \hfill & \le \frac{1}{3}\left(\frac{8a+6b+b^2}{4\eta }\right)\hfill \\ \hfill & \le \alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Sa)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Sa)].\hfill \end{array}$$

From the above inequality, it is clear that Condition (10) holds for S and T, that there is a fixed point in common, and that this point is $a=0$.

3.2. Fixed Point Theorems in Modular Ultrametric Spaces

If we set $S=T$ in Theorems 3–5, we obtain the following results.

Theorem 6.

Let $(E_{\omega },\omega )$ be a complete modular ultra-metric space and let $T:E_{\omega }\to E_{\omega }$ be a continuous self-map satisfying the following contraction:

$$\begin{array}{ccc}\hfill {\omega }_{\eta }(Ta,Tb)& \le & \alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Ta)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Sa)+{\omega }_{\eta }(b,Tb)]\hfill \\ & & +\lambda [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Ta)]+\eta [{\omega }_{\eta }(a,Ta)+{\omega }_{\eta }(a,b)],\hfill \end{array}$$

(11)

where $\alpha ,\beta ,\gamma ,\delta ,\lambda ,\eta \in [0,1)$ with $\alpha +\beta +\gamma +2\delta +2\lambda +2\eta <1$. Then, T has exactly one fixed point.

Proof. 

Let $a_0$ be chosen arbitrarily in $E_{\omega }$ with an arbitrary point $a_0$. Further, define a sequence $\left\{a_n\right\}$ with $a_{n+1}=T{a}_n$ for every $\mathfrak{n}\in \mathbb{N}$.

Now, our aim is to show that $\left\{a_n\right\}$ is a Cauchy sequence in $E_{\omega }$. For this, we take

$$\begin{array}{ccc}\hfill {\omega }_{\eta }(a_{n+1},a_n)& =& {\omega }_{\eta }(T{a}_n,T{a}_{n-1})\hfill \\ \hfill {\omega }_{\eta }(a_{n+1},a_n)& \le & \alpha {\omega }_{\eta }(a_n,a_{n-1})+\beta {\omega }_{\eta }(a_n,T{a}_n)\hfill \\ & & +\gamma {\omega }_{\eta }(a_{n-1},T{a}_{n-1})+\delta [{\omega }_{\eta }(a_n,T{a}_{n-1})\hfill \\ & & +{\omega }_{\eta }(a_{n-1},T{a}_n)]\hfill \\ & & +\lambda [{\omega }_{\eta }(a_n,T{a}_n)+{\omega }_{\eta }(a_{n-1},T{a}_{n-1})]\hfill \\ & & +\eta [{\omega }_{\eta }(a_n,T{a}_n)+{\omega }_{\eta }(a_n,a_{n-1})]\hfill \\ & \le & \alpha {\omega }_{\eta }(a_n,a_{n-1})+\beta {\omega }_{\eta }(a_n,a_{n+1})+\gamma {\omega }_{\eta }(a_{n-1},a_n)\hfill \\ & & +\delta [{\omega }_{\eta }(a_n,a_n)+{\omega }_{\eta }(a_{n-1},a_{n+1})]\hfill \\ & & +\lambda [{\omega }_{\eta }(a_n,a_{n+1})+{\omega }_{\eta }(a_{n-1},a_n)]+\eta [{\omega }_{\eta }(a_n,a_{n+1})\hfill \\ & & +{\omega }_{\eta }(a_n,a_{n-1})]\hfill \\ & \le & \alpha {\omega }_{\eta }(a_n,a_{n-1})+\beta {\omega }_{\eta }(a_n,a_{n+1})+\gamma {\omega }_{\eta }(a_{n-1},a_n)\hfill \\ & & +\delta max[{\omega }_{\eta }(a_{n-1},a_n),{\omega }_{\eta }(a_n,a_{n+1})]\hfill \\ & & +\lambda [{\omega }_{\eta }(a_n,a_{n+1})+{\omega }_{\eta }(a_{n-1},a_n)]+\eta [{\omega }_{\eta }(a_n,a_{n+1})\hfill \\ & & +{\omega }_{\eta }(a_n,a_{n-1})].\hfill \end{array}$$

(12)

Case 1: If $max\left\{{\omega }_{\eta }(a_{n-1},a_n),{\omega }_{\eta }(a_n,a_{n+1})\right\}={\omega }_{\eta }(a_{n-1},a_n)$, then we have

$$\begin{array}{ccc}\hfill {\omega }_{\eta }(a_{n+1},a_n)& \le & \alpha {\omega }_{\eta }(a_n,a_{n-1})+\beta {\omega }_{\eta }(a_n,a_{n+1})\hfill \\ & & +\gamma {\omega }_{\eta }(a_{n-1},a_n)+\delta {\omega }_{\eta }(a_{n-1},a_n)\hfill \\ & & +\lambda [{\omega }_{\eta }(a_n,a_{n+1})+{\omega }_{\eta }(a_{n-1},a_n)]\hfill \\ & & +\eta [{\omega }_{\eta }(a_n,a_{n+1})+{\omega }_{\eta }(a_n,a_{n-1})],\hfill \end{array}$$

which implies that

$$\begin{array}{cc}\hfill {\omega }_{\eta }(a_{n+1},a_n)& \le {\mathsf{k}}_1{\omega }_{\eta }(a_{n-1},a_n),\hfill \end{array}$$

where ${\mathsf{k}}_2=\frac{\alpha +\gamma +\delta +\lambda +\eta }{1-(\beta +\lambda +\eta )}<1$. Thus,

$$\begin{array}{cc}\hfill {\omega }_{\eta }(a_{n+1},a_n)& \le {\mathsf{k}}_2^n{\omega }_{\eta }(a_{n-1},a_n).\hfill \end{array}$$

(13)

Case 2: If $max\left\{{\omega }_{\eta }(a_{n-1},a_n),{\omega }_{\eta }(a_n,a_{n+1})\right\}={\omega }_{\eta }(a_n,a_{n+1})$, then we have

$$\begin{array}{ccc}\hfill {\omega }_{\eta }(a_{n+1},a_n)& \le & \alpha {\omega }_{\eta }(a_n,a_{n-1})+\beta {\omega }_{\eta }(a_n,a_{n+1})\hfill \\ & & +\gamma {\omega }_{\eta }(a_{n-1},a_n)+\delta {\omega }_{\eta }(a_n,a_{n+1})\hfill \\ & & +\lambda [{\omega }_{\eta }(a_n,a_{n+1})+{\omega }_{\eta }(a_{n-1},a_n)]\hfill \\ & & +\eta [{\omega }_{\eta }(a_n,a_{n+1})+{\omega }_{\eta }(a_n,a_{n-1})],\hfill \end{array}$$

which implies that

$$\begin{array}{cc}\hfill {\omega }_{\eta }(a_{n+1},a_n)& \le {\mathsf{h}}_2{\omega }_{\eta }(a_{n-1},a_n),\hfill \end{array}$$

where ${\mathsf{h}}_2=\frac{\alpha +\gamma +\lambda +\eta }{1-(\beta +\delta +\lambda +\eta )}<1$. Thus,

$$\begin{array}{cc}\hfill {\omega }_{\eta }(a_{n+1},a_n)& \le {\mathsf{h}}_2^n{\omega }_{\eta }(a_{n-1},a_n).\hfill \end{array}$$

(14)

Because ${\mathsf{k}}_2,{\mathsf{h}}_2<1$, we have $\underset{n\to \infty }{lim}{\mathsf{k}}_2^n=\underset{n\to \infty }{lim}{\mathsf{h}}_2^n=0$. In both cases, we can conclude that $\left\{a_n\right\}$ is a Cauchy sequence in $E_{\omega }$. Because $E_{\omega }$ is complete, there exists a point $\upsilon \in E_{\omega }$ such that $\underset{n\to \infty }{lim}{a}_n=\upsilon$. Now, applying Condition (5), we have

$$\begin{array}{ccc}\hfill {\omega }_{\eta }(\upsilon ,T\upsilon )& \le & max\{{\omega }_{\eta }(\upsilon ,a_{n+1}),{\omega }_{\eta }(a_{n+1},T\upsilon )\}\hfill \\ & \le & max\{{\omega }_{\eta }(\upsilon ,a_{n+1}),{\omega }_{\eta }(T{a}_n,T\upsilon )\}\hfill \\ & \le & max\{{\omega }_{\eta }(\upsilon ,a_{n+1}),\alpha {\omega }_{\eta }(a_n,\upsilon )+\beta {\omega }_{\eta }(a_n,T{a}_n)+\gamma {\omega }_{\eta }(\upsilon ,T\upsilon )\hfill \\ & & +\delta [{\omega }_{\eta }(a_n,T\upsilon )+{\omega }_{\eta }(\upsilon ,T{a}_n)]+\lambda [{\omega }_{\eta }(a_n,T{a}_n)+{\omega }_{\eta }(\upsilon ,T\upsilon )]\hfill \\ & & +\eta [{\omega }_{\eta }(a_n,T{a}_n)+{\omega }_{\eta }(a_n,\upsilon )]\}.\hfill \end{array}$$

Taking the limit $n\to \infty$, we obtain

$$\begin{array}{c}\hfill {\omega }_{\eta }(\upsilon ,T\upsilon )\le (\gamma +\delta +\lambda ){\omega }_{\eta }(\upsilon ,T\upsilon ).\end{array}$$

As $\gamma +\delta +\lambda <1$, it can easily be seen that $\upsilon$ is a fixed point of T, as indicated by $\upsilon =T\upsilon$. To prove the uniqueness, suppose that T has an another fixed point with $\mathsf{w}\ne \upsilon$. Then, we have

$$\begin{array}{ccc}\hfill {\omega }_{\eta }(\upsilon ,\mathsf{w})& =& {\omega }_{\eta }(T\upsilon ,T\mathsf{w})\hfill \\ & \le & \alpha {\omega }_{\eta }(\upsilon ,\mathsf{w})+\beta {\omega }_{\eta }(\upsilon ,T\upsilon )+\gamma {\omega }_{\eta }(\mathsf{w},T\mathsf{w})\hfill \\ & & +\delta [{\omega }_{\eta }(\upsilon ,T\mathsf{w})+{\omega }_{\eta }(\mathsf{w},T\upsilon )]\hfill \\ & & +\lambda [{\omega }_{\eta }(\upsilon ,T\upsilon )+{\omega }_{\eta }(\mathsf{w},T\mathsf{w})]\hfill \\ & & +\eta [{\omega }_{\eta }(\upsilon ,T\upsilon )+{\omega }_{\eta }(\upsilon ,\mathsf{w})]\hfill \\ & \le & (\alpha +2\delta +\eta ){\omega }_{\eta }(\upsilon ,\mathsf{w}),\hfill \end{array}$$

and as $\alpha +2\delta +\eta <1$, we can conclude that $\mathsf{w}=\upsilon$. Therefore, T has a unique fixed point in $E_{\omega }$. □

Theorem 7.

Let $(E_{\omega },\omega )$ be a complete modular ultra-metric space and let $T:E_{\omega }\to E_{\omega }$ be a continuous self-map satisfying the following contraction:

$$\begin{array}{ccc}\hfill {\omega }_{\eta }(Ta,Tb)& \le & \alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Ta)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Ta)+{\omega }_{\eta }(b,Tb)]\hfill \\ & & +\lambda [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Ta)],\hfill \end{array}$$

(15)

where $\alpha ,\beta ,\gamma ,\delta ,\lambda \in [0,1)$ with $\alpha +\beta +\gamma +2\delta +2\lambda <1$. Then, T has exactly one fixed point.

Theorem 8.

Let $(E_{\omega },\omega )$ be a complete modular ultra-metric space and let $T:E_{\omega }\to E_{\omega }$ be a continuous self-map satisfying the following contraction:

$$\begin{array}{c}\hfill {\omega }_{\eta }(Ta,Tb)\le \alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Ta)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Ta)],\end{array}$$

(16)

where $\alpha ,\beta ,\gamma ,\delta \in [0,1)$ with $\alpha +\beta +\gamma +2\delta <1$. Then, T has a unique fixed point.

Example 4.

Let $E_{\omega }=[0,1]$ be equipped with the modular ultrametric

$$\begin{array}{c}\hfill {\omega }_{\eta }(a,b)=\left\{\begin{array}{ccc}\hfill \frac{a+b}{\eta }& for& a\ne b;\hfill \\ \hfill 0& for& otherwise;\hfill \end{array}\right.\end{array}$$

for all $a,b\in E_{\omega }$ and $\eta >0$. Now, define a map $T:E_{\omega }\to E_{\omega }$ by $Ta=\frac{a}{2}$ for all $a\in E_{\omega }$ and take $\alpha =\beta =\gamma =\delta =\frac{1}{6}$. Now, we have $\alpha +\beta +\gamma +2\delta <1$. Further, we obtain

$$\begin{array}{cc}\hfill {\omega }_{\eta }(Ta,Tb)& =\frac{Ta+Tb}{\eta }\hfill \\ \hfill & =\frac{a+b}{2\eta }\hfill \\ \hfill & \le \frac{4}{3}\left(\frac{a+b}{2\eta }\right)\hfill \\ \hfill & \le \alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Ta)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Ta)].\hfill \end{array}$$

From the above inequality, it is clear that Condition (16) holds for T; thus, it has a fixed point, which is $a=0$.

From Figure 3, it is clear that T has a fixed point.

Figure 3. Fixed point.

Example 5.

Let $E_{\omega }=\mathbb{R}$ be endowed with the modular ultrametric

$$\begin{array}{c}\hfill {\omega }_{\eta }(a,b)=\left\{\begin{array}{cc}\frac{1}{\eta }\left(\right|a|+\left|b\right|),\hfill & if a\ne b\hfill \\ 0,\hfill & if a=b\hfill \end{array}\right.\end{array}$$

for all $a,b\in E_{\omega }$ and $\eta >0$. Define $T:E_{\omega }\to E_{\omega }$ by

$$\begin{array}{c}\hfill Ta=\left\{\begin{array}{cc}2a^{10},\hfill & if a\in (-\infty ,0)\hfill \\ \frac{1}{8}{a}^2,\hfill & if a\in [0,1)\hfill \\ \frac{1}{8}{a}^{,}\hfill & if a\in [1,2)\hfill \\ \frac{1}{4},\hfill & if a\in [2,+\infty ).\hfill \end{array}\right.\end{array}$$

Clearly, $E_{\omega }$ is a complete modular space. Let $\alpha =\beta =\gamma =\delta =\frac{1}{6}$; then, we have $\alpha +\beta +\gamma +2\delta <1$.

Now, we consider the following cases:

• Let $a,b\in [0,1)$; then,

$$\begin{array}{cc}\hfill {\omega }_{\eta }(Ta,Tb)& =\frac{1}{8}{a}^2+\frac{1}{8}{b}^2\hfill \\ \hfill & =\frac{1}{8}(a^2+b^2)\hfill \\ \hfill & <\frac{1}{24}(a^2+b^2+12a+12b)\hfill \\ \hfill & <\alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Ta)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Ta)].\hfill \end{array}$$

• Let $a,b\in [1,2)$; then,

$$\begin{array}{cc}\hfill {\omega }_{\eta }(Ta,Tb)& =\frac{1}{8}a+\frac{1}{8}b\hfill \\ \hfill & =\frac{1}{8}(a+b)\hfill \\ \hfill & <\frac{13}{24}(a+b)\hfill \\ \hfill & <\alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Ta)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Ta)].\hfill \end{array}$$

• Let $a,b\in [2,\infty )$; then,

$$\begin{array}{cc}\hfill {\omega }_{\eta }(Ta,Tb)& =\frac{1}{4}+\frac{1}{4}\hfill \\ \hfill & =\frac{1}{2}\hfill \\ \hfill & <\frac{1}{2}(a+b+\frac{1}{3})\hfill \\ \hfill & <\alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Ta)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Ta)].\hfill \end{array}$$

• Let $a\in [0,1)$ and $b\in [1,2)$; then,

$$\begin{array}{cc}\hfill {\omega }_{\eta }(Ta,Tb)& =\frac{1}{8}{a}^2+\frac{1}{8}b\hfill \\ \hfill & =\frac{1}{8}(a^2+b)\hfill \\ \hfill & <\frac{1}{24}(a^2+12a+13b)\hfill \\ \hfill & <\alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Ta)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Ta)].\hfill \end{array}$$

• Let $a\in [0,1)$ and $b\in [2,\infty )$; then,

$$\begin{array}{cc}\hfill {\omega }_{\eta }(Ta,Tb)& =\frac{1}{8}{a}^2+\frac{1}{4}\hfill \\ \hfill & =\frac{1}{8}(a^2+2)\hfill \\ \hfill & <\frac{1}{24}(a^2+12a+12b+2)\hfill \\ \hfill & <\alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Ta)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Ta)].\hfill \end{array}$$

• Let $a\in \left[1.2\right)$ and $b\in [2,\infty )$; then,

$$\begin{array}{cc}\hfill {\omega }_{\eta }(Ta,Tb)& =\frac{1}{8}a+\frac{1}{4}\hfill \\ \hfill & =\frac{1}{8}(a+2)\hfill \\ \hfill & <\frac{1}{24}(13a+12b+2)\hfill \\ \hfill & <\alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Ta)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Ta)].\hfill \end{array}$$

Hence, all conditions of Theorem 8 hold and T has a fixed point. Here, $a=0$ is the fixed point of T.

4. Applications

4.1. Application to Well-Posedness

The concept of well-posedness is crucial in studying fixed point problems, as it provides a rigorous framework to analyze solutions’ existence, uniqueness, and stability. When a fixed point problem is well-posed, it possesses a unique solution. The French mathematician Jacques Hadamard introduced the concept of well-posedness in the early 20th century to distinguish between mathematically significant and poorly defined problems. A well-posed problem has three fundamental properties: existence, uniqueness, and stability. Well-posedness is particularly substantial in numerical analysis and scientific computing, as it enables accurate and efficient solutions using numerical methods. The solutions obtained from well-posed problems can be relied upon to make predictions and draw meaningful conclusions. To establish well-posedness in fixed point problems, the underlying properties of the mapping or function must be analyzed using mathematical techniques and tools such as contraction mapping theorems, topological methods, etc. Blasi and Myjak have presented a study on the well-posedness of fixed point problems [39]. This section deals with the concept of well-posedness and investigates the well-posedness of CFP problems.

Definition 5

([23,33]). Let T be a self-mapping of $E_{\omega }$. Then, the fixed point problem of T is called well-posed if:

(1) 

T has precisely one fixed point $a_0\in E_{\omega }$

(2) 

For every sequence, $\left\{a_n\right\}\in E_{\omega }$ and $\underset{n\to \infty }{lim}{\omega }_{\eta }(a_n,T{a}_n)=0$, implying that $\underset{n\to \infty }{lim}{\omega }_{\eta }(a_n,a_0)=0$.

Let the family of all common fixed points of S and T be denoted by CFP$(T,S)$.

Definition 6

([23,33]). Let $T,S:E_{\omega }\to E_{\omega }$. Then, CFP$(T,S)$ is called well-posed if:

(1) 

For every sequence, $a_n\in E_{\omega }$ with $a^{*}\in CFP(T,S)$ and

$$\underset{n\to \infty }{lim}{\omega }_{\eta }(a_n,T{a}_n)=0=\underset{n\to \infty }{lim}{\omega }_{\eta }(a_n,S{a}_n),$$

implying that

$$a^{*}=\underset{n\to \infty }{lim}{a}_n.$$

(2) 

CFP$(T,S)$ is a singleton.

Theorem 9.

Let $(E_{\omega },\omega )$ be a complete modular ultra-metric space and let S, T be the self-mappings on $E_{\omega }$ such that

$$\begin{array}{c}\hfill {\omega }_{\eta }(Sa,Tb)\le \alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Sa)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Sa)]\end{array}$$

(17)

for all $a,b\in E_{\omega }$. Then, the problem of the CFP of $S,T$ is well-posed.

Proof. 

In Theorem 5, we have proved that the CFP of S and T exists and is unique. Now, let $a^{*}$ be a unique CFP of S and T and let $\left\{a_n\right\}$ be a sequence in $E_{\omega }$ and

$$\underset{n\to \infty }{lim}{\omega }_{\eta }(a_n,T{a}_n)=0=\underset{n\to \infty }{lim}{\omega }_{\eta }(a_n,S{a}_n).$$

Assume that, for the sake of simplicity, $a^{*}\ne a_n$ for any non-negative integer n. By utilizing Inequality (10), we can derive the following:

$$\begin{array}{ccc}\hfill {\omega }_{\eta }(a^{*},a_n)& \le & max\left\{{\omega }_{\eta }(a^{*},T{a}_n),{\omega }_{\eta }(T{a}_n,a_n)\right\}\hfill \\ & \le & max\left\{{\omega }_{\eta }(T{a}^{*},T{a}_n),{\omega }_{\eta }(T{a}_n,a_n)\right\}\hfill \\ & \le & max\{\alpha {\omega }_{\eta }(a^{*},a_n)+\beta {\omega }_{\eta }(a^{*},S{a}^{*})+\gamma {\omega }_{\eta }(a_n,T{a}_n)\hfill \\ & & +\delta [{\omega }_{\eta }(a^{*},T{a}_n)+{\omega }_{\eta }(a_n,S{a}^{*})],{\omega }_{\eta }(T{a}_n,a_n)\}.\hfill \end{array}$$

Taking the limit as $n\to \infty$, we have

$$\begin{array}{c}\hfill {\omega }_{\eta }(a^{*},a_n)\le (\alpha +2\delta ){\omega }_{\eta }(a^{*},a_n),\end{array}$$

which yields $\underset{n\to \infty }{lim}{\omega }_{\eta }(a^{*},a_n)=0$, as $\alpha +2\delta <1$. □

Theorem 10.

Let $(E_{\omega },\omega )$ be a complete modular ultra-metric space and let T be a self-map on $E_{\omega }$ such that

$$\begin{array}{c}\hfill {\omega }_{\eta }(Ta,Tb)\le \alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Ta)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Ta)]\end{array}$$

(18)

for all $a,b\in E_{\omega }$. Then, the problem of FP of T is well-posed.

Theorem 11.

Let $(E_{\omega },\omega )$ be a complete modular ultra-metric space and let $S,T$ be the self-mappings on $E_{\omega }$ such that

$$\begin{array}{ccc}\hfill {\omega }_{\eta }(Sa,Tb)& \le & \alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Sa)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Sa)+{\omega }_{\eta }(b,Tb)]\hfill \\ & & +\lambda [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Sa)]\hfill \end{array}$$

for all $a,b\in E_{\omega }$. Then. the problem of the CFP of $S,T$ is well-posed.

Proof. 

In Theorem 4, we have proved that the CFP of S and T exists and is unique. Now, let $a^{*}$ be a unique CFP of S and T, let $\left\{a_n\right\}$ be a sequence in $E_{\omega }$, and let

$$\underset{n\to \infty }{lim}{\omega }_{\eta }(a_n,T{a}_n)=0=\underset{n\to \infty }{lim}{\omega }_{\eta }(a_n,S{a}_n).$$

Assume for the sake of simplicity that $a^{*}\ne a_n$ for any non-negative integer n. Utilizing Inequality (9), we can derive the following:

$$\begin{array}{cc}\hfill {\omega }_{\eta }(a^{*},a_n)& \le max\left\{{\omega }_{\eta }(a^{*},T{a}_n),{\omega }_{\eta }(T{a}_n,a_n)\right\}\hfill \\ \hfill & \le max\left\{{\omega }_{\eta }(T{a}^{*},T{a}_n),{\omega }_{\eta }(T{a}_n,a_n)\right\}\hfill \\ \hfill & \le max\{\alpha {\omega }_{\eta }(a^{*},a_n)+\beta {\omega }_{\eta }(a^{*},S{a}^{*})+\gamma {\omega }_{\eta }(a_n,T{a}_n)+\delta [{\omega }_{\eta }(a^{*},S{a}^{*})+{\omega }_{\eta }(a_n,T{a}_n)]\hfill \\ \hfill & +\lambda [{\omega }_{\eta }(a^{*},T{a}_n)+{\omega }_{\eta }(a_n,S{a}^{*})],{\omega }_{\eta }(T{a}_n,a_n)\}.\hfill \end{array}$$

Taking the limit as $n\to \infty$, we have

$$\begin{array}{c}\hfill {\omega }_{\eta }(a^{*},a_n)\le (\alpha +2\lambda ){\omega }_{\eta }(a^{*},a_n),\end{array}$$

which yields $\underset{n\to \infty }{lim}{\omega }_{\eta }(a^{*},a_n)=0$, as $\alpha +2\lambda <1$. □

Theorem 12.

Let $(E_{\omega },\omega )$ be a complete modular ultra-metric space and let T be a self-map on $E_{\omega }$ such that

$$\begin{array}{cc}\hfill {\omega }_{\eta }(Ta,Tb)\le & \alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Ta)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Ta)+{\omega }_{\eta }(b,Tb)]\hfill \\ \hfill & +\lambda [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Ta)]\hfill \end{array}$$

(19)

for all $a,b\in E_{\omega }$. Then, the problem of the FP of T is well-posed.

Theorem 13.

Let $(E_{\omega },\omega )$ be a complete modular ultra-metric space and let $S,T$ be the self-mappings on $E_{\omega }$ such that

$$\begin{array}{cc}\hfill {\omega }_{\eta }(Sa,Tb)\le \alpha {\omega }_{\eta }(a,b)& +\beta {\omega }_{\eta }(a,Sa)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Sa)+{\omega }_{\eta }(b,Tb)]\hfill \\ \hfill & +\lambda [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Sa)]+\eta [{\omega }_{\eta }(a,Sa)+{\omega }_{\eta }(a,b)]\hfill \end{array}$$

(20)

for all $a,b\in E_{\omega }$. Then, the problem of the CFP of $S,T$ is well-posed.

Proof. 

In Theorem 3, we proved that the CFP of S and T exists and is unique. Now, let $a^{*}$ be a unique CFP of S and T, let $\left\{a_n\right\}$ be a sequence in $E_{\omega }$, and let

$$\underset{n\to \infty }{lim}{\omega }_{\eta }(a_n,T{a}_n)=0=\underset{n\to \infty }{lim}{\omega }_{\eta }(a_n,S{a}_n).$$

Assume for the sake of simplicity that $a^{*}\ne a_n$ for any non-negative integer n. Utilizing Condition (5), we can derive the following:

$$\begin{array}{cc}\hfill {\omega }_{\eta }(a^{*},a_n)& \le max\left\{{\omega }_{\eta }(a^{*},T{a}_n),{\omega }_{\eta }(T{a}_n,a_n)\right\}\hfill \\ \hfill & \le max\left\{{\omega }_{\eta }(T{a}^{*},T{a}_n),{\omega }_{\eta }(T{a}_n,a_n)\right\}\hfill \\ \hfill & \le max\{\alpha {\omega }_{\eta }(a^{*},a_n)+\beta {\omega }_{\eta }(a^{*},S{a}^{*})+\gamma {\omega }_{\eta }(a_n,T{a}_n)+\delta [{\omega }_{\eta }(a^{*},S{a}^{*})+{\omega }_{\eta }(a_n,T{a}_n)]\hfill \\ \hfill & +\lambda [{\omega }_{\eta }(a^{*},T{a}_n)+{\omega }_{\eta }(a_n,S{a}^{*})]+\eta [{\omega }_{\eta }(a^{*},S{a}^{*})+{\omega }_{\eta }(a^{*},a_n)],{\omega }_{\eta }(T{a}_n,a_n)\}.\hfill \end{array}$$

Taking the limit as $n\to \infty$, we have

$$\begin{array}{c}\hfill {\omega }_{\eta }(a^{*},a_n)\le (\alpha +2\lambda +\eta ){\omega }_{\eta }(a^{*},a_n),\end{array}$$

which yields $\underset{n\to \infty }{lim}{\omega }_{\eta }(a^{*},a_n)=0$, as $\alpha +2\lambda +\eta <1$. □

Theorem 14.

Let $(E_{\omega },\omega )$ be a complete modular ultra-metric space and let T be a self-map on $E_{\omega }$ such that

$$\begin{array}{cc}\hfill {\omega }_{\eta }(Ta,Tb)\le & \alpha {\omega }_{\eta }(a,b)+\beta {\omega }_{\eta }(a,Ta)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Sa)+{\omega }_{\eta }(b,Tb)]\hfill \\ \hfill & +\lambda [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Ta)]+\eta [{\omega }_{\eta }(a,Ta)+{\omega }_{\eta }(a,b)]\hfill \end{array}$$

(21)

for all $a,b\in E_{\omega }$. Then, the problem of FP of T is well-posed.

4.2. Application to Integral Equations

Integral equations arise in many scientific and engineering problems. A large class of initial and boundary value problem can be converted to integral equation.

Theorem 15.

Let $(E_{\omega },\omega )$ be a complete modular ultra-metric space and let S, $T:E_{\omega }\to E_{\omega }$ be continuous mapping such that

$$\begin{array}{cc}\hfill {\omega }_{\eta }(Sa,Tb)\le \alpha {\omega }_{\eta }(a,b)& +\beta {\omega }_{\eta }(a,Sa)+\gamma {\omega }_{\eta }(b,Tb)+\delta [{\omega }_{\eta }(a,Tb)+{\omega }_{\eta }(b,Sa)]\hfill \\ \hfill & +\lambda [{\omega }_{\eta }(a,Sa)+{\omega }_{\eta }(b,Tb)]+\eta [{\omega }_{\eta }(a,Sa)+{\omega }_{\eta }(a,b)]\hfill \end{array}$$

(22)

with $\alpha +\beta +\gamma +2\delta +2\lambda +2\eta <1$, where $\alpha ,\beta ,\gamma ,\delta ,\lambda ,\eta \in [0,1)$. Then, T and S admit a unique common fixed point.

Let $W=C([0,1],{\mathbb{R}}^{+})$ be the family of continuous functions defined on $[0,1]$. The following are two integral equations:

$$\begin{array}{c}\hfill a\left(e\right)={\int }_0^{e}H(e,f,a\left(f\right))df\end{array}$$

(23)

$$\begin{array}{c}\hfill b\left(e\right)={\int }_0^{e}G(e,f,b\left(f\right))df\end{array}$$

(24)

for all $e\in [0,1]$, where $H,G:[0,1]\times [0,1]\times W\to \mathbb{R}$. For $a\in C([0,1],{\mathbb{R}}^{+})$, define the supremum norm as ${∥a∥}_{\eta }={sup}_{s\in [0,1]}\left\{\right|a\left(s\right)|e^s\}$, and for all $a,b\in C([0,1],{\mathbb{R}}^{+})$ define

$$\begin{array}{cc}\hfill {\omega }_{\eta }(a,b)& =\frac{1}{2}\underset{s\in [0,1]}{sup}\left\{\right|a\left(s\right)+b\left(s\right)|e^s\}\hfill \\ \hfill & =\frac{1}{2}{∥a+b∥}_{\eta }.\hfill \end{array}$$

It is clear that $\mathsf{C}([0,1],{\mathbb{R}}^{+},d)$ is a complete modular ultrametric space; thus, we have the following result.

Theorem 16.

Suppose that

(i) 

$H,G:[0,1]\times [0,1]\times W\to \mathbb{R}$;

(ii) 

Define

$$\begin{array}{cc}\hfill \left(Sa\right)\left(e\right)& ={\int }_0^{e}H(e,f,a\left(f\right))df,\hfill \\ \hfill \left(Tb\right)\left(e\right)& ={\int }_0^{e}G(e,f,b\left(f\right))df,\hfill \end{array}$$

such that

$$\begin{array}{c}\hfill \left|H(e,f,a(f\left)\right)+G(e,f,b(f\left)\right)\right|\le \frac{M(a,b)}{M(a,b)+1}\end{array}$$

for all $e,f\in [0,1]$ and $a,b\in C([0,1],{\mathbb{R}}^{+})$, where

$$\begin{array}{cc}\hfill M(a,b)=(\alpha {∥a+b∥}_{\eta }+\beta {∥a+Sa∥}_{\eta }+& \gamma {∥b+Tb∥}_{\eta }+\delta ({∥a+Tb∥}_{\eta }+{∥b+Sa∥}_{\eta })+\hfill \\ \hfill & \lambda ({∥a+Sa∥}_{\eta }+{∥b+Tb∥}_{\eta })+\eta ({∥a+Sa∥}_{\eta }+{∥a+b∥}_{\eta })).\hfill \end{array}$$

Then, (23) and (24) possess a unique solution.

Proof. 

Per (ii) above,

$$\begin{array}{cc}\hfill \left|Sa+Tb\right|& ={\int }_0^e\left|H(e,f,a(f\left)\right)+G(e,f,b(f\left)\right)\right|df\hfill \\ \hfill & \le {\int }_0^e\frac{M(a,b)}{M(a,b)+1}{e}^{f}df\hfill \\ \hfill & \le \frac{M(a,b)}{M(a,b)+1}{\int }_0^e{e}^{f}df\hfill \\ \hfill & \le \frac{M(a,b)}{M(a,b)+1}{e}^e\hfill \end{array}$$

implying that

$$\begin{array}{cc}\hfill \left|Sa+Tb\right|& \le \frac{M(a,b)}{M(a,b)+1},\hfill \\ \hfill {∥Sa+Tb∥}_{\eta }& \le \frac{M(a,b)}{M(a,b)+1},\hfill \\ \hfill \frac{M(a,b)+1}{M(a,b)}& \le \frac{1}{{∥Sa+Tb∥}_{\eta }},\hfill \\ \hfill 1+\frac{1}{M(a,b)}& \le \frac{1}{{∥Sa+Tb∥}_{\eta }},\hfill \\ \hfill 1-\frac{1}{{∥Sa\left(e\right)+Tb\left(e\right)∥}_{\eta }}& \le \frac{-1}{M(a,b)}.\hfill \end{array}$$

All the conditions of Theorem 15 hold, and ${\omega }_{\eta }(a,b)=\frac{1}{2}{∥a+b∥}_{\eta }$; hence both of the integral Equations (23) and (24) admit a unique common solution. □

5. Conclusions

In our research, conducted within the framework of modular ultrametric spaces, we have successfully established several significant fixed point and common fixed point theorems by employing the powerful concept of the generalized contraction principle. This work represents a notable extension of previously proved theorems within modular metric and ultrametric spaces. Our contributions are marked by including a more comprehensive set of parameters, namely, $\alpha ,\beta ,\gamma ,\delta ,\lambda$, and $\eta$.

By introducing these and other parameters into the analysis, we have effectively broadened the scope and applicability of these theorems. This expansion opens up new avenues for research and provides a deeper understanding of the dynamics within modular ultrametric spaces.

Furthermore, our work suggests promising directions for future research endeavors. By exploring various contractive conditions tailored to the specific characteristics of modular ultrametric spaces, a plethora of novel fixed point results can be derived. This could lead to a more profound understanding of the underlying mathematical structures and their practical implications, with potential applications in various fields.