A Cubic B-Spline Collocation Method for Barrier Options under the CEV Model

Abstract

In this paper, we construct a new numerical algorithm for the partial differential equation of up-and-out put barrier options under the CEV model. In this method, we use the Crank-Nicolson scheme to discrete temporal variables and the cubic B-spline collocation method to discrete spatial variables. The method is stable and has second-order convergence for both time and space variables. The convergence analysis of the proposed method is discussed in detail. Finally, numerical examples verify the stability and accuracy of the method.

1. Introduction

With the further acceleration of economic globalization, the price turbulence in the financial market is becoming more and more serious, and various risks caused by it have become a hot issue concerned and studied by economists and investors. In recent years, the derivatives market has become increasingly important in the financial and investment fields. Options have become an important tool for companies and investors to hedge assets and investment portfolios to control the risks brought by stock price fluctuations. There are many types of options, such as European options, American options, Asian options, barrier options, exotic options, lookback options, etc. European options are options that one party of the call option must exercise on the expiration date of the option. American options and barrier options are path-dependent options, and the return of these two options depends on the volatility path of the underlying asset price, not just the asset price on the maturity date.

The famous Black-Scholes option pricing model was proposed by Fischer Black and Myron Scholes in 1973 [1]. This model assumes that the underlying asset price follows the geometric Brownian motion, i.e., its distribution is logarithmic normal, and when it focuses on option pricing under the premise that its volatility is constant, it can meet option pricing in most cases. Since the required preconditions are too strict, the conditions proposed by the Black-Scholes model do not conform to the reality. In 1975, Cox [2] first considered the characteristics of the relationship between the volatility of assets winning the bid in the market and their price level, and established the Constant Elasticity of Variance (CEV) model. Schroder’s [3] empirical research showed that the CEV model can more accurately describe the changes in the price of underlying assets. Therefore, applying the CEV model to option pricing can obtain a better solution.

The option pricing model used in this section is the CEV model. The stock price process satisfies:

$$\begin{array}{c}\hfill \mathrm{d}{S}_t=\mu S_t\mathrm{d}t+\sigma S_t^{\delta }\mathrm{d}{W}_t,\end{array}$$

where $\delta$ is a constant coefficient, $0⩽\delta ⩽1$, $\mu$ is expected rate of return, $W_t$ is standard Brownian motion.

The differential equation that the option price satisfies is

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial \mathcal{U}}{\partial t}}+rS{\displaystyle \frac{\partial \mathcal{U}}{\partial S}}+{\displaystyle \frac{1}{2}}{\sigma }^2{S}^{2\delta }{\displaystyle \frac{{\partial }^2\mathcal{U}}{\partial S^2}}-r\mathcal{U}=0,(S,t)\in (0,B)\times (0,T),\end{array}$$

(1)

where $\mathcal{U}(S,t)$ is the value of options at the asset price S and at time t, T is the maturity date, $\sigma$ is the volatility and r is the risk-free interest rate.

Barrier options are a kind of European option, and their final benefit depends not only on the price of the underlying asset on the expiration date of the option, but also on whether the price of the underlying asset reaches a certain level (barrier B) during the entire option validity period. When the price of the underlying asset reaches the barrier, the option terminates. This type of option is called a knock-out option. If the underlying price of the original asset is higher than the barrier, it is called a down knock-out barrier option; if the underlying price of the original asset is lower than the barrier, it is called an up knock-out barrier option. When the price of the underlying asset reaches the barrier period, the option becomes effective, and this type of option is called a knock-in option. Similarly, there are down knock-in options and up knock-in options. European options can be divided into call options and put options.

Let us consider the up-and-out put barrier options, the initial condition

$$\begin{array}{c}\hfill \mathcal{U}(S,0)=max(K-S,0),S\in (0,S_{max}),S_{max}<B,\end{array}$$

(2)

and boundary conditions

$$\begin{array}{cc}\hfill & \mathcal{U}(0,t)=K,t\in [0,T],\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & \mathcal{U}(S_{max},t)=max(K-S_{max},0),t\in [0,T].\hfill \end{array}$$

(4)

where K is the exercise price.

Due to the fact that the initial condition is not smooth, the obtained solution is not smooth enough to perform the convergence of numerical approximations. We replace $max(K-S,0)$ by a smooth function $\psi \left(S\right)$. We obtain

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial \mathcal{Z}}{\partial t}}+rS{\displaystyle \frac{\partial \mathcal{Z}}{\partial S}}+{\displaystyle \frac{1}{2}}{\sigma }^2{S}^{2\delta }{\displaystyle \frac{{\partial }^2\mathcal{Z}}{\partial S^2}}-r\mathcal{Z}=0,(S,t)\in (0,S_{max})\times (0,T),\end{array}$$

(5)

the initial condition

$$\begin{array}{c}\hfill \mathcal{Z}(S,0)=\psi \left(S\right),S\in (0,S_{max}),\end{array}$$

(6)

and boundary conditions

$$\begin{array}{cc}\hfill & \mathcal{Z}(0,t)=K,t\in [0,T],\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & \mathcal{Z}(S_{max},t)=max(K-S_{max},0),t\in [0,T].\hfill \end{array}$$

(8)

Using the transformation: $S=exp\left(x\right)$. We obtain

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial \mathcal{V}}{\partial t}}+(r-{\displaystyle \frac{1}{2}}{\sigma }^2{e}^{(2\delta x-2x)}){\displaystyle \frac{\partial \mathcal{V}}{\partial x}}+{\displaystyle \frac{1}{2}}{\sigma }^2{e}^{(2\delta x-2x)}{\displaystyle \frac{{\partial }^2\mathcal{V}}{\partial x^2}}-r\mathcal{V}=0,(x,t)\in (-\infty ,x_{max})\times (0,T),\end{array}$$

(9)

with initial condition

$$\begin{array}{c}\hfill \mathcal{V}(x,0)=\psi \left(exp\left(x\right)\right),x\in (-\infty ,x_{max}),x_{max}<lnB,\end{array}$$

(10)

and boundary conditions

$$\begin{array}{cc}\hfill & \mathcal{V}(x,t)=K,asx\to -\infty ,t\in [0,T],\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & \mathcal{V}(x_{max},t)=max(K-e^{x_{max}},0),t\in [0,T].\hfill \end{array}$$

(12)

where

$$\begin{array}{c}\hfill \mathcal{V}(x,t)=\mathcal{Z}(S,t)=\mathcal{Z}\left(exp\right(x),t)\end{array}$$

Now, to solve the problem given in (9)–(12), we truncate the infinite domain $(-\infty ,x_{max})$ into a finite domain $(x_{min},x_{max})$, where $x_{min}$ is a sufficiently small negative real number. Then, we consider a general form of (9)–(12) on the truncated region $\Omega =(x_{min},x_{max})\times (0,T)$:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial v(x,t)}{\partial t}}=\alpha {\displaystyle \frac{{\partial }^{2}v(x,t)}{\partial x^2}}+\beta {\displaystyle \frac{\partial v(x,t)}{\partial x}}+\gamma v(x,t)+f(x,t),(x,t)\in \Omega ,\end{array}$$

(13)

where

$$\begin{array}{c}\hfill \alpha =-{\displaystyle \frac{1}{2}}{\sigma }^2{e}^{(2\delta x-2x)},\beta =-(r-{\displaystyle \frac{1}{2}}{\sigma }^2{e}^{(2\delta x-2x)}),\gamma =r.\end{array}$$

with initial and boundary conditions

$$\begin{array}{cc}\hfill & v(x,0)={\psi }_0\left(x\right),x\in [x_{min},x_{max}],\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & v(x_{min},t)={\psi }_L\left(t\right),t\in [0,T],\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & v(x_{max},t)={\psi }_R\left(t\right),t\in [0,T].\hfill \end{array}$$

(16)

In order to ensure the existence of a unique solution $v\in C\left(\overline{\Omega }\right)\cap C^{2,1}\left(\Omega \right)$ of the above problem, we assume that [4]

$$\begin{array}{c}\hfill \left|{\displaystyle \frac{{\partial }^{l+n}v(x,t)}{\partial x^l\partial t^n}}\right|⩽Kon\overline{\Omega },0⩽n⩽3and0⩽l⩽4.\end{array}$$

There are numerous studies about the numerical methods of solving barrier options under the CEV model. For example, Thakoor et al. [5] provided a highly accurate and efficient numerical scheme for barrier options under CEV. In order to achieve the fourth order convergence, it is necessary to refine the grid at both the strike and barriers, and obtain oscillation-free hedging parameters; a full implicit time integration technique with extrapolation is employed. Ahmadian and Ballestra [6] developed a numerical method to price discrete barrier options based on an underlying described by the constant elasticity of variance model with jump-diffusion (CEVJD). This method is allowed to approximate differential terms and jump integral by means of two different numerical techniques. Dias [7] has developed two new methods for pricing and hedging European barrier option contracts under the Jump to Default Extended Constant Elasticity of Variance (JDCEV) model, i.e., the stopping time method based on the first passage time densities of the underlying asset price process through the barrier level, as well as a static hedging portfolio method in which the barrier option is replicated by a portfolio of plain-vanilla and binary options. Guo and Chang [8] proposed an accelerated static replication method for continuous European barrier options by using the repeated Richardson extrapolation technique for Romberg sequences.

The main motivation of this work is to develop a third-order numerical method for solving the CEV model given in (13)–(16). In this method, the Crank-Nicolson scheme is used to discrete the temporal variables, and the cubic B-spline configuration method is used to discrete the spatial variables. The stability of this method is analyzed. In addition, we prove that the proposed method is second order convergent in space and time. The theoretical results are verified by numerical experiments and the applicability of the method is illustrated. B-spline was originally proposed by Schoenherg [9] in 1946. B-spline has strong local control capabilities, as well as many advantages such as convexity preservation, convex hull, geometric invariance, and variability reduction. Nowadays, B-spline has become one of the most important numerical methods used to study and solve partial differential equations. For example, Shallu et al. [10] proposed an improved extrapolation collocation method based on cubic B-splines. The method is applied to a class of self adjoint singularly perturbed boundary value problems, with the equispaced discretization of the domain. Since the standard B-spline collocation method cannot achieve the optimal convergence order, the cubic B-spline interpolant and its higher-order derivatives are corrected later. The proposed technology can be applied to high-order linear, nonlinear problems, and partial differential equations. Shallu and V.K. Kukreja [11] obtained a numerical solution to the nonlinear modified Burgers equation using an improvised collocation technique with cubic B-spline as basis functions. In this method, the cubic B-spline is forced to satisfy interpolant conditions with some specific end conditions. Shallu and V.K. Kukreja [12] uses an improvised cubic B-spline collocation technique to solve the Benjamin-Bona-Mahony-Burgers (BBMB) equation due to the inability to achieve optimal accuracy and convergence order using the standard B-spline collocation method. Therefore, improvised cubic B-splines are formed by making a posteriori corrections to cubic B-spline interpolants and their higher-order derivatives. We note that numerical methods based on B-spline basis functions have been used to solve option pricing problems. For example, the authors of [13,14,15] used the B-spline basis function for solving the generalized Black Scholes equation.

The rest of this paper is organized as follows: In Section 2, the time variable is discretized by the Crank-Nicolson format, and the convergence analysis is carried out. In the Section 3, we describe spatial discretization by the cubic B-spline collocation method, and discuss the stability and convergence analysis of this method. Numerical experiments are carried out in Section 4. The results will be discussed in Section 5.

2. Temporal Discretization

In order to solve the CEV model given in (13)–(16) more conveniently, we consider a uniform partition of the domain $\Omega =(x_{min},x_{max})\times (0,T)$ with node points $(x_l,t_n)$, where $x_l=x_{min}+lh,h=(x_{max}-x_{min})/M,l=0,1,\cdots ,M$ and $\tau =T/N$ with $t_n=n\tau$ and $n=0,1,2,\cdots ,N$. We first discretize the problem (13)–(16) in the temporal direction.

2.1. Description of the Crank-Nicolson Method of Time Variable

We use the Crank-Nicolson method to discretize Equations (13)–(16). This discretization yields the following system of differential equations:

$$\begin{array}{c}\hfill {\displaystyle \frac{v^{n+1}\left(x\right)-v^n\left(x\right)}{\tau }}-{\displaystyle \frac{1}{2}}{L}_x^n{v}^{n+1}\left(x\right)-{\displaystyle \frac{1}{2}}{L}_x^n{v}^n\left(x\right)=f^{n+\frac{1}{2}}\left(x\right),n=0,1,\cdots ,N-1,\end{array}$$

or

$$\begin{array}{c}\hfill (I-{\displaystyle \frac{\tau }{2}}{L}_x^n)v^{n+1}\left(x\right)=(I+{\displaystyle \frac{\tau }{2}}{L}_x^n)v^n\left(x\right)+\tau f^{n+\frac{1}{2}}\left(x\right),n=0,1,\cdots ,N-1.\end{array}$$

(17)

$$\begin{array}{cc}\hfill & v^0\left(x\right)={\psi }_0\left(x\right),\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & v^{n+1}\left(x_{min}\right)={\psi }_L^{n+1},\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & v^{n+1}\left(x_{max}\right)={\psi }_R^{n+1}.\hfill \end{array}$$

(20)

Here, $v^n\left(x\right)$ approximate the exact solution $v(x,t_n)$ at the nth time level $t_n$ and

$$\begin{array}{cc}\hfill & L_x^n\equiv \alpha {\displaystyle \frac{{\partial }^2}{\partial x^2}}+\beta {\displaystyle \frac{\partial }{\partial x}}+\gamma I,\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & f^{n+\frac{1}{2}}\left(x\right)=f(x,t_n+{\displaystyle \frac{\tau }{2}}).\hfill \end{array}$$

(22)

2.2. Convergence Analysis

Next, we will conduct convergence analysis for the case of using the CN model discrete temporal variables.

The local truncation error of the temporal discretization method (17) is defined by

$$\begin{array}{c}\hfill e^{n+1}=v(x,t_{n+1})-{\tilde{v}}^{n+1}\end{array}$$

(23)

where ${\tilde{v}}^{n+1}$ is the approximate solution of the problem (17)–(20) obtained after one step of the semi-discrete scheme taking the exact value $v(x,t_n)$, instead of $v^n$ as the initial data, i.e.,

$$\begin{array}{cc}\hfill & (I-{\displaystyle \frac{\tau }{2}}{L}_x^n){\tilde{v}}^{n+1}=(I+{\displaystyle \frac{\tau }{2}}{L}_x^n)v(x,t_n)+\tau f^{n+\frac{1}{2}}\left(x\right),\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill & \tilde{v}(x_{min},t)={\psi }_L^{n+1},\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & \tilde{v}(x_{max},t)={\psi }_R^{n+1}.\hfill \end{array}$$

(26)

We define the global truncation error $E^{n+1}$ at time $t_{n+1}$ as

$$\begin{array}{c}\hfill E^{n+1}=v(x,t_{n+1})-v^{n+1}\end{array}$$

(27)

Lemma 1. 

Let the operator ${(I-{\displaystyle \frac{\tau }{2}}{L}_x^n)}^{-1}\equiv {\tilde{L}}_x^{-1}:R\left({\tilde{L}}_x\right)\subseteq C\left({\Omega }_x\right)\to C\left(\overline{{\Omega }_x}\right)\cap C^2\left({\Omega }_x\right)$ be such that ${\tilde{L}}_x^{-1}\left(w\right)$ is the solution ‘u’ of:

$$\begin{array}{cc}\hfill & {\tilde{L}}_x\left(u\right)=win{\Omega }_x,\hfill \\ \hfill & u=0on\overline{{\Omega }_x}\setminus {\Omega }_x.\hfill \end{array}$$

Then

$$\begin{array}{c}\hfill \parallel {\tilde{L}}_x^{-1}{\parallel }_{\infty }⩽{\displaystyle \frac{1}{1+\frac{\tau }{2}\tilde{\gamma }}},\end{array}$$

where $R\left({\tilde{L}}_x\right)\subseteq C\left({\Omega }_x\right)$ denotes the range of the linear operator ${\tilde{L}}_x$.

Proof. 

(see, [16]). □

Lemma 2. 

If

$$\begin{array}{c}\hfill \left|{\displaystyle \frac{{\partial }^{l+n}v(x,t)}{\partial x^l\partial t^n}}\right|⩽Kon\overline{\Omega },0⩽n⩽3and0⩽l⩽4.\end{array}$$

(28)

then there holds

$$\begin{array}{cc}\hfill & \parallel e^n{\parallel }_{\infty }⩽K{\tau }^3\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill & \parallel E^n{\parallel }_{\infty }⩽K{\tau }^2,\hfill \end{array}$$

(30)

where K is a constant independent of N.

Proof. 

Because $|v_{ttt}| ⩽K$ and v is a smooth function, hence by Taylor series expansion, we obtain

$$\begin{array}{cc}\hfill & v(x,t_{n+1})=v(x,t_{n+\frac{1}{2}})+{\displaystyle \frac{\tau }{2}}{v}_t(x,t_{n+\frac{1}{2}})+{\displaystyle \frac{{\tau }^2}{8}}{v}_{tt}(x,t_{n+\frac{1}{2}})+O\left({\tau }^3\right),\hfill \\ \hfill & v(x,t_n)=v(x,t_{n+\frac{1}{2}})-{\displaystyle \frac{\tau }{2}}{v}_t(x,t_{n+\frac{1}{2}})+{\displaystyle \frac{{\tau }^2}{8}}{v}_{tt}(x,t_{n+\frac{1}{2}})+O\left({\tau }^3\right).\hfill \end{array}$$

Using the above extension, we obtain

$$\begin{array}{c}\hfill {\displaystyle \frac{v(x,t_{n+1})-v(x,t_n)}{\tau }}=v_t(x,t_{n+\frac{1}{2}})+O\left({\tau }^2\right).\end{array}$$

(31)

Using relations (13) and (21) gives

$$\begin{array}{c}\hfill v_t(x,t_{n+\frac{1}{2}})=L_x^{n}v(x,t_{n+\frac{1}{2}})+f^{n+\frac{1}{2}}\left(x\right)\end{array}$$

(32)

By relations (31) and (32), we obtain

$$\begin{array}{c}\hfill {\displaystyle \frac{v(x,t_{n+1})-v(x,t_n)}{\tau }}=L_x^{n}v(x,t_{n+\frac{1}{2}})+f^{n+\frac{1}{2}}\left(x\right)+O\left({\tau }^2\right).\end{array}$$

(33)

Now, because

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}}v(x,t_{n+1})+{\displaystyle \frac{1}{2}}v(x,t_n)=v(x,t_{n+\frac{1}{2}})+{\displaystyle \frac{{\tau }^2}{8}}{v}_{tt}(x,t_{n+\frac{1}{2}})+O\left({\tau }^3\right),\end{array}$$

and $|L_x^n{v}_{tt}| ⩽K$ on $\overline{\Omega }$, we obtain

$$\begin{array}{c}\hfill L_x^n[{\displaystyle \frac{1}{2}}v(x,t_{n+1})+{\displaystyle \frac{1}{2}}v(x,t_n)]=L_x^{n}v(x,t_{n+\frac{1}{2}})+O\left({\tau }^2\right).\end{array}$$

This means

$$\begin{array}{c}\hfill L_x^{n}v(x,t_{n+\frac{1}{2}})=L_x^n[{\displaystyle \frac{1}{2}}v(x,t_{n+1})+{\displaystyle \frac{1}{2}}v(x,t_n)]+O\left({\tau }^2\right).\end{array}$$

It follows by (33) that

$$\begin{array}{c}\hfill (I-{\displaystyle \frac{\tau }{2}}{L}_x^n)v(x,t_{n+1})=(I+{\displaystyle \frac{\tau }{2}}{L}_x^n)v(x,t_n)+\tau f^{n+\frac{1}{2}}\left(x\right)+O\left({\tau }^3\right).\end{array}$$

By using relation (24), we obtain

$$\begin{array}{cc}\hfill & (I-{\displaystyle \frac{\tau }{2}}{L}_x^n)e^{n+1}=O\left({\tau }^3\right),\hfill \\ \hfill & e^{n+1}\left(x_{min}\right)=0,\hfill \\ \hfill & e^{n+1}\left(x_{max}\right)=0.\hfill \end{array}$$

By directly application of Lemma 1, we obtain

$$\begin{array}{c}\hfill \parallel e^n{\parallel }_{\infty }⩽K{\tau }^3.\end{array}$$

In addition, we can decompose the global truncation error at time $t_n$ in the following form

$$\begin{array}{c}\hfill E^n=v(x,t_n)-v^n=(v(x,t_n)-{\tilde{v}}^n)+({\tilde{v}}^n-v^n).\end{array}$$

(34)

By relations (17) and (24), we obtain

$$\begin{array}{c}\hfill (I-{\displaystyle \frac{\tau }{2}}{L}_x^{n-1})({\tilde{v}}^n-v^n)=(I+{\displaystyle \frac{\tau }{2}}{L}_x^{n-1})(v(x,t_{n-1})-v^{n-1}),\end{array}$$

(35)

(34) and (35) gives the recurrence relation as

$$\begin{array}{c}\hfill E^n=E^0\left(\prod _{j=0}^{n-1}{R}_{n-j}\right)+e^n+\sum _{i=1}^{n-1}\left(\prod _{j=0}^{i-1}{R}_{n-j}\right)e_{n-i},E^0=v(x,t_0)-v^0=0,\end{array}$$

Here, we use the notation ${\prod }_{j=0}^{n-1}{R}_{n-j}=R_n{R}_{n-1}\cdots R_1$.

The operator ‘$R_n\equiv R\left(\tau L_x^{n-1}\right),1⩽n⩽N$’ is defined by which $v_2\equiv R_{n}v$ is the solution of

$$\begin{array}{cc}\hfill & (I-{\displaystyle \frac{\tau }{2}}{L}_x^{n-1})v_2=(I-{\displaystyle \frac{\tau }{2}}{L}_x^{n-1})v,\hfill \\ \hfill & v_2=0on\overline{{\Omega }_x}\setminus {\Omega }_x.\hfill \end{array}$$

Now, according to Gonzalez and Palencia (see, [17]) for the operator ‘$R_n\equiv R\left(\tau L_x^{n-1}\right)$’, where $R\left(z\right)$ is a rational A-acceptable function (see, [18]), such that

$$\begin{array}{c}\hfill \parallel \prod _{j=0}^{m-1}{R}_{n-j}{\parallel }_{\infty }⩽K\forall m=1,2,3,\cdots ,n;1⩽n⩽N.\end{array}$$

Thus, we obtain

$$\begin{array}{c}\hfill \parallel E^n{\parallel }_{\infty }⩽n·K·\underset{1⩽i⩽n}{max}\parallel e^i{\parallel }_{\infty }=n\tau ·{\displaystyle \frac{K}{\tau }}·\underset{1⩽i⩽n}{max}\parallel e^i{\parallel }_{\infty }⩽TK·{\displaystyle \frac{1}{\tau }}\underset{1⩽i⩽n}{max}{\parallel e^i\parallel }_{\infty }.\end{array}$$

This imples that (30) follows. □

We can see that the discrete scheme is consistent by Lemma 2. Thus we obtain the following result with the help of Lax equivalence theorem (see, [19]) and Lemma 2.

Theorem 1. 

The method defined by (17)–(20) is second order convergent.

3. Spatial Discretization

3.1. Description of Cubic B-Spline Method

First, we consider a uniform partition $\pi :x_{min}=x_0<x_1<\cdots <x_{M-1}<x_M=x_{max}$ over the finite interval $\overline{{\Omega }_x}=(x_{min},x_{max})$. Then we extend the uniform partition $\pi$ in order to construct the cubic B-spline for the partition $\Pi :x_{-2}<x_{-1}<x_0=x_{min}<x_1<\cdots <x_M=x_{max}<x_{M+1}<x_{M+2}$, by adding four additional nodes $x_{-2},x_{-1},x_{M+1},x_{M+2}$.

Let $Q^{n+1}\left(x\right)$ be the approximation to the exact solution $v^{n+1}\left(x\right)$ at the $(n+1)$-th time level. Then, $Q^{n+1}\left(x\right)$ can be defined by

$$\begin{array}{c}\hfill Q^{n+1}\left(x\right)=\sum _{k=-1}^{M+1}{c}_k^{n+1}{B}_k\left(x\right),\end{array}$$

(36)

where $c_k^{n+1}$ are unknown parameters.

Following [20], we can obtain the representations of cubic B-splines $B_k$ with the required attributes:

$$B_k\left(x\right)={\displaystyle \frac{1}{h^3}}\left\{\begin{array}{cc}{(x-x_{k-2})}^3,\hfill & x\in [x_{k-2},x_{k-1}],\hfill \\ {(x-x_{k-2})}^3-4{(x-x_{k-1})}^3,\hfill & x\in \left[x_{k-1,x_k}\right],\hfill \\ {(x_{k-2}-x)}^3-4{(x_{k+1}-x)}^3,\hfill & x\in [x_k,x_{k+1}],\hfill \\ {(x_{k+2}-x)}^3,\hfill & x\in [x_{k+1},x_{k+2}],\hfill \\ 0,\hfill & otherwise,\hfill \end{array}\right.$$

(37)

Each basis function is twice continuously differentiable on the entire real line.

If we consider ${\mathcal{B}}_3\left(\pi \right):=span\{B_{-1},B_0,B_1,\cdots ,B_M,B_{M+1}\}\subseteq C^2\left({\Omega }_x\right)$. Since one can easily see that the basis functions in $\{B_{-1},B_0,B_1,\cdots ,B_M,B_{M+1}\}$ are linearly independent on ${\Omega }_x$. Then ${\mathcal{B}}_3\left(\pi \right)$ is a finite dimensional linear sub-space of $C^2\left({\Omega }_x\right)$ of dimension $M+3$ with basis $\{B_{-1},B_0,B_1,\cdots ,B_M,B_{M+1}\}$.

By using (37), the values of basis functions $B_k\left(x\right)$, $B_k^{\prime }\left(x\right)$, $B_k^{\prime \prime }\left(x\right)$ at the grid points $x_l$ are listed in Table 1. By using (36) and Table 1, $Q^{n+1}$, $Q_x^{n+1}$ and $Q_{xx}^{n+1}$ at the mesh points $x_l$ are obtained as

$$\begin{array}{cc}\hfill & Q^{n+1}\left(x_l\right)=c_{l-1}^{n+1}+4c_l^{n+1}+c_{l+1}^{n+1},\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill & Q_x^{n+1}\left(x_l\right)={\displaystyle \frac{1}{h}}(-3c_{l-1}^{n+1}+3c_{l+1}^{n+1}),\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill & Q_{xx}^{n+1}\left(x_l\right)={\displaystyle \frac{1}{h^2}}(6c_{l-1}^{n+1}-12c_l^{n+1}+6c_{l+1}^{n+1}).\hfill \end{array}$$

(40)

Table 1. The values of basis functions $B_k\left(x\right)$, $B_k^{\prime }\left(x\right)$, $B_k^{\prime \prime }\left(x\right)$ at the grid points $x_l$.

x	${\mathit{x}}_{\mathit{k}-2}$	${\mathit{x}}_{\mathit{k}-1}$	${\mathit{x}}_{\mathit{k}}$	${\mathit{x}}_{\mathit{k}+1}$	${\mathit{x}}_{\mathit{k}+2}$
$B_k(x$)	0	1	4	1	0
$B_k^{\prime }\left(x\right)$	0	$3/h$	0	$-3/h$	0
$B_k^{\prime \prime }\left(x\right)$	0	$6/h^2$	$-12/h^2$	$6/h^2$	0

3.2. Formulation of Cubic B-Spline Collocation Method

In this part, we construct the cubic B-spline collocation method for the solution of the problem (17)–(20). Firstly, we write Equation (17) as:

$$\begin{array}{c}\hfill {\displaystyle \frac{\alpha }{2}}{v}_{xx}^{n+1}\left(x\right)+{\displaystyle \frac{\beta }{2}}{v}_x^{n+1}\left(x\right)+({\displaystyle \frac{\gamma }{2}}-{\displaystyle \frac{1}{\tau }})v^{n+1}\left(x\right)=F^{n+\frac{1}{2}}\left(x\right),\end{array}$$

(41)

where

$$\begin{array}{c}\hfill F^{n+\frac{1}{2}}\left(x\right)=-{\displaystyle \frac{\alpha }{2}}{v}_{xx}^n\left(x\right)-{\displaystyle \frac{\beta }{2}}{v}_x^n\left(x\right)-({\displaystyle \frac{\gamma }{2}}+{\displaystyle \frac{1}{\tau }})v^n\left(x\right)-f^{n+\frac{1}{2}}\left(x\right),\end{array}$$

(42)

the boundary conditions

$$\begin{array}{c}\hfill v^{n+1}\left(x_{min}\right)={\psi }_L^{n+1},v^{n+1}\left(x_{max}\right)={\psi }_R^{n+1}.\end{array}$$

(43)

Then, we force the function $Q^{n+1}\left(x\right)$ to satisfy Equations (41) and (43) at the node points $x_l$, according to the cubic B-spline collocation technique. Thus, we have

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\displaystyle \frac{\alpha }{2}}{Q}_{xx}^{n+1}\left(x_l\right)+{\displaystyle \frac{\beta }{2}}{Q}_x^{n+1}\left(x_l\right)+({\displaystyle \frac{\gamma }{2}}-{\displaystyle \frac{1}{\tau }})Q^{n+1}\left(x_l\right)=F^{n+\frac{1}{2}}\left(x_l\right),l=0,1,\cdots ,M,n=0,1,\dots ,N-1,\end{array}\end{array}$$

(44)

$$\begin{array}{c}\hfill Q^{n+1}\left(x_0\right)={\psi }_L^{n+1},Q^{n+1}\left(x_M\right)={\psi }_R^{n+1}.\end{array}$$

(45)

Substituting the expressions for $Q^{n+1}\left(x_l\right)$, $Q_x^{n+1}\left(x_l\right)$ and $Q_{xx}^{n+1}\left(x_l\right)$ from Equations (38)–(40), respectively into Equation (44), we obtain a system of m + 1 equations in m + 1 unknowns

$$\begin{array}{c}\hfill p{c}_{l-1}^{n+1}+q{c}_l^{n+1}+r{c}_{l+1}^{n+1}=F_l^{n+\frac{1}{2}},l=0,1,\cdots ,M,\end{array}$$

(46)

where

$$\begin{array}{cc}\hfill & p=\frac{3\alpha }{h^2}-\frac{3\beta }{2h}+\frac{\gamma }{2}-\frac{1}{\tau },q=-\frac{6\alpha }{h^2}+2\gamma -\frac{4}{\tau },r=\frac{3\alpha }{h^2}+\frac{3\beta }{2h}+\frac{\gamma }{2}-\frac{1}{\tau },\hfill \\ \hfill & F_l^{n+\frac{1}{2}}=\left\{-\frac{2}{\tau }-p\right\}{c}_{l-1}^n+\left\{-\frac{8}{\tau }-q\right\}{c}_l^n+\left\{-\frac{2}{\tau }-r\right\}{c}_{l+1}^n-f^{n+\frac{1}{2}}\left(x_l\right).\hfill \end{array}$$

By using (45), we obtain

$$\begin{array}{cc}\hfill & c_{-1}^{n+1}+4c_0^{n+1}+c_1^{n+1}={\psi }_L^{n+1},\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill & c_{M-1}^{n+1}+4c_M^{n+1}+c_{M+1}^{n+1}={\psi }_R^{n+1}.\hfill \end{array}$$

(48)

By using Equations (47)–(48), we eliminate $c_{-1}^{n+1}$, $c_{-1}^n$, $c_{M+1}^{n+1}$ and $c_{M+1}^n$, such that

$$\begin{array}{cc}\hfill & (q-4p)c_0^{n+1}+(r-p)c_1^{n+1}=F_0^{n+\frac{1}{2}}-p{\psi }_L^{n+1},\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill & p{c}_{l-1}^{n+1}+q{c}_l^{n+1}+r{c}_{l+1}^{n+1}=F_l^{n+\frac{1}{2}},l=1,2,\cdots ,M-1,\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill & (p-r)c_{M-1}^{n+1}+(q-4r)c_M^{n+1}=F_M^{n+\frac{1}{2}}-r{\psi }_R^{n+1},\hfill \end{array}$$

(51)

where

$$\begin{array}{cc}\hfill & F_0^{n+\frac{1}{2}}=(4p-q)c_0^n+(p-r)c_1^n+(-\frac{2}{\tau }-p){\psi }_L^n-f^{n+\frac{1}{2}}\left(x_0\right),\hfill \\ \hfill & F_M^{n+\frac{1}{2}}=(r-p)c_{M-1}^n+(4r-q)c_M^n+(-\frac{2}{\tau }-r){\psi }_R^n-f^{n+\frac{1}{2}}\left(x_M\right).\hfill \end{array}$$

The system produced by Equations (49)–(51) can be expressed in matrix form as follows

$$\begin{array}{c}\hfill P{C}^{n+1}={\tilde{F}}^n,n=0,1,\cdots ,N-1,\end{array}$$

(52)

where

$$\begin{array}{c}\hfill P=\left(\begin{array}{cccccccccc}{P}_{1,1}& P_{1,2}& 0& 0& 0& \cdots & \cdots & 0& 0& 0\\ P_{2,1}& P_{2,2}& P_{2,3}& 0& 0& \cdots & \cdots & 0& 0& 0\\ 0& P_{3,2}& P_{3,3}& P_{3,4}& 0& \cdots & \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & \cdots & \cdots & 0& P_{m,m-1}& P_{m,m}& P_{m,m+1}\\ 0& 0& 0& \cdots & \cdots & \cdots & 0& 0& P_{m+1,m}& P_{m+1,m+1}\end{array}\right)\end{array}$$

with

$$\begin{array}{cc}\hfill & P_{1,1}=q-4p,P_{1,2}=r-p,\hfill \\ \hfill & P_{l,l-1}=p,P_{l,l}=q,P_{l,l+1}=r,l=2,3,\cdots ,M,\hfill \\ \hfill & P_{M+1,M}=p-r,P_{M+1,M+1}=q-4r,\hfill \end{array}$$

$$\begin{array}{c}\hfill {\tilde{F}}^n=\left(\begin{array}{c}{F}_0^{n+\frac{1}{2}}-p{\psi }_L^{n+1}\\ F_1^{n+\frac{1}{2}}\\ F_2^{n+\frac{1}{2}}\\ ⋮\\ F_M^{n+\frac{1}{2}}-r{\psi }_R^{n+1}\end{array}\right)\end{array}$$

and

$$C^{n+1}={[c_0^{n+1},c_1^{n+1},\cdots ,c_{M-1}^{n+1},c_M^{n+1}]}^T$$

where

$$\begin{array}{cc}\hfill & F_0^{n+\frac{1}{2}}=(4p-q)c_0^n+(p-r)c_1^n+(-\frac{2}{\tau }-p){\psi }_L^n-f^{n+\frac{1}{2}}\left(x_0\right),\hfill \\ \hfill & F_l^{n+\frac{1}{2}}=\left\{-\frac{2}{\tau }-p\right\}{c}_{l-1}^n+\left\{-\frac{8}{\tau }-q\right\}{c}_l^n+\left\{-\frac{2}{\tau }-r\right\}{c}_{l+1}^n-f^{n+\frac{1}{2}}\left(x_l\right),l=1,2,\cdots ,M-1,\hfill \\ \hfill & F_M^{n+\frac{1}{2}}=(r-p)c_{M-1}^n+(4r-q)c_M^n+(-\frac{2}{\tau }-r){\psi }_R^{n+1}-f^{n+\frac{1}{2}}\left(x_M\right),\hfill \\ \hfill & p=\frac{3\alpha }{h^2}-\frac{3\beta }{2h}+\frac{\gamma }{2}-\frac{1}{\tau },q=-\frac{6\alpha }{h^2}+2\gamma -\frac{4}{\tau },r=\frac{3\alpha }{h^2}+\frac{3\beta }{2h}+\frac{\gamma }{2}-\frac{1}{\tau }.\hfill \end{array}$$

One can easily see that for sufficiently large m, the matrix P is strictly diagonally dominant by rows. Hence P is invertible (see, [21]), and

$$\begin{array}{c}\hfill \parallel P^{-1}{\parallel }_{\infty }<{\displaystyle \frac{1}{\underset{l}{min}\left(|P_{l,l}|-{\sum }_{l\ne k}\left|P_{l,k}\right|\right)}}={\displaystyle \frac{1}{6\underset{1⩽l⩽M-1}{min}(-{\displaystyle \frac{\gamma }{2}}+{\displaystyle \frac{1}{\tau }})}}⩽\mathcal{M}.\end{array}$$

We need obtain the initial vector $C^0={[c_0^0,c_1^0,\cdots ,c_M^0]}^T$ to solve the system of matrix (52).

By solving the following interpolation problem can find the vector $C^0$

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial Q^0\left(x\right)}{\partial x}}{|}_{x=x_0}={\displaystyle \frac{\partial {\psi }_0\left(x\right)}{\partial x}}{|}_{x=x_0},\hfill \\ \hfill & Q^0\left(x_l\right)={\psi }^0\left(x_l\right);0⩽l⩽M,\hfill \\ \hfill & {\displaystyle \frac{\partial Q^0\left(x\right)}{\partial x}}{|}_{x=x_M}={\displaystyle \frac{\partial {\psi }_0\left(x\right)}{\partial x}}{|}_{x=x_M},\hfill \end{array}$$

where

$$\begin{array}{c}\hfill Q^0\left(x\right)=\sum _{k=-1}^{M+1}{c}_k^0{B}_k\left(x\right)\subseteq {\mathcal{B}}_3\left(\pi \right).\end{array}$$

Thus we obtain the following system of matrix

$$\begin{array}{c}\hfill A{\widehat{C}}^0=B,\end{array}$$

where

$$\begin{array}{cc}\hfill & A={\left(\begin{array}{cccccccccc}-3/h& 0& 3/h& 0& 0& \cdots & \cdots & 0& 0& 0\\ 1& 4& 1& 0& 0& \cdots & \cdots & 0& 0& 0\\ 0& 1& 4& 1& 0& \cdots & \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & \cdots & \cdots & 0& 1& 4& 1\\ 0& 0& 0& \cdots & \cdots & \cdots & 0& -3/h& 0& 3/h\end{array}\right)}_{(M+3)\times (M+3)},\hfill \\ \hfill & {\widehat{C}}^0={[c_{-1}^0,c_0^0,\cdots ,c_M^0,c_{M+1}^0]}^T,\hfill \\ \hfill & B={\left[{\displaystyle \frac{\partial {\psi }_0\left(x\right)}{\partial x}}{|}_{x=x_0},{\psi }_0\left(x_0\right),{\psi }_0\left(x_1\right),\cdots ,{\psi }_0\left(x_M\right),{\displaystyle \frac{\partial {\psi }_0\left(x\right)}{\partial x}}{|}_{x=x_M}\right]}^T.\hfill \end{array}$$

Now, since matrix A is diagonally dominant with strict diagonal dominance in all rows except the first row and the last row, it can be concluded from Gershgorin’s theorem (see [22]) that A is nonsingular. Therefore, the vector ${\widehat{C}}^0$ giving the initial vector $C^0$ can be uniquely found.

3.3. Stability Analysis

In this subsection, we use the Von-Neumann stability method to analyze the stability of the scheme defined by (52).

Theorem 2. 

The proposed method defined by (52) for solving the problem (13)–(16) is unconditionally stable.

Proof. 

We set $f^{n+\frac{1}{2}}\left(x\right)=0$ to establish the stability result of method (52). We define $c_l^n$ as

$$\begin{array}{c}\hfill c_l^n={\mu }^n{e}^{il\rho h},\end{array}$$

(53)

where $i=\sqrt{-1}$, $\rho$ is the time related parameter and the exponential term represents spatial correlation. Substituting Equation (53) into Equation (46), we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\mu }^{n+1}{e}^{il\rho h}\left\{e^{-i\rho h}p+q+e^{i\rho h}r\right\}=\hfill \\ \hfill & {\mu }^n{e}^{il\rho h}\left\{e^{-i\rho h}\left(-{\displaystyle \frac{2}{\tau }}-p\right)+\left(-{\displaystyle \frac{8}{\tau }}-q\right)+e^{i\rho h}\left(-{\displaystyle \frac{2}{\tau }}-r\right)\right\},n=0,1,\cdots ,N-1.\hfill \end{array}\end{array}$$

(54)

Re-write above equation as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \mu \left\{cos\left(\rho h\right)(p+r)+isin\left(\rho h\right)(-p+r)+q\right\}=\hfill \\ \hfill & \left\{cos\left(\rho h\right)\left(-{\displaystyle \frac{4}{\tau }}-p-r\right)+isin\left(\rho h\right)(p-r)+\left(-{\displaystyle \frac{8}{\tau }}-q\right)\right\},n=0,1,\cdots ,N-1.\hfill \end{array}\end{array}$$

(55)

For the convenience of calculation, we introduce $E_1$, $E_2$ and $E_3$ as

$$\begin{array}{c}\hfill E_1={\displaystyle \frac{2}{\tau }}+p+r,E_2=-p+r,E_3={\displaystyle \frac{4}{\tau }}+q.\end{array}$$

By reducing Equation (55), we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \mu \left\{\left[cos\left(\rho h\right)\left(-{\displaystyle \frac{2}{\tau }}+E_1\right)+\left(-{\displaystyle \frac{4}{\tau }}+E_3\right)\right]+isin\left(\rho h\right)E_2\right\}=\hfill \\ \hfill & \left\{\left[cos\left(\rho h\right)\left(-{\displaystyle \frac{2}{\tau }}-E_1\right)+\left(-{\displaystyle \frac{4}{\tau }}-E_3\right)\right]+isin\left(\rho h\right)(-E_2)\right\}\hfill \end{array}\end{array}$$

(56)

Equation (56) means that

$$\begin{array}{c}\hfill \mu ={\displaystyle \frac{(L_2-L_1)-i{L}_3}{(L_2+L_1)+i{L}_3}}\end{array}$$

(57)

with

$$\begin{array}{cc}\hfill & L_1=E_{1}cos\left(\rho h\right)+E_3,\hfill \\ \hfill & L_2=-{\displaystyle \frac{1}{\tau }}(2cos\left(\rho h\right)+4),\hfill \\ \hfill & L_3=E_{2}sin\left(\rho h\right).\hfill \end{array}$$

By taking the absolute value on both sides of Equation (57) we obtain

$$\begin{array}{c}\hfill {\left|\mu \right|}^2⩽{\displaystyle \frac{{(L_2-L_1)}^2+{(-L_3)}^2}{{(L_2+L_1)}^2+{\left(L_3\right)}^2}}.\end{array}$$

(58)

As ${(L_2+L_1)}^2+{\left(L_3\right)}^2>0$ and ${(L_2-L_1)}^2+{(-L_3)}^2⩽{(L_2+L_1)}^2+{\left(L_3\right)}^2$. This means

$$\begin{array}{c}\hfill \left|\mu \right|⩽1.\end{array}$$

(59)

□

Thus, we can see that the scheme is unconditionally stable by Equation (59).

3.4. Convergence Analysis

Lemma 3. 

Let ${\mathcal{S}}_3\left(\pi \right):=$ set of all functions $s\left(x\right)\in C^2\left({\Omega }_x\right)$ that reduces to cubic polynomials on each subintervals $(x_l,x_{l+1})$, $0⩽l⩽M-1$, of ${\Omega }_x$ then

$$\begin{array}{c}\hfill {\mathcal{S}}_3\left(\pi \right)={\mathcal{B}}_3\left(\pi \right)\end{array}$$

and, there exists a unique cubic spline $s\left(x\right)\in {\mathcal{S}}_3\left(\pi \right)$ solving the interpolation problem-

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial s\left(x\right)}{\partial x}}{|}_{x=x_0}={\displaystyle \frac{\partial v^n\left(x\right)}{\partial x}}{|}_{x=x_0},\hfill \\ \hfill & s\left(x_l\right)=v^n\left(x_l\right);0⩽l⩽M,\hfill \\ \hfill & {\displaystyle \frac{\partial s\left(x\right)}{\partial x}}{|}_{x=x_M}={\displaystyle \frac{\partial v^n\left(x\right)}{\partial x}}{|}_{x=x_M},\hfill \end{array}$$

where, $v^n\left(x\right)$ is the solution of the discretized problem (41)–(43) at the time level n. The function ‘s’ is called the cubic spline interpolate to $v^n\left(x\right)$.

Proof. 

(see, [23]). □

Theorem 3. 

The collocation approximation $Q^n\left(x\right)$ from the space ${\mathcal{B}}_3\left(\pi \right)$ to the solution $v_n\left(x\right)$ of the boundary value problem (41)–(43) satisfies the following error estimate

$$\begin{array}{c}\hfill \parallel v^n-Q^n{\parallel }_{\infty }⩽K{h}^2,\end{array}$$

for sufficiently small h (i.e., for sufficiently large m) where K is a positive constant.

Proof. 

In order to find error estimate, let ${\overline{Q}}^n\left(x\right)$ be the unique spline interpolate from ${\mathcal{Q}}_3\left(\pi \right)$ to the solution $v^n\left(x\right)$ of the boundary value problem (41)–(43) at the nth-time level. Here, ${\overline{Q}}^n\left(x\right)\in {\mathcal{S}}_3\left(\pi \right)={\mathcal{B}}_3\left(\pi \right)$ (see, Lemma 3), is given by

$$\begin{array}{c}\hfill {\overline{Q}}^n\left(x\right)=\sum _{k=-1}^{M+1}{\overline{c}}_k^n{B}_k\left(x\right).\end{array}$$

(60)

The boundary value problem (41)–(43) can be rewritten as

$$\begin{array}{cc}\hfill & {\mathcal{L}}_x^n{v}^{n+1}={\mathcal{F}}^{n+\frac{1}{2}},\hfill \end{array}$$

(61)

$$\begin{array}{cc}\hfill & v^{n+1}\left(x_{min}\right)={\psi }_L^{n+1},\hfill \end{array}$$

(62)

$$\begin{array}{cc}\hfill & v^{n+1}\left(x_{max}\right)={\psi }_R^{n+1}.\hfill \end{array}$$

(63)

where

$$\begin{array}{cc}\hfill & {\mathcal{L}}_x^n:={\displaystyle \frac{\alpha }{2}}{\displaystyle \frac{{\partial }^2}{\partial x^2}}+{\displaystyle \frac{\beta }{2}}{\displaystyle \frac{\partial }{\partial x}}+({\displaystyle \frac{\gamma }{2}}-{\displaystyle \frac{1}{\tau }})I,\hfill \\ \hfill & {\mathcal{F}}^{n+\frac{1}{2}}:=-{\displaystyle \frac{\alpha }{2}}{v}_{xx}^n-{\displaystyle \frac{\beta }{2}}{v}_x^n-({\displaystyle \frac{\gamma }{2}}+{\displaystyle \frac{1}{\tau }})v^n-f^{n+\frac{1}{2}}.\hfill \end{array}$$

If $f^{n+\frac{1}{2}}$, $\forall n$, $0⩽n⩽N$, lie in $C^2\left({\Omega }_x\right)$ then $v^n\in C^4\left({\Omega }_x\right)$, $\forall n$, $0⩽n⩽N$. Therefore, according to Hall and Meyer error estimate (see, [24]), we can obtain

$$\begin{array}{c}\hfill \parallel D^r(v^n-{\overline{S}}^n){\parallel }_{\infty }⩽{\epsilon }_r\parallel {\displaystyle \frac{d^4{v}^n}{d{x}^4}}{\parallel }_{\infty }{h}^{4-r},r=0,1,2,3;0⩽n⩽N\end{array}$$

(64)

where, ${\epsilon }_0=\frac{5}{384}$, ${\epsilon }_1=\frac{1}{24}$, ${\epsilon }_2=\frac{3}{8}$, ${\epsilon }_3=1$. Since

$$\begin{array}{cc}\hfill & \left|{\displaystyle \frac{{\partial }^{l+n}v(x,t)}{\partial x^l\partial t^n}}\right|⩽K;0⩽n⩽3,0⩽l+n⩽4\hfill \end{array}$$

(65)

$$\begin{array}{cc}\hfill & \parallel D^r(v^n-{\overline{Q}}^n){\parallel }_{\infty }⩽K{h}^{4-r},r=0,1,2,3;0⩽n⩽N\hfill \end{array}$$

(66)

$$\begin{array}{cc}\hfill & \Rightarrow |D^r(v^n\left(x_l\right)-{\overline{Q}}^n\left(x_l\right))|⩽K{h}^{4-r},r=0,1,2,3;0⩽n⩽N,0⩽l⩽M.\hfill \end{array}$$

(67)

Thus,

$$\begin{array}{cc}\hfill & |{\mathcal{L}}_x^n(v^n\left(x_l\right)-{\overline{Q}}^n\left(x_l\right))|⩽K{h}^2,\forall l,0⩽l⩽M,and,\forall n,0⩽n⩽N\hfill \end{array}$$

(68)

$$\begin{array}{cc}\hfill & \Rightarrow \parallel {\mathcal{L}}_x^n(v^n-{\overline{Q}}^n){\parallel }_{\infty }⩽K{h}^2,\forall n,0⩽n⩽N.\hfill \end{array}$$

(69)

At the $(n+1)$th-time level, we write

$$\begin{array}{cc}\hfill & {\mathcal{L}}_x^n{\overline{Q}}^{n+1}\left(x_l\right)={\mathcal{L}}_x^n{v}^{n+1}\left(x_l\right)+g^{n+1}\left(x_l\right);0⩽l⩽M,\hfill \end{array}$$

(70)

$$\begin{array}{cc}\hfill & {\overline{Q}}^{n+1}\left(x_0\right)=v^{n+1}\left(x_0\right)+{\overline{\psi }}_L^{n+1}\left(x_0\right),\hfill \end{array}$$

(71)

$$\begin{array}{cc}\hfill & {\overline{Q}}^{n+1}\left(x_M\right)=v^{n+1}\left(x_M\right)+{\overline{\psi }}_R^{n+1}\left(x_M\right).\hfill \end{array}$$

(72)

where $g^{n+1}$ is an error function which order of magnitude is $O\left(h^2\right)$ and ${\overline{\psi }}_L^{n+1}$, ${\overline{\psi }}_R^{n+1}$ are error functions which order of magnitude are $O\left(h^4\right)$.

Since $v^{n+1}\left(x_l\right)=Q^{n+1}\left(x_l\right)$; $\forall l,0⩽l⩽m$, therefore we can re-write the system (70)–(72) in the following matrix form

$$\begin{array}{c}\hfill P{\overline{C}}^{n+1}=P{C}^{n+1}+G^n\end{array}$$

(73)

where,

$$\begin{array}{c}\hfill G^n={[g^{n+1}\left(x_0\right),g^{n+1}\left(x_1\right),\cdots ,g^{n+1}\left(x_{M-1}\right),g^{n+1}\left(x_M\right)]}^T-{[p{\overline{\psi }}_L^{n+1}\left(x_0\right),0,\cdots ,0,r{\overline{\psi }}_R^{n+1}\left(x_M\right)]}^T,\end{array}$$

this implies

$$\begin{array}{c}\hfill \parallel G^n{\parallel }_{\infty }⩽K{h}^2.\end{array}$$

(74)

By using (52) and (73), we obtain

$$\begin{array}{cc}\hfill & P({\overline{C}}^{n+1}-C^{n+1})=G^n\hfill \\ \hfill & \Rightarrow \parallel C^{n+1}-{\overline{C}}^{n+1}{\parallel }_{\infty }⩽\parallel P^{-1}{\parallel }_{\infty }{\parallel G^n\parallel }_{\infty }.\hfill \end{array}$$

A simple use of Equation (74) and bound of $\parallel P^{-1}{\parallel }_{\infty }$ derived in Section 3.2 gives

$$\begin{array}{c}\hfill \parallel C^{n+1}-{\overline{C}}^{n+1}{\parallel }_{\infty }⩽K{h}^2;0⩽n⩽N-1\end{array}$$

(75)

where $\parallel C^{n+1}-{\overline{C}}^{n+1}{\parallel }_{\infty }={max}_{0⩽k⩽M}\left\{\right|c_k^{n+1}-{\overline{c}}_k^{n+1}\left|\right\}$.

In addition, with the help of Equations (71), (72) and (75), we obtain

$$\begin{array}{cc}\hfill & |c_{-1}^{n+1}-{\overline{c}}_{-1}^{n+1}|⩽K{h}^2,\hfill \\ \hfill & |c_{M+1}^{n+1}-{\overline{c}}_{M+1}^{n+1}|⩽K{h}^2.\hfill \end{array}$$

Thus

$$\begin{array}{c}\hfill \underset{-1⩽k⩽M+1}{max}\left\{\right|c_k^{n+1}-{\overline{c}}_k^{n+1}\left|\right\}⩽K{h}^2;0⩽n⩽N-1.\end{array}$$

(76)

Now,

$$\begin{array}{cc}\hfill & Q^{n+1}\left(x\right)-{\overline{Q}}^{n+1}\left(x\right)=\sum _{k=-1}^{M+1}(c_k^{n+1}-{\overline{c}}_k^{n+1})B_k\left(x\right)\hfill \\ \hfill & \Rightarrow |Q^{n+1}\left(x_l\right)-{\overline{Q}}^{n+1}\left(x_l\right)|⩽\underset{-1⩽k⩽M+1}{max}\left\{\right|c_k^{n+1}-{\overline{c}}_k^{n+1}\left|\right\}\sum _{k=-1}^{M+1}\left|B_k\left(x_l\right)\right|;0⩽l⩽M.\hfill \end{array}$$

By using $B_k\left(x_l\right)$ given in Section 3.1, we can easily see that ${\sum }_{k=-1}^{M+1}\left|B_k\left(x_l\right)\right|⩽K=10$, $0⩽l⩽M$, hence

$$\begin{array}{c}\hfill |Q^{n+1}\left(x_l\right)-{\overline{Q}}^{n+1}\left(x_l\right)| ⩽K{h}^2;\forall l,0⩽l⩽M\end{array}$$

(77)

$$\begin{array}{c}\hfill \Rightarrow \parallel Q^{n+1}-{\overline{Q}}^{n+1}{\parallel }_{\infty }⩽K{h}^2;0⩽n⩽N-1.\end{array}$$

(78)

In the following triangular inequality, we discuss the relations (66) and (78)

$$\begin{array}{c}\hfill \parallel v^{n+1}-Q^{n+1}{\parallel }_{\infty }⩽\parallel v^{n+1}-{\overline{Q}}^{n+1}{\parallel }_{\infty }+{\parallel {\overline{Q}}^{n+1}-Q^{n+1}\parallel }_{\infty },\end{array}$$

we obtain

$$\begin{array}{c}\hfill \parallel v^{n+1}-Q^{n+1}{\parallel }_{\infty }⩽K{h}^2;0⩽n⩽N-1.\end{array}$$

(79)

□

Theorem 4. 

Let $v(x,t)$ be the solution of the initial boundary value problem (13)–(16) and $Q^n\left(x\right)$ be the collocation approximation to the solution $v^n\left(x\right)$ after the temporal discretization stage. Then under the hypothesis of Lemma 2 and Theorem 3 the error estimate of the totally discrete scheme is given by

$$\begin{array}{c}\hfill {\parallel v-Q\parallel }_{\infty }⩽K({\tau }^2+h^2)\end{array}$$

where K are positive constants.

4. Numerical Experiments

In this section, we mainly use RStudio version 4.2.0 to verify the feasibility of the obtained pricing model (52).

Consider the following issue of PDE of up-and-out put barrier options under the CEV model:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial v(x,t)}{\partial t}}=\alpha {\displaystyle \frac{{\partial }^{2}v(x,t)}{\partial x^2}}+\beta {\displaystyle \frac{\partial v(x,t)}{\partial x}}+\gamma v(x,t),(x,t)\in (-2,2)\times (0,1)\end{array}$$

subject to the initial and boundary conditions

$$\begin{array}{cc}\hfill & v(x,0)=exp\left(x\right),x\in (-2,2)\hfill \\ \hfill & v(-2,t)=exp(-2-t),v(2,t)=exp(2-t),t\in (0,1).\hfill \end{array}$$

Figure 1 shows the change trend of Spatial Variable x and Option Price Q for $\delta =1/4,1/3,1/2$ when $r=0.05,\sigma =0.05$. When $\delta$ takes different values, it is noted that the changes in option prices are basically consistent, indicating that the obtained pricing model is feasible. Figure 2 shows the change trend of Spatial Variable x and Option Price Q for $r=0.05, 0.075, 0.1$ when $\delta =1/2, \sigma =0.05$. When the value of x approaches 2, the option price gradually increases as r increases, and the change trend of Spatial Variable x and Option Price Q is roughly the same in the rest of the time. Figure 3 shows the change trend of Spatial Variable x and Option Price Q for $\sigma =0.05, 0.075, 0.1$ when $\delta =1/2, r=0.05$. When the value of x is less than $-1$, the option price gradually increases as $\sigma$ increases, and the change trend of Spatial Variable x and Option Price Q is roughly the same in the rest of the time. Overall, the option price gradually increases with the increase of spatial variable x, and the rate of growth also gradually increases. Figure 4 shows the change trend of Time Variable t and Option Price Q for $r=0.05, 0.075, 0.1$ when $\delta =1/2, \sigma =0.05$. The option price gradually increases as the time variable t increases. As can be seen from the figure, as r increases, the slope of the line gradually steepens, and the option price increases more quickly. When $\delta =1/2, \sigma =0.05$ and $r=0.05$, the surface plot of the approximate solution for $M=N=30$ is given in Figure 5.

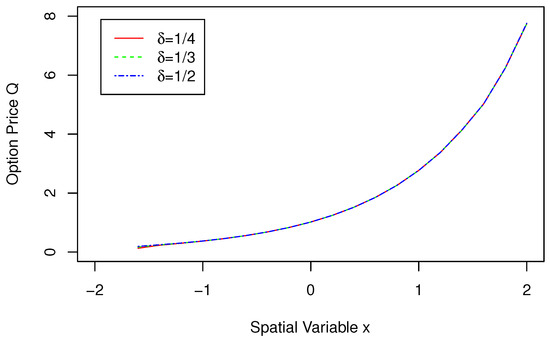
Figure 1. Approximate solutions with different values of $\delta$ and x in $[-2,2]$.

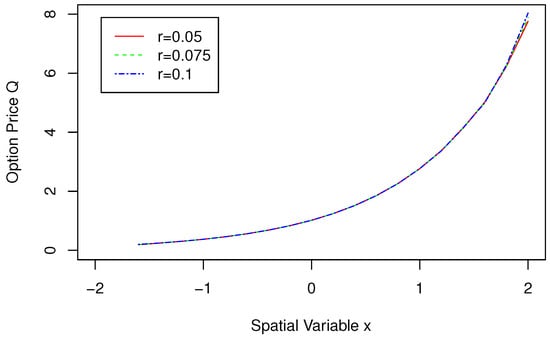
Figure 2. Approximate solutions with different values of r and x in $[-2,2]$.

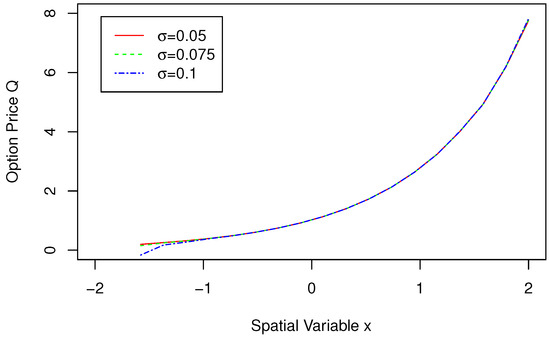
Figure 3. Approximate solutions with different values of $\sigma$ and x in $[-2,2]$.

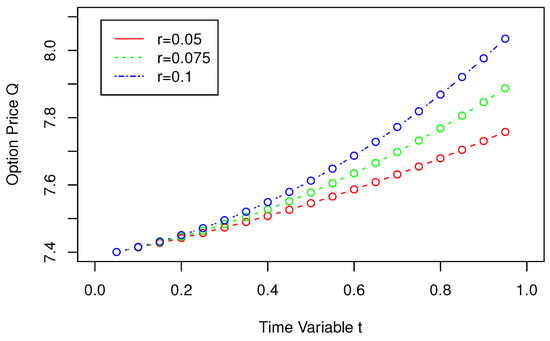
Figure 4. Approximate solutions with different values of r and t in $[0,1]$.

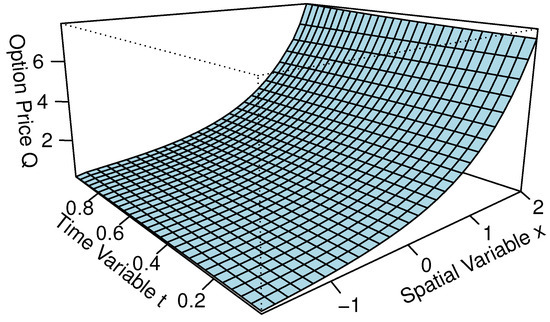
Figure 5. Approximate solution for $M=30,N=30$.

Based on the studied option pricing model, in this section we considers the relationship between the time variable x and the spatial variable t and the option price, and select different parameters $\delta$, r and $\sigma$. Based on the selected parameters, the trend chart of the option price was obtained, and the changes in the image were observed. The numerical simulation results were consistent with theoretical analysis.

5. Conclusions and Dicussion

In this paper, we study the cubic B-spline method for the barrier option problem under the CEV model. The time variable is discretized using the Crank-Nicolson method. On this basis, the spatial variable is discretized using the cubic B-spline collocation method to obtain a pricing model for barrier options. The time discretization of barrier options is analyzed for convergence, and the space discretization is analyzed for stability and convergence. The trend of log price of stock and option price for each parameter is analyzed in RStudio version 4.2.0, and the results show that cubic B-spline is feasible for solving barrier option problems under CEV models.

At present, there are still some shortcomings in this article. When truncating the infinite domain into the finite domain, some errors may occur. However, according to references [13,14,15], these errors are controllable. Thus, in the data experiment section, we make the error $f(x,t)=0$. Additionally, in this article, there is no comparison between the B-spline method used in this article and other methods for option pricing, which is also a limitation of this article.