Algebraic Structure Graphs over the Commutative Ring ${\mathbb{Z}}_m$: Exploring Topological Indices and Entropies Using $\mathbb{M}$-Polynomials

Abstract

The field of mathematics that studies the relationship between algebraic structures and graphs is known as algebraic graph theory. It incorporates concepts from graph theory, which examines the characteristics and topology of graphs, with those from abstract algebra, which deals with algebraic structures such as groups, rings, and fields. If the vertex set of a graph $\widehat{G}$ is fully made up of the zero divisors of the modular ring ${\mathbb{Z}}_n$, the graph is said to be a zero-divisor graph. If the products of two vertices are equal to zero under (modn), they are regarded as neighbors. Entropy, a notion taken from information theory and used in graph theory, measures the degree of uncertainty or unpredictability associated with a graph or its constituent elements. Entropy measurements may be used to calculate the structural complexity and information complexity of graphs. The first, second and second modified Zagrebs, general and inverse general Randics, third and fifth symmetric divisions, harmonic and inverse sum indices, and forgotten topological indices are a few topological indices that are examined in this article for particular families of zero-divisor graphs. A numerical and graphical comparison of computed topological indices over a proposed structure has been studied. Furthermore, different kinds of entropies, such as the first, second, and third redefined Zagreb, are also investigated for a number of families of zero-divisor graphs.

1. Introduction

Topological indices and algebraic graph theory are two closely linked subjects that focus on the mathematical study of graphs, having applications in chemistry, physics, computer science and social networks. Topological indices and algebraic graph theory are linked by a shared interest in graph analysis and representation. Although topological indices are a specific set of numerical measurements obtained from graph topology, algebraic graph theory gives mathematical tools and notions for studying graph features, which can be used to analysis and understand topological indices and vice versa.

A molecular graph is a type of topological representation of a molecule that represents the structure and connections of a molecule. These molecular graphs characterize numerous chemical aspects of molecules, such as their organic, chemical, or physical properties. They are critical in applications such as quantitative structure–activity relationship (QSAR) and quantitative structure–property relationship (QSPR) research, digital screens, and computational drug design [1,2]. Many topological indices have been used to characterize molecular graphs and many of these indices are good graph descriptors [3,4]. Furthermore, several of these indices have been discovered to correspond well with the organic, chemical, or physical characteristics of molecules [5,6,7,8,9,10,11,12,13,14,15,16,17]. As a result, they serve an important role in understanding and predicting molecular behavior and characteristics in a variety of chemical and pharmacological situations.

Graphs in mathematics are made up of vertices (which represent atoms) and edges (which represent chemical bonds). A molecular graph is a graph that represents the structure and connectivity of molecules and acts as a topological representation of the molecule. These molecular graphs are analyzed using a variety of topological indices, including distance-based topological indices, degree-based topological indices, and other derived indices. Distance-based topological indices, in particular, have an important role in chemical graph theory, notably in chemistry [18,19]. Each type of topological index offers unique information about the molecular graph and many have been presented to study different aspects of chemical compounds. Topological indices help in the analysis of molecular structures, property prediction, drug design, and other areas of chemical research.

Degree-based topological indices have undergone extensive research and have shown significant connections to various properties of the molecular compounds under study. The relationship between these indices is remarkably strong. Among the topological indexes derived from distance and degree in [20], degree-based topological indices stand out as the most widely recognized examples of such invariants. Numerical values exist that establish connections between the molecular structure and various physical properties, chemical reactivities and biological activities. These numerical values, known as topological indices, associate the molecular shape with specific physical properties, artificial reactivities, and natural biological activities [21,22].

In 1948, Shannon introduced the concept of entropy through his seminal paper [23]. Entropy, when applied to a probability distribution, serves as a measure of the predictability of information content or the uncertainty of a system. Subsequently, the application of entropy extended to graphs and chemical networks, enabling a deeper understanding of their structural information. Graph entropies have recently gained significance in various domains, including biology, chemistry, ecology, sociology, among others. The idea of entropy, which derives from statistical mechanics and information theory, quantifies how random or unpredictable a system is. Even though entropy is most frequently related to information theory, it may also be used to examine complex systems, networks, and patterns in algebraic structures and graphs. A detailed survey on the application of algebraic entropies over algebraic structure has been presented in [24]. The degree of each atom holds paramount importance, leading to substantial research in graph theory and network theory to explore invariants that have long served as information functionals in scientific studies. The chronological sequence of graph entropy measurements utilized to analyze biological and chemical networks [25,26,27]. Further, Das et al. investigated various results on topological indices and entropies in their research articles [28,29,30,31,32,33].

A graph that depends on algebraic structures such as group theory, number theory, and ring theory is known as an algebraic graph. In the field of algebraic graph theory, various problems are still open; the number of components problem of a graph, which depends on the modular relation, still remains a conjuncture. There are several algebraic graphs based on the algebraic structure that has been studied, but here we are going to discuss a zero-divisor graph that depends on the set of zero divisors of a ring R. A graph $\widehat{G}$ is known as a zero-divisor graph whose vertex set is the zero divisors of the modular ring ${\mathbb{Z}}_n$, and two vertices will be adjacent to each other if their product will be zero under (mod n) [34]. The zero-divisor graph for ${\mathbb{Z}}_{18}$ is shown in Figure 1. For further understanding related to algebraic structure graphs and their properties, reader should can study [35,36,37,38,39,40].

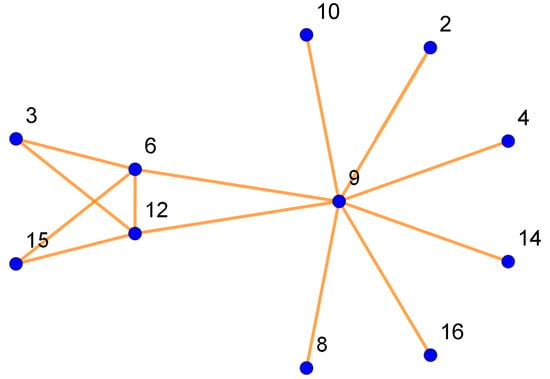
Figure 1. The zero-divisor graph for ${\mathbb{Z}}_{18}$.

The rest of the work is arranged as follows: In Section 2, some basic terminology related to topological indices are given to understand the proposed work. In Section 3 and Section 4, various topological indices over zero-divisor graphs $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$ and $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^3{\wp }_2}\right)$ are discussed, respectively. Further, in these sections the behavior of investigated topological indices via numeric tables and three-dimensional discrete plotting are observed numerically and graphically. In Section 5, three kinds of entropies, i.e., first, second, and third redefined entropies, are founded over the families of zero-divisor graphs. In the last section, concluding remarks and further future works are discussed with detail.

2. Basic Terminology Related to Topological Indices and Entropies

In this section, we will discuss some well-known existing topological indices for various families of graphs [41,42,43,44,45,46,47,48,49] and M -polynomial [3,8], namely, first Zagreb $M_1\left(G\right)$, second Zagreb $M_2\left(G\right)$, second modified Zagreb ${}^m{M}_2\left(G\right)$, general Randics $R_{\alpha }\left(G\right)$, inverse general Randics $R{R}_{\alpha }\left(G\right)$, third symmetric divisions $SS{D}_3\left(G\right)$, fifth symmetric divisions $SS{D}_5\left(G\right)$, harmonic $H\left(G\right)$, inverse sum $I\left(G\right)$, and forgotten topological index $F\left(G\right)$.

$$\begin{array}{ccc}\hfill M_1\left(G\right)& =& \sum _{u_i{v}_j\in E\left(G\right)}(d_{u_i}+d_{v_j}),M_2\left(G\right)=\sum _{u_i{v}_j\in E\left(G\right)}(d_{u_i}\times d_{v_j}).\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill {}^m{M}_2\left(G\right)& =& \sum _{u_i{v}_j\in E\left(G\right)}\left(\frac{1}{d_{u_i}\times d_{v_j}}\right),R_{\alpha }\left(G\right)=\sum _{u_i{v}_j\in E\left(G\right)}\left(\frac{1}{{(d_{u_i}\times d_{v_j})}^{\alpha }}\right),\alpha \in {\mathrm{R}}^{+}.\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill R{R}_{\alpha }\left(G\right)& =& \sum _{u_i{v}_j\in E\left(G\right)}\left({(d_{u_i}\times d_{v_j})}^{\alpha }\right),\alpha \in {\mathrm{R}}^{+},SS{D}_3\left(G\right)=\sum _{u_i{v}_j\in E\left(G\right)}\left(d_{u_i}{d}_{v_j}(d_{u_i}+d_{v_j})\right).\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill SS{D}_5\left(G\right)& =& \sum _{u_i{v}_j\in E\left(G\right)}(\frac{d_{u_i}}{d_{v_j}}+\frac{d_{v_j}}{d_{u_i}}),H\left(G\right)=\sum _{u_i{v}_j\in E\left(G\right)}\left(\frac{2}{d_{v_j}+d_{v_j}}\right).\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill I\left(G\right)& =& \sum _{u_i{v}_j\in E\left(G\right)}\left(\frac{d_{v_j}{d}_{v_j}}{d_{v_j}+d_{v_j}}\right),F\left(G\right)=\sum _{u_i{v}_j\in E\left(G\right)}\left((d_{u_i}^2+d_{v_j}^2)\right).\hfill \end{array}$$

(5)

In chemical graph theory, the $\mathbb{M}$-polynomial is a topological index used to characterize the molecular structure of organic molecules. Researchers can acquire insights into the structural factors that determine the properties of molecules by analyzing the coefficients of different terms in the $\mathbb{M}$-polynomial. The $\mathbb{M}$-polynomial is defined as [3,8]

$$\begin{array}{c}\hfill M(G,x,y)=\sum _{ij\in E\left(G\right)}{m}_{ij}\left(G\right)x^i{y}^j.\end{array}$$

(6)

The relationship between $\mathbb{M}$-polynomial and topological indices are given in Table 1.

Table 1. Relation between $\mathbb{M}$-polynomial and topological indices.

Topological Indices	$\mathit{f}(\mathit{u},\mathit{v})$	$\mathit{M}(\mathit{G};\mathit{u},\mathit{v})$
$\begin{array}{c}{M}_1\left(G\right)\hfill \\ M_2\left(G\right)\hfill \\ {}^m{M}_2\left(G\right)\hfill \\ R_{\alpha }\left(G\right),\alpha \ne 0\hfill \\ R{R}_{\alpha }\left(G\right),\alpha \ne 0\hfill \\ SS{D}_3\left(G\right)\hfill \\ SS{D}_5\left(G\right)\hfill \\ H\left(G\right)\hfill \\ I\left(G\right)\hfill \\ F\left(G\right)\hfill \end{array}$	$\begin{array}{c}u+v\\ u_i{v}_j\\ 1/uvs.\\ {\left(uv\right)}^{\alpha }\\ 1/{\left(uv\right)}^{\alpha }\\ uvs.(u^2+v^2)\\ \left(u^2+v^2\right)/uvs.\\ 2/(u+v)\\ uvs./(u+v)\\ u^2+v^2\end{array}$	$\begin{array}{c}{M}_1(G;u,v)={\left.\left(D_u+D_v\right)M(G;u,v)\right|}_{u=v=1}\\ M_2(G;u,v)=\left(D_u{D}_{}\right){M(G;u,v)|}_{u=v=1}\\ {}^m{M}_2(G;u,v)=\left({\delta }_u{\delta }_v\right){M(G;u,v)|}_{u=v=1}\\ R_{\alpha }\left(G\right)=\left(D_u^{\alpha }{D}_v^{\alpha }\right){M(G;u,v)|}_{u=v=1}\\ R{R}_{\alpha }\left(G\right)=\left({\delta }_u^{\alpha }{\delta }_v^{\alpha }\right){M(G;u,v)|}_{u=v=1}\\ SS{D}_3\left(G\right)=D_u{D}_v(D_u+D_v)M(G,u,v){|}_{u=v=1}\\ SS{D}_5\left(G\right)=\left(D_u{\delta }_v+{\delta }_u{D}_v\right){M(G;u,v)|}_{u=v=1}\\ H\left(G\right)=2{\delta }_{u}JM{(G;u,v|}_{u=1}\\ I\left(G\right)={\delta }_{u}J{D}_u{D}_v{M(G;u,v)|}_{u=1}\\ F\left(G\right)=\left(D_u^2+D_v^2\right){M(G;u,v)|}_{u=v=1}\end{array}$

Where, $D_u=u\left(\frac{\partial M(G;u,v)}{\partial u}\right),D_v=v\left(\frac{\partial M(G;u,v)}{\partial v}\right),{\delta }_u={\int }_0^u\frac{M(G;y,v)}{y}\mathrm{d}y,{\delta }_v={\int }_0^v\frac{M(G;u,y)}{y}\mathrm{d}y$, $J=M(G;u,u)$, $Q_{\alpha }=x^{\alpha }M(G;u,v),\alpha \ne 0$.

In 2013, Ranjini et al. introduced the first, second, and third redefined version of the Zagreb indices [50],

$$\begin{array}{ccc}\hfill ReZ{G}_1\left(G\right)& =& \sum _{x_i{y}_j\in E\left(G\right)}{\displaystyle \frac{d_{x_i}+d_{y_j}}{d_{x_i}{d}_{y_j}}}.\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill ReZ{G}_2\left(G\right)& =& \sum _{x_i{y}_j\in E\left(G\right)}{\displaystyle \frac{d_{x_i}{d}_{y_j}}{d_{x_i}+d_{y_j}}}.\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill ReZ{G}_3\left(G\right)& =& \sum _{x_i{y}_j\in E\left(G\right)}\left(d_{x_i}{d}_{y_j}\right)\left(d_{x_i}+d_{y_j}\right).\hfill \end{array}$$

(9)

The concept of entropy was introduced by Chen et al. in 2014 [51], and is defined as

$$\begin{array}{c}\hfill EN{T}_{\Psi \left(G\right)}=\sum _{x_i{y}_j\in E\left(G\right)}{\displaystyle \frac{\Psi \left(x_i{y}_j\right)}{{\displaystyle \sum _{x_i{y}_j\in E\left(G\right)}}\Psi \left(x_i{y}_j\right)}}log\left\{{\displaystyle \frac{\Psi \left(x_i{y}_j\right)}{{\displaystyle \sum _{x_i{y}_j\in E\left(G\right)}}\Psi \left(x_i{y}_j\right)}}\right\}.\end{array}$$

(10)

The remaining entropies were found in [52], which are defined as

• First redefined Zagreb entropy: if

  $$\Psi \left(x_i{y}_j\right)={\displaystyle \frac{d_{x_i}+d_{y_j}}{d_{x_i}{d}_{y_j}}}.$$
  Then

  $$ReZ{G}_1\left(G\right)=\sum _{x_i{y}_j\in E\left(G\right)}\left\{{\displaystyle \frac{d_{x_i}+d_{y_j}}{d_{x_i}{d}_{y_j}}}\right\}=\sum _{x_i{y}_j\in E\left(G\right)}\Psi \left(x_i{y}_j\right).$$

  (11)
  Now, by using (11) in (10), the first redefined Zagreb entropy is

  $$EN{T}_{ReZ{G}_1}=log\left(ReZ{G}_1\right)-{\displaystyle \frac{1}{ReZ{G}_1}}log\left\{\prod _{x_i{y}_j\in E\left(G\right)}{\left[{\displaystyle \frac{d_{x_i}+d_{y_j}}{d_{x_i}{d}_{y_j}}}\right]}^{\left[d_{x_i}+d_{y_j}/d_{x_i}{d}_{y_j}\right]}\right\}.$$

  (12)
• Second redefined Zagreb entropy: if

  $$\Psi \left(x_i{y}_j\right)={\displaystyle \frac{d_{x_i}{d}_{y_j}}{d_{x_i}+d_{y_j}}}.$$
  Then

  $$ReZ{G}_2\left(G\right)=\sum _{x_i{y}_j\in E\left(G\right)}\left\{{\displaystyle \frac{d_{x_i}{d}_{y_j}}{d_{x_i}+d_{y_j}}}\right\}=\sum _{x_i{y}_j\in E\left(G\right)}\Psi \left(x_i{y}_j\right).$$

  (13)
  Now, by using (13) in (10), the second redefined Zagreb entropy is

  $$EN{T}_{ReZ{G}_1}=log\left(ReZ{G}_2\right)-{\displaystyle \frac{1}{ReZ{G}_2}}log\left\{\prod _{x_i{y}_j\in E\left(G\right)}{\left[{\displaystyle \frac{d_{x_i}{d}_{y_j}}{d_{x_i}+d_{y_j}}}\right]}^{\left[d_{x_i}{d}_{y_j}/d_{x_i}+d_{y_j}\right]}\right\}.$$

  (14)
• Third redefined Zagreb entropy: if

  $$\Psi \left(x_i{y}_j\right)=\left(d_{x_i}{d}_{y_j}\right)(d_{x_i}+d_{y_j}).$$
  Then

  $$ReZ{G}_3\left(G\right)=\sum _{x_i{y}_j\in E\left(G\right)}\left\{\left(d_{x_i}{d}_{y_j}\right)(d_{x_i}+d_{y_j})\right\}=\sum _{x_i{y}_j\in E\left(G\right)}\Psi \left(x_i{y}_j\right).$$

  (15)
  Now, by using (15) in (10), the third redefined Zagreb entropy is

  $$EN{T}_{ReZ{G}_3}=log\left(ReZ{G}_3\right)-{\displaystyle \frac{1}{ReZ{G}_3}}log\left\{\prod _{x_i{y}_j\in E\left(G\right)}{\left[\left(d_{x_i}{d}_{y_j}\right)(d_{x_i}+d_{y_j})\right]}^{\left[\left(d_{x_i}{d}_{y_j}\right)(d_{x_i}+d_{y_j})\right]}\right\}.$$

  (16)

3. $\mathbb{M}$-Polynomial and Topological Indices for Zero-Divisor Graph $\widehat{\mathit{G}}\left({\mathbb{Z}}_{{\wp }_{\mathbf{1}}^{\mathbf{2}}{\wp }_{\mathbf{2}}}\right)$

Let ${\mathbb{Z}}_n$ be a modular ring with unity and ${\mathbb{Z}}_n\times {\mathbb{Z}}_m$ be the product of two modular rings. A non-zero element z of a modular ring ${\mathbb{Z}}_n$ is said to be a zero divisor if there exists another non-zero element y of ${\mathbb{Z}}_n$ such that the product of z and y will be zero under the modulo n. In other words, two non-zero elements will be zero divisors to each other if their product will be zero. Similarly, two non-zero elements $(x_1,y_1)$, $(x_2,y_2)$ from ${\mathbb{Z}}_n\times {\mathbb{Z}}_m$ will be zero, divisors to each other if the product of both will be zero such that $(x_1,y_1)\times (x_2,y_2)=(0,0)$ under modulo $mn$. In this section, $\mathbb{M}-$ polynomial and topological indices for the zero-divisor graph $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$ with numerically and graphically behavior are discussed. The zero-divisor graph $\widehat{G}\left({\mathbb{Z}}_{5^2\times 3}\right)$ as shown in Figure 2.

Figure 2. The zero-divisor graph $\widehat{G}\left({\mathbb{Z}}_{5^2\times 3}\right)$.

Lemma 1.

Let $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$ be a zero-divisor graph over ${\mathbb{Z}}_{{\wp }_1^2{\wp }_2}$ with distinct primes (${\wp }_1>{\wp }_2$), then M-polynomial is

$$\begin{array}{ccc}\hfill M(G;x;y)& =& -x^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}-{\wp }_1^2{x}^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}+2{\wp }_1{x}^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}+{\wp }_2{x}^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}+{\wp }_1^2{\wp }_2{x}^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & -& 2{\wp }_1{\wp }_2{x}^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}+x^{{\wp }_1^2-1}{y}^{{\wp }_2-1}-{\wp }_1^2{x}^{{\wp }_1^2-1}{y}^{{\wp }_2-1}-{\wp }_2{x}^{{\wp }_1^2-1}{y}^{{\wp }_2-1}+{\wp }_1^2{\wp }_2{x}^{{\wp }_1^2-1}{y}^{{\wp }_2-1}\hfill \\ & +& x^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}+\frac{1}{2}{\wp }_1^2{x}^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}-\frac{3}{2}{\wp }_1{x}^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

(17)

Proof. 

Let $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$ be a zero-divisor graph over ${\mathbb{Z}}_{{\wp }_1^2{\wp }_2}$ with distinct primes (${\wp }_1>{\wp }_2$). The cardinality function of edge partition for $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$ is;

$$\begin{array}{c}\hfill |m_{(i,j)}|=\left\{\begin{array}{c}\begin{array}{cc}{\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right),\hfill & \mathrm{if}i={\wp }_1^2-1,j={\wp }_2-1,\hfill \\ {\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right),\hfill & \mathrm{if}i={\wp }_1-1,j={\wp }_1{\wp }_2-2,\hfill \\ \left({\wp }_1-1\right)\left({\wp }_2-1\right),\hfill & \mathrm{if}i={\wp }_1^2-1,j={\wp }_1{\wp }_2-2,\hfill \\ \frac{1}{2}\left({\wp }_1^2-3{\wp }_1+2\right),\hfill & \mathrm{if}i={\wp }_1{\wp }_2-2,j={\wp }_1{\wp }_2-2.\hfill \end{array}\hfill \end{array}\right.\end{array}$$

(18)

By Equation (6);

$$\begin{array}{ccc}\hfill M(G,x,y)& =& \sum _{ij\in E\left(G\right)}{m}_{(i,j)}{x}^i{y}^j\hfill \\ & =& \sum _{{\wp }_2-1\le {\wp }_2{\wp }_1^2-1}|m_{({\wp }_2-1,{\wp }_1^2-1)}|x^{{\wp }_2-1}{y}^{{\wp }_1^2-1}+\sum _{{\wp }_1-1\le {\wp }_2{\wp }_1{\wp }_{1}2-2}|m_{({\wp }_1-1,{\wp }_1{\wp }_2-2)}|x^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \sum _{{\wp }_1{\wp }_2-2\le {\wp }_2{\wp }_1^2-1}|m_{({\wp }_1{\wp }_2-2,{\wp }_1^2-1)}|x^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1^2-1}+\sum _{{\wp }_1{\wp }_2-2\le {\wp }_2{\wp }_1{\wp }_2-2}|m_{({\wp }_1{\wp }_2-2,{\wp }_1{\wp }_2-2)}|x^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

Substituting the value from (18) in above equation, we then have

$$\begin{array}{ccc}\hfill M(G,x,y)& =& {\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right)x^{{\wp }_1^2-1}{y}^{{\wp }_2-1}+{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)x^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \left({\wp }_1-1\right)\left({\wp }_2-1\right)x^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-2}+\frac{1}{2}\left({\wp }_1^2-3{\wp }_1+2\right)x^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & =& -x^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}-{\wp }_1^2{x}^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}+2{\wp }_1{x}^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}+{\wp }_2{x}^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}+{\wp }_1^2{\wp }_2{x}^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & -& 2{\wp }_1{\wp }_2{x}^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}+x^{{\wp }_1^2-1}{y}^{{\wp }_2-1}-{\wp }_1^2{x}^{{\wp }_1^2-1}{y}^{{\wp }_2-1}-{\wp }_2{x}^{{\wp }_1^2-1}{y}^{{\wp }_2-1}+{\wp }_1^2{\wp }_2{x}^{{\wp }_1^2-1}{y}^{{\wp }_2-1}\hfill \\ & +& x^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}+\frac{1}{2}{\wp }_1^2{x}^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}-\frac{3}{2}{\wp }_1{x}^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

This one is a desired relation (17). □

Theorem 1.

Let $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$ be a zero-divisor graph over ${\mathbb{Z}}_{{\wp }_1^2{\wp }_2}$ with distinct primes (${\wp }_1>{\wp }_2$); then

$$\begin{array}{ccc}\hfill M_1\left(G\right)& =& {\wp }_1^3{\wp }_2^2-{\wp }_1{\wp }_2^2+{\wp }_1^4{\wp }_2+{\wp }_1^3{\wp }_2-11{\wp }_1^2{\wp }_2+9{\wp }_1{\wp }_2-{\wp }_1^4-{\wp }_1^3+6{\wp }_1^2-4.\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill M_2\left(G\right)& =& \frac{7}{2}{\wp }_1^4{\wp }_2^2-\frac{13}{2}{\wp }_1^3{\wp }_2^2+2{\wp }_1^2{\wp }_2^2+{\wp }_1{\wp }_2^2-4{\wp }_1^4{\wp }_2+14{\wp }_1^2{\wp }_2-10{\wp }_1{\wp }_2\hfill \\ & +& {\wp }_1^4+3{\wp }_1^3-7{\wp }_1^2-{\wp }_1+4.\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill {}^m{M}_2\left(G\right)& =& \frac{2+{\wp }_1(7+{\wp }_1(2+{\wp }_1-2(6+{\wp }_1){\wp }_2+4{\wp }_1{\wp }_2^2))}{2(1+{\wp }_1){(-2+{\wp }_1{\wp }_2)}^2}.\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill R_{\alpha }\left(G\right)& =& ({\wp }_1-1)({\wp }_2-1)\left({\wp }_1{\left({\wp }_1^2{\wp }_2-{\wp }_1^2-{\wp }_2+1\right)}^{\alpha }+{\left({\wp }_1^3{\wp }_2-2{\wp }_1^2-{\wp }_1{\wp }_2+2\right)}^{\alpha }\right)\hfill \\ & +& {({\wp }_1-1)}^2({\wp }_2-1){\left({\wp }_1^2{\wp }_2-2{\wp }_1-{\wp }_1{\wp }_2+2\right)}^{\alpha }+\frac{1}{2}\left({\wp }_1^2-3{\wp }_1+2\right){\left({\wp }_1{\wp }_2-2\right)}^{2\alpha }.\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill R{R}_{\alpha }\left(G\right)& =& ({\wp }_1-1)({\wp }_2-1)\left(\frac{{\wp }_1}{{\left({\wp }_1^2{\wp }_2-{\wp }_1^2-{\wp }_2+1\right)}^{\alpha }}+\frac{{\wp }_1-1}{{\left({\wp }_1^2{\wp }_2-2{\wp }_1-{\wp }_1{\wp }_2+2\right)}^{\alpha }}\right)\hfill \\ & +& \frac{{\wp }_1^2-3{\wp }_1+2}{2{({\wp }_1{\wp }_2-2)}^{2\alpha }}+({\wp }_1-1)({\wp }_2-1)\left(\frac{1}{{\left({\wp }_1^3{\wp }_2-2{\wp }_1^2-{\wp }_1{\wp }_2+2\right)}^{\alpha }}\right).\hfill \end{array}$$

(23)

Proof. 

Let $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$ be a zero-divisor graph over ${\mathbb{Z}}_{{\wp }_1^2{\wp }_2}$ with distinct primes (${\wp }_1>{\wp }_2$). First, we will find the following terms: $D_x$, $D_y$, $D_x+D_y$${\delta }_x{\delta }_y$, $D_x^{\alpha }{D}_y^{\alpha }$, and ${\delta }_x^{\alpha }{\delta }_y^{\alpha },(\alpha \ne 0)$ by using the $\mathbb{M}$-polynomial from Equation (17). Let $M(G,x,y)=f(x,y)$; then

$$\begin{array}{ccc}\hfill D_x& =& \frac{\partial f(x,y)}{\partial x}x\hfill \\ \hfill & =& {\wp }_1\left({\wp }_1^2-1\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)x^{{\wp }_1^2-1}{y}^{{\wp }_2-1}+{\left({\wp }_1-1\right)}^3\left({\wp }_2-1\right)x^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \left({\wp }_1^2-1\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)x^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-2}+\frac{1}{2}\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1^2-3{\wp }_1+2\right)x^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill D_y& =& \frac{\partial f(x,y)}{\partial y}y\hfill \\ \hfill & =& {\wp }_1\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^2{x}^{{\wp }_1^2-1}{y}^{{\wp }_2-1}+\left({\wp }_1{\wp }_2-2\right){\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)x^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \left({\wp }_1{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)x^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-2}+\frac{1}{2}\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1^2-3{\wp }_1+2\right)x^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill D_x{D}_y& =& x\frac{\partial f(x,y)}{\partial x}\left(D_y\right)\hfill \\ \hfill & =& {\wp }_1\left({\wp }_1^2-1\right)\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^2{x}^{{\wp }_1^2-1}{y}^{{\wp }_2-1}+\left({\wp }_1{\wp }_2-2\right){\left({\wp }_1-1\right)}^3\left({\wp }_2-1\right)x^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \left({\wp }_1^2-1\right)\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)x^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \frac{1}{2}{\left({\wp }_1{\wp }_2-2\right)}^2\left({\wp }_1^2-3{\wp }_1+2\right)x^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill D_x^{\alpha }{D}_y^{\alpha }& =& {\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right){\left(({\wp }_1^2-1)({\wp }_2-1)\right)}^{\alpha }{x}^{{\wp }_1^2-1}{y}^{{\wp }_2-1}\hfill \\ \hfill & +& {\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right){\left(({\wp }_1-1)({\wp }_1{\wp }_2-2)\right)}^{\alpha }{x}^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \left({\wp }_1-1\right)\left({\wp }_2-1\right){\left(({\wp }_1^2-1)({\wp }_1{\wp }_2-2)\right)}^{\alpha }{x}^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \frac{1}{2}\left({\wp }_1^2-3{\wp }_1+2\right){\left({\wp }_1{\wp }_2-2\right)}^{2\alpha }{x}^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill {\delta }_y& =& {\int }_0^y\frac{f(x,t)}{t}\mathrm{d}t\hfill \\ \hfill & =& {\wp }_1\left({\wp }_1-1\right)x^{{\wp }_1^2-1}{y}^{{\wp }_2-1}+\frac{{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\wp }_1{\wp }_2-2}{x}^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}+\frac{\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1{\wp }_2-2}{x}^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \frac{\left({\wp }_1^2-3{\wp }_1+2\right)}{2({\wp }_1{\wp }_2-2)}{x}^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill {\delta }_x{\delta }_y& =& {\int }_0^x\frac{{\delta }_y}{t}\mathrm{d}t\hfill \\ \hfill & =& \frac{{\wp }_1\left({\wp }_1-1\right)}{{\wp }_1^2-1}{x}^{{\wp }_1^2-1}{y}^{{\wp }_2-1}+\frac{\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1{\wp }_2-2}{x}^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}+\frac{\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1^2-1\right)}{x}^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \frac{\left({\wp }_1^2-3{\wp }_1+2\right)}{2{({\wp }_1{\wp }_2-2)}^2}{x}^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill {\delta }_x^{\alpha }{\delta }_y^{\alpha }& =& \frac{{\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\left(({\wp }_1^2-1)({\wp }_2-1)\right)}^{\alpha }}{x}^{{\wp }_1^2-1}{y}^{{\wp }_2-1}+\frac{{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\left(({\wp }_1-1)({\wp }_1{\wp }_2-2)\right)}^{\alpha }}{x}^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ \hfill & +& \frac{\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\left(({\wp }_1^2-1)({\wp }_1{\wp }_2-2)\right)}^{\alpha }}{x}^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-2}+\frac{\left({\wp }_1^2-3{\wp }_1+2\right)}{2{({\wp }_1{\wp }_2-2)}^{2\alpha }}{x}^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

(30)

By adding Equations (24) and (25), then substituting $x=y=1$.

$$\begin{array}{ccc}\hfill M_1(G;x,y)& =& \left(D_x+D_y\right){M(G;x,y)|}_{x=y=1}\hfill \\ & =& {\wp }_1\left({\wp }_1^2-1\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)+{\left({\wp }_1-1\right)}^3\left({\wp }_2-1\right)\hfill \\ & +& \left({\wp }_1^2-1\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)+\frac{1}{2}\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1^2-3{\wp }_1+2\right)\hfill \\ & +& {\wp }_1\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^2+\left({\wp }_1{\wp }_2-2\right){\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)\hfill \\ & +& \left({\wp }_1{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)+\frac{1}{2}\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1^2-3{\wp }_1+2\right)\hfill \\ & =& {\wp }_1^3{\wp }_2^2-{\wp }_1{\wp }_2^2+{\wp }_1^4{\wp }_2+{\wp }_1^3{\wp }_2-11{\wp }_1^2{\wp }_2+9{\wp }_1{\wp }_2-{\wp }_1^4-{\wp }_1^3+6{\wp }_1^2-4.\hfill \end{array}$$

(31)

By substituting $x=y=1$ in Equation (26);

$$\begin{array}{ccc}\hfill M_2(G;x,y)& =& \left(D_y{D}_x\right){M(G;x,y)|}_{x=y=1}\hfill \\ & =& {\wp }_1\left({\wp }_1^2-1\right)\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^2+\left({\wp }_1{\wp }_2-2\right){\left({\wp }_1-1\right)}^3\left({\wp }_2-1\right)\hfill \\ & +& \left({\wp }_1^2-1\right)\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)+\frac{1}{2}{\left({\wp }_1{\wp }_2-2\right)}^2\left({\wp }_1^2-3{\wp }_1+2\right)\hfill \\ & =& \frac{7}{2}{\wp }_1^4{\wp }_2^2-\frac{13}{2}{\wp }_1^3{\wp }_2^2+2{\wp }_1^2{\wp }_2^2+{\wp }_1{\wp }_2^2-4{\wp }_1^4{\wp }_2+14{\wp }_1^2{\wp }_2-10{\wp }_1{\wp }_2+{\wp }_1^4\hfill \\ & +& 3{\wp }_1^3-7{\wp }_1^2-{\wp }_1+4.\hfill \end{array}$$

(32)

By substituting $x=y=1$ in Equation (29);

$$\begin{array}{ccc}\hfill {}^m{M}_2(G;x,y)& =& \left({\delta }_x{\delta }_y\right){M(G;x,y)|}_{x=y=1}\hfill \\ & =& \frac{{\wp }_1\left({\wp }_1-1\right)}{{\wp }_1^2-1}+\frac{\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1{\wp }_2-2}+\frac{\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1^2-1\right)}+\frac{\left({\wp }_1^2-3{\wp }_1+2\right)}{2{({\wp }_1{\wp }_2-2)}^2}\hfill \\ & =& \frac{2+{\wp }_1(7+{\wp }_1(2+{\wp }_1-2(6+{\wp }_1){\wp }_2+4{\wp }_1{\wp }_2^2))}{2(1+{\wp }_1){(-2+{\wp }_1{\wp }_2)}^2}.\hfill \end{array}$$

(33)

By substituting $x=y=1$ in Equation (27);

$$\begin{array}{ccc}\hfill R_{\alpha }\left(G\right)& =& \left(D_y^{\alpha }{D}_x^{\alpha }\right)M(G;x,y){|}_{x=y=1}\hfill \\ & =& {\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right){\left(({\wp }_1^2-1)({\wp }_2-1)\right)}^{\alpha }+{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right){\left(({\wp }_1-1)({\wp }_1{\wp }_2-2)\right)}^{\alpha }\hfill \\ & +& \left({\wp }_1-1\right)\left({\wp }_2-1\right){\left(({\wp }_1^2-1)({\wp }_1{\wp }_2-2)\right)}^{\alpha }+\frac{1}{2}\left({\wp }_1^2-3{\wp }_1+2\right){\left({\wp }_1{\wp }_2-2\right)}^{2\alpha }\hfill \\ & =& ({\wp }_1-1)({\wp }_2-1)\left({\wp }_1{\left({\wp }_1^2{\wp }_2-{\wp }_1^2-{\wp }_2+1\right)}^{\alpha }+({\wp }_1-1){\left({\wp }_1^2{\wp }_2-2{\wp }_1-{\wp }_1{\wp }_2+2\right)}^{\alpha }\right)\hfill \\ & +& ({\wp }_1-1)({\wp }_2-1)\left({\left({\wp }_1^3{\wp }_2-2{\wp }_1^2-{\wp }_1{\wp }_2+2\right)}^{\alpha }\right)+\frac{1}{2}\left({\wp }_1^2-3{\wp }_1+2\right){\left({\wp }_1{\wp }_2-2\right)}^{2\alpha }.\hfill \end{array}$$

(34)

By substituting $x=y=1$ in Equation (30);

$$\begin{array}{ccc}\hfill R{R}_{\alpha }\left(G\right)& =& \left({\delta }_y^{\alpha }{\delta }_x^{\alpha }\right)M(G;x,y){|}_{x=y=1}\hfill \\ & =& \frac{{\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\left(({\wp }_1^2-1)({\wp }_2-1)\right)}^{\alpha }}+\frac{{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\left(({\wp }_1-1)({\wp }_1{\wp }_2-2)\right)}^{\alpha }}\hfill \\ & +& \frac{\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\left(({\wp }_1^2-1)({\wp }_1{\wp }_2-2)\right)}^{\alpha }}+\frac{\left({\wp }_1^2-3{\wp }_1+2\right)}{2{({\wp }_1{\wp }_2-2)}^{2\alpha }}\hfill \\ & =& ({\wp }_1-1)({\wp }_2-1)\left(\frac{{\wp }_1}{{\left({\wp }_1^2{\wp }_2-{\wp }_1^2-{\wp }_2+1\right)}^{\alpha }}+\frac{{\wp }_1-1}{{\left({\wp }_1^2{\wp }_2-2{\wp }_1-{\wp }_1{\wp }_2+2\right)}^{\alpha }}+\frac{1}{{\left({\wp }_1^3{\wp }_2-2{\wp }_1^2-{\wp }_1{\wp }_2+2\right)}^{\alpha }}\right)\hfill \\ & +& \frac{{\wp }_1^2-3{\wp }_1+2}{2{({\wp }_1{\wp }_2-2)}^{2\alpha }}.\hfill \end{array}$$

(35)

□

The numerical and graphical comparisons of $M_1\left(G\right)$, $M_2\left(G\right)$, ${}^m{M}_2\left(G\right)$, $R_{\alpha }\left(G\right)$, and $R{R}_{\alpha }\left(G\right)$ over zero-divisor graphs $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$ are given in Table 2 and Figure 3, respectively.

Table 2. Numerical comparison between topological indices, namely, $M_1\left(G\right)$, $M_2\left(G\right)$, ${}^m{M}_2\left(G\right)$, $R_{\alpha }\left(G\right)$, and $R{R}_{\alpha }\left(G\right)$ over zero-divisor graphs $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$.

${\mathit{\wp }}_1$	${\mathit{\wp }}_2$	${\mathit{M}}_1\left(\mathit{G}\right)$	${\mathit{M}}_2\left(\mathit{G}\right)$	${}^{\mathit{m}}{\mathit{M}}_2\left(\mathit{G}\right)$	${\mathit{R}}_{\mathit{\alpha }}\left(\mathit{G}\right)$	${\mathit{RR}}_{\mathit{\alpha }}\left(\mathit{G}\right)$
3	2	110	160	1.375	160	1.375
5	3	2036	7094	1.50986	7094	1.50986
7	5	17,286	115,119	1.6312	115,119	1.6312
11	7	152,610	$1.71833\times {10}^6$	1.73133	$1.71833\times {10}^6$	1.73133
13	11	553,692	$9.21199\times {10}^6$	1.78802	$9.21199\times {10}^6$	1.78802
17	13	$1.85102\times {10}^6$	$3.99098\times {10}^7$	1.8267	$3.99098\times {10}^7$	1.8267
19	17	$4.1092\times {10}^6$	$1.10518\times {10}^8$	1.85117	$1.10518\times {10}^8$	1.85117
23	19	$9.53667\times {10}^6$	$3.04601\times {10}^8$	1.87162	$3.04601\times {10}^8$	1.87162
29	23	$2.87815\times {10}^7$	$1.16254\times {10}^9$	$1.89494$	$1.16254\times {10}^9$	1.89494
31	29	$5.14282\times {10}^7$	$2.45143\times {10}^9$	1.90672	$2.45143\times {10}^9$	1.90672
37	31	$1.05938\times {10}^8$	$5.76021\times {10}^9$	1.91809	$5.76021\times {10}^9$	1.91809

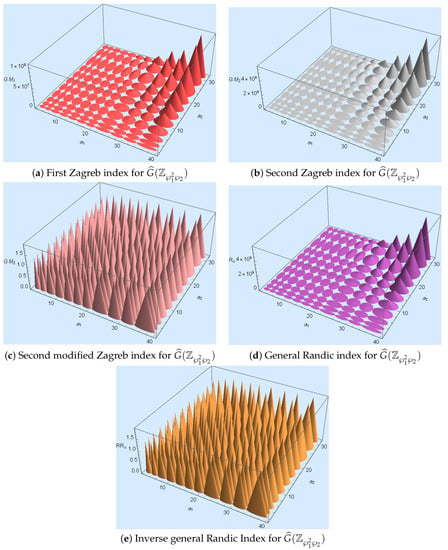
Figure 3. The three-dimensional discrete plot of first Zagreb, second Zagreb, second modified Zagreb, general Randic, and Inverse general Randic index for $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$.

Theorem 2.

Let $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$ be a zero-divisor graph over ${\mathbb{Z}}_{{\wp }_1^2{\wp }_2}$ with distinct primes (${\wp }_1>{\wp }_2$); then

$$\begin{array}{ccc}\hfill SS{D}_3\left(G\right)& =& 3{\wp }_1^5{\wp }_2^3-6{\wp }_1^4{\wp }_2^3+3{\wp }_1^3{\wp }_2^3-{\wp }_1^2{\wp }_2^3+{\wp }_1{\wp }_2^3+2{\wp }_1^6{\wp }_2^2-3{\wp }_1^5{\wp }_2^2-21{\wp }_1^4{\wp }_2^2+45{\wp }_1^3{\wp }_2^2-19{\wp }_1^2{\wp }_2^2\hfill \\ & -& 4{\wp }_1{\wp }_2^2-3{\wp }_1^6{\wp }_2+21{\wp }_1^4{\wp }_2+{\wp }_1^3{\wp }_2-62{\wp }_1^2{\wp }_2+43{\wp }_1{\wp }_2+{\wp }_1^6+{\wp }_1^5-3{\wp }_1^4-17{\wp }_1^3\hfill \\ & +& 26{\wp }_1^2+8{\wp }_1-16.\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill S{D}_5\left(G\right)& =& \frac{-4-2{\wp }_1^5+{\wp }_1^6{\wp }_2-4{\wp }_1^3(-1+{\wp }_2^2)-2{\wp }_1(2-4{\wp }_2+{\wp }_2^2)}{({\wp }_1+1)({\wp }_1{\wp }_2-2)}+\hfill \\ \hfill & & \frac{{\wp }_1^2(2+3{\wp }_2-2{\wp }_2^2+{\wp }_2^3)+{\wp }_1^4(-2+{\wp }_2-{\wp }_2^2+{\wp }_2^3)}{({\wp }_1+1)({\wp }_1{\wp }_2-2)}.\hfill \end{array}$$

(37)

$$\begin{array}{ccc}\hfill H\left(G\right)& =& \frac{2{\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^2+{\wp }_2-2}+\frac{2{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\wp }_1{\wp }_2+{\wp }_1-3}+\frac{2\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^2+{\wp }_1{\wp }_2-3}+\frac{\left({\wp }_1^2-3{\wp }_1+2\right)}{2{\wp }_1{\wp }_2-4}.\hfill \end{array}$$

(38)

$$\begin{array}{ccc}\hfill I\left(G\right)& =& \frac{{\wp }_1\left({\wp }_1^2-1\right)\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^2}{{\wp }_1^2+{\wp }_2-2}+\frac{\left({\wp }_1{\wp }_2-2\right){\left({\wp }_1-1\right)}^3\left({\wp }_2-1\right)}{{\wp }_1{\wp }_2+{\wp }_1-3}\hfill \\ & +& \frac{\left({\wp }_1^2-1\right)\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^2+{\wp }_1{\wp }_2-3}+\frac{1}{4}\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_1-2\right).\hfill \end{array}$$

(39)

$$\begin{array}{ccc}\hfill F\left(G\right)& =& \left({\wp }_1-1\right)\left[{\wp }_1^5\left({\wp }_2-1\right)+{\wp }_1^4\left({\wp }_2-1\right)+{\wp }_1^3\left({\wp }_2^3-{\wp }_2+1\right)-{\wp }_1^2\left(6{\wp }_2^2+5{\wp }_2-5\right)\right]\hfill \\ & +& \left({\wp }_1-1\right)\left[{\wp }_1\left({\wp }_2^3-3{\wp }_2^2+19{\wp }_2-5\right)-8\right].\hfill \end{array}$$

(40)

Proof. 

Let $\widehat{G}\left({\mathbb{Z}}_{p^2{\wp }_2}\right)$ be a zero-divisor graph over ${\mathbb{Z}}_{p^2{\wp }_2}$ with distinct primes ($p>{\wp }_2$). By adding (24) and (25);

$$\begin{array}{ccc}\hfill D_x+D_y& =& \left[{\wp }_1\left({\wp }_1^2-1\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)+{\wp }_1\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^2\right]x^{{\wp }_1^2-1}{y}^{{\wp }_2-1}\hfill \\ & +& \left[{\left({\wp }_1-1\right)}^3\left({\wp }_2-1\right)+\left({\wp }_1{\wp }_2-2\right){\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)\right]x^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \left[\left({\wp }_1^2-1\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)+\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)\right]x^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \left({\wp }_1{\wp }_2-2\right)\left({\wp }_1^2-3{\wp }_1+2\right)x^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

(41)

Differentiating with respect to y of Equation (41);

$$\begin{array}{ccc}\hfill D_y\left(D_x+D_y\right)& =& \left[{\wp }_1\left({\wp }_1^2-1\right)\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^2+{\wp }_1\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^3\right]x^{{\wp }_1^2-1}{y}^{{\wp }_2-1}\hfill \\ & +& \left[\left({\wp }_1{\wp }_2-2\right){\left({\wp }_1-1\right)}^3\left({\wp }_2-1\right)+{\left({\wp }_1{\wp }_2-2\right)}^2{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)\right]x^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \left[\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1^2-1\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)+{\left({\wp }_1{\wp }_2-2\right)}^2\left({\wp }_1-1\right)\left({\wp }_2-1\right)\right]x^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& {\left({\wp }_1{\wp }_2-2\right)}^2\left({\wp }_1^2-3{\wp }_1+2\right)x^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

(42)

Differentiating with respect to y of Equation (42);

$$\begin{array}{ccc}\hfill D_x{D}_y\left(D_x+D_y\right)& =& \left[{\wp }_1{\left({\wp }_1^2-1\right)}^2\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^2+{\wp }_1\left({\wp }_1^2-1\right)\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^3\right]x^{{\wp }_1^2-1}{y}^{{\wp }_2-1}\hfill \\ & +& \left[\left({\wp }_1{\wp }_2-2\right){\left({\wp }_1-1\right)}^4\left({\wp }_2-1\right)+{\left({\wp }_1{\wp }_2-2\right)}^2{\left({\wp }_1-1\right)}^3\left({\wp }_2-1\right)\right]x^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \left[\left({\wp }_1{\wp }_2-2\right){\left({\wp }_1^2-1\right)}^2\left({\wp }_1-1\right)\left({\wp }_2-1\right)+\left({\wp }_1^2-1\right){\left({\wp }_1{\wp }_2-2\right)}^2\left({\wp }_1-1\right)\left({\wp }_2-1\right)\right]x^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& {\left({\wp }_1{\wp }_2-2\right)}^3\left({\wp }_1^2-3{\wp }_1+2\right)x^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

(43)

By substituting $x=y=1$ in Equation (43) the third symmetric division index becomes;

$$\begin{array}{ccc}\hfill SS{D}_3\left(G\right)& =& D_x{D}_y\left(D_x+D_y\right){M(G;x,y)|}_{x=y=1}\hfill \\ \hfill SS{D}_3\left(G\right)& =& {\wp }_1{\left({\wp }_1^2-1\right)}^2\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^2+{\wp }_1\left({\wp }_1^2-1\right)\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^3\hfill \\ & +& \left({\wp }_1{\wp }_2-2\right){\left({\wp }_1-1\right)}^4\left({\wp }_2-1\right)+{\left({\wp }_1{\wp }_2-2\right)}^2{\left({\wp }_1-1\right)}^3\left({\wp }_2-1\right)\hfill \\ & +& \left({\wp }_1{\wp }_2-2\right){\left({\wp }_1^2-1\right)}^2\left({\wp }_1-1\right)\left({\wp }_2-1\right)+\left({\wp }_1^2-1\right){\left({\wp }_1{\wp }_2-2\right)}^2\left({\wp }_1-1\right)\left({\wp }_2-1\right)\hfill \\ & +& {\left({\wp }_1{\wp }_2-2\right)}^3\left({\wp }_1^2-3{\wp }_1+2\right).\hfill \end{array}$$

(44)

After some more simplification, we have

$$\begin{array}{ccc}\hfill SS{D}_3\left(G\right)& =& 3{\wp }_1^5{\wp }_2^3-6{\wp }_1^4{\wp }_2^3+3{\wp }_1^3{\wp }_2^3-{\wp }_1^2{\wp }_2^3+{\wp }_1{\wp }_2^3+2{\wp }_1^6{\wp }_2^2-3{\wp }_1^5{\wp }_2^2-21{\wp }_1^4{\wp }_2^2\hfill \\ & +& 45{\wp }_1^3{\wp }_2^2-19{\wp }_1^2{\wp }_2^2-4{\wp }_1{\wp }_2^2-3{\wp }_1^6{\wp }_2+21{\wp }_1^4{\wp }_2+{\wp }_1^3{\wp }_2-62{\wp }_1^2{\wp }_2+43{\wp }_1{\wp }_2\hfill \\ & +& {\wp }_1^6+{\wp }_1^5-3{\wp }_1^4-17{\wp }_1^3+26{\wp }_1^2+8{\wp }_1-16.\hfill \end{array}$$

(45)

By applying $D_x$ on Equation (28);

$$\begin{array}{ccc}\hfill D_x{\delta }_y& =& x\frac{\partial }{\partial x}\left({\delta }_y\right)\hfill \\ & =& {\wp }_1\left({\wp }_1^2-1\right)\left({\wp }_1-1\right)x^{{\wp }_1^2-1}{y}^{{\wp }_2-1}+\frac{{\left({\wp }_1-1\right)}^3\left({\wp }_2-1\right)}{{\wp }_1{\wp }_2-2}{x}^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \frac{\left({\wp }_1^2-1\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1{\wp }_2-2}{x}^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-2}+\frac{1}{2}\left({\wp }_1^2-3{\wp }_1+2\right)x^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

(46)

Similarly;

$$\begin{array}{ccc}\hfill {\delta }_x{D}_y& =& {\int }_0^x\frac{D_y}{t}\mathrm{d}t\hfill \\ & =& \frac{{\wp }_1\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^2}{{\wp }_1^2-1}{x}^{{\wp }_1^2-1}{y}^{{\wp }_2-1}+\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)x^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \frac{\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^2-1}{x}^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-2}+\frac{1}{2}\left({\wp }_1^2-3{\wp }_1+2\right)x^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

(47)

Adding Equations (46) and (47);

$$\begin{array}{ccc}\hfill D_x{\delta }_y+{\delta }_x{D}_y& =& \left[{\wp }_1\left({\wp }_1^2-1\right)\left({\wp }_1-1\right)+\frac{{\wp }_1\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^2}{{\wp }_1^2-1}\right]x^{{\wp }_1^2-1}{y}^{{\wp }_2-1}\hfill \\ & +& \left[\frac{{\left({\wp }_1-1\right)}^3\left({\wp }_2-1\right)}{{\wp }_1{\wp }_2-2}+\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)\right]x^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \left[\frac{\left({\wp }_1^2-1\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1{\wp }_2-2}+\frac{\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^2-1}\right]x^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \left({\wp }_1^2-3{\wp }_1+2\right)x^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

(48)

By substituting $x=y=1$ in Equation (48) the fifth symmetric division index becomes;

$$\begin{array}{ccc}\hfill S{D}_5\left(G\right)& =& (D_y{\delta }_x+D_x{\delta }_y)M(G;x,y){|}_{x=y=1}\hfill \\ & =& {\wp }_1\left({\wp }_1^2-1\right)\left({\wp }_1-1\right)+\frac{{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\wp }_1{\wp }_2-2}+\frac{\left({\wp }_1^2-1\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1{\wp }_2-2}\hfill \\ & +& \frac{{\wp }_1\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^2}{{\wp }_1^2-1}+\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)+\frac{\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^2-1}\hfill \\ & +& \left({\wp }_1^2-3{\wp }_1+2\right).\hfill \end{array}$$

(49)

After some more simplification, we have the desired result.

For the harmonic index, we will first find the value of J;

$$\begin{array}{ccc}\hfill J& =& f(x,x)={\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right)x^{{\wp }_1^2+{\wp }_2-2}+{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)x^{{\wp }_1{\wp }_2+{\wp }_1-3}+\left({\wp }_1-1\right)\left({\wp }_2-1\right)x^{{\wp }_1^2+{\wp }_1{\wp }_2-3}\hfill \\ & +& \frac{1}{2}\left({\wp }_1^2-3{\wp }_1+2\right)x^{2{\wp }_1{\wp }_2-4}.\hfill \end{array}$$

(50)

Applying ${\delta }_y$ on (50), we have

$$\begin{array}{ccc}\hfill {\delta }_{x}J& =& {\int }_0^x\frac{J}{t}\mathrm{d}t\hfill \\ & =& \frac{{\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^2+{\wp }_2-2}{x}^{{\wp }_1^2+{\wp }_2-2}+\frac{{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\wp }_1{\wp }_2+{\wp }_1-3}{x}^{{\wp }_1{\wp }_2+{\wp }_1-3}\hfill \\ & +& \frac{\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^2+{\wp }_1{\wp }_2-3}{x}^{{\wp }_1^2+{\wp }_1{\wp }_2-3}+\frac{\left({\wp }_1^2-3{\wp }_1+2\right)}{4({\wp }_1{\wp }_2-2)}{x}^{2{\wp }_1{\wp }_2-4}.\hfill \\ \hfill 2\left({\delta }_{x}J\right)& =& \frac{2\left({\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right)\right)}{{\wp }_1^2+{\wp }_2-2}{x}^{{\wp }_1^2+{\wp }_2-2}+\frac{2\left({\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)\right)}{{\wp }_1{\wp }_2+{\wp }_1-3}{x}^{{\wp }_1{\wp }_2+{\wp }_1-3}\hfill \\ & +& \frac{2\left(\left({\wp }_1-1\right)\left({\wp }_2-1\right)\right)}{{\wp }_1^2+{\wp }_1{\wp }_2-3}{x}^{{\wp }_1^2+{\wp }_1{\wp }_2-3}+\frac{\left({\wp }_1^2-3{\wp }_1+2\right)}{2({\wp }_1{\wp }_2-2)}{x}^{2{\wp }_1{\wp }_2-4}.\hfill \end{array}$$

(51)

The harmonic index is,

$$\begin{array}{ccc}\hfill H\left(G\right)& =& 2\left({\delta }_{x}J\right)M(G,x,y){|}_{x=y=1}\hfill \\ & =& \frac{2{\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^2+{\wp }_2-2}+\frac{2{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\wp }_1{\wp }_2+{\wp }_1-3}+\frac{2\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^2+{\wp }_1{\wp }_2-3}+\frac{\left({\wp }_1^2-3{\wp }_1+2\right)}{2{\wp }_1{\wp }_2-4}.\hfill \end{array}$$

(52)

For the inverse sum index, firsy applying J on (26);

$$\begin{array}{ccc}\hfill J{D}_x{D}_y& =& {\wp }_1\left({\wp }_1^2-1\right)\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^2{x}^{{\wp }_1^2+{\wp }_2-2}+\left({\wp }_1{\wp }_2-2\right){\left({\wp }_1-1\right)}^3\left({\wp }_2-1\right)x^{{\wp }_1{\wp }_2+{\wp }_1-3}\hfill \\ & +& \left({\wp }_1^2-1\right)\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)x^{{\wp }_1^2+{\wp }_1{\wp }_2-3}+\frac{1}{2}{\left({\wp }_1{\wp }_2-2\right)}^2\left({\wp }_1^2-3{\wp }_1+2\right)x^{2{\wp }_1{\wp }_2-4}.\hfill \end{array}$$

(53)

Applying ${\delta }_x$ on (53), we have

$$\begin{array}{ccc}\hfill {\delta }_{x}J{D}_x{D}_y& =& \frac{{\wp }_1\left({\wp }_1^2-1\right)\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^2}{{\wp }_1^2+{\wp }_2-2}{x}^{{\wp }_1^2+{\wp }_2-2}+\frac{\left({\wp }_1{\wp }_2-2\right){\left({\wp }_1-1\right)}^3\left({\wp }_2-1\right)}{{\wp }_1{\wp }_2+{\wp }_1-3}{x}^{{\wp }_1{\wp }_2+{\wp }_1-3}\hfill \\ & +& \frac{\left({\wp }_1^2-1\right)\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^2+{\wp }_1{\wp }_2-3}{x}^{{\wp }_1^2+{\wp }_1{\wp }_2-3}+\frac{{\left({\wp }_1{\wp }_2-2\right)}^2\left({\wp }_1^2-3{\wp }_1+2\right)}{4({\wp }_1{\wp }_2-2)}{x}^{2{\wp }_1{\wp }_2-4}.\hfill \end{array}$$

The inverse sum index is,

$$\begin{array}{ccc}\hfill I\left(G\right)& =& \left({\delta }_{x}J{D}_x{D}_y\right){M(G;x,y)|}_{x=y=1}\hfill \\ & =& \frac{{\wp }_1\left({\wp }_1^2-1\right)\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^2}{{\wp }_1^2+{\wp }_2-2}+\frac{\left({\wp }_1{\wp }_2-2\right){\left({\wp }_1-1\right)}^3\left({\wp }_2-1\right)}{{\wp }_1{\wp }_2+{\wp }_1-3}\hfill \\ & +& \frac{\left({\wp }_1^2-1\right)\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^2+{\wp }_1{\wp }_2-3}+\frac{1}{4}\left({\wp }_1{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_1-2\right)\hfill \end{array}$$

(54)

For the forgotten topological index, we will first compute $D_x^2$ and $D_y^2$. Applying $D_x$ on (24);

$$\begin{array}{ccc}\hfill D_x^2& =& x\frac{\partial }{\partial x}\left(D_x\right)\hfill \\ & =& {\wp }_1{\left({\wp }_1^2-1\right)}^2\left({\wp }_1-1\right)\left({\wp }_2-1\right)x^{{\wp }_1^2-1}{y}^{{\wp }_2-1}+{\left({\wp }_1-1\right)}^4\left({\wp }_2-1\right)x^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& {\left({\wp }_1^2-1\right)}^2\left({\wp }_1-1\right)\left({\wp }_2-1\right)x^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-2}+\frac{1}{2}{\left({\wp }_1{\wp }_2-2\right)}^2\left({\wp }_1^2-3{\wp }_1+2\right)x^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

(55)

$$\begin{array}{ccc}\hfill D_y^2& =& {\wp }_1\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^3{x}^{{\wp }_1^2-1}{y}^{{\wp }_2-1}+{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right){\left({\wp }_1{\wp }_2-2\right)}^2{x}^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \left({\wp }_1-1\right)\left({\wp }_2-1\right){\left({\wp }_1{\wp }_2-2\right)}^2{x}^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-2}+\frac{1}{2}{\left({\wp }_1{\wp }_2-2\right)}^2\left({\wp }_1^2-3{\wp }_1+2\right)x^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

(56)

By adding Equations (55) and (56).

$$\begin{array}{ccc}\hfill (D_x^2+D_y^2)M(G;x,y)& =& \left[{\wp }_1{\left({\wp }_1^2-1\right)}^2\left({\wp }_1-1\right)\left({\wp }_2-1\right)+{\wp }_1\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^3\right]x^{{\wp }_1^2-1}{y}^{{\wp }_2-1}\hfill \\ & +& \left[{\left({\wp }_1-1\right)}^4\left({\wp }_2-1\right)+{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right){\left({\wp }_1{\wp }_2-2\right)}^2\right]x^{{\wp }_1-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& \left[{\left({\wp }_1^2-1\right)}^2\left({\wp }_1-1\right)\left({\wp }_2-1\right)+\left({\wp }_1-1\right)\left({\wp }_2-1\right){\left({\wp }_1{\wp }_2-2\right)}^2\right]x^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-2}\hfill \\ & +& {\left({\wp }_1{\wp }_2-2\right)}^2\left({\wp }_1^2-3{\wp }_1+2\right)x^{{\wp }_1{\wp }_2-2}{y}^{{\wp }_1{\wp }_2-2}.\hfill \end{array}$$

(57)

The forgotten topological index is,

$$\begin{array}{ccc}\hfill F\left(G\right)& =& \left(D_x^2+D_y^2\right){M(G;x,y)|}_{x=y=1}\hfill \\ & =& {\wp }_1{\left({\wp }_1^2-1\right)}^2\left({\wp }_1-1\right)\left({\wp }_2-1\right)+{\wp }_1\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^3\hfill \\ & +& {\left({\wp }_1-1\right)}^4\left({\wp }_2-1\right)+{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right){\left({\wp }_1{\wp }_2-2\right)}^2\hfill \\ & +& {\left({\wp }_1^2-1\right)}^2\left({\wp }_1-1\right)\left({\wp }_2-1\right)+\left({\wp }_1-1\right)\left({\wp }_2-1\right){\left({\wp }_1{\wp }_2-2\right)}^2\hfill \\ & +& {\left({\wp }_1{\wp }_2-2\right)}^2\left({\wp }_1^2-3{\wp }_1+2\right)\hfill \\ & =& \left({\wp }_1-1\right)\left[{\wp }_1^5\left({\wp }_2-1\right)+{\wp }_1^4\left({\wp }_2-1\right)+{\wp }_1^3\left({\wp }_2^3-{\wp }_2+1\right)-{\wp }_1^2\left(6{\wp }_2^2+5{\wp }_2-5\right)\right]\hfill \\ & +& \left({\wp }_1-1\right)\left[{\wp }_1\left({\wp }_2^3-3{\wp }_2^2+19{\wp }_2-5\right)-8\right].\hfill \end{array}$$

(58)

□

The numerical and graphical comparisons of $SS{D}_3\left(G\right)$, $SS{D}_5\left(G\right)$, $H\left(G\right)$, $I\left(G\right)$, $F\left(G\right)$, and $R{R}_{\alpha }\left(G\right)$ over zero-divisor graphs $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$ are given in Table 3 and Figure 4, respectively.

Table 3. Numerical comparison between topological indices, namely, $SS{D}_3\left(G\right)$, $SS{D}_5\left(G\right)$, $H\left(G\right)$, $I\left(G\right)$, and $F\left(G\right)$ over zero-divisor graphs $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$.

${\mathit{\wp }}_1$	${\mathit{\wp }}_2$	${\mathit{SSD}}_3\left(\mathit{G}\right)$	${\mathit{SSD}}_5\left(\mathit{G}\right)$	$\mathit{H}\left(\mathit{G}\right)$	$\mathit{I}\left(\mathit{G}\right)$	$\mathit{F}\left(\mathit{G}\right)$
3	2	1520	65.75	3.25	18	662
5	3	196,924	628.282	7.7356	278.188	37,108
7	5	$6.94669\times {10}^6$	2929.59	14.8933	2068.22	665,862
11	7	$2.41394\times {10}^8$	18,036.5	25.8092	13,522.3	$1.46705\times {10}^7$
13	11	$2.08766\times {10}^9$	43,719.1	37.5964	44,500.5	$8.14183\times {10}^7$
17	13	$1.45742\times {10}^{10}$	121,383	49.21	120,432	$4.55966\times {10}^8$
19	17	$5.4791\times {10}^{10}$	216,988	61.0129	245,611	$1.34495\times {10}^9$
23	19	$2.10981\times {10}^{11}$	441,448	72.843	485,667	$4.46761\times {10}^9$
29	23	$1.24732\times {10}^{12}$	$1.09494\times {10}^6$	92.6126	$1.20073\times {10}^6$	$2.12959\times {10}^{10}$
31	29	$3.29134\times {10}^{12}$	$1.65044\times {10}^6$	108.471	$2.02461\times {10}^6$	$4.64677\times {10}^{10}$
37	31	$1.0328\times {10}^{13}$	$3.06433\times {10}^6$	124.42	$3.56393\times {10}^6$	$1.3093\times {10}^{11}$

Figure 4. The three-dimensional discrete plot of third symmetric division, fifth symmetric division, harmonic, inverse sum and forgotten topological index for $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$.

4. $\mathbb{M}$-Polynomial and Topological Indices for Zero-Divisor Graph $\widehat{\mathit{G}}\left({\mathbb{Z}}_{{\wp }_{\mathbf{1}}^{\mathbf{3}}{\wp }_{\mathbf{2}}}\right)$

In this section, $\mathbb{M}-$ polynomial and topological indices for zero-divisor graph $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^3{\wp }_2}\right)$ with numerically and graphically behavior are discussed. The zero-divisor graph $\widehat{G}\left({\mathbb{Z}}_{3^3\times 2}\right)$ as shown in Figure 5.

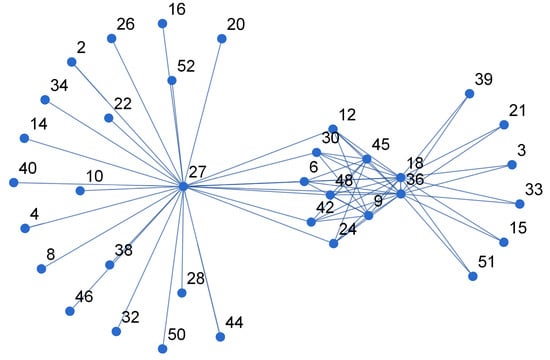
Figure 5. The zero-divisor graph $\widehat{G}\left({\mathbb{Z}}_{3^3\times 2}\right)$.

Lemma 2.

Let $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^3{\wp }_2}\right)$ be a zero-divisor graph over ${\mathbb{Z}}_{{\wp }_1^3{\wp }_2}$ with distinct primes (${\wp }_1>{\wp }_2$), then M-polynomial is

$$\begin{array}{ccc}\hfill M(G;x;y)& =& {\wp }_1^2\left({\wp }_1-1\right)\left({\wp }_2-1\right)x^{{\wp }_2-1}{y}^{{\wp }_1^3-1}+{\wp }_1{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)x^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-1}\hfill \\ & +& {\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right)x^{{\wp }_1^3-1}{y}^{{\wp }_1{\wp }_2-1}+{\wp }_1{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)x^{{\wp }_1-1}{y}^{{\wp }_1^2{\wp }_2-2}\hfill \\ & +& {\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)x^{{\wp }_1^2-1}{y}^{{\wp }_1^2{\wp }_2-2}+\left({\wp }_1-1\right)\left({\wp }_2-1\right)x^{{\wp }_1^3-1}{y}^{{\wp }_1^2{\wp }_2-2}\hfill \\ & +& {\wp }_1{\left({\wp }_1-1\right)}^2{x}^{{\wp }_1{\wp }_2-1}{y}^{{\wp }_1^2{\wp }_2-2}+\frac{1}{2}\left({\wp }_1-1\right)\left({\wp }_1-2\right)x^{{\wp }_1^2{\wp }_2-2}{y}^{{\wp }_1^2{\wp }_2-2}.\hfill \end{array}$$

(59)

Proof. 

Let $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^3{\wp }_2}\right)$ be a zero-divisor graph over ${\mathbb{Z}}_{{\wp }_1^3{\wp }_2}$ with distinct primes (${\wp }_1>{\wp }_1$). The cardinality function of edge partition for $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$ is;

$$\begin{array}{c}\hfill |m_{(i,j)}|=\left\{\begin{array}{c}\begin{array}{cc}{\wp }_1^2\left({\wp }_1-1\right)\left({\wp }_2-1\right),\hfill & \mathrm{if}i={\wp }_2-1,j={\wp }_1^3-1,\hfill \\ {\wp }_1{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right),\hfill & \mathrm{if}i={\wp }_1^2-1,j={\wp }_1{\wp }_2-1,\hfill \\ {\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right),\hfill & \mathrm{if}i={\wp }_1^3-1,j={\wp }_1{\wp }_2-1,\hfill \\ {\wp }_1{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right),\hfill & \mathrm{if}i={\wp }_1-1,j={\wp }_1^2{\wp }_2-2,\hfill \\ {\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right),\hfill & \mathrm{if}i={\wp }_1^2-1,j={\wp }_1{\wp }_2-1,\hfill \\ \left({\wp }_1-1\right)\left({\wp }_2-1\right),\hfill & \mathrm{if}i={\wp }_1^3-1,j={\wp }_1^2{\wp }_2-2,\hfill \\ {\wp }_1{\left({\wp }_1-1\right)}^2,\hfill & \mathrm{if}i={\wp }_1{\wp }_2-1,j={\wp }_1^2{\wp }_2-2,\hfill \\ \frac{1}{2}\left({\wp }_1-1\right)\left({\wp }_1-2\right),\hfill & \mathrm{if}i={\wp }_1^2{\wp }_2-2,j={\wp }_1^2{\wp }_2-2.\hfill \end{array}\hfill \end{array}\right.\end{array}$$

(60)

By using Equation (6),

$$\begin{array}{ccc}\hfill M(G,x,y)& =& \sum _{i\leftrightarrow j\in E\left(G\right)}|m_{(i,j)}|x^i{y}^j\hfill \\ & =& \sum _{{\wp }_2-1\leftrightarrow {\wp }_1^3-1}|m_{({\wp }_2-1,{\wp }_1^3-1)}|x^{{\wp }_2-1}{y}^{{\wp }_1^3-1}+\sum _{{\wp }_1^2-1\leftrightarrow {\wp }_1{\wp }_2-1}|m_{({\wp }_1^2-1,{\wp }_1{\wp }_2-1)}|x^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-1}\hfill \\ & +& \sum _{{\wp }_1^3-1\leftrightarrow {\wp }_1{\wp }_2-1}|m_{({\wp }_1^3-1,{\wp }_1{\wp }_2-1)}|x^{{\wp }_1^3-1}{y}^{{\wp }_1{\wp }_2-1}+\sum _{{\wp }_1-1\leftrightarrow {\wp }_1^2{\wp }_2-2}|m_{({\wp }_1-1,{\wp }_1^2{\wp }_2-2)}|x^{{\wp }_1-1}{y}^{{\wp }_1^2{\wp }_2-2}\hfill \\ & +& \sum _{{\wp }_1^2-1\leftrightarrow {\wp }_1^2{\wp }_2-2}|m_{({\wp }_1^2-1,{\wp }_1^2{\wp }_2-2)}|x^{{\wp }_1^2-1}{y}^{{\wp }_1^2{\wp }_2-2}+\sum _{{\wp }_1^3-1\leftrightarrow {\wp }_1^2{\wp }_2-2}|m_{({\wp }_1^3-1,{\wp }_1^2{\wp }_2-2)}|x^{{\wp }_1^3-1}{y}^{{\wp }_1^2{\wp }_2-2}\hfill \\ & +& \sum _{{\wp }_1{\wp }_2-1\leftrightarrow {\wp }_1^2{\wp }_2-2}|m_{({\wp }_1{\wp }_2-1,{\wp }_1^2{\wp }_2-2)}|x^{{\wp }_1{\wp }_2-1}{y}^{{\wp }_1^2{\wp }_2-2}\hfill \\ & +& \sum _{{\wp }_1^2{\wp }_2-2\leftrightarrow {\wp }_1^2{\wp }_2-2}|m_{({\wp }_1^2{\wp }_2-2,{\wp }_1^2{\wp }_2-2)}|x^{{\wp }_1^2{\wp }_2-2}{y}^{{\wp }_1^2{\wp }_2-2}.\hfill \end{array}$$

Using the data from Equation (60), we have

$$\begin{array}{ccc}\hfill M(G;x;y)& =& {\wp }_1^2\left({\wp }_1-1\right)\left({\wp }_2-1\right)x^{{\wp }_2-1}{y}^{{\wp }_1^3-1}+{\wp }_1{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)x^{{\wp }_1^2-1}{y}^{{\wp }_1{\wp }_2-1}\hfill \\ & +& {\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right)x^{{\wp }_1^3-1}{y}^{{\wp }_1{\wp }_2-1}+{\wp }_1{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)x^{{\wp }_1-1}{y}^{{\wp }_1^2{\wp }_2-2}\hfill \\ & +& {\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)x^{{\wp }_1^2-1}{y}^{{\wp }_1^2{\wp }_2-2}+\left({\wp }_1-1\right)\left({\wp }_2-1\right)x^{{\wp }_1^3-1}{y}^{{\wp }_1^2{\wp }_2-2}\hfill \\ & +& {\wp }_1{\left({\wp }_1-1\right)}^2{x}^{{\wp }_1{\wp }_2-1}{y}^{{\wp }_1^2{\wp }_2-2}+\frac{1}{2}\left({\wp }_1-1\right)\left({\wp }_1-2\right)x^{{\wp }_1^2{\wp }_2-2}{y}^{{\wp }_1^2{\wp }_2-2}.\hfill \end{array}$$

This one is a desired relation (59). □

Theorem 3.

Let $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^3{\wp }_2}\right)$ be a zero-divisor graph over ${\mathbb{Z}}_{{\wp }_1^3{\wp }_2}$ with distinct primes (${\wp }_1>{\wp }_2$), then

$$\begin{array}{ccc}\hfill M_1\left(G\right)& =& M_1\left(G\right)={\wp }_1^5{\wp }_2^2-{\wp }_1^2{\wp }_2^2+{\wp }_1^6{\wp }_2+{\wp }_1^5{\wp }_2-15{\wp }_1^3{\wp }_2+13{\wp }_1^2{\wp }_2-{\wp }_1^6-{\wp }_1^5+8{\wp }_1^3-5{\wp }_1^2+3{\wp }_1-4.\hfill \end{array}$$

(61)

$$\begin{array}{ccc}\hfill M_2\left(G\right)& =& \frac{1}{2}\left(15{\wp }_1^6{\wp }_2^2-27{\wp }_1^5{\wp }_2^2\right)+5{\wp }_1^4{\wp }_2^2+{\wp }_1^2{\wp }_2^2-7{\wp }_1^6{\wp }_2+8{\wp }_1^5{\wp }_2-8{\wp }_1^4{\wp }_2+22{\wp }_1^3{\wp }_2-15{\wp }_1^2{\wp }_2+{\wp }_1^6+{\wp }_1^5\hfill \\ & +& 3{\wp }_1^4-11{\wp }_1^3+6{\wp }_1^2-4{\wp }_1+4.\hfill \end{array}$$

(62)

$$\begin{array}{ccc}\hfill {}^m{M}_2\left(G\right)& =& \frac{{\wp }_1^2\left({\wp }_1-1\right)}{{\wp }_1^3-1}+\frac{{\wp }_1{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{\left({\wp }_1{\wp }_2-1\right)\left({\wp }_1^2-1\right)}+\frac{{\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{\left({\wp }_1{\wp }_2-1\right)\left({\wp }_1^3-1\right)}+\frac{{\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^2{\wp }_2-2}\hfill \\ & +& \frac{{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{\left({\wp }_1^2{\wp }_2-2\right)\left({\wp }_1^2-1\right)}+\frac{\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{\left({\wp }_1^2{\wp }_2-2\right)\left({\wp }_1^3-1\right)}+\frac{{\wp }_1{\left({\wp }_1-1\right)}^2}{\left({\wp }_1^2{\wp }_2-2\right)\left({\wp }_1{\wp }_2-1\right)}+\frac{\left({\wp }_1-1\right)\left({\wp }_1-2\right)}{2{({\wp }_1^2{\wp }_2-2)}^2}.\hfill \end{array}$$

(63)

$$\begin{array}{ccc}\hfill R_{\alpha }\left(G\right)& =& {\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right)[{\wp }_1{\left(\left({\wp }_2-1\right)\left({\wp }_1^3-1\right)\right)}^{\alpha }+\left({\wp }_1-1\right){\left(\left({\wp }_1^2-1\right)\left({\wp }_1{\wp }_2-1\right)\right)}^{\alpha }\hfill \\ & +& {\left(\left({\wp }_1^3-1\right)\left({\wp }_1{\wp }_2-1\right)\right)}^{\alpha }+\left({\wp }_1-1\right){\left(\left({\wp }_1-1\right)\left({\wp }_1^2{\wp }_2-2\right)\right)}^{\alpha }]\hfill \\ & +& \left({\wp }_1-1\right)\left({\wp }_2-1\right)[\left({\wp }_1-1\right){\left(\left({\wp }_1^2-1\right)\left({\wp }_1^2{\wp }_2-2\right)\right)}^{\alpha }+{\left(\left({\wp }_1^3-1\right)\left({\wp }_1^2{\wp }_2-2\right)\right)}^{\alpha }]\hfill \\ & +& \left({\wp }_1-1\right)[{\wp }_1\left({\wp }_1-1\right){\left(\left({\wp }_1{\wp }_2-1\right)\left({\wp }_1^2{\wp }_2-2\right)\right)}^{\alpha }+\frac{1}{2}\left({\wp }_1-2\right){\left({\wp }_1^2{\wp }_2-2\right)}^{2\alpha }].\hfill \end{array}$$

(64)

$$\begin{array}{ccc}\hfill R{R}_{\alpha }\left(G\right)& =& \frac{{\wp }_1^2\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\left(\left({\wp }_1^3-1\right)\left({\wp }_2-1\right)\right)}^{\alpha }}+\frac{{\wp }_1{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\left(\left({\wp }_1{\wp }_2-1\right)\left({\wp }_1^2-1\right)\right)}^{\alpha }}+\frac{{\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\left(\left({\wp }_1{\wp }_2-1\right)\left({\wp }_1^3-1\right)\right)}^{\alpha }}+\frac{{\wp }_1{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\left(\left({\wp }_1^2{\wp }_2-2\right)\left({\wp }_1-1\right)\right)}^{\alpha }}\hfill \\ & +& \frac{{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\left(\left({\wp }_1^2{\wp }_2-2\right)\left({\wp }_1^2-1\right)\right)}^{\alpha }}+\frac{\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\left(\left({\wp }_1^2{\wp }_2-2\right)\left({\wp }_1^3-1\right)\right)}^{\alpha }}+\frac{{\wp }_1{\left({\wp }_1-1\right)}^2}{\left(\left({\wp }_1^2{\wp }_2-2\right)\left({\wp }_1{\wp }_2-1\right)\right)}+\frac{\left({\wp }_1-1\right)\left({\wp }_1-2\right)}{2{({\wp }_1^2{\wp }_2-2)}^{2\alpha }}\hfill \end{array}$$

(65)

Theorem 4.

Let $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^3{\wp }_2}\right)$ be a zero-divisor graph over ${\mathbb{Z}}_{{\wp }_1^3{\wp }_2}$ with distinct primes (${\wp }_1>{\wp }_2$), then

$$\begin{array}{ccc}\hfill SS{D}_3\left(G\right)& =& 5{\wp }_1^8{\wp }_2^3-8{\wp }_1^7{\wp }_2^3+2{\wp }_1^6{\wp }_2^3+{\wp }_1^4{\wp }_2^3-{\wp }_1^3{\wp }_2^3+{\wp }_1^2{\wp }_2^3+3{\wp }_1^9{\wp }_2^2-4{\wp }_1^8{\wp }_2^2-41{\wp }_1^6{\wp }_2^2+80{\wp }_1^5{\wp }_2^2\hfill \\ & -& 33{\wp }_1^4{\wp }_2^2-{\wp }_1^3{\wp }_2^2-4{\wp }_1^2{\wp }_2^2-4{\wp }_1^9{\wp }_2+{\wp }_1^8{\wp }_2+{\wp }_1^7{\wp }_2+35{\wp }_1^6{\wp }_2-43{\wp }_1^5{\wp }_2+45{\wp }_1^4{\wp }_2-96{\wp }_1^3{\wp }_2\hfill \\ & +& 61{\wp }_1^2{\wp }_2+{\wp }_1^9+2{\wp }_1^7-5{\wp }_1^6-4{\wp }_1^5-17{\wp }_1^4+43{\wp }_1^3-22{\wp }_1^2+18{\wp }_1-16.\hfill \end{array}$$

(66)

$$\begin{array}{ccc}\hfill S{D}_5\left(G\right)& =& \frac{{\wp }_1^2\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^2}{{\wp }_1^3-1}+\frac{{\wp }_1\left({\wp }_1^2-1\right){\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\wp }_1{\wp }_2-1}+\frac{{\wp }_1\left({\wp }_1^3-1\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1{\wp }_2-1}\hfill \\ & +& \frac{{\wp }_1{\left({\wp }_1-1\right)}^3\left({\wp }_2-1\right)}{{\wp }_1^2{\wp }_2-2}+\frac{\left({\wp }_1^2-1\right){\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\wp }_1^2{\wp }_2-2}\hfill \\ & +& \frac{\left({\wp }_1^3-1\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^2{\wp }_2-2}+\frac{{\wp }_1\left({\wp }_1{\wp }_2-1\right){\left({\wp }_1-1\right)}^2}{{\wp }_1^2{\wp }_2-2}+{\wp }_1^2\left({\wp }_1^3-1\right)\left({\wp }_1-1\right)\hfill \\ & +& \frac{{\wp }_1\left({\wp }_1{\wp }_2-1\right){\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\wp }_1^2-1}+\frac{{\wp }_1\left({\wp }_1{\wp }_2-1\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^3-1}\hfill \\ & +& {\wp }_1\left({\wp }_1^2{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)+\frac{\left({\wp }_1^2{\wp }_2-2\right){\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\wp }_1^2-1}\hfill \\ & +& \frac{\left({\wp }_1^2{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^3-1}+\frac{{\wp }_1\left({\wp }_1^2{\wp }_2-2\right){\left({\wp }_1-1\right)}^2}{{\wp }_1{\wp }_2-1}+\left({\wp }_1-1\right)\left({\wp }_1-2\right).\hfill \end{array}$$

(67)

$$\begin{array}{ccc}\hfill H\left(G\right)& =& \frac{2{\wp }_1^2\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^3+{\wp }_2-2}+\frac{2{\wp }_1{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\wp }_1^2+{\wp }_1{\wp }_2-2}+\frac{2{\wp }_1\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^3+{\wp }_1{\wp }_2-2}+\frac{2{\wp }_1{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\wp }_1^2{\wp }_2+{\wp }_1-3}\hfill \\ & +& \frac{2{\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\wp }_1^2{\wp }_2+{\wp }_1^2-3}+\frac{2\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^3+{\wp }_1^2{\wp }_2-3}+\frac{2{\wp }_1{\left({\wp }_1-1\right)}^2}{{\wp }_1^2{\wp }_2+{\wp }_1{\wp }_2-3}+\frac{2\left({\wp }_1-1\right)\left({\wp }_1-2\right)}{2\left(2{\wp }_1^2{\wp }_2-4\right)}.\hfill \end{array}$$

(68)

$$\begin{array}{ccc}\hfill I\left(G\right)& =& \frac{{\wp }_1^2\left({\wp }_1^3-1\right)\left({\wp }_1-1\right){\left({\wp }_2-1\right)}^2}{{\wp }_1^3+{\wp }_2-2}+\frac{{\wp }_1\left({\wp }_1^2-1\right)\left({\wp }_1{\wp }_2-1\right){\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\wp }_1^2+{\wp }_1{\wp }_2-2}\hfill \\ & +& \frac{{\wp }_1\left({\wp }_1^3-1\right)\left({\wp }_1{\wp }_2-1\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^3+{\wp }_1{\wp }_2-2}+\frac{{\wp }_1\left({\wp }_1^2{\wp }_2-2\right){\left({\wp }_1-1\right)}^3\left({\wp }_2-1\right)}{{\wp }_1^2{\wp }_2+{\wp }_1-3}\hfill \\ & +& \frac{\left({\wp }_1^2-1\right)\left({\wp }_1^2{\wp }_2-2\right){\left({\wp }_1-1\right)}^2\left({\wp }_2-1\right)}{{\wp }_1^2{\wp }_2+{\wp }_1^2-3}+\frac{\left({\wp }_1^3-1\right)\left({\wp }_1^2{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_2-1\right)}{{\wp }_1^3+{\wp }_1^2{\wp }_2-3}\hfill \\ & +& \frac{{\wp }_1\left({\wp }_1{\wp }_2-1\right)\left({\wp }_1^2{\wp }_2-2\right){\left({\wp }_1-1\right)}^2}{{\wp }_1^2{\wp }_2+{\wp }_1{\wp }_2-3}+\frac{\left({\wp }_1^2{\wp }_2-2\right)\left({\wp }_1-1\right)\left({\wp }_1-2\right)}{4}.\hfill \end{array}$$

(69)

$$\begin{array}{ccc}\hfill F\left(G\right)& =& {\wp }_1^7{\wp }_2^3-{\wp }_1^6{\wp }_2^3+{\wp }_1^5{\wp }_2^3-{\wp }_1^4{\wp }_2^3+{\wp }_1^3{\wp }_2^3-{\wp }_1^2{\wp }_2^3-6{\wp }_1^5{\wp }_2^2+3{\wp }_1^4{\wp }_2^2+3{\wp }_1^2{\wp }_2^2\hfill \\ & +& {\wp }_1^9{\wp }_2+{\wp }_1^7{\wp }_2-4{\wp }_1^6{\wp }_2-2{\wp }_1^5{\wp }_2-{\wp }_1^4{\wp }_2+30{\wp }_1^3{\wp }_2-25{\wp }_1^2{\wp }_2-{\wp }_1^9-{\wp }_1^7\hfill \\ & +& 4{\wp }_1^6+2{\wp }_1^5+{\wp }_1^4-13{\wp }_1^3+7{\wp }_1^2-7{\wp }_1+8.\hfill \end{array}$$

(70)

The numerically and graphically comparison of $M_1\left(G\right)$, $M_2\left(G\right)$, ${}^m{M}_2\left(G\right)$, $R_{\alpha }\left(G\right)$ and $R{R}_{\alpha }\left(G\right)$ over zero-divisor graphs $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$ is given in Table 4 and Figure 6, respectively.

Table 4. Numerically comparison between topological indices namely $SS{D}_3\left(G\right)$, $SS{D}_5\left(G\right)$, $H\left(G\right)$, $I\left(G\right)$ and $F\left(G\right)$ over zero-divisor graphs $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$.

${\mathit{\wp }}_1$	${\mathit{\wp }}_2$	${\mathit{SSD}}_3\left(\mathit{G}\right)$	${\mathit{SSD}}_5\left(\mathit{G}\right)$	$\mathit{H}\left(\mathit{G}\right)$	$\mathit{I}\left(\mathit{G}\right)$	$\mathit{F}\left(\mathit{G}\right)$
3	2	125,552	683.877	6.53385	195.608	27,608
5	3	$5.29581\times {10}^7$	16,629.1	18.9935	5022.67	$5.53815\times {10}^6$
7	5	$4.45476\times {10}^9$	147,929	43.326	54,329.2	$2.5046\times {10}^8$
11	7	$5.55416\times {10}^{11}$	$2.21016\times {10}^6$	98.3333	652,906	$2.03022\times {10}^{10}$
13	11	$7.76304\times {10}^{12}$	$7.45386\times {10}^6$	163.917	$2.72455\times {10}^6$	$1.83766\times {10}^{11}$
17	13	$1.18842\times {10}^{14}$	$3.52665\times {10}^7$	260.899	$1.10572\times {10}^7$	$2.27682\times {10}^{12}$
19	17	$6.20879\times {10}^{14}$	$7.86567\times {10}^7$	356.206	$2.68999\times {10}^7$	$9.34205\times {10}^{12}$
23	19	$4.203\times {10}^{15}$	$2.34202\times {10}^8$	495.172	$7.22103\times {10}^7$	$5.48381\times {10}^{13}$
29	23	$4.94125\times {10}^{16}$	$9.2254\times {10}^8$	763.816	$2.61585\times {10}^8$	$5.22303\times {10}^{14}$
31	29	$1.59476\times {10}^{17}$	$1.58854\times {10}^9$	956.485	$4.96969\times {10}^8$	$1.39087\times {10}^{15}$
37	31	$8.45941\times {10}^{17}$	$4.1998\times {10}^9$	1276.08	$1.18128\times {10}^9$	$6.65469\times {10}^{15}$

Figure 6. Three-dimensional discrete plot of third symmetric division, fifth symmetric division, harmonic, inverse sum, and forgotten topological index for $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^3{\wp }_2}\right)$.

5. Entropies for the Zero-Divisor Graphs $\widehat{\mathit{G}}\left({\mathit{Z}}_{{\wp }_{\mathbf{1}}^{\mathbf{2}}{\wp }_{\mathbf{2}}}\right)$

In this section, three kind of entropies—namely the first, second, and third redefined Zagreb entropies—are founded over zero-divisor graphs $\widehat{G}\left(Z_{{\wp }_1^2{\wp }_2}\right)$.

Lemma 3.

Let $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$ be a zero-divisor graph over ${\mathbb{Z}}_{{\wp }_1^2{\wp }_2}$ with distinct primes (${\wp }_1>{\wp }_2$); then

$$\begin{array}{ccc}\hfill ReZ{G}_1\left(\widehat{G}\left({\mathbb{Z}}_{p^{2}q}\right)\right)& =& {\wp }_1^2+{\wp }_1({\wp }_2-1)-1.\hfill \end{array}$$

(71)

$$\begin{array}{ccc}\hfill ReZ{G}_2\left(\widehat{G}\left({\mathbb{Z}}_{p^{2}q}\right)\right)& =& \frac{1}{4}({\wp }_1-1)\left(\frac{4{\wp }_1({\wp }_1^2-1){({\wp }_2-1)}^2}{{\wp }_1^2+{\wp }_2-2}+({\wp }_1-2)({\wp }_1{\wp }_2-2)+\frac{4{({\wp }_1-1)}^2({\wp }_2-1)({\wp }_1{\wp }_2-2)}{{\wp }_1{\wp }_2+{\wp }_1-3}\right.\hfill \\ & +& \left.\frac{4({\wp }_1^2-1)({\wp }_2-1)({\wp }_1{\wp }_2-2)}{{\wp }_1^2+{\wp }_1{\wp }_2-3}\right).\hfill \end{array}$$

(72)

$$\begin{array}{ccc}\hfill ReZ{G}_3\left(\widehat{G}\left({\mathbb{Z}}_{p^{2}q}\right)\right)& =& ({\wp }_1-1)\left({\wp }_1^5(2{\wp }_2^2-3{\wp }_2+1)+{\wp }_1^4(3{\wp }_2^3-{\wp }_2^2-3{\wp }_2+2)-{\wp }_1^3(3{\wp }_2^3+22{\wp }_2^2-18{\wp }_2+1)\right.\hfill \\ & +& \left.{\wp }_1^2(23{\wp }_2^2+19{\wp }_2-18)-{\wp }_1({\wp }_2^3-4{\wp }_2^2+43{\wp }_2-8)+16\right).\hfill \end{array}$$

(73)

Proof. 

$$\begin{array}{ccc}\hfill ReZ{G}_1(\widehat{G}\left({\mathbb{Z}}_{p^{2}q}\right)& =& \sum _{x_i{y}_j\in E}\frac{d_{x_i}+d_{y_j}}{d_{x_i}{d}_{y_j}}\hfill \\ \hfill ReZ{G}_1(\widehat{G}\left({\mathbb{Z}}_{p^{2}q}\right)& =& {\wp }_1({\wp }_1-1)({\wp }_2-1)\left[\frac{{\wp }_1^2+{\wp }_2-2}{({\wp }_1^2-1)({\wp }_2-1)}\right]+{({\wp }_1-1)}^2({\wp }_2-1)\left[\frac{{\wp }_1{\wp }_2+{\wp }_1-3}{({\wp }_1-1)({\wp }_1{\wp }_2-2)}\right]\hfill \\ & +& ({\wp }_1-1)({\wp }_2-1)\left[\frac{{\wp }_1^2+{\wp }_1{\wp }_2-3}{({\wp }_1^2-1)({\wp }_1{\wp }_2-2)}\right]+({\wp }_1-1)({\wp }_1-2)\left[\frac{1}{{\wp }_1{\wp }_2-2}\right]\hfill \\ & =& {\wp }_1^2+{\wp }_1({\wp }_2-1)-1.\hfill \end{array}$$

(74)

$$\begin{array}{ccc}\hfill ReZ{G}_2(\widehat{G}\left({\mathbb{Z}}_{p^{2}q}\right)& =& \sum _{x_i{y}_j\in E}{\displaystyle \frac{d_{x_i}{d}_{y_j}}{d_{x_i}{d}_{y_j}}}\hfill \\ \hfill ReZ{G}_2(\widehat{G}\left({\mathbb{Z}}_{p^{2}q}\right)& =& {\wp }_1({\wp }_1-1)({\wp }_2-1)\left[{\displaystyle \frac{({\wp }_1^2-1)({\wp }_2-1)}{{\wp }_1^2+{\wp }_2-2}}\right]+{({\wp }_1-1)}^2({\wp }_2-1)\left[\frac{({\wp }_1-1)({\wp }_1{\wp }_2-2)}{{\wp }_1{\wp }_2+{\wp }_1-3}\right]\hfill \\ & +& ({\wp }_1-1)({\wp }_2-1)\left[\frac{({\wp }_1^2-1)({\wp }_1{\wp }_2-2)}{{\wp }_1^2+{\wp }_1{\wp }_2-3}\right]+1/2({\wp }_1-1)({\wp }_1-2)\left[\frac{{\wp }_1{\wp }_2-2}{2}\right]\hfill \\ & =& \frac{1}{4}({\wp }_1-1)\left(\frac{4{\wp }_1({\wp }_1^2-1){({\wp }_2-1)}^2}{{\wp }_1^2+{\wp }_2-2}+({\wp }_1-2)({\wp }_1{\wp }_2-2)+\frac{4{({\wp }_1-1)}^2({\wp }_2-1)({\wp }_1{\wp }_2-2)}{{\wp }_1{\wp }_2+{\wp }_1-3}\right.\hfill \\ & +& \left.\frac{4({\wp }_1^2-1)({\wp }_2-1)({\wp }_1{\wp }_2-2)}{{\wp }_1^2+{\wp }_1{\wp }_2-3}\right).\hfill \end{array}$$

(75)

$$\begin{array}{ccc}\hfill ReZ{G}_3(\widehat{G}\left({\mathbb{Z}}_{p^{2}q}\right)& =& \sum _{x_i{y}_j\in E}\left(d_{x_i}{d}_{y_j}\right)(d_{x_i}+d_{y_j})\hfill \\ \hfill ReZ{G}_3(\widehat{G}\left({\mathbb{Z}}_{p^{2}q}\right)& =& {\wp }_1({\wp }_1-1){({\wp }_2-1)}^2({\wp }_1^2-1)({\wp }_1^2+{\wp }_2-2)+{({\wp }_1-1)}^3({\wp }_2-1)({\wp }_1{\wp }_2+{\wp }_1-3)({\wp }_1{\wp }_2-2)\hfill \\ & +& ({\wp }_1-1)({\wp }_2-1)({\wp }_1^2+{\wp }_1{\wp }_2-3)({\wp }_1^2-1)({\wp }_1{\wp }_2-2)+({\wp }_1-1)({\wp }_1-2){({\wp }_1{\wp }_2-2)}^3\hfill \\ & =& ({\wp }_1-1)\left({\wp }_1^5(2{\wp }_2^2-3{\wp }_2+1)+{\wp }_1^4(3{\wp }_2^3-{\wp }_2^2-3{\wp }_2+2)-{\wp }_1^3(3{\wp }_2^3+22{\wp }_2^2-18{\wp }_2+1)\right.\hfill \\ & +& \left.{\wp }_1^2(23{\wp }_2^2+19{\wp }_2-18)-{\wp }_1({\wp }_2^3-4{\wp }_2^2+43{\wp }_2-8)+16\right).\hfill \end{array}$$

(76)

□

Theorem 5.

Let $\widehat{G}\left({\mathbb{Z}}_{{\wp }_1^2{\wp }_2}\right)$ be a zero-divisor graph over ${\mathbb{Z}}_{{\wp }_1^2{\wp }_2}$ with distinct primes (${\wp }_1>{\wp }_2$); then

$$\begin{array}{ccc}& & EN{T}_{ReZ{G}_1}\left(Z_{{\wp }_1^2{\wp }_2}\right)=log({\wp }_1^2+{\wp }_1({\wp }_2-1)-1)\hfill \\ & & -\frac{1}{{\wp }_1^2+{\wp }_1({\wp }_2-1)-1}log\left\{{\wp }_1({\wp }_1-1)({\wp }_2-1){\left[\frac{{\wp }_1^2+{\wp }_2-2}{({\wp }_1^2-1)({\wp }_2-1)}\right]}^{\left[\frac{{\wp }_1^2+{\wp }_2-2}{({\wp }_1^2-1)({\wp }_2-1)}\right]}\right.\hfill \\ & & \times {({\wp }_1-1)}^2({\wp }_2-1){\left[\frac{{\wp }_1{\wp }_2+{\wp }_1-3}{({\wp }_1-1)({\wp }_1{\wp }_2-2)}\right]}^{\left[\frac{{\wp }_1{\wp }_2+{\wp }_1-3}{({\wp }_1-1)({\wp }_1{\wp }_2-2)}\right]}\hfill \\ & & \left.\times ({\wp }_1-1)({\wp }_2-1){\left[\frac{{\wp }_1^2+{\wp }_1{\wp }_2-3}{({\wp }_1^2-1)({\wp }_1{\wp }_2-2)}\right]}^{\left[\frac{{\wp }_1^2+{\wp }_1{\wp }_2-3}{({\wp }_1^2-1)({\wp }_1{\wp }_2-2)}\right]}\times 1/2(p1-1)(p1-2){\left[\frac{2}{{\wp }_1{\wp }_2-2}\right]}^{\left[\frac{2}{{\wp }_1{\wp }_2-2}\right]}\right\}\hfill \end{array}$$

(77)

$$\begin{array}{ccc}& & EN{T}_{ReZ{G}_2}\left(Z_{{\wp }_1^2{\wp }_2}\right)=\hfill \\ & & log\left[\frac{1}{4}({\wp }_1-1)\left(\frac{4{\wp }_1({\wp }_1^2-1){({\wp }_2-1)}^2}{{\wp }_1^2+{\wp }_2-2}+({\wp }_1-2)({\wp }_1{\wp }_2-2)+\frac{4{({\wp }_1-1)}^2({\wp }_2-1)({\wp }_1{\wp }_2-2)}{{\wp }_1{\wp }_2+{\wp }_1-3}\right.\right.\hfill \\ & & \left.\left.+\frac{4({\wp }_1^2-1)({\wp }_2-1)({\wp }_1{\wp }_2-2)}{{\wp }_1^2+{\wp }_1{\wp }_2-3}\right)\right]-\hfill \\ & & \frac{4}{\left[({\wp }_1-1)\left(\frac{4{\wp }_1({\wp }_1^2-1){({\wp }_2-1)}^2}{{\wp }_1^2+{\wp }_2-2}+({\wp }_1-2)({\wp }_1{\wp }_2-2)+\frac{4{({\wp }_1-1)}^2({\wp }_2-1)({\wp }_1{\wp }_2-2)}{{\wp }_1{\wp }_2+{\wp }_1-3}+\frac{4({\wp }_1^2-1)({\wp }_2-1)({\wp }_1{\wp }_2-2)}{{\wp }_1^2+{\wp }_1{\wp }_2-3}\right)\right]}\times \hfill \\ & & log\left\{{\wp }_1({\wp }_1-1)({\wp }_2-1){\left[\frac{({\wp }_1^2-1)({\wp }_2-1)}{{\wp }_1^2+{\wp }_2-2}\right]}^{\left[\frac{({\wp }_1^2-1)({\wp }_2-1)}{{\wp }_1^2+{\wp }_2-2}\right]}\right.\times {({\wp }_1-1)}^2({\wp }_2-1){\left[\frac{({\wp }_1-1)({\wp }_1{\wp }_2-2)}{{\wp }_1{\wp }_2+{\wp }_1-3}\right]}^{\left[\frac{({\wp }_1-1)({\wp }_1{\wp }_2-2)}{{\wp }_1{\wp }_2+{\wp }_1-3}\right]}\hfill \\ & & \left.\times ({\wp }_1-1)({\wp }_2-1){\left[\frac{({\wp }_1^2-1)({\wp }_1{\wp }_2-2)}{{\wp }_1^2+{\wp }_1{\wp }_2-3}\right]}^{\left[\frac{({\wp }_1^2-1)({\wp }_1{\wp }_2-2)}{{\wp }_1^2+{\wp }_1{\wp }_2-3}\right]}\times 1/2(p1-1)(p1-2){\left[\frac{{\wp }_1{\wp }_2-2}{2}\right]}^{\left[\frac{{\wp }_1{\wp }_2-2}{2}\right]}\right\}.\hfill \end{array}$$

(78)

$$\begin{array}{ccc}\hfill EN{T}_{ReZ{G}_3}\left(Z_{{\wp }_1^2{\wp }_2}\right)& =& log\left[({\wp }_1-1)\left({\wp }_1^5(2{\wp }_2^2-3{\wp }_2+1)+{\wp }_1^4(3{\wp }_2^3-{\wp }_2^2-3{\wp }_2+2)-{\wp }_1^3(3{\wp }_2^3+22{\wp }_2^2-18{\wp }_2+1)\right.\right.\hfill \\ & +& \left.\left.{\wp }_1^2(23{\wp }_2^2+19{\wp }_2-18)-{\wp }_1({\wp }_2^3-4{\wp }_2^2+43{\wp }_2-8)+16\right)\right]\hfill \\ & -& \frac{1}{ReZ{G}_3}log\left\{{\wp }_1({\wp }_1-1)({\wp }_2-1){\left[({\wp }_1^2+{\wp }_2-2)({\wp }_1^2-1)({\wp }_2-1)\right]}^{\left[({\wp }_1^2+{\wp }_2-2)({\wp }_1^2-1)({\wp }_2-1)\right]}\right.\hfill \\ & \times & {({\wp }_1-1)}^2({\wp }_2-1){\left[({\wp }_1{\wp }_2+{\wp }_1-3)({\wp }_1-1)({\wp }_1{\wp }_2-2)\right]}^{\left[({\wp }_1{\wp }_2+{\wp }_1-3)({\wp }_1-1)({\wp }_1{\wp }_2-2)\right]}\hfill \\ & \times & ({\wp }_1-1)({\wp }_2-1){\left[({\wp }_1^2+{\wp }_1{\wp }_2-3)({\wp }_1^2-1)({\wp }_1{\wp }_2-2)\right]}^{\left[({\wp }_1^2+{\wp }_1{\wp }_2-3)({\wp }_1^2-1)({\wp }_1{\wp }_2-2)\right]}\hfill \\ & \times & \left.1/2(p1-1)(p1-2){\left[2{({\wp }_1{\wp }_2-2)}^3\right]}^{\left[2{({\wp }_1{\wp }_2-2)}^3\right]}\right\}.\hfill \end{array}$$

(79)

6. Conclusions

The mathematical framework used to analyze graphs and their characteristics using algebraic structures and techniques is known as algebraic graph theory. It enables researchers to conduct more systematic and rigorous graph analysis, allowing them to discover correlations between graph attributes and comprehend how different symmetries and structural aspects of molecules and crystals impact their behavior. Entropy is a notion adopted from information theory and statistical mechanics in graph theory. It quantifies the degree of uncertainty or unpredictability associated with a graph or a particular attribute of a graph. We have investigated several topological indices, namely first Zagreb, second Zagreb, second modified Zagreb, general Randic, inverse general Randic, third symmetric division, fifth symmetric division, harmonic, inverse sum, and forgotten topological by means of $\mathbb{M}$-polynomial for certain families.

For $\alpha =1$, from Table 2 and Figure 3, we conclude that

$${}^m{M}_2\left(G\right)=R{R}_{\alpha }\left(G\right)<M_1\left(G\right)<M_2\left(G\right)=R_{\alpha }\left(G\right).$$

From Table 3 and Figure 4, we conclude that

$$H\left(G\right)<I\left(G\right)<SS{D}_5\left(G\right)<F\left(G\right)<SS{D}_3\left(G\right).$$

From Table 4 and Figure 6, we conclude that

$$H\left(G\right)<I\left(G\right)<M_2\left(G\right)<SS{D}_5\left(G\right)<F\left(G\right)<SS{D}_3\left(G\right).$$

Further, different kinds of entropies such as the first, second, and third redefined Zagreb are investigated over proposed families of graphs. In future work, if anyone can generalize this study for each zero-divisor graph, then this result is very interesting for researchers working in the area of algebraic graph theory.