Abstract
The results of a theoretical study on Benjamin–Ono (BO) soliton evolution are presented in a simple model of a two-layer ocean with a shear flow and viscosity. The upper layer is assumed to move with a constant speed relative to the lower layer with a tangential discontinuity in the flow profile. It is shown that in the long-wave approximation, such a model can be appropriate. If the flow is supercritical, i.e., its speed (U) exceeds the speed of long linear waves (), then BO solitons experience “explosive-type” enhancement due to viscosity, such that their amplitudes increase to infinity in a finite time. In the subcritical regime, when , BO solitons experience very slow decay due to viscosity. Soliton amplitude decays with time as or , depending on whether both layers are weakly viscous (the former case) or only the lower layer is viscous (the latter case). Estimates of "explosion time" are presented for real oceanic parameters.
Keywords:
ocean waves; Benjamin–Ono equation; soliton; explosive instability; stratified ocean; viscous fluid MSC:
76B25; 76B55; 76D17; 76D33
1. Introduction
As is well known, weakly nonlinear internal waves in the ocean can be described with the Benjamin–Ono (BO) equation if one of the layers is relatively thin compared with the wavelength [1,2,3]. Such a situation is rather ubiquitous in oceans. The BO equation is a very useful model that provides both periodic and solitary solutions describing stationary waves close to observable waves in the ocean and laboratory [4]. The equation is completely integrable and possesses many remarkable mathematical properties, such as the infinite set of integrals of motion; for example, see [3].
In the meantime, there are many factors in the ocean that are not accounted for in the BO model; among them are shear flows, dissipation, bottom topography, the geometrical spreading of waves, etc. Some of these factors have been considered in applications of BO solitons, for example, the influence of different types of dissipation and radiative losses caused by global water rotation [5]. In this paper, we study the influence of two other specific factors, shear flow and water viscosity. Using the well-known method of separate derivation of small nonlinear, dispersion, and dissipation terms [6,7], we derive the generalized BO equations for the case when the shallow upper layer moves with a uniform velocity profile relative to the immovable lower layer. We show that viscosity can play a destabilizing role that leads to the growth in soliton amplitude if the flow in the upper layer is supercritical, i.e., its speed (U) exceeds the speed of long linear waves () at the interface between the layers. In such a situation, one of the branches of the dispersion relations corresponds to negative-energy waves [8,9,10,11]. Such co-current-propagating waves can grow in the course of propagation due to the influence of viscosity in the lower layer. We show that within the framework of the simplified model, the amplitudes of BO solitons turn to infinity in a finite time. The “explosion time” of solitons is estimated for realistic ocean parameters. Interfacial waves decay due to viscosity if the upper-layer flow is subcritical, i.e., if . As is well known, the presence of shear flows can drastically change the character of wave equations. The essence of physical effects related to the presence of shear flows can be understood with the help of simple flow models with piece-wise linear or even piece-wise constant profiles. As an example, we refer to publications [12,13], where nonlinear waves in a three-layer model with a shear flow were considered in a rotating fluid.
The paper structure is as follows: In Section 2, we derive a dispersion relation for interfacial waves in a two-layer model of an ocean with a uniformly moving upper layer using the rigid-lid approximation to filter out the surface mode. We analyze the derived dispersion equation in the long-wave approximation and consider the influence of layer viscosity values. Then, in Section 3, we derive the generalized BO equation, which is augmented with different dissipative terms; the structure of these terms depends on water-flow criticality (either or ) and viscosity in the layers. In Section 4, we study BO soliton evolution under the influence of viscosity and show that they can grow in the supercritical case when . Such growth is of the “explosion type” when soliton amplitude turns to infinity in a finite time. We estimate the “explosion time” for realistic ocean parameters. In the Conclusions section, we summarize the results obtained and discuss factors that can restrict the infinite growth of solitons.
2. Dispersion Relations for a Two-Layer Fluid with a Shear Flow
Let us consider a two-layer model of an ocean with a shear flow. For the sake of simplicity, we assume that the shear flow has a tangential discontinuity at the interface between the layers, as shown in Figure 1. The fluid density in the upper layer is assumed to be , and the thickness of the upper layer is , whereas the fluid density in the lower layer is assumed to be and the thickness of the lower layer is . We also assume that the upper layer fluid is perfect and the lower layer is viscous, with kinematic viscosity . Our interest is related to internal waves propagating at the interface between the layers; therefore, we apply a rigid-lid approximation to the surface to filter out surface waves.
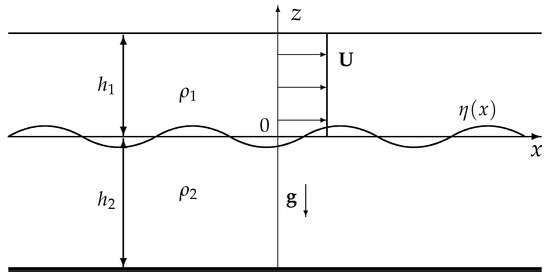
Figure 1.
Sketch of a fluid flow in the two-layer model with infinitely deep and immovable lower layer.
The basic set of hydrodynamic equations for two-dimensional motion in the linear approximation is
where subscripts 1 and 2 refer to the upper and lower layers, respectively; g is the acceleration due to gravity; and are pressure values in the corresponding layers. Further, and are the horizontal and vertical velocity components, respectively. The boundary conditions are
The dynamic condition follows from the equality of the tangential and normal stresses [14]:
A solution to the above-presented set of equations can be sought in the form
Here, . Using the equation for the tangential stress as given in Equation (8), we derive the dispersion relation for the interfacial waves: In the case of weak viscosity, , the dispersion relation yields
where is the density ratio.
Similarly, the dispersion relation, in the case when the upper layer is viscous and the lower layer is ideal , is derived as
If both layers are viscous, then a rigorous solution to the problem in linear approximation leads to the investigation of the eigenvalues of a fourth-order Orr–Sommerfeld equation [15]. In a viscous fluid, a flow with a discontinuous profile cannot exist. However, in the initial stage of the development of the shear flow, when the boundary layers on either side of the interface between the layers are small in comparison with a wavelength, the velocity profile can be approximated by a profile with a tangential velocity discontinuity. This is even more true when the characteristic wavelength is much greater than not only the boundary layer thickness but also the total depth of the upper layer. A similar approximation is not infrequently used in the theory of instabilities of a homogeneous liquid [15]. To obtain an approximate dispersion relation with allowance for the weak viscosity in both layers, we represent the dispersion relation in the functional form , where is the dispersion relation for an ideal fluid as per Equations (15) and (16). We expand function F in a series in terms of and and restrict ourselves to the first terms in the expansion:
The form of the expansion coefficients is obtained from the solution to the “half-viscous” problems for each of the layers, as presented in Equations (15) and (16). Assuming that imaginary correction to the frequency is small compared with real part (it is in this case where the viscosity of the layers is assumed to be small), can be easily derived by summing up the imaginary parts of Equations (15) and (16) [16]. Therefore, the resultant dispersion relation in the case of both upper and lower layers being weakly viscous can readily be obtained as a combination of the viscous effects on both layers:
In the next subsection, we present the analysis of dispersion relation (18).
Analysis of the Dispersion Relation
Dispersion Equation (18) can be re-written in the following equivalent forms:
where are the roots of the dispersion relation without viscosity, that is,
Assuming that the viscosity is small in both layers, the correction to the lower branch of the dispersion relation () can be derived for , where . By substituting this in Equation (19), we obtain
Taking into account Equation (20), we derive the imaginary correction to :
Similarly, the imaginary correction to can be derived:
We shall now focus on the particular case suitable to the typical oceanic situation when the upper layer is relatively shallow compared with the characteristic length of internal waves, i.e., , and the lower layer is infinitely deep, i.e., . Then, for the real parts of the dispersion relation, we obtain, up to inclusive,
where is the Froude number and is the speed of long waves. When there is no shear flow, , or the shear flow is relatively weak, , long waves travel in the opposite direction, whereas when , long waves propagate in the same direction as the current. Waves corresponding to the lower branch of the dispersion relation possess negative energy when (see, e.g., Refs. [10,11] and references therein). Graphics of approximate dispersion relations are shown in Figure 2.
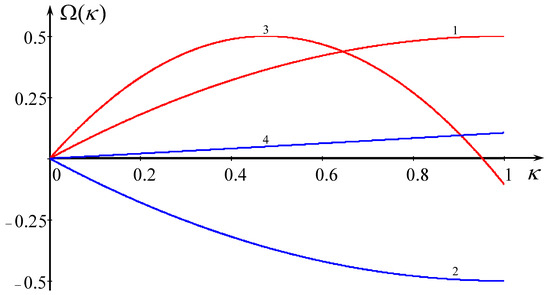
Figure 2.
(Color online). Real parts of approximate dispersion relations (25) in terms of dimensionless variables , where and . Lines 1 and 2 pertain to and , respectively, with . Lines 3 and 4 pertain to and , respectively, with .
The first terms of the Taylor expansions of the dispersion relation in parameter depend on the viscosity. If we assume that the upper layer of a fluid is perfect and the lower layer is viscous, which yields and , then the first non-zero terms of the imaginary parts of the dispersion relations are reduced to
In Equation (26), the negative sign of corresponds to wave decay, whereas the positive sign corresponds to wave growth. Therefore, co-current-propagating waves of the upper branch of the dispersion relation with and that possess positive energy decay in the course of propagation. Counter-current-propagating internal waves of the lower branch of the dispersion relation with and with and also possess positive energy and decay in the course of propagation. However, co-current-propagating waves of the lower branch of the dispersion relation with and with and that possess negative energy grow in the course of propagation. The restriction of only quadratic terms on in the real parts of the dispersion relation is consistent with the cubic terms in the imaginary parts of the dispersion relation. Simple estimates for the upper branch of the dispersion relation, , show that this can occur when a characteristic scale of a wave process is subjected to
For m, , and this requires /s. In the ocean, eddy turbulent viscosity can attain up to /s (Ref. [17]). Nevertheless, such a condition with an inviscid upper layer and a highly viscous lower layer is hardly realistic for the ocean. Similar estimates for the lower branch of the dispersion relation, , show that this can occur when
These conditions look quite realistic, especially when the Froude number is close to unity. Moreover, viscosity leads to wave decay if and to wave enhancement if . In the former case, waves indeed propagate in a counter-current manner and have positive energy, whereas in the latter case, waves actually propagate in a co-current manner and have negative energy. We focus below on this mode and consider its evolution in the nonlinear regime.
On the other hand, if the upper layer fluid is viscous, , and the lower layer is perfect, , then waves of both upper and lower branches decay under the influence of viscosity, because the imaginary parts of the corresponding dispersion equation do not depend on the Froude number and are negative in the principal order on parameter :
Finally, when fluids in both layers are viscous and , then and are determined with the same formula (29).
3. Generalized Benjamin–Ono Equations with Dissipative Terms
A preliminary analysis of the dispersion relation reveals that waves of the lower branch of the dispersion relation, , can exponentially grow with time in the course of propagation when , , and . The growth rate is determined as . In the nonlinear regime, wave growth can be different. This is, apparently, the most interesting case and is studied below. We first restore a linear evolution equation describing interfacial waves of the lower branch of the dispersion relation; then, we augment it with a nonlinear term to describe a nonlinear regime of wave evolution. In the derivation of the nonlinear term, we use a well-known approach, which consists in the separate consideration of small terms of the same order of magnitude [6,7]. In such a case, small terms can be involved in the equation only additively, i.e., independently of each other, because their products are terms of a higher order of smallness.
3.1. Linear Evolution Equations
Using the approximate dispersion equations derived above, one can construct linear evolution equations that possess such dispersion equations [18]. If the viscosity in both layers is ignored, then the evolution equation is reduced to the linearized Benjamin–Ono equation. This equation, augmented with a viscous term in the case where and , yields
where the integral terms (in the sense of a principal value) represent the Hilbert transform of . The coefficients of this equation are
In the subcritical case, for , coefficient is positive, which corresponds to the decay of counter-current-propagating waves with positive energy. However, in the supercritical case, when , coefficient is negative, which corresponds to the enhancement in co-current-propagating waves of negative energy [8,9,10,11]. The first two terms in Equation (31) are of zeroth order of magnitude on the small parameter , whereas the other two terms, the dispersive and dissipative ones, are of the first order of magnitude.
3.2. Derivation of the Nonlinear Term in the BO Equation
Here, we derive a nonlinear term for Equation (30), assuming that it is of the same order of smallness as the dispersive term. To this end, we consider the basic set of equations neglecting dispersion and dissipation. For the upper shallow layer, the basic equations are
On the other hand, for the lower infinitely deep layer, the governing equations are
The kinematic boundary conditions at the interface, , yield
Additionally, the dynamic boundary condition at the interface, , is given by
Finally, the boundary condition as z approaches is reduced to the absence of any perturbation, which yields
As we neglect viscosity, the fluid flow in the lower layer becomes a flow of the potential type, and we introduce velocity potential such that and . Subsequently, Equation (34) is reduced to
The first kinematic condition in Equation (37) in terms of the velocity potential is reduced to
Thus, by eliminating and from Equations (32) and (41) using dynamic boundary condition (38), we obtain
By differentiating the above equation with respect to x, it can be easily derived that
The right-hand side of Equation (44) contains high-order derivatives in comparison with the left-hand side, which corresponds to the dispersive term, and we neglect the same in accordance with our decision to keep only linear and nonlinear terms. Consequently, we obtain
By applying operator to Equation (33), we obtain
Equations (45) and (46) are combined into one with the elimination of the second terms, which yields
where . The left-hand side of this equation can be factorized as
The above equation describes dispersionless weakly nonlinear waves propagating in the opposite direction with respect to calm water (or in the reference frame moving with the upper layer). Our main interest is in the description of the counter-current-propagating waves that are described in the linear approximation given by
Next, by combining Equation (49) with the linearized Equation (33), we derive
which on integration gives . This relationship is used to eliminate in the nonlinear terms in Equation (50), which are of high order of smallness with respect to the wave perturbation. Subsequently, Equation (50) yields
Thus, Equation (52) gives the small nonlinear correction to Equation (49) describing counter-current wave propagation to the left without dispersion. Consequently, by combining Equation (52) and Equation (30), we finally obtain the generalized BO (genBO) equation describing counter-current wave propagation that contains small nonlinear, dispersive, and dissipative terms of the same order of smallness:
where and the other coefficients are given in Equation (31). On the other hand, for , , and , the generalized BO equation differs from Equation (53) by the viscosity term on the right-hand side (see Equation (29)):
4. Dynamics of a Solitary Wave Under the Influence of Dissipation
As is well known, the BO equation, when , is completely integrable [3]. It has a family of periodic stationary solutions as well as solitary solutions called BO solitons. A BO soliton has a simple algebraic structure and is described by the following function [3]:
where A is the soliton amplitude, is its velocity, and is its characteristic width.
Under the influence of small dissipation, a soliton undergoes adiabatic evolution when its shape remains unchanged but its parameters (amplitude, width, velocity) slowly vary with time, preserving the relationship between parameters and [5]. To determine the time variation of the soliton parameter, one can use the asymptotic approach [19], which is reduced to the energy balance equation. In terms of a multiple-scale analysis, the energy balance equation is the condition for the elimination of secular terms. To obtain this equation, we multiply Equation (53) or Equation (54) by and integrate with respect to x, which yields
where “wave energy” E and dissipative functions are given by
The Hilbert transform of soliton (55) is
Wave energy E is obviously conserved when there is no dissipation (). For BO soliton (55), the energy is given by
Now, dissipative functions can be easily evaluated using solution (55):
4.1. Soliton Decay Due to Reynolds-Type Dissipation
Let us first consider the case of Reynolds-type dissipation described by dissipative function . By substituting the expressions for soliton energy E and dissipative function into energy balance Equation (56), we derive the ODE for soliton amplitude:
By integrating the above equation, we obtain the time dependence of soliton amplitude as
It is worth mentioning that a linear wave decays exponentially due to Reynolds-type dissipation, , where k is the wavenumber.
The theoretical dependence of normalized soliton amplitude , where is the initial soliton amplitude at , is depicted in Figure 3, together with the direct numerical solution of genBO Equation (54) with the initial condition in the form of BO soliton (55). As one can see, the agreement between numerical data and adiabatic theory is very good, even for a relatively large dissipation coefficient, . Such big dissipation can occur if turbulent viscosity is taken instead of molecular water viscosity. Note that the simple estimate of the relative strength of the dissipative term () in comparison with the nonlinear or dispersive terms () does not depend on time and remains small, , at all times if it is small at .
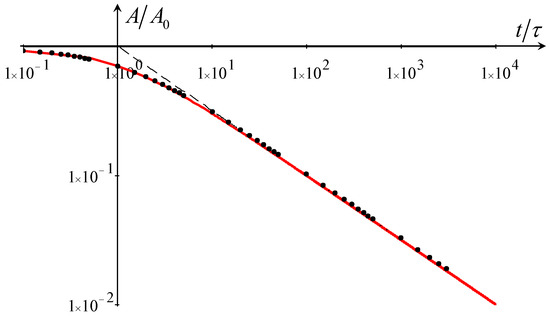
Figure 3.
(Color online). Soliton amplitude’s dependence on normalized time () for Reynolds dissipation. Solid line—theoretical dependence (62); dots—numerical data; dashed line—asymptotic dependence .
Figure 4 illustrates the solitary wave profile (line 1) at = 3000 (line 1). At this large time, the wave profile deviates slightly from the BO soliton of the same amplitude (line 2). One can clearly see the formation of a shelf behind the leading pulse in the near field, whereas in the far field, a decaying quasi-periodic trailing wave forms (similar results were obtained in Ref. [5]).
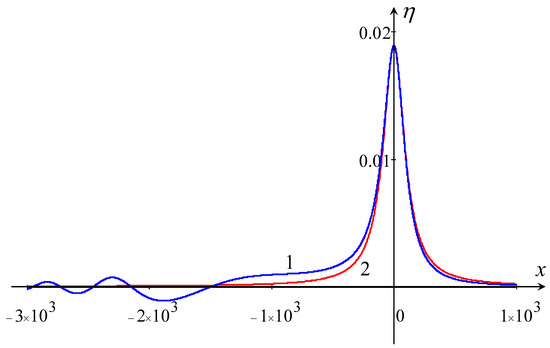
Figure 4.
(Color online). Solitary wave profile (line 1) at = 3000 for BO Equation (54) with Reynolds-type dissipation. Line 2 represents a BO soliton of the same amplitude as the leading pulse shown by line 1.
4.2. Soliton Dynamics under the Influence of Viscosity in a Moving Upper Layer
Let us now consider the most interesting case of soliton dynamics under the influence of integral term describing dissipation due to viscosity in the moving upper layer. This case is of special interest because the dissipation can change its sign when the Froude number passes through the unity. By substituting the expressions for soliton energy E and dissipative function into energy balance Equation (56), we obtain the ODE for soliton amplitude:
After the integration of this equation, we obtain the time dependence of soliton amplitude:
If , i.e., if , then this formula describes soliton decay, but if , i.e., if , then the formula predicts soliton-amplitude enhancement, formally up to infinity; the explosive instability occurs in finite time . The dependence of soliton amplitude on positive and negative are shown in Figure 5.
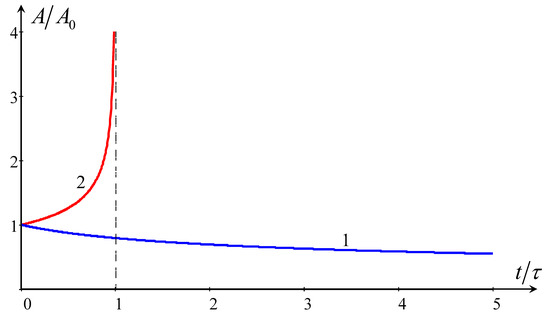
In reality, an infinite enhancement in soliton amplitude is, certainly, impossible due to several reasons. First of all, the weakly nonlinear genBO model becomes inapplicable. Secondly, the adiabatic theory describing wave amplification also ceases to work because the dissipative term becomes not small in comparison with the nonlinear and dispersive terms. Indeed, a simple estimate of the relative strength of the dissipative term (∼) and dispersive term (∼) shows that their ratio is proportional to . If soliton amplitude decreases with time when , then this ratio also decreases; therefore, the applicability of the asymptotic theory becomes better and better. Otherwise, when , the dissipative term becomes dominant in the genBO equation, and the asymptotic theory ceases to work.
Let us estimate the characteristic time of soliton “explosion”( ) for a realistic oceanic condition. Let us set m, m/s, kg/m, kg/m, m/s (conditional turbulent viscosity), m (initial soliton amplitude), m/s. Then, we obtain (see Equation (31)) m/s, , m/s, 1/s, m/s, m/s. This gives “explosion time”
Thus, if the Froude number exceeds the critical value by 2%, then even a small-amplitude soliton formally “blows up” in approximately three days. This can lead to the efficient mixing and turbulization of a flow. As follows from Equation (65), the “explosion time” strongly depends on supercriticality parameter . This can be explained by the strong dependence of the dispersion coefficient on supercriticality parameter . In particular, when , the moderating effect of dispersion on the “explosion time” vanishes.
A similar analysis can be performed for periodic perturbation; the corresponding calculations are presented in the Appendix A.
5. Discussion and Conclusions
In this paper, we have demonstrated that within a simple model of a two-layer ocean with a shear flow in the upper layer, BO solitons can experience an enhancement due to viscosity if the flow is supercritical, i.e., its speed (U) exceeds the speed of long linear waves (). BO solitons, in this case, possess negative energy, and the lower layer’s viscosity leads to their amplification. Other mechanisms of energy loss can also lead to soliton enhancement. One more possible mechanism of energy loss is related to the radiation of internal waves from the interface between the layers to the bulk of the lower layer if the latter is continuously stratified [9,10,11,20]. However, in the subcritical regime, when , BO solitons experience very slow decay due to viscosity. Soliton amplitude decays with time as or as , depending on whether both layers are weakly viscous (the former case) or only the lower layer is viscous (the latter case). A similar analysis can be performed for the case when the lower layer is shallow, whereas the upper layer is infinite; such a situation can also occur in real oceans. We derived the same equations as Equations (53) and (54) and obtained similar solutions for the adiabatic evolution of BO solitons. The results obtained are not included in the paper just for the sake of avoiding article extension.
Here, we only demonstrated a principal possibility of soliton enhancement within the simplest model of a shear flow with a tangential discontinuity of velocity and presented an estimate of a characteristic time of soliton-amplitude growth from a small value up to infinity. Such “explosive instability” of solitons can only occur in the early stage of soliton evolution. In a later stage, when soliton amplitude becomes big enough, the weakly nonlinear model becomes invalid, and a more advanced model (see, for example, Ref. [21]) should be used. This incurs, however, significant complications, because in the next order of smallness of wave amplitude, not only additional nonlinear terms appear but also dispersive, dissipative, and mixed terms do. Generalization can also include two-dimensional effects in the Kadomtsev–Petviashvili approximation [21,22,23], as well as a more realistic, smooth shear-flow profile. Higher-order effects, apparently, can restrict the infinite growth in soliton amplitude and lead to either soliton stabilization at a certain level or wave breaking and the turbulization of a flow. All this requires a more comprehensive analysis, which is beyond the scope of this paper.
Author Contributions
Conceptualization, Y.S.; methodology, Y.S.; validation, Y.S. and T.S.; formal analysis, Y.S. and P.N.; investigation, Y.S. and P.N.; data curation, Y.S.; writing and editing—original draft preparation, Y.S. and P.N.; writing—review & editing, Y.S. and T.S.; visualization, N.S.; supervision, Y.S. and T.S.; project administration, T.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Education, Government of India via Apex Committee of SPARC, grant number SPARC/2018-2019/P751/SL, as well as by the State task program in the sphere of scientific activity of the Ministry of Science and Higher Education of the Russian Federation (grant No. FSWE-2023-0004) and the RF Council on Grants for the state support of Leading Scientific Schools of the Russian Federation (grant No. NSH-70.2022.1.5).
Data Availability Statement
The data that support the findings of this study are available within the article.
Acknowledgments
The authors acknowledge the partial support received from the Ministry of Education, Government of India through the Apex Committee of SPARC, grant number SPARC/2018-2019/P751/SL. Y.S. acknowledges the funding of this study provided by the State task program in the sphere of scientific activity of the Ministry of Science and Higher Education of the Russian Federation (grant No. FSWE-2023-0004) and the RF Council on Grants for the state support of Leading Scientific Schools of the Russian Federation (grant No. NSH-70.2022.1.5).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A. Dynamics of Periodic Waves within the genBO Equation with Dissipative Terms
The BO equation has both solitary and periodic solutions [24]. We have presented solitary wave dynamics under the action of dissipative factors. Here, we present the dynamics of periodic waves under the influence of the same factors. A periodic solution of the BO equation with wavelength and zero mean value is
where , , and is the parameter of “nonsinusoidality”. When , the wave shape is close to sinusoidal, whereas when , the wave shape resembles a periodic sequence of solitary waves, as shown in Figure A1.
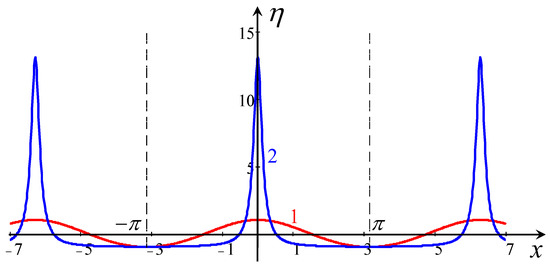
Figure A1.
(Color online). Shapes of periodic solutions of the BO equation of the same wavelength () and zero mean values but with different parameter . Line 1—quasi-sinusoidal wave with (wave amplitude multiplied by 10 to make it clearly visible); line 2—a periodic sequence of quasi-soliton waves with .
Now, let us first calculate the dissipation function per one period as per Equation (57):
Thus, the solution is , where is the initial value of parameter . This formula shows that even if, initially, this parameter is close to unity and the wave shape is close to the periodic set of solitons, then exponentially quickly decreases with time; wave amplitude also decreases; and the shape becomes sinusoidal.
Similar but more cumbersome calculations can be performed with function in Equation (57). This gives
and the corresponding equation for becomes
This equation can be hardly solved analytically but can be easily solved numerically. The typical plots of are shown in Figure A2, where .
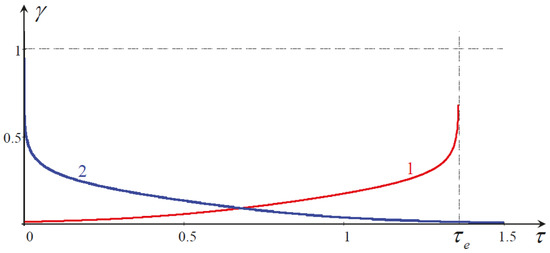
Figure A2.
(Color online). Dependence of parameter on normalized time (). Line 1 shows the increase in parameter from to for the supercritical case of a flow. Line 2 shows the decrease in parameter from to zero for the subcritical case of a flow.
Thus, in a supercritical flow, a small-amplitude sinusoidal wave increases and transforms into a periodic sequence of solitons, which subsequently blow up within the framework of this simplified model. In a subcritical flow, perturbations decay, so that even an initial periodic sequence of solitons gradually decay and transform into a quasi-sinusoidal wave, which then completely disappears.
References
- Benjamin, T. Internal waves of permanent form in fluids of great depth. J. Fluid Mech. 1967, 29, 559–592. [Google Scholar] [CrossRef]
- Ono, H. Algebraic solitary waves in stratified fluids. J. Phys. Soc. Jpn. 1975, 39, 1082–1091. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Segur, H. Solitons and the Inverse Scattering Transform; SIAM: Philadelphia, PA, USA, 1981. [Google Scholar]
- Ostrovsky, L.A.; Stepanyants, Y.A. Internal solitons in laboratory experiments: Comparison with theoretical models. Chaos 2005, 15, 37111. [Google Scholar] [CrossRef] [PubMed]
- Grimshaw, R.; Smyth, N.; Stepanyants, Y. Decay of Benjamin–Ono solitons under the influence of dissipation. Wave Motion 2018, 78, 98–115. [Google Scholar] [CrossRef]
- Korpel, A.; Banerjee, P. A heuristic guide to nonlinear dispersive wave equations and soliton-type solutions. In Proceedings of the IEEE, Bangalore, India, 9–12 December 1984; Volume 72, pp. 1109–1130. [Google Scholar]
- Benjamin, T.B. A new kind of solitary wave. J. Fluid Mech. 1992, 245, 401–411. [Google Scholar] [CrossRef]
- Nezlin, M.V. Negative-energy waves and the anomalous Doppler effect. Sov. Phys. Uspekhi 1976, 19, 946. [Google Scholar] [CrossRef]
- Ostrovski, L.A.; Rybak, S.A.; Tsimring, L.S. Negative energy waves in hydrodynamics. Sov. Phys. Uspekhi 1986, 29, 1040. [Google Scholar] [CrossRef]
- Fabrikant, A.L.; Stepanyants, Y.A. Propagation of Waves in Shear Flows; World Scientific Publishing Company: Singapore, 1998. [Google Scholar]
- Maïssa, P.; Rousseaux, G.; Stepanyants, Y. Negative energy waves in shear flow with a linear profile. Eur. J. Mech. B/Fluids 2016, 56, 1082–1091. [Google Scholar] [CrossRef]
- Alias, A.; Grimshaw, R.; Khusnutdinova, K. Coupled Ostrovsky equations for internal waves in a shear flow. Phys. Fluids 2014, 26, 126603. [Google Scholar] [CrossRef]
- Alias, A.; Grimshaw, R.; Khusnutdinova, K. Coupled Ostrovsky equations for internal waves, with a background shear flow. Proc. IUTAM 2014, 11, 3–14. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshits, E.M. Fluid Mechanics; Butterworth-Heinemann: Burlington, MA, USA, 1987. [Google Scholar]
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ostrovsky, L.A.; Stepanyants, Y.A. Nonlinear stage of the shearing instability in a stratified liquid of finite depth. Izv. Acad. Sci. Ussr. Fluid Dyn. 1983, 17, 540–546. [Google Scholar] [CrossRef]
- Jochum, M.; Danabasoglu, G.; Holland, M.; Kwon, Y.O.; Large, W.G. Ocean viscosity and climate. J. Geophys. Res. 2008, 113, 84. [Google Scholar]
- Whitham, G.B. Linear and Nonlinear Waves; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Ostrovsky, L.A. Asymptotic Perturbation Theory of Waves; Imperial College Press: London, UK, 2015. [Google Scholar]
- Ostrovsky, L.A.; Stepanyants, Y.A.; Tsimring, L.S. Radiation instability in a stratified shear flow. Iny. J. Nonlin. Mech. 1984, 19, 151–161. [Google Scholar]
- Matsuno, Y. Oblique interaction of interfacial solitary waves in a two-layer deep fluid. Proc. R. Soc. Lond. A 1998, 454, 835–856. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Segur, H. Long internal waves in fluids of great depth. Stud. Appl. Math. 1980, 62, 249–262. [Google Scholar] [CrossRef]
- Grimshaw, R.; Zhu, Y. Oblique interaction between internal solitary waves. Stud. Appl. Math. 1994, 92, 249–270. [Google Scholar] [CrossRef]
- Satsuma, J.; Ishimori, Y. Periodic wave and rational soliton solutions of the Benjamin–One equation. J. Phys. Soc. Jpn. 1979, 46, 681–687. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).