Abstract
In this study, we investigated a new zeta formula in which the zeta function can be expressed as the sum of an infinite series of delta and cosine functions. Our findings demonstrate that this formula possesses duality characteristics and we established a direct connection between the Riemann hypothesis and this new formula. Additionally, we explored the behavior of energy or particles in quantum physics within the proposed mathematical model framework based on the new formula. Our model provides a valuable understanding of several important physics inquiries, including the collapse of the wave function during measurement and quantum entanglement, as well as the double slits experiment.
Keywords:
zeta function; Riemann hypothesis; duality; wave collapse; entanglement; double slits experiment MSC:
11M06; 11M26
1. Introduction
The zeta or Dirichlet series can be expressed in the following form,
It generally takes a function form as [1,2]. The significance of this function can be observed in both applied scientific fields and mathematics [3]. Its importance dates to the nineteenth century, when mathematicians sought to understand the distribution of prime numbers. One of the major advantages of the zeta series is that its product formula includes all prime numbers as factors,
This is known as Euler’s product formula. In 1859, the German mathematician Riemann utilized this formula to establish a relationship that expresses the distribution of prime numbers, denoted by the function,
The function determines the number of primes less than or equal to a real number . Using Euler’s product formula, Riemann transformed the zeta series into a function and established that it is a polynomial function. He then computed the roots (zeros) of this polynomial and conjectured that all of these zeros have the form , where t is a real number. While these zeros have different imaginary parts, they all share the same real value, . These roots are known as the non-trivial zeros (Note that the zeta function has two types of zeros depending on the region of definition. For the region , it equals zero for the values and these zeros can be easily calculated. However, for the definition region , the zeta function has another type of zero known as the non-trivial zeros, which are mentioned in the Riemann hypothesis. It is important to note that these non-trivial zeros are specific to the zeta function as a function.). The Riemann hypothesis states that all non-trivial zeros of the zeta function lie on the line (see [1,4]).
In 1914, Hardy provided a significant result regarding the non-trivial zeros of the zeta function. Specifically, he proved that there are infinitely many roots of on the critical line , as noted in [1,4]. This was a groundbreaking result, as prior to the numerical work of Gram and Backlund, it was the first concrete result concerning zeros on the line [1]. Further progress was made in this area, as noted in [4], where it is mentioned that Selberg demonstrated that a positive proportion of the zeros of lie on the critical line [5]. Levinson subsequently elaborated upon Selberg’s work by proving that of the zeros lie on the critical line [6]. Most recently, Conrey showed that of the zeros lie on the critical line, which is considered the best and most recent result in this area [7].
The unexpected appearance of the zeros of the Zeta function in the field of nuclear physics was first discovered by Montgomery in 1973. He linked these zeros to random matrices, which are commonly used to model the nuclear energy levels for higher excitation [8]. Montgomery suspected that the local fluctuation properties of the zeros on the line were the same as those of the eigenvalues of these matrices [8]. Subsequently, Odlyzko conducted a numerical study of the distribution of spacings between the zeros of the Riemann zeta function and demonstrated that these zeros behave like the eigenvalues of random Hermitian matrices [9]. Applications of random matrices have since appeared in many areas of applied physics, particularly in relation to atoms and molecules [10]. This has led to the expansion of the applied areas of the zeta function beyond pure mathematics.
This study was divided into two parts. The first part involves the derivation of a novel formula for the zeta function, called the Zeta-cosine formula, which serves as the main focus of the research. The Zeta-cosine formula is primarily applicable in the strip region and can be extended to cover the entire s-domain. Next, the Zeta-cosine formula was tested by deriving formulas for the Zeta function that are already known to assess the reliability of the new formula. Furthermore, it will be proven that the Zeta-cosine function is only defined for in the strip region (as per Theorem 2), and that may prove the Riemann hypothesis.
In the physics section, we will explore the application of the zeta function as a mathematical model in quantum physics. We will discuss the various aspects and possibilities of the model to verify the following concepts:
- Planck’s law and exploration of the concept of wave–particle duality.
- Heisenberg’s uncertainty principle.
- Superposition and states.
- Entanglement phenomenon.
- Double-slit experiment.
Although there are many formulas developed for the zeta function, the new formula introduced herein is the first to express the zeta function as the sum of an infinite series of delta and cosine functions, which can provide a duality in mathematics. By inspecting the application of the new formula of the zeta function in the main concepts of quantum physics, this study offers a novel perspective and potential insights into the interplay between mathematical formulas and physical phenomena. It aims to contribute to the advancement of both mathematical and physical understanding in the realm of quantum physics.
2. Development of New Zeta Formula
In this section, the new zeta formula will be derived starting with the following theory:
Theorem 1.
For , the Dirichlet series form of zeta function,
can be expressed as
Proof.
The approach involves utilizing the integral representation of the combination of and , followed by extracting the function from the right-hand side of the integral and then canceling it from both sides. This leads to a new form of . We have the gamma function as:
By combining the gamma function with zeta, we get
or
Now, our next step is to extract the gamma function from the right-hand side of the integral, giving us
Next, by making the internal terms a Laplace transform, we get
By taking the integration with respect to x, we obtain
On setting , we obtain
since for , 2, 3,…
Hence
By removing gamma from both sides, we obtain
□
Corollary 1.
For , we have
Proof.
Since for [11] (Page 61). The first term in (15) in the right-hand-side can be expressed as
Therefore,
□
We claim that the function defined for . To test this hypothesis, we will use the function to derive some zeta function relations that are already defined in this strip region as will be provided in the next subsections. To do this, we will use the fact that the kernel function in Equation (18) can be written in the form
where is the Dirac comp starting from . Then, Equation (18) can be re-written as
2.1. First Test
Here, we want to derive the following equation (see Titchmarsh [2] ch2):
Proof.
By multiplying , the new form, with , we get
By setting , we obtain
□
2.2. Second Test
Here, we derive Hardy’s equation (Hardy derived this formula while attempting to prove the Riemann hypothesis and demonstrated that there are an infinite number of zeros for zeta on the vertical line (Edwards [1])).
Proof.
First, we need to define
By multiplying the new form of with , we get
For , one obtains
By using the equality
and by setting in the second term in the right-hand-side,
Since the integral
then
□
However, when applying the new formula to derive the zeta function equation for , an unexpected result was obtained. So, further development of the equation is required, as will be discussed in the next subsection.
2.3. The Integral-Pair Form of the Zeta Function
The zeta functional equation is
We want to multiply the new formula by to get and make sure it has the same structure.
Further, to restrict this study to only the strip region, we will define the first part as a Millen transform for , so
Then, we have
On setting , then
This is an unexpected result because it is supposed to be
Furthermore, the kernel function of the first integral on the right-hand-side resembles the zeta function, which raises questions about its nature. Therefore, we need to reconsider the main Function (18) from a different perspective. One way to study this summation is by considering the summation of as a geometric series [12]. So, it can be calculated as
Then, for , the first term,
The second integral
We notice that the first integral in the right-hand-side is defined only for , otherwise it will be zero. On the other hand, the second integral is defined for . So, and are defined as two different domains. If we define in the interval , where and {x} are the integral and fractional parts of x, respectively, the series could be expressed as two independent functions,
So, the zeta function can be re-written as
For the second integral in the right-hand-side, we have
By setting and using Equation (36), then
On setting in the first integral and in the second one, we obtain
The integrals in the right-hand-side can be solved by selecting an appropriate contour, and both would equal for , (see Appendix A); then,
This is the zeta functional equation and this part can be expressed as a Mellin transform of () for , and this term can be written as
or by setting , then
Then,
Therefore, the condition of in the integral can be achieved by making the integration first, then the summation. Conversely, if the summation is taken first, then the kernel should be expressed as . It seems that the convergence in the strip region is related to the term-wise function in zeta.
Now, back to the problem of the zeta functional equation in Equation (32). For simplicity, will be defined by two functions (discontinuous kernel) and (continuous kernel) for the kernels and , respectively, then
where
Thus,
Hence, for , we get
and for , we obtain
Hence
This is the anticipated outcome. The zeta function, represented in this way, will be referred to as the Zeta-cosine form, and its integrals will be called the Zeta integral-pair or the Zeta function-pair.
Some remarks can be summarized based on the previous results. First, the difference between this form of and the original one in Equation (18). Zeta in the Function (18) is defined for all , while in the Function (45), it separates the definition of zeta into two separate integrals corresponding to these two parts. In other words, the second integral in Equation (45) expresses the solution for , where all values of are excluded as poles. These poles are taken into account in the first integral in Equation (45) and expressed by the delta function. Second, both integrals provide a representation of on their own. Hence, the poles of the function contain the same information as the remaining parts of the function. In other words, the integral of can be evaluated for the values that correspond to the poles, as well as for the values where . Third, there is a relation between the zeta function-pair, where each of them is the Fourier transform of the other.
2.4. The Zeta Self-Operator
The zeta self-operator is defined as the operator, which converts to its conjugate and vice versa. The word “self” is used here because it is a part of the zeta functional equation (It can be also named the convert operator because it converts to and vice versa). It will be denoted by , and it can be expressed in two forms, denoted as and . Their equations are as follows:
They take the integral forms
The operator satisfies the following relation
Applying in (47), we have
The Self-Operator as a Unitary Operator
The self operators in general are related as
For , it will be a unitary operator, where
and
Hence,
In the case of unitary, we will denote it by .
3. Zeta Function in the Strip Region
In this section, we will start by proving that the zeta function in the strip region is only defined for .
Theorem 2.
For , we have
Which is only defined for .
Proof.
From equation here, we can write
However, can be derived by multiplying the operator by .
As a result of Equation (51), we have
So, n and m are equivalent and therefore there is a term-wise equality between both functions of Zeta. Then, we can write
or
For , we get
The left-hand-side will equal 1 for any value of s, whereas the right-hand-side is solved as and this term is equal 1 only for . □
The crucial observation here is that this proof relies on both functions of the zeta formula. The interdependence between these two functions restricts both integrals to be defined only for . This value is not obtained by solving the integrals or taking into account convergence conditions, but rather by requiring both sides of the equation to be equal. Therefore, the difficulty of this problem stems from attempting to solve it with only one of the integrals, highlighting the difference between the zeta function in this new form and all other forms.
Corollary 2.
For in the , the self-operator is always equal 1 regardless of the t value.
Proof.
As the zeta function has term-wise equality, then for the first term (), we have
Since the right-hand-side is equal to and the left-hand-side will be solved as regardless of the t value, this result should be the same for the right-hand-side. □
This result leads to the next important outcome.
Corollary 3.
For in the , prove that the zeta integral-pair are complex conjugate to each other, where
and vice versa.
Proof.
Since, in general, we have
As the integral-pair in in Equation (45) are equal,
For , we have , whatever the t value is. Then,
So, the corollary holds. □
This corollary also shows that the relation between the imaginary parts of s in both integrals is symmetrical. Additionally, the equality of both integrals in Equation (70) does not mean , should be identical or , which means . In addition, there is an interesting relation in the next corollary.
Corollary 4.
For , the Fourier transform of , for we have the equality
Proof.
Since
Both integrals in the right-hand-side should be equal and this requires a restricted condition where the Poisson summation formula is given as [13,14]:
where
So, the restricted condition is
Since both integrals in the right-hand-side are equal, and for , this equality is achieved only for as follows:
By setting in the right-hand-side integral, we get
Therefore, the only solution is . By calculating the integrals Equation (75) for , we have
By taking the largest power for both numerator and denominator in the region , then
The value of the limit cannot be ∞ or 0 because , therefore, there is only one solution, which is , or . Then, we have a term-wise equality.
The Relation between Zeta Function-Pair in x-Domain
Referring to the main Formula (45), the variable x in the kernel functions is expressed in two ways, namely and , for the first and second integrals, respectively, which represents the domains of the zeta function, in the x-domain, for its integrals. They are independent, as shown in Equation (37) but, despite this, each integral has a definite equivalent image in the other domain, which is illustrated by the relation Equation (69). In the next theory, we will use this relation to explore the connection between both domains and .
Theorem 3.
For , the kernel function in x-domain for
spans a complex isometric plane.
Proof.
Since we have
The idea of the proof would be proving that the right-hand-integral in this equality can be derived by setting in the left hand-integral.
Since is only defined for (Theorem 2) and for that value, we have , then the right-hand-integral in Equation (82) will be the same as the second integral in formula (same kernel function). Then, for Equation (82), we have
By setting in the first integral and in the second one, we get
Since
Hence,
Then, for we finally get
□
Therefore, we can conclude that the zeta function has two corresponding representations, which are equal. One is in real coordinates and the other is in complex coordinates. In addition, this also gives a clue about the independent nature of both and as domains for the zeta function-pair. They are conjugated to each other as the conjugation between the real and imaginary parts of a complex number.
Based on the new Zeta formula, we utilize it as a model to describe some properties of matter in quantum mechanics (QM) as will be presented in the following section. We used this model to investigate Planck’s law and the Heisenberg uncertainty principle in an abstract mathematical manner. By doing so, we gained insight into the behavior of matter and energy, including their mechanisms of motion and translation. This understanding may help us address outstanding questions in physics, including the nature of superposition and states, the phenomenon of entanglement, and the interpretation of the double-slit experiment and its results.
4. Quantum Mechanics Concepts in the New Zeta model
In this section, we will go over the fundamental principles of quantum mechanics and see how they are related to the new model.
4.1. Planck’s Law and the Concept of Wave-Particle Duality
Wave–particle duality is a concept in quantum mechanics according to which every particle or quantum entity may be described as either a particle or a wave [15]. This concept can be described clearly via the model by the kernel functions, where a particle (as delta function) associates with a wave, where we can write
Now, if the delta function is characterized as a localized energy shape E, this energy is quantized and transmitted by quantum number r by the unitary operator (self-operator) action (Equation (69)). So, we have , (h the Planck’s constant and its value gives the minimum amount of energy confined by the delta function (we assume ). This energy is transmitted as two plane waves in opposite directions .
Heisenberg’s Uncertainty Principle
The statement of Heisenberg’s uncertainty principle is as follows: If the x-component of the momentum of a particle is measured with an uncertainty , then its x-position cannot, at the same time, be measured more accurately than [16].
According to the model described in Equation (88), a particle can be represented by a localized energy in the delta function. In this case, the position of the particle can be determined accurately. However, its momentum (where k is the wave number; ), can be determined accurately by the wave form on the right-hand-side. The problem arises when we try to measure both the position and momentum of the particle. Essentially, we measured only one domain directly, while measuring the other domain is derived indirectly from the first. The concept is that the particle exists simultaneously in both particle and wave forms but, when observed and measured, it manifests on only one side, which is the localized part of the equation in the left-hand function space. In this case, the delta function is represented on the left-hand side integral. What we measure is the quantity that we have successfully localized from the wave space, allowing us to determine it in the left-hand space.
Mathematically, the measurement corresponds to determining the solution of the equation. It is important to note that the integral solution of the wave function within its domain is formally zero ( (see 10.5 Edwards [1]). This integral represents the wave function part (Equation (39))). This result may serve as a justification for the inability to directly measure or quantify this particular part.
In addition, the uncertainty principle in wave mechanics can be mathematically expressed as the uncertainty relation between position and momentum, which arises from the fact that the expressions of the wave function in the two corresponding orthonormal bases in Hilbert space are Fourier transforms of one another. This concept has been described in [17] and it is precisely what the model conveys mathematically.
4.2. The Concept of the Wave Function Collapse
Energy in this context possesses an intrinsic transitional nature. This is precisely what the equation describes, as it incorporates a self-transfer operator (the self operator ) that is an essential part of it. This operator characterizes the continuous transformation of energy, as it transitions from one form to another during transmission. The measurement process, on the other hand, involves the extraction of this energy, effectively halting its flow. This cessation of flow corresponds to the collapse of the wave function.
Superposition and States
In quantum mechanics, the concept of superposition and states is one of the most peculiar and often difficult to understand [16,18]. It marks the boundary between two schools of thought: classical determinism and probability. However, the model presented in this paper has the potential to bridge these two schools by providing a new perspective on these concepts. In this subsection, we will explore how the model accomplishes this.
To illustrate the probability idea, we need to go to the Zeta picture (20) and rewrite it as
The periodic function in the right-hand-side is constant for all periods and therefore does not require summation. However, after careful consideration, we assigned a probability adding to this term comparable to an algebraic adding to the terms in the corresponding integral. In other words, if we add as an algebraic term, which means (), we will get infinity. However, what we did is as it is a probability summation process. The reason is that the function, defined over the entire , is commonly understood as comprising distinct consecutive periods, which are not combined. However, in the other integral, we found that each period number (n) has a corresponding real term represented by . The count number (n) will be taken as a description of the state number and represents the energy level (i.e., energy state) of the particle.
Therefore, if we have, for instance, , this system will be described either as three particles that have different energies or one particle that has three states of energy, and we will read it as or or . When we measure, we will get one of them and the system collapses because they are connected as one function. This is the quantum mechanics point of view. Regarding the classical point of view, these values of energy are added algebraically to give one particle with 6 units of energy . So, in quantum mechanics, the sign means the probability (), in Classical mechanics, the sign means an algebraic sign.
Furthermore, we can read the function in another way: as represents a state n, also represents that state and the previous equation can be written as:
In this form, for any state n, the particle can take any wave with a frequency m by the probability distribution function . Then, the function can be written as:
Here, is not denoted as but it is denoted as any value of x, and we know . The kernel function in the second integral in this case will be considered as the probability distribution function (PDF) for the particle. In the case of translation, we get , so the particle will transmit only by the wave frequency that has the same value of its energy state, .
So, the wide picture is that, for every particle, we have a corresponding field Equation (90) (Dirac Quantum Field Theory perspective) [19]. This particle, when translating, will take one wave form (wave–particle duality).
4.3. The Entanglement Phenomenon
The entanglement phenomenon can be attributed to a novel term that we shall call the connection term. This term elucidates the relationship between the various forms of matter, i.e., its localized and non-localized forms, and can be derived from the original form of the zeta function. Referring to the Zeta-cosine function, we can state that the connection term is defined as follows:
[Noting that, for small x goes to , as same as, , which defines the delta function ]
Thus, we can write the zeta equation as
This term establishes the internal connection between the states within the function, which we define as entangled states. Furthermore, we believe that the system of particles that are influenced by each other is entangled and, mathematically speaking, belongs to the same s-domain. In the event of measurement (wave collapse) (Here, we consider that the measurement process happens by solving the integrals of the equation. Solving the integrals are equivalent to disappear (x) variable (the space variable). So, all the quantum phenomena will disappear and the function will only have the variable (n) and that gives a numerical result), this term will vanish.
According to what we measure, the action and its speed will be determined. Our interpretation is that the speed of light represents the boundary for the transition between localized and non-localized forms for each particle. By converting from the function shape to the shape by the unitary operator (self-operator) (Section 2.4), we believe that the maximum velocity for this transfer is the speed of light. Furthermore, all associated properties of this process will also be transmitted at this velocity, thus satisfying the locality principle in the classical sense. However, in the case of the collapsing measurement process, which is related to the entanglement of the particles, the speed of the action is directly proportional to the strength of the internal connection term (there no converting process). In the case of the Zeta-cosine function, where the connection term has infinite energy, the speed of the collapsing process is instantaneous, which explains the phenomenon.
Interpretation of Double Slits Experiment
The double slits act as a device that interacts with waves, causing a change in their path. This interaction leads to the emergence of two wave sources that are not independent, as one might initially assume, due to their interconnected field. The waves interfere with each other beyond the slits, reconstructing the original wave and ultimately manifesting as particles on the screen. While there are no destructive waves, there exist regions where the waves do not interfere with each other, resulting in blank areas. The presence of every particle on the screen provides evidence for the presence of only constructive points. The particles follow various paths determined by the incident angle when the wave encounters the slits and the probabilities associated with these paths contribute to the formation of the striped pattern.
When we observe or monitor a particle, it often results in field–field interaction. These interactions involve factors such as the self-operator (unitary operator), which influences the particle’s wave form and leads to its localization once again (see Equation (82)). Mathematically, the act of monitoring involves taking a Fourier transform of the particle’s wave, causing the waveform to immediately disappear and return to its localized shape, regardless of whether the detection occurs before or after passing through the slits.
5. Conclusions
The most challenging aspect of the zeta function lies in comprehending the transformation of a series expressed in integer numbers into a function with a continuous variable. This fundamental concept is clearly manifested in the new representation of the zeta function, presented in a simple form. It serves as a significant study that bridges the connected realm (function) and the separate realm (series), demonstrating how they can align and transform into one another.
In this context, the zeta function is described in two interrelated forms, and , interconnected through Operator S. These three components are unified and inseparable. The simplified form has been expressed by the trigonometric series function. This function is defined as two separate functions, each with its own domain: the Dirac delta function, which is defined for the integer part , and the remaining part of the series, which is defined for the fractional part . As a result, the function successfully distinguishes between the definitions within the integer part of the domain and those within the fractional part. The development of this fractional part has provided the function with a new representation, shedding light on some enigmatic properties previously associated with it.
The most significant outcome of this formula is that the zeta function, when applied to the domains of and , takes the form of a “function-pair” with a Fourier transform relation. When these two functions are set equally in the zeta function, we obtain the condition that restricts the zeta function to being defined only for , and that may prove the Riemann hypothesis. In addition, the zeta kernel function in x-domain spans a complex isometric plane.
Regarding the function as a model for the particle in quantum mechanics, the model highlights the inherent trade-off between accurately determining the position and momentum of a particle, as measurement collapses one function while the other becomes uncertain. This uncertainty principle can be interpreted due to the Fourier transform relationship between the wave function expressions in the position and momentum bases. The speed of light serves as the boundary between localized and non-localized forms of particles, with the conversion from to shapes occurring through the unitary operator. This maximum velocity for transformation satisfies the locality principle, but in the collapsing measurement process related to particle entanglement, the speed of action depends on the strength of the internal connection term and, in cases such as the Zeta-cosine function, where the connection term has infinite energy, the collapsing process happens instantaneously.
Author Contributions
Conceptualization, S.A.; methodology, S.A.; validation, S.A. and A.S.; formal analysis, S.A.; investigation, S.A. and A.S.; resources, S.A. and M.M.S.; writing—original draft preparation, S.A. and A.S.; writing—review and editing, S.A., A.S. and M.M.S.; funding acquisition, M.M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Calculation of Gamma Integral
We can show that the following integrals are equivalent
Proof.
We will prove that
The second integral can be proved by the same procedure and with similar contour.
By solving the complex integral
In the following contour [Figure A1]
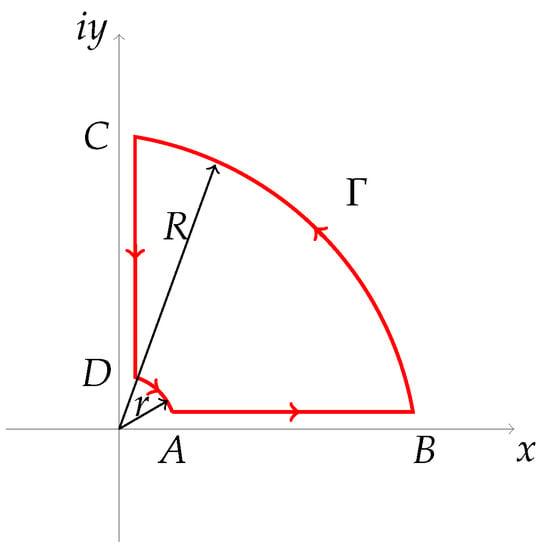 For and , then we have
The integral by and , according to the second integral, we have
We have in interval then
Hence
or
For and , then we have
The integral by and , according to the second integral, we have
We have in interval then
Hence
or

Figure A1.
A quarter circular contour of radii r and R.
□
References
- Edwards, H.M. Riemann’s Zeta Function; Dover Publications: Mineola, NY, USA, 2001. [Google Scholar]
- Titchmarsh, E.C.; Heath-Brown, D.R. The Theory of the Riemann Zeta-Function, 2nd ed.; Heath-Brown, D.R., Ed.; Oxford University Press: Oxford, UK, 1986. [Google Scholar]
- Kirsten, K. Basic zeta functions and some applications in physics. MSRI Publ. 2010, 57, 101–143. [Google Scholar] [CrossRef]
- Borwein, P.; Choi, S.; Rooney, B.; Weirathmueller, A. The Riemann Hypothesis; Springer: New York, NY, USA, 2006. [Google Scholar]
- Baluyot, S.A.C. On the zeros of Riemann’s zeta-function on the critical line. J. Number Theory 2016, 165, 203–269. [Google Scholar] [CrossRef]
- Levinson, N. More than one third of zeros of Riemann’s zeta-function are on ρ = . Adv. Math. 1974, 13, 383–436. [Google Scholar] [CrossRef]
- Conrey, J. More than two fifths of the zeros of the Riemann zeta function are on the critical line. J. Reine Angew. Math. 1989, 1989, 1–26. [Google Scholar] [CrossRef]
- Mehta, M.L. Random Matrices, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Odlyzko, A.M. On the distribution of spacings between zeros of the zeta function. Math. Comp. 1987, 48, 273–308. [Google Scholar] [CrossRef]
- Palese, L. Random Matrix Theory in molecular dynamics analysis. Biophys. Chem. 2014, 196, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Arakawa, T.; Ibukiyama, T.; Kaneko, M.; Zagier, D. Bernoulli Numbers and Zeta Functions; Springer Monographs in Mathematics; Springer: Tokyo, Japan, 2014. [Google Scholar]
- Zygmund, A.; Fefferman, R. Trigonometric Series, 3rd ed.; Cambridge Mathematical Library; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar] [CrossRef]
- Carslaw, H.S. Introduction to the Theory of Fourier’s Series and Integrals. Nature 1921, 126, 643. [Google Scholar]
- Guinand, A.P. On Poisson’s Summation Formula. Ann. Math. 1941, 42, 591–603. [Google Scholar] [CrossRef]
- Einstein, A.; Infeld, L. The Evolution of Physics. The Growth of Ideas from Early Concepts to Relativity and Quanta; Cambridge University Press: Cambridge, UK, 1938; Volume 4. [Google Scholar]
- Zettili, N. Quantum Mechanics: Concept and Application; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Jaeger, G. What in the (quantum) world is macroscopic? Am. J. Phys. 2014, 82, 896–905. [Google Scholar] [CrossRef]
- Griffiths, D.J.; Schroeter, D.F. Introduction to Quantum Mechanics, 3rd ed.; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar] [CrossRef]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; Westview Press: Boulder, CO, USA; Addison-Wesley: Reading, PA, USA, 1995; 842p. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).