On Characterization of Balance and Consistency Preserving d-Antipodal Signed Graphs

Abstract

A signed graph is an ordered pair $\Sigma =(G,\sigma )$, where G is a graph and $\sigma :E\left(G\right)⟶\{+1,-1\}$ is a mapping. For $e\in E\left(G\right)$, $\sigma \left(e\right)$ is called the sign of e and for any sub-graph H of G, $\sigma \left(H\right)={\displaystyle \prod _{e\in E\left(H\right)}}\sigma \left(e\right)$ is called the sign of H. A signed graph having a sign of each cycle $+1$ is called balanced. Two vertices in a graph G are called antipodal if $d_G(u,v)=diam\left(G\right)$. The antipodal graph $A\left(G\right)$ of a graph G is the graph with a vertex set that is the same as that of G, and two vertices $u,v$ in $A\left(G\right)$ are adjacent if $u,v$ are antipodal. By the d-antipodal graph $G_d^A$ of a graph G, we refer to the union of G and $A\left(G\right)$. Given a signed graph $\Sigma =(G,\sigma )$, the signed graph ${\Sigma }_d^A=(G_d^A,{\sigma }_d)$ is called the d-antipodal signed graph of G, where ${\sigma }_d$ is defined as follows: ${\sigma }_d\left(e\right)=\sigma \left(e\right)\mathrm{if}e\in E\left(G\right)\mathrm{and}\mathrm{otherwise},{\sigma }_d\left(e\right)={\displaystyle \prod _{P\in {\mathcal{P}}_e}}\sigma \left(P\right)$, where ${\mathcal{P}}_e$ is the collection of all diametric paths in $\Sigma$ connecting the end vertices of an antipodal edge e in ${\Sigma }_d^A$. In this article, the balance property and canonical consistency of d-antipodal signed graphs of Smith signed graphs (connected graphs having a highest eigenvalue of 2) are studied.

1. Introduction

The book [1] by Harary may be referred for basic terminologies in graph theory. A graph G is an ordered pair $(V,E)$, where V is a non-empty set whose elements are called vertices and E is a collection of unordered pair of distinct vertices whose elements are called edges of the graph G. We use $V\left(G\right)$ and $E\left(G\right)$ to denote the vertex set and the edge set of the graph G. By a signature on a graph G, we mean a function $\sigma :E\left(G\right)\to \{+1,-1\}$. A graph G together with a signature $\sigma$ is called a signed graph and will be denoted by $\Sigma =(G,\sigma )$. The graph G is referred as the underlying graph of the signed graph $\Sigma =(G,\sigma )$. The signed graph with all positive (negative) edges having the underlying graph G is denoted by $G^{+}\left(G^{-}\right)$. By the vertex set of $\Sigma$, we refer to the vertex set of the underlying graph G. For any edge $e\in E\left(G\right)$, $\sigma \left(e\right)$ is referred to as the sign of the edge e in $\Sigma$.

By the sign of a sub-graph H of a signed graph $\Sigma =(G,\sigma )$, we mean the product of the sign of the edges in H, and it is denoted by $\sigma \left(H\right)$. The concept of a signed graph was first introduced by Harary in [2] to model social problems. A signed graph is said to be balanced if every cycle in it has the sign $+1$. In [2], Harary characterized balanced signed graphs as the signed graph whose vertex set can be partitioned into $V_1,V_2$ such that any negative edge connects a vertex from $V_1$ to a vertex in $V_2$ and a positive edge connects a pair of vertices either from $V_1$ or from $V_2$. We refer to such a partition of a balanced signed graph as Harary’s partition.

The term “antipodal” was first coined by R. Singleton [3] to refer to a pair of vertices, the distance between which is equal to the diameter of the graph. By antipodes of a vertex in a graph, we refer to the vertices that are antipodal to it. Given a graph $G(V,E)$, by its antipodal graph $A\left(G\right)$, we refer to the graph with vertex set $V\left(A\right(G\left)\right)=V\left(G\right)$ such that for $u,v\in V\left(A\right(G\left)\right),\{u,v\}\in E\left(A\right(G\left)\right)$ if u and v are antipodes in G. The concept of an antipode was first used to establish regularity in Moore graphs, i.e., finite undirected graphs which are regular, connected with diameter $k\ge 1$ and girth $2k+1$. D H Smith [4] had used a version of antipodal graphs while studying distance transitive graphs to characterize primitive and imprimitive graphs. R Aravamudhan [5] studied the behavior of antipodal graphs with regard to completeness, connectedness, etc., and they derived necessary and sufficient conditions for a graph to be an antipodal graph of a graph in terms of its compliment. Acharya and Acharya [6] have studied self antipodal graphs and given important characterizations. Further works can be found in [7]. S-antipodal graphs have been introduced by Nair and Vijaykumar [8] as an induced sub-graph of antipodal graphs whose vertex set comprises those vertices having maximum eccentricity in which two vertices are joined by an edge if they are at a diametrical distance. P S K Reddy et al. [9] introduced Smarandachely antipodal signed digraphs and obtained some structural characterizations. In [10], Reddy and Prashanth have introduced the S-antipodal signed graph $A^{\ast }(\Sigma )$ of a signed graph $\Sigma =(G,\sigma )$ inspired by the complement of a graph in which the sign of an edge $uv$ is the product of canonical marking of u and v and reported several characterizations of the balanced S-antipodal signed graph of a signed graph.

In this article, the concept of a d-antipodal graph of a graph has been introduced. This has been inspired by real-life situations where we want to study the changes brought in the network by introducing antipodal edges while retaining the original edges of the network. Such a graph has many real-life applications in networking, defense, diplomatic relationships, etc. For example, consider a graph representing the diplomatic relationship among various countries. It might be interesting to investigate how the network will behave if diplomatic relationship develops between its antipodes.

2. Preliminaries

Given a graph G, its antipodal graph, $A\left(G\right)$, is a graph that has a vertex set that is the same as that of G, and two vertices in $A\left(G\right)$ are adjacent if they are at a distance of $diam\left(G\right)$ in G. By the d-antipodal graph $G_d^A$ of a graph G, we refer to the union of the graphs G and $A\left(G\right)$.

Remark 1. 

The following are true for d-antipodal graphs:

• The d-antipodal graph of an even cycle is 3-regular because each vertex in an even cycle has exactly one antipodal vertex.
• The d-antipodal graph of an odd cycle is 4-regular because each vertex in an even cycle has exactly two antipodal vertices.
• The d-antipodal graph of $K_{1,n}$ for $n\ge 2$ is n-regular because every pair of pendant vertices in $K_{1,n}$ consists of antipodes.
• $C_n$ and $K_{1,4}$ are the only Smith graphs whose d-antipodal graphs are regular.

Given a signed graph $\Sigma =(G,\sigma )$, the d-antipodal signed graph of $\Sigma$, denoted by ${\Sigma }_d^A$, is the signed graph $(G_d^A,{\sigma }_d)$ with sign function ${\sigma }_d$ defined as follows:

$${\sigma }_d\left(e\right)=\left\{\begin{array}{cc}\sigma \left(e\right),\hfill & \mathrm{if}e\in E\left(G\right)\hfill \\ {\displaystyle \prod _{P\in {\mathcal{P}}_e}}\sigma \left(P\right),\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

and ${\mathcal{P}}_e$ is the collection of all diametric paths in $\Sigma$ connecting the end vertices of an antipodal edge e in ${\Sigma }_d^A$.

Remark 2. 

Restriction of ${\sigma }_d$ to $\Sigma =(G,\sigma )$ is σ.

A marking on a graph G is a function $\mu :V\left(G\right)\to \{+1,-1\}$. A graph G provided with a marking $\mu$ is called a marked graph. A signed graph $\Sigma =(G,\sigma )$ provided with a marking $\mu$ is called a marked signed graph, and it is denoted by ${\Sigma }_{\mu }.$

Let $\mu$ be a marking on a graph G. By the mark of a sub-graph H of G, we mean the product of the marks of the vertices in H, and it is denoted by $\mu \left(H\right)$. The concept of a marked graph was first introduced by Harary and Cartwright in [11] to model a social problem. A marked graph is said to be consistent if every cycle in it has the mark $+1$. The following theorem characterizes marked graphs.

Theorem 1 

([12]). Any marked graph with a mark of each vertex $+1$ is consistent.

Proof. 

Let $\Sigma$ be a marked graph with a mark of each vertex $+1$. Since in any cycle of $\Sigma$, each vertex will have a mark $+1$, it will be consistent. Hence, $\Sigma$ is consistent. □

Theorem 2 

([12]). Any marked graph with a mark of each vertex $-1$ is consistent if and only if its underlying graph is bipartite.

Proof. 

Let $\Sigma$ be a marked graph with a mark of each vertex $-1$. Then, each cycle in $\Sigma$ will be consistent if and only if it has an even number of vertices. Since a graph is bipartite if and only if each of its cycles is even, so the result follows. □

The following corollary is immediate from Theorem 2.

Corollary 1. 

If a marked graph is consistent, then the sub-graph induced by its vertices with a mark $-1$ is bipartite.

Furthermore, in [13], it was noted that a marked graph is consistent if and only if for any spanning tree T of it, all its fundamental cycles are positive and all common paths shared by a pair of fundamental cycles have end points with the same marking. For more literature on consistency, we refer to [13,14,15,16,17,18].

Given a signed graph $\sum =(G,\sigma )$, we can associate a natural marking

$$\mu :V(\Sigma )\to \{-1,+1\}$$

as follows: For any vertex $v\in V(\Sigma )$

$$\mu \left(v\right)=\left\{\begin{array}{cc}+1,\hfill & \mathrm{if}v\mathrm{is}\mathrm{isolated};\hfill \\ {\displaystyle \prod _{u\in N\left(v\right)}}\sigma \left(uv\right),\hfill & \mathrm{otherwise};\hfill \end{array}\right.$$

where $N\left(v\right)$ is the set of all vertices adjacent to v in $\Sigma$. This marking $\mu$ is known as the canonical marking of the signed graph $\Sigma$, and we use ${\Sigma }_{\mu }$ to denote the corresponding marked signed graph. A signed graph $\Sigma$ is said to be canonically consistent if it is consistent with respect to the canonical marking.

Remark 3. 

All signed cycles are canonically consistent.

Unless otherwise stated, for a given signed graph $\Sigma$, we use $\mu$ to represent the canonical marking on $\Sigma$ and ${\mu }_d$ to represent the canonical marking on ${\Sigma }_d^A.$

Throughout this article, edges of the underlying graph are represented by bold lines, antipodal edges are represented by dotted lines and paths are represented by dashed lines. A blue color used to represent edges with the $+1$ sign, and a red color is used to represent edges with the $-1$ sign of a signed graph.

3. d-Antipodal Signed Graphs

In the theory of graph spectra, an important role is played by graphs with the largest eigenvalue of 2. In the literature, these graphs are known as Smith graphs [19]. There are six different classes of Smith graphs, as shown in Figure 1.

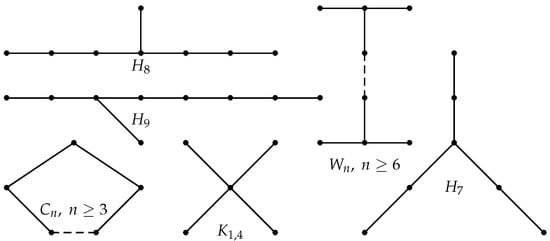
Figure 1. All classes of Smith graphs.

Remark 4. 

A Smith signed graph is balanced and consistent if and only if either it is acyclic or it has an even number of negative edges.

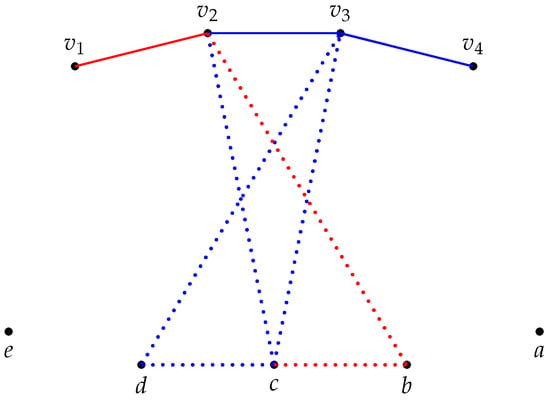
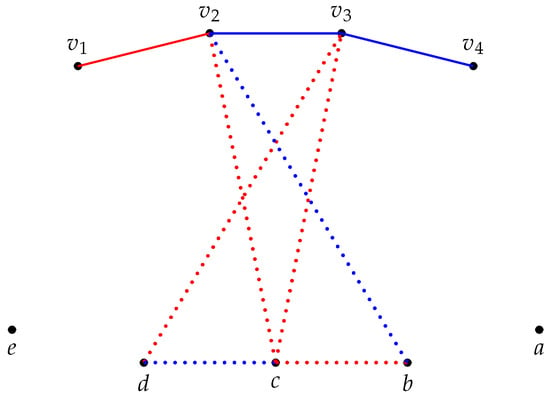
The Smith signed graph $(C_n^{+},\sigma )$ is balanced and consistent, and so is its d-antipodal ${\Sigma }_d^A$. The Smith signed graph $\Sigma$ shown in Figure 2 is balanced and consistent, but its d-antipodal ${\Sigma }_d^A$ is neither balanced nor consistent. In this article, the balanced and consistent Smith signed graphs are characterized that have balanced and consistent d-antipodal values.

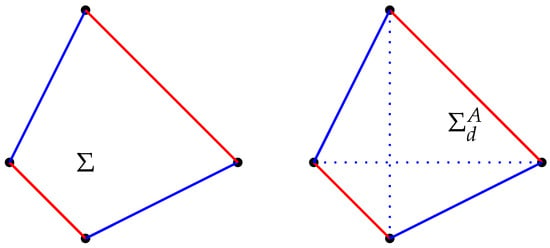
Figure 2. A Smith signed graph $\Sigma$ and its d-antipodal ${\Sigma }_d^A$.

Theorem 3. 

Let $\Sigma =(G,\sigma )$ be a balanced signed graph and $V_1,V_2$ be Harary’s partition of its vertex set. Then, ${\Sigma }_d^A$ is balanced if and only if for each pair of antipodes $u\in V_1$, $v\in V_2$, the number of distinct diametric paths in Σ joining $u,v$ with a sign of $-1$ is odd.

Proof. 

Suppose ${\Sigma }_d^A$ is balanced. Let $u,v\in V$ be two antipodes. On the contrary, let us assume that there is even number of distinct negative $u-v$ diametric paths $P_1,P_2,\dots ,P_n$ in $\Sigma$. Let a be the antipodal edge joining u and v in ${\Sigma }_d^A$. Clearly, ${\sigma }_d\left(a\right)=+1$ is the product of the signs of an even number of diametric paths with a sign of $-1$. Consider a cycle $P_{i}a,1\le i\le n$, then ${\sigma }_d\left(P_{i}a\right)=-1.$ This contradicts that ${\Sigma }_d^A$ is balanced. Hence, the number of distinct negative paths must be odd.

Conversely, suppose that for each pair of antipodes $u\in V_1$, $v\in V_2$, the number of distinct $u-v$ diametric paths in $\Sigma$ with a sign of $-1$ is odd. We want to show that ${\Sigma }_d^A$ is balanced. We complete the proof by showing that $V_1$ and $V_2$ is Harary’s partition for ${\Sigma }_d^A$.

Let $e=\{u,v\}$ be any edge in ${\Sigma }_d^A$. If $e\in E(\Sigma )$, then there is nothing to prove. So, let e be an antipodal edge.

Case 1: ${\sigma }_d\left(e\right)=-1$. In this case, there is a $u-v$ diametric path in $\Sigma$ with a negative sign and hence with an odd number of negative edges. Since each negative edge in $\Sigma$ connects a vertex from $V_1$ to a vertex from $V_2$, so $u,v$ cannot be from the same set of the partition $V_1,V_2$.

Case 2: ${\sigma }_d\left(e\right)=+1$. In this case, either all the diametric $u-v$ paths in $\Sigma$ has a sign of $+1$ or the number of distinct $u-v$ diametric paths in $\Sigma$ with a sign of $-1$ is even. The existence of $u-v$ diametric paths in $\Sigma$ with a sign of $-1$ demands that $u,v$ should be from different parts of the partition. So, by assumption, the second possibility is ruled out. Hence, either $u,v\in V_1$ or $u,v\in V_2$.

Thus every edge in ${\Sigma }_d^A$ with sign $+1$ connects two vertices from the same part of the partition $V_1,V_2$ and every edge in ${\Sigma }_d^A$ with sign $-1$ connects a vertex from $V_1$ to a vertex in $V_2$. Therefore, $V_1,V_2$ is a Harary’s partition of the vertex set of ${\Sigma }_d^A$ and so it is balanced. □

Remark 5. 

For any tree T, its antipodal edges are the chords of $T_d^A$ with respect to the spanning tree T.

Remark 6. 

For any tree T, the fundamental cycles of $T_d^A$ with respect to the spanning tree T are balanced.

4. Smith Signed Graphs

Let $\Sigma =(C_n,\sigma )$. The d-antipodal graph of a cycle does not have any new edge for $n=3$. However, $diam\left(C_n\right)=\lfloor n/2\rfloor$, where $\lfloor n/2\rfloor$ stands for the greatest integer less than or equal to $n/2$. However

$$|E\left({\Sigma }_d^A\right)|=\left\{\begin{array}{cc}3n/2,\hfill & \mathrm{if}n\mathrm{is}\mathrm{even}\hfill \\ 2n,\hfill & \mathrm{if}n\mathrm{is}\mathrm{odd}.\hfill \end{array}\right.$$

An immediate question is whether the d-antipodal signed graph of a balanced cycle is balanced or not? Here, we have characterized the d-antipodal signed graph of cycles and obtained some results on balancedness, consistency and regularity.

Proposition 1. 

Let $\Sigma =C_{2n}^{-}$. Then, ${\Sigma }_d^A$ is balanced if and only if $2|n$.

Proof. 

Let the vertices of $\Sigma$ be labeled by $v_1,v_2,\dots ,v_{2n}$ in cyclic order. Then, $V_1=\left\{v_i\right|i=1,3,\cdots ,2n-1\}$ and $V_2=\left\{v_i\right|i=2,4,\cdots ,2n\}$ gives a partition of $V(\Sigma )$ in which each edge of G connects a vertex from $V_1$ to a vertex from $V_2$. Since $\Sigma$ is balanced, this partition also serves as Harary’s partition of the balanced graph $\Sigma$. We note that if e is an antipodal edge in ${\Sigma }_d^A$, then ${\sigma }_d\left(e\right)=+1$.

First, assume that ${\Sigma }_d^A$ is balanced. Then, the cycle $v_1{v}_2\cdots v_{n+1}{v}_1$ in ${\Sigma }_d^A$ must be balanced. As this cycle contains n negative edges, so n must be even.

Conversely, suppose that n is even. Then, each antipodal edge in ${\Sigma }_d^A$ is positive and both the end vertices of such an edge is either from $V_1$ or from $V_2$. So, $V_1,V_2$ forms a partition of $V\left({\Sigma }_d^A\right)$ such that each negative edge connects a vertex from $V_1$ to a vertex from $V_2$ and positive edges connect vertices within the same set. Hence, ${\Sigma }_d^A$ is balanced. □

Proposition 2. 

Let $\Sigma =(C_{2n},\sigma )$ be a balanced cycle with Harary’s partition $V_1,V_2$ of $V(\Sigma )$. Then, ${\Sigma }_d^A$ is balanced if and only if $v_i\mathrm{and}{v}_{i+n}$ are in the same partition for each $1\le i\le n$.

Proof. 

First, suppose ${\Sigma }_d^A$ is balanced and let $V_1,V_2$ be Harary’s partition of $V\left({\Sigma }_d^A\right)$. Then, each cycle in ${\Sigma }_d^A$ is balanced and hence $\Sigma$ is also balanced. Furthermore, since $E(\Sigma )\subset E\left({\Sigma }_d^A\right)$, so $V_1,V_2$ is also Harary’s partition of $V(\Sigma )$. Since $\Sigma$ has an even number of negative edges, so each antipodal edge in ${\Sigma }_d^A$ must have a sign of $+1$. As for each $i=1,2,\cdots ,n$, the vertices $v_i$, $v_{i+n}$ are antipodes, so both must be either in $V_1$ or in $V_2$.

Conversely, since $\Sigma$ is balanced, so it has even number of negative edges. Hence each antipodal edges in ${\Sigma }_d^A$ must have sign $+1$. Since the antipodal vertices of $\Sigma$ are $v_i$, $v_{i+n}$ for each $i=1,2,\cdots ,n$, so $V_1,V_2$ also forms Harary’s partition of $V\left({\Sigma }_d^A\right)$. So, ${\Sigma }_d^A$ is balanced. □

We have the following characterization for odd cycles.

Proposition 3. 

Let $\Sigma =(C_{2n+1},\sigma )$; then, ${\Sigma }_d^A$ is balanced if and only if Σ is balanced.

Proof. 

First, suppose that $\Sigma$ is balanced with Harary’s partition of $V(\Sigma )$ as $V_1$, $V_2$. In $\Sigma$, each diametric path has a length of n and there is exactly one diametric path between each pair of antipodes. Let us label the vertices of $\Sigma$ using $v_1,v_2,\cdots ,v_{2n+1}$ in cyclic order.

Each vertex $v_i\in V,1\le i\le n$ has two antipodes $v_{i+n},v_{i+n+1}$. Without a loss of generality, suppose that $v_i\in V_1$ and let $e=\{v_i,v_{i+n}\},e^{\prime }=\{v_i,v_{i+n+1}\}$ be the two associated antipodal edges.

Case 1: Suppose, ${\sigma }_d\left(e\right)=+1$. Then, the number of negative edges in the diametric path joining the vertices $v_i$ and $v_{i+n}$ in $\Sigma$ must be even. Since each negative edge in $\Sigma$ joins a vertex from $V_1$ to a vertex from $V_2$, so both the end vertices of e must be in the same part, i.e., $v_{i+n}\in V_1$.

Case 2: Suppose, ${\sigma }_d\left(e\right)=-1$. Then, the number of negative edges in the diametric path joining the vertices $v_i$ and $v_{i+n}$ in $\Sigma$ must be odd. Since each negative edge in $\Sigma$ joins a vertex from $V_1$ to a vertex from $V_2$, so the two end vertices of e must be from different parts, i.e., $v_{i+n}\in V_2$.

A similar argument holds for the end vertices of the antipodal edge $e^{\prime }$.

Thus, each antipodal edge with a sign of $+1$ connects vertices from the same part and an antipodal edge with a sign of $-1$ connects a vertex from $V_1$ to a vertex from $V_2$. Hence, $V_1$ and $V_2$ gives a partition of $V\left({\Sigma }_d^A\right)$ such that each negative edge of ${\Sigma }_d^A$ connects vertices from different sets and each positive edge connects vertices from the same set. That is, $V_1,V_2$ serves as Harary’s partition of the vertices in ${\Sigma }_d^A$. Hence, ${\Sigma }_d^A$ is balanced. □

Remark 7. 

If the sign of each edge in a signed graph Σ is $+1$, then Σ and ${\Sigma }_d^A$ both are canonically consistent.

However, $(\Sigma ,\mu )$ being canonically consistent need not imply that its d-antipodal marked graph is canonically consistent. For example, the graph in Figure 2 is canonically consistent but its d-antipodal is not canonically consistent. Hence, the conditions under which the canonical consistency of signed graphs is invariant under the d-antipodal operation of canonically consistent signed graphs is essential. The following results give some characterization for signed cycles.

Proposition 4. 

If $\Sigma =(C_n^{-},\sigma )$, then ${\Sigma }_d^A$ is canonically consistent for any $n\in \mathbb{N}$.

Proof. 

We observe that $\mu \left(v_i\right)=+1,v_i\in V(\Sigma )$ for each i.

Case 1: n is even. Suppose $n=2l$ for some $l\in N$. Then, ${\sigma }_d\left(a_{il}\right)=+1$; hence, ${\mu }_d\left(v_i\right)=+1$ remains positive in $({\Sigma }_d^A,{\mu }_d)$. Thus, it is canonically consistent.

Case 2: n is odd. In this case, each antipodal edge in ${\Sigma }_d^A$ will have the same sign. Since each vertex is incident with exactly two antipodal edges, so each vertex in ${\Sigma }_d^A$ has a canonical marking of $+1$. Hence, the result follows.

□

Corollary 2. 

Let $\Sigma =C_{2n}^{-}$. Then, ${\Sigma }_d^A$ is balanced and canonically consistent if and only if $2|n$.

Lemma 1. 

Let $\Sigma =(C_{2n},\sigma )$. If there exist antipodes $u,v\in V(\Sigma )$ such that $\mu \left(u\right)\mu \left(v\right)=-1$, then ${\Sigma }_d^A$ is not canonically consistent.

Proof. 

Let $\Sigma =(C_{2n},\sigma )$ have antipodes $u,v\in V(\Sigma )$ with $\mu \left(u\right)\mu \left(v\right)=-1$. Since in ${\Sigma }_d^A$, $\{u,v\}$ is the only edge that is incident with u or v apart from the edges that were present in $\Sigma$, so the marks of u and v remain opposite in ${\Sigma }_d^A$. At most, their marks may become interchanged depending on whether $\Sigma$ is balanced or not. Therefore, ${\mu }_d\left(u\right){\mu }_d\left(v\right)=-1$. Let $P_{uv}$ and $P_{uv}^{\prime }$ be the two diametric paths in $\Sigma$ joining u to v.

If possible, suppose that ${\Sigma }_d^A$ is canonically consistent. Let $C_1,C_2$ be the cycles in ${\Sigma }_d^A$ consisting of the edge $\{u,v\}$ and the paths $P_{uv}$, $P_{uv}^{\prime }$, respectively. Then, by the consistency of ${\Sigma }_d^A$, each of the cycles $C_1,C_2$ has an even number of vertices with a mark of $-1$. However, these two cycles have exactly one vertex with the mark of $-1$ in common, namely u or v. So, the cycle $\Sigma$ in ${\Sigma }_d^A$ which the symmetric difference of $C_1$ and $C_2$ has an odd number of vertices with a mark of $-1$. This contradicts our assumption that ${\Sigma }_d^A$ is consistent. Hence, the result follows. □

Proposition 5. 

Let $\Sigma =(C_{2n},\sigma )$ be balanced. Then, ${\Sigma }_d^A$ is canonically consistent if and only if $\Sigma =C_{2n}^{-}$ or $\Sigma =C_{2n}^{+}$.

Proof. 

First, assume that $\Sigma =C_{2n}^{-}$ or $\Sigma =C_{2n}^{+}$. In each case, the number of negative edges in $\Sigma$ is even. Since the two diametric paths connecting a pair of antipodes contain each edge of $\Sigma$ exactly once, so the sign of an antipodal edge in ${\Sigma }_d^A$ is $+1$. Hence,

$${\mu }_d\left(v\right)=\mu \left(v\right)=+1\mathrm{for}\mathrm{all}v\in V\left({\Sigma }_d^A\right).$$

So, ${\Sigma }_d^A$ is canonically consistent.

Conversely, suppose that $\Sigma$ has edges with a sign of $+1$ as well as with a sign of $-1$. Since $\Sigma$ is balanced, so the total number of negative edges in both the diametric paths connecting a pair of antipodes is even. Hence, the sign of each antipodal edge in ${\Sigma }_d^A$ is positive. If we have antipodes $u,v\in V(\Sigma )$ such that $\mu \left(u\right)\mu \left(v\right)=-1$, then by Lemma 1, ${\Sigma }_d^A$ is not canonically consistent.

So, let for each pair of antipodes $u,v\in V(\Sigma )$, $\mu \left(u\right)=\mu \left(v\right)$. Then, $\Sigma$ must have a pair of antipodes with negative marking.

If for all $u\in V(\Sigma )$, $\mu \left(u\right)=-1$, then the signs of the edges of $\Sigma$ are alternately $+1$ or $-1$. Since $\Sigma$ is balanced and half of the edges in it are negative, so n must be even. Thus, both the cycles in ${\Sigma }_d^A$ that are generated by an antipodal edge consist of an odd number of vertices each with mark $-1$ and so, ${\Sigma }_d^A$ is not canonically consistent.

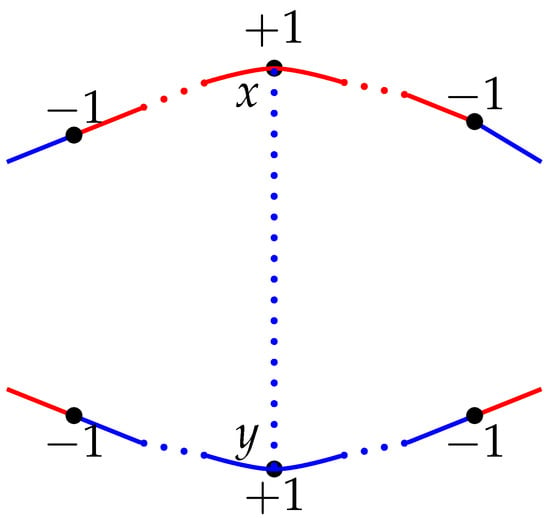
Otherwise, let $x,y\in V(\Sigma )$ be antipodes such that $\mu \left(x\right)=\mu \left(y\right)=+1$. Then, both the edges incident with x are of the same sign and those with y are of same sign. We consider the following cases:

Case 1. The edges incident with x and those incident with y are opposite in sign, as shown in Figure 3. In this case, each of the cycles in ${\Sigma }_d^A$ generated by the antipodal edge $\{x,y\}$ contains an odd number of vertices with a mark of $-1$, and so, both are not consistent. Hence, ${\Sigma }_d^A$ is not canonically consistent.

Figure 3. Mark distribution after introducing antipodal edge $\{x,y\}$ in $\Sigma$.

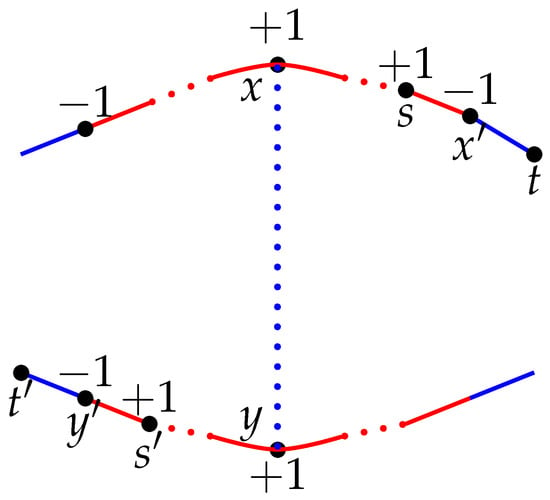
Case 2. The edges incident with x and those incident with y are of the same sign. As we move along the cycle clockwise, starting from x, let $x^{\prime }$ be the first vertex with $\mu \left(x^{\prime }\right)=-1$. The existence of $x^{\prime }$ is guaranteed, because it has at least two edges with different signs. Furthermore, we must obtain such a vertex before reaching y, because antipodes have the same sign. Notice that the signs of all the edges in the x–$x^{\prime }$ path in $\Sigma$ not containing y are the same.

Let $s,t$ be the vertices adjacent to $x^{\prime }$ in $\Sigma$, as shown in Figure 4. Let $s^{\prime },y^{\prime },t^{\prime }$ be the antipodes of $s,x^{\prime },t$ in $\Sigma$, respectively. Since antipodal vertices have the same marking, the signs of all the edges in the $y-y^{\prime }$ path in $\Sigma$ not containing x are the same sign as that of the edges incident with x. So, the pair of edges $\{s,x^{\prime }\},\left\{s^{\prime }{y}^{\prime }\right\}$ has the same sign and the pair of edges $\{x^{\prime },t\},\{y^{\prime },t^{\prime }\}$ has the same sign. Since $\mu \left(x^{\prime }\right)=\mu \left(y^{\prime }\right)=-1$, each of the cycles generated by introducing the antipodal edge $\{x^{\prime },y^{\prime }\}$ in $\Sigma$ will have an odd number of vertices with a mark of $-1$ in ${\Sigma }_d^A$, and hence, these cycles are not consistent in ${\Sigma }_d^A$. So, ${\Sigma }_d^A$ is not canonically consistent. Hence, the proof is complete. □

Figure 4. Mark distribution after introducing antipodal edge $\{x,y\}$ in $\Sigma$.

Corollary 3. 

Let $\Sigma =(C_{2n},\sigma )$ be balanced. Then, ${\Sigma }_d^A$ is balanced and canonically consistent if and only if either of the following holds:

1. 

$\Sigma =C_{2n}^{-}$ and n is even.

2. 

$\Sigma =C_{2n}^{+}$.

Theorem 4. 

Let $\Sigma =(C_{2n+1},\sigma )$ and $n>1$. Then, ${\Sigma }_d^A$ is canonically consistent if and only if ${\mu }_d\left(u\right)=+1$ for every vertex u in ${\Sigma }_d^A$.

Proof. 

Let $\Sigma =(C_{2n+1},\sigma )$. If ${\mu }_d\left(u\right)=+1$ for every vertex u in ${\Sigma }_d^A$, then obviously ${\Sigma }_d^A$ is consistent.

Conversely, let ${\Sigma }_d^A$ have a vertex u with ${\mu }_d\left(u\right)=-1$. We need to show that ${\Sigma }_d^A$ is not consistent. We shall prove this by the method of contradiction. If possible, suppose that ${\Sigma }_d^A$ is consistent. Let $v,w$ be the antipodes of u. Let x be the vertex adjacent to v other than w and let y be the vertex adjacent to w other than v in $\Sigma$.

Let $C_1$ be the cycle in ${\Sigma }_d^A$ consisting of the antipodal edge $\{u,v\}$ and let $u-v$ be the sub-path of $\Sigma$ containing x. Let $C_2$ be the cycle in ${\Sigma }_d^A$ consisting of the antipodal edge $\{u,w\}$ and let $u-w$ be the sub-path of $\Sigma$ containing y. Let $C_3$ be the triangle $uvwu$. As ${\Sigma }_d^A$ is consistent, each $C_1,C_2,C_3$ and $\Sigma$ are consistent. Now, $C_3$ is consistent, which implies ${\mu }_d\left(v\right){\mu }_d\left(w\right)=-1.$ Without a loss of generality, let ${\mu }_d\left(v\right)=-1$. Then, ${\mu }_d\left(w\right)=+1$ and the $u-v$ sub-path in $\Sigma$ containing x should have an even number of vertices with a mark of $-1$ in ${\Sigma }_d^A$. In addition, the $u-w$ sub-path in $\Sigma$ containing y should have an even number of vertices with a mark of $-1$ in ${\Sigma }_d^A$. Therefore, the number of vertices in ${\Sigma }_d^A$ with a mark of $-1$ is odd and hence ${\mu }_d(\Sigma )=-1$, which is a contradiction. Hence, ${\Sigma }_d^A$ cannot be consistent. □

Proposition 6. 

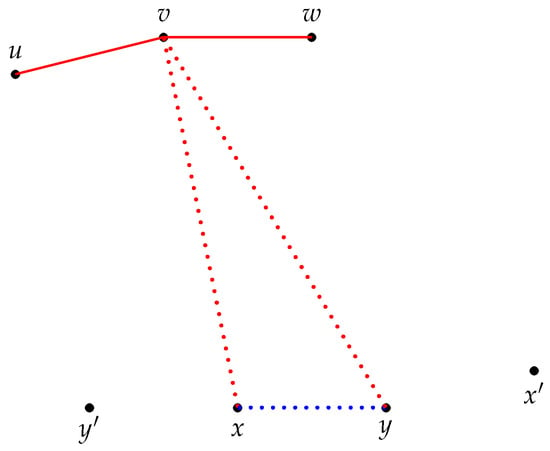
Let $\Sigma =(C_{2n+1},\sigma )$ be balanced and $n>1$. If Σ has three consecutive edges with signs in the order $\left(i\right)-1,+1,+1$ or $\left(ii\right)+1,-1,+1$ or $\left(iii\right)-1,-1,-1$, then ${\Sigma }_d^A$ is not consistent.

Proof. 

Consider four vertices $v_1,v_2,v_3,v_4$ in $\Sigma$ such that

$$\{v_1,v_2\},\{v_2,v_3\},\{v_3,v_4\}\in E(\Sigma ).$$

Let the antipodes of $v_1,v_2,v_3,v_4$ be $a,b;b,c;c,d;d,e$, respectively.

$\left(i\right)$ Let $\sigma \left(\{v_1,v_2\}\right)=-1,\sigma \left(\{v_2,v_3\}\right)=+1,\sigma \left(\{v_3,v_4\}\right)=+1.$ Then, by Theorem 4

$${\mu }_d\left(v\right)=+1,\forall v\in V\left({\Sigma }_d^A\right)$$

and so ${\sigma }_d\left(\{v_3,c\}\right)={\sigma }_d\left(\{v_3,d\}\right).$ If possible, let ${\Sigma }_d^A$ be consistent.

Case 1. ${\sigma }_d\left(\{v_3,c\}\right)={\sigma }_d\left(\{v_3,d\}\right)=+1$. Since $\Sigma$ is balanced, so ${\sigma }_d\left(\{d,c\}\right)=+1$. Now, ${\sigma }_d\left(\{v_3,c\}\right)={\sigma }_d\left(\{d,c\}\right)={\sigma }_d\left(\{v_2,v_3\}\right)=+1$ implies that ${\sigma }_d\left(\{v_2,c\}\right)=+1$ and using the consistency of ${\Sigma }_d^A$, we conclude ${\sigma }_d\left(\{v_2,b\}\right)=-1$. So, ${\sigma }_d\left(\{b,c\}\right)=-1$. Hence, ${\mu }_d\left(c\right)=-1$, which is a contradiction to Theorem 4. Thus, ${\Sigma }_d^A$ is not consistent. (Figure 5 is a representation of this case.)

Figure 5. Representative diagram: Case 1.

Case 2. ${\sigma }_d\left(\{v_3,c\}\right)={\sigma }_d\left(\{v_3,d\}\right)=-1$. Since $\Sigma$ is balanced, so ${\sigma }_d\left(\{d,c\}\right)=+1$. Now, ${\sigma }_d\left(\{v_3,v_2\}\right)={\sigma }_d\left(\{d,c\}\right)=+1$ and ${\sigma }_d\left(\{v_3,d\}\right)=-1$ implies that ${\sigma }_d\left(\{v_2,c\}\right)=-1$ and using the consistency of ${\Sigma }_d^A$, we conclude ${\sigma }_d\left(\{v_2,b\}\right)=+1$. So, ${\sigma }_d\left(\{b,c\}\right)=-1$ (Refer to the Figure 6). Hence, ${\mu }_d\left(c\right)=-1$, which is a contradiction to Theorem 4. Thus, ${\Sigma }_d^A$ is not consistent.

Figure 6. Representative diagram: Case 2.

$\left(ii\right)$ Let $\sigma \left(\{v_1,v_2\}\right)=+1,\sigma \left(\{v_2,v_3\}\right)=-1,\sigma \left(\{v_3,v_4\}\right)=+1.$ Then, by Theorem 4

$${\mu }_d\left(v\right)=+1,\forall v\in V\left({\Sigma }_d^A\right)$$

and so ${\sigma }_d\left(\{v_2,c\}\right){\sigma }_d\left(\{v_2,b\}\right)=-1.$ If possible, let ${\Sigma }_d^A$ be consistent.

Case 1: ${\sigma }_d\left(\{v_2,c\}\right)=-1$ and ${\sigma }_d\left(\{v_2,b\}\right)=+1$. Since $\Sigma$ is balanced, so ${\sigma }_d\left(\{b,c\}\right)=-1$. Therefore, ${\sigma }_d\left(\{v_3,c\}\right)=+1$ and a consistency of ${\Sigma }_d^A$ implies ${\sigma }_d\left(\{v_3,d\}\right)=-1$. Hence, ${\sigma }_d\left(\{d,c\}\right)=+1$, which in turn implies that ${\sigma }_d\left(\{v_3,d\}\right)=+1$. Therefore, ${\mu }_d\left(v_3\right)=-1$.

Case 2: ${\sigma }_d\left(\{v_2,c\}\right)=+1$ and ${\sigma }_d\left(\{v_2,b\}\right)=-1$. In this case also, applying an argument similar to Case 1, we can show that ${\mu }_d\left(v_3\right)=-1$.

Hence, in either case, ${\Sigma }_d^A$ has a vertex with a sign of $-1$, which is a contradiction. So, ${\Sigma }_d^A$ is not consistent.

$\left(iii\right)$ Let $\sigma \left(\{v_1,v_2\}\right)=-1,\sigma \left(\{v_2,v_3\}\right)=-1,\sigma \left(\{v_3,v_4\}\right)=-1.$ Then, by Theorem 4

$${\mu }_d\left(v\right)=+1,\forall v\in V\left({\Sigma }_d^A\right)$$

and so ${\sigma }_d\left(\{v_2,c\}\right)={\sigma }_d\left(\{v_2,b\}\right).$ If possible, let ${\Sigma }_d^A$ be consistent. Since $\Sigma$ is balanced, it has at least one edge with sign $+1$.

Case 1: ${\sigma }_d\left(\{v_2,c\}\right)={\sigma }_d\left(\{v_2,b\}\right)=-1$. In this case, since $\Sigma$ is balanced and each of the antipodal paths connecting $v_2,c$ and $v_2,b$ has an odd number of negative edges, so ${\sigma }_d\left(\{b,c\}\right)=+1$. Now, ${\sigma }_d\left(\{v_2,b\}\right)=-1$ implies that the antipodal path connecting $v_2$ and c has an odd number of negative edges and hence the antipodal path joining $v_3$ and c has an even number of edges with a sign of $-1$. So, ${\sigma }_d\left(\{v_3,c\}\right)=+1$. Now, the consistency of ${\Sigma }_d^A$ implies that ${\sigma }_d\left(\{v_3,d\}\right)=+1$, which in turn implies that ${\sigma }_d\left(\{c,d\}\right)=-1$. Finally, ${\sigma }_d\left(\{v_3,c\}\right)={\sigma }_d\left(\{v_3,d\}\right)=+1$ implies that each of the antipodal paths connecting $v_3,c$ and $v_3,d$ has an aeven number of edges with a sign of $-1$. Since the union of the antipodal paths connecting $v_3,c$ and $v_3,d$ together with the edge $\{c,d\}$ is $\Sigma$, so ${\sigma }_d(\Sigma )=-1$, which is a contradiction.

Case 2: ${\sigma }_d\left(\{v_2,c\}\right)={\sigma }_d\left(\{v_2,b\}\right)=+1$. Proceeding in the way as we have taken in case 1, we can show that $\Sigma$ is not consistent, which is a contradiction.

Hence, ${\Sigma }_d^A$ is not consistent. □

Theorem 5. 

Let $\Sigma =(C_{2n+1},\sigma )$ be balanced and $\Sigma \ne C_{2n+1}^{+}$. Then, ${\Sigma }_d^A$ is canonically consistent if and only if the signs of any three consecutive edges has the pattern either $-1,-1,+1$ or $-1,+1,-1$ or $+1,-1,-1$.

Proof. 

First, suppose that $\Sigma$ has three consecutive edges with a sign pattern different from $-1,-1,+1$; $-1,+1,-1$ and $+1,-1,-1$. Since $\Sigma$ is balanced, so it must have an edge with sign $+1$. So, $\Sigma$ must have three consecutive edges with a sign pattern of either $-1,+1,+1$ or $+1,-1,+1$ or $-1,-1,-1$. In each of these cases, ${\Sigma }_d^A$ is not consistent.

Conversely, let the sign of the edges follow the given patterns. Then, for every single edge with a sign of $+1$ in the graph, there will be two exclusive edges with a sign of $-1$. This implies that $2n+1$ is a multiple of 3. Let $2n+1=3k$. Then, k must be odd and the number of edges in $\Sigma$ with a sign of $-1$ is $2k$. We claim that ${\sigma }_d\left(v\right)=+1,\forall v\in {\Sigma }_d^A$. On the contrary, assume that ${\mu }_d\left(v\right)=-1$ for some $v\in {\Sigma }_d^A$. Let $u,w$ be the vertices adjacent to v in $\Sigma$. Let $x,y$ be the antipodes of v, as shown in Figure 7. We consider the following cases:

Figure 7. Representation diagram: Case 1.

Case 1: ${\sigma }_d\left(\{u,v\}\right)={\sigma }_d\left(\{v,w\}\right)=-1$. Then, by the assumption of sign pattern, ${\sigma }_d\left(\{x,y\}\right)=+1$. So, each of the diametric paths connecting $v,x$ and $v,y$ should have an odd number of edges with a sign of $-1$. Therefore, ${\sigma }_d\left(\{v,x\}\right)={\sigma }_d\left(\{v,y\}\right)=-1$, which is a contradiction to our assumption that ${\mu }_d\left(v\right)=-1$.

Case 2: ${\sigma }_d\left(\{u,v\}\right)=+1$ and ${\sigma }_d\left(\{v,w\}\right)=-1$. Then, by the assumption of a sign pattern, ${\sigma }_d\left(\{x,y\}\right)=-1$. So, if the diametric path connecting v to x has an odd number of negative edges, then the diametric path connecting v to y should have an even number of negative edges and vice versa. Thus, either ${\sigma }_d\left(\{v,x\}\right)=-1,{\sigma }_d\left(\{v,y\}\right)=+1$ or ${\sigma }_d\left(\{v,x\}\right)=+1,{\sigma }_d\left(\{v,y\}\right)=-1$. In either case, ${\mu }_d\left(v\right)=+1$, which is a contradiction.

Thus, in each case, we have arrived at a contradiction. Hence, ${\Sigma }_d^A$ is canonically consistent. □

5. The Smith Graph ${\mathit{H}}_{\mathbf{7}}$

Consider the labeling of the vertices of $H_7$ using $v_1,v_2,v_3,v_4,v_5,v_6,v_7$, as shown in Figure 8. Let $\Sigma =(H_7,\sigma )$. We shall investigate the conditions under which $\Sigma$ is balanced and canonical consistent.

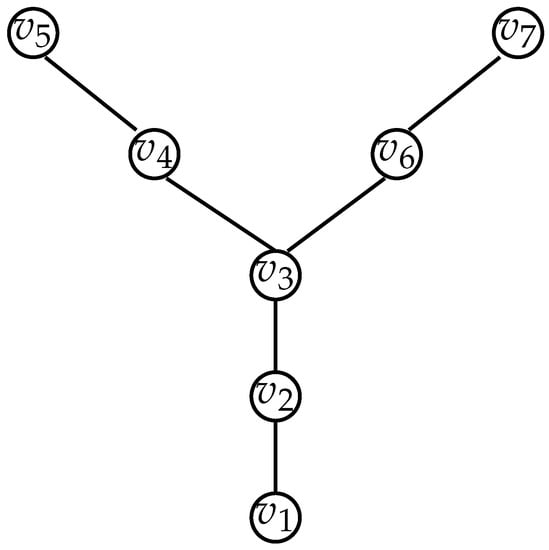
Figure 8. The Smith graph $H_7$.

Proposition 7. 

If $\Sigma =(H_7,\sigma )$, then ${\Sigma }_d^A$ is balanced.

Proof. 

Since $\Sigma$ is acyclic, so it is balanced. Let $V_1$ and $V_2$ be Harary’s partition of vertices. We claim that $V_1$ and $V_2$ also serve as Harary’s partition of vertices for ${\Sigma }_d^A$. Let $a_{15},a_{17}$ and $a_{57}$ be the antipodal edges joining the pair of antipodal vertices $v_1,v_5;v_1,v_7$ and $v_5,v_7$, respectively. Now, ${\sigma }_d\left(a_{ij}\right)=-1$ implies that the path in $\Sigma$ joining $v_i$ and $v_j$ has an odd number of edges with a sign of $-1$ and so $v_i$ and $v_j$ belongs to different partitions. In addition, ${\sigma }_d\left(a_{ij}\right)=+1$ implies that the path in $\Sigma$ joining $v_i$ and $v_j$ has an even number of edges with a sign of $-1$ and so $v_i$ and $v_j$ belong to the same partition. Hence, $V_1$, $V_2$ serves as the desired Harary’s partition of ${\Sigma }_d^A$ and so it is balanced. □

Lemma 2. 

If $\Sigma =(H_7,\sigma )$ has an edge with a sign of $-1$, then there exists a vertex in ${\Sigma }_d^A$ with a mark of $-1$.

Proof. 

Consider the labeling of $H_7$, as shown in Figure 8. Let e be any edge in $\Sigma$ with $\sigma \left(e\right)=-1$. If possible, let ${\mu }_d\left(v\right)=+1$ for all $v\in V\left({\Sigma }_d^A\right)$. We consider the following cases:

Case 1: e is a pendant edge. Without loss of generality, let $e=\{v_1,v_2\}$. Then, ${\sigma }_d\left(\{v_2,v_3\}\right)=-1$, otherwise ${\mu }_d\left(v_2\right)=-1$, and hence, exactly one of the edges $\{v_4,v_3\},$$\{v_6,v_3\}$ has a sign of $-1$; otherwise, ${\mu }_d\left(v_3\right)=-1$. Without a loss of generality, assume that ${\sigma }_d\left(\{v_4,v_3\}\right)=-1$ and ${\sigma }_d\left(\{v_6,v_3\}\right)=+1$. Then, ${\sigma }_d\left(\{v_6,v_7\}\right)=+1$ and ${\sigma }_d\left(\{v_4,v_5\}\right)=-1$; otherwise, at least one of $v_4,v_6$ will have a mark of $-1$. In this case, both the antipodal edges incident with $v_1$ has a sign of $+1$ and so ${\mu }_d\left(v_1\right)=-1$, which is a contradiction.

Case 2: e is a non-pendant edge. Without a loss of generality, let $e=\{v_3,v_2\}$. Then, ${\sigma }_d\left(\{v_2,v_1\}\right)=-1$; otherwise, ${\mu }_d\left(v_2\right)=-1$. Since $\{v_2,v_1\}$ is a pendant edge, so as in case 1, it will lead to a contradiction.

Hence, the result follows. □

Theorem 6. 

If $\Sigma =(H_7,\sigma )$, then ${\Sigma }_d^A$ is balanced and canonically consistent if and only if $\Sigma =H_7^{+}$.

Proof. 

By Proposition 7, ${\Sigma }_d^A$ is always balanced. So, first suppose that ${\Sigma }_d^A$ is canonically consistent. First, we show that ${\mu }_d\left(v_3\right)=+1$. On the contrary, let us assume that ${\mu }_d\left(v_3\right)=-1$. Since ${\Sigma }_d^A$ is canonically consistent, so ${\mu }_d\left(v_1{v}_2{v}_3{v}_4{v}_5{v}_1\right)=+1$, and this in turn implies that ${\mu }_d\left(v_1\right){\mu }_d\left(v_2\right)\ne {\mu }_d\left(v_4\right){\mu }_d\left(v_5\right)$. Similarly,

$${\mu }_d\left(v_1{v}_2{v}_3{v}_6{v}_7{v}_1\right)=+1\Rightarrow {\mu }_d\left(v_1\right){\mu }_d\left(v_2\right)\ne {\mu }_d\left(v_6\right){\mu }_d\left(v_7\right).$$

Consequently, ${\mu }_d\left(v_4\right){\mu }_d\left(v_5\right)={\mu }_d\left(v_6\right){\mu }_d\left(v_7\right)$. Then

$${\mu }_d\left(v_5{v}_4{v}_3{v}_6{v}_7{v}_5\right)={\mu }_d\left(v_5\right){\mu }_d\left(v_4\right){\mu }_d\left(v_3\right){\mu }_d\left(v_6\right){\mu }_d\left(v_7\right)=-1$$

This implies that ${\Sigma }_d^A$ is not consistent, which is a contradiction. So, the only possibility is ${\mu }_d\left(v_3\right)=+1.$

We now claim that the canonical marking of each of the vertices $v_1,v_5,v_7$ is $+1$. Without a loss of generality, let ${\mu }_d\left(v_1\right)=-1$. Since ${\Sigma }_d^A$ is canonically consistent, so the mark of the cycle $v_1{v}_5{v}_7{v}_1$ must be $+1$, and hence ${\mu }_d\left(v_5\right){\mu }_d\left(v_7\right)=-1$. Then, at least one of the pairs of cycles $v_1{v}_2{v}_3{v}_6{v}_7{v}_1$, $v_1{v}_2{v}_3{v}_6{v}_7{v}_5{v}_1$ or $v_1{v}_2{v}_3{v}_4{v}_5{v}_1$, $v_1{v}_2{v}_3{v}_4{v}_5{v}_7{v}_1$ has an opposite canonical marking. So, ${\Sigma }_d^A$ is not consistent, which is a contradiction. This proves our claim.

We now claim that the canonical marking of each of the vertices $v_2,v_4,v_6$ is $+1$. Without a loss of generality, let ${\mu }_d\left(v_2\right)=-1$. The canonical consistency of ${\Sigma }_d^A$ implies that ${\mu }_d\left(v_4\right)={\mu }_d\left(v_6\right)=-1$. Now, ${\mu }_d\left(v_2\right)=-1$ implies that ${\sigma }_d\left(\{v_1,v_2\}\right)=-1$ or ${\sigma }_d\left(\{v_3,v_2\}\right)=-1$. If ${\sigma }_d\left(\{v_1,v_2\}\right)=-1$, then ${\sigma }_d\left(\{v_5,v_7\}\right)=-1$. Since ${\mu }_d\left(v_5\right)={\mu }_d\left(v_7\right)=+1$, so ${\sigma }_d\left(\{v_6,v_7\}\right)=-1$ and ${\sigma }_d\left(\{v_4,v_5\}\right)=+1$. This in turn implies that ${\sigma }_d\left(\{v_3,v_4\}\right)=-1$ and ${\sigma }_d\left(\{v_3,v_6\}\right)=+1$. However, ${\sigma }_d\left(\{v_3,v_2\}\right)=+1$. Therefore, ${\mu }_d\left(v_3\right)=-1$, a contradiction. If ${\sigma }_d\left(\{v_3,v_2\}\right)=-1$, then ${\sigma }_d\left(\{v_4,v_3\}\right){\sigma }_d\left(\{v_6,v_3\}\right)=-1$ because ${\sigma }_d\left(v_3\right)=+1$. Without a loss of generality, let ${\sigma }_d\left(\{v_4,v_3\}\right)=+1$ and ${\sigma }_d\left(\{v_6,v_3\}\right)=-1$. Then, the cycles $v_1{v}_2{v}_3{v}_6{v}_7{v}_1$, $v_1{v}_2{v}_3{v}_4{v}_5{v}_1$ will have opposite canonical markings, which is a contradiction. So, the canonical marking of each of the vertices $v_2,v_4,v_6$ must be $+1$.

Thus, each of the vertices in ${\Sigma }_d^A$ has a canonical marking of $+1$ and so, by the Lemma 2, $\Sigma =H_7^{+}$. □

Remark 8. 

If $\Sigma =(H_i,\sigma )$, $i=8,9$ then ${\Sigma }_d^A$ will have exactly one cycle, and so it is always balanced. However, ${\Sigma }_d^A$ will be canonically consistent if and only if the non-diametric edge in Σ has a sign of $+1$.

Double-Headed Snake $\left(W_n\right),n\ge 6$

In this section, we consider the d-antipodal graph of the Smith graph $W_n,n\ge 6$. We label the vertices of $W_n$ using $v_1,v_2,\cdots ,v_n$, as shown in Figure 9. The antipodal pairs in $W_n$ are $v_1,v_3;v_1,v_4;v_2,v_3;v_2,v_4$ and the antipodal edges are represented by dotted lines. Let $a_{i,j}$ be the antipodal edge joining a pair of antipodes $v_i,v_j$.

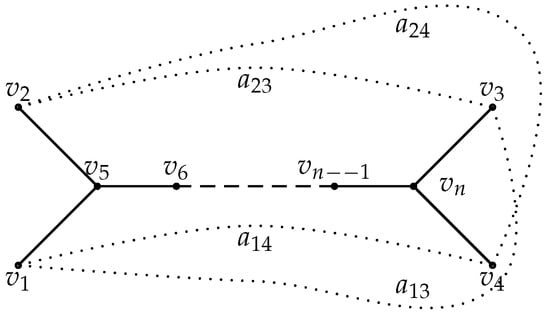
Figure 9. d-Antipodal graph of the Smith graph $W_n,n\ge 6$.

The following remark about the d-antipodal graph of the Smith graph $W_n,n\ge 6$ follows from Theorem 3.

Remark 9. 

Let $\Sigma =(W_n,\sigma )$, for $n\ge 6$. Then, ${\Sigma }_d^A$ is balanced.

Proposition 8. 

If $\Sigma =(W_n,\sigma )$, then ${\Sigma }_d^A$ is canonically consistent if and only if all the six edges incident with both the vertices of degree 3 in Σ are of the same sign.

Proof. 

First, assume that ${\Sigma }_d^A$ is canonically consistent. If possible, let there be a pair of edges $e,e^{\prime }$ among the six edges incident with the two vertices of degree 3 in $\Sigma$ that have opposite signs. We consider the following two cases:

Case 1: e and $e^{\prime }$ are pendant edges with a vertex in common. Without a loss of generality, let $e=\{v_1,v_5\}$ and $e^{\prime }=\{v_2,v_5\}$. In this case, ${\sigma }_d\left(a_{13}\right){\sigma }_d\left(a_{23}\right)=-1$ and ${\sigma }_d\left(a_{14}\right){\sigma }_d\left(a_{24}\right)=-1$. Therefore,

$$\begin{array}{ccc}\hfill {\mu }_d\left(v_1\right)& =& {\sigma }_d\left(e\right){\sigma }_d\left(a_{13}\right){\sigma }_d\left(a_{14}\right)\hfill \\ & =& [-{\sigma }_d\left(e^{\prime }\right)][-{\sigma }_d\left(a_{23}\right)][-{\sigma }_d\left(a_{24}\right)]\hfill \\ & =& -{\mu }_d\left(v_2\right)\hfill \end{array}$$

Since ${\Sigma }_d^A$ is consistent, both the cycles $v_1{v}_5{v}_2{v}_3{v}_1$ and $v_1{v}_5{v}_2{v}_4{v}_1$ should have a mark of $+1$, and this is possible only if ${\mu }_d\left(v_3\right)={\mu }_d\left(v_4\right)\ne {\mu }_d\left(v_5\right)$. Hence,

$${\mu }_d\left(v_1{v}_3{v}_2{v}_4{v}_1\right)={\mu }_d\left(v_1\right){\mu }_d\left(v_3\right){\mu }_d\left(v_2\right){\mu }_d\left(v_4\right))={\mu }_d\left(v_1\right){\mu }_d\left(v_2\right)=-1,$$

which is a contradiction. Therefore, $\sigma \left(e\right)=\sigma \left(e^{\prime }\right)$—that is, pendant edges in $\Sigma$ sharing a common vertex should have the same sign.

Case 2: e and $e^{\prime }$ are pendant edges with no vertex in common. Without a loss of generality, let $e=\{v_1,v_5\}$ and $e^{\prime }=\{v_n,v_3\}$. By case 1, ${\sigma }_d\left(\{v_1,v_5\}\right)={\sigma }_d\left(\{v_2,v_5\}\right)$ and ${\sigma }_d\left(\{v_n,v_3\}\right)={\sigma }_d\left(\{v_n,v_4\}\right)$, which in turn implies that all the antipodal edges have the same sign. Hence, ${\mu }_d\left(v_1\right)={\mu }_d\left(v_2\right)$ and ${\mu }_d\left(v_3\right)={\mu }_d\left(v_4\right)$. However,

$$\begin{array}{ccc}\hfill {\mu }_d\left(v_1\right)& =& {\sigma }_d\left(e\right){\sigma }_d\left(a_{13}\right){\sigma }_d\left(a_{14}\right)\hfill \\ & =& -{\sigma }_d\left(e^{\prime }\right){\sigma }_d\left(a_{13}\right){\sigma }_d\left(a_{23}\right)\hfill \\ & =& -{\mu }_d\left(v_3\right)\hfill \end{array}$$

Since the mark of the cycle $v_1{v}_5{v}_2{v}_3{v}_1$ is $+1$, so ${\mu }_d\left(v_5\right)=+1$. In addition, the mark of the cycle $v_3{v}_n{v}_4{v}_2{v}_3$ is $+1$, so ${\mu }_d\left(v_n\right)=-1$. Therefore, the mark of the cycle $v_1{v}_5{v}_2{v}_4{v}_n{v}_3{v}_1$ is −1, which is a contradiction. Hence, all the four pendant edges should have the same sign in $\Sigma$.

Case 3: e and $e^{\prime }$ have a vertex in common, and only one of these edges is a pendant. Without a loss of generality, let $e=\{v_1,v_5\}$ and $e^{\prime }=\{v_5,v_6\}$. By case 2, all pendant edges have the same sign and all the four vertices $v_1,v_2,v_3,v_4$ have the same marking. Therefore, ${\mu }_d\left(v_1\right)\ne {\mu }_d\left(v_5\right)$ and so the mark of the cycle $v_1{v}_5{v}_2{v}_3{v}_1$ is $-1$, which is a contradiction. Hence, the result follows.

Conversely, let all the edges in $\Sigma$ incident with both the vertices of degree 3 have the same sign. Then,

$${\mu }_d\left(v_i\right)=+1,\mathrm{for}i=1,2,3,4,5,n.$$

Since each cycle in ${\Sigma }_d^A$ consists of either an even number of vertices entirely from the set $\{v_i:i=1,2,3,4,5,n\}$ or an even number of vertices from the set $\{v_i:i=1,2,3,4,5,n\}$ and the vertices on the path connecting $v_6$ to $v_{n-1}$, so the mark of each cycle in ${\Sigma }_d^A$ must be positive. Hence, ${\Sigma }_d^A$ is canonically consistent. □

6. Conclusions

In this paper, the concept of d-antipodal signed graphs has been introduced. The underlying graph of the d-antipodal signed graph of a signed graph $\Sigma =(G,\sigma )$ is the union of G and its antipodal graph $A\left(G\right)$. The sign assignment to the antipodal edges is inspired by similar works available in the literature. We have characterized balanced and canonically consistent Smith signed graphs whose d-antipodal signed graphs are balanced and canonically consistent. In particular, it is shown that

• For any sign assignment to the cycle $C_{2n+1}$, its d-antipodal is canonically consistent and each vertex in the d-antipodal has a sign of $+1$.
• For any sign assignment to the double-headed snake $W_n$, its d-antipodal is canonically consistent if and only if both the degree three vertices are of the same sign.
• For any sign assignment to the Smith graph $H_7$, its d-antipodal is canonically consistent if and only if all its edges have a sign of $+1$.