Tail Value-at-Risk-Based Expectiles for Extreme Risks and Their Application in Distributionally Robust Portfolio Selections

Abstract

Empirical evidence suggests that financial risk has a heavy-tailed profile. Motivated by recent advances in the generalized quantile risk measure, we propose the tail value-at-risk (TVaR)-based expectile, which can capture the tail risk compared with the classic expectile. In addition to showing that the risk measure is well-defined, the properties of TVaR-based expectiles as risk measures were also studied. In particular, we give the equivalent characterization of the coherency. For extreme risks, usually modeled by a regularly varying survival function, the asymptotic expansion of a TVaR-based expectile (with respect to quantiles) was studied. In addition, motivated by recent advances in distributionally robust optimization in portfolio selections, we give the closed-form of the worst-case TVaR-based expectile based on moment information. Based on this closed form of the worst-case TVaR-based expectile, the distributionally robust portfolio selection problem is reduced to a convex quadratic program. Numerical results are also presented to illustrate the performance of the new risk measure compared with classic risk measures, such as tail value-at-risk-based expectiles.

1. Introduction

A risk measure involves mapping $\rho :\mathcal{X}\to \mathbb{R}=(-\infty ,\infty )$, where $\mathcal{X}$ is a set of loss random variables or risks. Risk measures were well used in solvency risk management to determine the required capital for risks. Among others, expectile, introduced in Newey and Powell [1] as the minimizers of asymmetric quadratic loss functions in the context of regression, is one of the most important risk measures in risk management. For a risk X with $\mathbb{E}\left[X^2\right]<\infty$, the expectile of X at a confidence level $\alpha \in (0,1)$, written as $e_{\alpha }\left(X\right)$, is defined as the unique minimizer of the following problem:

$$\begin{array}{c}\hfill e_{\alpha }\left(X\right)=arg\underset{x\in \mathbb{R}}{min}\left\{\alpha \mathbb{E}\left[{(X-x)}_{+}^2\right]+(1-\alpha )\mathbb{E}\left[{(x-X)}_{+}^2\right]\right\},\end{array}$$

where ${\left(x\right)}_{+}:=max\{x,0\}$. Equivalently, $e_{\alpha }\left(X\right)$ is the unique solution to the equation

$$\begin{array}{c}\hfill \alpha \mathbb{E}\left[{(X-x)}_{+}\right]=(1-\alpha )\mathbb{E}\left[{(X-x)}_{-}\right],x\in \mathbb{R}.\end{array}$$

(1)

Note that the above definition (1) is well-defined for any risk X with finite mean.

Bellini et al. [2] showed that the expectile for $\alpha ⩾1/2$ is a coherent risk measure (whose definition, as introduced by Artzner et al. [3], will be given later). Starting from this seminal paper in risk management, expectiles are gaining popularity in econometric literature studies and actuarial science (e.g., Bellini et al. [2] and Cai and Weng [4]). An expectile has the property of elicitability, which is an essential and desirable property in backtesting and forecasting (e.g., Gneiting [5] and Kratz et al. [6]). In addition, Ziegel [7] showed that the expectile is the only coherent risk measure class that has elicitability. See Bellini et al. [2], Ziegel [7], Embrechts et al. [8], and the references therein for more discussions on the properties of expectiles.

From the point view of solvency risk management, based on the definition of (1), if x is the required capital for the risk X, then ${(X-x)}_{+}$ and ${(X-x)}_{-}$ are viewed as the shortfall risk and the over-required capital risk, respectively. For $\alpha \in (0,1)$, we can rewrite (1) as $\mathbb{E}\left[{(X-x)}_{+}\right]/\mathbb{E}\left[{(X-x)}_{-}\right]=\beta$, $\beta :=\left(1-\alpha \right)/\alpha$. With $e_{\alpha }\left(X\right)$ serving as the required capital, the ratio of the expected shortfall risk to the expected over-required capital risk is $\beta$. Obviously, it is desired that the expected shortfall risk is not larger than the expected over-required capital risk or that the ratio satisfies $\beta =\left(1-\alpha \right)/\alpha ⩽1$ or equivalent $\alpha ⩾\frac{1}{2}$, which is a necessary and sufficient condition for the expectile $e_{\alpha }\left(X\right)$ to be a coherent risk measure.

As argued by Mao and Cai [9], the shortfall risk and the over-required capital risk in the expectile definition are evaluated under the probability measure or the distribution of X. A decision-maker may have different attitudes toward the different outcomes of risks, and it is reasonable to employ more conservative risk measures than expectations to evaluate the risks. The tail value-at-risk (TVaR), the expected shortfall (ES), and the conditional VaR (CVaR) of X at a confidence level $\beta \in (0,1)$, defined as

$$\begin{array}{c}\hfill {\mathrm{TVaR}}_{\beta }\left(X\right)=\frac{1}{1-\beta }{\int }_{\beta }^1{F}_X^{-1}\left(t\right)\mathrm{d}t,\end{array}$$

(2)

are other important examples of coherent risk measures used in finance and insurance risk management, where $F_X^{-1}$ is the left-continuous inverse of $F_X$, defined by $F_X^{-1}\left(\alpha \right)=inf\{x:F_X\left(x\right)⩾\alpha \}$ for $\alpha \in (0,1]$. One can verify that ${\mathrm{TVaR}}_{\beta }⩾\mathbb{E}$ for any $\beta ⩾0$ and it reduces to the expectation when $\beta =0$, which is a natural alternative conservative risk measure compared to the expectation of evaluating the risk. In this paper, we intend to employ TVaR instead of the expectation to evaluate the two risks in (1) and require the ratio to be equal to a given confidence level in which we generalize the definition of the classic expectile. The new risk measure is called the TVaR-based expectile.

In this paper, we first show that the TVaR-based expectile is well-defined, and we study its basic properties as risk measures. In particular, we give the equivalent characterization of the TVaR-based expectile being a coherent risk measure. As a generalization of the expectile, the TVaR-based expectile does not admit a closed form, which makes the estimation of the risk measure difficult. When the prudentiality level is close to 1, a preliminary step to the estimation involves the obtention of asymptotic expansions for the target risk measure. Such expansions allow quantifying bias terms and are fundamental in the derivation of asymptotic normality results for estimators at extreme levels, see, e.g., Cai et al. [10], Daouia et al. [11], and Zhao et al. [12]. Such asymptotic expansions can lead to better understanding of the risk measures and plug-in estimators at extreme levels (Daouia et al. [11]), and are very useful in practice as there is empirical evidence that financial risks have the properties of heavy tails. In this paper, we study the asymptotic expansions of TVaR-based expectiles for heavy-tailed risks with confidence levels close to 1. The results obtained in this paper recover the asymptotic expansions of the expectile given by Mao et al. [13].

The work of Delage and Ye [14] involves distributionally robust optimization (DRO) and has been recognized as the diagram in modeling distribution uncertainty. Motivated by recent advances in DRO in risk management (Blanchet et al. [15] and Li [16]), we studied the worst-case TVaR-based expectile based on moment information, which recovers the worst-case expectile. Based on this closed form of the worst-case TVaR-based expectile, we reduce the distributionally robust portfolio selection problem to a convex quadratic program. Numerical results are also presented to illustrate the performance of the new risk measures compared with classic risk measures, such as tail value-at-risk-based expectiles.

Throughout the paper, let $(\Omega ,\mathcal{B},\mathbb{P})$ be an atomless probability space, where $\Omega$ is a set of possible states of nature and $\mathcal{B}$ is $\sigma$-algebra on $\Omega$. Let $L^1=L^1(\Omega ,\mathcal{B},\mathbb{P})$ be the spaces of all random variables and the spaces of all integrable random variables on $(\Omega ,\mathcal{B},\mathbb{P})$, respectively, i.e., $L^0=\{X:\Omega \to \mathbb{R}:X\mathrm{is}\mathrm{measurable}\mathrm{with}\mathrm{respect}\mathrm{to}\mathcal{B}\}$ and $L^1=\{X:\Omega \to \mathbb{R}\left|X\mathrm{is}\mathrm{measurable}\mathrm{with}\mathrm{respect}\mathrm{to}\mathcal{B},{\int }_{\Omega }\left|X\right|\mathrm{d}\mathbb{P}<\infty \right.\}$. For a random variable $X\in L^1$, we denote by $F_X$ the cumulative distribution function (cdf) of X under the probability $\mathbb{P}$, i.e., $F_X\left(x\right)=\mathbb{P}(X⩽x)$, $x\in \mathbb{R}$.

2. TVaR-Based Expectile

In this section, we present the formal definition of the TVaR-based expectile and study its properties as risk measures. We first give an auxiliary lemma, which guarantees that the definition of the TVaR-based expectile is well-defined.

Lemma 1. 

For $\alpha \in [0,1]$, $X\in L^1$, the equation of x:

$$\alpha {\mathrm{TVaR}}_{{\beta }_1}\left[{(X-x)}_{+}\right]=\left(1-\alpha \right){\mathrm{TVaR}}_{{\beta }_2}\left[{(X-x)}_{-}\right]$$

has a unique solution, which also equals the unique solution to

$$\alpha {\int }_x^{\infty }min\left\{\frac{1-F\left(u\right)}{1-{\beta }_1},1\right\}\mathrm{d}u=(1-\alpha ){\int }_{-\infty }^{x}min\left\{\frac{F\left(u\right)}{1-{\beta }_2},1\right\}\mathrm{d}u,$$

(3)

where F is the distribution function of X.

Proof. 

We first show that for $X\in L^1$ and $x\in \mathbb{R}$, it holds that

$${\mathrm{TVaR}}_{\beta }\left({(X-x)}_{+}\right)={\int }_x^{\infty }min\left\{\frac{1-F\left(u\right)}{1-\beta },1\right\}\mathrm{d}u$$

(4)

and

$${\mathrm{TVaR}}_{\beta }\left({(X-x)}_{-}\right)={\int }_{-\infty }^{x}min\left\{\frac{F\left(u\right)}{1-\beta },1\right\}\mathrm{d}u,$$

(5)

where F is the distribution function of X. Note that

$$\begin{array}{c}\hfill {\mathrm{TVaR}}_{\alpha }\left({(X-d)}_{+}\right)=\left\{\begin{array}{cc}{\mathrm{TVaR}}_{\alpha }\left(X\right)-d,\hfill & d⩽{\mathrm{VaR}}_{\alpha }\left(X\right),\hfill \\ \frac{1}{1-\alpha }\mathbb{E}\left[{(X-d)}_{+}\right],\hfill & d⩾{\mathrm{VaR}}_{\alpha }\left(X\right).\hfill \end{array}\right.\end{array}$$

(6)

Note that ${\mathrm{VaR}}_u\left(Y\right)=-{\mathrm{VaR}}_{1-u}(-Y)$. We have

$$\begin{array}{cc}\hfill {\mathrm{TVaR}}_{\beta }\left({(X-x)}_{-}\right)& =\frac{1}{1-\beta }{\int }_{\beta }^1{\mathrm{VaR}}_u\left({(X-x)}_{-}\right)\mathrm{d}u\hfill \\ \hfill & =\frac{1}{1-\beta }{\int }_{\beta }^1-{\mathrm{VaR}}_{1-u}(-{(X-x)}_{-})\mathrm{d}u\hfill \\ \hfill & =-\frac{1}{1-\beta }{\int }_0^{1-\beta }{\mathrm{VaR}}_u(-{(X-x)}_{-})\mathrm{d}u\hfill \\ \hfill & =\frac{1}{1-\beta }{\int }_0^{1-\beta }{({\mathrm{VaR}}_u\left(X\right)-x)}_{-}\mathrm{d}u\hfill \end{array}$$

where the last equality follows from ${\mathrm{VaR}}_u(-{(X-x)}_{-})=-{({\mathrm{VaR}}_u\left(X\right)-x)}_{-}$. We next consider two cases. If $x⩽{\mathrm{VaR}}_{1-\beta }\left(X\right)$, then ${({\mathrm{VaR}}_u\left(X\right)-x)}_{-}=0$ for $u⩾1-\beta$ and, thus,

$$\begin{array}{cc}\hfill {\mathrm{TVaR}}_{\beta }\left({(X-x)}_{-}\right)& =\frac{1}{1-\beta }{\int }_0^1{({\mathrm{VaR}}_u\left(X\right)-x)}_{-}\mathrm{d}u=\frac{1}{1-\beta }\mathbb{E}\left[{(X-x)}_{-}\right].\hfill \end{array}$$

For $x⩾{\mathrm{VaR}}_{1-\beta }\left(X\right)$, then

$$\begin{array}{cc}\hfill {\mathrm{TVaR}}_{\beta }\left({(X-x)}_{-}\right)& =\frac{1}{1-\beta }{\int }_0^{1-\beta }x-{\mathrm{VaR}}_u\left(X\right)\mathrm{d}u\hfill \\ \hfill & =x-\frac{1}{1-\beta }{\int }_0^{1-\beta }{\mathrm{VaR}}_u\left(X\right)\mathrm{d}u\hfill \\ \hfill & =x-\frac{1}{1-\beta }{\int }_0^{1-\beta }-{\mathrm{VaR}}_{1-u}(-X)\mathrm{d}u\hfill \\ \hfill & =x+\frac{1}{1-\beta }{\int }_{\beta }^1{\mathrm{VaR}}_z(-X)\mathrm{d}z=x+{\mathrm{TVaR}}_{\beta }(-X).\hfill \end{array}$$

By taking the derivatives of ${\mathrm{TVaR}}_{\beta }\left({(X-x)}_{+}\right)$ and ${\mathrm{TVaR}}_{\beta }\left({(X-x)}_{-}\right)$, we have (4) and (5) holding. It, thus, follows that the equation $\alpha {\mathrm{TVaR}}_{{\beta }_1}\left[{(X-x)}_{+}\right]=\left(1-\alpha \right){\mathrm{TVaR}}_{{\beta }_2}\left[{(X-x)}_{-}\right]$ is equivalent to (3). It suffices to show the solution is unique. Denote

$$h\left(x\right):=\alpha {\int }_x^{\infty }min\left\{\frac{1-F\left(u\right)}{1-{\beta }_1},1\right\}\mathrm{d}u-(1-\alpha ){\int }_{-\infty }^{x}min\left\{\frac{F\left(u\right)}{1-{\beta }_2},1\right\}\mathrm{d}u.$$

It can be verified that $h\left(x\right)$ is a strictly decreasing function in the support of F, ${lim}_{x\to \infty }h\left(x\right)=-\infty$ and ${lim}_{x\to -\infty }h\left(x\right)=\infty$. Moreover, note that the solution to (3) must lie in the support of F. Hence, the solution to $h\left(x\right)=0$, i.e., Equation (3), is unique. This completes the proof. □

Now, we introduce the TVaR-based risk measure of the expectile as follows.

Definition 1. 

For a risk X, $\alpha \in (0,1)$, and ${\beta }_1,{\beta }_2\in [0,1)$,the TVaR-based expectile of X, denoted by $e_{\alpha ;{\beta }_1,{\beta }_2}\left(X\right)$, is the unique solution to the equation

$$\begin{array}{c}\hfill \alpha {\mathrm{TVaR}}_{{\beta }_1}\left({(X-x)}_{+}\right)=(1-\alpha ){\mathrm{TVaR}}_{{\beta }_2}\left({(X-x)}_{-}\right),x\in \mathbb{R}.\end{array}$$

(7)

When ${\beta }_1={\beta }_2=0$, then $e_{\alpha ;0,0}$ reduces to the classic expectile with level $\alpha$. In particular, we identify the following two special classes of TVaR-based expectiles.

(i)

If ${\beta }_1={\beta }_2=\beta$, i.e., the decision-maker has the same risk attitude to the shortfall risk ${(X-x)}_{+}$ and the over-required capital risk ${(X-x)}_{-}$, and he/she uses the same TVaR to evaluate the two risks, in this case, the TVaR-based expectile of X, denoted by $e_{\alpha ;\beta }\left(X\right)$, is the unique solution to the equation

$$\begin{array}{c}\hfill \alpha {\mathrm{TVaR}}_{\beta }\left({(X-x)}_{+}\right)=(1-\alpha ){\mathrm{TVaR}}_{\beta }\left({(X-x)}_{-}\right),x\in \mathbb{R}.\end{array}$$

(8)

(ii)

If ${\beta }_1=0$, ${\beta }_2=\beta$, i.e., the decision maker is risk neutral to the shortfall risk ${(X-x)}_{+}$ and is risk averse to the over-required capital risk ${(X-x)}_{-}$, and he/she uses the expectation and TVaR to evaluate the two risks, respectively, in this case, the TVaR-based expectile of X, denoted by $e_{\alpha ;\beta }^I\left(X\right)$, is the unique solution to the equation

$$\begin{array}{c}\hfill \alpha \mathbb{E}\left[{(X-x)}_{+}\right]=(1-\alpha ){\mathrm{TVaR}}_{\beta }\left({(X-x)}_{-}\right),x\in \mathbb{R}.\end{array}$$

(9)

By changing the parameters in the definition of the TVaR-based expectile, we can flexibly obtain different risk measures based on the purpose of risk evaluation. In the next subsection, we will study the properties of TVaR-based expectiles as risk measures.

2.1. Basic Properties

We next study the basic properties of the TVaR-based expectile introduced in Definition 1 as a risk measure. We list some desired properties of the risk measures as follows.

(P1)

Monotonicity: $\rho \left(X\right)⩽\rho \left(Y\right)$ for all $X,Y\in \mathcal{X}$, such that $X⩽Y$ is almost surely (a.s.).

(P2)

Translation invariance: $\rho (X+c)=\rho \left(X\right)+c$ for all $X\in \mathcal{X}$ and all $c\in \mathbb{R}$.

(P3)

Positive homogeneity: $\rho \left(\lambda X\right)=\lambda \rho \left(X\right)$ for all $X\in \mathcal{X}$ and all $\lambda \in {\mathbb{R}}_{+}=[0,\infty )$.

(P4)

Subadditivity: $\rho (X+Y)⩽\rho \left(X\right)+\rho \left(Y\right)$ for all $X,Y\in \mathcal{X}$.

It is well-known that a risk measure satisfying the above four properties is called a coherent risk measure, which is introduced by Artzner et al. [3].

Proposition 1. 

For $X\in L^1$, let $e_{\alpha ;{\beta }_1,{\beta }_2}\left(X\right)$ be defined by (7). We have the following result.

(i) 

$e_{\alpha ;{\beta }_1,{\beta }_2}$ satisfies (P1) monotonicity, (P2) translation-invariance, and (P3) positive homogeneity.

(ii) 

$e_{\alpha ;{\beta }_1,{\beta }_2}$ satisfies (P4) subadditivity if and only if ${\beta }_1={\beta }_2=0$ and $\alpha ⩾1/2$.

(iii) 

$e_{\alpha ;{\beta }_1,{\beta }_2}$ increases in α and ${\beta }_1$ and decreases in ${\beta }_2$.

(iv) 

$e_{\alpha ;{\beta }_1,{\beta }_2}\left(X\right)=-e_{1-\alpha ;{\beta }_2,{\beta }_1}(-X)$.

Proof. 

(i)

The results follow from standard manipulation based on the definition (7).

(ii)

The necessary and sufficient conditions follow directly from Theorem 3.2 of Mao and Cai [9].

(iii)

The result can be verified directly based on (3).

(iv)

Note that for any $x\in \mathbb{R}$, ${(-X+x)}_{+}={(X-x)}_{-}$ and ${(-X+x)}_{-}={(X-x)}_{+}$ and, thus, ${\mathrm{TVaR}}_{{\beta }_1}\left({(-X+x)}_{+}\right)={\mathrm{TVaR}}_{{\beta }_1}\left({(X-x)}_{-}\right)$ and ${\mathrm{TVaR}}_{{\beta }_2}\left({(-X+x)}_{-}\right)={\mathrm{TVaR}}_{{\beta }_2}\left({(X-x)}_{+}\right).$ Therefore, by the definition of $e_{\alpha ;{\beta }_1,{\beta }_2}\left(X\right)$, we have

$${\mathrm{TVaR}}_{{\beta }_1}\left({(-X+e_{\alpha ;{\beta }_1,{\beta }_2}\left(X\right))}_{+}\right)(1-\alpha )=\alpha {\mathrm{TVaR}}_{{\beta }_1}\left({(-X+e_{\alpha ;{\beta }_1,{\beta }_2}\left(X\right))}_{-}\right)$$

and, thus, $e_{\alpha ;{\beta }_1,{\beta }_2}\left(X\right)=-e_{1-\alpha ;{\beta }_2,{\beta }_1}(-X)$. This completes the proof. □

By Proposition 1, we immediately obtain the following result.

Corollary 1. 

For $\alpha ,{\beta }_1,{\beta }_2\in (0,1)$, the TVaR-based expectile $e_{\alpha ;{\beta }_1,{\beta }_2}$ is a coherent risk measure if and only if $\alpha ⩾1/2$ and ${\beta }_1={\beta }_2=0$. In this case, the TVaR-based expectile reduces to the expectile at level α.

2.2. Asymptotic Expansion of TVaR-Based Expectile for Extreme Risks

We investigate the asymptotic properties of $e_{\alpha ;{\beta }_1,{\beta }_2}$ defined by (7) for extreme risks. We first view $\alpha$ as a fixed weight on the shortfall risk and let ${\beta }_1={\beta }_2=:\beta$ in the definition of $e_{\alpha ;{\beta }_1,{\beta }_2}$. In this case, we denote that $e_{\alpha ;\beta }:=e_{\alpha ;\beta ,\beta }$, i.e., $e_{\alpha ;\beta }$ is the unique solution to the following equation

$$\begin{array}{c}\hfill \frac{{\mathrm{TVaR}}_{\beta }\left({(X-x)}_{+}\right)}{{\mathrm{TVaR}}_{\beta }\left({(X-x)}_{-}\right)}=\frac{1-\alpha }{\alpha },x\in \mathbb{R}.\end{array}$$

(10)

We study the asymptotic properties of $e_{\alpha ;\beta }$ when the confidence level $\beta$ converges to 1.

We first recall the definition of regular variation, which is an essential concept in defining the heavy-tailed risks. A function h is said to be regularly varying at point $x\in \mathbb{R}$, denoted as $h\in {\mathrm{RV}}_{-\gamma }^x$, $\gamma >0$, if

$$\underset{t\to x}{lim}\frac{h\left(ts\right)}{h\left(t\right)}=s^{-\gamma },\mathrm{for}\mathrm{all}s>0.$$

For a random variable X, let $F=1-\overline{F}$ be its cumulative distribution function. X is said to be regularly varying at both tails, denoted as $X\in {\mathrm{RV}}_{{\gamma }_1,{\gamma }_2}$, ${\gamma }_1,{\gamma }_2>0$, if $\overline{F}\in {\mathrm{RV}}_{-{\gamma }_1}^{-\infty }$ and $F\in {\mathrm{RV}}_{-{\gamma }_2}^{\infty }$. Here, ${\gamma }_1$ and ${\gamma }_2$ are called the indexes of regular variations. To state the results, let ${\mathrm{VaR}}_{\alpha }\left(X\right)$ denote the quantile of X at level $\alpha \in (0,1)$, defined by

$${\mathrm{VaR}}_{\alpha }\left(X\right)=F^{-1}\left(\alpha \right)=inf\{x:F\left(x\right)⩽\alpha \},$$

where F is the distribution of X.

Proposition 2. 

Let X be a random variable, such that it regularly varies at both tails with indexes ${\gamma }_1,{\gamma }_2>0$ and $e_{\alpha ;\beta }\left(X\right)$ defined by the solution to (10). Then we have if ${\gamma }_1<{\gamma }_2$,

$$\underset{\beta \to 1}{lim}\frac{e_{\alpha ;\beta }\left(X\right)}{{\mathrm{VaR}}_{\beta }\left(X\right)}=\left\{\begin{array}{cc}\frac{\alpha {\gamma }_1}{{\gamma }_1-1},\hfill & \frac{\alpha {\gamma }_1}{{\gamma }_1-1}<1,\hfill \\ {\left(\frac{\alpha }{(1-\alpha )({\gamma }_1-1)}\right)}^{1/{\gamma }_1},\hfill & \frac{\alpha {\gamma }_1}{{\gamma }_1-1}⩾1,\hfill \end{array}\right.$$

and if ${\gamma }_1>{\gamma }_2$,

$$\underset{\beta \to 1}{lim}\frac{e_{\alpha ;\beta }\left(X\right)}{{\mathrm{VaR}}_{1-\beta }\left(X\right)}=\left\{\begin{array}{cc}\frac{(1-\alpha ){\gamma }_2}{{\gamma }_2-1},\hfill & \frac{\alpha {\gamma }_2}{{\gamma }_2-1}<1,\hfill \\ {\left(\frac{1-\alpha }{\alpha ({\gamma }_2-1)}\right)}^{1/{\gamma }_2},\hfill & \frac{\alpha {\gamma }_2}{{\gamma }_2-1}⩾1.\hfill \end{array}\right.$$

Proof. 

We only show the case that ${\gamma }_1<{\gamma }_2$ is the proof for ${\gamma }_1>{\gamma }_2$ and is similar by taking $X^{\ast }=-X$. When ${\gamma }_1<{\gamma }_2$, we have $\beta \to 1-$, then $e_{\alpha ;\beta }\left(X\right)\to \infty$, which is larger than ${\mathrm{VaR}}_{1-\beta }\left(X\right)$. Hence, we have $e_{\alpha ;\beta }\left(X\right)$ as the solution to

$$\alpha h\left(x\right)=(1-\alpha )(x-{\mathrm{TVaR}}_{\beta }(-X)),$$

where

$$h\left(x\right)=\left\{\begin{array}{cc}{\mathrm{TVaR}}_{\beta }\left(X\right)-x,\hfill & x⩽{\mathrm{VaR}}_{\beta }\left(X\right)\hfill \\ \frac{1}{1-\beta }\mathbb{E}\left[{(X-x)}_{+}\right],\hfill & x⩾{\mathrm{VaR}}_{\beta }\left(X\right).\hfill \end{array}\right.$$

If $x⩽{\mathrm{VaR}}_{\beta }\left(X\right)$, then the equation is

$$\alpha ({\mathrm{TVaR}}_{\beta }\left(X\right)-x)=(1-\alpha )(x-{\mathrm{TVaR}}_{\beta }(-X)),$$

and the solution is $x^{\ast }=\alpha {\mathrm{TVaR}}_{\beta }\left(X\right)+(1-\alpha ){\mathrm{TVaR}}_{\beta }(-X)$. It is well-known that

$$\underset{\beta \to 1}{lim}\frac{{\mathrm{TVaR}}_{\beta }\left(X\right)}{{\mathrm{VaR}}_{\beta }\left(X\right)}=\frac{{\gamma }_1}{{\gamma }_1-1}\mathrm{and}\underset{\beta \to 1}{lim}\frac{{\mathrm{TVaR}}_{\beta }(-X)}{{\mathrm{VaR}}_{\beta }\left(X\right)}=0.$$

Hence, we have ${lim}_{\beta \to 1}{x}^{\ast }/{\mathrm{VaR}}_{\beta }\left(X\right)=\alpha {\gamma }_1/({\gamma }_1-1)$. If $\alpha {\gamma }_1/({\gamma }_1-1)<1$, then we have for $\beta$ close to 1, $e_{\alpha ;\beta }\left(X\right)=\alpha {\mathrm{TVaR}}_{\beta }\left(X\right)+(1-\alpha ){\mathrm{TVaR}}_{\beta }(-X),$ and, thus,

$$\underset{\beta \to 1}{lim}\frac{e_{\alpha ;\beta }\left(X\right)}{{\mathrm{VaR}}_{\beta }\left(X\right)}=\frac{\alpha {\gamma }_1}{{\gamma }_1-1}.$$

(11)

If $\alpha {\gamma }_1/({\gamma }_1-1)⩾1$, then $e_{\alpha ;\beta }\left(X\right)$ is the solution to

$$\frac{\alpha }{1-\beta }\mathbb{E}\left[{(X-x)}_{+}\right]=(1-\alpha )(x-{\mathrm{TVaR}}_{\beta }(-X)),$$

that is,

$$x={\mathrm{TVaR}}_{\beta }(-X)+\frac{\alpha }{(1-\alpha )(1-\beta )}{\int }_x^{\infty }\overline{F}\left(u\right)\mathrm{d}u.$$

(12)

By Proposition 1.1 of Zhu [17] or Mao et al. [18], we have

$$\underset{x\to \infty }{lim}\frac{{\int }_x^{\infty }\overline{F}\left(u\right)\mathrm{d}u}{x\overline{F}\left(x\right)}=\frac{1}{{\gamma }_1-1}.$$

(13)

Substituting this into (12) yields

$$\underset{\beta \to 1}{lim}\frac{e_{\alpha ;\beta }\left(X\right)}{{\mathrm{VaR}}_{\beta }\left(X\right)}={\left(\frac{\alpha }{(1-\alpha )({\gamma }_1-1)}\right)}^{1/{\gamma }_1}.$$

Combining this with (11), we complete the proof. □

Remark 1. 

(i) 

In general, we could not obtain similar asymptotic results for the case ${\gamma }_1={\gamma }_2$. The reason is that even if ${\gamma }_1={\gamma }_2$, we may have ${\mathrm{VaR}}_{\beta }\left(X\right)/{\mathrm{VaR}}_{\beta }(-X)$ converging to ∞ or 0 as $\beta \to 1$. Let X be a symmetric distribution about $x_0$ and $\alpha =1/2$. Then $e_{\alpha ;\beta }\left(X\right)\equiv 0$.

(ii) 

From Proposition 2, we have ${\gamma }_1<{\gamma }_2$, which means the right tail is heavier than the left tail of X, then the $e_{\alpha ;\beta }\left(X\right)$ is asymptotically determined by the right tail and is asymptotic equivalent to ${\mathrm{VaR}}_{\beta }\left(X\right)$, multiplied by some constant. In contrast, if ${\gamma }_1>{\gamma }_2$, which means the right-tail is lighter than the left tail of X, then the $e_{\alpha ;\beta }\left(X\right)$ is asymptotically determined by the left tail and is asymptotic equivalent to ${\mathrm{VaR}}_{1-\beta }\left(X\right)$, multiplied by some constant.

In the following proposition, we investigate the asymptotic properties of $e_{\alpha ;\beta }$ as $\alpha$ goes to 1.

Proposition 3. 

Let X be a random variable with the survival function $\overline{F}=1-F$, such that $\overline{F}\in {\mathrm{RV}}_{\gamma }$, $\gamma >0$ and $e_{\alpha ;\beta }\left(X\right)$ are defined by the solution to (10), $\alpha \in (0,1),\beta \in (0,1)$. Then we have

$$\underset{\alpha \to 1}{lim}\frac{e_{\alpha ;\beta }\left(X\right)}{{\mathrm{VaR}}_{\alpha }\left(X\right)}={\left((1-\beta )(\gamma -1)\right)}^{-1/\gamma }.$$

(14)

Proof. 

First note that as $\alpha \to 1$, $e_{\alpha ;\beta }\left(X\right)$ converges to infinity. Then, for the $\alpha$ that is large enough, we have $e_{\alpha ;\beta }\left(X\right)$ as no less than ${\mathrm{VaR}}_{\beta }\left(X\right)$ and ${\mathrm{VaR}}_{1-\beta }\left(X\right)$. Hence, for the $\alpha$ that is large enough, we have $e_{\alpha ;\beta }\left(X\right)$ as the unique solution to

$$\frac{\alpha }{1-\beta }\mathbb{E}\left[{(X-x)}_{+}\right]=(1-\alpha )(x-{\mathrm{TVaR}}_{\beta }(-X)),$$

i.e., (12). Similar to the proof of Proposition 2, substituting (13) into (12) yields (14). We complete the proof. □

If $\beta =0$, then $e_{\alpha ;0}\left(X\right)$ reduces to the classic expectile $e_{\alpha }$. The asymptotics result in (14) reducing to

$$\underset{\alpha \to 1}{lim}\frac{e_{\alpha }\left(X\right)}{{\mathrm{VaR}}_{\beta }\left(X\right)}={\left(\gamma -1\right)}^{-1/\gamma }.$$

It is worth mentioning that this recovers the asymptotic expansion of the classic expectile in Mao et al. [13].

3. Distributionally Robust Optimization with the TVaR-Based Expectile

3.1. Worst-Case TVaR-Based Expectile

Motivated by recent advances in distributionally robust optimization (DRO), in this section, we study the worst-case TVaR-based expectile with respect to the moment constraint. DRO has arisen as a modeling paradigm for addressing the issue of distributional ambiguity in risk management (see, e.g., Delage and Ye [14]). The power of DRO lies in its flexibility in characterizing one’s (partial) knowledge of the distribution through specifying an ambiguity set. In particular, one common way of defining the ambiguity set is by specifying the moments of the distribution, i.e., we confine the possible distributions to the following ambiguity set

$$\mathcal{P}(\mu ,\sigma )=\{F\mathrm{is}\mathrm{a}\mathrm{distribution}:{\mathbb{E}}^F\left[X\right]=\mu ,{\mathrm{var}}^F\left(X\right)={\sigma }^2\},$$

where ${\mathbb{E}}^F\left[X\right]$ and ${\mathrm{var}}^F\left(X\right)$ represent the mean and variance of X, respectively, under the constraint that X has the distribution F.

One special case of the TVaR-based expectile of X, denoted by $e_{\alpha ;\beta }\left(X\right)$, is the unique solution to the equation

$$\begin{array}{c}\hfill \alpha \mathbb{E}\left[{(X-x)}_{+}\right]=(1-\alpha ){\mathrm{TVaR}}_{\beta }\left({(X-x)}_{-}\right)x\in \mathbb{R}.\end{array}$$

(15)

We study the worst-case TVaR-based expectile given the expectation $\mu$ and variance ${\sigma }^2$. That is, we aim to find

$$e_{\alpha ;\beta }^{\uparrow }\left(X\right)=\underset{F\in \mathcal{P}(\mu ,\sigma )}{sup}{e}_{\alpha ;\beta }\left(X_F\right),$$

where $X_F$ is the random variable with the distribution F. Note that $e_{\alpha ;\beta }$ satisfies the translation–invariance and positive homogeneity, i.e.,

$$e_{\alpha ;\beta }(X+c)=e_{\alpha ;\beta }\left(X\right)+c,e_{\alpha ;\beta }\left(\lambda X\right)=\lambda e_{\alpha ;\beta }\left(X\right),c\in \mathbb{R},\lambda \in {\mathbb{R}}_{+}.$$

Then ${sup}_{F\in \mathcal{P}(\mu ,\sigma )}{e}_{\alpha ;\beta }\left(X_F\right)=\mu +\sigma {sup}_{F\in \mathcal{P}(0,1)}{e}_{\alpha ;\beta }\left(X_F\right)$. It suffices to investigate the special case that $\mu =0$ and $\sigma =1$. To show our main result, we need the following lemmas.

Lemma 2. 

Let ρ be a risk measure satisfying translation–invariance and positive homogeneity and ${\rho }^{\uparrow }$ be the worst-case of ρ. If ${\rho }^{\uparrow }\left(X\right)⩾\mu$, then we have ${\rho }^{\uparrow }$ as increasing in μ and σ. Hence,

$${\rho }^{\uparrow }\left(X\right)=\underset{F\in {\mathcal{P}}_0(\mu ,\sigma )}{sup}\rho \left(X_F\right),$$

where ${\mathcal{P}}_0(\mu ,\sigma )$ is the set of all possible distributions of X, such that it has a mean no larger than μ and variance no larger than ${\sigma }^2$.

Lemma 3. 

Let $e_{\alpha ;\beta }\left(X\right)$ be the TVaR-based expectile of X defined by (7). Then $e_{\alpha ;\beta }^{\uparrow }\left(X\right)⩾\mu$.

Proof. 

It suffices to show the case for $\mu =0$. Consider a random variable $X_{\gamma }$ given by

$$\mathbb{P}\left(X_{\gamma }=-\sqrt{\frac{1-\gamma }{\gamma }}\right)=\gamma ,\mathbb{P}\left(X_{\gamma }=\sqrt{\frac{\gamma }{1-\gamma }}\right)=1-\gamma ,\gamma \in (0,1).$$

It is obvious that $\mathbb{E}\left[X_{\gamma }\right]=0$ and $\mathrm{Var}\left(X_{\gamma }\right)=1$. Letting $\gamma \to 1^{-}$, one can verify that $e_{\alpha ;\beta }\left(X_{\gamma }\right)$ goes to 0. To see it, suppose that ${lim\; inf}_{\gamma \to 1^{-}}{e}_{\alpha ;\beta }\left(X_{\gamma }\right)<-\delta$ for some $\delta >0$. Then there exists ${\gamma }_0<1$, such that $-\sqrt{(1-\gamma )/\gamma }>-\delta$ for $\gamma >{\gamma }_0$, and in this case, ${(X_{\gamma }+\delta )}_{-}\equiv 0$. Denote

$$h\left(x\right):=\alpha \mathbb{E}\left[{(X-x)}_{+}\right]-(1-\alpha ){\mathrm{TVaR}}_{\beta }\left({(X-x)}_{-}\right),x\in \mathbb{R}.$$

Then

$$h(-\delta )=\alpha \mathbb{E}\left[{(X+\delta )}_{+}\right]>0.$$

Note that $h\left(x\right)$ is a decreasing function in x and $e_{\alpha ;\beta }\left(X_{\gamma }\right)$ is the solution to $h\left(x\right)=0$. It then follows that $e_{\alpha ;\beta }\left(X_{\gamma }\right)>-\delta$ for $\gamma >{\gamma }_0$. That is, ${lim\; inf}_{\gamma \to 1^{-}}{e}_{\alpha ;\beta }\left(X_{\gamma }\right)>-\delta$ for $\gamma >{\gamma }_0$, which yields a contradiction. Hence, this completes the proof. □

Combining Lemmas 2 and 3, we have that $e_{\alpha ;\beta }^{\uparrow }\left(X\right)$ is increasing in $\alpha$ and $\sigma$ and, hence, $e_{\alpha ;\beta }^{\uparrow }\left(X\right)={sup}_{F\in {\mathcal{P}}_0(\mu ,\sigma )}{e}_{\alpha ;\beta }\left(X_F\right).$

Remark 2. 

Note that (7) can be rewritten as

$$x=\mathbb{E}\left[X\right]+\mathbb{E}\left[{(X-x)}_{-}\right]-\frac{1-\alpha }{\alpha }{\mathrm{TVaR}}_{\beta }\left({(X-x)}_{-}\right).$$

If $\alpha ⩽1/2$, it is obvious that $(1-\alpha )/\alpha ⩾1$ and $\mathbb{E}\left[{(X-x)}_{-}\right]⩽{\mathrm{TVaR}}_{\beta }\left({(X-x)}_{-}\right)$, which implies that $e_{\alpha ,\beta }\left(X\right)⩽\mathbb{E}\left[X\right]$ for any random variable X. Hence, by Lemma 3, we have $e_{\alpha ,\beta }^{\uparrow }\left(X\right)=\mu$. Therefore, in the following, we only consider the case that $\alpha >1/2$.

Lemma 4. 

Let $e_{\alpha ;\beta }\left(X\right)$ be the TVaR-based expectile of X defined by (7). Then the worst-case distribution is a bivariate distribution. Specifically, we have

$${\rho }^{\uparrow }\left(X\right)=\underset{F\in {\mathcal{P}}^b(\mu ,\sigma )}{sup}\rho \left(X_F\right),$$

where ${\mathcal{P}}^b(\mu ,\sigma )$ is the set of all bivariate distributions in $\mathcal{P}(\mu ,\sigma )$.

Proof. 

By Lemmas 2 and 3, it suffices to show that for any distribution in $\mathcal{P}(\mu ,\sigma )$, we can find a bivariate distribution in ${\mathcal{P}}_0(\mu ,\sigma )$, such that its value of risk measure is no less than that of the original distribution. Let $X_F$ be a random variable with distribution $F\in \mathcal{P}(\mu ,\sigma )$ and $x_0=e_{\alpha ;\beta }^{\uparrow }\left(X_F\right)$. Define

$$X_F^{\ast }=\left\{\begin{array}{cc}\mathbb{E}\left[X_F\right|X_F⩽x_0],\hfill & X_F⩽x_0,\hfill \\ \mathbb{E}\left[X_F\right|X_F>x_0],\hfill & X_F>x_0.\hfill \end{array}\right.$$

It is obvious that $\mathbb{E}\left[X_F^{\ast }\right]=\mathbb{E}\left[X_F\right]=\mu$ and $\mathrm{Var}\left(X_F^{\ast }\right)⩽{\sigma }^2$, i.e., the distribution of $X_F^{\ast }$ belongs to ${\mathcal{P}}_0(\mu ,\sigma )$. Note that $x_0-X_F^{\ast }{\prec }_{\mathrm{cx}}{x}_0-X_F$ and, thus, ${(x_0-X_F^{\ast })}_{+}{\prec }_{\mathrm{icx}}{(x_0-X_F)}_{+}$ (let X and Y be two random variables X is said to be smaller than Y in increasing convex order, denoted by $X{\prec }_{\mathrm{icx}}Y$, if $\mathbb{E}\left[\varphi \right(X\left)\right]⩽\mathbb{E}\left[\varphi \right(Y\left)\right]$ for any increasing convex function $\varphi$. X is said to be smaller than Y in convex order, denoted by $X{\prec }_{\mathrm{cx}}Y$, if $\mathbb{E}\left[X\right]=\mathbb{E}\left[Y\right]$ and $X{\prec }_{\mathrm{icx}}Y$.), which implies

$${\mathrm{TVaR}}_{\beta }\left({(X_F^{\ast }-x_0)}_{-}\right)⩽{\mathrm{TVaR}}_{\beta }\left({(X_F-x_0)}_{-}\right).$$

Moreover, note that $\mathbb{E}\left[{(X_F^{\ast }-x_0)}_{+}\right]=\mathbb{E}\left[{(X_F-x_0)}_{+}\right]$. Then we have

$$\alpha \mathbb{E}\left[{(X_F^{\ast }-x_0)}_{+}\right]-(1-\alpha ){\mathrm{TVaR}}_{\beta }\left({(X_F^{\ast }-x_0)}_{-}\right)⩾0.$$

This implies $e_{\alpha ;\beta }\left(X_F^{\ast }\right)⩾x_0$. Hence, we complete the proof. □

By Lemma 4, we only need to find the worst-case distribution in the set ${\mathcal{P}}^b(\mu ,\sigma )$. Now we are ready to show the main result.

Theorem 1. 

For $\alpha >1/2$, let $e_{\alpha ;\beta }$ be defined by (7). Then we have

$$e_{\alpha ;\beta }^{\uparrow }\left(X\right)=\mu +\sigma K_{\alpha ,\beta },$$

where

$$\begin{array}{c}\hfill K_{\alpha ,\beta }=\left\{\begin{array}{cc}\frac{2\alpha -\alpha \beta -1}{2\sqrt{\alpha (1-\alpha )(1-\beta )}},\hfill & \beta ⩽{\beta }_{\alpha }^{\ast },\hfill \\ s_{\alpha },\hfill & \beta ⩾{\beta }_{\alpha }^{\ast },\hfill \end{array}\right.\end{array}$$

(16)

with

$$s_{\alpha }=\left(\frac{\alpha }{1-\alpha {\gamma }^{\ast }}-1\right)\sqrt{\frac{1-{\gamma }^{\ast }}{{\gamma }^{\ast }}},{\beta }_{\alpha }^{\ast }=1-\frac{1-\alpha }{\alpha }{\left(\sqrt{1+s_{\alpha }^2}+s_{\alpha }\right)}^2$$

$${\gamma }^{\ast }=\frac{3\alpha -2+s}{2\alpha },\mathrm{and}s=\sqrt{9{\alpha }^2-16\alpha +8}.$$

Proof . 

Without loss of generality, we assume $\mu =0$ and $\sigma =1$. Then

$${\mathcal{P}}^b(0,1)=\left\{\mathrm{df}\mathrm{of}{X}_{\gamma }\left|\mathbb{P}\left(X_{\gamma }=-\sqrt{\frac{1-\gamma }{\gamma }}\right)=\gamma ,\mathbb{P}\left(X_{\gamma }=\sqrt{\frac{\gamma }{1-\gamma }}\right)=1-\gamma ,\gamma \in (0,1)\right.\right\}.$$

We next calculate $e_{\alpha ,\beta }\left(X_{\gamma }\right)$ for $\gamma \in [0,1]$ for the following two cases. If $\gamma ⩽1-\beta$, then $e_{\alpha ,\beta }\left(X_{\gamma }\right)$ satisfies the equation

$$\alpha (1-\gamma )\left(\sqrt{\frac{\gamma }{1-\gamma }}-x\right)=(1-\alpha )\frac{\gamma }{1-\beta }\left(\sqrt{\frac{1-\gamma }{\gamma }}+x\right),x\in \left[-\sqrt{\frac{1-\gamma }{\gamma }},\sqrt{\frac{\gamma }{1-\gamma }}\right].$$

and if $\gamma ⩾1-\beta$, then $e_{\alpha ,\beta }\left(X_{\gamma }\right)$ satisfies the equation

$$\alpha (1-\gamma )\left(\sqrt{\frac{\gamma }{1-\gamma }}-x\right)=(1-\alpha )\left(\sqrt{\frac{1-\gamma }{\gamma }}+x\right),x\in \left[-\sqrt{\frac{1-\gamma }{\gamma }},\sqrt{\frac{\gamma }{1-\gamma }}\right].$$

That is,

$$e_{\alpha ,\beta }\left(X_{\gamma }\right)=\left\{\begin{array}{cc}\frac{\alpha (1-\beta )-(1-\alpha )}{\alpha (1-\beta )(1-\gamma )+(1-\alpha )\gamma }\sqrt{\gamma (1-\gamma )},\hfill & \gamma ⩽1-\beta \hfill \\ \frac{\alpha \gamma +\alpha -1}{\gamma (1-\alpha \gamma )}\sqrt{\gamma (1-\gamma )},\hfill & \gamma ⩾1-\beta .\hfill \end{array}\right.$$

(17)

Denote by $h_1\left(\gamma \right)$ and $h_2\left(\gamma \right)$ the two functions of the right-hand side of (17), respectively. By taking derivatives of $h_1\left(\gamma \right)$ with respect to $\gamma$, it is easy to see that $h_1\left(\gamma \right)$ takes its maximum value

$$h_1\left({\gamma }_1^{\ast }\right)=\frac{2\alpha -\alpha \beta -1}{2\sqrt{\alpha (1-\alpha )(1-\beta )}}\mathrm{at}{\gamma }_1^{\ast }=\frac{\alpha (1-\beta )}{\alpha (1-\beta )+1-\alpha }=\frac{\alpha (1-\beta )}{1-\alpha \beta },$$

and $h_1\left(\gamma \right)$ is increasing in $\gamma ⩽{\gamma }_1^{\ast }$ and decreasing in $\gamma ⩾{\gamma }_1^{\ast }$. On the other hand, by taking derivatives of $h_2\left(\gamma \right)$ with respect to $\gamma$, one can verify that $h_2\left(\gamma \right)$ takes its maximum value

$$h_2\left({\gamma }^{\ast }\right)=\frac{(2-\alpha )(3\alpha -2)+\alpha s}{4\sqrt{2}{(1-\alpha )}^{3/2}}\sqrt{\alpha s-3{\alpha }^2+4\alpha -2}.$$

at

$${\gamma }^{\ast }=\frac{3\alpha -2+s}{2\alpha }\mathrm{with}s=\sqrt{9{\alpha }^2-16\alpha +8},$$

and $h_2\left(\gamma \right)$ is increasing in $\gamma ⩽{\gamma }^{\ast }$ and decreasing in $\gamma ⩾{\gamma }^{\ast }$. Hence, by (17), the maximum value of $e_{\alpha ,\beta }\left(X_{\gamma }\right)$ could be attained at one of the points $\{0,{\gamma }_1^{\ast },1-\beta ,{\gamma }^{\ast },1\}$. We next consider the following three cases.

(i)

If $\beta ⩽1-{\gamma }^{\ast }$, then one can find that confining on $\{\gamma ⩾1-\beta \}$, $e_{\alpha ,\beta }\left(X_{\gamma }\right)$ takes its maximum value at point $\gamma =1-\beta$. On the other hand, note that

$$1-{\gamma }^{\ast }=\frac{1}{\alpha }-1-\frac{s}{2\alpha }+\frac{1}{2},$$

and $s>\alpha$, which imply $1-{\gamma }^{\ast }⩽1/\alpha -1.$ Hence, we have in this case, $\alpha <1/(1+\beta )$. Then one can easily verify that ${\gamma }_1^{\ast }⩽1-\beta$. This implies that confining on $\{\gamma ⩽1-\beta \}$, $e_{\alpha ,\beta }\left(X_{\gamma }\right)$ takes its maximum value at point $\gamma ={\gamma }_1^{\ast }$ and the corresponding maximum value is no less than $e_{\alpha ,\beta }\left(X_{1-\beta }\right)$. Therefore, $e_{\alpha ,\beta }\left(X_{\gamma }\right)$ takes its maximum value at ${\gamma }_1^{\ast }$.

(ii)

If $1-{\gamma }^{\ast }⩽\beta ⩽1/\alpha -1$, then one can verify that confining on $\{\gamma ⩾1-\beta \}$, $e_{\alpha ,\beta }\left(X_{\gamma }\right)$ takes its maximum value at point $\gamma ={\gamma }_1^{\ast }$, while confining on $\{\gamma ⩾1-\beta \}$, $e_{\alpha ,\beta }\left(X_{\gamma }\right)$ takes its maximum value at point $\gamma ={\gamma }^{\ast }$. Hence, to find the maximum value at the whole interval $\gamma \in [0,1]$, we need to compare the values of $e_{\alpha ,\beta }\left(X_{\gamma }\right)$ at ${\gamma }_1^{\ast }$ and ${\gamma }^{\ast }$. Note that

$$e_{\alpha ,\beta }\left(X_{{\gamma }_1^{\ast }}\right)=\frac{2\alpha -\alpha \beta -1}{2\sqrt{\alpha (1-\alpha )(1-\beta )}}\mathrm{and}{e}_{\alpha ,\beta }\left(X_{{\gamma }^{\ast }}\right)=\left(\frac{\alpha }{1-\alpha {\gamma }^{\ast }}-1\right)\sqrt{\frac{1-{\gamma }^{\ast }}{{\gamma }^{\ast }}}.$$

One can verify that for $\alpha >1/2$,

$$e_{\alpha ,\beta }\left(X_{{\gamma }_1^{\ast }}\right)=\frac{1}{2}\sqrt{\frac{\alpha (1-\beta )}{1-\alpha }}-\frac{1}{2}\sqrt{\frac{1-\alpha }{\alpha (1-\beta )}}$$

is decreasing in $\beta$. Hence, $e_{\alpha ,\beta }\left(X_{{\gamma }_1^{\ast }}\right)$ takes its minimum value at $\beta =1/\alpha -1$ and its maximum value at $\beta =1-{\gamma }^{\ast }$. Note that $e_{\alpha ,1/\alpha -1}\left(X_{{\gamma }_1^{\ast }}\right)⩽e_{\alpha ,\beta }\left(X_{{\gamma }^{\ast }}\right)$. Moreover, we have $e_{\alpha ,1-{\gamma }^{\ast }}\left(X_{{\gamma }_1^{\ast }}\right)⩾0$, i.e., when $\alpha -1+\alpha {\gamma }^{\ast }⩾0$,

$$\begin{array}{cc}\hfill e_{\alpha ,1-{\gamma }^{\ast }}\left(X_{{\gamma }_1^{\ast }}\right)-e_{\alpha ,\beta }\left(X_{{\gamma }^{\ast }}\right)& =\frac{\alpha -1+\alpha {\gamma }^{\ast }}{\sqrt{{\gamma }^{\ast }}}\left(\frac{1}{2\sqrt{\alpha (1-\alpha )}}-\frac{\sqrt{1-{\gamma }^{\ast }}}{1-\alpha {\gamma }^{\ast }}\right)\hfill \\ \hfill & ⩾\frac{\alpha -1+\alpha {\gamma }^{\ast }}{\sqrt{{\gamma }^{\ast }}}\left(\frac{1}{2\sqrt{\alpha (1-\alpha )}}-\frac{\sqrt{1-(2-1/\alpha )}}{1-\alpha (2-1/\alpha )}\right)=0,\hfill \end{array}$$

where the first inequality follows from the mapping $v\mapsto \sqrt{1-v}/\left(1-\alpha v\right)$ and is decreasing in $v⩾2-1/\alpha$. Then there exists a unique $\beta \in [1-{\gamma }^{\ast },1/\alpha -1]$, such that it is the solution to the equation $e_{\alpha ,\beta }\left(X_{{\gamma }_1^{\ast }}\right)=e_{\alpha ,\beta }\left(X_{{\gamma }^{\ast }}\right)$, i.e., $\beta ={\beta }_{\alpha }^{\ast }$, such that if $\beta ⩽{\beta }_{\alpha }^{\ast }$, then $e_{\alpha ,\beta }\left(X_{{\gamma }_1^{\ast }}\right)⩾e_{\alpha ,\beta }\left(X_{{\gamma }^{\ast }}\right)$ and, thus, $e_{\alpha ,\beta }\left(X_{\gamma }\right)$ takes its maximum value at ${\gamma }_1^{\ast }$. If $\beta >{\beta }_{\alpha }^{\ast }$, then $e_{\alpha ,\beta }\left(X_{{\gamma }_1^{\ast }}\right)<e_{\alpha ,\beta }\left(X_{{\gamma }^{\ast }}\right)$ and, thus, $e_{\alpha ,\beta }\left(X_{\gamma }\right)$ takes its maximum value at ${\gamma }^{\ast }$.

(iii)

If $\beta ⩾1/\alpha -1$, one can verify that ${\gamma }_1^{\ast }⩾1-\beta$ and $\alpha \beta (2-\alpha -\alpha \beta )⩾(1-\alpha )(2\alpha -1)$, i.e., ${\gamma }^{\ast }⩾1-\beta$. This implies that $e_{\alpha ,\beta }\left(X_{\gamma }\right)$ is increasing in $\gamma ⩽{\gamma }^{\ast }$ and decreasing in $\gamma >{\gamma }^{\ast }$. Therefore, $e_{\alpha ,\beta }\left(X_{\gamma }\right)$ takes its maximum value at ${\gamma }^{\ast }$.

Combining the above three cases, we complete the proof. □

Note that when $\beta =0$, the TVaR-based expectile $e_{\alpha ,0}$ reduces to the classic expectile. By Li [16], we can show the following result for the expectile.

Corollary 2. 

The worst-case expectile is given by

$$e_{\alpha }^{\uparrow }\left(X\right)=\mu +\sigma \frac{2\alpha -1}{2\alpha }\sqrt{\frac{\alpha }{1-\alpha }}$$

and the worst-case distribution F is given by

$$F^{-1}\left(u\right)=\mu -\sigma \sqrt{\frac{1-\alpha }{\alpha }}{1}_{\{u<\alpha \}}+\sigma \sqrt{\frac{\alpha }{1-\alpha }}{1}_{\{u⩾\alpha \}}.$$

Proof. 

For completeness, we give another direct proof. By Bellini et al. [2], we have the following dual representation,

$$\begin{array}{cc}\hfill e_{\alpha }\left(X\right)& =\underset{\gamma \in [1/\beta ,1]}{sup}\left\{(1-\gamma ){\mathrm{ES}}_{(\beta -1/\gamma )/(\beta -1)}\left(X\right)+\gamma \mathbb{E}\left[X\right]\right\}\hfill \\ \hfill & =\underset{\gamma \in [1/\beta ,1]}{sup}{\int }_0^1{\mathrm{VaR}}_u\left(X\right)\mathrm{d}{h}_{\gamma }\left(u\right),\hfill \end{array}$$

where $\beta =\alpha /(1-\alpha )$ and $h_{\gamma }^{\prime }\left(u\right)=\frac{1-\gamma }{1-\xi }{1}_{\{u⩾\xi \}}+\gamma$ with $\xi =(\beta -1/\gamma )/(\beta -1)$. Note that

$$\begin{array}{cc}\hfill \parallel h_{\gamma }^{\prime }{-1\parallel }_2& =(1-\gamma ){∥\frac{1}{1-\xi }{1}_{\{u⩾\xi \}}-1∥}_2\hfill \\ \hfill & =(1-\gamma )\sqrt{{\int }_0^1{\left(\frac{1}{1-\xi }{1}_{\{u⩾\xi \}}-1\right)}^2\mathrm{d}u}\hfill \\ \hfill & =(1-\gamma )\sqrt{\frac{\xi }{1-\xi }}=\sqrt{\frac{\beta \gamma -1}{1-\gamma }}.\hfill \end{array}$$

By Lemma 2, we have

$$\begin{array}{cc}\hfill e_{\alpha }^{\uparrow }\left(X\right)& =\mu +\sigma \underset{\gamma \in [1/\beta ,1]}{sup}(1-\gamma )\sqrt{\frac{\beta \gamma -1}{1-\gamma }}\hfill \\ \hfill & =\mu +\sigma \underset{\gamma \in [1/\beta ,1]}{sup}\sqrt{\beta (1-\gamma )(\gamma -1/\beta )}\hfill \\ \hfill & =\mu +\sigma \sqrt{\beta {\left(\frac{\beta -1}{2\beta }\right)}^2}=\mu +\sigma \frac{2\alpha -1}{2\alpha }\sqrt{\frac{\alpha }{1-\alpha }}.\hfill \end{array}$$

Note that in the above equation, the supremum is attained at the optimal ${\gamma }^{\ast }=(\beta +1)/\left(2\beta \right)=1/\left(2\alpha \right)$. The corresponding distortion function has the left derivative function $h_{{\gamma }^{\ast }}^{\prime }\left(u\right)=\frac{1}{2\alpha }{1}_{\{u⩽\alpha \}}+\frac{1}{2(1-\alpha )}{1}_{\{u>\alpha \}}$. Hence, the worst-case distribution F is given by

$$F^{-1}\left(u\right)=\frac{c}{2\alpha }{1}_{\{u<\alpha \}}+\frac{c}{2(1-\alpha )}{1}_{\{u⩾\alpha \}}+\mu -c,$$

where $c=\frac{2\sigma }{2\alpha -1}\sqrt{\alpha (1-\alpha )}$ is a constant. Then the result follows by taking variance as ${\sigma }^2$. This completes the proof. □

3.2. Application in the Portfolio Selection

In this subsection, we are interested in the following distributionally robust portfolio optimization problem under the mean-variance uncertainty set:

$$\underset{\mathbf{w}\in \mathbb{W}}{inf}\underset{F\in \mathcal{P}(\mathbf{\mu },\Sigma )}{sup}{e}_{\alpha ,\beta }^F\left({\mathbf{w}}^{\top }\mathbf{X}\right)$$

(18)

where

$$\mathbb{W}=\{\mathbf{w}=(w_1,\dots ,w_d):w_i⩾0,{\mathbf{1}}^{\top }\mathbf{w}=1\},$$

$$\begin{array}{c}\hfill \mathcal{P}(\mathbf{\mu },\Sigma ):=\{F:{\mathbb{E}}^F\left[\mathbf{X}\right]=\mathbf{\mu },{\mathrm{Var}}^F\left(\mathbf{X}\right)=\Sigma \},\end{array}$$

and $e_{\alpha ,\beta }^F$ represents the TVaR-based expectile of ${\mathbf{w}}^{\top }\mathbf{X}$ that is calculated under the constraint that the distribution of $\mathbf{X}$ is F. This kind of distributionally robust portfolio optimization problem under different principles was recently studied by Sim et al. [19], Blanchet et al. [15] and the references therein. By Theorem 1 and the projection result on the moment-based ambiguity set by Chen et al. [20], we can reduce Problem (18). We first recall the projection result from Chen et al. [20]: For $\mathbf{w}\in {\mathbb{R}}^d$, it holds that

$$\mathcal{S}(\mathbf{w},\mathbf{\mu },\Sigma )={\mathcal{S}}_{\mathbf{w}}(\mathbf{\mu },\Sigma ),$$

where

$$\begin{array}{cc}\hfill \mathcal{S}(\mathbf{w},\mathbf{\mu },\Sigma )=\{& F_{\mathbf{w}}:F\in \mathcal{S}(\mathbf{\mu },\Sigma )\hfill \\ & F_{\mathbf{w}}\mathrm{is} \mathrm{the} \mathrm{distribution} \mathrm{of} {\mathbf{w}}^{\top }\mathbf{X} \mathrm{when} \mathrm{the} \mathrm{distribution} \mathrm{of} \mathbf{X} \mathrm{is} F\}\hfill \end{array}$$

and

$${\mathcal{S}}_{\mathbf{w}}(\mathbf{\mu },\Sigma )=\{F:{\mathbb{E}}^F\left[\mathbf{X}\right]={\mathbf{w}}^{\top }\mathbf{\mu },{\mathrm{Var}}^F\left(\mathbf{X}\right)={\mathbf{w}}^{\top }\Sigma \mathbf{w}\}.$$

In the following theorem, we solve the inner problem of Problem (18) and give a equivalent optimization problem to Problem (18) in the sense that two problems have the same optimal solution.

Theorem 2. 

Given $c\in \mathbb{R}$, $\mathbf{w}\in \mathbb{W}$, $\mu \in {\mathbb{R}}^d$ and Σ, a positive semi-defined matrix of ${\mathbb{R}}^{d\times d}$, we assume ${\mathbf{w}}^{\top }\mu ⩾c$. Problem (18) is equivalent to the following optimization problem:

$$\underset{\mathbf{w}\in \mathbb{W}}{min}{\mathbf{w}}^{\top }\mu +K_{\alpha ,\beta }\sqrt{{\mathbf{w}}^{\top }\Sigma \mathbf{w}},$$

(19)

where $K_{\alpha ,\beta }$ is given by (16).

Note that $K_{\alpha ,\beta }$ given by (16) is a constant independent from the decision variable $\mathbf{w}$. Problem (19) is a convex quadratic program. We reduce Problem (18) to a convex quadratic program.

4. Empirical Results

To demonstrate the viability and robustness of the proposed approach, a robust optimal portfolio strategy was determined using Python programming. A total of 10 stocks from diverse sectors of the Chinese stock market were selected to comprise the portfolio. The stock codes that make up the portfolio in the empirical study are shown in the Table 1 and $X={(X_1,\dots ,X_{10})}^T$ is a 10-dimensional vector where $X_i$ represents the ith stock return for $i=1,\dots ,10.$

Table 1. The assets from the Chinese stock market.

Stock Code	Return	Stock Code	Return	Stock Code	Return	Stock Code	Return	Stock Code	Return
000596	$X_1$	600519	$X_2$	601788	$X_3$	002315	$X_4$	002959	$X_5$
603868	$X_6$	688068	$X_7$	300760	$X_8$	600988	$X_9$	000688	$X_{10}$

We obtained the daily closing prices for these 485 stocks from cn.investing.com for the period from 1 January 2020 to 31 December 2021. The Table 2 shows key characteristics of the 10 stock returns, such as the mean, variance, and correlation coefficients.

Table 2. Means, variance, and correlation coefficients of stock returns.

Stock	Mean	Variance	Correlation Coefficient
$X_1$	0.001702	0.001027	1	0.58	0.23	0.13	0.3	0.33	0.05	0.33	0.08	−0.04
$X_2$	0.001452	0.000442	0.58	1	0.31	0.16	0.34	0.31	0.07	0.45	0.1	−0.08
$X_3$	0.000643	0.000808	0.23	0.31	1	0.34	0.23	0.2	0.01	0.17	0.17	0.12
$X_4$	0.000632	0.001076	0.13	0.16	0.34	1	0.2	0.18	0.06	0.12	0.16	0.17
$X_5$	0.000921	0.001193	0.3	0.34	0.23	0.2	1	0.3	0.08	0.27	0.11	0.04
$X_6$	0.000532	0.000538	0.33	0.31	0.2	0.18	0.3	1	0.08	0.23	0.1	0.07
$X_7$	0.002461	0.002833	0.05	0.07	0.01	0.06	0.08	0.08	1	0.22	0.06	0.07
$X_8$	0.001962	0.000825	0.33	0.45	0.17	0.12	0.27	0.23	0.22	1	0.07	−0.08
$X_9$	0.002818	0.001215	0.08	0.1	0.17	0.16	0.11	0.1	0.06	0.07	1	0.21
$X_{10}$	0.000559	0.001037	−0.04	−0.08	0.12	0.17	0.04	0.07	0.07	−0.08	0.21	1

We present below the comparative models used in the empirical studies, mainly the classical portfolio model, the $\frac{1}{n}$ equally weighted portfolio model, and the portfolio model based on the risk measure CVaR. According to Harry Markowitz [21], the core idea of the traditional portfolio model is the strategy of minimizing variance to achieve the optimal weighting based on the presumption that the expected return is greater than the risk-free return. The $\frac{1}{n}$ equally weighted model is an equally weighted investment strategy in which the total capital is dynamically allocated equally to each asset in the portfolio. This is a simple but highly effective strategy. However, in the presence of large stocks with high volatility, many optimal strategies will be biased toward the investment strategy. The primary idea of the CVaR-based portfolio model is to determine the optimal weights based on the available data in order to minimize the CVaR under conditions of returns that are greater than predicted.

We obtain the worst-case TVaR-based expectile by setting various anticipated returns and inserting them into the theorem, where $\alpha =0.85,0.90,0.95$, and $\beta =0,0.1,0.95$, respectively. The Figure 1 displays the worst-case efficiency bounds generated by the robust portfolio and classical portfolio models. Note that the classical portfolio model is based on the mean-variance model to compute the optimal weights to bring into Equation (19) in order to obtain the largest risk exposure achievable using the classical portfolio strategy.

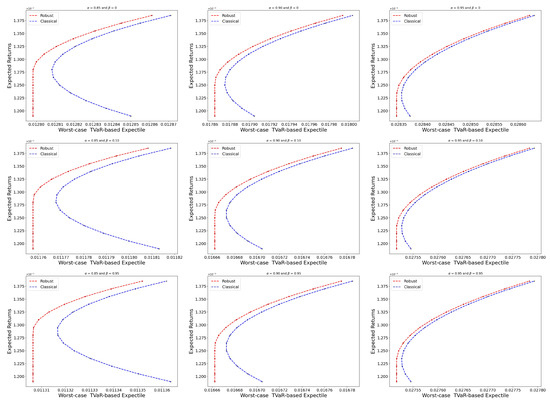
Figure 1. The effective boundaries of the classical investment strategy and robust investment strategy based on the worst-case TVaR-based expectile.

Given the same desired return, the worst-case TVaR-based expectile of a robust portfolio strategy is less than the corresponding risk of a classical portfolio strategy. This is intuitive, as the objective of the robust model is to minimize the worst-case TVaR-based expectile. The following is an empirical examination of the performance of the robust portfolio model.

Using the first 30 days of stock data, and assuming an initial asset value of 1 and a sliding time window of 30 days, we determine the optimal weight vector for the various strategy models. Then, we utilize this weight vector for the following day’s investment and the return vector for that day to obtain the new asset value. Following this approach and advancing the data, we can finally obtain the cumulative returns for the various investment strategies from 2020 to 2022. The results are displayed in the Figure 2.

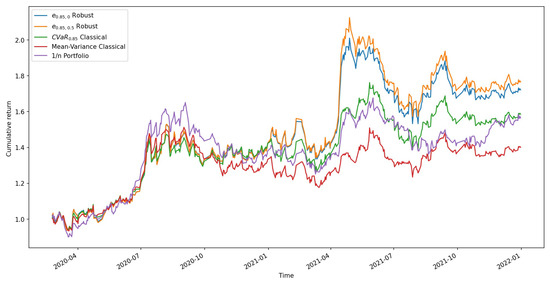
Figure 2. Cumulative returns of optimal portfolio strategies under different strategies.

The general trend in cumulative return values indicates a minor decline in the market in early 2020 due to COVID-19. During the decline, the robust portfolio was much more stable than other investment strategies, experiencing smaller decreases than other strategies. Due to the well-controlled epidemic in China, the subsequent swift recovery of the Chinese economy, and the general outstanding performance of the stock market, the portfolio has steadily gained value, with the $\frac{1}{n}$ equal-weighted investment model demonstrating the highest returns.

Nevertheless, due to market volatility, the other investment strategies lost more than the robust investment strategy during the stock market decline in 2021; therefore, the final findings indicate that the robust portfolio has the best cumulative return, followed by the CVaR-based portfolio model and finally the $\frac{1}{n}$ equal-weighted model and the mean-variance model. As a result, the robust investment model performs admirably in terms of both its robustness and its cumulative returns.

5. Conclusions

In this paper, to better capture the tail risk, we propose a class of new risk measures called TVaR-based expectiles. The basic properties of risk measures, such as monotonicity, translation invariance, positive homogeneity, and subadditivity are studied. In particular, the equivalent characterization of coherency is given. For a better understanding of TVaR-based expectiles for extreme risks, asymptotic expansions with respect to quantiles were investigated. In addition, the closed-form of the worst-case TVaR-based expectile under the moment uncertainty set was obtained, and based on this closed-form, the distributionally robust portfolio selection problem with the principle of the TVaR-based expectile was reduced to a convex quadratic program. The empirical results for financial data were given to illustrate the performance of the new risk measure compared with the classic expectile and TVaR. Compared with the classic expectile, our TVaR-based expectiles employ more conservative risk measures than expectations to evaluate the risks and, thus, put more weight on the tail risk, which is more reasonable in practice.