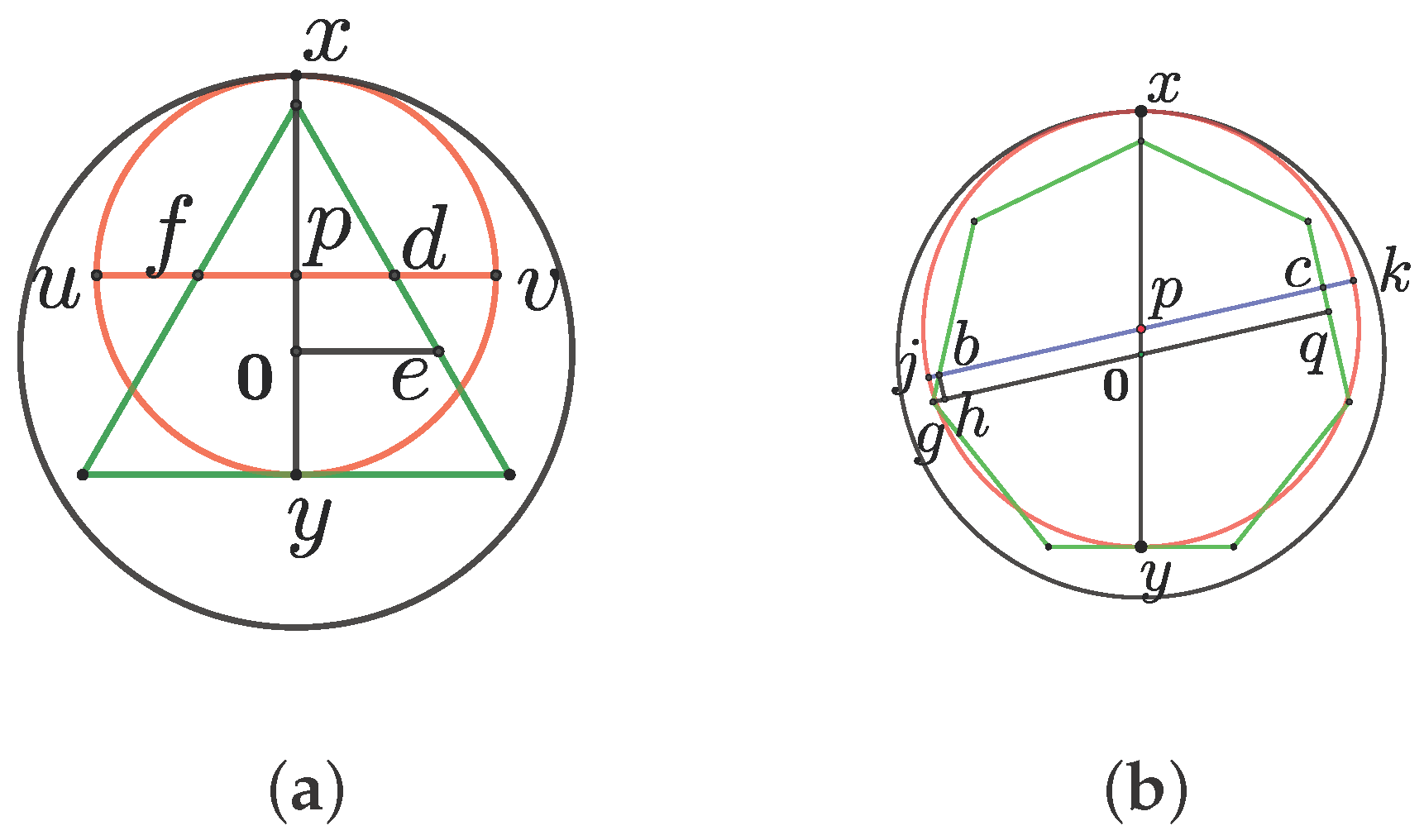Right Quadruple Convexity of Complements

Abstract

Let $\mathcal{F}$ be a family of sets in ${\mathbb{R}}^d$ (always $d\ge 2$). A set $M\subset {\mathbb{R}}^d$ is called $\mathcal{F}$-convex, if for any pair of distinct points $x,y\in M$, there is a set $F\in \mathcal{F}$, such that $x,y\in F$ and $F\subset M$. A set of four points $\{w,x,y,z\}\subset {\mathbb{R}}^d$ is called a rectangular quadruple, if $\mathrm{conv}\{w,x,y,z\}$ is a non-degenerate rectangle. If $\mathcal{F}$ is the family of all rectangular quadruples, then we obtain the right quadruple convexity, abbreviated as $rq$-convexity. In this paper we focus on the $rq$-convexity of complements, taken in most cases in balls or parallelepipeds.

1. Introduction

In 1974, the third author proposed at the meeting on Convexity in Oberwolfach the investigation of the following general convexity concept. Let $\mathcal{F}$ be a family of sets in ${\mathbb{R}}^d$ (always $d\ge 2$). A set $M\subset {\mathbb{R}}^d$ is called $\mathcal{F}$-convex, if for any pair of distinct points $x,y\in M$, there is a set $F\in \mathcal{F}$, such that $x,y\in F$ and $F\subset M$ [1].

Let $M\subset {\mathbb{R}}^d$. If, for $x,y\in M$, there exists a set $F\in \mathcal{F}$, such that $x,y\in F$ and $F\subset M$, then we say that $x,y$ enjoy the $\mathcal{F}$-property in M.

If, for any $x,y\in M$, there exists a non-degenerate rectangle F, such that $x,y\in F$ and $F\subset M$, then we call the set M rectangularly convex, or r-convex, for short.

In [1] a very simple characterization of planar convex bodies which are r-convex is presented, but only as a conjecture. The characterization in the unbounded case is given in [1], not only in the plane, but also in the much harder 3-dimensional case.

For the case of planar convex bodies, the characterization was proven only for some particular families of sets, in [1] and by K. Böröczky in [2]. The general conjecture from 1980 is still open.

A set of four points $\{w,x,y,z\}\subset {\mathbb{R}}^d$ is called a rectangular quadruple, if $\mathrm{conv}\{w,x,y,z\}$ is a non-degenerate rectangle. If $\mathcal{F}$ is the family of all rectangular quadruples, then we obtain the right quadruple convexity, abbreviated as $rq$-convexity. This notion has been introduced by Li, Yuan and Zamfirescu in [3], where the $rq$-convexity was also investigated in several directions. The motivation for studying the $rq$-convexity mainly came from the astonishing lack of knowledge about the rectangular convexity. More generalizations of r-convexity can be seen in [4].

For distinct points $x,y\in {\mathbb{R}}^d$, let $xy$ denote the line-segment from x to y, $\overline{xy}$ the line through $x,y$, $H_{xy}$ the hyperplane through x orthogonal to $\overline{xy}$, and $C_{xy}$ the hypersphere of diameter $xy$. For any compact set $K\subset {\mathbb{R}}^d$, the circumsphere $C_K$ of K is the smallest hypersphere containing K in its convex hull.

For any two affine subspaces $H_1,H_2\subset {\mathbb{R}}^d$, $H_1\Vert H_2$ means that $H_1$ is parallel to $H_2$, and $H_1\perp H_2$ means that they are orthogonal.

For a point $x\in {\mathbb{R}}^d$ and an affine subspace $L\subset {\mathbb{R}}^d$, let ${\phi }_L\left(x\right)$ denote the orthogonal projection of x on L.

For $M\subset {\mathbb{R}}^d$, we denote by $\mathrm{conv}M$ its convex hull, by $\mathrm{aff}M$ its affine hull and by $\mathrm{int}M,\mathrm{bd}M,\mathrm{cl}M$ its relative interior, boundary and closure, which means in the topology of $\mathrm{aff}M$. Put $a_1{a}_2\dots a_n=\mathrm{conv}\{a_1,a_2,\dots ,a_n\}$, for $a_1,\dots ,a_n\in {\mathbb{R}}^d$. Such a set is called a polytope (polygon for $d=2$). We call a polytope, which is congruent with the Cartesian product of line-segments on the coordinate axes, a parallelepiped. Thus, all (planar) angles at the vertices of a parallelepiped are right.

A convex body is a compact convex set in ${\mathbb{R}}^d$ with non-empty interior.

The space $\mathcal{K}$ of all convex bodies in ${\mathbb{R}}^d$, equipped with the Pompeiu-Hausdorff metric, is a Baire space. We say that most convex bodies have a property $\mathbf{P}$, if those not enjoying P form a set of first Baire category in $\mathcal{K}$.

For a convex body $M\subset {\mathbb{R}}^d$, let $\mathrm{ext}M$ denote the set of all its extreme points, i.e. points not interior to any line-segment included in M.

For any real number $r>0$ and point $x\in {\mathbb{R}}^d$, let $B_r\left(x\right)$ be the ball (always considered compact) of centre x and radius r.

In this short paper we focus on the $rq$-convexity of complements, taken in most cases in balls or parallelepipeds.

2. $\mathit{rq}$-Convexity of Complements

Li, Yuan and Zamfirescu [3] proved that the complement of any bounded set in ${\mathbb{R}}^d$ is $rq$-convex. Here, we obtain the same, for open convex sets instead of bounded sets.

Theorem 1. 

If $Q\subset {\mathbb{R}}^d$ is an open set and $L\subset Q$ an open convex set different from Q, then $Q\setminus L$ is $rq$-convex.

Proof. 

Let $M=Q\setminus L$ and $a,b\in M$. Suppose $a,b\in \mathrm{bd}L$. At a and b, consider the supporting hyperplanes $H_a$ and $H_b$ of $\mathrm{cl}L$, respectively. For $d\ge 3$, if $H_a\ne H_{ab}$, then at least one (closed) half-hyperplane $P_a\subset H_{ab}$ with $\mathrm{bd}{P}_a=H_a\cap H_{ab}$, does not meet L. If $H_a=H_{ab}$, then take $P_a\subset H_{ab}$ with $a\in \mathrm{bd}{P}_a$, arbitrarily. Consider the analogous half-hyperplane $P_b$. Its orthogonal projection $P_b^{{}^{\prime }}$ onto $H_{ab}$ meets $P_a$. Now, choose $a^{\prime }\in P_a\cap P_b^{{}^{\prime }}\setminus \left\{a\right\}$ and $b^{\prime }=b+a^{\prime }-a$, both in M. Then $\{a,a^{\prime },b,b^{\prime }\}$ is a suitable rectangular quadruple.

For $d=2$, if $H_a\ne H_{ab}$ and $H_b\ne H_{ba}$, then perhaps $P_a$ and $P_b$ cannot be chosen such that the intersection of $P_a$ with $P_b^{\prime }$ be more than $\left\{a\right\}$. In that case, $C_{ab}$ has two small diametrically opposite arcs, one starting at a and the other at b, both in M. Thus, $ab$ is the diagonal of a rectangle with all its vertices in M.

If $\{a,b\}\neg \subset \mathrm{bd}L$, the proof is easy. □

Notice that Q and L may be unbounded; also, M may be simply connected.

Theorem 2. 

If $K\subset {\mathbb{R}}^d$ is a parallelepiped and $L\subset \mathrm{int}K$ a convex body, then $K\setminus \mathrm{int}L$ is $rq$-convex.

Proof. 

Assume $x,y\in \left(\mathrm{int}K\right)\setminus \mathrm{int}L$; by Theorem 1, $x,y$ have the $rq$-property in $M=K\setminus \mathrm{int}L$.

Now, suppose that at least one of $x,y$, say x, belongs to the boundary of K. If $x\in \mathrm{ext}K$, then we are done for any $y\in M$, by using the orthogonal projections of y on an edge $E_x$ and a facet $F_x$ of K meeting at x, with $E_x\perp F_x$.

Suppose $x\in \left(\mathrm{bd}K\right)\setminus \mathrm{ext}K$. If $x,y$ lie on parallel facets $F_x,F_y$ of K respectively, then there are another two points in $F_x\cup F_y$ forming with $x,y$ a rectangular quadruple. If y lies on a facet $F_y$ orthogonal to $F_x\ni x$ or in $\mathrm{int}M$, then take two points $z,w\in M$, such that $z\in H_{xy}$ and $w=y+z-x$. Again, $\{x,y,z,w\}$ is a rectangular quadruple.

Let now $x\in \left(\mathrm{bd}K\right)\setminus \mathrm{ext}K$, $y\in \mathrm{bd}L$. First, assume $d=2$. Consider $I_x=H_{xy}\cap M,I_y=H_{yx}\cap M$. If $H_{yx}$ is a supporting line of L, we can choose $z\in I_x$ distinct from x, such that $w=y+z-x\in I_y$. If not, we choose a short line-segment $yw\subset I_y$ disjoint from $L\setminus \left\{y\right\}$. If $F_x\subset H_{xy}$, then take $z=x+w-y$. Suppose $F_x\cap H_{xy}=\left\{x\right\}$. For $I_x,yw$ in the same half-plane of boundary $\overline{xy}$, take $z=x+w-y$. For $I_x,yw$ in different half-planes, there are two antipodal points $z^{\prime },w^{\prime }$ in $C_{xy}\cap M$ close to $x,y$. In all cases, $\{x,y,z,w\}$ (or $\{x,y,z^{\prime },w^{\prime }\}$ in the latter case) is a suitable rectangular quadruple.

For $d\ge 3$, consider a plane $H\ni x,y$ parallel to an edge of a facet containing x. Now, working in the rectangle $K\cap H$, we are in the case $d=2$, if $L\cap H$ is a planar convex body. If not, the proof becomes trivial. □

Theorem 3. 

Let $B\subset {\mathbb{R}}^d$ be a ball. If $L\subset \mathrm{int}B$ is a closed set, then $B\setminus L$ is $rq$-convex.

Proof. 

Let $M=B\setminus L$ and $x,y\in M$. If $x,y\in \mathrm{int}M$ or $x,y\in \mathrm{bd}B$, then we can easily find another two points in M forming with $x,y$ a rectangular quadruple.

Suppose $x\in \mathrm{bd}B,y\in \mathrm{int}M$. Then $C_{xy}$ has two small opposite arcs of a great circle in M, starting at $x,y$. They provide rectangular quadruples. □

Theorem 4. 

Suppose $K\subset {\mathbb{R}}^d$ is a parallelepiped. If $L\subset \mathrm{int}K$ is a closed set, then $K\setminus L$ is $rq$-convex.

Proof. 

Let $M=K\setminus L$ and $x,y\in M$.

Case 1. $x\in \mathrm{ext}K$. We find $x^{\prime },y^{\prime }\in \mathrm{bd}K$ forming together with $x,y$ a rectangular quadruple.

Case 2. $x,y\notin \mathrm{ext}K$. We find a rectangle $xy{y}^{\prime }{x}^{\prime }$ (or $x{x}^{\prime }y{y}^{\prime }$) of small width, with all vertices in M. □

3. Complements of Polygons

Theorem 5. 

If $D\subset {\mathbb{R}}^2$ is a disc and $P\subset \mathrm{int}D$ a regular n-gon $(n\ge 3)$ concentric with D, then $D\setminus \mathrm{int}P$ is $rq$-convex.

Proof. 

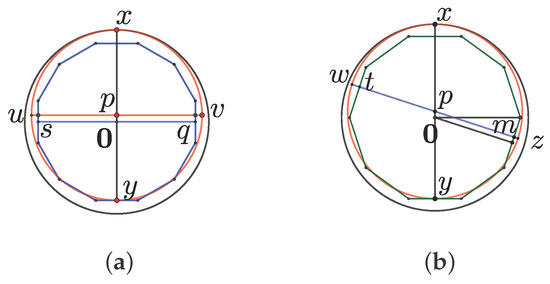
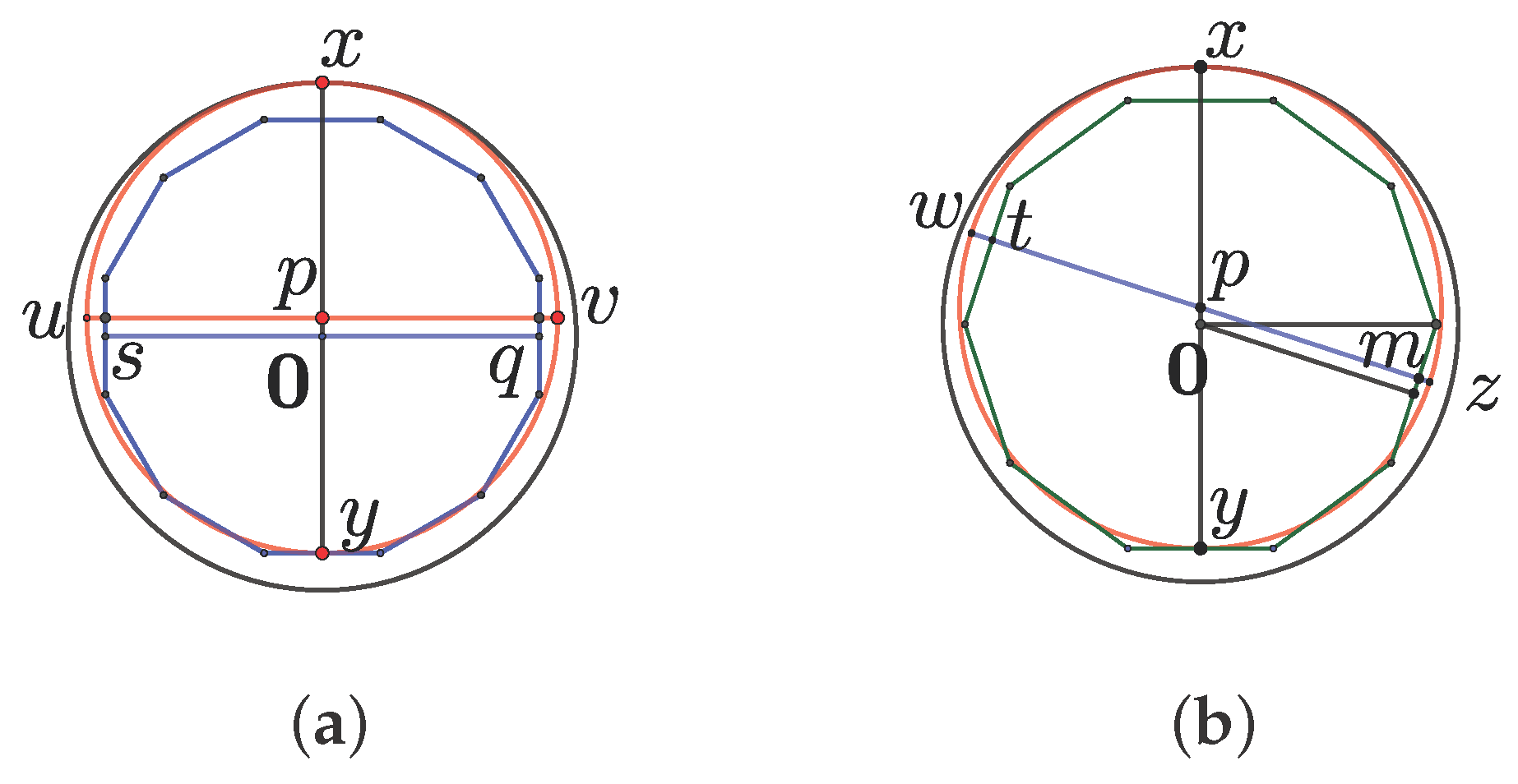
Assume that the centre of D is $\mathbf{0}$ and its radius 1. For any $x\in \mathrm{bd}D$, let $L_x$ be the supporting line of D at x. For any $y\in \left(\mathrm{bd}P\right)\setminus \mathrm{ext}P$, denote by $I_y$ the edge of $\mathrm{bd}P$ containing y. Suppose $xy$ orthogonal to both $L_x$ and $I_y$, and $\mathbf{0}\in xy$. Let the diameter $uv$ of $C_{xy}$ be orthogonal to $xy$, and set $L=\overline{uv}\cap P$. If the side-length of P is $2a$, we have $\parallel u-v\parallel =1+a/tan(\pi /n)$. Put $p=(x+y)/2$.

If $n\equiv 0\left(\mathrm{mod}4\right)$, then $L\subset uv$, because $\parallel p-u\parallel =\parallel p-v\parallel =\parallel p-y\parallel >\parallel y\parallel =\parallel s\parallel =\parallel q\parallel$, where $s,q$ are the midpoints of the edges of P met by $\overline{uv}$, see Figure 1a. For $n\equiv 2\left(\mathrm{mod}4\right)$, we consider a diameter $wz$ of $C_{xy}$ forming with $uv$ the angle $\pi /n$, see Figure 1b. Let $mt=\overline{wz}\cap P$, such that $\{m,z\}$ and $\{t,w\}$ are separated by p on $\overline{wz}$. We have $\parallel p-z\parallel =(1+a/tan(\pi /n\left)\right)/2$ and

$$\parallel p-m\parallel =\frac{1-\frac{a}{tan\frac{\pi }{n}}}{2}sin\frac{\pi }{n}+\frac{a}{tan\frac{\pi }{n}}<\frac{1-\frac{a}{tan\frac{\pi }{n}}}{2}+\frac{a}{tan\frac{\pi }{n}}=\frac{1+\frac{a}{tan\frac{\pi }{n}}}{2}.$$

Figure 1. n is even. (a) $n\equiv 0\left(\mathrm{mod}4\right)$; (b) $n\equiv 2\left(\mathrm{mod}4\right)$.

Hence, $z\notin P$. A fortiori, $w\notin P$, as $\parallel p-t\parallel <\parallel p-m\parallel$.

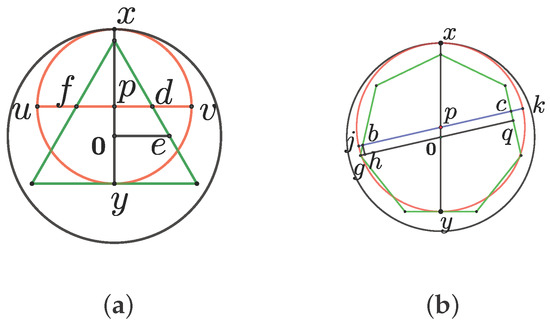
Suppose n is odd. If $n=3$, then $L\subset uv$, see Figure 2a.

Figure 2. n is odd. (a) $n=3$; (b) $n\ge 5$.

This is immediately seen. Thus, $u,v\notin \mathrm{int}P$.

If $n\ge 5$, then take a diameter $jk$ of $C_{xy}$ forming with $xy$ the angle $(2\pi /n)(\lfloor n/4\rfloor +(1/2\left)\right)$, see Figure 2b. Let $bc=\overline{jk}\cap P$. The choice of $jk$ guarantees the existence of $g\in \mathrm{ext}P$ and $q\in \mathrm{bd}P$, such that $\mathbf{0}\in gq$ and $\overline{gq}\Vert \overline{jk}$. Note that q is the midpoint of a side of P. Because

$$\parallel p-c\parallel \le \parallel q\parallel =\frac{a}{tan\frac{\pi }{n}}<\frac{1+\frac{a}{tan\frac{\pi }{n}}}{2}=\parallel p-k\parallel ,$$

$k\notin P$. Let $h={\phi }_{\overline{gq}}\left(b\right).$

We have

$$\parallel b-c\parallel =\parallel h-q\parallel =\parallel g-q\parallel -\parallel g-h\parallel =\parallel g-q\parallel -\parallel b-h\parallel tan\frac{\pi }{n}.$$

The inequality $\angle \mathbf{0}p{\phi }_{\overline{gq}}\left(p\right)<\pi /n$ yields

$$\parallel b-h\parallel =\parallel p-{\phi }_{\overline{gq}}\left(p\right)\parallel =\parallel p\parallel cos\angle \mathbf{0}p{\phi }_{\overline{gq}}\left(p\right)>\parallel p\parallel cos\frac{\pi }{n}.$$

Because $a\le sin(\pi /n)$,

$$\parallel b-c\parallel \le \frac{a}{sin\frac{\pi }{n}}+\frac{a}{tan\frac{\pi }{n}}-\frac{1-\frac{a}{tan\frac{\pi }{n}}}{2}sin\frac{\pi }{n}<1+\frac{a}{tan\frac{\pi }{n}}=\parallel k-j\parallel ,$$

which implies that $j\notin P$. For all cases, we find $u,v$(or $w,z$ or $j,k)$ in $C_{xy}$, forming together with $x,y$ a rectangular quadruple lying in $D\setminus \mathrm{int}P$. □

Is the restriction to regular polygons in Theorem 5 essential? Take $n=3$. Is a result similar to Theorem 5 valid for arbitrary triangles? Our next theorem affirmatively answers this question, but adds a condition on the size.

Theorem 6. 

Let $D\subset {\mathbb{R}}^2$ be a unit disc, T a triangle with its circumcircle $C_T$ concentric with D. If the radius of $C_T$ is no more than $\sqrt{3}/2$, then $D\setminus \mathrm{int}T$ is $rq$-convex.

Proof. 

Let $T=abc$, $\mathbf{0}$ be the centre of D and $x\in \mathrm{bd}D,y\in \left(\mathrm{bd}T\right)\setminus \mathrm{ext}T$. Consider $xy$ orthogonal to both $L_x$ and $I_y$, defined as in the preceding proof.

Suppose T is a non-acute triangle; thus, $\mathbf{0}$ is the midpoint of $ab$. Assume that the radius $r_{C_T}$ of $C_T$ is $\sqrt{3}/2$. If $x\mathbf{0}\perp ab$ and $C_T\cap C_{x\mathbf{0}}=\{e,f\}$, such that b and e are not separated by $\overline{x\mathbf{0}}$, we find out that $a,x/2,e$ are collinear. Only in case $c=e$, $T\cap C_{x\mathbf{0}}$ is a half-circle. Then the four points $ae\cap C_{x\mathbf{0}}$, x and $\mathbf{0}$ lie in $M=D\setminus \mathrm{int}T$. In case T is obtuse, we have the same rectangular quadruple in M. If $r_{C_T}<\sqrt{3}/2$, then the intersection of $ac$ and $C_{x\mathbf{0}}$ can not determine a diameter of $C_{x\mathbf{0}}$. We can easily choose two antipodal points of $C_{xy}$ in M different from $x,y$.

If T is an acute triangle and y is the midpoint of $ab$, then $C_{xy}$ is lager than $C_{x\mathbf{0}}$. Assume that $T\cap C_{xy}$ contains a half-circle of $C_{xy}$. Then $\angle acb$ is at least $\pi /2$, contradicting the assumption that T is an acute triangle. Hence, there are always two antipodal points of $C_{xy}$, forming together with $x,y$ a rectangular quadruple in M. □

4. Generic Results

In this section, like in the previous one, we consider complements of interiors of convex bodies in discs. We want now to see what happens with most of them.

Consider a convex body $K\subset {\mathbb{R}}^2$. Let ${\psi }_K$ be the set of all points $v\in \mathrm{bd}K$, such that the vector v is external normal at v to K. In other words, $\mathbf{0}v$ and some supporting line H at v are orthogonal, and H does not separate $\mathbf{0}$ from $\mathrm{int}K$.

For $x\in \mathrm{bd}K$, ${\varrho }_i(K,x)$ and ${\varrho }_s(K,x)$ denote the lower and the upper curvature radius of $\mathrm{bd}K$ at x (see H. Busemann [2], p. 14). If ${\varrho }_i(K,x)={\varrho }_s(K,x)$, the common value is the curvature radius and its inverse is the curvature of K at x.

Theorem 7. 

Let $D\subset {\mathbb{R}}^2$ be a disc of centre $\mathbf{0}$. For most convex bodies $K\subset D$, at each point $x\in {\psi }_K$, the upper curvature of $\mathrm{bd}K$ is at least $1/\parallel x\parallel$.

Proof. 

We may consider only convex bodies K with $\mathbf{0}\notin \mathrm{bd}K$ and $K\subset \mathrm{int}D$, as those K not satisfying these conditions form a nowhere dense set.

For $n\in \mathbb{N}$, let ${\mathcal{K}}_n$ be the set of all $K\subset \mathrm{int}D$, such that, for some $x\in {\psi }_K$, $B_{n^{-1}}\left(x\right)\cap D_n\left(x\right)\subset K$, where $D_n\left(x\right)$ is the disc of centre o, such that $\mathbf{0}\in ox,\parallel o\parallel =1/n$ and $x\in \mathrm{bd}{D}_n\left(x\right)$. Clearly, at such a point x, the lower radius of curvature of $\mathrm{bd}K$ is at least $\parallel x\parallel +n^{-1}$.

We show now that, for every n, ${\mathcal{K}}_n$ is nowhere dense in $\mathcal{K}$.

Let $\mathcal{O}\subset \mathcal{K}$ be open. We choose a polygon $P\in \mathcal{O}$. Every point $x\in {\psi }_P$ is a vertex of P or lies on an edge $E_x$ orthogonal to x. We may choose P such that no point of ${\psi }_P$ is a vertex of P belonging to an edge orthogonal to x.

If $x\in E_x$, take $a,b\in \left(\mathrm{bd}P\right)\setminus E_x$ close to the endpoints of $E_x$ and replace P by

$$Q_x=\mathrm{conv}((\left(\mathrm{ext}P\right)\setminus E_x)\cup \{a,b\}\cup (B_{n^{-1}}\left(x\right)\cap B_{\parallel x\parallel }\left(\mathbf{0}\right))).$$

After doing so for all (finitely many) points $x\in {\psi }_P$ which are not vertices of P, we obtain a convex body $Q\in \mathcal{O}$.

It is easily checked that $Q\notin {\mathcal{K}}_n$. As ${\mathcal{K}}_n$ is closed, a whole neighborhood of Q is disjoint from ${\mathcal{K}}_n$. Thus, ${\mathcal{K}}_n$ is nowhere dense. Therefore, ${\bigcup }_{n\in \mathbb{N}}{\mathcal{K}}_n$ is of first Baire category.

This implies that, for most $K\in \mathcal{K}$, at every $x\in {\psi }_K$, the lower radius of curvature of $\mathrm{bd}K$ is at most $\parallel x\parallel$. The theorem is proved. □

Theorem 8. 

Let $D\subset {\mathbb{R}}^2$ be the unit disc of centre $\mathbf{0}$ and $K\subset \mathrm{int}D$ a convex body. If, at each point $x\in {\psi }_K$, ${\varrho }_i(K,x)\le (\parallel x\parallel +1)/2$, then $D\setminus \mathrm{int}K$ is $rq$-convex.

Proof. 

We verify the $rq$-property at $x,y\in D\setminus \mathrm{int}K$. The only interesting case is for $xy$ (internal) normal to both K and D ($x\in \mathrm{bd}K,y\in \mathrm{bd}D$). In this case, $\mathbf{0}\in xy$. By hypothesis, ${\varrho }_i(K,x)\le (\parallel x\parallel +1)/2$. So, $C_{xy}$ has points outside of K arbitrarily close to x, and includes a whole arc in $D\setminus K$ containing y. Thus, diametrally opposite points different from $x,y$ can be found in $C_{xy}\setminus K$. The $rq$-property at $x,y$ is verified. □

Theorem 9. 

Let $D\subset {\mathbb{R}}^2$ be a disc. For most convex bodies $K\subset D$, $D\setminus \mathrm{int}K$ is $rq$-convex.

Proof. 

We may assume that D is the unit disc of centre $\mathbf{0}$. For most convex bodies $K\subset D$, $\mathbf{0}\notin \mathrm{bd}K$ and $K\subset \mathrm{int}D$. By Theorem 7, at each point $x\in {\psi }_K$, ${\varrho }_i(K,x)\le \parallel x\parallel <(\parallel x\parallel +1)/2$.

Hence, by Theorem 8, $D\setminus \mathrm{int}K$ is $rq$-convex. □

5. Conclusions

The conjectured characterization of r-convexity in the plane does not leave much hope for a great variety of convex bodies to be $rq$-convex, the two notions being equivalent in the convex case. But for non-convex sets our paper revealed a lot of diversity.