Delayed Impulsive Control for μ-Synchronization of Nonlinear Multi-Weighted Complex Networks with Uncertain Parameter Perturbation and Unbounded Delays

Abstract

The global $\mu$-synchronization problem for nonlinear multi-weighted complex dynamical networks with uncertain parameter perturbation and mixed time-varying delays is investigated in this paper. Unlike other existing works, all delays, including sampling and internal and coupling delays, are assumed to be unbounded, making the considered model more general and practical. Based on the generalized impulsive comparison principles, a time-varying impulsive controller with sampling delays is designed, and some new sufficient conditions are obtained to make drive–response multi-weighted networks reach $\mu$-synchronization. In addition, the external coupling matrices do not need to meet the requirement of zero-row sum, and the limitation of time delay on pulse interval is weakened. The results obtained in this article can be seen as extensions of previous related research.

1. Introduction

Recently, complex networks have been widely investigated because of their realistic applications in various fields, such as image encryption, filtering, secure communication, stability analysis, etc. [1,2,3,4,5,6,7]. Considerable attention from scholars has been cast on the dynamic behaviors of complex networks, and numerous remarkable achievements have been reached [8,9,10]. Synchronization, as a kind of interesting and significant collective behavior of complex dynamical networks, has become a hot object gradually [11,12]. To date, various synchronization modes have been studied, including pinning synchronization [13], exponential synchronization [14], finite-time synchronization [15], impulsive synchronization [16,17], etc.

Unfortunately, most existing results about synchronization problems only pay attention to the complex network model with a single weight, which may lead to inaccurate modeling of real networks. Multi-weighted networks are ubiquitous in our work and life. For example, in a logistics network, each city is regarded as a separate node, and goods are transported from one node to another by different means such as highways, railways, and airways. It is obvious that such a multichannel network cannot be precisely modeled by a single weighted system. In a social network, taking each person as a single node, individuals can connect with each other through different tools such as telephone, email, Facebook, etc. Clearly, it is more suitable to apply multi-weighted systems to describe the social network since each communication tool has its features forming a different subnetwork. Considering the practicality and universality of multi-weighted complex networks, some researchers have attempted to study such networks and some preliminary results have been obtained recently. For instance, in [18], Zhang et al. investigated the asymptotic synchronization of stochastic multi-weighted systems. In [19], the authors studied the synchronization of multi-weighted complex networks with noise based on graph theory methods. In [20], Guo et al. derived the finite-time synchronization criteria of multi-weighted switching dynamical networks by using quantized intermittent control. It is worth noting that the delay effect was not considered in the multi-weighted models developed in [18,19,20].

As a matter of fact, in real multi-weighted networks, various time delays are non-negligible since different subsystems have different limited transmission speeds. Taking the logistics network as an instance, it is composed of the highway network, railway network, and air network (see Figure 1). Each subnetwork has its distinctive transmission speeds, which may result in different time delays. To describe real multi-weighted networks better, internal and coupling time delays were introduced in the models of [21], and several useful synchronization criteria were derived for delayed multi-weighted systems based on the stability theory. In [22], aperiodically adaptive intermittent synchronization for stochastic multi-weighted complex networks with hybrid delays was considered using extended stochastic differential inequalities. Moreover, in [23], Zheng et al. studied the decay synchronization of multi-weighted neural networks including internal and coupling delays by constructing a novel Lyapunov–Krasovskii function. Besides internal and coupling delays, sampling delays also should be considered in the control process because it is difficult to immediately complete the sampling and transferring of impulse information at several discrete instants in the practical application environment. Hence, it is particularly important to utilize the recent information on drive systems to replace the real-time information in the impulsive control process. In recent years, based on delayed impulsive control schemes, some research results on synchronization problems of complex networks have been obtained. For instance, in [24], delayed impulsive control methods were used to deal with the synchronization of linear complex systems. In [25], delayed impulsive controllers were applied to the synchronization of nonlinear complex networks. Zhang et al. [26] derived the asymptotic chaotic synchronization criteria of stochastic complex-valued dynamical systems via delayed impulsive control. We should note that the delayed complex networks above always assumed that time delays were bounded or even constants. However, in some practical applications, there is no prior condition on the bound of time delays, which shows that it may be unpredictable or unbounded. In ecosystems, the unbounded delay is used to describe the effect of predator behavior on predator population growth, and ignoring the boundlessness of time delay will lead to inaccurate or even wrong results. Therefore, when we model the complex network with time-varying delays, removing the assumption that the delays are bounded can obtain more reasonable results.

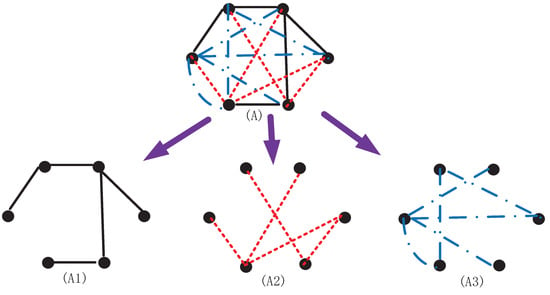
Figure 1. The schematic diagram of the logistic network: (A) complete logistic network; (A1) highway network; (A2) railway network; (A3) air network.

To cope with the synchronization issues of single-weighted systems including unbounded delays, Chen and Wang [27] considered the $\mu$-stability scheme. As an extension of Lyapunov stability, it always is applied to analyze the stability issue of dynamical systems including unknown delays by correlating the historical and current information of network nodes through $\mu$-function [28]. For instance, Xu et al. [29] considered the $\mu$-synchronization of dynamical networks including unknown delays. The authors in [30] studied the $\mu$-stability issue for impulsive networks with time-varying delays of unknown bound. Global $\mu$-synchronization criteria of impulsive complex-valued networks with leakage delay and distributed delay were gained in [31] based on $\mu$-stability. In addition, unknown parameter perturbations caused by modeling errors, measurement inaccuracies, and changes in ambient temperature and humidity widely exist in complex networks, which brings challenges to synchronization control. Specifically, each node in a complex network has its own dynamic behavior, which can be described by various differential dynamical systems, and the standard parameters of these systems may be difficult to determine in certain cases. To construct a more generalized network, parameter uncertainties should be considered. For instance, Wang et al. [32] studied the synchronous motion of networked robotic systems, which have uncertain kinematic and dynamic information in the task space. In [33], Rakkiyappan et al. discussed the robust synchronization of neural networks with Markovian jumping and stochastic uncertainties by constructing a new Lyapunov–Krasovskii function. In [34], Huang et al. considered the synchronization of uncertain Cohen–Grossberg neural networks with delayed couplings under fixed time. Lately, the bipartite synchronization issues of neural networks with uncertain parameters were studied [35]. However, the theoretical results obtained in [27,28,29,30,31,32,33,34,35] are based on the assumption that the model is a single weight. Compared with single-weighted networks, multi-weighted networks have more complex and unpredictable dynamic behavior, which is more valuable to consider and research. To the best of our knowledge, very few works focus on the $\mu$-synchronization issues of multi-weighted complex networks with unbounded mixed time delays and uncertainties via impulsive control including sampling delays, which is the primary motivation of this article.

Taking the facts above into consideration, this paper studies the $\mu$-synchronization for multi-weighted dynamical networks including three kinds of time delays and uncertain perturbation by using delayed impulsive control. To be more practical, nonlinear couplings are considered in this paper. The main highlights of this article include three aspects: (1) To prefer the more practical significance of our results, in this article, a more generalized uncertain multi-weighted model including unbounded internal delay, sampling delay, and coupling delay is discussed. (2) Different from the impulsive control schemes in [24,25,26], a delayed impulsive controller with unbounded sampling delay is devised, and new synchronization criteria are gained for the concerned multi-weighted networks. (3) The topological matrices of the multi-weighted systems in this paper do not need to meet the condition of zero-row sum, and the constriction of time delay on pulse interval is weakened.

Besides the first section, the network model description and preliminaries are given in Section 2. In Section 3, some new $\mu$-synchronization criteria for a complicated multi-weighted model are obtained. In Section 4, numerical examples are provided to show the correctness of our theorem and corollaries. Section 5 is the conclusion of this article.

Notation 1.

I represents an identity matrix. $A\le 0$ means that A represents a semi-negative definite matrix. Let ${\mathsf{\Omega }}_1\subseteq \mathbb{R},{\mathsf{\Omega }}_2\subseteq {\mathbb{R}}^m,1\le m\le n,C^1({\mathsf{\Omega }}_1,{\mathsf{\Omega }}_2)=\{\omega :{\mathsf{\Omega }}_1\to {\mathsf{\Omega }}_2,\omega$ is continuously differentible}. $PC({\mathsf{\Omega }}_1,{\mathsf{\Omega }}_2)=\{\omega :{\mathsf{\Omega }}_1\to {\mathsf{\Omega }}_2,\omega$ is piecewise continuous apart from some limited moments $t\mathit{with}\omega \left(t^{+}\right)=\omega \left(t\right),\mathit{and}\omega \left(t^{-}\right)\mathit{exists}\}.$ Let $PC{B}_{\tau }=\{\overline{\omega }\in PC([-\tau ,0],{\mathbb{R}}^n),\overline{\omega }\mathit{is}\mathit{bounded}\}$, and the norm of $\overline{\omega }$ is expressed as $|\overline{\omega }| = {\mathit{sup}}_{-\tau \le s\le 0}\parallel \overline{\omega }\left(s\right)\parallel$. $[-\tau ,0]$ converts into $(-\infty ,0]$ if $\tau =\infty .$ Let $\chi =\{\mu \left(t\right)\in C^1({\mathbb{R}}_{+},[1,\infty )):\mu \left(t\right)$ is nondecreasing on $[0,+\infty )\mathit{and}\mathit{\mu }\left(t\right)\to \infty \mathit{as}t\to \infty \}.$ ${\lambda }_{min}\left(B\right)$ and ${\lambda }_{max}\left(B\right)$ denote the minimum and maximum eigenvalues of B, respectively.

2. Mathematical Model and Preknowledge

Consider a nonlinear multi-weighted dynamical network including unbounded delays and parametric uncertainties, which can be expressed as

$$\begin{array}{cc}\hfill {\dot{x}}_i\left(t\right)=& -(D+\mathsf{\Delta }D\left(t\right))x_i\left(t\right)+(A+\mathsf{\Delta }A\left(t\right))f\left(x_i\left(t\right)\right)+(B+\mathsf{\Delta }B\left(t\right))g\left(x_i(t-{\tau }_0\left(t\right))\right)\hfill \\ & + c_0\sum _{j=1}^N{C}_{ij}^{\left(0\right)}\psi \left(x_j\left(t\right)\right)+c_1\sum _{j=1}^N{C}_{ij}^{\left(1\right)}\psi \left(x_j(t-{\tau }_1\left(t\right))\right)\hfill \\ & + c_2\sum _{j=1}^N{C}_{ij}^{\left(2\right)}\psi \left(x_j(t-{\tau }_2\left(t\right))\right)+\cdots +c_{m-1}\sum _{j=1}^N{C}_{ij}^{(m-1)}\psi \left(x_j(t-{\tau }_{m-1}\left(t\right))\right)\hfill \\ \hfill =& -\tilde{D}{x}_i\left(t\right)+\tilde{A}f\left(x_i\left(t\right)\right)+\tilde{B}g\left(x_i(t-{\tau }_0\left(t\right))\right)\hfill \\ & + c_0\sum _{j=1}^N{C}_{ij}^{\left(0\right)}\psi \left(x_j\left(t\right)\right)+\sum _{q=1}^{m-1}\sum _{j=1}^N{c}_q{C}_{ij}^{\left(q\right)}\psi \left(x_j(t-{\tau }_q\left(t\right))\right),i=1,2,\dots ,N,\hfill \end{array}$$

(1)

where $x_i\left(t\right)={(x_{i1}\left(t\right),x_{i2}\left(t\right),\dots ,x_{in}\left(t\right))}^T\in {\mathbb{R}}^n$ is the state vector of node i, $\tilde{D}=D+\mathsf{\Delta }D\left(t\right)$, $\tilde{A}=A+\mathsf{\Delta }A\left(t\right)$ and $\tilde{B}=B+\mathsf{\Delta }B\left(t\right)$. $D=diag\{d_1,d_2$$,\dots ,d_n\} >0$. $A\in {\mathbb{R}}^{n\times n}$ and $B\in {\mathbb{R}}^{n\times n}$ are connection weight matrices. $\mathsf{\Delta }D\left(t\right)\in {\mathbb{R}}^{n\times n}$, $\mathsf{\Delta }A\left(t\right)\in {\mathbb{R}}^{n\times n}$ and $\mathsf{\Delta }B\left(t\right)\in {\mathbb{R}}^{n\times n}$ represent uncertain parameter perturbation. $f(·)\in {\mathbb{R}}^n$ and $g(·)\in {\mathbb{R}}^n$ stand for nonlinear vector-valued functions characterizing the nonlinear dynamic behavior of nodes, and $\psi (·)\in {\mathbb{R}}^n$ denotes the nonlinear coupling function. The internal delay ${\tau }_0\left(t\right)$ and the coupling delays ${\tau }_q\left(t\right)$ have no bound, which means $0\le {\tau }_0\left(t\right)\le \infty ,0\le {\tau }_q\left(t\right)\le \infty ,(q=1,2,\dots ,m-1)$. The constant $c_r(r=0,1,\dots ,m-1)$ represents the coupling strength for the rth coupling form. In addition, $C^{\left(r\right)}=\left(C_{ij}^{\left(r\right)}\right)\in {\mathbb{R}}^{N\times N}(r=0,1,\dots ,m-1)$ is the outer coupling matrix of the rth subnetwork, where $\left(C_{ij}^{\left(r\right)}\right)$ is defined as follows: if there exists a connection link from node i to node j, then $\left(C_{ij}^{\left(r\right)}\right)\ne 0$; otherwise, $\left(C_{ij}^{\left(r\right)}\right)=0(i\ne j)$. The initial value of model (1) is given by $x_i\left(s\right)={\varphi }_i\left(s\right),s\in (-\infty ,0]$, and ${\varphi }_i\in PC{B}_{\tau }$.

Take model (1) as the drive system, then the concerned response system can be described as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left\{\begin{array}{cc}{\dot{y}}_i\left(t\right)=\hfill & -\tilde{D}{y}_i\left(t\right)+\tilde{A}f\left(y_i\left(t\right)\right)+\tilde{B}g\left(y_i(t-{\tau }_0\left(t\right))\right)\hfill \\ \hfill & +c_0{\displaystyle \sum _{j=1}^N}{C}_{ij}^{\left(0\right)}\psi \left(y_j\left(t\right)\right)+{\displaystyle \sum _{q=1}^{m-1}}{\displaystyle \sum _{j=1}^N}{c}_q{C}_{ij}^{\left(q\right)}\psi \left(y_j(t-{\tau }_q\left(t\right))\right),t\ne t_k,k\in {\mathbb{Z}}_{+},\hfill \\ e_i\left(t\right)=\hfill & M{e}_i(t^{-}-{\iota }_k),t=t_k,k\in {\mathbb{Z}}_{+},\hfill \end{array}\right.\end{array}\end{array}$$

(2)

where $i=1,2,\dots ,N$, and $y_i\left(t\right)={(y_{i1}\left(t\right),y_{i2}\left(t\right),\dots ,y_{in}\left(t\right))}^T\in {\mathbb{R}}^n$ is the ith state variable for response system (2). The initial value of model (2) is given by $y_i\left(s\right)={\phi }_i\left(s\right),s\in (-\infty ,0]$, and ${\phi }_i\in PC{B}_{\tau }$. The equation

$$e_i\left(t\right)=M{e}_i(t^{-}-{\iota }_k),t=t_k,k\in {\mathbb{Z}}_{+},$$

(3)

represents the impulsive controller with unbounded sampling delay, where $e_i(·)=y_i(·)-x_i(·)$ indicates the system error of node i. $M\in {\mathbb{R}}^{n\times n}$ represents the impulsive gain matrix. ${\iota }_k$ denotes the sampling delay at impulsive points, which satisfies $0\le {\iota }_k\le +\infty ,k\in {\mathbb{Z}}_{+}$. The impulsive instants $\{t_k,k\in {\mathbb{Z}}_{+}\}$ meet $0=t_0<t_1<\cdots <t_k<\cdots$ and $t_k\to \infty$ as $k\to \infty$. The set of impulsive instants is expressed as ${\delta }_0$. For any $T>0,$ let $\delta \left(T\right)=\{t_k\in {\delta }_0|t_k-t_{k-1}\le T,k\in {\mathbb{Z}}_{+}\}$.

Remark 1.

In addition to nonlinear coupling and uncertainty perturbations, three types of unbounded time-varying delays, including impulse sampling delays and internal and coupling delays, are introduced into our complex system. At the same time, the topologies of the whole network are not restricted by the condition of zero-row sum, which shows our results are more generalized than other related results.

Combining models (1) and (2), and $e_i(·)=y_i(·)-x_i(·)$, we can obtain the following error system

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left\{\begin{array}{cc}{\dot{e}}_i\left(t\right)=\hfill & -\tilde{D}{e}_i\left(t\right)+\tilde{A}f\left(e_i\left(t\right)\right)+\tilde{B}g\left(e_i(t-{\tau }_0\left(t\right))\right)\hfill \\ \hfill & +c_0{\displaystyle \sum _{j=1}^N}{C}_{ij}^{\left(0\right)}\psi \left(e_j\left(t\right)\right)+{\displaystyle \sum _{q=1}^{m-1}}{\displaystyle \sum _{j=1}^N}{c}_q{C}_{ij}^{\left(q\right)}\psi \left(e_j(t-{\tau }_q\left(t\right))\right),t\ne t_k,k\in {\mathbb{Z}}_{+},\hfill \\ e_i\left(t\right)=\hfill & M{e}_i(t^{-}-{\iota }_k),t=t_k,k\in {\mathbb{Z}}_{+},\hfill \\ e_i\left(s\right)=\hfill & {\phi }_i\left(s\right)-{\varphi }_i\left(s\right),s\in (-\infty ,0],\hfill \end{array}\right.\end{array}\end{array}$$

(4)

for $i=1,2,\dots ,N$, where $f\left(e_i\left(t\right)\right)=f\left(y_i\left(t\right)\right)-f\left(x_i\left(t\right)\right)$, $g\left(e_i(t-{\tau }_0\left(t\right))\right)=g\left(y_i(t-{\tau }_0\left(t\right))\right)-g\left(x_i(t-{\tau }_0\left(t\right))\right)$, $\psi \left(e_j\left(t\right)\right)=\psi \left(y_j\left(t\right)\right)-\psi \left(x_j\left(t\right)\right)$ and $\psi \left(e_j(t-{\tau }_q\left(t\right))\right)=\psi \left(y_j(t-{\tau }_q\left(t\right))\right)-\psi \left(x_j(t-{\tau }_q\left(t\right))\right)$. It is assumed that the solution of system (4) is right continuous, namely, $e_i\left(t_k\right)=e_i\left(t_k^{+}\right),k\in {\mathbb{Z}}_{+}$. Then, the synchronization issue of drive–response systems (1) and (2) is equivalent to constructing a suitable control gain matrix M such that error system (4) is $\mu$-stable.

Definition 1.

Response network (2) and drive network (1) are said to be global μ-synchronization, namely, error system (4) is globally μ-stable, if there is a function $\mu \left(t\right)\in \chi$ and a scalar $K>0$ such that

$$\parallel e_i\left(t\right)\parallel \le \frac{K}{\mu \left(t\right)},t\ge 0,i=1,2,\dots ,N.$$

Remark 2.

Most synchronization modes are closely related to μ-synchronization. When $\mu \left(t\right)={(1+p_{1}t)}^{\varsigma },p_1>0,\varsigma >0,$ the μ-synchronization becomes power synchronization; when $\mu \left(t\right)=exp\left(\rho t\right),\rho >0$, the μ-synchronization changes into exponential synchronization; when $\mu \left(t\right)=ln(e+\theta t)$, $\theta >0$, the μ-synchronization is log synchronization;

Assumption 1.

There exist three nonnegative constants $l_f,l_g,$ and $l_{\psi }$ such that

$$\parallel f\left(x\right)-f\left(y\right)\parallel \le l_f\parallel x-y\parallel ,\parallel g\left(x\right)-g\left(y\right)\parallel \le l_g\parallel x-y\parallel ,\parallel \psi \left(x\right)-\psi \left(y\right)\parallel \le l_{\psi }\parallel x-y\parallel$$

hold for any vectors $x\in {\mathbb{R}}^n$ and $y\in {\mathbb{R}}^n$.

Assumption 2.

For each outer coupling matrix $C^{\left(r\right)}(r=0,1,\dots ,m-1)$, there exist a corresponding nonnegative constant $L_r(r=0,1,\dots ,m-1)$ such that

$$\sum _{j=1}^N{\left(C_{ij}^{\left(r\right)}\right)}^2\le L_r,i=1,2,\dots ,N.$$

Assumption 3.

The uncertain system matrices $\mathsf{\Delta }D\left(t\right)$, $\mathsf{\Delta }A\left(t\right)$ and $\mathsf{\Delta }B\left(t\right)$ are norm bounded and have the following form

$$\mathsf{\Delta }D\left(t\right)=E_D\Phi \left(t\right)F_D,\mathsf{\Delta }A\left(t\right)=E_A\Phi \left(t\right)F_A,\mathsf{\Delta }B\left(t\right)=E_B\Phi \left(t\right)F_B,$$

where $\Phi \left(t\right)$ stands for the unknown time-varying matrix satisfying ${\Phi }^T\left(t\right)\Phi \left(t\right)\le I$ and $E_D,E_A,E_B$, $F_D,F_A,F_B$ are constant matrices.

Assumption 4.

There exist some constants ${\mu }_a\ge 1,{\mu }_i\ge 1,(i=0,1,\dots ,n)$, and ${\mu }_b\ge 1$ such that $\mu \left(t\right)\in \chi$ satisfies

$$\frac{\mu \left(t_k\right)}{\mu \left(t_{k-1}\right)}\le {\mu }_a,\frac{\mu \left(t\right)}{{\mu }^{*}(t-{\tau }_0\left(t\right))}\le {\mu }_0,\cdots ,\frac{\mu \left(t\right)}{{\mu }^{*}(t-{\tau }_n\left(t\right))}\le {\mu }_n,\frac{\mu \left(t_k\right)}{{\mu }^{*}(t_k-{\iota }_k)}\le {\mu }_b,k\in {\mathbb{Z}}_{+},$$

where ${\mu }^{*}\left(t\right)=\mu \left(t\right)$ when $t\ge 0$ and ${\mu }^{*}\left(t\right)=1$ when $t<0$.

Lemma 1

([35]). For any $n\times n$ real matrix $W>0$ and vectors $u,v\in {\mathbb{R}}^n$, one can obtain

$$2u^{T}v\le u^{T}Wu+v^T{W}^{-1}v.$$

Lemma 2

([11]). The following matrix inequality

$$\left[\begin{array}{cc}{B}_{11}& B_{12}\\ B_{12}^T& B_{22}\end{array}\right]<0$$

equals to one of the conditions as follows:

$$\left(\mathrm{a}\right)B_{11}<0,B_{22}-B_{12}^T{B}_{11}^{-1}{B}_{12}<0;$$

$$\left(\mathrm{b}\right)B_{22}<0,B_{11}-B_{12}{B}_{22}^{-1}{B}_{12}^T<0,$$

where $B_{11}^T=B_{11}$ and $B_{22}^T=B_{22}.$

Lemma 3

([28]). Under Assumption 4, $v\left(t\right)\in PC(\mathbb{R},{\mathbb{R}}_{+})$ satisfies the following condition

$$\left\{\begin{array}{c}{D}^{+}v\left(t\right)\le \alpha v\left(t\right)+{\beta }_{0}v(t-{\tau }_0\left(t\right))+{\beta }_{1}v(t-{\tau }_1\left(t\right))+\cdots +{\beta }_{n}v(t-{\tau }_n\left(t\right)),t\ne t_k,\hfill \\ v\left(t\right)\le {\gamma }_{k}v(t^{-}-{\iota }_k),t=t_k,k\in {\mathbb{Z}}_{+},\hfill \end{array}\right.$$

(5)

where $\alpha \in \mathbb{R},{\beta }_i\in {\mathbb{R}}_{+},{\gamma }_k\in {\mathbb{R}}_{+},0\le {\tau }_i\left(t\right)\le \infty$ for $i=0,1,2,\dots ,n$, $0\le {\iota }_k\le \infty$, and $0=t_0<t_1<\cdots <t_k<\cdots ,k\in {\mathbb{Z}}_{+}$. If one can find suitable parameters $\sigma >1$ and $T>0$ such that

$$ln{\mu }_a+\left[\right|\alpha |+\sigma ({\beta }_0{\mu }_0+{\beta }_1{\mu }_1+\cdots +{\beta }_n{\mu }_n)]T<ln\sigma ,$$

(6)

and

$$\sigma {\mu }_b{\gamma }_k\le 1.$$

(7)

Then any solution of (5) meets

$$v\left(t\right)\le \frac{\sigma \mu \left(0\right)\overline{v}\left(0\right)}{\mu \left(t\right)},t\ge 0,$$

(8)

where $\overline{v}\left(0\right)={\sup }_{-\infty <s\le 0}v\left(s\right).$

3. Main Results

This section gives the global $\mu$-synchronization criteria between the response system (2) and the drive system (1) by using impulsive control with unbounded sampling delays. The main theorem and corollaries are gained below.

Theorem 1.

Under Assumptions 1–4, if there exists a function $\mu \left(t\right)\in \chi ,n\times n$ matrices $G,P>0$, a constant $\sigma >1$ and several nonnegative constants $T,{\xi }_0,{\xi }_1,{\xi }_2,{\zeta }_1,{\zeta }_2,\alpha ,{\sigma }_0,{\beta }_0,{\sigma }_q$, ${\beta }_q$, such that

$$\begin{array}{cc}\hfill \left(\mathrm{i}\right)& \left(\alpha +\sigma {\beta }_0{\mu }_0+\sigma \sum _{q=1}^{m-1}{\beta }_q{\mu }_q\right)T<\ln (\sigma /{\mu }_a),\hfill \\ \hfill \left(\mathrm{ii}\right)& -2PD+P\left({\xi }_0{E}_D{E}_D^T+{\xi }_{1}A{A}^T+{\xi }_2{E}_A{E}_A^T+{\zeta }_{1}B{B}^T+{\zeta }_2{E}_B{E}_B^T+I\sum _{r=0}^{m-1}{\sigma }_r{c}_r{L}_r\right)P\hfill \\ & +{\xi }_0^{-1}{\lambda }_{max}\left(F_D^T{F}_D\right)I+c_0{\sigma }_0^{-1}{l}_{\psi }^{2}NI+l_f^2\left({\xi }_1^{-1}+{\xi }_2^{-1}{\lambda }_{max}\left(F_A^T{F}_A\right)\right)I\le \alpha P,\hfill \\ \hfill \left(\mathrm{iii}\right)& l_g^2\left({\zeta }_1^{-1}+{\zeta }_2^{-1}{\lambda }_{max}\left(F_B^T{F}_B\right)\right)I\le {\beta }_{0}P,\hfill \\ \hfill \left(\mathrm{iv}\right)& c_q{\sigma }_q^{-1}{l}_{\psi }^{2}NI\le {\beta }_{q}P,q=1,2,\dots ,m-1,\hfill \\ \hfill \left(\mathrm{v}\right)& \left[\begin{array}{cc}-\frac{1}{\sigma {\mu }_b}P& \Xi \\ {\Xi }^T& -P\end{array}\right]\le 0.\hfill \end{array}$$

Then, drive–response systems (1) and (2) can realize the global μ-synchronization through the impulsive controller (3) with matrix $M=P^{-1}{\Xi }^T$.

 Proof. 

Choose the following Lyapunov function:

$$V\left(t\right)=\sum _{i=1}^N{e}_i^T\left(t\right)P{e}_i\left(t\right).$$

(9)

When $t\ne t_k,k\in {\mathbb{Z}}_{+}$, calculating the Dini derivative of $V\left(t\right)$ along the solution of (4) yields

$$\begin{array}{cc}\hfill D^{+}& V\left(t\right)\hfill \\ \hfill =& 2\sum _{i=1}^N{e}_i^T\left(t\right)P{\dot{e}}_i\left(t\right)\hfill \\ \hfill =& 2\sum _{i=1}^N{e}_i^T\left(t\right)P[-\tilde{D}{e}_i\left(t\right)+\tilde{A}f\left(e_i\left(t\right)\right)+\tilde{B}g\left(e_i(t-{\tau }_0\left(t\right))\right)\hfill \\ \hfill & +c_0\sum _{j=1}^N{C}_{ij}^{\left(0\right)}\psi \left(e_j\left(t\right)\right)+\sum _{q=1}^{m-1}\sum _{j=1}^N{c}_q{C}_{ij}^{\left(q\right)}\psi \left(e_j(t-{\tau }_q\left(t\right))\right)].\hfill \end{array}$$

(10)

By Assumption 1, Assumption 3 and Lemma 1, we have

$$\begin{array}{cc}\hfill & 2\sum _{i=1}^N{e}_i^T\left(t\right)P[-(D+\mathsf{\Delta }D\left(t\right))]e_i\left(t\right)\hfill \\ \hfill =& -2\sum _{i=1}^N{e}_i^T\left(t\right)P\left[(D+E_D\Phi \left(t\right)F_D)\right]e_i\left(t\right)\hfill \\ \hfill \le & -2\sum _{i=1}^N{e}_i^T\left(t\right)PD{e}_i\left(t\right)+\sum _{i=1}^N[{\xi }_0{e}_i^T\left(t\right)P{E}_D{E}_D^{T}P{e}_i\left(t\right)+{\xi }_0^{-1}{e}_i^T\left(t\right){\lambda }_{max}\left(F_D^T{F}_D\right)e_i\left(t\right)],\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & 2\sum _{i=1}^N{e}_i^T\left(t\right)P(A+\mathsf{\Delta }A\left(t\right))f\left(e_i\left(t\right)\right)\hfill \\ \hfill =& 2\sum _{i=1}^N{e}_i^T\left(t\right)PAf\left(e_i\left(t\right)\right)+2\sum _{i=1}^N{e}_i^T\left(t\right)P{E}_A\Phi \left(t\right)F_{A}f\left(e_i\left(t\right)\right)\hfill \\ \hfill \le & \sum _{i=1}^N[{\xi }_1{e}_i^T\left(t\right)PA{A}^{T}P{e}_i\left(t\right)+{\xi }_1^{-1}\parallel f\left(e_i\left(t\right)\right){\parallel }^2]\hfill \\ \hfill & +\sum _{i=1}^N[{\xi }_2{e}_i^T\left(t\right)P{E}_A{E}_A^{T}P{e}_i\left(t\right)+{\xi }_2^{-1}{f}^T\left(e_i\left(t\right)\right)F_A^T{F}_{A}f\left(e_i\left(t\right)\right)\hfill \\ \hfill \le & \sum _{i=1}^N[{\xi }_1{e}_i^T\left(t\right)PA{A}^{T}P{e}_i\left(t\right)+{\xi }_2{e}_i^T\left(t\right)P{E}_A{E}_A^{T}P{e}_i\left(t\right)]+\sum _{i=1}^N[{\xi }_1^{-1}+{\xi }_2^{-1}{\lambda }_{max}\left(F_A^T{F}_A\right)]l_f^2{e}_i^T\left(t\right)e_i\left(t\right).\hfill \end{array}$$

(12)

Similarly, we can obtain

$$\begin{array}{cc}\hfill & 2\sum _{i=1}^N{e}_i^T\left(t\right)P(B+\mathsf{\Delta }B\left(t\right))g\left(e_i(t-{\tau }_0\left(t\right))\right)\hfill \\ \hfill =& 2\sum _{i=1}^N{e}_i^T\left(t\right)PBg\left(e_i(t-{\tau }_0\left(t\right))\right)+2\sum _{i=1}^N{e}_i^T\left(t\right)P{E}_B\Phi \left(t\right)F_{B}g\left(e_i(t-{\tau }_0\left(t\right))\right)\hfill \\ \hfill \le & \sum _{i=1}^N[{\zeta }_1{e}_i^T\left(t\right)PB{B}^{T}P{e}_i\left(t\right)+{\zeta }_1^{-1}\parallel g\left(e_i(t-{\tau }_0\left(t\right))\right){\parallel }^2]\hfill \\ \hfill & +\sum _{i=1}^N[{\zeta }_2{e}_i^T\left(t\right)P{E}_B{E}_B^{T}P{e}_i\left(t\right)+{\zeta }_2^{-1}{g}^T\left(e_i(t-{\tau }_0\left(t\right))\right)F_B^T{F}_{B}g\left(e_i(t-{\tau }_0\left(t\right))\right)]\hfill \\ \hfill \le & \sum _{i=1}^N[{\zeta }_1{e}_i^T\left(t\right)PB{B}^{T}P{e}_i\left(t\right)+{\zeta }_2{e}_i^T\left(t\right)P{E}_B{E}_B^{T}P{e}_i\left(t\right)]\hfill \\ \hfill & +\sum _{i=1}^N[{\zeta }_1^{-1}+{\zeta }_2^{-1}{\lambda }_{max}\left(F_B^T{F}_B\right)]l_g^2{e}_i^T(t-{\tau }_0\left(t\right))e_i(t-{\tau }_0\left(t\right)).\hfill \end{array}$$

(13)

By Assumptions 1–2 and Lemma 1, we have

$$\begin{array}{cc}\hfill & 2\sum _{i=1}^N{e}_i^T\left(t\right)P{c}_0\sum _{j=1}^N{C}_{ij}^{\left(0\right)}\psi \left(e_j\left(t\right)\right)\hfill \\ \hfill \le & \sum _{i=1}^N\sum _{j=1}^N{c}_0{\sigma }_0{e}_i^T\left(t\right)P{\left(C_{ij}^{\left(0\right)}\right)}^{2}P{e}_i\left(t\right)+\sum _{i=1}^N\sum _{j=1}^N{c}_0{\sigma }_0^{-1}{\parallel \psi \left(e_j\left(t\right)\right)\parallel }^2\hfill \\ \hfill \le & \sum _{i=1}^N{c}_0{\sigma }_0{L}_0{e}_i^T\left(t\right)PP{e}_i\left(t\right)+l_{\psi }^{2}N\sum _{i=1}^N{c}_0{\sigma }_0^{-1}{e}_i^T\left(t\right)e_i\left(t\right).\hfill \end{array}$$

(14)

Similarly, one can obtain

$$\begin{array}{cc}\hfill & 2\sum _{i=1}^N{e}_i^T\left(t\right)P\sum _{q=1}^{m-1}\sum _{j=1}^N{c}_q{C}_{ij}^{\left(q\right)}\psi \left(e_j(t-{\tau }_q\left(t\right))\right)\hfill \\ \hfill \le & \sum _{i=1}^N\sum _{j=1}^N\sum _{q=1}^{m-1}{c}_q{\sigma }_q{e}_i^T\left(t\right)P{\left(C_{ij}^{\left(q\right)}\right)}^{2}P{e}_i\left(t\right)+\sum _{i=1}^N\sum _{j=1}^N\sum _{q=1}^{m-1}{c}_q{\sigma }_q^{-1}{\parallel \psi \left(e_j(t-{\tau }_q\left(t\right))\right)\parallel }^2\hfill \\ \hfill \le & \sum _{i=1}^N\sum _{q=1}^{m-1}{c}_q{\sigma }_q{L}_q{e}_i^T\left(t\right)PP{e}_i\left(t\right)+l_{\psi }^{2}N\sum _{i=1}^N\sum _{q=1}^{m-1}{c}_q{\sigma }_q^{-1}{e}_i^T(t-{\tau }_q\left(t\right))e_i(t-{\tau }_q\left(t\right)).\hfill \end{array}$$

(15)

Substituting inequalities (11)–(15) into (10), we can derive that

$$\begin{array}{cc}\hfill D^{+}& V\left(t\right)\hfill \\ \hfill \le & \sum _{i=1}^N{e}_i^T\left(t\right)[-2PD+P({\xi }_0{E}_D{E}_D^T+{\xi }_{1}A{A}^T+{\xi }_2{E}_A{E}_A^T+{\zeta }_{1}B{B}^T+{\zeta }_2{E}_B{E}_B^T\hfill \\ \hfill & +I\sum _{r=0}^{m-1}{\sigma }_r{c}_r{L}_r)P+{\xi }_0^{-1}{\lambda }_{max}\left(F_D^T{F}_D\right)I+c_0{\sigma }_0^{-1}{l}_{\psi }^{2}NI+l_f^2({\xi }_1^{-1}+{\xi }_2^{-1}{\lambda }_{max}\left(F_A^T{F}_A\right))I]e_i\left(t\right)\hfill \\ \hfill & +\sum _{i=1}^N{e}_i^T(t-{\tau }_0\left(t\right))\left[l_g^2({\zeta }_1^{-1}+{\zeta }_2^{-1}{\lambda }_{max}\left(F_B^T{F}_B\right))I\right]e_i(t-{\tau }_0\left(t\right))\hfill \\ \hfill & +\sum _{i=1}^N\sum _{q=1}^{m-1}{e}_i^T(t-{\tau }_q\left(t\right))\left(c_q{\sigma }_q^{-1}{l}_{\psi }^{2}NI\right)e_i(t-{\tau }_q\left(t\right))\hfill \\ \hfill \le & \alpha V\left(t\right)+{\beta }_{0}V(t-{\tau }_0\left(t\right))+\sum _{q=1}^{m-1}{\beta }_{q}V(t-{\tau }_q\left(t\right)).\hfill \end{array}$$

(16)

Denote $e_i\left(t\right)={[e_1^T\left(t\right),e_2^T\left(t\right),\dots ,e_N^T\left(t\right)]}^T$. When $t=t_k,k\in {\mathbb{Z}}_{+}$, we obtain

$$\begin{array}{cc}\hfill V\left(t_k\right)& =\sum _{i=1}^N{e}_i^T\left(t_k\right)P{e}_i\left(t_k\right)=\sum _{i=1}^N{\left[M{e}_i(t_k^{-}-{\iota }_k)\right]}^{T}P\left[M{e}_i(t_k^{-}-{\iota }_k)\right]\hfill \\ \hfill & =\sum _{i=1}^N{e}_i^T(t_k^{-}-{\iota }_k)M^{T}PM{e}_i(t_k^{-}-{\iota }_k).\hfill \end{array}$$

(17)

Based on Lemma 2 and condition (v) in Theorem 1, we have

$$M^{T}PM-\frac{1}{\sigma {\mu }_b}P\le 0,$$

(18)

which implies

$$\begin{array}{cc}\hfill V\left(t_k\right)& \le \frac{1}{\sigma {\mu }_b}\sum _{i=1}^N{e}_i^T(t_k^{-}-{\iota }_k)P{e}_i(t_k^{-}-{\iota }_k)\hfill \\ \hfill & =\frac{1}{\sigma {\mu }_b}V(t_k^{-}-{\iota }_k).\hfill \end{array}$$

(19)

By Lemma 3, combining (16) and (19), we have

$$V\left(t\right)\le \frac{\sigma \mu \left(0\right){\sup }_{-\infty <s\le 0}V\left(s\right)}{\mu \left(t\right)},t\ge 0,$$

(20)

which further implies

$$\parallel e\left(t\right)\parallel \le \sqrt{\frac{\sigma \mu \left(0\right){\lambda }_{max}\left(P\right){\left|e\left(0\right)\right|}^2}{{\lambda }_{min}\left(P\right)\mu \left(t\right)}}.$$

(21)

Since $\sigma >1$ and $P>0$, the $\mu$-synchronization between the drive system (1) and the response system (2) can be realized, and the proof is finished. □

Remark 3.

Compared with the existing impulse synchronization results [12,16,17], which require the parameter T to be restricted by the bound of time delay, that is, as the time delay increases, the impulsive interval needs to be gradually reduced. In this article, the impulsive interval T is no longer limited by the delay size, which can be seen in condition (i).

Remark 4.

The synchronization problem of complex networks with time delay is studied [21,22,23,24,25,26]. However, these results are all based on the assumption that there exist positive scalars τ or $\overline{\tau }$ such that $0\le {\tau }_i\left(t\right)\le \tau$ or $0\le {\dot{\tau }}_i\left(t\right)\le \overline{\tau }<1$. On the contrary, in this paper, the three kinds of time delays are all unbounded, i.e., $0\le {\tau }_0\left(t\right)\le \infty$, $0\le {\tau }_q\left(t\right)\le \infty$, and $0\le {\iota }_k\le \infty$.

Remark 5.

The existing results about μ-stability or μ-synchronization in [27,28,29,30,31] mainly focused on single-weighted networks rather than multi-weighted networks. Furthermore, the network topologies must meet dissipative coupling conditions and system uncertain perturbation was ignored in these works. In this paper, the μ-synchronization criteria for multi-weighted networks including unbounded mixed delays and uncertainties are derived via a delayed impulsive control scheme.

Particularly, if the mixed time-varying delays in drive–response systems (1) and (2) have more limitations, then we can gain two important corollaries as follows:

Corollary 1.

Under Assumptions 1–3 and inequalities $\left(\mathrm{ii}\right)$–$\left(\mathrm{iv}\right)$, suppose $\mu \left(t\right)={(1+p_{1}t)}^{\varsigma }$, ${\tau }_0\left(t\right)={\pi }_{0}t$, ${\tau }_q\left(t\right)={\pi }_{q}t$,$(q=1,2,\dots ,m-1)$, and ${\iota }_k=\pi t_k$, $k\in {\mathbb{Z}}_{+}$, where $p_1>0,\varsigma >0,0\le {\pi }_0<1,0\le \pi <1,$ and $0\le {\pi }_q<1,(q=1,2,\dots ,m-1).$ If there are two scalars $\sigma >1,T>0$ to make the following conditions:

$$\alpha T+\sigma [\frac{{\beta }_0}{{(1-{\pi }_0)}^{\varsigma }}+\sum _{q=1}^{m-1}\frac{{\beta }_q}{{(1-{\pi }_q)}^{\varsigma }}]T<ln\left[\sigma {(1+p_{1}T)}^{-\varsigma }\right],$$

and

$$\left[\begin{array}{cc}-\frac{{(1-\pi )}^{\varsigma }}{\sigma }P& \Xi \\ {\Xi }^T& -P\end{array}\right]\le 0.$$

hold, then complex systems (1) and (2) can achieve global power synchronization via the control matrix $M=P^{-1}{\Xi }^T.$

 Proof. 

In fact, only Assumption 4 needs to be verified. For any $t\ge 0,$ we can obtain

$$\begin{array}{cc}\hfill & \frac{\mu \left(t_k\right)}{\mu (t_{k-1)}}={\left[\frac{1+p_1{t}_k}{1+p_1{t}_{k-1}}\right]}^{\varsigma }={\left[\frac{1+p_1{t}_{k-1}+p_1(t_k-t_{k-1})}{1+p_1{t}_{k-1}}\right]}^{\varsigma }\le {(1+p_{1}T)}^{\varsigma },\hfill \\ \hfill & \frac{\mu \left(t\right)}{{\mu }^{*}(t-{\tau }_0\left(t\right))}={\left[\frac{1+p_{1}t}{1+p_1(1-{\pi }_0)t}\right]}^{\varsigma }=\frac{1}{{\left[\frac{1+p_1(1-{\pi }_0)t}{1+p_{1}t}\right]}^{\varsigma }}\le \frac{1}{{(1-{\pi }_0)}^{\varsigma }},\hfill \\ \hfill & \frac{\mu \left(t\right)}{{\mu }^{*}(t-{\tau }_q\left(t\right))}={\left[\frac{1+p_{1}t}{1+p_1(1-{\pi }_q)t}\right]}^{\varsigma }=\frac{1}{{\left[\frac{1+p_1(1-{\pi }_q)t}{1+p_{1}t}\right]}^{\varsigma }}\le \frac{1}{{(1-{\pi }_q)}^{\varsigma }},\hfill \\ \hfill & \frac{\mu \left(t_k\right)}{{\mu }^{*}(t_k-{\iota }_k)}={\left[\frac{1+p_1{t}_k}{1+p_1(1-\pi )t_k}\right]}^{\varsigma }=\frac{1}{{\left[\frac{1+p_1(1-\pi )t_k}{1+p_1{t}_k}\right]}^{\varsigma }}\le \frac{1}{{(1-\pi )}^{\varsigma }}.\hfill \end{array}$$

Set ${\mu }_a={(1+p_{1}T)}^{\varsigma },{\mu }_0=\frac{1}{{(1-{\pi }_0)}^{\varsigma }}$, ${\mu }_q=\frac{1}{{(1-{\pi }_q)}^{\varsigma }}$, $(q=1,2,\dots ,m-1),$ and ${\mu }_b=\frac{1}{{(1-\pi )}^{\varsigma }}$. Utilizing the similar proof method of Theorem 1, we can conclude that drive system (1) and response system (2) can achieve global power synchronization. □

Corollary 2.

Under Assumptions 1–3 and inequalities $\left(\mathrm{ii}\right)$–$\left(\mathrm{iv}\right)$, suppose $\mu \left(t\right)=ln(e+\theta t),$${\tau }_0\left(t\right)=t+[e-{(t+e)}^{{\lambda }_0}]/\theta ,{\tau }_q\left(t\right)=t+[e-{(t+e)}^{{\lambda }_q}]/\theta ,(q=1,2,\dots ,m-1)$, and ${\iota }_k=\pi t_k,$$k\in {\mathbb{Z}}_{+}$, where $0<\theta <1,0<{\lambda }_0<1,0<{\lambda }_q<1,(q=1,2,\dots ,m-1),\mathrm{and}0\le \pi <1.$ If there are two scalars $\sigma >1,T>0$ to make the following conditions

$$\left(\alpha +\frac{\sigma {\beta }_0}{{\lambda }_0}+\sigma \sum _{q=1}^{m-1}\frac{{\beta }_q}{{\lambda }_q}\right)T<ln\left[\frac{\sigma }{1+ln(1+\theta T/e)}\right],$$

and

$$\begin{array}{c}\hfill \left[\begin{array}{cc}-\frac{1}{\sigma [1-ln(1-\pi \left)\right]}P& \Xi \\ {\Xi }^T& -P\end{array}\right]\le 0.\end{array}$$

hold, then complex systems (1) and (2) can achieve the global log synchronization via the control matrix $M=P^{-1}{\Xi }^T.$

 Proof. 

Similarly, we just verify Assumption 4. For any $t\ge 0$, one has

$$\begin{array}{cc}\hfill & \frac{\mu \left(t_k\right)}{\mu \left(t_{k-1}\right)}=\frac{ln(e+\theta t_k)}{ln(e+\theta t_{k-1})}\le 1+\frac{ln[1+\frac{\theta (t_k-t_{k-1})}{e+\theta t_{k-1}}]}{ln(e+\theta t_{k-1})}\le 1+ln(1+\theta T/e),\hfill \\ \hfill & \frac{\mu \left(t\right)}{{\mu }^{*}(t-{\tau }_0\left(t\right))}=\frac{ln(e+\theta t)}{{\mu }^{*}[({(t+e)}^{{\lambda }_0}-e)/\theta ]}=\frac{ln(e+\theta t)}{{\lambda }_{0}ln(e+t)}\le \frac{1}{{\lambda }_0},\hfill \\ \hfill & \frac{\mu \left(t\right)}{{\mu }^{*}(t-{\tau }_q\left(t\right))}=\frac{ln(e+\theta t)}{{\mu }^{*}[({(t+e)}^{{\lambda }_q}-e)/\theta ]}=\frac{ln(e+\theta t)}{{\lambda }_{q}ln(e+t)}\le \frac{1}{{\lambda }_q},\hfill \\ \hfill & \frac{\mu \left(t_k\right)}{{\mu }^{*}(t_k-{\iota }_k)}=\frac{ln(e+\theta t_k)}{ln(e+\theta (t_k-\pi t_k))}=1+\frac{ln\left[\frac{e+\theta t_k}{[e+\theta (1-\pi )t_k]}\right]}{ln[e+\theta (1-\pi )t_k]}\le 1-ln(1-\pi ).\hfill \end{array}$$

Set ${\mu }_a=1+ln(1+\theta T/e),{\mu }_0=\frac{1}{{\lambda }_0},{\mu }_q=\frac{1}{{\lambda }_q}$, $(q=1,2,\dots ,m-1)$, and ${\mu }_b=1-ln(1-\pi )$. We can easily derive Corollary 2. □

Corollary 3.

Under Assumptions 1–3 and inequalities $\left(\mathrm{ii}\right)$–$\left(\mathrm{iv}\right)$, suppose $\mu \left(t\right)=exp\left(\rho t\right),0\le {\tau }_0\left(t\right)\le \tau ,0\le {\tau }_q\left(t\right)\le \tau ,(q=1,2,\dots ,m-1),0\le {\iota }_k\le \iota ,k\in {\mathbb{Z}}_{+}$, where $\rho >0,\tau <\infty ,$ and $\iota <\infty$. If there are two scalars $\sigma >1,T>0$ to make the following conditions:

$$\rho T+\left[\alpha +\sigma ({\beta }_0+\sum _{q=1}^{m-1}{\beta }_q)exp\left(\rho t\right)\right]T<ln\sigma ,$$

and

$$\begin{array}{c}\hfill \left[\begin{array}{cc}-\frac{1}{\sigma exp\left(\rho \iota \right)}P& \Xi \\ {\Xi }^T& -P\end{array}\right]\le 0.\end{array}$$

hold, then complex systems (1) and (2) can achieve the global exponential synchronization via the control matrix $M=P^{-1}{\Xi }^T.$

 Proof. 

Similarly, we just verify Assumption 4. For any $t\ge 0$, we have

$$\begin{array}{cc}\hfill & \frac{\mu \left(t_k\right)}{\mu \left(t_{k-1}\right)}=\frac{exp\left(\rho t_k\right)}{exp\left(\rho t_{k-1}\right)}=exp\left[\rho (t_k-t_{k-1})\right]\le exp\left(\rho T\right),\hfill \\ \hfill & \frac{\mu \left(t\right)}{{\mu }^{*}(t-{\tau }_0\left(t\right))}=\frac{exp\left(\rho t\right)}{exp\left[\rho (t-{\tau }_0\left(t\right))\right]}=exp\left[\rho {\tau }_0\left(t\right)\right]\le exp\left(\rho \tau \right),\hfill \\ \hfill & \frac{\mu \left(t\right)}{{\mu }^{*}(t-{\tau }_q\left(t\right))}=\frac{exp\left(\rho t\right)}{exp\left[\rho (t-{\tau }_q\left(t\right))\right]}=exp\left[\rho {\tau }_q\left(t\right)\right]\le exp\left(\rho \tau \right),\hfill \\ \hfill & \frac{\mu \left(t_k\right)}{{\mu }^{*}(t_k-{\iota }_k)}=\frac{exp\left(\rho t_k\right)}{exp\left[\rho (t_k-{\iota }_k)\right]}=exp\left[\rho {\iota }_k\right]\le exp\left(\rho \iota \right).\hfill \end{array}$$

Set ${\mu }_a=exp\left(\rho T\right),{\mu }_0=exp\left(\rho \tau \right),{\mu }_q=exp\left(\rho \tau \right),$$(q=1,2,\dots ,m-1),$ and ${\mu }_b=exp\left(\rho \iota \right)$. We can easily derive Corollary 3. □

4. Numerical Simulations

Two numerical examples are given to illustrate the validity of the synchronization criteria obtained above. Consider the following neural network consisting of 6 nodes with mixed delays and uncertainties, which could be described by

$$\begin{array}{cc}\hfill {\dot{x}}_i\left(t\right)=& -\tilde{D}{x}_i\left(t\right)+\tilde{A}f\left(x_i\left(t\right)\right)+\tilde{B}g\left(x_i(t-{\tau }_0\left(t\right))\right)\hfill \\ & +c_0\sum _{j=1}^6{C}_{ij}^{\left(0\right)}\psi \left(x_j\left(t\right)\right)+\sum _{q=1}^2\sum _{j=1}^6{c}_q{C}_{ij}^{\left(q\right)}\psi \left(x_j(t-{\tau }_q\left(t\right))\right),i=1,2,\dots ,6,\hfill \end{array}$$

(22)

where $x_i\left(t\right)={(x_{i1}\left(t\right),x_{i2}\left(t\right))}^T$ is the state vector of the ith node. The nonlinear functions are $f\left(x_i\left(t\right)\right)=g\left(x_i\left(t\right)\right)=\psi \left(x_i\left(t\right)\right)=1/5{(\tan \mathrm{h}\left(x_{i1}\left(t\right)\right),\tan \mathrm{h}\left(x_{i2}\left(t\right)\right))}^T$. Take the above equation as the drive network, and the corresponding response network is described as follows:

$$\begin{array}{cc}\hfill {\dot{y}}_i\left(t\right)=& -\tilde{D}{y}_i\left(t\right)+\tilde{A}f\left(y_i\left(t\right)\right)+\tilde{B}g\left(y_i(t-{\tau }_0\left(t\right))\right)\hfill \\ & +c_0\sum _{j=1}^6{C}_{ij}^{\left(0\right)}\psi \left(y_j\left(t\right)\right)+\sum _{q=1}^2\sum _{j=1}^6{c}_q{C}_{ij}^{\left(q\right)}\psi \left(y_j(t-{\tau }_q\left(t\right))\right),i=1,2,\dots ,6.\hfill \end{array}$$

(23)

Respectively, the connection matrices $D,A,B$ and parametric uncertainties are selected as

$$D=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],A=\left[\begin{array}{cc}2.0& -0.1\\ -3.0& 1.5\end{array}\right],B=\left[\begin{array}{cc}-1.5& -0.1\\ -0.2& -2.0\end{array}\right],$$

$$\mathsf{\Delta }D\left(t\right)=E_D\Phi \left(t\right)F_D=\left[\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right]\left[\begin{array}{cc}sin\left(t\right)& 0\\ 0& cos\left(t\right)\end{array}\right]\left[\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right],$$

$$\mathsf{\Delta }A\left(t\right)=E_A\Phi \left(t\right)F_A=\left[\begin{array}{cc}0.2& 0\\ 0& 0.2\end{array}\right]\left[\begin{array}{cc}sin\left(t\right)& 0\\ 0& cos\left(t\right)\end{array}\right]\left[\begin{array}{cc}0.2& 0\\ 0& 0.2\end{array}\right],$$

$$\mathsf{\Delta }B\left(t\right)=E_B\Phi \left(t\right)F_B=\left[\begin{array}{cc}0.3& 0\\ 0& 0.3\end{array}\right]\left[\begin{array}{cc}sin\left(t\right)& 0\\ 0& cos\left(t\right)\end{array}\right]\left[\begin{array}{cc}0.3& 0\\ 0& 0.3\end{array}\right].$$

By simple calculation, one can easily obtain $l_f=l_g=l_{\psi }=1/5$, such that Assumption 1 holds. The outer coupling matrices $C^{\left(0\right)},C^{\left(1\right)}$, and $C^{\left(2\right)}$ are chosen from left to right as follows:

$$\left[\begin{array}{cccccc}1& 1& 0& 0& 0& 0\\ 0& 1& 1& 0& 0& 0\\ 0& 0& 1& 1& 0& 0\\ 0& 0& 0& 1& 1& 0\\ 0& 0& 0& 0& 1& 1\\ 1& 0& 0& 0& 1& 2\end{array}\right],\left[\begin{array}{cccccc}1& 0& 1& 0& 0& 0\\ 0& 1& 0& 1& 0& 0\\ 0& 0& 1& 0& 1& 0\\ 0& 1& 0& 2& 0& 1\\ 0& 0& 0& 0& 1& 1\\ 0& 1& 0& 0& 0& 1\end{array}\right],\left[\begin{array}{cccccc}2& 1& 1& 0& 0& 0\\ 0& 1& 1& 0& 0& 0\\ 0& 0& 1& 1& 0& 0\\ 0& 0& 1& 2& 1& 0\\ 0& 0& 0& 0& 1& 1\\ 0& 0& 0& 1& 0& 1\end{array}\right].$$

Clearly, Assumption 2 is satisfied with $L_r=6$. The other parameters are set as ${\tau }_0\left(t\right)=0.05t,{\tau }_1\left(t\right)={\tau }_2\left(t\right)=0.01t,\mu \left(t\right)=\sqrt{1+3t},{\iota }_k=t_k/6,k\in Z_{+}$, ${\xi }_0={\xi }_1=2,{\xi }_2=4,$${\zeta }_1={\zeta }_2=0.1,T=0.01,$$\alpha =228,{\beta }_0=1.01,{\beta }_1=1.12,{\beta }_2=1.13,$$c_0=0.05,c_1=c_2=0.1,\sigma =18.83,{\sigma }_0=3,{\sigma }_1=1,{\sigma }_2=0.5$. By calculation, one can gain that ${\mu }_a=1.0149,{\mu }_0=1.0260,{\mu }_1={\mu }_2=1.0050$ and ${\mu }_b=1.0954$. To solve the rest of the conditions in Corollary 1, Matlab LMI Toolbox is used and we can obtain the feasible solutions as follows.

$$P=\left[\begin{array}{cc}4.3121& 0\\ 0& 8.0812\end{array}\right],\Xi =\left[\begin{array}{cc}0.5912& 0.8121\\ 0& 1.0510\end{array}\right].$$

Then control gain matrix M could be designed as

$$M=\left[\begin{array}{cc}0.1371& 0\\ 0.1005& 0.1301\end{array}\right].$$

The initial values of networks are produced stochastically from [−50, 0]. By the fourth-order Runge–Kutta technology, the simulation results of Corollary 1 can be seen in Figure 2. Figure 2a displays the time evolution of $\parallel e_i\left(t\right)\parallel$ through the effective matrix M, which demonstrates that the response system (23) can achieve synchronization with (22) by using delayed impulsive control. In case there exists some change for the gain matrix $M^{*}=M+0.1I$, which breaks the corresponding conditions, then Figure 2b shows the synchronization target between the drive system (22) and the response system (23) cannot be achieved.

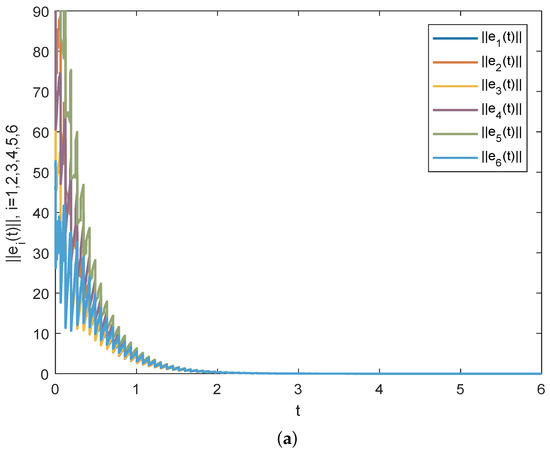
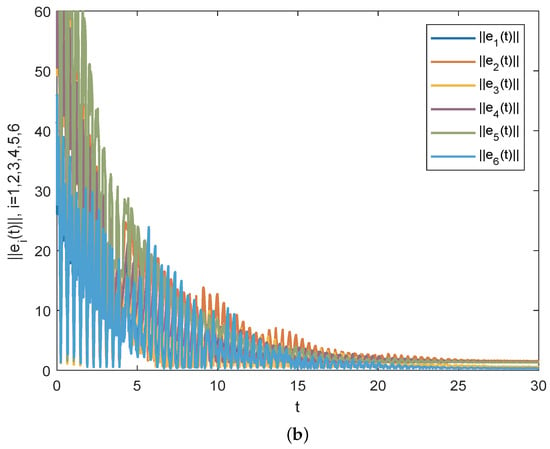
Figure 2. (a) Time evolution of $\parallel e_i\left(t\right)\parallel$ through the effective impulsive matrix M. One can see that $\parallel e_i\left(t\right)\parallel$ approach zero over time, which shows complex networks (23) and (22) can achieve synchronization in this case. (b) Time evolution of $\parallel e_i\left(t\right)\parallel$ through the impulsive gain matrix $M^{*}=M+0.1I$. Since $M^{*}$ breaks the conditions of Corollary 1, one can see that $\parallel e_i\left(t\right)\parallel$ cannot approach zero over time and the synchronization fails in this instance.

Next, to verify the effect of different parameter forms on the synchronization process, we change the uncertain parameters, coupling parts, and delay expressions. The uncertain matrix and the coupling matrices $C^{\left(0\right)},C^{\left(1\right)}$, $C^{\left(2\right)}$ are set, respectively, as

$$\mathsf{\Delta }D\left(t\right)=E_D\Phi \left(t\right)F_D=\left[\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right]\left[\begin{array}{cc}sin\left(t\right)& 0\\ 0& sin\left(t\right)\end{array}\right]\left[\begin{array}{cc}0.2& 0\\ 0& 0.2\end{array}\right],$$

$$\mathsf{\Delta }A\left(t\right)=E_A\Phi \left(t\right)F_A=\left[\begin{array}{cc}0.2& 0\\ 0& 0.2\end{array}\right]\left[\begin{array}{cc}sin\left(t\right)& 0\\ 0& sin\left(t\right)\end{array}\right]\left[\begin{array}{cc}0.15& 0\\ 0& 0.15\end{array}\right],$$

$$\mathsf{\Delta }B\left(t\right)=E_B\Phi \left(t\right)F_B=\left[\begin{array}{cc}0.15& 0\\ 0& 0.15\end{array}\right]\left[\begin{array}{cc}sin\left(t\right)& 0\\ 0& sin\left(t\right)\end{array}\right]\left[\begin{array}{cc}0.25& 0\\ 0& 0.25\end{array}\right],$$

$$\left[\begin{array}{cccccc}1& 1& 0& 0& 0& 1\\ 0& 1& 1& 0& 0& 0\\ 0& 0& 1& 1& 0& 0\\ 0& 0& 0& 1& 1& 0\\ 0& 0& 0& 0& 1& 1\\ 1& 1& 0& 0& 1& 1\end{array}\right],\left[\begin{array}{cccccc}1& 0& 1& 0& 0& 1\\ 0& 1& 0& 1& 0& 0\\ 0& 0& 1& 0& 1& 0\\ 0& 1& 0& 1& 0& 1\\ 0& 0& 0& 0& 1& 1\\ 1& 1& 0& 0& 0& 1\end{array}\right],\left[\begin{array}{cccccc}1& 1& 1& 0& 0& 1\\ 0& 1& 1& 0& 0& 0\\ 0& 0& 1& 1& 0& 0\\ 0& 0& 1& 2& 1& 0\\ 1& 0& 0& 0& 1& 1\\ 0& 0& 0& 1& 0& 1\end{array}\right].$$

We choose nonlinear variable delays rather than linear delays, such as ${\tau }_0\left(t\right)={\tau }_1\left(t\right)={\tau }_2\left(t\right)=t+5[e-{(t+e)}^{0.5}]$. Set $\mu \left(t\right)=ln(e+t/5),{\iota }_k=t_k/5,k\in Z_{+},\alpha =243,{\xi }_0=1,{\xi }_1=2,$${\xi }_2=3$, ${\beta }_0={\beta }_1={\beta }_2=0.45$, $\sigma =20.83,{\sigma }_0=1,{\sigma }_1={\sigma }_2=0.5$. By calculation, one can obtain that ${\mu }_a=1.0007,{\mu }_0={\mu }_1={\mu }_2=2,$ and ${\mu }_b=1.2231.$ The remaining parameters are identical to the first example. To solve the rest of the conditions in Corollary 2, by using LMI Toolbox, we can obtain the feasible solutions as follows:

$$P=\left[\begin{array}{cc}7.3011& 0\\ 0& 8.0832\end{array}\right],\Xi =\left[\begin{array}{cc}0.8923& 0.8142\\ 0& 0.8225\end{array}\right].$$

Then control gain matrix M could be designed as

$$M=\left[\begin{array}{cc}0.1222& 0\\ 0.1007& 0.1018\end{array}\right].$$

The initial values of networks are produced stochastically as before and the simulation results of Corollary 2 are gained in Figure 3. Figure 3a displays the time evolution of $\parallel e_i\left(t\right)\parallel$ through the useful impulsive matrix M, and it implies that complex networks (23) and (22) realize synchronization by using the proposed impulsive control methods. If there exists some change for the impulsive matrix $M^{*}=M-0.1I$, which makes the corresponding conditions unsatisfied, then synchronization cannot be achieved between complex networks (22) and (23), as displayed in Figure 3b.

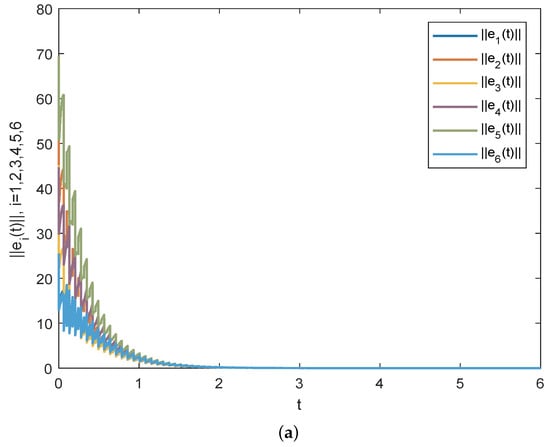
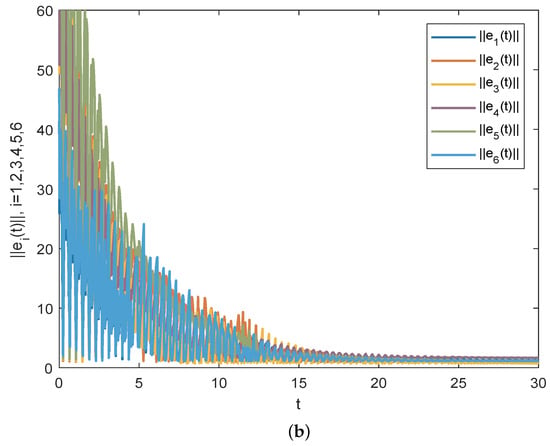
Figure 3. (a) Time evolution of $\parallel e_i\left(t\right)\parallel$ through the effective impulsive matrix M. One can see that synchronization errors $\parallel e_i\left(t\right)\parallel$ approach zero over time, which implies response network (23) achieves synchronization with drive network (22) in this case. (b) Time evolution of $\parallel e_i\left(t\right)\parallel$ under impulsive gain matrix $M^{*}=M-0.1I$. Since matrix $M^{*}$ breaks the conditions of Corollary 2, one can see that $\parallel e_i\left(t\right)\parallel$ cannot approach zero over time and the synchronization fails in this situation.

5. Conclusions

We investigated the $\mu$-synchronization issues of nonlinearly coupled multi-weighted drive–response networks with unbounded mixed time-varying delays and uncertain parameter perturbation in this article. By designing a suitable $\mu$-function and the impulsive controller including unbounded sampling delays, several new sufficient conditions were gained to ensure the $\mu$-synchronization of the concerned multi-weighted network. The restrictions between delays and impulsive intervals were weakened, and the coupling matrices were not confined by zero-row sum requirement, which made our results more general. Ultimately, numerical simulations were provided to verify the correctness and effectiveness of our theoretical analysis.