Describing Water Wave Propagation Using the $\frac{{\mathit{G}}^{\mathbf{\prime }}}{{\mathit{G}}^{\mathbf{2}}}$–Expansion Method

Abstract

In the present study, our focus is to obtain the different analytical solutions to the space–time fractional Bogoyavlenskii equation in the sense of the Jumaries-modified Riemann–Liouville derivative and to the conformable time–fractional-modified nonlinear Schrödinger equation that describes the fluctuation of sea waves and the propagation of water waves in ocean engineering, respectively. The $\frac{G^{\prime }}{G^2}$–expansion method is applied to investigate the dynamics of solitons in relation to governing models. Moreover, the restriction conditions for the existence of solutions are reported. In addition, we note that the accomplished solutions are useful to the description of wave fluctuation and the wave propagation survey and are also significant for experimental and numerical verification in ocean engineering.

1. Introduction

Lately, it has become significant for scholars and researchers to investigate the analytical solutions to NLPDEs with the assistance of computational bundles, which simplify boring and tedious mathematical calculations. NLPDEs arise when one describes the physical mechanisms of natural phenomena in optical fibres, geochemistry, ocean engineering, geophysics, fluid mechanics, and many other fields. As a result, nonlinear phenomena are now, considered by many scholars in this novel field of science.

The nonlinear Schrödinger equation (NLSE), one of NLPDEs, has been investigated in such areas as nonlinear optics and condensed matter physics due to its potential physical applications and mathematical properties. It was found that the NLSE can illustrate the dynamic of nonlinear localized waves generally associated with breather, soliton, and rogue waves. Indeed, rogue waves can be informally thought of as rare events arising from the constructive interference of the surrounding waves. This construction interference can eventuate in waves with heights as large as ninth times that of the surrounding free surface. Multitude real-world consequences of these large spontaneous events exist, which can disrupt and damage human lives, commercial shipping, and many other nautical operations.

The modified nonlinear Schrödinger equation (MNSE) [1], which models rogue waves in ocean engineering, is given by

$$i{\mathsf{\Phi }}_{\tau }+{\sigma }_1{\mathsf{\Phi }}_{\chi \chi }+{\sigma }_2{\left|\mathsf{\Phi }\right|}^2\mathsf{\Phi }-i{\delta }_1{\mathsf{\Phi }}_{\chi \chi \chi }-i{\delta }_2{\mathsf{\Phi }}^2{\mathsf{\Phi }}_{\chi }^{*}+i{\delta }_3{\left|\mathsf{\Phi }\right|}^2{\mathsf{\Phi }}_{\chi }-{\delta }_4\mathsf{\Phi }=0,$$

(1)

where ${\sigma }_1={\displaystyle \frac{{\Xi }_0}{8{\Omega }_0^2(-3cos\left(\theta \right)+2)}},{\sigma }_2={\displaystyle \frac{-{\Xi }_0{\Omega }_0^2}{2}},{\delta }_1={\displaystyle \frac{{\Xi }_{0}cos\left(\theta \right)}{16{\Omega }_0^3(-5{cos}^2\left(\theta \right)-6)}},{\delta }_2={\displaystyle \frac{{\Xi }_0{\Omega }_{0}cos\left(\theta \right)}{4}},{\delta }_3={\displaystyle \frac{3{\Xi }_0{\Omega }_0}{2}},{\delta }_4={\Omega }_0{\left|\mathsf{\Phi }\right|}_{\chi }^2{|}_{\chi =0}$, and ${\Omega }_0$ and ${\Xi }_0$ are the wave number and the frequency of the carrier wave, respectively.

The simplified form of this equation was first discovered by Rogister (1971), starting with a Vlasov kinetic explanation for the particle species. Next, it was proposed by Mjølhus (1976) and Mio et al. (1976) on the basis of Hall magnetohydrodynamics (MHD) for cold plasmas, and by Spangler and Sheerin (1982) and Sakai and Sonnerup (1983) from warm-fluid models.

The nonlinear spatio-temporal evolution of gravity water-surface waves can be predicted by the nonlinear Bogoyavlenskii equation. In 1990, the following NPDE was given, later called the Bogoyavlenskii equation [2], to describe some kinds of waves on the sea surface.

$$\begin{array}{ccc}& & 4{\mathsf{\Phi }}_{\tau }+{\mathsf{\Phi }}_{\chi \chi \mathcal{Y}}-4{\mathsf{\Phi }}^2{\mathsf{\Phi }}_{\mathcal{Y}}-4{\mathsf{\Phi }}_{\chi }\mathsf{\Psi }=0,\hfill \end{array}$$

(2)

$$\begin{array}{ccc}& & \mathsf{\Phi }{\mathsf{\Phi }}_{\mathcal{Y}}={\mathsf{\Psi }}_{\chi }.\hfill \end{array}$$

(3)

Fractional calculus (FC) was formulated in 1695 after the development of classical calculus. For a long time, FC was regarded as a pure mathematical area without any real applications, but over the last few decades FC was recognized as a useful tool for understanding and modeling several artificial and natural phenomena. Scientific areas where FC concepts are applied include not only physics and mathematics but also finance, human sciences, engineering, economics, chemistry, and biology.

Starting from the earlier stage of FCs, various fractional operators have been presented during the last 300 years. For instance, the Caputo derivative [3] appeared naturally in the work of Liouville and Abel, and it was proposed by Caputo to solve a practical problem.

The study of fractional-order nonlinear systems of physical models relies on the analysis of wave solutions for nonlinear equations. Recently, numerous and varied techniques have been used to solve nonlinear fractional equations, such as the functional variable method [4], the trial equation method and the modified trial method [5], and the bifurcation method [6].

The objective of the present paper is to apply an interesting method, namely, the $\frac{G^{\prime }}{G^2}$–expansion method [7], to obtain novel exact solutions for the following nonlinear time-fractional equations:

• The conformable time-modified nonlinear Schrödinger equation (CTFMNLSE), given by [8]

  $$\mathrm{i}{D}_{\tau }^{\alpha }\mathsf{\Phi }+{\sigma }_1{\mathsf{\Phi }}_{\chi \chi }+{\sigma }_2{\left|\mathsf{\Phi }\right|}^2\mathsf{\Phi }-\mathrm{i}{\delta }_1{\mathsf{\Phi }}_{\chi \chi \chi }-\mathrm{i}{\delta }_2{\mathsf{\Phi }}^2{\mathsf{\Phi }}_{\chi }^{*}+\mathrm{i}{\delta }_3{\left|\mathsf{\Phi }\right|}^2{\mathsf{\Phi }}_{\chi }-{\delta }_4\mathsf{\Phi }=0,0<\alpha \le 1,$$

  (4)

  where ${\sigma }_1,{\sigma }_2,{\delta }_1,{\delta }_2,{\delta }_3,{\delta }_4$, ${\Omega }_0$ and ${\Xi }_0$ are defined in Equation (1),
• The space–time fractional Bogoyavlenskii equation in the sense of the Jumarie’s modified the Riemann–Liouville derivative defined by [9]

  $$\begin{array}{ccc}\hfill & & 4D_{\tau }^{\alpha }\mathsf{\Phi }+{\mathsf{\Phi }}_{\chi \chi \mathcal{Y}}-4{\mathsf{\Phi }}^2{\mathsf{\Phi }}_{\mathcal{Y}}-4{\mathsf{\Phi }}_{\chi }\mathsf{\Psi }=0,0<\alpha \le 1\hfill \\ & & \mathsf{\Phi }{\mathsf{\Phi }}_{\mathcal{Y}}={\mathsf{\Psi }}_{\chi }.\hfill \end{array}$$

  (5)

2. The Basic Idea of the $\frac{{\mathit{G}}^{\prime }}{{\mathit{G}}^{\mathbf{2}}}$–Expansion Method

Here, we propose the algorithm of the $\frac{G^{\prime }}{G^2}$–expansion procedure [7] for an NPDE, as follows:

• We assume a common nonlinear PDE of the type:

$$\begin{array}{c}\hfill \mathsf{N}(u,D_t^{\alpha }u,D_x^{\alpha }u,D_x^{\beta }u,D_x^{\alpha }{D}_x^{\beta }u,D_t^{\alpha }{D}_t^{\beta }u,\cdots )=0,0<\alpha ,\beta ⩽1,\end{array}$$

(6)

where $u=u(x,t).$

• Convert the nonlinear PDE (6) into an ODE through

$$\begin{array}{c}\hfill \mu ={\displaystyle \frac{d{x}^{d\beta }}{\mathsf{\Gamma }(1+\beta )}}+{\displaystyle \frac{c{x}^{c\alpha }}{\mathsf{\Gamma }(1+\alpha )}},u(x,t)=u\left(\mu \right),\end{array}$$

(7)

where d and c are constants.

• Rewrite Equation (6) in the following nonlinear ODE form:

$$\begin{array}{c}\hfill \tilde{\mathsf{N}}(u,u^{\prime },u^{″},u^{‴},\dots )=0.\end{array}$$

(8)

• Assume that the general solution of Equation (8) can be expressed in terms of $\frac{G^{\prime }}{G^2}$ as

$$\begin{array}{c}\hfill u\left(\mu \right)=a_0+\sum _{i=1}^N\left[a_i{\left(\frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}\right)}^i+b_i{\left(\frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}\right)}^{-i}\right],\end{array}$$

(9)

where $G\left(\mu \right)$ satisfies the following Riccati equation:

$$\begin{array}{c}\hfill {\left(\frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}\right)}^{\prime }=\eta +\lambda {\left(\frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}\right)}^2,\end{array}$$

(10)

in which $\eta \ne 1,\lambda \ne 0.$ The passive constants $b_N$ or $a_N$ may be zero, but they cannot be zero at the same time. Note, $a_0,\underset{i=1,\dots ,N}{\underbrace{b_i}},\underset{i=1,\dots ,N}{\underbrace{a_i}}$ are passive constants to be determined in the next step. Additionally, the value of $N\in \mathbb{N}$ can be computed through the homogeneous balance principle.

Notice that Equation (10) results in

$$\begin{array}{ccc}& & G^{″}\left(\mu \right)={\displaystyle \frac{\eta G^4+{\left(G^{\prime }\right)}^2(2G+\lambda )}{G^2}},\hfill \end{array}$$

(11)

$$\begin{array}{ccc}& & G^{‴}\left(\mu \right)=G^{\prime }(6G\eta +2\lambda \eta )+{\displaystyle \frac{{\left(G^{\prime }\right)}^3}{G^2}}(6+6\lambda {\displaystyle \frac{1}{G}}+2{\lambda }^2{\displaystyle \frac{1}{G^2}}).\hfill \end{array}$$

(12)

• Insert Equation (9), along with Equation (10), into Equation (8). Collect all of the coefficients of the same power of $\underset{i=1,\dots ,N}{\underbrace{{\left(\frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}\right)}^{\pm i}}}$, and set all of the obtained coefficients to zero. Then, solve the system of algebraic equations on variables $a_0,\underset{i=1,\dots ,N}{\underbrace{b_i}},\underset{i=1,\dots ,N}{\underbrace{a_i}},\eta ,\lambda ,c$, and $d.$

• Based on $\eta$ and $\lambda ,$ the solutions of Equation (10) are given by

  Case 1: $\lambda \eta >0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=\sqrt{{\displaystyle \frac{\eta }{\lambda }}}\left({\displaystyle \frac{Ccos\left(\sqrt{\eta \lambda }\mu \right)+Dsin\left(\sqrt{\eta \lambda }\mu \right)}{Dcos\left(\sqrt{\eta \lambda }\mu \right)-Csin\left(\sqrt{\eta \lambda }\mu \right)}}\right),\end{array}$$

(13)

  Case 2: $\lambda \ne 0,\eta =0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=-{\displaystyle \frac{C}{\lambda (C\mu +D)}},\end{array}$$

(14)

  Case 3: $\lambda \eta <0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=-{\displaystyle \frac{\sqrt{\left|\eta \lambda \right|}}{\lambda }}\left({\displaystyle \frac{Ccosh\left(2\sqrt{\left|\eta \lambda \right|}\mu \right)+Csinh\left(2\sqrt{\left|\eta \lambda \right|}\mu \right)+D}{Csinh\left(2\sqrt{\left|\eta \lambda \right|}\mu \right)+Ccosh\left(2\sqrt{\left|\eta \lambda \right|}\mu \right)-D}}\right),\end{array}$$

(15)

where $C,D\ne 0.$

• By substituting the obtained values of $a_0,\underset{i=1,\dots ,N}{\underbrace{b_i}},\underset{i=1,\dots ,N}{\underbrace{a_i}},\eta ,\lambda ,c,d$ and the solutions Equations (13)–(15) into Equation (9) with the transformation Equation (7), the exact traveling-wave solutions of Equation (6) can be obtained.

3. Application of the $\frac{{\mathit{G}}^{\prime }}{{\mathit{G}}^{\mathbf{2}}}$–Expansion Method for Equations (1) and (4)

Consider CTFMNLSE (4), where $D^{\alpha },$ is the conformable derivative of order $\alpha$ given by [10]

$$\begin{array}{c}\hfill D_{\xi }^{\alpha }\left(\varpi \right)=\underset{ϵ⟶0}{lim}{\displaystyle \frac{\varpi (\xi +ϵ{\xi }^{1-\alpha })-\varpi \left(\xi \right)}{ϵ}},\xi >0,0<\alpha ⩽1,\end{array}$$

in which $\varpi :[0,\infty )⟶\mathbb{R}$ is a given function.

If the above limit exists, then $\varpi$ is called $\alpha$-differentiable. Assume $0<\alpha ⩽1,$ and $\varpi$ and ${\varpi }^{\prime }$ are $\alpha$-differentiable at $\xi >0,$ then we obtain the following results:

∘$D_{\xi }^{\alpha }(c\varpi +d{\varpi }^{\prime })=c{D}_{\xi }^{\alpha }\left(\varpi \right)+d{D}_{\xi }^{\alpha }\left({\varpi }^{\prime }\right)$ where $c,d\in \mathbb{R},$

∘$D_{\xi }^{\alpha }\left({\varpi }^n\right)=n{\varpi }^{n-\alpha }$, where $n\in \mathbb{R},$

∘$D_{\xi }^{\alpha }\left(\vartheta \right)=0⟹\varpi \left(\xi \right)=\vartheta \left(\mathrm{is}\mathrm{a}\mathrm{constant}\right),$

∘$D_{\xi }^{\alpha }\left(\varpi {\varpi }^{\prime }\right)=\varpi D_{\xi }^{\alpha }\left({\varpi }^{\prime }\right)+{\varpi }^{\prime }{D}_{\xi }^{\alpha }\left(\varpi \right),$

∘$D_{\xi }^{\alpha }\left(\varpi \right)\left(\xi \right)={\xi }^{1-\alpha }{\displaystyle \frac{d\varpi }{d\xi }}\left(\xi \right),$

∘$D_{\xi }^{\alpha }\left({\displaystyle \frac{\varpi }{{\varpi }^{\prime }}}\right)={\displaystyle \frac{{\varpi }^{\prime }{D}_{\xi }^{\alpha }\left(\varpi \right)-\varpi D_{\xi }^{\alpha }\left({\varpi }^{\prime }\right)}{{\left({\varpi }^{\prime }\right)}^2}}.$

We start with the following traveling-wave assumption:

$$\mathsf{\Phi }(\chi ,\tau )=\psi \left(\mu \right){\mathrm{e}}^{\mathrm{i}\varphi }$$

(16)

where $\mu =\eta (-{\displaystyle \frac{\rho }{\alpha }}{\tau }^{\alpha }+\chi )$; $\varphi =-\omega \chi +{\displaystyle \frac{\varsigma }{\alpha }}{\tau }^{\alpha }+\epsilon$; and $\varsigma ,\epsilon$, and $\omega$ are the frequency, phase constant, and wave number, correspondingly. Inserting Equation (16) into Equation (4), we obtain the imaginary and real parts as [8]

$${\eta }^2({\sigma }_1-3{\delta }_1\omega ){\psi }^{″}+({\sigma }_2+({\delta }_2+{\delta }_3)\omega ){\psi }^3+(-\varsigma -{\sigma }_1{\omega }^2+{\delta }_1{\omega }^3-{\delta }_4)\psi =0,$$

(17)

and

$$(3{\delta }_1{\omega }^2-\rho -2{\sigma }_1\omega ){\psi }^{\prime }-{\delta }_1{\eta }^2{\psi }^{‴}+({\delta }_3-{\delta }_2){\psi }^2{\psi }^{\prime }=0.$$

(18)

By integrating the imaginary part and taking the constant equal to zero, we obtain

$$3(3{\delta }_1{\omega }^2-\rho -2{\sigma }_1\omega )\psi -3{\delta }_1{\eta }^2{\psi }^{″}+({\delta }_3-{\delta }_2){\psi }^3=0.$$

(19)

From Equations (17) and (19), we have that

$${\displaystyle \frac{{\omega }^3{\delta }_1-\varsigma -{\sigma }_1{\omega }^2-{\delta }_4}{3(3{\delta }_1{\omega }^2-\rho -2{\sigma }_1)\omega }}={\displaystyle \frac{{\sigma }_1-3{\delta }_1\omega }{-3{\delta }_1}}={\displaystyle \frac{\omega {\delta }_2+\omega {\delta }_3+{\sigma }_2}{{\delta }_3-{\delta }_2}}.$$

(20)

From the above, we have that

$$\rho =-{\displaystyle \frac{{\delta }_1\varsigma +{\delta }_1{\delta }_4+2\omega {({\sigma }_1-2{\delta }_1\omega )}^2}{{\sigma }_1-3{\delta }_1\omega }},$$

$$\omega ={\displaystyle \frac{{\sigma }_1({\delta }_2-{\delta }_3)-3{\sigma }_2{\delta }_1}{6{\delta }_1{\delta }_2}}.$$

Rewrite Equation (17) in the following form:

$${\psi }^{″}+c_1{\psi }^3-c_2\psi =0$$

(21)

or

$${\psi }^{″}=c_2\psi -c_1{\psi }^3$$

(22)

where $c_1={\displaystyle \frac{{\sigma }_2+({\delta }_2+{\delta }_3)\omega }{{\eta }^2({\sigma }_1-3{\delta }_1\omega )}}$ and $c_2=-{\displaystyle \frac{-\varsigma -{\sigma }_1{\omega }^2+{\delta }_1{\omega }^3-{\delta }_4}{{\eta }^2({\sigma }_1-3{\delta }_1\omega )}}$.

We can obtain the precise solution of Equation (19) in a similar way.

Balancing ${\psi }^{″}$ in Equation (22) with ${\psi }^3$, we obtain the balancing number $3N=N+2$ or $N=1.$

Suppose that the solution of Equation (22) can be given by

$$\begin{array}{c}\hfill \psi \left(\mu \right)=a_0+a_1\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)+b_1{\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^{-1},\end{array}$$

(23)

in which $a_0,b_1,a_1$ are constants to be determined later.

Inserting Equation (23) with Equation (10) into Equation (22) and collecting all of the terms with the same powers of ${\displaystyle \frac{G^{\prime }}{G^2}},$ and then equating every coefficient of the polynomial to zero, we obtain a system of algebraic equations, as follows:

$$\begin{array}{ccc}& & {\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^{-3}:b_1^3{c}_1+2{\eta }^2{b}_1=0,\hfill \\ & & {\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^{-2}:3c_1{a}_0{b}_1^2=0,\hfill \\ & & {\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^{-1}:3a_0^2{b}_1{c}_1+3a_1{b}_1^2{c}_1-b_1{c}_2\eta \lambda b_1=0,\hfill \\ & & {\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^0:a_0^3{c}_1+6a_0{a}_1{b}_1{c}_1+a_0{c}_2=0,\hfill \\ & & {\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^1:3a_0^2{a}_1{c}_1+3a_1^2{b}_1{c}_1+2\eta \lambda a_1-a_1{c}_2=0,\hfill \\ & & {\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^2:3c_1{a}_0{a}_1^2=0,\hfill \\ & & {\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^3:a_1^3{c}_1+2{\lambda }^2{a}_1=0.\hfill \end{array}$$

Solving the above system of nonlinear algebraic equations, we have

$$\begin{array}{ccc}& & \eta =\eta ,\lambda =\frac{1}{2}\frac{c_2}{\eta },a_0=0,a_1=\pm \frac{c_2}{\sqrt{-2c_1}\eta },b_1=0,\hfill \end{array}$$

(24)

$$\begin{array}{ccc}& & \eta =\frac{1}{2}\frac{c_2}{\lambda },\lambda =\lambda ,a_0=0,a_1=0,b_1=\pm \frac{c_2}{\sqrt{-2c_1}\lambda },\hfill \end{array}$$

(25)

$$\begin{array}{ccc}& & \eta =\pm \frac{1}{4}\frac{c_2}{\sqrt{-2c_1}{a}_1},\lambda =\pm \frac{1}{\sqrt{-2c_1}},a_0=0,a_1=a_1,b_1=\frac{1}{4}\frac{c_2}{c_1{a}_1},\hfill \end{array}$$

(26)

$$\begin{array}{ccc}& & \eta =\pm \frac{1}{2}\frac{c_2}{\sqrt{-2c_1}{a}_1},\lambda =\pm \frac{1}{\sqrt{-2c_1}}:a_0=0,a_1=a_1,b_1=\frac{1}{2}\frac{c_2}{c_1{a}_1},\hfill \end{array}$$

(27)

$$\begin{array}{ccc}& & \eta =\eta ,\lambda =\lambda ,a_0=\pm \frac{\sqrt{-c_1{c}_2}}{c_1},a_1=0,b_1=0,\hfill \end{array}$$

(28)

$$\begin{array}{ccc}& & \eta =\eta ,\lambda =\lambda ,a_0=0,a_1=0,b_1=0.\hfill \end{array}$$

(29)

Inserting Equation (24) into Equation (23), we obtain

$$\begin{array}{c}\hfill {\mathsf{\Phi }}_1\left(\mu \right)=\left(\pm \frac{c_2}{\sqrt{-2c_1}\eta }\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)\right)e^{i\varphi }.\end{array}$$

(30)

Therefore, we obtain three types of traveling-wave solutions, as follows:

  Case 1: $\lambda \eta >0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=\sqrt{{\displaystyle \frac{\eta }{\frac{1}{2}\frac{c_2}{\eta }}}}\left({\displaystyle \frac{Ccos\left(\sqrt{\frac{1}{2}{c}_2}\mu \right)+Dsin\left(\sqrt{\frac{1}{2}{c}_2}\mu \right)}{Dcos\left(\sqrt{\frac{1}{2}{c}_2}\mu \right)-Csin\left(\sqrt{\frac{1}{2}{c}_2}\mu \right)}}\right),\end{array}$$

(31)

  Case 2: $\lambda \eta <0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=-{\displaystyle \frac{\sqrt{|\frac{1}{2}{c}_2|}}{\frac{1}{2}\frac{c_2}{\eta }}}\left({\displaystyle \frac{Csinh\left(2\sqrt{|\frac{1}{2}{c}_2|}\mu \right)+Ccosh\left(2\sqrt{|\frac{1}{2}{c}_2|}\mu \right)+D}{Ccosh\left(2\sqrt{|\frac{1}{2}{c}_2|}\mu \right)+Csinh\left(2\sqrt{|\frac{1}{2}{c}_2|}\mu \right)-D}}\right),\end{array}$$

(32)

  Case 3: $\lambda \ne 0,\eta =0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=-{\displaystyle \frac{C}{\frac{1}{2}\frac{c_2}{\eta }(C\mu +D)}},\end{array}$$

(33)

where $C,D\ne 0.$

The Figure 1 and Figure 2 display the plots of Equation (30), for $\alpha =1,$ and two different cases $\lambda \eta >0$ and $\lambda \eta <0$, respectively.

Figure 1. The plots of Equation (30), for $\lambda \eta >0$ and $\alpha =1.$ Now, [a1] and [a3] are imaginary and real parts of Equation (30), and [a2], [a4], [a5], and [a6] display the z-axis orientation, the contour plot, the 2d for $x=2$, and the 2d for $t=2$, of the imaginary part of [a1], respectively.

Figure 2. The plots of Equation (30), for $\lambda \eta <0$ and $\alpha =1.$ Now, [b1] and [b3] are the imaginary and real parts of Equation (30), and [b2], [b4], [b5], and [b6] display the z-axis orientation, the contour plot, the 2d for $x=2$, and the 2d for $t=2$, of the imaginary part of [b1], respectively.

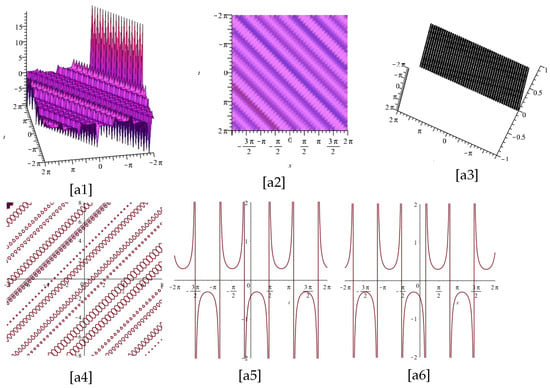
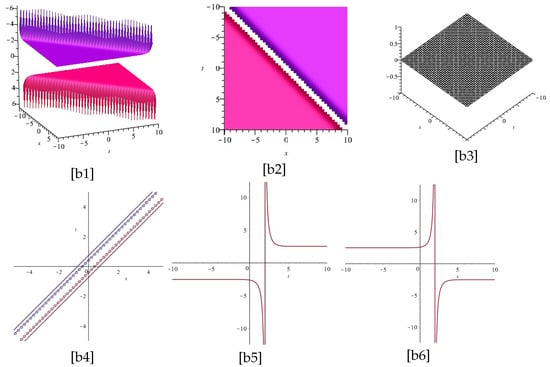
The Figure 3 and Figure 4 display the plots of Equation (30), for $\alpha =0.75,$ and two different cases $\lambda \eta >0$ and $\lambda \eta <0$, respectively.

Figure 3. The plots of Equation (30), for $\lambda \eta >0$ and $\alpha =0.75.$ Now, [c1] and [c3] are the imaginary and real parts of Equation (30), and [c2], [c4], [c5], and [c6] display the z-axis orientation, the contour plot, the 2d for $x=2$, and the 2d for $t=2$, of the imaginary part of [c1], respectively.

Figure 4. The plots of Equation (30), for $\lambda \eta <0$ and $\alpha =0.75.$ Now, [d1] and [d3] are the imaginary and real parts of Equation (30), and [d2], [d4], [d5], and [d6] display the z-axis orientation, the contour plot, the 2d for $x=2$, and the 2d for $t=2$, of the imaginary part of [d1], respectively.

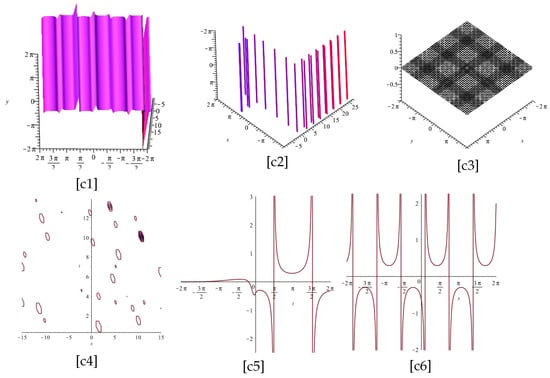
The Figure 5 and Figure 6 display the plots of Equation (30), for $\alpha =0.5,$ and two different cases $\lambda \eta >0$ and $\lambda \eta <0$, respectively.

Figure 5. The plots of Equation (30), for $\lambda \eta >0$ and $\alpha =0.5.$ Now, [e1] and [e3] are imaginary and real parts of Equation (30), and [e2], [e4], [e5], and [e6] display the z-axis orientation, the contour plot, the 2d for $x=2$, and the 2d for $t=2$, of the imaginary part of [e1], respectively.

Figure 6. The plots of Equation (30), for $\lambda \eta <0$ and $\alpha =0.5.$ Now, [f1] and [f3] are imaginary and real parts of Equation (30), and [f2], [f4], [f5], and [f6] display the z-axis orientation, the contour plot, the 2d for $x=2$, and the 2d for $t=2$, of the imaginary part of [f1], respectively.

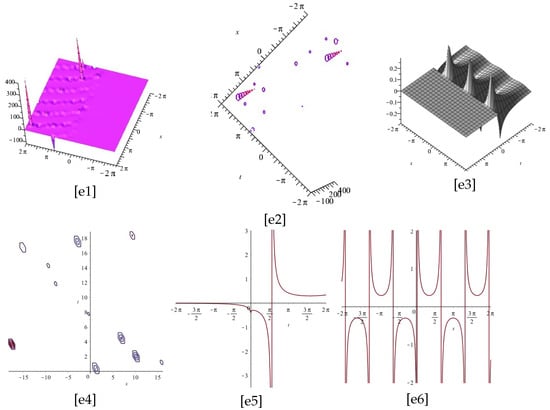
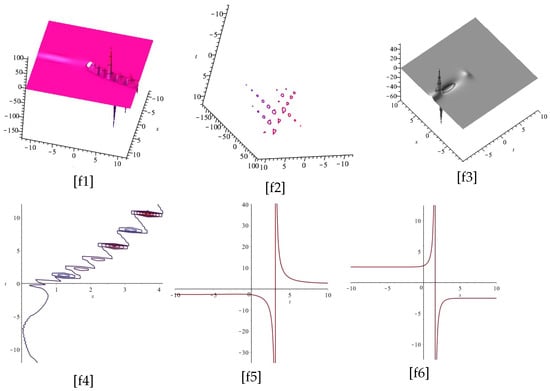
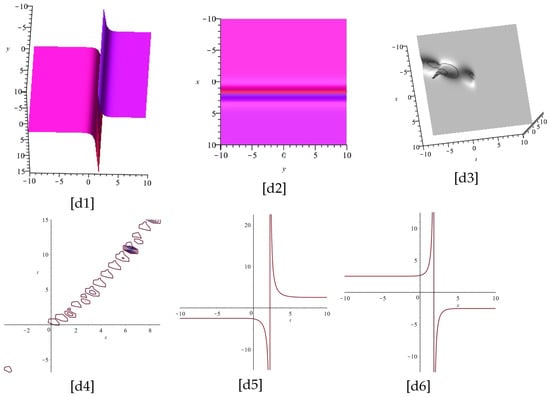
The Figure 7 and Figure 8 display the plots of Equation (30), for $\alpha =0.25,$ and two different cases $\lambda \eta >0$ and $\lambda \eta <0$, respectively.

Figure 7. The plots of Equation (30), for $\lambda \eta >0$ and $\alpha =0.25.$ Now, [g1] and [g3] are imaginary and real parts of Equation (30), and [g2], [g4], [g5], and [g6] display the z-axis orientation, the contour plot, the 2d for $x=2$, and the 2d for $t=2$, of the imaginary part of [g1], respectively.

Figure 8. The plots of Equation (30), for $\lambda \eta <0$ and $\alpha =0.25.$ Now, [h1] and [h3] are imaginary and real parts of Equation (30), and [h2], [h4], [h5], and [h6] display the z-axis orientation, the contour plot, the 2d for $x=2$, and the 2d for $t=2$, of the imaginary part of [h1], respectively.

Notice that [1] and [3] are the imaginary and real part of Equation (30), and [2], [4], [5], and [6] display the z-axis orientation, the contour plot, the 2d for $x=2$, and the 2d for $t=2$, of the imaginary part of [1], respectively.

By considering Equation (25), we obtain three types of traveling-wave solutions, as follows:

$$\begin{array}{c}\hfill {\mathsf{\Phi }}_2\left(\mu \right)=\left(\pm \frac{c_2}{\sqrt{-2c_1}\lambda }{\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^{-1}\right)e^{i\varphi },\end{array}$$

(34)

  Case 1: $\lambda \eta >0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=\sqrt{{\displaystyle \frac{\frac{1}{2}\frac{c_2}{\lambda }}{\lambda }}}\left({\displaystyle \frac{Ccos\left(\sqrt{\frac{1}{2}\frac{c_2}{\lambda }\lambda }\mu \right)+Dsin\left(\sqrt{\frac{1}{2}\frac{c_2}{\lambda }\lambda }\mu \right)}{Dcos\left(\sqrt{\frac{1}{2}\frac{c_2}{\lambda }\lambda }\mu \right)-Csin\left(\sqrt{\frac{1}{2}\frac{c_2}{\lambda }\lambda }\mu \right)}}\right),\end{array}$$

(35)

  Case 2: $\lambda \eta <0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=-{\displaystyle \frac{\sqrt{|\frac{1}{2}\frac{c_2}{\lambda }\lambda |}}{\lambda }}\left({\displaystyle \frac{Ccosh\left(2\sqrt{|\frac{1}{2}\frac{c_2}{\lambda }\lambda |}\mu \right)+Csinh\left(2\sqrt{|\frac{1}{2}\frac{c_2}{\lambda }\lambda |}\mu \right)+D}{Csinh\left(2\sqrt{|\frac{1}{2}\frac{c_2}{\lambda }\lambda |}\mu \right)+Ccosh\left(2\sqrt{|\frac{1}{2}\frac{c_2}{\lambda }\lambda |}\mu \right)-D}}\right),\end{array}$$

(36)

  Case 3: $\lambda \ne 0,\eta =0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=-{\displaystyle \frac{C}{\lambda (C\mu +D)}},\end{array}$$

(37)

where $C,D\ne 0.$

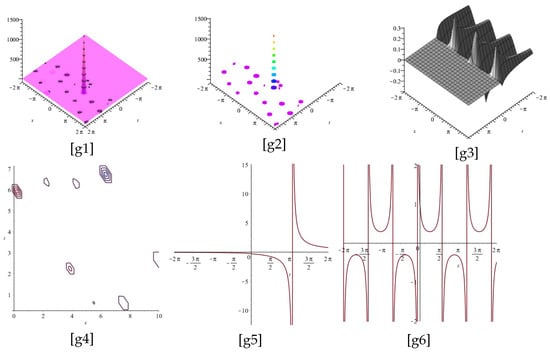
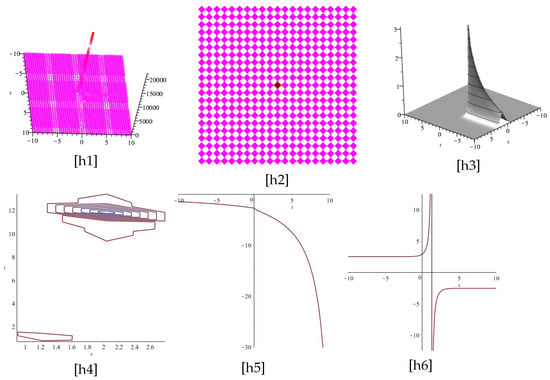
In Figure 9, Figure 10, Figure 11 and Figure 12, the imaginary parts of Equation (34) are displayed for two different cases $\lambda \eta >0$ and $\lambda \eta <0$, and different values of $\alpha ,$ respectively.

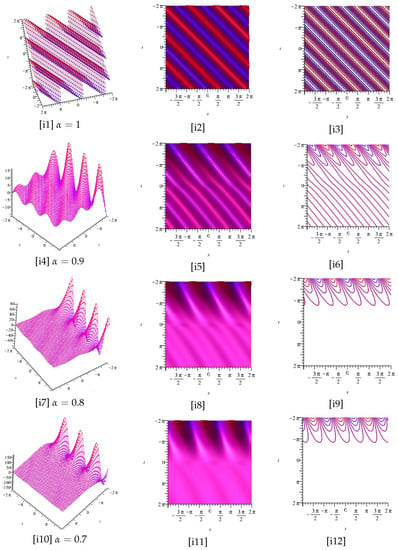
Figure 9. Now, [i1], [i4], [i7], [i10] display the plots of the imaginary part of Equation (34), for $\lambda \eta >0$, and [i2], [i5], [i8], [i11] as well as [i3], [i6], [i9], [i12] display the z-axis orientation and the contour plot, respectively.

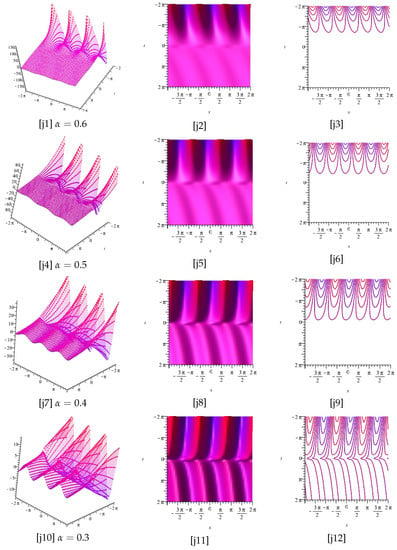
Figure 10. Now, [j1], [j4], [j7], [j10] display the plots of the imaginary part of Equation (34), for $\lambda \eta >0$, and [j2], [j5], [j8], [j11] as well as [j3], [j6], [j9], [j12] display the z-axis orientation and the contour plot, respectively.

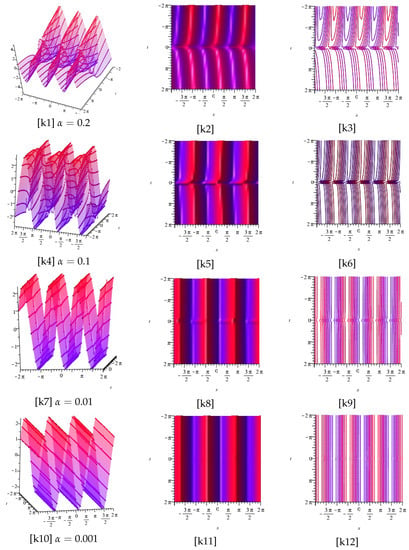
Figure 11. Now, [k1], [k4], [k7], and [k10] display the plots of the imaginary part of Equation (34), for $\lambda \eta >0$, and [k2], [k5], [k8], and [k11], as well as [k3], [k6], [k9], and [k12], display the z-axis orientation and the contour plot, respectively.

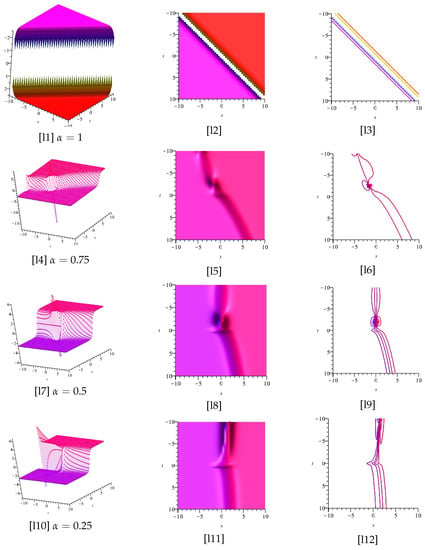
Figure 12. Now, [l1], [l4], [l7], and [l10] display the plots of the imaginary part of Equation (34), for $\lambda \eta <0$, and [l2], [l5], [l8], and [l11], as well as [l3], [l6], [l9], and [l12], display the z-axis orientation and the contour plot, respectively.

By considering Equation (26), we obtain three types of traveling-wave solutions, as follows:

$$\begin{array}{c}\hfill {\mathsf{\Phi }}_3\left(\mu \right)=\left(a_1\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)+\frac{1}{4}\frac{c_2}{c_1{a}_1}{\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^{-1}\right)e^{i\varphi },\end{array}$$

(38)

  Case 1: $\lambda \eta >0;$

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=\sqrt{{\displaystyle \frac{\pm \frac{1}{4}\frac{c_2}{\sqrt{-2c_1}{a}_1}}{\pm \frac{1}{\sqrt{-2c_1}}}}}\hfill \\ & & \left({\displaystyle \frac{Ccos\left(\sqrt{\pm \frac{1}{4}\frac{c_2}{\sqrt{-2c_1}{a}_1}(\pm \frac{1}{\sqrt{-2c_1}})}\mu \right)+Dsin\left(\sqrt{\pm \frac{1}{4}\frac{c_2}{\sqrt{-2c_1}{a}_1}(\pm \frac{1}{\sqrt{-2c_1}})}\mu \right)}{Dcos\left(\sqrt{\pm \frac{1}{4}\frac{c_2}{\sqrt{-2c_1}{a}_1}(\pm \frac{1}{\sqrt{-2c_1}})}\mu \right)-Csin\left(\sqrt{\pm \frac{1}{4}\frac{c_2}{\sqrt{-2c_1}{a}_1}(\pm \frac{1}{\sqrt{-2c_1}})}\mu \right)}}\right),\hfill \end{array}$$

(39)

  Case 2: $\lambda \eta <0;$

$$\begin{array}{ccc}\hfill & & {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=-{\displaystyle \frac{\sqrt{|\pm \frac{1}{4}\frac{c_2}{\sqrt{-2c_1}{a}_1}(\pm \frac{1}{\sqrt{-2c_1}})|}}{(\pm \frac{1}{\sqrt{-2c_1}})}}\hfill \\ & & \left({\displaystyle \frac{Csinh\left(2\sqrt{|\pm \frac{1}{4}\frac{c_2}{\sqrt{-2c_1}{a}_1}(\pm \frac{1}{\sqrt{-2c_1}})|}\mu \right)+Ccosh\left(2\sqrt{|\pm \frac{1}{4}\frac{c_2}{\sqrt{-2c_1}{a}_1}(\pm \frac{1}{\sqrt{-2c_1}})|}\mu \right)+D}{Ccosh\left(2\sqrt{|\pm \frac{1}{4}\frac{c_2}{\sqrt{-2c_1}{a}_1}(\pm \frac{1}{\sqrt{-2c_1}})|}\mu \right)+Csinh\left(2\sqrt{|\pm \frac{1}{4}\frac{c_2}{\sqrt{-2c_1}{a}_1}(\pm \frac{1}{\sqrt{-2c_1}})|}\mu \right)-D}}\right),\hfill \end{array}$$

(40)

  Case 3: $\lambda \ne 0,\eta =0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=-{\displaystyle \frac{C}{(\pm \frac{1}{\sqrt{-2c_1}})(C\mu +D)}},\end{array}$$

(41)

where $C,D\ne 0.$

In Figure 13 and Figure 14, the real part of Equation (38) is displayed for two different cases $\lambda \eta >0$ and $\lambda \eta <0$, and different values of $\alpha ,$ respectively.

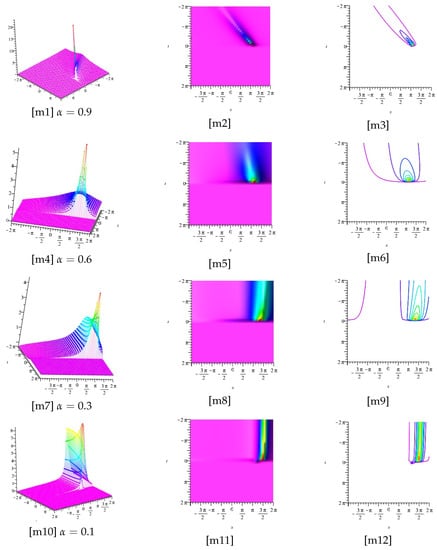
Figure 13. Now, [m1], [m4], [m7], and [m10] display the plots of the real part of Equation (38), for $\lambda \eta >0$, and [m2], [m5], [m8], and [m11], as well as [m3], [m6], [m9], and [m12], display the z-axis orientation and the contour plot, respectively.

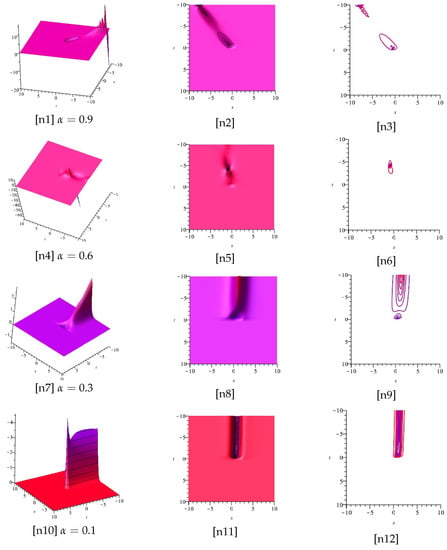
Figure 14. Now, [n1], [n4], [n7], and [n10] display the plots of the real part of Equation (38), for $\lambda \eta <0$, and [n2], [n5], [n8], and [n11], as well as [n3], [n6], [n9], and [n12], display the z-axis orientation and the contour plot, respectively.

3.1. Modulation Instability Analysis

Here, we deduce the modulation instability of Equation (4) for the special case $\alpha =1,$ through employing the criterion of linear stability analysis in [11].

Assume the steady-state solutions of Equation (4) for the special case $\alpha =1,$ which is given by

$$\begin{array}{c}\hfill \mathsf{\Phi }(\chi ,\tau )=(\sqrt{{ϵ}_0}+\psi (\chi ,\tau ))e^{i{\Omega }_0\tau },\end{array}$$

(42)

in which ${\Omega }_0$ is the normalized optical power.

By inserting Equation (42) in Equation (4), and by linearizing, we obtain

$$\begin{array}{ccc}\hfill & & i{\psi }_{\tau }+{\sigma }_1{\psi }_{\chi \chi }-({\Omega }_0+{\delta }_4-3{\Omega }_0{\sigma }_2)(\psi +{\psi }^{*})\hfill \\ & & -i{\delta }_1{\psi }_{\chi \chi \chi }-i{\Omega }_0{\delta }_2{\psi }_{\chi }^{*}+i{\Omega }_0{\delta }_3{\psi }_{\chi }=0.\hfill \end{array}$$

(43)

Assume that the solution to Equation (43) is as follows:

$$\begin{array}{c}\hfill \psi (\chi ,\tau )={ϵ}_1{e}^{i\left(\right(\mathbb{k}\chi -w\tau \left)\right)}+{ϵ}_2{e}^{-i\left(\right(\mathbb{k}\chi -w\tau \left)\right)},\end{array}$$

(44)

in which w is the frequency of perturbation and $\mathbb{k}$ is the normalized wave number.

By inserting Equation (44) into Equation (43) and splitting the coefficients of $e^{i\left(\right(\mathbb{k}\chi -w\tau \left)\right)}$ and $e^{-i\left(\right(\mathbb{k}\chi -w\tau \left)\right)}$ and solving the determinant of the coefficient matrix, we have

$$\begin{array}{ccc}\hfill & & 2{\mathbb{k}}^{3}w{\delta }_1-w^2-{\mathbb{k}}^6{\delta }_1^2+{\mathbb{k}}^2{\mathbb{k}}_0^2{\delta }_2^2+2\mathbb{k}w{\Omega }_0{\delta }_3\hfill \\ & & -2{\mathbb{k}}^4{\Omega }_0{\delta }_1{\delta }_3-{\mathbb{k}}^2{\Omega }_0^2{\delta }_3^2+2{\mathbb{k}}^2{\Omega }_0{\sigma }_1+2{\mathbb{k}}^2{\delta }_4{\sigma }_1\hfill \\ & & +{\mathbb{k}}^4{\sigma }_1^2-6{\mathbb{k}}^2{\Omega }_0{\sigma }_1{\sigma }_2=0.\hfill \end{array}$$

(45)

By solving Equation (45) for w, we obtain

$$\begin{array}{ccc}\hfill & & w={\mathbb{k}}^3{\delta }_1+\mathbb{k}{\Omega }_0{\delta }_3\hfill \\ & & +\sqrt{{\mathbb{k}}^2{\Omega }_0^2{\delta }_2^2+2{\mathbb{k}}^2{\Omega }_0{\sigma }_1+2{\mathbb{k}}^2{\delta }_4{\sigma }_1^2+{\mathbb{k}}^4{\sigma }_1^2-6{\mathbb{k}}^2{\Omega }_0{\sigma }_1{\sigma }_2}.\hfill \end{array}$$

(46)

If

$${\mathbb{k}}^2{\Omega }_0^2{\delta }_2^2+2{\mathbb{k}}^2{\Omega }_0{\sigma }_1+2{\mathbb{k}}^2{\delta }_4{\sigma }_1^2+{\mathbb{k}}^4{\sigma }_1^2-6{\mathbb{k}}^2{\Omega }_0{\sigma }_1{\sigma }_2>0,$$

$w\in \mathbb{R},$ for any $\underset{i=1,\cdots ,4}{\underbrace{{\delta }_i}}$, $\underset{i=1,2}{\underbrace{{\sigma }_i}},{\Omega }_0\in \mathbb{R},$ then the steady-state is stable if the perturbations are small. In other words, small changes in the system input do not result in a large change in the system output. In addition, the steady-state solution is unstable if

$${\mathbb{k}}^2{\Omega }_0^2{\delta }_2^2+2{\mathbb{k}}^2{\Omega }_0{\sigma }_1+2{\mathbb{k}}^2{\delta }_4{\sigma }_1^2+{\mathbb{k}}^4{\sigma }_1^2<6{\mathbb{k}}^2{\Omega }_0{\sigma }_1{\sigma }_2;$$

here, w is imaginary, and the perturbation grows exponentially.

Therefore, the growth rate of the modulation stability gain spectrum $\Delta \left(\mathbb{k}\right)$ is defined as

$$\begin{array}{ccc}\hfill \Delta \left(\mathbb{k}\right)& =& 2\Im \left(w\right)\hfill \\ & =& 2\Im ({\mathbb{k}}^3{\delta }_1+\mathbb{k}{\Omega }_0{\delta }_3+\sqrt{{\mathbb{k}}^2{\Omega }_0^2{\delta }_2^2+2{\mathbb{k}}^2{\Omega }_0{\sigma }_1+2{\mathbb{k}}^2{\delta }_4{\sigma }_1^2+{\mathbb{k}}^4{\sigma }_1^2-6{\mathbb{k}}^2{\Omega }_0{\sigma }_1{\sigma }_2}).\hfill \end{array}$$

3.2. Discussion

The imaginary and real parts of solutions of Equation (4) are obtained by the $\frac{G^{\prime }}{G^2}$-expansion method, whose diverse point sources, though arbitrary, and $\alpha =0.90,$ are displayed in Table 1, Table 2 and Table 3. As you can see, for fixed $\chi$ by changing $\tau$, the $\frac{G^{\prime }}{G^2}–$expansion method results in minor changes for solutions ${\psi }_{1,2}^{\Im }(\lambda \eta >0),{\psi }_{3,4}^{\Im }(\lambda \eta >0,\lambda \eta <0),{\psi }_{5,6}^{\Im },{\psi }_{5,6}^{\Re }(\lambda \eta >0)$. In other words, the mentioned solutions are stable against small perturbations. However, overall, for $\alpha =0.90,$ the governing method cannot properly describe all of the real parts of the solutions of Equation (4).

Table 1. The imaginary and real parts of the analytical solutions of Equation (4) are obtained by the $\frac{G^{\prime }}{G^2}–$expansion method, with diverse point sources, though arbitrary, and $\alpha =0.90$.

		$\mathit{\lambda }\mathit{\eta }>0$		$\mathit{\lambda }\mathit{\eta }<0$
$\mathbf{\chi }$	$\mathbf{\tau }$	${\mathsf{\Phi }}_{\mathbf{1},\mathbf{2}}^{\Re }(\mathbf{\chi },\mathbf{\tau })$	${\mathsf{\Phi }}_{\mathbf{1},\mathbf{2}}^{\Im }(\mathbf{\chi },\mathbf{\tau })$	${\mathsf{\Phi }}_{\mathbf{1},\mathbf{2}}^{\Re }(\mathbf{\chi },\mathbf{\tau })$	${\mathsf{\Phi }}_{\mathbf{1},\mathbf{2}}^{\Im }(\mathbf{\chi },\mathbf{\tau })$
0.012	0.012	0.00000	±0.41523	0.00000	±339.37846
	0.037	0.00000	±0.39534	0.00000	±60.70046
	0.062	0.00000	±0.37942	0.00000	±34.48412
	0.087	0.00000	±0.36610	0.00000	±24.41456
0.037	0.012	0.00000	±0.43195	0.00000	∓143.18583
	0.037	0.00000	±0.40963	0.00000	±152.62498
	0.062	0.00000	±0.39181	0.00000	±52.34274
	0.087	0.00000	±0.37694	0.00000	±32.14308
0.062	0.012	0.00000	±0.45078	0.00000	∓59.15192
	0.037	0.00000	±0.42565	0.00000	∓295.98183
	0.062	0.00000	±0.40568	0.00000	±108.85178
	0.087	0.00000	±0.38904	0.00000	±47.11727
0.087	0.012	0.00000	±0.47207	0.00000	∓37.30504
	0.037	0.00000	±0.44368	0.00000	∓75.16017
	0.062	0.00000	±0.42122	0.00000	∓1346.22816
	0.087	0.00000	±0.40258	0.00000	±88.41972

Table 2. The imaginary and real parts of the analytical solutions of Equation (4) are obtained by the $\frac{G^{\prime }}{G^2}$-expansion method, with diverse point sources, though arbitrary, and $\alpha =0.90$.

		$\mathit{\lambda }\mathit{\eta }>0$		$\mathit{\lambda }\mathit{\eta }<0$
$\mathbf{\chi }$	$\mathbf{\tau }$	${\mathsf{\Phi }}_{\mathbf{3},\mathbf{4}}^{\Re }(\mathbf{\chi },\mathbf{\tau })$	${\mathsf{\Phi }}_{\mathbf{3},\mathbf{4}}^{\mathbf{\Im }}\mathbf{(}\mathbf{\chi }\mathbf{,}\mathbf{\tau }\mathbf{)}$	${\mathsf{\Phi }}_{\mathbf{3},\mathbf{4}}^{\Re }(\mathbf{\chi },\mathbf{\tau })$	${\mathsf{\Phi }}_{\mathbf{3},\mathbf{4}}^{\Im }(\mathbf{\chi },\mathbf{\tau })$
0.012	0.012	0.00000	±1.69922	0.00000	∓0.01884
	0.037	0.00000	±1.78472	0.00000	∓0.10537
	0.062	0.00000	±1.85962	0.00000	∓0.18548
	0.087	0.00000	±1.92724	0.00000	∓0.26198
0.037	0.012	0.00000	±1.63346	0.00000	±0.04467
	0.037	0.00000	±1.72247	0.00000	∓0.04190
	0.062	0.00000	±1.80079	0.00000	∓0.12219
	0.087	0.00000	±1.87184	0.00000	∓0.19898
0.062	0.012	0.00000	±1.56523	0.00000	±0.10813
	0.037	0.00000	±1.65763	0.00000	±0.02160
	0.062	0.00000	±1.73925	0.00000	∓0.05876
	0.087	0.00000	±1.81361	0.00000	∓0.13574
0.087	0.012	0.00000	±1.49464	0.00000	±0.17145
	0.037	0.00000	±1.59028	0.00000	±0.085100
	0.062	0.00000	±1.67509	0.00000	±0.00475
	0.087	0.00000	±1.75264	0.00000	∓0.07233

Table 3. The imaginary and real parts of the analytical solutions of Equation (4) are obtained by the $\frac{G^{\prime }}{G^2}–$expansion method, with diverse point sources, though arbitrary, and $\alpha =0.90$.

		$\mathit{\lambda }\mathit{\eta }>0$		$\mathit{\lambda }\mathit{\eta }<0$
$\mathbf{\chi }$	$\mathbf{\tau }$	${\mathbf{\Phi }}_{\mathbf{5},\mathbf{6}}^{\mathbf{\Re }}(\mathbf{\chi },\mathbf{\tau })$	${\mathsf{\Phi }}_{\mathbf{5},\mathbf{6}}^{\Im }(\mathbf{\chi },\mathbf{\tau })$	${\mathsf{\Phi }}_{\mathbf{5},\mathbf{6}}^{\Re }(\mathbf{\chi },\mathbf{\tau })$	${\mathsf{\Phi }}_{\mathbf{5},\mathbf{6}}^{\Im }(\mathbf{\chi },\mathbf{\tau })$
0.012	0.012	∓ 1.00391	±0.00085	0.00000	∓214.23208
	0.037	∓ 1.00383	±0.00478	0.00000	∓38.34451
	0.062	∓1.00366	±0.00843	0.00000	∓21.81747
	0.087	∓1.00342	±0.01193	0.00000	∓15.48189
0.037	0.012	∓1.00390	∓0.00202	0.00000	±90.39569
	0.037	∓1.00390	±0.00190	0.00000	∓96.35426
	0.062	∓1.00380	±0.00555	0.00000	∓33.07337
	0.087	∓1.00363	±0.00905	0.00000	∓20.34337
0.062	0.012	∓1.00383	∓0.00491	0.00000	±37.36776
	0.037	∓1.00391	∓0.00098	0.00000	±186.83944
	0.062	∓1.00389	±0.00267	0.00000	∓68.72668
	0.087	∓1.00378	±0.00617	0.00000	∓29.77853
0.087	0.012	∓1.00370	∓0.00779	0.00000	±23.59434
	0.037	∓1.00386	∓0.00386	0.00000	±47.46651
	0.062	∓1.00391	∓0.00021	0.00000	±849.78525
	0.087	∓1.00387	±0.00328	0.00000	∓55.83294

4. Application of the $\frac{{\mathit{G}}^{\prime }}{{\mathit{G}}^{\mathbf{2}}}$–Expansion Method for Equation (5)

Consider the time fractional Bogoyavlenskii Equation (5), where $D^{\alpha }$ is the Jumaries-modified Riemann-Liouville derivative of order $\alpha$ given by [12]

$$\begin{array}{c}\hfill D_{\tau }^{\alpha }\mathsf{\Phi }\left(\tau \right)={\displaystyle \frac{1}{\mathsf{\Gamma }(1-\alpha )}}{\displaystyle \frac{d}{d\tau }}{\int }_0^{\tau }{(\tau -\rho )}^{-\alpha }(\mathsf{\Phi }\left(\rho \right)-\mathsf{\Phi }\left(0\right))d\rho ,0<\alpha \le 1.\end{array}$$

Some important properties of Jumarie’s derivative are

$$\begin{array}{ccc}& & D_{\tau }^{\alpha }{\chi }^{\gamma }=\frac{\mathsf{\Gamma }(1+\gamma )}{\mathsf{\Gamma }(\gamma -\alpha +1)},\hfill \\ & & D_{\tau }^{\alpha }\left[\mathsf{\Phi }\left(\tau \right)\mathsf{\Psi }\left(\tau \right)\right]=\mathsf{\Psi }\left(\tau \right)D_{\tau }^{\alpha }\mathsf{\Phi }\left(\tau \right)+\mathsf{\Phi }\left(\tau \right)D_{\tau }^{\alpha }\mathsf{\Psi }\left(\tau \right),\hfill \\ & & D_{\tau }^{\alpha }\mathsf{\Phi }\left[\mathsf{\Psi }\left(\tau \right)\right]={\mathsf{\Phi }}_{\mathsf{\Psi }}^{\prime }\left[\mathsf{\Psi }\left(\tau \right)\right]D_{\tau }^{\alpha }\mathsf{\Psi }\left(\tau \right).\hfill \end{array}$$

Through the following transformations:

$$\begin{array}{ccc}& & \mathsf{\Phi }(\chi ,\mathcal{Y},\tau )=\mathsf{\Phi }\left(\mu \right),\hfill \\ & & \mathsf{\Psi }(\chi ,\mathcal{Y},\tau )=\mathsf{\Psi }\left(\mu \right),\hfill \\ & & \mu =\chi +\mathcal{Y}-{\displaystyle \frac{c}{\mathsf{\Gamma }(1+\alpha )}}{\tau }^{\alpha },\hfill \end{array}$$

(47)

integrating the second equation of Equation (5) once, and inserting the constant of integration to zero, we obtain

$$\begin{array}{ccc}\hfill & & -4\varpi {\mathsf{\Phi }}^{\prime }+{\mathsf{\Phi }}^{‴}-4{\mathsf{\Phi }}^2{\mathsf{\Phi }}^{\prime }-4{\mathsf{\Phi }}^{\prime }\mathsf{\Psi },\hfill \\ & & {\displaystyle \frac{{\mathsf{\Phi }}^2}{2}}=\mathsf{\Psi }.\hfill \end{array}$$

(48)

Now, setting the second equation of Equation (48) into the first equation, integrating the gained result with respect to $\mu$, and substituting the integration constant to zero, we obtain

$$\begin{array}{ccc}& & {\mathsf{\Phi }}^{″}-2{\mathsf{\Phi }}^3-4\varpi \mathsf{\Phi }=0.\hfill \end{array}$$

(49)

We now obtain the balancing number $N=1.$ Suppose the solution of Equation (49) can be given by

$$\begin{array}{c}\hfill \mathsf{\Phi }\left(\mu \right)=a_0+a_1\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)+b_1{\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^{-1},\end{array}$$

(50)

in which $a_0,b_1,a_1$ are constants to be determined later.

Letting equation Equation (50) with Equation (10) into Equation (49), collecting all terms with the same powers of ${\displaystyle \frac{G^{\prime }}{G^2}}$, and next equating every coefficient of the polynomial to zero, we obtain the following system of algebraic equations:

$$\begin{array}{ccc}& & {\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^{-3}:2{\eta }^2{b}_1-2b_1^3=0,\hfill \\ & & {\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^{-2}:-6a_0{b}_1^2=0,\hfill \\ & & {\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^{-1}:2\eta \lambda b_1-6a_0^2{b}_1-6a_1{b}_1^2-4c{b}_1=0,\hfill \\ & & {\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^0:-2a_0^3-12a_0{a}_1{b}_1-4c{a}_0=0,\hfill \\ & & {\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^1:2\eta \lambda a_1-6a_0^2{a}_1-6a_1^2{b}_1-4c{a}_1=0,\hfill \\ & & {\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^2:-6a_0{a}_1^2=0,\hfill \\ & & {\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^3:2{\lambda }^2{a}_1-2a_1^3=0.\hfill \end{array}$$

Solving the system of nonlinear algebraic equations, we have

$$\begin{array}{ccc}& & \eta =\eta ,\lambda =\lambda ,a_0=\mp \sqrt{-2c},a_1=0,b_1=0,\hfill \end{array}$$

(51)

$$\begin{array}{ccc}& & \eta =\frac{2c}{\lambda },\lambda =\lambda ,a_0=0,a_1=0,b_1=\pm \frac{2c}{\lambda },\hfill \end{array}$$

(52)

$$\begin{array}{ccc}& & \eta =\pm \frac{c}{a_1},\lambda =\mp a_1,a_0=0,a_1=a_1,b_1=-\frac{c}{a_1},\hfill \end{array}$$

(53)

$$\begin{array}{ccc}& & \eta =\pm \frac{1}{2}\frac{c}{a_1},\lambda =\pm a_1,a_0=0,a_1=a_1,b_1=-\frac{1}{2}\frac{c}{a_1},\hfill \end{array}$$

(54)

$$\begin{array}{ccc}& & \eta =\eta ,\lambda =\frac{2c}{\eta },a_0=0,a_1=\pm \frac{2c}{\eta },b_1=0.\hfill \end{array}$$

(55)

Inserting Equation (51) in Equation (50), we obtain

$$\begin{array}{c}\hfill {\mathsf{\Phi }}_1\left(\mu \right)=\mp \sqrt{-2c}.\end{array}$$

(56)

Inserting Equation (52) in Equation (50), we obtain

$$\begin{array}{c}\hfill {\mathsf{\Phi }}_2\left(\mu \right)=\pm \frac{2c}{\lambda }{\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^{-1}.\end{array}$$

(57)

Therefore, we obtain three types of traveling-wave solutions, as follows:

  Case 1: $\lambda \eta >0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=\sqrt{{\displaystyle \frac{2c}{{\lambda }^2}}}\left({\displaystyle \frac{Ccos\left(\sqrt{2c}\mu \right)+Dsin\left(\sqrt{2c}\mu \right)}{Dcos\left(\sqrt{2c}\mu \right)-Csin\left(\sqrt{2c}\mu \right)}}\right),\end{array}$$

(58)

  Case 2: $\lambda \eta <0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=-{\displaystyle \frac{\sqrt{\left|2c\right|}}{\lambda }}\left({\displaystyle \frac{Ccosh\left(2\sqrt{\left|2c\right|}\mu \right)+Csinh\left(2\sqrt{\left|2c\right|}\mu \right)+D}{Csinh\left(2\sqrt{\left|2c\right|}\mu \right)+Ccosh\left(2\sqrt{\left|2c\right|}\mu \right)-D}}\right),\end{array}$$

(59)

  Case 3: $\lambda \ne 0,\eta =0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=-{\displaystyle \frac{C}{\lambda (C\mu +D)}},\end{array}$$

(60)

where $C,D\ne 0.$

Inserting Equation (53) in Equation (50), we obtain

$$\begin{array}{c}\hfill {\mathsf{\Phi }}_3\left(\mu \right)=a_1\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)-\frac{c}{a_1}{\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^{-1}.\end{array}$$

(61)

Therefore, we obtain three types of traveling-wave solutions, as follows:

  Case 1: $\lambda \eta >0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=\sqrt{\pm {\displaystyle \frac{c}{a_1^2}}}\left({\displaystyle \frac{Ccos\left(\sqrt{\pm c}\mu \right)+Dsin\left(\sqrt{\pm c}\mu \right)}{Dcos\left(\sqrt{\pm c}\mu \right)-Csin\left(\sqrt{\pm c}\mu \right)}}\right),\end{array}$$

(62)

  Case 2: $\lambda \eta <0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=\pm {\displaystyle \frac{\sqrt{\left|c\right|}}{a_1}}\left({\displaystyle \frac{Ccosh\left(2\sqrt{\left|c\right|}\mu \right)+Csinh\left(2\sqrt{\left|c\right|}\mu \right)+D}{Csinh\left(2\sqrt{\left|c\right|}\mu \right)+Ccosh\left(2\sqrt{\left|c\right|}\mu \right)-D}}\right),\end{array}$$

(63)

  Case 3: $\lambda \ne 0,\eta =0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=\pm {\displaystyle \frac{C}{a_1(C\mu +D)}},\end{array}$$

(64)

where $C,D\ne 0.$

Inserting Equation (54) in Equation (50), we obtain

$$\begin{array}{c}\hfill {\mathsf{\Phi }}_4\left(\mu \right)=a_1\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)-\frac{1}{2}\frac{c}{a_1}{\left({\displaystyle \frac{G^{\prime }}{G^2}}\right)}^{-1}.\end{array}$$

(65)

Therefore, we obtain three types of traveling-wave solutions, as follows:

  Case 1: $\lambda \eta >0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=\sqrt{{\displaystyle \frac{\eta }{\pm a_1}}}\left({\displaystyle \frac{Ccos\left(\sqrt{\pm \frac{c}{2}}\mu \right)+Dsin\left(\sqrt{\pm \frac{c}{2}}\mu \right)}{Dcos\left(\sqrt{\pm \frac{c}{2}}\mu \right)-Csin\left(\sqrt{\pm \frac{c}{2}}\mu \right)}}\right),\end{array}$$

(66)

  Case 2: $\lambda \eta <0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=\pm {\displaystyle \frac{\sqrt{|\frac{c}{2}|}}{a_1}}\left({\displaystyle \frac{Csinh\left(2\sqrt{|\frac{c}{2}|}\mu \right)+Ccosh\left(2\sqrt{|\frac{c}{2}|}\mu \right)+D}{Ccosh\left(2\sqrt{|\frac{c}{2}|}\mu \right)+Csinh\left(2\sqrt{|\frac{c}{2}|}\mu \right)-D}}\right),\end{array}$$

(67)

  Case 3: $\lambda \ne 0,\eta =0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=\pm {\displaystyle \frac{C}{a_1(C\mu +D)}},\end{array}$$

(68)

where $C,D\ne 0.$

Inserting Equation (55) in Equation (50), we obtain

$$\begin{array}{c}\hfill {\mathsf{\Phi }}_5\left(\mu \right)=\pm \frac{2c}{\eta }\left({\displaystyle \frac{G^{\prime }}{G^2}}\right).\end{array}$$

(69)

Therefore, we obtain three types of traveling-wave solutions, as follows:

  Case 1: $\lambda \eta >0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=\sqrt{{\displaystyle \frac{{\eta }^2}{2c}}}\left({\displaystyle \frac{Ccos\left(\sqrt{2c}\mu \right)+Dsin\left(\sqrt{2c}\mu \right)}{Dcos\left(\sqrt{2c}\mu \right)-Csin\left(\sqrt{2c}\mu \right)}}\right),\end{array}$$

(70)

  Case 2: $\lambda \eta <0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=-{\displaystyle \frac{\sqrt{\left|2c\right|}}{\frac{2c}{\eta }}}\left({\displaystyle \frac{Csinh\left(2\sqrt{\left|2c\right|}\mu \right)+Ccosh\left(2\sqrt{\left|2c\right|}\mu \right)+D}{Ccosh\left(2\sqrt{\left|2c\right|}\mu \right)+Csinh\left(2\sqrt{\left|2c\right|}\mu \right)-D}}\right),\end{array}$$

(71)

  Case 3: $\lambda \ne 0,\eta =0;$

$$\begin{array}{c}\hfill {\displaystyle \frac{G^{\prime }\left(\mu \right)}{G^2\left(\mu \right)}}=-{\displaystyle \frac{C}{\frac{2c}{\eta }(C\mu +D)}},\end{array}$$

(72)

where $C,D\ne 0.$

5. Conclusions

We successfully obtained the different analytical solutions to the space–time fractional Bogoyavlenskii equation in the sense of the Jumaries-modified Riemann–Liouville derivative and the CTFMNLSE that describes the fluctuation of sea waves and the propagation of water waves in marine engineering, respectively. The gained results are very helpful in ocean sciences to understand the study of wave fluctuation and wave propagation and are also essential for the validity of experimental and numerical results. We displayed 2–D and 3–D plots for the better realization of the physical existence of the gained solutions by via the appropriate selection of the variables. These solutions are desirable for illustrating various natural phenomena. Our obtained solutions represented that the presented method can be applied to obtain analytical solutions for diverse kinds of NLPDEs.