Germeier’s Scalarization for Approximating Solution of Multicriteria Matrix Games

Abstract

In this paper, we study the properties of Germeier’s scalarization applied for solving multicriteria games. The equilibria and the equilibrium values of such games, as a rule, make sets, and the problems of parametrizing and approximating these sets arise. Shapley proved that Nash equilibrium of multicriteria matrix game can be found by solving a two-parametric family of scalar games obtained with the help of linear scalarization of the criteria vector. We show that Germeier’s scalarization parametrizes the equilibria of the multicriteria game by using one-parametric family of scalar games. Germeier’s scalarization has certain advantages over the linear one, and we suggest it for approximating the multicriteria game equilibria with a finite set. For two-criteria games with $2\times 2$ matrices, we show by examples that there is no continuity of the values of scalar games in the scalarizing parameters. We prove one-sided (from the left or from the right) continuity for the game values. As a result, we come to convergence in Hausdorff metric for the set of equilibrium values obtained for $ϵ$-net on the simplex of scalarizing parameters to the value of the multicriteria game as $ϵ\to 0$. The constructed finite approximation may be helpful in practical applications, where players try to find a compromise in an iterative negotiating procedure under multiple criteria.

1. Introduction

A multicriteria game is usually considered as the extension of a scalar game in the case when players have vector valued payoff functions. Such problems appear when players, or, in general, decision makers, have more than one goal and these goals cannot be a priori reduced to the only criterion (see Refs. [1,2,3,4] for recent models, problems, and settings). For example, the two criteria auction is considered in the evaluation of the mortgage loans with minimizing both the term of the contract and the monthly premium [5]. Matrix games with multicriteria payoffs were firstly considered by Shapley [6]. He proposed to extent the idea of Nash equilibrium for such games (see Definition 2 below). Then this idea was developed by many researches including [7,8,9,10,11]. The definition of Nash equilibrium in the multicriteria case leads to a multicriteria optimization, which is a rather complicated problem with a lot of research done in the area mostly devoted to approximating the nondominated set [12,13] or to techniques of choosing a decision from the set of nondominated alternatives [14,15].

The main problem for multicriteria games is that the best responses of a player form a very wide set, and the equilibrium points also form a set, and it may be hard for players to find a compromise solution. Thus, it is interesting to propose a method for finding a finite approximation for the set of equilibria of the multicriteria game to make any practical application possible. Our idea is to use the scalarizing method because, at first, it was successfully used by Shapley for parametrizing the solution of a multicriteria matrix game and, secondly, it allows to parametrize the nondominated set.

Many papers are devoted to the selection of a proper equilibrium from the set. For example, in Ref. [16], the Nash arbitration scheme is applied. The authors of Ref. [17] use an approach based on additional utility functions. These functions are scalar; therefore, they may be considered as a particular case of scalarizing functions without scalarizing the whole set (this approach corresponds to the choice from the set). Nevertheless, the nature of multicriteriality appears in the fact that utility functions are not known a priori. Any vector from the multicriteria game solution (called agnostic Nash equilibrium in Ref. [17]) may be chosen. However, here, a question arises: is it possible to approximate Shapley’s solution with the union of the solutions obtained from some finite set of utility functions? We try to answer this question in the present paper.

Further to illustrate the idea, we limit ourselves with two person zero-sum finite multicriteria game. Such games are widely used, as may be seen in the review of Ref. [18].

To make our reasoning clear, we introduce some definitions and the main results for multicriteria optimization and the scalarizing method.

1.1. Multicriteria Optimization

Multicriteria maximization considers the problem of finding

$$\mathrm{Max}F\left(x\right),F\left(x\right)=(f_1\left(x\right),\dots ,f_K\left(x\right)),x\in X\subseteq \mathrm{I}{\mathrm{R}}^n.$$

It is usually assumed that F is a continuous vector function and X is a compact set of alternatives. The set of all possible values of F for the given set X is denoted by $F\left(X\right)=\{z|\exists x\in X:z=F\left(x\right)\}$ and it is called the feasible set. To solve the multicriteria problem means to find nondominated alternatives and/or nondominated values of the vector function. Dominance is usually considered with respect to Pareto relation or weak Pareto relation, and Max (or Min) of a vector function is understood as the set of efficient (Pareto) or weakly efficient points in the criterion space [12,19,20,21].

Definition 1. 

Pareto optimal (efficient) alternatives in multicriteria maximization forms the set

$$P_F\left(X\right)=\{x^{*}\in X|\forall x\in X,f\left(x\right)\ne f\left(x^{*}\right),\exists k:f_k\left(x\right)<f_k\left(x^{*}\right)\}.$$

The set of all Pareto optimal (efficient) points $F\left(P_F\left(X\right)\right)$ is called the Pareto frontier (Pareto front or Pareto set).

Further we consider the set of weakly efficient (nondominated) alternatives

$$\begin{array}{c}{\displaystyle \mathrm{Arg}\underset{x\in X}{\mathrm{Max}}F\left(x\right)\stackrel{\mathrm{def}}{=}\{x^0\in X|\forall x\in X\exists k:f_k\left(x\right)\le f_k\left(x^0\right)\},}\hfill \\ {\displaystyle \mathrm{Arg}\underset{x\in X}{\mathrm{Min}}F\left(x\right)\stackrel{\mathrm{def}}{=}\{x^0\in X|\forall x\in X\exists k:f_k\left(x\right)\ge f_k\left(x^0\right)\}}\hfill \end{array}$$

(1)

and the corresponding weakly efficient values ${\displaystyle F(\mathrm{Arg}\underset{x\in X}{\mathrm{Max}}F\left(x\right))}$ and ${\displaystyle F(\mathrm{Arg}\underset{x\in X}{\mathrm{Min}}F\left(x\right))}$ of the vector function F in multicriteria maximization and minimization, respectively. These sets include all Pareto points and also weakly nondominated ones.

1.2. Scalarization

Scalarization [12,14,20,21] is one of the methods applied for multicriteria optimization. This method reduces the problem of finding one of the sets in (1) or the Pareto frontier (which is also the set) to a parametric family of scalar optimization problems. Linear scalarizing function (LS) changes the initial vector function with the weighted sum of its partial criteria:

$$F\left(x\right)\to \sum _{k=1}^K{\lambda }_k{f}_k\left(x\right),\lambda \stackrel{\mathrm{def}}{=}({\lambda }_1,\dots ,{\lambda }_K),\lambda \in \Lambda \stackrel{\mathrm{def}}{=}\{\lambda \in \mathrm{I}{\mathrm{R}}_{+}^K|\sum _{k=1}^K{\lambda }_k=1\}.$$

It is well-known [14,21] that the Pareto frontier of a convex feasible set Z is parametrized with linear scalarizing function: for a Pareto point $z^0\in Z$ there exists such $\lambda \in \Lambda$ that

$$\sum _{k=1}^K{\lambda }_k{z}_k^0=\underset{z\in Z}{max}\sum _{k=1}^K{\lambda }_k{z}_k$$

and if this equality is satisfied for some $\lambda \in \Lambda$, $\lambda >0$, then $z^0$ is Pareto efficient.

Convexity requirement for the feasible set restricts the application of the linear scalarization. It is especially important for multicriteria games, because the set of possible game values in multicriteria case is not convex [8,9]. Therefore we consider a scalarizing function suitable for nonconvex sets [14,20]. The idea was put forward by Yu.B. Germeier at the end of the 1960s. It corresponds to the concept of fair allocation of limited resources introduced by Rawls [22] and is widely used for decision making (in particular, in data networks [23]). It realizes the idea of measuring, for example, social welfare or network users’ demands as (weighted) the worst-off member of society or user. Germeier proved that for $F\left(x\right)>0$, $x^{*}$ is weakly efficient if and only if there exists the vector $\mu >0,\mu \in \Lambda$, such that ${\displaystyle x^{*}\in \mathrm{Arg}\underset{x}{max}\underset{k}{min}{\mu }_k{f}_k\left(x\right)}$. The function ${\displaystyle \underset{k}{min}{\mu }_k{f}_k\left(x\right)}$ is called the Germeier’s combination (in Russian literature) and the weighed Chebyshev metric (in English language literature). Further investigations [11,24,25,26] have widened Germeier’s result for the modified function

$${\displaystyle \underset{k\in I\left(\mu \right)}{min}\frac{f_k\left(x\right)}{{\mu }_k},I\left(\mu \right)\stackrel{\mathrm{def}}{=}\{k=1\dots K|{\mu }_k>0\},\mu \in \Lambda .}$$

(2)

We refer to it as Germeier scalarizing function (GS). Here and further $1\dots K$ (and similar) denotes the interval of all integers between 1 and K included.

Figure 1 illustrates how GS (2) works in a multicriteria maximization problem. The feasible set $F\left(X\right)$ (the set of all feasible values of the vector function) is shown (shaded) in the criterion space, i.e., on $(f_1,f_2)$ plane. Level curves of the function ${\displaystyle min\left(\frac{f_1}{{\mu }_1},\frac{f_2}{{\mu }_2}\right)}$ are presented for the given $\mu =({\mu }_1,{\mu }_2)$. The particular level curve is a cone with the vertex determined by the equality ${\displaystyle \frac{f_1}{{\mu }_1}=\frac{f_2}{{\mu }_2}=const}$. The maximal value of ${\displaystyle min\left(\frac{f_1}{{\mu }_1},\frac{f_2}{{\mu }_2}\right)}$ along the ray $\overline{0,\mu }$ is achieved at the point, where the cone vertex lies on the Pareto frontier of $F\left(X\right)$ (in bold). This point has the coordinates ${\displaystyle \left({\mu }_1\underset{x\in X}{max}min\left(\frac{f_1\left(x\right)}{{\mu }_1},\frac{f_2\left(x\right)}{{\mu }_2}\right),{\mu }_2\underset{x\in X}{max}min\left(\frac{f_1\left(x\right)}{{\mu }_1},\frac{f_2\left(x\right)}{{\mu }_2}\right)\right)}$.

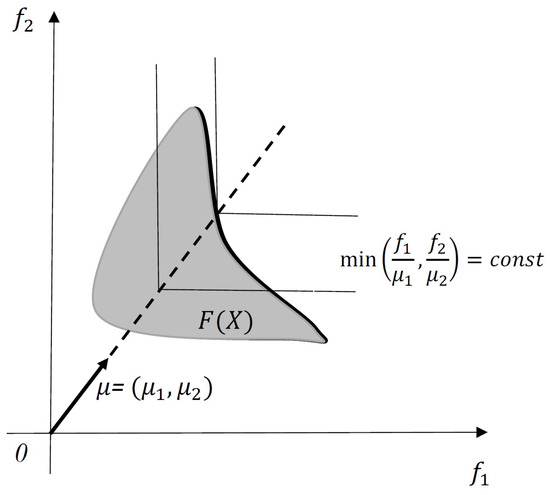
Figure 1. Germeier’s scalarization in the two-criteria max problem.

The function ${\displaystyle \underset{x\in X}{max}\underset{k\in I\left(\mu \right)}{min}\frac{f_k\left(x\right)}{{\mu }_k}}$ is continuous in $\mu$ while F is continuous, and

$$\underset{x\in X}{\mathrm{Max}}F\left(x\right)=\bigcup _{\mu \in \Lambda }\mu \underset{x\in X}{max}\underset{k\in I\left(\mu \right)}{min}\frac{f_k\left(x\right)}{{\mu }_k}$$

under some regularity conditions [25]. Therefore Germeier’s scalarizing function is successfully used for parametrizing and approximating nonconvex weakly efficient sets. Further development of Germeier’s idea leads to a combination of GS and LS [27,28] and to the scalarizing functions of the form ${\displaystyle {(\sum _k{\lambda }_k{z}_k^s)}^{1/s}}$ (see [19]). Nevertheless, GS (2) looks better for finite approximation [25] than other types of scalarizing functions.

1.3. Two Person Zero-Sum Multicriteria Game

Consider a multicriteria (MC) game of two players having opposite goals: Player 1 wants to maximize a vector function $F(x,y)=(f_1(x,y),\dots ,f_K(x,y))$ and Player 2 tries to minimize the same function. Player 1 chooses strategy $x\in X$ and Player 2’s strategy is $y\in Y$, and we come to the game $\Gamma =⟨X,Y,F(x,y)⟩$. Following classic game theoretic concepts it is easy to rewrite the definition of Nash equilibrium for multicriteria case [7].

Definition 2. 

A pair of strategies $(x^{*},y^{*})$, $x^{*}\in X$, $y^{*}\in Y$ is called the multicriteria Nash equilibrium outcome or just multicriteria Nash equilibrium if

$$x^{*}\in \mathrm{Arg}\underset{x\in X}{\mathrm{Max}}F(x,y^{*})and{y}^{*}\in \mathrm{Arg}\underset{y\in Y}{\mathrm{Min}}F(x^{*},y).$$

As mentioned above, here and from now on we will consider Max and Min as the sets of weakly nondominated values of the vector function. Such an approach defines the widest possible of MC game solutions [7]. Shapley [6] proved that the set of MC equilibria for an MC finite game can be represented as a set of solutions of scalar games.

Another idea for solving MC games comes from the attempts of using maxmin and minmax in multicriteria case [29]. In a scalar game, maxmin defines a player’s security strategy [30], and the equilibrium in a zero-sum scalar game exists when maxmin of the payoff is equal to minmax of the payoff. However, what should be understood by maxmin for a vector function? There are two competing approaches for combining the sets of Min and Max. One of them unites the feasible sets for each particular player’s strategy [31,32], the other considers the intersection of such sets widened with nonfeasible points (evaluations) [19,24,33]. The main disadvantage of the first approach is a lack of meaningful interpretation, while the second one leads to underestimated values.

In our papers [24,26] we have developed a second approach. Based on the approach, we consider vector evaluations for the points from the initial feasible set. This allows us to formulate the concept of the solution for an MC game with opposite interests [34] as the set of points in criterion space belonging both to MC maxmin and minmax. We find the class of MC games “in evaluations” for which such a solution is not empty. Zero-sum games have empty intersections of Player 1’s MC maxmin and Player 2’s MC minmax in the nondegenerate case [34,35]. To overcome this problem, we introduce [36,37] a new concept of MC mixed extension for which MC maxmin and minmax are equal for the same player. For this concept, relations between MC mixed strategy equilibrium set and MC maxmin are presented in Ref. [38]. A detailed analysis of different concepts for MC game value can be found in Ref. [11]. In the present paper, we turn back to the classic (initial) concept of a mixed strategy solution of an MC matrix game introduced by Shapley (see Definition 2).

Consider a finite multicriteria zero-sum two person game. In this case, kth partial criterion forms an $(n\times m)$-matrix $A_k$, $k=1\dots K$. Component $a_{ij}\left(k\right)$ of the matrix $A_k$ stands for Player 1’s gain and Player 2’s loss for kth criterion when Player 1 chooses strategy i (matrix row) and Player 2 chooses strategy j (matrix column), $i=1\dots n$, $j=1\dots m$. The chosen pair $(i,j)$ is the pure strategy outcome of the game. It determines vector $(a_{ij}\left(1\right),\dots ,a_{ij}\left(K\right))$ of Player 1’s gains and Player 2’s losses. When the players use mixed strategies, assuming that $p_i$ is the probability that Player 1 chooses row i and $q_j$ is the probability that Player 2 chooses column j, we come to the mixed strategy outcome $(p,q)$ with $p\in P$ and $q\in Q$, where

$$P\stackrel{\mathrm{def}}{=}\{p\in \mathrm{I}{\mathrm{R}}_{+}^n|\sum _{i=1}^n{p}_i=1\},Q\stackrel{\mathrm{def}}{=}\{q\in \mathrm{I}{\mathrm{R}}_{+}^m|\sum _{j=1}^m{q}_j=1\}.$$

The averaged criteria vector ($p{A}_{1}q,\dots ,p{A}_{K}q$) is the gain of Player 1 and the loss of Player 2 according to standard mixed extension of the multicriteria game [6]. We obtain multicriteria zero-sum game ${\Gamma }^0\stackrel{\mathrm{def}}{=}⟨P,Q,\Phi ⟩$ with gain/loss vector function

$$\Phi (p,q)=({\phi }_1(p,q),\dots ,{\phi }_K(p,q)),{\phi }_k(p,q)\stackrel{\mathrm{def}}{=}p{A}_{k}q,k=1\dots K.$$

Shapley [6] studied game ${\Gamma }^0$, assuming that its solution is the Nash equilibrium generalized for the multicriteria case. As a rule, the solution and the value of the MC game are sets. According to Shapley, the solution (or set of equilibria) of ${\Gamma }^0$ is the set of outcomes

$$R^0\stackrel{\mathrm{def}}{=}\{(p^0,q^0)\in P\times Q|p^0\in \mathrm{Arg}\underset{p\in P}{\mathrm{Max}}\Phi (p,q^0)\mathrm{and}{q}^0\in \mathrm{Arg}\underset{q\in Q}{\mathrm{Min}}\Phi (p^0,q)\},$$

(3)

and the value (or set of equilibrium values) of ${\Gamma }^0$ is the set

$$Z^0\stackrel{\mathrm{def}}{=}\{\Phi (p^0,q^0)|(p^0,q^0)\in R^0\}.$$

Any pair of strategies $(p^0,q^0)\in R^0$ in (3) is called MC equilibrium in the game ${\Gamma }^0$, and the corresponding $\Phi (p^0,q^0)$ is called the equilibrium value.

According to Refs. [6,7], the sets $R^0$ and $Z^0$ can be obtained with the aid of linear scalarization applied to the partial criteria of $\Phi (p,q)$. Equilibrium outcomes and equilibrium values of the scalar games

$${\Gamma }_S[\Phi ,(\lambda ,\gamma )]\stackrel{\mathrm{def}}{=}⟨P,Q,\sum _{k=1}^K{\lambda }_k{\phi }_k,-\sum _{k=1}^K{\gamma }_k{\phi }_k⟩\forall \lambda ,\gamma \in \Lambda \stackrel{\mathrm{def}}{=}\{\lambda \in \mathrm{I}{\mathrm{R}}_{+}^K|\sum _{k=1}^K{\lambda }_k=1\},$$

(4)

form the sets of equilibrium outcomes and equilibrium values of the MC game ${\Gamma }^0$. Here and further for a normal form scalar game [30,39], we write minus in the payoff function of Player 2 because she/he minimizes her/his losses (in (4), the payoff is equal to convex combination of partial criteria).

The scalar games in (4) are not zero-sum for $\lambda \ne \gamma$. Nevertheless, the equilibrium exists in each of the games due to Nash’s theorem [40]. For each pair of parameters, it can be found as a mixed strategy equilibrium of the finite bimatrix game with matrices ${\displaystyle \sum _{k=1}^K{\lambda }_k{A}_k}$ and ${\displaystyle -\sum _{k=1}^K{\gamma }_k{A}_k}$ by solving a system of linear equations (see, for example, in Ref. [30]). However, parametrization of the sets $R^0$ and $Z^0$ by the equilibria of scalar games (4) may be not convenient, in particular, due to practical reasons [10,36]. In addition, such a parametrization does not allow to compare the set $Z^0$ of MC game equilibrium values with MC maxmin and MC minmax, because the latter cannot be parametrized by maxmins and minmaxes of the LS [11,41,42]. The present paper studies parametrization of $R^0$ and $Z^0$ based on Germeier’s scalarization with the main purpose of proposing the finite approximation of $Z^0$.

In Section 2, we apply Germeier’s scalarization to the solution (3) of the MC matrix game in mixed strategies and substantiate the parametrization of $Z^0$ with the aid of Germeier’s scalarizing function. In Section 3, we discuss the obtained result and compare $Z^0$ with MC maxmin and MC minmax parametrized with GS. In Section 4, we examine a finite approximation of the set of equilibria (and the equilibrium values) of the MC game. In Section 5, we give a short review of the close results, and the conclusions in Section 6 summarize our research.

2. Germeier’s Scalarization in MC Games

Scalarization is not only useful for parametrizing and approximating MC game value, as may also be used by a decision maker who wants to compare nondominated vector payoffs, keeping in mind some certain meaning. For example, she/he may consider weights of relative importance of the criteria or coefficients that show the degree of achievements of some target values. When the decision maker uses LS, she/he solves the problem of total profit maximization, while GS improves the worst compliance with the target among the criteria. According to Rawls [22], the latter is called a fair allocation.

The MC game may be considered as a competition between two teams, and their members rely on the partial criteria. The criteria values depend on the strategies of the members of both teams. In this case, fair optimization leads to GS as a measure for efficiency of the decisions made [10]. In addition, GS is a useful tool for searching, analyzing, and describing the solutions of MC games.

In a zero-sum multicriteria game, Player 1 faces the multicriteria maximization

$$\underset{p\in P}{\mathrm{Max}}\Phi (p,q^0)$$

(for the fixed $q^0$). Germeier’s scalarization (2) specifies the corresponding parametric family of scalar functions

$$G_1[\Phi ,\mu ](p,q^0)\stackrel{\mathrm{def}}{=}\underset{k\in I\left(\mu \right)}{min}\frac{{\phi }_k(p,q^0)}{{\mu }_k},\mu \in \Lambda .$$

For the fixed $p^0$, the minimizing Player 2 solves the multicriteria minimization

$$\underset{q\in Q}{\mathrm{Min}}\Phi (p^0,q)$$

that is reduced to parametric minimization of GS

$${\displaystyle G_2[\Phi ,\mu ](p^0,q)\stackrel{\mathrm{def}}{=}\underset{k\in I\left(\mu \right)}{max}\frac{{\phi }_k(p^0,q)}{{\mu }_k},\mu \in \Lambda .}$$

To further simplify the reasoning, we suppose that all elements $a_{ij}\left(k\right)$ of matrices $A_k$ ($k=1\dots K$) are positive rational numbers. For definiteness, let them be no less than 1 and no greater than 10. Then $1\le {\phi }_k(p,q)\le 10$, $k=1\dots K$. The payoff of Player 2 is negative, and this leads to some distinctions between proofs of the results in the current section and those given for the weak equilibrium in Ref. [10].

Now we show that Germeier’s scalarization allows us to describe $R^0$ and $Z^0$ in multicriteria zero-sum game with one-parametric family of scalar games

$${\Gamma }_G\left(\mu \right)\stackrel{\mathrm{def}}{=}⟨P,Q,G_1[\Phi ,\mu ](p,q),-G_2[\Phi ,\mu ](p,q)⟩,\mu \in \Lambda .$$

(5)

Proposition 1. 

For all $(p^0,q^0)\in R^0$ there exists ${\mu }^0\in \Lambda$ such that $(p^0,q^0)$ is Nash equilibrium in ${\Gamma }_G\left({\mu }^0\right)$.

Proof. 

Let us choose, as in Refs. [20,25], the vector of Germeier’s scalarizing function ${\mu }^0\in \Lambda$ having components

$${\mu }_k^0\stackrel{\mathrm{def}}{=}\frac{{\phi }_k(p^0,q^0)}{{\displaystyle \sum _{k=1}^K}{\phi }_k(p^0,q^0)}.$$

(6)

1. We obtain

$$p^0\in \mathrm{Arg}\underset{p\in P}{max}{G}_1[\Phi ,{\mu }^0](p,q^0).$$

(7)

Indeed, let $p^{*}\in P$ be a maximizer in (7). Then ${\displaystyle G_1[\Phi ,{\mu }^0](p^{*},q^0)\ge G_1[\Phi ,{\mu }^0](p^0,q^0).}$ If the equality is satisfied, then (7) is proven. If strong inequality is satisfied, then, by definitions of $G_1$ and ${\mu }^0$,

$$\underset{k\in I\left({\mu }^0\right)}{min}\frac{{\phi }_k(p^{*},q^0)}{{\mu }_k^0}>\underset{k\in I\left({\mu }^0\right)}{min}\frac{{\phi }_k(p^0,q^0)}{{\mu }_k^0}=\sum _{k=1}^K{\phi }_k(p^0,q^0)\mathrm{and}\underset{k\in I\left({\mu }^0\right)}{min}\frac{{\phi }_k(p^{*},q^0)}{{\phi }_k(p^0,q^0)}>1,$$

i.e., ${\phi }_k(p^{*},q^0)>{\phi }_k(p^0,q^0)$$\forall k=1\dots K$, since ${\phi }_k(p^0,q^0)>0$ under the assumptions made. Hence,

$${\displaystyle \sum _{k=1}^K{\lambda }_k{\phi }_k(p^{*},q^0)>\sum _{k=1}^K{\lambda }_k{\phi }_k(p^0,q^0)\mathrm{for} \mathrm{any}\lambda \ne 0.}$$

However, according to Refs. [6,7], $(p^0,q^0)$ is an equilibrium in a game from (4), i.e., there exists such $\lambda \in \Lambda$ that

$$p^0\in \mathrm{Arg}\underset{p\in P}{max}\sum _{k=1}^K{\lambda }_k{\phi }_k(p,q^0).$$

The obtained contradiction proves (7).

2. Similarly ${\displaystyle q^0\in \mathrm{Arg}\underset{q\in Q}{max}\{-G_2[\Phi ,{\mu }^0](p^0,q)\}}$, i.e., ${\displaystyle q^0\in \mathrm{Arg}\underset{q\in Q}{min}{G}_2[\Phi ,{\mu }^0](p^0,q)}$, if

$$q^0\in \mathrm{Arg}\underset{q\in Q}{min}\sum _{k=1}^K{\gamma }_k{\phi }_k(p^0,q),\gamma \in \Lambda .$$

(8)

Let ${\displaystyle q^{*}\in \mathrm{Arg}\underset{q\in Q}{min}{G}_2[\Phi ,{\mu }^0](p^0,q)}$. Then $G_2[\Phi ,{\mu }^0](p^0,q^{*})\le G_2[\Phi ,{\mu }^0](p^0,q^0)$. However, for strict inequality we have

$$\underset{k\in I\left({\mu }^0\right)}{max}\frac{{\phi }_k(p^0,q^{*})}{{\mu }_k^0}<\sum _{k=1}^K{\phi }_k(p^0,q^0)\mathrm{and}\underset{k\in I\left({\mu }^0\right)}{max}\frac{{\phi }_k(p^0,q^{*})}{{\phi }_k(p^0,q^0)}<1,$$

i.e., ${\phi }_k(p^0,q^{*})<{\phi }_k(p^0,q^0)\forall k\in I\left({\mu }^0\right)$. Since $I\left({\mu }^0\right)=\{k=1\dots K\}$ then

$$\sum _{k=1}^K{\gamma }_k{\phi }_k(p^0,q^{*})<\sum _{k=1}^K{\gamma }_k{\phi }_k(p^0,q^0),$$

i.e., $q^0$ does not minimize LS, which contradicts (8). As a result, we prove that there exists an equilibrium in the game ${\Gamma }_G\left({\mu }^0\right)$ that coincides with the MC equilibrium $(p^0,q^0)$. □

Remark 1. 

If we do not suppose ${\phi }_k(p^0,q^0)>0$, part 2 of the proof is not true for ${\gamma }_k\ne 0$.

Thus, any MC equilibrium in the MC game ${\Gamma }^0$ can be obtained with the aid of GS with the same value of a scalarizing parameter for both players. Under the assumptions ${\phi }_k(p^0,q^0)>0$ the inverse statement is true.

Proposition 2. 

For any $\mu \in \Lambda$, Nash equilibrium in the game ${\Gamma }_G\left(\mu \right)$ belongs to $R^0$.

Proof. 

Let $\mu \in \Lambda$ and ${\displaystyle p^{*}\in \mathrm{Arg}\underset{p\in P}{max}{G}_1[\Phi ,\mu ](p,q^{*})}$, ${\displaystyle q^{*}\in \mathrm{Arg}\underset{q\in Q}{min}{G}_2[\Phi ,\mu ](p^{*},q)}$ (note that ${\displaystyle \mathrm{Arg}\underset{q\in Q}{max}\{-G_2[\Phi ,\mu ](p^{*},q)\}=\mathrm{Arg}\underset{q\in Q}{min}{G}_2[\Phi ,\mu ](p^{*},q)}$). Then, according to GS properties (see Section 1.2 and Ref. [25] for details),

$$p^{*}\in \mathrm{Arg}\underset{p\in P}{\mathrm{Max}}\Phi (p,q^{*})\mathrm{and}{q}^{*}\in \mathrm{Arg}\underset{q\in Q}{\mathrm{Min}}\Phi (p^{*},q),\mathrm{i}.\mathrm{e}.,(p^{*},q^{*})\in R^0.$$

□

Let us emphasize that existence of Nash equilibrium in the scalar game ${\Gamma }_G\left(\mu \right)$ for any $\mu \in \Lambda$ follows from Nash’s theorem [30], because in the considered case of the finite game, $G_1[\Phi ,\mu ](p,q)$ is concave in p and $-G_2[\Phi ,\mu ](p,q)$ is concave in q on the convex compact set $P\times Q$.

It follows from the proof of Proposition 1 that $G_1[\Phi ,{\mu }^0](p^0,q^0)=G_2[\Phi ,{\mu }^0](p^0,q^0)$ at equilibrium for ${\mu }^0$ (6), i.e., Germeier’s scalarizing functions for both players are equal. One can also see the equality between the partial criteria divided by the corresponding scalarizing coefficients. It means the equality between the normalized partial gains for Player 1 and losses for Player 2. The value they are equal to is the sum of the vector function components at the MC equilibrium. Furthermore, the following interesting result takes place.

Proposition 3. 

For any $\mu \in \Lambda$ at any Nash equilibria $(p^{*},q^{*})$ of the game ${\Gamma }_G\left(\mu \right)$ either

$$G_1[\Phi ,\mu ](p^{*},q^{*})=G_2[\Phi ,\mu ](p^{*},q^{*}),$$

and $\mu G_i[\Phi ,\mu ](p^{*},q^{*})=\Phi (p^{*},q^{*}),$$i=1,2$, or μ does not satisfy (6) for $(p^{*},q^{*})$, and

$$\mu G_i[\Phi ,\mu ](p^{*},q^{*})\ne \Phi (p^{*},q^{*}),i=1,2.$$

Proof. 

Let us choose $\mu \in \Lambda$ and let $(p^{*},q^{*})$ be an equilibrium in the game ${\Gamma }_G\left(\mu \right)$ (5). For the equilibrium, we construct ${\mu }^{*}$ according to (6) (replacing index 0 with *). Then we have $\Phi (p^{*},q^{*})={\mu }^{*}{G}_1[\Phi ,{\mu }^{*}](p^{*},q^{*})$. On the other hand, since $p^{*}$ maximizes $G_1[\Phi ,\mu ](p,q^{*})$, then ${\phi }_k(p^{*},q^{*})/{\mu }_k\ge G_1[\Phi ,\mu ](p^{*},q^{*})$$\forall k=1\dots K$ and $\Phi (p^{*},q^{*})\ge \mu G_1[\Phi ,\mu ](p^{*},q^{*})$, i.e., ${\mu }^{*}{G}_1[\Phi ,{\mu }^{*}](p^{*},q^{*})\ge \mu G_1[\Phi ,\mu ](p^{*},q^{*})$. If the vectors are equal, then $\mu ={\mu }^{*}$, because $G_1[\Phi ,{\mu }^{*}](p^{*},q^{*})$ and $G_1[\Phi ,\mu ](p^{*},q^{*})$ are positive and $\mu ,{\mu }^{*}\in \Lambda$. Hence, $\mu$ has the same properties as ${\mu }^{*}$. If there exists k such that ${\phi }_k(p^{*},q^{*})>{\mu }_k{G}_1[\Phi ,\mu ](p^{*},q^{*})$, i.e.,

$${\mu }_k^{*}{G}_1[\Phi ,{\mu }^{*}](p^{*},q^{*})>{\mu }_k{G}_1[\Phi ,\mu ](p^{*},q^{*}),$$

then it follows from $\mu ,{\mu }^{*}\in \Lambda$ that $G_1[\Phi ,{\mu }^{*}](p^{*},q^{*})>G_1[\Phi ,\mu ](p^{*},q^{*})$. Thus, the equality $\Phi (p^{*},q^{*})=\mu G_1[\Phi ,\mu ](p^{*},q^{*})$ is impossible.

Notice that, by definitions of $G_i$, when $G_1[\Phi ,\mu ](p^{*},q^{*})\ne G_2[\Phi ,\mu ](p^{*},q^{*})$ there exist such k and l, for which ${\phi }_k(p^{*},q^{*})>{\mu }_k{G}_1[\Phi ,\mu ](p^{*},q^{*})$ and ${\phi }_l(p^{*},q^{*})<{\mu }_l{G}_2[\Phi ,\mu ](p^{*},q^{*})$. Therefore, $\Phi (p^{*},q^{*})\ne \mu G_1[\Phi ,\mu ](p^{*},q^{*})$ and $\Phi (p^{*},q^{*})\ne \mu G_2[\Phi ,\mu ](p^{*},q^{*})$ from what was proved above. We have that $\mu \ne {\mu }^{*}$ for this $(p^{*},q^{*})$. □

It follows from Proposition 3 and the proof of Proposition 1 that for the description of the set $R^0$, it is enough to consider only those $\mu \in \Lambda$, for which $G_1[\Phi ,\mu ](p^{*},q^{*})=G_2[\Phi ,\mu ](p^{*},q^{*})$ for some equilibrium $(p^{*},q^{*})$ of the game ${\Gamma }_G\left(\mu \right)$. We denote the set of these GS parameters by $M^{*}$. In particular, under the assumptions we have made, ${\mu }_k\ge 0.1/K>0,k=1\dots K,$ for $\mu \in M^{*}$. The solutions of game (5) for $\mu \in \Lambda \backslash M^{*}$ do not add any new MC equilibrium to $R^0$ in comparison to those obtained for $\mu \in M^{*}$. Further, we denote by ${\Lambda }_0\stackrel{\mathrm{def}}{=}\{\mu \in \Lambda |{\mu }_k\ge 0.1/K,k=1\dots K\}$ the set of GS’s scalarizing parameters that contain $M^{*}$ for certain.

If $\mu \in M^{*}$, then all ratios ${\phi }_k/{\mu }_k$ are equal at the equilibrium $(p^{*},q^{*})$, for which $G_1[\Phi ,\mu ](p^{*},q^{*})=G_2[\Phi ,\mu ](p^{*},q^{*})$. Thus, GS allows us to obtain the following necessary conditions of $(p,q)$ being MC equilibrium in the multicriteria matrix game. There exists $\mu \in M^{*}$ such that

$$p(A_k-{\mu }_k\sum _{k=1}^K{A}_k)q=0,k=1\dots K.$$

(9)

We have $K-1$ equations for $n-1+m-1$ variables. In particular, for two criteria games $2\times 2$, p and q satisfy the equality $p\{A_1-{\mu }_1(A_1+A_2)\}q=0$. Further we write $a_{i,j}^{\mathrm{I}}$ or $a_{i,j}^{\mathrm{II}}$ instead of $a_{ij}\left(k\right)$ in the case of $K=2$. In these notations, (9) takes the form $\{p_1(a_{1,1}^{\mathrm{I}}(1-{\mu }_1)-{\mu }_1{a}_{1,1}^{\mathrm{II}})+(1-p_1)(a_{2,1}^{\mathrm{I}}(1-{\mu }_1)-{\mu }_1{a}_{2,1}^{\mathrm{II}})\}{q}_1+\{p_1(a_{1,2}^{\mathrm{I}}(1-{\mu }_1)-{\mu }_1{a}_{1,2}^{\mathrm{II}})+(1-p_1)(a_{2,2}^{\mathrm{I}}(1-{\mu }_1)-{\mu }_1{a}_{2,2}^{\mathrm{II}})\}(1-q_1)=0.$ This relation allows us to express $p_1$ in terms of $q_1$ and vice versa. However, one should take into account $p\in P$ and $q\in Q$.

The number of equations grows together with K (no matter how many pure strategies the players have), and it is not obvious that system (9) is compatible. Nevertheless, it is compatible for $\mu ={\mu }^0$ from (6) and its solution leads (by the proof of Proposition 1) to at least one vector of mixed strategies $(p^0,q^0)$, that is an equilibrium in the scalar game ${\Gamma }_G\left(\mu \right)$, i.e., the equilibrium of the MC game. Thus, a solution of (9) that belongs to $P\times Q$ exists for all $\mu \in M^{*}$ (by Proposition 3). The question of how to use (9) for finding $(p^0,q^0)\in R^0$ is still open. It is clear that the set $M^{*}$ is not described explicitly. Besides, it is not enough to use (9) for obtaining an equilibrium in the game ${\Gamma }_G\left(\mu \right)$. However, Equation (9) help to find all pure strategy MC equilibria for the multicriteria matrix game.

Proposition 4. 

If $p_i^0=1,q_j^0=1$ for $(p^0,q^0)\in R^0$, then $(p^0,q^0)$ is Nash equilibrium in the scalar game ${\Gamma }_G\left({\mu }^{ij}\right)$ with

$${\displaystyle {\mu }_k^{ij}\stackrel{\mathrm{def}}{=}\frac{a_{ij}\left(k\right)}{{\displaystyle \sum _{l=1}^K}{a}_{ij}\left(l\right)},k=1\dots K.}$$

Proof. 

Conditions (9) for pure strategies $(p^0,q^0)$ take the form

$$a_{ij}\left(k\right)-{\mu }_k\sum _{l=1}^K{a}_{ij}\left(l\right)=0,k=1\dots K,$$

and allow us to write ${\mu }^{ij}$ in the needed way. □

Thus, if $(i,j)$ is a pure strategy MC equilibrium, then it is also a pure strategy equilibrium in the bimatrix game with matrices $G_1[(A_1,\dots ,A_K),{\mu }^{ij}]$ and $-G_2[(A_1,\dots ,A_K),{\mu }^{ij}]$, where

$$G_1[(A_1,\dots ,A_K),\mu ](i,j)=\underset{k=1\dots K}{min}\frac{a_{ij}\left(k\right)}{{\mu }_k},G_2[(A_1,\dots ,A_K),\mu ](i,j)=\underset{k=1\dots K}{max}\frac{a_{ij}\left(k\right)}{{\mu }_k}.$$

The inverse is also true by Proposition 2. Therefore, if we find pure strategy equilibria (if exist) for the games ${\Gamma }_G\left({\mu }^{ij}\right)$, $i=1\dots n,j=1\dots m$, we construct all pure strategy MC equilibria for the MC game ${\Gamma }^0$. A fast algorithm for finding a pure strategy equilibrium in a bimatrix game is suggested in Ref. [43]. Assuming $a_{ij}\left(k\right)$ to be integer or rational numbers for all $k=1\dots K$, we can choose ${\mu }^{ij}$ at once from Proposition 4 as basic knots of $ϵ$-net for approximating $R^0$ (see Section 4).

Notice that the game ${\Gamma }_G\left({\mu }^{ij}\right)$ has the pure strategy equilibrium $p_i^0=1$, $q_j^0=1$ if the corresponding pair $(i,j)$ is a pure strategy saddle point (solution) of the zero-sum matrix game with the matrix ${\displaystyle A\stackrel{\mathrm{def}}{=}\sum _k{A}_k}$. Indeed, let $(i,j)$ be a pure strategy equilibrium in the game with the matrix A. Then for the bimatrix game with payoff functions

$$G_1[(A_1,\dots ,A_K),{\mu }^{ij}](i^{\prime },j^{\prime }),-G_2[(A_1,\dots ,A_K),{\mu }^{ij}](i^{\prime },j^{\prime })$$

for ${\mu }^{ij}$ defined in Proposition 4, we obtain

$$\underset{i^{\prime }=1\dots n}{max}{G}_1[(A_1,\dots ,A_K),{\mu }^{ij}](i^{\prime },j)=\underset{i^{\prime }=1\dots n}{max}\underset{k=1\dots K}{min}\frac{a_{i^{\prime }j}\left(k\right)}{{\mu }_k^{ij}}\ge \sum _{l=1}^K{a}_{ij}\left(l\right).$$

For strict inequality, we have ${\displaystyle \underset{k=1\dots K}{min}{a}_{i^{\prime }j}\left(k\right)/a_{ij}\left(k\right)>1,}$ hence, $a_{i^{\prime }j}\left(k\right)>a_{ij}\left(k\right)$$\forall k=1\dots K$ and ${\displaystyle \sum _{l=1}^K{a}_{i^{\prime }j}\left(k\right)>\sum _{l=1}^K{a}_{ij}\left(l\right)}$. The latter contradicts to the fact that $(i,j)$ is a saddle point for A. The same reasoning can be performed for Player 2.

This property may be convenient for finding MC equilibria, although it follows from the parametrization of $R^0$ with linear scalarizing function, and any convex combination of $A_k$ may provide sufficient condition instead of the sum of the matrices. As a reminder, we cannot limit ourselves with saddle points of the similar matrix games when we construct the whole set $R^0$ using LS. All equilibria of the bimatrix games for different weights used by different players should be found as well [6]. There is no need to solve games with mismatched scalarizing parameters when GS is used.

3. Properties of GS-Based Parametrization for Multicriteria Game Value

3.1. MC Maxmin and MC Minmax

The constructed one-parametric representation of the set $R^0$ gives a similar parametrization for the value $Z^0$ of the MC game ${\Gamma }^0$. Namely, for the positive payoff vector function,

$$Z^0=\{z^0\left[\mu \right]\stackrel{\mathrm{def}}{=}\Phi (p^{*}\left[\mu \right],q^{*}\left[\mu \right])|(p^{*}\left[\mu \right],q^{*}\left[\mu \right])\mathrm{is}\mathrm{the}\mathrm{equilibrium}\mathrm{in}{\Gamma }_G\left(\mu \right),\mu \in {\Lambda }_0\}.$$

(10)

For $\mu \in M^{*}$, the equalities

$$\Phi (p^{*}\left[\mu \right],q^{*}\left[\mu \right])=\mu G_1[\Phi ,\mu ](p^{*}\left[\mu \right],q^{*}\left[\mu \right])=\mu G_2[\Phi ,\mu ](p^{*}\left[\mu \right],q^{*}\left[\mu \right])$$

are satisfied (for some $(p^{*}\left[\mu \right],q^{*}\left[\mu \right])$), and vector inequalities (for all equilibria of the game ${\Gamma }_G\left(\mu \right)$) are fulfilled for all other positive $\mu$ according to Proposition 3. In addition, it follows from the proof of Proposition 1 that $Z^0$ is not changed if we take only $\mu \in M^{*}$ in (10). Formula (10) allows us to obtain the following parametric relations between the value of zero-sum MC game and MC maxmin and MC minmax.

According to Ref. [26], MC maxmin and MC minmax of the vector payoff $\Phi (p,q)$ for Player 1 are the sets $V_1$ and $W_1$ that can be parametrized using GS in the following way:

$$V_1=\{v_1\left[\mu \right]\stackrel{\mathrm{def}}{=}\mu \underset{p\in P}{max}\underset{q\in Q}{min}{G}_1[\Phi ,\mu ](p,q)|\mu \in {\Lambda }_0\},$$

$$W_1=\{w_1\left[\mu \right]\stackrel{\mathrm{def}}{=}\mu \underset{q\in Q}{min}\underset{p\in P}{max}{G}_1[\Phi ,\mu ](p,q)|\mu \in {\Lambda }_0\}.$$

We do not consider $\mu \in \Lambda \backslash {\Lambda }_0$ because the corresponding $v_1\left[\mu \right]$ and $w_1\left[\mu \right]$ do not belong to the feasible set $\Phi (P,Q)\stackrel{\mathrm{def}}{=}\{\Phi (p,q)|p\in P,q\in Q\}$ for certain. MC maxmin and MC minmax of Player 2’s vector loss $\Phi (p,q)$ are represented as

$$W_2=\{w_2\left[\mu \right]\stackrel{\mathrm{def}}{=}\mu \underset{p\in P}{max}\underset{q\in Q}{min}{G}_2[\Phi ,\mu ](p,q)|\mu \in {\Lambda }_0\},$$

$$V_2=\{v_2\left[\mu \right]\stackrel{\mathrm{def}}{=}\mu \underset{q\in Q}{min}\underset{p\in P}{max}{G}_2[\Phi ,\mu ](p,q)|\mu \in {\Lambda }_0\},$$

respectively. The following inequalities take place:

$$\forall \mu \in {\Lambda }_0{v}_1\left[\mu \right]\le w_1\left[\mu \right]\le z^0\left[\mu \right]\le w_2\left[\mu \right]\le v_2\left[\mu \right].$$

(11)

Indeed, it is well-known that maxmin is not greater than minmax for scalar functions [20,30], therefore $v_1\left[\mu \right]\le w_1\left[\mu \right]$ and $w_2\left[\mu \right]\le v_2\left[\mu \right]$. One can see that

$${\beta }_1\left[\mu \right]\stackrel{\mathrm{def}}{=}\underset{q\in Q}{min}\underset{p\in P}{max}{G}_1[\Phi ,\mu ](p,q)\le \underset{p\in P}{max}{G}_1[\Phi ,\mu ](p,q^{*}\left[\mu \right])=G_1[\Phi ,\mu ](p^{*}\left[\mu \right],q^{*}\left[\mu \right]),$$

i.e., $w_1\left[\mu \right]=\mu {\beta }_1\left[\mu \right]\le \mu G_1[\Phi ,\mu ](p^{*}\left[\mu \right],q^{*}\left[\mu \right])\le \Phi (p^{*}\left[\mu \right],q^{*}\left[\mu \right])$. The same reasoning leads to $z^0\left[\mu \right]\le w_2\left[\mu \right]$, so all the inequalities in (11) are proved. Inequalities (11) justify the possibility to interpret $Z^0$ (and $R^0$) as the set of compromise values (and outcomes) in the MC matrix game.

Notice that based on the approach by Refs. [24,38], we can consider the wider concept of MC game value with the same $R^0$. For (1), weakly efficient values of the vector function F can be represented as weakly efficient points of the Edgeworth–Pareto hull (eph) [13,19] of the function. For the considered settings, eph is defined as

$${eph}_{\le }\left(F\right)\stackrel{\mathrm{def}}{=}\{0\le \psi \le 11|\psi \le \underset{x\in X}{\mathrm{Max}}F\left(x\right)\}\mathrm{and}{eph}_{\ge }\left(F\right)\stackrel{\mathrm{def}}{=}\{0\le \psi \le 11|\psi \ge \underset{x\in X}{\mathrm{Min}}F\left(x\right)\}.$$

Then we obtain the following enveloping sets for MC maximum and minimum:

$$\overline{{\mathrm{Max}}_{x\in X}}F\left(x\right)\stackrel{\mathrm{def}}{=}\{{\psi }^0\in {eph}_{\le }\left(F\right)|\forall \psi \in {eph}_{\le }\left(F\right)\exists k:{\psi }_k\le {\psi }_k^0\},$$

(12)

$$\overline{{\mathrm{Min}}_{x\in X}}F\left(x\right)\stackrel{\mathrm{def}}{=}\{{\psi }^0\in {eph}_{\ge }\left(F\right)|\forall \psi \in {eph}_{\ge }\left(F\right)\exists k:{\psi }_k\ge {\psi }_k^0\}.$$

(13)

Some weakly efficient points may not belong to $F\left(X\right)$ (or $\Phi (P,Q)$ in our case), but they may serve as evaluations that make sense for compromise or when both players are faced with additional uncertainty. Here we do not focus on obviously unreal evaluations and limit ourselves with an intersection with $\Phi (P,Q)$.

Using the extended sets of evaluations (12), (13) instead of standard MC maximum and MC minimum and applying results from Refs. [24,38], we come to the following MC game value “in evaluations” for Player 1:

$$Z_1^{*}=\{z^{1*}\left[\mu \right]\stackrel{\mathrm{def}}{=}\mu G_1[\Phi ,\mu ](p^{*}\left[\mu \right],q^{*}\left[\mu \right])|(p^{*}\left[\mu \right],q^{*}\left[\mu \right])\mathrm{is}\mathrm{equilibrium}\mathrm{in}{\Gamma }_G\left(\mu \right),\mu \in {\Lambda }_0\}.$$

For Player 2 a similar set is

$$Z_2^{*}=\{z^{2*}\left[\mu \right]\stackrel{\mathrm{def}}{=}\mu G_2[\Phi ,\mu ](p^{*}\left[\mu \right],q^{*}\left[\mu \right])|(p^{*}\left[\mu \right],q^{*}\left[\mu \right])\mathrm{is}\mathrm{equilibrium}\mathrm{in}{\Gamma }_G\left(\mu \right),\mu \in {\Lambda }_0\}.$$

As it is proved in Proposition 3, the sets have common points for $\mu \in M^{*}$ and $Z^0\subseteq Z_1^{*}\bigcap Z_2^{*}$. For other $\mu$, only inequalities $z^{1*}\left[\mu \right]\le z^0\left[\mu \right]\le z^{2*}\left[\mu \right]$ are satisfied. Thus $Z_1^{*}\subseteq {eph}_{\le }\left(Z^0\right)$ and $Z_2^{*}\subseteq {eph}_{\ge }\left(Z^0\right)$, and consequently, $Z_1^{*}\bigcap Z_2^{*}\subseteq {eph}_{\le }\left(Z^0\right)\bigcap {eph}_{\ge }\left(Z^0\right)$. However, this inclusion does not imply the equality between $Z^0$ and $Z_1^{*}\bigcap Z_2^{*}$ because $Z^0$ is not convex. Nevertheless, let us emphasize once again that the MC equilibrium set $R^0$ is the same for both statements. The difference is in different evaluations for the same $(p^{*}\left[\mu \right],q^{*}\left[\mu \right])$. However, the players may prefer to use $Z_i^{*}$ instead of $Z^0$. For these sets, inequalities (11) are also fulfilled.

Vector functions $v_1,v_2,w_1,w_2$ are continuous because functions ${\beta }_1\left[\mu \right]$ and

$${\displaystyle \underset{p\in P}{max}\underset{q\in Q}{min}{G}_1[\Phi ,\mu ](p,q)}$$

are continuous in $\mu$ on ${\Lambda }_0$ (see [24]), and the same is satisfied for $G_2[\Phi ,\mu ](p,q)$: its maxmin and minmax are continuous in $\mu \in {\Lambda }_0$.

Further we investigate the continuity of $z^0\left[\mu \right]$ taking into account the possible plurality of equilibrium values in the scalar game ${\Gamma }_G\left(\mu \right)$. Denote the set of all equilibrium values for a given $\mu$ by

$$Z\left(\mu \right)\stackrel{\mathrm{def}}{=}\{z^0\left[\mu \right]=\Phi \left((p^0,q^0)\left[\mu \right]\right)|(p^0,q^0)\left[\mu \right]\mathrm{is}\mathrm{an}\mathrm{equilibrium}\mathrm{in}\mathrm{the}\mathrm{game}{\Gamma }_G\left(\mu \right)\}.$$

3.2. Geometric Presentation and Examples

Let us see what we can say about $M^{*}$ as a subset of ${\Lambda }_0$. According to definition of $M^{*}$, for any ${\mu }^0\in M^{*}$, there exists the equilibrium $(p^0,q^0)$ in the game ${\Gamma }_G\left({\mu }^0\right)$ so that it is related with ${\mu }^0$ via (6). Condition (6) means that $\Phi (p^0,q^0)$ belongs to the ray $\overline{0,{\mu }^0}$ in the criterion space (the plane $({\phi }_1,{\phi }_2)$ is similar to Figure 1). The ray goes from the origin in the direction of ${\mu }^0$ (see Figure 2 on the right for ${\mu }^0$ with ${\mu }_1^0=1/2,5/8$, 5/9, and 3/4 for the Example (14) below). It is obvious that if the ray $\overline{0,{\mu }^{\prime }}$, ${\mu }^{\prime }\in {\Lambda }_0$, does not intersect the feasible set $\Phi (P,Q)$, then (according to definition of $M^{*}$) ${\mu }^{\prime }\in {\Lambda }_0\backslash M^{*}$. However, the inverse statement is not true: there may be no equilibrium values on the ray $\overline{0,\mu }$ that intersects $\Phi (P,Q)$. In particular, if $R^0$ is a singleton that consists of the only pure strategy outcome, then this specific outcome is the equilibrium in the game ${\Gamma }_G\left(\mu \right)$ for all $\mu$ (whether the ray $\overline{0,\mu }$ intersects with the feasible set $\Phi (P,Q)$ or not). In this case, $M^{*}$ consists of the only one ${\mu }^0$ that corresponds to this outcome according to (6). The uniqueness of MC equilibrium is possible for singular MC case when all matrices $A_k$ of the game ${\Gamma }^0$ have the same pure strategy outcome as the saddle point (for example, equilibrium in dominant strategies [30]). The uniqueness of the equilibrium for all $\mu$ means its continuity in $\mu$.

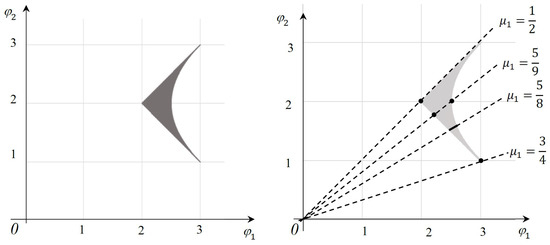
Figure 2. Game (14). Criterion space with the feasible set $\Phi (P,Q)$ (on the left) and the sets of equilibrium values (in bold) for scalar games ${\Gamma }_G\left(\mu \right)$, $\mu =1/2,5/8,5/9$, and $3/4$ (on the right).

More complicated situations are illustrated by the MC game with the following bimatrix payoff:

$$(A_1,A_2)=\left(\begin{array}{c}(3,3)(2,2)\\ (2,2)(3,1)\end{array}\right).$$

(14)

Applying mixed strategies we come to bilinear criteria of the payoff function $\Phi$ with

$${\phi }_1(p,q)=2p_1{q}_1-p_1-q_1+3,{\phi }_2(p,q)=p_1+q_1+1.$$

Here and further in two-criteria $2\times 2$ games we write only the first component of the strategy vector and of the parameter vector because the second components are defined uniquely. The feasible set $\Phi (P,Q)$ for (14) is shown in Figure 2 on the left in the criterion space, i.e., on the plane of partial criteria $({\phi }_1,{\phi }_2)$.

For $\mu =(1/2,1/2)$, the unique outcome $(p_1=1,q_1=0)$ is the equilibrium in the game ${\Gamma }_G(1/2,1/2)$. The corresponding equilibrium value is equal to (2, 2), i.e., $Z(1/2,1/2)=\left\{z^0\left[(1/2,1/2)\right]\right\}=\left\{(2,2)\right\}$. However, solving (9), we find the outcomes ($p_1=1$, $q_1\in [0,1]$) and ($p_1\in [0,1]$, $q_1=1$), and the corresponding values of $\Phi (p,q)$ form the segment connecting points (2, 2) and (3, 3) in the criterion space. This segment is the intersection of the ray $\overline{0,(1/2,1/2)}$ with the set $\Phi (P,Q)$, but the equilibrium is only (2, 2). There is no intersection of the ray $\overline{0,\mu }$ with $\Phi (P,Q)$ for ${\mu }_1<1/2$, and there is only the equilibrium $(p_1=1,q_1=0)$ for such $\mu$ in the game ${\Gamma }_G\left(\mu \right)$ for (14). It gives the MC equilibrium value (2, 2), i.e., $Z\left(\mu \right)=\left\{z^0\left[\mu \right]\right\}=\left\{(2,2)\right\}$$\forall \mu \le 1/2$ that is already found for $(1/2,1/2)\in M^{*}$.

Notice that there is no convergence of the values of $\Phi$ on the solutions of (9) for ${\mu }_1\to 1/2-0$, i.e., values $\Phi$ on the solutions of (9) are not continuous in $\mu$. All such $\mu$ (with ${\mu }_1<1/2$) do not belong to $M^{*}$, but they allow to find MC equilibrium for game (14) as the solution of the game ${\Gamma }_G\left(\mu \right)$. On the other hand, $\Phi$ for the solutions of (9) and the corresponding segments in the criterion space converge in Hausdorff metric to the mentioned segment (between (2, 2) and (3, 3)) for ${\mu }_1\to 1/2+0$. The equilibrium value in the scalar games ${\Gamma }_G\left(\mu \right)$ with (14) (see Figure 3 on the right) is unique for ${\mu }_1\in (1/2,5/9)$ and moves to south-east from $(2,2)$. For the equilibrium values, we obtain that $z^0\left[\mu \right]\to z^0\left[{\mu }^0\right]$ when $\mu \to {\mu }^0$ for ${\mu }_1^0\in (0,5/9)$, although it is not true for the values of $\Phi$ on the solutions of (9) for ${\mu }_1^0=1/2$.

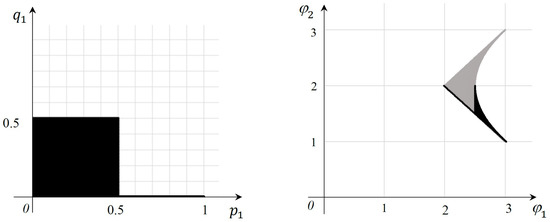
Figure 3. Game (14). The set of equilibrium outcomes $R^0$ in the plane of the first strategies’ components (on the left) and equilibrium values $Z^0$ (in bold) in the criterion space (on the right).

Continuity of $Z\left(\mu \right)$ in the Hausdorff metric is also correct for ${\mu }_1\in (5/9,3/4)$. There are two or more equilibria for ${\mu }_1\in [5/9,3/4)$ in the game ${\Gamma }_G\left(\mu \right)$ with (14) and the only one exists for $\mu$ with ${\mu }_1=3/4$. The set $M^{*}$ is composed of all $\mu$ with ${\mu }_1\in [1/2,3/4]$. Continuity of $Z\left(\mu \right)$ at ${\mu }_1=5/9$ is one-sided: $Z\left(\mu \right)$ converges in Hausdorff metric for ${\mu }_1\to 5/9+0$. This property is sufficient for approximating $Z^0$ in the game (14). The set of equilibrium values for the MC game with (14) is shown in bold in Figure 3 on the right. Further we solve the game in explicit form (see $R^0$ in Figure 3 on the left).

Notice that ${\phi }_1(p,q)$ and ${\phi }_2(p,q)$ (i.e., $G_2$) increase in $q_1$ for all $p_1>1/2$. Therefore, the only optimal response of Player 2 is $q_1=0$ for all $\mu \in {\Lambda }_0$. The best response strategy for Player 1 depends on $\mu$. It is easy to see that $(3-p_1)/{\mu }_1=(p_1+1)/(1-{\mu }_1)$, i.e., $p_1=3-4{\mu }_1$, and $1/2\le {\mu }_1<5/8$ because $p_1\in (1/2,1]$ Thus, the first part of $R^0$ for the game with (14) is the set of equilibria

$$R_1=\{(p,q)with(p_1=3-4{\mu }_1,q_1=0)|{\mu }_1\in [1/2,5/8)\}.$$

The corresponding values of $\Phi$ (with ${\phi }_1+{\phi }_2=4$) form the segment with the endpoints (2, 2) and (2.5, 1.5) (see Figure 3 on the right). For ${\mu }_1=1/2$, we have $p_1=1$ and the unique solution $(p,q)$ with $p_1=1$, $q_1=0$. The equilibrium value $z^0\left[(1/2,1/2)\right]$ coincides with the left angle point of $\Phi (P,Q)$ (see Figure 2). For ${\mu }_1=5/8$, the solution has $p_1=1/2$, $q_1=0$, but it is not unique as we will discuss. For intermediate value ${\mu }_1=5/9$, one can find the equilibrium with $p_1=7/9$, $q_1=0$.

If $q_1>1/2$, Player 1’s payoff function $G_1$ increases in $p_1$ for all $\mu \in {\Lambda }_0$, and the optimal strategy has $p_1=1$. However, the corresponding Player 2’s optimal response is $q_1=0$, which does not satisfy the considered case, hence there is no equilibrium. For $q_1=1/2$ we have $G_1=min\{2.5/{\mu }_1,(p_1+1.5)/(1-{\mu }_1)\}$. Any $p_1\le 1/2$ is suitable for ${\mu }_1\ge 5/9$ if it leads to $q_1=1/2$, and for other ${\mu }_1$ we have $p_1=1$ again. In particular, for ${\mu }_1=5/9$, we come to the second equilibrium with $p_1=q_1=1/2$. If $p_1=1/2$, we have $G_2=max\{2.5/{\mu }_1,(q_1+1.5)/(1-{\mu }_1)\}$, and the optimal response is $q_1=2.5/{\mu }_1-4$ for ${\mu }_1\in [1/2,5/9]$. Thus, we come to ${\mu }_1=5/9$. Notice that $\mu =(5/9,4/9)$ belongs to $M^{*}$ with both equilibrium outcomes differing in the sum of partial criteria equal to 4 and 4.5, respectively.

If $p_1<1/2$, one of the criterion of Player 2 increases and the other decreases in $q_1$. Therefore, we find the possible pair for $p_1<1/2$ from the equality of the weighted criteria, which gives

$$q_1=\frac{3-4{\mu }_1-p_1}{1-2p_1+2p_1{\mu }_1}.$$

(15)

Conditions $0\le q_1\le 1/2$ and $p_1\le 1/2$ imply ${\mu }_1\in [5/9,3/4)$. Hence, for ${\mu }_1\in [1/2,5/9)$, all equilibrium outcomes are in $R_1$. Similarly, for $q_1<1/2$, the optimal response for Player 2 is found from (15) in the form

$$p_1=\frac{3-4{\mu }_1-q_1}{1-2q_1+2q_1{\mu }_1},0\le p_1\le 1/2$$

with the same conditions for ${\mu }_1$. The set of equilibria of the game ${\Gamma }_G\left(\mu \right)$ can be obtained for all ${\mu }_1\in [5/9,3/4)$ as the set of solutions of the system

$$p\in \mathrm{Arg}\underset{p^{\prime }\in P}{max}{G}_1[\Phi ,\mu ](p^{\prime },q),q\in \mathrm{Arg}\underset{q^{\prime }\in Q}{min}{G}_2[\Phi ,\mu ](p,q^{\prime }).$$

(16)

For $0<p_1,q_1<1/2$, (16) is equivalent to an arbitrary of inclusions and therefore may have many solutions. In particular, for $p_1=q_1$, we find all the symmetric equilibria $(p,q)$ from (15): $p_1=q_1=x$ is a root of the quadratic equation $2(1-{\mu }_1)x^2-2x+3-4{\mu }_1=0$ under the condition $0\le x\le 1/2$. This parametric family of equilibria is denoted by $R_2$. The corresponding equilibrium values form a curved line in the criterion space (see Figure 3 on the right). Its upper point corresponds to the equilibrium $p_1=q_1=1/2$ found for ${\mu }_1=5/9$ in the above. The second equilibrium for ${\mu }_1=5/8$ is symmetric one. The unique equilibrium $p_1=q_1=0$ is for ${\mu }_1=3/4$ and for all ${\mu }_1>3/4$.

It follows from (15) that for each $\mu$ with $3/4>{\mu }_1\ge 5/8$, the equilibrium values form the whole segment, connecting an equilibrium value on the curved line $\Phi \left(R_2\right)$ for symmetric equilibria $R_2$ with a point on the line continuing $\Phi \left(R_1\right)$ on the bound of $\Phi (P,Q)$. The line corresponds to $q_1=0$. These segments are the values of $\Phi$ calculated for solutions of (9) for ${\mu }_1\in [5/8,3/4]$. For example, for ${\mu }_1=5/8$, (15) gives the family of outcomes such that $q_1=2(1-2p_1)/(4-3p_1),p_1=2(1-2q_1)/(4-3q_1)$. Here, $p_1$ varies from 1/2 to 0 for all $q_1\in [0,1/2]$, and both values satisfied the inequalities of the case under consideration. In particular, $q_1=4/13$ composes the equilibrium pair with $p_1=1/4$, and $p_1=4/13$ makes the equilibrium pair with $q_1=1/4$, and so on.

The set $Z\left(\mu \right)$ for ${\mu }_1\in (5/9,5/8)$ consists of not only points from $\Phi \left(R_1\right)$, but also from the segment adjoining to the curved line corresponding to the set of symmetrical equilibria $R_2$. The left end points of all such segments lie on the perpendicular, dropped from (2.5, 2) into (2.5, 1.5) inside $\Phi (P,Q)$ in the criterion space (see Figure 3 on the right). These points correspond to the solutions of (15) for $p_1=1/2$, $q_1=2.5/{\mu }_1-4$. The set of these equilibrium outcomes is denoted by $R_3$ (in $R_3$, $q_1$ varies from 1/2 to 0 when ${\mu }_1$ runs from 5/9 to 5/8). The remaining points of the segments of equilibrium values for ${\mu }_1\in (5/9,5/8)$ are obtained when $q_1$ varies from $2.5/{\mu }_1-4$ to 0 together with $p_1$ running from 0 to $(3-4{\mu }_1-q_1)/(1-2q_1+2q_1{\mu }_1)$.

Thus, we construct $R^0$ for the multicriteria game (14). The whole set is shown in Figure 3 on the left ($p_1$ is abscissa and $q_1$ is ordinate), its part $R_1$ corresponds to the horizontal segment, the part $R_2$ is the diagonal of the shaded square, and $R_3$ is its right side. The segment $R_1$ gives south-west bound of the feasible set $\Phi (P,Q)$ and $R_2$ provides the lower part of its east bound. On the curved line $\Phi \left(R_2\right)$, the value ${\phi }_1+{\phi }_2=2x^2+4$ decreases from 4.5 to 4 when $x=p_1=q_1$ decreases from 1/2 to 0, i.e., when ${\mu }_1$ increases from 5/9 to 3/4. The sum ${\phi }_1+{\phi }_2$ also decreases from 4.5 to 4 on the vertical segment $\Phi \left(R_3\right)$ in the criterion space, but this segment is interior for the feasible set (although $R_3$ is on the bound of $R^0$). Figure 2 and Figure 3 demonstrate nontriviality of the form of the set of equilibrium values even in a very simple MC game (14), for which multicriteriality is significant for only one outcome in pure strategies.

Another interesting example is the complete multicriteria matrix game with

$$(A_1,A_2)=\left(\begin{array}{c}(2,5)(5,2)\\ (3,1)(1,3)\end{array}\right)$$

(17)

(see Figure 4 and Figure 5). The feasible set $\Phi (P,Q)$ for (17) is shown in Figure 4 on the left. The equilibrium values $Z(1/3,2/3)$, $Z(3/4,1/4)$, and $Z(1/2,1/2)$ of the corresponding scalar games ${\Gamma }_G\left(\mu \right)$ are presented in Figure 4 on the right. The set $Z^0$ is given in Figure 5 on the right. The set of solutions $R^0$ is shown in Figure 5 on the left on the coordinate plane $(p_1,q_1)$. There are a lot of equilibrium values in this game, but $Z^0\ne \Phi (P,Q)$ (in contrast to the example from Ref. [41]). We also notice that $R^0$ is asymmetrical (it does not include the interval (0.2, 0.8) of the ordinate axis), despite the symmetry in bimatrix (17). We can see that $Z\left(\mu \right)$ is continuous in $\mu$ although the sets of equilibrium values are nonconvex (disconnected) for the scalar games ${\Gamma }_G\left(\mu \right)$. Continuity means that GS may be used for approximating the set of MC equilibrium values. It should be emphasized that (14) and (17) are rather representative examples of two-person two criteria MC games $2\times 2$ (in Ref. [8], they are called envelope and butterfly, respectively).

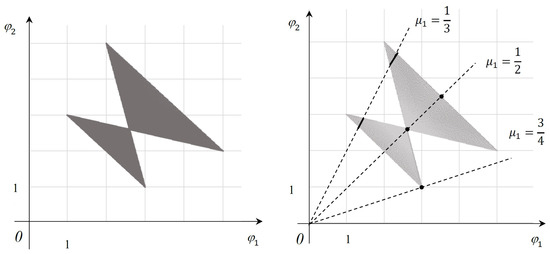
Figure 4. Game (17). The feasible set (on the left) and the sets of equilibrium values (in bold) for some scalar games ${\Gamma }_G\left(\mu \right)$ (on the right).

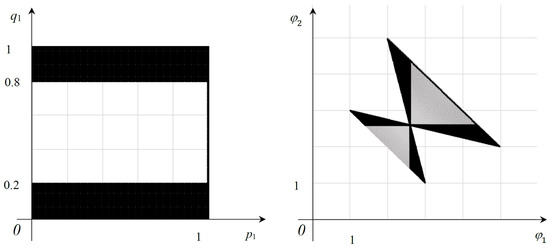
Figure 5. Game (17). The set of equilibrium outcomes (on the left) and the set of equilibrium values (on the right).

As it is known, the set of Nash equilibria of an arbitrary scalar game is not necessarily continuous in its parameters in general case [30,44]. Unfortunately, the set $Z\left(\mu \right)$ of equilibrium values of the game ${\Gamma }_G\left(\mu \right)$ is not necessarily continuous in $\mu$ in our (particular) case, as the example of game (14) shows for ${\mu }_1\to 5/9-0$. However, one-sided continuity of $Z(·)$ is satisfied for this game. Thus, the specificity of the MC matrix game gives the hope that it is possible to use GS for approximating the set $Z^0$ of equilibrium values of the MC game without continuity of $Z\left(\mu \right)$ in $\mu$.

4. Approximating the Set of Equilibrium Values Using GS

We suggest the following idea of approximation for $M^{*}$ and the set of equilibrium values. Let $M^{ϵ}$ be a finite $ϵ$-net on ${\Lambda }_0$ consisting of the points ${\mu }^t$, $t=1\dots T$, such that $\forall \mu \in {\Lambda }_0\exists t$: $\parallel {\mu }^t-\mu \parallel \le ϵ$. Here and further $\parallel ·\parallel$ denotes $L_{\infty }$ norm in $\mathrm{I}{\mathrm{R}}^K$ (i.e., the maximum absolute of a vector components) and ${\parallel ·\parallel }_1$ denotes $L_1$ norm in $\mathrm{I}{\mathrm{R}}^K$, i.e., ${\displaystyle \parallel z\parallel \stackrel{\mathrm{def}}{=}\underset{k}{max}|z_k|}$, ${\parallel z\parallel }_1\stackrel{\mathrm{def}}{=}{\sum }_k|z_k|$. At first, we include all vectors determined in Proposition 4 into $M^{ϵ}$. Elements of the $ϵ$-net between these vectors and between the vectors and bound vectors of ${\Lambda }_0$ may be chosen uniformly component-wise under the condition ${\parallel \mu \parallel }_1=1$. Let $Z^{\delta }\left({\mu }^t\right)$ denote a $\delta$-net on $Z\left({\mu }^t\right)$ for each $t=1\dots T$. Find a solution $(p^t,q^t)$ of the game ${\Gamma }_G\left({\mu }^t\right)$ and let $\Phi (p^t,q^t)\in Z^{\delta }\left({\mu }^t\right)$. If $G_1[\Phi ,{\mu }^t](p^t,q^t)=G_2[\Phi ,{\mu }^t](p^t,q^t)$, then ${\mu }^t\in M^{*}$ and turn to the next point from $Z^{\delta }\left({\mu }^t\right)$. If the equality is not satisfied, then find such indices k for which ${\phi }_k(p^t,q^t)/{\mu }_k^t>G_1[\Phi ,{\mu }^t](p^t,q^t)$ and/or ${\phi }_k(p^t,q^t)/{\mu }_k^t<G_2[\Phi ,{\mu }^t](p^t,q^t)$. After all points from $Z^{\delta }\left({\mu }^t\right)$ are analyzed, we turn to the neighboring point from $M^{ϵ}$ nearest to ${\mu }^t$ on the component k.

Consider the case $K=2$ in detail. Here, if ${\displaystyle \frac{{\phi }_1(p^t,q^t)}{{\mu }_1^t}>G_1[\Phi ,{\mu }^t](p^t,q^t)}$, then

$$\frac{{\phi }_2(p^t,q^t)}{{\mu }_2^t}=G_1[\Phi ,{\mu }^t](p^t,q^t)$$

and

$$G_2[\Phi ,{\mu }^t](p^t,q^t)=\frac{{\phi }_1(p^t,q^t)}{{\mu }_1^t}>\frac{{\phi }_2(p^t,q^t)}{{\mu }_2^t}.$$

Consequently, for rather small $\epsilon >0$ such that ${\displaystyle \frac{{\phi }_1(p^t,q^t)}{{\mu }_1^t+\epsilon }>\frac{{\phi }_2(p^t,q^t)}{{\mu }_2^t-\epsilon },}$ we still have

$$\frac{{\phi }_1(p^t,q^t)}{{\mu }_1^{\prime }}>G_1[\Phi ,{\mu }^{\prime }](p^t,q^t),\frac{{\phi }_2(p^t,q^t)}{{\mu }_2^{\prime }}=G_1[\Phi ,{\mu }^{\prime }](p^t,q^t)$$

for ${\mu }_1^{\prime }\stackrel{\mathrm{def}}{=}{\mu }_1^t+\epsilon$. Hence, $p^t$, which maximizes $G_1[\Phi ,{\mu }^t](p,q^t)$, also maximizes ${\phi }_2(p,q^t)$ and $G_1[\Phi ,{\mu }^{\prime }](p,q^t)$. Similarly, $q^t$, which minimizes $G_2[\Phi ,{\mu }^t](p^t,q)$, also minimizes ${\phi }_1(p^t,q)$ and $G_2[\Phi ,{\mu }^{\prime }](p^t,q)$, as for ${\mu }^t$. Thus, $(p^t,q^t)$ is still a solution of the new game ${\Gamma }_G\left({\mu }^{\prime }\right)$. The values of $G_1$ and $G_2$ change for this solution at the new point ${\mu }^{\prime }$, moreover $G_1$ increases and $G_2$ decreases, tending to the equality for $\mu \in M^{*}.$ The equilibrium value is $z^0\left[{\mu }^{\prime }\right]=z^0\left[{\mu }^t\right]=\Phi (p^t,q^t)$. If ${\displaystyle \frac{{\phi }_1(p^t,q^t)}{{\mu }_1^t}<\frac{{\phi }_2(p^t,q^t)}{{\mu }_2^t}}$, then let ${\mu }_1^{\prime }\stackrel{\mathrm{def}}{=}{\mu }_1^t-\epsilon$. We may run by the points from $M^{ϵ}$ for $ϵ<\epsilon$. Notice that inequality between components of GS remains for $\epsilon <0$, and the difference between new values of $G_1$ and $G_2$ increases after the recalculation. Therefore, if $\epsilon <0$ is used for choosing a new point ${\mu }^{t^{\prime }}\in M^{ϵ}$, then the obtained ${\mu }^{t^{\prime }}$ does not belong to $M^{*}$ for $(p^t,q^t)$ and there is no sense to consider this point. The relation between partial criteria may be changed for other equilibrium outcomes of the game ${\Gamma }_G\left({\mu }^t\right)$.

For an arbitrary K, ${\mu }^{t^{\prime }}$ is also obtained from ${\mu }^t$ in such a way that kth component for which

$$\frac{{\phi }_k(p^t,q^t)}{{\mu }_k^t}=G_2[\Phi ,{\mu }^t](p^t,q^t)>G_1[\Phi ,{\mu }^t](p^t,q^t)$$

increases, and ${\mu }_l^t$, for which ${\displaystyle \frac{{\phi }_l(p^t,q^t)}{{\mu }_l^t}=G_1[\Phi ,{\mu }^t](p^t,q^t)<G_2[\Phi ,{\mu }^t](p^t,q^t)}$, decreases. If the component which realizes $G_i$ changes, then we possibly obtain a new MC equilibrium. For $G_1[\Phi ,{\mu }^t](p^t,q^t)=G_2[\Phi ,{\mu }^t](p^t,q^t)$ (i.e., for ${\mu }^t\in M^{*}$), we fix the equilibrium outcome $(p^t,q^t)$ and consider the next one until the approximation $Z^{\delta }\left({\mu }^t\right)$ of the equilibrium values set $Z\left({\mu }^t\right)$ of the game ${\Gamma }_G\left({\mu }^t\right)$ is constructed. Then we turn to any of the neighboring ${\mu }^{t^{\prime }}$ in $M^{ϵ}$ not chosen previously. If the equality of $G_1$ and $G_2$ is not satisfied for several considered equilibrium outcomes of ${\Gamma }_G\left({\mu }^t\right)$, then ${\mu }^{t^{\prime }}$ may be chosen for any of them. Thus, turning from ${\mu }^t$ to ${\mu }^{t^{\prime }}$ and calculating the equilibria $(p^t,q^t)$ of the scalar game ${\Gamma }_G\left({\mu }^t\right)$ that form $Z^{\delta }\left({\mu }^t\right)$, we obtain the representative set of equilibrium values of the MC game ${\Gamma }^0$. Further, we investigate when these values make a $\delta$-net on the set $Z^0$, i.e., we justify the possibility of approximation theoretically.

Let $R\left(\mu \right)$ be the set of equilibria in the game ${\Gamma }_G\left(\mu \right)$. In addition, we denote an outcome $(p,q)$ by r for brevity. Consider an arbitrary vector $\mu \in {\Lambda }_0$ and define the function

$$f(x,y)\left[\mu \right]\stackrel{\mathrm{def}}{=}{G}_1[\Phi ,\mu ](x_1,y_2)-G_1[\Phi ,\mu ]\left(y\right)-G_2[\Phi ,\mu ](y_1,x_2)+G_2[\Phi ,\mu ]\left(y\right),x,y\in P\times Q.$$

Then

$$R\left(\mu \right)=\mathrm{Arg}\underset{y\in P\times Q}{min}\{\underset{x\in P\times Q}{max}f(x,y)\left[\mu \right]\}.$$

(18)

Indeed, according to the proof [30] of Nash theorem on existence of the equilibrium,

$$R\left(\mu \right)=\bigcap _{x\in P\times Q}\{y\in P\times Q|f(x,y)\left[\mu \right]\le 0\}.$$

Consequently, $\forall r\in R\left(\mu \right)$

$$g(r,\mu )\stackrel{\mathrm{def}}{=}\underset{x\in P\times Q}{max}f(x,r)\left[\mu \right]\le 0.$$

Since $f(r,r)\left[\mu \right]=0$, then this maximum is equal to 0 (for the equilibrium outcomes). Hence

$$R\left(\mu \right)=\{r\in P\times Q|\underset{x\in P\times Q}{max}f(x,r)\left[\mu \right]=0\},$$

and we come to (18). Now we prove the following lemma.

Lemma 1. 

The set of equilibrium outcomes $R\left(\mu \right)$ in the game ${\Gamma }_G\left(\mu \right)$ is upper semicontinuous on ${\Lambda }_0$ in the Hausdorff metric.

Proof. 

The function $f(x,r)\left[\mu \right]$ is continuous in both variables simultaneously. The function $g(r,\mu )$ is continuous in r and $\mu$ simultaneously (see, for example, in Ref. [28]). The set $R\left(\mu \right)$ is not empty for all $\mu \in {\Lambda }_0$. Representation

$$R\left(\mu \right)=\{r\in P\times Q|min\left\{g\right(r,\mu ),0\}\ge 0\}$$

allows to prove upper semicontinuity of the mapping $R\left(\mu \right)$ on ${\Lambda }_0$ (strict proof also may be found in Ref. [28]). □

We may directly prove that $R\left(\mu \right)$ is upper semicontinuous since it is closed (because $g(r,\mu )$ is continuous). Besides, we notice that closeness of $R\left(\mu \right)$ and continuity of $\Phi$ imply closeness of $Z\left(\mu \right)$, i.e., the latter mapping is also upper semicontinuous on ${\Lambda }_0$. We come to the following property.

Property 1. 

Let ${\mu }^0\in M^{*}$ be an isolated point on $M^{*}$ (i.e., there are no points from $M^{*}$ in the sufficiently small neighborhood in ${\Lambda }_0$), corresponding to MC equilibrium $(p^0,q^0)$ according to (6). If there is only the equilibrium in the game ${\Gamma }_G\left({\mu }^0\right)$, then for all ${\mu }^t\to {\mu }^0$, starting from some t, we have $(p^t,q^t)=(p^0,q^0)$ for any solution $(p^t,q^t)$ of the game ${\Gamma }_G\left({\mu }^t\right)$.

Proof. 

Assuming the contrary, we obtain by Lemma 1 the sequence of equilibria $\left\{(p^{t_s},q^{t_s})\right\}$ of the game ${\Gamma }_G\left({\mu }^{t_s}\right)$. This is the sequence of MC equilibria for which $(p^{t_s},q^{t_s})\to (p^0,q^0)$ and $(p^{t_s},q^{t_s})\ne (p^0,q^0)$. However, this contradicts the isolation of ${\mu }^0$. Indeed, $\Phi (p^{t_s},q^{t_s})\to \Phi (p^0,q^0)$, and ${\mu }^{*t_s}\to {\mu }^0$ for ${\mu }^{*t_s}$ corresponding to $(p^{t_s},q^{t_s})$ according to (6). If ${\mu }^{*t_s}={\mu }^0$, then $(p^{t_s},q^{t_s})\in R\left({\mu }^{*t_s}\right)=R\left({\mu }^0\right)$. We come to contradiction with the uniqueness of $(p^0,q^0)$ in the game ${\Gamma }_G\left({\mu }^0\right)$. Otherwise ${\mu }^0$ is not isolated. □

The isolated MC equilibrium can be found with the use of points from $M^{ϵ}$. Similarly, based on Lemma 1, we prove that points from $M^{ϵ}$ allow us to find an approximation of the outcome that gives the unique equilibrium value for some ${\Gamma }_G\left({\mu }^0\right)$.

Property 2. 

If the set $Z\left({\mu }^0\right)$ consists of the only point $z^0\left[{\mu }^0\right]$ for ${\mu }^0\in M^{*}$, then for all ${\mu }^t\to {\mu }^{0}Z\left({\mu }^t\right)\to \left\{z^0\left[{\mu }^0\right]\right\}$ in the Hausdorff metric.

Proof. 

According to Lemma 1, any convergent sub-sequence of equilibrium outcomes $\left\{(p^{t_s},q^{t_s})\right\}$ of the games ${\Gamma }_G\left({\mu }^{t_s}\right)$, which are MC equilibria, has a MC equilibrium as a limit. This MC equilibrium belongs to $Z\left({\mu }^0\right)$. The uniqueness of such a value leads to the statement of the property. □

In particular, there exists $z^0\left[{\mu }^{t_s}\right]=z^0\left[{\mu }^0\right]$ for ${\mu }^{t_s}\notin M^{*}$. This solves the problem of approximating partially isolated (from one side for $K=2$) equilibrium values $z^0$ in the case of the unique equilibrium for a game ${\Gamma }_G\left({\mu }^0\right)$.

The case of nonunique equilibria is more complicated. Lemma 1 only allows to state that

$$R\left({\mu }^t\right)\to R^{\prime }\subseteq R\left({\mu }^{\prime }\right)\forall {\mu }^t\to {\mu }^{\prime },$$

and the inclusion may be strict. Below we show for $K=2$ case that strict inclusion is fulfilled not for all variants of approaching ${\mu }^t$ to ${\mu }^{\prime }$. For a general MC matrix game, we notice the following.

For $\delta \ge 10Kϵ$, there exists $\delta$-approximation (constructed with the help of GS) on $ϵ$-net in ${\Lambda }_0$ for the equilibrium values ${\Phi }^{*}$ that belongs to $Z^0$ with their $\delta$-neighborhood (in $\parallel ·\parallel$ norm) in the criterion space. Indeed, consider ${\displaystyle {\mu }^{*}\stackrel{\mathrm{def}}{=}\frac{{\Phi }^{*}}{\parallel {\Phi }^{*}{\parallel }_1}}$ and $\mu \in M^{ϵ}$, which is the nearest to ${\mu }^{*}$ in the norm $\parallel ·\parallel$. We have $\mu ={\mu }^{*}+h$, ${\displaystyle \sum _{k=1}^K{h}_k=0}$, $\parallel h\parallel \le ϵ$ according to the construction of $M^{ϵ}$. Then for $h^{*}\stackrel{\mathrm{def}}{=}h{\parallel {\Phi }^{*}\parallel }_1$

$$\mu =\frac{{\Phi }^{*}+h{\parallel {\Phi }^{*}\parallel }_1}{\parallel {\Phi }^{*}{\parallel }_1}=\frac{{\Phi }^{*}+h^{*}}{{\displaystyle \sum _{k=1}^K}({\phi }_k^{*}+h_k\parallel {\Phi }^{*}{\parallel }_1)}=\frac{{\Phi }^{*}+h^{*}}{{\displaystyle \sum _{k=1}^K}({\phi }_k^{*}+h_k^{*})}.$$

(19)

The denominator of the last fraction in (19) is equal to $\parallel {\Phi }^{*}+h^{*}{\parallel }_1$ because components of h are small. Since $\parallel h^{*}\parallel \le 10Kϵ$ under the assumption of the initial problem, then for $ϵ\le \delta /\left(10K\right)$ we have ${\Phi }^{*}+h^{*}\in Z^0$. With (19) and (7), this leads to ${\Phi }^{*}+h^{*}\in Z\left(\mu \right)$.

The performed reasoning may be generalized to the case of the one-sided $\delta$-neighborhood of ${\Phi }^{*}$ in $Z^0$, because there are at least two points from $M^{ϵ}$ in the neighborhood of ${\mu }^{*}$, which is not situated on the bound of ${\Lambda }_0$.

Consider the case $K=2$.

Property 3. 

If for $z^0\in Z^{*}\left({\mu }^0\right)\subset Z^0$ there exists such ${\Delta }^0>0$ that for all $\Delta \in (0,{\Delta }^0]$$z(\Delta )\stackrel{\mathrm{def}}{=}(z_1^0+\Delta ,z_2^0-\Delta )\in Z^0$, then for ${\mu }_1\to {\mu }_1^0+0$ there exists $z\left[\mu \right]\in Z\left(\mu \right)$ such that $z\left[\mu \right]\to z^0$. Similarly for ${\Delta }^0$, $\Delta <0$ when ${\mu }_1\to {\mu }_1^0-0$.

Here and further $Z^{*}\left({\mu }^0\right)$ denotes the subset of the set of equilibrium values $Z\left({\mu }^0\right)$, connected with the given ${\mu }^0$ according to (6). The upper index 0 is omitted for equilibrium values if it does not lead to misunderstanding.

Proof. 

It is obvious for $\Delta =({\mu }_1-{\mu }_1^0){\parallel z^0\parallel }_1$ and $z\left[\mu \right]=z(\Delta )$. (Since ${\displaystyle {\mu }^0=\frac{z^0}{\parallel z^0{\parallel }_1}}$, then ${\displaystyle \mu =\frac{(z_1^0+\Delta ,z_2^0-\Delta )}{\parallel z^0{\parallel }_1}=\frac{z(\Delta )}{{\parallel z(\Delta )\parallel }_1}}$, i.e., $z(\Delta )\in Z^{*}\left(\mu \right)$.) □

For two criteria case, Property 3 may also be generalized in the following way.

Property 4. 

For $K=2$, if for $z^0\in Z^{*}\left({\mu }^0\right)$ there exists ${\Delta }^0>0$ such that for all $\Delta \in (0,{\Delta }^0]$ there exists $z^{\Delta }\in Z^0$ such that $z^{\Delta }\ne z^0,\parallel z^{\Delta }-z^0\parallel <\Delta$, then there exist $\{\mu \in {\Lambda }_0\}$ and $z\left[\mu \right]\in Z\left(\mu \right)$ such that $z\left[\mu \right]\to z^0$ for ${\mu }_1\to {\mu }_1^0$.

Proof. 

Choose ${\displaystyle {\mu }^{\Delta }=\frac{z^{\Delta }}{\parallel z^{\Delta }{\parallel }_1}}$, then for ${\displaystyle {\mu }^0=\frac{z^0}{\parallel z^0{\parallel }_1}}$ we obtain ${\mu }^{\Delta }\to {\mu }^0$ for $\Delta \to 0$, because $z^{\Delta }\to z^0,\Delta \to 0$. If ${\mu }^{\Delta }={\mu }^0$, then $z^{\Delta }\in Z^{*}\left({\mu }^0\right)$. If ${\mu }^{\Delta }\ne {\mu }^0,\Delta \to 0$, then ${\mu }_1^{\Delta }\ne {\mu }_1^0,{\mu }_1^{\Delta }\to {\mu }_1^0,\Delta \to 0$. □

Lemma 2. 

In $K=2$ case, if for $z^0\in Z^0$ there exists ${\Delta }^0>0$ such that for all $\Delta \in [0,{\Delta }^0]$ there exists $z^0(\Delta )\in Z^0$ such that the function $z^0(\Delta )$ is continuous on $[0,{\Delta }^0]$, $z^0\left(0\right)=z^0$, $z^0(\Delta )\ne z^0$ for all $\Delta \in (0,{\Delta }^0]$, then for any $\epsilon >0$ there exist $ϵ>0$, $\mu \in M^{ϵ}$, and $z\left[\mu \right]\in Z\left(\mu \right)$ such that $\parallel z\left[\mu \right]-z^0\parallel <\epsilon$.

Proof. 

Choosing ${\displaystyle {\mu }^{\Delta }=\frac{z^0(\Delta )}{\parallel z^0{(\Delta )\parallel }_1}}$ and ${\displaystyle {\mu }^0=\frac{z^0}{\parallel z^0{\parallel }_1}}$, we come to ${\mu }^{\Delta }\to {\mu }^0$ for $\Delta \to 0$, and ${\mu }^{\Delta }$ is continuous on $[0,{\Delta }^0]$ as the function of $\Delta$. If ${\mu }^{\Delta }\ne {\mu }^0,\Delta \to 0$, then ${\mu }_1^{\Delta }\ne {\mu }_1^0$, ${\mu }_1^{\Delta }\to {\mu }_1^0$, $\Delta \to 0$, and the statement of the Lemma follows from continuity of ${\mu }_1^{\Delta }$. Assume that all different values of $z^0(\Delta )$ form the segment on the ray $\overline{0,{\mu }^0}$ in the criterion space (i.e., ${\mu }^{\Delta }={\mu }^0$$\forall \Delta \in (0,{\Delta }^0]$), and there is no other sequence $z^0(\Delta )\to z^0$. However, such a situation is impossible (see Appendix A for proof). □

Notice that Proof of Lemma 2 (see Appendix A) considers all the possible variants of the equilibrium outcomes $r^0$ and the corresponding values $z^0$ independently of the presence of other equilibria in the neighborhood of $z^0$. In particular, there may be only two equilibrium values on the ray $\overline{0,{\mu }^0}$, as it is in the game (14) for ${\mu }_1^0=5/9$. Existence of $r\left[\mu \right]\in R\left(\mu \right)$ and $z\left[\mu \right]\in Z\left(\mu \right)$ such that $r\left[\mu \right]\to r^0$ and $z\left[\mu \right]\to z^0=\Phi \left(r^0\right)\in Z^{*}\left({\mu }^0\right)$ for all $\mu \ne {\mu }^0$ in the neighborhood of ${\mu }^0$, for which ${\mu }_1\to {\mu }_1^0$ from the left or from the right, is proved for all $r^0\in R^0$, $z^0\in Z^0$ in the two criteria $2\times 2$ games. Therefore, the Proof of Lemma 2 directly leads to

Proposition 5. 

For $K=n=m=2$, for all $r^0\in R^0$, $z^0\in Z^0$ there exists ${\epsilon }^0>0$ such that for any $\epsilon >0$, $\epsilon <{\epsilon }^0$ there exist $ϵ>0$, $\mu \in M^{ϵ}$, $r\left[\mu \right]\in R\left(\mu \right)$, $z\left[\mu \right]\in Z\left(\mu \right)$ such that $\parallel r\left[\mu \right]-r^0\parallel <\epsilon$ and $\parallel z\left[\mu \right]-z^0\parallel <\epsilon$.

In addition, it may be noticed from Appendix A that there exists an equilibrium outcome in the neighborhood of a pure strategy equilibrium or equilibrium with a pure strategy of one of the players with one strategy remaining unchanged (for two criteria $2\times 2$ games).

It follows from Proposition 5 that the mappings $R\left(\mu \right)$ and $Z^{*}\left(\mu \right)$ are one-sided lower semicontinuous on ${\Lambda }_0$ at points $\mu \in M^{*}$. The set ${\Lambda }_0$ is compact, and this leads to uniform one-sided lower semicontinuity for the considered mappings, and, as a sequence, to their uniform one-sided (from the left or from the right) continuity due to Lemma 1. Thus, we prove the possibility of approximating the set of equilibrium values for the simplest case of MC zero-sum game.

Proposition 6. 

For $K=n=m=2$, there exists ${\epsilon }^0>0$ such that for any $\epsilon >0$, $\epsilon <{\epsilon }^0$ there exists such that $ϵ>0$ for all $z^0\in Z^0$ there exist $\mu \in M^{ϵ}$, $z\left[\mu \right]\in Z\left(\mu \right)$ such that $\parallel z\left[\mu \right]-z^0\parallel <\epsilon$.

Proposition 7. 

For $K=n=m=2$, there exists ${\epsilon }^0>0$ such that for any $\epsilon >0$, $\epsilon <{\epsilon }^0$ there exists $ϵ>0$ such that for all $r^0\in R^0$ there exist $\mu \in M^{ϵ}$, $r\left[\mu \right]\in R\left(\mu \right)$ such that $\parallel r\left[\mu \right]-r^0\parallel <\epsilon$.

Corollary 1. 

For $K=n=m=2$, the sets $\{r\in R\left(\mu \right)|\mu \in M^{ϵ}\}$ and $\{z\in Z\left(\mu \right)|\mu \in M^{ϵ}\}$ converge in Hausdorff metric to $R^0$ and $Z^0$, respectively, for $ϵ\to 0$, where $M^{ϵ}$ is ϵ-net on the set ${\Lambda }_0$.

We do not generalize the obtained results for arbitrary $K,n,m>2$ in this paper. Our main aim is to show the principal possibility of GS being used for approximating the solution of a MC game. Even for the considered simplest case of a two-criteria $2\times 2$ game, the equilibrium set and the set of equilibrium values of the game have nontrivial forms (see Figure 3 and Figure 5). In particular, the set $Z^0$ on Figure 3 is not only nonconvex but also contains curved parts. However, $Z^0$ may be considered as a set of compromises in the MC zero-sum game, and therefore it is important to not miss the equilibrium outcomes acceptable for both players even when they correspond to the isolated equilibrium value. We prove that GS helps to do this.

A lot of papers are devoted to the problem of finding the equilibrium in scalar games (parametric games ${\Gamma }_G\left(\mu \right)$ and ${\Gamma }_S(\lambda ,\gamma )$ are scalar for the fixed values of parameters), in particular [45,46,47,48]. Therefore, we do not pay attention to the problem as well as to the numerical methods of finding optimum (see Refs. [49,50] for review).

5. Discussion

The sets $R^0$ and $Z^0$ are represented with the aid of parametric families of the sets of equilibrium outcomes and values of scalar games. However, these sets are not continuous in scalarizing parameters. In Ref. [44], the author suggests to extend the set of equilibrium outcomes and considers the approximate (not exact) equilibria. Continuity in the Hausdorff metric of the set of approximate equilibria in parameters is proved in Ref. [44]. This fact allows us to construct the corresponding approximation for $R^0$ and $Z^0$. After that the $ϵ$-net (finite approximation) of the set of approximate equilibria may be applied, as we suggested in the above. However, the question is whether the approximation of the approximate equilibrium is exact equilibrium.

The papers [36,37] suggest another definition of the set of equilibrium values in MC matrix games in mixed strategies. It is justified from the point of decision-making that averaging over the partner’s mixed strategy may be done, not before, but after scalarization (a similar setting is considered in Ref. [17]). In this case, LS and GS lead to different sets of MC game value. Moreover, LS gives the standard set $Z^0$, and GS lets us construct a wider set of evaluations of equilibria values for Players 1 and 2 in the forms

$$\{\mu {\overline{G}}_1^{*}\left(\mu \right)|\mu \in {\Lambda }_0\}and\{\mu {\overline{G}}_2^{*}\left(\mu \right)|\mu \in {\Lambda }_0\}.$$

Here $G_1^{*}\left(\mu \right)$ and $G_2^{*}\left(\mu \right)$ are equilibrium values for the parametric family of scalar games

$$\{⟨P,Q,{\overline{G}}_1\left[\mu \right](p,q),-{\overline{G}}_2\left[\mu \right](p,q)⟩|\mu \in {\Lambda }_0\}.$$

(20)

According to Ref. [37],

$${\displaystyle {\overline{G}}_1\left[\mu \right](p,q)\stackrel{\mathrm{def}}{=}\sum _{j=1}^m\underset{k\in I\left(\mu \right)}{min}\frac{{\phi }_k(p,q^j)}{{\mu }_k},{\overline{G}}_2\left[\mu \right](p,q)\stackrel{\mathrm{def}}{=}\sum _{i=1}^n\underset{k\in I\left(\mu \right)}{max}\frac{{\phi }_k(p^i,q)}{{\mu }_k},}$$

where $p_i^i=1$, $q_j^j=1$. The possibility of finite approximation for the introduced sets is not studied yet.

Approximation properties for the sets $V_l$ and $W_l$, $l=1,2$ from Section 3.1 are proved in Refs. [24,26]. The possibility of approximating $Z_l^{*}$ (based on its parametrization with GS) is proved in the present paper for the same cases as $Z^0$, in particular, for two criteria $2\times 2$ games. The proof follows from the uniform continuity of $G_l$ in $r\in P\times Q$, $\mu \in {\Lambda }_0$ and from Proposition 7 about finite approximation of $R^0$ with solutions $r^{*}\left[\mu \right]\in R\left(\mu \right)$ of scalar games ${\Gamma }_G\left(\mu \right)$ (which are used for defining $Z_l^{*}$, $l=1,2$), if for small enough $ϵ$, we limit ourselves with $\mu \in M^{ϵ}$.

The set $Z^0$ that was introduced by Shapley is the widest of the concepts of MC game equilibrium values, except what we obtain for (20). Therefore, this set is not empty. For Pareto efficient MC maximum and minimum, conditions for nonemptiness of the MC game solutions and values are represented in Ref. [51]. Such solutions are called strong equilibria. In addition, the authors of Ref. [51] find the conditions for stability of the set of strong equilibria with respect of the perturbation of MC game parameters. We plan to investigate the stability of GS-based parametrization of $Z^0$ in our future research.

6. Conclusions

In this paper, we prove some properties of the Germeier’s scalarization, which is applied for parametrizing the sets of equilibrium outcomes and equilibrium values of MC matrix games. In particular, we find a one-parametric family of scalar two-person games to represent MC game equilibria. We obtain the inequalities between parameterized values of MC game, MC maxmin, and MC minmax, which allow us to interpret the equilibrium value as a set of compromises in a zero-sum MC game. Thus, we are interested in a finite approximation of the set (to assist the players to come to an agreement). However, examples in Section 3 demonstrate that the approximation problem is not trivial (see also examples in Refs. [8,9]). Despite this, we prove the possibility of approximating the sets of equilibrium values and equilibrium outcomes with GS in the case of two criteria matrix game $2\times 2$. We hope that the obtained results encourage researchers to further study GS and its application to MC problems.