An Accelerated Convex Optimization Algorithm with Line Search and Applications in Machine Learning

Abstract

In this paper, we introduce a new line search technique, then employ it to construct a novel accelerated forward–backward algorithm for solving convex minimization problems of the form of the summation of two convex functions in which one of these functions is smooth in a real Hilbert space. We establish a weak convergence to a solution of the proposed algorithm without the Lipschitz assumption on the gradient of the objective function. Furthermore, we analyze its performance by applying the proposed algorithm to solving classification problems on various data sets and compare with other line search algorithms. Based on the experiments, the proposed algorithm performs better than other line search algorithms.

1. Introduction

The convex minimization problem in the form of the sum of two convex functions plays a very important role in machine learning. This problem has been analyzed and studied by many authors because of its applications in various fields such as data science, computer science, statistics, engineering, physics, and medical science. Some examples of these applications are signal processing, compressed sensing, medical image reconstruction, digital image processing, and data prediction and classification; see [1,2,3,4,5,6,7,8].

As we know in machine learning, especially in data prediction and classification problems, the main objective is to minimize loss functions. Many loss functions can be viewed as convex functions; thus by employing convex minimization, one could find the minimum of such functions, which in turn solve data prediction and classification problems. Many works have implemented this strategy; see [9,10,11] and the references therein for more information. In this work, we apply extreme learning machine together with the least absolute shrinkage and selection operator to solve classification problems; more detail will be discussed in a later section. First, we introduce a convex minimization problem, which can be formulated as the following form:

$$\underset{x\in H}{min}\{f\left(x\right)+g\left(x\right)\},$$

(1)

where $f:H\to \mathbb{R}\cup \{+\infty \}$ is proper, convex differentiable on an open set containing $dom\left(g\right)$ and $g:H\to \mathbb{R}\cup \{+\infty \}$ is a proper, lower semicontinuous convex function defined on a real Hilbert space H.

A solution of (1) is in fact a fixed point of the operator $pro{x}_{\alpha g}(I-\alpha ▿f)$, i.e.,

$$x^{*}=pro{x}_{\alpha g}(I-\alpha ▿f)\left(x^{*}\right),$$

(2)

where $\alpha >0,$ and $pro{x}_{\alpha g}(I-\alpha ▿f)\left(x\right)=arg{min}_{y\in H}\{g\left(y\right)+\frac{1}{2\alpha }{\parallel (x-\alpha ▿f\left(x\right))-y\parallel }^2\},$ which is known as the forward–backward operator. In order to solve (1), the forward–backward algorithm [12] was introduced as follows:

$$x_{n+1}=\underset{\mathrm{backward}}{\underbrace{pro{x}_{{\alpha }_{n}g}}}\underset{\mathrm{forward}}{\underbrace{(I-{\alpha }_n▿f)}}\left(x_n\right),foralln\in \mathbb{N},$$

(3)

where ${\alpha }_n$ is a positive number. If $▿f$ is L-Lipschitz continuous and ${\alpha }_n\in (0,\frac{2}{L})$, then a sequence generated by (3) converges weakly to a solution of (1). There are several techniques that can improve the performance of (3). For instance, we could utilize an inertial step, which was first introduced by Polyak [13], to solve smooth convex minimization problems. Since then, there have been several works that included an inertial step in their algorithms to accelerate the convergence behavior; see [14,15,16,17,18,19] for examples.

One of the most famous forward–backward-type algorithms that implements an inertial step is the fast iterative shrinkage–thresholding algorithm (FISTA) [20]. It is defined as the following Algorithm 1.

Algorithm 1. FISTA.

1: Input Given $y_1=x_0\in {\mathbb{R}}^n$, and $t_1=1,$ for $n\in \mathbb{N},$ $$\begin{array}{c}\hfill x_n=pro{x}_{\frac{1}{L}g}(y_n-\frac{1}{L}▿f\left(y_n\right)),\\ t_{n+1}=\frac{1+\sqrt{1+4t_n^2}}{2},{\theta }_n=\frac{t_n-1}{t_{n+1}},\\ y_{n+1}=x_n+{\theta }_n(x_n-x_{n-1}),\end{array}$$ where L is a Lipschitz constant of $▿f$.

The term $x_n+{\theta }_n(x_n-x_{n-1})$ is known as an inertial term with an inertial parameter ${\theta }_n$. It has been shown that FISTA performs better than (3). Later, other forward–backward-type algorithms have been introduced and studied by many authors; see for instance [2,8,18,21,22]. However, most of these works assume the Lipschitz assumption on $▿f$, which is difficult for computation in general. Therefore, in this paper, we focus on another approach where $▿f$ is not necessarily Lipschitz continuous.

In 2016, Cruz and Nghia [23] introduced a line search technique as the following Algorithm 2.

Algorithm 2. Line search 1. $(x,\delta ,\sigma ,\theta )$

1: Input Given $x\in dom\left(g\right),$$\delta >0,$$\sigma >0$ and $\theta \in (0,1).$ 2: Set $\gamma =\sigma .$ 3: while$\gamma \parallel ▿f\left(pro{x}_{\gamma g}(x-\gamma ▿f\left(x\right))\right)-▿f\left(x\right)\parallel >\delta \parallel pro{x}_{\gamma g}(x-\gamma ▿f\left(x\right))-x\parallel$do 4:     Set $\gamma =\theta \gamma$ 5: end while 6: Output$\gamma .$

   They asserted that Line Search 1 stops after finitely many steps and proposed the following Algorithm 3.

Algorithm 3. Algorithm with Line Search 1.

1: Input Given $x_0\in dom\left(g\right),$$\delta \in (0,\frac{1}{2}),$$\sigma >0,$ and $\theta \in (0,1),$ for all $n\in \mathbb{N},$ $$x_{n+1}=pro{x}_{{\gamma }_{n}g}(I-{\gamma }_n▿f)\left(x_n\right),$$ where ${\gamma }_n:=$ Line Search 1$(x_n,\delta ,\sigma ,\theta ).$

They also showed that the sequence $\left\{x_n\right\}$ defined by Algorithm 3 converges weakly to a solution of (1) under Assumptions A1 and A2 where:

A1.

$f,g$ are proper lower semicontinuous convex functions with $dom\left(g\right)\subseteq dom\left(f\right);$

A2.

f is differentiable on an open set containing $dom\left(g\right),$ and $▿f$ is uniformly continuous on any bounded subset of $dom\left(g\right)$ and maps any bounded subset of $dom\left(g\right)$ to a bounded set in $H.$

It is noted that the L-Lipschitz continuity of $▿f$ is not necessarily assumed. Moreover, if $▿f$ is L-Lipschitz continuous, then A2 is satisfied.

   In 2019, Kankam et al. [3] proposed the new line search as the following Algorithm 4.

Algorithm 4. Line search 2. $(x,\delta ,\sigma ,\theta )$

1: Input Given $x\in dom\left(g\right),$$\delta >0,$$\sigma >0$ and $\theta \in (0,1)$. Set $$L(x,\gamma )=pro{x}_{\gamma g}(x-\gamma ▿f\left(x\right)), \mathrm{and}$$ $$S(x,\gamma )=pro{x}_{\gamma g}(L(x,\gamma )-\gamma ▿f\left(L(x,\gamma )\right)).$$ 2: Set $\gamma =\sigma .$ 3: while $$\begin{array}{cc}\hfill \gamma max\{\parallel ▿f(S(x,\gamma ))-▿f(L(x& ,\gamma \left)\right)\parallel ,\parallel ▿f\left(L\right(x,\gamma \left)\right)-▿f\left(x\right)\parallel \}\hfill \\ & \hfill >\delta (\parallel S(x,\gamma )-L(x,\gamma )\parallel +\parallel L(x,\gamma )-x\parallel )\end{array}$$ do 4:     Set $\gamma =\theta \gamma ,L(x,\gamma )=L(x,\theta \gamma ),S(x,\gamma )=S(x,\theta \gamma )$ 5: end while 6: Output$\gamma .$

They also asserted that Line Search 2 stops at finitely many steps and proposed the following Algorithm 5.

Algorithm 5. Algorithm with Line Search 2.

1: Input Given $x_0\in dom\left(g\right),$$\delta \in (0,\frac{1}{8}),$$\sigma >0$ and $\theta \in (0,1),$ for all $n\in \mathbb{N},$ $$\begin{array}{c}\hfill y_n=pro{x}_{{\gamma }_{n}g}(x_n-{\gamma }_n▿f\left(x_n\right)),\\ \hfill x_{n+1}=pro{x}_{{\gamma }_{n}g}(y_n-{\gamma }_n▿f\left(y_n\right)),\end{array}$$ where ${\gamma }_n:=LineSearch2(x_n,\delta ,\sigma ,\theta ).$

A weak convergence result of this algorithm was obtained under Assumptions A1 and A2. Although Algorithms 3 and 5 obtained weak convergence results without the Lipschitz assumption on $▿f$, the two algorithms did not utilize an inertial step yet. Therefore, some improvements of their convergence behavior using this technique are interesting to investigate.

Motivated by the works mentioned earlier, we aim to introduce a new line search technique and prove that it is well-defined. Then, we employ it to construct a novel forward–backward algorithm that utilizes an inertial step to improve its performance to be better than the other line search algorithms. We prove a weak convergence theorem of the proposed algorithm without the Lipschitz assumption on $▿f$ and apply it to solve classification problems on various data sets. We also compare its performance with Algorithms 3 and 5 to show that the proposed algorithm performs better.

This work is organized as follows: In Section 2, we recall some important definitions and lemmas used in later sections. In Section 3, we introduce a new line search technique and algorithm for solving (1). Then, we analyze the convergence and complexity of the proposed algorithm under Assumptions A1 and A2. In Section 4, we apply the proposed algorithm to solve data classification problems and compare its performance with other algorithms. Finally, the conclusion of this work is presented in Section 5.

2. Preliminaries

In this section, some important definitions and lemmas, which will be used in later sections, are presented.

Let $\left\{x_n\right\}$ be a sequence in H and $x\in H$. We denote $x_n\to x$ and $x_n\rightharpoonup x$ as a strong and weak convergence of $\left\{x_n\right\}$ to x, respectively. Let $f:H\to \mathbb{R}\cup \{+\infty \}$ be a proper lower semicontinuous and convex function. We denote $dom\left(f\right)=\{x\in H:f(x)<+\infty \}$.

A subdifferential of f at x is defined by

$$\partial f\left(x\right):=\{u\in H:⟨u,y-x⟩+f(x)\le f(y),y\in H\}.$$

A proximal operator $pro{x}_{\alpha f}:H\to dom\left(f\right)$ is defined as follows:

$$pro{x}_{\alpha f}\left(x\right)={(I+\alpha \partial f)}^{-1}\left(x\right),$$

where I is an identity mapping and $\alpha$ is a positive number. It is well known that this operator is single-valued, nonexpansive, and

$$\frac{x-pro{x}_{\alpha f}\left(x\right)}{\alpha }\in \partial f\left(pro{x}_{\alpha f}\left(x\right)\right),\mathrm{for} \mathrm{all}x\in H \mathrm{and} \alpha >0;$$

(4)

see [23] for more details. Next, we present some important lemmas for this work.

Lemma 1

([24]). Let $\partial f$ be a subdifferential of f. Then, the following hold:

(i) 

$\partial f$ is maximal monotone;

(ii) 

$Gph(\partial f):=\left\{\right(x,y)\in H\times H:y\in \partial f(x\left)\right\}$ is demiclosed, i.e., for any sequence $\left\{(x_n,y_n)\right\}\subseteq Gph(\partial f)$ such that $\left\{x_n\right\}\rightharpoonup x$ and $\left\{y_n\right\}\to y,$ then $(x,y)\in Gph(\partial f)$.

Lemma 2

([25]). Let $f,g:H\to \mathbb{R}\cup \{+\infty \}$ be proper lower semicontinuous convex functions with $dom\left(g\right)\subseteq dom\left(f\right)$ and $J(x,\alpha )=pro{x}_{\alpha g}(x-\alpha ▿f\left(x\right)).$ Then, for any $x\in dom\left(g\right)$ and ${\alpha }_2\ge {\alpha }_1>0,$ we have

$$\frac{{\alpha }_2}{{\alpha }_1}\parallel x-J(x,{\alpha }_1)\parallel \ge \parallel x-J(x,{\alpha }_2)\parallel \ge \parallel x-J(x,{\alpha }_1)\parallel .$$

Lemma 3

([26]). Let H be a real Hilbert space. Then, for all $a,b,c\in H$ and $\zeta \in [0,1],$ the following hold:

(i) 

${\parallel a\pm b\parallel }^2={\parallel a\parallel }^2\pm 2⟨a,b⟩+{\parallel b\parallel }^2;$

(ii) 

${\parallel \zeta a+(1-\zeta )b\parallel }^2={\zeta \parallel a\parallel }^2+{(1-\zeta )\parallel b\parallel }^2-\zeta (1-\zeta ){\parallel a-b\parallel }^2;$

(iii) 

${\parallel a+b\parallel }^2\le {\parallel a\parallel }^2+2⟨b,a+b⟩;$

(iv) 

$⟨a-b,b-c⟩=\frac{1}{2}{(\parallel a-c\parallel }^2{-\parallel a-b\parallel }^2{-\parallel b-c\parallel }^2).$

Lemma 4

([8]). Let $\left\{a_n\right\}$ and $\left\{b_n\right\}$ be sequences of non-negative real numbers such that

$$a_{n+1}\le (1+b_n)a_n+b_n{a}_{n-1},foralln\in \mathbb{N}.$$

Then, the following holds:

$${\displaystyle a_{n+1}\le K\prod _{j=1}^n(1+2b_j),whereK=max\{a_1,a_2\}.}$$

Moreover, if ${\displaystyle \sum _{n=1}^{+\infty }{b}_n<+\infty ,}$ then $\left\{a_n\right\}$ is bounded.

Lemma 5

([26]). Let $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ be sequences of non-negative real numbers such that

$${\alpha }_{n+1}\le (1+{\gamma }_n){\alpha }_n+{\beta }_n,foralln\in \mathbb{N}.$$

If ${\displaystyle \sum _{n=1}^{+\infty }{\gamma }_n<+\infty }$ and ${\displaystyle \sum _{n=1}^{+\infty }{\beta }_n<+\infty ,}$ then ${\displaystyle \underset{n\to +\infty }{lim}{\alpha }_n}$ exists.

Lemma 6

([27], Opial). Let $\left\{x_n\right\}$ be a sequence in a Hilbert space H. If there exists a nonempty subset Ω of H such that the following hold:

(i)

For any ${\displaystyle x^{*}\in \Omega ,\underset{n\to +\infty }{lim}\parallel x_n-x^{*}\parallel }$ exists;

(ii)

Every weak-cluster point of $\left\{x_n\right\}$ belongs to $\Omega .$

Then, $\left\{x_n\right\}$ converges weakly to an element in Ω.

3. Main Results

In this section, we define a new line search technique and a new accelerated algorithm with the new line search for solving (1). We denote $S_{*}$ the set of all solutions of (1) and suppose that $f,g:H\to \mathbb{R}\cup \{+\infty \}$ are two convex functions that satisfy Assumptions A1 and A2, and $dom\left(g\right)$ is closed. Furthermore, we also suppose that $S_{*}\ne \varnothing$.

We first introduce a new line search technique as the following Algorithm 6.

Algorithm 6. Line Search 3 $(x,\delta ,\sigma ,\theta )$.

1: Input Given $x\in dom\left(g\right),$$\delta >0,$$\sigma >0$ and $\theta \in (0,1)$. Set $$L(x,\gamma )=pro{x}_{\gamma g}(x-\gamma ▿f\left(x\right)), \mathrm{and}$$ $$S(x,\gamma )=pro{x}_{\gamma g}(L(x,\gamma )-\gamma ▿f\left(L(x,\gamma )\right)).$$ 2: Set $\gamma =\sigma .$ 3: while $$\begin{array}{cc}\frac{\gamma }{2}(\parallel ▿f\left(S(x,\gamma )\right)-▿f\left(L(x,\gamma )\right)\parallel \hfill & +\parallel ▿f\left(L\right(x,\gamma \left)\right)-▿f\left(x\right)\parallel )\hfill \\ & >\delta (\parallel S(x,\gamma )-L(x,\gamma )\parallel +\parallel L(x,\gamma )-x\parallel ),\hfill \end{array}$$ $$\mathbf{or}\gamma \parallel ▿f\left(L\right(x,\gamma \left)\right)-▿f\left(x\right)\parallel >4\delta \parallel L(x,\gamma )-x\parallel .$$ do 4:     Set $\gamma =\theta \gamma ,L(x,\gamma )=L(x,\theta \gamma ),S(x,\gamma )=S(x,\theta \gamma )$ 5: end while 6: Output$\gamma .$

We first show that Line Search 3 terminates at finitely many steps.

Lemma 7.

Line Search 3 stops at finitely many steps.

Proof. 

If $x\in S_{*}$, then $x=L(x,\sigma )=S(x,\sigma )$, so Line Search 3 stops with zero steps. If $x\notin S_{*}$, suppose by contradiction that, for all $n\in \mathbb{N},$ the following hold:

$$\begin{array}{cc}\hfill \frac{\sigma {\theta }^n}{2}& (\parallel ▿f\left(S(x,\sigma {\theta }^n)\right)-▿f\left(L(x,\sigma {\theta }^n)\right)\parallel +\parallel ▿f\left(L(x,\sigma {\theta }^n)\right)-▿f\left(x\right)\parallel )\hfill \\ \hfill & >\delta (\parallel S(x,\sigma {\theta }^n)-L(x,\sigma {\theta }^n)\parallel +\parallel L(x,\sigma {\theta }^n)-x\parallel ),\hfill \end{array}$$

(5)

or

$$\sigma {\theta }^n\parallel ▿f\left(L(x,\sigma {\theta }^n)\right)-▿f\left(x\right)\parallel >4\delta \parallel L(x,\sigma {\theta }^n)-x\parallel .$$

(6)

Then, from these assumptions, we can find a subsequence $\left\{\sigma {\theta }^{n_k}\right\}$ of $\left\{\sigma {\theta }^n\right\}$ such that (5) or (6) holds. First, we show that

$$\{\parallel ▿f\left(L(x,\sigma {\theta }^n)\right)-▿f\left(x\right)\parallel \left\}\mathrm{and}\right\{\parallel ▿f\left(S(x,\sigma {\theta }^n)\right)-▿f\left(L(x,\sigma {\theta }^n)\right)\parallel \}$$

are bounded. It follows from Lemma 2 that

$$\parallel L(x,\sigma {\theta }^n)-x\parallel \le \parallel L(x,\sigma )-x\parallel ,$$

for all $n\in \mathbb{N}.$ In combination with A2, we conclude that $\{\parallel ▿f\left(L(x,\sigma {\theta }^n)\right)-▿f\left(x\right)\parallel \}$ is bounded. Next, we prove that $\{\parallel ▿f\left(S(x,\sigma {\theta }^n)\right)-▿f\left(L(x,\sigma {\theta }^n)\right)\parallel \}$ is bounded. Since $pro{x}_{\gamma g}$ is nonexpansive, for any $\gamma >0$, then

$$\begin{array}{cc}\hfill \parallel S(x,\sigma {\theta }^n)& -▿L(x,\sigma {\theta }^n)\parallel \hfill \\ \hfill & =\parallel pro{x}_{\sigma {\theta }^{n}g}(L(x,\sigma {\theta }^n)-\sigma {\theta }^n▿f\left(L(x,\sigma {\theta }^n)\right))-pro{x}_{\sigma {\theta }^{n}g}(x-\sigma {\theta }^n▿f\left(x\right))\parallel \hfill \\ \hfill & \le \parallel (L(x,\sigma {\theta }^n)-\sigma {\theta }^n▿f\left(L(x,\sigma {\theta }^n)\right)-(x-\sigma {\theta }^n▿f\left(x\right))\parallel \hfill \\ \hfill & \le \parallel L(x,\sigma {\theta }^n)-x\parallel +\sigma {\theta }^n\parallel ▿f(L(x,\sigma {\theta }^n)-▿f\left(x\right))\parallel \hfill \\ \hfill & \le \parallel L(x,\sigma {\theta }^n)-x\parallel +\sigma \parallel ▿f(L(x,\sigma {\theta }^n)-▿f\left(x\right))\parallel ,\hfill \end{array}$$

for all $n\in \mathbb{N}$; hence, $\{\parallel S(x,\sigma {\theta }^n)-▿L(x,\sigma {\theta }^n)\parallel \}$ is bounded. Again, it follows from A2 that $\{\parallel ▿f\left(S(x,\sigma {\theta }^n)\right)-▿f\left(L(x,\sigma {\theta }^n)\right)\parallel \}$ is bounded. To complete the proof, we consider the only two possible cases to find a contradiction.

Case 1: Suppose that there exists a subsequence $\left\{\sigma {\theta }^{n_k}\right\}$ of $\left\{\sigma {\theta }^n\right\}$ such that (5) holds, for all $k\in \mathbb{N}$. Then, it follows that $\parallel S(x,\sigma {\theta }^{n_k})-L(x,\sigma {\theta }^{n_k})\parallel \to 0$ and $\parallel L(x,\sigma {\theta }^{n_k})-x\parallel \to 0$, as $k\to +\infty$. Since $▿f$ is uniformly continuous, we obtain:

$$\parallel ▿f\left(S(x,\sigma {\theta }^{n_k})\right)-▿f\left(L(x,\sigma {\theta }^{n_k})\right)\parallel \to 0\mathrm{and}\parallel ▿f\left(L(x,\sigma {\theta }^{n_k})\right)-▿f\left(x\right)\parallel \to 0,$$

as $k\to +\infty .$ Therefore, it follows from (5) that $\frac{\parallel L(x,\sigma {\theta }^{n_k})-x\parallel }{\sigma {\theta }^{n_k}}\to 0,$ as $k\to +\infty .$ By (4), we obtain

$$\frac{x-\sigma {\theta }^{n_k}▿f\left(x\right)-L(x,\sigma {\theta }^{n_k})}{\sigma {\theta }^{n_k}}\in \partial g\left(L(x,\sigma {\theta }^{n_k})\right).$$

Thus, $\frac{L(x,\sigma {\theta }^{n_k})-x}{\sigma {\theta }^{n_k}}-▿f\left(x\right)\in \partial g\left(L(x,\sigma {\theta }^{n_k})\right).$ Since $L(x,\sigma {\theta }^{n_k})\to x$, as $k\to +\infty$, we obtain from Lemma 1 that $0\in ▿f\left(x\right)+\partial g\left(x\right)\subseteq \partial (f+g)\left(x\right).$ Hence, $x\in S_{*}$, which is a contradiction.

Case 2: Suppose that there is a subsequence $\left\{\sigma {\theta }^{n_k}\right\}$ of $\left\{\sigma {\theta }^n\right\}$ satisfying (6), for all $k\in \mathbb{N}$. Then, $\parallel L(x,\sigma {\theta }^{n_k})-x\parallel \to 0$, as $k\to +\infty$. Again, from the uniform continuity of $▿f$, we have

$$\parallel ▿f\left(L(x,\sigma {\theta }^{n_k})\right)-▿f\left(x\right)\parallel \to 0,$$

as $k\to +\infty .$ From (6), we conclude that

$$\frac{\parallel L(x,\sigma {\theta }^{n_k})-x\parallel }{\sigma {\theta }^{n_k}}\to 0,$$

as $k\to +\infty .$ By the same argument as in Case 1, we can show that $0\in \partial (f+g)\left(x\right),$ and hence, $x\in S_{*},$ a contradiction. Therefore, we conclude that Line Search 3 stops with finite steps, and the proof is complete.    □

We propose a new inertial algorithm with Line Search 3 as following Algorithm 7.

Algorithm 7. Inertial algorithm with Line Search 3.

1: Input Given $x_0,x_1\in dom\left(g\right),{\alpha }_n\in [0,1],{\beta }_n\ge 0,\sigma >0,\theta \in (0,1)$ and $\delta \in (0,\frac{1}{8}),$ for $n\in \mathbb{N},$ $$\begin{array}{c}{y}_n=x_n+{\beta }_n(x_n-x_{n-1}),\\ z_n=P_{dom\left(g\right)}{y}_n,\\ w_n=pro{x}_{{\gamma }_{n}g}(z_n-{\gamma }_n▿f\left(z_n\right)),\\ x_{n+1}=(1-{\alpha }_n)w_n+{\alpha }_{n}pro{x}_{{\gamma }_{n}g}(w_n-{\gamma }_n▿f\left(w_n\right)),\end{array}$$ where ${\gamma }_n:=\mathrm{Line}\mathrm{Search}3(z_n,\delta ,\sigma ,\theta ),$ and $P_{dom\left(g\right)}$ is a metric projection map onto $dom\left(g\right).$

The diagram of Algorithm 7 can be seen in Figure 1.

Figure 1. Diagram of Algorithm 7.

Next, we prove the following lemma, which will play a crucial role in our main theorems.

Lemma 8.

Let ${\gamma }_n:=LineSearch3(z_n,\delta ,\sigma ,\theta ).$ Then, for all $n\in \mathbb{N}$ and $x\in dom\left(g\right)$, the following hold:

(I) 

$\parallel z_n{-x\parallel }^2-\parallel w_n{-x\parallel }^2\ge 2{\gamma }_n[(f+g)\left(w_n\right)-(f+g)\left(x\right)]+(1-8\delta ){\parallel w_n-z_n\parallel }^2;$

(II) 

$\parallel z_n{-x\parallel }^2-{\parallel v_n-x\parallel }^2\ge 2{\gamma }_n[(f+g)\left(w_n\right)+(f+g)\left(v_n\right)-2(f+g)\left(x\right)]$

                            $+(1-8\delta )(\parallel w_n-z_n{\parallel }^2+\parallel v_n-w_n{\parallel }^2).$

where $v_n=pro{x}_{{\gamma }_{n}g}(w_n-{\gamma }_n▿f\left(w_n\right)).$

Proof. 

First, we show that $\left(I\right)$ is true. From (4), we know that

$$\frac{z_n-w_n}{{\gamma }_n}-▿f\left(z_n\right)\in \partial g\left(w_n\right),\mathrm{for}\mathrm{all}n\in \mathbb{N}.$$

Moreover, it follows from the definitions of $\partial g\left(w_n\right),▿f\left(z_n\right)$ and $▿f\left(w_n\right)$ that

$$g\left(x\right)-g\left(w_n\right)\ge ⟨\frac{z_n-w_n}{{\gamma }_n}-▿f\left(z_n\right),x-w_n⟩,$$

$$f\left(x\right)-f\left(z_n\right)\ge ⟨▿f\left(z_n\right),x-z_n⟩ \mathrm{and} f\left(z_n\right)-f\left(w_n\right)\ge ⟨▿f\left(w_n\right),z_n-w_n⟩,$$

for all $n\in \mathbb{N}$. Consequently,

$$\begin{array}{cc}\hfill f\left(x\right)-f\left(z_n\right)+g\left(x\right)-g\left(w_n\right)& \ge \frac{1}{{\gamma }_n}⟨z_n-w_n,x-w_n⟩+⟨▿f\left(z_n\right),w_n-z_n⟩\hfill \\ \hfill & =\frac{1}{{\gamma }_n}⟨z_n-w_n,x-w_n⟩+⟨▿f\left(z_n\right)-▿f\left(w_n\right),w_n-z_n⟩\hfill \\ \hfill & +⟨▿f\left(w_n\right),w_n-z_n⟩\hfill \\ \hfill & \ge \frac{1}{{\gamma }_n}⟨z_n-w_n,x-w_n⟩-\parallel ▿f\left(z_n\right)-▿f\left(w_n\right)\parallel \parallel w_n-z_n\parallel \hfill \\ \hfill & +⟨▿f\left(w_n\right),w_n-z_n⟩\hfill \\ \hfill & \ge \frac{1}{{\gamma }_n}⟨z_n-w_n,x-w_n⟩-\frac{4\delta }{{\gamma }_n}{\parallel w_n-z_n\parallel }^2+f\left(w_n\right)-f\left(z_n\right),\hfill \end{array}$$

for all $n\in \mathbb{N}$. It follows that

$$\frac{1}{{\gamma }_n}⟨z_n-w_n,w_n-x⟩\ge (f+g)\left(w_n\right)-(f+g)\left(x\right)-\frac{4\delta }{{\gamma }_n}{\parallel w_n-z_n\parallel }^2,\mathrm{for}\mathrm{all}n\in \mathbb{N}.$$

From Lemma 3, we have $⟨z_n-w_n,w_n-x⟩=\frac{1}{2}(\parallel z_n{-x\parallel }^2-\parallel z_n-w_n{\parallel }^2-\parallel w_n-x{\parallel }^2)$, and hence,

$$\frac{1}{2{\gamma }_n}(\parallel z_n{-x\parallel }^2-\parallel z_n-w_n{\parallel }^2-\parallel w_n{-x\parallel }^2)\ge (f+g)\left(w_n\right)-(f+g)\left(x\right)-\frac{4\delta }{{\gamma }_n}{\parallel w_n-z_n\parallel }^2,$$

for all $n\in \mathbb{N}.$ Then, it follows that, for any $x\in dom\left(g\right),$

$$\begin{array}{cc}\hfill \parallel z_n{-x\parallel }^2-{\parallel w_n-x\parallel }^2& \ge 2{\gamma }_n[(f+g)\left(w_n\right)-(f+g)\left(x\right)]+(1-8\delta ){\parallel w_n-z_n\parallel }^2,\hfill \end{array}$$

and $\left(I\right)$ is proven. Next, we show $\left(II\right)$. From (4), we have that

$$\frac{z_n-w_n}{{\gamma }_n}-▿f\left(z_n\right)\in \partial g\left(w_n\right),\mathrm{and}$$

$$\frac{w_n-v_n}{{\gamma }_n}-▿f\left(w_n\right)\in \partial g\left(v_n\right).$$

Then,

$$g\left(x\right)-g\left(w_n\right)\ge ⟨\frac{z_n-w_n}{{\gamma }_n}-▿f\left(z_n\right),x-w_n⟩,\mathrm{and}$$

$$g\left(x\right)-g\left(v_n\right)\ge ⟨\frac{w_n-v_n}{{\gamma }_n}-▿f\left(w_n\right),x-v_n⟩,\mathrm{for}\mathrm{all}n\in \mathbb{N}.$$

Moreover,

$$f\left(x\right)-f\left(z_n\right)\ge ⟨▿f\left(z_n\right),x-z_n⟩,$$

$$f\left(x\right)-f\left(w_n\right)\ge ⟨▿f\left(w_n\right),x-w_n⟩,$$

$$f\left(z_n\right)-f\left(w_n\right)\ge ⟨▿f\left(w_n\right),z_n-w_n⟩,\mathrm{and}$$

$$f\left(w_n\right)-f\left(v_n\right)\ge ⟨▿f\left(v_n\right),w_n-v_n⟩,\mathrm{for}\mathrm{all}n\in \mathbb{N}.$$

The above inequalities imply

$$\begin{array}{cc}\hfill & f\left(x\right)-f\left(z_n\right)+f\left(x\right)-f\left(w_n\right)+g\left(x\right)-g\left(w_n\right)+g\left(x\right)-g\left(v_n\right)\hfill \\ \hfill & \ge \frac{1}{{\gamma }_n}⟨z_n-w_n,x-w_n⟩+⟨▿f\left(z_n\right),w_n-z_n⟩+\frac{1}{{\gamma }_n}⟨w_n-v_n,x-v_n⟩+⟨▿f\left(w_n\right),v_n-w_n⟩\hfill \\ \hfill & =\frac{1}{{\gamma }_n}⟨z_n-w_n,x-w_n⟩+⟨▿f\left(z_n\right)-▿f\left(w_n\right),w_n-z_n⟩+⟨▿f\left(w_n\right),w_n-z_n⟩\hfill \\ \hfill & +\frac{1}{{\gamma }_n}⟨w_n-v_n,x-v_n⟩+⟨▿f\left(w_n\right)-▿f\left(v_n\right),v_n-w_n⟩+⟨▿f\left(v_n\right),v_n-w_n⟩\hfill \\ \hfill & \ge \frac{1}{{\gamma }_n}⟨z_n-w_n,x-w_n⟩+\frac{1}{{\gamma }_n}⟨w_n-v_n,x-v_n⟩-\parallel ▿f\left(w_n\right)-▿f\left(z_n\right)\parallel \parallel w_n-z_n\parallel \hfill \\ \hfill & +⟨▿f\left(w_n\right),w_n-z_n⟩-\parallel ▿f\left(v_n\right)-▿f\left(w_n\right)\parallel \parallel v_n-w_n\parallel +⟨▿f\left(v_n\right),v_n-w_n⟩\hfill \\ \hfill & \ge \frac{1}{{\gamma }_n}⟨z_n-w_n,x-w_n⟩+\frac{1}{{\gamma }_n}⟨w_n-v_n,x-v_n⟩\hfill \\ \hfill & -\parallel ▿f\left(w_n\right)-▿f\left(z_n\right)\parallel (\parallel w_n-z_n\parallel +\parallel v_n-w_n\parallel )+⟨▿f\left(w_n\right),w_n-z_n⟩\hfill \\ \hfill & -\parallel ▿f\left(v_n\right)-▿f\left(w_n\right)\parallel (\parallel w_n-z_n\parallel +\parallel v_n-w_n\parallel )+⟨▿f\left(v_n\right),v_n-w_n⟩\hfill \\ \hfill & =\frac{1}{{\gamma }_n}⟨z_n-w_n,x-w_n⟩+\frac{1}{{\gamma }_n}⟨w_n-v_n,x-v_n⟩+⟨▿f\left(w_n\right),w_n-z_n⟩+⟨▿f\left(v_n\right),v_n-w_n⟩\hfill \\ \hfill & -(\parallel ▿f\left(w_n\right)-▿f\left(z_n\right)\parallel +\parallel ▿f\left(v_n\right)-▿f\left(w_n\right)\parallel \left)\right(\parallel w_n-z_n\parallel +\parallel v_n-w_n\parallel )\hfill \\ \hfill & \ge \frac{1}{{\gamma }_n}⟨z_n-w_n,x-w_n⟩+\frac{1}{{\gamma }_n}⟨w_n-v_n,x-v_n⟩+⟨▿f\left(w_n\right),w_n-z_n⟩\hfill \\ \hfill & +⟨▿f\left(v_n\right),v_n-w_n⟩-\frac{2\delta }{{\gamma }_n}(\parallel w_n-z_n\parallel +\parallel v_n-w_n{\parallel )}^2\hfill \\ \hfill & \ge \frac{1}{{\gamma }_n}⟨z_n-w_n,x-w_n⟩+\frac{1}{{\gamma }_n}⟨w_n-v_n,x-v_n⟩+f\left(v_n\right)-f\left(z_n\right)\hfill \\ \hfill & -\frac{4\delta }{{\gamma }_n}(\parallel w_n-z_n{\parallel }^2+\parallel v_n-w_n{\parallel }^2),\hfill \end{array}$$

for all $x\in dom\left(g\right)$ and $n\in \mathbb{N}.$ Hence,

$$\begin{array}{cc}\hfill \frac{1}{{\gamma }_n}& ⟨z_n-w_n,w_n-x⟩+\frac{1}{{\gamma }_n}⟨w_n-v_n,v_n-x⟩\hfill \\ \hfill & \ge (f+g)\left(w_n\right)+(f+g)\left(v_n\right)-2(f+g)\left(x\right)-\frac{4\delta }{{\gamma }_n}\parallel w_n-z_n{\parallel }^2-\frac{4\delta }{{\gamma }_n}{\parallel v_n-w_n\parallel }^2.\hfill \end{array}$$

Moreover, from Lemma 3, we have, for all $n\in \mathbb{N},$

$$⟨z_n-w_n,w_n-x⟩=\frac{1}{2}(\parallel z_n{-x\parallel }^2-\parallel z_n-w_n{\parallel }^2-\parallel w_n-x{\parallel }^2),\mathrm{and}$$

$$⟨w_n-v_n,v_n-x⟩=\frac{1}{2}(\parallel w_n{-x\parallel }^2-\parallel w_n-v_n{\parallel }^2-\parallel v_n-x{\parallel }^2).$$

As a result, we obtain

$$\begin{array}{cc}\hfill \frac{1}{2{\gamma }_n}& (\parallel z_n{-x\parallel }^2-\parallel z_n-w_n{\parallel }^2)-\frac{1}{2{\gamma }_n}(\parallel w_n-v_n{\parallel }^2+\parallel v_n-x{\parallel }^2)\hfill \\ \hfill & \ge (f+g)\left(w_n\right)+(f+g)\left(v_n\right)-2(f+g)\left(x\right)-\frac{4\delta }{{\gamma }_n}\parallel w_n-z_n{\parallel }^2-\frac{4\delta }{{\gamma }_n}{\parallel v_n-w_n\parallel }^2,\hfill \end{array}$$

for all $x\in dom\left(g\right),$ and $n\in \mathbb{N}$. Therefore,

$$\begin{array}{cc}\hfill \parallel z_n{-x\parallel }^2-{\parallel v_n-x\parallel }^2\ge & 2{\gamma }_n[(f+g)\left(w_n\right)+(f+g)\left(v_n\right)-2(f+g)\left(x\right)]\hfill \\ \hfill & +(1-8\delta )(\parallel w_n-z_n{\parallel }^2+\parallel v_n-w_n{\parallel }^2),\hfill \end{array}$$

for all $x\in dom\left(g\right),$ and $n\in \mathbb{N}$, and hence, $\left(II\right)$ is proven.    □

Next, we prove the weak convergence result of Algorithm 7.

Theorem 9.

Let $\left\{x_n\right\}$ be a sequence generated by Algorithm 7. Suppose that the following hold:

B1. 

${\displaystyle \sum _{n=1}^{+\infty }{\beta }_n<+\infty ;}$

B2. 

There exists $\gamma >0$ such that ${\gamma }_n\ge \gamma ,$ for all $n\in \mathbb{N}.$

Then, $\left\{x_n\right\}$ converges weakly to some point in $S_{*}$.

Proof. 

Let $x^{*}\in S_{*}$; obviously, $x^{*}\in dom\left(g\right).$ The following are direct consequences of Lemma 8:

$$\begin{array}{cc}\hfill \parallel z_n-x^{*}{\parallel }^2-{\parallel w_n-x^{*}\parallel }^2& \ge 2{\gamma }_n[(f+g)\left(w_n\right)-(f+g)\left(x^{*}\right)]+(1-8\delta ){\parallel w_n-z_n\parallel }^2\hfill \\ \hfill & \ge (1-8\delta )\parallel w_n-z_n{\parallel }^2,\hfill \end{array}$$

(7)

and

$$\begin{array}{cc}\hfill \parallel z_n-x^{*}{\parallel }^2-{\parallel v_n-x^{*}\parallel }^2& \ge 2{\gamma }_n[(f+g)\left(w_n\right)+(f+g)\left(v_n\right)-2(f+g)\left(x^{*}\right)]\hfill \\ \hfill & +(1-8\delta )(\parallel w_n-z_n{\parallel }^2+\parallel v_n-w_n{\parallel }^2)\hfill \\ \hfill & \ge (1-8\delta )(\parallel w_n-z_n{\parallel }^2+\parallel v_n-w_n{\parallel }^2),\hfill \end{array}$$

(8)

where $v_n=pro{x}_{{\gamma }_{n}g}(w_n-{\gamma }_n▿f\left(w_n\right)).$ Then, we have

$$\begin{array}{cc}\hfill \parallel x_{n+1}-x^{*}\parallel & \le (1-{\alpha }_n)\parallel w_n-x^{*}\parallel +{\alpha }_n\parallel v_n-x^{*}\parallel \hfill \\ \hfill & \le (1-{\alpha }_n)\parallel w_n-x^{*}\parallel +{\alpha }_n\parallel z_n-x^{*}\parallel \hfill \\ \hfill & \le \parallel z_n-x^{*}\parallel .\hfill \end{array}$$

(9)

Next, we show that ${\displaystyle \underset{n\to \infty }{lim}\parallel x_n-x^{*}\parallel }$ exists. Since $P_{dom\left(g\right)}$ is nonexpansive, we have

$$\begin{array}{cc}\hfill \parallel x_{n+1}-x^{*}\parallel & \le \parallel z_n-x^{*}\parallel \hfill \\ \hfill & =\parallel P_{dom\left(g\right)}{y}_n-P_{dom\left(g\right)}{x}^{*}\parallel \hfill \\ \hfill & \le \parallel y_n-x^{*}\parallel \hfill \\ \hfill & \le \parallel x_n-x^{*}\parallel +{\beta }_n\parallel x_n-x_{n-1}\parallel \hfill \\ \hfill & \le (1+{\beta }_n)\parallel x_n-x^{*}\parallel +{\beta }_n\parallel x_{n-1}-x^{*}\parallel ,\mathrm{for}\mathrm{all}n\in \mathbb{N}.\hfill \end{array}$$

(10)

By using Lemma 4, we have that $\left\{x_n\right\}$ is bounded. Consequently, ${\displaystyle \sum _{n=1}^{+\infty }{\beta }_n\parallel x_n-x_{n-1}\parallel <+\infty ,}$ and

$$\parallel y_n-x_n\parallel ={\beta }_n\parallel x_n-x_{n-1}\parallel \to 0,\mathrm{as}n\to +\infty .$$

By (10) together with Lemma 5, we conclude that ${\displaystyle \underset{n\to +\infty }{lim}\parallel x_n-x^{*}\parallel }$ exists. Since $x_n\in dom\left(g\right),$ for all $n\in \mathbb{N}$, we obtain

$$\parallel y_n-z_n\parallel \le \parallel y_n-x_n\parallel ,\mathrm{for}\mathrm{all}n\in \mathbb{N},$$

which implies that ${\displaystyle \underset{n\to +\infty }{lim}\parallel y_n-z_n\parallel =0.}$ Consequently, ${\displaystyle \underset{n\to +\infty }{lim}\parallel x_n-z_n\parallel =0,}$ and hence, ${\displaystyle \underset{n\to +\infty }{lim}\parallel x_n-x^{*}\parallel =\underset{n\to +\infty }{lim}\parallel z_n-x^{*}\parallel .}$ Now, we will show that ${\displaystyle \underset{n\to +\infty }{lim}\parallel x_n-w_n\parallel =0.}$ To do this, we consider the following two cases.

Case 1. ${\displaystyle \underset{n\to +\infty }{lim\; sup}{\alpha }_n=c<1}$, then from (9), we obtain

$${\displaystyle \underset{n\to +\infty }{lim\; sup}\parallel w_n-x^{*}\parallel =\underset{n\to +\infty }{lim\; sup}\parallel x_n-x^{*}\parallel =\underset{n\to +\infty }{lim\; sup}\parallel z_n-x^{*}\parallel .}$$

Therefore, we obtain from (7) that ${\displaystyle \underset{n\to +\infty }{lim}\parallel w_n-z_n\parallel =0.}$ As a result, we have ${\displaystyle \underset{n\to +\infty }{lim}\parallel x_n-w_n\parallel =0.}$

Case 2. ${\displaystyle \underset{n\to +\infty }{lim\; sup}{\alpha }_n=1}$, then it follows from (9) that

$${\displaystyle \underset{n\to +\infty }{lim\; sup}\parallel v_n-x^{*}\parallel =\underset{n\to +\infty }{lim\; sup}\parallel x_n-x^{*}\parallel =\underset{n\to +\infty }{lim\; sup}\parallel z_n-x^{*}\parallel .}$$

It follows from (8) that ${\displaystyle \underset{n\to +\infty }{lim}\parallel w_n-z_n\parallel =0,}$ and hence, ${\displaystyle \underset{n\to +\infty }{lim}\parallel x_n-w_n\parallel =0.}$

We claim that every weak-cluster point of $\left\{x_n\right\}$ belongs to $S_{*}.$ To prove this claim, let w be a weak-cluster point of $\left\{x_n\right\}.$ Then, there exists a subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$ such that $x_{n_k}\rightharpoonup w,$ and hence, $w_{n_k}\rightharpoonup w$. Next, we show that $w\in S_{*}.$ From A2, we know that $▿f$ is uniformly continuous, so ${\displaystyle \underset{k\to +\infty }{lim}\parallel ▿f{w}_{n_k}-▿f{z}_{n_k}\parallel =0.}$ From (4), we also have

$$\frac{z_{n_k}-{\gamma }_{n_k}▿f{z}_{n_k}-w_{n_k}}{{\gamma }_{n_k}}\in \partial g\left(w_{n_k}\right),\mathrm{for}\mathrm{all}k\in \mathbb{N}.$$

Hence,

$$\frac{z_{n_k}-w_{n_k}}{{\gamma }_{n_k}}-▿f{z}_{n_k}+▿f{w}_{n_k}\in \partial g\left(w_{n_k}\right)+▿f{w}_{n_k}=\partial (f+g)\left(w_{n_k}\right),\mathrm{for}\mathrm{all}k\in \mathbb{N}.$$

By letting $k\to +\infty$ in the above inequality, we can conclude from (1) that $0\in \partial (f+g)\left(w\right),$ and hence, $w\in S_{*}.$ It follows directly from Lemma 6 that $\left\{x_n\right\}$ converges weakly to a point in $S_{*}$, and the proof is now complete.    □

If we set ${\beta }_n=0,$ for all $n\in \mathbb{N},$ in Algorithm 7, we obtain the following Algorithm 8.

Algorithm 8. Algorithm with Line Search 3.

1: Input Given $x_0\in dom\left(g\right),\sigma >0,\theta \in (0,1)$, $\delta \in (0,\frac{1}{8})$ and ${\alpha }_n\in [0,1]$, for $n\in \mathbb{N},$ $$\begin{array}{c}\hfill w_n=pro{x}_{{\gamma }_{n}g}(x_n-{\gamma }_n▿f\left(x_n\right)),\\ \hfill x_{n+1}=(1-{\alpha }_n)w_n+{\alpha }_{n}pro{x}_{{\gamma }_{n}g}(w_n-{\gamma }_n▿f\left(w_n\right)),\end{array}$$ where ${\gamma }_n:=\mathrm{Line}\mathrm{Search}3(x_n,\delta ,\sigma ,\theta ).$

The diagram of Algorithm 8 can be seen in Figure 2.

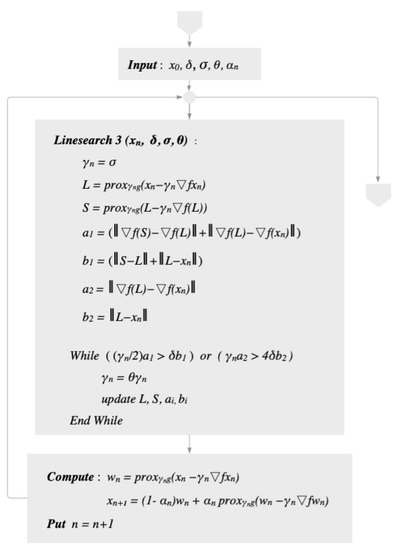
Figure 2. Diagram of Algorithm 8.

We next prove the complexity of Algorithm 8.

Theorem 10.

Let $\left\{x_n\right\}$ be a sequence generated by Algorithm 8. Suppose that there exists $\gamma >0$ such that ${\gamma }_n\ge \gamma ,$ for all $n\in \mathbb{N},$ then $\left\{x_n\right\}$ converges weakly to a point in $S_{*}.$ In addition, if $\delta \in (0,\frac{1}{16}),$ then the following also holds:

$${\displaystyle (f+g)\left(x_n\right)-\underset{x\in H}{min}(f+g)\left(x\right)\le \frac{1}{2\gamma }\frac{{\left[d(x_0,S_{*})\right]}^2}{n},}$$

(11)

for all $n\in \mathbb{N}.$

Proof. 

A weak convergence of $\left\{x_n\right\}$ is guaranteed by Theorem 9. It remains to show that (11) is true. Let $v_n=pro{x}_{{\gamma }_{n}g}(w_n-{\gamma }_n▿f\left(w_n\right))$ and $x^{*}\in S_{*}$.

We first show that $f\left(x_{k+1}\right)\le f\left(x_k\right),$ for all $k\in \mathbb{N}.$ We know that $x_k=z_k$ in Lemma 8, so for any $x\in dom\left(g\right)$ and $k\in \mathbb{N}$, we have:

$$\parallel x_k{-x\parallel }^2-\parallel w_k{-x\parallel }^2\ge 2{\gamma }_k[(f+g)\left(w_k\right)-(f+g)\left(x\right)]+(1-8\delta ){\parallel w_k-x_k\parallel }^2,$$

(12)

and

$$\begin{array}{cc}\hfill \parallel x_k{-x\parallel }^2-{\parallel v_k-x\parallel }^2& \ge 2{\gamma }_k[(f+g)\left(w_k\right)+(f+g)\left(v_k\right)-2(f+g)\left(x\right)]\hfill \\ \hfill & +(1-8\delta )(\parallel w_k-x_k{\parallel }^2+\parallel v_k-w_k{\parallel }^2).\hfill \end{array}$$

(13)

Putting $x=x_k$ in (12) and (13), we obtain

$$-\parallel w_k-x_k{\parallel }^2\ge 2{\gamma }_k[(f+g)\left(w_k\right)-(f+g)\left(x_k\right)]+(1-8\delta ){\parallel w_k-x_k\parallel }^2,$$

(14)

and

$$\begin{array}{cc}\hfill -\parallel v_k-x_k{\parallel }^2& \ge 2{\gamma }_k[(f+g)\left(w_k\right)+(f+g)\left(v_k\right)-2(f+g)\left(x_k\right)]\hfill \\ \hfill & +(1-8\delta )(\parallel w_k-x_k{\parallel }^2+\parallel v_k-w_k{\parallel }^2),\hfill \end{array}$$

(15)

respectively. Substituting x with $w_k$ in (13), we obtain

$$\begin{array}{cc}\hfill \parallel x_k-w_k{\parallel }^2-{\parallel v_k-w_k\parallel }^2& \ge 2{\gamma }_k[(f+g)\left(v_k\right)-(f+g)\left(w_k\right)]\hfill \\ \hfill & +(1-8\delta )(\parallel w_k-x_k{\parallel }^2+\parallel v_k-w_k{\parallel }^2).\hfill \end{array}$$

(16)

By summing (15) and (16), we obtain

$$\begin{array}{c}\hfill (16\delta -1)\parallel x_k-w_k{\parallel }^2+(16\delta -4){\parallel v_k-w_k\parallel }^2\ge 4{\gamma }_k[(f+g)\left(v_k\right)-(f+g)\left(x_k\right)].\end{array}$$

(17)

It follows from (14) and (17) that

$$(f+g)\left(w_k\right)\le (f+g)\left(x_k\right)\mathrm{and}(f+g)\left(v_k\right)\le (f+g)\left(x_k\right),$$

respectively, for all $k\in \mathbb{N}.$ Hence,

$$(f+g)\left(x_{k+1}\right)-(f+g)\left(x_k\right)\le (1-{\alpha }_k)(f+g)\left(w_k\right)+{\alpha }_k(f+g)\left(v_k\right)-(f+g)\left(x_k\right)\le 0,$$

(18)

for all $k\in \mathbb{N}.$ Hence, $\left\{(f+g)\left(x_k\right)\right\}$ is a non-increasing sequence. Now, put $x=x^{*}$ in (12) and (13), then we obtain

$$\parallel w_k-x^{*}{\parallel }^2-{\parallel x_k-x^{*}\parallel }^2\le 2{\gamma }_k[(f+g)\left(x^{*}\right)-(f+g)\left(w_k\right)],$$

(19)

and

$$\begin{array}{cc}\hfill \parallel v_k-x^{*}{\parallel }^2-{\parallel x_k-x^{*}\parallel }^2& \le 2{\gamma }_k[2(f+g)\left(x^{*}\right)-(f+g)\left(w_k\right)-(f+g)\left(v_k\right)]\hfill \\ \hfill & \le 2{\gamma }_k[(f+g)\left(x^{*}\right)-(f+g)\left(v_k\right)].\hfill \end{array}$$

(20)

Inequalities (19) and (20) imply that

$$\begin{array}{cc}\hfill \parallel x_{k+1}-x^{*}{\parallel }^2-{\parallel x_k-x^{*}\parallel }^2& \le (1-{\alpha }_k)\parallel w_k-x^{*}{\parallel }^2+{\alpha }_k\parallel v_k-x^{*}{\parallel }^2-{\parallel x_k-x^{*}\parallel }^2\hfill \\ \hfill & \le 2{\gamma }_k(1-{\alpha }_k)[(f+g)\left(x^{*}\right)-(f+g)\left(w_k\right)]\hfill \\ \hfill & +2{\gamma }_k{\alpha }_k[(f+g)\left(x^{*}\right)-(f+g)\left(v_k\right)]\hfill \\ \hfill & =2{\gamma }_k(f+g)\left(x^{*}\right)-2{\gamma }_k[(1-{\alpha }_k)(f+g)\left(w_k\right)+{\alpha }_k(f+g)\left(v_k\right)]\hfill \\ \hfill & \le 2{\gamma }_k[(f+g)\left(x^{*}\right)-(f+g)\left(x_{k+1}\right)],\hfill \end{array}$$

for all $k\in \mathbb{N}.$ Since ${\gamma }_k\ge \gamma ,$ we obtain

$$\begin{array}{cc}\hfill 0\ge (f+g)\left(x^{*}\right)-(f+g)\left(x_{k+1}\right)& \ge \frac{1}{2{\gamma }_k}(\parallel x_{k+1}-x^{*}{\parallel }^2-\parallel x_k-x^{*}{\parallel }^2)\hfill \\ \hfill & \ge \frac{1}{2\gamma }(\parallel x_{k+1}-x^{*}{\parallel }^2-\parallel x_k-x^{*}{\parallel }^2),\hfill \end{array}$$

(21)

for all $k\in \mathbb{N}.$ Summing the above inequality over $k=1,2,3,...,n-1,$ we obtain

$${\displaystyle n(f+g)\left(x^{*}\right)-\sum _{k=0}^{n-1}(f+g)\left(x_k\right)\ge \frac{1}{2\gamma }\parallel x_n-x^{*}{\parallel }^2-{\parallel x_0-x^{*}\parallel }^2,}$$

for all $n\in \mathbb{N}$. Since, $\left\{(f+g)\left(x_k\right)\right\}$ is a non-increasing, we have

$$n(f+g)\left(x^{*}\right)-n(f+g)\left(x_n\right)\ge \frac{1}{2\gamma }\parallel x_n-x^{*}{\parallel }^2-{\parallel x_0-x^{*}\parallel }^2,$$

for all $n\in \mathbb{N}$. Hence,

$$(f+g)\left(x_n\right)-(f+g)\left(x^{*}\right)\le \frac{1}{2\gamma }\frac{\parallel x_0-x^{*}{\parallel }^2}{n}$$

(22)

Since $x^{*}$ is arbitrarily chosen from $S_{*}$, we obtain

$${\displaystyle (f+g)\left(x_n\right)-\underset{x\in H}{min}(f+g)\left(x\right)\le \frac{1}{2\gamma }\frac{{\left[d(x_0,S_{*})\right]}^2}{n},}$$

for all $n\in \mathbb{N},$ and the proof is now complete. □

4. Some Applications on Data Classification

In this section, we apply Algorithms 3, 5, 7, and 8 to solve some classification problems based on a learning technique called extreme learning machine (ELM) introduced by Huang et al. [28]. It is formulated as follows:

Let $\{(x_k,t_k):x_k\in {\mathbb{R}}^n,t_k\in {\mathbb{R}}^m,k=1,2,\dots ,N\}$ be a set of N samples where $x_k$ is an input and $t_k$ is a target. A simple mathematical model for the output of ELM for SLFNs with M hidden nodes and activation function G is defined by

$${\displaystyle o_j=\sum _{i=1}^M{\eta }_{i}G(⟨w_i,x_j⟩+b_i),}$$

where $w_i$ is the weight that connects the i-th hidden node and the input node, ${\eta }_i$ is the weight connecting the i-th hidden node and the output node, and $b_i$ is the bias. The hidden layer output matrix $\mathbf{H}$ is defined by

$$\mathbf{H}=\left[\begin{array}{ccc}G(⟨w_1,x_1⟩+b_1)& \cdots & G(⟨w_M,x_1⟩+b_M)\\ ⋮& \ddots & ⋮\\ G(⟨w_1,x_N⟩+b_1)& \cdots & G(⟨w_M,x_N⟩+b_M)\end{array}\right].$$

The main objective of ELM is to calculate an optimal weight $\eta ={[{\eta }_1^T,\dots ,{\eta }_M^T]}^T$ such that $\mathbf{H}\eta =\mathbf{T},$ where $\mathbf{T}={[t_1^T,\dots ,t_N^T]}^T$ is the training target. If the Moore–Penrose generalized inverse${\mathbf{H}}^{†}$ of $\mathbf{H}$ exists, then $\eta ={\mathbf{H}}^{†}\mathbf{T}$ is the solution. However, in general cases, ${\mathbf{H}}^{†}$ may not exist or be difficult for computation. Thus, in order to avoid such difficulties, we transformed the problem into a convex minimization problem and used our proposed algorithm to find the solution $\eta$ without ${\mathbf{H}}^{†}$.

In machine learning, a model can be overfit in the sense that it is very accurate on a training sets, but inaccurate on a testing set. In other words, it cannot be used to predict unknown data. In order to prevent overfitting, the least absolute shrinkage and selection operator (LASSO) [29] is used. It can be formulated as follows:

$${\mathrm{Minimize}:\parallel \mathbf{H}\eta -\mathbf{T}\parallel }_2^2+\lambda {\parallel \eta \parallel }_1,$$

(23)

where $\lambda$ is a regularization parameter. If we set $f\left(x\right):={\parallel \mathbf{H}x-\mathbf{T}\parallel }_2^2$ and $g\left(x\right):={\lambda \parallel x\parallel }_1,$ then the problem (Section 4) is reduced to the problem (1). Hence, we can use our algorithm as a learning method to find the optimal weight $\eta$ and solve classification problems.

In the experiments, we aim to classify three data sets from https://archive.ics.uci.edu (accessed on 15 November 2021):

• Iris data set [30]. Each sample in this data set has four attributes, and the set contains three classes with 50 samples for each type.
• Heart disease data set [31]. This data set contains 303 samples each of which has 13 attributes. In this data set, we classified two classes of data.
• Wine data set [32]. In this data set, we classified three classes of 178 samples. Each sample contains 13 attributes.

In all experiments, we used the sigmoid as the activation function. The number of hidden nodes $M=30.$ We calculate the accuracy of the output data by:

$$\mathrm{accuracy}=\frac{\mathrm{correctly} \mathrm{predicted} \mathrm{data}}{\mathrm{all} \mathrm{data}}\times 100.$$

We chose control parameters for each algorithm as seen in Table 1.

Table 1. Chosen parameters of each algorithm.

	Algorithm 3	Algorithm 5	Algorithm 7	Algorithm 8
$\sigma$	0.49	0.124	0.124	0.124
$\delta$	0.1	0.1	0.1	0.1
$\theta$	0.1	0.1	0.1	0.1
${\alpha }_n$	-	-	$\frac{1}{2}$	$\frac{1}{3}$

In our experiments, the inertial parameters ${\beta }_n$ for Algorithm 7 were chosen as follows:

$${\beta }_n=\left\{\begin{array}{c}0.95, \mathrm{if} n\le 1000\hfill \\ \frac{1}{n^2}, \mathrm{if} n\ge 1001.\hfill \end{array}\right.$$

In the first experiment, we chose the regularization parameter $\lambda =0.1$ for all algorithms and data sets. Then, we used 10-fold cross-validation and utilized Average ACC and ERR${}_{\%}$ for evaluating the performance of each algorithm.

$${\displaystyle \mathrm{Average} \mathrm{ACC}=\sum _{i=1}^N\frac{x_i}{y_i}\times 100\%/N,}$$

where N is the number of folds ($N=10$), $x_i$ is the number of data correctly predicted at fold i, and $y_i$ is the number of all data at fold i.

Let err${}_{Lsum}$ = the sum of errors in all 10 training sets, err${}_{Tsum}$ = the sum of errors in all 10 testing sets, $Lsum=$ the sum of all data in all 10 training sets, and $Tsum=$ the sum of all data in all 10 testing sets. Then,

$${\mathrm{ERR}}_{\%}=({\mathrm{err}}_{L\%}+{\mathrm{err}}_{T\%})/2,$$

where err${}_{L\%}$ = $\frac{{\mathrm{err}}_{Lsum}}{Lsum}\times 100\%$ and err${}_{T\%}$ = $\frac{{\mathrm{err}}_{Tsum}}{Tsum}\times 100\%$.

With these evaluation tools, we obtained the results for each data set as seen in Table 2, Table 3 and Table 4.

Table 2. The performance of each algorithm in the first experiment at the 200th iteration with 10-fold cv. on the Iris data set.

	Algorithm 3		Algorithm 5		Algorithm 7		Algorithm 8
	acc.train	acc.test	acc.train	acc.test	acc.train	acc.test	acc.train	acc.test
Fold 1	87.41	86.67	93.33	86.67	97.78	100	97.04	93.33
Fold 2	88.15	93.33	92.59	100	96.30	100	96.30	100
Fold 3	88.15	100	92.59	100	97.78	93.33	96.30	100
Fold 4	88.15	100	92.59	100	97.78	100	96.30	100
Fold 5	86.67	86.67	93.33	86.67	97.78	100	96.30	100
Fold 6	88.15	73.33	92.59	80	99.26	86.67	97.78	86.67
Fold 7	87.41	100	92.59	100	97.78	100	96.30	100
Fold 8	88.15	86.67	93.33	93.33	97.04	93.33	97.78	86.67
Fold 9	88.89	80	93.33	93.33	98.52	93.33	96.30	93.33
Fold 10	88.15	73.33	92.59	93.33	97.78	100	95.56	100
Average acc.	87.93	88	92.89	93.33	97.78	96.67	96.59	96
ERR${}_{\%}$	12.04		6.89		2.78		3.70
Time	0.0609		0.0901		0.0781		0.0767

Table 3. The performance of each algorithm in the first experiment at the 200th iteration with 10-fold cv. on the Heart disease data set.

	Algorithm 3		Algorithm 5		Algorithm 7		Algorithm 8
	acc.train	acc.test	acc.train	acc.test	acc.train	acc.test	acc.train	acc.test
Fold 1	79.85	86.67	81.32	86.67	83.15	93.33	82.05	86.67
Fold 2	80.15	80.65	80.15	80.65	84.19	83.87	81.62	83.87
Fold 3	81.25	77.42	82.35	77.42	84.93	77.42	83.09	80.65
Fold 4	80.51	83.87	82.35	87.10	84.56	80.65	82.72	90.32
Fold 5	79.85	90	81.32	90	84.98	86.67	82.42	86.67
Fold 6	81.68	80	83.15	83.33	84.62	86.67	83.52	83.33
Fold 7	80.22	86.67	81.68	83.33	84.25	83.33	82.05	83.33
Fold 8	82.05	66.67	82.42	66.67	84.98	73.33	82.42	66.67
Fold 9	81.32	70	81.68	70	86.08	73.33	82.05	70
Fold 10	80.95	76.67	82.05	80	84.25	83.33	82.05	80
Average acc.	80.78	79.86	81.85	80.52	84.60	82.19	82.40	81.15
ERR${}_{\%}$	19.67		18.81		16.61		18.21
Time	0.0726		0.1048		0.1004		0.0921

Table 4. The performance of each algorithm in the first experiment at the 200th iteration with 10-fold cv. on the Wine data set.

	Algorithm 3		Algorithm 5		Algorithm 7		Algorithm 8
	acc.train	acc.test	acc.train	acc.test	acc.train	acc.test	acc.train	acc.test
Fold 1	96.89	100	96.89	100	99.38	100	98.14	100
Fold 2	96.88	100	97.50	100	99.38	100	98.13	100
Fold 3	97.50	100	98.13	100	99.38	100	98.13	100
Fold 4	97.50	100	96.88	100	99.38	100	98.13	100
Fold 5	96.88	100	97.50	100	99.38	100	98.13	100
Fold 6	97.50	94.44	96.88	100	99.38	100	98.13	100
Fold 7	97.50	94.44	98.13	94.44	100	94.44	98.75	94.44
Fold 8	97.50	100	96.88	100	99.38	100	98.13	100
Fold 9	98.75	88.89	98.13	88.89	99.38	88.89	99.38	88.89
Fold 10	98.76	88.24	98.76	88.24	99.38	100	98.14	100
Average acc.	97.57	96.60	97.57	97.16	99.44	98.33	98.31	98.33
ERR${}_{\%}$	2.90		2.62		1.12		1.69
Time	0.0624		0.0997		0.0870		0.0810

As seen in Table 2, Table 3 and Table 4, with the same regularization $\lambda =0.1$, Algorithms 7 and 8 perform better than Algorithms 3 and 5 in terms of accuracy, while the computation times are relatively close among the four algorithms.

In the second experiment, the regularization parameters $\lambda$ for each algorithm and data set were chosen using 10-fold cv. We compared the error of each model and data set with various $\lambda$, then chose the $\lambda$ that gives the lowest error ($ER{R}_{\%}$) for the particular model and data set. Hence, the parameter $\lambda$ varies depending on the algorithm and data set. The choice of parameters $\lambda$ can be seen in Table 5.

Table 5. Chosen $\lambda$ of each algorithm.

	Regularization Parameter $\mathit{\lambda }$
	Iris	Heart Disease	Wine
Algorithm 3	$0.001$	$0.003$	$0.02$
Algorithm 5	$0.01$	$0.03$	$0.006$
Algorithm 7	$0.003$	$0.13$	$0.0001$
Algorithm 8	$0.01$	$0.008$	$0.003$

With the chosen $\lambda$, we also evaluated the performance of each algorithm using 10-fold cross-validation and similar evaluation tools as in the first experiment. The results can be seen in the following Table 6, Table 7 and Table 8.

Table 6. The performance of each algorithm in the second experiment at the 200th iteration with 10-fold cv. on the Iris data set.

	Algorithm 3		Algorithm 5		Algorithm 7		Algorithm 8
	acc.train	acc.test	acc.train	acc.test	acc.train	acc.test	acc.train	acc.test
Fold 1	88.15	86.67	93.33	86.67	98.52	100	97.04	93.33
Fold 2	88.15	93.33	92.59	100	98.52	100	96.30	100
Fold 3	88.89	100	93.33	100	98.52	100	96.30	100
Fold 4	88.15	100	92.59	100	98.52	100	96.30	100
Fold 5	86.67	86.67	93.33	86.67	98.52	100	96.30	100
Fold 6	88.15	73.33	93.33	80	99.26	86.67	97.78	86.67
Fold 7	87.41	100	92.59	100	98.52	100	96.30	100
Fold 8	88.15	86.67	93.33	93.33	97.78	100	97.78	86.67
Fold 9	88.89	80	93.33	93.33	98.52	100	96.30	93.33
Fold 10	88.15	73.33	92.59	93.33	98.52	100	95.56	100
Average acc.	88.07	88	93.04	93.33	98.52	98.67	96.59	96
ERR${}_{\%}$	11.96		6.81		1.41		3.70
Time	0.0618		0.0973		0.0793		0.0783

Table 7. The performance of each algorithm in the second experiment at the 200th iteration with 10-fold cv. on the Heart disease data set.

	Algorithm 3		Algorithm 5		Algorithm 7		Algorithm 8
	acc.train	acc.test	acc.train	acc.test	acc.train	acc.test	acc.train	acc.test
Fold 1	79.49	86.67	82.05	86.67	84.25	80	82.05	86.67
Fold 2	80.15	80.65	80.51	83.87	83.82	87.10	81.62	83.87
Fold 3	81.62	77.42	81.99	80.65	84.56	80.65	83.46	80.65
Fold 4	80.51	83.87	82.72	90.32	83.82	87.10	83.09	87.10
Fold 5	79.85	90	82.42	86.67	86.45	76.67	82.78	86.67
Fold 6	81.68	80	83.52	83.33	85.35	86.67	83.52	83.33
Fold 7	80.22	86.67	81.68	83.33	84.98	73.33	82.05	83.33
Fold 8	82.42	66.67	82.42	66.67	83.15	90	82.78	66.67
Fold 9	80.95	70.00	82.05	70	84.62	83.33	82.42	70
Fold 10	80.95	76.67	82.05	80	84.98	90	82.78	83.33
Average acc.	80.78	79.86	82.14	81.15	84.60	83.48	82.66	81.16
ERR${}_{\%}$	19.67		18.34		15.95		18.08
Time	0.0794		0.1129		0.1013		0.097

Table 8. The performance of each algorithm in the second experiment at the 200th iteration with 10-fold cv. on the Wine data set.

	Algorithm 3		Algorithm 5		Algorithm 7		Algorithm 8
	acc.train	acc.test	acc.train	acc.test	acc.train	acc.test	acc.train	acc.test
Fold 1	96.89	100	97.52	100	99.38	100	98.14	100
Fold 2	96.88	100	97.50	100	100	100	98.75	100
Fold 3	97.50	100	97.50	100	100	100	98.13	100
Fold 4	97.50	100	98.13	100	99.38	100	98.13	100
Fold 5	97.50	100	98.13	100	99.38	100	98.13	100
Fold 6	97.50	94.44	98.13	100	99.38	100	98.13	100
Fold 7	97.50	94.44	98.75	94.44	100	94.44	98.75	94.44
Fold 8	97.50	100	97.50	100	99.38	100	98.13	100
Fold 9	98.75	88.89	98.75	88.89	99.38	100	99.38	88.89
Fold 10	98.76	88.24	98.14	88.24	100	100	98.14	100
Average acc.	97.63	96.60	98	97.16	99.63	99.44	98.38	98.33
ERR${}_{\%}$	2.87		2.40		0.47		1.65
Time	0.0644		0.0971		0.0874		0.0819

With the chosen regularization parameters $\lambda$ as in Table 5, we see that the $ER{R}_{\%}$ of each algorithm in Table 6, Table 7 and Table 8 is lower than that of Table 2, Table 3 and Table 4. We can also see that Algorithms 7 and 8 perform better than Algorithms 3 and 5 in terms of accuracy in all experiments conducted.

In Figure 3, we show the graph of $ER{R}_{\%}$ for each algorithm of the second experiment. As we can see, Algorithms 7 and 8 have lower $ER{R}_{\%}$, which means they perform better than Algorithm 3 and 5.

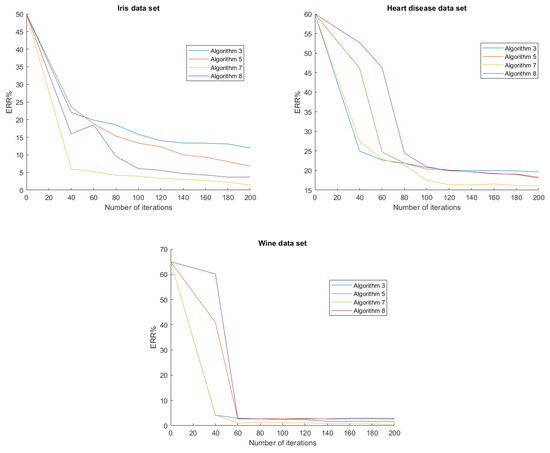
Figure 3. ERR${}_{\%}$ of each algorithm and data set of the second experiment.

From Table 6, Table 7 and Table 8, we can notice that the computational time of Algorithms 7 and 8 is $30\%$ slower than Algorithm 3 at the same number of iterations. However, from Figure 3, we see that at the 120th iteration, both Algorithms 7 and 8 have lower $ER{R}_{\%}$ than Algorithm 3 at the 200th iteration. Therefore, the time needed for Algorithms 7 and 8 to achieve the same accuracy as or higher accuracy than Algorithm 3 is actually lower because we can compute the 120-step iteration much faster than the 200-step iteration.

5. Conclusions

We introduced a new line search technique and employed it in order to introduce new algorithms, namely Algorithms 7 and 8. Furthermore, Algorithm 7 also utilizes an inertial step to accelerate its convergence behavior. Both algorithms converge weakly to a solution of (1) without the Lipschitz assumption on $▿f$. The complexity of Algorithm 8 was also analyzed and studied. Then, we applied the proposed algorithms to the data classification of the Iris, Heart disease, and Wine data set, then their performances were evaluated and compared with other line search algorithms, namely Algorithms 3 and 5. We observed from our experiments that Algorithm 7 achieved the highest accuracy in all data sets under the same number of iterations. Moreover, Algorithm 8, which is not an inertial algorithm, also performed better than Algorithms 3 and 5. Furthermore, from Figure 3, we see that at a lower number of iterations, the proposed algorithms were more accurate than the other algorithms at a higher iteration number.

Based on the experiments on various data sets, we conclude that the proposed algorithms perform better than the previously established algorithms. Therefore, for our future works, we would like to implement the proposed algorithm to predict and classify the data of patients with non-communicable diseases (NCDs) collected from Sriphat Medical Center, Faculty of Medicine, Chiang Mai University, Thailand. We aim to make an innovation for screening and preventing non-communicable diseases, which will be used in hospitals in Chiang Mai, Thailand.