Abstract
The publication opportunities in science require knowing the existing gaps in the academic debate. In recent decades, scholars specializing in fuzzy theory and applied methodologies have experienced an unprecedented evolution of the field. The Sustainable Development Goals (SDGs) have shaped the way socio-technical transitions use fuzzy methodologies to solve environmental problems. This study conducts a systematic literature review of articles published in the Journal Citations Report on these specific fields. The Web of Science (Core Collection) was used and a database was assembled (N = 1956) that allowed the evaluation of the evolution of the research agenda and detecting high-impact publication opportunities. A model of analysis of successful strategies in academic influence is proposed. The model is tested with a configurational methodology through fuzzy-set Qualitative Comparative Analysis (fsQCA). The conditions used are: number of authors, underlying interest of the researchers, standardized citations per year, age of the articles and link of the research with sustainability. The results are solid and inform five paths that ensure the success of academic publications in high-impact journals. The robustness of the model allows its extrapolation to other fields of research. The contribution of this article allows knowledge of the academic conversation and its research opportunities. In addition, it clarifies the different paths that guarantee high impact research articles. This article offers important recommendations for academics and journal editors, allowing them to guide and advise academic production in the scholarly debate of the future.
MSC:
03E72
1. Introduction
Mathematics is at the base of Boolean logic and it is a field of knowledge that has actively contributed to the promotion of fuzzy theory and the development of methodologies based on fuzzy set, as well as its applications to multiple related areas related with engineering and management.
Since its origins, the development of the Fuzzy Sets Theory has provided tools that facilitate the construction of useful conceptual frameworks for understanding complexity, beyond recognizing patterns and processing and classifying information [1]. Thus, the theory achieved important developments, evolving as fuzzy sets and fuzzy logic in multi-criteria decision making in the last half century [2].
Academics need to know the best publishing practices from the benchmark that determines the success factors of a published article. The purpose of all academic research is to achieve the maximum possible dissemination. The total citations of an article is a standardized indicator to evaluate the success of a publication strategy. The impact of an article is measured according to its ability to influence academic conversation, modeling the lines of research, methodologies and applications. A configurational analysis of the article is carried out and the five successful strategies applied by academics to maximize the impact of their research are identified.
This work is structured as follows: first, a review of the theoretical framework is carried out. Second, the Materials and Methods Section presents the data sources used and the analysis procedure, with the formulation of the proposed model to understand the strategies for success in the academic publication on Fuzzy Sets Theory. In this section, the configurational methodology chosen to test the proposed model is described. Third, the Results and the Discussion Sections analyze the evidence found and its implications for the academic community. Fourth, the Conclusions Section draws general implications to consider about the opportunities for publication, as well as future lines of research to evaluate emerging issues, especially in the application of fuzzy methodologies for solving problems related to sustainability, climate change and the context proposed by the Sustainable Development Goals (SDGs). Finally, to facilitate the reading of this article, two appendices with relevant complementary information are incorporated, both to detect publication opportunities and also to know the details of the success strategies applied by the best academics in the research agenda of fuzzy sets and math.
The theory of fuzzy sets provides logical-mathematical frameworks that allow the rigorous study of phenomena with the use of precise methodologies [3,4,5,6,7,8,9,10], according to a duly modeled notion of imprecision. It permits the study of problems to be easily approached when there is an absence of univocal criteria for belonging to the observable variables to the categories that constitute the phenomena [11]. In recent decades, Fuzzy Sets Theory has expanded with its own ideas and original concepts while, in parallel, it extended to reach classical areas of mathematics such as algebra, graph theory or topology, among others. In parallel, it has been developed as “fuzzy technology” as an orientation to modeling and problem solving [4,10], being complementary to other existing methodologies, sometimes with controversial compared results [12].
2. Materials and Methods
Authors such as Ragin [13], Rihoux and Ragin [14] and Schneider and Wagemann [15] contributed to popularizing the fuzzy-set Qualitative Comparative Analysis (fsQCA) and Qualitative Comparative Analysis (QCA) methodologies, known as csQCA since popularization of fsQCA. In addition, in recent decades other approaches such as multi-value Qualitative Comparative Analysis (mvQCA) [16] and time series analysis using fuzzy sets [17] have become popular.
The fsQCA variant is based on applying a new algebra, making comparative case analyzes more refined [15]. fsQCA does not require dichotomizing the study variables or distinguishing the presence or absence within a set, but rather establishes membership [13,18] according to different thresholds. Thus, with adequate methodological control, fsQCA allows it to be possible to identify existing connections between the cases studied, highlighting underlying asymmetric relationships that would be discarded with the use of conventional statistical methodologies when registering statistically non-significant values of one or more dependent variables [19]. Since it allows improving the knowledge of the cases under study, fsQCA has undergone notable development in recent years [20], having been applied in multiple fields of research related to management [21].
This study used a systematic review of academic publications of scientific articles published in the Core Collection of the Web of Science (WoS-CC). The search was carried out in any period and in all languages, limiting the type of document to articles published in the Journal Citation Reports® (SSCI and SCIE). The academic literature on fuzzy set links to Boolean logic, set theory and mathematical logic. The specific analysis implemented focused on academic publications on fuzzy theory from the field of mathematics research and its applications.
The search strategy applied two different scopes. On the one hand, a broad one was defined consisting of the co-occurrence of terms such as fuzzy set or fsQCA and subject mathematics (N = 1956). In this way, the search terms included within the scope were connected with Boolean operators OR according to the attributes Title (TI), Topic (TS), Abstract (AB), Author Keywords (AK) and Keyword Plus® (KP), and the Boolean operator AND according to the Subject (SU) attribute. On the other hand, a restricted scope was defined, only for studies related to sustainability and published in journals indexed in the Journal Citation Reports®, as a subset of the wide-scope search (Top10). This second search focuses its analysis on the evaluation of articles on fuzzy set, fuzzy logic and mathematics with an application oriented to Sustainability Oriented Innovations (SOIs) [22,23].
There are multiple methodologies for carrying through systematic literature reviews and bibliographic reviews, such as PRISMA [24]. To achieve the bibliographic review, the methodology proposed by Thomé et al. [25], backward and forward searches were performed, in an attempt to locate documents that could have been generated as bias from the initial keyword search. Figure 1 shows the review methodology applied in this article. The first search returned 1989 results. The application of quality and contextual threshold performs an evaluation of the search results, in-depth review and residual search, configuring a database of 1956 articles. The search added articles according to the Boolean search (“fuzzy set” OR fsQCA) in journals in the mathematics area indexed in the Science Citation Index Expanded (SCIE) or the Social Sciences Citation Index (SSCI). The type of document selected was article, and no chapters or proceedings were included. Therefore, if an article did not meet both requirements, it was not included in the database of this study, even in the case of seminal articles on Fuzzy Sets Theory, whose origin dated back to 1956, that is, two decades prior to the first article located.
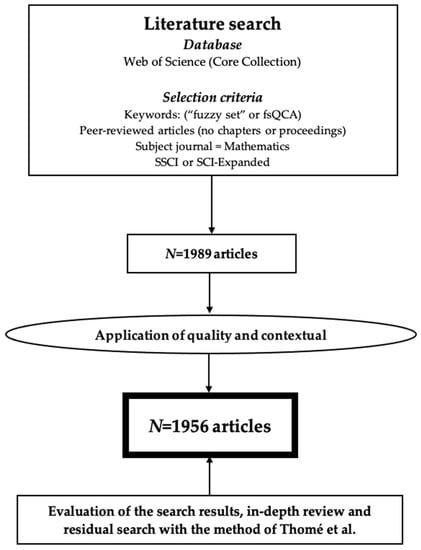
Figure 1.
Systematic research approach.
Figure 1 shows the activity workflow followed. From top to bottom: first, activity flow and search criteria applied; second, preliminary results obtained; third and fifth, filtering activity with application of quality and contextual criteria; fourth, final results that constitute the research database used in this article.
The robustness of the search was demonstrated by not finding new additional studies and by confirming that the methodology used identified the main research topics on fuzzy set, fsQCA in mathematics fields and the restricted search for the subset of articles on sustainability. Subsequently, the data were analyzed from a double approach, according to the static and dynamic evaluation of the research agenda. Both analyzes evaluated the production of documents and academic impact, for the entire period (1977–2021) and for two different sub-periods (1977–2007; 2008–2021). The sub-periods were constructed applying as the threshold the beginning of the great financial crisis (GFC), the year in which the VUCA approach began to be generalized [26] in engineering and management studies, according to a persistent vector that is based on four dimensions: Volatility (V), Uncertainty (U), Complexity (C) and Ambiguity (A).
In addition, three variables were calculated that allowed the capture of the academic impact of the research published in the last few decades. The first variable was the total number of citations achieved by an article since its publication (Total or absolute impact; IMP). The second variable was an indicator of relative impact (Normalized Impact per Year; NIY), which divides the total impact by the number of years that have elapsed since the publication of the article. The third variable was another indicator of relative impact regarding the impact of a journal (Normalized Impact per Article; NIA), calculated as the sum of citations achieved by all the articles published by a journal, divided by the number of articles published by the journal, in all periods.
The bibliometric analysis used the VOS Viewer 1.6.17 software [27] to study the networks of keywords, countries and journals. VOS Viewer has been used in multiple previous studies and is a tool with high precision of results [28,29,30]. The evaluation of specific articles on fuzzy set, fuzzy logic, mathematics and sustainability was carried out with a systematic review that allowed identifying publication opportunities on new emerging topics. Additionally, a configurational analysis was carried out to find out what the success and failure strategies were, maximizing the impact of the articles analyzed (N = 1956).
Equation (1):
IMP = f (YEARS, NIY, UC, CRC, SUST, OA)
Outcome is measured as the absolute impact (IMP). The weight of the article’s age in the WoS-CC database, expressed as the years that have elapsed since its publication. An anchoring effect is assumed based on the accumulated citations’ spiral (YEARS). The Normalized Impact per Year (NIY) is also considered, assuming that the impact of novel articles should be considered as a contingent variable that helps to explain successful strategies. In addition, according to Clarivate® data, the usage count since 2013 (UC) is identified. This variable explains the latent interest of researchers in an article, and may not be manifested as a citation, either because it is a cross-sectional article whose ultimate impact is minimal but it is a relevant article (e.g., review of the literature), or because it is an article that is very recent and UC is presented as an advanced variable of citations, since academics have cited the article in manuscripts that are in the revision phase and have not yet been published. The count of cited references included in the article (CRC) is also used as an independent variable. It is assumed that the articles with more references could be more citable, insofar as they represent bibliometric studies or systematic reviews of academic literature. However, another path of academic relevance and impact comes from articles with very few cited references included, usually because they are seminal studies in the field or, in any case, because they have contributed in a disruptive way to the fuzzy set discipline. Finally, two control variables designed as dichotomous variables are included. On the one hand, the SUST condition encodes if an article is related to sustainability (specific Boolean operators were applied in the title, abstract, keyword and keyword plus attributes, according to the terms: climat*, sustainab*, waste*, SDG*, warming, 2020, environments), showing 0 if the article is not related to sustainability issues and 1 if the article is related to sustainability. On the other hand, the OA condition determines the number of authors of an article: the value 1 reports the authorship of a single academic and the value 0 reports collective authorship (more than one author).
The model was tested with fuzzy set Qualitative Comparative Analysis (fsQCA) according to the standards and best practices of the methodology [13,14,15,18,19,20,31,32,33,34,35,36,37]. This methodology is based on quantitative and qualitative analysis and Boolean algebra, and allows the identification of the safe pathways for the design and execution of successful strategies in the high impact articles in the field of mathematics and fuzzy logic. A QCA performs a set theory analysis to look at all potential relationships between the outcome and the possible binary combinations of predictive conditions. The analysis produces attributes both necessary and sufficient to explain the result, giving causally asymmetric elements. Therefore, sometimes, the combinations of the conditions that explain the result are different from those that indicate the lack of the result. Boolean logic offers important factual and counterfactual implications for the analysis of reality. Dialogue with the cases makes it possible to establish the scope and definition of the objective of the investigation.
In addition to large samples, QCA methodology is suitable for small and medium samples [38]. QCA overcomes the limitations of inferential statistical techniques [19], since it is not necessary that the relationship be given with a minimum intensity to achieve statistical significance, and, consequently, it allows the advancement of knowledge from the study of particular cases [13,14,36]. In this study, the purpose is to know how the cases of articles published in high-impact academic journals followed specific recipes that guaranteed relevance among academics.
The solutions to the model tested with QCA establish the pathways that allow an increase in the impact of a scientific article published in journals indexed in the JCR®. QCA allows improvement in the profiling of the theoretical scheme [39]. In fact, the QCA analysis offers an unconventional vision to evaluate theoretical relationships not yet studied and the study of counterfactuals allows influencing issues not yet explained by the theory. The study of causal configurations is based on the principle of asymmetry and equifinality [33]. The same result can be achieved through various combinations of attributes and the configurations are not necessarily symmetrical. However, the research question of this study focuses on the analysis of successful strategies in generating impact. As a consequence, only the presence of the outcome (IMP) was analyzed. It allows a systematic study of the crossover cases resulting from all the possible combinations of relationships between the different types of explanatory and explained conditions for recipes followed by academics to maximize the impact of their research. They are used as explanatory variables (attributes or conditions).
According to Fiss [33], the QCA analysis process follows four steps: (1) define the property space; (2) create joint membership measures; (3) evaluate the coherence between global relationships and (4) logically reduce the different results. Our study used the fuzzy-set QCA variant (fsQCA), especially recommended for the study of multilevel theory. The fsQCA assesses whether the membership of cases to causal conditions is related to the result, considering a continuum calibrated between 0 and 1 for all the dependent and independent variables. The belonging of the data established a zone of maximum ambiguity (0.5) that establishes the cross-point that delimits in a qualitative-conceptual way if a case is located within or outside of a set. After the calibration process, the values of each variable are configured in fuzzy sets. The analysis based on fuzzy sets preserves the properties of sharp sets [35], and makes it possible to model cyclical causality [33], analyzing the relationships between theoretical sets based on the specificity of the cases.
On the other hand, according to Fiss [33], a fsQCA allows modeling of the concept of cyclical causality since it allows us to understand the influence of causal conditions of successful strategies on the impact publication of the articles analyzed. This fact is true even when several combinations of chance conditions occur for the same result, introducing the concept of equifinality.
Finally, this method allows for the asymmetry between the attributes that explains the success and failure of think tank strategies. A fsQCA allows for more refined and thoughtful analysis than other quantitative techniques aimed at explaining success and failure from a symmetrical perspective.
The fsQCA analysis evaluates the necessary conditions for the outcome to be given and the set of pathways that are explained, by analyzing sufficient conditions that configure the different solutions to the proposed model. The calibration process was carried out using percentiles, assigning different degrees of membership following the fuzzy set of three values that delimit fully inside, maximum ambiguity and fully outside, and the dichotomous variables were coded using binary and metric values [32], with assignment to the fully inside (1) and fully outside (0) sets, respectively. Success strategies were analyzed to achieve impact on the academic publications in the WoS-CC. The variables were defined by calibration following the method proposed by [19], using the 95th, 50th and 5th percentiles. Table 1 reports the descriptive statistics of the variables, as well as the thresholds that delimit the full-inside points. (0.95), maximum ambiguity (0.5) and full-outside (0.05).

Table 1.
Calibration and descriptive statistics.
The methodological process followed the best practices for fsQCA analysis, allowing adequate results for the connection and extension of the theoretical framework through empirical support based on evidence.
3. Results
3.1. Bibliometric Analysis
The WoS-CC search returned 1956 articles published during the last 44 years. The first available registry was published in 1977 and the last in 2021. Figure 2 shows the number of articles published throughout the period, as well as the regression and the coefficient of determination R2. The trend is growing, especially in the last four years.
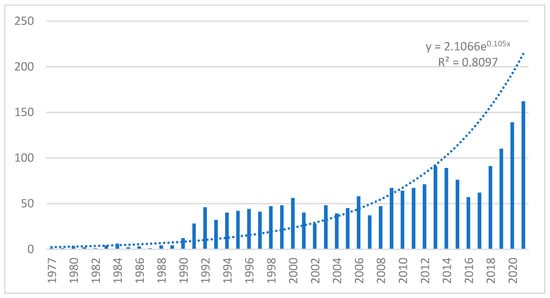
Figure 2.
Impact scholarly publication trend on fuzzy sets.
The studies published in WoS-CC obtained 55,995 citations, registering an average of 28.61 citations per article. Table 2 shows the evolution of the fuzzy set research agenda in the field of mathematics, showing articles, citations and citations by year according to groupings made by decades. A notable evolution of articles, citations and NIY is observed, reaching the maximum number of articles and NIY in the decade 2010–2019 and the maximum number of citations per article in the decade 2000–2009.

Table 2.
Intertemporal analysis. Articles, citations and Normalized Impact per Years (NIY).
The “citations per year” ratio was calculated in order to capture relevant information on the implicit impact of academic production. For each article, the total citations were divided by age and article, calculated as years elapsed from its publication date to 2021. The evidence suggests a constant increase in the production of articles per year, with the decade 2010–2019 being the one that collected the most articles (778), while the period with the most citations was the decade 2000–2009. However, the decade 2010–2019 concentrated on more citations per year, improving the efficiency and impact of mathematical production on fuzzy logic, fuzzy systems and fuzzy sets.
Figure 3 shows the total citations according to the year of publication of the article.
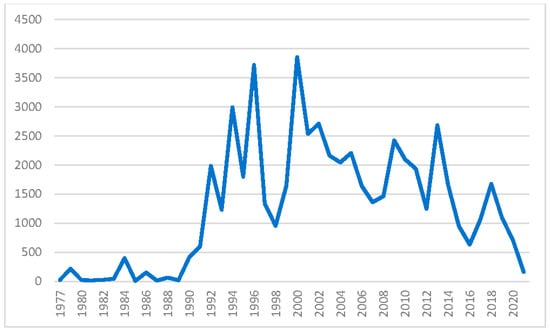
Figure 3.
Intertemporal evolution of citations per article and per year.
Figure 4 shows the standardized citations per year, according to the articles published in each year.
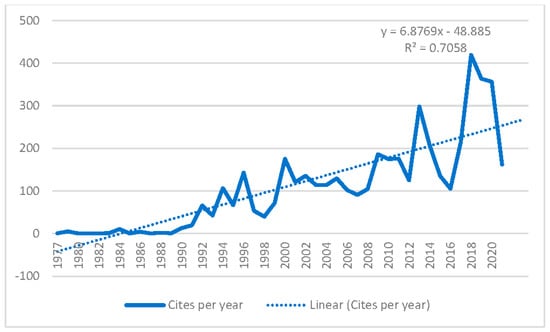
Figure 4.
Intertemporal evolution of citations per year.
Next, the results obtained are analyzed from a double perspective. Thematic clusters, main countries contributing to the academic debate and main journals are analyzed. In all three cases, the network map and its inter-temporal evolution are presented. The network map shows the connections between topics, countries and journals. The intertemporal analysis shows the forefront of scientific knowledge and the protagonists of evolution.
Table 3 reports the academic impact of the articles according to their journal, showing the number of articles per journal, their absolute impact and their relative impact (citations per article).

Table 3.
High-impact journals.
The journal Fuzzy Sets and Systems stands out in the first level of academic production and citations. Computers & Mathematics with Applications, Applied Mathematical Modeling and the Iranian Journal of Fuzzy Systems follow in absolute impact level. The top five absolute impact magazines concentrates 50% of the total citations.
The co-occurrence map captured information for both the author keywords and keyword plus, added by WoS. Figure 5 clearly identifies four thematic clusters based on keywords of the published articles. Cluster 1 (red): fuzzy set, mapping, fixed points, algebra, analysis of existence, convergence and representation, and evaluation of categories and unique classifications; Cluster 2 (blue): sets, aggregation operators, accuracy and score functions, membership evaluation, numbers, information and decision-making; Cluster 3 (green): models, selection, AHP, management and supply chain, and performance and Cluster 4 (brown): archetypes and ideal profiles, sub-groups, filters and elements. Cluster 1 focuses on the core of the Fuzzy Sets Theory; Cluster 2, on methodological application on sets and information systems; Cluster 3, on management and engineering applications and Cluster 4, on evaluation of the ideal and counterfactual configurations.
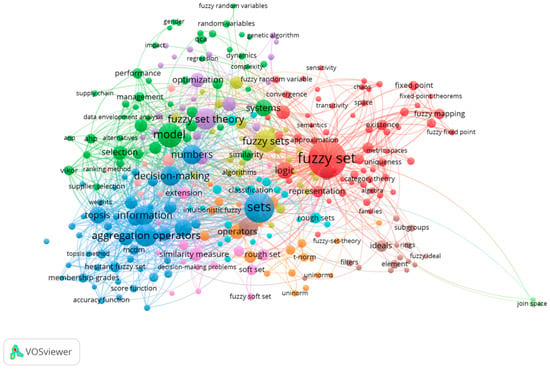
Figure 5.
Co-occurrences for all keywords. Network visualization.
The intertemporal analysis (Figure 6) allows us to check the change in academic discourse and how the research agenda has changed during the last decade. The analysis of the Fuzzy Sets Theory and the algorithms has developed the interest of academics on the operators of the models and hierarchical methods, such as AHP or the fuzzy-soft-set variant. Finally, in recent years, the trend has focused on the analysis and evaluation of membership grades, aggregation operators, extensions of the applications of the fuzzy-set methodology and the fuzzy MCDM based on ideal and anti-ideal concepts.
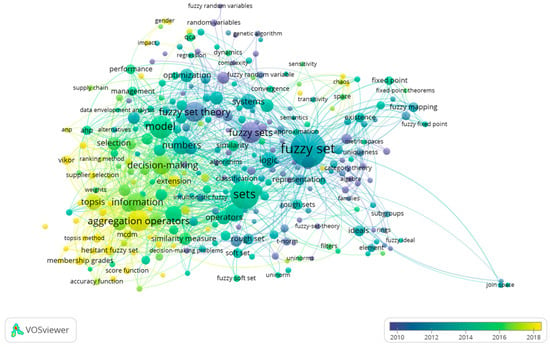
Figure 6.
Co-occurrences for all keywords. Overlay visualization.
Figure 7 and Figure 8 report the connections between the countries of the universities of affiliation of the authors of the articles. Specifically, Figure 7 shows the connection by affinity and Figure 8 the intertemporal evolution of the associations of universities and authors.
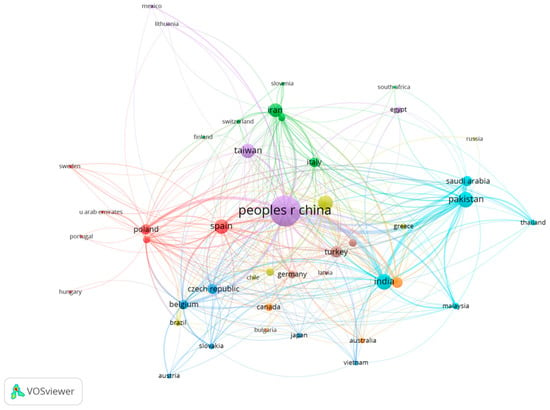
Figure 7.
Bibliographic coupling for countries. Network visualization.
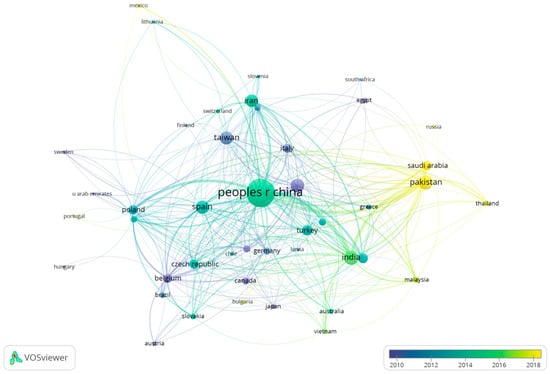
Figure 8.
Bibliographic coupling for countries. Overlay visualization.
The connection of academic collaboration between India, Malaysia, Pakistan, South Arabia and Thailand is confirmed. The connection between China and Taiwan is strong, and China’s production volume takes on special importance. On the other hand, the European connection between the Czech Republic, Belgium, Slovakia and Austria stands out. In addition, the authors of articles published by the institutions of Iran, Italy, Switzerland, Finland, Slovenia and South Africa are linked. Finally, there is an important connection between Spain, Poland, Sweden, United Arab Emirates, Portugal and Hungary.
The intertemporal evolution that has pivoted from precursor countries in 2010, such as Taiwan, Italy, Bekguynm Canada, Japan or Austria stands out. It passed through China, Spain and Iran in 2015–2016, and moved towards the vanguard of fuzzy set research led by Pakistan, Saudi Arabia and Thailand.
Figure 9 and Figure 10 report the existing connections between journals. Figure 8 shows the formal connections and Figure 9 shows their intertemporal evolution and the change of associations produced in the long term in the academic discourses of impact.
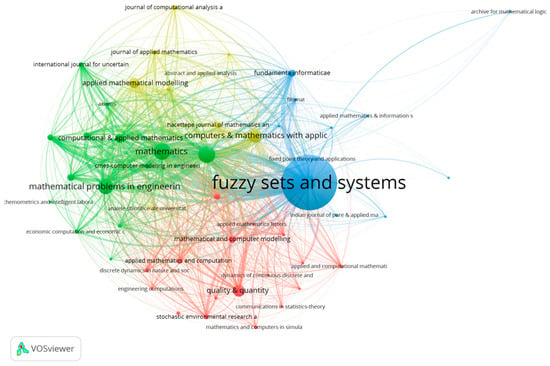
Figure 9.
Bibliographic coupling for journals. Network visualization.
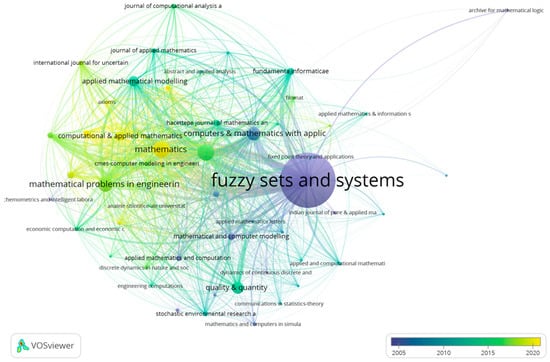
Figure 10.
Bibliographic coupling for journals. Overlay visualization.
The connection networks between journals are clear. Figure 8 reports four consolidated networks. First, with blue color, this connection given by Fuzzy Sets and Systems leads the connections. Second, with green color, this connection is co-led by Mathematics, Mathematical Problems in Engineering, and Computational and Applied Mathematics. Third, with red color, is led by Quality & Quantity. Fourth, with yellow color, is led by Applied Mathematical Modeling.
There is a clear evolution in the leadership of publications from the perspective of journals. In the last 15 years, the avant-garde has pivoted from Fuzzy Sets and Systems (still prominent in the number of published articles), to Mathematics, which has gained volume in recent years, in addition to standing alongside Computational and Applied Mathematics in the most advanced trend line in fuzzy set, fuzzy logic and fsQCA.
Appendix A (Table A1) reports the top articles by absolute impact (total citations), presenting research opportunities in this field, and including the complete reference of each article. The detailed analysis of the mathematical development carried out on the fuzzy knowledge area allows the evaluation of the scientific production published in indexed journals in the area of mathematics’ knowledge in WoS based on fuzzy sets and sustainability, presenting research opportunities in this field.
3.2. Strategies for Impact
3.2.1. Analysis of Necessary Conditions
The analysis of necessary conditions reports that for an article to be successful it is necessary that it is not related to sustainability. Table 4 reports consistency and coverage for each attribute tested with the proposed model.

Table 4.
Analysis of Necessary Conditions. Outcome variable: IMP.
According to the best practice standards in fsQCA, a consistency greater than 0.9 of a condition represents that it is necessary for the result to occur. Thus, for a fuzzy set article to achieve great academic impact, it must not be related to sustainability issues. This evidence is consistent with the period analyzed (44 years) and the incipient nature of research on sustainability using methodologies based on fuzzy logic (e.g., fsQCA). In fact, the formulation of the Sustainable Development Goals (SDGs) is recent, having approved the 2030 Agenda in September 2015 and having been put into operation in January 2016. Thus, it is expected that over the years it will increase the academic impact of articles based on fuzzy methodologies.
3.2.2. Analysis of Sufficient Conditions
The parsimonious and intermediate solutions to the proposed model are reported. In accordance with the best practices in fsQCA, only the intermediate solution is considered for the analysis of the model solutions. The combination of the analysis of intermediate and parsimonious solutions allows knowledge of the core conditions, according to Fiss [33]. Table 5 shows the results of the sufficient conditions’ analysis. Appendix B reports the results of the Quine–McCluskey algorithm for complex, parsimonious and intermediate solutions. This algorithm arises from the need to simplify truth functions [40]. The use of the Quine–McCluskey algorithm in the fsQCA methodology allows applying a logical reduction of the specified configurations and their different options [14,18,34,36,37], extending the general solutions of the model to configurations of more complicated solutions. In this way, it is possible to obtain a logical description of the necessary conditions that allow an analyzed result to be produced. In addition, the Quine–McCluskey algorithm shows the coverage statistics of each reduced configuration and of the general solutions of the proposed model [18,34]. Following Ragin [34,36,37], the Quine–McCluskey algorithm allows minimization of Boolean functions in QCA, such that one Boolean expression implies another if the membership of the second is a subset of the membership of the first. Taking as an example a truth table that relates three causal variables (A, B, C) and an outcome (S), it can be reduced to a three-term primitive Boolean equation (S = AC + AB + BC), and in this sense, the Quine–McCluskey algorithm contributes to solving and optimizing the problem by devising a general mechanical procedure for reducing any formula to its simplest equivalent.

Table 5.
Solutions to the proposed model to evaluate successful strategies. Intermediate solution.
The solution to the model is robust and reports adequate coverage (>0.25) and consistency (>0.75) according to the best practices of fsQCA. Following the principle of equifinality, it was observed that many articles followed several pathways (see raw coverage), since unique coverage concentrates levels between 0.04% and 10.73%, while the raw coverage group concentrates thresholds about the sample between 10.9% and 63.34%. The consistency of all causal configurations is very robust, improving on the minimum of 0.75 established by Ragin [13,14,36] (Pathway 1: 0.929386; Pathway 2: 0.996607; Pathway 3: 0.888357; Pathway 4: 0.896791; Pathway 5: 0.931918). Following Fiss [33], core conditions are present in the five causal configurations. The results of this study do not report SUST as core conditions for pathways 1 and 2. The core conditions are those that help to explain the phenomenon studied, while the peripheral conditions can help to explain some causal configurations from the perspective of the intermediate solution, but allow permutations and are not determinative [31]. In our study, SUST are considered peripheral conditions for recipes 1 and 2, applied by researchers to enhance the impact and influence capacity of their studies.
4. Discussion
Regarding the relative impact expressed in citations per journal article, it is found that the highest relative impact indexes are concentrated in journals with scientific production of less than five articles during the 44 years analyzed. The relative impact of these journals ranges from 204 citations per article from Computational Mechanics to 95.5 citations per article from Annals of Mathematics and Artificial Intelligence. The other journals with a much higher production and with a higher number of citations in absolute terms register lower relative citation rates. Journals with more than 50 published articles are divided into two different groups. On the one hand, journals with publication of articles above the average, which register a high capacity for relative impact: Fuzzy Sets and Systems (751 articles; 43.80 citations per article) and Computers & Mathematics with Applications (71 articles; 62.32 citations per article). On the other hand, journals that register between 50 and 100 articles and very moderate levels of relative impact expressed in citations per article (e.g., the Iranian Journal of Fuzzy Systems, 9.72; Quality & Quantity, 9.46; Mathematics, 7.30; Mathematical Problems in Engineering, 5.77).
On the other hand, the results show that the journals that published fewer than five articles concentrate 988 citations in only 8 articles (Annals of Mathematics and Artificial Intelligence, 382; Journal of Statistical Planning and Inference, 223; Computational Mechanics, 204; Environmental and Ecological Statistics, 179).
The bibliometric analysis of the articles published on fuzzy sets, fuzzy logic, fsQCA and mathematics reports the following results for the evaluation of the topic clusters from the evaluation of the keywords. Figure 4 analyzes the thematic connections by colors and Figure 5 analyzes the intertemporal evolution of discourse and the constellations of keywords.
This study detects publication opportunities in the following tracks: decision making problems [41,42,43], intuitionistic fuzzy sets [42,44,45,46,47,48,49,50,51,52,53], parameterization reduction of soft sets [54], fuzzy theory boost [55], fuzzy time series [56], fuzzy rough sets [57], correlation coefficients of hesitant fuzzy sets [58], defuzzification [59], vague sets [47,60], interval-valued fuzzy set [61], fuzzy clustering [62], entropy and measures of fuzzy sets [46,48,63], and other lines of research based on the semantics of fuzzy sets [64] or fuzzy rules [65].
The most prominent publishers are Univ. Sistan and Baluchestan, Amer Inst. Mathematical sciences-AIMS, MDPI, Hindawi Publishing, Springer and Elsevier. Appendix A (Table A2) reports the top 10 mathematics articles within the emerging subset of sustainability topics, presenting research opportunities in this field, and including the complete reference of each article.
From the perspective of sustainability, the fight against climate change and the promotion of the Sustainable Development Goals (SDG), the evidence found reports of lines of research with great research opportunities, such as: fuzzy set-OWA approaches for integrated air pollution risk assessment [66], integrated multi-criteria decision-making [67,68,69], fuzzy TOPSIS [70], fuzzy cellular prey-predator models [71], interval-valued intuitionistic fuzzy synthetic measures (I-VIFSM), hybrid MCDM, trapezoidal fuzzy numbers [72] or hybrid inconsistent sustainable chemical industry evaluation methods [73].
The academics who achieved high impact in JCR® journals by publishing articles on fuzzy logic, fuzzy systems, fuzzy sets or fsQCA, did so by following five different pathways. On the one hand (Pathway 1), they published articles not related to sustainability, with few cited references and reached a high normalized impact per year. These articles became mainstream, since in addition to gaining widespread attention from the international scientific community, the academics who cited them did so, on average, in a very short time, taking as a reference the years that have elapsed since their publication. In addition (Pathway 2), other academics made their research relevant in the long term, assuming seminal publications from the first decades of fuzzy theory development, with great normalized impact per year and on issues not related to sustainability. Another pathway that explains the success of great academic impact (Pathway 3) is evidenced by many seminal articles that were precursors of the later development of the theory, were continuously consulted by academics and were not linked to sustainability or climate change. Academics who combined great impact normalized per year, which could be new or initial articles, also published unsustainable topics (Pathway 4). Finally (Pathway 4), the recipe followed by the academics who published without co-authorship was based on research related to issues not related to sustainability and registered a high normalized impact per year, including in this causal configuration both basic and seminal articles as well as new and disruptive. The proposed model has adequate robustness to be tested in other fields.
5. Conclusions
Research in mathematics and fuzzy logic is an emerging field in academia. Analyzing the cutting edge of math-driven fuzzy set research and fuzzy logic ensures important recipes for the successful publication of articles in the best JCR® journals. Academics need to analyze the successful strategies to achieve greater impact shown by the paths followed by authors with greater academic impact. This study aims to guide and advise future research in the field of fuzzy sets, fuzzy logic and fsQCA. This article also develops the academic debate on the evolution of the fuzzy logic research agenda and contributes to guiding and advising researchers and journal editors on the best practices that will increase the impact of their research, recommending strategies and reporting journals with greater academic projection and more opportunities for publication.
The academic community need to know that this evolution from the motor approach of mathematics and identification of high-impact publication opportunities can help them. This study presents evidence on the evolution of the research agenda in fuzzy set within the area of mathematics, given that mathematical science is at the base of creation, development and promotion of the different emerging methodologies.
The main contribution of this article is to clarify the evolution of the research agenda in Fuzzy Sets Theory and its different associated tracks. In addition, this study provides guidance and advice for authors in their future articles, offering a guide to improve the impact of their research, according to the paths of success suggested by the empirical evidence found by the proposed causal model.
A limitation of this research is its thematic concentration in the specific field of fuzzy theory and mathematics. Fuzzy theory and fuzzy logic are emerging issues with great impact, given their cross-sectional applications, both in engineering and management. Recent developments in fuzzy methodologies have spread from STEM-based knowledge areas to other areas such as social sciences, business organization, innovation, entrepreneurship, corporate finance or strategic management, among others. The research roadmap presented in this article is limited to the emerging field of fuzzy theory and its applications, mainly in engineering. The proposed model has adequate robustness to be tested in other fields. The threats to the validity of the study are due to the sample under study. Future research should expand the field of study and the thematic scope of applicability of the Fuzzy Sets Theory.
Future lines of research should analyze the research agenda in these other scientific fields and multidisciplinary links that contribute to promoting the forefront of fuzzy methodologies and their applications, both in the exact sciences and in the social sciences. In fact, a major trend reaffirmed after the global COVID-19 pandemic is developing in accordance with the acceleration of sustainable strategies. Future research should expand this study from a cutting-edge social science research approach, connecting policy design, fuzzy methodologies with citizen concerns about sustainability, global warming and Sustainable Development Goals (SDGs).
Funding
This research was funded by ESIC Business and Marketing School under grant number 1-V-2021 and is part of the SEDDeS Research Group (Society, Digital Economy and Sustainable Development).
Acknowledgments
I want to thank the reviewers for all the suggestions that made it possible to substantially improve this article.
Conflicts of Interest
The author declare no conflict of interest.
Appendix A. Higher-Impact Elements for Restricted and Wide Scopes

Table A1.
Higher-impact articles for a wide scope and research opportunities.
Table A1.
Higher-impact articles for a wide scope and research opportunities.
| Citations | NIY | Article Title | Year | Authors | Journal | References |
|---|---|---|---|---|---|---|
| 996 | 49.80 | An application of soft sets in a decision-making problem [42] | 2002 | Maji, Pk; Roy, Ar | Computers & Mathematics With Applications | 16 |
| 969 | 44.05 | Distances between intuitionistic fuzzy sets [44] | 2000 | Szmidt, E; Kacprzyk, J | Fuzzy Sets and Systems | 13 |
| 911 | 32.54 | Handling multicriteria fuzzy decision-making problems based on vague set-theory [41] | 1994 | Chen, Sm; Tan, Jm | Fuzzy Sets and Systems | 20 |
| 846 | 38.45 | Multicriteria fuzzy decision-making problems based on vague set theory [43] | 2000 | Hong, Dh; Choi, Ch | Fuzzy Sets and Systems | 14 |
| 756 | 29.08 | Vague sets are intuitionistic fuzzy sets [47] | 1996 | Bustince, H; Burillo, P | Fuzzy Sets and Systems | 46 |
| 736 | 36.80 | A comparative study of fuzzy rough sets [57] | 2002 | Radzikowska, Am; Kerre, Ee | Fuzzy Sets and Systems | 23 |
| 686 | 32.67 | Entropy for intuitionistic fuzzy sets [46] | 2001 | Szmidt, E; Kacprzyk, J | Fuzzy Sets and Systems | 24 |
| 679 | 26.12 | Forecasting enrollments based on fuzzy time series [56] | 1996 | Chen, SM | Fuzzy Sets and Systems | 12 |
| 593 | 31.21 | On the relationship between some extensions of fuzzy set theory [55] | 2003 | Deschrijver, G; Kerre, Ee | Fuzzy Sets and Systems | 11 |
| 575 | 27.38 | An application of intuitionistic fuzzy sets in medical diagnosis [45] | 2001 | De, Sk; Biswas, R; Roy, Ar | Fuzzy Sets and Systems | 17 |
| 548 | 19.57 | New operations defined over the intuitionistic fuzzy-sets [49] | 1994 | Atanassov, Kt | Fuzzy Sets and Systems | 7 |
| 504 | 19.38 | Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy sets [48] | 1996 | Burillo, P; Bustince, H | Fuzzy Sets and Systems | 11 |
| 497 | 17.75 | Operators over interval valued intuitionistic fuzzy-sets [50] | 1994 | Atanassov, Kt | Fuzzy Sets and Systems | 10 |
| 451 | 26.53 | The parameterization reduction of soft sets and its applications [54] | 2005 | Chen, Dg; Tsang, Ecc; Yeung, Ds; Wang, Xz | Computers & Mathematics With Applications | 8 |
| 412 | 22.89 | Distances between intuitionistic fuzzy sets and/or interval-valued fuzzy sets based on the hausdorff metric [51] | 2004 | Grzegorzewski, P | Fuzzy Sets and Systems | 26 |
| 392 | 13.07 | Entropy, distance measure and similarity measure of fuzzy-sets and their relations [63] | 1992 | Liu, Xc | Fuzzy Sets and Systems | 10 |
| 380 | 42.22 | Correlation coefficients of hesitant fuzzy sets and their applications to clustering analysis [58] | 2013 | Chen, N; Xu, Zs; Xia, Mm | Applied Mathematical Modelling | 59 |
| 379 | 16.48 | Defuzzification: criteria and classification [59] | 1999 | Van Leekwijck, W; Kerre, Ee | Fuzzy Sets and Systems | 16 |
| 360 | 16.36 | Some operations on intuitionistic fuzzy sets [52] | 2000 | De, Sk; Biswas, R; Roy, Ar | Fuzzy Sets and Systems | 18 |
| 355 | 13.15 | Measures of similarity between vague sets [60] | 1995 | Chen, Sm | Fuzzy Sets and Systems | 12 |
| 341 | 31.00 | Cosine similarity measures for intuitionistic fuzzy sets and their applications [53] | 2011 | Ye, J | Mathematical and Computer Modelling | 19 |
| 334 | 25.69 | Combination of interval-valued fuzzy set and soft set [61] | 2009 | Yang, Xb; Lin, Ty; Yang, Jy; Li, Y; Yu, Dj | Computers & Mathematics With Applications | 16 |
| 334 | 13.36 | The three semantics of fuzzy sets [64] | 1997 | Dubois, D; Prade, H | Fuzzy Sets and Systems | 59 |
| 316 | 10.90 | A survey of fuzzy clustering [62] | 1993 | Yang, Ms | Mathematical and Computer Modelling | 103 |
| 282 | 10.85 | What are fuzzy rules and how to use them [65] | 1996 | Dubois, D; Prade, H | Fuzzy Sets and Systems | 37 |

Table A2.
Higher-impact articles for a scope restricted to sustainability and research opportunities.
Table A2.
Higher-impact articles for a scope restricted to sustainability and research opportunities.
| Citations | Article Title | Year | Authors | Journal |
|---|---|---|---|---|
| 40 | An integrated multi-criteria decision-making methodology based on type-2 fuzzy sets for selection among energy alternatives in turkey [67] | 2015 | Erdogan, M; Kaya, I | Iranian Journal of Fuzzy Systems |
| 33 | Bipolar fuzzy topsis and bipolar fuzzy electre-i methods to diagnosis [70] | 2020 | Akram, M; Shumaiza; Arshad, M | Computational and Applied Mathematics |
| 12 | A model-based fuzzy set-owa approach for integrated air pollution risk assessment [66] | 2015 | Wang, Bz; Chen, Z | Stochastic Environmental Research and Risk Assessment |
| 9 | An integrated fuzzy multi-criteria decision-making approach for evaluating business process information systems [68] | 2019 | Kang, Hy; Lee, Ahi; Chan, Yc | Mathematics |
| 8 | Hydrogen production technologies evaluation based on interval-valued intuitionistic fuzzy multiattribute decision making method [69] | 2014 | Yu, DJ | Journal of Applied Mathematics |
| 3 | A fuzzy cellular prey-predator model for pest control under sustainable bio-economic equilibrium: a formal description and simulation analysis study [71] | 2015 | Leal-Ramirez, C; Castillo, O; Melin, P; Echavarria-Heras, H | Applied Mathematical Modelling |
| 2 | An advanced decision support framework to assess sustainable transport projects using a new uncertainty modeling tool: interval-valued pythagorean trapezoidal fuzzy numbers [72] | 2021 | Aghamohagheghi, M; Hashemi, Sm; Tavakkoli-Moghaddam, R | Iranian Journal of Fuzzy Systems |
| 1 | A hybrid inconsistent sustainable chemical industry evaluation method [73] | 2019 | Han, Y; Lu, Zy; Chen, S | Journal of Industrial and Management Optimization |
Appendix B. Complex, Parsimonious and Intermediate Solutions to the Proposed Model, according to the Quine–McCluskey Algorithm
**********************
*TRUTH TABLE ANALYSIS*
**********************
Model: IMP = f(YEARS, NIY, UC, CRC, SUST, OA)
Algorithm: Quine–McCluskey
--- COMPLEX SOLUTION ---
frequency cutoff: 1
consistency cutoff: 0.85959
| raw | unique | ||
| coverage | coverage | consistency | |
| NIY*~CRC*~SUST | 0.567855 | 0.0136701 | 0.929386 |
| YEARS*NIY*~SUST | 0.606232 | 0.022215 | 0.996607 |
| YEARS*UC*~SUST | 0.483854 | 0.0316306 | 0.888357 |
| NIY*UC*~SUST | 0.633418 | 0.107339 | 0.896791 |
| NIY*~SUST*OA | 0.199042 | 0.00488454 | 0.931918 |
solution coverage: 0.839251
solution consistency: 0.842801
**********************
*TRUTH TABLE ANALYSIS*
**********************
Model: IMP = f(YEARS, NIY, UC, CRC, SUST, OA)
Algorithm: Quine–McCluskey
--- PARSIMONIOUS SOLUTION ---
frequency cutoff: 1
consistency cutoff: 0.85959
| raw | unique | ||
| coverage | coverage | consistency | |
| NIY*~CRC | 0.571883 | 0.0145642 | 0.927335 |
| YEARS*NIY | 0.610278 | 0.0228849 | 0.99654 |
| YEARS*UC*~SUST | 0.483854 | 0.0316306 | 0.888357 |
| NIY*UC*~SUST | 0.633418 | 0.107339 | 0.896791 |
| NIY*~SUST*OA | 0.199042 | 0.00394869 | 0.931918 |
| NIY*~UC*OA | 0.138233 | 0.000204623 | 0.93561 |
solution coverage: 0.844395
solution consistency: 0.841905
**********************
*TRUTH TABLE ANALYSIS*
**********************
Model: IMP = f(YEARS, NIY, UC, CRC, SUST, OA)
Algorithm: -Quine–McCluskey
--- INTERMEDIATE SOLUTION ---
frequency cutoff: 1
consistency cutoff: 0.85959
Assumptions:
| raw | unique | ||
| coverage | coverage | consistency | |
| NIY*~CRC*~SUST | 0.567855 | 0.0136701 | 0.929386 |
| YEARS*NIY*~SUST | 0.606232 | 0.022215 | 0.996607 |
| YEARS*UC*~SUST | 0.483854 | 0.0316306 | 0.888357 |
| NIY*UC*~SUST | 0.633418 | 0.107339 | 0.896791 |
| NIY*~SUST*OA | 0.199042 | 0.00488454 | 0.931918 |
solution coverage: 0.839251
solution consistency: 0.842801
Appendix C. Acronyms Used in this Article
| Acronym | Description |
| AB | Abstract |
| AHP | Analytical Hierarchy Process |
| AK | Author keywords |
| CRC | Count of cited references |
| csQCA | Crisp-set Qualitative Comparative Analysis |
| fsQCA | Fuzzy-set Qualitative Comparative Analysis |
| GFC | Great financial crisis |
| IMP | Absolute impact |
| INA | Relative impact expressed as citations per article |
| I-VIFSM | Interval-Valued Intuitionistic Fuzzy Synthetic Measures |
| JCR® | Journal Citation Reports® |
| KP | Keyword Plus® |
| MCDM | Multiple Criteria Decision Making |
| mvQCA | Multi-value Qualitative Comparative Analysis |
| NIA | Normalized Impact per Article |
| NIY | Normalized Impact per Year |
| OA | Single authorship |
| PRISMA | Preferred Report. Items for Systematic Reviews & Meta-Analyses |
| QCA | Qualitative Comparative Analysis |
| SDG | Sustainable Development Goal |
| SDGs | Sustainable Development Goals |
| SCIE | Science Citation Index Expanded |
| SEDDeS | Society, Digital Economy and Sustain. Develop. Research Group |
| SOI | Sustainability Oriented Innovation |
| SOIs | Sustainability Oriented Innovations |
| SSCI | Social Sciences Citation Index |
| STEM | Science (S), Technology (T), Engineering (E) and Mathematics (M) |
| SU | Subject |
| SUST | Articles related to sustainability |
| TI | Title |
| TS | Topic |
| UC | Usage count |
| VUCA | Volatility (V), Uncertainty (U), Complexity (C) and Ambiguity (A) |
| WoS | Web of Science |
| WoS-CC | Web of Science Core Collection |
| YEARS | Accumulated citations per year |
References
- Goguen, J.A. The logic of inexact concepts. Synthese 1969, 19, 325–373. [Google Scholar] [CrossRef]
- Herrera-Viedma, E. Fuzzy sets and fuzzy logic in multi-criteria decision making. The 50th anniversary of Prof. Lotfi Zadeh’s theory: Introduction. Technol. Econ. Dev. Econ. 2015, 21, 677–683. [Google Scholar] [CrossRef]
- Zimmermann, H.-J. Applications of fuzzy set theory to mathematical programming. Inf. Sci. 1985, 36, 29–58. [Google Scholar] [CrossRef]
- Zimmermann, H.-J. Fuzzy set theory. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 317–332. [Google Scholar] [CrossRef]
- Zimmermann, H.-J. Fuzzy set theory and mathematical programming. In Fuzzy Sets Theory and Applications; Springer: Dordrecht, The Netherlands, 1986; pp. 99–114. [Google Scholar]
- Zimmermann, H.J. Results of empirical studies in fuzzy set theory. In Applied General Systems Research; Springer: Cham, Switzerland, 1978; pp. 303–312. [Google Scholar]
- Zimmermann, H.-J. Fuzzy Sets, Decision Making, and Expert Systems; Springer Science & Business Media: Berlin, Germany, 1987; Volume 10. [Google Scholar]
- Zimmermann, H.-J. Description and optimization of fuzzy systems. Int. J. Gen. Syst. 1975, 2, 209–215. [Google Scholar] [CrossRef]
- Zimmermann, H.-J. Fuzzy mathematical programming. Comput. Oper. Res. 1983, 10, 291–298. [Google Scholar] [CrossRef]
- Zimmermann, H.-J. Fuzzy control. In Fuzzy Set Theory—and Its Applications; Springer: Cham, Switzerland, 2001; pp. 223–264. [Google Scholar]
- Zadeh, L.A. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1999, 100, 9–34. [Google Scholar] [CrossRef]
- Zhang, L.; Zhan, J. Fuzzy soft β-covering based fuzzy rough sets and corresponding decision-making applications. Int. J. Mach. Learn. Cybern. 2019, 10, 1487–1502. [Google Scholar] [CrossRef]
- Ragin, C.C. Fuzzy-Set Social Science; University of Chicago Press: Chicago, IL, USA, 2000; ISBN 0226702774. [Google Scholar]
- Rihoux, B.; Ragin, C.C. Configurational Comparative Methods: Qualitative Comparative Analysis (QCA) and Related Techniques; Sage Publications: Thousand Oaks, CA, USA, 2008; ISBN 1452210314. [Google Scholar]
- Schneider, C.Q.; Wagemann, C. Set-Theoretic Methods for the Social Sciences: A Guide to Qualitative Comparative Analysis; Cambridge University Press: Cambridge, UK, 2012; ISBN 1139560611. [Google Scholar]
- Cronqvist, L.; Berg-Schlosser, D. Multi-value QCA (mvQCA). Config. Comp. Methods Qual. Comp. Anal. Relat. Tech. 2009, 51, 69–86. [Google Scholar]
- Verweij, S.; Vis, B. Three strategies to track configurations over time with Qualitative Comparative Analysis. Eur. Polit. Sci. Rev. 2021, 13, 95–111. [Google Scholar]
- Ragin, C.C. Qualitative Comparative Analysis and Fuzzy Sets; University of Arizona: Tucson, AZ, USA, 2008. [Google Scholar]
- Woodside, A.G. Moving beyond multiple regression analysis to algorithms: Calling for adoption of a paradigm shift from symmetric to asymmetric thinking in data analysis and crafting theory. J. Bus. Res. 2013, 66, 463–472. [Google Scholar] [CrossRef]
- Rihoux, B. Qualitative comparative analysis (QCA), anno 2013: Reframing the comparative method’s seminal statements. Swiss Polit. Sci. Rev. 2013, 19, 233–245. [Google Scholar] [CrossRef]
- Kraus, S.; Ribeiro-Soriano, D.; Schüssler, M. Fuzzy-set qualitative comparative analysis (fsQCA) in entrepreneurship and innovation research--the rise of a method. Int. Entrep. Manag. J. 2018, 14, 15–33. [Google Scholar] [CrossRef]
- Scarpellini, S.; Ortega-Lapiedra, R.; Marco-Fondevila, M.; Aranda-Usón, A. Human capital in the eco-innovative firms: A case study of eco-innovation projects. Int. J. Entrep. Behav. Res. 2017, 23, 919–933. [Google Scholar] [CrossRef] [Green Version]
- Pierce, P.; Ricciardi, F.; Zardini, A. Smart cities as organizational fields: A framework for mapping sustainability-enabling configurations. Sustainability 2017, 9, 1506. [Google Scholar] [CrossRef] [Green Version]
- Page, M.J.; Moher, D.; McKenzie, J.E. Introduction to PRISMA 2020 and implications for research synthesis methodologists. Res. Synth. Methods 2022, 13, 156–163. [Google Scholar] [CrossRef]
- Thomé, A.M.T.; Scavarda, L.F.; Scavarda, A.; de Souza Thomé, F.E.S. Similarities and contrasts of complexity, uncertainty, risks, and resilience in supply chains and temporary multi-organization projects. Int. J. Proj. Manag. 2016, 34, 1328–1346. [Google Scholar] [CrossRef]
- Mack, O.; Khare, A.; Krämer, A.; Burgartz, T. Managing in a VUCA World; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Hammad, M.A.; Elgazzar, S.; Obrecht, M.; Sternad, M. Compatibility about the concept of energy hub: A strict and visual review. Int. J. Energy Sect. Manag. 2021, 16, 1–20. [Google Scholar] [CrossRef]
- Lafuente-Lechuga, M.; Cifuentes-Faura, J.; Faura-Martínez, U. Sustainability, Big Data and Mathematical Techniques: A Bibliometric Review. Mathematics 2021, 9, 2557. [Google Scholar] [CrossRef]
- Xie, L.; Chen, Z.; Wang, H.; Zheng, C.; Jiang, J. Bibliometric and visualized analysis of scientific publications on atlantoaxial spine surgery based on Web of Science and VOSviewer. World Neurosurg. 2020, 137, 435–442. [Google Scholar] [CrossRef]
- Ersozlu, Z.; Karakus, M. Mathematics anxiety: Mapping the literature by bibliometric analysis. EURASIA J. Math. Sci. Technol. Educ. 2019, 15, em1673. [Google Scholar] [CrossRef]
- Rihoux, B. Qualitative Comparative Analysis: Discovering Core Combinations of Conditions in Political Decision Making. In Oxford Research Encyclopedia of Politics; Oxford University Press: Oxford, UK, 2020. [Google Scholar]
- Kent, R. Using fsQCA: A Brief Guide and Workshop for Fuzzy-Set Qualitative Comparative Analysis; Context; University of Stirling: Stirling, UK, 2008; Volume 45, pp. 489–503. [Google Scholar]
- Fiss, P.C. Building better causal theories: A fuzzy set approach to typologies in organization research. Acad. Manag. J. 2011, 54, 393–420. [Google Scholar] [CrossRef] [Green Version]
- Ragin, C.C. Measurement versus calibration: A set-theoretic approach. In The Oxford Handbook of Political Methodology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Ragin, C.C.; Pennings, P. Fuzzy sets and social research. Sociol. Methods Res. 2005, 33, 423–430. [Google Scholar] [CrossRef] [Green Version]
- Ragin, C.C. Reflections on casing and case-oriented research. In The SAGE Handbook of Case-Based Methods; Sage Publications: Thousand Oaks, CA, USA, 2009; Volume 31, pp. 522–534. [Google Scholar]
- Ragin, C.C. The Comparative Method; University of California Press: Berkley, CA, USA, 2014. [Google Scholar]
- Cezar, R.F. Compliance in “exceptional” trade disputes: A set-theoretical approach. Rev. Bras. Política Int. 2020, 63, e003. [Google Scholar] [CrossRef] [Green Version]
- Redding, K.; Viterna, J.S. Political demands, political opportunities: Explaining the differential success of left-libertarian parties. Soc. Forces 1999, 78, 491–510. [Google Scholar] [CrossRef]
- Quine, W.V. The problem of simplifying truth functions. Am. Math. Mon. 1952, 59, 521–531. [Google Scholar] [CrossRef]
- Chen, S.; Tan, J.-F. Handling multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets Syst. 1994, 67, 163–172. [Google Scholar] [CrossRef]
- Maji, P.K.; Roy, A.R.; Biswas, R. An application of soft sets in a decision making problem. Comput. Math. Appl. 2002, 44, 1077–1083. [Google Scholar] [CrossRef] [Green Version]
- Hong, D.H.; Choi, C.-H. Multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets Syst. 2000, 114, 103–113. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. Distances between intuitionistic fuzzy sets. Fuzzy Sets Syst. 2000, 114, 505–518. [Google Scholar] [CrossRef]
- De, S.K.; Biswas, R.; Roy, A.R. An application of intuitionistic fuzzy sets in medical diagnosis. Fuzzy Sets Syst. 2001, 117, 209–213. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. Entropy for intuitionistic fuzzy sets. Fuzzy Sets Syst. 2001, 118, 467–477. [Google Scholar] [CrossRef]
- Bustince, H.; Burillo, P. Vague sets are intuitionistic fuzzy sets. Fuzzy Sets Syst. 1996, 79, 403–405. [Google Scholar] [CrossRef]
- Burillo, P.; Bustince, H. Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy sets. Fuzzy Sets Syst. 1996, 78, 305–316. [Google Scholar] [CrossRef]
- Atanassov, K.T. New operations defined over the intuitionistic fuzzy sets. Fuzzy Sets Syst. 1994, 61, 137–142. [Google Scholar] [CrossRef]
- Atanassov, K.T. Operators over interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1994, 64, 159–174. [Google Scholar] [CrossRef]
- Grzegorzewski, P. Distances between intuitionistic fuzzy sets and/or interval-valued fuzzy sets based on the Hausdorff metric. Fuzzy Sets Syst. 2004, 148, 319–328. [Google Scholar] [CrossRef]
- De, S.K.; Biswas, R.; Roy, A.R. Some operations on intuitionistic fuzzy sets. Fuzzy Sets Syst. 2000, 114, 477–484. [Google Scholar] [CrossRef]
- Ye, J. Cosine similarity measures for intuitionistic fuzzy sets and their applications. Math. Comput. Model. 2011, 53, 91–97. [Google Scholar] [CrossRef]
- Chen, D.; Tsang, E.C.C.; Yeung, D.S.; Wang, X. The parameterization reduction of soft sets and its applications. Comput. Math. Appl. 2005, 49, 757–763. [Google Scholar] [CrossRef] [Green Version]
- Deschrijver, G.; Kerre, E.E. On the relationship between some extensions of fuzzy set theory. Fuzzy Sets Syst. 2003, 133, 227–235. [Google Scholar] [CrossRef]
- Chen, S.-M. Forecasting enrollments based on fuzzy time series. Fuzzy Sets Syst. 1996, 81, 311–319. [Google Scholar] [CrossRef]
- Radzikowska, A.M.; Kerre, E.E. A comparative study of fuzzy rough sets. Fuzzy Sets Syst. 2002, 126, 137–155. [Google Scholar] [CrossRef]
- Chen, N.; Xu, Z.; Xia, M. Correlation coefficients of hesitant fuzzy sets and their applications to clustering analysis. Appl. Math. Model. 2013, 37, 2197–2211. [Google Scholar] [CrossRef]
- Van Leekwijck, W.; Kerre, E.E. Defuzzification: Criteria and classification. Fuzzy Sets Syst. 1999, 108, 159–178. [Google Scholar] [CrossRef]
- Chen, S.-M. Measures of similarity between vague sets. Fuzzy Sets Syst. 1995, 74, 217–223. [Google Scholar] [CrossRef]
- Yang, X.; Lin, T.Y.; Yang, J.; Li, Y.; Yu, D. Combination of interval-valued fuzzy set and soft set. Comput. Math. Appl. 2009, 58, 521–527. [Google Scholar] [CrossRef] [Green Version]
- Yang, M.-S. A survey of fuzzy clustering. Math. Comput. Model. 1993, 18, 1–16. [Google Scholar] [CrossRef]
- Xuecheng, L. Entropy, distance measure and similarity measure of fuzzy sets and their relations. Fuzzy Sets Syst. 1992, 52, 305–318. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. The three semantics of fuzzy sets. Fuzzy Sets Syst. 1997, 90, 141–150. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. What are fuzzy rules and how to use them. Fuzzy Sets Syst. 1996, 84, 169–185. [Google Scholar] [CrossRef]
- Wang, B.; Chen, Z. A model-based fuzzy set-OWA approach for integrated air pollution risk assessment. Stoch. Environ. Res. Risk Assess. 2015, 29, 1413–1426. [Google Scholar] [CrossRef]
- Erdogan, M.; Kaya, I. An integrated multi-criteria decision-making methodology based on type-2 fuzzy sets for selection among energy alternatives in Turkey. Iran. J. Fuzzy Syst. 2015, 12, 1–25. [Google Scholar]
- Kang, H.-Y.; Lee, A.H.I.; Chan, Y.-C. An integrated fuzzy multi-criteria decision-making approach for evaluating business process information systems. Mathematics 2019, 7, 982. [Google Scholar] [CrossRef] [Green Version]
- Yu, D. Hydrogen production technologies evaluation based on interval-valued intuitionistic fuzzy multiattribute decision making method. J. Appl. Math. 2014, 2014, 751249. [Google Scholar] [CrossRef]
- Akram, M.; Arshad, M. Others Bipolar fuzzy TOPSIS and bipolar fuzzy ELECTRE-I methods to diagnosis. Comput. Appl. Math. 2020, 39, 1–21. [Google Scholar] [CrossRef]
- Leal-Ramirez, C.; Castillo, O.; Melin, P.; Echavarria-Heras, H. A fuzzy cellular prey--predator model for pest control under sustainable bio-economic equilibrium: A formal description and simulation analysis study. Appl. Math. Model. 2015, 39, 1794–1803. [Google Scholar] [CrossRef]
- Aghamohagheghi, M.; Hashemi, S.M.; Tavakkoli-Moghaddam, R. An advanced decision support framework to assess sustainable transport projects using a new uncertainty modeling tool: Interval-valued Pythagorean trapezoidal fuzzy numbers. Iran. J. Fuzzy Syst. 2021, 18, 53–73. [Google Scholar]
- Han, Y.; Lu, Z.; Chen, S. A hybrid inconsistent sustainable chemical industry evaluation method. J. Ind. Manag. Optim. 2019, 15, 1225. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).