Abstract
With an empirical study, we explore the process of designing modeling tasks for teaching mathematics in a Dynamic Geometry environment. We address the research questions: What are the characteristics of the tasks that pre-service teachers design to teach mathematics in digital and modeling environments? What are the activities like that these tasks encourage in students? By means of a qualitative methodology, we characterize the tasks designed by secondary pre-service mathematics teachers and identify the activities that these tasks encourage in students. By analyzing the process of designing and planning a class, we can determine how the characteristics of the modeling tasks are modified based on the software used. In this context, the software also acts as a medium that reflects aspects of the models involved, the objectives of the tasks, and the activities intended for the students. The results contribute to the discussion regarding task design, where technology is a means of supporting the exploration, understanding, and study of different phenomena.
1. Introduction
The design of modeling tasks for supporting the development of skills that provide students with an approach for solving real problems both in their classes and in their life environment has been one of the main research topics in mathematics education in recent years [1,2]. Simultaneously, the exploration of the use of digital tools for addressing mathematical problems and modelling and simulating phenomena constitutes a field of study that seeks to expand the opportunities students have to learn mathematics [3]. However, with the variety of technological resources available today, traditional teaching practices end up adapting to work with technology, instead of allowing technology to redefine classroom practices, as was recommended several years ago [4]. Computers are still being used in classrooms to replace paper printouts with computer screens without modifying the tasks. This has a negative impact on learning since it ignores the opportunities offered by technologies to reconnect students with useful contexts that give meaning to the mathematical knowledge they build [5].
The search for alternatives that better integrate the use of technology for learning mathematics can be approached from different points of view. In this paper, we focus on two relevant points associated with the tasks for teaching mathematics: modeling and the use of digital technologies. In addition, we keep in mind that the efficient use of technology and the design of activities that promote mathematical learning largely depend on the teacher’s knowledge, skills, and beliefs [6,7]. In particular, to teach modeling, teachers must first have experimented with similar activities that provide them with knowledge on how to design and implement tasks effectively, as noted by Goldsmith, Doerr, and Lewis [8]. Teachers have to be encouraged to take part in exploring and developing techniques that let them use artifacts as digital tools and as tools for understanding specific concepts of the domain [9]. From this perspective, the design of tasks based on the experience resulting from modeling and simulating different situations represents an opportunity for in-service and pre-service teachers to build a set of knowledge associated with content, technology, and pedagogy for teaching mathematics [10]. In this research, we present the results obtained by characterizing tasks that integrate the use of a Dynamic Geometry System (DGS) designed by pre-service secondary mathematics teachers. The objective is to show the potential that the process of designing modeling tasks has for creating teaching material. The research questions that guide this work are:
What are the characteristics of the tasks that pre-service teachers design to teach mathematics in digital and modeling environments?
What kind of activities do these tasks encourage in students?
Therefore, the answers to these questions allow us to identify the intentions that the teacher has regarding the modeling activities for the students and the potentials and limitations introduced by the DGS in the design of the task. To answer these questions, a review of the research literature is presented in the following section in order to determine the challenges that in-service and pre-service teachers encounter when designing tasks and to understand the role of digital tools as mediators for learning mathematics. These elements provide feedback for constructing a conceptual framework and the research methodology. Finally, we describe how the data were analyzed and present the conclusions. This research provides empirical and comprehensive evidence of how modeling activities and processes are reorganized in technological environments from the point of view of task design by pre-service mathematics teachers. The results also allow us to establish categories for designing tasks where technology is a means for supporting the exploration, understanding, and study of different phenomena.
2. Task and Modeling Task
In mathematics education, there are different definitions of models, mathematical models, and modeling. In this document, we define a model as a simplified representation of a part of reality that reflects some of its particular aspects. A mathematical model is a representation of a part of reality that allows the application of mathematical methods. Mathematical modeling refers to the process of representing a problem from reality through mathematical means for processing it mathematically and obtaining an answer to the problem [11]. In addition, we will refer to a modeling task as that which encourages the activity of modeling so as to understand, describe, intervene, respond to, and reflect on a situation that occurs in the real world.
The tasks for teaching mathematics have been classified in different ways, there being no consensus regarding the various existing classifications [12]. Sullivan, Clarke, and Clarke [13] show three categories of tasks: purposeful representational tasks, mathematical tasks that emerge from a context, and open-ended tasks. The goal of the first group of tasks is to develop and consolidate mathematical understanding through the use of models and representations, where the model or representation must be related to the mathematical concept that is the focus of the task. The models in this case can be concrete materials, graphics, and images. In the second type of task, the context is intended to show how mathematics is used and to give it meaning. Contexts are considered that are of interest to students. In an open-ended task, more than one answer is expected to be found for a given situation. The students need to reflect on the meaning of the concepts involved, make decisions about the processes, consider the possibility of multiple responses, and think about ways to communicate the results. Although the classification by Sullivan, Clarke, and Clarke [13] refers to the role of the context of tasks and the use of tools or models to achieve a mathematical goal, it does not explicitly state the multiple ways of looking at modeling processes [14,15]. With regard to modeling, there is also no consensus as to its definition, although most researchers agree that it entails a transition between reality and mathematics, with different ways of representing the processes involved [16]. Some of these include phases along the modeling cycle that will depend on the perspective taken, such as situation and real problem, model of the situation, model and real problem, model and mathematical problem, and mathematical results and real results [17]. In this area, tasks seek to provide the skills for solving a problem in the real world by using mathematics and by fostering creative and reflective thinking. In addition, these types of tasks are unique in that they can enhance the relationships between different fields of knowledge and promote critical thinking [13].
Some researchers emphasize that the design of modeling tasks should focus on favoring the process and reasoning more than the results [18,19]. Geiger [1] provides some general principles for the design process. Fit to circumstance: the tasks must consider the local conditions, such as the specifications of the local curriculum, resources of the institution, and the particular characteristics of the students. Challenge: the tasks must challenge the students’ way of thinking and propose open-ended and realistic problems. The tasks should offer students opportunities to explore, justify their actions, and make decisions. Tasks should be challenging yet accessible, meaning the end goal of the task should be attainable. Students should know what is expected of them in terms of the tasks in order to be successful and fully involved in them (transparency). In addition, Geiger indicates some relevant points in task design that have been observed by teachers: syllabus compliance, authenticity and relevance, connectivity, and accessibility. These aspects are relevant to curricular demands and connect with other areas of knowledge, as well as with the knowledge and interest of the students who carry out the tasks.
Following the framework of the Anthropological Theory of the Didactic (ATD), Quiroz-Rivera and Rodríguez-Gallegos [20] characterized the modeling tasks presented in basic education textbooks. They did so by considering the existence of a real domain, a pseudo-concrete domain, and a physical domain. The first contains problems as they are presented in reality, while in the second domain these problems are also related to the real context, but their data have been modified to achieve a didactic purpose, thus yielding a didactic transposition. In addition, the physical domain is associated with the nature of the mathematical content involved. From their analysis of textbooks, the authors presented six types of tasks associated with modeling: problems in real situations, problems in pseudo-concrete situations, tasks that require the creation of a mathematical model, tasks that foster the work with a mathematical model, tasks that analyze mathematical results in pseudo-concrete situations, and tasks that analyze mathematical results in real situations.
Elsewhere, based on a thorough review of the literature, Maaß [21] developed a scheme for characterizing the design of modeling tasks that can be used to reach predefined objectives for a certain target group. This characterization mainly considers: the focus of the modeling activity (it refers to the work in the phases of the modeling process), the data (superfluous, missing, inconsistent), the relationship with reality (authentic, close to reality, artificial, imaginative), the type of model used (descriptive, normative), the type of representation (text, images, drawings, material), openness of a task (solved example, ascertaining task, reversal task, complex problem, finding a situation, open problem), cognitive demand (extra mathematical modeling, intra-mathematical modeling, dealing with text containing mathematics, reasoning mathematically, dealing with mathematical representations), and mathematical content (mathematical area, school level).
In the above characterizations, the use of technology in modeling tasks is not made explicit, even though it may be present. Molina-Toro, Rendón-Mesa, and Villa-Ochoa [22] classify the roles of technology in modeling processes based on two aspects: technology as a resource for the development of modeling processes and technology as a reorganizer of the modeling process. They also identify uses of digital technologies in modeling processes. These classifications involve zooming in and out of the modeling process and identifying how the use of technology impacts the phases of the process. Moreover, technology can be viewed as an additional domain that supports working with complex mathematical models. A more general approach underscores the role of technology as a mediator that modifies learning and the activities carried out by students.
Although, in the works mentioned, the authors make significant contributions to our knowledge of the characteristics of modeling tasks and activities, the classifications presented do not explore the design processes, nor do they consider their relationship with the knowledge of those who design the tasks. Our contribution to this area through our research is based on empirical data on task design that reveal information about the particular characteristics regarding the mathematical content and ways of exploiting technology in tasks that are designed in a Dynamic Geometry environment.
3. Conceptual Framework
3.1. Modelling and Digital Tools
Task design poses a challenge for teachers since they must choose which activities will be performed by students and which will be performed by technology. They must also make decisions regarding the feedback provided by technology [23]. When designing tasks in which technology is involved, teachers have to assess its function as an artifact or instrument for teaching and learning mathematics since its particular characteristics can shape the conceptual development of users [1]. Accordingly, emphasis has been placed on the importance of proposing tasks in which technology promotes more qualitative reasoning and on reducing the reproduction of algorithms or mathematical applications that trivialize the task [24]. Hence the need to explore the possibilities offered by technology to model, to develop experiments and simulations, and to act as a support for the development of numerical solutions, visualizations, and graphs and for accessing information. We are referring to design in terms of Leung [25], who points out that
The word “design” carries a meaning of accomplishing goals in a particular environment satisfying a set of requirements or subject to a set of constraints; it is a strategic approach (roadmap) towards achieving a certain expectation. Design necessarily creates boundary; a structure or framework on which meaning and knowledge can grow.(p. 4)
When designing tasks, the teacher/researcher is involved in defining and organizing activities in didactic teaching and learning environments. Like Leung, we view technology as an element that defines the limits, but that also shapes the activities that students and teachers carry out [26]. We can thus find tasks in which students use the tool as a support for solving the task, but it is not essential, and the situation or context that generates the activities does not arise in a technological environment. By contrast, there are tasks that are approached in such a way that the use of technology is required, or the situation is set in a technological context. In lessons with modeling assignments, five categories of patterns and modes of calculator use have also been found: computational tool, transformational tool, data collection and analysis tool, visualizing tool, and checking tool [27].
Greefrath, Hertleif, and Siller [28] have studied the role of a DGS in the phases of the modeling process, noting its potential for understanding the problem through simplification and mathematization, as well as its use for validation and the support it offers to investigate, experiment, visualize, draw, measure, etc. They further distinguish that a mathematical work takes place when digital tools are used once the mathematical expressions have been translated into a language that technology understands and that the results offered by the tool must be reinterpreted and translated into a mathematical language. This idea has been represented in the modeling cycle by including a technological world alongside the mathematical world [28].
When modeling in digital environments, the nature of the activities and the knowledge involved are transformed based on the potential offered by the tools to carry out experiments with computational models that may involve the interaction between physical phenomena (or empirical data), simulation (or computational data), and analysis (or explanatory theory) [16]. As a result, digital tools, on the one hand, provide support for the development of mathematical work, and on the other hand, they shape a kind of microworld in which individuals engage in mathematical work and carry out explorations.
Computational media both empower the mathematical processes involved in modeling activities by providing new “worlds” to explore and potentially shape the world we try to model.[16] (p. 79)
We understand simulation as the creation of an analog to a real-world situation, whose function is to explore or experience the processes that take place in the original environment. By simulating phenomena, we create the opportunity to answer questions that would otherwise be difficult to answer [29].
One goal of a simulation is to explore and obtain data from the simulated system for the purpose of optimizing or understanding said system. When simulating a situation, this undeniably creates an interpretation of the language in which the situation is presented, as well as a transformation of the information to be represented in the language that the software understands. A simulation may involve the use of different types of mathematical and non-mathematical models. There are also different types of simulations. In this work, we consider dynamic and static simulations. The former is time-dependent, whereas time does not play a fundamental role in the latter [29]. For Doerr, Ärlebäck, and Misfeldt [16], there are three ways in which technology influences modeling processes: simulation and new digital realities to be investigated, digital technology shaping reality, and support in modeling processes. Some of these will be reflected in the task design.
3.2. Teacher Knowledge for Designing Tasks
The design and implementation of teaching activities that involve modeling and the use of technologies involves different areas of knowledge that the teacher must bring to bear, a knowledge that we call complex and that is organized in a network that associates knowledge of technology, pedagogy, and content [6,10,25]. This knowledge also depends on the teacher’s experience with digital tools and his/her beliefs regarding the use of technology [7]. In particular, when teaching about modeling, these elements of knowledge have been observed to manifest themselves in the tasks the teacher designs and proposes to guide learning [10], the way in which the teacher manages and organizes the class, and the interventions and explanations the teacher makes [30].
As a result, based on experience, we believe that the construction of modeling tasks in digital environments encourages pre-service teachers to, through the involvement of and feedback from technology, reflect on those aspects of the situation that are simplified and idealized. This also makes them able to “virtually” sketch and dynamically represent their mental representations of situations. Of key importance when designing tasks in a DGS environment is the teacher’s ability to bridge the gap between the characteristics and properties he/she recognizes in the situation, which are transferred to a representation that stands out for its visual perception and for the restrictions that the software itself imposes when representing it. The teacher must not lose sight of the goal that the task should ultimately offer opportunities to understand the situations and encourage mathematical work to answer questions that emerge from the situation in reality.
The teacher must thus take into account the processes that the software can develop and the relevant feedback for the user [23], since otherwise the students could lose sight of the relevant mathematical ideas [31]. Joubert [23] underscores that the teacher must be able to differentiate between the work carried out by the students and that performed by the computer, pointing out that “If computers are able to do the ‘work’ for the students, then what is the work of the students?” Regarding this same idea, Nevile et al. [32] indicate that it is particularly important to look “at the software” together with looking “through the software”.
4. Methodology
This study is part of a broader investigation that is exploring the Technological Pedagogical Content Knowledge (TPACK) for teaching mathematics. As a continuation, this research focuses on characterizing the tasks for modeling and using technology employed by 45 students of pedagogy in mathematics with extensive knowledge of mathematics. Employing a qualitative approach [33], we developed an instrumental case study [34] that allows us to analyze, classify, compare, and interpret the work carried out by pre-service mathematics teachers, and thus understand their teaching practice in a natural environment for designing teaching tasks. In this environment, it is assumed that when a teacher constructs modeling tasks, they have to delve into activities to research, model, and use technology, and then explore and select mathematical content for teaching. The result of the above is the activity for the students, in which the types of questions, the uses of tools, and the cognitive load of the task stand out. Some aspects of relevance when designing tasks are shown in Figure 1.
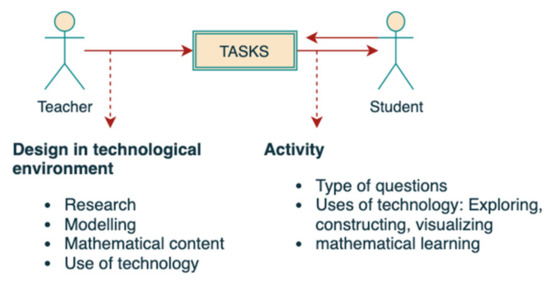
Figure 1.
Actions of the teacher when designing tasks and activities for students.
Organizing the scenario for designing tasks consisted of an introductory phase to the DGS and a design phase, which are described in the following section.
4.1. Introductory Phase for Working with Dynamic Geometry Systems
Before the tasks were designed, and during twelve 90 min sessions, the participants worked to construct and explore various geometric configurations in the DGS environment related to problem solving (with and without extra-mathematical context). In these sessions, participants were introduced to using and experimenting with various DGS components, such as the point, point-on-object, line-through-two-points, angle, slider, locus, and conic tools, and the mathematical definitions associated with the DGS tools were presented. In addition, relevance was given to identifying relationships between objects and conditions that can be used to move geometric constructions, as in a type of hierarchy or nesting of the objects used in the construction. For example, the following process related to Figure 2 allows represent the movement of a wheel: Using the slider tool, a circumference C with center A and radius r is constructed. The circumference is intersected by the horizontal line h, yielding point B. Then, with the angle tool and given its amplitude (-a/r), point B′ is constructed. Now, when slider a is moved, the circle slides horizontally and point B′ moves by the angle α, generating “the illusion” of rolling the circle and the locus of the cycloid described by B′.
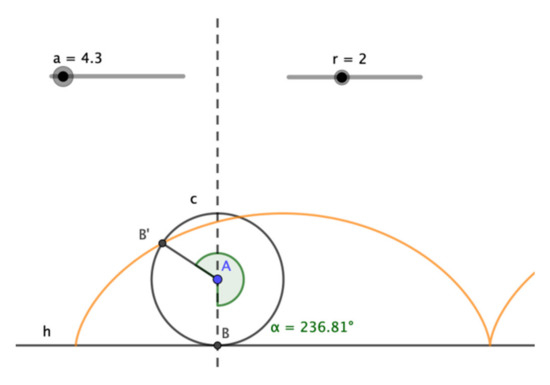
Figure 2.
Generating the illusion of a rolling circle.
The geometric configuration that generates this movement consists of nested actions—that is, the characteristics of the circumference C (radius and perimeter) depend on the sliders, and the movement of point B′ in turn depends on the circumference C. These are actions that are frequently used to simulate and study certain phenomena in a DGS environment.
4.2. Tasks Design Phase
For two months, the participants worked in groups (3 per group) to design and plan a modeling activity. When designing this activity, they had to select and justify the need for studying a particular situation (identify a problem of interest). This led them to study the characteristics and variables associated with the real situation and its behavior and relevance both for society and for fostering student learning. In this way, the designers were introduced to exploring the mathematical and extra-mathematical knowledge involved in creating tasks with specific contexts. After selecting the situation, the participants identified the relevant information and then simplified and idealized the situation. This gave way to exploring the modeling process and designing the teaching task, accompanied by a simulation (Figure 3). It has been shown that it is in these moments when the pre-service teacher brings to bear and builds their Technological Pedagogical Content Knowledge and modeling knowledge [10].

Figure 3.
Process carried out by the participants to design the task.
The set of activities carried out by the participants (Figure 3) yielded the data that are analyzed as described below.
4.3. Data Collection and Analysis
The participants presented their design process through a written report, which included a description of the research and modeling stages (Figure 3). It also contained a description of the teaching task and a preliminary analysis specifying the use of the DGS. They also included an electronic file in GeoGebra with the simulation for the student to use or build. Fifteen written reports were received, one per group, with their respective electronic files. Four papers were excluded because the goals of the tasks were unclear or the electronic file did not contain findings of use for the data analysis.
Table 1 shows the information requested from the participants, indicating the elements they had to include.

Table 1.
Information collected with the instruments.
To analyze the data, the content of the written report was divided into episodes based on the points shown on the left side of Table 1. These episodes offer information about the origin of the task and its materialization into a teaching activity. It also explains the main achievements made by the participants as they stepped through the stages indicated in Figure 3.
Subsequently, during the initial coding, the data were categorized according to didactic and pedagogical objectives evidenced in the tasks. A second categorization of the data led us to identify characteristics of the modeling processes and the elements associated with the mathematical work in a DGS. Finally, the resulting categories were compared against the literature.
One example of the analysis carried out is as follows, for the “objective of the modeling task” category. Initially, arguments were found that could be coded as: development of skills to find solutions to a problem and activities to find applications to mathematics or to motivate students (Table 2). Subsequently, during recoding, the categories emerged for classifying the modeling tasks that focus on the activities intended for the students (Table 3 and Table 4). This is shown in detail in the next section.

Table 2.
Coding example.
5. Discussion and Analysis of the Results
In this section we answer the questions:
Q1: What are the characteristics of the tasks that pre-service teachers design to teach mathematics in digital and modeling environments?
Q2: What are the activities like that these tasks encourage in students?
The results are initially organized based on how the DGS tools are used to approach the teaching of mathematics through modeling tasks (exploitation mode), described in Table 3 and Table 4. Table 5 shows the coding of the 12 tasks, considering the goal of the model, the actions for the students, the type of model used, and the type of simulation involved in the task. Subsequently, two examples of the tasks designed exemplify the characterization.
5.1. Characteristics Elements of the Tasks
To answer the first research question (Q1), we assume that the intended activity for the students and the actions they will take when working with the task will be determined by the characteristics of the software and, in turn, will be subject to the restrictions and limitations imposed by said software. In addition, the activities that are designed for the students, together with the use of the DGS, are considered to have a didactical intention. Taking the above into account, the data were classified and coded according to the intended modes of use (or exploitation mode). A mode of use (performance) can be regarded as part of the design of a hypothetical learning trajectory. It is defined as the way in which the teacher exploits the didactic configuration according to his/her didactic intentions, including decisions about the way in which a task is introduced and practiced, about the roles of artifacts, and about the schemes and techniques that the students will develop and establish [35]. The latter is consistent with the answer to the second research question (Q2).
Two relevant categories associated with the modeling tasks were identified that are related to the modeling objective and the actions intended for the students (Table 3). In relation to the interaction and scopes allowed by the DGS, three categories associated with the types of simulation, models, and expected solutions were identified (Table 4). The first two categories correspond to the dimension of the intentions that the teacher has regarding the modeling activities for the student. The other three categories are grouped into one dimension that combines the design of the task and the potentials and limitations introduced by the DGS.
The modeling objective defines the direction taken by the activities planned by the pre-service teachers for the students. Its intention is reflected in the mathematical work proposed in the DGS environment, in the sense that the objective of the task can give more or less relevance to describing, predicting, understanding, representing, and intervening in the situation in question (Table 3). In this way, the geometric configuration (or model) discovers some of these purposes associated with the task.
Different types of models are identified in the literature; among them are descriptive and normative models. As their name indicates, the former are intended to describe a situation and are also predictive. Some of them seek to simulate and represent elements of one part of reality in an effort to understand and explain the situation and solve problems. Normative models seek to explore and create mathematical rules for supporting decision-making [11]. Generally, the models have more than one purpose. For our study, we considered the purpose declared by the participants, together with the intention that we identified in the proposed work with the DGS. As Table 5 shows, one of the main objectives of most of the tasks proposed is for the model given by the geometric configuration to aid in understanding the situation. This characteristic of the model is favored by the possibility that the DGS offers to manipulate the simulations and observe the consequences of these actions. Meanwhile, the construction of a simulation whose objective is to describe and predict is present to a lesser extent.
Very close to the purpose of modeling are the actions that are encouraged through tasks, which is explained as per the distinction made by Doerr [36] between exploratory models and model building. An exploratory model is one built by experts to represent knowledge in some content domain, where the learner interacts with the models and explores the consequences of their actions within the boundaries of the model defined beforehand by the designer. In the words of Doerr, “These models are in essence microworlds that provide the student with a set of simulated, idealized worlds that embody for example, the Newtonian laws of motion while allowing the student to explore the consequences of changes in the simulation’s parameters [36] (p. 266)”. While building models, students are provided with opportunities to express their thoughts by representing concepts, defining relationships, and exploring the consequences of those relationships, which thus entails a greater cognitive demand [21]. Only three of the eleven tasks analyzed promote the construction of models to a certain extent (code I5 Table 3 and Table 5). Exploration (I3) is promoted to a greater extent in eight of the tasks analyzed. In addition, the identification (I2) and application (I4) actions were identified only in tasks T1 and T2.

Table 3.
Intentional ways of exploiting the DGS.
Table 3.
Intentional ways of exploiting the DGS.
| Category | Code | Explanation |
|---|---|---|
| Modeling objective | MO1—Describe | Intended to establish the description of the system’s characteristics |
| MO2—Predict | Seeks to predict the behavior of the system | |
| MO3—Understand | Seeks to understand the impact of certain modifications on the characteristics of the system | |
| MO4—Represent | Seeks to build a reproduction of the system in a medium other than the original | |
| MO5—Intervene | Seeks to understand the system in order to intervene in it | |
| Activity intended for the student | I1—Solve | These actions are specific to each task and depend on the modeling objective and the learning objective |
| I2—Identify | ||
| I3—Explore | ||
| I4—Apply | ||
| I5—Build | ||
| I6—Model | ||
| I7—Work mathematically | ||
| I8—Interpret | ||
| I9—Observe |
In previous sections, we described how a model and mathematical model are defined in the literature. However, the characteristics of modeling tasks in a DGS environment provide new elements for building a definition of a model and computational model for these particular cases. In ten of the eleven tasks analyzed, there is a change in the environment in which the task is carried out, transitioning from its representation in “reality” to the construction of a mental image of the situation, and finally to a representation in the micro world of the DGS [10]. Then, the computational model is given by the geometric configuration that represents the situation in the DGS in a kind of simulation of a part of reality that allows exploring the results of a series of actions within the borders of the model, previously defined by the designer. At this point, there is no proper mathematical model in the sense of Doerr [36]; however, the construction of the configuration by using mathematical objects highlights and represents those aspects of reality that are the focus of the study. The configuration or structure of the relationships between the objects of the DGS is what constitutes the model in the context of task design that we explore in this paper. The computational model, in our perspective, represents the characteristics and behaviors of the situation, while the mathematical model comprises the relationships between the software objects established with a mathematical intention.
All of these considerations lead us to characterize the computational models that are part of the set of geometric configurations analyzed (Table 4). We thus establish two categories of characteristics: one that associates the elements considered for its construction (M1 and M2) and another that describes how the context influences the type of model (M3 and M4). The two groups of characteristics refer to those concepts or elements of reality that shape the structure of the model and are not mutually exclusive. These characteristics indicate (for example, in tasks T1, T6, T9, and T11) that the model is built by identifying components and behaviors in the context of the system to be studied (M2) using DGS objects to represent them. As a result, “the situation” gives rise to the construction of the model (M4). In tasks T2, T5, T7, and T8, the construction of the model uses theoretical knowledge (M1) suggested by the context of the task (M3). In these cases, the context of the task may be related to some area of science. In addition, in relation to the above, the tasks analyzed show two types of user interactions with the simulation: one where the user has control and can manipulate the objects at his/her convenience (S1) and another where the simulation is used to show a certain behavior and the user uses it to take data and work with that data (S2). We use the word “user” to refer the students who will work with the simulation.

Table 4.
Characteristics of the model and simulation.
Table 4.
Characteristics of the model and simulation.
| Category | Code | Description |
|---|---|---|
| Model | M1—based on theoretical knowledge | In addition to the geometric tools of the DGS, the model considers theoretical elements such as formulas or known behaviors associated with the phenomenon. |
| M2—based on the characteristics of the situation | Using the geometric tools of the DGS, the model mainly considers the characteristics and behaviors of the situation. | |
| M3—theoretical origin | The context gives rise to building the model with theoretical elements. | |
| M4—situational origin | The context gives rise to building the model by selecting elements and behaviors of the situation to represent. | |
| Type of simulation | S1—motion controlled by the user | The user controls the motion of certain objects present in the simulation. |
| S2—motions defined by the designer | The user’s actions are limited by the geometric configuration of the simulation. | |
| Type of solution | TS1—unique solution | Right answer determined by the design of the task. |
| TS2—dynamic open solution | The dynamism of DGS favors multiple responses. | |
| TS3—subjective answers | Answers that are difficult to classify as correct or incorrect. | |
| TS4—solution path determined by the geometric configuration | The dynamic configuration favors only one type of solution strategy. | |
| TS5—multiple solution paths | The dynamic configuration favors different solution strategies. |
A key point when designing tasks involves decisions regarding its structure. Sullivan et al. [13] refer to this as the degree of openness in tasks. Two types of questions are recognized in the literature as part of the task structure: one that scaffolds student engagement with a task in a more prescribed way and another that allows students greater opportunity to make strategic decisions on pathways and destinations for themselves. Thus, the structure of the tasks defines the path by which the solver finds a type of answer to said task. One type of answer that we might expect is that which can have clearly defined objectives but different solution strategies and responses [12]. Accordingly, the tasks analyzed can be classified as those that have a correct answer, determined by the design of the task (TS1), or those that have multiple correct answers, which we have called an open and dynamic solution (TS2), determined by the dynamism of the DGS. Now, in modeling, questions are often presented whose answers cannot be said to be correct or not. Yao [12] calls these subjective answers. In modeling, an answer may be said to be more or less correct, while the mathematical model is the one that best describes the system. The tasks that exhibited this characteristic were coded as TS3, while the tasks that favored different strategies for finding the solution were categorized as TS5, and those where the rigidity of the dynamic configuration only favored one type of strategy were categorized as TS4.
The main characteristics of each task are summarized in Table 5. We note that the objective of most of the tasks is focused on teaching mathematical concepts more than on teaching the modeling process. In addition, except for task T10, they all have the characteristic that they can only exist in the context of the DGS [37] and that it is the dynamism of the software that gives meaning to the task through experimentation when moving objects and observing their properties.

Table 5.
Summary of the tasks analyzed. The first column shows the name of the task and the group that designed it; the second column indicates the coding of the task. The third and fourth columns indicate the intended student activities. The fifth, sixth, seventh, and eighth columns indicate the modeling objective, the characteristics of the model, the type of simulation, and the type of solutions of the tasks.
Table 5.
Summary of the tasks analyzed. The first column shows the name of the task and the group that designed it; the second column indicates the coding of the task. The third and fourth columns indicate the intended student activities. The fifth, sixth, seventh, and eighth columns indicate the modeling objective, the characteristics of the model, the type of simulation, and the type of solutions of the tasks.
| Task/Group | Task Code | Activity Intended for the Student/Code | Objective Intended to Model | Characteristic of the Model | Type of Simulation | Solutions | |
|---|---|---|---|---|---|---|---|
| Bus in tunnel G1 | T1 | Solve an intersection problem between geometric objects, interpret the result. | I1 I3 I4 I8 | MG2 MG3 MG5 | M2 M4 | S1 | TS2 TS4 |
| Planetary motion G2 | T2 | Identify the behavior of planetary motion. Identify properties of the ellipse. | I2 I7 I9 | MG4 | M1 M3 | S2 | TS2 TS4 |
| Basketball G4 | T4 | Build the geometric model. Explore possible answers to the task. Add distances, use axial symmetry. | I3 I5 I6 | MG3 MG5 | M2 M1 M4 | S1 | TS2 TS5 |
| Motion of an inner circle G5 | T5 | Explore, given a geometric configuration, the geometric locus described by certain defined points based on the motion of inscribed circles. | I3 I7 I9 | MG1 MG3 MG4 | M1 M3 | S2 | TS2 TS4 |
| Harvest G6 | T6 | Build and solve a situation involving areas and perimeters and proportionality ratios. | I1 I3 I5 I6 | MG2 MG3 MG5 | M2 M4 | S1 | TS2 TS3 |
| Height of a building G7 | T7 | Solve using Thales’s theorem and trigonometric ratios. | I1 I3 I4 I7 | MG3 | M1 M3 | S2 | TS1 TS4 |
| Launch G8 | T8 | Explore and relate the behavior of a parabola with the value of its parameters. | I3 I7 I9 | MG3 MG4 | M1 M3 | S2 | TS1 TS4 |
| Speed bump G9 | T9 | Simplify and build the simulation. Study possible solutions algebraically in the context of software. | I5 I6 I7 I8 | MG2 MG3 MG5 | M2 M4 | S1 | TS2 TS3 TS5 |
| Seat arrangement G10 | T10 | Explore the geometric configuration, paying attention to the combination of distances and angles to find the optimal solution. | I3 I8 | MG3 MG5 | M2 M1 M4 | S1 | TS2 TS3 TS4 |
| Lift gate G11 | T11 | Explore different cases. Find the optimal solution or determine whether there is no solution. | I3 | MG3 MG5 | M2 M4 | S1 | TS2 TS3 TS4 |
| Wind power G12 | T12 | Perform algebraic operations and calculations using a given mathematical expression. | I1 I7 I9 | MG4 | M1 | S2 | TS1 |
In short, we find that the set of tasks promotes exploration (I3) and mathematical work (I7) to a greater extent, at 73% and 55%, respectively. The exploration promoted by the tasks is explained by the dynamism of the software, which naturally favors this activity. The most common modeling objectives are understanding (MO3) and intervening (MO5), at 82% and 55%, respectively. It is thus natural for the software-enhanced exploration (I3) to have a strong presence (in 73% of the cases) for understanding the situation (MO3). Also of note are the tasks in which the context induces the use of specific theoretical knowledge (M1, M3) related to some domain of science. In the set of tasks, the expected solutions exhibit different nuances (TS1–TS5), which are related to the different contexts and objectives in the tasks. Finally, in 55% of the tasks, the user is free to modify elements of the configuration (S1).
5.2. Two Examples
5.2.1. Speed Bump
The context that gives rise to this task originated in a study of the impact between the undercarriage of a car and a speed bump as it crosses over it (Figure 4), a very frequent situation in Latin American countries. Simulating this situation implies initially ruling out external aspects associated with environmental conditions, such as temperature, tire pressure, and the height of the car, which is considered fixed, thus ignoring the effect of the suspension, vehicle weight, the speed of car, exact shape of the bump, etc. Although this situation could be modeled from the perspective of mechanics involving force, velocity acceleration, and other elements, the participants decided to focus on reproducing the visual aspects of the situation. The simulation thus considers an idealization of the shapes of the objects and their motion.

Figure 4.
Task (T9) designed by G9 ([…] a speed bump is to be installed on the street […]. Raúl, who lives near the area, has to drive on that street daily with his Nissan v16, and he notices that the undercarriage of his car impacts the speed bump heavily. Annoyed by this situation, he decides to take his car to the garage to modify its suspension and make sure that the height of the car (distance between the ground and the bodywork) is sufficient to prevent this situation from happening again. What is the minimum car height required so the undercarriage does not impact the speed bump again?).
This task was proposed by group G9 for students aged 15–16 who are somewhat proficient in DGS. The procedure that incentivizes the modeling activity is shown in Figure 4. The intention of the pre-service teachers is for the students to look for a way to solve this situation in the context of the DGS. They are expected to model the situation (Figure 5a) to understand the motion of the undercarriage of the car (MO3) and predict (MO2) when the impact occurs (Figure 5b) and intervene in the situation (MO5). Since this task proposes having the students build the configuration, as shown in Figure 5a,b and Figure 6, and the students make the decisions about the movements represented, this task is classified as S1, in which the movements are defined and controlled by the user.
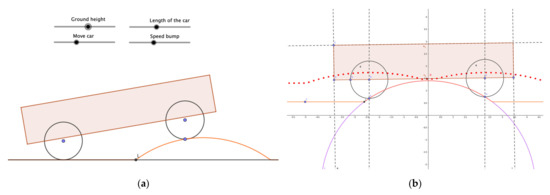
Figure 5.
(a) Representation of the situation. (b) Construction of a computational model.
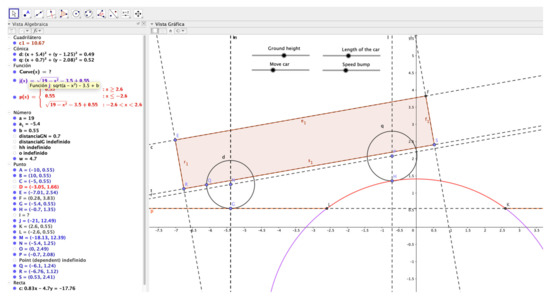
Figure 6.
Mathematical elements associated with building the computational model.
To address the situation, the students have to model (I6) it in the DGS environment, which will lead them to build (I5) a computational model. Both the construction of the model and the search for an answer to the problem involve mathematical work (I7), the results of which must be interpreted to provide an answer to the problem.
The computational model is built using DGS tools to represent the situation (M2), in an effort to represent the elements of the situation. Figure 5a shows the use of DGS elements to represent the speed bump (arc of a circle), as well as the automobile (quadrilateral and circles for the wheels) and its motion. As a result, this situation may be said to have a situational origin (M4).
In turn, the computational model consists of the geometric configuration (Figure 6) that corresponds to the mathematical model and that uses tools such as sliders, lines, segments, circles and functions, which are related and operated to intersect and transfer distances. These tools can also appear to be dependent on one another. These construction actions are part of the mathematical work carried out by the participants (I7) to build (I5) the computational model.
Another aspect related to mathematical work (I7) that students are expected to develop involves the solution process to determine an answer, which can only be developed in the DGS environment (TS2 and TS3) and/or with help from algebraic tools (TS5). In Figure 5a, point D has been constructed on the side of the quadrilateral that represents the undercarriage of the car. By sliding the dot on this side, students can experiment and identify the position at which the car will hit the speed bump. This makes it possible to use a table to record the values of the points or to search for the curve that best describes the geometric locus formed by the points, and then, by using the intersection, to determine the height. Another solution path is given by using trigonometric elements, as shown in Figure 7a, where it is assumed that the arc of the circumference that conforms the speed bump and the circles that represent the wheels of the car are tangent, which yields information of relevance for solving the problem (Figure 7b).
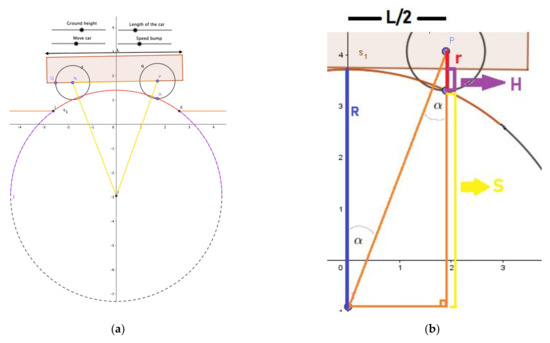
Figure 7.
(a) Representation of the situation with geometric elements. (b) To solve the situation, the participants regard the circles as tangents.
The above reveals that by modifying the height of the speed bump or the length of the car, different answers to the situation are obtained (TS2) that vary in precision (TS3) as the mathematical model improves in describing the system.
Although it is not the focus of this research, difficulties are also evident in the construction of the simulations. For example, it was not possible to fully convey visually the circles that represent the wheels as being tangent to the arc that represents the speed bump, while also keeping the circles tangent to the ground (represented by the graph of a linear function) (Figure 5b). However, the problem can be solved mathematically by assuming that the circles are tangent (Figure 7b), without forgetting that in reality the tangency at a point does not occur.
5.2.2. Height of a Building
The T7 task was designed by group G7 for students aged 15–16 to practice applications of trigonometry.
In the simulation that accompanies task 7 (Figure 8a), point G represents the position from which a beam (laser light) is projected towards an arc, representing a convex mirror. Then, using the law of reflection for convex mirrors (M1; specifically: (a) the reflection of a ray parallel to the focal axis passing through the focal point F of a convex mirror, (b) a ray traveling toward the focal point F and being reflected parallel to the focal axis, and (c) a ray along the radius through the center of curvature intersecting the surface in the normal direction and being reflected back along its original path (Figure 8b), the simulation shows ray m, which must hit the highest part of the photograph of the building by modifying the height h from which ray k is projected. The description of the assignment for the students is as follows:
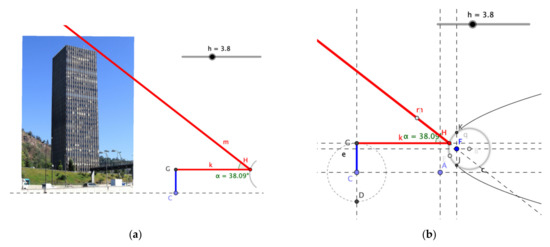
Figure 8.
(a) Reproduction of the simulation built by G7. (b) Construction of the computational model using the law of reflection.
We want to calculate the height of a building by using a laser and a convex mirror with a certain curvature, expressed in the attached GeoGebra file. If the distance between the building and the mirror is 10 (m), is it possible to calculate the height of the building? Prove your answer. If the answer is yes, how would you do it? Explain your procedure.
In contrast with task T9, the computational model is built using theoretical concepts of the phenomenon of light reflecting in concave mirrors (Figure 8b), which is why it is characterized as M1. In Figure 8b, a ray is horizontally projected from G to the mirror (represented by a parabolic curve), then at point H, the ray reflects with angle α (ray m), the extension of ray m (dashed line) passes through point F (focus of the parabola). The circumference with center B intends to show the case for a spherical mirror. In addition, the interest of the participants in constructing a task with interdisciplinary characteristics gives rise to a type of task that in reality would hardly be solved in the way they expect. The context of the task that creates the geometric configuration originates from a theoretical or interdisciplinary interest that the designers have (M3).
Even though when designing task T7 the participants developed a modeling process, the intended activity for the students boils down to exploration (I3) by modifying the height h and the distance k to understand (MO3) the situation presented. The central activity for students is to give an answer about the height of the building (I1). To this end, two expected solution strategies were identified. Both strategies depend on the configuration of the DGS environment (TS4), meaning that the presentation of the situation in the DGS environment guides the students to take solution paths that were predetermined by the designers of the task. The simplest strategy is to directly measure the height of the figure by drawing additional elements such as lines and intersection points. The other expected strategy is for the students to use trigonometric ratios. These two strategies are part of the mathematical work desired (I7) and both lead to a single solution (TS1). Finally, as described, the motions that the students can make are limited (S2) and more related to understanding the phenomenon of reflection than to solving a problem.
The main difference between tasks T7 and T9 is that the former proposes the use of a geometric configuration to enhance mathematical work (I7), explore (I3), and solve (I1) a particular situation. In this case, the exploration is particularly helpful for understanding the reflection phenomenon (MO3). Meanwhile, in task T9, the students are mainly asked to model (I5, I6, I7, I8) a situation to understand the situation in general (MO3) and to predict (MO2) and intervene in the situation (MO5).
6. Conclusions
The nature of the activities that emerge from the task design process undertaken by pre-service teachers allows us to initially recognize in their creations the use of technology as a reorganizer of the modeling process [22]. In the future, we would like to further study the ways in which the processes associated with modeling are reorganized.
The participants’ designs are an example of how the environment provided by the DGS provides a means for creating a simulated context of the phenomenon—an objective developed with the intention of creating new learning environments. In this artificial microworld, in which we have explored the characteristics of the tasks designed for teaching mathematics in digital and modeling environments and the kinds of activities that these tasks encourage in students, two relevant elements associated with the context of the tasks were observed that define their characteristics.
The first has to do with the teaching–learning of modeling and mathematics, in which there are two currents that can be associated with the intentions of the designer: one that considers modeling as a content to be taught and another that views it as a vehicle for learning mathematics. These currents have an impact on the pedagogical decisions that the designer makes regarding the objectives of the task. These two perspectives can be developed in a complementary fashion; however, factors determined by the formulation of study programs, such as giving greater relevance to covering mathematical concepts than to problem solving and modeling, mark a trend towards the use of modeling as a means for teaching mathematics. This fact is reflected in the participants’ lower tendency to propose tasks that encourage modeling activity (I6) in relation to the tasks that require exploration (I3) and mathematical work (I7), in which the teaching of mathematical objects is acknowledged as the main objective. Five main objectives are identified in the tasks that drive the students’ activities: describe (MO1), predict (MO2), understand (MO3), represent (MO4), and intervene (MO5). These characteristics have also been recognized in the mathematical models by various researchers [38].
In addition, it is important to consider that the characteristics of the tasks and the activity that these tasks encourage in the students are permeated by the experience that the participants had with modeling activities at the time of the study. As mentioned earlier, this work is part of a broader research effort that is studying the construction of the TPACK for teaching mathematics and mathematical modeling [10], where we have found that participation of pre-service teachers in mathematical problem-solving activities and the still scarce experience with modeling activities influence the type of tasks designed. As teacher educators, we hope that the continuous participation of future mathematics teachers in the design of modeling tasks in DGS environments will prompt them to consider more realistic situations, where the challenge is to bridge the gap between the tangible of the real world and its representation in a simulation.
The second element has to do with the way in which the DGS impacts the design characteristics of the tasks and the activity that the students can perform within the limitations of the software and the built configuration. One contribution of this paper involving the design of the work environment intended for students is the definition of a computational model and a mathematical model. A computational model, in our case, is made up of the geometric configuration that seeks to simulate selected aspects of the situation at hand, previously defined by the designer. In turn, the structure of the computational model consists of a set of DGS-specific objects that, by themselves, may or may not have a mathematical intention. The configuration may only seek to represent the situation with no obvious mathematical intention for the user, as in Figure 5a and Figure 8a, or it may seek to make mathematical aspects evident, as in Figure 6, Figure 7a and Figure 8b. The case in which the geometric configuration presents a structure built with mathematical intention, and which relies on intentional relationships between the DGS objects, we refer to as a mathematical model.
These characteristics of the models reflect the intentions of the person designing the task, which is why we also considered an origin (M3 and M4) or an interest in highlighting certain elements of the situation (M1 and M2). This means that if the focus of the designer of the task is on the situation as such, then the computational model will strive to represent details of the situation that are perhaps more superficial (visual or physical features), although this does not mean that it cannot involve a relatively interesting mathematical model. If, however, the designer has more specific knowledge of the situation, associated to a certain extent with the discipline in which said situation is framed, then there is a greater likelihood that the model built will be based on theoretical foundations. Thus, a computational model, as we conceptualize it, has two aspects: one mathematical and the other more associated with the specifics of the situation. Along these same lines, we observe that when the tasks are proposed in a digital environment (as in the cases shown), they are transformed. In other words, the task starts out in a situation selected and conceptualized by the designer in the context of the real world. It is then transformed into a teaching situation and, by involving the use of the DGS, the students’ work takes place mostly in the context of a microworld. The objectives of the task are reflected in the interactions they can have with the simulation and the kinds of answers they can find in this environment.
The work planned in the DGS environment provides feedback to students in different ways. On the one hand, the use of tools such as measure, drag, locus, etc., can be used to suggest and test conjectures involving the situation being analyzed. On the other, the construction of a dynamic configuration that represents part of a situation supports the complementarity of the representations offered by the DGS through its algebraic, graphic, tabular, and 3D screens. It also stimulates students to recognize and represent the dependence between objects, both in reality and in the microworld of the DGS, thus facilitating the processes of situational understanding and simplification. These aspects show how the DGS offers opportunities for students to explore, manipulate, simplify, and build models by giving them access to features of the situation that would otherwise be impossible to address.
Finally, it should be noted that the characterization of tasks, as identified in this research, provides a reference for studying the design of modeling tasks in DGS environments and for reflecting on the use of DGS and its influence on modeling processes.
Author Contributions
Conceptualization, C.G.-O.; methodology, C.G.-O.; formal analysis, C.G.-O. and M.C.-M.; investigation, C.G.-O. and M.C.-M.; writing—original draft preparation, C.G.-O. and M.C.-M.; writing—review and editing, C.G.-O. and M.C.-M.; visualization, C.G.-O. and M.C.-M.; project administration, C.G.-O. and M.C.-M.; funding acquisition, C.G.-O. and M.C.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by EDU2017-84276-R, Spain, and Fondecyt/iniciación No. 11200169, Chile.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the support received from project of National Plan of MICINN of the Spanish Government with reference EDU2017-84276-R and Agencia Nacional de Investigación y Desarrollo Fondecyt/iniciación No. 11200169 from Chile during the development of this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Geiger, V. Designing for Mathematical Applications and Modelling Tasks in Technology Rich Environments. In Digital Technologies in Designing Mathematics Education Tasks; Mathematics Education in the Digital Era; Leung, A., Baccaglini-Frank, A., Eds.; Springer: Cham, Switzerland, 2017; Volume 8, pp. 285–301. [Google Scholar] [CrossRef]
- Schukajlow, S.; Kaiser, G.; Stillman, G. Empirical research on teaching and learning of mathematical modelling: A survey on the current state-of-the-art. ZDM 2018, 50, 5–18. [Google Scholar] [CrossRef]
- Swidan, O.; Faggiano, E. Constructing shared mathematical meanings in the classroom with digital artifacts that simulate real-world phenomena. Math Ed. Res. J. 2021. [Google Scholar] [CrossRef]
- Kaput, J.; Thompson, P. Technology in Mathematics Education Research: The First 25 Years in the JRME. J. Res. Math. Educ. 1994, 25, 676–684. [Google Scholar] [CrossRef]
- Olive, J.; Makar, K.; Hoyos, V.; Kor, L.; Kosheleva, O.; Sträßer, R. Mathematical Knowledge and Practices Resulting from Access to Digital Technologies. In Mathematics Education and Technology-Rethinking the Terrain; Hoyles, C., Lagrange, J.-B., Eds.; Springer: Boston, MA, USA, 2010; pp. 133–177. [Google Scholar]
- Koh, J.H.L. Articulating teachers’ creation of Technological Pedagogical Mathematical Knowledge (TPMK) for supporting mathematical inquiry with authentic problems. Int. J. Sci. Math. Educ. 2019, 17, 1195–1212. [Google Scholar] [CrossRef]
- Thurm, D.; Barzel, B. Effects of a professional development program for teaching mathematics with technology on teachers’ beliefs, self-efficacy. ZDM 2020, 52, 1411–1422. [Google Scholar] [CrossRef]
- Goldsmith, L.; Doerr, H.; Lewis, C. Mathematics teachers’ learning: A conceptual framework and synthesis of research. J. Math. Teach. Educ. 2014, 17, 5–36. [Google Scholar] [CrossRef]
- Van Dijke-Droogers, M.; Drijvers, P.; Bakker, A. Statistical modeling processes through the lens of instrumental genesis. Educ. Stud. Math. 2021, 107, 235–260. [Google Scholar] [CrossRef]
- Guerrero-Ortiz, C. Pre-service Mathematics Teachers’ Technological Pedagogical Content Knowledge: The Case of Modelling. In Mathematical Modelling Education in East and West; International Perspectives on the Teaching and Learning of Mathematical Modelling; Leung, F.K.S., Stillman, G.A., Kaiser, G., Wong, K.L., Eds.; Springer Nature: Cham, Switzerland, 2021; pp. 141–151. [Google Scholar] [CrossRef]
- Greefrath, G.; Vorhölter, K. Teaching and Learning Mathematical Modelling: Approaches and Developments from German Speaking Countries. In Teaching and Learning Mathematical Modelling; ICME-13 Topical Surveys; Springer International Publishing AG: Cham, Switzerland, 2016. [Google Scholar]
- Yeo, J.B.W. Development of a Framework to Characterise the Openness of Mathematical Tasks. Int. J. Sci. Math. Educ. 2017, 15, 175–191. [Google Scholar] [CrossRef]
- Sullivan, P.; Clarke, D.; Clarke, B. Teaching with Tasks for Effective Mathematics Learning; Springer: New York, NY, USA, 2013. [Google Scholar]
- Blomhøj, M.; Jensen, T.H. What’s all the fuss about competencies? In Modelling and Applications in Mathematics Education; Blum, W., Galbraith, P., Henn, H., Niss, M., Eds.; Springer: New York, NY, USA, 2007; pp. 45–56. [Google Scholar]
- Borromeo, F. Theoretical and empirical differentiations of phases in the modelling process. Zent. Für Didakt. Der Math. 2006, 38, 86–95. [Google Scholar]
- Doerr, H.; Ärlebäck, J.; Misfeldt, M. Representations of modelling in mathematics education. In Mathematical Modelling and Applications: Crossing and Researching Boundaries in Mathematics Education; Springer: Cham, Switzerland, 2017; pp. 71–82. [Google Scholar]
- Blum, W.; Leiß, D. How do students and teachers deal with modelling problems? In Mathematical Modelling: Education, Engineering and Economics; Haines, C., Galbraith, P., Blum, W., Khan, S., Eds.; Horwood: Chichester, UK, 2007; pp. 222–231. [Google Scholar]
- Lesh, R.; Doerr, H.M. Foundations of a models and modeling perspective on mathematics teaching, learning, and problem solving. In Beyond Constructivism: Models and Modeling Perspectives on Mathematics Teaching, Learning, and Problem Solving; Lesh, R., Doerr, H.M., Eds.; Lawrence Erlbaum Associates Inc.: Mahwah, NJ, USA, 2003; pp. 3–33. [Google Scholar]
- Swan, M.; Burkhardt, H. A Designer Speaks. Educational Designer. 2012. Available online: http://www.educationaldesigner.org/ed/volume2/issue5/article19 (accessed on 2 March 2022).
- Quiroz-Rivera, S.; Rodríguez, R. Análisis de praxeologías de modelización matemática en libros de texto de educación primaria. Educ. Matemática 2015, 27, 45–79. Available online: http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S1665-58262015000300045&lng=es&tlng=es (accessed on 1 June 2019).
- Maaß, K. Classification Scheme for Modelling Tasks. J. Math. Didakt. 2010, 31, 285–311. [Google Scholar] [CrossRef]
- Molina-Toro, J.F.; Rendón-Mesa, P.A.; Villa-Ochoa, J.A. Research Trends in Digital Technologies and Modeling in Mathematics Education. Eurasia J. Math. Sci. Technol. Educ. 2019, 15, em1736. [Google Scholar] [CrossRef]
- Joubert, M. Revisiting Theory for the Design of Tasks: Special Considerations for Digital Environments. In Digital Technologies in Designing Mathematics Education Tasks; Mathematics Education in the Digital Era; 2016; Volume 8, pp. 14–17. [Google Scholar] [CrossRef] [Green Version]
- Lingefjärd, T.; Holmquist, M. Mathematical modelling and technology in teacher education—Visions and reality. In Modelling and Mathematics Education ICTMA 9: Applications in Science and Technology; Matos, J., Blum, W., Houston, K., Carreira, S., Eds.; Horwood: Chichester, UK, 2001; pp. 205–215. [Google Scholar]
- Leung, A. Exploring Techno-Pedagogic Task Design in the Mathematics Classroom. In Digital Technologies in Designing Mathematics Education Tasks, Mathematics Education in the Digital Era; Leung, A., Baccaglini-Frank, A., Eds.; Springer International Publishing: Cham, Switzerland, 2017; Volume 8, pp. 3–16. [Google Scholar] [CrossRef]
- Moreno-Armella, L.; Santos-Trigo, M. The use of digital technologies in mathematical practices: Reconciling traditional and emerging approaches. In Handbook of International Research in Mathematics Education, 3rd ed.; English, L., Kirshner, D., Eds.; Taylor and Francis: New York, NY, USA, 2016; pp. 595–616. [Google Scholar]
- Doerr, H.M.; Zangor, R. Creating Meaning for and with the Graphing Calculator. Educ. Stud. Math. 2000, 41, 143–163. [Google Scholar] [CrossRef]
- Greefrath, G.; Hertleif, C.; Siller, H. Mathematical modelling with digital tools -a quantitative study on mathematising with dynamic geometry software. ZDM 2018, 50, 233–244. [Google Scholar] [CrossRef]
- Greefrath, G.; Siller, H. Modelling and simulation with the help of digital tools. In Mathematical Modelling and Applications; Stillman, G.A., Blum, W., Kaiser, G., Eds.; ICTMA 17; Springer: Dordrecht, The Netherlands, 2017; pp. 529–539. [Google Scholar]
- Borromeo, R. Learning How to Teach Mathematical Modeling in School and Teacher Education; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Love, E.; Burton, L.; Jaworski, B. Software for Mathematics Education; Chartwell-Bratt: Lund, Sweden, 1995. [Google Scholar]
- Nevile, L.; Burton, L.; Jaworski, B. Looking at, through, Back at: Useful Ways of Viewing Mathematical Software; Chartwell-Bratt: Lund, Sweden, 1995. [Google Scholar]
- Cohen, L.; Manion, L. Métodos de Investigación Educative, 2nd ed.; La Muralla: Madrid, Spain, 2002. [Google Scholar]
- Stake, R. Investigación con Estudio de Casos, 4th ed.; Ediciones Morata: Madrid, Spain, 2007. [Google Scholar]
- Drijvers, P.; Doorman, M.; Boon, P.; Reed, H.; Gravemeijer, K. The teacher and the tool: Instrumental orchestrations in the technology-rich mathematics classroom. Educ. Stud. Math. 2010, 75, 213–234. [Google Scholar] [CrossRef] [Green Version]
- Doerr, H. Experiment, simulation and analysis: An integrated instructional approach to the concept of force. Int. J. Sci. Educ. 1997, 19, 265–282. [Google Scholar] [CrossRef]
- Venturini, M.; Sinclair, N. Designing Assessment Tasks in a Dynamic Geometry Environment. In Digital Technologies in Designing Mathematics Education Tasks; Mathematics Education in the Digital Era; Leung, A., Baccaglini-Frank, A., Eds.; Springer International Publishing: Cham, Switzerland, 2017; Volume 8, pp. 77–98. [Google Scholar] [CrossRef]
- Gainsburg, J. Learning to Model in Engineering. Math. Think. Learn. 2013, 15, 259–290. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).