A Tensor Splitting AOR Iterative Method for Solving a Tensor Absolute Value Equation

Abstract

In this paper, a tensor splitting AOR iterative method for solving the ${\mathcal{H}}^{+}$-tensor absolute value equation is presented. Some sufficient conditions for the existence of the solution to the tensor absolute value equation are given. Under suitable conditions, the new method is proved to be convergent. Finally, some numerical examples demonstrate that our new method is effective.

1. Introduction

Recently, the study of tensors has become a hot research field due to its numerous fields of application, such as tensor complementary problems [1,2,3], numerical partial differential equations [4], image processing [5] and data mining [6]. With the development of the tensor problem, the solution to the tensor absolute value equation has been paid more and more attention. In this paper, we consider the tensor absolute value equation (TAVE):

$$\mathcal{A}{\mathbf{x}}^{m-1}-{\left|\mathbf{x}\right|}^{[m-1]}=\mathbf{b},$$

(1)

where $\mathcal{A}=\left(a_{i_1{i}_2\cdots i_m}\right)$ is an m-order, n-dimensional tensor; $\mathbf{x}={(x_1,x_2,\dots ,x_n)}^T$ and the right-hand $\mathbf{b}={(b_1,b_2,\dots ,b_n)}^T$ are both n-dimensional vectors; and ${|\mathbf{x}|}^{[m-1]}=(|x_1{|}^{m-1},$$|x_2{|}^{m-1},\dots ,|x_n{{|}^{m-1})}^T$. The tensor absolute value equation is a further extension of the matrix absolute value equation. Du et al. [7] proved that TAVE (1) is equal to a certain class of structural tensor complementarity problems, and they solved it with the Levenberg–Marquardt method. Bu and Ma [8] proposed some tensor splitting methods and proved the existence of positive solutions for solving TAVE (1), with $\mathcal{A}$ being a nonsingular $\mathcal{M}$-tensor. Ning et al. [9] studied a tensor-type successive over-relaxation method and tensor-type accelerated over-relaxation method for solving TAVE (1) when $\mathcal{A}$ is a nonsingular $\mathcal{M}$-tensor. More generally, Guo and Gu [10] introduced the following tensor generalized absolute value equation (TGAVE):

$$\mathcal{A}{\mathbf{x}}^{m-1}-\mathcal{B}{\left|\mathbf{x}\right|}^{[m-1]}=\mathbf{b},$$

(2)

where $\mathcal{B}=\left(b_{i_1{i}_2\cdots i_m}\right)$ is also an m-order n-dimensional tensor, and they proposed a smoothing Newton method to solve it. Ling et al. [11] provided the existence of solutions of TGAVE (2) with the help of degree theory and proved that TGAVE (2) has at least one solution under some checkable conditions. Jiang and Li [12] analyzed the existence of solutions of TGAVE (2) and proposed a SOR iterative algorithm to solve this equation. Apparently, (2) covers (1), when $\mathcal{B}$ is an m-order n-dimensional unit tensor.

In addition, when $\mathcal{B}$ is a zero tensor, TGAVE (2) is expressed as the tensor equation:

$$\mathcal{A}{\mathbf{x}}^{m-1}=\mathbf{b}.$$

(3)

There are many methods for solving (3) when $\mathcal{A}$ is a nonsingular $\mathcal{M}$-tensor. For example, the Jacobi method, the Gauss–Seidel method, the Newton method [13], the tensor splitting method [14], and the preconditioned tensor splitting method [15]. The $\mathcal{H}$-tensor has been widely used in evolutionary game dynamics and high-order Markov chains. Wang et al. [16] proposed a preprocessing AOR iterative method for solving (3) when the coefficient tensor $\mathcal{A}$ is a nonsingular $\mathcal{H}$-tensor. When $\mathcal{A}$ is an ${\mathcal{H}}^{+}$-tensor, Wang et al. [17] theoretically proved that (3) has a unique positive solution with positive right-hand side $\mathbf{b}$, and also proved that (3) has a negative solution.

To our knowledge, TAVE (1) has been studied in recent years, and there is not much literature on it. It is observed that many of the current research works aim at TAVE (1), which $\mathcal{A}$ is an $\mathcal{M}$-tensor, and the results of studies about TAVE (1) with $\mathcal{A}$ as an ${\mathcal{H}}^{+}$-tensor are relatively rare. Additionally, TAVE (1) of the ${\mathcal{H}}^{+}$-tensor is a further extension of the $H^{+}$-matrix absolute value equation [18]. Based on these motivations, a tensor splitting AOR iterative method to solve TAVE (1) when $\mathcal{A}$ is an ${\mathcal{H}}^{+}$-tensor is intensively studied in this paper, and we illustrate the effectiveness of this method through some numerical examples in Section 4.

The main structure of this paper is as follows. In Section 2, we introduce some notation, definitions, and lemmas. In Section 3, we give some sufficient conditions for the existence of the solution of TAVE (1). Then we give a tensor splitting AOR iterative algorithm and prove the convergence of the algorithm. In Section 4, the results of some numerical examples are given.

2. Preliminaries

We first introduce some notation relevant to this paper. Let $\mathbb{R}$, ${\mathbb{R}}^n$, and ${\mathbb{R}}^{[m,n]}$ be the real field, the set of all n-dimensional real vectors, and the set of all m-order n-dimensional real tensors, respectively. Remember $\mathbf{0}$, O, and $\mathcal{O}$ are a null vector, a null matrix, and a null tensor, respectively. Let $\mathcal{A},\mathcal{B}\in {\mathbb{R}}^{[m,n]}$. The order $\mathcal{A}\ge \mathcal{B}$ means that $a_{i_1{i}_2\cdots i_m}\ge b_{i_1{i}_2\cdots i_m}$. If $\mathcal{A}\ge \mathcal{O}$, that is, $a_{i_1{i}_2\cdots i_m}\ge 0$, the tensor $\mathcal{A}$ is called a nonnegative tensor. An m-order n-dimensional unit tensor ${\mathcal{I}}_m=\left({\delta }_{i_1{i}_2\cdots i_m}\right)$ is given by

$${\delta }_{i_1{i}_2\cdots i_m}=\left\{\begin{array}{cc}1,\hfill & i_1=i_2=\cdots =i_m,\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

Next, we summarize some definitions and lemmas related to this paper. We introduce the definitions of $\mathcal{M}$-tensor, $\mathcal{H}$-tensor, and ${\mathcal{H}}^{+}$-tensor.

Definition 1

([19]). $\mathcal{A}\in {\mathbb{R}}^{[m,n]}$ is called an $\mathcal{M}$-tensor if there exist a nonnegative tensor $\mathcal{B}$ and a positive real number $\eta \ge \rho \left(\mathcal{B}\right)$ such that

$$\mathcal{A}=\eta {\mathcal{I}}_m-\mathcal{B}.$$

If $\eta >\rho \left(\mathcal{B}\right)$, then $\mathcal{A}$ is called a nonsingular $\mathcal{M}$-tensor.

Definition 2

([19]). Let $\mathcal{A}\in {\mathbb{R}}^{[m,n]}$. We call another tensor $⟨\mathcal{A}⟩=\left(m_{i_1{i}_2\dots i_m}\right)$ the comparison tensor of $\mathcal{A}$ if

$$m_{i_1{i}_2\dots i_m}=\left\{\begin{array}{cc}|a_{i_1{i}_2\dots i_m}|,\hfill & (i_1{i}_2\dots i_m)=(i_1{i}_1\dots i_1),\hfill \\ -|a_{i_1{i}_2\dots i_m}|,\hfill & (i_1{i}_2\dots i_m)\ne (i_1{i}_1\dots i_1).\hfill \end{array}\right.$$

Definition 3

([19,20]). Let $\mathcal{A}\in {\mathbb{R}}^{[m,n]}$. We call a tensor $\mathcal{A}$ an $\mathcal{H}$-tensor, if its comparison tensor is an $\mathcal{M}$-tensor; we call it a nonsingular $\mathcal{H}$-tensor, if its comparison tensor is a nonsingular $\mathcal{M}$-tensor. We call $\mathcal{A}$ an ${\mathcal{H}}^{+}$-tensor, if it is a nonsingular $\mathcal{H}$-tensor with all the diagonal elements $a_{ii\dots i}>0.$

The following introduces the majorization matrix and the order-2 left-inverse of the tensor.

Definition 4

([21]). Let $\mathcal{A}\in {\mathbb{R}}^{[m,n]}$. The majorization matrix $M\left(\mathcal{A}\right)$ of $\mathcal{A}$ is defined as an $n\times n$ matrix with its entries

$$M{\left(\mathcal{A}\right)}_{ij}=\left(a_{ij\cdots j}\right),i,j=1,2,\cdots ,n.$$

Definition 5

([22]). Let $\mathcal{A}\in {\mathbb{R}}^{[m,n]}$. If $M\left(\mathcal{A}\right)$ is a nonsingular matrix and $\mathcal{A}=M\left(\mathcal{A}\right){\mathcal{I}}_m$, we call $M{\left(\mathcal{A}\right)}^{-1}$ the order-2 left-inverse of $\mathcal{A}$.

Definition 6

([14]). Let $\mathcal{A}\in {\mathbb{R}}^{[m,n]}$. If $\mathcal{A}$ has an order-2 left-inverse, then $\mathcal{A}$ is called a left-invertible tensor or left-nonsingular tensor.

Tensor H-splitting and H-compatible splitting are introduced next.

Definition 7

([14]). Let $\mathcal{A},\mathcal{E},\mathcal{F}\in {\mathbb{R}}^{[m,n]}$. $\mathcal{A}=\mathcal{E}-\mathcal{F}$ is said to be a splitting of $\mathcal{A}$ if $\mathcal{E}$ is left-nonsingular, or a convergent splitting if $\rho \left(M{\left(\mathcal{E}\right)}^{-1}\mathcal{F}\right)<1$.

Definition 8

([16]). Let $\mathcal{A},\mathcal{E},\mathcal{F}\in {\mathbb{R}}^{[m,n]}$. The splitting $\mathcal{A}=\mathcal{E}-\mathcal{F}$ is called

(1) 

H-splitting if $⟨\mathcal{E}⟩$ is a left-nonsingular tensor and $⟨\mathcal{E}⟩-\left|\mathcal{F}\right|$ is a nonsingular $\mathcal{M}$-tensor;

(2) 

H-compatible splitting if $⟨\mathcal{E}⟩$ is a left-nonsingular tensor and $⟨\mathcal{A}⟩=⟨\mathcal{E}⟩-\left|\mathcal{F}\right|$.

Lemma 1

([16]). Let $\mathcal{A},\mathcal{E},\mathcal{F}\in {\mathbb{R}}^{[m,n]}$. If $\mathcal{A}=\mathcal{E}-\mathcal{F}$ is an H-splitting, then $\mathcal{A}$ and $\mathcal{E}$ are nonsingular $\mathcal{H}$-tensors and $\rho \left(M{\left(\mathcal{E}\right)}^{-1}\mathcal{F}\right)\le \rho (M{\left(⟨\mathcal{E}⟩\right)}^{-1}\left|\mathcal{F}\right|)<1$.

Lemma 2

([16]). Let $\mathcal{A},\mathcal{E},\mathcal{F}\in {\mathbb{R}}^{[m,n]}$. If the splitting $\mathcal{A}=\mathcal{E}-\mathcal{F}$ is an H-compatible splitting and $\mathcal{A}$ is a nonsingular $\mathcal{H}$-tensor, then it is an H-splitting and $\rho \left(M{\left(\mathcal{E}\right)}^{-1}\mathcal{F}\right)<1$.

From the above Lemmas 1 and 2, we have the following lemma.

Lemma 3.

Let $\mathcal{A}$ is an ${\mathcal{H}}^{+}$-tensor. Then all H-(compatible) splittings of $\mathcal{A}$ are convergent.

Proof. 

Assume that $\mathcal{A}=\mathcal{E}-\mathcal{F}$ is an H-(compatible) splitting. Since $\mathcal{A}$ is an ${\mathcal{H}}^{+}$-tensor, $\mathcal{A}$ is a nonsingular $\mathcal{H}$-tensor. By Lemmas 1 and 2, we get $\rho \left(M{\left(\mathcal{E}\right)}^{-1}\mathcal{F}\right)<1$.    □

Finally, for tensor Equation (3) with $\mathcal{A}$ as an ${\mathcal{H}}^{+}$-tensor, the existence theorem for a positive solution and a negative solution is in the following lemmas.

Lemma 4

([17]). If $\mathcal{A}$ is an ${\mathcal{H}}^{+}$-tensor, then for every positive vector $\mathbf{b}$, the tensor Equation (3) has a unique positive solution.

Lemma 5

([17]). Let $\mathcal{A}$ be an ${\mathcal{H}}^{+}$-tensor. For every positive vector $\mathbf{b}$ and an odd m, if $\mathbf{x}$ is a solution of

$$\mathcal{A}{\mathbf{x}}^{m-1}-\mathbf{b}=\mathbf{0},$$

then the tensor equation (3) has a negative solution: $-\mathbf{x}$.

3. Main Results

3.1. Existence and Uniqueness of Solutions of TAVE (1)

First of all, we discuss the conditions for the existence and uniqueness of the solution of TAVE (1).

Theorem 1.

Let $\mathcal{A}=\left(a_{i_1{i}_2\cdots i_m}\right),\mathcal{B},{\mathcal{I}}_m\in {\mathbb{R}}^{[m,n]}$. If the diagonal elements $a_{ii\dots i}>1$ and the comparison matrix $⟨\mathcal{A}⟩$ can be written as $⟨\mathcal{A}⟩=c{\mathcal{I}}_m-\mathcal{B}$ with $\mathcal{B}\ge \mathcal{O}$ and $c>\rho \left(\mathcal{B}\right)+1$, then for every positive vector $\mathbf{b}$, TAVE (1) has a unique positive solution.

Proof. 

Since $a_{ii\dots i}>1$, we get

$$⟨\mathcal{A}-{\mathcal{I}}_m⟩=\left\{\begin{array}{cc}|a_{i_1{i}_2\dots i_m}|-1,\hfill & (i_1{i}_2\dots i_m)=(i_1{i}_1\dots i_1),\hfill \\ -|a_{i_1{i}_2\dots i_m}|,\hfill & (i_1{i}_2\dots i_m)\ne (i_1{i}_1\dots i_1),\hfill \end{array}\right.$$

and then we obtain $⟨\mathcal{A}-{\mathcal{I}}_m⟩=⟨\mathcal{A}⟩-{\mathcal{I}}_m$. Suppose that $s=c-1$. According to $⟨\mathcal{A}⟩=c{\mathcal{I}}_m-\mathcal{B}$, we have

$$⟨\mathcal{A}⟩-{\mathcal{I}}_m=s{\mathcal{I}}_m-\mathcal{B},\mathcal{B}\ge \mathcal{O},s>\rho \left(\mathcal{B}\right),$$

which means that $⟨\mathcal{A}⟩-{\mathcal{I}}_m$ is a nonsingular $\mathcal{M}$-tensor; that is, $⟨\mathcal{A}-{\mathcal{I}}_m⟩$ is also a nonsingular $\mathcal{M}$-tensor. Thus, $\mathcal{A}-{\mathcal{I}}_m$ is an ${\mathcal{H}}^{+}$-tensor. By Lemma 4, the tensor equation

$$(\mathcal{A}-{\mathcal{I}}_m){\mathbf{x}}^{m-1}=\mathbf{b}$$

(4)

has a unique positive solution for every positive vector $\mathbf{b}$. Additionally, TAVE (1) can be converted to the tensor Equation (4) when $\mathbf{x}>\mathbf{0}$. Hence, for every positive vector $\mathbf{b}$, TAVE (1) has a unique positive solution.    □

Theorem 2.

Let $\mathcal{A}=\left(a_{i_1{i}_2\cdots i_m}\right),\mathcal{B},{\mathcal{I}}_m\in {\mathbb{R}}^{[m,n]}$, and $\mathbf{x}$ is a solution of TAVE (1). If the diagonal elements $a_{ii\dots i}>1$, the comparison matrix $⟨\mathcal{A}⟩$ can be written as $⟨\mathcal{A}⟩=c{\mathcal{I}}_m-\mathcal{B}$ with $\mathcal{B}\ge \mathcal{O}$ and $c>\rho \left(\mathcal{B}\right)+1$, so TAVE (1) has a negative solution $-\mathbf{x}$ for every positive vector $\mathbf{b}$ and an odd m.

Proof. 

It is known from the proof of Theorem 1 that $\mathcal{A}-{\mathcal{I}}_m$ is an ${\mathcal{H}}^{+}$-tensor. By Lemma 5, it follows that for every positive vector $\mathbf{b}$ and an odd m, if $\mathbf{x}>\mathbf{0}$ is a solution of the tensor Equation (4), then so is $-\mathbf{x}$; that is,

$$(\mathcal{A}-{\mathcal{I}}_m){(-\mathbf{x})}^{m-1}=\mathbf{b}.$$

Hence, for every positive vector $\mathbf{b}$ and an odd m, if $\mathbf{x}$ is a solution of TAVE (1), then TAVE (1) has a negative solution $-\mathbf{x}$.    □

From the conditions of Theorems 1 and 2, we proved that $\mathcal{A}-{\mathcal{I}}_m$ is an ${\mathcal{H}}^{+}$-tensor. Therefore, we have the following two corollaries.

Corollary 1.

Let $\mathcal{A},{\mathcal{I}}_m\in {\mathbb{R}}^{[m,n]}$. If $\mathcal{A}-{\mathcal{I}}_m$ is an ${\mathcal{H}}^{+}$-tensor, then for every positive vector $\mathbf{b}$, TAVE (1) has a unique positive solution.

Corollary 2.

Let $\mathcal{A},{\mathcal{I}}_m\in {\mathbb{R}}^{[m,n]}$ and $\mathbf{x}$ is a solution of TAVE (1). If $\mathcal{A}-{\mathcal{I}}_m$ is an ${\mathcal{H}}^{+}$-tensor, then TAVE (1) has a negative solution $-\mathbf{x}$ for every positive vector $\mathbf{b}$ and an odd m.

3.2. Tensor Splitting AOR Iterative Method

In [16], the preconditioned tensor splitting AOR iterative method was proposed to solve the tensor Equation (3) by Wang et al. Next, based on the method of [16], we give a tensor splitting AOR iterative method for solving TAVE (1).

From Theorems 1 and 2, we proved that TAVE (1) can be converted to the tensor Equation (4) when $\mathbf{x}>\mathbf{0}$ or m is an odd number and $\mathbf{x}<\mathbf{0}$, where $\mathbf{x}$ is the solution of (4). Thus, we can get the solution of TAVE (1) by solving the tensor Equation (4). First of all, a splitting of the tensor $\mathcal{A}-{\mathcal{I}}_m$ into

$$\mathcal{A}-{\mathcal{I}}_m=\mathcal{E}-\mathcal{F}.$$

(5)

If ${\left(M\left(\mathcal{E}\right)\right)}^{-1}$ exists, then an iterative formula for solving the tensor Equation (4) can be written as

$${\mathbf{x}}_k={(\mathcal{T}{\mathbf{x}}_{k-1}^{m-1}+f)}^{\left[\frac{1}{m-1}\right]},k=1,2,\cdots ,$$

where $\mathcal{T}=M{\left(\mathcal{E}\right)}^{-1}\mathcal{F}$ and $f=M{\left(\mathcal{E}\right)}^{-1}\mathbf{b}$. The tensor $\mathcal{T}$ denotes the iterative tensor of the splitting method. Let

$$\mathcal{A}-{\mathcal{I}}_m=\mathcal{D}-\mathcal{L}-\mathcal{U},$$

where $\mathcal{D}=D{\mathcal{I}}_m$; $\mathcal{L}=L{\mathcal{I}}_m$; and D and $-L$ are the diagonal and the strictly lower triangle part of $M(\mathcal{A}-{\mathcal{I}}_m)$, respectively. If

$$\mathcal{E}=\frac{1}{\omega }(\mathcal{D}-r\mathcal{L}),\mathcal{F}=\frac{1}{\omega }[(1-\omega )\mathcal{D}+(\omega -r)\mathcal{L}+\omega \mathcal{U}],$$

then the splitting method (5) is called the AOR method. Additionally, the iteration tensor of the AOR method is given by ${\mathcal{T}}_{AOR}=M{\left(\mathcal{E}\right)}^{-1}\mathcal{F}=M{(\mathcal{D}-r\mathcal{L})}^{-1}·[(1-\omega )\mathcal{D}+(\omega -r)\mathcal{L}+\omega \mathcal{U}]$, where $\omega ,r$ are real parameters with $\omega \ne 0$. In particular, the AOR method becomes the SOR method when $r=\omega$, the AOR method becomes the Gauss–Seidel method when $r=\omega =1$, and the AOR method becomes the Jacobi method when $r=0$ and $\omega =1$. The corresponding tensor splitting AOR iterative method for solving TAVE (1) is given as follows.

Next, we give the convergence theorem of Algorithm 1.

Algorithm 1 Tensor splitting AOR iterative method.

1. Given an ${\mathcal{H}}^{+}$-tensor $\mathcal{A}$, a splitting $\mathcal{A}-{\mathcal{I}}_m=\mathcal{E}-\mathcal{F}$, a right-hand vector $\mathbf{b}>\mathbf{0}$, a maximal iteration number $k_{max}$, a machine precision $\epsilon$, and a positive initial vector ${\mathbf{x}}_0$. Initialize $k:=1$. 2. While $k<k_{max}$ $${\mathbf{x}}_k={(M{\left(\mathcal{E}\right)}^{-1}\mathcal{F}{\mathbf{x}}_{k-1}^{m-1}+M{\left(\mathcal{E}\right)}^{-1}\mathbf{b})}^{\left[\frac{1}{m-1}\right]},k=1,2,\cdots .$$ 3. If $\Vert (\mathcal{A}-{\mathcal{I}}_m){\mathbf{x}}_k^{m-1}{-\mathbf{b}\Vert }_2\le \epsilon$, output the solution ${\mathbf{x}}_{\mathit{k}}$. 4. Let $k=k+1$, return to step 2.

Theorem 3.

Let $\mathcal{A}-{\mathcal{I}}_m\in {\mathbb{R}}^{[m,n]}$ be an ${\mathcal{H}}^{+}$-tensor.

(1) If $0\le r\le \omega \le 1(\omega \ne 0)$, then $\rho \left({\mathcal{T}}_{AOR}\right)<1$;

(2) If $0\le r\le \omega \le 2$ ($\omega >1,\omega \ne 0)$ and $(\frac{2}{\omega }-1)\left|\mathcal{D}\right|-\left|\mathcal{L}\right|-\left|\mathcal{U}\right|$ is a nonsingular $\mathcal{M}$-tensor, then $\rho \left({\mathcal{T}}_{AOR}\right)<1$.

Proof. 

According to the AOR splitting of (5), we have

$$⟨\mathcal{E}⟩=\frac{1}{\omega }\left(\right|\mathcal{D}|-r\left|\mathcal{L}\right|),|\mathcal{F}|=\frac{1}{\omega }\left[\right|(1-\omega )|·\left|\mathcal{D}\right|+(\omega -r)\left|\mathcal{L}\right|+\omega \left|\mathcal{U}\right|].$$

(1) Due to $0\le r\le \omega \le 1(\omega \ne 0)$, we obtain

$$\begin{array}{cc}\hfill ⟨\mathcal{E}⟩-\left|\mathcal{F}\right|& =\frac{1}{\omega }\left(\right|\mathcal{D}|-r\left|\mathcal{L}\right|)-\frac{1}{\omega }\left[(1-\omega )\right|\mathcal{D}|+(\omega -r)\left|\mathcal{L}\right|+\omega \left|\mathcal{U}\right|]\hfill \\ & =\left|\mathcal{D}\right|-\left|\mathcal{L}\right|-\left|\mathcal{U}\right|\hfill \\ & =⟨\mathcal{A}-{\mathcal{I}}_m⟩.\hfill \end{array}$$

Since $\mathcal{A}-{\mathcal{I}}_m$ is an ${\mathcal{H}}^{+}$-tensor, the diagonal tensor $\mathcal{D}$ is nonsingular. Additionally, $r\le \omega$, so $⟨\mathcal{E}⟩$ is a left-nonsingular tensor. Therefore, the splitting of $\mathcal{A}-{\mathcal{I}}_m=\mathcal{E}-\mathcal{F}$ is an H-compatible splitting. From Lemma 3, we can get that the AOR splitting of (5) is convergent. So $\rho \left({\mathcal{T}}_{AOR}\right)<1$.

(2) It can be seen from the proof of (1) that $⟨\mathcal{E}⟩$ is a left-nonsingular tensor. While $0\le r\le \omega \le 2$ ($\omega >1,\omega \ne 0)$, we have

$$⟨\mathcal{E}⟩-\left|\mathcal{F}\right|=(\frac{2}{\omega }-1)\left|\mathcal{D}\right|-\left|\mathcal{L}\right|-\left|\mathcal{U}\right|.$$

As $(\frac{2}{\omega }-1)\left|\mathcal{D}\right|-\left|\mathcal{L}\right|-\left|\mathcal{U}\right|$ is a nonsingular $\mathcal{M}$-tensor, $\mathcal{A}-{\mathcal{I}}_m=\mathcal{E}-\mathcal{F}$ is an H-splitting. Hence, by Lemma 3, we know that the AOR splitting of (5) is convergent. In other words, $\rho \left({\mathcal{T}}_{AOR}\right)<1$. □

4. Numerical Examples

In this section, we verify the effectiveness of Algorithm 1 through some numerical examples. All tests were performed in Matlab 2018b with configuration: Intel(R) Core(TM)i5-8265 CPU @ 1.60 GHz 1.80 GHz. The number of iterations is denoted by IT, and the CPU time in seconds is denoted by CPU(s). We set the maximum number of iterations as $k_{max}=1000$ and the stopping tolerance as $\epsilon ={10}^{-11}$.

Example 1.

Let an ${\mathcal{H}}^{+}$-tensor

$$\mathcal{A}=\left[\begin{array}{ccccccccc}3& -0.36& 0.40& -0.16& 0.10& 0.13& -0.06& 0.04& 0.08\\ -0.12& 0.10& 0.20& 0.05& 4& -0.80& -0.04& 0.12& 0.05\\ 0.13& 0.12& -0.20& -0.06& 0.08& -0.04& 0.04& -0.02& 2\end{array}\right],$$

and the right-hand side $\mathbf{b}={(1,1,1)}^T$.

It is easy to prove that $\mathcal{A}-{\mathcal{I}}_3$ is also an ${\mathcal{H}}^{+}$-tensor and the AOR splitting of $\mathcal{A}-{\mathcal{I}}_3=\mathcal{E}-\mathcal{F}$ is convergent when $0\le r\le \omega \le 1.2$ and $\omega \ne 0$. Let the initial value ${\mathbf{x}}_0={(\frac{1}{3},\frac{1}{3},\frac{1}{3})}^T$. The numerical results of Algorithm 1 are shown in Figure 1, where the values of $\omega$ range from $0.1$ to $1.2$ in intervals of 0.1 and the values of r from 0 to $\omega$ in intervals of 0.1.

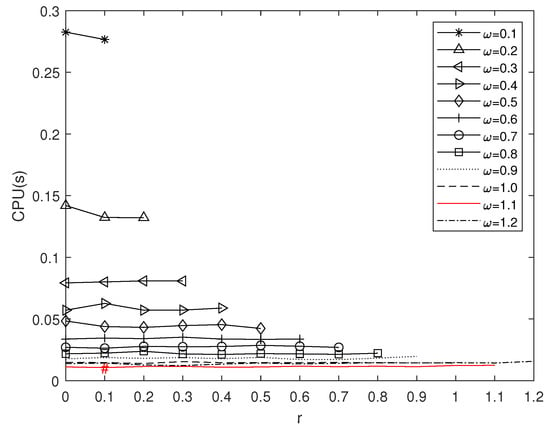
Figure 1. The numerical results of Example 1.

As can be seen in Figure 1, Algorithm 1 effectively solves TAVE (1). Of the parameters $\omega$ and r in this experiment, the value of $\omega$ has a greater impact on the running time of the algorithm. The values of optimal parameters $\omega$ and r in Example 1 were between 1.1 and 0.1. The minimum CPU time was 0.01042 s, which is represented by “#” in Figure 1, and the number of iteration steps was 13.

Example 2.

Let

$$\mathcal{A}=|(n^2+1){\mathcal{I}}_3-\mathcal{B}|\in {\mathbb{R}}^{[3,n]},$$

where $\mathcal{B}\in {\mathbb{R}}^{[3,n]}$ is a nonnegative tensor with $b_{i_1{i}_2{i}_3}=|sin(i_1+i_2+i_3)|$ and the right-hand side $\mathbf{b}={(1,1,\dots ,1)}^T\in {\mathbb{R}}^n$.

By [23], we know that $⟨\mathcal{A}-{\mathcal{I}}_3⟩=n^2{\mathcal{I}}_3-\mathcal{B}$ is a nonsingular $\mathcal{M}$-tensor, so $\mathcal{A}-{\mathcal{I}}_3$ is an ${\mathcal{H}}^{+}$-tensor. Let the initial value ${\mathbf{x}}_0={(\frac{1}{2n},\frac{1}{2n},\dots ,\frac{1}{2n})}^T\in {\mathbb{R}}^n$. For the SOR method, we took the values of $\omega$ range from 0.1 to 1.0 in intervals of 0.1. For the AOR method, we took the values of $\omega$ range from $0.1$ to $1.0$ in intervals of 0.1 and the values of r from 0 to $\omega$ in intervals of 0.1. For $n=3,5,10,30,50,100,150,200$, and 300, we solved TAVE (1) by the Jacobi method, Gauss–Seidel method, SOR method, and AOR method. The numerical results are shown in Table 1, where $\omega$ and r are the optimal parameters.

Table 1. The numerical results of Example 2.

n	Jacobi		Gauss–Seidel		SOR			AOR
	CPU(s)	IT	CPU(s)	IT	$\mathit{\omega }$	CPU(s)	IT	($\mathit{\omega }$,r)	CPU(s)	IT
3	0.044761	52	0.026841	31	0.8	0.012209	15	(0.8, 0.8)	0.012209	15
5	0.048811	54	0.033353	40	0.7	0.015901	17	(0.7, 0.3)	0.014624	17
10	0.041475	47	0.034756	41	0.7	0.013918	16	(0.7, 0.3)	0.013632	16
30	0.056128	44	0.064641	42	0.7	0.014826	13	(0.7, 0.5)	0.012868	12
50	0.051478	42	0.044186	41	0.7	0.014656	12	(0.7, 0.1)	0.010484	10
100	0.080886	40	0.10691	39	0.7	0.018922	10	(0.7, 0.3)	0.017542	10
150	0.25923	39	0.19730	38	0.7	0.045011	10	(0.7, 0.3)	0.044049	10
200	0.39142	38	0.33626	37	0.7	0.072017	9	(0.7, 0.7)	0.072017	9
300	0.99464	36	1.0196	36	0.7	0.24692	9	(0.6, 0.1)	0.21801	8

It can be seen in Table 1 that if we take the optimal parameters $\omega$ and r, the AOR method and SOR method are more effective than the Jacobi method and Gauss–Seidel method for solving TAVE (1) with $n=3,5,10,30,50,100,150,200$, and 300. In particular, the AOR method is optimal. Furthermore, we found that the number of iteration steps decreases as n ($n\ge 5$) increases in these four methods. Therefore, our algorithm may be more efficient for solving the large-scale problems.

Example 3.

Let $\mathcal{B}\in {\mathbb{R}}^{[4,n]}$ be generated randomly by MATLAB and

$$s=1+(1+0.01)\underset{i=1,2,\cdots ,n}{max}{\left(\mathcal{B}{\mathbf{e}}^3\right)}_i,$$

where, $\mathbf{e}={(1,1,\dots ,1)}^T\in {\mathbb{R}}^n$. Let $\mathcal{A}=\left(a_{i_1{i}_2{i}_3{i}_4}\right)$, $\tilde{\mathcal{A}}=s{\mathcal{I}}_4-\mathcal{B}=\left({\tilde{a}}_{i_1{i}_2{i}_3{i}_4}\right)$, and

$$a_{i_1{i}_2{i}_3{i}_4}={(-1)}^{i_1+i_2+i_3+i_4}·{\tilde{a}}_{i_1{i}_2{i}_3{i}_4},1\le i_1,i_2,i_3,i_4\le n.$$

The right-hand side is $\mathbf{b}=\mathbf{e}$.

It is easy to see that $s>\rho \left(\mathcal{B}\right)+1$, $⟨\mathcal{A}⟩=\tilde{\mathcal{A}}$, so $\mathcal{A}-{\mathcal{I}}_4$ is an ${\mathcal{H}}^{+}$-tensor. We took the initial value ${\mathbf{x}}_0={(\frac{1}{n+1},\frac{1}{n+1},\frac{1}{n+1},\frac{1}{n+1})}^T$. We took the values of $\omega$ from $0.1$ to $1.0$ with intervals of 0.1 and the values of r from 0 to $\omega$ with intervals of 0.1. For different $\omega$ and r, we solved TAVE (1) with $n=4,10,30$, and 50 by Algorithm 1. All numerical results are depicted in Figure 2, and the numerical results under the optimal parameters $\omega$ and r are shown in Table 2.

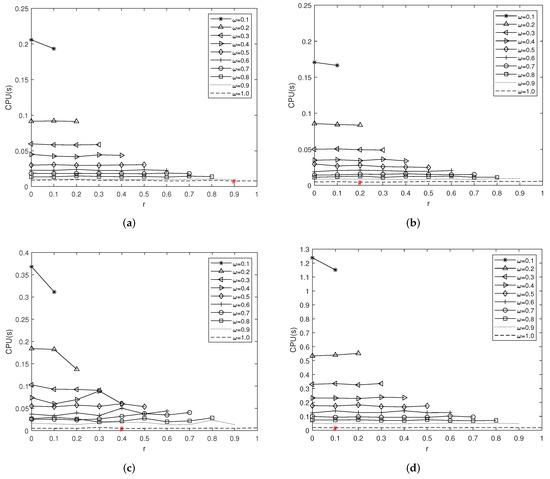
Figure 2. The numerical results of Example 3. (a) n = 4; (b) n = 10; (c) n = 30; (d) n = 50.

Table 2. The numerical results of Example 3 with optimal parameters $\omega$ and r.

n	AOR
	($\mathit{\omega }$,r)	CPU(s)	IT
4	(1.0, 0.9)	0.0075531	9
10	(1.0, 0.2)	0.0042066	5
30	(1.0, 0.4)	0.0049098	3
50	(1.0, 0.1)	0.017581	3

Figure 2 and Table 2 show that Algorithm 1 is efficient for solving TAVE (1) when $\mathcal{A}$ is a 4-order ${\mathcal{H}}^{+}$-tensor. In Figure 2, the minimum CPU time is represented by “#” for $n=4,10,30$, and 50. We observe that Algorithm 1 performs more efficiently as $\omega$ increases, and reaches the optimum when $\omega =1.0$.

5. Conclusions

In this paper, a tensor splitting AOR iterative method was presented to solve the ${\mathcal{H}}^{+}$-tensor absolute value equation. The convergence of the new method was analyzed. Some numerical examples verified the effectiveness of the new method. In the future, we will explore theoretical optimal parameters for our algorithm, and study more efficient algorithms for solving TAVE (1). Our AOR iterative method may be applied to control problems [24,25,26,27,28], which will be research by our team in future.