The Extremal Structures of r-Uniform Unicyclic Hypergraphs on the Signless Laplacian Estrada Index

Abstract

$SLEE$ has various applications in a large variety of problems. The signless Laplacian Estrada index of a hypergraph H is defined as $SLEE\left(H\right)={\sum }_{i=1}^n{e}^{{\lambda }_i\left(Q\right)}$, where ${\lambda }_1\left(Q\right),{\lambda }_2\left(Q\right),\dots ,{\lambda }_n\left(Q\right)$ are the eigenvalues of the signless Laplacian matrix of H. In this paper, we characterize the unique r-uniform unicyclic hypergraphs with maximum and minimum $SLEE$.

1. Introduction

1.1. Basic Concepts

Let $H=\left(V\right(H),E(H\left)\right)$ be a hypergraph, $V\left(H\right)=\{v_1,v_2,\dots ,v_n\}$ and $E\left(H\right)=\{e_1,e_2,\dots ,e_m\}\subseteq \mathcal{P}\left(V\right)$ be the vertex set and edge set, and $\mathcal{P}\left(V\right)$ be the power set of $V\left(H\right)$. If each edge $e_i\in E\left(H\right)$ has precisely r vertices $(r\ge 2)$, H is a r-uniform hypergraph. If $r=2$, H is an ordinary graph. Let $d_H\left(v\right)$ be the degree of a vertex v, which is the number of edges containing v. Let $\Delta \left(H\right)$, $\delta \left(H\right)$ and $d\left(H\right)=\frac{{\sum }_{v\in V\left(H\right)}{d}_H\left(v\right)}{n}$ be the maximum, minimum and average degrees.

The cyclomatic number of a graph is defined as $E+P-N$, where E is the number of edges, P is the number of parts and N is the number of nodes. For a r-uniform connected hypergraph H, the cyclomatic number $c\left(H\right)$ of H is $m(r-1)-n+1$. If $c\left(H\right)=0$ (resp. 1), the corresponding r-uniform connected hypergraph H is exactly a hypertree (resp. unicyclic hypergraph). Denote $S_{n,r}$ as the r-uniform hyperstar with one common vertex for all edges. ${\mathcal{T}}_{n,r}$ (resp. ${\mathcal{U}}_{n,r}$) denotes the set of r-uniform hypertrees (resp. unicyclic hypergraph) with n vertices. For $v\in V\left(H\right)$, $H-v$ denotes the hypergraph obtained from H by deleting v and all the edges incident with v. For a subset $A\subseteq V\left(H\right)$ with $A\ne \varnothing$, $H\left[A\right]$ denotes the subgraph of H induced by A, where $H\left[A\right]$ has the vertex set A and the edge set $\{V\left(e_i\right)\cap A|e_i\in E\left(H\right),1\le i\le m\}$. For a vertex $v\in e\in E\left(H\right)$ with $|e|\ge 3$, we apply a v-shrinking on e when we just remove v from the edge e.

For $u,v\in V\left(H\right)$, a $(u,v)$-semi-walk [1] is a vertex–edge alternative sequence $u(=u_1),e_1,u_2,e_2,\dots ,u_s,$ $e_s,u_{s+1}(=v)$, where $u_i,u_{i+1}\in e_i$ ($u_i,u_{i+1}$ is not necessarily distinct) for $i\in \left[s\right]=\{1,2,\cdots ,s\}$. If $u_i\ne u_{i+1}$ for $i\in \left[s\right]$, the $(u,v)$-semi-walk is called a $(u,v)$-walk. Further, we name the $(u,v)$-walk as a $(u,v)$-path, if $u_1,u_2,\dots ,u_{s+1}$ are distinct vertices and $e_1,e_2,\dots ,e_s$ are distinct edges. If $v\in e_i\setminus \{u_i,u_{i+1}\}$ for $i\in \left[s\right]$, the degree of v is 1, we call the $(u,v)$-path a loose $(u,v)$-path. A loose $(u,u)$-path is also called a loose cycle. We call the smallest length of all $(u,v)$-paths the distance $d_H(u,v)$ between u and v. For a hypergraph $H=\left(V\right(H),E(H\left)\right)$, its incidence matrix is $I\left(H\right)={\left(I_{ij}\right)}_{n\times m}$, where

$$\begin{array}{c}\hfill I_{ij}=\left\{\begin{array}{cc}1\hfill & if{v}_i\in e_j,\hfill \\ 0\hfill & otherwise,\hfill \end{array}\right.\end{array}$$

and its adjacent matrix is $A\left(H\right)={\left(a_{ij}\right)}_{n\times n}$, where $a_{ii}=0$ and $a_{ij}=|\{e\in E\left(H\right),v_i,v_j\in e\}|$ for $i\ne j$. The signless Laplacian matrix $Q\left(H\right)=\left({\left(Q\left(H\right)\right)}_{ij}\right)$ of H is $I\left(H\right)I{\left(H\right)}^T$. It is obvious that ${\left(Q\left(H\right)\right)}_{ii}=d_H\left(v_i\right)$ for $i\in \left[n\right]$ and ${\left(Q\left(H\right)\right)}_{ij}=a_{ij}$ for $i\ne j$. The signless Laplacian Estrada index $SLEE\left(H\right)$ [1] of a hypergraph H is defined as

$$\begin{array}{c}\hfill SLEE\left(H\right)=\sum _{i=1}^n{e}^{{\lambda }_i\left(Q\right)},\end{array}$$

where ${\lambda }_1\left(Q\right),{\lambda }_2\left(Q\right),\dots ,{\lambda }_n\left(Q\right)$ are the eigenvalues of the signless Laplacian matrix $Q\left(H\right)$. We denote by $T_k\left(H\right)$ the k-th signless Laplacian spectral moment of a hypergraph H, that is, $T_k\left(H\right)={\sum }_{i=1}^n{\lambda }_i^k\left(Q\right)$, then the signless Laplacian Estrada index can be rewritten as $SLEE\left(H\right)={\sum }_{k=0}^{\infty }\frac{T_k\left(H\right)}{k!}$. From [1], we know that $T_k\left(H\right)$ is exactly equal to the number of closed semi-walks of length k.

1.2. Background and Related Works

Let $G=(V,E)$ be a molecular graph (2-uniform hypergraph) represented by a molecular structure, where vertex set V is corresponding to the set of its atoms, and edge set E to its chemical bonds. It is widely used in theoretical chemical research and computational chemistry. A topological index is a single number, which is used to characterize some properties of the graph of a molecule structure. Topological indices are mainly used for the nonempirical quantitative structure–property/activity relationship (QSPR/QSAR) [2,3,4].

Based on the adjacency matrix A of 2-uniform hypergraph G, Estrada [5] put forward the Estrada index $EE\left(H\right)$ as follows:

$$\begin{array}{c}\hfill EE\left(G\right)=\sum _{i=1}^n{e}^{{\mu }_i\left(A\right)},\end{array}$$

where ${\mu }_1\left(A\right),{\mu }_2\left(A\right),\dots ,{\mu }_n\left(A\right)$ are the eigenvalues of A. Many applications in a large variety of problems on this index have been proposed. For examples, it was successfully employed to quantify the degree of folding of long-chain molecules, especially proteins [6,7], and to measure the centrality of complex (reaction, metabolic, communication, social, etc.) networks [8,9,10], network robustness against failures/attacks [11,12]. There is also a connection between the Estrada index and the extended atomic branching of molecules [13].

The signless Laplacian matrix $Q\left(G\right)$ has many positive properties, such as being symmetric, irreducible, positive semi-definite, the multiplicity of 0 as a eigenvalue of $Q\left(G\right)$ is equal to the number of bipartite connected components of G, and so on. The study on $Q\left(G\right)$ has received extensive attention by many researchers. For example, in [14], Ayyaswamy et al. generalized the definition of the Estrada index to the signless Laplacian Estrada index, many extremal and mathematics properties on this index were obtained [15,16,17,18,19,20].

Graph models are widely used to represent pairwise relationships between entities; however, real-world phenomena can be rich in multi-way relationships involving interactions among more than two entities. Then graph models do not adequately describe these types of applications [21]. Hypergraphs are generalizations of graphs in which edges may connect any number of vertices, and as such, hypergraphs are the natural model of multi-way relationships. It is natural to generalize the signless Laplacian Estrada index $SLEE$ of graphs to hypergraphs. However, we obtained a few results on $SLEE$ of hypergraphs. This paper is a new attempt to study on this topic and is expected to attract more and more attention in the near future. Recently, H.Y. Lu et al. [1] provided lower and upper bounds for $SLEE$ on r-uniform hypergraphs, and characterized the hypertrees with the largest and the smallest $SLEE$ among all r-uniform hypertrees, respectively. Along this line, in this paper, we continue to study $SLEE$ for r-uniform unicyclic hypergraphs.

2. Preliminaries

In this section, we will introduce some lemmas to prove our main results.

In a hypergraph H, let $S{W}_k(H;u,v)$ be the set of all $(u,v)$-semi walks of length k, and $S{W}_k(H;u)$ be the set of all $(u,u)$-semi walks of length k. Denote $S{W}_k\left(H\right)={\cup }_{u\in V\left(H\right)}S{W}_k(H;u)$, then $|S{W}_k\left(H\right)|=T_k\left(H\right)$, that is, the number of closed semi-walks of length k in H.

For two hypergraphs G and H with $x,y\in V\left(G\right)$ and $u,v\in V\left(H\right)$, if $|S{W}_k(G;x,y)|\le |S{W}_k(H;u,v)|$ for any $k\ge 0$, we say $(G;x,y){⪯}_s(H;u,v)$. Moreover, if $(G;x,y){⪯}_s(H;u,v)$ and there exists some $k_0$ such that $|S{W}_{k_0}(G;x,y)|<|S{W}_{k_0}(H;u,v)|$, then we write $(G;x,y){\prec }_s(H;u,v)$. Similarly, if $|S{W}_k(G;x)|\le |S{W}_k(G;y)|$ for any $k\ge 0$, we call $(G;x){⪯}_s(G;y)$, further if $(G;x){⪯}_s(G;y)$, and there is some $k_0$ such that $|S{W}_{k_0}(G;x)|<|S{W}_{k_0}(G;y)|$, we write $(G;x){\prec }_s(G;y)$.

For a hypergraph H, let $E^{\prime }=\{e_i^{\prime }\in E\left(H\right),u_i\in e_i^{\prime }\}$. By applying the $u_i$-shrinking on each edge $e_i^{\prime }$ in $E^{\prime }$, denote the resulted edge by $e_i$, let $E_0=\{e_i:e_i^{\prime }\in E^{\prime }\}$. For $u,v\in V\left(H\right)\setminus \{V\left(e_i\right):e_i\in E_0\}$, let $E_u=\{e_i\cup \left\{u\right\},e_i\in E_0\}$ and $E_v=\{e_i\cup \left\{v\right\},e_i\in E_0\}$, respectively. Further, $H_u=H-E_0+E_u$ denotes the hypergraph obtained from H by deleting edges in $E_0$ and adding edges in $E_u$. Similarly, we can attain hypergraph $H_v=H-E_0+E_v$.

Lemma 1

([1]). For a hypergraph H, let $E_0,H_u,H_v$ be defined as above, respectively. For $u,v\in V\left(H\right)\setminus \{V\left(e_i\right):e_i\in E_0\}$ and $w\in \{V\left(e_i\right):e_i\in E_0\}$, if $(H;u){\prec }_s(H;v)$ and $(H;w,u){⪯}_s(H;w,v)$, then $SLEE\left(H_u\right)\le SLEE\left(H_v\right)$.

$H_1$ and $H_2$ denote two disjoint connected hypergraphs and $v\in V\left(H_1\right)$, $w\in V\left(H_2\right)$, respectively. $H_1\left(v\right)\circ \left(w\right)H_2$ denotes the hypergraph obtained from $H_1$ and $H_2$ by identifying v of $H_1$ with w of $H_2$.

Lemma 2

([1]). Let $H_1$ and $H_2$ be two disjoint connected hypergraphs with $u,v\in V\left(H_1\right)$ and $w\in V\left(H_2\right)$, respectively. If $(H_1;u){\prec }_s(H_1;v)$, then $SLEE(H_1\left(u\right)\circ \left(w\right)H_2)<SLEE(H_1\left(v\right)\circ \left(w\right)H_2)$.

Lemma 3

([1]). Let e be a cut edge of hypergraph H with $u,v\in e$ and $|e|\ge 3$. When $d_H\left(u\right)\ge 2$ and $d_H\left(v\right)=1$, $(H;v){⪯}_s(H;u)$.

H is a connected r-uniform hypergraph. Let $u\in V\left(H\right)$ and

$$\begin{array}{ccc}\hfill P_{p(r-1)+1,r}& =& u_0,e_1,u_1,e_2,\dots ,e_{p-1},u_{p-1},e_p,u_{p+1}\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill P_{q(r-1)+1,r}& =& v_0,f_1,v_1,f_2,\dots ,f_{q-1},v_{q-1},f_q,v_{q+1}\hfill \end{array}$$

(2)

be two disjoint r-uniform loose paths, where $p,q\ge 1$. Denote $H_u(p,q)$ as the hypergraph obtained from H, $P_{p(r-1)+1,r}$ and $P_{q(r-1)+1,r}$ by coalescing $u,u_0,v_0$ as a new vertex, denoted by u. Obviously, if $G=P_{p(r-1)+1,r}\left(u_0\right)\circ \left(v_0\right)P_{q(r-1)+1,r}$, then $H_u(p,q)=G\left(u_0\right)\circ \left(u\right)H$ (as shown in Figure 1).

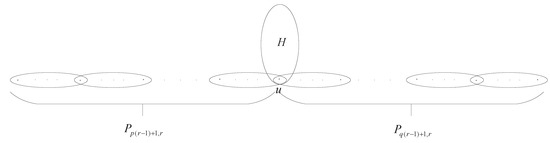
Figure 1. $H_u(p,q)$.

Lemma 4.

Let $H_u(p,q)$ be a hypergraph defined as above (as shown in Figure 1). If $p\ge q\ge 1$, $SLEE\left(H_u(p+1,q-1)\right)<SLEE\left(H_u(p,q)\right)$.

Proof. 

Let $P_{p(r-1)+1,r},P_{q(r-1)+1,r}$ be the loose paths defined in (1) and (2), respectively. In $G=P_{p(r-1)+1,r}\left(u_0\right)\circ \left(v_0\right)P_{q(r-1)+1,r}$, if $q=1$, $d_G\left(v_1\right)=1$, and if $q\ge 2$, $d_G\left(v_1\right)=2$. Let $f_1\setminus \{v_0,v_1\}=\{w_1,w_2,\dots ,w_{r-2}\}$. After applying the $v_0$-shrinking on $f_1$ of $P_{q(r-1)+1,r}$, the resulting hypergraph is denoted by $Q_1$. Let Q be the hypergraph obtained from $P_{p(r-1)+1,r}$ by adding $f_1$ at $u_0$. After applying the $v_1$-shrinking on $f_1$ of Q, the resulting hypergraph is denoted by $Q_2$. In G, we have

$$\begin{array}{c}\hfill S{W}_k(G;v_1)=S{W}_k(Q_1;v_1)\cup S{W}_k(G;v_1,\left[v_0\right])\\ \hfill S{W}_k(G;v_0)=S{W}_k(Q_2;v_0)\cup S{W}_k(G;v_0,\left[v_1\right])\end{array}$$

Suppose that $k_1,k_2\ge 1$ and $1\le i\le r-2$. For any $W\in S{W}_k(G;v_1,\left[v_0\right])$, W can be decomposed into $W_1{W}_2$, where $W_1$ is either a walk which consists of a $(v_1,v_1)$-section of $Q_1$ with length $(k_1-1)$ and a $(v_1,f_1,v_0)$-section of length 1, or a walk which consists of a $(v_1,w_i)$-section of $Q_1$ with length $(k_1-1)$ and a $(w_i,f_1,v_0)$-section of length 1, and $W_2$ is a $(v_0,v_1)$-section of G with length $k_2$. Then, we have

$$\begin{array}{ccc}\hfill |S{W}_k(G;v_1)|& =& |S{W}_k(Q_1;v_1)|+|S{W}_k(G;v_1,\left[v_0\right])|\hfill \\ & =& |S{W}_k(Q_1;v_1)|+\sum _{k_1+k_2=k}|S{W}_{k_1-1}(Q_1;v_1)||S{W}_{k_2}(G;v_0,v_1)|+\hfill \\ & & \sum _{i=1}^{r-2}\sum _{k_1+k_2=k}|S{W}_{k_1-1}(Q_1;v_1,w_i)||S{W}_{k_2}(G;v_0,v_1)|\hfill \\ \hfill |S{W}_k(G;v_0)|& =& |S{W}_k(Q_2;v_0)|+|S{W}_k(G;v_0,\left[v_1\right])|\hfill \\ & =& |S{W}_k(Q_2;v_0)|+\sum _{k_1+k_2=k}|S{W}_{k_1-1}(Q_2;v_0)||S{W}_{k_2}(G;v_1,v_0)|+\hfill \\ & & \sum _{i=1}^{r-2}\sum _{k_1+k_2=k}|S{W}_{k_1-1}(Q_2;v_0,w_i)||S{W}_{k_2}(G;v_1,v_0)|\hfill \end{array}$$

For $p\ge q\ge 1$, $Q_1$ is isomorphic to a proper subgraph of $Q_2$, then we have $|S{W}_k(Q_1;v_1)|$$\le |S{W}_k(Q_2;v_0)|$ for $k\ge 0$ and $|S{W}_{k_1-1}(Q_1;v_1,w_i)|\le |S{W}_{k_1-1}(Q_2;v_0,w_i)|$ for $k_1\ge 1$ and $1\le i\le r-2$. Furthermore, we find $|S{W}_{2(q+1)}(Q_1;v_1)|<|S{W}_{2(q+1)}(Q_2;v_0)|$. Therefore, we obtain $|S{W}_k(G;v_1)|\le |S{W}_k(G;v_0)|$ for $k\ge 0$ and there exists an integer $k_0=2(q+1)$ such that $|S{W}_k(G;v_1)|<|S{W}_k(G;v_0)|$. Thus, we obtain $(G;v_1){\prec }_s(G;v_0)$. By Lemma 2, we obtain $SLEE(G\left(v_1\right)\circ \left(u\right)H)<SLEE(G\left(v_0\right)\circ \left(u\right)H)$. Since $H_u(p+1,q-1)\cong G\left(v_1\right)\circ \left(u\right)H$ and $H_u(p,q)\cong G\left(v_0\right)\circ \left(u\right)H$, thus we have $SLEE\left(H_u(p+1,q-1)\right)<SLEE\left(H_u(p,q)\right)$. □

Let $P_{p(r-1)+1,r},P_{q(r-1)+1,r}$ be the two loose paths defined in (1) and (2) respectively. For convenience, let $c=p(r-1)+1,d=q(r-1)+1$, $V\left(P_{p(r-1)+1,r}\right)=\{x_1,x_2,\dots ,x_c\}$ and $V\left(P_{q(r-1)+1,r}\right)=\{y_1,y_2,\dots ,y_d\}$, respectively. Let $e=\{w_1,w_2,\dots ,w_r\}$ be an edge of a connected r-uniform hypergraph H. Denote $H_{w_r,w_1}(p,q)$ as the r-uniform hypergraph obtained from H, $P_{c,r}$ and $P_{d,r}$ by identifying $w_r$ of H with $x_c$ of $P_{c,r}$ and identifying $w_1$ of H with $y_d$ of $P_{d,r}$, as shown in Figure 2.

Figure 2. $H_{w_r,w_1}(p,q)$.

Lemma 5.

Let $H_{w_r,w_1}(p,q)$ be the r-uniform hypergraph as shown in Figure 2. If $H\ne P_{r,r}$ and $p>q\ge 0$, $SLEE\left(H_{w_r,w_1}(p+1,q)\right)<SLEE\left(H_{w_r,w_1}(p,q+1)\right)$.

Proof. 

If $q=0$ in $H_{w_r,w_1}(p,q)$, let $w_1=y_1$. For simplicity, let $\tilde{H}=H_{w_r,w_1}(p,q)$. We obtain $R_1$ by applying the $x_c$-shrinking of $P_{c,r}$. Denote $V_2=V\left(\tilde{H}\right)\setminus \{x_1,x_2,\dots ,x_{d+r-1}\}$ and $R_2=\tilde{H}\left[V_2\right]=(V_2,E_2)$, where $E_2=\{e\subseteq V_2,e\in E\left(\tilde{H}\right)\}$. Since $H\ne P_{r,r}$ and $p>q$, $R_1$ is isomorphic to a proper subgraph $R_2$. For any $W\in S{W}_k(\tilde{H};x_1)$, W can be decomposed into two sections according to whether it passes $x_c$ (namely $w_r$) or not. Then

$$\begin{array}{c}\hfill S{W}_k(\tilde{H};x_1)=S{W}_k(R_1;x_1)\cup S{W}_k(\tilde{H};x_1,\left[x_c\right]).\end{array}$$

Suppose that W passes through $x_i(1\le i\le c)$, then we construct a mapping f as follows:

(i)

If $1\le i\le d$, we replace $x_i$ in W by $y_i$;

(ii)

If $d+1\le i\le d+r-2$, we replace $x_i$ in W by $w_{i-(d-1)}$;

(iii)

If $d+r-1\le i\le c$, we replace $x_i$ in W by $x_{(c+d+r-1)-i}$.

If $W\in S{W}_k(R_1;x_1)$, we construct a mapping $f_1$ as follows: $f_1\left(W\right)=f\left(W\right)$. Obviously, $f_1\left(W\right)\in S{W}_k(R_2;y_1)\subseteq S{W}_k(\tilde{H};y_1)$. Since $R_1$ is isomorphic to a proper subgraph of $R_2$, $f_1$ is an injection but not a bijection from $S{W}_k(R_1;x_1)$ to $S{W}_k(R_2;y_1)$.

If $W\in S{W}_k(\tilde{H};x_1,\left[x_c\right])$, we can decompose W into $W_1{W}_2{W}_3{W}_4{W}_5$, where

(i)

$W_1$ is the longest $(x_1,x_{d+r-1})$-section;

(ii)

$W_2$ is the longest $(x_{d+r-1},x_c)$-section;

(iii)

$W_3$ is the longest $(x_c,x_c)$-section;

(iv)

$W_4$ is the longest $(x_c,x_{d+r-1})$-section;

(v)

$W_5$ is the longest $(x_{d+r-1},x_1)$-section.

Now, we construct a mapping $f_2\left(W\right)=f\left(W_1\right)W_{3}f\left(W_2\right)f\left(W_4\right)f\left(W_5\right)$, where

(i)

$f\left(W_1\right)$ is the longest $(y_1,w_r)$-section;

(ii)

$f\left(W_2\right)$ is the longest $(w_r,x_{d+r-1})$-section;

(iii)

$f\left(W_4\right)$ is the longest $(x_{d+r-1},w_r)$-section;

(iv)

$f\left(W_5\right)$ is the longest $(w_r,y_1)$-section.

Then $f_2\left(W\right)\in S{W}_k(\tilde{H};y_1,\left[x_{d+r-1}\right])\subseteq S{W}_k(\tilde{H};y_1)$. Further, we construct a mapping $f^{\ast }$,

$$\begin{array}{c}\hfill f^{\ast }\left(W\right)=\left\{\begin{array}{cc}{f}_1\left(W\right)\hfill & W\in S{W}_k(R_1;x_1)\hfill \\ f_2\left(W\right)\hfill & W\in S{W}_k(\tilde{H};x_1,\left[x_c\right])\hfill \end{array}\right.\end{array}$$

Obviously, $f^{\ast }\left(W\right)\in S{W}_k(\tilde{H};y_1)$ and $f^{\ast }$ is injective but not bijective from $S{W}_k(\tilde{H};x_1)$ to $S{W}_k(\tilde{H};y_1)$. Then $(\tilde{H};x_1){\prec }_s(\tilde{H};y_1)$, that is, $(H_{w_r,w_1}(p,q);x_1){\prec }_s(H_{w_r,w_1}(p,q);y_1)$. By Lemma 2, we have $SLEE\left(H_{w_r,w_1}(p+1,q)\right)<SLEE\left(H_{w_r,w_1}(p,q+1)\right)$. □

Lemma 6.

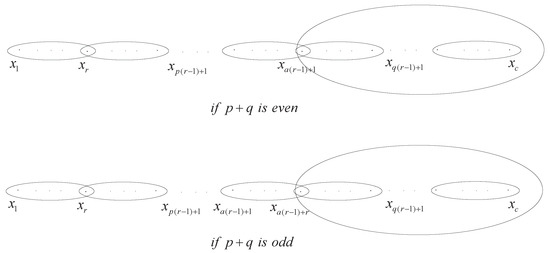
Let $p,q,l$ be three integers with $0\le p<q$, $p+q\le l-1$ and $a=\left[\frac{p+q}{2}\right]$ (that is, the largest integer is no more than $\frac{p+q}{2}$). In a connected r-uniform hypergraph H, let $P=x_1,e_1,x_r,e_2,\dots ,e_l,x_{l(r-1)+1}$ be a path with length l and $d_H\left(x_1\right)=1$, and $v=x_{p(r-1)+1}$ and $u=x_{q(r-1)+1}$. Further if $p+q$ is even, $Q=x_1{e}_1{x}_r{e}_2\dots e_a{x}_{a(r-1)+1}$ is a loose path; if $p+q$ is odd, $Q=x_1{e}_1{x}_r{e}_2\dots e_{a+1}{x}_{a(r-1)+r}$ is a loose path (as shown in Figure 3). Then $(H;v){\prec }_s(H;u)$ and $(H;v,w){\prec }_s(H;u,w)$ for any $w\in \{x_{t(r-1)+1},t>a\}$.

Figure 3. An illustration of graph H in Lemma 6.

Proof. 

If $p+q$ is even, by applying the $x_{a(r-1)+1}$-shrinking of P, let $R_1$ be the component containing $x_1$ and $R_2$ be the component containing $x_c$. Obviously, $R_1$ is a loose path and $R_1$ is isomorphic to a proper subgraph of $R_2$.

In H, we can classify $(v,v)$-closed walks of length $k\ge 1$ into two types according to whether they pass $x_{a(r-1)+1}$ or not. Namely, we obtain $S{W}_k(H;v)=S{W}_k(R_1;v)\cup S{W}_k(H;v,\left[x_{a(r-1)+1}\right])$. Let W be a walk passing $x_{t(r-1)+1}$, where $1\le t<a$. We construct a mapping $\phi$ as follows: we replace $x_{t(r-1)+1}$ for $1\le t<a$ by $x_{t^{\prime }(r-1)+1}$ for $t^{\prime }=p+q-t$ in W.

For $W\in S{W}_k(R_1;v)$, we construct a mapping ${\phi }_1$ as follows: let ${\phi }_1\left(W\right)=\phi \left(W\right)$. We can check ${\phi }_1\left(W\right)\in S{W}_k(R_2;u)\subseteq S{W}_k(H;u)$. Since $R_1$ is isomorphic to a proper subgraph of $R_2$, ${\phi }_1$ is an injection but not a bijection from $S{W}_k(R_1;v)$ to $S{W}_k(R_2;u)$.

For $W\in S{W}_k(H;v;\left[x_{a(r-1)+1}\right])$, we decompose W into $W_1{W}_2{W}_3$, where $W_1$ and $W_3$ are semi-edge walks in P, and $W_2\in S{W}_k(H;x_{a(r-1)+1})$ is as long as possible. Let ${\phi }_2\left(W\right)=W_1{W}_2{W}_3$, and we can check ${\phi }_2\left(W\right)\in S{W}_k(H;u;\left[x_a\right])\subseteq S{W}_k(H;u)$.

Finally, for $W\in S{W}_k(H;x_p)$, we can construct a mapping ${\phi }^{\ast }$ as follows:

$$\begin{array}{c}\hfill {\phi }^{\ast }\left(W\right)=\left\{\begin{array}{cc}{\phi }_1\left(W\right)\hfill & W\in S{W}_k(R_1;v)\hfill \\ {\phi }_2\left(W\right)\hfill & W\in S{W}_k(\tilde{H};v,\left[x_{a(r-1)+1}\right])\hfill \end{array}\right.\end{array}$$

Obviously, ${\phi }^{\ast }\left(W\right)\in S{W}_k(H;u)$. Since ${\phi }_1$ is an injection but not bijective,

$$S{W}_k(R_2;u)\cap S{W}_k(H;u;\left[x_{a(r-1)+1}\right])=\varnothing .$$

${\phi }^{\ast }$ is an injection but not bijective from $S{W}_k(H;v)$ to $S{W}_k(H;u)$. Then we obtain $(H;v){\prec }_s(H;u)$.

By the same procedure as that for $p+q$ being even, we can prove that Lemma 6 holds for $p+q$ being odd. □

Corollary 1.

For an integer $l\ge 3$, let $C=x_1{e}_1{x}_r{e}_2\cdots x_{(l-1)(r-1)+1}{e}_l{x}_1$ be the unique cycle in a unicyclic r-uniform hypergraph H. Suppose that $H^{\prime }$ is the hypergraph obtained from H by moving edges in $E\left(x_1\right)\setminus e_1$ from $x_1$ to $x_r$. Then $SLEE\left(H\right)<SLEE\left(H^{\prime }\right)$.

Proof. 

Let $P=x_1{e}_1{x}_r{e}_2{x}_{2(r-1)+1}\cdots x_{(l-1)(r-1)+1}$. Applying Lemma 6 for $p=0$ and $q=1$ implies that $(H^{\prime };v){\prec }_s(H^{\prime };u)$. Now the result follows from Lemma 2. □

Note that the result of Corollary 1 holds for any $v=v_{i(r-1)+1}$ and $u=v_{(i+1)(r-1)+1}$ because we can rewrite the cycle C as $x_{i(r-1)+1}{e}_{i+1}{x}_{(i+1)(r-1)+1}\cdots e_l{x}_1{e}_1\cdots x_{(i-1)(r-1)+1}{e}_{i+1}$$x_{i(r-1)+1}$.

3. Extremal $\mathbf{r}$-Uniform Unicyclic Hypergraph on Minimum $\mathbf{SLEE}$

In this section, we determine the extremal r-uniform unicyclic hypergraph with minimum $SLEE$.

Let ${\mathcal{U}}_{n,r}^g$ be the class of the connected r-uniform unicyclic hypergraph with order n and unique cycle $C_{g(r-1),r}$, where $r\ge 3$ and $g\ge 2$. For convenience, for any $H\in {\mathcal{U}}_{n,r}^g$, let $E\left(C_{g(r-1),r}\right)=\{e_1,e_2,\dots ,e_g\}$ and $e_i=\{v_{(i-1)(r-1)+1},\cdots ,v_{(i-1)(r-1)+r}\}$ for $i\in \left[g\right]$ and $v_{(g-1)(r-1)+r}=v_1$. If $n=g(r-1)$, it is easy to see that $H\cong C_{n,r}$. Let $H_1,\dots ,H_{g(r-1)}$ be the components of $H-E\left(C_{g(r-1),r}\right)$, where $v_i\in V\left(H_i\right)$ for $i\in \left[g\right(r-1\left)\right]$. So we can denote H by $C_{g(r-1)}^r(H_1,\dots ,H_{g(r-1)})$.

Lemma 7.

Let $H=C_{g(r-1)}^r(H_1,\dots ,H_{g(r-1)})\in {\mathcal{U}}_{n,r}^g$. Then for $i\in \left[g\right(r-1\left)\right]$

$$\begin{array}{ccc}& & SLEE\left(C_{g(r-1)}^r(H_1,\dots ,H_{i-1},P_i,H_{i+1},\dots ,H_{g(r-1)})\right)\hfill \\ & \le & SLEE(C_{g(r-1)}^r(H_1,\dots ,H_{i-1},H_i,H_{i+1},\dots ,H_{g(r-1)}).\hfill \end{array}$$

The equality holds if, and only if, $P_i\cong H_i$, where $P_i$ is a loose path of length $|E(H_i)|$.

Proof. 

It is trivial if $|E(H_i)|=1$ or 2. Suppose that $|E(H_i)|\ge 3$.

Case 1. There is at least one vertex in $V\left(H_i\right)\setminus \left\{v_i\right\}$ with a degree of at least 3. Denote u as a vertex of a degree of at least 3. The distance $d_{H_i}(u,v_i)$ is as large as possible in $H_i$. Denote $f_1,f_2,\dots ,f_{d_H\left(u\right)}$ as all the edges containing u in H. By u-shrinking on $f_i$ for $i\in \left[d_H\left(u\right)\right]$, denote the components by $T_1,\dots ,T_{d_H\left(u\right)}$. Without loss of generality, let $v_i\in V\left(T_1\right)$.

Subcase 1.1 If $r=2$, $2\le j\le d_H\left(u\right)$, $H[V\left(T_j\right)\cup \left\{u\right\}]$ is a pendant path at u. Repeatedly by Lemma 4, we obtain a hypergraph $H^{\ast }$ with smaller $SLEE$ by replacing ${\cup }_{j=2}^{d_H\left(u\right)}H[V\left(T_j\right)\cup \left\{u\right\}]$ by a pendant path P of length $|E({\cup }_{j=2}^{d_H\left(u\right)}H[V\left(T_j\right)\cup \left\{u\right\}])|$ at u.

If $H^{\ast }\cong C_{g(r-1)}^r(H_1,\dots ,H_{i-1},P_i,H_{i+1},\dots ,H_{g(r-1)})$, we obtain the desirable result.

Subcase 1.2 If $r\ge 3$, $j\in \{2,\cdots ,d_H\left(u\right)\}$,$H[V\left(T_j\right)\cup \left\{u\right\}]$ is not a pendant path at u, then there is at least one edge in $H[V\left(T_j\right)\cup \left\{u\right\}]$ with at least three vertices of degree 2. We choose such an edge $e=\{w_1,\cdots ,w_r\}$ by requiring that $d_H(u,w_1)$ is as large as possible, where $d_H(u,w_1)=d_H(u,w_l)-1$ for $2\le l\le r$. Then, there are two pendant paths at different vertices of e; let P and Q be pendant paths at vertices $w_s$ and $w_t$ of e$(2\le s<t\le r)$, respectively. Denote p and q$(p\ge q\ge 1)$ as the lengths of P and Q. Then $H\cong G_{w_s,w_t}(p,q)$, and $G=H[V\left(H\right)\setminus (V(P\cup Q)\setminus \{w_s,w_t\})]$. Let $H^{\prime }=G_{w_s,w_t}(p+1,q-1)$, by Lemma 5, $SLEE\left(H^{\prime }\right)<SLEE\left(H\right)$, we can obtain a hypergraph $H_1$ with smaller $SLEE$ by reusing Lemma 5, where $H[V\left(T_j\right)\cup \left\{u\right\}]$ is a pendant path at u for any $j\in \{2,\cdots ,d_H\left(u\right)\}$.

Denote $a_j$ as the lengths of the pendant path $P_j$ at u in $H_1$, where $2\le j\le d_H\left(u\right)$ and $a_j\ge 1$. Suppose without loss of generality that $a_2\ge a_3$. Then $H_1\cong G_u^{\prime }(a_2,a_3)$, where $G^{\prime }=H_1[V\left(H\right)\setminus (V\left(T_2\right)\cup V\left(T_3\right))]$. Let $H_2=G_u^{\prime }(a_2+1,a_3-1)$, by Lemma 5, $SLEE\left(H_1\right)<SLEE\left(H_2\right)$.

We can obtain a hypergraph $H_3$ with smaller $SLEE$ by attaching a pendant path P of length $|E({\cup }_{j=2}^{d_H\left(u\right)}H[V\left(T_j\right)\cup \left\{u\right\}])|$ at u by reusing Lemma 4.

If $H_3\cong (C_{g(r-1)}^r(H_1,\dots ,H_{i-1},P_i,H_{i+1},\dots ,H_{g(r-1)})$, we obtain the desired result. Otherwise, repeating the above process on $H_3$, we will obtain our desired result.

Case 2. There is no vertex with degree at least 3 in $V\left(H_i\right)\setminus \left\{v_i\right\}$.

It is trivial for $r=2$. When $r\ge 3$, similar to the proof in Subcase 1.2, we obtain the desirable result. □

Applying Lemma 7, we have the following results.

Corollary 2.

Let $H_1=C_{g(r-1)}^r(P_1,P_2,\dots ,P_{g(r-1)})$ be a hypergraph obtained from $H=C_{g(r-1)}^r$$(H_1,\dots ,H_{g(r-1)})$ by replacing each $H_i$ by a loose path $P_i$ with $|E\left(H_i\right)|=|E\left(P_i\right)|$ for $i\in \left[g\right(r-1\left)\right]$. Then $SLEE\left(H_1\right)\le SLEE\left(H\right)$, and the equality holds if, and only if, $H\cong H_1$.

Theorem 1.

Let $H_1=C_{g(r-1)}^r(P_1,P_2,\dots ,P_{r-1},P_r,\dots ,P_{g(r-1)})$ be a connected r-uniform unicyclic hypergraph with $r\ge 3$ and $g\ge 2$, where $P_i$ is a path attached at $v_i$ in $V\left(C_{g(r-1)}^r\right)$ for $1\le i\le g(r-1)$. Then

$$\begin{array}{c}\hfill SLEE\left(C_{n,r}\right)<SLEE\left(H_1\right)\end{array}$$

Proof. 

Without loss of generality, let $P_1=v_1{e}_1^{\prime }{u}_2{e}_2^{\prime }\cdots u_{n_1-1}{e}_{n_1-1}^{\prime }{u}_{n_1}$ be the pendant path at $v_1$. $H_2$ is the unicyclic hypergraph obtained from $H_1$ by moving $e_1$ from $v_1$ to $u_{n_1}$. By Lemma 2 and Corollary 1, $SLEE\left(H_2\right)<SLEE\left(H_1\right)$. By repeating the process on every pendant path, we conclude that $SLEE\left(C_{n,r}\right)<SLEE\left(H_1\right)$. □

The following theorem shows that the extremal r-uniform unicyclic hypergraph with minimum $SLEE$ is $C_{n,r}$.

Theorem 2.

For $\frac{n}{r-1}\ge 3$, let H be a r-uniform unicyclic hypergraph with n vertices, then

$$\begin{array}{c}\hfill SLEE\left(C_{n,r}\right)\le SLEE\left(H\right),\end{array}$$

and the equality holds if, and only if, $H\cong C_{n,r}$.

4. Extremal $\mathbf{r}$-Uniform Unicyclic Hypergraph on Maximum $\mathbf{SLEE}$

In this section, we obtain the extremal r-uniform unicyclic hypergraphs with the largest $SLEE$.

Lemma 8.

Let $H=C_{g(r-1)}^r(H_1,\dots ,H_{g(r-1)})\in {\mathcal{U}}_{n,r}^g$. Then

$$\begin{array}{ccc}& & SLEE\left(C_{g(r-1)}^r(H_1,\dots ,H_{i-1},H_i,H_{i+1},\dots ,H_{g(r-1)})\right)\hfill \\ & \le & SLEE\left(C_{g(r-1)}^r(S_1,\dots ,S_{i-1},S_i,S_{i+1},\dots ,S_{g(r-1)})\right),\hfill \end{array}$$

and the equality holds if, and only if, $S_i\cong H_i$, where $S_i$ is a hyperstar with center $v_i$ and $|E\left(S_i\right)|=|E\left(H_i\right)|$.

Proof. 

It is trivial if $|E(H_i)|\le 1$. Now we assume $|E(H_i)|\ge 2$.

Let $\check{H}$ be the hypergraph with largest $SLEE$ in ${\mathcal{U}}_{n,r}^g$ and the diameter of $H_i$ be $d_i$ for $i\in \left[g\right(r-1\left)\right)]$. Next, we prove $d_i=2$ for $i\in \left[g\right(r-1\left)\right]$.

Without loss of generality, let $P=u_0,h_1,u_1,\cdots ,u_{d_1-1},h_{d_1},u_{d_1}$ be a diametral path of $H_1$, where $u_{i-1},u_i\in h_i\in E\left(H_1\right)(i\in \left[d_1\right])$ and $d_1\ge 3$.

We denote by R the component of $\check{H}-h_{d_1-1}$ which contains $u_{d_1-1}$. Let $G=\check{H}[V\left(\check{H}\right)\setminus (V\left(R\right)\setminus \left\{u_{d_1-1}\right\})]$. Then, we have $d_G\left(v_{d-1}\right)=1$ and $d_G\left(v_{d-2}\right)\ge 2$. By Lemma 4, we obtain $(G;v_{d-1})\prec (G;v_{d-2})$. Obviously, $G\left(v_{d-1}\right)\circ \left(v_{d-1}\right)R\cong \check{H}$. By Lemma 3, we have $SLEE(G\left(v_{d-2}\right)\circ \left(v_{d-1}\right)R)>SLEE\left(\check{H}\right)$. This contradicts the maximality of $\check{H}$. So we obtain $d_1=2$. By the same procedure, we have $d_i=2$, for $i=2,\cdots ,g(r-1)$. Thus, we have $\check{H}\cong C_{g(r-1)}^r{S}_1,\dots ,S_{i-1},S_i,S_{i+1},\dots ,S_{g(r-1)})$. □

Lemma 9.

Let $\check{H}=C_{g(r-1)}^r(S_1,S_2\dots ,S_{r-1},S_r,\dots ,S_{g(r-1)}))$ be a connected r-uniform unicyclic hypergraph with $r\ge 3$ and $g\ge 2$, where $S_i$ is a r-uniform hyperstar with center $v_i$ for $1\le i\le g(r-1)$. Then

$$\begin{array}{c}\hfill SLEE\left(\check{H}\right)<SLEE\left(C_{g(r-1)}^r(S_1^{\prime },v_2,v_3,\dots ,v_{r-1},S_r,\dots ,S_{g(r-1)})\right)\end{array}$$

where $S_1^{\prime }$ is a hyperstar with center $v_1$ and $|E\left(S_1^{\prime }\right)|=|E\left(S_1\right)|+|E\left(S_2\right)|+\cdots +|E\left(S_{r-1}\right)|$.

Proof. 

We denote by $R^{\prime }$ the component of $\check{H}-e_1$ which contains $v_2$. Let $G^{\prime }=\check{H}[V\left(\check{H}\right)\setminus (V\left(R^{\prime }\right)\setminus \left\{v_2\right\})]$. Then, we have $d_{G^{\prime }}\left(v_2\right)=1$ and $d_{G^{\prime }}\left(v_1\right)\ge 2$. By Lemma 4, we obtain $(G^{\prime };v_2)\prec (G^{\prime };v_1)$. Obviously, $G^{\prime }\left(v_2\right)\circ \left(v_2\right)R^{\prime }\cong \check{H}$. By Lemma 3, we have $SLEE\left(\check{H}\right)<SLEE(G^{\prime }\left(v_1\right)\circ \left(v_2\right)R^{\prime })$. That is to say, $SLEE\left(\check{H}\right)<SLEE\left(C_{g(r-1)}^r\right(S_1^{\prime \prime },v_2,S_3,\dots ,S_{r-1},S_r,\dots ,$$S_{g(r-1)}\left)\right)$, where $S_1^{\prime \prime }$ is a hyperstar with center $v_1$ and $|E\left(S_1^{\prime \prime }\right)|=|E\left(S_1\right)|+|E\left(S_2\right)|$.

Repeatedly by the above process on $S_3,S_4,\cdots ,S_{r-1}$, we will obtain the desirable result. □

Lemma 10.

For $r\ge 3$ and $g\ge 3$, $H=C_{g(r-1)}^r(S_1,v_2,\dots ,v_{r-1},S_r,v_{r+1},\dots ,S_{(i-1)(r-1)+r},\dots ,$$v_{g(r-1)})$, where $S_{(i-1)(r-1)+r}$ are hyperstars with centers $v_{(i-1)(r-1)+r}$ for $i=1,2,\dots ,m$. Let e be the edge containing $v_1,v_r$. Let $H^{\prime }=C_{2(r-1)}^r(S_1,v_2,\dots ,v_{r-1},S_r,v_{r+1},\dots ,v_{2(r-1)})$ be the r-uniform unicyclic hypergraph obtained from H by moving each edge of $E\left(C_{g(r-1)}^r\right)\setminus e$ from $v_{(i-1)(r-1)+r}$ to $v_1$. Then, $SLEE\left(H\right)<SLEE\left(H^{\prime }\right)$.

Proof. 

If $g=2$, the equality holds. Let $g\ge 3$, and $C_{g(r-1)}^r$ be the unique cycle of H. Applying Lemma 9, $SLEE\left(H\right)<C_{(g-1)(r-1)}^r(S_1^{\prime },v_{r+1},\dots ,\dots ,S_{(i-1)(r-1)+r},\dots ,v_{g(r-1)})$, where $|S_1^{\prime }|=|S_1|+|S_r|+1$. Repeatedly by the above process, we have $SLEE\left(H\right)<SLEE\left(H^{\prime }\right)$. □

Lemma 11.

For $r\ge 3$, $H^{\prime }=C_{2(r-1)}^r(S_1,v_2,\dots ,v_{r-1},S_r,v_{r+1},\dots ,v_{2(r-1)})$, where $S_1$ and $S_r$ are two hyperstars with centers $v_1$ and $v_r$ and $|E\left(S_1\right)|\ge |E\left(S_r\right)|$. Let $H^{\ast }=C_{2(r-1)}^r(S_1,v_2,v_3,\dots ,$$v_{2(r-1)})$ be the r-uniform unicyclic hypergraph obtained from $H^{\prime }$ by moving all edges in $E\left(S_r\right)$ from $v_r$ to $v_1$. Then, $SLEE\left(H^{\prime }\right)<SLEE\left(H^{\ast }\right)$.

Proof. 

Let $V_1=V\left(S_1\right)\cup \{v_2,v_3,\dots ,v_{r-1},v_{r+1},\dots ,v_{2r-2}\}$, $V_2=V\left(S_r\right)\cup \{v_2,v_3,\dots ,v_{r-1},$$v_{r+1},\dots ,v_{2r-2}\}$. Let $Q_1=H^{\prime }\left[V_1\right]$ and $Q_2=H^{\prime }\left[V_2\right]$. We have $S{W}_k(H^{\prime };v_1)=S{W}_k(Q_1;v_1)\cup S{W}_k(H^{\prime };v_1,\left[v_r\right])$ and $S{W}_k(H^{\prime };v_r)=S{W}_k(Q_2;v_r)\cup S{W}_k(H^{\prime };v_r,\left[v_1\right])$. Then we obtain

$$\begin{array}{ccc}\hfill |S{W}_k(H^{\prime };v_1)|& =& |S{W}_k(Q_1;v_1)|+|S{W}_k(H^{\prime };v_1,\left[v_r\right])|\hfill \\ & =& |S{W}_k(Q_1;v_1)|+\sum _{k_1+k_2=k}|S{W}_{k_1-1}(Q_1;v_1)||S{W}_{k_2}(H^{\prime };v_r,v_1|)+\hfill \\ & & \sum _{i=1}^{r-2}\sum _{k_1+k_2=k}|S{W}_{k_1-1}(Q_1;v_1,w_i)||S{W}_{k_2}(H^{\prime };v_r,v_1|)\hfill \\ \hfill |S{W}_k(H^{\prime };v_r)|& =& |S{W}_k(Q_2;v_r)|+|S{W}_k(H^{\prime };v_r,\left[v_1\right])|\hfill \\ & =& |S{W}_k(Q_2;v_r)|+\sum _{k_1+k_2=k}|S{W}_{k_1-1}(Q_2;v_r)||S{W}_{k_2}(H^{\prime };v_1,v_r|)+\hfill \\ & & \sum _{i=1}^{r-2}\sum _{k_1+k_2=k}|S{W}_{k_1-1}(Q_2;v_r,w_i)||S{W}_{k_2}(H^{\prime };v_1,v_r|)\hfill \end{array}$$

Since $|E\left(S_1\right)|\ge |E\left(S_r\right)|\ge 2$, $Q_2$ is isomorphic to a proper subgraph of $Q_1$. Then we have $|S{W}_{k_1-1}(Q_1;v_1)|\ge |S{W}_{k_1-1}(Q_2;v_r)|$ for $k_1\ge 1$, $|S{W}_{k_1-1}(Q_1;v_1,w_i)|\ge |S{W}_{k_1-1}(Q_2;$$v_r,w_i)|$ for $k_1\ge 1$ and $1\le i\le r-2$ and $|S{W}_{k_2}(H^{\prime };v_r,v_1|=|S{W}_{k_2}(H^{\prime };v_1,v_r|$ for $k_2\ge 1$. Furthermore, we have $|S{W}_k(Q_1;v_1)|\ge |S{W}_k(Q_2;v_2)|$. Thus, we obtain $(H^{\prime };v_r){\prec }_s(H^{\prime };v_1)$. By Lemma 3, we have $SLEE(H^{\prime }\left(v_r\right)\circ \left(u_1\right)e)<SLEE(H^{\prime }\left(v_1\right)\circ \left(u_1\right)e)$, where $e=\{u_1,u_2,\dots ,u_r\}$ is an edge.

Then we show that the hypergraph obtained from $H^{\prime }$ has a larger $SLEE$ by moving an edge in $E\left(S_r\right)$ from $v_r$ to $v_1$. Repeat the above process to obtain the desired result. □

Theorem 3.

For $\frac{n}{r-1}\ge 3$, let H be a r-uniform unicyclic hypergraph with n vertices. Then

$$\begin{array}{c}\hfill SLEE\left(H\right)\le SLEE\left(C_{2(r-1)}^r(S_1,v_2,v_3,\dots ,v_{2(r-1)})\right)\end{array}$$

with equality if, and only if, $H\cong C_{2(r-1)}^r(S_1,v_2,v_3,\dots ,v_{2(r-1)})$, where $S_1$ is a hyperstar with center $v_1$.

Proof. 

Denote H as a r-uniform unicyclic hypergraph with n vertices; we denote it by $C_{g(r-1)}^r(H_1,\dots ,H_{g(r-1)})$ with $r\ge 3$ and $g\ge 2$, where $H_i$ is a r-uniform hypertree for $1\le i\le g(r-1)$.

Case 1.$g=2$.

By repeating the use of Lemmas 8, 9 and 11, it is easy to obtain our desirable result.

Case 2.$g\ge 3$.

By repeating our use of Lemmas 8 and 9, we can obtain a r-uniform unicyclic hypergraph $H^{\prime }$ satisfying $SLEE\left(H\right)\le SLEE\left(H^{\prime }\right)$, where $H^{\prime }\cong C_{g(r-1)}^r(S_1^{\prime },v_2,\cdots ,v_{r-1},S_r^{\prime },v_{r+1},\cdots ,$$S_{g(r-1)}^{\prime })$. we obtain a r-uniform unicyclic hypergraph $H^{\prime \prime }$ with $SLEE\left(H^{\prime }\right)\le SLEE\left(H^{\prime \prime }\right)$ by Lemma 10, where $H^{\prime \prime }\cong C_{2(r-1)}^r(S_1^{\prime \prime },v_2,\cdots ,v_{r-1},S_r^{\prime \prime },v_{r+1}\cdots ,v_{2(r-1)})$ and $S_1^{\prime \prime }$ is a hyperstar with center $v_1$, and $S_r^{\prime \prime }$ is a hyperstar with center $v_r$.

By Lemma 11, we obtain a r-uniform unicyclic hypergraph $H^{\ast }$ satisfying $SLEE\left(H^{\prime \prime }\right)\le SLEE\left(H^{\ast }\right)$, where $H^{\ast }\cong C_{2(r-1)}^r(S_1^{\prime \prime \prime },v_2,v_3,\cdots ,v_{2(r-1)})$. We can obtain our desirable result. □

5. Conclusions

$SLEE$ is one of the important chemical topological indices and has various applications in a large variety of problems. In addition, molecular structures that cannot be represented in ordinary graphs need to be represented by hypergraphs. It is necessary to study $SLEE$ of hypergraphs. On the basis of the study of r-uniform hypergraphs with respect to $SLEE$, we study the extremal structures of r-uniform unicyclic hypergraphs. In this paper, we characterize the extremal hypergraphs with maximum and minimum $SLEE$ among r-uniform unicyclic hypergraphs, respectively. Few results on the $SLEE$ of hypergraphs have been obtained. $SLEE$ can be studied by the structure and method of hypergraphs.