A Note of Jessen’s Inequality and Their Applications to Mean-Operators

Abstract

A variant of Jessen’s type inequality for a semigroup of positive linear operators, defined on a Banach lattice algebra, is obtained. The corresponding mean value theorems lead to a new family of mean-operators.

1. Introduction

The idea behind the main contents of this article is not very unusual but has been an active area of research in the present decade [1,2,3,4]. The theory of inequalities is not only limited to the real numbers or the basic real functions. In the past few years, the generalization of known inequalities to the operators has become the topic of active research in the field of applied analysis. In recent years, there has been considerable interest in the generalization of “functional-inequalities” and “type-inequalities” to the semigroups of operators defined on a Banach space [5,6]. Due to the mathematical structure and physical applications of operator semigroups, it is significant to find the new expressions and relations among them.

The Banach lattice was introduced to get a general abstract setting within which the ordering of elements can be considered. Therefore, the phenomena related to positivity can be generalized. For a detailed introduction to the Banach lattice, we refer our readers to the introductions of [5,6] and the references therein.

A linear mapping $\psi :E\to E$ is said to be positive (denoted by: $\psi \ge 0$) if $\psi \left(E_{+}\right)\subset E_{+}$. The set of all positive linear mappings forms a convex cone in the space $L\left(E\right)$ of all linear mappings from E into itself, defining the natural ordering of $L\left(E\right)$. The absolute value of $\psi$, if it exists, is given by

$$\left|\psi \right|\left(f\right)=sup\{\psi \left(h\right):|h|\le f\},(f\in E_{+}).$$

Thus $\psi :E\to E$ is positive if and only if $\left|\psi \right(f\left)\right|\le \psi \left(\right|f\left|\right)$ holds for any $f\in E$.

Each of the following definitions is used in our investigation.

Definition 1.

A (one parameter) $C_0$-semigroup (or strongly continuous semigroup) of operators on a Banach space E is a family ${\left\{S\left(t\right)\right\}}_{t\ge 0}\subset B\left(E\right)$ such that

(1) 

$S\left(s\right)S\left(t\right)=S(s+t)$ for all $s,t\in {\mathbb{R}}^{+}$;

(2) 

S(0)=I, the identity operator on E;

(3) 

for each fixed $f\in E$, $S\left(t\right)f\to f$(with respect to the norm on E) as $t\to 0^{+}$,

where $B\left(E\right)$ denotes the space of all bounded linear operators defined on a Banach space E.

Definition 2.

Let U be a nonempty open convex subset of E. An operator $L:U\to E$ is convex if it satisfies

$$L(tf+(1-t\left)g\right)\le tL\left(f\right)+(1-t)L\left(g\right),$$

(1)

where $f,g\in U$ and $0\le t\le 1$.

The (infinitesimal) generator of ${\left\{S\left(t\right)\right\}}_{t\ge 0}$ is the densely defined closed linear operator $A:E\supseteq D\left(A\right)\to R\left(A\right)\subseteq E$ such that

$$D\left(A\right)=\{f:f\in E,\underset{t\to 0^{+}}{lim}{A}_{t}f\mathrm{exists}\mathrm{in}E\}$$

$$Af=\underset{t\to 0^{+}}{lim}{A}_{t}f(f\in D\left(A\right))$$

where, for $t>0$,

$$A_{t}f=\frac{\left[S\right(t)-I]f}{t}(f\in E).$$

Let ${\left\{S\left(t\right)\right\}}_{t\ge 0}$ be the strongly continuous positive semigroup, defined on a Banach lattice E. The positivity of the semigroup is equivalent to

$$\left|S\right(t\left)f\right|\le S\left(t\right)\left|f\right|,t\ge 0,f\in E.$$

For positive contraction semigroups ${\left\{S\left(t\right)\right\}}_{t\ge 0}$, defined on a Banach lattice E, we have

$${\parallel \left(S\left(t\right)f\right)}^{+}\parallel \le \parallel f^{+}\parallel ,\mathrm{for}\mathrm{all}f\in E.$$

For details, we refer the reader to [7]. The strongly continuous semigroup ${\left\{S\left(t\right)\right\}}_{t\ge 0}$ defined on unital Banach algebra X is called a normalized semigroup and satisfies [6]

$$\left[S\right(t\left)\right]\left(e\right)=e,\mathrm{for}\mathrm{all}t>0$$

(2)

where e is identity in $X.$

Let ${\mathcal{D}}_c\left(E\right)$ denote the set of all differentiable convex operators $\varphi :E\to E$. The following Jessen’s type inequality of $c_0$-semigroup of operators has been proved in [6].

Theorem 1.

(Jessen’s Type Inequality) Let ${\left\{S\left(t\right)\right\}}_{t\ge 0}$ be the positive $C_0$-semigroup on E such that it satisfies (2). For an operator $\varphi \in {\mathcal{D}}_c\left(E\right)$ and $t\ge 0$;

$$\varphi \left(S\right(t\left)f\right)\le S\left(t\right)\left(\varphi f\right),f\in E.$$

(3)

2. Main Results

Our first main results are asserted in the following Theorem.

Theorem 2.

(Converse Jessen’s Type Inequality) Let ${\left\{S\left(t\right)\right\}}_{t\ge 0}$ be the positive $C_0$-semigroup on E such that it satisfies (2). For an ordered interval $K=[u,U]\subseteq E$, let $\varphi :K\to E$ be a convex operator. Then, for all $f\in E$, such that $u\le \varphi \left(f\right)\le U$, we have

$$S\left(t\right)\left[\varphi \left(f\right)\right]\le \frac{U-S\left(t\right)\left[f\right]}{U-u}\varphi \left(u\right)+\frac{S\left(t\right)\left[f\right]-u}{U-u}\varphi \left(U\right).$$

(4)

Proof. 

From the definition of convex functions, we have

$$\varphi \left(x_2\right)\le \frac{x_3-x_2}{x_3-x_1}\varphi \left(x_1\right)+\frac{x_2-x_1}{x_3-x_1}\varphi \left(x_3\right),(x_1\le x_2\le x_3,x_1<x_3)$$

Now, let $x_1=u$, $x_2=f$ and $x_3=U$; we have

$$\varphi \left(f\right)\le \frac{U-f}{U-u}\varphi \left(u\right)+\frac{f-u}{U-u}\varphi \left(U\right)$$

Since $u,U,\varphi \left(u\right)$ and $\varphi \left(U\right)$ are fixed in E, using the positivity and property (2), we finally reach the assertion (4). □

Now, let us consider the following example to present a better illustration.

Example 1.

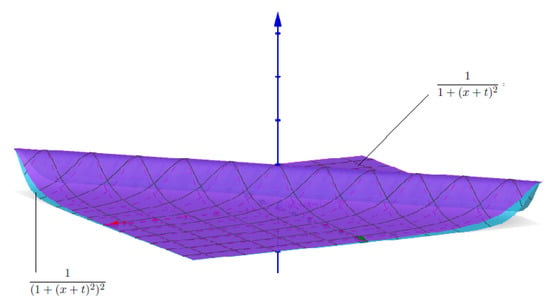
Let $E:=C\left(\mathbb{R}\right)$, $S{\left(t\right)}_{t\ge 0}$ be the left shift semigroup of operators defined on E. Let ϕ be the squaring operator; i.e, maps f to $f^2$ for each $f\in E$. Clearly, the existence of identity element $e\in E$ such that $e\left(x\right)=1$ for all $x\in \mathbb{R}$ is assured. Now, consider the function $f:\mathbb{R}\to \mathbb{R}$, defined as

$$f\left(x\right)=\frac{1}{1+x^2}.$$

Clearly, $0<f\left(x\right)\le 1$ so set $u\left(x\right)=0$ and $U\left(x\right)=1$ for all $x\in \mathbb{R}$ and hence, $\varphi \left(u\right)=0$ and $\varphi \left(U\right)=1$.

It follows that $\varphi \left(f\right)=f$ and

$$\left(S\left(t\right)\varphi f\right)\left(x\right)=\frac{1}{{(1+{(x+t)}^2)}^2}\le \frac{1-\frac{1}{1+{(x+t)}^2}}{1-0}\left(0\right)+\frac{\frac{1}{1+{(x+t)}^2}-0}{1-0}\left(1\right)=\frac{1}{1+{(x+t)}^2}=S\left(t\right)f\left(x\right),$$

with equality at $x=-t.$ See Figure 1 below.

Figure 1. Visualization of converse Jessen’s type inequality.

Next we present an extension of results in [8].

Theorem 3.

Let ${\left\{S\left(t\right)\right\}}_{t\ge 0}$ be the positive $C_0$-semigroup on E such that it satisfies (2). Let ϕ be a continuous convex operator on an ordered interval $K=[u,U]\subseteq E$; then, for all $f\in E$ such that $\varphi \left(f\right),\varphi (u+U-f)\in E$ (so that $u\le f\le U$), we have the following variant of Jessen’s inequality:

$$\varphi [u+U-S(t\left)\right(f\left)\right]\le \varphi \left(u\right)+\varphi \left(U\right)-S\left(t\right)\left(\varphi \right(f\left)\right).$$

This actually gives a series of inequalities:

$$\begin{array}{cc}\hfill \varphi [u+U-S(t\left)\right(f\left)\right]& \le S\left(t\right)\left[\varphi \right[u+U-\left(f\right)\left]\right]\hfill \\ \hfill & \le \frac{U-S\left(t\right)\left(f\right)}{U-u}\varphi \left(U\right)+\frac{S\left(t\right)\left(f\right)-u}{U-u}\varphi \left(u\right)\hfill \\ \hfill & \le \varphi \left(u\right)+\varphi \left(U\right)-S\left(t\right)\left[\varphi \right(f\left)\right]\hfill \end{array}$$

(5)

Proof. 

Let $\psi \left(f\right)=\varphi [u+U-(f\left)\right]$, the continuity and convexity of $\varphi$ imply the same for $\psi :[u,U]\to E$. Using Theorem 1,

$$\psi \left(S\right(t\left)f\right)\le S\left(t\right)\left(\psi f\right),f\in E$$

or

$$\varphi [u+U-S(t\left)\right(f\left)\right]\le \varphi \left(u\right)+\varphi \left(U\right)-S\left(t\right)\left(\varphi \right(f\left)\right).$$

Applying Theorem 2 to $\psi$ and then to $\varphi$, we obtain

$$\begin{array}{cc}\hfill S\left(t\right)\left[\varphi \right[u+U-\left(f\right)\left]\right]& =S\left(t\right)\left[\psi \right(f\left)\right]\hfill \\ \hfill & \le \frac{U-S\left(t\right)\left(f\right)}{U-u}\psi \left(u\right)+\frac{S\left(t\right)\left(f\right)-u}{U-u}\psi \left(U\right)\hfill \\ \hfill & =\frac{U-S\left(t\right)\left(f\right)}{U-u}\varphi \left(U\right)+\frac{S\left(t\right)\left(f\right)-u}{U-u}\varphi \left(u\right)\hfill \\ \hfill & =\varphi \left(u\right)+\varphi \left(U\right)-\left[\frac{U-S\left(t\right)\left(f\right)}{U-u}\varphi \left(u\right)+\frac{S\left(t\right)\left(f\right)-u}{U-u}\varphi \left(U\right)\right]\hfill \\ \hfill & \le \varphi \left(u\right)+\varphi \left(U\right)-S\left(t\right)\left[\varphi \right(f\left)\right],\hfill \end{array}$$

which completes the proof of Theorem 3. □

Let the arithmetic mean of the $C_0$-semigroup ${\left\{S\left(t\right)\right\}}_{t\ge 0}$ defined on E be denoted as

$$m_t\left(f\right)=m(S,f,t)=\frac{1}{t}{\int }_0^{t}S\left(\tau \right)fd\tau ,f\in E.$$

Corollary 1.

Let ${\left\{S\left(t\right)\right\}}_{t\ge 0}$ be the positive $C_0$-semigroup on E such that it satisfies (2). Let ϕ be a continuous convex operator; then,

$$\varphi [u+U-m_t\left(f\right)]\le \varphi \left(u\right)+\varphi \left(U\right)-m_t\left(\varphi \left(f\right)\right),f\in E.$$

(6)

Proof. 

Straightforward calculation would yield

$$\begin{array}{cc}\hfill \varphi [u+U-m_t\left(f\right)]& =\varphi \left[\frac{1}{t}{\int }_0^{t}S\left(\tau \right)ud\tau +\frac{1}{t}{\int }_0^{t}S\left(\tau \right)Ud\tau -\frac{1}{t}{\int }_0^{t}S\left(\tau \right)fd\tau \right]\hfill \\ \hfill & =\varphi \left[\frac{1}{t}{\int }_0^{t}S\left(\tau \right)[u+U-f]d\tau \right]\hfill \\ \hfill & \le \frac{1}{t}{\int }_0^t\varphi \left[S\left(\tau \right)[u+U-f]\right]d\tau \hfill \\ \hfill & \le \frac{1}{t}{\int }_0^{t}S\left(\tau \right)\left[\varphi [u+U-f]\right]d\tau \hfill \\ \hfill & \le \varphi \left(u\right)+\varphi \left(U\right)-m_t\left(\varphi \left(f\right)\right).\hfill \end{array}$$

□

3. Applications

In the sequel, we apply the Theorem 3 to generate inequalities involving power means and generalized means taking inspiration from [8].

3.1. Generalized Power Mean-Operators

Let ${\left\{S\left(t\right)\right\}}_{t\ge 0}$ be the positive $C_0$-group on E such that it satisfies (2) and let $f\in [u,U]\subset E$. Then, we define the generalized power mean as follows:

$${\mathcal{Q}}_r(S,f,t)=\left\{\begin{array}{cc}{\left[S\left(t\right)\left[f^r\right]\right]}^{1/r},\hfill & r\ne 0\hfill \\ \\ exp\left[S\right(t\left)\right[logf\left]\right],\hfill & r=0.\hfill \end{array}\right.$$

(7)

Now, for $r,s\in \mathbb{R},$ we present the following family of functions corresponding to the above-defined generalized power mean:

$${\overline{\mathcal{Q}}}_r(S,f,t):=\left\{\begin{array}{cc}{\left\{u^r+U^r-S\left(t\right)\left(f^r\right)\right\}}^{1/r},\hfill & r\ne 0\hfill \\ \\ \frac{uU}{exp\left[S\right(t\left)\right(log\left(f\right)\left)\right]},\hfill & r=0,\hfill \end{array}\right.$$

(8)

$${\overline{R}}_{r,s}(S,f,t):=\left\{\begin{array}{cc}{\left\{S\left(t\right)\left({[u^r+U^r-f^r]}^{\frac{s}{r}}\right)\right\}}^{1/s},\hfill & r\ne 0,s\ne 0\hfill \\ \\ exp\left\{S\left(t\right)(log{[u^r+U^r-f^r]}^{\frac{1}{r}})\right\},\hfill & r\ne 0,s=0\hfill \\ \\ {\left\{S\left(t\right)\left({\left[\frac{uU}{f}\right]}^s\right)\right\}}^{\frac{1}{s}},\hfill & r=0,s\ne 0\hfill \\ \\ exp\left\{S\left(t\right)(log\left[\frac{uU}{f}\right])\right\},\hfill & r=s=0,\hfill \end{array}\right.$$

(9)

$${\overline{S}}_{r,s}(S,f,t):=\left\{\begin{array}{cc}{\left\{\frac{U^r-S\left(t\right)\left(f^r\right)}{U^r-u^r}.U^s+\frac{S\left(t\right)\left(f^r\right)-u^r}{U^r-u^r}.u^s\right\}}^{1/s},\hfill & r\ne 0,s\ne 0\hfill \\ \\ exp\left\{\frac{U^r-S\left(t\right)\left(f^r\right)}{U^r-u^r}.logU+\frac{S\left(t\right)\left(f^r\right)-u^r}{U^r-u^r}.logu\right\},\hfill & r\ne 0,s=0\hfill \\ \\ {\left\{\frac{log\left(U\right)-S\left(t\right)(log(f\left)\right)}{log\left(U\right)-log\left(u\right)}.U^s+\frac{S\left(t\right)(log(f)-log(u\left)\right)}{log\left(U\right)-log\left(u\right)}.u^s\right\}}^{1/s},\hfill & r=0,s\ne 0\hfill \\ \\ exp\left\{\frac{log\left(U\right)-S\left(t\right)(log(f\left)\right)}{log\left(U\right)-log\left(u\right)}.log\left(U\right)+\frac{S\left(t\right)(log(f\left)\right)-log\left(u\right)}{log\left(U\right)-log\left(u\right)}.log\left(u\right)\right\},\hfill & r=s=0,\hfill \end{array}\right.$$

(10)

Theorem 4.

If $r,s\in \mathbb{R}$ and $r\le s$, then

$${\overline{\mathcal{Q}}}_r(S,f,t)\le {\overline{\mathcal{Q}}}_s(S,f,t).$$

Moreover,

$${\overline{\mathcal{Q}}}_r(S,f,t)\le {\overline{R}}_{r,s}(S,f,t)\le {\overline{S}}_{r,s}(S,f,t)\le {\overline{\mathcal{Q}}}_s(S,f,t).$$

(11)

Proof. 

We know that

$$u^r\le f^r\le U^r.$$

Five cases are present: Case I: Let $0<r\le s$. Then

$$u^r\le f^r\le U^r.$$

By applying Theorem 3 to the continuous convex operator $\varphi$, where

$$\varphi \left(f\right)=f^{\frac{s}{r}},\mathrm{for}\mathrm{all}f\in E.$$

Then, we have

$$\begin{array}{cc}\hfill {[u^r+U^r-S\left(t\right)\left(f^r\right)]}^{\frac{s}{r}}& \le S\left(t\right){\left[u^r+U^r-f^r\right]}^{\frac{s}{r}}\hfill \\ \hfill & \le \frac{U^r-S\left(t\right)\left[f^r\right]}{U^r-u^r}{U}^s+\frac{S\left(t\right)\left(\left[f^r\right]\right)-u^r}{U^r-u^r}{u}^s\hfill \\ \hfill & \le u^s+U^s-S\left(t\right)\left[f^s\right]\hfill \end{array}$$

Hence,

$${\overline{\mathcal{Q}}}_r(S,f,t)\le {\overline{R}}_{r,s}(S,f,t)\le {\overline{S}}_{r,s}(S,f,t)\le {\overline{\mathcal{Q}}}_s(S,f,t).$$

Case II: Let $r\le s<0$. Then we have,

$$U^r\le f^r\le u^r.$$

By applying Theorem 3 to the continuous concave operator $\varphi$ (observe that $0<\frac{s}{r}\le 1$), where

$$\varphi \left(f\right)=f^{\frac{s}{r}},f\in E.$$

Therefore,

$$\begin{array}{cc}\hfill {[U^r+u^r-S\left(t\right)\left(f^r\right)]}^{\frac{s}{r}}& \ge S\left(t\right)\left[{(U^r+u^r-f^r)}^{\frac{s}{r}}\right]\hfill \\ \hfill & \ge \frac{u^r-S\left(t\right)\left(f^r\right)}{u^r-U^r}.u^s+\frac{S\left(t\right)\left(f^r\right)-U^r}{u^r-U^r}.U^s\hfill \\ \hfill & \ge U^s+u^s-S\left(t\right)\left(f^s\right).\hfill \end{array}$$

Since $r\le s<0,$ we get

$$\begin{array}{cc}\hfill {[u^r+U^r-S\left(t\right)\left(f^r\right)]}^{\frac{1}{r}}& \le {\left[S\left(t\right)\left[{(u^r+U^r-f^r)}^{\frac{s}{r}}\right]\right]}^{\frac{1}{s}}\hfill \\ \hfill & \le {[\frac{U^r-S\left(t\right)\left(f^r\right)}{U^r-u^r}{U}^s+\frac{S\left(t\right)\left(f^r\right)-u^r}{U^r-u^r}{u}^s]}^{\frac{1}{s}}\hfill \\ \hfill & \le {[u^s+U^s-S\left(t\right)\left(f^s\right)]}^{\frac{1}{s}}.\hfill \end{array}$$

Consequently,

$${\overline{\mathcal{Q}}}_r(S,f,t)\le {\overline{R}}_{r,s}(S,f,t)\le {\overline{S}}_{r,s}(S,f,t)\le {\overline{\mathcal{Q}}}_s(S,f,t).$$

Case III: Let $r<0<s$. Thus we get

$$U^r\le f^r\le u^r.$$

From Theorem 3 to the continuous convex operator $\varphi$ (observe that $\frac{s}{r}<0$), where

$$\varphi \left(f\right)=f^{\frac{s}{r}},f\in E$$

we have

$$\begin{array}{cc}\hfill {[U^r+u^r-S\left(t\right)\left(f^r\right)]}^{\frac{s}{r}}& \ge S\left(t\right)\left[{(U^r+u^r-f^r)}^{\frac{s}{r}}\right]\hfill \\ \hfill & \ge \frac{u^r-S\left(t\right)\left(f^r\right)}{u^r-U^r}.u^s+\frac{S\left(t\right)\left(f^r\right)-U^r}{u^r-U^r}.U^s\hfill \\ \hfill & \ge U^s+u^s-S\left(t\right)\left(f^s\right).\hfill \end{array}$$

Moreover, since $r\le s<0,$ it follows

$$\begin{array}{cc}\hfill {[u^r+U^r-S\left(t\right)\left(f^r\right)]}^{\frac{1}{r}}& \le {\left[S\left(t\right)\left[{(u^r+U^r-f^r)}^{\frac{s}{r}}\right]\right]}^{\frac{1}{s}}\hfill \\ \hfill & \le {[\frac{U^r-S\left(t\right)\left(f^r\right)}{U^r-u^r}{U}^s+\frac{S\left(t\right)\left(f^r\right)-u^r}{U^r-u^r}{u}^s]}^{\frac{1}{s}}\hfill \\ \hfill & \le {[u^s+U^s-S\left(t\right)\left(f^s\right)]}^{\frac{1}{s}}.\hfill \end{array}$$

Hence

$${\overline{\mathcal{Q}}}_r(S,f,t)\le {\overline{R}}_{r,s}(S,f,t)\le {\overline{S}}_{r,s}(S,f,t)\le {\overline{\mathcal{Q}}}_s(S,f,t).$$

Case IV: Let $r<0,s=0.$ Again,

$$U^r\le f^r\le u^r.$$

By means of Theorem 3 to the continuous concave operator $\varphi$, where

$$\varphi \left(f\right)=\frac{1}{r}logf,f\in E.$$

we have

$$\begin{array}{cc}\hfill \frac{1}{r}log[U^r+u^r-S\left(t\right)\left(f^r\right)]& \le S\left(t\right)(\frac{1}{r}log[U^r+u^r-f^r])\hfill \\ \hfill & \le \frac{u^r-S\left(t\right)\left(f^r\right)}{u^r-U^r}.\frac{1}{r}log\left(u^r\right)+\frac{S\left(t\right)\left(f^r\right)-U^r}{u^r-U^r}{u}^s.\frac{1}{r}log\left(U^r\right)\hfill \\ \hfill & \le \frac{1}{r}log\left(U^r\right)+\frac{1}{r}log\left(u^r\right)-S\left(t\right)(\frac{1}{r}log\left(f^r\right)),\hfill \end{array}$$

which implies

$$log\left[{\overline{\mathcal{Q}}}_r(S,f,t)\right]\le log\left[{\overline{R}}_{r,0}(S,f,t)\right]\le log\left[{\overline{S}}_{r,0}(S,f,t)\right]\le log\left[{\overline{\mathcal{Q}}}_0(S,f,t)\right].$$

Therefore,

$${\overline{\mathcal{Q}}}_r(S,f,t)\le {\overline{R}}_{r,0}(S,f,t)\le {\overline{S}}_{r,0}(S,f,t)\le {\overline{\mathcal{Q}}}_0(S,f,t).$$

Case V: Let $r=0,s>0.$ Since

$$u\le f\le U,$$

it follows

$$log\left(u\right)\le log\left(f\right)\le log\left(U\right).$$

By applying Theorem 3 to the continuous convex operator $\varphi$, where

$$\varphi \left(f\right)=exp\left(sf\right),f\in E.$$

We have

$$\begin{array}{cc}\hfill exp\left(s\right(log\left(u\right)+log\left(M\right)-S\left(t\right)(log(f\left)\right))& \le S\left(t\right)(exp(s(log(u)+log(U)-log(f\left)\right))\hfill \\ \hfill & \le \frac{log\left(U\right)-S\left(t\right)(log(f\left)\right)}{log\left(U\right)-log\left(u\right)}exp(slog\left(U\right))\hfill \\ & +\frac{S\left(t\right)(log(f\left)\right)-log\left(u\right)}{log\left(U\right)-log\left(u\right)}exp(slog\left(u\right))\hfill \\ \hfill & \le exp(slog(u\left)\right)+exp(slog(U\left)\right)-S\left(t\right)(exp(slog\left(f\right)\left)\right),\hfill \end{array}$$

which implies

$${\left[{\overline{\mathcal{Q}}}_0(S,f,t)\right]}^s\le {\left[{\overline{R}}_{0,s}(S,f,t)\right]}^s\le {\left[{\overline{S}}_{0,s}(S,f,t)\right]}^s\le {\left[{\overline{\mathcal{Q}}}_s(S,f,t)\right]}^s,$$

and since $s\ge 0$, we get

$${\overline{\mathcal{Q}}}_0(S,f,t)\le {\overline{R}}_{0,s}(S,f,t)\le {\overline{S}}_{0,s}(S,f,t)\le {\overline{\mathcal{Q}}}_s(S,f,t).$$

Finally, in the case $r=s=0,$ it follows

$${\overline{\mathcal{Q}}}_0(S,f,t)={\overline{R}}_{0,0}(S,f,t)={\overline{S}}_{0,0}(S,f,t).$$

□

Corollary 2.

Let

$$m_t(T,f)=\frac{1}{t}{\int }_0^{t}T\left(\tau \right)fd\tau$$

be the arithmetic mean for $C_0$ group, and let $u\le T\left(\tau \right)f\le U.$ Let $S\left(t\right)$ be defined as $S\left(t\right)\left(f\right)=m_t(T,f)$. Then, for any continuous convex operator $\varphi :[u,U]\to E,$ and any $r,s\in \mathbb{R}$ with $r\le s$,the inequality (11) holds.

3.2. Generalized Mean-Operators

In this section, we assume the following assertions:

• (i). E denotes unital Banach lattice algebra;
• (ii). $S\left(t\right)$ is a positive bounded linear operator satisfying (2);
• (iii). $\psi ,\chi$ are continuous and strictly monotonic operators on $[u,U]\subset E$, such that $\psi ,\chi$ are invertible;
• (iv). $\psi \left(f\right),\chi \left(f\right),\chi \left({\psi }^{-1}(\psi \left(u\right)+\psi \left(U\right)-\psi \left(f\right))\right)\in E.$

Under the above-stated assumptions, we define the generalized mean of f with respect to the operator $S\left(t\right)$, belonging to the $C_0$ semigroup family, and $\psi$ by,

$$M_{\psi }(S,f)={\psi }^{-1}\left(S\left(t\right)\left(\psi \left(f\right)\right)\right).$$

Note that if $\psi \left(u\right)\le \psi \left(f\right)\le \psi \left(U\right)$, then by (2), we have,

$$\psi \left(u\right)\le S\left(t\right)\left(\psi \right(T\left(\tau \right)f\left)\right)\le \psi \left(U\right),$$

so that $M_{\psi }$ is well defined. Now, let us define

$${\overline{M}}_{S,f}={\psi }^{-1}(\psi \left(u\right)+\psi \left(U\right)-S\left(t\right)\left(\psi \left(f\right)\right)).$$

From assumption (iv), we see that

$$\psi \left(u\right)\le \psi \left(u\right)+\psi \left(U\right)-S\left(t\right)\left(\psi \right(T\left(\tau \right)f\left)\right)\le \psi \left(U\right).$$

Consequently, ${\overline{M}}_{T,f,S}$ is well defined.

Theorem 5.

Assume that hypotheses (i)–(iv) are satisfied. If either $\chi \circ {\psi }^{-1}$ is convex and χ is strictly increasing or $\chi \circ {\psi }^{-1}$ is concave and χ is strictly decreasing, then

$${\overline{M}}_{\psi }(S,f)\le {\overline{M}}_{\chi }(S,f).$$

(12)

Furthermore, the following inequalities hold true:

$$\begin{array}{cc}\hfill {\overline{M}}_{\psi }(S,f)& \le {\chi }^{-1}\left[\left(S\left(t\right)\left({\psi }^{-1}(\psi \left(u\right)+\psi \left(U\right)-\psi \left(f\right))\right)\right)\right]\hfill \\ \hfill & \le {\chi }^{-1}(\frac{\psi \left(U\right)-S\left(t\right)\left(\psi \right(f\left)\right)}{\psi \left(U\right)-\psi \left(u\right)}\chi \left(U\right)+\frac{S\left(t\right)\left(\psi \right(f)-\psi (u\left)\right)}{\psi \left(U\right)-\psi \left(u\right)}\chi \left(u\right))\hfill \\ \hfill & \le {\overline{M}}_{\chi }(S,f).\hfill \end{array}$$

(13)

In addition, if either $\chi \circ {\psi }^{-1}$ is concave and χ is strictly increasing or $\chi \circ {\psi }^{-1}$ is convex and χ is strictly decreasing, then the inequality (13) is reversed.

Proof. 

Since $\psi$ is strictly monotonic and $u\le f\le U$, we have

$$\psi \left(u\right)\le \psi \left(f\right)\le \psi \left(U\right).$$

Now suppose that $\chi \circ {\psi }^{-1}$ is convex. Letting $\varphi =\chi \circ {\psi }^{-1}$ in Theorem 3, we get

$$\begin{array}{cc}\hfill \chi \circ {\psi }^{-1}(\psi \left(u\right)+\psi \left(U\right)-S\left(t\right)\left(\psi \left(f\right)\right))& \le S\left(t\right)\left((\chi \circ {\psi }^{-1})(\psi \left(u\right)+\psi \left(U\right)-\psi \left(f\right))\right)\hfill \\ \hfill & \le \frac{\psi \left(U\right)-S\left(t\right)\left(\psi \right(f\left)\right)}{\psi \left(U\right)-\psi \left(u\right)}(\chi \circ {\psi }^{-1})\left(\psi \left(U\right)\right)\hfill \\ & +\frac{S\left(t\right)\left(\psi \right(f)-\psi (u\left)\right)}{\psi \left(U\right)-\psi \left(u\right)}(\chi \circ {\psi }^{-1})\left(\psi \left(u\right)\right)\hfill \\ \hfill & \le (\chi \circ {\psi }^{-1})\left(\psi \left(u\right)\right)+(\chi \circ {\psi }^{-1})\left(\psi \left(U\right)\right)\hfill \\ & -S\left(t\right)\left((\chi \circ {\psi }^{-1})\left(\psi \left(f\right)\right)\right).\hfill \end{array}$$

Alternatively, we have

$$\begin{array}{cc}\hfill (\chi \left({\psi }^{-1}(\psi \left(u\right)+\psi \left(U\right)-S\left(t\right)\left(\psi \left(f\right)\right))\right)& \le S\left(t\right)\left(\chi \left({\psi }^{-1}(\psi \left(u\right)+\psi \left(U\right)-\psi \left(f\right))\right)\right)\hfill \\ \hfill & \le \frac{\psi \left(U\right)-S\left(t\right)\left(\psi \right(f\left)\right)}{\psi \left(U\right)-\psi \left(u\right)}\left(\chi \left(U\right)\right)\hfill \\ & +\frac{S\left(t\right)\left(\psi \right(f)-\psi (u\left)\right)}{\psi \left(U\right)-\psi \left(u\right)}\left(\chi \left(u\right)\right)\hfill \\ \hfill & \le \left(\chi \right(u\left)\right)+\left(\chi \right(U\left)\right)-S\left(t\right)\left(\chi \right(f\left)\right).\hfill \end{array}$$

(14)

Finally, by the same method, we have the reverse of inequalities (14) if $\chi \circ {\psi }^{-1}$ is concave. □

Remark 1.

If χ is strictly increasing, then the inverse function ${\chi }^{-1}$ is also strictly increasing, so (14) implies (13). If χ is strictly decreasing, then the inverse function ${\chi }^{-1}$ is also strictly decreasing, and so the reverse of (14) implies (13) (i.e., $\chi \circ {\psi }^{-1}$ is concave). Similarly, if either $\chi \circ {\psi }^{-1}$ is convex and χ is strictly decreasing or $\chi \circ {\psi }^{-1}$ is concave and χis strictly increasing, we get the reverse of (13).

Remark 2.

Upon setting in Theorem 5

$$\psi \left(f\right):=\left\{\begin{array}{cc}{f}^r,\hfill & r\ne 0\hfill \\ ln\left(f\right),\hfill & r=0\hfill \end{array}\right.$$

and

$$\chi \left(f\right):=\left\{\begin{array}{cc}{f}^s,\hfill & s\ne 0\hfill \\ ln\left(f\right),\hfill & s=0\hfill \end{array}\right.,$$

we get Theorem 4.