Abstract
When we face real problems using computational resources, we understand that it is common to find combinatorial problems in binary domains. Moreover, we have to take into account a large number of possible candidate solutions, since these can be numerous and make it complicated for classical algorithmic techniques to address them. When this happens, in most cases, it becomes a problem due to the high resource cost they generate, so it is of utmost importance to solve these problems efficiently. To cope with this problem, we can apply other methods, such as metaheuristics. There are some metaheuristics that allow operation in discrete search spaces; however, in the case of continuous swarm intelligence metaheuristics, it is necessary to adapt them to operate in discrete domains. To perform this adaptation, it is necessary to use a binary scheme to take advantage of the original moves of the metaheuristics designed for continuous problems. In this work, we propose to hybridize the whale optimization algorithm metaheuristic with the Q-learning reinforcement learning technique, which we call (the QBWOA). By using this technique, we are able to realize an smart and fully online binarization scheme selector, the results have been statistically promising thanks to the respective tables and graphs.
MSC:
90C27
1. Introduction
In recent years, metaheuristics have proven their effectiveness in solving complex problems, especially combinatorial problems. Numerous examples can be found in biology [1], logistics [2], civil engineering [3,4], transit [5] and machine learning [6]. Within these complex problems, discrete domain or binary problems are getting more and more attention with increasing numbers to be solved. In this sense, the use of exact methods may not be the right choice because of the long computational time, therefore, approximate methods such as metaheuristics have become more popular in the scientific community, because although they do not guarantee optimality, they achieve solutions closer to the optimum in a reasonable computational time. It is necessary to add that there are metaheuristics specifically designed to address these problems with binary domain, however, it has been shown that metaheuristics designed to work in continuous domains assisted by a discretization scheme outperform the classical approaches based on binarization [7]. The classical design includes transforming domains through two-step techniques, despite the higher efficiency, and partly because many combinatorial problems are very large, it is critical to maintain the robustness of metaheuristic techniques.
Among the main approaches to integrate metaheuristics, some hybrid learning-based approaches have been discovered [8,9,10,11], in which the focus is on improving the transformation process and performance. Mathematization is another intriguing hybrid approach [12], which mixes mathematical programming techniques with metaheuristic algorithms. Ref. [13] examined the truck routing problem using mixed integer linear programming and metaheuristic approaches. In general, these methods do not make use of the auxiliary data generated by the metaheuristics to produce more accurate conclusions. Metaheuristics provide useful auxiliary data during the solution search process that can be used to inform machine learning algorithms. Artificial intelligence, and in particular machine learning, has gained importance in recent years, with applications in a variety of fields [14,15,16]. The combination of machine learning techniques and metaheuristic algorithms is a relatively new area of research that has gained popularity in recent years [9]. For example, in [17], the authors addressed several approaches to combine machine learning and metaheuristic techniques. To name a few; in [18], they make use of the Q-learning technique for the Cooperative Water Wave Optimization algorithm, called CWWO, to address the Distributed Assembly No-Idle Flow-shop Scheduling Problem (DANIFSP) and they minimize the maximum assembly completion time. In [19], Q-Learning (QL) in Hyper Simulated Annealing (HSA) is used to select the appropriate heuristic to address the mixed-model sequencing problem with stochastic processing times (MMSPSP). In both cases, the results stand out compared to traditional deterministic approaches.
Three main areas in which machine learning algorithms use metaheuristic data are presented in [9], they are: item Low-level integrations, High-level integrations and Optimization problems. In this work, we focus on low-level integrations. This group corresponds to general binarization techniques in which the metaheuristic moves are not modified, but after their execution, the binarization of the solutions is applied. Putting these concepts into practice, we specifically engaged 2 activities. (1) The authors in [20,21] proposed SARSA as a dynamic binarization scheme selector in the continuous metaheuristic. Motivated by the first point and seeking to answer our research question: “Does an increase of the transfer functions to be used in the binarization scheme selector positively affect the optimization process?” is that we propose a reimplementation and instance of the algorithm where we added new actions to the pool of SARSA selection possibilities, and (2) We use other dynamic binarization selector called Q-Learning [22] with the same actions pool that SARSA. This proposed approach combines the original metaheuristic moves and their continuous nature solutions with reinforcement learning to obtain a robust and competitive binary version. The proposed algorithm was applied to the set covering problem. The research contributions of this work are as follows:
- A new smart binarization scheme selector is proposed.
- The Q-learning technique, proposed in [21], is used to binarize the whale optimization algorithm.
- A selector with a much wider repertoire in its actions is obtained from the literature.
The following is a summary of the contents of this study: The Section 2 addresses with the set covering problem and some of its applications in different areas. Section 3 outlines the techniques used and re-implemented from Q-learning and SARSA. The basics of the whale optimization algorithm and its binary version are covered in Section 4 and Section 5 respectively. In Section 6, the details of the numerical experiments and comparisons are developed. Finally, conclusions and possible future lines of research are discussed in Section 7.
2. Set Covering Problem
The set covering problem (SCP) is a well-known optimization problem that may be used to represent a variety of different applications and domains, such as assignment problems, and transport networks. This is an NP-hard problem [23] that entails finding the set of elements with the lowest cost that fulfills a certain number of requirements. The Set Covering Problem’s mathematical model is represented as follows:
Subject to the following restrictions:
where A is a binary matrix of size m-rows and n-columns and is value of each cell in the matrix A. The i and j are size m-rows and n-columns. In the event that column j satisfies a row i then is equal to 1, otherwise, it is 0. In addition has an associated a cost , where together with that and are the sets of rows and columns, respectively. Finally, x corresponds to the area to be covered.
In order to understand how the SCP operates and as an example, we have implemented the following practical explanation. Intentionally, we have selected an instance of SCP with and to represent it graphically in Figure 1 and Figure 2 and by Equations (4) to (15).
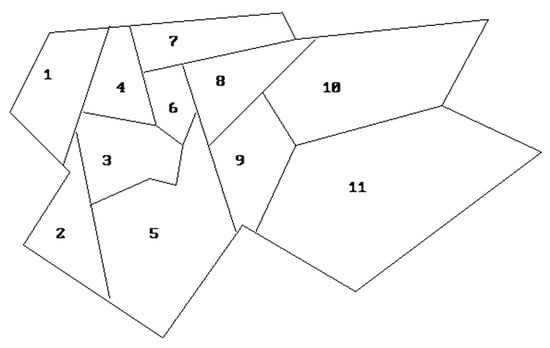
Figure 1.
An example of SCP.
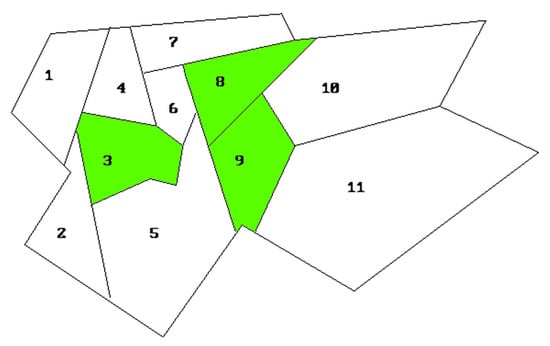
Figure 2.
Solution to the practical example of SCP.
Subject to:
The SCP allows the modeling of real-life optimization problems such as the location of gas detectors for industrial plants [24], the location of electric vehicle charging points in California [25], the optimal UAV locations for the purpose of generating wireless communication networks in disaster areas [26], the optimal location of first aid centers in Japan [27] and the location of stations to cover a network of reels [28]. These studies allow us to appreciate the importance of solving this problem with optimization techniques that guarantee good results.
3. Reinforcement Learning
Reinforcement learning is a subsection of Machine Learning in which an agent performs several actions in various states with the purpose of determining which action is the best for each state based on the consequences of completing each of the actions. Some of the classic examples are QL [29], Monte Carlo RL [30] and SARSA [31].
3.1. Q-Learning
QL was proposed by Watkins et al. [29] in 1992 and is one of the most well-known reinforcement learning approaches. The primary goal is to maximize the cumulative reward of an action in a given state and to discover the optimal action for that state.
The agent goes through several states, and in each one, an action is experienced instantly obtaining a reward or a penalty, and the point at which an action is done in a given condition is referred to as an episode.
The Q-learning method attempts to determine the amount of cumulative reward the agent will receive for each pair of action states in the long run. The action-state function is denoted by , which returns the reward that the agent will receive while performing an action in state s, assuming that the agent will continue to follow the Q-function’s policy until the conclusion of the episode; this value is referred to as the Q-Value [30]. These Q-Values are recorded in the Q-Table, a matrix with rows representing states and columns representing actions. For the mathematical model, please see the article [29].
3.2. SARSA
SARSA has been explained in the work of [20]; however, we want to give an explanation in this work to have all the concepts within reach that are related to reinforcement learning and the techniques used or reimplemented.
Therefore, SARSA is a slight variation of the popular Q-learning algorithm. It is necessary to mention that for a learning agent in any reinforcement learning algorithm, its policy can be of two types: (1) on-policy and (2) off-policy. For (1) the learning agent learns the value function according to the current action derived from the policy currently in use, while for (2) the agent learns the value function according to the action derived from another policy.
The SARSA technique is on-policy and uses the action performed by the current policy to learn the q-value; that is, for its update, it will depend on the current state (s), the current action (a), the reward obtained (r), the next state (s’) and the next action (a’), referring to the tuple (s, a, r, s’, a’). On the other hand, the Q-learning technique is an off-policy technique and uses the greedy approach to learn the q-value.
4. Whale Optimization Algorithm: Fundamentals
The Whale Optimization Algorithm (WOA) is inspired by the hunting behavior of humpback whales, in particular how they search (Section 4.1), encircle (Section 4.2) and attack (Section 4.3) their prey with a technique known as “bubble nets”. Mirjalili and Lewis devised this algorithm in 2015 [32]. The WOA metaheuristic has also been used in the following works [33,34,35].
The WOA metaheuristic begins with a set of randomly generated solutions. At the end of each iteration, the whales’ locations are updated in relation to a randomly picked whale or the best whale acquired thus far.
4.1. Identifying the Prey
Humpback whales start by searching for and identifying the target prey; this prey is algorithmically assumed to be the current best search agent; therefore, the whales update their position toward this agent in the course of nomerous iterations. This behavior can be reflected mathematically as follows:
where and are coefficient vectors and t denotes the current iteration, is a random whale of the population. The coefficient vectors and can be computed according to Equations (17) and (18):
where decreases linearly from 2 to 0 over the course of the iterations (both in the exploration and exploitation phases) and corresponds to a random vector of values between .
The main goal of the Equations presented in (17) and (18) is to balance the exploration and exploitation of the search space. r, being a random value and same for both Eqs., provides us with the stochastic behavior in updating the future position of the population. Therefore, thanks to Equation (17), the exploration is present when the value of and exploitation when . Finally, thanks to Equation (18), parameter , by taking random values between , helps us to reduce the probability of being permanently trapped in local solutions. In this way, we can also enhance exploration of the exploitation at any stage of the optimization.
4.2. Encircling the Prey
Once the prey is identified, humpback whales move to close to their prey, forcing them to swim upward and making it impossible for them to escape. Mathematically, it is represented by the following equation
where is the best whale obtained so far and is the i-th whale in the t-th iteration. The vector and are calculated as in Equations (17) and (18). It is worth mentioning that must be updated at each iteration if a better solution exists.
4.3. Bubble Netting Technique
The way in which they force their prey to climb to the top and make it impossible for them to escape is because, during the entire course of the encirclement, humpback whales expel bubbles forming a spiral that becomes narrower and narrower until it finally traps its prey. For WOA, this behavior is achieved by decreasing the linear value of a. The manner in which this behavior is imitated is as follows:
where is the distance of the i-th whale from the prey (the best solution obtained so far), b is a constant to define the shape of the logarithmic spiral. l is a random number between .
Humpback whales swim around the prey within a shrinking circle and along a spiral trajectory simultaneously. To model this simultaneous behavior, there is a 50% probability of choosing between the encircling prey mechanism (Section 4.2) or the spiral model (Section 4.3) to update the position of the whales during optimization. The mathematical model is as follows:
In summary, the pseudocode of the WOA is illustrated in Algorithm 1.
| Algorithm 1 Whale Optimization Algorithm |
Input: The population Output: The updated population and
|
5. Whale Optimization Algorithm: Q-Binary Version
The WOA was designed to solve continuous optimization problems. To solve a combinatorial problem such as the SCP with WOA, we need to translate the continuous solutions generated by WOA to the binary domain [7]. One of the most widely used techniques in the literature is the two-step technique [36]. As the name implies, it transfers the continuous solutions to the binary domain in two steps. First, it transfers the continuous solutions to the domain using transfer functions and then discretizes the solutions in the domain using binarization functions. The transfer functions and binarization techniques used in this work can be visualized in Table 1 and Table 2.
The Authors propose in [37] to hybridize Q-learning with WOA to dynamically select binarization schemes. In these cases the actions to be selected are the different combinations between the transfer functions and binarization functions. Specifically, 40 combinations or actions obtained from the 8 transfer functions (4 S-Shaped and 4 V-Shaped) and 5 binarization functions (Standard, Complement, Static Probability, Elitist and Elitist Roulette) were used. This hybrid can be seen in Algorithm 2.

Table 1.
Transfer Functions.
Table 1.
Transfer Functions.
| Type | Transfer Function |
|---|---|
| S1 [38,39] | |
| S2 [39,40] | |
| S3 [38,39] | |
| S4 [38,39] | |
| V1 [39,41] | |
| V2 [39,41] | |
| V3 [38,39] | |
| V4 [38,39] | |
| X1 [42,43] | |
| X2 [42,43] | |
| X3 [42,43] | |
| X4 [42,43] | |
| Z1 [44,45] | |
| Z2 [44,45] | |
| Z3 [44,45] | |
| Z4 [44,45] |

Table 2.
Binarization Functions.
Table 2.
Binarization Functions.
| Type | Binarization |
|---|---|
| Standard | |
| Complement | |
| Static Probability | |
| Elitist | |
| Roulette Elitist |
| Algorithm 2 Q-Binary Whale Optimization Algorithm |
Input: The population Output: The updated population and
|
5.1. Exploration and Exploitation of Actions
As explained previously, reinforcement learning algorithms seek to find the best action for a particular state. Therefore, it is necessary to efficiently define the pool of actions to be considered so that the algorithm can have different alternatives to consider in a given state. With this in mind, our proposal seeks to demonstrate that by increasing the alternatives to consider when selecting actions, Q-learning performs better. That is why we will use the same approach proposed in [37], where they use as actions the combination between the transfer functions and the binarization functions of the two-step technique. The authors proposed in [37] 8 transfer functions (4 S-Shaped and 4 V-Shaped) and 5 binarization functions (Standard, Complement, Probalistic Static, Elitist and Elitist Roulette), thus obtaining a total of 40 actions. In our proposals, we consider these 40 actions and add 9 transfer functions, thus obtaining 40 new actions and having a total of 80 actions to select. The transfer functions used can be seen in Table 1 and the binarization functions used can be seen in Table 2.
5.2. Feasibility and Repair Heuristic
When working with stochastic algorithms such as metaheuristics, there is a possibility that perturbing the solutions may generate a solution that does not satisfy all the constraints of the problem. The probability of generating infeasible solutions increases in our proposal since we transfer continuous solutions to the binary domain when applying binarization schemes. In this session we will discuss the repair heuristic applied in our proposal and the solution feasibility verification heuristic.
First, we need to know whether the solution is feasible or not. To this end, we use the incidence matrix A of the Set Covering Problem instance and the solution to be checked. Algorithm 3 outlines all steps for feasibility validation. The objective of this algorithm is to identify constraints that are not covered by any dimension of the solution. As a result we get two things. First, a boolean that tells us whether the solution is feasible or not. Secondly, we get the number of columns that cover a given constraint. If we get a 0 for a constraint it indicates that we have an infeasible solution.
| Algorithm 3 Feasibility Heuristic |
Input: Matrix A of incidence and solution Output: coverage, is number of columns covering a row and feasibility
|
After validating feasibility, we must repair solutions that are not feasible. Repair consists of turning infeasible solutions into feasible ones by applying certain particular criteria to the problem. The detail of the repair used in our proposal is shown in Algorithm 4. The repair consists of calculating a percentage based on the cost of column j over the sum of all the rows of the constraint matrix covered by a column j. This equation is as follows:
where is the cost of the j-th column and is the value of the incidence matrix.
Unfeasible solutions are repaired by summing the columns of the solution that had the lowest percentage. Once we have activated a column, we run the feasibility test again. This process is repeated until a feasible solution is obtained.
| Algorithm 4 Repair heuristics |
Input: Matrix A of incidence and unfeasible solution Output: feasible solution
|
5.3. Complexity Analysis
A very critical area in software development is the computation time of our solutions. The Big-O asymptotic notation helps us to quantify the algorithmic complexity in terms of worst-case execution time. To determine the algorithm competence of our proposal, we divide the implementation into 3 phases. The first is the initialization phase, the second is the perturbation phase and the third is the repair phase.
For the initialization of solutions we have a complexity of where N denotes the number of individuals in the population. For the initialization of the Q-Table used in Q-Learning and SARSA we have a complexity of where A indicates the number of actions and S the number of states. To determine the initial state of the population we need to calculate the diversity. The complexity of calculating the population diversity is where D is the number of decision variables in the problem. Thus, the complexity of the initialization phase is .
For solution perturbation, solution binarization, diversity calculation and fitness calculation at each iteration we have a complexity of where T indicates the total number of iterations executed. For the selection of actions and the updating of the Q-Values in the Q-Table we have a complexity of . For the perturbation phase we obtain an algorithmic complexity of .
For the feasibility of solutions we obtain a complexity of , where R is the number of constraints of the problem. For the repair heuristic we have a complexity of . To this end, the complexity of the repair phase is of ).
Taking into account the initialization phase, the perturbation phase and the repair phase, we obtain the following algorithm complexity for our proposal:
6. Experimentation Results
To validate the performance of our proposal, we used 4 different instances of WOA. The first, called QBWOA, incorporates Q-Learning to dynamically select the 80 binarization schemes. The second, called BSWOA, we incorporated SARSA to dynamically select the 80 binarization schemes. The third, called BCL, is a version with binarization scheme based on the recommendation of the authors in their work [46], the fixed scheme is V4-Elitist. The fourth, called MIR, is a version with fixed binarization scheme based on the recommendation of the authors in their work, the fixed scheme is V4-Complement [39].
The benchmark instances of the Set Covering Problem solved are those proposed in Beasley’s OR-Library [47]. These instances are widely known and used to test the performance of different algorithms when solving a combinatorial optimisation problem such as the Set Covering Problem. In particular, we solved 45 instances delivered in this library.
The code was coded in Python 3.8 and executed using the free Google Colaboratory [48] services. The results were stored and processed from databases provided by the Google Cloud Platform. The authors in [46] suggest making 40000 calls to the objective function. To this end, we use 40 population individuals and 1000 iterations for all instances WOA run. Thirty-one independent runs were performed for each instance of WOA executed. All parameters used for WOA, Q-Learning and SARSA are detailed in Table 3.

Table 3.
Parameters setting.
Table 4 shows the results obtained in this work. To read the table it is necessary to understand what each acronym means, so we proceed to explain it. In the first column (Inst.) is the name of each of the instances. The next four columns are replicated for each technique; thus, for QL, SARSA, BCL and MIR, we have (Opt.) is the known optimum for each of the instances, (Best) represents the best results of the 31 independent runs, and the mean of the results is in (Avg). We have also considered the average relative percentage deviation (RPD) as a quality metric according to Equation (24) which quantifies how close a solution is to the optimum, and finally, the last row is the sum of each column. As for the colors used, we have used a light shade of gray with bold text to represent and imply those that obtained the best results in the corresponding instance. As mentioned above, the comparison is a reimplementation and extension of the proposed algorithm and named BSWOA in [20]; by extension we mean the number of actions or the combinatorics existing between the transfer functions (16) plus the binarization techniques (5) that can be taken by the smart selector.

Table 4.
Comparison of the metaheuristics WOA.
We have also studied whether there are significant differences between the different techniques used in this work. As the samples are independent and the data do not follow a normal distribution, we assumed the Wilcoxon-Mann-Whitney test. The p-values obtained were analyzed considering a significance level of 0.05. From this analysis and for each set of cases, the Table 5 presents the total average of the cases analyzed.

Table 5.
Averages Statistical Test Comparison.
The table is composed as follows: the first column presents the techniques used, the following columns is the competition, explained otherwise, for the second row of the first column [QBWOA] is compared with the first of [BSWOA], [BCL], [MIR], [40QBWOA] and finally with [40BSWOA], these last two are comparisons of the original version of 40 actions proposed in [20]. If the value of this comparison is greater than the significance value of 0.05 it is presented as “≥”, for the comparison between itself the symbol “-” and finally the values, which have been approximated to the third decimal place. The color shade is maintained as in the previous table of results.
Analyses of Exploration and Exploitation
It is widely known that metaheuristics perform the search process in two important phases: exploration and exploitation. Therefore, it is of great interest to evaluate the behavior of metaheuristics in terms of exploration and exploitation.
Morales-Castañeda et al. in [49] propose some Equations which can obtain a percentage of exploration (XPL%) and a percentage of exploitation (XPT%) based on the diversity of the population. These Equations are as follows:
where corresponds to the current diversity in the t-th iteration and corresponds to the maximum diversity obtained in the entire search process.
Authors in [37,50,51] use Dimensional-Hussan Diversity [52] in order to calculate the diversity of the population at each iteration. Dimensional-Hussain Diversity is a diversity based on central measurements and is defined as:
where corresponds to the Dimensional-Hussan Diversity of the population X, is average of the d-th dimension, n is the number of search agents in the population X and l is the number of dimension of the optimization problem.
Based on the above and following these forms of measurement, we have obtained the graphs presented in Figure 3 denominated as “Exploration and exploitation graphs”, where the X axis is the number of total iterations, while the Y axis is the percentage of exploration and exploitation, results obtained by applying the Equations (25) and (26).
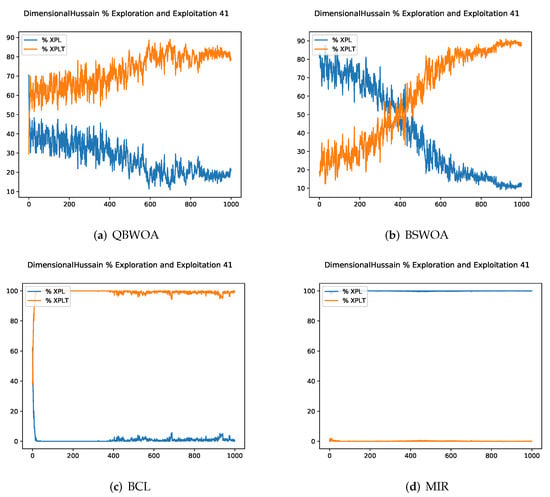
Figure 3.
Percentage of exploration and exploitation of algorithms resolving the 41 instance.
These graphs allow us to better understand the results obtained. The algorithms where we included a dynamic selection technique of binarization schemes had a better exploration and exploitation balance. The algorithms that executed fixed binarization techniques had unbalanced behaviors. On the one hand, the algorithm called MIR had an explorative behavior being unable to find the promising regions within the search space. On the other hand, the algorithm called BCL had an exploitative behavior leading it to drop to local optima prematurely.
7. Conclusions
In this work, we have implemented QL and reimplemented SARSA as smart binarization scheme selectors in the metaheuristic whale optimization algorithm, a new and novel way of binarizing metaheuristics that specializes in working on continuous domains. We solved 45 instances of the OR library of the set covering problem. When compared with its closest version BSWOA, it is observed that QBWOA obtains better results.
On average we can conclude thanks to the statistical tests (Table 5) that the versions of QL, SARSA and BCL compared to each other do not present any significant statistical difference, however, when we compare these 3 with the version of MIR (V4-Complement) we can observe a different behavior, in this case, there are statistically significant better solutions concluding that the versions of QL, SARSA and BCL (V4-Elitist) have statistically better results.
This also helps us to answer the research question, implying that, despite having more transfer functions, or, in other words, more actions, at first glance it seems that there is an improvement, however, we realize that despite obtaining competitive results and solutions these are not statistically significant. Therefore, this implies that the path of increasing the number of actions does not necessarily lead to better performance (at least for this research, i.e., number of actions and problem solved), i.e., it is valid to continue exploring other combinations of actions, to try the same actions in another problem or to decrease the pool of actions.
When observing the behavior of the exploration and exploitation percentages (Figure 3) for the whale metaheuristic, it can be clearly observed that for the cases there are 4 different exploration and exploitation behaviors, where for the case of QBWOA, we can notice that only the first iterations it begins to explore and gradually goes on to exploit until ending with high values during the rest of the iterations. While in the case of BSWOA, it happens that the exploration percentage starts high and begins to decrease until a break point to become exploited in the rest of iterations. For the BCL version (V4-Supplement) a clear beginning of exploration is noticed in the first iterations, while the exploitation increases until maintaining high values during the rest of the iterations, this behavior together with QBWOA and BSWOA is the one recommended by [49]. Finally, the behavior similar to random searches is reflected by the MIR version (V4-Complement), where the exploration percentage remains at high values during all iterations.
As for transfer functions, V-shaped or Z-shaped functions are suitable for solving limited search or exploit problems and S-shaped or X-shaped functions are suitable for solving large search space or explore problems. As the problem size increases, discretization techniques with a better exploration-to-exploitation ratio outperform the others. We recommend the use of Standard, Elitist Roulette and Elitist to solve all problems. Finally, it is especially significant to select a binarization approach suitable for solving large problems, it is for this reason, that we recommend BQWOA as a possible testing bench for future work, as they reduce tuning times by not having to evaluate the combinations of the different binarization schemes present in the literature, facilitating the implementation of these techniques. As future lines of research, it would be interesting to consider other metaheuristics, including some that give the best results solving the SCP in the current literature and solve other problems.
Author Contributions
M.B.-R.: Project administration, Writing—original draft, Investigation, Formal analysis, Conceptualization, Methodology, Writing—review & editing. F.C.-C.: Writing—original draft, Investigation, Formal analysis, Conceptualization, Methodology, Writing—review & editing. B.C.: Validation, Resources, Writing—review & editing, Supervision, Funding acquisition. R.S.: Validation, Resources, Supervision, Funding acquisition. J.G.: Validation, Resources G.A.: Investigation, Validation, Resources, Visualization. W.P.: Validation, Resources, Funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
Crawford, Ricardo Soto, Gino Astorga and Wenceslao Palma are supported by Grant ANID/FONDECYT/REGULAR/1210810. Marcelo Becerra-Rozas is supported by National Agency for Research and Development (ANID)/Scholarship Program/DOCTORADO NACIONAL/2021-21210740. Felipe Cisternas-Caneo is supported by Beca INF-PUCV.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The code used can be found in: https://github.com/imaberro/BSS-QL-80actions (accessed on 4 September 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guo, H.; Liu, B.; Cai, D.; Lu, T. Predicting protein–protein interaction sites using modified support vector machine. Int. J. Mach. Learn. Cybern. 2018, 9, 393–398. [Google Scholar] [CrossRef]
- Korkmaz, S.; Babalik, A.; Kiran, M.S. An artificial algae algorithm for solving binary optimization problems. Int. J. Mach. Learn. Cybern. 2018, 9, 1233–1247. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Yepes, V. Robust design optimization for low-cost concrete box-girder bridge. Mathematics 2020, 8, 398. [Google Scholar] [CrossRef]
- Crawford, B.; Soto, R.; Lemus-Romani, J.; Astorga, G.; Matus de la Parra, S.; Peña-Fritz, A.; Valenzuela, M.; García, J.; de la Fuente-Mella, H.; Castro, C.; et al. Investigating the efficiency of swarm algorithms for bridge strengthening by conversion to tied-arch: A numerical case study on San Luis bridge. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 45, 2345–2357. [Google Scholar] [CrossRef]
- Lemus-Romani, J.; Alonso, B.; Moura, J.L.; Crawford, B.; Soto, R.; González, F. Limited Stop Services Design Considering Variable Dwell Time and Operating Capacity Constraints. IEEE Access 2021, 9, 30359–30373. [Google Scholar] [CrossRef]
- Al-Madi, N.; Faris, H.; Mirjalili, S. Binary multi-verse optimization algorithm for global optimization and discrete problems. Int. J. Mach. Learn. Cybern. 2019, 10, 3445–3465. [Google Scholar] [CrossRef]
- Crawford, B.; Soto, R.; Astorga, G.; García, J.; Castro, C.; Paredes, F. Putting continuous metaheuristics to work in binary search spaces. Complexity 2017, 2017, 8404231. [Google Scholar] [CrossRef]
- Talbi, E.G. Combining metaheuristics with mathematical programming, constraint programming and machine learning. Ann. Oper. Res. 2016, 240, 171–215. [Google Scholar] [CrossRef]
- Talbi, E.G. Machine learning into metaheuristics: A survey and taxonomy. ACM Comput. Surv. (CSUR) 2021, 54, 1–32. [Google Scholar] [CrossRef]
- García, J.; Crawford, B.; Soto, R.; Castro, C.; Paredes, F. A k-means binarization framework applied to multidimensional knapsack problem. Appl. Intell. 2018, 48, 357–380. [Google Scholar] [CrossRef]
- García, J.; Moraga, P.; Valenzuela, M.; Crawford, B.; Soto, R.; Pinto, H.; Peña, A.; Altimiras, F.; Astorga, G. A Db-Scan Binarization Algorithm Applied to Matrix Covering Problems. Comput. Intell. Neurosci. 2019, 2019, 3238574. [Google Scholar] [CrossRef] [PubMed]
- Caserta, M.; Voß, S. Metaheuristics: Intelligent problem solving. In Matheuristics; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–38. [Google Scholar]
- Schermer, D.; Moeini, M.; Wendt, O. A matheuristic for the vehicle routing problem with drones and its variants. Transp. Res. Part Emerg. Technol. 2019, 106, 166–204. [Google Scholar] [CrossRef]
- Roshani, M.; Phan, G.; Roshani, G.H.; Hanus, R.; Nazemi, B.; Corniani, E.; Nazemi, E. Combination of X-ray tube and GMDH neural network as a nondestructive and potential technique for measuring characteristics of gas-oil–water three phase flows. Measurement 2021, 168, 108427. [Google Scholar] [CrossRef]
- Roshani, S.; Jamshidi, M.B.; Mohebi, F.; Roshani, S. Design and modeling of a compact power divider with squared resonators using artificial intelligence. Wirel. Pers. Commun. 2021, 117, 2085–2096. [Google Scholar] [CrossRef]
- Nazemi, B.; Rafiean, M. Forecasting house prices in Iran using GMDH. Int. J. Hous. Mark. Anal. 2020. [Google Scholar] [CrossRef]
- Karimi-Mamaghan, M.; Mohammadi, M.; Meyer, P.; Karimi-Mamaghan, A.M.; Talbi, E.G. Machine Learning at the service of Meta-heuristics for solving Combinatorial Optimization Problems: A state-of-the-art. Eur. J. Oper. Res. 2022, 296, 393–422. [Google Scholar]
- Zhao, F.; Zhang, L.; Cao, J.; Tang, J. A cooperative water wave optimization algorithm with reinforcement learning for the distributed assembly no-idle flowshop scheduling problem. Comput. Ind. Eng. 2021, 153, 107082. [Google Scholar] [CrossRef]
- Mosadegh, H.; Ghomi, S.F.; Süer, G.A. Stochastic mixed-model assembly line sequencing problem: Mathematical modeling and Q-learning based simulated annealing hyper-heuristics. Eur. J. Oper. Res. 2020, 282, 530–544. [Google Scholar] [CrossRef]
- Becerra-Rozas, M.; Lemus-Romani, J.; Crawford, B.; Soto, R.; Cisternas-Caneo, F.; Embry, A.T.; Molina, M.A.; Tapia, D.; Castillo, M.; Misra, S.; et al. Reinforcement Learning Based Whale Optimizer. In Proceedings of the International Conference on Computational Science and Its Applications, Cagliari, Italy, 13–16 September 2021; pp. 205–219. [Google Scholar]
- Becerra-Rozas, M.; Lemus-Romani, J.; Crawford, B.; Soto, R.; Cisternas-Caneo, F.; Embry, A.T.; Molina, M.A.; Tapia, D.; Castillo, M.; Rubio, J.M. A New Learnheuristic: Binary SARSA-Sine Cosine Algorithm (BS-SCA). In Proceedings of the International Conference on Metaheuristics and Nature Inspired Computing, Marrakech, Morocco, 27–30 October 2021; pp. 127–136. [Google Scholar]
- Cisternas-Caneo, F.; Crawford, B.; Soto, R.; de la Fuente-Mella, H.; Tapia, D.; Lemus-Romani, J.; Castillo, M.; Becerra-Rozas, M.; Paredes, F.; Misra, S. A Data-Driven Dynamic Discretization Framework to Solve Combinatorial Problems Using Continuous Metaheuristics. In Innovations in Bio-Inspired Computing and Applications; Abraham, A., Sasaki, H., Rios, R., Gandhi, N., Singh, U., Ma, K., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 76–85. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability; Freeman: San Francisco, CA, USA, 1979; Volume 174. [Google Scholar]
- Vianna, S.S. The set covering problem applied to optimisation of gas detectors in chemical process plants. Comput. Chem. Eng. 2019, 121, 388–395. [Google Scholar] [CrossRef]
- Zhang, L.; Shaffer, B.; Brown, T.; Samuelsen, G.S. The optimization of DC fast charging deployment in California. Appl. Energy 2015, 157, 111–122. [Google Scholar] [CrossRef]
- Park, Y.; Nielsen, P.; Moon, I. Unmanned aerial vehicle set covering problem considering fixed-radius coverage constraint. Comput. Oper. Res. 2020, 119, 104936. [Google Scholar] [CrossRef]
- Alizadeh, R.; Nishi, T. Hybrid set covering and dynamic modular covering location problem: Application to an emergency humanitarian logistics problem. Appl. Sci. 2020, 10, 7110. [Google Scholar] [CrossRef]
- Vieira, B.S.; Ferrari, T.; Ribeiro, G.M.; Bahiense, L.; Orrico Filho, R.D.; Abramides, C.A.; Júnior, N.F.R.C. A progressive hybrid set covering based algorithm for the traffic counting location problem. Expert Syst. Appl. 2020, 160, 113641. [Google Scholar] [CrossRef]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Lazaric, A.; Restelli, M.; Bonarini, A. Reinforcement learning in continuous action spaces through sequential monte carlo methods. In Proceedings of the 20th International Conference on Neural Information Processing Systems 2007, Vancouver, BC, Canada, 3–6 December 2007; Volume 20. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Dewi, S.K.; Utama, D.M. A new hybrid whale optimization algorithm for green vehicle routing problem. Syst. Sci. Control. Eng. 2021, 9, 61–72. [Google Scholar] [CrossRef]
- Utama, D.M.; Widodo, D.S.; Ibrahim, M.F.; Hidayat, K.; Baroto, T.; Yurifah, A. The hybrid whale optimization algorithm: A new metaheuristic algorithm for energy-efficient on flow shop with dependent sequence setup. J. Phys. Conf. Ser. IOP Publ. 2020, 1569, 022094. [Google Scholar] [CrossRef]
- Utama, D. Minimizing Number of Tardy Jobs in Flow Shop Scheduling Using A Hybrid Whale Optimization Algorithm. J. Phys. Conf. Ser. IOP Publ. 2021, 1845, 012017. [Google Scholar] [CrossRef]
- Lanza-Gutierrez, J.M.; Caballe, N.; Crawford, B.; Soto, R.; Gomez-Pulido, J.A.; Paredes, F. Exploring further advantages in an alternative formulation for the set covering problem. Math. Probl. Eng. 2020, 2020, 5473501. [Google Scholar] [CrossRef]
- Crawford, B.; Soto, R.; Lemus-Romani, J.; Becerra-Rozas, M.; Lanza-Gutiérrez, J.M.; Caballé, N.; Castillo, M.; Tapia, D.; Cisternas-Caneo, F.; García, J.; et al. Q-learnheuristics: Towards data-driven balanced metaheuristics. Mathematics 2021, 9, 1839. [Google Scholar] [CrossRef]
- Crawford, B.; Soto, R.; Olivares-Suarez, M.; Palma, W.; Paredes, F.; Olguin, E.; Norero, E. A binary coded firefly algorithm that solves the set covering problem. Rom. J. Inf. Sci. Technol. 2014, 17, 252–264. [Google Scholar]
- Mirjalili, S.; Lewis, A. S-shaped versus V-shaped transfer functions for binary particle swarm optimization. Swarm Evol. Comput. 2013, 9, 1–14. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Rajalakshmi, N.; Padma Subramanian, D.; Thamizhavel, K. Performance enhancement of radial distributed system with distributed generators by reconfiguration using binary firefly algorithm. J. Inst. Eng. (India) Ser. B 2015, 96, 91–99. [Google Scholar] [CrossRef]
- Ghosh, K.K.; Singh, P.K.; Hong, J.; Geem, Z.W.; Sarkar, R. Binary social mimic optimization algorithm with x-shaped transfer function for feature selection. IEEE Access 2020, 8, 97890–97906. [Google Scholar] [CrossRef]
- Beheshti, Z. A novel x-shaped binary particle swarm optimization. Soft Comput. 2021, 25, 3013–3042. [Google Scholar] [CrossRef]
- Guo, S.s.; Wang, J.s.; Guo, M.w. Z-shaped transfer functions for binary particle swarm optimization algorithm. Comput. Intell. Neurosci. 2020, 2020, 6502807. [Google Scholar] [CrossRef]
- Sun, W.Z.; Zhang, M.; Wang, J.S.; Guo, S.S.; Wang, M.; Hao, W.K. Binary Particle Swarm Optimization Algorithm Based on Z-shaped Probability Transfer Function to Solve 0-1 Knapsack Problem. IAENG Int. J. Comput. Sci. 2021, 48, 294–303. [Google Scholar]
- Lanza-Gutierrez, J.M.; Crawford, B.; Soto, R.; Berrios, N.; Gomez-Pulido, J.A.; Paredes, F. Analyzing the effects of binarization techniques when solving the set covering problem through swarm optimization. Expert Syst. Appl. 2017, 70, 67–82. [Google Scholar] [CrossRef]
- Beasley, J.; Jörnsten, K. Enhancing an algorithm for set covering problems. Eur. J. Oper. Res. 1992, 58, 293–300. [Google Scholar] [CrossRef]
- Bisong, E. Google Colaboratory. In Building Machine Learning and Deep Learning Models on Google Cloud Platform: A Comprehensive Guide for Beginners; Apress: Berkeley, CA, USA, 2019; pp. 59–64. [Google Scholar] [CrossRef]
- Morales-Castañeda, B.; Zaldivar, D.; Cuevas, E.; Fausto, F.; Rodríguez, A. A better balance in metaheuristic algorithms: Does it exist? Swarm Evol. Comput. 2020, 54, 100671. [Google Scholar] [CrossRef]
- Crawford, B.; Soto, R.; Cisternas-Caneo, F.; Tapia, D.; de la Fuente-Mella, H.; Palma, W.; Lemus-Romani, J.; Castillo, M.; Becerra-Rozas, M. A Comparison of Learnheuristics Using Different Reward Functions to Solve the Set Covering Problem. In Optimization and Learning; Dorronsoro, B., Amodeo, L., Pavone, M., Ruiz, P., Eds.; Springer International Publishing: Cham, Switzerlan, 2021; pp. 74–85. [Google Scholar] [CrossRef]
- Lemus-Romani, J.; Becerra-Rozas, M.; Crawford, B.; Soto, R.; Cisternas-Caneo, F.; Vega, E.; Castillo, M.; Tapia, D.; Astorga, G.; Palma, W.; et al. A Novel Learning-Based Binarization Scheme Selector for Swarm Algorithms Solving Combinatorial Problems. Mathematics 2021, 9, 2887. [Google Scholar] [CrossRef]
- Hussain, K.; Zhu, W.; Salleh, M.N.M. Long-term memory Harris’ hawk optimization for high dimensional and optimal power flow problems. IEEE Access 2019, 7, 147596–147616. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).