Two Approaches to the Traffic Quality Intuitionistic Fuzzy Estimation of Service Compositions

Abstract

Recently, intuitionistic fuzzy pairs have been used as uncertainty estimations of the request services in service systems. In the present paper, three intuitionistic fuzzy characterizations of virtual service devices are specified: intuitionistic fuzzy traffic estimation, intuitionistic fuzzy flow estimation and intuitionistic fuzzy estimation about probability. Discussed herein are two approaches to the intuitionistic fuzzy estimation of the uncertainty of compositions of services. One of the approaches is based on the definitions of the intuitionistic fuzzy pairs for one service device. The other approach is based on the aggregation operators over intuitionistic fuzzy pairs. A total of six intuitionistic fuzzy estimations of the uncertainty of comprise service device are proposed. The proposed uncertainty estimations allow for the definition of new Quality of Service (QoS) indicators and can be used to determine the quality of service compositions across a wide range of service systems.

1. Introduction

Quality of Service (QoS) in service compositions is an important criterion for the selection of services in the process flow in order to maintain a certain level of quality. The QoS of a composition of services can be considered as a complex service provision scheme where the service cost varies depending on its partnership with another service [1]. In [2], the design and implementation of QoS-aware and adaptive frameworks for service compositions are developed. The focus is on self-optimization through which the composite services seek to restore and maintain their QoS levels. A survey of QoS-aware service composition is conducted in [3]. The composition of several services represents a new service. The embedded services may share similar functionality but different QoS. Therefore, it is important to define and derive QoS of the various compositions of services. Web service composition issues are considered a significant area of research for selecting the appropriate web services that provide the expected QoS and attain the clients’ Service Level Agreement (SLA, see [4]). A model that helps the selection and composition of web services through minimization of the number of integrated services is proposed in [5].

The Service Quality Agreement (SQA) is a formalized program to monitor, measure and set targets that are intended to satisfy customers and service providers. In the standardization SQA documents of ITU-T and ETSI, in force, the uncertain service results are not considered, but service compositions are foreseen [6]. On the other hand, service termination due to an uncertainty reason and/or uncertainty service result is not rare (e.g., ‘abandoned service’). In greater detail, we herein consider the definitions and usage of intuitionistic fuzzy characterization of the traffic of service requests and methods for intuitionistic fuzzy estimation of service compositions. The importance of the intuitionistic fuzzy approach for the Fourth Industrial Revolution is discussed in [7]. To the best of our knowledge, the approach to the representation of uncertainty in the service of requests proposed in [8] and further developed in [9,10], and in the present paper, is a novel one that outlines a prospective area of research.

The problem regarding the representation of uncertainty in the service of requests is studied in [8] where the apparatus of the Intuitionistic Fuzzy Sets (IFSs, see [11]) is proposed as an approach to quantifying the uncertainty. The problem is further studied in [9], where three IF characterizations of uncertainty of the service of requests are proposed: IF flow, IF traffic and IF time characterizations. The advantages of using Intuitionistic Fuzzy Pairs (IFP, see [12]) are illustrated in the case of a consecutive composition of two services. In [10], IF estimation of a parallel composition of services is obtained.

In the present paper, the intuitionistic fuzzy estimations of the uncertainty of a service device are specified and their analytical expressions are derived. A total of two approaches to the estimation of uncertainty of comprise service devices are discussed. The first approach is based on the definition of intuitionistic fuzzy estimations of a single service device. It has been applied to a parallel composition of two services in [10] and analytical expressions of the degrees of membership, non-membership and uncertainty of the composition are expressed through the corresponding degrees of the embedded devices. The second approach described in the present paper is based on the aggregation operators on IFPs. A new aggregation operator is also defined.

The two approaches are important for the estimation of traffic quality in complex service systems and in particular in overall telecommunication systems consisting of a large number of embedded service devices on several levels.

2. Preliminaries

In the present paper, the overall approach described in [8] is used for the conceptual modeling of service systems. It is based on the notion of base virtual service devices.

2.1. Service Modeling Virtual Devices

Different types of virtual service devices are used similar to those used in the modeling language GPSS [13], Generalized Nets [14] and Petri Nets [15]. Their graphical representations are shown in Figure 1.

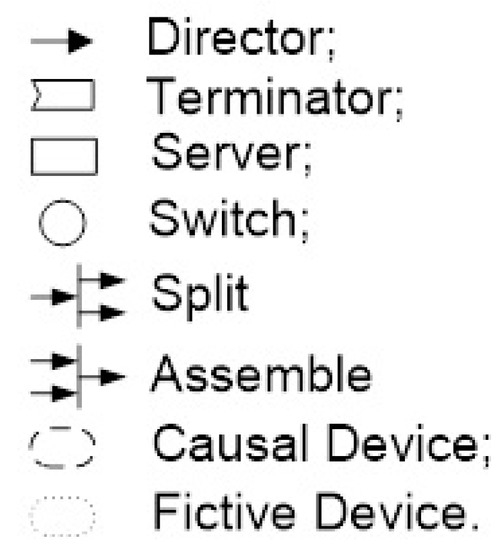
Figure 1. Virtual devices.

Every base virtual device type is characterized by a specific function (see [8]):

• Director—used to show the next device to which the requests are tranferred. It does not delay, change or transfer the requests.
• Terminator—removes from the model every request that has been tranferred to it.
• Server—models the delay in the service of requests. It does not remove or generate requests. It is also used to model time and traffic characteristics in the process of servicing of requests.
• Switch—for every request transfer it receives, it selects one exit. In this way, it determines the next device to which the request is transferred.
• Split Transition—eliminates from the model an incoming request and simultaneously generates (inducts) two different analogous (similar) requests.
• Assemble Transition—eliminates simultaneously the two incoming requests and generates (induces) a different analogous request.
• Causal device—represents the causes of a service ending, e.g., successful (carried) or not (interrupted, abandoned, etc.).
• Fictive device—represents fictive traffic used for engineering purposes (e.g., device dimensioning).

2.2. Naming System for the Devices and Their Parameters

According to the principles of structured programming (see [16]), we assume that each block-schematic representation, according to the above-mentioned information, can be decomposed to virtual devices (with the exception of the transitions) which have only one entrance and one exit and do not contain any other virtual devices (see Figure 2).

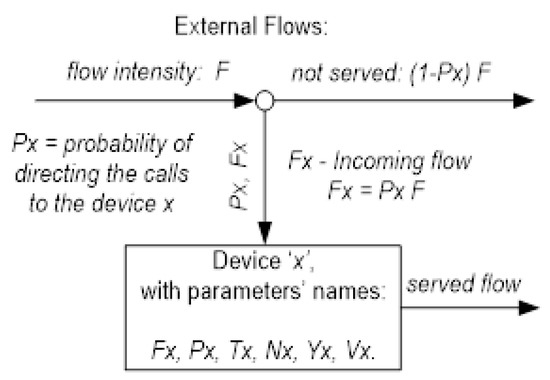
Figure 2. Virtual device parameters.

2.3. Causal and Intuitionistic Fuzzy Traffic Classification

In the papers [8,10], causal and intuitionistic fuzzy traffic characterization is proposed (see Figure 3).

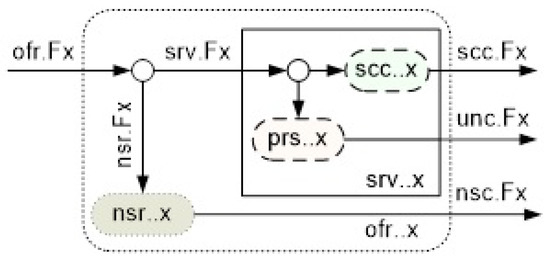
Figure 3. Causal and intuitionistic fuzzy traffic classification.

In the papers [8,17], the notion of generalized comprising causal device is used. It encompasses the causes of service ending and the corresponding causal devices. It is shown that only three causal traffic qualificators are sufficient to represent the service of requests: “parasitic”, “carried” and “served” (see [18]). For completeness, the meaning of each qualificator is given below (see [17]).

In a pool of resources, the traffic that is not successfully served is referred to as parasitic traffic. Usually, the parasitic traffic does not result in a useful service execution, but it always occupies real resources. The qualifier “uncertain” is used in the present paper as a more adequate term from the analyzer’s point of view.

In a pool of resources, the succesfully served traffic that is consequently carried to the next device is referred to as carried traffic.

The served traffic in a pool of resources is any traffic occupying (using) resources in the pool. It must be mentioned that the served traffic is the sum of the carried and parasitic traffic.

There are two additional and important traffic characterizations that warrant explanation. These are not served traffic and offered traffic.

In a pool of resources, the traffic that does not occupy any resources is called not served traffic. For example,‘blocking’ due to a lack of service places in the pool [18]. The intensity of the not served traffic is a product of the flow intensity of the not served requests and the mean service time of the served requests.

In a pool of resources, the sum of the served and not served traffic intensities is called offered traffic.

A naming system is proposed in [17] for the devices’ parameters names. According to this naming system, the name of the parameter is a concatenation of one or two qualifiers, one of the symbols $P,F,T,Y,V,N$ and the name of the device:

Causal name = <qualifier><qualifier>.<Parameter’s Symbol>.<Device Name>.

Some of the used qualifiers are:

• crr. = carried;
• nsr. = not served;
• ofr. = offered;
• prs. = parasitic;
• srv. = served.

‘Parameter’s symbol’ is one symbol used to denote the parameters, i.e., $P,F,T,Y,V,N$. The qualifiers are used to characterize the parameters of the devices. The number of qualifiers used to characterize a particular parameter can be two, one or zero. When the parameter symbol is absent, it is assumed that the causal name is the name of a device (see Figure 3).

In the names of the devices, only small or subscript letters are used. For example, $srv.Fx$ is the flow intensity of the served requests of the device x (see Figure 3). In the graphical representations, only the names of causal devices can be present. The names of the device parameters are implicit.

A conceptual model of a service network portion ‘x’ is shown in Figure 3. Let the embedded virtual device $srv.x$ have a limited capacity. Because of the limited device capacity, requests are rejected when there are no service places. It is important to note that the device $nsr.x$ does not belong to the service device. In fact, it is a part of the comprise fictive device $ofr.x$ which is used for dimensioning and traffic estimation. Moreover, three more characterizations of the service of requests should be specified:

• successful—a service that is part of a fully completed target service (qualifier $scc.$);
• not successful (abortive)—a service that has not finished all service stages (with no final result) or has received a random denial (qualifiers $nsr.$, $nsc.$).;
• uncertain—is a service which has passed all service stages with partial, unclear, etc., results (qualifier $unc.$).

For the qualifier $unc.$, a more detailed explanation is needed. It is used when the reasons for the parasitic load cannot be determined explicitly. Some possible reasons are:

• Abandonment/Failure by the users.
• Unsatisfying terms of service according to the users’ opinion.
• Technical (objective) reasons—electricity failure, equipment failure, etc.
• Preempted—overtaken by a higher priority request.

In the case of uncertain service, it is assumed that the service of the requests is terminated.

2.4. General Assumptions

The following assumptions should be stated explicitly.

Assumption 1 (A1).

Each service device performs only the operations described in Section 2.1 and there are no hidden operations or effects.

Assumption 2 (A2).

In all models studied in the present paper, the modeled system is considered to be in a stationary state. This allows for the Little’s theorem (see [19]) to be applied to every virtual device, i.e.,:

$$Y=FT,$$

(1)

where if t is the length of the time interval in which the mean values of the parameters are considered, then

$${\displaystyle Y=\underset{t\to \infty }{lim}Y\left(t\right);F=\underset{t\to \infty }{lim}F\left(t\right);t=\underset{T\to \infty }{lim}T\left(t\right).}$$

(2)

Equation (1) is invariant with respect to the probability distributions of the parameters.

Assumption 3 (A3). 

Every request is serviced by every device independently from the rest of the requests in the model.

Note 1. With regard to the servicing of requests in a buffer and in the case of managing feedback, all dependencies are represented explicitly in the graphical, mathematical and text representations of the models.

2.5. Basic Types of Parameters in the Intuitionistic Fuzzy Classification of the Traffic

2.5.1. Partial Parameters

The systematic introduction of new useful indicators requires a development of the concept of partial parameters of the service devices. The partial time has already been used as a Quality of Service (QoS) indicator while the other partial parameters have been used in [17]. Partial parameters for intuitionistic fuzzy estimations are used in the paper [9].

Let us consider an arbitrary virtual device denoted by x with one entrance, k exits and arbitrary internal structure (see Figure 4).

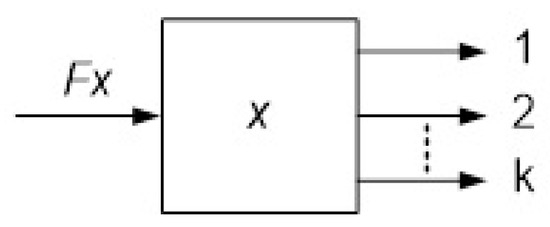
Figure 4. Virtual device with one entrance and k exits.

Let the state of the device x, according to assumption A2, be characterized by the values $Fx,Tx,Yx$. There are many ways in which the internal structure of the device can be presented, independently from the values of the state and the actual internal structure of the device x. One useful representation for generalized characterization of the functioning of the device is shown in Figure 5.

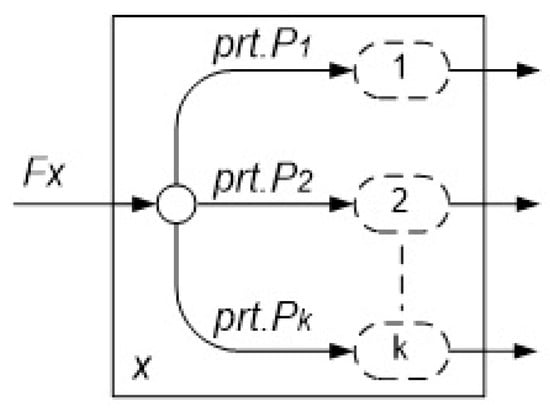
Figure 5. Generalized representation of the functioning of a virtual device.

To every exit (i), a virtual embedded device with number i is juxtaposed. A part of the flow of requests entering the device x ($Fx$) is directed towards this embedded device. After the completion of the service by the device i, this flow with intensity $Fi$ immediately leaves the service device x. Considering that there are no other subdevices in the service device x, it is evident that

$$Fx=\sum _{i=1}^{k}Fi,$$

(3)

$$Yx=\sum _{i=1}^{k}Yi.$$

(4)

Definition 1. 

Partial parameter of an embedded device i with respect to comprise device x is the ratio of the traffic characterization of the embedded virtual device (i) to the corresponding value of the device x.

The sum of all partial parameters from one and the same type for all embedded devices in x is equal to 1. This means that the value of the corresponding parameter of x is fully represented by the partial parameters of the embedded devices. According to Definition 1 and Figure 5, we have at least the following types of partial parameters for one service device which we denote using the prefix “prt.”: $prt.Fi,prt.Yi,prt.Pi,prt.Ti$. From Definition 1, we have

$$prt.Fi=\frac{Fi}{Fx}.$$

(5)

From (3) and (5) if follows:

$$\sum prt.Fi=1.$$

(6)

From the well-known definition of the value of transition probability and Figure 5, it follows

$$prt.Pi=\frac{Fi}{Fx}.$$

(7)

From (5) and (7) we obtain:

$$prt.Fi=prt.Pi.$$

(8)

Now, using Definition 1 we obtain:

$$prt.Yi=\frac{Yi}{Yx}.$$

(9)

From (4) and (9), we have

$$\sum _{i=1}^{k}prt.Yi=1.$$

(10)

Using (9) and the Little’s theorem, we obtain

$$prt.Yi=\frac{FiTi}{Yx}=\frac{FiTi}{FxTx}.$$

(11)

From (5) and (11), it follows directly that

$$prt.Yi=\frac{prt.PiTi}{Tx}.$$

(12)

By combining (10) and (12), we obtain

$$1=\sum _{i=1}^k\frac{prt.PiTi}{Tx}.$$

(13)

Therefore, from Definition 1 and (13) we obtain

$$prt.Ti=\frac{prt.PiTi}{Tx}.$$

(14)

From (12) and (14), we obtain

$$prt.Yi=prt.Ti.$$

(15)

Finally, from (15) and (10) we obtain

$$\sum _{i=1}^{k}prt.Ti=1.$$

(16)

Equation (16) corresponds to Definition 1.

Proposition 1. 

Out of the four considered partial characteristics of one virtual device, the values of the parameters $prt.Fi$ and $prt.Pi$ coincide for every virtual embedded device. The values of the parameters $prt.Yi$ and $prt.Ti$ also coincide for every virtual embedded device.

Proof. 

The validity of the proposition follows from the derivation of Equations (8) and (12). □

2.5.2. Intuitionistic Fuzzy Characterization of a Virtual Device

The concept of partial traffic parameters and the correspondence between causal and fuzzy service qualification of the fictive device $ofr.x$ (see Figure 3) allows for a correct introduction of the notion of intuitionistic fuzzy characterization of the service. According to Proposition 1, we select out of the four considered characterizations, those based on flow and traffic intensity (Equations (8) and (15), respectively). The reason for this is because they use fundamental and clearly defined concepts of the Teletraffic theory (see [18,20]).

According to (8) and Figure 3, we define in accordance with the causal structure of device traffic x intuitionistic fuzzy estimations of the belonging to the flow of the successfully served requests (degree of membership ${\mu }_x^f$) in device x, as well as the corresponding degree of membership of the intuitionistic fuzzy estimation regarding probability (${\mu }_x^p$):

$$prt.scc.Px=prt.scc.Fx=\frac{scc.Fx}{ofr.Fx}={\mu }_x^p={\mu }_x^f.$$

(17)

From (17) and by following the flows in Figure 3, we obtain:

$${\mu }_x^p=\frac{scc.Fx}{ofr.Fx}=(1-nsr.Px)(1-prs.Px).$$

(18)

Analogously, for the degree of uncertainty of the intuitionistic fuzzy estimation regarding probability (${\pi }_x^p$) we obtain:

$${\pi }_x^p=\frac{unc.Fx}{ofr.Fx}=(1-nsr.Px)prs.Px.$$

(19)

In a similar way, for the degree of non-membership of the intuitionistic fuzzy estimation about probability (${\nu }_x^p$) we have:

$${\nu }_x^p=\frac{nsc.Fx}{ofr.Fx}=nsr.Px.$$

(20)

After adding together Equations (18)–(20), we get:

$${\mu }_x^p+{\pi }_x^p+{\nu }_x^p=1.$$

(21)

From (21) it is clear that the pair $⟨{\mu }_x^p,{\nu }_x^p⟩$ is an Intuitionistic Fuzzy Pair (IFP, see [12]).

Analogously, according to (15) and Figure 3, an intuitionistic fuzzy traffic intensity estimation of the service can be defined in the form of an IFP $⟨{\mu }_x^y,{\nu }_x^y⟩$ and degree of uncertainty ${\pi }_x^y$. Using the Little’s theorem and the definition of equivalent offered traffic (see [20]), for the intuitionistic fuzzy traffic estimation, we obtain the following expressions.

$${\mu }_x^y=\frac{scc.Yx}{ofr.Yx}=\frac{ofr.Fx(1-nsc.Px)(1-prs.Px)scc.Tx}{ofr.Fxofr.Tx}=\frac{(1-nsc.Px)(1-prs.Px)scc.Tx}{ofr.Tx}.$$

(22)

Analogously, for the degree of uncertainty of the intuitionistic fuzzy traffic estimation we obtain:

$${\pi }_x^y=(1-nsr.Px)prs.Px\frac{prs.Tx}{ofr.Tx}.$$

(23)

Finally, the degree of non-membership of the intuitionistic fuzzy traffic characterization is given by

$${\nu }_x^y=nsr.Px\frac{nsr.Tx}{ofr.Tx}.$$

(24)

After adding together Equations (22)–(24), we obtain

$${\mu }_x^y+{\pi }_x^y+{\nu }_x^y=\frac{(1-nsr.Px)\left[\right(1-prs.Px)scc.Tx+prs.Pxprs.Tx]+nsr.Pxnsr.Tx}{ofr.Tx}.$$

(25)

On the other hand, according to the definition of equivalent offered traffic (see [20]) we have

$$ofr.Tx=srv.Tx.$$

(26)

From the graphical representation in Figure 3, it is evident that

$$srv.Tx=prs.Pxprs.Tx+(1-prs.Px)scc.Tx.$$

(27)

By combining (25)–(27), we obtain

$${\mu }_x^y+{\pi }_x^y+{\nu }_x^y=\frac{(1-nsr.Px)srv.Tx+nsr.Pxsrv.Tx}{srv.Tx}=1.$$

(28)

Equation (28) shows that the pair $⟨{\mu }_x^y,{\nu }_x^y⟩$ is indeed an IFP with degree of uncertainty ${\pi }_x^y$. Taking into account Equation (26) and comparing directly Equations (18)–(20) with (22)–(24), we obtain the following expressions for the intuitionistic fuzzy traffic estimation:

$${\mu }_x^y={\mu }_x^p\frac{scc.Tx}{srv.Tx}.$$

(29)

$${\pi }_x^y={\pi }_x^p\frac{prs.Tx}{srv.Tx}.$$

(30)

$${\nu }_x^y={\nu }_x^p\frac{nsr.Tx}{srv.Tx}.$$

(31)

Equations (29)–(31) are new dependencies between different intuitionistic fuzzy characterizations of one virtual device with limited capacity. They allow for the obtainment of intuitionistic fuzzy traffic estimations from pointwise intuitionistic fuzzy estimations and vice versa.

3. Intuitionistic Fuzzy Estimation of the Uncertainty of Comprise Service Devices

The problem regarding the obtainment of intuitionistic fuzzy estimations of the uncertainty for parallel and serial compositions of two services is studied in [9,10]. The degrees of membership, non-membership and uncertainty for the composition are expressed, respectively, through the degrees of membership, non-membership and uncertainty of the embedded devices. In this section, two approaches to the estimations of uncertainty of comprise service devices are presented.

3.1. First Approach

The first approach to the intuitionistic fuzzy estimation of the uncertainty of comprise devices is based on the definitions of the degrees of membership, non-membership and uncertainty of the intuitionistic fuzzy characterizations. We shall illustrate the approach in the case of a parallel composition of two services. A conceptual model of a parallel composition of two services is described in [10]. The graphical representation of the model is shown in Figure 6.

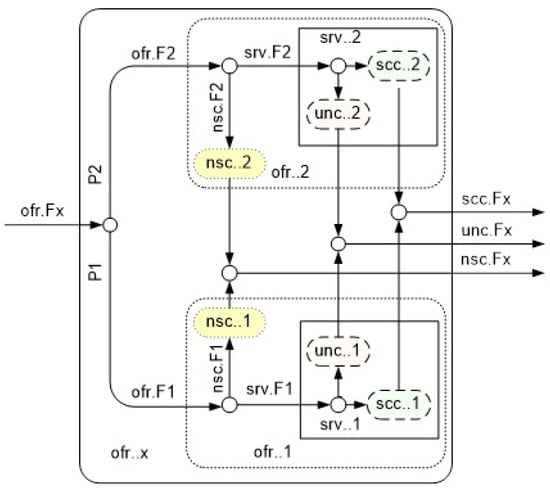
Figure 6. Parallel composition of two services (see [10]).

On the basis of this model, in [10] expressions for the degrees of membership, non-membership and uncertainty of the traffic and flow characterizations of the comprise device are obtained through the degrees of membership, non-membership and uncertainty of the embedded devices. They are presented below.

$${\mu }_x^y=\frac{ofr.Fx[P_1{\mu }_1^{y}srv.T_1+P_2{\mu }_2^{y}srv.T_2]}{ofr.Fx[P_{1}srv.T_1+P_{2}srv.T_2]}$$

$$=k_1{\mu }_1^y+k_2{\mu }_2^y,$$

(32)

where $k_1$ and $k_2$ do not depend on the input flow intensity $ofr.Fx$:

$$k_1=\frac{P_{1}srv.T_1}{P_{1}srv.T_1+P_{2}srv.T_2};k_2=\frac{P_{2}srv.T_2}{P_{1}srv.T_1+P_{2}srv.T_2}.$$

(33)

The degree of non-membership of the intuitionistic fuzzy traffic estimation of the composition is given by

$${\nu }_x^y=k_1{\nu }_1^y+k_2{\nu }_2^y.$$

(34)

The degree of uncertainty of the intuitionistic fuzzy traffic estimation of the composition is given by

$${\pi }_x^y=k_1{\pi }_1^y+k_2{\pi }_2^y.$$

(35)

The degrees of membership non-membership and uncertainty of the intuitionistic fuzzy flow estimation are given by

$${\mu }_x^f=P_1{\mu }_1^f+P_2{\mu }_2^f,$$

(36)

$${\nu }_x^f=P_1{\nu }_1^f+P_2{\nu }_2^f,$$

(37)

$${\pi }_x^f=P_1{\pi }_1^f+P_2{\pi }_2^f.$$

(38)

3.2. Second Approach

For more complex compositions consisting of a much larger number of embedded devices, it is considerably harder to obtain an estimation of the uncertainty of the comprise device through estimations of the embedded devices using definitions of the intuitionistic fuzzy traffic and flow estimations and the estimation about probability. In such cases, an estimation of the service uncertainty of the requests by the comprise device can be obtained through approximate aggregation approach.

Let a comprise service device x consist of k embedded service devices with intuitionistic fuzzy traffic estimations given by the intuitionistic fuzzy pairs: $⟨{\mu }_1^y,{\nu }_1^y⟩$, $⟨{\mu }_2^y,{\nu }_2^y⟩$,..., $⟨{\mu }_k^y,{\nu }_k^y⟩$. Following [21], we introduce the following estimations of the uncertainty of the comprise service device x.

Definition 2. 

Strongly optimistic intuitionistic fuzzy traffic estimation of the comprise service device x is the intuitionistic fuzzy pair $⟨{\mu }_x^{y,++},{\nu }_x^{y,++}⟩$, where

$${\mu }_x^{y,++}=1-\prod _{i=1}^k(1-{\mu }_i),$$

(39)

$${\nu }_x^{y,++}=\prod _{i=1}^k{\nu }_i.$$

(40)

Definition 3. 

Optimistic intuitionistic fuzzy traffic estimation of the comprise service device x is the intuitionistic fuzzy pair $⟨{\mu }_x^{y,+},{\nu }_x^{y,+}⟩$, where

$${\mu }_x^{y,+}=\underset{i\in \{1,2,\cdots ,k\}}{max}{\mu }_i,$$

(41)

$${\nu }_x^{y,+}=\underset{i\in \{1,2,\cdots ,k\}}{min}{\nu }_i.$$

(42)

Definition 4. 

Average intuitionistic fuzzy traffic estimation of the comprise service device x is the intuitionistic fuzzy pair $⟨{\mu }_x^{y,av},{\nu }_x^{y,av}⟩$, where

$${\mu }_x^{y,av}=\frac{1}{k}\sum _{i=1}^k{\mu }_i,$$

(43)

$${\nu }_x^{y,av}=\frac{1}{k}\sum _{i=1}^k{\nu }_i.$$

(44)

Definition 5. 

Pessimistic intuitionistic fuzzy traffic estimation of the comprise service device x is the intuitionistic fuzzy pair $⟨{\mu }_x^{y,-},{\nu }_x^{y,-}⟩$, where

$${\mu }_x^{y,-}=\underset{i\in \{1,2,\cdots ,k\}}{min}{\mu }_i,$$

(45)

$${\nu }_x^{y,-}=\underset{i\in \{1,2,\cdots ,k\}}{max}{\nu }_i.$$

(46)

Definition 6. 

Strongly pessimistic intuitionistic fuzzy traffic estimation of the comprise service device x is the intuitionistic fuzzy pair $⟨{\mu }_x^{y,--},{\nu }_x^{y,--}⟩$, where

$${\mu }_x^{y,--}=\prod _{i=1}^k{\mu }_i,$$

(47)

$${\nu }_x^{y,--}=1-\prod _{i=1}^k(1-{\nu }_i).$$

(48)

In the following definition, a new aggregation operator over intuitionistic fuzzy pairs is defined.

Definition 7. 

Intuitionistic fuzzy traffic confidence coefficient of the comprise service device x is an intuitionistic fuzzy pair $⟨{\overline{\mu }}_x^y,{\overline{\nu }}_x^y⟩$, where

$${\overline{\mu }}_x^y=\frac{1}{k}\sum _{i=1}^k\varphi ({\mu }_i,{\nu }_i),$$

(49)

$${\overline{\nu }}_x^y=\frac{1}{k}\sum _{i=1}^k\varphi ({\nu }_i,{\mu }_i),$$

(50)

where

$$\varphi (a,b)=\left\{\begin{array}{cc}1,\hfill & ifa>\frac{1}{2}.\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

(51)

To see that $⟨{\overline{\mu }}_x^y,{\overline{\nu }}_x^y⟩$ is an IFP, it is sufficient to observe that

$$\sum _i^k[\varphi ({\mu }_i,{\nu }_i)+\varphi ({\nu }_i,{\mu }_i)]\le k.$$

(52)

Similarly, by substituting the symbol “y” in the above definitions with “f” or “p”, the corresponding intuitionistic fuzzy estimations about flow and probability are obtained.

We shall provide a geometric interpretation of the above introduced estimations. Let $z=⟨a,b⟩$ be an intuitionistic fuzzy pair. One possible geometrical interpretation of the pair is shown in Figure 7. Every intuitionistic fuzzy pair is represented by a point inside the isosceles right-angled triangle with edges equal to 1.

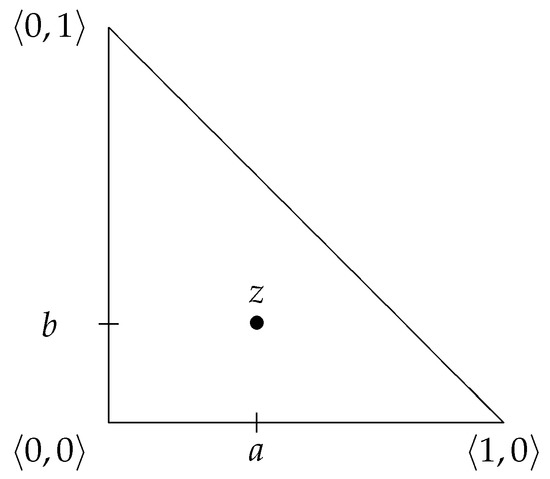
Figure 7. Geometric interpretation of the intuitionistic fuzzy pair $z=⟨a,b⟩$.

Let z and t now be two intuitionistic fuzzy estimations of two embedded virtual devices with geometrical interpretation shown in Figure 8.

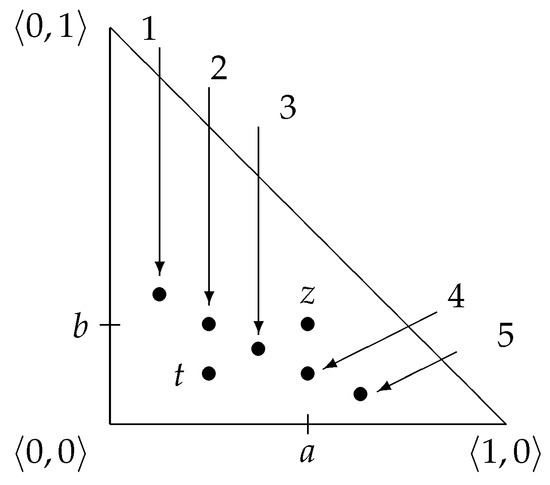
Figure 8. Geometric interpretation of the intuitionistic fuzzy pairs representing the strongly optimistic (5), optimistic (4), average (3), pessimistic (2) and strongly pessimistic (1) estimations.

The intuitionistic fuzzy estimations of a comprise service device consisting of two embedded devices with intuitionistic fuzzy estimations z and t are represented in Figure 8 as follows: 1—strongly pessimistic; 2—pessimistic; 3—average; 4 –optimistic; 5–strongly optimistic.

4. Discussion

The two approaches to the intuitionistic fuzzy estimation of uncertainty of service compositions bear their own advantages and disadvantages.

The first approach uses the definitions of the degrees of membership, non-membership and uncertainty of the intuitionistic fuzzy pairs characterizing the uncertainty. In addition, the estimations of the embedded devices also require the values of parameters internal to the embedded devices ($k_1,k_2,P_1,P_2$). The second approach requires only the intuitionistic fuzzy estimations of the embedded devices.

The accuracy of the approximate aggregation approach is lower. It can be employed in cases when fast approximate estimation of the uncertainty of the comprise device is needed. The selection of the aggregation operator to use depends on the modeled process.

The proposed approaches to the traffic quality intuitionistic fuzzy estimation of composition of services will be used for the QoS estimation of overall telecommunication systems including users and telecommunication networks. The models of such systems consist of many embedded virtual service devices in various compositions and, therefore, the study of QoS compositions is important for determining the overall network QoS.