Generalized Hukuhara Weak Solutions for a Class of Coupled Systems of Fuzzy Fractional Order Partial Differential Equations without Lipschitz Conditions

Abstract

As is known to all, Lipschitz condition, which is very important to guarantee existence and uniqueness of solution for differential equations, is not frequently satisfied in real-world problems. In this paper, without the Lipschitz condition, we intend to explore a kind of novel coupled systems of fuzzy Caputo Generalized Hukuhara type (in short, gH-type) fractional partial differential equations. First and foremost, based on a series of notions of relative compactness in fuzzy number spaces, and using Schauder fixed point theorem in Banach semilinear spaces, it is naturally to prove existence of two classes of gH-weak solutions for the coupled systems of fuzzy fractional partial differential equations. We then give an example to illustrate our main conclusions vividly and intuitively. As applications, combining with the relevant definitions of fuzzy projection operators, and under some suitable conditions, existence results of two categories of gH-weak solutions for a class of fire-new fuzzy fractional partial differential coupled projection neural network systems are also proposed, which are different from those already published work. Finally, we present some work for future research.

1. Introduction

Let E be a fuzzy number space and $E_c$ is a space of fuzzy number $\varpi \in E$, which has the property that the function $\tau \mapsto {\left[\varpi \right]}^{\tau }$ is continuous with respect to Hausdorff metric (in short, H-continuous) on $[0,1]$, where ${\left[\varpi \right]}^{\tau }=\{x\in \mathbb{R}|\varpi \left(x\right)\ge \tau \}$ for $0<\tau \le 1$ is $\tau$-level set of $\varpi$. From now on, we will introduce and investigate a brand-new fuzzy fractional partial differential coupled projection neural network system as follows

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}_{gH}^C{\mathcal{D}}_k^{\alpha }u(x,y)=-u(x,y)+P_{F\left(D\right)}\left(m(x,y)v(x,y)\right),\hfill \\ {}_{gH}^C{\mathcal{D}}_k^{\beta }v(x,y)=\widehat{g}(x,y,u(x,y)),\hfill \\ u(x,0)={\xi }_1\left(x\right),v(x,0)={\eta }_1\left(x\right),\hfill \\ u(0,y)={\xi }_2\left(y\right),v(0,y)={\eta }_2\left(y\right),\hfill \end{array}\right.\end{array}$$

(1)

for all $(x,y)\in J=[0,a]\times [0,b]$ and $k=1,2$, where $P_{F\left(D\right)}:E_c\to F\left(D\right)$ is a fuzzy projection operator (see [1]), $m(x,y)$ is a continuous real-valued function defined on J and $F\left(D\right)\subset E_c$ represents the set of all fuzzy numbers defined on $D\subset \mathbb{R}$ with H-continuous, ${}_{gH}^C{\mathcal{D}}_k^{\gamma }$ is a Caputo generalized Hukuhara type (in short, $gH$-type) derivative operator with the fractional order $\gamma =({\gamma }_1,{\gamma }_2)\in (0,1]\times (0,1]$ for $\gamma =\alpha ,\beta$, and ${\xi }_1,{\eta }_1:[0,a]\to E_c$ and ${\xi }_2,{\eta }_2:[0,b]\to E_c$ are continuous. It is worth noting that ${}_{gH}^C{\mathcal{D}}_k^{\alpha }$ and ${}_{gH}^C{\mathcal{D}}_k^{\beta }$ in (1) assume the presence of Hukuhara difference (in short, H-difference) and $gH$-type difference.

Clearly, if the right-hand side of the first equation in (1) is generalized to a nonlinear function $\widehat{f}\left(x,y\right.$, $\left.u(x,y),v(x,y)\right)$ for any $(x,y)\in J$ and all $u,v\in E$, then the system (1) is extended to the following new coupled system of fuzzy fractional order partial differential equation (in short, FFPDC): For each $(x,y)\in J$ and $k=1,2$,

$$\left\{\begin{array}{c}{}_{gH}^C{\mathcal{D}}_k^{\alpha }u(x,y)=\widehat{f}\left(x,y,u(x,y),v(x,y)\right),\hfill \\ {}_{gH}^C{\mathcal{D}}_k^{\beta }v(x,y)=\widehat{g}(x,y,u(x,y)),\hfill \\ u(x,0)={\xi }_1\left(x\right),v(x,0)={\eta }_1\left(x\right),\hfill \\ u(0,y)={\xi }_2\left(y\right),v(0,y)={\eta }_2\left(y\right),\hfill \end{array}\right.$$

(2)

where J, $\alpha ,\beta$, ${}_{gH}^C{\mathcal{D}}_k^{\alpha }$, ${}_{gH}^C{\mathcal{D}}_k^{\beta }$, and ${\xi }_i$ and ${\eta }_i$ for $i=1,2$ are the same as in (1).

Remark 1. 

When $\widehat{f}\left(x,y,u,v\right)\equiv \widehat{h}\left(x,y,v\right)$ for all $(x,y)\in J$ and each $u,v\in E$, the form (2) reduces to the fuzzy fractional coupled partial differential equations considered by Zhang et al. [2]. Further, one can easily see that the right side of the first equation for (1) or (2) is a function of $u(x,y)$ and $v(x,y)$, which widen the scope of solvable problems comparing with [2] and other corresponding work in the literatures. In particular, as a special case of the FFPDC (2), the coupled projection neural network system (1) depends on fuzzy projection operator, which can be applied to solve some concerned fuzzy optimization problems [1]. Thus, (1) and (2) are fire-new and worth studying.

The research of the above forms (1) and (2) is firstly motivated by an increasing interest in partial differential equations (in short, PDEs) and their applications. In fact, PDEs have a wide range of applications in the fields of engineering, biology and so on, and are considered as one of the most ideal methods to solve practical problems. For some related details, one can refer to [2,3,4,5,6,7,8,9] and the references therein.

Since theory of fractional differential equations (in short, FDEs) derived from the ideas of Leibnitz and Euler (see [10]), can better describe the genetic characteristics of various substances and processes, FDEs have been shown to be a valuable modelling tool in the fields of mechanics and physics, electrochemistry and hydrodynamic flow modelling [11]. Thus, fractional PDEs fully describe real world problems in theory [4]. Further, as an excellent tool, fractional PDEs are employed to describe complex phenomena in electromagnetic waves, diffusion equations and other fields [10].

It is well known that fuzzy analysis theory, as an extension of extreme value theory [12], has flourished in the past 30 years. The dynamic representations of models related to natural events are often losing important information. The fuzzy numbers with the basic attributes of membership functions around clear data can well avoid such problems during transmission [8]. In deed, Zadeh [13] pointed out that the interpretability and simplicity of fuzzy systems make the modelling close to natural language. In 2017, Wang et al. [14] pointed out that fuzzy set theory is a powerful tool for modelling uncertainty and dealing with subjective information in mathematical models. Humaira et al. [15] established fixed-point results of multivalued mappings with least upper bound property under contractive condition in complex-valued fuzzy metric spaces, which opened the door for the study of ideal-type shrinkage in complex-valued fuzzy metric spaces. With its unique convenience, flexibility and simplicity in describing uncertain features [7], fuzzy set theory creates unique opportunities for optimal control research [16].

In addition, practical engineering problems such as optimal control systems can be transformed into constrained optimization problems, which in turn can be changed into projection neural networks, that is to solve equations in essence. In recent decades, many neural networks have been utilized to solve optimization problems have been studied intensively and extensively [1]. In 2016, Eshaghnezhad et al. [17] discussed the following nonlinear projection equation:

$$x=P_{\mathrm{\Omega }}[x-\alpha F\left(x\right)],$$

where $F:{\mathbb{R}}^n\to {\mathbb{R}}^n$ is a continuous vector function, $\mathrm{\Omega }=\{x\in {\mathbb{R}}^n|d_i\le x_i\le h_i,\forall i\in \widehat{I}\subseteq \mathbb{N}\}\subseteq {\mathbb{R}}^n$ is a closed convex set, $\mathbb{N}=\{1,2,\dots ,n\}$, $\alpha >0$, and projection map $P_{\mathrm{\Omega }}(·)$ is defined by

$$P_{\mathrm{\Omega }}\left(x\right)=\underset{y\in \mathrm{\Omega }}{argmin}\Vert x-y\Vert .$$

Here, the projection method due to projection operators, helps us establish the equivalence between variational inequalities and fixed point problems. Based on the concepts of projection, classical projection equations are equivalent to optimality conditions of the variational inequalities and the optimization problems. In other words, solving a variational inequality system is equivalent to solving the equilibrium point of projection neural network. Hence, the concept of fuzzy projection can be generalized and applied to solve fuzzy optimization problems [1].

By the combination of fuzzy method with FDEs, a more accurate and precise proof of natural event complex system in applied science has been obtained (see [8]). In fact, there is always inconsistency between the actual physical process and the measured physical process, which leads to uncertainty of data sets. In dealing with dynamic systems containing uncertain phenomena, such as epidemiology, economics and finance, the fuzzy PDEs proposed by Buckley and Feuring [18] in 1999 are better choices than deterministic PDEs [9].

Since concept of the H-difference has an important drawback, the use of classical Hukuhara derivative in fuzzy differential equations has been criticized [19]. Stefanini and Bede [20] pointed out that a set or a fuzzy differential equation may have only solutions with increasing length of their support, and uncertainty increases with time, then the solution of a set or a fuzzy differential equation is irreversibility under uncertainty and the diameter of natural fuzzy solution of the classical Hukuhara differentiability decreases monotonically. Therefore, based on the above shortcomings of the H-difference, they first proposed the $gH$-type difference concept for studying the interval differential equations modeled by dynamic systems, whose functions diameter length do not monotonically increase monotonically with time. As Bede and Stefanini [19] indicated again, the conditions for existence of H-difference between two fuzzy numbers are very strict, but the $gH$-type difference exists under conditions with few restrictions, and the interval of the $gH$-type difference is always present.

In the other direction, the relationship arising from the interaction and influence of two or more kinds of things is called “coupling”. Generally speaking, a single differential equation cannot model a complex system or process, and so coupled systems containing FDEs have attracted intense attention. See, for example, [2,4,5,21,22].

Since most fractional differential equations do not have exact analytical solutions, approximate numerical solutions must be obtained by numerical techniques [23]. The development of direct methods for constructing mathematical problems is an important branch of mathematics [24]. However, traditional numerical methods such as finite difference and finite element exist some problems, for example, difficulty in grid generation and large amount of calculation. Thereupon, Aslefallah and Shivanian [23,24], and Aslefallah et al. [25,26] adopted meshless methods such as radial basis functions, spectral meshless radial point interpolation and singular boundary method to simulate numerical problems. In recent years, this meshless technique, which does not need to divide the grid domain and boundary, has been widely developed, and has attracted extensive attention in both mathematics and engineering fields. For some related details, one can refer to [23,24,25,26] and the references therein. By means of Buckley-Feuring strategy and fuzzing deterministic solutions, a $\left(l\right)$-weak solution of (2) for $l=†$ and ‡ is obtained. These solutions are the exact analytical solutions of (2). Therefore, the solution method in this paper is different from the meshless technique.

On the other hand, it is easy to see that there are many relevant classical results of existence and uniqueness of solutions for differential equations, which are based on Lipschitz condition. In 2017, based on Banach fixed point theorem and the Lipschitz condition of function on the right-hand side of the equation, Long et al. [3] established the first result on the existence of two kinds of $gH$-weak solutions of the fuzzy fractional partial differential equations. And then, using Banach fixed point theorem and on the strength of the work from [3,22], under the Lipschitz condition, Zhang et al. [2] proved the existence and uniqueness of two kinds of $gH$-weak solutions of the coupled system of the form (2) with a particular $\widehat{f}\left(x,y,u,v\right)\equiv \widehat{h}\left(x,y,v\right)$ for every $(x,y)\in J$ and any $u,v\in E$. But in reality, for most functions, the Lipschitz condition is relatively strong and is often difficult to satisfy (see [27,28]). Thus, by virtue of the nonlinear alternative of the Schauder type for fuzzy-valued continuous functions without the Lipschitz condition, Long et al. [3] also obtained the second result on the existence of two kinds of $gH$-weak solutions for the special coupled system. Hence, in order to enhance the practicability and utility of the functions in the absence of Lipschitz condition, it is necessary to explore existence of solutions for the systems (1) and (2).

Inspired by the previous work of predecessors such as Long et al. [3], Zhang et al. [2] and other pioneers, in this paper, in order to obtain existence of two kinds of $gH$-weak solutions for (1) without Lipschitz conditions, it is of great value to explore (2). Moreover, a numerical example is given and illustrated main results presented in this paper.

2. Preliminaries

In this section, we present the notions of fractional integral and fractional Caputo $gH$-type derivative of fuzzy value multivariable functions, as well as some concepts of relative compactness in fuzzy number spaces. Some of them were detailed further in previous papers [2,3,29,30].

Throughout this paper, denote E by the space of fuzzy numbers $\varpi :\mathbb{R}\to [0,1]$, which satisfies properties as follows: (a) $\varpi$ is normal, i.e., $\{x\in \mathbb{R}|\varpi \left(x\right)=1\}\ne \varnothing$; (b) $\varpi$ is fuzzy convex, namely, $\varpi (\lambda x+(1-\lambda \left)y\right)\ge min\left\{\varpi \right(x),\varpi (y\left)\right\}$ for all $x,y\in \mathbb{R}$ and any $\lambda \in [0,1]$; (c) $\varpi$ is upper semi-continuous on $\mathbb{R}$; (d) ${\left[\varpi \right]}^0=cl\{x\in \mathbb{R}|\varpi \left(x\right)>0\}=supp\varpi$, called the support of $\varpi$, is compactly supported, where $cl$ is the closure of the sets.

It is easy to see that the Hausdorff metric $d_H$ can be extended to the supremum metric $d_{\infty }$ on E by mean

$$\begin{array}{ccc}\hfill d_{\infty }(\varpi ,\omega )& & =\underset{\tau \in [0,1]}{sup}{d}_H\left({\left[\varpi \right]}^{\tau },{\left[\omega \right]}^{\tau }\right)\hfill \\ & & =\underset{\tau \in [0,1]}{sup}max\left\{|{\varpi }_{\tau }^{-}-{\omega }_{\tau }^{-}|,|{\varpi }_{\tau }^{+}-{\omega }_{\tau }^{+}|\right\},\forall \varpi ,\omega \in E,\hfill \end{array}$$

(3)

where ${\left[\varpi \right]}^{\tau }=[{\varpi }_{\tau }^{-},{\varpi }_{\tau }^{+}]$ for any $\varpi \in E$. And in $C(J,E)$, it follows from (3) that the supremum metric $\rho$ is considered by

$$\begin{array}{c}\hfill \rho (u,v)=\underset{(x,y)\in J}{sup}{d}_{\infty }(u(x,y),v(x,y)),\end{array}$$

(4)

here J is the same as in (1). Thus, $(E,d_{\infty })$ and $(E,\rho )$ are complete metric spaces (see [3,31]).

For all $\varpi ,\omega \in E$, $\tau \in [0,1]$, by [32], one can see that $\varpi \ominus \omega \ne \varpi +(-1)\omega$, where $\varpi \ominus \omega$ is H-difference of fuzzy numbers $\varpi$ and $\omega$, and then (i) ${[\varpi +\omega ]}^{\tau }={\left[\varpi \right]}^{\tau }+{\left[\omega \right]}^{\tau }$; (ii) ${\left[k\varpi \right]}^{\tau }=k{\left[\varpi \right]}^{\tau }$ for any $k\in \mathbb{R}\backslash \left\{0\right\}$; (iii) if $\varpi \ominus \omega$ exists, then

$$\begin{array}{c}\hfill {[\varpi \ominus \omega ]}^{\tau }=\left[{\varpi }_{\tau }^{-}-{\omega }_{\tau }^{-},{\varpi }_{\tau }^{+}-{\omega }_{\tau }^{+}\right].\end{array}$$

(5)

In this paper, we assume that the H-difference always exists and for $i=1,2$, define $E_c^i$ as a space of fuzzy numbers $\varpi \in E$ with H-continuous. According to [29,31,33], fuzzy number spaces E and $E_c^1$ are semilinear spaces having the cancellation property. i.e., for any $\zeta ,\theta ,\varphi \in S$, where S is a semilinear space, if $\zeta +\theta =\varphi +\theta$, then $\zeta =\varphi$. Furthermore, it is proved that fuzzy numbers spaces E and $E_c^1$ with metric $d_{\infty }$ are complete metric semilinear spaces. Hence, the fuzzy-valued continuous functions space $C(J,E_c^1)$ is complete metric semilinear space, which is a Banach semilinear space with the cancellation property. At the same time, we point out that $L^1(J,E_c^1)$ represents the Lebesgue integrable space of fuzzy valued continuous functions.

For each positive real number r, $B(\widehat{0},r)=\{\varpi \in E_c^1:\rho (\varpi ,\widehat{0})\le r\}$ denotes the closed sphere in $\left(C(J,E_c^1),\rho \right)$, here the metric $\rho$ is defined by (4) and $\widehat{0}=\varpi \ominus \varpi$ for all $\varpi \in E_c^1$, where $\widehat{0}\left(x\right)=1$ if $x=0$, and otherwise $\widehat{0}\left(x\right)=0$.

In the sequel, we present some lemmas and definitions which are needed to solve (1) and (2).

Lemma 1 

([3]). For all $\nu ,\theta ,\omega ,e\in E_c^1$, one has the following presentations:

(i) 

$d_{\infty }(\nu +\theta ,\omega +e)\le d_{\infty }(\nu ,\omega )+d_{\infty }(\theta ,e)$.

(ii) 

If $\nu \ominus \theta$ and $\omega \ominus e$ exist, then $d_{\infty }(\nu \ominus \theta ,\omega \ominus e)\le d_{\infty }(\nu ,\omega )+d_{\infty }(\theta ,e)$.

(iii) 

If $\nu \ominus (\theta +\omega )$ exists then $\nu \ominus \theta \ominus \omega$ exists and $\nu \ominus (\theta +\omega )=\nu \ominus \theta \ominus \omega$.

(iv) 

If $\nu \ominus \theta$ and $\theta \ominus \omega$ exist then $\nu \ominus (\theta \ominus \omega )$ exists and $\nu \ominus (\theta \ominus \omega )=(\nu \ominus \theta )+\omega$.

(v) 

If $u\ominus v$ exists then $(-1)u\ominus (-1)v$ exists and $(-1)(u\ominus v)=(-1)u\ominus (-1)v$.

Remark 2. 

The conclusions of Lemma 1 (ii)–(v) are based on the existence of H-difference, which will be used to obtain our main results.

Definition 1 

([20]). For any $n\in \mathbb{N}$, a fuzzy valued mapping $w\in C(J,E_c^1)$ is called $gH$-type differentiable of the $n^{th}$-order with respect to x at $(x_0,y_0)\in J$ whenever the function ω is $gH$-type differentiable of the order i ($i=1,2,\dots ,n-1$) at $(x_0,y_0)$ provided that $gH$-type differentiable has no change, if there exists an element $\frac{{\partial }^{n}w(x_0,y_0)}{\partial x^n}\in E_c^1$ such that for all $h>0$ sufficiently close to 0, $(x_0+h,y_0)\in J$, $w^{n-1}(x_0+h,y_0){\ominus }_{gH}{w}^{n-1}(x_0,y_0)$ exists and

$$\begin{array}{c}\hfill \underset{h\to 0}{lim}\frac{w^{n-1}(x_0+h,y_0){\ominus }_{gH}{w}^{n-1}(x_0,y_0)}{h}=\frac{{\partial }^{n}w(x_0,y_0)}{\partial x^n}\end{array}$$

(6)

owns, where $w{\ominus }_{gH}\varpi$ denotes the $gH$-type difference ([34]) of $w,\varpi \in E_c^1$, which is the fuzzy number ζ if it exists such that

$$\begin{array}{c}\hfill w{\ominus }_{gH}\varpi =\zeta ⟺\left\{\begin{array}{c}(†)w=\varpi +\zeta or\hfill \\ (‡)\varpi =w+(-1)\zeta .\hfill \end{array}\right.\end{array}$$

(7)

Under this circumstance, $\frac{{\partial }^{n}w(x_0,y_0)}{\partial x^n}\in E_c^1$ is said to be the n-order $gH$-type derivative of w at $(x_0,y_0)$ with respect to x, assume that the limit in the left side exists.

The higher fuzzy $gH$-type partial derivative of w with respect to y is defined similarly. If $n=1$, (6) degenerates to

$$\underset{h\to 0}{lim}\frac{w(x_0+h,y_0){\ominus }_{gH}w(x_0,y_0)}{h}=\frac{\partial w(x_0,y_0)}{\partial x},$$

which represents the first partial derivative of ω at $(x_0,y_0)$ with respect to x.

Definition 2 

([2]). Let $\theta =({\theta }_1,{\theta }_2)\in (0,1]\times (0,1]$, $\omega (x,y)\in C(J,E_c^i)\bigcap$$L^1(J,E_c^i),i=1,2$, ${\left[\omega (x,y)\right]}^{\lambda }=\left[{\omega }_{\lambda }^{-}(x,y),{\omega }_{\lambda }^{+}(x,y)\right]$ for $(x,y)\in J$ and $\lambda \in [0,1]$. Then the mixed Riemann-Liouville fractional integral of orders θ for fuzzy-valued multivariable function $\omega (x,y)$ is defined by

$$\begin{array}{c}\hfill {}_F^{RL}{\mathcal{I}}_{0^{+}}^{\theta }\omega (x,y)=\frac{1}{\mathrm{\Gamma }\left({\theta }_1\right)\mathrm{\Gamma }\left({\theta }_2\right)}\underset{0}{\overset{x}{\int }}\underset{0}{\overset{y}{\int }}{(x-s)}^{{\theta }_1-1}{(y-t)}^{{\theta }_2-1}\omega (s,t)dtds.\end{array}$$

(8)

Definition 3. 

If for any $\epsilon >0$, there exist ${\delta }_1,{\delta }_2>0$ such that for all $(x,y,u,v)\in J\times C(J,E_c^1)\times C(J,E_c^2)$ and $(x,y,u)\in J\times C(J,E_c^1)$ with $|x-x_0|+$ $|y-y_0|+d_{\infty }(u,\psi )+d_{\infty }(v,\phi )<{\delta }_1$, $|x-x_0|+|y-y_0|+d_{\infty }(v,\phi )<{\delta }_2$, $d_{\infty }(f(x,y,u,v),f(x_0,y_0,\psi ,\phi ))<ϵ$ and $d_{\infty }(g(x,y,u),$$g(x_0,y_0,\psi ))<ϵ$, then the mappings $f:J\times C(J,E_c^1)\times C(J,E_c^2)\to E_c^1$ and $g:J\times C(J,E_c^1)\to E_c^2$ are called jointly continuous at point $(x_0,y_0,\psi ,\phi )\in J\times C(J,E_c^1)\times C(J,E_c^2)$ and $(x_0,y_0,\psi )\in J\times C(J,E_c^1)$, respectively.

For all $(x,y)\in J=[0,a]\times [0,b]$, let

$$\begin{array}{c}\hfill \psi (x,y)={\xi }_2\left(y\right)+[{\xi }_1\left(x\right)\ominus {\xi }_1\left(0\right)],\end{array}$$

(9)

$$\begin{array}{c}\hfill \phi (x,y)={\eta }_2\left(y\right)+[{\eta }_1\left(x\right)\ominus {\eta }_1\left(0\right)],\end{array}$$

(10)

here ${\xi }_1\in C([0,a],E_c^1)$, ${\eta }_1\in C([0,a],E_c^2)$, ${\xi }_2\in C([0,b],E_c^1)$ and ${\eta }_2\in C([0,b],E_c^2)$ are given functions such that ${\xi }_2\left(y\right)\ominus {\xi }_1\left(0\right)$ and ${\eta }_2\left(y\right)\ominus {\eta }_1\left(0\right)$ exist in several. Then we call

$$\begin{array}{ccc}\hfill {\widehat{C}}_{\phi }^{\widehat{g}}(J,E_c^1)=\{u\in C(J,E_c^1)|& & \phi (x,y)\ominus (-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\beta }\widehat{g}(x,y,u(x,y))\hfill \\ & & \mathrm{exists} \mathrm{for} \mathrm{all} (x,y)\in J\},\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill & {\widehat{C}}_{\psi }^{\widehat{f}}(J,E_c^2)=\{v\in C(J,E_c^2)|& \psi (x,y)\ominus (-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\alpha }\widehat{f}(x,y,u(x,y),v(x,y))\mathrm{exists},\hfill \\ & & \forall (x,y)\in J,u(x,y)\in {\widehat{C}}_{\phi }^{\widehat{g}}(J,E_c^1)\},\hfill \end{array}$$

(12)

where $\psi (·,·)$ and $\phi (·,·)$ are alone defined by (9) and (10).

For $k,j=0,1,2$, denote $C_{gH}^{k,j}(j,E_c^i)$ by the sets of all the functions $\varrho :j\subset {\mathbb{R}}^2\to E_c^i,\mathrm{i}=1,2$, which have the partial $gH$-type derivatives up to order k and j with respect to x and y in j, respectively.

Definition 4 

([2]). Let $\theta =({\theta }_1,{\theta }_2)\in (0,1]\times (0,1]$, and $\omega (x,y)\in C_{gH}^{2,2}(J,E_c^i),i=1,2$. Then the Caputo $gH$-type derivative of order θ with respect to x and y for the function ω is defined by

$$\begin{array}{c}\hfill {}_{gH}^C{\mathcal{D}}^{\theta }\omega (x,y)={}_F^{RL}{\mathcal{I}}_{0^{+}}^{1-\theta }\left(\frac{{\partial }^2\omega (x,y)}{\partial x\partial y}\right),\end{array}$$

which the expression on the right hand side is well-defined, where $1-\theta =(1-{\theta }_1,1-{\theta }_2)\in [0,1)\times [0,1)$.

Particularly, it is necessary for us to distinguish two cases homologizing to $(†)$ and $(‡)$ in (7), for any $\zeta \in E_c^1$, ζ is

(i) 

$(†)$-Caputo $gH$-type differentiable of order θ with respect to x and y if $\frac{{\partial }^2\zeta }{\partial x\partial y}(·,·)$ as a $gH$-type derivative in type 1 (i.e., $k=1$ in (2)) at $(x,y)$ and denotes ${}_{gH}^C{\mathcal{D}}_1^{\theta }\zeta (x,y)$.

(ii) 

$(‡)$-Caputo $gH$-type differentiable of order θ with respect to $x,y$ when $\frac{{\partial }^2\zeta }{\partial x\partial y}(·,·)$ is a $gH$-type derivative in type 2 (i.e., $k=2$ in (2)) at $(x,y)$. One can denote it by ${}_{gH}^C{\mathcal{D}}_2^{\theta }\zeta (x,y)$.

Afterwards, we give some important concepts of relative compactness in the fuzzy number space $E_c^1$.

Definition 5 

([30]). A subset $S\subset E_c^1$, is equicontinuous at ${\varpi }_0$ if for all $\epsilon >0$, there exists $\delta >0$ such that $d_{\infty }(w,{\varpi }_0)<\delta$ implies $d_{\infty }(T\left(w\right),T\left({\varpi }_0\right))<\epsilon$ for all $w\in E_c^1$ and $T\in S$. We say that S is equicontinuous if S is equicontinuous at every ${\varpi }_0\in E_c^1$.

Definition 6 

([30]). For all $\varpi \in S$, S is a subset of $E_c^1$, if there exists a compact set $K\subseteq \mathbb{R}$ such that ${\left[\varpi \right]}^0\subseteq K$, then S is said to be compact-supported.

Definition 7 

([30]). A subset $S\subseteq E_c^1$ is called level-equicontinuous at ${\tau }_0\in [0,1]$, if for all $\epsilon >0$, there exists $\delta >0$ such that $|\tau -{\tau }_0|<\delta$ means $d_H({\left[\varpi \right]}^{\tau },{\left[\varpi \right]}^{{\tau }_0})<\epsilon$ for each $\varpi \in S$. Further, S is said to be level-equicontinuous on $[0,1]$ if S is level-equicontinuous at every $\tau \in [0,1]$.

Definition 8. 

For any two fuzzy number spaces $U_c$ and $V_c$ with H-continuous, the continuous function $\mathrm{\Lambda }:U_c\to V_c$ defined on $U_c$ is said to be compact, if for any bounded subset $S_c\subseteq U_c$, $\mathrm{\Lambda }\left(S_c\right)$ is relatively compact in $V_c$, i.e., $\overline{\mathrm{\Lambda }\left(S_c\right)}$(the closure of $\mathrm{\Lambda }\left(S_c\right)$)is a compact subset in $V_c$.

Lemma 2 

([30], Theorem 4.5). S is a compact supported subset on $E_c^1$, if and only if S is a relatively compact subset of $(E_c^1,d_{\infty })$ and S is level-equicontinuous on $[0,1]$.

We note that this result presented in Lemma 2 states that when S is relatively compact in $(E_c^1,d_{\infty })$, S is compact-supported and level-equicontinuous on $[0,1]$. Conversely, if S is compact-supported in $E_c^1$ and level-equicontinuous on $[0,1]$, S is relatively compact in $(E_c^1,d_{\infty })$.

Lemma 3. 

Let $\psi (·,·)$ and $\phi (·,·)$ be the same as in (9) and (10), let the functions $\widehat{f}$ and $\widehat{g}$ be jointly continuous according to Definition 3, and let the functions $u\in C_{gH}^{2,2}(J,E_c^1)$ and $v\in C_{gH}^{2,2}(J,E_c^2)$ be fuzzy value. Then (2) is equivalent to the following nonlinear fractional Volterra integro-differential coupled system: For any $(x,y)\in J$,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}u(x,y)=\psi (x,y)+{}_F^{RL}{\mathcal{I}}_{0^{+}}^{\alpha }\widehat{f}(x,y,u(x,y),v(x,y))\hfill \\ v(x,y)=\phi (x,y)+{}_F^{RL}{\mathcal{I}}_{0^{+}}^{\beta }\widehat{g}(x,y,u(x,y))\hfill \end{array}\right.whenk=1\end{array}$$

(13)

or

$$\begin{array}{c}\hfill \left\{\begin{array}{c}u(x,y)=\psi (x,y)\ominus (-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\alpha }\widehat{f}(x,y,u(x,y),v(x,y))\hfill \\ v(x,y)=\phi (x,y)\ominus (-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\beta }\widehat{g}(x,y,u(x,y))\hfill \end{array}\right.whenk=2.\end{array}$$

(14)

Proof. 

The proving process of the equivalence is similar to the proof of ([2], Lemma 3), and so it is omitted. □

3. Main Results

In this section, employing fire-new proof method, which is different from those already published work, that is, using Schauder fixed point in Banach semilinear spaces, without Lipschitz conditions for the functions $\widehat{f}$ and $\widehat{g}$, we present existence of $(†)$-weak solutions and $(‡)$-weak solutions for the more general coupled system (2).

Lemma 4. 

Suppose that there exists a positive real number κ such that (i) $\widehat{f}:J\times B(\widehat{0},\kappa )\times B(\widehat{0},\kappa )\to E_c^1$ and $\widehat{g}:J\times B(\widehat{0},\kappa )\to E_c^2$ are compact operators; (ii) $\psi ,\phi \in C(J,B(\widehat{0},\frac{\kappa }{2}))$. Then there exist $\widehat{a}\in [0,a]$ and $\widehat{b}\in [0,b]$ such that an operator ${\tilde{H}}_1:\overline{\mathrm{\Omega }}\to \overline{\mathrm{\Omega }}$ defined as

$$\begin{array}{c}\hfill {\tilde{H}}_1(u,v)=\left(\begin{array}{c}{\tilde{T}}_1(u,v)\\ {\tilde{G}}_1(u,v)\end{array}\right)\end{array}$$

(15)

for all $(u,v)\in \overline{\mathrm{\Omega }}:=\left\{(\omega ,\varpi )\in C(\widehat{J},E_c^1)\times C(\widehat{J},E_c^2)|max\left\{\rho (\omega ,\widehat{0}),\rho (\varpi ,\widehat{0})\right\}\le \kappa \right\}$ is continuous, where $\widehat{J}:=[0,\widehat{a}]\times [0,\widehat{b}]$, ${\tilde{T}}_1:\overline{\mathrm{\Omega }}\to C(\widehat{J},E_c^1)$, ${\tilde{G}}_1:\overline{\mathrm{\Omega }}\to C(\widehat{J},E_c^2)$ are respectively decided by

$$\begin{array}{c}\hfill \begin{array}{cc}& {\tilde{T}}_1(u,v):=\psi (x,y)+{}_F^{RL}{\mathcal{I}}_{0^{+}}^{\alpha }\widehat{f}(x,y,u(x,y),v(x,y)),\hfill \\ & {\tilde{G}}_1(u,v):=\phi (x,y)+{}_F^{RL}{\mathcal{I}}_{0^{+}}^{\beta }\widehat{g}(x,y,u(x,y)).\hfill \end{array}\end{array}$$

(16)

Proof. 

For each $\left(\begin{array}{c}{u}_1(x,y)\\ v_1(x,y)\end{array}\right)$, $\left(\begin{array}{c}{u}_2(x,y)\\ v_2(x,y)\end{array}\right)\in C(J,E_c^1)\times C(J,E_c^2)$,

$$\begin{array}{ccc}\hfill & & \rho \left({\tilde{H}}_1(u_1,v_1),{\tilde{H}}_1(u_2,v_2)\right)\hfill \\ & & =max\left\{\rho \left({\tilde{T}}_1(u_1,v_1),{\tilde{T}}_1(u_2,v_2)\right),\rho \left({\tilde{G}}_1(u_1,v_1),{\tilde{G}}_1(u_2,v_2)\right)\right\}\hfill \\ & & \begin{array}{cc}\hfill =max& \left\{\underset{(x,y)\in J}{sup}{d}_{\infty }\left({\tilde{T}}_1(u_1(x,y),v_1(x,y)),{\tilde{T}}_1(u_2(x,y),v_2(x,y))\right),\right.\hfill \\ & \left.\underset{(x,y)\in J}{sup}{d}_{\infty }\left({\tilde{G}}_1(u_1(x,y),v_1(x,y)),{\tilde{G}}_1(u_2(x,y),v_2(x,y))\right)\right\}.\hfill \end{array}\hfill \end{array}$$

(17)

Since $\widehat{f}$ and $\widehat{g}$ are compact operators, $\widehat{f}$ and $\widehat{g}$ are bounded by Definition 8. Setting

$$\begin{array}{ccc}\hfill M_1& & =\underset{((x,y),\omega ,\varpi )\in J\times B(\widehat{0},\kappa )\times B(\widehat{0},\kappa )}{sup}\rho \left(\widehat{f}(x,y,\omega ,\varpi ),\widehat{0}\right),\hfill \\ \hfill M_2& & =\underset{((x,y),\omega )\in J\times B(\widehat{0},\kappa )}{sup}\rho \left(\widehat{g}(x,y,\omega ),\widehat{0}\right),\hfill \end{array}$$

then for all $\alpha =({\alpha }_1,{\alpha }_2)$, $\beta =({\beta }_1,{\beta }_2)\in (0,1]\times (0,1]$, there exist constants $a_1,a_2,b_1,b_2>0$ such that $\frac{M_1{a}_1^{{\alpha }_1}{b}_1^{{\alpha }_2}}{\mathrm{\Gamma }({\alpha }_1+1)\mathrm{\Gamma }({\alpha }_2+1)}\le \frac{\kappa }{2}$ and $\frac{M_2{a}_2^{{\beta }_1}{b}_2^{{\beta }_2}}{\mathrm{\Gamma }({\beta }_1+1)\mathrm{\Gamma }({\beta }_2+1)}\le \frac{\kappa }{2}$ because $a^{\iota }{b}^{\upsilon }$ is a polynomial with positive powers for any $a,b\in \mathbb{R}$ and all $\iota ,\upsilon \in (0,1]$. Let $\widehat{a}=min\left\{a,a_1,a_2\right\}$, and $\widehat{b}=min\left\{b,b_1,b_2\right\}$, and denote $[0,\widehat{a}]\times [0,\widehat{b}]:=\widehat{J}$. Thus, one can get $\widehat{J}\subset J$ and

$$\begin{array}{c}\hfill \frac{M_1{\widehat{a}}^{{\alpha }_1}{\widehat{b}}^{{\alpha }_2}}{\mathrm{\Gamma }({\alpha }_1+1)\mathrm{\Gamma }({\alpha }_2+1)}\le \frac{\kappa }{2},\frac{M_2{\widehat{a}}^{{\beta }_1}{\widehat{b}}^{{\beta }_2}}{\mathrm{\Gamma }({\beta }_1+1)\mathrm{\Gamma }({\beta }_2+1)}\le \frac{\kappa }{2}.\end{array}$$

(18)

First of all, we show that ${\tilde{H}}_1(u,v)$ is a mapping from the set $\overline{\mathrm{\Omega }}$ to itself, i.e., ${\tilde{H}}_1\left(\overline{\mathrm{\Omega }}\right)\subset \overline{\mathrm{\Omega }}$. In fact, it follows from (17) that for all $(u,v)\in \overline{\mathrm{\Omega }}$,

$$\begin{array}{c}\hfill d_{\infty }\left({\tilde{H}}_1(u,v),\widehat{0}\right)=max\left\{d_{\infty }\left({\tilde{T}}_1(u,v),\widehat{0}\right),\left({\tilde{G}}_1(u,v),\widehat{0}\right)\right\}.\end{array}$$

(19)

By Lemma 1 (i), we have

$$\begin{array}{ccc}\hfill & & d_{\infty }\left({\tilde{T}}_1(u(x,y),v(x,y)),\widehat{0}\right)\hfill \\ & & \begin{array}{cc}\hfill \le & d_{\infty }\left(\psi (x,y),\widehat{0}\right)\hfill \\ & +\frac{1}{\mathrm{\Gamma }\left({\alpha }_1\right)\mathrm{\Gamma }\left({\alpha }_2\right)}\underset{0}{\overset{x}{\int }}\underset{0}{\overset{y}{\int }}{(x-s)}^{{\alpha }_1-1}{(y-t)}^{{\alpha }_2-1}·d_{\infty }(\widehat{f}(s,t,u(s,t),v(s,t)),\widehat{0})dtds\hfill \end{array}\hfill \\ & & \le \rho (\psi ,\widehat{0})+\frac{M_1{\widehat{a}}^{{\alpha }_1}{\widehat{b}}^{{\alpha }_2}}{\mathrm{\Gamma }({\alpha }_1+1)\mathrm{\Gamma }({\alpha }_2+1)}.\hfill \end{array}$$

(20)

Since $\psi \in C(J\times B(\widehat{0},\frac{\kappa }{2}))$, one knows that $\rho (\psi ,\widehat{0})\le \frac{\kappa }{2}$, which implies with substituting (18) into (20) that

$$\begin{array}{c}\hfill d_{\infty }\left({\tilde{T}}_1(u,v),\widehat{0}\right)\le \frac{\kappa }{2}+\frac{\kappa }{2}=\kappa .\end{array}$$

(21)

By the same token, it is easy to see that

$$\begin{array}{c}\hfill d_{\infty }\left({\tilde{G}}_1(u,v),\widehat{0}\right)\le \kappa .\end{array}$$

(22)

Combining (21), (22) with (19), we get $\rho \left({\tilde{H}}_1\left(u,v\right),\widehat{0}\right)\le \kappa$ and so ${\tilde{H}}_1(u,v)\in \overline{\mathrm{\Omega }}$.

The next proof is that the mapping ${\tilde{H}}_1$ is continuous. It can be known from Lemma 1 (i) that

$$\begin{array}{ccc}\hfill & & d_{\infty }\left({\tilde{T}}_1\left(u_n,v_n\right),{\tilde{T}}_1\left(u,v\right)\right)\hfill \\ & & \begin{array}{cc}\hfill \le 0+\frac{1}{\mathrm{\Gamma }\left({\alpha }_1\right)\mathrm{\Gamma }\left({\alpha }_2\right)}& \underset{0}{\overset{x}{\int }}\underset{0}{\overset{y}{\int }}{(x-s)}^{{\alpha }_1-1}{(y-t)}^{{\alpha }_2-1}\hfill \\ & \times d_{\infty }(\widehat{f}(s,t,u_n(s,t),v_n(s,t)),\widehat{f}(s,t,u(s,t),v(s,t)))dtds\hfill \end{array}\hfill \\ & & \begin{array}{c}\hfill \le \frac{{\widehat{a}}^{{\alpha }_1}{\widehat{b}}^{{\alpha }_2}}{\mathrm{\Gamma }({\alpha }_1+1)\mathrm{\Gamma }({\alpha }_2+1)}\times \underset{(s,t)\in \widehat{J}}{sup}{d}_{\infty }(\widehat{f}(s,t,u_n(s,t),v_n(s,t)),\widehat{f}(s,t,u(s,t),v(s,t))).\end{array}\hfill \end{array}$$

(23)

Because $\widehat{f}$ is a compact operator, $\widehat{f}$ is continuous. Hence, ${\tilde{T}}_1$ is continuous. Similarly,

$$\begin{array}{ccc}\hfill & & d_{\infty }\left({\tilde{G}}_1\left(u_n,v_n\right),{\tilde{G}}_1\left(u,v\right)\right)\hfill \\ & & \le \frac{{\widehat{a}}^{{\beta }_1}{\widehat{b}}^{{\beta }_2}}{\mathrm{\Gamma }({\beta }_1+1)\mathrm{\Gamma }({\beta }_2+1)}\times \underset{(s,t)\in \widehat{J}}{sup}{d}_{\infty }(\widehat{g}(s,t,u_n(s,t)),\widehat{g}(s,t,u(s,t))),\hfill \end{array}$$

(24)

which intends that the operator ${\tilde{G}}_1$ is also continuous. Making $(u_n,v_n)$ tends to $(u,v)$ in $\overline{\mathrm{\Omega }}$, then from (23), (24) and (17), it follows that $d_{\infty }\left({\tilde{H}}_1\left(u_n,v_n\right),{\tilde{H}}_1\left(u,v\right)\right)\to 0$. This completes the proof. □

Lemma 5. 

If all the assumptions in Lemma 4 are true, ψ and φ are compact-supported, then ${\tilde{H}}_1\left(\overline{\mathrm{\Omega }}\right)$ is relatively compact in $C(\widehat{J},E_c^1)\times C(\widehat{J},E_c^2)$.

Proof. 

The proof is divided into two steps as follows.

Step 1: To begin with, it is proved that ${\tilde{H}}_1\left(\overline{\mathrm{\Omega }}\right)$ is equicontinuous in $C(\widehat{J},E_c^1)\times C(\widehat{J},E_c^2)$. Considering $(x_1,y_1),(x_2,y_2)\in \widehat{J}$ make $x_1<x_2$, $y_1<y_2$ and $(u,v)\in \overline{\mathrm{\Omega }}$. To simplify the expression, let $s_1=x_1-s$, $s_2=x_2-s$, $t_1=y_1-t$ and $t_2=y_2-t$. Since

$$\begin{array}{ccc}& & \begin{array}{c}\hfill d_{\infty }\left(\underset{0}{\overset{x_1}{\int }}\underset{0}{\overset{y_1}{\int }}{s}_2^{{\alpha }_1-1}{t}_2^{{\alpha }_2-1}\widehat{f}(s,t,u(s,t),v(s,t))dtds,\underset{0}{\overset{x_1}{\int }}\underset{0}{\overset{y_1}{\int }}{s}_1^{{\alpha }_1-1}{t}_1^{{\alpha }_2-1}\widehat{f}(s,t,u(s,t),v(s,t))dtds\right)\end{array}\hfill \\ & & \begin{array}{cc}\hfill =d_{\infty }& \left(\underset{0}{\overset{x_1}{\int }}\underset{0}{\overset{y_1}{\int }}(s_2^{{\alpha }_1-1}{t}_2^{{\alpha }_2-1}-s_1^{{\alpha }_1-1}{t}_1^{{\alpha }_2-1})\widehat{f}(s,t,u(s,t),v(s,t))dtds,\right.\hfill \\ & \left.\underset{0}{\overset{x_1}{\int }}\underset{0}{\overset{y_1}{\int }}(s_2^{{\alpha }_1-1}{t}_2^{{\alpha }_2-1}-s_1^{{\alpha }_1-1}{t}_1^{{\alpha }_2-1})·\widehat{0}dtds\right)\hfill \end{array}\hfill \\ & & \le M_1·\underset{0}{\overset{x_1}{\int }}\underset{0}{\overset{y_1}{\int }}\left(s_2^{{\alpha }_1-1}{t}_2^{{\alpha }_2-1}-s_1^{{\alpha }_1-1}{t}_1^{{\alpha }_2-1}\right)dtds,\hfill \end{array}$$

$$\begin{array}{c}\hfill d_{\infty }\left(\underset{x_1}{\overset{x_2}{\int }}\underset{0}{\overset{y_1}{\int }}{s}_2^{{\alpha }_1-1}{t}_2^{{\alpha }_2-1}\widehat{f}(s,t,u(s,t),v(s,t))dtds,\widehat{0}\right)\le M_1·\underset{x_1}{\overset{x_2}{\int }}\underset{0}{\overset{y_1}{\int }}{s}_2^{{\alpha }_1-1}{t}_2^{{\alpha }_2-1}dtds,\end{array}$$

$$\begin{array}{c}\hfill d_{\infty }\left(\underset{0}{\overset{x_1}{\int }}\underset{y_1}{\overset{y_2}{\int }}{s}_2^{{\alpha }_1-1}{t}_2^{{\alpha }_2-1}\widehat{f}(s,t,u(s,t),v(s,t))dtds,\widehat{0}\right)\le M_1·\underset{0}{\overset{x_1}{\int }}\underset{y_1}{\overset{y_2}{\int }}{s}_2^{{\alpha }_1-1}{t}_2^{{\alpha }_2-1}dtds\end{array}$$

and

$$\begin{array}{c}\hfill d_{\infty }\left(\underset{x_1}{\overset{x_2}{\int }}\underset{y_1}{\overset{y_2}{\int }}{s}_2^{{\alpha }_1-1}{t}_2^{{\alpha }_2-1}\widehat{f}(s,t,u(s,t),v(s,t))dtds,\widehat{0}\right)\le M_1·\underset{x_1}{\overset{x_2}{\int }}\underset{y_1}{\overset{y_2}{\int }}{s}_2^{{\alpha }_1-1}{t}_2^{{\alpha }_2-1}dtds,\end{array}$$

one obtains

$$\begin{array}{ccc}& & \begin{array}{c}\hfill d_{\infty }\left(\underset{0}{\overset{x_2}{\int }}\underset{0}{\overset{y_2}{\int }}{s}_2^{{\alpha }_1-1}{t}_2^{{\alpha }_2-1}\widehat{f}(s,t,u(s,t),v(s,t))dtds,\underset{0}{\overset{x_1}{\int }}\underset{0}{\overset{y_1}{\int }}{s}_1^{{\alpha }_1-1}{t}_1^{{\alpha }_2-1}\widehat{f}(s,t,u(s,t),v(s,t))dtds\right)\end{array}\hfill \\ & & \begin{array}{cc}& \begin{array}{cc}\hfill \le d_{\infty }& \left(\underset{0}{\overset{x_1}{\int }}\underset{0}{\overset{y_1}{\int }}{s}_2^{{\alpha }_1-1}{t}_2^{{\alpha }_2-1}\widehat{f}(s,t,u(s,t),v(s,t))dtds,\right.\hfill \\ & \left.\underset{0}{\overset{x_1}{\int }}\underset{0}{\overset{y_1}{\int }}{s}_1^{{\alpha }_1-1}{t}_1^{{\alpha }_2-1}\widehat{f}(s,t,u(s,t),v(s,t))dtds\right)\hfill \end{array}\hfill \\ & +d_{\infty }\left(\underset{x_1}{\overset{x_2}{\int }}\underset{0}{\overset{y_1}{\int }}{s}_2^{{\alpha }_1-1}{t}_2^{{\alpha }_2-1}\widehat{f}(s,t,u(s,t),v(s,t))dtds,\widehat{0}\right)\hfill \\ & +d_{\infty }\left(\underset{0}{\overset{x_1}{\int }}\underset{y_1}{\overset{y_2}{\int }}{s}_2^{{\alpha }_1-1}{t}_2^{{\alpha }_2-1}\widehat{f}(s,t,u(s,t),v(s,t))dtds,\widehat{0}\right)\hfill \\ & +d_{\infty }\left(\underset{x_1}{\overset{x_2}{\int }}\underset{y_1}{\overset{y_2}{\int }}{s}_2^{{\alpha }_1-1}{t}_2^{{\alpha }_2-1}\widehat{f}(s,t,u(s,t),v(s,t))dtds,\widehat{0}\right)\hfill \end{array}\hfill \\ & & \le \frac{M_1}{{\alpha }_1{\alpha }_2}·\left(x_2^{{\alpha }_1}{y}_2^{{\alpha }_2}-x_1^{{\alpha }_1}{y}_1^{{\alpha }_2}\right),\hfill \end{array}$$

by virtue of Lemma 1 (i), which implies that

$$\begin{array}{ccc}& & d_{\infty }\left({\tilde{T}}_1(u(x_2,y_2),v(x_2,y_2)),{\tilde{T}}_1(u(x_1,y_1),v(x_1,y_1))\right)\hfill \\ & & \begin{array}{cc}\hfill \le & d_{\infty }\left(\psi (x_2,y_2),\psi (x_1,y_1)\right)\hfill \\ & \begin{array}{cc}\hfill +\frac{1}{\mathrm{\Gamma }\left({\alpha }_1\right)\mathrm{\Gamma }\left({\alpha }_2\right)}\times d_{\infty }& \left(\underset{0}{\overset{x_2}{\int }}\underset{0}{\overset{y_2}{\int }}{s}_2^{{\alpha }_1-1}{t}_2^{{\alpha }_2-1}\widehat{f}(s,t,u(s,t),v(s,t))dtds,\right.\hfill \\ & \left.\underset{0}{\overset{x_1}{\int }}\underset{0}{\overset{y_1}{\int }}{s}_1^{{\alpha }_1-1}{t}_1^{{\alpha }_2-1}\widehat{f}(s,t,u(s,t),v(s,t))dtds\right)\hfill \end{array}\hfill \end{array}\hfill \\ & & \le d_{\infty }\left(\psi (x_2,y_2),\psi (x_1,y_1)\right)+\frac{M_1\left(x_2^{{\alpha }_1}{y}_2^{{\alpha }_2}-x_1^{{\alpha }_1}{y}_1^{{\alpha }_2}\right)}{\mathrm{\Gamma }({\alpha }_1+1)\mathrm{\Gamma }({\alpha }_2+1)}.\hfill \end{array}$$

This deduces from the continucity of $\psi$ that

$$\begin{array}{c}\hfill d_{\infty }\left({\tilde{T}}_1(u(x_2,y_2),v(x_2,y_2)),{\tilde{T}}_1(u(x_1,y_1),v(x_1,y_1))\right)\to 0as\left(x_1,y_1\right)\to \left(x_2,y_2\right).\end{array}$$

(25)

In the same way, we acquire that when $(x_1,y_1)\to (x_2,y_2)$,

$$\begin{array}{ccc}\hfill & & d_{\infty }\left({\tilde{G}}_1(u(x_2,y_2),v(x_2,y_2)),{\tilde{G}}_1(u(x_1,y_1),v(x_1,y_1))\right)\hfill \\ & & \le d_{\infty }\left(\phi (x_2,y_2),\phi (x_1,y_2)\right)+\frac{M_2\left(x_2^{{\beta }_1}{y}_2^{{\beta }_2}-x_1^{{\beta }_1}{y}_1^{{\beta }_2}\right)}{\mathrm{\Gamma }({\beta }_1+1)\mathrm{\Gamma }({\beta }_2+1)}\to 0\hfill \end{array}$$

(26)

is known based on the continuity of $\phi$. Further, by (4), (17), (25) and (26), now one knows that $d_{\infty }\left({\tilde{H}}_1(u(x_2,y_2),v(x_2,y_2)),{\tilde{H}}_1(u(x_1,y_1),v(x_1,y_1))\right)\to 0$. This suggests that ${\tilde{H}}_1\left(\overline{\mathrm{\Omega }}\right)$ is equicontinuous on $C(\widehat{J},E_c^1)\times C(\widehat{J},E_c^2)$.

Step 2: The following proof is to show that ${\tilde{H}}_1\left(\overline{\mathrm{\Omega }}\right)$ is relatively compact on $C(\widehat{J},E_c^1)\times C(\widehat{J},E_c^2)$. According to Lemma 2, we only need to prove that the following two conditions are satisfied: (${\mathbf{C}}_{\mathbf{1}}$) ${\tilde{H}}_1\left(\overline{\mathrm{\Omega }}\right)$ is level-equicontinuous; (${\mathbf{C}}_2$) ${\tilde{H}}_1\left(\overline{\mathrm{\Omega }}\right)$ is a compact-supported subset of $E_c^1\times E_c^2$.

(i) Give evidence of the condition (${\mathbf{C}}_{\mathbf{1}}$). In fact, for every fixed pair of $(x,y)\in \widehat{J}$, ${\tilde{H}}_1\left(\overline{\mathrm{\Omega }}\right)\in C(\widehat{J},E_c^1)\times C(\widehat{J},E_c^2)$. If ${(\mu ,\nu )}^T\in {\tilde{H}}_1\left(\overline{\mathrm{\Omega }}\right)$, then there exists ${(u,v)}^T\in \overline{\mathrm{\Omega }}$ which makes for any $(x,y)\in \widehat{J}$,

$$\mu (x,y)=\psi (x,y)+{}_F^{RL}{\mathcal{I}}_{0^{+}}^{\alpha }\widehat{f}(x,y,u(x,y),v(x,y)),$$

$$\nu (x,y)=\phi (x,y)+{}_F^{RL}{\mathcal{I}}_{0^{+}}^{\beta }\widehat{g}(x,y,u(x,y)).$$

Since $\widehat{f}$ and $\widehat{g}$ are compact operators, $\widehat{f}(\widehat{J}\times \overline{\mathrm{\Omega }})$ is relatively compact on $E_c^1$ and so is $\widehat{g}(\widehat{J}\times {\overline{\mathrm{\Omega }}}_{*})$ in $E_c^2$, here ${\overline{\mathrm{\Omega }}}_{*}:=\{\vartheta \in C(\widehat{J},E_c^2):\rho (\vartheta ,\widehat{0})\le \kappa \}$, and one can see from Lemma 2 that $\widehat{f}(\widehat{J}\times \overline{\mathrm{\Omega }})$ and $\widehat{g}(\widehat{J}\times {\overline{\mathrm{\Omega }}}_{*})$ are level-equicontinuous. Thus, for any $\epsilon >0$, there exists $\delta >0$ such that for all $(x,y)\in \widehat{J}$ and each $(u,v)\in \overline{\mathrm{\Omega }}$,

$$\begin{array}{ccc}& & d_H\left({\left[\widehat{f}(x,y,u(x,y),v(x,y))\right]}^{\lambda },{\left[\widehat{f}(x,y,u(x,y),v(x,y))\right]}^{\tau }\right)<{\displaystyle \frac{\mathrm{\Gamma }({\alpha }_1+1)\mathrm{\Gamma }({\alpha }_2+1)}{a^{{\alpha }_1}{b}^{{\alpha }_2}}}·\frac{\epsilon }{2},\hfill \\ & & d_H\left({\left[\widehat{g}(x,y,u(x,y))\right]}^{\lambda },{\left[\widehat{g}(x,y,u(x,y))\right]}^{\tau }\right)<{\displaystyle \frac{\mathrm{\Gamma }({\beta }_1+1)\mathrm{\Gamma }({\beta }_2+1)}{a^{{\beta }_1}{b}^{{\beta }_2}}}·\frac{\epsilon }{2}\hfill \end{array}$$

and

$$\begin{array}{c}\hfill d_H\left({\left[\psi (x,y)\right]}^{\lambda },{\left[\psi (x,y)\right]}^{\tau }\right)\le \frac{\epsilon }{2},d_H\left({\left[\phi (x,y)\right]}^{\lambda },{\left[\phi (x,y)\right]}^{\tau }\right)\le \frac{\epsilon }{2}\end{array}$$

when $|\lambda -\tau |<\delta$. Since

$$\begin{array}{ccc}\hfill & & d_H\left({\left[\mu \right]}^{\lambda },{\left[\mu \right]}^{\tau }\right)\hfill \\ & & =d_H\left({\left[{\tilde{T}}_1(u,v)\right]}^{\lambda },{\left[{\tilde{T}}_1(u,v)\right]}^{\tau }\right)\hfill \\ & & \begin{array}{cc}\hfill \le & d_H\left({\left[\psi (x,y)\right]}^{\lambda },{\left[\psi (x,y)\right]}^{\tau }\right)\hfill \\ & \begin{array}{cc}\hfill +\frac{1}{\mathrm{\Gamma }\left({\alpha }_1\right)\mathrm{\Gamma }\left({\alpha }_2\right)}{d}_H& \left({\left[\underset{0}{\overset{x}{\int }}\underset{0}{\overset{y}{\int }}{(x-s)}^{{\alpha }_1-1}{(y-t)}^{{\alpha }_2-1}\widehat{f}(s,t,u(s,t),v(s,t))dtds\right]}^{\lambda },\right.\hfill \\ & \left.{\left[\underset{0}{\overset{x}{\int }}\underset{0}{\overset{y}{\int }}{(x-s)}^{{\alpha }_1-1}{(y-t)}^{{\alpha }_2-1}\widehat{f}(s,t,u(s,t),v(s,t))dtds\right]}^{\tau }\right)\hfill \end{array}\hfill \end{array}\hfill \\ & & \le \frac{\epsilon }{2}+\frac{\epsilon }{2}=\epsilon \hfill \end{array}$$

(27)

and

$$\begin{array}{c}\hfill d_H\left({\left[\nu \right]}^{\lambda },{\left[\nu \right]}^{\tau }\right)=d_H\left({\left[{\tilde{G}}_1(u,v)\right]}^{\lambda },{\left[{\tilde{G}}_1(u,v)\right]}^{\tau }\right)<\epsilon \end{array}$$

(28)

are valid, it can be known from (27) and (28) that for each small $\epsilon >0$, there exists $\delta >0$ such that

$$\begin{array}{ccc}& & d_H\left({\left[{\tilde{H}}_1(u,v)\right]}^{\lambda },{\left[{\tilde{H}}_1(u,v)\right]}^{\tau }\right)\hfill \\ & & \begin{array}{c}\hfill :=max\left\{d_H\left({\left[{\tilde{T}}_1(u,v)\right]}^{\lambda },{\left[{\tilde{T}}_1(u,v)\right]}^{\tau }\right),\right.\left.d_H\left({\left[{\tilde{G}}_1(u,v)\right]}^{\lambda },{\left[{\tilde{G}}_1(u,v)\right]}^{\tau }\right)\right\}<\epsilon \end{array}\hfill \end{array}$$

when $|\lambda -\tau |<\delta$, exists, that is, ${\tilde{H}}_1\left(\overline{\mathrm{\Omega }}\right)$ is level-equicontinuous over $E_c^1\times E_c^2$.

(ii) Demonstrate the condition (${\mathbf{C}}_2$). Since $\widehat{f}(\widehat{J}\times \overline{\mathrm{\Omega }})$, $\widehat{g}(\widehat{J}\times {\overline{\mathrm{\Omega }}}_{*})$ are relatively compact, it can be seen from Lemma 2 that $\widehat{f}(\widehat{J}\times \overline{\mathrm{\Omega }})$ and $\widehat{g}(\widehat{J}\times {\overline{\mathrm{\Omega }}}_{*})$ are compact supports and level-equicontinuous on $[0,1]$. According to Definition 6, there exists $K_{11}$ and $K_{21}$, the compact subset of $\mathbb{R}$ such that ${\left[\widehat{f}(x,y,u(x,y),v(x,y))\right]}^0\subseteq K_{11}$ is true for any $(x,y,\varphi ,\phi )\in \widehat{J}\times \overline{\mathrm{\Omega }}$, ${\left[\widehat{g}(x,y,u(x,y))\right]}^0\subseteq K_{21}$ is true for all $(x,y,\varphi )\in \widehat{J}\times {\overline{\mathrm{\Omega }}}_{*}$.

Given that $\psi ,\phi$ have compact supports, then from Definition 6, ${\left[\psi (x,y)\right]}^0\subseteq K_{12}$, ${\left[\phi (x,y)\right]}^0\subseteq K_{22}$ are valid for any $(x,y)\in \widehat{J}$ by the existence of $K_{12}$, $K_{22}$, the compact subsets of $\mathbb{R}$. Thus, one has

$$\begin{array}{ccc}& & {\left[{\tilde{T}}_1(u,v)\right]}^0\hfill \\ & & \begin{array}{c}\hfill ={\left[\psi (x,y)\right]}^0+\frac{1}{\mathrm{\Gamma }\left({\alpha }_1\right)\mathrm{\Gamma }\left({\alpha }_2\right)}\underset{0}{\overset{x}{\int }}\underset{0}{\overset{y}{\int }}{(x-s)}^{{\alpha }_1-1}{(y-t)}^{{\alpha }_2-1}{\left[\widehat{f}(s,t,u(s,t),v(s,t))\right]}^{0}dtds\end{array}\hfill \\ & & \subseteq K_{12}+\frac{K_{11}{x}^{{\alpha }_1}{y}^{{\alpha }_2}}{\mathrm{\Gamma }({\alpha }_1+1)\mathrm{\Gamma }({\alpha }_2+1)}.\hfill \end{array}$$

And because $x^{{\alpha }_1}{y}^{{\alpha }_2}$ is bounded on $\widehat{J}$, there exists a compact subset $K_1\subseteq \mathbb{R}$ such that ${\left[{\tilde{T}}_1(u,v)\right]}^0$$\subseteq K_1$, which indicates that ${\tilde{T}}_1\left(\overline{\mathrm{\Omega }}\right)$ is a compact-supported.

Similarly, ${\left[{\tilde{G}}_1(u,v)\right]}^0\subseteq K_{22}+\frac{K_{21}{x}^{{\beta }_1}{y}^{{\beta }_2}}{\mathrm{\Gamma }({\beta }_1+1)\mathrm{\Gamma }({\beta }_2+1)}$ hold, then there exists $K_2\subseteq \mathbb{R}$ such that ${\left[{\tilde{G}}_1(u,v)\right]}^0\subseteq K_2$. This shows that ${\tilde{G}}_1\left(\overline{\mathrm{\Omega }}\right)$ is compact-supported.

From (15), it follows that

$${\left[{\tilde{H}}_1(u,v)\right]}^0\subseteq \left\{K_i\subseteq \mathbb{R}|K_i\subseteq K_j,i,j=1,2\right\},$$

and ${\tilde{H}}_1(u,v)$ is a compact-supported set.

To sum up, ${\tilde{H}}_1\left(\overline{\mathrm{\Omega }}\right)$ is relatively compact on $E_c^1\times E_c^2$. Therefore, ${\tilde{H}}_1\left(\overline{\mathrm{\Omega }}\right)$ is relatively compact on $C(\widehat{J},E_c^1)\times C(\widehat{J},E_c^2)$ according to the Ascoli-Arzelá theorem. □

Lemma 6 

([35], Theorem 3.4) Schauder fixed point theorem for semilinear spaces). Let S be a nonempty, bounded, closed and convex subset of a Banach semilinear space $C(J,E_c^1)$ with cancellation property, and h is a compact operator from S to itself. Then h has at least one fixed point on S.

Remark 3. 

From Lemmas 4 and 5, we can obtain that ${\tilde{H}}_1\left(\overline{\mathrm{\Omega }}\right)$ is a relatively compact operator. Thus, applying Lemma 6 on Banach semilinear space but not based on Banach fixed point theorem in the product spaces of all fuzzy-valued continuous functions, which is the key to obtain the existence of $(†)$-weak solution on $C(\widehat{J},E_c^1)\times C(\widehat{J},E_c^2)$.

Theorem 1. 

Assume that there exists $\kappa >0$ such that (i) $\widehat{f}:J\times B(\widehat{0},\kappa )\times B(\widehat{0},\kappa )\to E_c^1$ and $\widehat{g}:J\times B(\widehat{0},\kappa )\to E_c^2$ are compact operators; (ii) $\psi ,\phi \in C(J\times B(\widehat{0},\frac{\kappa }{2}))$ and ψ, φ are compact-supported. Then there exist $\widehat{a}\in (0,a]$ and $\widehat{b}\in (0,b]$ such that (2) has at least a $(†)$-weak solution on $C(\widehat{J},E_c^1)\times C(\widehat{J},E_c^2)$, where $\widehat{J}=[0,\widehat{a}]\times [0,\widehat{b}]\subset J$.

Proof. 

Define an operator ${\tilde{H}}_1:\overline{\mathrm{\Omega }}\to C(\widehat{J},E_c^1)\times C(\widehat{J},E_c^2)$ by the same as (15) and two operators ${\tilde{T}}_1:\overline{\mathrm{\Omega }}\to C(\widehat{J},E_c^1)$ and ${\tilde{G}}_1:\overline{\mathrm{\Omega }}\to C(\widehat{J},E_c^2)$ as in (16). One can easily see that the operators ${\tilde{T}}_1$ and ${\tilde{G}}_1$ are well-defined and so is ${\tilde{H}}_1$. By Lemma 4, we know that ${\tilde{H}}_1:\overline{\mathrm{\Omega }}\to \overline{\mathrm{\Omega }}$ is a continuous operator. By means of the Ascoli-Arzelá theorem, it follows form Lemma 5 that ${\tilde{H}}_1\left(\overline{\mathrm{\Omega }}\right)$ is relatively compact in $C(\widehat{J},E_c^1)\times C(\widehat{J},E_c^2)$. Thus, ${\tilde{H}}_1$ is a compact operator by Definition 8. Hence, it is known from Lemma 6 that ${\tilde{H}}_1$ has at least one fixed point in $\overline{\mathrm{\Omega }}$, which is a $(†)$-weak solution of (2). □

Remark 4. 

The proposed proof in Theorem 1 is completely different from Theorem 1 in [2]. Indeed, there is no Lipschitz conditions to the functions $\widehat{f}$ and $\widehat{g}$ in Theorem 1, and we apply Lemmas 4–6 and Ascoli-Arzelá Theorem in Banach semilinear space to obtain the existence of $(†)$-weak solutions to (2). But the existence result of $(†)$-weak solutions in ([2], Theorem 1) has to be premised on the Lipschitz conditions.

Next, we shall present existence of the $(‡)$-weak solution for (2) under the following hypotheses:

• $(h_1) {\widehat{C}}_{\psi }^{\widehat{f}}(J,E_c^2)\ne \varnothing$, ${\widehat{C}}_{\phi }^{\widehat{g}}(J,E_c^1)\ne \varnothing$.
• $(h_2) \mathrm{If}u(·,·)\in {\widehat{C}}_{\phi }^{\widehat{g}}(J,E_c^1)$, then for any $(x,y)\in J$ and each $v(x,y)\in {\widehat{C}}_{\psi }^{\widehat{f}}(J,E_c^2)$, one has

  $$U(x,y)=\psi (x,y)\ominus (-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\alpha }\widehat{f}(x,y,u(x,y),v(x,y))\in {\widehat{C}}_{\phi }^{\widehat{g}}(J,E_c^1)$$

  and

  $$V(x,y)=\phi (x,y)\ominus (-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\beta }\widehat{g}(x,y,u(x,y))\in {\widehat{C}}_{\psi }^{\widehat{f}}(J,E_c^2),\forall (x,y)\in J,$$

  when $v(·,·)\in {\widehat{C}}_{\psi }^{\widehat{f}}(J,E_c^2)$, where ${\widehat{C}}_{\phi }^{\widehat{g}}(J,E_c^1)$ and ${\widehat{C}}_{\psi }^{\widehat{f}}(J,E_c^2)$ are confirmed by (11) and (12) in several.

Remark 5. 

By [2], it is easy to see that it is not easy to solve the existence of (‡)-weak solution for (2) under H-difference and the case corresponding to $(‡)$ of (7). However, the hypotheses($h_1$)and($h_2$)solve this problem well.

Lemma 7. 

Suppose that ($h_1$) and ($h_2$) are satisfied, and there is a positive real number κ such that (i) $\widehat{f}:J\times B(\widehat{0},\kappa )\times B(\widehat{0},\kappa )\to E_c^1$ and $\widehat{g}:J\times B(\widehat{0},\kappa )\to E_c^2$ are compact operators; (ii) $\psi ,\phi \in C(J\times B(\widehat{0},\frac{\kappa }{2}))$. Then there exist $\widehat{a}\in [0,a]$ and $\widehat{b}\in [0,b]$ such that an operator ${\tilde{H}}_2$ decided by ${\tilde{H}}_2(u,v)=\left(\begin{array}{c}{\tilde{T}}_2(u,v)\\ {\tilde{G}}_2(u,v)\end{array}\right),$ is a continuous operator from $\tilde{\mathrm{\Omega }}$ to itself, where $\tilde{\mathrm{\Omega }}:=\left\{(u,v)\in {\widehat{C}}_{\phi }^{\widehat{g}}(\widehat{J},E_c^1)\times \right.$ $\left.{\widehat{C}}_{\psi }^{\widehat{f}}(\widehat{J},E_c^2):max\left\{\rho (u,\widehat{0}),\rho (v,\widehat{0})\right\}\le \kappa \right\}$, ${\tilde{T}}_2:\tilde{\mathrm{\Omega }}\to {\widehat{C}}_{\phi }^{\widehat{g}}(\widehat{J},E_c^1)$, ${\tilde{G}}_2:\tilde{\mathrm{\Omega }}\to {\widehat{C}}_{\psi }^{\widehat{f}}(\widehat{J},E_c^2)$ are separately defined by

$${\tilde{T}}_2(u,v):=\psi (x,y)\ominus (-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\alpha }\widehat{f}(x,y,u(x,y),v(x,y)),$$

$${\tilde{G}}_2(u,v):=\phi (x,y)\ominus (-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\beta }\widehat{g}(x,y,u(x,y)),$$

for each $(x,y)\in \widehat{J}=[0,\widehat{a}]\times [0,\widehat{b}]\subset J$.

Proof. 

Since the hypotheses ($h_1$) and ($h_2$) are true for any $(x,y)\in J$ and all $\left(\begin{array}{c}{u}_1(x,y)\\ v_1(x,y)\end{array}\right)$, $\left(\begin{array}{c}{u}_2(x,y)\\ v_2(x,y)\end{array}\right)\in {\widehat{C}}_{\phi }^{\widehat{g}}(J,E_c^1)\times {\widehat{C}}_{\psi }^{\widehat{f}}(J,E_c^2)$, one has

$$\begin{array}{ccc}& & \rho \left({\tilde{H}}_2(u_1,v_1),{\tilde{H}}_2(u_2,v_2)\right)\hfill \\ & & \begin{array}{cc}\hfill =max& \left\{\underset{(x,y)\in J}{sup}{d}_{\infty }\left({\tilde{T}}_2(u_1(x,y),v_1(x,y)),{\tilde{T}}_2(u_2(x,y),v_2(x,y))\right),\right.\hfill \\ & \left.\underset{(x,y)\in J}{sup}{d}_{\infty }\left({\tilde{G}}_2(u_1(x,y),v_1(x,y)),{\tilde{G}}_2(u_2(x,y),v_2(x,y))\right)\right\}.\hfill \end{array}\hfill \end{array}$$

Thus, one can clearly know that the proof is similar to Lemma 4 and so it is omitted. □

By the similar proof to Lemma 5, we have the following results.

Lemma 8. 

Under the premise that all the assumptions in Lemma 7 are true, ψ and φ are compact-supported, then ${\tilde{H}}_2\left(\tilde{\mathrm{\Omega }}\right)$ is relatively compact on ${\widehat{C}}_{\phi }^{\widehat{g}}(\widehat{J},E_c^1)\times {\widehat{C}}_{\psi }^{\widehat{f}}(\widehat{J},E_c^2)$.

Theorem 2. 

Let all the conditions in Theorem 1 satisfy. In addition, suppose that ($h_1$) and ($h_2$) meet. Then there exist $\widehat{a}\in (0,a]$ and $\widehat{b}\in (0,b]$ such that (2) has at least a $(‡)$-weak solution on ${\widehat{C}}_{\phi }^{\widehat{g}}(\widehat{J},E_c^1)\times {\widehat{C}}_{\psi }^{\widehat{f}}(\widehat{J},E_c^2)$, where $\widehat{J}$ is the same as in Lemma 7.

Proof. 

The proving process of this theorem is exactly similar to that of Theorem 1, thus, it is omitted. □

Remark 6. 

Inspired by the work in the second aspect of [3], in the absence of the Lipschitz conditions, Lemmas 6–8 and Ascoli-Arzelá Theorem in Banach semilinear space are applied. Therefore, the proof for the existence of $(‡)$-weak solutions in this paper is totally different from that of ([2], Theorem 2).

4. A Numerical Example and Applications

This section presents a numerical example to verify that Theorems 1 and 2 hold. Then some applications of Theorems 1 and 2 to projection neural network systems are given.

Example 1. 

We now consider the following coupled system of fuzzy fractional PDEs: For each $(x,y)\in \widehat{J}=[0,1]\times [0,1]$ and $k=1,2$,

$$\left\{\begin{array}{c}\begin{array}{c}\hfill {}_{gH}^C{\mathcal{D}}_k^{\frac{1}{2}}u(x,y)=-\frac{1}{{\left[\mathrm{\Gamma }\left(\frac{1}{2}\right)\right]}^2}{x}^{\frac{1}{2}}{y}^{\frac{1}{2}}v(x,y)+\frac{1}{{\left[\mathrm{\Gamma }\left(\frac{1}{2}\right)\right]}^2}xyu(x,y)+\frac{A}{{\left[\mathrm{\Gamma }\left(\frac{1}{2}\right)\right]}^2}{x}^{\frac{3}{2}}{y}^{\frac{3}{2}}+\frac{5A}{9{\left[\mathrm{\Gamma }\left(\frac{1}{2}\right)\right]}^2}{x}^2{y}^2,\end{array}\hfill \\ {}_{gH}^C{\mathcal{D}}_k^{\frac{1}{2}}v(x,y)=\frac{{\left[\mathrm{\Gamma }\left(\frac{1}{2}\right)\right]}^2}{4}u(x,y)+\frac{4A}{{\left[\mathrm{\Gamma }\left(\frac{1}{2}\right)\right]}^2}{x}^{\frac{1}{2}}{y}^{\frac{1}{2}},\hfill \\ u(x,0)=u(0,y)=u(0,0)=-A,\hfill \\ v(x,0)=v(0,y)=v(0,0)=4A,\hfill \end{array}\right.$$

(29)

where $u(x,y)$ and $v(x,y)$ are fuzzy functions and A is a fuzzy number.

It is easy to check that the functions $\widehat{f}(x,y,u(x,y),v(x,y)):=-\frac{1}{{\left[\mathrm{\Gamma }\left(\frac{1}{2}\right)\right]}^2}{x}^{\frac{1}{2}}{y}^{\frac{1}{2}}v(x,y)+\frac{1}{{\left[\mathrm{\Gamma }\left(\frac{1}{2}\right)\right]}^2}xyu(x,y)+\frac{A}{{\left[\mathrm{\Gamma }\left(\frac{1}{2}\right)\right]}^2}{x}^{\frac{3}{2}}{y}^{\frac{3}{2}}+\frac{5A}{9{\left[\mathrm{\Gamma }\left(\frac{1}{2}\right)\right]}^2}{x}^2{y}^2$, $\widehat{g}(x,y,u(x,y)):=\frac{{\left[\mathrm{\Gamma }\left(\frac{1}{2}\right)\right]}^2}{4}u(x,y)+\frac{4A}{{\left[\mathrm{\Gamma }\left(\frac{1}{2}\right)\right]}^2}{x}^{\frac{1}{2}}{y}^{\frac{1}{2}}$ in (29) are compact operators.

From (9) and (10), $\psi (x,y)=-A$ and $\phi (x,y)=4A$ can be lightly obtained.

Letting triangle fuzzy function $A=(1,2,3)$, then from [21], one knows that

$${\left[A\right]}^{\lambda }=[A_{\lambda }^{-},A_{\lambda }^{+}]=[\lambda +1,3-\lambda ],{\left[A\right]}^{\tau }=[A_{\tau }^{-},A_{\tau }^{+}]=[\tau +1,3-\tau ],$$

and

$${\left[\psi (x,y)\right]}^{\lambda }={[-A]}^{\lambda }=-[\lambda +1,3-\lambda ]=[-\lambda -1,-3+\lambda ],$$

$${\left[\phi (x,y)\right]}^{\tau }={\left[4A\right]}^{\tau }=4[\tau +1,3-\tau ]$$

hold. According to Definition 6,

$${\left[\psi (x,y)\right]}^0=(-1)[1,3]\subseteq [-3,-1],{\left[\phi (x,y)\right]}^0=4[1,3]\subseteq [4,12].$$

Let $K_1=[-3,-1]$, $K_2=[4,12]$. Then $K_1,K_2$ are obviously compact sets and so we know that $\psi (x,y)$ and $\phi (x,y)$ have compact-supported sets. Taking ${\kappa }_1=2\rho (A,\widehat{0})$, ${\kappa }_2=8\rho (A,\widehat{0})$ and $\kappa =max\{{\kappa }_1,{\kappa }_2\}=8\rho (A,\widehat{0})$, then $\rho (\psi (x,y),\widehat{0})=\rho (-A,\widehat{0})=\rho (A,\widehat{0})\le \frac{{\kappa }_1}{2}$, $\rho (\phi (x,y),\widehat{0})=\rho (4A,\widehat{0})=4\rho (A,\widehat{0})\le \frac{{\kappa }_2}{2}$ are obtained and $\psi (x,y)$, $\phi (x,y)\in C\left(J,B(\widehat{0},\frac{\kappa }{2})\right)$ are established.

(Case I) When $k=1$, with the aid of Buckley-Feuring strategy and fuzzifying the deterministic solution, it follows from (13), Definition 4.1 of [6] and [3] that the following BF solution of (29) is obtained:

$$\begin{array}{c}\hfill \left(u(x,y),v(x,y)\right)=\left(-A-Axy,4A-A{x}^{\frac{1}{2}}{y}^{\frac{1}{2}}-\frac{4A}{9}{x}^{\frac{3}{2}}{y}^{\frac{3}{2}}+Axy\right),\forall (x,y)\in \widehat{J}.\end{array}$$

Combining with the conclusions that $\psi (x,y)$ and $\phi (x,y)$ have compact-supported sets and $\psi (x,y),\phi (x,y)\in C\left(J,B(\widehat{0},\frac{\kappa }{2})\right)$, it can be concluded from Theorem 1 that (29) has a $(†)$-weak solution in $C(\widehat{J},E_c^1)\times C(\widehat{J},E_c^2)$ as follows

$$\left\{\begin{array}{cc}\hfill u(x,y)& =-A-Axy,\hfill \\ \hfill v(x,y)& =4A-A{x}^{\frac{1}{2}}{y}^{\frac{1}{2}}-\frac{4A}{9}{x}^{\frac{3}{2}}{y}^{\frac{3}{2}}+Axy.\hfill \end{array}\right.$$

(Case II) When $k=2$, according to Lemma 1 (iii)–(v) and (14), using the same strategy as (Case I), we get the BF solution of (29) as

$$\left(u(x,y),v(x,y)\right)=\left(-A\ominus Axy,4A\ominus A{x}^{\frac{1}{2}}{y}^{\frac{1}{2}}-\frac{4A}{9}{x}^{\frac{3}{2}}{y}^{\frac{3}{2}}\ominus (-1)Axy\right).$$

The continuity of the extended principle shows that the level sets of fuzzy solutions of (29) are

$$\begin{array}{ccc}\hfill & {[\Delta (x,y,A)]}^{\lambda }& =\left[-\left(\lambda +1\right)-\left(\lambda +1\right)xy,-\left(3-\lambda \right)-\left(3-\lambda \right)xy\right]\hfill \end{array}$$

(30)

and

$$\begin{array}{ccc}\hfill & {\left[\Theta (x,y,A)\right]}^{\tau }& =\left[4\left(\tau +1\right)-(\tau +1)x^{\frac{1}{2}}{y}^{\frac{1}{2}}-\frac{4(\tau +1)}{9}{x}^{\frac{3}{2}}{y}^{\frac{3}{2}}+\left(\tau +1\right)xy\right.,\hfill \\ \hfill & & \left.4\left(3-\tau \right)-(3-\tau )x^{\frac{1}{2}}{y}^{\frac{1}{2}}-\frac{4(3-\tau )}{9}{x}^{\frac{3}{2}}{y}^{\frac{3}{2}}+\left(3-\tau \right)xy\right].\hfill \end{array}$$

(31)

The simulation of the level sets of $\lambda$ and $\tau$ for the fuzzy solutions are shown in Figure 1. The left and right pictures of Figure 1 represent the six level sets of fuzzy solutions $\Theta (x,y,A)$ and $\Delta (x,y,A)$ when six constant values of x are fixed, respectively. That is, each group of corresponding surfaces represent a $\lambda$ or $\tau$ level set, and the distance between each group of corresponding faces represent the fuzzy solution $\Theta (x,y,A)$ and $\Delta (x,y,A)$. By observing (30) and (31), it can be found that the changes of the level sets of $\Theta (x,y,A)$ and $\Delta (x,y,A)$ with x and $\lambda$ or $\tau$ when y is fixed to six constant values are exactly the same as in Figure 1. The curves of $\lambda Oy$ and $\tau Oy$ planes in the two pictures of Figure 1 represent contour lines of ${\left[\Theta (x,y,A)\right]}^{\tau }$ and ${[\Delta (x,y,A)]}^{\lambda }$, respectively.

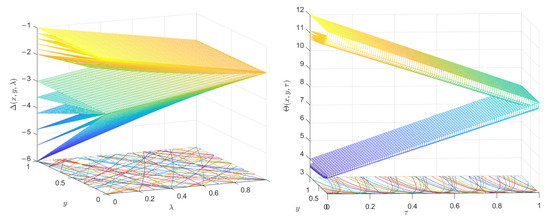
Figure 1. Numerical simulation for fuzzy solutions of (29).

Moreover, we need to make sure that ($h_1$) and ($h_2$) are true.

For simplicity, take $L=\frac{1}{\mathrm{\Gamma }\left(\frac{1}{2}\right)\mathrm{\Gamma }\left(\frac{1}{2}\right)}$. Since

$$\begin{array}{c}\hfill {\left[u\right]}^{\tau }={[-A\ominus Axy]}^{\tau }=[-(\tau +1)-(\tau +1)xy,-(3-\tau )-(3-\tau )xy],\end{array}$$

(32)

$$\begin{array}{ccc}\hfill {\left[v\right]}^{\lambda }& & ={\left[4A\ominus A{x}^{\frac{1}{2}}{y}^{\frac{1}{2}}-\frac{4A}{9}{x}^{\frac{3}{2}}{y}^{\frac{3}{2}}\ominus (-1)Axy\right]}^{\lambda }\hfill \\ & & =\left(4-x^{\frac{1}{2}}{y}^{\frac{1}{2}}-\frac{4}{9}{x}^{\frac{3}{2}}{y}^{\frac{3}{2}}+xy\right)[\lambda +1,3-\lambda ],\hfill \end{array}$$

(33)

we have

$$len{\left[u\right]}^{\tau }=(-2+2\tau )(1+xy),len{\left[v\right]}^{\lambda }=(2-2\lambda )\left(4-x^{\frac{1}{2}}{y}^{\frac{1}{2}}-\frac{4}{9}{x}^{\frac{3}{2}}{y}^{\frac{3}{2}}+xy\right)$$

and based on (5), one gets

$$\begin{array}{ccc}& & len{\left[(-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\frac{1}{2}}\widehat{g}(x,y,u(x,y))\right]}^{\tau }=-L{x}^{\frac{1}{2}}{y}^{\frac{1}{2}}·len{\left[u\right]}^{\tau }-Lxy·len{\left[A\right]}^{\tau }\le \frac{2}{\pi }(2-2\tau ),\hfill \end{array}$$

$$len{\left[\phi (x,y)\right]}^{\tau }=4(2-2\tau ),$$

furthermore,

$$len{\left[\phi (x,y)\right]}^{\tau }\ge len{\left[(-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\frac{1}{2}}\widehat{g}(x,y,u(x,y))\right]}^{\tau }.$$

It is known from ([32], Proposition 21) (a) that there exists H-difference

$$\phi (x,y)\ominus (-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\frac{1}{2}}\widehat{g}(x,y,u(x,y)).$$

Choosing

$$U(x,y)=\psi (x,y)\ominus (-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\frac{1}{2}}\widehat{f}(x,y,u(x,y),v(x,y)),$$

then

$$\begin{array}{ccc}& & {\left[U(x,y)\right]}^{\tau }=\left(-1-xy+\frac{9{\pi }^2-64}{36{\pi }^2}{x}^{\frac{3}{2}}{y}^{\frac{3}{2}}-\frac{7}{64}{x}^2{y}^2-\frac{464}{405{\pi }^2}{x}^{\frac{5}{2}}{y}^{\frac{5}{2}}\right)[\tau +1,3-\tau ],\hfill \\ & & len{\left[U(x,y)\right]}^{\tau }=(2-2\tau )\left(-1-xy+\frac{9{\pi }^2-64}{36{\pi }^2}{x}^{\frac{3}{2}}{y}^{\frac{3}{2}}-\frac{7}{64}{x}^2{y}^2-\frac{464}{405{\pi }^2}{x}^{\frac{5}{2}}{y}^{\frac{5}{2}}\right).\hfill \end{array}$$

Similar to the previous calculation method, we can obtain

$${\left[(-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\frac{1}{2}}\widehat{g}(x,y,U(x,y))\right]}^{\tau }=L{\left[U\right]}^{\tau }{x}^{\frac{1}{2}}{y}^{\frac{1}{2}}+L{\left[A\right]}^{\tau }xy$$

and

$$\begin{array}{ccc}& & len{\left[(-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\frac{1}{2}}\widehat{g}(x,y,U(x,y))\right]}^{\tau }\le \frac{2}{\pi }(2-2\tau ).\hfill \end{array}$$

It is shown that H-difference $\phi (x,y)\ominus (-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\frac{1}{2}}\widehat{g}(x,y,U(x,y))$ exists.

Analogously, based on (32) and (33), we have

$$\begin{array}{ccc}& & {\left[(-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\frac{1}{2}}\widehat{f}(x,y,u(x,y),v(x,y))\right]}^{\lambda }\hfill \\ & & \begin{array}{cc}\hfill =& \frac{L{\left[v\right]}^{\lambda }}{\mathrm{\Gamma }\left(\frac{1}{2}\right)\mathrm{\Gamma }\left(\frac{1}{2}\right)}·\underset{0}{\overset{x}{\int }}\underset{0}{\overset{y}{\int }}{(x-s)}^{-\frac{1}{2}}{(y-t)}^{-\frac{1}{2}}{s}^{\frac{1}{2}}{t}^{\frac{1}{2}}dtds\hfill \\ & -\frac{L{\left[u\right]}^{\lambda }}{\mathrm{\Gamma }\left(\frac{1}{2}\right)\mathrm{\Gamma }\left(\frac{1}{2}\right)}·\underset{0}{\overset{x}{\int }}\underset{0}{\overset{y}{\int }}{(x-s)}^{-\frac{1}{2}}{(y-t)}^{-\frac{1}{2}}stdtds\hfill \\ & -\frac{L{\left[A\right]}^{\lambda }}{\mathrm{\Gamma }\left(\frac{1}{2}\right)\mathrm{\Gamma }\left(\frac{1}{2}\right)}·\underset{0}{\overset{x}{\int }}\underset{0}{\overset{y}{\int }}{(x-s)}^{-\frac{1}{2}}{(y-t)}^{-\frac{1}{2}}{s}^{\frac{3}{2}}{t}^{\frac{3}{2}}dtds\hfill \\ & -\frac{5L{\left[A\right]}^{\lambda }}{9\mathrm{\Gamma }\left(\frac{1}{2}\right)\mathrm{\Gamma }\left(\frac{1}{2}\right)}·\underset{0}{\overset{x}{\int }}\underset{0}{\overset{y}{\int }}{(x-s)}^{-\frac{1}{2}}{(y-t)}^{-\frac{1}{2}}{s}^2{t}^{2}dtds\hfill \end{array}\hfill \\ & & =\left(xy-\frac{9{\pi }^2-64}{36{\pi }^2}{x}^{\frac{3}{2}}{y}^{\frac{3}{2}}+\frac{7}{64}{x}^2{y}^2+\frac{464}{405{\pi }^2}{x}^{\frac{5}{2}}{y}^{\frac{5}{2}}\right){\left[A\right]}^{\lambda },\hfill \end{array}$$

and then we can get

$$\begin{array}{ccc}& & len{\left[\psi (x,y)\right]}^{\lambda }=-(2-2\lambda ),\hfill \\ & & len{\left[(-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\frac{1}{2}}\widehat{f}(x,y,u(x,y),v(x,y))\right]}^{\lambda }\ge -\frac{1}{2}(2-2\lambda ).\hfill \end{array}$$

This implies

$$len{\left[\psi (x,y)\right]}^{\lambda }\le len{\left[(-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\frac{1}{2}}\widehat{f}(x,y,u(x,y),v(x,y))\right]}^{\lambda }.$$

It follows that $V(x,y)=\phi (x,y)\ominus (-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\frac{1}{2}}\widehat{g}(x,y,u(x,y))$ exists via (b) of ([32], Proposition 21). So using the same calculation method, we find

$$\begin{array}{c}\hfill len{\left[V(x,y)\right]}^{\lambda }=\left(4-\frac{1}{\pi }{x}^{\frac{1}{2}}{y}^{\frac{1}{2}}-\frac{1}{\pi }{x}^{\frac{3}{2}}{y}^{\frac{3}{2}}+\frac{1}{\pi }xy\right)(2-2\lambda ),\end{array}$$

and then one establishes

$$\begin{array}{c}\hfill len{\left[(-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\frac{1}{2}}\widehat{f}(x,y,u(x,y),V(x,y))\right]}^{\lambda }\ge -\frac{1}{2}(2-2\lambda ).\end{array}$$

The above procedure demonstrates existence of H-difference $\psi (x,y)\ominus (-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\frac{1}{2}}\widehat{f}(x,$$y,u(x,y),V(x,y))$. So far, these validate the assumptions of ($h_1$) and ($h_2$) in Theorem 2. Because of $\psi (x,y)$ and $\phi (x,y)$ have compact-supported sets, and $\psi (x,y),\phi (x,y)\in C\left(J,B(\widehat{0},\frac{\kappa }{2})\right)$, it can be known from Theorem 2 that on ${\widehat{C}}_{\phi }^{\widehat{g}}(J,E_c^1)\times {\widehat{C}}_{\psi }^{\widehat{f}}(J,E_c^2)$, (29) exists a $(‡)$-weak solution

$$\left\{\begin{array}{cc}\hfill u(x,y)& =-A\ominus Axy,\hfill \\ \hfill v(x,y)& =4A\ominus A{x}^{\frac{1}{2}}{y}^{\frac{1}{2}}-\frac{4A}{9}{x}^{\frac{3}{2}}{y}^{\frac{3}{2}}\ominus (-1)Axy.\hfill \end{array}\right.$$

In the following, we shall give some applications of Theorems 1 and 2 to the projection neural network system (1). It is concluded that there exists at least one $(†)$-weak solution or $(‡)$-weak solution for fuzzy fractional coupled partial differential systems with projection operators under some suitable conditions.

To begin with, similar to [1], we define the concept of fuzzy projection for fuzzy functions on fuzzy sets.

Definition 9. 

For any fuzzy function $\zeta (x,y)\in E_c^1$, its projection on $F\left(D\right)\subset E_c^1$ is defined as

$$\begin{array}{c}\hfill P_{F\left(D\right)}\left(\zeta (x,y)\right)=\underset{\varsigma \in F\left(D\right)}{argmin}\rho (\zeta ,\varsigma ),\end{array}$$

which is a fuzzy mapping from $E_c^1$ to $F\left(D\right)$, where $F\left(D\right)$ represents the set of all fuzzy numbers with H-continuous defined on $D\subset \mathbb{R}$ and ρ is defined by (4).

Remark 7. 

Because of $u(x,y)\in C(J,E_c^1)$ and $P_{F\left(D\right)}(·):E_c^1\to F\left(D\right)$, we know from (1) that $F\left(D\right)$ in Definition 9 can only be included in $E_c^1$.

It is easy to see that $-u(x,y)+P_{F\left(D\right)}\left(m(x,y)v(x,y)\right)$ in (1) is a special case of $\widehat{f}\left(x,y,\right.$$\left.u(x,y),v(x,y)\right)$ in (2). Then, based on Definition 9, we can directly obtain two existence results of $\left(l\right)$-weak solutions of (1) for $l=†,‡$ as follows.

Theorem 3. 

For any positive real number κ, suppose that

(i) 

$P_{F\left(D\right)}\left(S\right)$ is a relatively compact subset of the fuzzy set $F\left(D\right)$, where $S\subset B(\widehat{0},\kappa )\subset E_c^1$, and $F\left(D\right)$ is a nonempty closed and convex subset of $E_c^1$;

(ii) 

$\widehat{g}:J\times B(\widehat{0},\kappa )\to E_c^2$ is a compact mapping;

(iii) 

$\psi ,\phi \in C(J,B(\widehat{0},\frac{\kappa }{2}))$, and $\psi ,\phi$ are compact-supported.

Then there exist $\widehat{a}\in (0,a]$ and $\widehat{b}\in (0,b]$ such that (1) has at least one $(†)$-weak solution defined on $C(\widehat{J},F\left(D\right))\times C(\widehat{J},E_c^2)$, where $\widehat{J}=[0,\widehat{a}]\times [0,\widehat{b}]$.

In order to show the existence theorem of $(‡)$-weak solution for (1) more specifically and intuitively, now we rewrite the hypotheses (${\mathit{h}}_{\mathit{1}}$) and (${\mathit{h}}_{\mathit{2}}$) to (${\mathit{s}}_{\mathit{1}}$) and (${\mathit{s}}_{\mathit{2}}$), the obtained two assumptions that guarantee the existence of the $(‡)$-weak solution for (1):

• $({\mathit{s}}_1) {\widehat{C}}_{\psi }^{P_{F\left(D\right)}}(J,E_c^2)\ne \varnothing$, $({\mathit{s}}_2) {\widehat{C}}_{\phi }^{\widehat{g}}(J,E_c^1)\ne \varnothing$.
• $({\mathit{s}}_2) \mathrm{If}u(·,·)\in {\widehat{C}}_{\phi }^{\widehat{g}}(J,E_c^1)$, then one has

  $$\begin{array}{c}\hfill U(x,y)=\psi (x,y)\ominus (-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\alpha }\left(-u(x,y)+P_{F\left(D\right)}\left(m(x,y)v(x,y)\right)\right)\in {\widehat{C}}_{\phi }^{\widehat{g}}(J,E_c^1)\end{array}$$

  for any $(x,y)\in J$ and each $v(x,y)\in {\widehat{C}}_{\psi }^{P_{F\left(D\right)}}(J,E_c^2)$, and for all $(x,y)\in J$,

  $$V(x,y)=\phi (x,y)\ominus (-1){}_F^{RL}{\mathcal{I}}_{0^{+}}^{\beta }\widehat{g}(x,y,u(x,y))\in {\widehat{C}}_{\psi }^{P_{F\left(D\right)}}(J,E_c^2)$$

  when $v(·,·)\in {\widehat{C}}_{\psi }^{P_{F\left(D\right)}}(J,E_c^2)$, where ${\widehat{C}}_{\phi }^{\widehat{g}}(J,E_c^1)$ is confirmed by (11) and ${\widehat{C}}_{\psi }^{P_{F\left(D\right)}}(J,E_c^2)$ is determined by

  $$\begin{array}{ccc}& & {\widehat{C}}_{\psi }^{P_{F\left(D\right)}}(J,E_c^2)\hfill \\ & & \begin{array}{cc}\hfill =\{v\in C(J,E_c^2\left)\right|& \psi (x,y)\ominus {(-1)}_F^{RL}{\mathcal{I}}_{0^{+}}^{\alpha }\left(-u(x,y)+P_{F\left(D\right)}\left(m(x,y)v(x,y)\right)\right)\hfill \\ & \mathrm{exists},\forall (x,y)\in J,u(x,y)\in {\widehat{C}}_{\phi }^{\widehat{g}}(J,E_c^1)\},\hfill \end{array}\hfill \end{array}$$

  where $\psi (·,·)$ is alone defined by (9).

Theorem 4. 

If all the assumptions in Theorem 3 are satisfied, and (${\mathbf{s}}_{\mathbf{1}}$) and (${\mathbf{s}}_2$) are also assumed to be true, then there exist $\widehat{a}\in (0,a]$ and $\widehat{b}\in (0,b]$ such that (1) has at least one $(‡)$-weak solution on ${\widehat{C}}_{\phi }^{\widehat{g}}(\widehat{J},F\left(D\right))\times {\widehat{C}}_{\psi }^{P_{F\left(D\right)}}(\widehat{J},E_c^2)$.

Remark 8. 

Theorems 3 and 4 are based on Definition 9. For projection operator $P_{F\left(D\right)}\left(\zeta (x,y)\right):B(\widehat{0},\kappa )$$\to F\left(D\right)$, if $P_{F\left(D\right)}\left(S\right)$ is relatively compact on $F\left(D\right)$, then $P_{F\left(D\right)}$ is a compact operator according to Definition 8. Further, the conclusions of Theorems 3 and 4 can be obtained from Theorems 1 and 2, respectively.

5. Conclusions

In this paper, we considered a class of new coupled systems of fuzzy fractional PDEs of the following form in the sense of Caputo $gH$-type derivative:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}_{gH}^C{\mathcal{D}}_k^{\alpha }u(x,y)=\widehat{f}\left(x,y,u(x,y),v(x,y)\right),\hfill \\ {}_{gH}^C{\mathcal{D}}_k^{\beta }v(x,y)=\widehat{g}(x,y,u(x,y)),\hfill \\ u(x,0)={\xi }_1\left(x\right),v(x,0)={\eta }_1\left(x\right),\hfill \\ u(0,y)={\xi }_2\left(y\right),v(0,y)={\eta }_2\left(y\right),\hfill \end{array}\right.\end{array}$$

(34)

for any $(x,y)\in J=[0,a]\times [0,b]$ and $k=1,2$. In the sense of $gH$-type differentiability, it is very important to extend the relevant conclusions of fuzzy fractional PDEs to coupled systems without Lipschitz conditions of the functions $\widehat{f}$ and $\widehat{g}$.

Based on $gH$-type derivatives, relative compactness concepts and without Lipschitz conditions, the brand new work of this paper is as follows:

•

Combining with some relative compactness concepts and using Schauder fixed point theorem, it is proved that (34) is equivalent to a nonlinear fractional Volterra integral-differential coupled system, which further proves the existence of two kinds of $gH$-weak solutions to (34). This greatly expands the range of solvable problems.

•

An example is given to visually demonstrate the existence of two kinds of $gH$-type weak solutions, and based on the found $(‡)$-weak solution, we give the numerical simulation of this weak solution.

•

Furthermore, based on the definition of fuzzy projection, we give some applications of the existence conclusions of two classes of $gH$-type weak solutions in the following projection neural network:

$$\left\{\begin{array}{c}{}_{gH}^C{\mathcal{D}}_k^{\alpha }u(x,y)=-u(x,y)+P_{F\left(D\right)}\left(m(x,y)v(x,y)\right),\hfill \\ {}_{gH}^C{\mathcal{D}}_k^{\beta }v(x,y)=\widehat{g}(x,y,u(x,y)),\hfill \end{array}\right.$$

with initial conditions $u(x,0)={\xi }_1\left(x\right),v(x,0)={\eta }_1\left(x\right)$, and $u(0,y)={\xi }_2\left(y\right),v(0,y)={\eta }_2\left(y\right)$.

We remark that comparing with the existing work, in this paper, we studied a class of more general coupled systems, and obtained some new conclusions using fire-new proof methods.

Moreover, as we all know, neural network is a powerful tool to solve signal processing, associative memory, pattern recognition and other mathematical and engineering problems. It can effectively solve optimization problems and variational inequalities. Based on the results of fuzzy fractional coupled partial differential systems with projection operators, how to establish existence and uniqueness of fuzzy optimal control solutions with parameters? This is an important work and is worth to explore in the future.