On a Combinatorial Approach to Studying the Steiner Diameter of a Graph and Its Line Graph

Abstract

In 1989, Chartrand, Oellermann, Tian and Zou introduced the Steiner distance for graphs. This is a natural generalization of the classical graph distance concept. Let $\Gamma$ be a connected graph of order at least 2, and $S\backslash V(\Gamma )$. Then, the minimum size among all the connected subgraphs whose vertex sets contain S is the Steiner distance $d_{\Gamma }\left(S\right)$ among the vertices of S. The Steiner k-eccentricity $e_k\left(v\right)$ of a vertex v of $\Gamma$ is defined by $e_k\left(v\right)=max\{d_{\Gamma }\left(S\right)|S\backslash V(\Gamma ),|S|=k,andv\in S\}$, where n and k are two integers, with $2\le k\le n$, and the Steiner k-diameter of $\Gamma$ is defined by ${sdiam}_k(\Gamma )=max\left\{e_k\left(v\right)\right|v\in V(\Gamma )\}$. In this paper, we present an algorithm to derive the Steiner distance of a graph; in addition, we obtain a relationship between the Steiner k-diameter of a graph and its line graph. We study various properties of the Steiner diameter through a combinatorial approach. Moreover, we characterize graph $\Gamma$ when ${sdiam}_k(\Gamma )$ is given, and we determine ${sdiam}_k(\Gamma )$ for some special graphs. We also discuss some of the applications of Steiner diameter, including one in education networks.

1. Introduction

In this paper, all the graphs are assumed to be undirected, finite and simple. The degree of a vertex v in graph $\Gamma$ is denoted by $de{g}_{\Gamma }\left(v\right)$. We denote by $\Delta (\Gamma )$ and $\delta (\Gamma )$ the maximum and minimum degrees of the vertices of $\Gamma$, respectively. A subdivision of $\Gamma$ is a graph obtained from $\Gamma$ by replacing edges with pairwise internally disjointed paths. We write $\Gamma =kH$ when $\Gamma$ is the disjointed union of k copies of a graph H. As usual, by $C_n$, $P_n$, $K_{1,n-1}$ and $K_n$, we denote, respectively, the cycle, path, star, and complete graph of order n. We also denote a complement graph of $\Gamma$ by $\overline{\Gamma }$. The connectivity $\kappa$ of a graph $\Gamma$ is the minimum size of a vertex set V such that $\Gamma -V$ is disconnected. The edge connectivity $\lambda$ of a graph $\Gamma$ is the minimum size of an edge set E such that $\Gamma -E$ is disconnected. The line graph of $\Gamma$ is the graph $L(\Gamma )$ with vertex set $E(\Gamma )$, where two elements $e,f\in V\left(L\right(\Gamma \left)\right)$ are adjacent in $L(\Gamma )$ if and only if they correspond to two edges in $\Gamma$ sharing a common endpoint. Let $L^0(\Gamma )=\Gamma$ and $L^1(\Gamma )=L(\Gamma )$. Then for $\ell \ge 2$, the ℓ-th iterated line graph $L^{\ell }(\Gamma )$ is defined by $L\left(L^{\ell -1}(\Gamma )\right)$. We skip the definitions of other standard graph-theoretical notions, which can be found in, e.g., [1,2,3,4].

1.1. The Generalized Concept of Distance

One of the most fundamental ideas in graph-theoretic subjects is distance. Let $\Gamma$ be a connected graph with $x,y\in V(\Gamma )$. Then the length of a shortest path between x and y is the distance $d(x,y)$. The eccentricity $e\left(v\right)$ of any vertex v in $\Gamma$ is defined by $e\left(v\right)=max\left\{d\right(u,v\left)\right|u\in V(\Gamma )\}$. Moreover, the diameter $diam(\Gamma )$ and radius $rad(\Gamma )$ of $\Gamma$ are defined by $diam(\Gamma )=max\left\{e\right(v\left)\right|v\in V(\Gamma )\}$ and $rad(\Gamma )=min\left\{e\right(v\left)\right|v\in V(\Gamma )\}$. These two graph invariants are related by the inequalities $rad(\Gamma )\le diam(\Gamma )\le 2rad(\Gamma )$. The center $C(\Gamma )$ of a connected graph $\Gamma$ is defined by $C(\Gamma )=\{u\in V(\Gamma \left)\right|e\left(u\right)=rad(\Gamma )\}$.

The minimum size of a connected subgraph containing two vertices x and y in a connected graph $\Gamma$ is equal to the distance between these two vertices x and y. This observation suggests a generalization of distance. The Steiner distance of a graph, first proposed in 1989 by Chartrand, Oellermann, Tian and Zou [5], is a natural and nice generalization of the concept of classical graph distance. An S-Steiner tree, or a Steiner tree connecting S (or simply, an S-tree), is a tree $T=(V^{\prime },E^{\prime })$ of $\Gamma$, $S\backslash V^{\prime }$ for a graph $\Gamma =(V,E)$ and a set $S\backslash V(\Gamma )$ $\left(\right|S|\ge 2)$. Let S be a nonempty set of vertices of a connected graph $\Gamma$. Then the Steiner distance $d_{\Gamma }\left(S\right)$ among the vertices of S (or simply the distance of S) is the minimum size among all connected subgraphs whose vertex sets contain S. Note that if G is a connected subgraph of $\Gamma$ such that $S\backslash V\left(G\right)$ and $\left|E\left(G\right)\right|=d_{\Gamma }\left(S\right)$, then G is a tree. Observe that $d_{\Gamma }\left(S\right)=min\left\{e\left(T\right)\right|S\backslash V\left(T\right)\}$, where T is a subtree of $\Gamma$. In particular, if $S=\{x,y\}$, then $d_{\Gamma }\left(S\right)=d(x,y)$. If there is no S-Steiner tree in $\Gamma$, then we assume that $d_{\Gamma }\left(S\right)=\infty$. For its basic mathematical properties including related results, see [6,7,8,9].

Observation 1.

Let Γ be a graph of order n with integer k such that $2\le k\le n$. If $S\backslash V(\Gamma )$ and $\left|S\right|=k$, then $d_{\Gamma }\left(S\right)\ge k-1$.

Let k and n be two integers such that $2\le k\le n$. The Steiner k-eccentricity $e_k\left(u\right)$ of a vertex u of $\Gamma$ is defined by $e_k\left(u\right)=max\{d_{\Gamma }\left(S\right)|S\backslash V(\Gamma ),|S|=k,andu\in S\}$. (If there are two graphs in the context, then we use $e_k^{\Gamma }\left(u\right)$ instead of $e_k\left(u\right)$.) The Steiner k-radius of $\Gamma$ is ${srad}_k(\Gamma )=min\left\{e_k\left(u\right)\right|u\in V(\Gamma )\}$, while the Steiner k-diameter of $\Gamma$ is ${sdiam}_k(\Gamma )=max\left\{e_k\left(u\right)\right|u\in V(\Gamma )\}$. Note that for every connected graph $\Gamma$, $e_2\left(u\right)=e\left(u\right)$ for all $u\in V(\Gamma )$, and hence, ${sdiam}_2(\Gamma )=diam(\Gamma )$ and ${srad}_2(\Gamma )$ $=rad(\Gamma )$. Let ${\Gamma }_1$ be a graph in Figure 1. For any $S\subset V\left({\Gamma }_1\right)$ and $\left|S\right|=3$, obviously, $d_{{\Gamma }_1}\left(S\right)\le 4$. If we take $S=\{u,v,x\}$, then the Steiner tree of ${\Gamma }_1$ is ${\Gamma }_2$ (see Figure 1), and hence, we have ${srad}_3\left({\Gamma }_1\right)=4$. Moreover, each vertex of the graph ${\Gamma }_3$ in Figure 1 is labeled with its Steiner 3-eccentricity, so that ${sdiam}_3\left({\Gamma }_3\right)=6$.

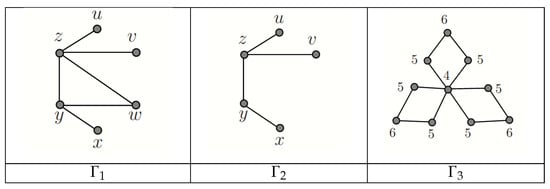
Figure 1. Three graphs ${\Gamma }_1,{\Gamma }_2$, and ${\Gamma }_3$.

Observation 2.

Let k and n be two integers, with$2\le k\le n$.

$\left(1\right)$ If H is a spanning subgraph of Γ, then ${sdiam}_k(\Gamma )\le sdia{m}_k\left(H\right)$.

$\left(2\right)$ For a connected graph Γ, ${sdiam}_k(\Gamma )\le {sdiam}_{k+1}(\Gamma )$.

1.2. Background and Recent Progress

In 1971, Hakimi [10] and Levi [11] introduced the Steiner tree problem in graphs. For an undirected and unweighted graph $\Gamma$, the problem is to find a minimal connected subgraph that contains the vertices in S, where $S\backslash V(\Gamma )$. More specifically, the determination of a Steiner tree in a graph is a discrete analogue of the well-known geometric Steiner problem: Find the shortest possible network of line segments interconnecting a set of given points in Euclidean space. Researchers have studied the computational part of this problem and have found it an NP-hard problem for general graphs (see [4]).

Chartrand, Okamoto and Zhang [12] presented the following result.

Theorem 1

([12]).Let Γ be a connected graph of order n with integer k such that $2\le k\le n$. Then $k-1\le {sdiam}_k(\Gamma )\le n-1$. Moreover, the upper and lower bounds are sharp.

Mao et al. [13] studied the problem of determining the minimum size of a graph of given order, Steiner diameter and maximum degree. Mao et al. [14] studied the Steiner distance of Cartesian and lexicographic product graphs. Dankelmann et al. [15] presented an upper bound on ${sdiam}_k(\Gamma )$: ${sdiam}_k(\Gamma )\le \frac{3n}{\delta +1}+3n$, where n is the order, and $\delta$ is the minimum degree of $\Gamma$. Mao [16] gave the upper and lower bounds for the Steiner diameter of graphs.

The Steiner k-center $C_k(\Gamma )(k\ge 2)$ of a connected graph $\Gamma$ is the subgraph induced by the vertices of minimum k-eccentricity in $\Gamma$. According to Oellermann and Tian [17], every graph is the k-center of another graph. The Steiner k-median of $\Gamma$ is the subgraph of $\Gamma$ induced by the vertices of $\Gamma$ of minimum Steiner k-distance. We refer interested readers to [17,18,19] for further discussions of Steiner medians and Steiner centers.

Dankelmann, Oellermann and Swart [20] introduced the average Steiner distance ${\mu }_k(\Gamma )$ of a graph $\Gamma$. It is defined as

$${\mu }_k(\Gamma )={\left(\genfrac{}{}{0pt}{}{n}{k}\right)}^{-1}\sum _{S\backslash V(\Gamma ),\left|S\right|=k}{d}_{\Gamma }\left(S\right).$$

For mathematical properties on average Steiner distance, see [20,21] and the references therein.

Let $\Gamma$ be a k-connected graph, and $x,y\in V(\Gamma )$. Let $P_k(x,y)$ be a family of k vertex-disjoint paths between x and y, i.e., $P_k(x,y)=\{P_i,1\le i\le k\}$. Let $p_i$ $(1\le i\le k)$ be the number of edges of path $P_i$ such that $p_1\le p_2\le \cdots \le p_k$. The k-distance $d_k(x,y)$ between vertices x and y is the minimum $p_k$ among all $P_k(x,y)$, and the k-diameter $d_k(\Gamma )$ of $\Gamma$ is defined as the maximum k-distance $d_k(x,y)$ over all pairs $x,y$ of vertices of $\Gamma$. The concept of k-diameter emerges rather naturally when one looks at the performance of routing algorithms. Several authors (Chung [22], Du, Lyuu and Hsu [23], Hsu [24,25], Meyer and Pradhan [26]) have studied and discussed applications of such notions as k-diameter to network routing in distributed and parallel processing.

In [27], Mao et al. obtained the following results, which are used later.

Lemma 1

([27]).Let Γ be a graph of order n. Then Γ is connected if and only if ${sdiam}_n(\Gamma )=n-1$.

Lemma 2

([27]).Let Γ be a connected graph with n vertices. Then

$\left(1\right)$ Γ is 2-connected if and only if ${sdiam}_{n-1}(\Gamma )=n-2$;

$\left(2\right)$ Γ contains at least one cut vertex if and only if ${sdiam}_{n-1}(\Gamma )=n-1$.

Lemma 3

([27]).Let Γ be a connected graph with $n(n\ge 4)$ vertices and connectivity κ. Then

$\left(1\right)$$\kappa (\Gamma )\ge 3$ if and only if ${sdiam}_{n-2}(\Gamma )=n-3$;

$\left(2\right)$$\kappa (\Gamma )=2$or Γ contains only one cut vertex if and only if ${sdiam}_{n-2}(\Gamma )=n-2$;

$\left(3\right)$there are at least two cut vertices in Γ if and only if ${sdiam}_{n-2}(\Gamma )=n-1$.

Lemma 4

([27]).Let Γ be a connected graph with n vertices and connectivity κ. Then

$\left(1\right)$there are at least three cut vertices in Γ if and only if ${sdiam}_{n-3}(\Gamma )=n-1$;

$\left(2\right)$$\kappa (\Gamma )\ge 4$ if and only if ${sdiam}_{n-3}(\Gamma )=n-4$.

$\left(3\right)$ If $\kappa (\Gamma )=3$, then ${sdiam}_{n-3}(\Gamma )=n-3$.

1.3. Three Problems

Let $A_i(1\le i\le 4)$ be the graphs shown in Figure 2.

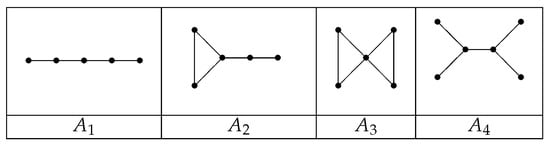
Figure 2. The forbidden subgraphs $A_i(1\le i\le 4)$.

In [28], Ramane et al. obtained the following results.

Theorem 2

([28]).Let Γ be a graph with $diam(\Gamma )\le 2$. If Γ does not contain $A_i(1\le i\le 3)$ as its induced subgraph, then $diam\left(L\right(\Gamma \left)\right)\le 2$.

Theorem 3

([28]).Let Γ be a graph with $diam(\Gamma )\le 2$. If Γ does not contain $A_i(1\le i\le 4)$ as its induced subgraph, then $L(\Gamma )$ does not contain $A_i(1\le i\le 4)$ as its induced subgraph.

Theorem 4

([28]).Let Γ be a graph with $diam(\Gamma )\le 2$. If Γ does not contain $A_i(1\le i\le 4)$ as its induced subgraph, then for $\ell \ge 1$,

$\left(1\right)$$diam\left(L^{\ell }(\Gamma )\right)\le 2$;

$\left(2\right)$$L^{\ell }(\Gamma )$ does not contain $A_i(1\le i\le 4)$ as its induced subgraph.

In this paper, to better understand this notion of the Steiner diameter of a graph and its associated line graphs, we propose and study the following problems.

Problem 1.

Let Γ be a graph with ${sdiam}_k(\Gamma )\le k$, and ℓ is an integer. Find some induced subgraphs such that if Γ does not contain such induced subgraphs, then ${sdiam}_k\left(L^{\ell }(\Gamma )\right)\le k$.

Problem 2.

Find some induced subgraphs that characterize ${sdiam}_k\left(L(\Gamma )\right)$.

The following observation is immediate from Theorem 1.

Observation 3.

Let Γ be a connected graph with m edges. Then

$$k-1\le {sdiam}_k\left(L(\Gamma )\right)\le m-1.$$

In 1979, Bauer and Tindell [29] studied graphs with prescribed connectivity and line-graph connectivity.

Theorem 5

([29]).For each $s,t$, $1<s<t$, there is a graph ${\Gamma }_{s,t}$ such that $\kappa \left({\Gamma }_{s,t}\right)=s$ and $\kappa \left(L\left({\Gamma }_{s,t}\right)\right)=t$.

Li and Mao [30] investigated this problem for generalized connectivity. In this paper, we consider the same problem for distance-edge-monitoring numbers.

Problem 3.

For each $s,t$, $2\le s\le t$, is there a graph ${\Gamma }_{s,t}$ such that ${sdiam}_k\left({\Gamma }_{s,t}\right)=s$ and ${sdiam}_k\left(L\left({\Gamma }_{s,t}\right)\right)=t$?

The rest of the paper is organized as follows. In Section 2, we present an algorithm to derive the Steiner distance of graph $\Gamma$. In Section 3, we obtain a relationship between the Steiner k-diameter of a graph and its line graph and provide a solution to Problem 1. In Section 4, we characterize the graphs $\Gamma$ when ${sdiam}_k(\Gamma )$ is given and provide an initial solution to Problem 2. In Section 5, we determine ${sdiam}_k(\Gamma )$ for some special graphs $\Gamma$, including cycles, paths, complete graphs, fan graphs and friendship graphs, and provide a solution to Problem 3; and finally, in Section 6, we discuss some applications of these aforementioned results, as well as the combinatorial approach that we applied in our studies.

2. A Steiner Tree Construction Algorithm

As pointed out in [31], this Steiner problem in networks was originally formulated in [10], where a straightforward algorithm was suggested: a solution to this problem can be found by the enumeration of the minimum spanning trees (MSTs) of subnetworks of $\Gamma (V,E)$ induced by subsets W of V such that $Z\backslash W\backslash V.$ Although $\left|E\right|log\left|V\right|$ algorithms for the MST problem do exist [32,33], it is well known that there are an exponential number of subsets in $V.$ Thus, this straightforward algorithm takes an exponential amount of time to finish. Many algorithms following different approaches, together with heuristics, for a more general problem when the involved graph is weighted, i.e., all the edges come with positive weights, have been presented in, e.g., [31]. Although some of these approaches do lead to a polynomial solution for some special classes of graphs/networks, they all lead to exponential algorithms in the general case. Indeed, the problem of finding the Steiner distance of a set of vertices, the Steiner Problem, is NP-complete [3,34]. On the other hand, to expose a constructive nature for finding this important quantity, we describe an alternative algorithm to find the Steiner distance for a given $S\backslash V$ in a graph $\Gamma (V,E).$

Calling any graph with just one vertex trivial, non-trivial otherwise [1], we start with the following well-known result.

Lemma 5

([1]).Every non-trivial tree has at least two leaves.

Corollary 1.

A graph $\Gamma (V,E)$ is a tree iff, for some vertices $u,v\in V,(u,v)\in E,$ $\Gamma (V,E)-\left\{v\right\}$ is a tree, and v is a leaf.

Proof. 

The sufficiency follows from Lemma 5. Let v be one of the two leaves, $\Gamma (V,E)-\left\{v\right\}$ has to be both connected and cycle free, otherwise, it would contradict the assumption that $\Gamma$ is a tree itself. Regarding the necessity, assume $\Gamma (V,E)-\left\{v\right\}$ is a tree; then by definition of a tree, it is connected and contains no cycle. It is clear that with the additional edge connecting u and $v,$ $\Gamma$ is still connected and cycle free, and is thus a tree.    □

Given a graph $\Gamma (V,E),$ $\varnothing \subset W\backslash V,$ the following algorithm Tree $(W,E)$ as shown in Algorithm 1, returns true if vertices in W form a tree in $\Gamma .$ Let W be $\{w_0,w_1,\dots ,w_{m-1}\},m\ge 1.$

Algorithm 1: Algorithm Tree$(W,E)$

1. If $m=1$ 2. //An isolated vertex is a tree 3.       return True 4. Else 5.         For $i\ge 0\&\&i\le m-1$ 6.             If $Tree(W-w_i,E)$ 7.                   For $j\ge 0\&\&j\le m-1\&\&j\ne i$ 8.                         If $w_i$ is adjacent to only one $w_j$ 9.                         // $w_i$ is a leaf in W 10.                               return True 11.          //No such a leaf exists 12.       return False

In terms of complexity, let $T\left(m\right)$ be the number of checks we need to do in Line 8 or the constant operation that we need to do in Line 1. It is clear that $T\left(1\right)=1.$ When $m\ge 1,$ with the worst-case scenario, we have to go through a loop m times in Line 5; for each loop, we have to recursively call Tree $(W-w_i,E)$, for which we have to go through another loop in Line 7 $m-1$ times. Hence,

$$\begin{array}{c}\hfill T\left(m\right)=m(m-1)T(m-1)\end{array}$$

It is thus easy to see that

$$T\left(m\right)=m(m-1)T(m-1)=m{(m-1)}^2(m-2)T(m-2)=\cdots ={[m!]}^2/m.$$

By the following Stirling’s approximation,

$$\begin{array}{ccc}\hfill n!& =& \sqrt{2\pi n}{\left(\frac{n}{e}\right)}^n\left(1+\Theta \left(\frac{1}{n}\right)\right),\hfill \end{array}$$

where e refers to the natural logarithm 2.71828..., we may conclude that $T\left(m\right)=\Theta \left({(m/e)}^m\right).$

We are now ready to present a Steiner algorithm in Algorithm 2, by definition, to construct a Steiner tree in a graph $\Gamma (V,E).$ We notice the remark that we quoted in Section 1.1, “...if $\Gamma$ is a connected subgraph of $\Gamma$ such that $S\backslash V(\Gamma )$ and $\left|E(\Gamma )\right|=d_{\Gamma }\left(S\right),$ then G is a tree. Obviously, if $S=\{u,v\},$ then $d_{\Gamma }\left(S\right)(=d(u,v))$ is simply the classical distance between u and $v.$” [14].

Algorithm 2: Steiner algorithm

0. Given $\Gamma (V,E)$, and $S\backslash V$ 1. $S_t=\infty$ 2. // Initially set St to infinite, by definition in the DMTC paper 3. for $i\ge 0\&\&i\le \left|V\right|-\left|S\right|$ 4. // With the number of the vertices to be added. 5. // Since we want to get the minimum size, we start with 0 and go up. 6. //We quit in Line 12 as soon as we find a Steiner tree. 7.      Choose a subset $S_1$, $|S_1|=i$, $S_1$ is a subset of V-S 8.      // Notice that the number of $s_1$ is $\left(\genfrac{}{}{0pt}{}{|V-S|}{i}\right)$. 9.      If $Tree(S\cup S_1,E)$ //If the so-chosen set $S\cup S_1$ is a tree, we 10.    //are done, and the size of this tree is $|S\cup S_1|-1$. 11.         $S_t=|S\cup S_1|-1$ 12.         break 13.    return $S_t$ 14.    //If none of the vertex subsets satisfy the condition in 9, 15.                                  we return ∞.

When applying the Steiner algorithm to ${\Gamma }_1$ as shown in Section 1.1, we start by picking $I=0$ in Line 3; $S=\varnothing$ in Line 7 since Tree($S,E$) returns True (In Tree(S, E)), $m=2;$ let $w_0=u,w_1=v;$ Tree($\left\{u\right\},$E) returns True; and since v is only adjacent to $u,$ we are done. $St$ is set to 1 in Line 11, and it then breaks in Line 12 and returns 1 in Line 13.

In terms of complexity, the best scenario is that the loop in Line 3 runs only once; i.e., when S itself is a Steiner tree with edges in $G,$ then its complexity is the same as that of Tree($S,E$), i.e., $\Theta \left({\left|S\right|/e}^{\left|S\right|}\right)$.

The worst case is that $\Gamma$ is a Steiner tree itself, or it does not contain any Steiner tree, in which case the algorithm will have to go through all the subsets of $V\setminus S.$ In this worst case, the inner loop in Line 2 and the outside loop in Line 7 would cost altogether $2^{\left|V\right|\setminus \left|S\right|}T\left(\right|V\left|\right)(={O\left(\right|V|}^{\left|V\right|}\left)\right).$ Since, as mentioned earlier, this Steiner problem is NP-complete, there is no way to significantly improve the efficiency of such an algorithm.

3. Steiner Diameter of a Graph and Its Line Graph

In this section, we address Problems 1 and 2, as suggested in Section 1.3. Chartrand and Steeart [35] investigated the relation between the connectivity and edge-connectivity of a graph and its line graph.

Lemma 6

([35]).Let Γ be a connected graph with connectivity κ and edge-connectivity λ. Then

$\left(1\right)$$\lambda (\Gamma )\le \kappa \left(L\right(\Gamma \left)\right)$ if $\lambda (\Gamma )\ge 2$;

$\left(2\right)$$\lambda \left(L\right(\Gamma \left)\right)\ge 2\lambda (\Gamma )-2$;

$\left(3\right)$$\kappa \left(L\right(L(\Gamma )\left)\right)\ge 2\kappa (\Gamma )-2$.

The following result is immediate from Theorem 1.

Proposition 1.

Let $n,k$ be two integers with $k=n$ or $k=n-1$. Additionally, let Γ be a connected graph of order n, and Γ is not a tree. Then ${sdiam}_k(\Gamma )\le k$, and ${sdiam}_k\left(L(\Gamma )\right)\ge k-1$.

Proof. 

Since $\Gamma$ is a connected graph of order n, we have $L(\Gamma )$ is a connected graph with $\left|V\right(L(\Gamma )\left)\right|=\left|E\right(\Gamma \left)\right|\ge n$. It follows that $n-1\le {sdiam}_n\left(L(\Gamma )\right)\le \left|V\left(L(\Gamma )\right)\right|-1$. From Theorem 1, we have $n-2\le {sdiam}_{n-1}(\Gamma )\le n-1$, and ${sdiam}_n(\Gamma )=n-1$. □

For $k=n-2$, we have the following result.

Proposition 2.

Let Γ be a connected graph of order n with edge-connectivity λ and integer k such that $n-2\le k\le n$.

$\left(1\right)$ For $\lambda (\Gamma )\ge 2$, then ${sdiam}_{n-2}\left(L(\Gamma )\right)\le n-2$.

$\left(2\right)$If $\lambda (\Gamma )=1$, there exists only one cut edge in Γ; then ${sdiam}_{n-2}\left(L(\Gamma )\right)=n-2$.

$\left(3\right)$ If $\lambda (\Gamma )=1$ and there exist at least two cut edges, then ${sdiam}_{n-2}\left(L(\Gamma )\right)=n-1$.

Proof. 

$\left(1\right)$ For $k=n-2$, since $\lambda (\Gamma )\ge 2$, by Lemma 6$\left(1\right)$, we have $\kappa \left(L\right(\Gamma \left)\right)\ge \lambda (\Gamma )\ge 2$. Using this result with Lemmas 3 $\left(1\right)$ and $\left(2\right)$, we obtain ${sdiam}_{n-2}\left(L(\Gamma )\right)\le n-2$.

$\left(2\right)$ Suppose $\lambda (\Gamma )=1$ and there exists only one cut edge in $\Gamma$. Then we have $\kappa (\Gamma )=1$, and there exists only one cut vertex in $L(\Gamma )$. From $\left(2\right)$ of Lemma 3, we have ${sdiam}_{n-2}\left(L(\Gamma )\right)=n-2$, as desired.

$\left(3\right)$ Suppose $\lambda (\Gamma )=1$ and there exist at least two cut edges in $\Gamma$. Then there exist at least two cut vertices in $L(\Gamma )$. From Lemma 3$\left(3\right)$, we have ${sdiam}_{n-2}\left(L(\Gamma )\right)=n-1$, as desired. □

Proposition 3.

Let Γ be a connected graph with n vertices and edge connectivity λ. If $\lambda (\Gamma )\ge 3$, then ${sdiam}_{n-3}\left(L(\Gamma )\right)\le n-3$. Moreover, the bound is sharp.

Proof. 

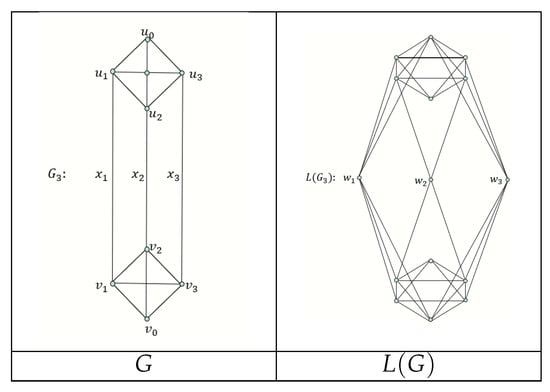
Since $\lambda (\Gamma )\ge 3$, it follows from $\left(1\right)$ of Lemma 6 that $\kappa \left(L\right(\Gamma \left)\right)\ge \lambda (\Gamma )\ge 3$. If $\kappa \left(L\right(\Gamma \left)\right)=3$, then from Lemma 4 (3), we have ${sdiam}_{n-3}\left(L(\Gamma )\right)=n-3$, as desired. Otherwise, $\kappa \left(L\right(\Gamma \left)\right)\ge 4$. From Lemma 4 (2), we have ${sdiam}_{n-3}\left(L(\Gamma )\right)=n-4$. This completes the proof of the result.

Moreover, if we take $\Gamma =G$ (see Figure 3), then we obtain $\kappa (\Gamma )=\kappa \left(L\right(\Gamma \left)\right)=3$. It follows from Lemma 4 (3) that we have ${sdiam}_{n-3}\left(L(\Gamma )\right)=n-3$, as desired. □

Figure 3. Graph G and its line graph $L\left(G\right)$.

We now focus our attention on the case of $k=3$. We now introduce nine graphs (see Figure 4), which are used later.

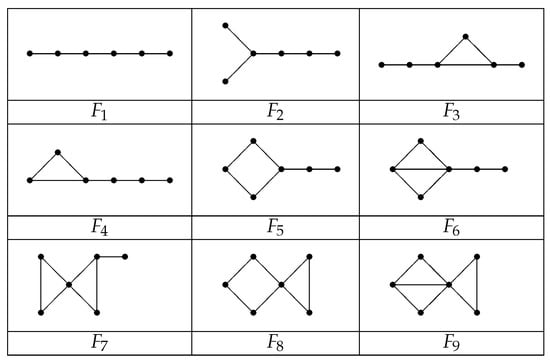
Figure 4. Graphs $F_i(1\le i\le 9)$.

• Let $F_1$ be a path of order 6;
• Let $F_2$ be the graph obtained by identifying a vertex of degree 2 in the 3-vertex path with one end vertex of the 4-vertex path;
• Let $F_3$ be the graph obtained by identifying a vertex of a cycle with one end vertex of the 3-vertex path and identifying the other vertex of this cycle with one end vertex of the 2-vertex path;
• Let $F_4$ be the graph obtained by identifying a vertex of a triangle with one end vertex of the 4-vertex path;
• Let $F_5$ be the graph obtained by identifying a vertex of a 4-vertex cycle with one end vertex of the 3-vertex path;
• Let $F_6$ be the graph obtained by identifying a vertex of degree 3 in $K_4^{-}$ with one end vertex of the 3-vertex path, where $K_4^{-}$ denotes the graph obtained from $K_4$ by deleting one edge;
• Let $F_7$ be the graph obtained by identifying a vertex of degree 2 of $F_7^{-}$ with one vertex of the 2-vertex path, where $F_7^{-}$ is the graph obtained by identifying a vertex of a triangle with one vertex of another triangle;
• Let $F_8$ be the graph obtained by identifying a vertex of 4-vertex cycle with one vertex of a triangle;
• Let $F_9$ be the graph obtained by identifying a vertex of degree 3 in $K_4^{-}$ with one vertex of a triangle, where $K_4^{-}$ denotes the graph obtained from $K_4$ by deleting one edge.

The following result provides a solution to Problem 1; that is, given a graph $\Gamma$ with ${sdiam}_k(\Gamma )\le k$, we want to find some induced subgraphs such that if $\Gamma$ does not contain such induced subgraphs, then ${sdiam}_k\left(L^{\ell }(\Gamma )\right)\le k$.

Theorem 6.

Let Γ be a connected graph with ${sdiam}_3(\Gamma )\le 3$. If Γ contains neither $F_2$ nor $3P_2$ as its induced subgraph, then ${sdiam}_3\left(L(\Gamma )\right)\le 3$.

Proof. 

Let $e_1,e_2,\dots ,e_m$ be the edges of a graph $\Gamma$. These are all the vertices of $L(\Gamma )$. Let $S=\{e_i,e_j,e_k\}$, where $e_i,e_j,e_k\in V\left(L(\Gamma )\right)=\{e_1,e_2,\dots ,e_m\}$. Note that $e_i,e_j,e_k$ are three edges in $\Gamma$. First, we assume that $\Gamma \left[S\right]$ is connected. This means that if one of them, say $e_i$, is adjacent to the other two edges, then vertex $e_i$ is adjacent to both vertex $e_j$ and vertex $e_k$ in $L(\Gamma )$. Thus, the tree T induced by the edges in $\{e_i{e}_j,e_i{e}_k\}$ is an S-Steiner tree in $L(\Gamma )$, which implies $d_{L(\Gamma )}\left(S\right)\le 2$, as desired.

Next, we assume that $\Gamma \left[S\right]$ is disconnected. We now may assume that $\Gamma \left[S\right]=P_3\cup P_2$ or $\Gamma \left[S\right]=3P_2$. Since $\Gamma$ does not contain $3P_2$ as its induced subgraph, we only need to consider the case $\Gamma \left[S\right]=P_3\cup P_2$. Let $e_i$ be adjacent to $e_j$ in $\Gamma$, and let $e_k$ be adjacent to neither $e_i$ nor $e_j$ in $\Gamma$. Set $e_i=xy$, $e_j=yz$ and $e_k=uv$. Suppose that one vertex in $\{x,y,z\}$ is adjacent to one vertex in $\{u,v\}$. Without loss of generality, let $e^{\prime }=xu\in E(\Gamma )$. Then the tree T induced by the edges in $\{e_i{e}_j,e_i{e}^{\prime },e_k{e}^{\prime }\}$ is an S-Steiner tree in $L(\Gamma )$, and hence $d_{L(\Gamma )}\left(S\right)\le 3$, as desired. Suppose that none of $\{x,y,z\}$ are adjacent to one vertex in $\{u,v\}$. Since ${sdiam}_3(\Gamma )\le 3$, it follows that there exists a vertex $w\in V(\Gamma )$ such that w is adjacent to one vertex in $\{x,y,z\}$ and w is adjacent to one vertex in $\{u,v\}$. By symmetry, we may assume that $xw,uw\in E(\Gamma )$ or $yw,uw\in E(\Gamma )$. Table 1 shows the edges between w and one element in $\{x,y,z,u,v\}$. By Figure 4, subgraphs $F_i(1\le i\le 9)$ induced by the vertices in $\{w,x,y,z,u,v\}$ are shown in Table 1. Note that $F_1$ and $F_i(3\le i\le 9)$ contains $3P_2$ as its subgraph. If $\Gamma$ contains neither $F_2$ nor $3P_2$ as its induced subgraph, then ${sdiam}_3\left(L(\Gamma )\right)\le 3$. □

Table 1. Edges between w and vertices in $\{x,y,z,u,v\}$ of $\Gamma$ and $\overline{\Gamma }$.

$\mathit{E}\left(\mathit{\Gamma }\right)$	$\mathit{E}\left(\overline{\mathit{\Gamma }}\right)$
$wx,wu$	$wz,wz,wv$	$F_1$
$wy,uw$	$wx,wz,wv$	$F_2$
$wx,wy,wu$	$wz,wv$	$F_3$
$wx,wu,wv$	$wy,wz$	$F_4$
$wx,wz,wu$	$wy,wv$	$F_5$
$wx,wy,wz,wu$	$wv$	$F_6$
$wx,wy,wu,wv$	$wz$	$F_7$
$wx,wz,wu,wv$	$wy$	$F_8$
$wx,wy,wz,wu,wv$		$F_9$

4. Line Graphs with Steiner Diameter

The following observation is immediate.

Observation 4.

Let Γ be a connected graph with $n(n\ge 5)$ vertices and m edges. Then ${sdiam}_k\left(L(\Gamma )\right)=k-1$ if and only if for any $S\backslash E(\Gamma )$ and $\left|S\right|=k$, the subgraph induced by the edges in S is connected.

Proposition 4.

Let Γ be a connected graph with n vertices, and $2\le k\le n-2$. Then ${sdiam}_k\left(L(\Gamma )\right)$ $=k-1$ if and only if $\Gamma =K_{1,n-1}$.

Proof. 

If $\Gamma =K_{1,n-1}$ for $2\le k\le n-2$, then ${sdiam}_k\left(L(\Gamma )\right)=k-1$. Conversely, let ${sdiam}_k\left(L(\Gamma )\right)=k-1$. We have to prove that $\Gamma =K_{1,n-1}$. Since $\Gamma$ is connected, it follows that $\Gamma$ contains a spanning tree, say T. If T is not a star, then there exists a non-leaf edge e. We choose k edges from different components of $T-e$. Then the subgraph induced by these k edges is not connected, contradicting Observation 4. Thus T is a star. Note that $\Gamma$ is a graph obtained from T by adding some edges. Suppose that u is the center of T. We claim that $\Gamma$ is a star. Otherwise, let $vw$ be an edge of $\Gamma -T.$ Then $T+vw-uv$ is a spanning tree but is not a star, which is a contradiction. This completes the proof of the result. □

Proposition 5.

Let Γ be a unicycle graph of order n with integer s $(3\le s\le n)$. Then ${sdiam}_{n-1}\left(L(\Gamma )\right)=n-2$ if and only if $\Gamma =C_s^{*}$, where $C_s^{*}$ is a cycle $C_s$ plus $n-s$ hanging edges into the cycle randomly.

Proof. 

If $\Gamma$ is $C_s^{*}$, then it follows from Observation 4 that ${sdiam}_{n-1}\left(L(\Gamma )\right)=n-2$. Conversely, let ${sdiam}_{n-1}\left(L(\Gamma )\right)=n-2$. Since $\Gamma$ is a unicyclic graph, it follows that $\Gamma$ contains a cycle, say $C_s$. We claim that the edge $e\in E(\Gamma )-V\left(C_s\right)$ must be a pendant edge. Otherwise, we can find a path $P_3:v_i{v}_j{v}_k$, and $v_i\in V\left(C_s\right)$. Then there exists a non-leaf edge $e=v_i{v}_j$. We choose $n-1$ edges from $E(\Gamma )-e$. Then the subgraph induced by these $n-1$ edges is not connected, contradicting Observation 4. Thus, we have $\Gamma =C_s^{*}$. □

Proposition 6.

Let Γ be a connected graph with size m and $d_{\Gamma }\left(v\right)\ge 2$ for all $v\in V(\Gamma )$. Then ${sdiam}_{m-1}\left(L(\Gamma )\right)=m-2$ if and only if $\lambda (\Gamma )\ge 2$.

Proof. 

From Lemma 2, ${sdiam}_{m-1}\left(L(\Gamma )\right)=m-2$ if and only if $L(\Gamma )$ is 2-connected. If $\lambda (\Gamma )\ge 2$, then it follows from Lemma 6 that $\kappa \left(L\right(\Gamma \left)\right)\ge \lambda (\Gamma )\ge 2$, and so ${sdiam}_{m-1}\left(L(\Gamma )\right)=m-2$.

Conversely, let ${sdiam}_{m-1}\left(L(\Gamma )\right)=m-2$; thus $\kappa \left(L\right(\Gamma \left)\right)=2$. If there exists a cut edge e in $\Gamma$, it follows that e is a cut vertex in $L(\Gamma )$, which means that $\kappa \left(L\right(\Gamma \left)\right)=1$, which is a contraction. Hence, $\lambda (\Gamma )\ge 2$. □

The following result provides a first step to address Problem 2, i.e., finding some induced subgraphs that characterize ${sdiam}_k\left(L(\Gamma )\right)$ when ${sdiam}_3\left(L(\Gamma )\right)=2$.

Corollary 2.

Let Γ be a connected graph with $n\ge 3$ vertices. Then ${sdiam}_3\left(L(\Gamma )\right)=2$ if and only if Γ satisfies one of the following conditions:

•$\Gamma =C_3$ for $n=3$;

•$\Gamma \in \{C_4,P_4,K_4^{-}\}$ for $n=4$;

•$\Gamma =K_{1,n-1}$ for $n\ge 5$.

5. Results for Some Special Graphs

For any graph $\Gamma$ with positive integer k, we now explore the relationship between $diam(\Gamma )$ and $sdia{m}_k(\Gamma )$ as follows:

Lemma 7.

For any graph Γ with positive integer $k(2\le k\le n)$, we have

$$sdia{m}_k(\Gamma )\le (k-1)diam(\Gamma )$$

with equality if and only if $\Gamma =K_n$ or $k=2$.

Proof. 

For $\Gamma =K_n$, $diam(\Gamma )=1$ and $sdia{m}_k(\Gamma )=k-1$, and hence $sdia{m}_k(\Gamma )=(k-1)diam(\Gamma )$; the equality holds. We already mentioned in Section 1.1, that $sdia{m}_2(\Gamma )=diam(\Gamma )$. For $k=2$, the equality thus also holds. Otherwise, $\Gamma \ne K_n$ and $k\ge 3$. For any $u,v\in V(\Gamma )$, we have $d_{\Gamma }(u,v)\le diam(\Gamma )$. Let $S\backslash V(\Gamma )$ be any set of vertices with $\left|S\right|=k$. First, we have to prove that

$$d_{\Gamma }\left(S\right)<(k-1)diam(\Gamma ).$$

(1)

Let T be a spanning tree of graph $\Gamma$. For $k=3$, $d_{\Gamma }\left(S\right)\le d_T\left(S\right)<2diam(\Gamma )$ as $\Gamma \ne K_n$. The strict inequality (1) holds. We now assume that $k\ge 4$. We prove the result (1) by mathematical induction on k. Assume that the result in (1) holds for k and prove it for $k+1$. For this, let $S^{\prime }\backslash V(\Gamma )$ be any set of vertices with $|S^{\prime }|=k+1$ such that $S^{\prime }\setminus S=\left\{v\right\}$. Then, there exists a vertex w in S such that $d_{\Gamma }\left(S^{\prime }\right)=d_{\Gamma }\left(S\right)+d_{\Gamma }(v,w)$. Therefore, by the mathematical induction hypothesis with the above result, we obtain

$$d_{\Gamma }\left(S^{\prime }\right)=d_{\Gamma }\left(S\right)+d_{\Gamma }(v,w)<(k-1)diam(\Gamma )+diam(\Gamma )=kdiam(\Gamma )$$

as $d_{\Gamma }(v,w)\le diam(\Gamma )$. Hence, the result (1) holds by induction when $k\ge 3$ and $\Gamma \ne K_n$. It follows that $sdia{m}_k(\Gamma )\le (k-1)diam(\Gamma )$ with equality if and only if $\Gamma =K_n$ or $k=2$. □

Theorem 7.

Let k, n be two integers.

$\left(1\right)$ Let Γ be a path $P_n$, and $2\le k\le n-1$, ${sdiam}_k\left(L(\Gamma )\right)=n-2$.

$\left(2\right)$ Let Γ be a cycle $C_n$, and $2\le k\le n$, ${sdiam}_k\left(L(\Gamma )\right)=⌊\frac{n(k-1)}{k}⌋$.

$\left(3\right)$ Let Γ be a star $S_n$, and $2\le k\le n-1$, ${sdiam}_k\left(L(\Gamma )\right)=k-1$.

Proof.

$\left(1\right)$ Let $V(\Gamma )=\{v_1,v_2,\dots ,v_n\}$ and $E(\Gamma )=\{e_1,e_2,\dots ,e_{n-1}|e_i=v_i{v}_{i+1}\}$. By the definition of a line graph $V\left(L\right(\Gamma \left)\right)=E(\Gamma )$. By Observation 3, we have ${sdiam}_k\left(L(\Gamma )\right)\le n-2$. We can assume that $S\backslash V\left(L\right(\Gamma \left)\right)$ is a set of vertices with $\left|S\right|=k\ge 2$ such that $e_1,e_{n-1}\in S$. Then, we have $d_{L(\Gamma )}\left(S\right)=n-2$. It follows that ${sdiam}_k\left(L(\Gamma )\right)\ge d_{L(\Gamma )}\left(S\right)=n-2$ and hence ${sdiam}_k\left(L(\Gamma )\right)=n-2$.

$\left(2\right)$ Since $L\left(C_n\right)\cong C_n$, we obtain ${sdiam}_k\left(L(\Gamma )\right)=⌊\frac{n(k-1)}{k}⌋$.

$\left(3\right)$ Since $L\left(S_n\right)\cong K_{n-1}$, we obtain ${sdiam}_k\left(L(\Gamma )\right)=k-1$. □

From Theorem 7 $\left(2\right)$, we have the following observation.

Observation 5.

Let $\Gamma =C_n$ be a cycle, and also let $n,\ell ,k(2\le k\le n)$ be positive integers. Then

$${sdiam}_k\left(L^{\ell }\left(C_n\right)\right)={sdiam}_k\left(C_n\right).$$

Proof. 

From Theorem 7 $\left(2\right)$, we have ${sdiam}_k\left(L\left(C_n\right)\right)=⌊\frac{n(k-1)}{k}⌋={sdiam}_k\left(C_n\right)$. Thus, we have

$${sdiam}_k\left(L^{\ell }\left(C_n\right)\right)={sdiam}_k\left(L^{\ell -1}\left(C_n\right)\right)=\cdots ={sdiam}_k\left(L\left(C_n\right)\right)={sdiam}_k\left(C_n\right).$$

□

The friendship graph, $F{r}_n$, can be constructed by joining n copies of the complete graph $K_3$ with a common vertex, which is called the universal vertex of $F{r}_n$.

Theorem 8.

Let $F{r}_n$ be a friendship graph with two positive integers k and n. Then

$${sdiam}_k\left(F{r}_n\right)=\left\{\begin{array}{cc}k\hfill & if 2\le k\le 2n,\hfill \\ k-1\hfill & if k=2n+1.\hfill \end{array}\right.$$

Proof. 

Let $\Gamma =F{r}_n$. Further, let $V(\Gamma )=\{v_0,v_1,u_1,\dots ,v_n,u_n\}$ and $E(\Gamma )=\{v_0{v}_i,v_0{u}_i|1\le i\le n\}\cup \left\{v_i{u}_i\right|1\le i\le n\}$, where $v_0$ is its universal vertex. We consider the following three cases:

• $\mathbf{Case}\mathbf{1}$: $k=2$. Let $S=\{v_i,v_j\}$ or $S=\{v_i,u_j\}$ or $S=\{u_i,u_j\}$, where $i\ne j$. If $1\le i\ne j\le n$, then $d_{\Gamma }\left(S\right)=2$. Otherwise, $S=\{u_i,v_i\}$ $(1\le i\le n)$ or $S=\{v_0,v_j\}$ $(1\le j\le n)$ or $S=\{v_0,u_j\}$ $(1\le j\le n)$. Then $d_{\Gamma }\left(S\right)=1$. Hence, ${sdiam}_2(\Gamma )=2$.
• $\mathbf{Case}\mathbf{2}$: $3\le k\le 2n$. Let $S=\left\{w\right|w\in V(\Gamma )-\left\{v_0\right\}\}$ such that $\left|S\right|=k$. Then, the subgraph $T_k$ induced by the edges in $E\left(T_k\right)=\left\{v_{0}w\right|w\in S\}$ is an S-Steiner tree; hence, $d_{\Gamma }\left(S\right)=\left|E\left(T_k\right)\right|=k$, and so ${sdiam}_k(\Gamma )\ge k$.

For any $S\backslash V(\Gamma )$, if $v_0\notin S$, then the subgraph $T_k$ induced by the edges in $E\left(T_k\right)=\left\{v_{0}w\right|w\in V(\Gamma )-\left\{v_0\right\}\}$ is an S-Steiner tree, and hence ${sdiam}_k(\Gamma )\le \left|S\right|=k$. If $v_0\in S$, then the subgraph $T_k$ induced by the edges in $E\left(T_k\right)=\left\{v_{0}w\right|w\in S-\left\{v_0\right\}\}$, and so $d\left(S\right)=|S-\left\{v_0\right\}|=k-1$; hence ${sdiam}_k(\Gamma )\le k$. Therefore, ${sdiam}_k(\Gamma )=k$.

• $\mathbf{Case}\mathbf{3}$: $k=2n+1$. Then, it follows from Theorem 1 that ${sdiam}_k\left((\Gamma )\right)=k-1$. □

Theorem 9.

Let k, n be two positive integers. Then,

$${sdiam}_k\left(L\left(F{r}_n\right)\right)=\left\{\begin{array}{cc}2k-1\hfill & \mathrm{i}\mathrm{f}2\le k\le n,\hfill \\ {\displaystyle \frac{k+3n-2}{2}}\hfill & \mathrm{i}\mathrm{f}n+1\le k\le 3n-2 \mathrm{a}\mathrm{n}\mathrm{d} k-n \mathrm{i}\mathrm{s} \mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n},\hfill \\ {\displaystyle \frac{k+3n-3}{2}}\hfill & \mathrm{i}\mathrm{f}n+1\le k\le 3n-3 \mathrm{a}\mathrm{n}\mathrm{d} k-n \mathrm{i}\mathrm{s} \mathrm{o}\mathrm{d}\mathrm{d},\hfill \\ k-1\hfill & \mathrm{i}\mathrm{f}3n-1\le k\le 3n.\hfill \end{array}\right.$$

Proof. 

Let $\Gamma =L\left(F{r}_n\right)$, $V(\Gamma )=\{v_1,u_1,\dots ,v_n,u_n$, $w_1,w_2,\dots ,w_n\}$ and $E(\Gamma )=\{v_i{v}_j,$ $u_i{u}_j|1\le i<j\le n\}\cup \left\{v_i{u}_j\right|1\le i,j\le n\}\cup \{w_i{v}_i,w_i{u}_i|1\le i\le n\}$. For any $w_i,w_j,v_s,v_t\in V(\Gamma )$, we have $d_{\Gamma }(v_s,v_t)=1$, $d_{\Gamma }(w_i,w_j)=3$, and

$$d_{\Gamma }(w_i,v_j)=d_{\Gamma }(w_i,u_j)=\left\{\begin{array}{cc}1\hfill & \mathrm{i}\mathrm{f} i=j,\hfill \\ 2\hfill & \mathrm{i}\mathrm{f} i\ne j.\hfill \end{array}\right.$$

(2)

We consider the following cases:

• $\mathbf{Case}\mathbf{1}$: $2\le k\le n$. First we assume that there is a set S with $\left|S\right|=k$ such that $S\cap \{v_1,u_1,\dots ,v_n,u_n\}\ne \varnothing$. Then, $d_{\Gamma }\left(S\right)\le 2(k-1)$.

Next, we assume that $S\cap \{v_1,u_1,\dots ,v_n,u_n\}=\varnothing$; that is, $S=\left\{w_i\right|1\le i\le k\}$. It follows from $\left(2\right)$ that $d_{\Gamma }\left(S\right)=3+2(k-2)=2k-1$, and hence $sdia{m}_k(\Gamma )=2k-1$.

• $\mathbf{Case}\mathbf{2}$: $n+1\le k\le 3n-2$, and $k-n$ is even. Let $\frac{k-n}{2}=t$. For any $S\backslash V(\Gamma )$ with $\left|S\right|=k$, let $D=S\cap \{v_1,u_1,\dots ,v_n,u_n\}$, $W_1=\left\{w_i\right|\{u_i,v_i\}\bigcap D\ne \varnothing ,w_i\in S-D\}$ and $W_2=\left\{w_i\right|\{u_i,v_i\}\bigcap D=\varnothing ,w_i\in S-D\}$. One can easily see that $\left|S\right|=\left|D\right|+|W_1|+|W_2|=k=n+2t$. Clearly, $d_{\Gamma }\left(D\right)=\left|D\right|-1$, and $|W_1|+|W_2|\le n$. Since $\left|S\right|=k=n+2t$, we have $\left|D\right|\ge 2t$, and hence, $|W_1|\ge t$. Therefore $|W_2|\le n-t$. Since $k\ge n+1$, it follows that there exists a vertex $u_i\in D$ or $v_i\in D$. If $w_j\in S$ and $u_j,v_j\notin D$ where $j\ne i$, then from (2), we have $d_{\Gamma }(w_i,u_j)=2$ or $d_{\Gamma }(w_i,v_j)=2$. If $u_i\in D$ or $v_i\in D$, then, $d_{\Gamma }(w_i,u_i)=1$. Thus we obtain

  $$d_{\Gamma }\left(S\right)=\left(\right|D|-1)+|W_1|+2|W_2|=n+2t-1+|W_2|\le 2n+t-1=\frac{k+3n-2}{2}.$$

Since S is any subset in $V(\Gamma )$ with $\left|S\right|=k$, we have ${\displaystyle sdia{m}_k(\Gamma )\le \frac{k+3n-2}{2}}$.

Let $S=\{v_j,u_j|1\le j\le t\}\cup \left\{w_i\right|1\le i\le n\}$. Then ${\displaystyle d_{\Gamma }\left(S\right)=(2t-1)+t+2(n-t)=t+2n-1=\frac{k+3n-2}{2}}$, and therefore ${\displaystyle sdia{m}_k(\Gamma )\ge \frac{k+3n-2}{2}}$. Hence, ${\displaystyle sdia{m}_k(\Gamma )=\frac{k+3n-2}{2}}$.

• $\mathbf{Case}\mathbf{3}$: $n+1\le k\le 3n-3$ and $k-n$ is odd. Let $\frac{k-n-1}{2}=t$. For any $S\backslash V(\Gamma )$ and $\left|S\right|=k$ and $k\ge n+1$, there exists a vertex $u_i\in S$ or $v_i\in S$. Similarly, as in the proof of $\mathbf{Case}\mathbf{1}$, we define D, $W_1$ and $W_2$. One can obtain easily that $\left|S\right|=\left|D\right|+|W_1|+|W_2|=k=n+2t+1$, $d_{\Gamma }\left(D\right)=\left|D\right|-1$, $|W_1|+|W_2|\le n$, $\left|D\right|\ge 2t+1$, $|W_1|\ge t+1$ and $|W_2|\le n-t-1$. From (2), we obtain

  $$d_{\Gamma }\left(S\right)=\left(\right|D|-1)+|W_1|+2|W_2|=n+2t+|W_2|\le 2n+t-1=\frac{k+3n-3}{2}.$$

Therefore, ${\displaystyle sdia{m}_k(\Gamma )\le \frac{k+3n-3}{2}}$.

Let $S=\{v_i,u_i|1\le i\le t\}\cup \left\{w_i\right|1\le i\le n\}\cup \left\{u_{t+1}\right\}$. Then, ${\displaystyle d_{\Gamma }\left(S\right)=2t+(t+1)+2(n-t-1)=\frac{3n+k-3}{2}}$, and hence ${\displaystyle sdia{m}_k(\Gamma )=\frac{3n+k-3}{2}}$.

• $\mathbf{Case}\mathbf{4}$: $3n-1\le k\le 3n$. Since $\kappa (\Gamma )=2$, it follows from Lemmas 2 and 3 that $sdia{m}_k(\Gamma )=k-1$. □

Theorem 10.

Let $K_{2,n}(n\ge 2)$ be a complete bipartite graph. Then,

$${sdiam}_k\left(L\left(K_{2,n}\right)\right)=\left\{\begin{array}{cc}k\hfill & \mathrm{i}\mathrm{f} 2\le k\le n,\hfill \\ k-1\hfill & \mathrm{i}\mathrm{f} n+1\le k\le 2n.\hfill \end{array}\right.$$

Proof. 

Let $V\left(L\left(K_{2,n}\right)\right)=U\cup V$ and $E\left(L\left(K_{2,n}\right)\right)={\displaystyle \bigcup _{1\le i<j\le n}}{u}_i{u}_j$ ${\displaystyle \bigcup _{1\le i<j\le n}}{v}_i{v}_j$ ${\displaystyle \bigcup _{1\le i\le n}}{u}_i{v}_i$, where $V=\{v_1,v_2,\dots ,v_n\}$ and $U=\{u_1,u_2,\dots ,u_n\}$. For any $S\backslash V\left(L\left(K_{2,n}\right)\right)$, let $U_1=U\cap S$ and $V_1=V\cap S$, where $|U_1|=s$, $|V_1|=t$ and $s+t=k$.

• $\mathbf{Case}\mathbf{1}$: $2\le k\le n$. First, we assume that there is no $i(1\le i\le n)$ such that $u_i\in U_1$ and $v_i\in V_1$. Without loss of generality, we can assume that if $S=\{u_1,u_2,\dots ,u_i,v_{i+1},\dots ,v_k\}$ $\left(\right|S|=k)$, there is a Steiner tree, T, obtained from $L\left(K_{2,n}\right)$ such that $E\left(T\right)={\displaystyle \bigcup _{1\le j\le i-1}}{u}_i{u}_j$ ${\displaystyle \bigcup _{i+2\le j\le k}}{v}_{i+1}{v}_j$ $\bigcup \{u_i{u}_{i+1},u_{i+1}{v}_{i+1}\}$. It follows that $d_{\Gamma }\left(S\right)=k$.

Next, we assume that there exists $i(1\le i\le n)$ such that $u_i\in U_1$ and $v_i\in V_1$. Then, we find a Steiner tree T such that $E\left(T\right)={\displaystyle \bigcup _{v_j\in V_1-\left\{v_i\right\}}}{v}_i{v}_j{\displaystyle \bigcup _{u_j\in U_1-\left\{u_i\right\}}}{u}_i{u}_j\bigcup \left\{v_i{u}_i\right\}$. Thus, $d_{\Gamma }\left(S\right)=(s-1)+(t-1)+1=k-1$. It follows that for $S\backslash V\left(L\left(K_{2,n}\right)\right)$ with $2\le \left|S\right|\le n$, we have $d_{\Gamma }\left(S\right)\le k$, and hence, ${sdiam}_k\left(L\left(K_{2,n}\right)\right)=k$.

• $\mathbf{Case}\mathbf{2}$: $n+1\le k\le 2n$. By the Nestle principle, there exists an $i(1\le i\le n)$ such that $u_i\in U_1$ and $v_i\in V_1$. Similar to $\mathbf{Case}\mathbf{1}$, $u_i\in U_1$, $v_i\in V_1$, and hence $d_{\Gamma }\left(S\right)\le k-1$, which means ${sdiam}_k\left(L\left(K_{2,n}\right)\right)\le k-1$. From Observation 3, ${sdiam}_k\left(L\left(K_{2,n}\right)\right)\ge k-1$, and hence, ${sdiam}_k\left(L\left(K_{2,n}\right)\right)=k-1$. □

Theorem 11.

Let $K_n$ be a complete graph of order n with positive integer k. Then

$${sdiam}_k\left(L\left(K_n\right)\right)=\left\{\begin{array}{cc}2(k-1)\hfill & \mathrm{i}\mathrm{f} 2\le k\le \lfloor \frac{n}{2}\rfloor ,\hfill \\ k\hfill & \mathrm{i}\mathrm{f} k=\left(\genfrac{}{}{0pt}{}{n}{2}\right)-2n+4,\hfill \\ k-1\hfill & \mathrm{i}\mathrm{f} \left(\genfrac{}{}{0pt}{}{n}{2}\right)-2n+5\le k\le \left(\genfrac{}{}{0pt}{}{n}{2}\right).\hfill \end{array}\right.$$

Let $\lfloor \frac{n}{2}\rfloor <k\le \left(\genfrac{}{}{0pt}{}{n}{2}\right)-2n+3$. Further, let t be a positive integer such that $n_t=2(t-1)t+\lfloor \frac{n}{2}\rfloor$, where $n_t<k\le n_{t+1}$. Then ${sdiam}_k\left(L\left(K_n\right)\right)\ge \lfloor \frac{n}{2}\rfloor +k-2t-1$.

Proof. 

Let $\Gamma =L\left(K_n\right)$. Then $V(\Gamma )=E\left(K_n\right)$. For any edge $e_1,e_2\in E\left(K_n\right)$, we have

$$d_{\Gamma }(e_1,e_2)=\left\{\begin{array}{cc}1\hfill & \mathrm{i}\mathrm{f} e_1,e_2 \mathrm{a}\mathrm{r}\mathrm{e} \mathrm{i}\mathrm{n}\mathrm{c}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{i}\mathrm{n} \Gamma ,\hfill \\ 2\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\hfill \end{array}\right.$$

Let M be a perfect matching or almost perfect matching in $K_n$. Then $\left|M\right|=\lfloor \frac{n}{2}\rfloor$.

• $\mathbf{Case}\mathbf{1}$: $2\le k\le \lfloor \frac{n}{2}\rfloor$. Let $S\backslash M$ with $\left|S\right|=k$. Recall that a Steiner tree connecting S is defined as a subgraph $T(V^{\prime },E^{\prime })$ of $\Gamma$, which is a subtree satisfying $S\backslash V^{\prime }$. Then $d_{\Gamma }\left(S\right)=2(k-1)$, and hence, ${sdiam}_k(\Gamma )\ge 2(k-1)$.

One can easily see that $diam(\Gamma )=2$. Together with Lemma 7, we obtain ${sdiam}_k(\Gamma )\le 2(k-1)$. Hence, ${sdiam}_k(\Gamma )=2(k-1)$.

• $\mathbf{Case}\mathbf{2}$: $k=\left(\genfrac{}{}{0pt}{}{n}{2}\right)-2n+4$. Let $V\left(K_n\right)=\{v_1,\dots ,v_n\}$. We denote by $N\left[v_i{v}_j\right]=\{v_i{v}_k,v_j{v}_{\ell }|$$1\le k,\ell \le n;k,\ell \notin \{i,j\}\}$, $1\le i\ne j\le n$. Let $C\subset V(\Gamma )$ be a subset of $\Gamma$ with $\left|C\right|=2n-4$. First, we assume that $C=N\left[v_i{v}_j\right],1\le i\ne j\le n$. Then C is a vertex cut of $\Gamma$. Let $S=V(\Gamma )-C$. Then $d_{\Gamma }\left(S\right)=\left|S\right|=k$.

Next, we assume that $C\ne N\left[v_i{v}_j\right],1\le i\ne j\le n$. For any $S_1=V(\Gamma )-C\subset V(\Gamma )$ with $|S_1|=k$, one can easily obtain that $d_{\Gamma }\left(S_1\right)=k-1$. Then ${sdiam}_k(\Gamma )=k$.

• $\mathbf{Case}\mathbf{3}$: $\left(\genfrac{}{}{0pt}{}{n}{2}\right)-2n+5\le k\le \left(\genfrac{}{}{0pt}{}{n}{2}\right)$. We have $\kappa (\Gamma )=2(n-2)$, and hence, $\Gamma \left[S\right]$ is connected for any $S=V(\Gamma )-C$, where $C\subset V(\Gamma )$ and $\left|C\right|<\kappa (\Gamma )$. Therefore, $\Gamma$ contains a spanning tree T of order $\left|S\right|$, and hence, ${sdiam}_k(\Gamma )=k-1$.

We now assume that $\lfloor \frac{n}{2}\rfloor <k\le \left(\genfrac{}{}{0pt}{}{n}{2}\right)-2n+3$ and $n_t=2(t-1)t+\lfloor \frac{n}{2}\rfloor$, where $n_t<k\le n_{t+1}$. Let $M=\{e_1,e_2,\dots ,e_t,e_{t+1},\dots ,e_{\lfloor \frac{n}{2}\rfloor }\}$. We denote by $E\left(\left[K_n\left[\{e_1,\dots ,e_t\}\right]\right]\right)$ the edge set of the subgraph induced by the edges in $\{e_1,\dots ,e_t\}$. Let $E_{K_n}[\left\{e_{t+1}\right\},\{e_1,e_2,\dots ,e_t\}]$ be the set of edges from $\left\{e_{t+1}\right\}$ to $\{e_1,e_2,\dots ,e_t\}$ in $K_n$.

Let $p_t$ be the number of edges in $M\cup E\left[K_n\left[\{e_1,\dots ,e_t\}\right]\right]$. Then $p_t-p_{t-1}=4(t-1)$ and $p_1=\left|M\right|=\lfloor \frac{n}{2}\rfloor$. It follows that

$$\begin{array}{cc}\hfill p_t=p_{t-1}+4(t-1)& =p_{t-2}+4(t-2)+4(t-1)\hfill \\ \hfill & =\cdots \cdots \hfill \\ \hfill & =p_1+4.1+4.2+\cdots +4(t-2)+4(t-1)\hfill \\ \hfill & =⌊\frac{n}{2}⌋+2t(t-1).\hfill \end{array}$$

Thus, we have $p_t=2(t-1)t+\lfloor \frac{n}{2}\rfloor =n_t$. Since $p_t=n_t<k\le n_{t+1}=p_{t+1}$, then we consider a set $S=M\cup E\left[K_n\left[\{e_1,\dots ,e_t\}\right]\right]\cup E_{K_n}[\left\{e_{t+1}\right\},\{e_1,\dots ,e_t\}]$, where $\left|S\right|=k$ and $|E_{K_n}[\left\{e_{t+1}\right\},\{e_1,\dots ,e_t\}]|=k-n_t$. By Observation 4, we have

$$d_G\left(S\right)=2\left(⌊\frac{n}{2}⌋-(t+1)\right)+\left(k-\left(\frac{n}{2}-(t+1)\right)-1\right)=k+⌊\frac{n}{2}⌋-t-2,$$

and hence ${sdiam}_k\left(L\left(K_n\right)\right)\ge \lfloor \frac{n}{2}\rfloor +k-t-2$. This completes the proof of the theorem. □

A general fan graph $F_{n_1,n_2}$ is defined as the graph join ${\overline{K}}_{n_1}\vee P_{n_2}$. We denote fan graph $F_{1,n-1}=K_1\vee P_{n-1}$ by $F_n$.

Theorem 12.

Let $F_n$ be a fan graph of order n with positive integer k. Then

$${sdiam}_k\left(F_n\right)=\left\{\begin{array}{cc}k\hfill & \mathrm{i}\mathrm{f}2\le k\le n-2,\hfill \\ k-1\hfill & \mathrm{i}\mathrm{f}n-1\le k\le n.\hfill \end{array}\right.$$

Proof. 

Let $V\left(F_n\right)=\{v_0,v_1,\cdots ,v_{n-1}\}$ and $E\left(F_n\right)=\left\{v_0{v}_i\right|1\le i\le n-1\}\cup \left\{v_i{v}_{i+1}\right|1\le i\le n-2\}$.

• $\mathbf{Case}\mathbf{1}$: $2\le k\le n-2$. Let $S\backslash V\left(F_n\right)$ with $\left|S\right|=k$. First, we assume that $v_0\notin S$. Let $S=\{v_{i_1},v_{i_2},\dots ,v_{i_k}\}$, where $1\le i_j\le n-1$ $(1\le j\le k)$. Then, the subgraph induced by the edges in $E\left(T_k\right)=\left\{v_0{v}_x\right|v_x\in S\}$ is an S-Steiner tree of $F_n$, and hence $d_{F_n}\left(S\right)=\left|S\right|=k$.

Next, we assume that $v_0\in S$. In this case, let $S=\{v_0,v_{i_1},\dots ,v_{i_{k-1}}\}$, where $1\le i_j\le n-1$ $(1\le j\le k-1)$. Then, the subgraph induced by the edges in $E\left(T_k\right)=\left\{v_0{v}_x\right|v_x\in S-\left\{v_0\right\}\}$ is an S-Steiner tree of $F_n$, and hence, $d_{F_n}\left(S\right)=\left|S\right|-1=k-1$. From the above result, one can easily see that $e_k\left(v\right)=k$ for $v\in S-\left\{v_0\right\}$, and $e_k\left(v_0\right)=k-1$. Hence, ${sdiam}_k\left(F_n\right)=k$ for $2\le k\le n-2$.

• $\mathbf{Case}\mathbf{2}$: $k=n-1$. First, we assume that $S=V\left(F_n\right)-\left\{v_i\right\}$ for $1\le i\le n-1$. Then, the subgraph induced by the edges in $E\left(T_{n-1}\right)=\left\{v_0{v}_i\right|v_i\in S\}$ is an S-Steiner tree, and hence, ${sdiam}_{n-1}\left(F_n\right)\le \left|E\left(T_{n-1}\right)\right|=n-2$. Next, we assume that $S=V\left(F_n\right)-\left\{v_0\right\}$. Then, the subgraph induced by the edges in $E\left(T_{n-1}\right)=\left\{v_i{v}_{i+1}\right|1\le i\le n-2\}$ is an S-Steiner tree, and hence, ${sdiam}_{n-1}\left(F_n\right)\le \left|E\left(T_{n-1}\right)\right|=n-2$. From Theorem 1, we have ${sdiam}_{n-1}\left(\left(F_n\right)\right)\ge n-2$, and hence, ${sdiam}_{n-1}\left(F_n\right)=n-2$.
• $\mathbf{Case}\mathbf{3}$: $k=n$. Then it follows from Lemma 1 that ${sdiam}_n\left(F_n\right)=n-1$. □

Theorem 13.

Let $F_n$ be a fan graph of order $n(\ge 5)$ with positive integer k. Then

$${sdiam}_k\left(L\left(F_n\right)\right)=\left\{\begin{array}{cc}2k-1\hfill & \mathrm{i}\mathrm{f}2\le k\le \lceil \frac{n-2}{3}\rceil ,\hfill \\ k\hfill & \mathrm{i}\mathrm{f}k=2n-6,\hfill \\ k-1\hfill & \mathrm{i}\mathrm{f}2n-5\le k\le 2n-3.\hfill \end{array}\right.$$

Proof. 

Let $L\left(F_n\right)=\Gamma$. Additionally, let $V(\Gamma )=\{v_1,v_2,\dots ,v_{n-1},$ $w_1,w_2,\dots ,w_{n-2}\}$ and $E\left(F_n\right)=\left\{v_i{v}_j\right|1\le i<j\le n-1\}\cup \{w_i{v}_i,w_i{v}_{i+1}|1\le i\le n-2\}\cup \left\{w_i{w}_{i+1}\right|1\le i\le n-3\}$. For any $w_i,w_j,v_s,v_t\in V(\Gamma )$, we have $d_{\Gamma }(v_s,v_t)=1$, and

$$d_{\Gamma }(w_i,w_j)=\left\{\begin{array}{cc}1\hfill & \mathrm{i}\mathrm{f}|i-j|=1,\hfill \\ 2\hfill & \mathrm{i}\mathrm{f}|i-j|=2,\hfill \\ 3\hfill & \mathrm{i}\mathrm{f}|i-j|\ge 3,\hfill \end{array}\right.$$

(3)

and

$$d_{\Gamma }(w_i,v_t)=\left\{\begin{array}{cc}1\hfill & \mathrm{i}\mathrm{f}|t-i|\le 1,\hfill \\ 2\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\hfill \end{array}\right.$$

(4)

• $\mathbf{Case}\mathbf{1}$: $2\le k\le \lceil \frac{n-2}{3}\rceil$. Since $n\ge 5$, we have $diam(\Gamma )=3$.

First, we assume that there is a set S with $\left|S\right|=k$ such that $S\cap \{v_1,v_2,\dots ,v_{n-1}\}\ne \varnothing$. From $\left(3\right)$ and $\left(4\right)$, we obtain $d_{\Gamma }\left(S\right)\le 2(k-1)$.

Next, we assume that $S\cap \{v_1,v_2,\dots ,v_{n-1}\}=\varnothing$. Then, one can easily see that $d_{\Gamma }\left(S\right)\le 1+2(k-1)=2k-1$. If we take $S=\left\{w_i\right|i\equiv 1(mod3)\mathrm{and}1\le i\le n-2\}$, then we obtain $d_{\Gamma }\left(S\right)=1+2(k-1)=2k-1$, and so ${sdiam}_k(\Gamma )=2k-1$.

• $\mathbf{Case}\mathbf{2}$: $k=2n-6$. Since $\kappa (\Gamma )=3$, it follows from Lemma 4 that ${sdiam}_k(\Gamma )=k$.
• $\mathbf{Case}\mathbf{3}$: $2n-5\le k\le 2n-3$. Since $\kappa (\Gamma )=3$, it follows from Lemmas 2 and 3 that ${sdiam}_k(\Gamma )=k-1$. □

We obtain the relation between the diameter of the line graph and the cardinal of vertex set S as follows.

Observation 6.

For any Γ and integer k, we have

$$k-1\le {sdiam}_k\left(L(\Gamma )\right)\le (k-1)(diam\left(L(\Gamma )\right).$$

Moreover, the bound is sharp.

Proof. 

From Observation 3 and Lemma 7, we have

$$k-1\le {sdiam}_k\left(L(\Gamma )\right)\le (k-1)(diam\left(L(\Gamma )\right).$$

□

We now address Problem 3 that we proposed in Section 1.3; that is, for integer $s,t$, $2\le s\le t$, is there a graph ${\Gamma }_{s,t}$ such that ${sdiam}_k\left({\Gamma }_{s,t}\right)=s$ and ${sdiam}_k\left(L\left({\Gamma }_{s,t}\right)\right)=t$?

In Table 2, we present some graphs $\Gamma$ such that ${sdiam}_k(\Gamma )=s$ and ${sdiam}_k\left(L(\Gamma )\right)=t$, which starts to provide a solution to Problem 3; that is, for each $s,t,$ $2\le s\le t$, is there a graph ${\Gamma }_{s,t}$ such that ${sdiam}_k\left({\Gamma }_{s,t}\right)=s$ and ${sdiam}_k\left(L\left({\Gamma }_{s,t}\right)\right)=t$?

Table 2. ${sdiam}_k\left({\Gamma }_{s,t}\right)=s$ and ${sdiam}_k\left(L\left({\Gamma }_{s,t}\right)\right)=t$.

Graph	s	t	k
$C_n$	s	s	$2\le k\le n$
$F{r}_n$	s	$2s-1$	$2\le k\le \lceil (n-2)/3\rceil$
$K_n$	s	$2(s-1)$	$2\le k\le \lfloor n/2\rfloor$

We indeed have the following general observations. For any graph $\Gamma$, let $u,v,w,z\in V(\Gamma )$ and $uv,wz\in E(\Gamma )$. Then

$$d_{L(\Gamma )}(uv,wz)=\left\{\begin{array}{cc}0\hfill & \mathrm{i}\mathrm{f} uv=wz,\hfill \\ 1+min\{d_{\Gamma }(u,w),d_{\Gamma }(u,z),d_{\Gamma }(v,w),d_{\Gamma }(v,z)\}\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\hfill \end{array}\right.$$

(5)

Observation 7.

Let Γ be a connected graph with $uv\in E(\Gamma )$. Then

$$|e_k^{L(\Gamma )}\left(uv\right)-e_k^{\Gamma }\left(v\right)|\le 2(k-1).$$

Proof. 

For any vertex $v\in V(\Gamma )$, we can assume that $S=\{v,u_1,\dots ,u_{k-1}\}\subset V(\Gamma )$ such that $e_k^{\Gamma }\left(v\right)=d_{\Gamma }\left(S\right)$. Let $S^{*}=\{u_i\in S|u_{i}y\in E(\Gamma ))$. Clearly, $d_{L(\Gamma )}\left(S^{*}\right)-d_{\Gamma }\left(S\right)\le 2(k-1)$, and hence $e_k^{L(\Gamma )}\left(uv\right)\le e_k^{\Gamma }\left(v\right)+2(k-1)$. □

Observation 8.

Let Γ be a graph of order n with positive integer k such that $2\le k\le n$. Then

$$0\le |{sdiam}_k\left(L(\Gamma )\right)-{sdiam}_k(\Gamma )|\le 2(k-1).$$

Moreover, the lower bound is sharp.

Theorem 14.

Let Γ be a graph of order n with size $m(\ge n)$ and positive integer k such that $2\le k\le n$. Then

$$0\le |{sdiam}_k\left(L(\Gamma )\right)-{sdiam}_k(\Gamma )|\le m-k.$$

Moreover, the bound is sharp.

Proof. 

From Observation 3, we have $k-1\le {sdiam}_k\left(L(\Gamma )\right)\le m-1$. From Theorem 1, we have $k-1\le {sdiam}_k(\Gamma )\le n-1$, and hence, ${sdiam}_k\left(L(\Gamma )\right)-{sdiam}_k(\Gamma )\le m-k$.

Let $\Gamma =C_n$. From Observation 5, the lower bound is sharp. If $k=n$, then the upper bound is sharp. □

6. Applications

During an economic debate on social networking technologies in education, Vicki A. Davis proposed the concept of education networks [36,37], where Steiner trees may find application. For instance, one may want to connect certain kinds of educational resources in a subnetwork that uses the smallest number of communication links. To do this, one needs a Steiner tree for the vertices of the subnetwork corresponding to the educational resources that need to be connected.

Combinatorial thinking, also known as “connected thinking” or “combined thinking”, is a way of thinking in which a number of seemingly unrelated things are connected so that they become a new and inseparable whole. Combinatorial thinking is innovative, contemporary and inheritable. Forms of combinatorial thinking include homogeneous combination, heterogeneous combination, recombination combination, shared substitution and concept combination.

Mathematics education researchers Rezaie and Gooya [38] speculated on the claim that learning combinatorial concepts requires a special way of thinking, and by reviewing the related literature in this area, they found that some researchers acknowledged this speculation and called it combinatorial thinking. In 2002, Graumann [39] regarded combinatorial thinking as a tool for solving problems when he was experimenting with children doing geometrical tasks.

As a more specific example related to the technical results that we report in this paper, graph operations such as line graphs are motivated by the desire to “construct” graphs with established properties to obtain new graphs that inherit those properties. From Proposition 2, we can get an upper bound of ${sdiam}_{n-2}(\Gamma )\le n-2$ from the upper bound of ${sdiam}_{n-2}\left(L(\Gamma )\right)$. One can also see from Theorem 5 that both ${sdiam}_3(\Gamma )\le 3$ and ${sdiam}_3\left(L(\Gamma )\right)\le 3$ hold. The teaching of graph operations is thus a good example for training combinatorial thinking ability.

7. Concluding Remarks

In this paper, we derived an algorithm to calculate the Steiner distance. Next, we provided a solution to Problem 1: that is, given a graph $\Gamma$ with ${sdiam}_k(\Gamma )\le k$, we wanted to find some induced subgraphs such that if $\Gamma$ did not contain such induced subgraphs, then ${sdiam}_k\left(L(\Gamma )\right)\le k$, where $k=3$. We also obtained a relationship between the Steiner k-diameter of a graph and its line graph and studied various properties of the Steiner diameter through a combinatorial approach. In addition, we obtained Steiner diameters for some special graphs. Moreover, whether for each $s,t$, $2\le s\le t$, there exists a graph ${\Gamma }_{s,t}$ such that ${sdiam}_k\left({\Gamma }_{s,t}\right)=s$ and ${sdiam}_k\left(L\left({\Gamma }_{s,t}\right)\right)=t$ is still open; we got several results, as shown in Table 2.