Abstract
This study contributes to the debate on accessibility of higher education in Chile, with a special focus on the geospatial dimension of access to university studies. This paper addresses the central question of whether geography (physical distance and neighborhood effects) plays a significant role in determining the accessibility of higher education to students in Chile. We use Heckman probit-type (Heckit) models to adjust for selection during application for higher education—that is, pre-selection among applications to study at university and, ultimately, admission (or denial) to a higher educational institution. Of all high school graduates who took the university selection test (PSU), only 37.9% were able to attend higher education. The results show that the geospatial elements—neighborhood characteristics and distance from the city of Santiago—have a significant local effect on the student’s application and access to Chilean universities. Specifically, the most significant local range for each candidate is 300 neighbors. We also find that, when distance to the capital city increases, the probability of applying to university increases to a threshold of 1400 km, at which point probability begins to decrease.
1. Introduction
Access to university education is a real concern for policymakers all over the world. This is particularly true in the case of Chile, where the government has invested intense efforts into providing equal access for students from families of different socioeconomic levels. Due to the stratification of education in Chile, admission to universities reflects an inequitable educational system [1,2]. At the same time, economic and demographic concentration in the central part of the country plays a large role in students’ performance, as is reflected in the results of the University Selection Test (PSU); the best results are clustered in the central area around the city of Santiago de Chile.
Unfortunately, an OECD report [3] concluded that differences in university access and student performance persist in Chile. Specifically, the report found indications that access to higher education depends on students’ socioeconomic status, secondary schooling, and region of origin. It is thus important to understand how personal characteristics, reflected in socioeconomic and geographic items, influence students’ enrollment in university education to generate empirical evidence that contributes to the design of public policies in the area of university education. To our knowledge, this conclusion has never been tested with real microdata in Chile. This paper’s goal is thus to examine access to university education in Chile using cross-sectional data for about 300,000 students who finished high school in 2016. The database we use contains information on students’ high school grades, selection test scores, applications to the university, as well as personal and family characteristics.
Our analysis focuses on the two stages each student must complete before he/she can begin university study in Chile. In the first stage, each student must pass a selection test; if they pass the test, they may apply to university. The university application implies the student’s deliberate decision or willingness to participate in university education, which is clearly conditional on passing the test. In the second stage, after the university application, each student must wait for their admission decision (admission/denial) to access university education. This decision is taken by the Department of Evaluation, Measurement, and Educational Registration (DEMRE) of the University of Chile in Santiago de Chile.
While sociology and psychology have highlighted the main role of the environment where students live and their social networks, the economic literature focuses mainly on the socioeconomic characteristics of the family as a key factor defining students’ probability of attending university. Our database on the PSU overcomes the difficulty of finding fine-scale georeferenced secondary statistics from which to build spatial models. We focus specifically on two types of potential socio-interaction effects on the student’s decisions: neighborhood and network (social capital).
To improve our understanding of the determinants of accessibility to higher education in Chile, we estimate a sequence of two Heckman probit (Heckit) models, one for each stage mentioned above. We estimate both non-spatial and spatial versions of the Heckit model, where the spatial application accounts for the potential impact of social interactions—in the form of local spatial spillovers—on the probability of passing the initial selection test and on the likelihood of applying to the university. We also employ a confirmatory factor analysis to create a latent variable for use in our model that would avoid collinearity and resolve the problem of choosing between four variables: (1) father’s education, (2) mother’s education, (3) household income, and (4) type of student’s secondary school. The new composite variable is one of the excluded variables (instrumental variables) in the selection equation of the two Heckman probit models. This variable is also considered a proxy variable for students’ social capital, as explained below. Estimation of the Heckit models provides evidence of significant differences in university access in Chile, depending on gender, social network/capital, and geographic location of the student’s home province.
This paper is organized as follows. After the introduction, we present a literature review on the determinants of access to higher education and the main characteristics of the university admission system in Chile. The third section presents the data sources and variable statistics. Section 4, Section 5 and Section 6 then develop the estimation strategy, the main results, and a discussion section, respectively. The conclusions, an appendix, and the references close this paper.
2. Literature Review
2.1. Determinants of Access to Higher Education
Access to higher education and its determinants have been studied extensively in analyses of countries all over the world of widely varying scopes. A Google Scholar search for the term “access to higher education” from 2018 onwards found almost 20,000 references. Despite logical differences in these studies’ perspectives, most converge toward identifying three main factors that cause a high school student to attend university [4]: socioeconomic status, primary and secondary schools, and public subsidies.
Socioeconomic status is considered the most important determinant of access to higher education. Despite sustained investments in access and applications to higher education, students continue to be stratified by socioeconomic status almost everywhere in the world. This trend has intensified since the Great Recession, as most states had to curb public spending on public colleges and universities, seriously jeopardizing affordability and access to low-income students, students of color, students from underrepresented minorities, and students with illiterate parents or parents with low education levels [5,6].
Students from backgrounds of lower socioeconomic status are almost three times more likely than advantaged students not to attain the baseline level of proficiency in science. Even if they manage to enter university, fewer than 5% of students from disadvantaged backgrounds matriculate at highly selective universities [4]. The decision to access higher education is also due to family structure, although to a lesser extent [7], which may explain some contradictory results on the influence of gender and students’ siblings on propensity to access the university [8,9].
A second determinant is the type of school attended, including quality of teachers. It is well-known that failure in school affects a child for life, ultimately excluding them from higher education and even the civic and democratic aspects of modern societies. Additionally, a body of literature on developing countries that compares low-cost private schools to state schools in India [10,11] and Kenya [12,13] shows that students from private schools are more likely to achieve better results than students in public schools. This gap between private and public schools may occur because students from wealthier families and of higher social status tend to attend private schools [14]. In Chile, where it was possible to compare students from public and private schools in similar environments, the advantage of private schools was less pronounced [15,16].
A third important factor influencing access to higher education is public and private subsidiarity and solidarity, which provides support for students who wish to go to university, prioritizing those from the most vulnerable social groups. Most countries have implemented government financial aid, such as cash transfers or fellowships to help low-income and pregnant teenagers as well as other candidates from underrepresented groups to complete high school and to attend university. This is also the case in Chile [17,18]. Once these students enter university, they must meet their financial responsibilities with the help of economic subsidies such as loans, scholarships, and free tuition designed to help them avoid dropping out and to encourage them to persist in completing their degrees.
Additionally, the literature has identified another important element to consider when analyzing access to higher education: the student’s place of origin. Individuals who share the same social space can act in a similar way because they present the same unobservable factors, such as cultural economic conditions, as well as the occupational structure and institutional framework of the environment [19,20]. In the case of education, geography and academic achievement are linked through the effects of social composition in local areas [21]. This connection is also explained in [22], which notes that average educational achievement would not vary spatially if groups of people were equally distributed across space and the provision of education were equally and homogeneously distributed across space. This achievement would only be affected by factors such as individual ability and family background. Studies [23,24] have investigated the expectations and academic achievement of young people living in urban and rural sectors of Canada, where students from rural areas have lower expectations and academic achievement than other students when we control for the variables parental background, gender, and education. Analyses of students’ decision to apply to university show that students’ decisions depend significantly on their geographical location and the score obtained (below or above average) on the US Scholastic Aptitude Test (SAT) [25]. Other studies highlight living close to a university as a determining factor [26].
From a geographical perspective, we find a constellation of papers reviewing the determinants of access to higher education on all five continents and in almost every country globally. Just a few of the studies performed in the last five years and not cited above include interesting cross-country analyses, such as [27,28], and many insightful studies of individual countries or regions. In Europe, studies [29,30,31,32,33] of Croatia, Portugal, Greece, Italy, and Russia focus on analyses of inequalities in access to university, with a special scope that includes the refugee crisis. In Asia, an analysis of the determinants of university access was complemented by studies of the unequal impact of expansion of higher education on university access and the implementation of policies to guarantee quotas for lower-class candidates at good universities [34,35,36]. Studies of Africa [37] and Latin America were also interested in detecting the influence of being part of a vulnerable group (illiterate parents, women, African Americans, etc.) on university access [38,39,40].
2.2. The Chilean Higher Education Admissions System
In Chile, the debate over higher education frequently mentions “equity.” Improving “equity access” is vital because students from low-income families are least likely to attend post-secondary studies [3]. As shown above, the problem of equity access stems from a multiplicity of related phenomena (e.g., [7,8]), but the most significant in Chile is socioeconomic status. The quality of secondary education varies significantly, as children from low-income families who cannot pay for a private school achieve less academic success and thus fall into the least advantaged student group. As this situation has repercussions for the university application process, an urgent need exists to reflect family background in the process [9,10].
The Chilean university admissions system has historically been based on two indicators [1]. The first is the score the student obtains on a standardized test (PSU) that measures skills in the areas of mathematics, language and communication, history, social science and geography, and sciences. The second is the grades that the student obtained in secondary education.
Until January 2021, the application process to access Chilean universities consisted of three steps:
- The students had to pass the PSU, organized by the “Departamento de Evaluación, Medición y Registro Educacional” (DEMRE) of the Universidad de Santiago. To pass, they have to obtain a minimum score of 475 points out of 850.
- Once they pass the PSU, prospective students must decide whether to apply to the universities that belong to the Unified Admission System (SUA). Historically, only traditional universities used this system. In 2011, non-traditional universities were allowed to participate after evaluation by the Council of Chilean University Vice-Chancellors (CRUCH) to determine whether they met the necessary quality standards.
- After submitting their application, students received an admission decision, based on their PSU score.
In [3], the standard tests in the application process to attend universities in Chile were analyzed. The authors noted the need to consider the geographical location of the students’ home, as its impact was not clear. More specifically, the OECD’s report observed that the PSU score might be explained by family income level, secondary school performance, and urbanization level. In fact, many rural areas have smaller numbers of schools and fewer resources.
Students who decide to apply to SUA universities may choose up to 10 options, applying to different programs at different universities. They must rank their selections to prioritize the programs in order of preference; once their score earns them acceptance to a university program, the other options are disqualified. Since acceptance/denial is based on the student’s PSU score, the students with the best scores are more likely to be accepted into the program of their choice.
3. Data and Variables
3.1. Data Source and Descriptive Statistics
Our data were provided by the Universidad de Antofagasta from the DEMRE. This entity holds the official PSU test score records with some information about all high school graduates who took this selection test in the year 2016. The database also contains information about students’ secondary school type and grades, PSU selection test scores and applications to the university, and basic personal characteristics. Initially, this database covered about 300,000 students, although only 267,233 students took the exam. After eliminating the records that contained missing values, the database retained a total of 260,775 “useable” observations, that is, the entire population sample of students potentially eligible for participation in higher education.
The database was georeferenced using an R script to construct the spatial weights matrices and to calculate the geographical distances to the centroid of Santiago de Chile city, which is also the socioeconomic center of the country. Rural–urban classification was taken from the Ministry of Education (MINEDU), which assigns this qualification to the schools according to the students’ origin.
Given that our main goal was to examine access to higher education in Chile and potential disparities in the process of university enrollment across different groups of high school graduates, we focused on a set of core variables representing basic student characteristics as well as geographical distance from students to universities. We also examined the role of the variable “social capital” in students’ decisions to apply to university.
3.1.1. Students’ Characteristics
Key variables in our analysis are individual characteristics of the high school graduates, such as gender and age. Two sets of characteristics of great interest in our analysis were used as proxy variables for latent ability and motivation/opportunities, respectively. As shown in Table 1, the first set comprises secondary school grades (“GRADE_PTS”) and PSU selection test scores (“LIT_SCORE” and “MATH_SCORE”), which evaluate cognitive skills related to literature and mathematics, respectively. The second set of characteristics includes the students’ employment status (“WORKING”) and their siblings’ education (“SIBL_UNIV”) [41,42].

Table 1.
Descriptive statistics for the sample of university candidates.
3.1.2. Location Factors
First, we distinguished between two types of students’ place of origin using information about the type of college (public, subsidized, and private). Students who graduated were represented as a dummy variable: “rural” if the students graduated from a rural high school or “urban” if they graduated from an “urban high school”.
Second, we considered the role of geographical distance as affecting access to higher education, through its relationship with success in passing the selection test and propensity to apply to study at university. To this end, we calculated the distances from each student’s home location to Santiago de Chile city centroid (“DISTANCE”). The average distance to the Santiago city centroid is about 310 km, ranging from 40 m to about 3800 km. Distance is an important variable because the best PSU selection test scores correspond to residents living in the center of the country, close to Santiago, perhaps due to the extreme socioeconomic concentration of Chile around the Metropolitan Region of Santiago. We thus expected that, the larger this distance, the smaller the probability of successfully passing the selection test and the propensity to apply to study at university.
3.1.3. Localized Social Capital
A strong correlation exists between parents’ (mother’s and father’s) education, family income, and type of student’s secondary school. This correlation causes a problem of multicollinearity when these variables are used in a regression model. To tackle this situation, we decided to build a latent variable with these four variables using confirmatory factor analysis (see in Appendix A the estimation results). The new composite variable is one of the excluded (instrumental) variables in the selection equation of the two Heckman probit models, but it can also be considered a variable representing students’ social capital.
The social capital variable is a complex variegated social mechanism. Parents garner social capital to give their children the best chance of success in personal and professional life. The notion of social capital presented in [43] is attractive because it provides a conceptual link between the attributes of individual actors and their immediate social contexts, most notably family, school, and neighborhood [44]. These authors provide a simple way to compute this variable, defining social capital as a mere combination of three variables—intellectual aspect, tangible economic aspect, and social networks—that can be approximated by mother’s and father’s education level, household income, and type of student’s secondary school, respectively. In Chile, the students’ ordinary school is, in effect, a good social “proxy” of social networks, since access to elitist private secondary schools is conditioned by household income and parents’ high education level [45].
Table 1 also presents basic sample descriptive statistics for the 267,233 high school graduates participating in the 2016 PSU selection test. The table also includes descriptive statistics for the model control variables. The variable “APPLICATION” includes the group of 18,885 students who did not pass the PSU. On average, only 2% of high school graduates come from rural and 30% have siblings in university. Additionally, only 9.8% of PSU candidates are working, probably because most people who work value their present incomes more than future earnings from a university degree.
3.2. Exploratory Data Analysis
3.2.1. Higher Education System Design: Selection—Application—Admission
Of all high school graduates who took the PSU selection test in 2016, only 53.9% passed (Figure 1). Next, of the 60.3% students who passed the selection test, only 46.6% applied to university. Finally, only 37.9% of the initial high school graduates who decided to take the PSU had access to higher education.
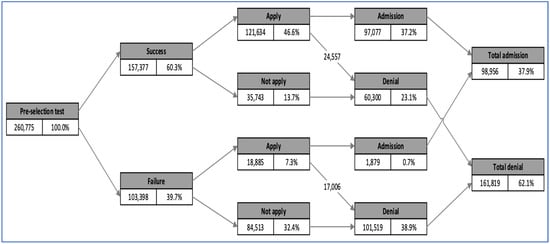
Figure 1.
Trajectory data distribution.
The minimum score for the pre-selection test is 475 points. A student must pass this pre-selection test before applying for university admission and accessing higher education. However, some universities make exceptions, admitting candidates with a score of 450.
3.2.2. Geography of Access to Higher Education: Distances and Neighborhoods
The detailed microlevel information provided by our database (i.e., each student’s postal address) enables us to examine the spatial dimension of university access in Chile. Students’ geospatial context is likely to determine their social class and identity, influencing their decision-making throughout the three stages of the process to access higher education in Chile.
Unfortunately, we encountered difficulties in georeferencing students’ locations. Several postal addresses contained odd characters, and some addresses registered did not exist. To solve these problems, we applied an R-function to geocode the addresses based on Google’s Application Programming Interface for the Geo-Coding Function. When we found erroneous addresses that we could not geocode exactly, we assigned these locations the centroid coordinates of their corresponding communes.
We checked this variable to ensure that all addresses were within the expected distance radius. In Figure 2, boxplots are used to visualize the outcome of the georeferencing process.
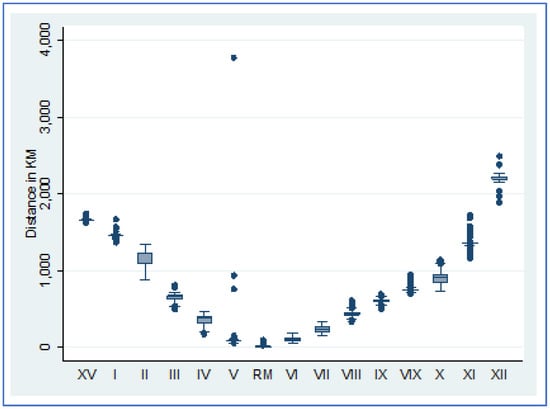
Figure 2.
Distance to Santiago distributions after the georeferencing process.
The boxplots represent the distribution of distances from each candidate’s home to the city of Santiago. There is one boxplot for each Chilean region. The horizontal axis plots the Chilean regions in Roman numerals. XV represents Arica and Parinacota, I represents Tarapacá, II represents Antofagasta, III represents Atacama, IV represents Coquimbo, V represents Valparaíso, RM represents Metropolitan Region of Santiago, VI represents O’Higgins, VII represents Maule, VIII represents Bío-Bío, IX represents Araucanía, XIV represents Los Ríos, X represents Los Lagos, XI represents Aysén, and XII represents Magallanes. The figure shows only a few outliers in the V region (Valparaíso). These outliers are accurate, as they correspond to some of the Pacific islands that fall under the Valparaíso Region’s administration.
4. Estimation Strategy
We are interested in the effects that individual student characteristics have on the probability that recent high school graduates—at least those who participated in the selection test—will access university education in Chile. This goal gives rise to two separate (sequential) procedures, visualized in the flowchart in Figure 3.
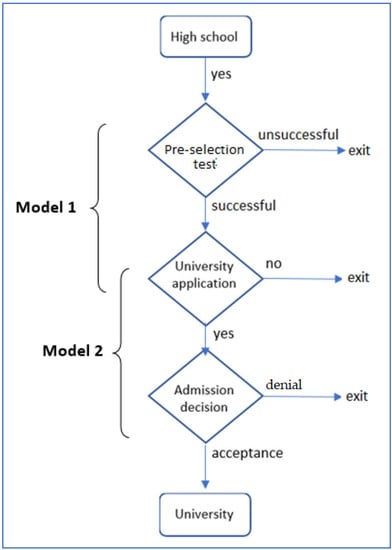
Figure 3.
Flowchart of the trajectory toward higher education.
4.1. Heckman Probit Models
We estimate two Heckman probit (Heckit) models. Both baseline models use the same sample population of (260,755) students potentially eligible for higher education in Chile in 2016.
4.1.1. Baseline Model 1
The modeling strategy assumption in Model 1 is that high school graduates’ primary decision is whether to take the (mandatory) country-wide pre-selection test. Only in the second stage, conditional upon successfully passing this pre-selection test, must the student decide whether to apply to the university. In the absence of longitudinal data, we use the natural estimation strategy, a Heckman correction procedure.
More specifically, we use the Heckit model ([46]; see also [47]), which allows for an estimation of the two probit models with controls for self-selection bias, which may arise due to the exclusion of students who exit the application process for higher education (i.e., insufficient score on the PSU or no application to university). We find two examples of Heckit estimations close to those in this paper in [48,49].
In Model 1, if the students who must decide whether to apply to university differ systematically from high school graduates who did not pass the pre-selection test, the estimated coefficients of the determinants of the application decision are likely to be biased. To address this potential selection bias in the probit estimation, we estimate two probit models, where each model consists of a (probit) selection equation and a (probit) outcome equation (see also [50]):
where Equation (1) is the main equation and Equation (2) the selection equation. The binary outcome in Equation (1), which is related to the student’s decision whether to apply to university, is of course only observed if the student passes the PSU. The dependent variable in Equation (2) is also a binary variable and takes a value of one for students who passed the PSU and zero otherwise.
It is further assumed that the error terms, representing idiosyncratic unobservable variables, are bivariate normal and independent of the explanatory variables (exogeneity) in both equations:
where the models are estimated using Maximum Likelihood (ML). The log likelihood is computed as follows:
where S is the set of observations for which yi is observed, is the cumulative bivariate normal distribution function (with mean [0 0]′), is the standard cumulative normal, and is an optional weight for observation i.
The selection-bias problem in Equation (1) occurs when the error terms in the two equations are correlated (. The Heckit approach should correct for such selection biases by also estimating Equation (2), thus providing consistent and asymptotically efficient estimates for the unknown parameters in the model.
4.1.2. Baseline Model 2
We follow the same approach as in Model 1. Along similar lines, the model encompasses the binary outcome in Equation (7). This outcome is related to the DEMRE’s final decision to admit or deny students access to higher education, where the binary outcome is only observed if the student in fact applies to university. The dependent variable in Equation (8) is also a binary variable that takes a value of one for students who applied to university and zero otherwise. If applicants admitted to university education differ systematically from high school graduates who did not apply to university, the estimated coefficients of the determinants of the admission decision are likely to be biased.
To address this potential selection bias, we again estimate two probit models, each model consisting of a (probit) selection equation and an (probit) outcome equation:
under similar assumptions to those in Model 1.
4.2. Heckman Probit Models with Spatial Effects
In this section, we augment the previous Heckit models to include spatially lagged explanatory variables to account for the student’s neighborhood and to address the endogeneity problem caused by spatial autocorrelation. We use GeoDa software [51] to estimate the spatial lag variables and Stata’s ‘heckprob’ command to estimate the Heckman probit models with sample selection.
More specifically, we consider two ways of including spatial effects in the Heckit model. First, we show that Moran’s I test is calculated on the residuals of the Heckit model. Second, we examine the role of localized social interactions between “neighbors” (nearby in a spatial sense) that occur in the context of information exchange and social context related to participation in higher education.
4.2.1. Endogeneity Issues and Spatial Autocorrelation Test of the Residuals
An endogeneity problem may arise because individual students who live in the same socio-spatial setting (social space) may act in a similar way because they share common unobservable factors or institutional environments [52]. This phenomenon creates spatial dependence that reflects a situation in which a given student’s values may be contingent on the values of students living nearby [53].
We thus calculate the Moran’s I test statistic to assess the presence of spatial error autocorrelation in the Heckit model. The general form of Moran’s I is given by the following:
where
in which is the n × 1 vector of the generalized residual of the Heckit model; W is the familiar n × n spatial weights matrix, which reflects the vicinity relations among the n spatial observations, where the main diagonal is equal to zero by convention; and is a normalizing factor [54]. The generalized residual values of the Heckit model are calculated as follows:
where , and are the maximum likelihood estimates of the variable parameters and inter-equation residual covariance, respectively, and and denote the probability density and cumulative distribution functions of the standard normal distribution. The term in curly brackets, known as the inverse Mills ratio, coincides with the generalized residual of the probit model [55].
4.2.2. A Spatial Heckit Model
The spatial version of Heckit Model 1 (university application) takes the form of a cross-sectional spatially lagged SLX model ([56]; see also [57,58]). This model incorporates an augmented outcome equation to account for the latent spatial structure of the decision-making process, reflected by , given by the following:
where contains the usual explanatory variables (as in the standard Heckit model), W is the spatial weights matrix indicating “nearest neighbors”, are the spatial lagged variables representing local “spillovers”, and γ1 is an additional vector of unknown parameters to capture interaction spatial effects [53].
Local spatial spillovers are appropriate when the proper spatial range of the explanatory variables is the location and its immediate neighbors (but not beyond), that is, the range of neighbors considered in the reference space—for example, only direct neighbors, not neighbors’ neighbors [59]. This concept is in line with [44], which used the nearby environment of students’ addresses (family, school, and neighborhood) as its main spatial contextual reference.
Similarly, we extend the selection equation in Model 1 by including an SLX term:
For Heckit Model 2, university application becomes the selection criterion. We thus extend the selection equation to include only SLX terms, not the outcome equation, because admission depends on the decision of the DEMRE (not of the student):
5. Estimation Results
5.1. Baseline Models
This section presents the results for two baseline models.
- Baseline Model 1
- Main equation:
- Selection equation:
This first baseline model uses the variables “RURAL”, “SIBL_UNIV”, and “SOCIAL_CAP” as exclusion criteria (instruments) that correlate with selection (“PRE-SELECTION”) but not with the binary outcome in the main equation (“APPLICATION”). In both models, the scores and distance variables are transformed in natural logarithms: “Log(LIT_SCORE)”, “Log(MATH_SCORE)”, “Log(GRADE_PTS)”, “Log(DISTANCE)”, and “[Log(DISTANCE)]2”.
- Baseline Model 2
- Main equation:
- Selection equation:
This model uses the variables “RURAL”, “Log(DISTANCE)”, “[Log(DISTANCE)]2”, “WORKING”, and “SOCIAL_CAP” as exclusion criteria (instruments) that correlate with selection (“APPLICATION”) but not with the binary outcome in the main equation (“ADMISSION”).
Table 2 shows the results of the baseline models, which can be replicated—along with estimations of the spatial models—using the database and coding available from [60]. For both models, we found a statistically significant selection of unobserved factors (non-negative correlation between the errors of the main and selection equations). That is, (i) applicants to university are systematically different from the students who did not pass the pre-selection test (Model 1) and (ii) applicants to university who are granted admission to higher education are likely to be systematically different from students who did not apply to university.

Table 2.
Estimated coefficients from Heckman probit—baseline models.
In the application model, as expected, the variables with considerable influence on the probability of being admitted into university are the test results, and the mathematics test has the most significant effect on the probability that a student will apply to university. Grades are another variable with considerable influence on the probability of a student applying to university.
Students’ characteristic variables are also important in explaining the probability of both being preselected and applying to university. Women are less likely to pass the PSU, but once they have passed this exam, they are more likely than men to apply to university. After the application process, however, the probability of being accepted into higher education is significantly lower for women.
Additionally, working students are less likely to pass the PSU and to apply to university. This phenomenon could reflect lower priority and/or interest in educating these candidates or higher opportunity cost of accessing the university.
As for the familial variables, students with siblings at university are more likely to pass the PSU, as are those with higher levels of social capital (a composite variable of parental education and family income). Candidates living in rural areas are less likely to pass the PSU.
Finally, distance to Santiago plays a different role in the pre-selection and application equations. On the one hand, the probability of passing the PSU declines linearly with distance to Santiago, but once students pass this exam, there is a non-linear positive relation between distance to Santiago and probability of applying to university (Figure 4).
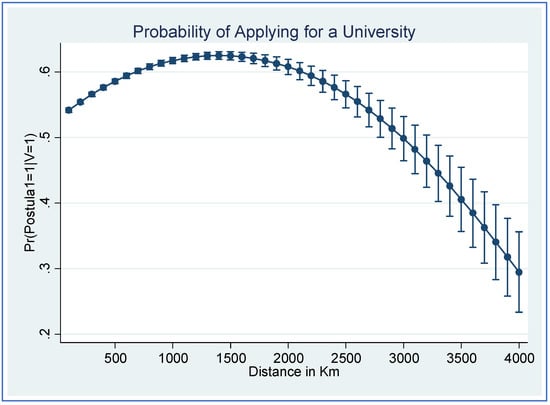
Figure 4.
Effect of distance from students’ home to Santiago city on the probability of applying to university.
Students living in peripheral areas are viewed as more likely to apply to university. The distance variable shows an inverted U effect on applying to the university. That is, when distance to Santiago increases, the probability of applying to university increases to a threshold of 1400 km (Antofagasta region, in the North and Aysén region, in the South), at which point it begins to decrease. Additionally, the probability of applying is an increasingly variable, from the distance threshold to the country limits. This variability can be explained by the many private universities concentrated in the Metropolitan Region. The private universities offer their residents more opportunities to access higher education once they pass the PSU than those that are available to people living farther from Santiago, who opt to apply to the traditional higher education system.
5.2. Spatial Models
5.2.1. Specification of the Spatial Weights Matrix
Based on the spatial distribution of the individual students in Chile, we identify spatial neighborhoods to be used in the construction of the spatial weights matrix. We use an exploratory approach to characterize the structure of the spatial weights matrix W. More specifically, based on the addresses of all the students, we performed Thiessen polygonization to define the spatial contiguity within the neighborhood. The most frequent number of neighbors was three, covering around 41% of the total number of students. Taking this into consideration, we specified three different W matrices: (i) dispersed matrix (few neighbors), 3 neighbors; (ii) dense matrix (more neighbors), 100 neighbors; (iii) very dense matrix, 300 neighbors.
Table 3 shows the results from Moran’s I test of the residuals of the baseline models—Equations (9) and (10)—using an inferential process based on the permutation approach (9999 permutations). Moran’s I is statistically significant for the three types of W matrices, and the dense matrix shows the most significant z-value.

Table 3.
Results of Moran’s I test on the baseline model residuals.
Despite the high significance of the tests, with pseudo p-values at 0.001, the slope of the regression line in the Moran scatterplot exhibits a weak and uniform pattern of spatial association. The Moran scatter plot was first outlined in [59]. It consists of a plot with the spatially lagged variable on the y-axis and the original variable on the x-axis. The slope of the linear fit to the scatter plot equals Moran’s I. Figure 5 represent these plots for the dense and most significant spatial weights matrix, .
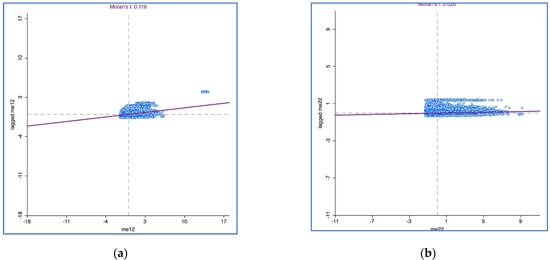
Figure 5.
Moran’s I test on the model residuals for . (a) Baseline model; (b) Spatial Model.
Spatial autocorrelation analysis of the baseline model residuals thus demonstrates the existence of statistically significant spatial neighborhood effects influencing the university access process in Chile, especially in the vicinity of 300 neighbors. This spatial effect is not very strong for the global spatial structure, however, suggesting the existence of local spatial externalities—spillovers—in this phenomenon. As stated above, the SLX model estimates local spatial spillovers, which are suitable for our purpose here. Additionally, as pointed out in [61], when spatial dependence is weak, the best fitting specification might be the SLX model.
5.2.2. SLX Heckit Model Results
Next, we present the specification of the SLX Heckit models for a spatial weights matrix of 300 neighbors (W300).
- Spatial Model 1
- Main equation:
- Selection equation:
This model uses the statistically significant variables “SIBL_UNIV” and “SOCIAL_CAP” as exclusion criteria (instruments) that correlate with selection (“PRE-SELECTION”) but not with the binary outcome in the main equation (“APPLICATION”).
- Spatial Model 2
- Main equation:
- Main equation:
This model uses the statistically significant variables “WORKING” and “SOCIAL_CAP” as exclusion criteria (instruments) that correlate with selection (“APPLICATION”) but not with the binary outcome in the main equation (“ADMISSION”).
Table 4 shows the main outcomes of the SLX Heckit models. In Spatial Model 1, each candidate’s social capital and having siblings already enrolled in the university have positives effect on the probability of successfully passing the PSU. Additionally, the spatial neighborhood of the 300 nearest candidates leverages the positive impact of these variables. That is, the existence of nearby applicants with high levels of social capital and siblings at the university influences a candidate positively to pass the PSU. Hence, a “good” social environment matters for success on the PSU.

Table 4.
Estimated coefficients of the spatial Heckman probit models.
Having good high school grades and not having a job are significant in explaining candidates’ probability of both passing the PSU and applying to university. In this case, however, students are also affected by their closest neighbors’ performance in high school and professional situation. The spatial effect of the variable “WORKING” in particular is significantly higher, indicating that the presence in a student’s neighborhood of many high school peer graduates already working discourage him/her from applying to university after passing the PSU.
In Spatial Model 2, social capital also has a significant positive effect on a student’s probability of applying to university, and having a job has a significant negative effect, as shown above. In this case, the candidates’ spatial neighborhood influences their decision to apply to university through social capital and professional situation. As for ultimate acceptance to a university and a career, spatial effects are not relevant, since this decision is made exclusively by the university.
A student’s spatial vicinity is thus crucial to ensuring that a candidate both passes the PSU exam and applies to university. Specifically, four variables have local spillovers: social capital, professional situation, having siblings studying at a university, and having good marks in high school. The best environment for a student to succeed in accessing higher education in Chile includes peers who obtained good marks in high school and do not have a job, high social capital, and siblings already studying at a university.
Conversely, the worst neighborhood for a higher education candidate includes peers who obtained bad grades in high school and have a job, a lack of good social capital status, or no siblings at university. We also add other environmental variables with a negative impact on higher education accessibility, such as living in rural areas and/or ultra-peripheral regions, over 1400 km from Santiago. It is thus important for the state to foster policies that motivate students living in working-class neighborhoods—understood as communities that have low social capital, few siblings studying in college, and many classmates who are employed—to see university as a valid option for their personal advancement. Students who live in environments with good secondary schools, where students earn good grades, are more likely to apply than others. This finding strengthens support for the abovementioned need to foster public policies to improve the quality of secondary education in the most disadvantaged neighborhoods.
The results indicate a problem of gender inequality. Although women’s likelihood of applying to university is higher than men’s, their probability of ultimately being accepted is significantly lower. This is clearly a serious problem that merits further in-depth study to see whether bias exists in the model used or in the type of education women receive. The effect of the candidates’ social capital, while statistically significant, does not seem as relevant as initially expected, perhaps due to its correlation with the effect of the variable of student grade-point average in secondary education and score on the PSU.
Distance to Santiago seems to have an inverted U-shaped effect, such that the greater the distance between students and Santiago, the greater students’ probability of applying to and being accepted at university. This trend continued up to a threshold distance of 1400 km or to the regions at the geographical extremes of Chile—region II in the north and region XI in the south. As stated above, the best university education system is clearly concentrated in the central region of Chile, as are many private universities that do not form part of the PSU admission system and to which students can apply if they are not admitted to traditional universities. This U shape again demonstrates the importance of improving the quality of secondary school instruction in the ultra-peripheral Chilean regions, especially rural ones, to increase the rates at which students in these regions attend university.
6. Discussion
A student’s spatial vicinity is thus crucial to ensuring that a candidate both passes the PSU exam and applies to university. This outcome has been studied in other countries, such as the United States. In [62], students’ academic performance depended not only on home and school but also on neighborhood and surrounding community at the local spatial resolution of blocks. Similar conclusions were reached in [63], where an analysis of county and commuting zone data showed “education deserts”, places where opportunities richly available in some communities are rare (or even nonexistent).
Specifically in our analysis, four variables have local spillovers: social capital, professional situation, having siblings studying at a university, and having good marks in high school. The best environment for a student to succeed in accessing higher education in Chile includes peers who obtained good marks in high school and do not have a job, high social capital, and siblings already studying at a university.
Conversely, the worst neighborhood for a higher education candidate includes peers who obtained bad grades in high school and have a job, lack of good social capital status, or no siblings at university. We also add other environmental variables with a negative impact on higher education accessibility, such as living in rural areas and/or ultra-peripheral regions, over 1400 km far from Santiago. It is thus important for the state to foster policies that motivate students living in working-class neighborhoods—understood as communities that have low social capital, no siblings studying in college, and many classmates who are employed—to see university as a valid option for their personal advancement. Students who live in environments with good secondary schools, where students earn good grades, are more likely to apply than others. This finding strengthens support for the abovementioned need to foster public policies to improve the quality of secondary education in the most disadvantaged neighborhoods.
Distance to Santiago seems to have an inverted U-shaped effect, such that, the greater the distance between students and Santiago, the greater students’ probability of applying to and being accepted at university. This trend continued up to a threshold distance of 1400 km or to regions at the geographical extremes of Chile—region II in the north and region XI in the south. This result contrasts with those of studies showing that, even in countries that grant every possible candidate access to higher education, spatial distance between residence of origin and location of the university acts as a deterrent because people from more isolated locations face more costs and those costs grow with spatial distance. Other findings (e.g., [32] for Italy) are more in line with the case of Chile in detecting a kind of inelastic demand at certain universities—regardless of their location—that offer significant benefits, such as dropping the requirement of an entrance examination.
As stated above, the best university education system is clearly concentrated in the central region of Chile, as are many private universities that do not form part of the PSU admission system and to which students can apply if they are not admitted to the traditional universities. This U shape again demonstrates the importance of improving the quality of secondary school instruction in the ultra-peripheral Chilean regions, especially rural ones, to increase the rates at which students in these regions attend university.
The results also indicate a problem of gender inequality. Although women’s likelihood of applying to university is higher than men’s, their probability of ultimately being accepted is significantly lower. Similar evidence is found for Chile in [40] using a different database: fewer women than men attend higher education, but those who do are more likely to follow through, yielding a fairly equal gender balance at the end of the university learning process. Although the distribution of skills during adolescence is similar among genders, a study of Peru shows that marginal expected returns on investment in human capital are lower among girls than boys [39]. Gender imbalance is clearly a serious problem that merits further in-depth study to see whether bias exists in the model used or in the type of education women receive.
Finally, the effect of the candidates’ social capital, while statistically significant, does not seem as relevant as initially expected, perhaps due to its correlation with the effect of the variable of student grade-point average in secondary education and score on the PSU. Conversely, many individual studies stress the role of parents’ education, household income, and quality of secondary school in determining access to university (e.g., [32,33,36,38]). Finally, our paper’s results align with other results for Chile, such as [17], where expectations and information provided by family (parents and siblings), society, peers, and high school are considered the main factors influencing students to access higher education.
7. Conclusions
This paper has two main objectives, implementation of a spatial Heckman probit model and validation of the importance of geography to education. This paper uses a discrete sample selection model augmented with local spatial spillover effects to explore the role of spatial interaction role of Chile’s educational economy.
The model was respecified as a spatial cross-regressive (SLX) model, which adds the spatially lagged explanatory variables to the standard Heckit model. This model can absorb and explain the effect of spatial dependence or proximity among students on their probability of accessing higher education. This model can be estimated directly using the maximum likelihood method appropriate to the Heckit model, given the exogenous character of the lagged spatially explanatory variables and the model’s suitability for explaining local spatial externalities even when they occur with weak intensity, as in this model.
The application process for admission to universities has two parts or models: the first is based on students’ decision to take the PSU test; this first step leads to the second, the DEMRE’s decision on the student’s application.
This study is limited in that it does not consider unobserved heterogeneity, that is, some nonrandom factors specific to the individuals that are not measurable or observable, such as students’ innate learning ability.
Our hope is that this paper serves as a starting point for future research that estimates a SAR-Heckit model to quantify global spatial externality effects, their direct and indirect effects at the national level, and new specifications of the spatial weight matrix based on social networks or socioeconomic factors.
Author Contributions
Conceptualization, J.L.Q., L.P., C.C. and P.A.; methodology, J.L.Q., L.P., C.C. and P.A.; software, J.L.Q., L.P. and C.C.; validation, J.L.Q., L.P., C.C. and P.A.; formal analysis, J.L.Q., L.P. and C.C.; investigation, J.L.Q. and L.P.; resources, J.L.Q.; data curation, J.L.Q. and C.C.; writing—original draft preparation, J.L.Q. and L.P.; writing—review and editing, C.C.; project administration, J.L.Q.; funding acquisition, C.C. and P.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the FONDECYT Project, grant number 1171230, the COES–FONDAP Project, grant number 15130009, and by the eS-MiData Project, grant number 447379001.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data and scripts are available in the Spatial and Regional Economics research group (ECONRES) of the Universidad Autónoma de Madrid at https://econresuam.wordpress.com/opendata, accessed on 11 January 2022.
Acknowledgments
We are grateful to the participants at the 9th Seminar of Spatial Econometric Jean Paelinck|6–7 October 2017, Cartagena, Spain and at the 2021 RSAI World Conference|25–28 May 2021, Virtual Conference for their valuable comments on several versions of this paper. We also acknowledge Andrés Vallone’s contribution of the postal address geocoding process and Carmen Pérez Esparrells, Mónica Navarrete, and Dusan Paredes for their invaluable comments during Juan Luis Quiroz’s dissertation defense.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
We developed a “proxy” variable for students’ social capital as a latent variable composed of four indicators: mother’s education level, father’s education level, household monthly income, and type of student’s secondary school (Table A1).

Table A1.
Coding of indicators of the latent variable social capital.
Table A1.
Coding of indicators of the latent variable social capital.
| Variable | Description | Coding | Year |
|---|---|---|---|
| Mother’s and father’s education level | No information | 0 | 2016 |
| Illiterate | 1 | ||
| Incomplete primary education | 2 | ||
| Complete primary education | 3 | ||
| Incomplete secondary education | 4 | ||
| Complete secondary education | 5 | ||
| Other studies | 6 | ||
| Incomplete technical school education | 7 | ||
| Complete technical school education | 8 | ||
| Incomplete high school education | 9 | ||
| Complete high school education | 10 | ||
| Incomplete university education | 11 | ||
| Complete university education | 12 | ||
| Household monthly income (USD) | 0–213 | 1 | 2016 |
| 213–425 | 2 | ||
| 425–638 | 3 | ||
| 638–851 | 4 | ||
| 851–1064 | 5 | ||
| 1064–1276 | 6 | ||
| 1276–1489 | 7 | ||
| 1489–1702 | 8 | ||
| 1702–1914 | 9 | ||
| 1914–2127 | 10 | ||
| 2127–2340 | 11 | ||
| 2340+ | 12 | ||
| Secondary school type | Public school | 1 | 2016 |
| Subsidized school | 2 | ||
| Private school | 3 |
These indicators correlate closely in socially segregated countries such as Chile, where only high-income parents (who are usually well-educated) can afford to send their children to private schools, while poorer and non-educated families must be content with public schools. We synthesized these indicators using a confirmatory factor analysis. Both the database and STATA code are available in [60].
The Cronbach’s alpha of the scale is 0.762, well above the value of 0.70 considered as sufficiently good to ensure reliability of the latent variable social capital (Table A2).

Table A2.
Cronbach’s alpha of social capital indicators.
Table A2.
Cronbach’s alpha of social capital indicators.
| Item | Obs. | Sign | Item–Test Correlation | Item–Rest Correlation | Average Inter–Item Correlation | Cronbach’s Alpha |
|---|---|---|---|---|---|---|
| Father’s education | 260,775 | + | 0.787 | 0.598 | 0.420 | 0.685 |
| Mother’s education | 260,775 | + | 0.768 | 0.567 | 0.439 | 0.701 |
| Family income | 260,775 | + | 0.799 | 0.616 | 0.408 | 0.674 |
| School types | 260,775 | + | 0.700 | 0.463 | 0.509 | 0.756 |
| Test scale | 0.444 | 0.762 |
Lastly, Table A3 presents the measurement coefficients (loadings) and intercepts. The structural equation model (SEM) was estimated using the Maximum Likelihood (ML) method for the 260,775 students who attended the PSU exam. All model loadings are highly significant at the 0.001 significance level, demonstrating the high capacity of the latent variable social capital to explain each of the four individual items.

Table A3.
Results for confirmatory factor analysis or measurement model.
Table A3.
Results for confirmatory factor analysis or measurement model.
| Social Capital Model | ||||
|---|---|---|---|---|
| Coefficient | Z | OIM S.E. | ||
| Father’s education | Factor score (CS) | 1 | - | - |
| Constant | 5.032 *** | 677.7 | 0.007 | |
| Mother’s education | Factor score (CS) | 0.850 *** | 307.9 | 0.003 |
| Constant | 5.536 *** | 828.0 | 0.007 | |
| Family income | Factor score (CS) | 0.774 *** | 258.9 | 0.003 |
| Constant | 4.349 *** | 702.1 | 0.006 | |
| High school type | Factor score (CS) | 0.116 *** | 204.4 | 0.001 |
| Constant | 1.770 *** | 1427.6 | 0.001 | |
| Var (Father’s Education) | Constant | 6.338 *** | 214.4 | 0.030 |
| Var (Mother’s Education) | Constant | 5.858 *** | 247.2 | 0.024 |
| Var (Family Income) | Constant | 5.190 *** | 239.4 | 0.022 |
| Var (School Type) | Constant | 0.292 *** | 309.8 | 0.001 |
| Var (CS) | Constant | 8.037 *** | 187.2 | 0.043 |
Note: *** means significant for p-value < 0.001.
It must be said, however, that the overall goodness of fit is not good. In the test of the “model versus saturated”, 21,342.40, a result that clearly rejects the null hypothesis that the fitted covariance matrix and mean vector of the observed variables are equal to the matrix and vector observed in the population.
References
- Espinoza, O. Creating (in) Equalities in Access to Higher Education in the Context of Structural Adjustment and Post-Adjustment Policies: The Case of Chile. High. Educ. 2008, 55, 269–284. [Google Scholar] [CrossRef]
- Koljatic, M.; Silva, M.; Cofré, R. Achievement versus Aptitude in College Admissions: A Cautionary Note Based on Evidence from Chile. Int. J. Educ. Dev. 2013, 33, 106–115. [Google Scholar] [CrossRef]
- OECD. World Bank Access and Equity. In Reviews of National Policies for Education: Tertiary Education in Chile 2009; OECD Publishing: Paris, France, 2009; pp. 73–121. [Google Scholar] [CrossRef]
- Speirs, N.M. Solidarity and Subsidiarity—How to Widen Access to Higher Education? In Social Responsibility and Sustainability: How Businesses and Organizations Can Operate in a Sustainable and Socially Responsible Way; Filho, W.L., Ed.; World Sustainability Series; Springer International Publishing: Cham, Germany; Hamburg, Germany, 2019; pp. 123–137. ISBN 978-3-030-03562-4. [Google Scholar]
- Millett, C. Designing Sustainable Funding for College Promise Initiatives. ETS Res. Rep. Ser. 2017, 2017, 1–55. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, M.; Leachman, M.; Masterson, K.; Waxman, S. Unkept Promises: State Cuts to Higher Education Threaten Access and Equity; Center for Budget and Policy Priorities, Virginia Tech: Washington, DC, USA, 2018; p. 23. [Google Scholar]
- Zarifa, D.; Hango, D.; Pizarro Milian, R. Proximity, Prosperity, and Participation: Examining Access to Postsecondary Education among Youth in Canada’s Provincial North. Rural Sociol. 2018, 83, 270–314. [Google Scholar] [CrossRef]
- DesJardins, S.L.; Dundar, H.; Hendel, D.D. Modeling the College Application Decision Process in a Land-Grant University. Econ. Educ. Rev. 1999, 18, 117–132. [Google Scholar] [CrossRef]
- Aguirre, J.; Matta, J. Walking in Your Footsteps: Sibling Spillovers in Higher Education Choices. Econ. Educ. Rev. 2021, 80, 102062. [Google Scholar] [CrossRef]
- Kingdon, G.G. The Private Schooling Phenomenon in India: A Review. J. Dev. Studies 2020, 56, 1795–1817. [Google Scholar] [CrossRef] [Green Version]
- McDonough, I.K.; Roychowdhury, P.; Dhamija, G. Measuring the Dynamics of the Achievement Gap Between Public and Private School Students During Early Life in India. J. Labor Res. 2021, 42, 78–122. [Google Scholar] [CrossRef]
- Zuilkowski, S.S.; Piper, B.; Ong’ele, S.; Kiminza, O. Parents, Quality, and School Choice: Why Parents in Nairobi Choose Low-Cost Private Schools over Public Schools in Kenya’s Free Primary Education Era. Oxf. Rev. Educ. 2018, 44, 258–274. [Google Scholar] [CrossRef]
- Ngware, M.W.; Mutisya, M. Demystifying Privatization of Education in Sub-Saharan Africa: Do Poor Households Utilize Private Schooling Because of Perceived Quality, Distance to School, or Low Fees? Comp. Educ. Rev. 2021, 65, 124–146. [Google Scholar] [CrossRef]
- UNESCO, G.E.M.R. Education for All 2000-2015: Achievements and Challenges; EFA Global Monitoring Report. 2015. Available online: https://unesdoc.unesco.org/ark:/48223/pf0000232205 (accessed on 22 December 2021).
- Lira, J. Mind the Gap: Irrevocable Wage Differentials in Chile; Universidad de Chile: Santiago, Chile, 2008. [Google Scholar]
- Molina, A.; Lamb, S. School Segregation, Inequality and Trust in Institutions: Evidence from Santiago. Comp. Educ. 2021, 58, 72–90. [Google Scholar] [CrossRef]
- Guzmán, P.; Cifuentes Gomez, G.; Santelices, M.V. Secondary Students’ Expectations on Transition to Higher Education. Educ. Res. 2021, 63, 164–179. [Google Scholar] [CrossRef]
- Von Hippel, P.T.; Hofflinger, A. The Data Revolution Comes to Higher Education: Identifying Students at Risk of Dropout in Chile. J. High. Educ. Policy Manag. 2021, 43, 2–23. [Google Scholar] [CrossRef]
- Ioannides, Y.M.; Topa, G. Neighborhood Effects: Accomplishments and Looking Beyond Them*. J. Reg. Sci. 2010, 50, 343–362. [Google Scholar] [CrossRef]
- Ivemark, B.; Ambrose, A. Habitus Adaptation and First-Generation University Students’ Adjustment to Higher Education: A Life Course Perspective. Sociol. Educ. 2021, 94, 191–207. [Google Scholar] [CrossRef]
- Dickerson, A.; McIntosh, S. The Impact of Distance to Nearest Education Institution on the Post-Compulsory Education Participation Decision. Urban Studies 2013, 50, 742–758. [Google Scholar] [CrossRef] [Green Version]
- Butler, T.; Hamnett, C. The Geography of Education: Introduction. Urban Studies 2007, 44, 1161–1174. [Google Scholar] [CrossRef]
- Zarifa, D.; Seward, B.; Milian, R.P. Location, Location, Location: Examining the Rural-Urban Skills Gap in Canada. J. Rural Studies 2019, 72, 252–263. [Google Scholar] [CrossRef]
- Hango, D.; Zarifa, D.; Pizarro Milian, R.; Seward, B. Roots and STEMS? Examining Field of Study Choices among Northern and Rural Youth in Canada. Studies High. Educ. 2021, 46, 563–593. [Google Scholar] [CrossRef]
- Weiler, W.C. Transition from Consideration of a College to the Decision to Apply. Res. High. Educ. 1994, 35, 631–646. [Google Scholar] [CrossRef]
- Helland, H.; Heggen, K. Regional Differences in Higher Educational Choice? Scand. J. Educ. Res. 2018, 62, 884–899. [Google Scholar] [CrossRef]
- Buckner, E.; Khoramshahi, C. Does the Private Sector Expand Access to Higher Education? A Cross-National Analysis, 1999–2017. Int. J. Educ. Dev. 2021, 84, 102410. [Google Scholar] [CrossRef]
- Wilson, J.Z.; Harvey, A.; Mendes, P. Changing Lives: Improving Care Leaver Access to Higher Education. Oxf. Rev. Educ. 2019, 45, 573–586. [Google Scholar] [CrossRef]
- Doolan, K.; Puzić, S.; Baranović, B. Social Inequalities in Access to Higher Education in Croatia: Five Decades of Resilient Findings. J. Furth. High. Educ. 2018, 42, 467–481. [Google Scholar] [CrossRef]
- Amorim, J.P. Mature Students’ Access to Higher Education: A Critical Analysis of the Impact of the 23+ Policy in Portugal. Eur. J. Educ. 2018, 53, 393–413. [Google Scholar] [CrossRef] [Green Version]
- Verdis, A.; Kalogeropoulos, K.; Chalkias, C. Regional Disparities in Access to Higher Education in Greece. Res. Comp. Int. Educ. 2019, 14, 318–335. [Google Scholar] [CrossRef]
- Türk, U. Socio-Economic Determinants of Student Mobility and Inequality of Access to Higher Education in Italy. Netw. Spat. Econ. 2019, 19, 125–148. [Google Scholar] [CrossRef] [Green Version]
- Prakhov, I.; Sergienko, D. Matching between Students and Universities: What Are the Sources of Inequalities of Access to Higher Education? Eur. J. Educ. 2020, 55, 261–274. [Google Scholar] [CrossRef]
- Chea, P. Does Higher Education Expansion in Cambodia Make Access to Education More Equal? Int. J. Educ. Dev. 2019, 70, 102075. [Google Scholar] [CrossRef]
- Fadhil, I.; Sabic-El-Rayess, A. Providing Equity of Access to Higher Education in Indonesia: A Policy Evaluation. Indones. J. Learn. Adv. Educ. IJOLAE 2021, 3, 57–75. [Google Scholar] [CrossRef]
- Bulbul, T. Socio-Economic Status and School Types as the Determinants of Access to Higher Education. Educ. Sci. 2021, 46, 303–334. [Google Scholar] [CrossRef]
- Carr-Hill, R. Inequalities in Access to Higher Education in Africa: How Large Are They? Do They Mirror the Situation in the Metropole 60 Years Ago? Int. J. Educ. Dev. 2020, 72, 102122. [Google Scholar] [CrossRef]
- Benavides, M.; León, J.; Galindo, C.; Herring, C. Access to Higher Education of Afro-Peruvians: Disentangling the Influence of Skin Color and Social Origins in the Peruvian Stratification System. Sociol. Race Ethn. 2019, 5, 354–369. [Google Scholar] [CrossRef]
- Molina, O.; Santa María, D.; Yamada, G. What Stops Poor Girls from Going to College? Skill Development and Access to Higher Education in a Developing Country; IZA Discussion Papers 12052; Institute of Labor Economics (IZA): Bonn, Germany, 2018; Available online: http://hdl.handle.net/10419/193346 (accessed on 30 December 2021).
- Gaentzsch, A.; Zapata-Román, G. Climbing the Ladder: Determinants of Access to and Returns from Higher Education in Chile and Peru; UNRISD Working Paper 2020-2; United Nations Research Institute for Social Development (UNRISD): Geneva, Switzerland, 2020; Available online: http://hdl.handle.net/10419/246234 (accessed on 30 December 2021).
- Looker, E.D.; Lowe, G.S. Post-Secondary Access and Student Financial Aid in Canada: Current Knowledge and Research Gaps (2001); Canada Millennium Scholarship Foundation: Otawa, ON, Canada, 2021; Available online: https://doi=10.1.1.482.7571 (accessed on 30 December 2021).
- Finnie, R.; Mueller, R.E.; Wismer, A. Access and Barriers to Postsecondary Education: Evidence from the Youth in Transition Survey. Can. J. High. Educ. 2015, 45, 229–262. [Google Scholar] [CrossRef]
- Coleman, J.S. Social Capital in the Creation of Human Capital. Am. J. Sociol. 1988, 94, S95–S120. [Google Scholar] [CrossRef]
- Furstenberg, F.F.; Hughes, M.E. Social Capital and Successful Development among At-Risk Youth. J. Marriage Fam. 1995, 57, 580–592. [Google Scholar] [CrossRef]
- Madrid, S. Diversidad sin Diversidad: Los Colegios Particulares Pagados de Elite y la Formación de la Clase Dominante en una Sociedad de Mercado. In Mercado Escolar y Oportunidad. Educacional. Libertad, Diversidad y Desigualdad; Corvalán, J., Carrasco, A., García-Huidobro, J.E., Eds.; Ediciones Universidad Católica de Chile: Santiago, Chile, 2016; pp. 269–299. [Google Scholar]
- Van de Ven, W.P.M.M.; Van Praag, B.M.S. The Demand for Deductibles in Private Health Insurance: A Probit Model with Sample Selection. J. Econom. 1981, 17, 229–252. [Google Scholar] [CrossRef]
- Wooldridge, J.M. Econometric Analysis of Cross Section and Panel Data, 2nd ed.; MIT Press: Cambridge, MA, USA, 2010; ISBN 978-0-262-23258-6. [Google Scholar]
- Pastore, F. To Study or to Work? East. Eur. Econ. 2012, 50, 49–78. [Google Scholar] [CrossRef]
- Ahlin, L.; Andersson, M.; Thulin, P. Human Capital Sorting: The “When” and “Who” of the Sorting of Educated Workers to Urban Regions. J. Reg. Sci. 2018, 58, 581–610. [Google Scholar] [CrossRef]
- Morrissey, K.; Kinderman, P.; Pontin, E.; Tai, S.; Schwannauer, M. Web Based Health Surveys: Using a Two Step Heckman Model to Examine Their Potential for Population Health Analysis. Soc. Sci. Med. 2016, 163, 45–53. [Google Scholar] [CrossRef] [Green Version]
- Anselin, L. GeoDa on Github. Available online: https://geodacenter.github.io/ (accessed on 30 December 2021).
- LeSage, J.; Pace, R.K. Introduction to Spatial Econometrics; Chapman and Hall/CRC: New York, USA, 2008; ISBN 978-1-4200-6424-7. [Google Scholar] [CrossRef] [Green Version]
- Kelejian, H.; Prucha, I.R. On the Asymptotic Distribution of the Moran I Test Statistic with Applications. J. Econom. 2001, 104, 219–257. [Google Scholar] [CrossRef] [Green Version]
- Vella, F. Estimating Models with Sample Selection Bias: A Survey. J. Hum. Resour. 1998, 33, 127–169. [Google Scholar] [CrossRef] [Green Version]
- Halleck Vega, S.; Elhorst, J.P. The Slx Model. J. Reg. Sci. 2015, 55, 339–363. [Google Scholar] [CrossRef]
- Fischer, M.M.; Scherngell, T.; Reismann, M. Knowledge Spillovers and Total Factor Productivity: Evidence Using a Spatial Panel Data Model. Geogr. Anal. 2009, 41, 204–220. [Google Scholar] [CrossRef] [Green Version]
- Chasco, C.; Le Gallo, J. Hierarchy and Spatial Autocorrelation Effects in Hedonic Models. Econ. Bull. 2012, 32, 1474–1480. [Google Scholar]
- Anselin, L. Spatial Externalities, Spatial Multipliers, And Spatial Econometrics. Int. Reg. Sci. Rev. 2003, 26, 153–166. [Google Scholar] [CrossRef]
- Anselin, L. The Moran Scatterplot as an ESDA Tool to Assess Local Instability in Spatial Association. In Spatial Analytical Perspectives on GIS; Fischer, M., Scholten, H.J., Unwin, D., Eds.; Routledge: London, UK, 1996; ISBN 978-0-203-73905-1. [Google Scholar] [CrossRef]
- Quiroz, J.L.; Peeters, L.; Aroca, P. Access the University. A Spatial Heckman Probit Model [Data Set]. Available online: https://b2share.eudat.eu/records/b434ff0201074090a9bea92563c8c59f (accessed on 5 January 2022).
- LeSage, J.P. What Regional Scientists Need to Know about Spatial Econometrics. Rev. Reg. Studies 2014, 44, 13–32. [Google Scholar] [CrossRef]
- Miller, P.M. Mapping Educational Opportunity Zones: A Geospatial Analysis of Neighborhood Block Groups. Urban Rev. 2012, 44, 189–218. [Google Scholar] [CrossRef]
- Hillman, N.W. Geography of College Opportunity: The Case of Education Deserts. Am. Educ. Res. J. 2016, 53, 987–1021. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).