Confidence Intervals for Assessing Non-Inferiority with Assay Sensitivity in a Three-Arm Trial with Normally Distributed Endpoints

Abstract

Various approaches including hypothesis test and confidence interval (CI) construction have been proposed to assess non-inferiority and assay sensitivity via a known fraction or pre-specified margin in three-arm trials with continuous or discrete endpoints. However, there is little work done on the construction of the non-inferiority margin from historical data and simultaneous generalized CIs (SGCIs) in a three-arm trial with the normally distributed endpoints. Based on the generalized fiducial method and the square-and-add method, we propose two simultaneous CIs for assessing non-inferiority and assay sensitivity in a three-arm trial. For comparison, we also consider the Wald-type Bonferroni simultaneous CI and parametric bootstrap simultaneous CI. An algorithm for evaluating the optimal sample size for attaining the pre-specified power is given. Simulation studies are conducted to investigate the performance of the proposed CIs in terms of their empirical coverage probabilities. An example taken from the mildly asthmatic study is illustrated using the proposed simultaneous CIs. Empirical results show that the proposed generalized fiducial method and the square-and-add method behave better than other two compared CIs.

1. Introduction

In modern clinical trials, it is extremely interesting to demonstrate whether a new treatment that is less toxic, less expensive or easier to administer is not inferior to an expensive and technical pathological reference treatment by more than a pre-specified margin. This is usually called a two-arm non-inferiority trial that does not include a placebo. Two-arm non-inferiority trials have been widely studied. For example, see [1,2,3]. However, two-arm non-inferiority trials have some shortcomings, such as the selection of the non-inferiority margin and the assessment of assay sensitivity (i.e., the ability to differentiate between an effective treatment and a less effective or ineffective treatment). If ethically acceptable and practically feasible, it is generally recognized that three-arm non-inferiority trials including a placebo can surmount the difficulties mentioned above [4].

There has been a growing interest in developing statistical inference on three-arm non-inferiority trials. For example, see [5], and [6] for the fractional margin, i.e., the non-inferiority margin is taken as a pre-specified fraction of unknown effect size of reference treatment. In particular, Tang, Yu and Tang [7] developed the exact and approximate unconditional test approaches for the assessment of the non-inferiority in a three-arm trial with binary endpoints. However, the aforementioned literature did not consider the assessment of assay sensitivity. To this end, simultaneously assessing non-inferiority and assay sensitivity via a fixed margin has received considerable attention in recent years. For example, Hide and Tango [8] investigated simultaneous testing for both non-inferiority and assay sensitivity via a pre-specified margin, which is defined as a difference between two treatment effects in the considered historical placebo-controlled trial with normally distributed endpoints in the presence of homoscedasticity. Here endpoint represents the observation of random variable, and the normally distributed endpoint means that endpoint comes from a normal distribution. Hida and Tango’s method may be improper due to the usage of the same margins for testing both non-inferiority and assay sensitivity. To solve the problem, Kwong et al. [9] considered a modified version of Hida and Tango’s testing procedure based on different margins for assessing both non-inferiority and assay sensitivity. M$\ddot{\mathrm{u}}$tze, Munk and Friede  [10] presented a Wald-type test procedure for assessing both non-inferiority and assay sensitivity in a three-arm trial with negative binomially distributed endpoints.

The aforementioned literature mainly focuses on the non-inferiority testing problem in a three-arm trial. However, there is little work on simultaneously considering the construction of non-inferiority margin from the historical data and confidence interval for simultaneously testing both non-inferiority and assay sensitivity. Moreover, it is difficult to invert to find simultaneous confidence intervals for simultaneously testing both non-inferiority and assay sensitivity based on the aforementioned test procedures. To address these issues, here we consider the construction problem of simultaneous confidence intervals (CIs) for assessing both non-inferiority and assay sensitivity based on the square-and-add method and the generalized fiducial method in a three-arm trial.

CI construction via the square-and-add method [11], which is also called the method of variance estimates recovery, has received considerable attention over the past years in that it does not depend on the large sample theory and has a computationally simple and closed expression. For example, Li et al.  [12] proposed an interval for the difference between two poisson rates based on the square-and-add method. Tang et al. [13] proposed five simultaneous CIs for risk differences in stratified matched-pair designs via the square-and-add method. Tang et al. [14] studied the problem of CI construction for the difference between two correlated proportions in the presence of incomplete paired binary data based on the square-and-add method. Zhang and Tang [15] extended the square-and-add method to CI construction of difference between two correlated areas under ROC curves in a matched-pair experiment. However, to our knowledge, there is little work done on simultaneous CI construction for assessing both non-inferiority and assay sensitivity in a three-arm trial using the square-and-add method.

Generalized CIs (GCIs) via generalized fiducial method [16] are widely studied in that it has been shown to be a useful tool for making inference in many practical problems. For example, see [17,18]. In particular, Schaarschmidt [19] discussed simultaneous CI construction for multiple comparisons among expected values of log-normal variables via the generalized fiducial method; Gamalo et al. [20] investigated the generalized CI construction problem for assessing non-inferiority in a three-arm trial with normally distributed endpoints in the presence of heteroscedasticity. However, Gamalo et al. [20] did not consider the assay sensitivity assessment problem. Moreover, to our knowledge, there is little work developed on simultaneous GCIs for assessing both non-inferiority and assay sensitivity in a three-arm trial with normally distributed endpoints. Hence, this paper proposes two simultaneous GCIs for simultaneously assessing non-inferiority and assay sensitivity by incorporating generalized fiducial pivotal quantity of [21] and the square-and-add approach in a three-arm non-inferiority trial with normally distributed endpoints, and presents their corresponding algorithms for evaluating GCIs. For comparison, we also consider Wald-type Bonferroni simultaneous CIs and parametric bootstrap simultaneous CIs introduced in [22]. In addition, we also discuss the problem of sample size determination, and present approximate formulae for determining sample size for attaining a pre-specified power.

The rest of this paper is organized as follows. Section 2 introduces the hypothesis testing problem for assessing both non-inferiority and assay sensitivity in a three-arm trial, discusses the problem of non-inferiority margin construction from historical data, presents four simultaneous CIs for assessing both non-inferiority and assay sensitivity based on generalized fiducial method, square-and-add approach, Wald-type Bonferroni method and parametric bootstrap method and gives the sample size formulae. Simulation studies and an example from the mildly asthmatic study are illustrated in Section 3. A brief discussion is given in Section 4. Technical details are presented in the Appendix A.

2. Materials and Methods

Following [9], we consider a one-way fixed effect model for endpoints in a three-arm non-inferiority trial with experimental, reference and placebo treatments. For notational simplicity, we denote experimental, reference and placebo treatments as E, R and P, respectively. Throughout this paper, we assume

$$\begin{array}{c}\hfill X_{ij}={\mu }_i+{ϵ}_{ij},i=\mathrm{E},\mathrm{R},\mathrm{P},j=1,\cdots ,n_i,\end{array}$$

(1)

where $X_{ij}$ is the endpoint of the jth individual for the ith treatment, ${\mu }_i$ is the fixed effect of the ith treatment, measurement errors ${ϵ}_{ij}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}}{\sim }\mathcal{N}(0,{\sigma }_i^2)$, and $n_i$ is the sample size of the ith treatment for $i=$ E, R, P. Without loss of generality, it is assumed that a larger value of ${\mu }_i$ indicates the better efficacy for the ith treatment. Under the above assumption, we have

$$X_{ij}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}}{\sim }\mathcal{N}({\mu }_i,{\sigma }_i^2),i=\mathrm{E},\mathrm{R},\mathrm{P},j=1,\cdots ,n_i,$$

(2)

To assess the non-inferiority (NI) and the assay sensitivity in a three-arm trial, Kwong et al.  [9] considered the following modified HT hypotheses:

$$\left\{\begin{array}{ccc}{H}_{\mathrm{NI}}^0:{\mu }_E-{\mu }_R\le -r\Delta \hfill & \mathrm{versus}\hfill & H_{\mathrm{NI}}^1:{\mu }_E-{\mu }_R>-r\Delta ,\hfill \\ K_{\mathrm{AS}}^0:{\mu }_R-{\mu }_P\le \Delta \hfill & \mathrm{versus}\hfill & K_{\mathrm{AS}}^1:{\mu }_R-{\mu }_P>\Delta ,\hfill \end{array}\right.$$

(3)

where $\Delta >0$ is a pre-specified margin, and r is some pre-specified constant and satisfies the restricted condition: $0<r\le 1$. In particular, when $r=1$, the hypotheses considered above are just those given in [8]. When $r<1$, the testing procedure for hypotheses (3) is more stringent than the testing procedure of [8] because of requiring assay sensitivity to be established. Clearly, if $H_{\mathrm{NI}}^0$ and $K_{\mathrm{AS}}^0$ are simultaneously rejected by some two-tailed test at the significance level $\alpha$ or two one-tailed tests at the significance level $\alpha /2$, we may draw a conclusion: ${\mu }_P+\Delta <{\mu }_R<{\mu }_E+r\Delta$, which indicates that (i) the NI of experimental treatment to reference one with respect to $r\Delta$ and (ii) the superiority of reference treatment to placebo by more than $\Delta$. Here $\Delta$ is the entire effect size of reference treatment over placebo, and ${\Delta }_{\mathrm{NI}}=r\Delta$ is the NI margin showing the NI of experimental treatment to reference one.

Generally, one can construct two appropriate statistics for testing hypotheses $H_{\mathrm{NI}}^0$ and $K_{\mathrm{AS}}^0$. Here, rather than hypothesis testing, we consider the problem of constructing simultaneous CIs for $\varphi ={\mu }_E-{\mu }_R$ and $\psi ={\mu }_R-{\mu }_P$ due to the duality of hypothesis testing and CI estimation. If the lower limits of the resultant $100(1-\alpha )\%$ one-sided simultaneous CIs for $\varphi$ and $\psi$ are larger than $-r\Delta$ and $\Delta$, respectively, we can simultaneously reject the null hypotheses $H_{\mathrm{NI}}^0$ and $K_{\mathrm{AS}}^0$ at the significance level $\alpha$. However, in clinical studies, ${\Delta }_{\mathrm{NI}}$ is usually unknown. In what follows, we consider the construction problem of the NI margin, denoted as ${\Delta }_{\mathrm{NI}}$, via the lower bound of the credible interval of treatment effect of reference treatment in historical trials.

2.1. Construction of NI Margin

In what follows, a historical-trial-based approach and the generalized fiducial method are adopted to determine the NI margin ${\Delta }_{\mathrm{NI}}$. To this end, we first consider the generalized fiducial CI construction problem as follows.

Let $S\in {\mathcal{R}}^k$ be a random vector whose distribution is indexed by parameter vector $\xi \in {\mathcal{R}}^p$. Suppose we are interested in making inference on $\theta =\pi \left(\xi \right)\in {\mathcal{R}}^q$. Let $S^{\ast }$ be an independent copy of S, and s and $s^{\ast }$ represent the observed values of S and $S^{\ast }$, respectively. A generalized fiducial pivotal quantity (GFPQ) for parameter $\theta$, denoted as $G_{\theta }(S,S^{\ast },\xi )$, is a function of $(S,S^{\ast },\xi )$, and satisfies the following conditions:

(i) The conditional distribution of $G_{\theta }(S,S^{\ast },\xi )$, given $S=s$, is free of $\xi$.

(ii) For every allowable $s\in {\mathcal{R}}^k$, $G_{\theta }(s,s,\xi )=\theta$.

Approximate percentiles of $G_{\theta }(S,S^{\ast },\xi )$ form a $100(1-\alpha )\%$ generalized fiducial CI for $\theta$. To wit, if the above conditions hold and there exist two statistics $L\left(s\right)$ and $U\left(s\right)$ such that

$$\begin{array}{c}\hfill \mathrm{Pr}\left\{L\left(s\right)\le G_{\theta }(S,S^{\ast },\xi )\le U\left(s\right)|S=s\right\}=1-\alpha ,\end{array}$$

(4)

thus the interval $\left(L\right(s),U(s\left)\right)$ is called the $100(1-\alpha )\%$ generalized fiducial CI for $\theta$. In what follows, we adapt the above definition of generalized fiducial CI to determine NI margin via a historical placebo-controlled trial for the reference treatment, which is a superiority trial for establishing the efficacy of the reference treatment.

Let $Y_{ij}^h$ be the endpoint of the jth individual for the ith treatment in the historical trial for $i=R,P$ and $j=1,\dots ,m_i$. Following the aforementioned one-way fixed effect model, we assume that $Y_{Pj}^h$ and $Y_{Rj}^h$ follow the normal distributions, i.e.,

$$\begin{array}{c}\hfill Y_{Pj}^h|{\nu }_P,{\xi }_P^2\sim \mathcal{N}({\nu }_P,{\xi }_P^2),j=1,\dots ,m_P,\end{array}$$

(5)

$$\begin{array}{c}\hfill Y_{Rj}^h|{\nu }_R,{\xi }_R^2\sim \mathcal{N}({\nu }_R,{\xi }_R^2),j=1,\dots ,m_R,\end{array}$$

(6)

where ${\nu }_P$ and ${\nu }_R$ denote the treatment effects for placebo and reference treatments in the considered historical trial, respectively, ${\xi }_P^2$ and ${\xi }_R^2$ denote their corresponding variances to be estimated, and $m_P$ and $m_R$ are their corresponding sample sizes. Our purpose is to construct GFPQ for mean difference $\eta ={\nu }_R-{\nu }_P$. To this end, we denote ${\overline{Y}}_k^h=m_k^{-1}{\sum }_{j=1}^{m_k}{Y}_{kj}^h$ and $S_{kh}^2={(m_k-1)}^{-1}{\sum }_{j=1}^{m_k}{(Y_{kj}^h-{\overline{Y}}_k^h)}^2$ for $k=R$, P. It is easily shown that ${\widehat{\nu }}_k={\overline{Y}}_k^h$ and ${\widehat{\xi }}_k^2=S_{kh}^2$ are unbaised estimators of ${\nu }_k$ and ${\xi }_k^2$, respectively. Thus, an unbaised estimator of $\eta$ is given by $\widehat{\eta }={\widehat{\nu }}_R-{\widehat{\nu }}_P={\overline{Y}}_R^h-{\overline{Y}}_P^h$. It is well known that ${\overline{Y}}_k^h$ and $S_{kh}^2$ are sufficient statstics of ${\nu }_k$ and ${\xi }_k^2$, respectively, and ${\overline{Y}}_k^h\sim \mathcal{N}({\nu }_k,{\xi }_k^2/m_k)$ and $(m_k-1)S_{kh}^2\sim {\xi }_k^2{\chi }^2(m_k-1)$ for $k=R$, P. Let

$$\begin{array}{c}\hfill W_k^h=\frac{{\overline{Y}}_k^{h\ast }-{\nu }_k}{{\xi }_k/\sqrt{m_k}},V_k^h=\frac{(m_k-1)S_{kh}^{2\ast }}{{\xi }_k^2}\end{array}$$

(7)

where ${\overline{Y}}_k^{h\ast }$ and $S_{kh}^{2\ast }$ are independent copies of ${\overline{Y}}_k^h$ and $S_{kh}^2$, respectively. Then, we have $W_k^h\sim \mathcal{N}(0,1)$, $V_k^h\sim {\chi }^2(m_k-1)$, and $W_k^h$ is independent of $V_k^h$. Hence, the GFPQs for ${\nu }_k$ and ${\xi }_k^2$ are

$$\begin{array}{c}\hfill R_{{\nu }_k}={\overline{Y}}_k^h-\sqrt{\frac{S_{kh}^2}{S_{kh}^{2\ast }}}({\overline{Y}}_k^{h\ast }-{\nu }_k)={\overline{Y}}_k^h-W_k^h\sqrt{\frac{(m_k-1)S_{kh}^2}{m_k{V}_k^h}},\end{array}$$

(8)

$$\begin{array}{c}\hfill R_{{\xi }_k^2}=\frac{S_{kh}^2}{S_{kh}^{2\ast }}{\xi }_k^2=\frac{(m_k-1)S_{kh}^2}{V_k^h},\end{array}$$

(9)

respectively. Using the GFPQs of ${\nu }_R$ and ${\nu }_P$ leads to

$$\begin{array}{cc}\hfill R_{\eta }& =({\overline{Y}}_R^h-{\overline{Y}}_P^h)-\left(W_R^h\sqrt{{\displaystyle \frac{(m_R-1)S_{Rh}^2}{m_R{V}_R^h}}}-W_P^h\sqrt{{\displaystyle \frac{(m_P-1)S_{Ph}^2}{m_P{V}_P^h}}}\right)\hfill \\ \hfill & =({\overline{Y}}_R^h-{\overline{Y}}_P^h)-\left(\sqrt{{\displaystyle \frac{S_{Rh}^2}{m_R}}}{\displaystyle \frac{W_R^h}{\sqrt{V_R^h/(m_R-1)}}}-\sqrt{{\displaystyle \frac{S_{Ph}^2}{m_P}}}{\displaystyle \frac{W_P^h}{\sqrt{V_P^h/(m_P-1)}}}\right)\hfill \\ \hfill & \stackrel{\Delta }{=}({\overline{Y}}_R^h-{\overline{Y}}_P^h)-\left(\sqrt{{\displaystyle \frac{S_{Rh}^2}{m_R}}}{T}_{m_R-1}-\sqrt{{\displaystyle \frac{S_{Ph}^2}{m_P}}}{T}_{m_P-1}\right),\hfill \end{array}$$

(10)

where $T_{m_R-1}\sim t(m_R-1)$ and $T_{m_P-1}\sim t(m_P-1)$. From Equation (10), it is easily shown that $R_{\eta }$ is a GFPQ of $\eta$. The $100(1-\alpha )\%$ two-sided GFCI for $\eta$ is $(R_{\eta ,\alpha /2},R_{\eta ,1-\alpha /2})$, where $R_{\eta ,\gamma }$ is the $100\gamma \%$ percentile point of sample observations of $R_{\eta }$.

Denote ${\Delta }_h=R_{\eta ,\alpha /2}$. Following the frequentist’s approach, we take the NI margin as ${\Delta }_{\mathrm{NI}}=(1-\lambda ){\Delta }_h$, where $\lambda \in [0,1]$ is a fraction representing the preservation level or desired proportion of the reference effect to the retained. Thus, the assay sensitivity margin can be expressed as $\Delta ={\Delta }_{\mathrm{NI}}/r=(1-\lambda ){\Delta }_h/r$. This shows that when $r<1-\lambda$ (i.e., $\Delta >{\Delta }_h>{\Delta }_{\mathrm{NI}}$), the assay sensitivity margin results in a more stringent rejection criterion than the historical placebo-controlled trial; when $r=1-\lambda$ and $\lambda \ne 0$ (i.e., $\Delta ={\Delta }_h>{\Delta }_{\mathrm{NI}}$), the assay sensitivity margin is equal to ${\Delta }_h$ and the NI margin is set as $(1-\lambda ){\Delta }_h$; when $r=1$ and $\lambda =0$, the hypothesis (3) reduces to the HT hypothesis.

2.2. Simultaneous CIs for $\varphi$ and $\psi$

2.2.1. Wald-Type Bonferroni Simultaneous CI

Generally, to construct simultaneous CI for $\varphi$ and $\psi$, one can consider the widely used and simple Bonferroni method based on the Wald-type statistics.

For the current trial data $X=\{X_{ij}:i=P,R,E,j=1,\dots ,n_i\}$ generated from model (2), we denote ${\overline{X}}_i=n_i^{-1}{\sum }_{j=1}^{n_i}{X}_{ij}$ and $S_i^2={(n_i-1)}^{-1}{\sum }_{j=1}^{n_i}{(X_{ij}-{\overline{X}}_i)}^2$. The unbiased estimators of ${\mu }_i$ and ${\sigma }_i^2$ are given by ${\widehat{\mu }}_i={\overline{X}}_i$ and ${\widehat{\sigma }}_i^2=S_i^2$, respectively, i.e., $E\left({\widehat{\mu }}_i\right)={\mu }_i$ and $E\left({\widehat{\sigma }}_i^2\right)={\sigma }_i^2$ for $i=P$, R, E. The unbiased estimators of $\varphi$ and $\psi$ are $\widehat{\varphi }={\overline{X}}_E-{\overline{X}}_R$ and $\widehat{\psi }={\overline{X}}_R-{\overline{X}}_P$, respectively, whose variances are $\mathrm{var}\left(\widehat{\varphi }\right)={\sigma }_E^2/n_E+{\sigma }_R^2/n_R$ and $\mathrm{var}\left(\widehat{\psi }\right)={\sigma }_R^2/n_R+{\sigma }_P^2/n_P$, respectively. The estimated variances of $\widehat{\varphi }$ and $\widehat{\psi }$ have the forms: $\widehat{\mathrm{var}}\left(\widehat{\varphi }\right)={\widehat{\sigma }}_E^2/n_E+{\widehat{\sigma }}_R^2/n_R$ and $\widehat{\mathrm{var}}\left(\widehat{\psi }\right)={\widehat{\sigma }}_R^2/n_R+{\widehat{\sigma }}_P^2/n_P$, respectively. It is easily shown that the Wald-type statistics $T_{\varphi }=(\widehat{\varphi }-\varphi )/\sqrt{\widehat{\mathrm{var}}\left(\widehat{\varphi }\right)}$ and $T_{\psi }=(\widehat{\psi }-\psi )/\sqrt{\widehat{\mathrm{var}}\left(\widehat{\psi }\right)}$ asymptotically follow the standard normal distribution. Thus, an approximate $100(1-\alpha )\%$ one-sided Wald-type Bonferroni simultaneous confidence region for $\varphi$ and $\psi$ is given by

$$\begin{array}{c}\hfill \{(\varphi ,\psi ):\varphi \in (L_{\varphi }^{WB},\infty ),\psi \in (L_{\psi }^{WB},\infty )\},\end{array}$$

(11)

where $L_{\varphi }^{WB}=\widehat{\varphi }-z_{1-\alpha /2}\sqrt{\widehat{\mathrm{var}}\left(\widehat{\varphi }\right)}$, and $L_{\psi }^{WB}=\widehat{\psi }-z_{1-\alpha /2}\sqrt{\widehat{\mathrm{var}}\left(\widehat{\psi }\right)}$. The above defined simultaneous confidence region is called the WB-SCI.

As Tang et al.  [13] pointed out, the Bonferroni simultaneous confidence region may behave poorly when $min\{n_E,n_R,n_P\}$ is small. To address the issue, three new simultaneous confidence regions are developed as follows.

2.2.2. Generalized Fiducial Simultaneous CI

For $k=E$, P, R, let ${\overline{X}}_k^{\ast }$ and $S_k^{2\ast }$ be independent copies of ${\overline{X}}_k$ and $S_k^2$, respectively, and define $W_k=\sqrt{n_k}({\overline{X}}_k^{\ast }-{\mu }_k)/{\sigma }_k$ and $V_k=(n_k-1)S_k^{2\ast }/{\sigma }_k^2$. It is easily shown that $W_k\sim \mathcal{N}(0,1)$, $V_k\sim {\chi }^2(n_k-1)$ and $W_k$ is independent of $V_k$. It follows from Section 2.1 that the GFPQs for ${\sigma }_k^2$ and ${\mu }_k$ can be expressed as

$$\begin{array}{c}\hfill R_{{\sigma }_k^2}=\frac{(n_k-1)S_k^2}{V_k},R_{{\mu }_k}={\overline{X}}_k-W_k\sqrt{\frac{(n_k-1)S_k^2}{n_k{V}_k}},\end{array}$$

(12)

respectively. Thus, the GFPQs of $\varphi$ and $\psi$ are

$$\begin{array}{cc}\hfill R_{\varphi }& ={\overline{X}}_E-{\overline{X}}_R-\left(W_E\sqrt{{\displaystyle \frac{(n_E-1)S_E^2}{n_E{V}_E}}}-W_R\sqrt{{\displaystyle \frac{(n_R-1)S_R^2}{n_R{V}_R}}}\right),\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill R_{\psi }& ={\overline{X}}_R-{\overline{X}}_P-\left(W_R\sqrt{{\displaystyle \frac{(n_R-1)S_R^2}{n_R{V}_R}}}-W_P\sqrt{{\displaystyle \frac{(n_P-1)S_P^2}{n_P{V}_P}}}\right),\hfill \end{array}$$

(14)

respectively. Define

$$R_D=max\left({\displaystyle \frac{\widehat{\varphi }-R_{\varphi }}{\sqrt{\widehat{\mathrm{var}}\left(\widehat{\varphi }\right)}}},{\displaystyle \frac{\widehat{\psi }-R_{\psi }}{\sqrt{\widehat{\mathrm{var}}\left(\widehat{\psi }\right)}}}\right).$$

(15)

Thus, the $100(1-\alpha )\%$ one-sided simultaneous generalized fiducial confidence region for $(\varphi ,\psi )$ is

$$\{(\varphi ,\psi ):\varphi \in (L_{\varphi }^F,\infty ),\psi \in (L_{\psi }^F,\infty )\}$$

(16)

where $L_{\varphi }^F=\widehat{\varphi }-d_{1-\alpha }\sqrt{\widehat{\mathrm{var}}\left(\widehat{\varphi }\right)}$, $L_{\psi }^F=\widehat{\psi }-d_{1-\alpha }\sqrt{\widehat{\mathrm{var}}\left(\widehat{\psi }\right)}$, and $d_{1-\alpha }$ is the $1-\alpha$ percentile point of statistic $R_D$’s distribution given sample observations. The above defined simultaneous confidence region is referred to as GF-SCI method.

Theorem 1.

Let $X_{k1},\dots ,X_{k{n}_k}$ be an independent and identically distributed sample from $\mathcal{N}({\mu }_k,{\sigma }_k^2)$ for k=P, R, E. Suppose that $r_k={lim}_{n\to \infty }{n}_k/n$ holds, where $n=n_E+n_R+n_P$ and $0<r_k<1$ for k=P, R, E. Then, we have

$$\begin{array}{c}\hfill \mathrm{Pr}(\varphi \ge L_{\varphi }^F,\psi \ge L_{\psi }^F)\approx 1-\alpha .\end{array}$$

(17)

The proof of Theorem 1 is given in Appendix A. Theorem 1 shows that the proposed GF-SCI can asymptotically attain the pre-specified coverage probability.

Combining the above argument, we form the following computing Algorithm 1 for evaluating empirical coverage probability (ECP) of the proposed GF-SCI.

Algorithm 1: Evaluating ECP of GF-SCI.

2.2.3. Hybrid Generalized Fiducial Simultaneous CI

The above presented GF-SCI for $\varphi$ and $\psi$ is computationally intensive in determining the percentile point of statistic $R_D$’s distribution. To solve this problem, we develop a hybrid generalized fiducial simultaneous CI by incorporating the square-and-add method and generalized fiducial method as follows.

The lower limits of the approximate $100(1-\alpha )\%$ Wald-type CIs for $\varphi$ and $\psi$ are given by

$$L_{\varphi }^W=\widehat{\varphi }-z_{1-\alpha }\sqrt{\widehat{\mathrm{var}}(\widehat{\varphi })},L_{\psi }^W=\widehat{\psi }-z_{1-\alpha }\sqrt{\widehat{\mathrm{var}}(\widehat{\psi })},$$

(18)

respectively, where $\widehat{\mathrm{var}}(\widehat{\varphi })=\widehat{\mathrm{var}}({\widehat{\mu }}_E)+\widehat{\mathrm{var}}({\widehat{\mu }}_R)$, $\widehat{\mathrm{var}}(\widehat{\psi })=\widehat{\mathrm{var}}({\widehat{\mu }}_R)+\widehat{\mathrm{var}}({\widehat{\mu }}_P)$, and $z_{1-\alpha }$ is the $1-\alpha$ percentile point of the standard normal distribution. It is easily shown that $\widehat{\mathrm{var}}(\widehat{\varphi })$ and $\widehat{\mathrm{var}}(\widehat{\psi })$ are consistent estimators of $\mathrm{var}(\widehat{\varphi })$ and $\mathrm{var}(\widehat{\psi })$ when the sample sizes $n_R$ and $n_P$ are sufficiently large, respectively. Hence, to recovery variances $\mathrm{var}(\widehat{\varphi })$ and $\mathrm{var}(\widehat{\psi })$ so that the resultant simultaneous CI behaves satisfactorily for small to moderate sample sizes, we develop the following hybrid method, which is similar to that given in [14].

Let $l_k$ and $u_k$ be the lower and upper limits of an approximate $100(1-\alpha )\%$ one-sided CI for ${\mu }_k$ for k = E, R, P. It follows from the Slutsky’s theorem that statistic $T_k=({\widehat{\mu }}_k-{\mu }_k)/\sqrt{\widehat{\mathrm{var}}\left({\widehat{\mu }}_k\right)}$ asymptotically follows the standard normal distribution for k = E, R, P. Thus, for k = E, R, P, we have $l_k={\widehat{\mu }}_k-z_{1-\alpha }\sqrt{\widehat{\mathrm{var}}\left({\widehat{\mu }}_k\right)}$ and $u_k={\widehat{\mu }}_k+z_{1-\alpha }\sqrt{\widehat{\mathrm{var}}\left({\widehat{\mu }}_k\right)}$, which lead to $\widehat{\mathrm{var}}\left({\widehat{\mu }}_k\right)={({\widehat{\mu }}_k-l_k)}^2/Z_{1-\alpha }^2$ for $l_k$ and $\widehat{\mathrm{var}}\left({\widehat{\mu }}_k\right)={(u_k-{\widehat{\mu }}_k)}^2/Z_{1-\alpha }^2$ for $u_k$, respectively. Following the argument of Howe [23] and Newcombe [11], we substitute the above equations into (18) and define the lower limits of the approximate $100(1-\alpha )\%$ one-sided hybrid CIs for $\varphi$ and $\psi$ as

$$L_{\varphi }^H=\widehat{\varphi }-\sqrt{{({\widehat{\mu }}_E-l_E)}^2+{(u_R-{\widehat{\mu }}_R)}^2},L_{\psi }^H=\widehat{\psi }-\sqrt{{({\widehat{\mu }}_R-l_R)}^2+{(u_P-{\widehat{\mu }}_P)}^2},$$

(19)

respectively, which imply that it is necessary to first evaluate the lower and upper limits $l_k$ and $u_k$ (k = E, R, P) for computing $L_{\varphi }^H$ and $L_{\psi }^H$. In what follows, the generalized fiducial method introduced above is employed to calculate $l_k$ and $u_k$ for k = E, R, P.

The lower and upper limits of an approximate $100(1-\alpha )\%$ one-sided GFCI of ${\mu }_k$ adjusted for multiplicity using the Bonferroni method have the forms

$$\begin{array}{c}\hfill l_k=R_{{\mu }_k,\alpha /2},u_k=R_{{\mu }_k,1-\alpha /2},\end{array}$$

(20)

where $R_{{\mu }_k,\alpha }$ represents the $\alpha$ percentile point of sample observations of $R_{{\mu }_k}$, which is the GFPQ of ${\mu }_k$ with $R_{{\mu }_k}={\overline{X}}_k-W_k\sqrt{(n_k-1)S_k^2/\left(n_k{V}_k\right)}$, $W_k\sim \mathcal{N}(0,1)$ and $V_k\sim {\chi }^2(n_k-1)$ for $k=E$, R, P.

Plugging the above defined lower and upper limits $l_k$ and $u_k$ ($k=E,R,P$) into $L_{\varphi }^H$ and $L_{\psi }^H$ defined in (19) leads to an approximate $100(1-\alpha )\%$ one-sided hybrid generalized fiducial simultaneous confidence region of $(\varphi ,\psi )$:

$$\begin{array}{c}\hfill \{(\varphi ,\psi ):\varphi \in (L_{\varphi }^H,\infty ),\psi \in (L_{\psi }^H,\infty )\}.\end{array}$$

(21)

The above defined simultaneous confidence region is referred to as HG-SCI method.

The approach to evaluate empirical coverage probability (ECP) of the defined HG-SCI is summarized as the Algorithm 2.

Algorithm 2: Evaluating ECP of HG-SCI.

2.2.4. Parametric Bootstrap Simultaneous CI

From Section 2.2.3, it is easily seen that the current data are repeatedly used in calculating hybrid generalized fiducial simultaneous confidence region. To address the issue, following [22], we consider the following parametric bootstrap simultaneous confidence region for $\varphi$ and $\psi$.

To this end, we denote

$$T_{\varphi }={\displaystyle \frac{\widehat{\varphi }-\varphi }{\sqrt{\widehat{\mathrm{var}}\left(\widehat{\varphi }\right)}}},T_{\psi }={\displaystyle \frac{\widehat{\psi }-\psi }{\sqrt{\widehat{\mathrm{var}}\left(\widehat{\psi }\right)}}},T_B=max\left(T_{\varphi },T_{\psi }\right).$$

(22)

Let $q_{1-\alpha }$ be the approximate $1-\alpha$ percentile point of statistic $T_B$’s distribution. Then, the lower limits of an approximate $100(1-\alpha )\%$ one-sided simultaneous confidence region for $\varphi$ and $\psi$ are given as

$$\begin{array}{c}\hfill L_{\varphi }^B=\widehat{\varphi }-q_{1-\alpha }\sqrt{\widehat{\mathrm{var}}\left(\widehat{\varphi }\right)},L_{\psi }^B=\widehat{\psi }-q_{1-\alpha }\sqrt{\widehat{\mathrm{var}}\left(\widehat{\psi }\right)},\end{array}$$

(23)

respectively. Clearly, the challenge for evaluating $L_{\varphi }^B$ and $L_{\psi }^B$ is to calculate $q_{1-\alpha }$. While $T_{\varphi }$ and $T_{\psi }$ are asymptotically distributed as the standard normal distribution, it is rather difficult to compute $q_{1-\alpha }$ from the joint distribution of $T_{\varphi }$ and $T_{\psi }$ in that $T_{\varphi }$ is not independent of $T_{\psi }$. To solve the problem, the parametric bootstrap approach given in [22] is adopted to approximate the distribution of statistic $T_B$.

Let $s_k^2$ denote the observed values of $S_k^2$ for $k=E$, P, R. Note that the distribution of $T_B$ depends on the nuisance parameters ${\sigma }_k^2$, but it dose not depend on the values of ${\mu }_k$ for $k=E$, R, P. Therefore, when inducing the distribution of $T_B$, we can take ${\mu }_k=0$ for $k=E$, R, P. The parametric bootstrap distribution of $T_B$ can be obtained from its resampling distribution when the values of ${\sigma }_k^2$’s are replaced by $s_k^2$ and the values of ${\mu }_k$’s are taken as zero. It follows from Equation (22) that the parametric bootstrap pivotal quantity for statistic $T_B$ is

$$T_B^{PI}=max\left({\displaystyle \frac{{\overline{X}}_E^B-{\overline{X}}_R^B}{\sqrt{{\widehat{\mathrm{var}}}_B\left(\widehat{\varphi }\right)}}},{\displaystyle \frac{{\overline{X}}_R^B-{\overline{X}}_P^B}{\sqrt{{\widehat{\mathrm{var}}}_B\left(\widehat{\psi }\right)}}}\right),$$

(24)

where

$$\begin{array}{c}\hfill {\widehat{\mathrm{var}}}_B\left(\widehat{\varphi }\right)={\displaystyle \frac{S_{E,B}^2}{n_E}}+\frac{S_{R,B}^2}{n_R},{\widehat{\mathrm{var}}}_B\left(\widehat{\psi }\right)={\displaystyle \frac{S_{R,B}^2}{n_R}}+\frac{S_{P,B}^2}{n_P},\end{array}$$

(25)

$$\begin{array}{c}\hfill {\overline{X}}_k^B\sim \mathcal{N}\left(0,\frac{s_k^2}{n_k}\right),S_{k,B}^2\sim \frac{s_k^2}{n_k-1}{\chi }^2(n_k-1).\end{array}$$

(26)

The distribution of $T_B^{PI}$ provides a parametric bootstrap approximation to the distribution of $T_B$. Let $q_{1-\alpha }^B$ be the $1-\alpha$ percentile point of bootstrap sample observations of $T_B^{PI}$. Thus, an approximate $100(1-\alpha )\%$ one-sided parametric bootstrap simultaneous confidence region for $(\varphi ,\psi )$ is given by

$$\begin{array}{c}\hfill \{(\varphi ,\psi ):\varphi \in (L_{\varphi }^B,\infty ),\psi \in (L_{\psi }^B,\infty )\},\end{array}$$

(27)

where $L_{\varphi }^B=\widehat{\varphi }-q_{1-\alpha }^B\sqrt{\widehat{\mathrm{var}}(\widehat{\varphi })}$, and $L_{\psi }^B=\widehat{\psi }-q_{1-\alpha }^B\sqrt{\widehat{\mathrm{var}}(\widehat{\psi })}$. The above defined simultaneous confidence region is referred to as PB-SCI method.

Theorem 2.

Let $X_{k1},\cdots ,X_{k{n}_k}$ be an independent and identically distributed sample from $\mathcal{N}({\mu }_k,{\sigma }_k^2)$ for k = P, R, E. Let $n=n_E+n_R+n_P$. Assume that there is a $r_k\in (0,1)$ such that $r_k={lim}_{n\to \infty }{n}_k/n$ holds for k = E, R, P. Then, we have

$$\begin{array}{c}\hfill \mathrm{Pr}(\varphi \ge L_{\varphi }^B,\psi \ge L_{\psi }^B)\approx 1-\alpha .\end{array}$$

(28)

Proof of Theorem 2 is given in Appendix B. Theorem 2 shows that the preceding proposed parametric bootstrap simultaneous confidence region can asymptotically attain the pre-specified confidence level $1-\alpha$.

2.3. Sample Size Determination

Due to the duality of hypothesis testing and interval estimation, we can obtain the rejection regions at the significance level $\alpha =0.05$ from the above proposed four simultaneous confidence regions, which are given as ${\mathbb{D}}_W=\{(x_E,x_R,x_P):{\overline{x}}_E-{\overline{x}}_R>-{\widehat{\Delta }}_{\mathrm{NI}}+z_{1-\alpha /2}\sqrt{\widehat{\mathrm{var}}(\widehat{\varphi })}\cup {\overline{x}}_R-{\overline{x}}_P>\widehat{\Delta }+z_{1-\alpha /2}\sqrt{\widehat{\mathrm{var}}(\widehat{\psi })}\}$, ${\mathbb{D}}_F=\{(x_E,x_R,x_P):{\overline{x}}_E-{\overline{x}}_R>-{\widehat{\Delta }}_{\mathrm{NI}}+d_{1-\alpha }\sqrt{\widehat{\mathrm{var}}(\widehat{\varphi })}\cup {\overline{x}}_R-{\overline{x}}_P>\widehat{\Delta }+d_{1-\alpha }\sqrt{\widehat{\mathrm{var}}(\widehat{\psi })}\}$, ${\mathbb{D}}_H=\{(x_E,x_R,x_P):{\overline{x}}_E-{\overline{x}}_R>-{\widehat{\Delta }}_{\mathrm{NI}}+\sqrt{{({\widehat{\mu }}_E-l_E)}^2+{(u_R-{\widehat{\mu }}_R)}^2}\cup {\overline{x}}_R-{\overline{x}}_P>\widehat{\Delta }+\sqrt{{({\widehat{\mu }}_R-l_R)}^2+{(u_P-{\widehat{\mu }}_P)}^2}\}$, ${\mathbb{D}}_B=\{(x_E,x_R,x_P):{\overline{x}}_E-{\overline{x}}_R>-{\widehat{\Delta }}_{\mathrm{NI}}+q_{1-\alpha }^B\sqrt{\widehat{\mathrm{var}}(\widehat{\varphi })}\cup {\overline{x}}_R-{\overline{x}}_P>\widehat{\Delta }+q_{1-\alpha }^B\sqrt{\widehat{\mathrm{var}}(\widehat{\psi })}\}$, respectively, where ${\overline{x}}_k$ denotes the sample mean for $k=E$, R, P, and ${\mathbb{D}}_W$, ${\mathbb{D}}_F$, ${\mathbb{D}}_H$ and ${\mathbb{D}}_B$ correspond to the WB-SCI, GF-SCI, HG-SCI and PB-SCI, respectively. The family wise error rate can be controlled at the significance level $\alpha$ via $\mathrm{Pr}\left({\mathbb{D}}_{\ell }\right|H_{\mathrm{NI}}^0,K_{\mathrm{AS}}^0)\approx \alpha$, and the power of $1-\beta$ can be computed by $\mathrm{Pr}\left({\mathbb{D}}_{\ell }\right|H_{\mathrm{NI}}^1,K_{\mathrm{AS}}^1)\approx 1-\beta$ for ℓ = W, F, H and B. The required sample size $n=n_E+n_R+n_P$ for attaining the pre-specified power $1-\beta$ at the given significance level $\alpha$ can be obtained by finding the solution to $\mathrm{Pr}\left({\mathbb{D}}_{\ell }\right|H_{\mathrm{NI}}^1,K_{\mathrm{AS}}^1)\approx 1-\beta$ with respect to n for ℓ = W, F, H and B. There is not a closed-form for n. To this end, Algorithm 3 is presented to compute the sample size n with the assumption: $n_E:n_R:n_P=c_1:c_2:1$ as follows.

Algorithm 3: Computing sample size.

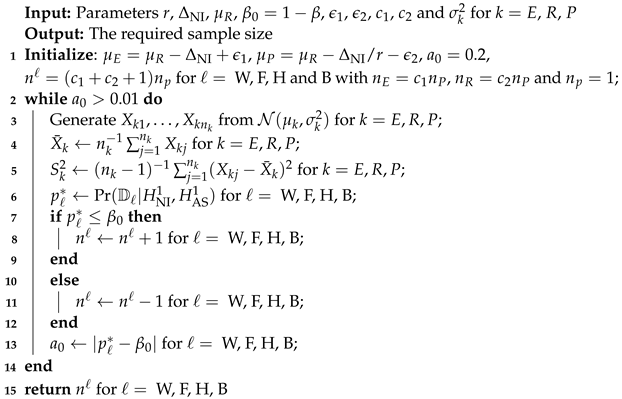3. Results

Simulation examples and a real example are provided to illustrate the efficiency of the preceding proposed methods in terms of empirical coverage probabilities. The lower limits of the approximate 95% one-sided simultaneous confidence region for the proposed methods are given in an application to mildly asthmatic study. Empirical results demonstrated that the GF-SCI and HG-SCI perform better than the WB-SCI and PB-SCI.

3.1. Simulation Results

In this section, two simulation studies are conducted to investigate the performance of the preceding proposed methodologies.

To compare the performance of the proposed simultaneous confidence regions in terms of their empirical coverage probabilities (ECPs), we conduct the first simulation study for $\mathcal{T}=5000$ replications. In this simulation study, we take ${\nu }_R$ = 4, ${\nu }_P$ = 1.5, ${\xi }_R^2$ = 1, ${\xi }_P^2$ = 2 and $m_P=m_R=20$ in generating historical data for determining ${\Delta }_{NI}$ and $\Delta ={\Delta }_{\mathrm{NI}}/r$ with $M=5000$, and ${\sigma }_P^2$ = 2.0, ${\sigma }_E^2$ = 1.5, ${\sigma }_R^2$ = 0.5, 1.0 and 3.0, ${\mu }_R=$3.0, 4.0 and 5.0, ${\mu }_E={\mu }_R-{\Delta }_{\mathrm{NI}}$ and ${\mu }_P={\mu }_R-\Delta$ indicating that the true values ${\varphi }_0$ and ${\psi }_0$ of $\varphi$ and $\psi$ are ${\varphi }_0=-{\Delta }_{\mathrm{NI}}$ and ${\psi }_0=\Delta$, respectively, in sampling the current trial data. We set r = 0.3 together with $\lambda =0.6$ and 0.7, and r = 0.6 together with $\lambda =0.3$ and 0.4, corresponding to the cases that $\Delta >{\Delta }_h>{\Delta }_{\mathrm{NI}}$ and $\Delta ={\Delta }_h>{\Delta }_{\mathrm{NI}}$, respectively; and r = 1.0 together with $\lambda =$ 0.0 corresponding to the case that $\Delta ={\Delta }_h={\Delta }_{\mathrm{NI}}$. We consider $n=n_E+n_R+n_P$ = 60, 150 and 300 with the following three allocation proportions: (L1) the balanced design $n_E:n_R:n_P=1:1:1$, (L2) the unbalanced design $n_E:n_R:n_P=2:2:1$ and (L3) the unbalanced design $n_E:n_R:n_P=3:2:1$.

For each of the aforementioned settings, the preceding proposed three algorithms for evaluating simultaneous confidence regions for $\varphi$ and $\psi$ are used to compute ECPs at the significance level $\alpha =0.05$. Results for $n=60$, 150 and 300 are given in Table 1, Table 2 and Table 3, respectively. Inspection of Table 1, Table 2 and Table 3 indicates that (i) the GF-SCI and HG-SCI methods behave better than the WB-SCI and PB-SCI methods regardless of the values of r, $\lambda$, ${\mu }_R$ and ${\sigma }_R^2$ and the sample sizes in that the ECPs of the former are quite closer to the pre-specified confidence level 95% than those of the latter; (ii) when the sample size n is small, the PB-SCI and WB-SCI methods are liberal regardless of the balanced and unbalanced designs in that their ECPs are less than the pre-specified confidence level 95%, but the PB-SCI method behaves better than the WB-SCI method in that the ECPs for the former are closer to the pre-specified confidence level than those for the latter; (iii) when the sample size is large (e.g., $n=150$ and 300), the PB-SCI method has the same performance as the GF-SCI and HG-SCI methods, but the WB-SCI method is liberal.

Table 1. Empirical coverage probabilities of four 95% simultaneous confidence regions for $\varphi$ and $\psi$ under various settings with $n=60$.

				${\mathit{n}}_{\mathit{E}}:{\mathit{n}}_{\mathit{R}}:{\mathit{n}}_{\mathit{P}}=1:1:1$				${\mathit{n}}_{\mathit{E}}:{\mathit{n}}_{\mathit{R}}:{\mathit{n}}_{\mathit{P}}=2:2:1$				${\mathit{n}}_{\mathit{E}}:{\mathit{n}}_{\mathit{R}}:{\mathit{n}}_{\mathit{P}}=3:2:1$
r	$\mathit{\lambda }$	${\mathit{\mu }}_{\mathit{R}}$	${\mathit{\sigma }}_{\mathit{R}}^2$	GF	HG	WB	PB	GF	HG	WB	PB	GF	HG	WB	PB
0.3	0.6	3	0.5	95.00	95.06	93.90	94.68	95.16	95.14	93.26	94.62	95.22	95.36	93.42	94.78
			1	95.34	95.44	94.02	94.66	95.34	95.28	93.34	94.66	95.52	95.60	93.62	94.98
			3	95.44	95.42	94.10	94.80	95.70	95.86	94.34	95.18	96.02	96.04	94.48	95.36
		4	0.5	94.98	95.10	93.62	94.50	95.42	95.66	93.82	95.14	95.20	95.32	93.38	94.74
			1	95.22	95.36	93.64	94.48	95.50	95.60	93.92	95.12	95.80	95.78	93.74	95.16
			3	95.44	95.60	94.26	95.04	95.58	95.64	94.26	95.04	95.72	95.76	93.90	95.14
		5	0.5	95.52	95.66	94.16	95.16	95.44	95.48	93.98	94.98	95.64	95.44	93.46	95.06
			1	95.70	95.74	94.40	95.12	95.54	95.44	93.90	94.98	95.86	95.88	93.98	95.28
			3	95.94	95.88	94.44	95.20	96.00	96.12	94.42	95.22	96.12	96.10	94.18	95.38
	0.7	3	0.5	95.46	95.56	94.16	95.00	95.60	95.70	94.10	95.24	95.64	95.52	93.84	95.14
			1	95.38	95.48	93.88	94.66	95.22	95.38	93.68	94.66	95.58	95.64	93.78	94.92
			3	95.50	95.62	94.18	95.04	95.36	95.46	93.86	94.88	96.20	96.44	94.46	95.42
		4	0.5	95.58	95.58	94.22	95.24	94.54	94.72	92.80	94.18	95.64	95.74	93.66	95.10
			1	95.86	95.92	94.28	95.12	95.82	95.76	94.12	95.32	95.36	95.42	93.50	94.70
			3	95.30	95.42	93.86	94.76	95.44	95.56	93.96	94.82	95.82	95.86	94.38	95.12
		5	0.5	95.68	95.82	94.38	95.42	95.26	95.46	93.76	95.06	95.34	95.46	93.32	95.12
			1	95.90	95.94	94.42	95.36	95.26	95.38	93.54	94.58	95.54	95.76	93.72	95.16
			3	95.92	95.94	94.46	95.34	95.64	95.62	93.94	94.86	95.82	95.82	94.06	95.10
0.6	0.3	3	0.5	94.80	94.96	93.48	94.32	94.84	95.00	93.26	94.42	95.12	95.16	93.16	94.44
			1	95.34	95.48	94.20	94.74	95.62	95.82	93.96	95.10	95.22	95.28	93.36	94.68
			3	95.62	95.64	94.24	95.10	96.08	96.26	94.76	95.54	95.40	95.46	93.40	94.90
		4	0.5	95.66	95.80	94.38	95.22	95.52	95.68	93.78	95.16	95.18	95.38	93.34	94.52
			1	95.26	95.52	93.72	94.74	95.06	95.24	93.36	94.60	95.86	95.98	94.26	95.38
			3	95.64	95.80	94.26	94.96	95.78	95.80	94.18	95.18	95.38	95.62	93.56	94.74
		5	0.5	94.60	94.70	93.44	94.18	94.90	95.16	93.46	94.62	95.04	95.00	92.86	94.42
			1	95.32	95.36	93.88	94.76	95.54	95.52	93.72	94.72	95.94	96.04	93.98	95.44
			3	95.18	95.26	93.68	94.60	95.66	95.74	94.38	95.10	95.66	95.58	93.80	94.94
	0.4	3	0.5	94.84	94.92	93.56	94.42	95.68	95.74	94.08	95.28	95.48	95.58	93.48	95.02
			1	95.14	95.36	93.94	94.78	95.28	95.28	94.12	94.96	95.22	95.36	93.34	94.46
			3	95.92	95.94	94.70	95.52	95.84	95.84	94.44	95.18	95.60	95.60	93.86	95.10
		4	0.5	95.28	95.34	93.88	94.84	95.10	95.18	93.26	94.70	95.20	95.16	93.46	94.70
			1	95.78	95.98	94.26	95.22	95.92	96.04	94.28	95.46	95.50	95.50	93.58	94.88
			3	95.50	95.64	94.00	94.82	95.72	95.90	94.58	95.20	95.58	95.60	93.92	94.98
		5	0.5	95.82	95.84	94.42	95.34	95.38	95.48	93.84	95.00	95.28	95.30	93.40	94.72
			1	94.56	94.66	93.56	94.08	95.66	95.78	94.00	95.00	95.16	95.36	93.44	94.76
			3	96.02	96.04	94.52	95.38	95.08	95.26	93.82	94.44	95.48	95.32	93.82	94.58
1.0	0.0	3	0.5	95.52	95.60	94.20	95.08	95.38	95.38	93.86	95.00	95.68	95.88	94.00	95.16
			1	95.64	95.70	94.10	95.02	94.98	95.16	93.54	94.44	95.46	95.58	93.28	94.74
			3	95.64	95.68	94.20	94.92	95.36	95.46	94.00	94.82	95.56	95.44	93.74	94.80
		4	0.5	95.32	95.46	93.90	94.90	95.52	95.60	94.08	95.26	95.10	95.52	93.20	94.78
			1	95.54	95.54	94.18	94.92	95.34	95.52	93.88	94.98	95.04	95.06	93.20	94.42
			3	95.68	95.68	94.32	95.02	95.28	95.46	94.14	94.78	95.68	95.62	94.06	94.88
		5	0.5	95.22	95.42	93.72	94.64	95.92	96.04	94.34	95.58	95.70	95.68	93.76	95.18
			1	95.66	95.62	94.38	95.18	95.46	95.52	93.84	94.90	95.30	95.36	93.60	94.96
			3	95.86	96.02	94.56	95.26	95.62	95.60	93.92	94.92	96.40	96.30	94.44	95.58

Table 2. Empirical coverage probabilities of four 95% simultaneous confidence regions for $\varphi$ and $\psi$ under various settings with $n=150$.

				${\mathit{n}}_{\mathit{E}}:{\mathit{n}}_{\mathit{R}}:{\mathit{n}}_{\mathit{P}}=1:1:1$				${\mathit{n}}_{\mathit{E}}:{\mathit{n}}_{\mathit{R}}:{\mathit{n}}_{\mathit{P}}=2:2:1$				${\mathit{n}}_{\mathit{E}}:{\mathit{n}}_{\mathit{R}}:{\mathit{n}}_{\mathit{P}}=3:2:1$
r	$\mathit{\lambda }$	${\mathit{\mu }}_{\mathit{R}}$	${\mathit{\sigma }}_{\mathit{R}}^2$	GF	HG	WB	PB	GF	HG	WB	PB	GF	HG	WB	PB
0.3	0.6	3	0.5	95.26	95.24	94.88	95.22	95.56	95.60	95.16	95.54	94.72	94.88	93.90	94.66
			1	94.66	94.70	94.10	94.46	94.68	94.86	94.06	94.44	95.24	95.32	94.42	94.88
			3	95.44	95.50	95.02	95.30	95.46	95.64	95.04	95.30	95.74	95.74	94.96	95.54
		4	0.5	95.02	95.08	94.50	94.76	94.78	94.92	94.26	94.70	95.42	95.38	94.72	95.38
			1	96.02	96.16	95.56	95.76	95.44	95.42	94.72	95.18	95.90	95.88	95.12	95.56
			3	95.42	95.42	94.74	95.10	95.02	95.06	94.48	94.88	95.20	95.34	94.66	94.98
		5	0.5	95.20	95.22	94.80	95.10	94.96	95.12	94.60	94.98	95.24	95.44	94.66	95.06
			1	94.66	94.76	94.26	94.54	95.08	95.20	94.52	94.90	95.50	95.48	94.86	95.30
			3	94.82	94.82	94.12	94.42	95.50	95.56	94.84	95.24	95.80	95.66	95.20	95.58
	0.7	3	0.5	95.16	95.28	94.74	95.00	95.70	95.66	95.02	95.64	95.04	95.14	94.50	94.96
			1	94.92	94.96	94.18	94.70	94.92	94.94	94.38	94.62	94.76	94.86	93.98	94.46
			3	95.48	95.42	94.94	95.20	95.08	95.14	94.60	94.88	95.40	95.52	94.98	95.26
		4	0.5	94.82	94.88	94.20	94.68	94.96	94.92	94.34	94.80	94.60	94.78	93.94	94.28
			1	94.50	94.56	94.08	94.30	95.46	95.50	94.78	95.08	95.10	95.22	94.32	94.88
			3	94.98	95.06	94.50	94.70	95.32	95.30	94.66	95.22	95.76	95.68	95.06	95.38
		5	0.5	95.14	95.20	94.64	95.06	95.36	95.32	94.78	95.08	95.22	95.26	94.54	95.08
			1	95.36	95.56	95.00	95.26	95.04	95.18	94.64	94.96	95.38	95.32	94.56	95.12
			3	95.16	95.06	94.56	94.88	95.24	95.26	94.62	94.86	95.42	95.52	94.86	95.12
0.6	0.3	3	0.5	95.46	95.52	94.86	95.28	95.24	95.24	94.46	95.00	94.82	94.88	94.16	94.82
			1	95.06	95.20	94.58	94.94	95.08	95.08	94.56	94.98	95.16	95.04	94.42	94.86
			3	95.14	95.04	94.70	94.92	94.84	94.78	94.22	94.54	95.46	95.54	94.78	95.26
		4	0.5	95.08	95.20	94.80	95.14	95.24	95.38	94.74	95.14	95.04	95.02	94.36	94.92
			1	95.40	95.42	94.92	95.10	95.50	95.62	94.92	95.28	95.30	95.24	94.40	95.08
			3	95.28	95.34	94.78	95.22	95.00	95.18	94.38	94.82	95.18	95.28	94.62	95.06
		5	0.5	95.52	95.44	94.98	95.34	94.72	94.66	93.98	94.42	94.84	94.86	94.22	94.58
			1	95.20	95.26	94.66	95.00	95.54	95.48	94.76	95.08	95.30	95.20	94.66	95.04
			3	95.32	95.32	94.82	95.08	95.60	95.66	94.94	95.32	95.58	95.60	95.02	95.36
	0.4	3	0.5	95.46	95.52	94.94	95.16	94.76	94.80	94.08	94.68	94.48	94.48	93.68	94.30
			1	94.82	94.84	94.32	94.56	94.68	94.80	93.82	94.54	95.64	95.64	94.88	95.38
			3	95.16	95.28	94.46	94.92	94.86	94.94	94.32	94.66	95.26	95.32	94.68	94.94
		4	0.5	95.54	95.70	94.92	95.32	94.82	94.82	94.22	94.56	94.68	94.64	94.10	94.50
			1	95.04	95.12	94.48	94.88	95.04	95.06	94.52	94.94	94.84	94.82	93.90	94.40
			3	95.06	95.06	94.62	94.88	95.40	95.36	94.86	95.04	95.38	95.46	94.82	95.14
		5	0.5	95.68	95.62	95.22	95.62	94.90	94.98	94.20	94.64	95.74	95.72	95.12	95.58
			1	95.22	95.32	94.90	95.10	95.16	95.20	94.46	94.86	94.52	94.54	93.96	94.40
			3	94.88	95.08	94.50	94.78	95.54	95.64	95.08	95.36	94.92	94.94	94.14	94.50
1.0	0.0	3	0.5	95.36	95.54	94.80	95.22	95.12	95.10	94.42	94.92	95.06	95.14	94.44	95.00
			1	94.60	94.78	93.94	94.46	95.20	95.40	94.80	95.12	95.14	95.24	94.34	94.86
			3	95.48	95.58	95.08	95.32	95.66	95.64	95.10	95.40	95.60	95.44	94.74	95.28
		4	0.5	95.36	95.32	94.78	95.06	95.00	95.02	94.40	94.80	95.04	95.16	94.44	94.86
			1	95.18	95.14	94.66	94.90	95.08	95.14	94.48	94.96	95.22	95.34	94.66	95.18
			3	95.64	95.60	95.26	95.50	95.06	95.10	94.78	94.92	95.38	95.44	94.88	95.18
		5	0.5	95.00	95.00	94.50	94.80	95.26	95.30	94.54	95.22	95.34	95.44	94.72	95.22
			1	95.54	95.66	95.18	95.44	95.40	95.54	94.66	95.04	95.34	95.34	94.68	95.10
			3	95.04	95.12	94.44	94.70	95.12	95.20	94.62	94.88	95.44	95.48	94.80	95.16

Table 3. Empirical coverage probabilities of four 95% simultaneous confidence regions for $\varphi$ and $\psi$ under various settings with $n=300$.

				${\mathit{n}}_{\mathit{E}}:{\mathit{n}}_{\mathit{R}}:{\mathit{n}}_{\mathit{P}}=1:1:1$				${\mathit{n}}_{\mathit{E}}:{\mathit{n}}_{\mathit{R}}:{\mathit{n}}_{\mathit{P}}=2:2:1$				${\mathit{n}}_{\mathit{E}}:{\mathit{n}}_{\mathit{R}}:{\mathit{n}}_{\mathit{P}}=3:2:1$
r	$\mathit{\lambda }$	${\mathit{\mu }}_{\mathit{R}}$	${\mathit{\sigma }}_{\mathit{R}}^2$	GF	HG	WB	PB	GF	HG	WB	PB	GF	HG	WB	PB
0.3	0.6	3	0.5	95.08	95.02	94.92	94.96	95.02	95.02	94.66	95.02	95.22	95.34	94.98	95.20
			1	95.58	95.64	95.40	95.46	94.84	94.82	94.54	94.76	95.16	95.20	94.94	95.12
			3	94.48	94.50	94.14	94.24	95.26	95.30	95.04	95.20	95.56	95.58	95.22	95.38
		4	0.5	95.40	95.38	95.12	95.28	94.76	94.84	94.42	94.72	94.18	94.38	93.92	94.18
			1	94.94	94.92	94.70	94.88	94.60	94.64	94.32	94.44	95.50	95.42	95.10	95.32
			3	95.32	95.32	94.88	95.16	95.24	95.28	95.10	95.16	94.74	94.82	94.50	94.70
		5	0.5	95.08	95.14	94.88	95.02	94.94	94.92	94.60	94.86	95.08	95.16	94.76	94.98
			1	95.18	95.18	94.84	95.00	95.42	95.32	95.14	95.36	95.72	95.72	95.40	95.60
			3	94.74	94.82	94.48	94.78	95.28	95.28	94.96	95.12	94.92	94.84	94.62	94.80
	0.7	3	0.5	95.04	95.08	94.86	94.92	94.84	94.84	94.54	94.76	95.28	95.26	95.04	95.16
			1	95.58	95.62	95.30	95.44	95.10	94.98	94.86	94.94	95.46	95.44	95.12	95.36
			3	95.32	95.34	94.98	95.14	95.50	95.48	95.28	95.40	95.48	95.46	95.12	95.30
		4	0.5	94.94	94.92	94.70	94.80	94.78	94.90	94.54	94.76	95.22	95.12	94.86	95.16
			1	95.42	95.46	95.32	95.42	95.12	95.16	94.92	95.20	95.18	95.18	94.92	95.12
			3	95.14	95.34	95.02	95.02	94.72	94.74	94.66	94.72	95.22	95.18	94.96	95.10
		5	0.5	94.86	94.92	94.76	94.92	94.98	95.00	94.78	94.90	95.20	95.26	94.80	95.14
			1	95.10	95.14	94.88	95.10	95.22	95.16	94.98	95.12	95.02	95.04	94.52	94.80
			3	95.40	95.32	95.08	95.38	95.26	95.40	94.94	95.08	94.94	94.94	94.62	94.72
0.6	0.3	3	0.5	95.56	95.70	95.36	95.66	94.92	95.06	94.68	94.94	94.46	94.60	94.08	94.34
			1	95.30	95.26	95.06	95.22	95.68	95.76	95.34	95.58	95.06	95.24	94.90	95.12
			3	94.88	95.00	94.76	94.86	95.14	95.20	94.90	95.06	94.88	94.94	94.64	94.92
		4	0.5	95.38	95.40	95.08	95.24	95.04	95.20	94.82	95.06	94.98	94.94	94.58	94.72
			1	94.92	95.00	94.64	94.82	94.84	94.92	94.60	94.86	95.04	95.10	94.82	94.96
			3	95.50	95.52	95.26	95.32	95.24	95.26	95.10	95.24	94.84	94.86	94.56	94.72
		5	0.5	95.50	95.56	95.34	95.36	94.94	94.86	94.72	94.84	95.02	95.16	94.80	94.96
			1	95.10	94.92	94.92	94.92	95.38	95.40	95.14	95.26	94.72	94.82	94.38	94.66
			3	95.00	95.06	94.84	94.88	94.92	94.96	94.68	94.88	94.94	95.00	94.52	94.66
	0.4	3	0.5	95.18	95.26	94.86	95.02	95.10	95.20	94.86	95.04	94.92	94.94	94.48	94.72
			1	95.16	95.18	94.94	95.10	94.92	94.98	94.70	94.80	94.72	94.76	94.42	94.64
			3	94.52	94.66	94.30	94.24	94.88	94.98	94.74	94.72	95.36	95.34	95.06	95.14
		4	0.5	95.26	95.24	94.96	95.18	95.12	95.06	94.82	95.02	95.06	95.10	94.78	95.06
			1	95.34	95.38	95.22	95.22	95.22	95.18	94.88	95.18	94.96	94.94	94.56	94.76
			3	94.96	94.80	94.62	94.78	94.52	94.64	94.26	94.52	95.20	95.18	94.94	95.02
		5	0.5	94.46	94.58	94.38	94.48	95.42	95.38	94.94	95.30	95.02	95.08	94.66	94.94
			1	95.26	95.38	95.06	95.26	94.74	94.92	94.30	94.44	94.56	94.74	94.34	94.54
			3	95.20	95.34	94.88	95.08	95.12	95.14	94.82	94.90	94.70	94.80	94.32	94.56
1.0	0.0	3	0.5	95.26	95.42	94.98	95.20	95.14	95.24	94.76	94.96	95.42	95.50	95.18	95.36
			1	95.48	95.46	95.28	95.36	94.30	94.30	93.90	94.16	94.96	95.00	94.56	94.80
			3	94.92	94.98	94.88	95.06	94.96	94.96	94.70	94.94	94.68	94.72	94.36	94.54
		4	0.5	94.90	94.86	94.56	94.72	95.30	95.34	95.06	95.16	95.32	95.48	95.00	95.22
			1	95.38	95.48	95.30	95.38	94.98	95.02	94.82	95.02	94.82	95.04	94.58	94.90
			3	95.04	95.06	94.82	95.02	94.88	94.98	94.68	94.76	95.12	95.20	94.64	94.82
		5	0.5	95.24	95.32	95.00	95.14	95.06	95.06	94.80	95.02	95.16	95.20	94.94	95.18
			1	94.50	94.50	94.26	94.36	95.10	95.10	94.78	95.04	94.60	94.68	94.42	94.48
			3	94.82	94.78	94.48	94.66	94.64	94.60	94.40	94.56	94.58	94.60	94.08	94.38

To investigate the performance of the sample size determination method introduced above (i.e., Algorithm 3), we conduct the second simulation study. Here the same settings as those given in the first simulation study including r and $\lambda$ are used to generate the historical data in determining the NI margin: ${\Delta }_{\mathrm{NI}}=(1-\lambda ){\Delta }_h$ and $\Delta =(1-\lambda ){\Delta }_h/r$, i.e., ${\nu }_R$ = 4, ${\nu }_P$ = 1.5, ${\xi }_R^2$ = 1, ${\xi }_P^2$ = 2, $m_P=m_R=20$, $M=5000$, $r=0.3$ and $\lambda =0.6$ and 0.7, $r=0.6$ and $\lambda =0.3$ and 0.4, and $r=1.0$ and $\lambda =0.0$. To calculate the required sample size for attaining the power ${\beta }_0=1-\beta =0.95$, we consider the following settings: ${\sigma }_P^2$ = 2.0, ${\sigma }_E^2$ = 1.5, ${\sigma }_R^2$ = 0.5, 1.0 and 3.0, ${\mu }_R=$3, 4 and 5, ${\mu }_E={\mu }_R-{\Delta }_{\mathrm{NI}}+{ϵ}_1$, ${\mu }_P={\mu }_R-\Delta -{ϵ}_2$ with $2{ϵ}_1={ϵ}_2$ = 0.4 and 0.6, and four allocation proportions: $n_E:n_R:n_P$ = 1:1:1 (the balanced design), and 2:1:1, 2:2:1 and 3:2:1 (the unbalanced design).

For each of the aforementioned settings, the above introduced Algorithm 3 is adopted to calculate the required sample sizes for the WB-SCI, GF-SCI, HG-SCI and PB-SCI methods. The powers $\mathrm{Pr}\left({\mathbb{D}}_{\ell }\right|H_{\mathrm{NI}}^1,H_{\mathrm{AS}}^1)$ for ℓ = W, F, H and B are computed by Monte Carlo method with $\mathcal{T}=5000$ random observations. Based on the required sample size, we also compute its corresponding empirical power for comparing the accuracy of the proposed sample size determination. Results for $\alpha =0.05$ are presented in Table 4 and Table 5. Examination of Table 4 and Table 5 shows that (i) the derived sample size formulae are rather accurate regardless of the values of r, $\lambda$ and ${ϵ}_2$, the balanced and unbalanced designs in that their corresponding empirical powers are quite close to the pre-specified true powers; (ii) the sample size increases as ${\sigma }_R^2$ increases; (iii) the value of ${\mu }_R$ has little effect on the sample size; (iv) the sample size decreases as ${ϵ}_2$ increases.

Table 4. The required sample sizes n for true power $1-\beta =$95% and its empirical powers $p^{\ast }$ under various settings with $ϵ=0.4$.

				${\mathit{n}}_{\mathit{E}}:{\mathit{n}}_{\mathit{R}}:{\mathit{n}}_{\mathit{P}}=1:1:1$								${\mathit{n}}_{\mathit{E}}:{\mathit{n}}_{\mathit{R}}:{\mathit{n}}_{\mathit{P}}=2:1:1$
				GF-SCI		HG-SCI		WB-SCI		PB-SCI		GF-SCI		HG-SCI		WB-SCI		PB-SCI
$\mathbf{r}$	$\mathbf{\lambda }$	${\mathbf{\mu }}_{\mathit{R}}$	${\mathbf{\sigma }}_{\mathit{R}}^{\mathbf{2}}$	${\mathit{n}}_{\mathbf{0}}$	${\mathit{p}}^{\ast }$	${\mathit{n}}_{\mathbf{0}}$	${\mathit{p}}^{\ast }$	${\mathit{n}}_{\mathbf{0}}$	${\mathit{p}}^{\ast }$	${\mathit{n}}_{\mathbf{0}}$	${\mathit{p}}^{\ast }$	${\mathit{n}}_{\mathbf{0}}$	${\mathit{p}}^{\ast }$	${\mathit{n}}_{\mathbf{0}}$	${\mathit{p}}^{\ast }$	${\mathit{n}}_{\mathbf{0}}$	${\mathit{p}}^{\ast }$	${\mathit{n}}_{\mathbf{0}}$	${\mathit{p}}^{\ast }$
0.3	0.6	3	0.5	486	95.78	486	95.70	450	94.92	468	95.00	548	95.20	548	95.08	548	95.20	548	95.22
			1	525	94.74	525	94.86	525	95.06	525	94.98	648	95.64	648	95.60	600	94.04	600	94.20
			3	786	94.84	786	94.70	750	94.32	786	95.38	1000	95.64	1000	95.56	948	94.88	1000	95.70
		4	0.5	486	95.52	486	95.48	450	94.12	450	94.40	548	95.26	548	95.28	500	94.18	548	95.54
			1	525	94.60	525	94.68	525	95.10	525	95.22	600	94.34	600	94.32	600	94.58	600	94.34
			3	750	94.36	750	94.40	750	94.42	786	94.88	1000	95.76	1000	95.74	1000	95.74	948	94.64
		5	0.5	450	94.20	450	94.06	450	94.08	450	94.40	500	94.10	548	95.52	500	94.40	548	95.38
			1	525	94.72	525	94.76	525	94.94	525	94.76	600	94.42	596	94.06	600	94.42	600	94.82
			3	825	95.96	786	94.88	825	95.92	825	95.86	1000	95.90	948	94.80	948	95.12	1000	95.48
	0.7	3	0.5	450	94.12	468	94.90	450	94.30	450	94.04	548	95.18	548	95.28	524	94.04	500	94.14
			1	525	94.40	525	94.50	525	94.38	525	94.56	600	94.10	600	94.48	600	94.42	600	94.66
			3	786	95.46	825	95.90	825	95.90	786	95.08	948	94.64	1000	95.58	1000	95.58	948	94.82
		4	0.5	486	95.44	486	95.52	450	94.70	450	94.38	548	95.52	548	95.48	500	94.18	548	95.00
			1	525	94.92	525	94.86	525	94.58	525	94.04	648	95.46	648	95.50	600	95.00	600	94.08
			3	825	95.86	825	95.78	750	94.24	825	95.86	1000	95.62	1000	95.66	1000	95.88	1000	95.78
		5	0.5	450	94.46	450	94.32	450	94.68	450	94.02	500	94.38	548	95.66	500	94.40	548	95.58
			1	525	94.22	561	95.54	525	94.66	525	94.34	600	94.04	600	94.66	600	94.18	600	94.40
			3	825	95.64	750	94.02	750	94.64	750	94.02	1000	95.72	1000	95.60	1000	95.36	1000	95.46
0.6	0.3	3	0.5	450	94.12	450	94.04	450	94.60	450	94.36	548	94.88	548	94.88	548	95.78	548	95.48
			1	525	95.10	525	95.04	525	94.78	525	94.20	600	94.34	600	94.40	600	94.64	648	95.48
			3	825	95.98	825	95.92	825	95.72	786	95.18	1000	95.62	1000	95.62	1000	95.92	1000	95.58
		4	0.5	486	95.76	486	95.72	486	95.46	450	94.26	500	94.36	500	94.26	500	94.18	548	95.20
			1	525	94.72	525	94.60	525	94.52	525	95.06	600	94.18	600	94.36	600	94.34	600	94.14
			3	786	94.80	786	94.62	825	95.92	750	94.10	1000	95.90	1000	95.94	1000	95.74	948	95.14
		5	0.5	450	94.04	486	95.44	450	94.54	486	95.68	548	95.52	548	95.62	524	94.76	524	94.72
			1	525	95.02	525	94.74	525	94.88	525	94.42	648	95.62	648	95.50	600	94.06	648	95.56
			3	825	95.62	825	95.74	750	94.24	750	94.32	948	95.12	1000	95.88	948	94.94	1000	95.56
	0.4	3	0.5	486	95.24	486	95.18	450	94.48	450	94.46	500	94.12	548	95.34	500	94.26	548	94.98
			1	525	94.50	525	94.42	525	94.62	525	94.90	600	94.04	648	95.54	600	94.36	648	95.86
			3	825	95.56	825	95.70	825	95.92	786	95.20	1000	95.98	1000	95.72	1000	95.84	1000	95.70
		4	0.5	450	94.74	450	94.66	450	94.44	450	94.34	548	95.24	548	95.20	548	95.50	548	95.52
			1	525	94.50	525	94.56	525	95.34	525	94.90	600	94.44	600	94.34	648	95.66	600	94.16
			3	786	94.90	786	94.76	750	94.60	750	94.56	1000	95.60	1000	95.60	1000	95.80	1000	95.90
		5	0.5	486	95.18	486	95.08	450	94.44	450	94.14	548	95.48	548	95.46	548	95.62	548	95.32
			1	525	94.78	525	94.82	525	94.66	525	94.42	600	94.36	600	94.36	600	94.32	600	94.42
			3	786	95.54	786	95.58	786	95.38	825	95.96	1000	95.74	1000	95.86	1000	95.94	900	94.14
1.0	0.0	3	0.5	450	94.22	450	94.08	450	94.40	468	94.88	548	95.06	548	95.02	548	95.50	500	94.06
			1	525	94.52	525	94.52	525	95.18	525	94.64	600	94.20	600	94.20	600	94.72	600	94.44
			3	825	95.72	825	95.68	786	95.36	786	94.80	1000	95.94	948	94.66	900	94.42	1000	95.54
		4	0.5	450	94.70	450	94.66	468	94.82	450	94.04	548	94.92	548	95.18	500	94.02	548	95.22
			1	525	94.32	525	94.20	525	94.92	525	94.38	600	94.56	648	95.74	600	94.48	600	94.36
			3	825	95.90	786	94.88	750	94.34	825	95.36	1000	95.80	1000	95.96	1000	95.46	1000	95.82
		5	0.5	486	95.14	486	95.08	450	94.46	486	95.84	548	95.30	548	95.20	500	94.10	548	95.24
			1	525	94.84	525	94.78	525	94.98	525	94.34	648	95.80	648	95.70	600	94.48	600	94.28
			3	825	95.74	825	95.64	750	94.54	825	95.74	1000	95.86	1000	95.88	1000	95.94	1000	95.88
0.3	0.6	3	0.5	625	95.42	625	95.44	625	95.68	625	95.62	672	95.78	672	95.74	672	95.20	672	95.46
			1	685	95.48	685	95.50	685	95.44	655	94.68	750	95.62	750	95.46	750	95.80	750	95.98
			3	875	95.12	875	95.14	875	95.20	875	94.28	1050	95.24	1050	95.32	972	94.34	1050	95.10
		4	0.5	625	95.30	625	95.22	625	95.46	625	94.98	672	95.48	672	95.36	672	95.92	636	94.72
			1	685	95.34	685	95.36	625	94.12	685	95.12	750	95.08	750	95.06	750	95.60	750	95.82
			3	875	94.82	875	94.84	875	94.48	875	94.42	1050	95.92	1050	95.96	972	94.70	1050	95.74
		5	0.5	625	95.36	625	95.36	625	95.48	625	95.02	672	95.48	672	95.52	672	95.70	672	95.86
			1	685	95.52	685	94.76	685	95.56	685	95.44	750	95.54	750	95.58	750	95.42	750	95.42
			3	875	94.76	875	94.70	875	94.88	875	94.74	972	94.60	1050	95.76	1050	95.88	1014	95.46
	0.7	3	0.5	625	95.18	625	95.28	625	95.40	625	95.10	672	95.62	672	95.68	672	95.50	636	94.74
			1	685	95.52	685	95.62	685	95.48	685	95.60	750	95.66	750	95.52	750	95.92	750	95.78
			3	875	94.72	875	94.88	875	94.68	875	94.46	1050	95.26	1050	95.38	1050	95.80	1050	95.82
		4	0.5	625	95.46	625	95.54	625	95.18	625	95.94	672	95.42	672	95.38	600	94.02	672	95.22
			1	685	94.92	685	95.04	685	94.86	685	95.46	750	95.26	750	95.22	750	95.54	750	95.56
			3	875	94.72	875	94.54	875	94.58	875	94.38	1050	95.44	1050	95.58	1050	95.94	1014	95.46
		5	0.5	625	95.00	625	95.24	625	95.26	625	95.96	672	95.12	672	95.38	600	94.24	672	95.46
			1	625	94.10	685	95.58	685	95.92	685	95.30	750	95.26	750	95.20	750	95.72	750	95.64
			3	875	94.14	875	94.54	875	94.78	875	95.04	1050	95.66	1050	95.96	972	94.42	972	94.20
0.6	0.3	3	0.5	625	95.14	625	94.98	625	95.48	625	95.82	672	95.72	672	95.66	672	95.56	672	95.60
			1	655	94.66	685	95.86	685	95.52	620	94.08	750	95.58	750	95.18	750	95.44	750	95.34
			3	875	94.16	875	95.04	875	95.34	875	95.34	1050	95.22	1050	95.94	1050	95.96	972	94.82
		4	0.5	625	95.26	625	95.24	625	95.36	625	95.26	672	95.14	672	95.18	672	95.42	672	95.42
			1	625	94.50	625	94.48	685	95.64	685	95.52	750	95.76	750	95.64	750	95.28	750	95.64
			3	875	94.84	875	94.62	875	95.20	875	95.24	1050	95.30	1050	95.36	1014	95.36	1050	95.68
		5	0.5	625	95.32	625	95.62	625	95.74	625	95.34	600	94.20	672	94.88	672	95.70	672	95.76
			1	625	94.20	685	95.26	685	95.48	685	95.42	750	95.36	750	95.52	714	94.56	750	94.90
			3	875	94.72	875	94.60	875	94.44	875	94.70	1050	95.98	972	94.40	972	94.20	972	94.34
	0.4	3	0.5	625	95.06	625	94.88	625	95.68	625	95.52	672	95.40	672	95.68	672	95.78	672	95.58
			1	685	95.44	685	95.88	685	95.10	685	95.42	750	95.02	750	95.70	750	95.82	750	95.28
			3	875	95.24	875	94.98	875	95.38	875	95.28	972	94.06	1050	95.92	972	94.62	1050	95.86
		4	0.5	625	95.16	625	94.96	625	95.86	625	95.46	672	95.48	672	95.38	672	95.54	672	95.42
			1	685	95.68	685	95.60	685	95.56	685	95.64	750	95.30	750	95.14	750	95.44	750	94.52
			3	875	95.04	875	94.88	875	95.54	875	94.74	1050	95.92	1050	95.80	972	95.18	1050	95.76
		5	0.5	625	95.10	625	95.04	625	95.12	625	95.42	672	95.80	672	95.74	636	94.68	672	95.54
			1	685	95.72	685	95.66	685	95.36	685	95.52	750	95.48	750	95.48	750	95.62	750	95.76
			3	875	94.76	875	94.68	875	94.12	875	94.74	1050	95.76	1050	95.60	1014	95.44	1050	95.94
1.0	0.0	3	0.5	625	95.48	625	94.76	625	95.48	625	95.34	672	95.06	672	95.20	672	95.66	600	94.22
			1	685	95.12	685	95.54	685	95.80	685	95.32	750	95.24	750	95.18	750	95.82	750	95.56
			3	875	94.44	875	95.24	875	94.92	875	95.22	1014	94.82	1050	95.00	972	94.16	972	94.48
		4	0.5	625	95.64	625	95.34	625	95.98	625	95.26	672	95.40	672	95.22	672	95.88	672	95.54
			1	685	95.80	685	95.12	685	95.14	685	95.14	750	95.78	750	95.60	750	95.20	750	95.82
			3	875	95.42	875	94.94	875	94.58	875	94.46	1014	95.20	1050	95.68	972	94.16	972	94.76
		5	0.5	625	95.18	625	95.16	625	95.52	625	95.80	672	95.56	672	95.52	600	94.08	672	95.84
			1	685	95.54	685	95.62	685	95.96	685	95.36	750	95.44	750	95.38	750	95.56	750	95.24
			3	875	95.04	875	95.02	875	95.10	875	94.54	1050	95.48	1050	95.44	1050	95.66	972	94.20

Table 5. The required sample sizes n for true power $1-\beta =$95% and its empirical powers $p^{\ast }$ under various settings with $ϵ=0.6$.

				${\mathit{n}}_{\mathit{E}}:{\mathit{n}}_{\mathit{R}}:{\mathit{n}}_{\mathit{P}}=1:1:1$								${\mathit{n}}_{\mathit{E}}:{\mathit{n}}_{\mathit{R}}:{\mathit{n}}_{\mathit{P}}=2:1:1$
				GF-SCI		HG-SCI		WB-SCI		PB-SCI		GF-SCI		HG-SCI		WB-SCI		PB-SCI
$\mathbf{r}$	$\mathbf{\lambda }$	${\mathbf{\mu }}_{\mathit{R}}$	${\mathbf{\sigma }}_{\mathit{R}}^{\mathbf{2}}$	${\mathit{n}}_{\mathbf{0}}$	${\mathit{p}}^{\ast }$	${\mathit{n}}_{\mathbf{0}}$	${\mathit{p}}^{\ast }$	${\mathit{n}}_{\mathbf{0}}$	${\mathit{p}}^{\ast }$	${\mathit{n}}_{\mathbf{0}}$	${\mathit{p}}^{\ast }$	${\mathit{n}}_{\mathbf{0}}$	${\mathit{p}}^{\ast }$	${\mathit{n}}_{\mathbf{0}}$	${\mathit{p}}^{\ast }$	${\mathit{n}}_{\mathbf{0}}$	${\mathit{p}}^{\ast }$	${\mathit{n}}_{\mathbf{0}}$	${\mathit{p}}^{\ast }$
0.3	0.6	3	0.5	207	94.90	207	94.82	225	95.98	207	94.14	248	95.34	248	95.42	248	95.64	248	95.80
			1	225	94.02	225	94.10	225	94.04	222	94.26	300	95.84	300	95.90	300	95.54	300	95.98
			3	357	95.10	375	95.86	336	94.38	375	95.68	448	95.54	448	95.90	448	95.74	448	95.54
		4	0.5	225	95.86	225	95.96	207	95.10	207	94.22	248	95.00	248	94.90	248	95.78	248	95.10
			1	243	95.54	243	95.50	222	94.18	243	95.70	276	94.68	276	94.62	276	95.36	300	95.92
			3	357	95.08	357	94.96	336	94.38	357	94.94	448	95.14	448	95.18	424	95.18	424	94.66
		5	0.5	225	95.80	207	94.48	207	94.96	216	95.62	252	95.74	248	94.84	248	95.72	248	95.90
			1	243	94.64	243	95.66	231	94.44	243	95.58	276	94.52	276	94.80	276	94.74	276	94.32
			3	357	94.96	375	95.68	336	94.04	357	95.10	448	95.48	448	95.88	424	94.98	448	95.56
	0.7	3	0.5	225	95.70	207	94.30	207	94.60	207	95.00	248	95.74	248	95.26	248	95.92	236	94.86
			1	243	95.18	243	94.86	243	95.22	243	95.04	300	95.88	276	94.04	276	95.28	276	94.18
			3	357	94.98	357	95.14	357	95.32	336	94.22	448	95.58	448	95.62	424	94.86	424	94.70
		4	0.5	225	95.92	225	95.88	207	95.10	207	94.22	248	95.32	248	95.26	248	95.56	236	95.14
			1	243	95.28	243	95.16	225	94.68	225	94.18	276	94.64	276	94.54	276	95.18	276	95.00
			3	375	95.98	375	95.98	336	94.04	336	94.14	448	95.54	448	95.48	448	95.74	424	94.82
		5	0.5	225	95.78	225	95.76	207	94.46	225	95.88	248	95.64	248	95.26	248	95.72	248	95.52
			1	243	94.72	243	94.94	243	95.44	261	95.82	276	94.60	300	95.94	276	95.24	276	94.92
			3	357	95.22	375	95.94	336	94.04	336	94.48	448	95.74	448	95.64	448	95.96	424	94.60
0.6	0.3	3	0.5	207	94.52	225	95.56	225	95.94	207	94.98	248	95.50	248	95.72	248	95.66	248	95.78
			1	225	94.14	261	95.92	243	95.50	243	95.20	276	95.24	300	95.98	276	94.90	276	94.46
			3	357	95.08	357	95.26	375	95.68	375	95.78	448	95.94	448	95.56	424	95.34	424	94.34
		4	0.5	225	95.96	225	95.94	207	94.92	207	94.80	248	95.34	248	95.26	248	95.84	248	95.02
			1	243	95.42	243	95.50	225	94.28	243	95.24	276	94.02	276	94.08	276	95.04	276	94.82
			3	375	95.72	375	95.64	336	94.68	357	95.40	448	95.96	448	95.90	448	95.68	448	95.92
		5	0.5	207	94.24	225	95.80	207	95.14	207	94.82	248	95.44	248	95.24	248	95.56	248	95.76
			1	243	95.14	243	95.64	225	94.24	243	95.08	300	95.90	276	94.58	300	95.98	276	94.26
			3	357	95.58	357	95.10	336	94.14	375	95.96	448	95.62	448	95.80	448	95.56	448	95.14
	0.4	3	0.5	207	94.44	225	95.58	207	95.14	207	94.60	248	95.28	248	95.54	248	95.28	248	95.72
			1	243	94.80	243	95.18	243	95.42	243	95.48	276	94.06	300	95.94	276	95.48	276	94.48
			3	375	95.90	375	95.86	375	95.82	336	94.20	448	95.70	424	94.66	448	95.98	448	95.22
		4	0.5	216	95.22	216	95.26	207	94.78	207	94.08	248	94.90	248	95.86	248	95.92	248	95.70
			1	222	94.26	222	94.18	243	94.92	243	95.00	276	94.48	276	94.72	276	95.38	276	94.02
			3	375	95.96	336	94.30	336	94.26	357	95.56	448	95.76	448	95.66	424	95.16	424	94.56
		5	0.5	225	95.90	225	95.74	207	94.78	207	94.32	248	95.26	248	95.04	248	95.52	248	95.38
			1	243	95.36	243	95.36	222	94.02	243	95.16	276	94.22	276	94.12	276	95.08	276	95.36
			3	357	95.38	357	95.40	336	94.02	336	94.06	448	95.72	448	95.66	424	94.72	448	95.52
1.0	0.0	3	0.5	225	95.96	225	95.92	207	94.68	207	95.10	248	95.38	248	95.42	248	95.48	248	95.26
			1	243	95.20	243	95.24	243	95.58	243	95.60	276	94.30	300	95.88	276	95.08	276	94.66
			3	357	95.26	357	94.94	336	94.12	357	95.34	448	95.82	448	95.62	424	94.92	424	94.86
		4	0.5	207	94.18	225	95.84	207	94.80	207	94.90	248	95.70	248	95.46	248	95.92	248	95.48
			1	243	94.82	243	95.24	243	95.32	243	95.34	300	95.96	276	94.82	276	95.28	276	95.18
			3	375	95.86	375	95.90	336	94.38	375	95.68	448	95.94	448	95.78	424	94.94	448	95.72
		5	0.5	225	95.52	225	95.48	207	94.52	207	94.92	248	95.28	248	95.32	224	94.20	248	95.06
			1	243	95.04	243	94.86	243	94.86	243	95.18	276	94.68	276	94.26	276	95.38	300	95.86
			3	336	94.04	357	95.28	336	94.34	375	95.94	448	95.78	448	95.64	424	95.08	448	95.70
0.3	0.6	3	0.5	280	95.40	280	95.10	280	95.86	280	95.32	300	95.70	300	95.26	300	95.60	300	95.68
			1	310	95.78	310	94.94	310	95.70	310	95.74	336	95.50	336	95.24	336	95.78	336	95.38
			3	405	95.58	405	95.26	370	94.22	405	95.32	450	95.08	450	95.30	450	95.42	450	95.04
		4	0.5	280	95.22	280	95.18	280	95.68	280	95.32	300	95.54	300	95.42	300	95.72	300	95.70
			1	310	94.70	310	94.60	310	95.44	310	95.86	336	95.84	336	95.70	336	95.98	336	95.16
			3	405	95.36	405	95.22	375	94.56	405	95.50	450	94.54	450	94.60	450	95.26	450	94.80
		5	0.5	280	95.02	280	95.72	280	95.84	280	95.44	300	94.90	300	95.06	300	95.72	300	95.58
			1	310	95.76	310	95.06	310	95.86	310	95.66	336	95.44	336	95.22	336	95.82	336	95.86
			3	405	95.60	405	95.28	385	94.60	405	95.52	450	94.78	450	94.74	450	94.86	450	94.94
	0.7	3	0.5	280	95.16	280	95.12	280	95.80	280	95.34	300	95.40	300	95.96	300	95.76	300	95.42
			1	310	95.70	310	95.18	310	95.48	310	95.84	336	95.26	336	95.58	336	95.66	336	95.36
			3	405	95.76	405	95.36	405	95.76	375	94.16	450	94.68	450	95.14	450	95.66	450	95.00
		4	0.5	280	95.22	280	95.10	280	95.88	280	94.88	300	94.72	300	94.66	300	95.42	300	95.28
			1	310	94.86	310	94.66	315	95.68	310	95.16	336	95.16	336	95.14	312	94.34	336	95.52
			3	405	95.22	405	95.28	375	94.16	405	95.56	450	95.28	450	95.34	450	95.24	450	95.54
		5	0.5	280	95.02	280	95.24	280	95.60	280	95.14	300	95.48	300	95.40	300	95.48	300	95.32
			1	310	95.74	310	95.42	310	95.90	310	95.70	336	95.74	336	94.80	336	95.36	336	95.22
			3	370	94.12	405	95.90	405	95.66	375	94.44	450	94.58	450	94.96	450	94.84	450	94.76
0.6	0.3	3	0.5	280	95.10	280	95.22	280	95.36	280	95.08	300	95.24	300	95.48	300	95.58	300	95.08
			1	310	95.12	310	95.96	310	95.36	310	95.92	336	94.80	336	95.12	336	95.66	336	95.60
			3	405	95.44	405	95.00	395	94.96	405	95.64	450	95.04	450	94.92	450	95.56	450	94.92
		4	0.5	280	94.62	280	94.60	280	95.16	280	95.18	300	95.18	300	95.12	300	95.94	300	95.34
			1	310	95.54	310	95.42	280	94.06	310	95.42	336	95.62	336	95.64	336	95.68	336	95.22
			3	405	95.42	405	95.36	405	95.24	405	95.38	450	95.16	450	95.20	450	95.84	450	94.60
		5	0.5	280	94.16	280	94.88	280	95.62	280	95.54	300	95.46	300	95.12	300	95.70	300	95.24
			1	310	95.62	310	95.46	310	95.66	280	94.06	336	95.72	336	95.12	336	95.26	336	95.34
			3	405	94.96	375	94.38	375	94.04	375	94.24	450	94.84	450	95.22	450	95.20	450	95.44
	0.4	3	0.5	280	95.74	280	95.16	280	95.16	280	95.38	300	95.56	300	95.26	300	95.92	300	95.26
			1	310	95.50	310	95.14	310	95.62	310	95.38	336	95.74	336	95.38	336	95.66	336	95.40
			3	370	94.08	405	95.24	385	94.52	375	94.08	450	94.94	450	94.90	450	94.96	450	94.68
		4	0.5	280	95.06	280	95.42	280	95.48	280	94.88	300	95.26	300	95.36	300	95.36	300	95.38
			1	310	95.54	310	95.00	310	95.54	295	94.26	336	95.10	336	94.82	336	95.52	336	95.52
			3	405	94.96	405	95.24	375	94.52	375	94.10	450	94.74	450	95.40	450	95.20	450	95.62
		5	0.5	280	95.00	280	94.94	280	95.56	280	94.74	300	95.44	300	95.30	300	95.62	300	95.22
			1	310	95.84	310	95.74	310	95.78	310	95.40	336	95.38	336	95.28	336	95.38	336	95.90
			3	405	95.08	405	95.00	375	94.08	370	94.32	450	94.66	450	94.60	450	94.96	450	94.36
1.0	0.0	3	0.5	280	95.06	280	95.00	280	95.68	280	94.96	300	95.42	300	94.90	300	95.72	300	95.62
			1	310	95.84	315	95.82	310	95.32	310	95.72	336	95.84	336	95.50	336	95.34	336	95.38
			3	405	95.74	405	95.40	405	95.40	405	95.58	450	95.26	450	94.90	450	95.36	450	95.42
		4	0.5	280	94.82	280	95.34	280	95.98	280	95.44	300	94.98	300	94.54	300	95.94	300	95.18
			1	310	95.28	310	95.86	310	95.64	310	95.38	336	94.50	336	95.78	336	95.86	312	94.12
			3	405	95.54	405	95.80	375	94.02	375	94.24	450	94.74	450	94.86	450	95.38	450	95.32
		5	0.5	280	95.26	280	95.82	280	94.96	280	95.40	300	95.00	300	95.46	300	95.76	300	95.30
			1	310	95.84	310	95.30	310	95.72	315	95.92	336	95.08	336	95.58	300	94.02	336	95.28
			3	405	95.58	405	95.60	370	94.48	405	95.46	450	94.84	450	94.84	456	95.10	450	95.06

3.2. Application to Mildly Asthmatic Study

As an illustration of the preceding proposed simultaneous confidence region, we consider a data set on “Mildly Asthmatic Study” taken from [5]. In the mildly asthmatic study, the primary outcome variable is the forced vital capacity (FVC), and the data set consists of experimental ($n_E=35$), reference ($n_R=19$), and placebo ($n_P=20$) groups. The means, standard deviations, minimum and maximum values for the FVC are 4.32, 1.16, 0.8 and 6.52 for E group, respectively; 4.86, 1.03, 2.94 and 6.90 for R group, respectively; and 3.14, 0.97, 1.41 and 4.99 for placebo group, respectively. Since [5] did not present the details on the historical trial, Ghosh et al. [24] independently simulated 5000 historical data sets from the normal distribution with the specified parameters and sample sizes in applying their proposed approach to the assessment of the NI of experimental to reference in a three-arm trial. Unlike [24], we here divide the considered data set into the historical and current data sets, its 30% is taken as the historical data randomly sampled from the considered data set without replacement, and the rest is regarded as the current data. Thus, the above developed approach to determine NI margin is applied to the historical data, and the preceding proposed four simultaneous confidence regions for $\varphi$ and $\psi$ are applied to the current data for simultaneously assessing both NI and assay sensitivity with the following specification: $\lambda =0.0$, 0.25, 0.5, 0.6, 0.75 and 0.9 together with $r=1-\lambda$ and $M=5000$. The lower limits of the approximate $95\%$ one-sided simultaneous confidence region of $(\varphi ,\psi )$ for the GF-SCI, HG-SCI, WB-SCI and PB-SCI methods are presented in Table 6. Examination of Table 6 shows that (i) the assay sensitivity can be established at the significance level $\alpha =5\%$ in that lower limits of four confidence regions are greater than $\Delta$ regardless of the values of $\lambda$; (ii) the NI cannot be established at the significance level 5% for the GF-SCI, HG-SCI, WB-SCI and PB-SCI methods in that lower limits of their corresponding confidence intervals are less than $-{\Delta }_{\mathrm{NI}}$ regardless of the values of $\lambda$, which is consistent with those given in [5].

Table 6. Lower limits of the approximate $95\%$ one-sided simultaneous confidence regions of $(\varphi ,\psi )$ for the GF-SCI, HG-SCI, WB-SCI and PB-SCI methods in the mildly asthmatic study.

			GF-SCI		HG-SCI		WB-SCI		PB-SCI
$\mathbf{\lambda }$	${\Delta }_{\mathrm{NI}}$	$\Delta$	$\mathbf{\varphi }$	$\mathbf{\psi }$	$\mathbf{\varphi }$	$\mathbf{\psi }$	$\mathbf{\varphi }$	$\mathbf{\psi }$	$\mathbf{\varphi }$	$\mathbf{\psi }$
0	0.5359	0.5359	−0.7413	1.7744	−0.9295	1.4548	−1.0836	1.3523	−0.7403	1.7756
0.25	0.9563	0.7172	−0.5438	1.3784	−0.7607	1.1330	−0.8785	0.9472	−0.5466	1.3748
0.5	0.9288	0.4644	−0.4105	1.5093	−0.6439	1.2028	−0.7676	1.0585	−0.4095	1.5106
0.6	0.9608	0.3843	−0.3641	1.1416	−0.6101	0.8457	−0.7305	0.7259	−0.3677	1.1376
0.75	0.4707	0.1177	−0.8854	1.7782	−1.0603	1.4066	−1.2334	1.3435	−0.8849	1.7789
0.9	0.7461	0.0746	−0.5859	1.6179	−0.7757	1.2700	−0.9613	1.1762	−0.5889	1.6145

4. Discussion

This paper studied the confidence interval construction problem for simultaneously assessing the non-inferiority and assay sensitivity in a three-arm trial with normally distributed endpoints, in which the non-inferiority margin is defined as a pre-specified fixed difference between treatment effects of experimental and reference treatments in the considered historical placebo-controlled trial. The generalized fiducial pivotal quantity method together with the historical-trial-based approach were utilized to determine the non-inferiority margin. However, there was no closed-form for the non-inferiority margin via the historical-trial-based approach. To overcome the difficulty, a Monte Carlo resampling method was adopted to determine the non-inferiority margin based on the percentile point of the drawn observations. Based on the constructed non-inferiority margin, we developed four simultaneous confidence intervals for parameters $(\varphi ,\psi )$ based on the Wald-type statistic together with the Bonferroni method, generalized fiducial pivotal quantity method, hybrid generalized fiducial method incorporating the square-and-add method and generalized fiducial method, and parametric bootstrap resampling method. The flexible algorithms for computing empirical coverage probabilities for the proposed four simultaneous confidence intervals were also given. Simulation studies were conducted to investigate the performance of the proposed four simultaneous confidence intervals under various settings including the moderate and large sample sizes, balanced and unbalanced designs, different hypotheses including the HT hypothesis. Empirical results demonstrated that the GF-SCI and HG-SCI methods perform better than the WB-SCI and PB-SCI methods, and the GF-SCI, PB-SCI and HG-SCI methods had the same performance when the sample size was large (i.e., n = 150 and 300) in terms of their empirical coverage probabilities. Hence, we recommended the usage of the hybrid generalized fiducial simultaneous confidence interval because its computational burden was less than that for the PB-SCI method, and the usage of the Wald-type Bonferroni simultaneous confidence interval when the sample size was large.

This paper did not consider the simultaneous confidence interval construction problem for simultaneously assessing both non-inferiority and assay sensitivity in a three-arm trial with normally distributed endpoints in the presence of missing endpoints, which are commonly encountered in the modern drug studies. We did not consider the usage of the prior information in determining the non-inferiority margin from the placebo-controlled data, which may improve the efficiency of the estimation for the non-inferiority margin.