On Strictly Positive Fragments of Modal Logics with Confluence

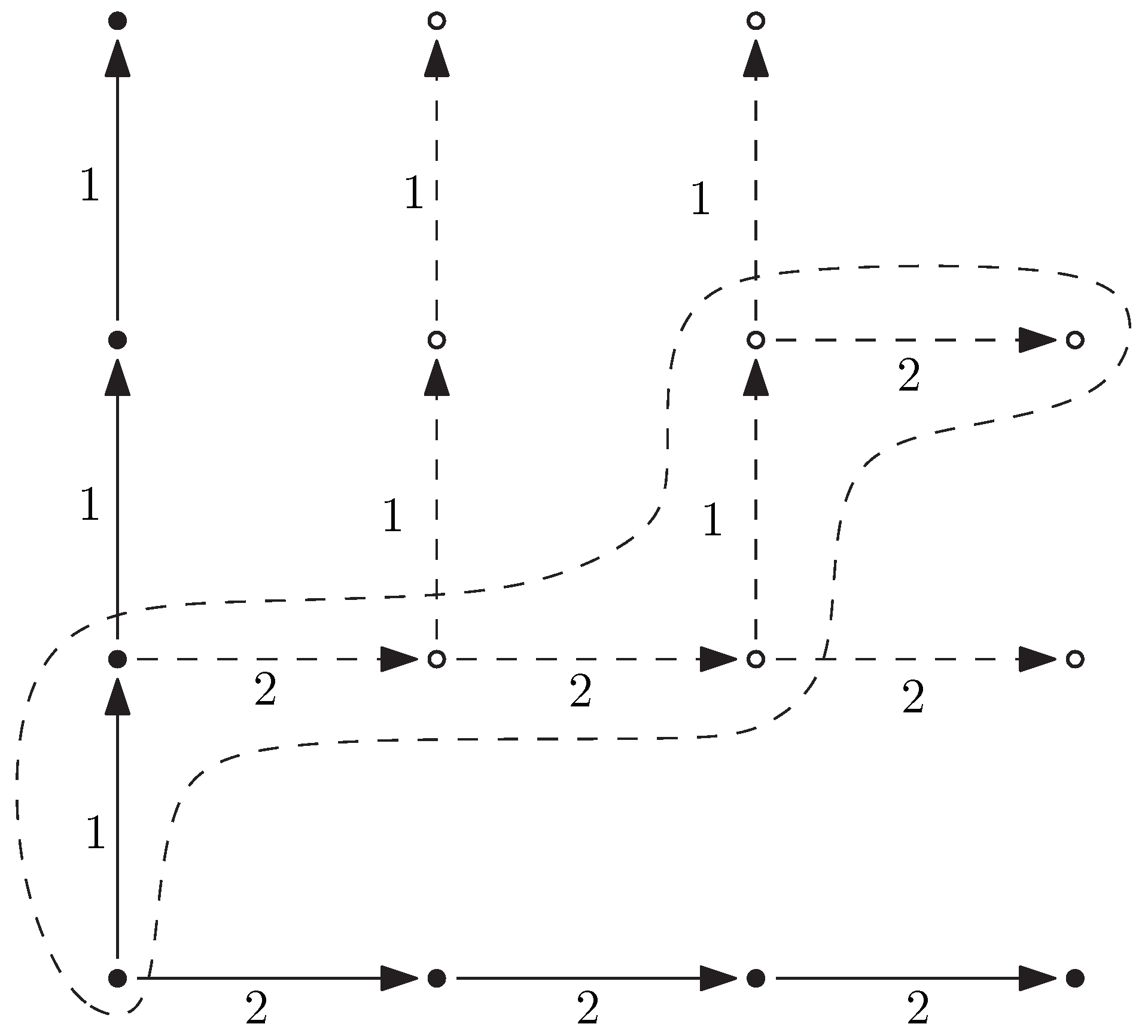
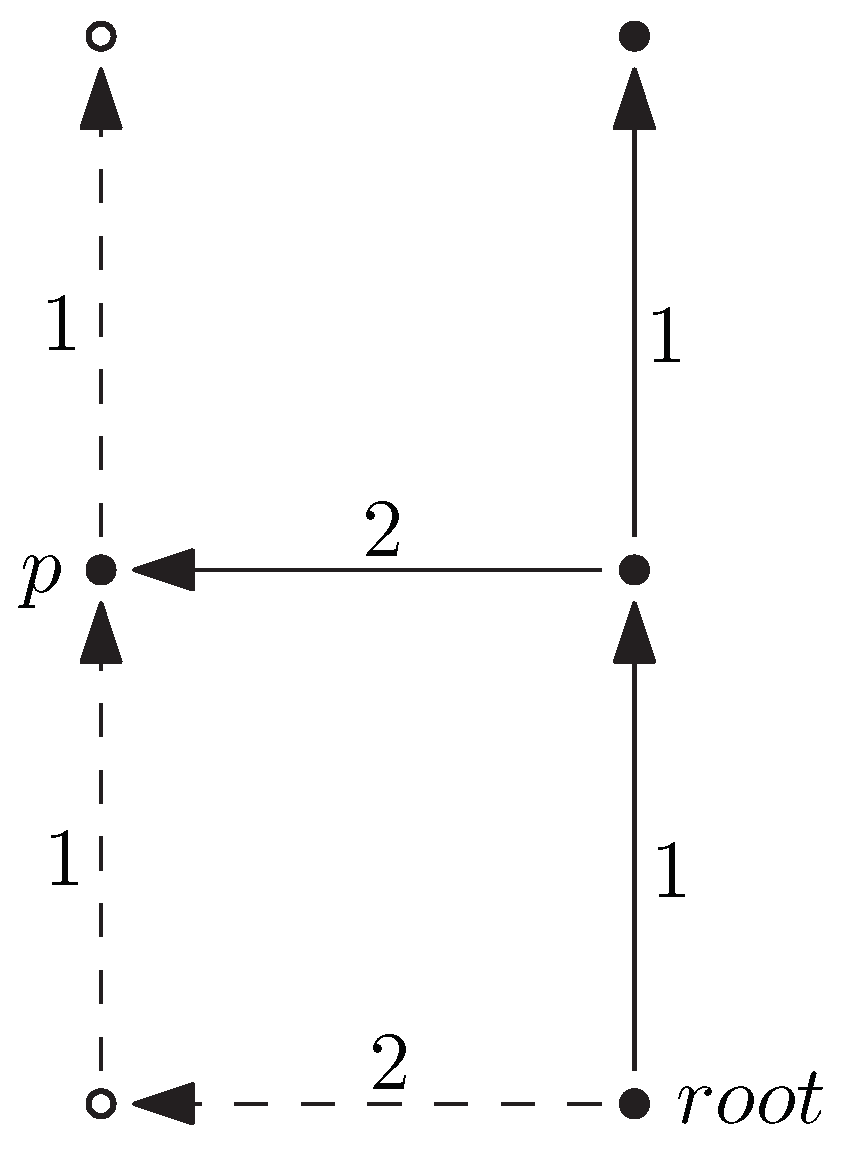
Abstract

We axiomatize strictly positive fragments of modal logics with the confluence axiom. We consider unimodal logics such as $\mathbf{K}.\mathbf{2}$, $\mathbf{D}.\mathbf{2}$, $\mathbf{D}\mathbf{4}.\mathbf{2}$ and $\mathbf{S}\mathbf{4}.\mathbf{2}$ with unimodal confluence $\diamond \square p\to \square \diamond p$ as well as the products of modal logics in the set $\left\{\mathbf{K},\mathbf{D},\mathbf{T},\mathbf{D}\mathbf{4},\mathbf{S}\mathbf{4}\right\}$, which contain bimodal confluence ${\diamond }_1{\square }_{2}p\to {\square }_2{\diamond }_{1}p$. We show that the impact of the unimodal confluence axiom on the axiomatisation of strictly positive fragments is rather weak. In the presence of $\top \to \diamond \top$, it simply disappears and does not contribute to the axiomatisation. Without $\top \to \diamond \top$ it gives rise to a weaker formula $\diamond \top \to \diamond \diamond \top$. On the other hand, bimodal confluence gives rise to more complicated formulas such as ${\diamond }_{1}p\wedge {\diamond }_2^n\top \to {\diamond }_1(p\wedge {\diamond }_2^n\top )$ (which are superfluous in a product if the corresponding factor contains $\top \to \diamond \top$). We also show that bimodal confluence cannot be captured by any finite set of strictly positive implications.

1. Introduction

Strictly positive modal formulas are constructed of propositional variables and the constant ⊤ using only conjunction and diamonds. Strictly positive logics consists of implications between strictly positive modal formulas. They were studied in the context of universal algebra [1], knowledge representation [2,3] and proof theory [4,5,6].

In this paper, we investigate strictly positive fragments of modal logics that include the confluence axiom $\diamond \square p\to \square \diamond p$ and its bimodal counterpart ${\diamond }_1{\square }_{2}p\to {\square }_2{\diamond }_{1}p$. The confluence axiom is an example of a simple but very useful formula. It appears in very different areas of modal logic, ranging from epistemic logic to the logic of space-time (cf. [7]) and the logic of forcing [8]. Bimodal confluence is valid in any product of two Kripke frames and plays an important role in multidimensional modal logic [9]. When ${\diamond }_1$ stands for $\exists x$ and ${\diamond }_2$ stands for $\exists y$, bimodal confluence turns into the principle $\exists x\forall y\varphi (x,y)\to \forall y\exists x\varphi (x,y)$, which is one of the basic axioms of first-order logic.

For a modal logic L by $SPF\left(L\right)$, we denote its strictly positive fragment; that is, the set of all strictly positive implications in L. The modal calculus $\mathbf{K}$ can be easily modified to work only with strictly positive implications yielding a natural calculus $K^{+}$. The question of whether, given a strictly positive implication $\varphi$, $K^{+}+\varphi$ axiomatises $SPF(\mathbf{K}+\varphi )$ was thoroughly investigated in [10]. For example, this is true for $p\to \diamond p$ and $\diamond \diamond p\to \diamond p$ but not for $\diamond p\to p$. The confluence axiom $\diamond \square p\to \square \diamond p$ cannot be rewritten as a strictly positive implication. This raises the question of how this axiom is reflected in strictly positive fragments of modal logic that contain it. This question is highly non-trivial. For example, Svyatlovskii showed in [11] that the strictly positive fragment of $\mathbf{K}\mathbf{4}.\mathbf{3}$ is axiomatised by $\diamond \diamond p\to \diamond p$ and $\diamond (p\wedge \diamond q)\wedge \diamond (p\wedge \diamond r)\to \diamond (p\wedge \diamond q\wedge \diamond r)$, which is a rather unexpected transformation of .3 axiom $\diamond p\wedge \diamond q\to \diamond (p\wedge \diamond q)\vee \diamond (p\wedge q)\vee \diamond (q\wedge \diamond p)$ (undefinable as a strictly positive implication as well as confluence axioms, see Section 9.1 of [10]).

In this paper, we show that the impact of the unimodal confluence axiom on the axiomatisation of strictly positive fragments is rather weak. In the presence of $\top \to \diamond \top$, it simply disappears and does not contribute to the axiomatisation. Without $\top \to \diamond \top$ it changes into a weaker formula $\diamond \top \to \diamond \diamond \top$. Some may find it unsurprising, but in our opinion, this is a remarkable property of the unimodal setting. In contrast, we show that the strictly positive fragment of ${\mathbf{K}}_2+{\diamond }_1{\square }_{2}p\to {\square }_2{\diamond }_{1}p$ is axiomatised by an infinite set of formulas of the form ${\diamond }_{1}p\wedge {\diamond }_2^n\top \to {\diamond }_1(p\wedge {\diamond }_2^n\top )$ and ${\diamond }_{2}p\wedge {\diamond }_1^n\top \to {\diamond }_2(p\wedge {\diamond }_1^n\top )$, and that it cannot be captured by any finite set of strictly positive implications. We also show that strictly positive fragments of two-dimensional products of modal logics in the set $\left\{\mathbf{K},\mathbf{D},\mathbf{T},\mathbf{D}\mathbf{4},\mathbf{S}\mathbf{4}\right\}$ also are axiomatised by these two infinite series of formulas, except for the cases when one or both of the factors contain $\diamond \top$, in which case some or all of these formulas become superfluous and can be omitted.

2. Preliminaries

2.1. Basic Modal Logic

Let $PV=\{p_1,p_2,\dots \}$ be a countable set of proposition letters, with typical members denoted by p, q, etc. Modal formulas over $PV$ are built using the constants ⊤ and ⊥, dual-modal operators ⋄ and □ and (classical) binary connectives ∨ and ∧ and →.

A normal modal logic is a set L of formulas that contains all classical propositional tautologies, the formula $\square (p\to q)\to (\square p\to \square q)$, and that is closed under the standard rules Modus ponens, Uniform substitution and Generalization (given $\varphi$ infer $\square \varphi$). The smallest normal modal logic is denoted by $\mathbf{K}$. For a set of modal formulas $\Gamma$ and a modal logic L, $L+\Gamma$ denotes the smallest normal modal logic containing $L\cup \Gamma$. For a modal formula, $\varphi$, $L+\varphi =L+\left\{\varphi \right\}$.

As usual, a Kripke frame is a pair $F=(W,R)$, where W is a non-empty set of worlds and R is a binary relation on W (that is $R\subseteq W\times W$). Sometimes, we refer to the W- and R-components of $Frame$ as $Frame.W$ and $Frame.R$. A point u in W is called final in F if u has no R-successors. A (Kripke) model based on F is a pair $M=(F,V)$, where V is a function assigning to each proposition letter p a subset $V\left(p\right)$ of W. The inductive definition of the truth value of a formula $\varphi$ at a point x in a model M is standard. The fact that $\varphi$ is true at x in M is denoted by $M,x\models \varphi$. In particular, boolean connectives are computed by classical truth tables within a point, $M,x\models \diamond \varphi$ if there is a point $y\in R\left(x\right)$ such that $M,y\models \varphi$ and $M,x\models \square \varphi$ if for all points y such that $(x,y)\in R$ we have $M,y\models \varphi$.

A formula $\varphi$ is said to be true in a model$M=(W,R,V)$, in symbols $M\models \varphi$, if $\varphi$ is true at all worlds in W; $\varphi$ is valid in a frame F, in symbols $F\models \varphi$, if $\varphi$ is true in all models based on F.

Each class of Kripke frames $\mathbf{C}$ gives rise to a normal modal logic $\mathrm{Log}\left(\mathbf{C}\right)=\{\varphi \mid F\models \varphi \mathrm{for} \mathrm{all} F \mathrm{in} \mathbf{C}\}$. It is known (cf. [12]) that $\mathbf{K}+\diamond \square p\to \square \diamond p$ is the logic of all Kripke frames satisfying $Conf=\left\{\forall x\forall y\forall z\left(R\right(x,y)\wedge R(x,z)\to \exists v(R(y,v)\wedge R(z,v)\left)\right)\right\}$.

In addition to $\mathbf{K}$, we consider the logics

$$\begin{array}{cccc}\hfill \mathbf{D}& =\mathbf{K}+\top \to \diamond \top ,\hfill & \hfill \mathbf{D}\mathbf{4}& =\mathbf{D}+\diamond \diamond p\to \diamond p,\hfill \\ \hfill \mathbf{T}& =\mathbf{K}+p\to \diamond p,\hfill & \hfill \mathbf{S}\mathbf{4}& =\mathbf{T}+\diamond \diamond p\to \diamond p.\hfill \end{array}$$

Their axioms $\top \to \diamond \top$, $p\to \diamond p$ and $\diamond \diamond p\to \diamond p$ are strictly positive implications and correspond to conditions $Ser=\left\{\forall x(\top \to \exists yR(x,y\left)\right)\right\}$, $Refl=\left\{\forall x(\top \to R(x,x\left)\right)\right\}$ and $Trans=\left\{\forall x\forall y\forall z\left(R\right(x,y)\wedge R(y,z)\to R(x,z\left)\right)\right\}$ in the same way as $\diamond \square p\to \square \diamond p$ corresponds to $Conf$.

2.2. Strictly Positive Implications

A strictly positive term (or sp-term) is a modal formula constructed from propositional variables, the constant ⊤, conjunction ∧, and the unary diamond operator ⋄. An SP-implication takes the form $\sigma \to \tau$, where $\sigma$ and $\tau$ are SP-terms. An SP-logic is a set of SP-implications that contains formulas

$$p\to p,p\to \top ,p\wedge q\to q\wedge p,p\wedge q\to p,$$

(1)

and is closed under uniform substitution (of sp-terms for propositional variables) and rules

$$\frac{\sigma \to \tau \tau \to \varrho }{\sigma \to \varrho },\frac{\sigma \to \tau \sigma \to \varrho }{\sigma \to \tau \wedge \varrho },\frac{\sigma \to \tau }{\diamond \sigma \to \diamond \tau }$$

(2)

(see also the Reflection Calculus $\mathbf{RC}$ of [4,5]). For an sp-implication $\varphi$, $K^{+}+\varphi$ denotes the smallest SP-logic containing $\varphi$. By $K_2^{+}$, we denote the natural modification of $K^{+}$ for strictly positive implications with two modal operators ${\diamond }_1$ and ${\diamond }_2$ with two versions of the third rule for each of the two diamonds. It is easy to see that the rule

$$\frac{{\sigma }_1\to {\tau }_1{\sigma }_2\to {\tau }_2}{{\sigma }_1\wedge {\sigma }_2\to {\tau }_1\wedge {\tau }_2}$$

(3)

is admissible in $K^{+}$.

For a normal modal logic $\mathbf{L}$, the strictly positive fragment of $\mathbf{L}$ is

$$SPF\left(\mathbf{L}\right)=\left\{\varphi \left|\varphi \mathrm{is}\mathrm{an}\mathrm{sp}-\mathrm{implication}\mathrm{and}\varphi \in \mathbf{L}\right.\right\}.$$

It is easy to check that $SPF\left(\mathbf{L}\right)$ is an SP-logic.

Given an sp-term $\rho$, we define by induction a Kripke model $M_{\rho }=(T_{\rho },V_{\rho })$ based on a finite tree $T_{\rho }=(W_{\rho },R_{\rho })$ with root $r_{\rho }$. For $\rho =\top$, $T_{\rho }$ consists of a single irreflexive point $r_{\rho }$ with $V_{\rho }\left(p\right)=\varnothing$ for all variables p. For $\rho =p$, $T_{\rho }$ consists of a single irreflexive point $r_{\rho }$, $V_{\rho }\left(p\right)=\left\{r_{\rho }\right\}$, and $V_{\rho }\left(q\right)=\varnothing$ for $q\ne p$. For $\rho ={\rho }_1\wedge {\rho }_2$, we first construct disjointed $M_{{\rho }_1}$ and $M_{{\rho }_2}$, and then merge their roots $r_{{\rho }_1}$ and $r_{{\rho }_2}$ into r such that $r\in V_{\rho }\left(q\right)$ iff $r_i\in V_{{\rho }_i}\left(q\right)$, for some $i=1,2$. Finally, for $\rho =\diamond {\rho }^{\prime }$, we add a fresh point r to $W_{{\rho }^{\prime }}$, and set $R_{\rho }=R_{{\rho }^{\prime }}\cup \left\{(r_{\rho },r_{{\rho }^{\prime }})\right\}$ and $V_{\rho }\left(p\right)=V_{{\rho }^{\prime }}\left(p\right)$ for all variables p. We refer to $M_{\rho }$ as the $\rho$-tree model.

Given two Kripke models, $M_1=(W_1,R_1,V_1)$ and $M_2=(W_2,R_2,V_2)$, a map $h:W_1\to W_2$ is a homomorphism from $M_1$ into $M_2$ if it satisfies the following conditions:

• for all $x,y$ in $W_1$, if $(x,y)\in R_1$, then $(h\left(x\right),h\left(y\right))\in R_2$
• for all x in $W_1$ and propositional variables p, $x\in V_1\left(p\right)$ implies $h\left(x\right)\in V_2\left(p\right)$

Proposition 1.

For any sp-term t, Kripke model M and point w in M, we have $M,w\models t$ if there is a homomorphism $h:M_t\to M$ with $h\left(r_t\right)=w$.

Proposition 2.

For any sp-terms s and t, the implication $s\to t$ is derivable in $K^{+}$ if there is a rooted homomorphism from $M_t$ into $M_s$.

Propositions 1 and 2 are well known and can be shown by induction on the length of the sp-term t. Proposition 2 can also be obtained as a consequence of a representation theorem for semilattices with monotone operators [13], but this is outside of the scope of this paper, where we prefer to approach the completeness of $K^{+}$-based calculi syntactically whenever it is possible.

2.3. The Chase

A tuple-generating dependency [14] is a first-order formula of the form

$$\forall \overline{x}\forall \overline{y}(\varphi (\overline{x},\overline{y})\to \exists \overline{z}\psi (\overline{x},\overline{z})),$$

(4)

where $\overline{x}$, $\overline{y}$ and $\overline{z}$ are disjoint tuples of variables and $\varphi$ and $\psi$ are possibly empty conjunctions of R-atoms in respective sets of variables. We call $\varphi$ the body and $\psi$ the head of the corresponding TGD. Examples of TGDs include $Conf$ and $Con{f}^{+}=\{\forall x\forall y(R(x,y)\to \exists z\exists v(R(x,z)\wedge R(z,v)))\}.$

For a conjunction $\chi$ of R-atoms (with variables and without constants) we introduce constants $c_v$ for all object variables v in $\chi$ and set ${\Delta }_{\chi }=(W^{\chi },R^{\chi })$ where $W^{\chi }=\{c_v\mid v \mathrm{occurs} \mathrm{in} \chi \}$ and $R^{\chi }=\{(c_u,c_v)\mid R(u,v) \mathrm{is} \mathrm{a} \mathrm{conjunct} \mathrm{of} \chi \}$.

Given a Kripke frame $F=(W,R)$ trigger h for a TGD of the form (4) is a homomorphism from ${\Delta }_{\varphi }$ into F. Trigger h is good if h cannot be extended to a homomorphism from ${\Delta }_{\varphi \wedge \psi }$ into F. An application of a good trigger h for $F=(W,R)$ to F is a frame $F^{\prime }=(W^{\prime },R^{\prime })$ where $W^{\prime }$ extends W with fresh constants $c_u$ for all $u\in \overline{z}$ and $R^{\prime }$ extends R with pairs $\left(f\right(u),f(v\left)\right)$ for all atoms $R(u,v)$ in $\psi$ where

$$f\left(u\right)=\left\{\begin{array}{cc}h\left(u\right)\hfill & \mathrm{if}u\mathrm{is}\mathrm{in}\overline{x},and\hfill \\ c_u\hfill & \mathrm{if}u\mathrm{is}\mathrm{in}\overline{z}.\hfill \end{array}\right.$$

For a set of TGDs $\Pi$ by $ChaseStep(F,\Pi )$ we mean the relational structure, which is the result of the simultaneous application of all good triggers for F for all TGDs in $\Pi$ to F. We define $Chase(F,\Pi )$ as the union or the inverse limit of infinite chain $F\to ChaseStep(F,\Pi )\to ChaseStep\left(ChaseStep\right(F,\Pi \left)\right)\to \dots$. This version of the chase is similar to the one defined in [15] and is known in the database literature as ‘standard chase’ (in [16]) or as ‘restricted chase’ (in recent papers). In papers on logic, good triggers are sometimes called ‘defects’ and the chase construction is then referred to as ‘defect elimination’.

It should be clear that $Chase(F,\Pi )$ always satisfies $\Pi$. For a Kripke model $M=(F,V)$, we define $Chase(M,\Pi )$ as $\left(Chase\right(F,\Pi ),V)$. Those points of $Chase(F,\Pi )$ that are already in F are called non-anonymous, and those that are not are called anonymous. Anonymous points are often referred to in the database literature as ‘labelled nulls’, but we like to think that Kripke models consist of points. The rank of an anonymous point is the number of the iteration when it was created. The rank of non-anonymous points is 0 by definition.

Proposition 3.

For any SP-implication $s\to t$ we have $(s\to t)\in Log\{F\mid F\models \Pi \}$ iff $Chase(M_s,\Pi ),root\models t$.

(⇒) Suppose that $Chase(M_s,\Pi ),root⊭t$. Clearly $Chase(M_s,\Pi ),root\models s$ and also $Chase(M_s,\Pi )\models \Pi$, so there exists a frame $F=Chase(M_s,\Pi )$ such that $F\models \Pi$, $F⊭s\to t$. Therefore, this F refutes $s\to t$, showing that $s\to t$ is not in $Log\{F\mid F\models \Pi \}$.

(⇐) Suppose that $Chase(M_s,\Pi ),root\models t$. Consider an arbitrary Kripke frame F satisfying $\Pi$, valuation V and its point w such that $F,V,w\models s$. Hence there is a homomorphism f from $M_s$ into F sending the root of $M_s$ to w. Now consider (potentially infinite) the step-by-step construction of $Chase(M_s,\Pi )$. Following this process in a step-by-step manner and using the fact that F satisfies $\Pi$ at each step, we extend f to a homomorphism h from $Chase(M_s,\Pi )$ to F. Since $Chase(M_s,\Pi ),root\models t$, it follows that $F,V,w\models t$. This shows that $s\to t$ is in $Log\{F\mid F\models \Pi \}$.

2.4. Two-Dimensional Products of Modal Logics

In this paper, we also consider modal formulas with two modalities: ${\square }_1$ and ${\square }_2$, and their dual modalities: ${\diamond }_1$ and ${\diamond }_2$.

The definition of a normal bimodal logic repeats the definition of normal modal logic except for the axioms ${\square }_i(p\to q)\to ({\square }_{i}p\to {\square }_{i}q)$ ($i\in \left\{1,2\right\}$) and the Generalization rules (given as $\varphi$ infer ${\square }_i\varphi$) ($i\in \left\{1,2\right\}$). The smallest bimodal logic is denoted by ${\mathbf{K}}_{\mathbf{2}}$. For a set of bimodal formulas $\Gamma$ and a bimodal logic L, $L+\Gamma$ denotes the smallest normal bimodal logic containing $L\cup \Gamma$.

Definition 1.

For Kripke frames $F_1=(W_1,R_1)$ and $F_2=(W_2,R_2)$ we define $F_1\times F_2=(W_1\times W_2,R_1^{\prime },R_2^{\prime })$, where

$$\begin{array}{cc}\hfill (x_1,x_2)R_1^{\prime }(y_1,y_2)& \iff x_1{R}_1{y}_{1}and{x}_2=y_2,\hfill \\ \hfill (x_1,x_2)R_2^{\prime }(y_1,y_2)& \iff x_1=y_{1}and{x}_2{R}_2{y}_2.\hfill \end{array}$$

Frame $F_1\times F_2$ is called the product of $F_1$ and $F_2$.

Definition 2.

For two normal modal logics, $L_1$ and $L_2$, we define the product

$$L_1\times L_2=\left\{A\left|\forall F_1\forall F_2(F_1\models L_1\wedge F_2\models L_2\Rightarrow F_1\times F_2\models A)\right.\right\}.$$

Definition 3.

Let $L_1$ and $L_2$ be two modal logics with one modality □, then the fusion of these logics is the following bimodal logic:

$$L_1\ast L_2={\mathbf{K}}_{\mathbf{2}}+L_1^{\prime }+L_2^{\prime };$$

where $L_i^{\prime }$ is the set of all additional axioms in $L_i$ where each □ is replaced by ${\square }_i$.

We consider the following formulas

$$\begin{array}{cc}\hfill co{m}_{12}& ={\diamond }_1{\diamond }_{2}p\to {\diamond }_2{\diamond }_{1}p,\hfill \\ \hfill co{m}_{21}& ={\diamond }_2{\diamond }_{1}p\to {\diamond }_1{\diamond }_{2}p,\hfill \\ \hfill chr& ={\diamond }_1{\square }_{2}p\to {\square }_2{\diamond }_{1}p.\hfill \end{array}$$

They correspond to the following TGDs:

$$\begin{array}{cc}\hfill Com12& =\left\{\forall x\forall y\forall z\left(R_1(x,y)\wedge R_2(y,z)\to \exists v(R_2(x,v)\wedge R_1(v,z))\right)\right\},\hfill \\ \hfill Com21& =\left\{\forall x\forall y\forall z\left(R_2(x,y)\wedge R_1(y,z)\to \exists v(R_1(x,v)\wedge R_2(v,z))\right)\right\},\hfill \\ \hfill ChRos& =\{\forall x\forall y\forall z(R_1(x,y)\wedge R_2(x,z)\to \exists v(R_2(x,v)\wedge R_1(y,v)))\}.\hfill \end{array}$$

Definition 4.

For two unimodal logics $L_1$ and $L_2$ we define the commutator of these logics by

$$\begin{array}{cc}\hfill \left[L_1,L_2\right]& =L_1\ast L_2+co{m}_{12}+co{m}_{21}+chr.\hfill \end{array}$$

Theorem 1

([17]). For logics $L_1,L_2\in \left\{\mathbf{K},\mathbf{D},\mathbf{T},\mathbf{K}\mathbf{4},\mathbf{D}\mathbf{4},\mathbf{S}\mathbf{4}\right\}$

$$L_1\times L_2=\left[L_1,L_2\right].$$

3. Two Conditions for TGDs

Consider the following two conditions for a set of TGDs $\Pi$:

(P1)

given an sp-term s and a propositional variable p, the valuation $V\left(p\right)$ in $Chase(M_s,\Pi )$ does not contain anonymous points of $Chase(M_s,\Pi )$ and

(P2)

given an sp-term s, every generated submodel rooted at an anonymous point of $Chase(M_s,\Pi )$ contains only anonymous points.

It will be explained later how (P1) and (P2) allow us to lift a homomorphism from $Chase(M_s,\Pi )$ into $Chase(M_s,{\Pi }^{\prime })$ for a simpler ${\Pi }^{\prime }$ (think of $\Pi =Conf$ and ${\Pi }^{\prime }=Con{f}^{+}$). What we mean by a ‘simpler $\Pi$’ will also be clear later. At this point, only note that,

Proposition 4.

Suppose Π is a subset of {Conf, Ser, Refl, Trans}. Then Π satisfies (P1) and (P2).

In fact, (P1) holds for all TGDs without unary predicates in the head. On the other hand, $Com12$ and $Com21$ violate (P2), and so logic with these two axioms will need a special approach.

4. Strictly Positive Fragments of Unimodal Logics with Confluence

In this section, we prove the following two theorems:

Theorem 2.

$SPF(\mathbf{K}+\diamond \square p\to \square \diamond p)=K^{+}+\diamond \top \to \diamond \diamond \top$.

Theorem 3.

For each L in the following set of logics $\left\{\mathbf{D},\mathbf{T},\mathbf{D}\mathbf{4},\mathbf{S}\mathbf{4}\right\}$ we have $SPF(L+\diamond \square p\to \square \diamond p)=SPF\left(L\right)$ (and so they both are axiomatised by $K^{+}$ with the strictly positive axioms of L due to a general result from [10]).

The proof of Theorem 2 is based on the following two lemmas. The following lemma can be called the completeness of $K^{+}+\diamond \top \to \diamond \diamond \top$ with respect to TGD $Con{f}^{+}$.

Lemma 1.

Suppose that s and t are sp-terms such that there is a rooted homomorphism h from $M_t$ into $Chase(M_s,Con{f}^{+})$. Then $s\to t$ is derivable in $K^{+}+\diamond \top \to \diamond \diamond \top$.

Proof. 

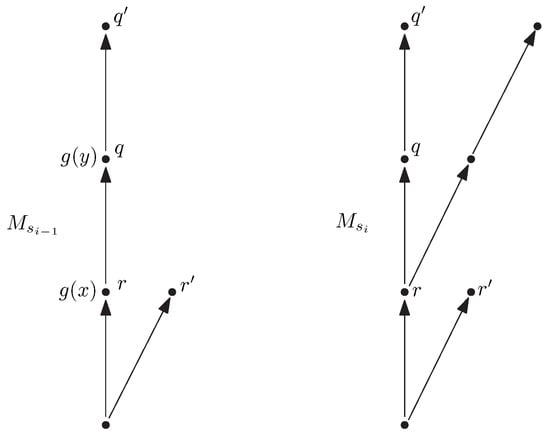
First note that in $K^{+}+\diamond \top \to \diamond \diamond \top$ we can derive $\diamond p\to \diamond p\wedge \diamond \diamond \top$:

$$\begin{array}{ccc}\left(1\right)& p\to \top & \left[axiomof{K}^{+}\right]\\ \left(2\right)& \diamond p\to \diamond \top & \left[rule3of{K}^{+}applied\left(1\right)\right]\\ \left(3\right)& \diamond \top \to \diamond \diamond \top & \left[additionalaxiom\right]\\ \left(4\right)& \diamond p\to \diamond \diamond \top & \left[rule1of{K}^{+}appliedto\left(2\right)and\left(3\right)\right]\\ \left(5\right)& p\to p& \left[axiomof{K}^{+}\right]\\ \left(6\right)& \diamond p\to \diamond p& \left[rule3of{K}^{+}appliedto\left(5\right)\right]\\ \left(7\right)& \diamond p\to \diamond p\wedge \diamond \diamond \top & \left[rule2of{K}^{+}appliedto\left(4\right)and\left(6\right)\right]\end{array}$$

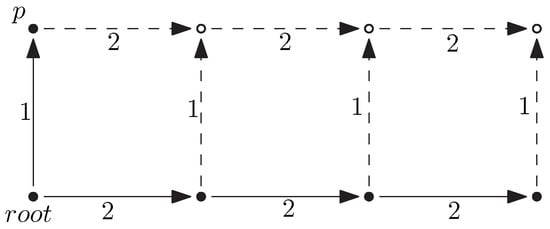
Then note that $Chase(M_s,Con{f}^{+})$ can be obtained from $M_s$ by a sequence of applications of individual triggers for $Con{f}^{+}$ in such a way that all intermediary models are of the form $M_{s^{\prime }}$ for some term $s^{\prime }$. (This is due to the fact that applications of $Con{f}^{+}$ preserve the ‘tree-shapedness’ of models.) Thus there exists a sequence of sp-terms $s=s_0,s_1,\cdots ,s_m$ such that $M_{s_i}$ is the result of the application of trigger g for $Con{f}^{+}$ to $M_{s_{i-1}}$ for $1\le i\le m$ and a rooted homomorphism from $M_t$ into $M_{s_m}$. Now we argue that all implications $s_{i-1}\to s_i$ are derivable in $K^{+}+\diamond \top \to \diamond \diamond \top$. To derive $s_{i-1}\to s_i$ it is sufficient to take $\diamond p\to \diamond p\wedge \diamond \diamond \top$, then substitute the term corresponding to the ‘part of $M_{s_{i-1}}$ sitting above $g\left(y\right)$’, which is common for $M_{s_{i-1}}$ and $M_{s_i}$, and then apply rules 3 and (3) of $K^{+}$ to derive ‘the part of $M_{s_{i-1}}$ sitting below $g\left(x\right)$’, which is again common for two models, on both sides of the resulting implication (here x and y are variables in the antecedent of $Con{f}^{+}$). This argument is illustrated in Figure 1. The implication $s_m\to t$ is derivable by Proposition 2. Now it remains to apply $m+1$ times the first rule of $K^{+}$. □

Figure 1. Suppose that $s_{i-1}=\diamond (r\wedge \diamond (q\wedge \diamond q^{\prime }))\wedge \diamond r^{\prime }$ and $s_i=\diamond (r\wedge \diamond (q\wedge \diamond q^{\prime })\wedge \diamond \diamond \top )\wedge \diamond r^{\prime }$ with $M_{s_{i-1}}$, $M_{s_i}$ and g as in the figure. Then the term corresponding to the ‘part of $M_{s_{i-1}}$ sitting above $g\left(y\right)$’ is $q\wedge \diamond q^{\prime }$. Therefore, we substitute $p:=q\wedge \diamond q^{\prime }$ in $\diamond p\to \diamond p\wedge \diamond \diamond \top$ and infer $\diamond (q\wedge \diamond q^{\prime })\to \diamond (q\wedge \diamond q^{\prime })\wedge \diamond \diamond \top$. Then by an admissible in $K^{+}$ rule (3) from the latter formula and the axiom $r\to r$ we infer $r\wedge \diamond (q\wedge \diamond q^{\prime })\to r\wedge \diamond (q\wedge \diamond q^{\prime })\wedge \diamond \diamond \top$. Then by rule 3 of $K^{+}$ we infer $\diamond (r\wedge \diamond (q\wedge \diamond q^{\prime }))\to \diamond (r\wedge \diamond (q\wedge \diamond q^{\prime })\wedge \diamond \diamond \top )$ and by rule (3) we infer $\diamond (r\wedge \diamond (q\wedge \diamond q^{\prime }))\wedge \diamond r^{\prime }\to \diamond (r\wedge \diamond (q\wedge \diamond q^{\prime })\wedge \diamond \diamond \top )\wedge \diamond r^{\prime }$ which is $s_{i-1}\to s_i$.

Lemma 2.

For each frame F we can define a partial function $succ$ on $Chase(F,Con{f}^{+})$ such that

• its domain contains all non-final points of F and the image of $succ$.
• if $succ\left(u\right)=v$, then $(u,v)\in Chase(F,Con{f}^{+}).R$.

Proof. 

Each non-final point u of F has a successor v, which gives rise to trigger h for $Con{f}^{+}$. If this trigger is good, we set $succ\left(u\right)$ to be $c_z$ introduced by an application of this trigger. Otherwise, we set $succ\left(u\right)$ to be $h^{\prime }\left(z\right)$, where h is an extension of h to the head of the rule. Then we define $succ$ on those points of $ChaseStep(F,Con{f}^{+})$ where it has not been defined so far. Then we deal similarly with $ChaseStep(ChaseStep(F,Con{f}^{+}),Con{f}^{+})$ and so on. □

Proof of Theorem 2.

It should be clear that every theorem of $K^{+}+\diamond \top \to \diamond \diamond \top$ is a strictly positive theorem of $\mathbf{K}+\diamond \square p\to \square \diamond p$ since $\diamond \top \to \diamond \diamond \top$ is a theorem of $\mathbf{K}+\diamond \square p\to \square \diamond p$. Therefore, it remains to show that every strictly positive theorem of $\mathbf{K}+\diamond \square p\to \square \diamond p$ is a theorem of $K^{+}+\diamond \top \to \diamond \diamond \top$. Now take a strictly positive implication $s\to t$ such that $s\to t\in \mathbf{K}+\diamond \square p\to \square \diamond p$. By Proposition 3, it follows that $Chase(M_s,Conf),root\models t$. Therefore, there exists a rooted homomorphism h from $M_t$ into $Chase(M_s,Conf)$. If $M_s$ is a singleton, then both $Chase(M_s,Conf)$ and $Chase(M_s,{Conf}^{+})$ are isomorphic to $M_s$, and we are done. Otherwise, note that $Conf$ satisfies (P1) and (P2). It follows that $Chase(M_s,Con{f}^{+}),root\models t$. Indeed, we can define a homomorphism $h^{\prime }$ from $M_t$ into $Chase(M_s,Con{f}^{+})$ by recursion. We set $h^{\prime }\left(u\right)=h\left(u\right)$ for non-anonymous $h\left(u\right)$. For anonymous $h\left(u\right)$ we look at the parent v of u in $M_s$ and set $h^{\prime }\left(u\right)=succ\left(h^{\prime }\left(v\right)\right)$ assuming that $h^{\prime }\left(v\right)$ is already defined. It should be clear that $h^{\prime }$ is a homomorphism, since due to (P1) and (P2), no points above an anonymous u in $M_t$ can be in $V\left(p\right)$ for any p. It remains to apply Lemma 1 to conclude that $s\to t$ is derivable in $K^{+}+\diamond \top \to \diamond \diamond \top$. □

The proof of Theorem 3 is similar. We use TGDs $Ser=\left\{\forall x(\top \to \exists yR(x,y\left)\right)\right\}$, $Refl=\left\{\forall x(\top \to R(x,x\left)\right)\right\}$ and $Trans=\left\{\forall x\forall y\forall z\left(R\right(x,y)\wedge R(y,z)\to R(x,z\left)\right)\right\}$ and the fact that properties (P1) and (P2) still hold in the setting of L. For example, for $s\to t\in \mathbf{S}\mathbf{4}.\mathbf{2}$, (P1) and (P2) hold for $Chase(M_s,Trans\cup Refl\cup Conf)$, and this allows us to transform a homomorphism $h:M_t\to Chase(M_s,Trans\cup Refl\cup Conf)$ into one $h^{\prime }:M_t\to Chase(M_s,Trans\cup Refl)$ using the fact that each point in $Chase(M_s,Trans\cup Refl)$ has a successor. We also use the ‘completeness lemma’ for strictly positive counterparts of $\left\{\mathbf{D},\mathbf{T},\mathbf{D}\mathbf{4},\mathbf{S}\mathbf{4}\right\}$ to go from the existence of $h^{\prime }$ to a derivation of $s\to t$ in the corresponding strictly positive logic:

Lemma 3.

Suppose that Φ is a subset of $\{\top \to \diamond \top ,\diamond \diamond p\to \diamond p,p\to \diamond p\}$ and that Π is the corresponding subset of $\{Ser,Refl,Trans\}$. Then for any sp-terms s and t, if there is a rooted homomorphism h from $M_t$ into $Chase(M_s,\Pi )$, then the implication $s\to t$ is derivable in $K^{+}+\Phi$.

We consider this lemma as folklore (cf. [1,2,5,10]) and leave it without a proof.

5. Strictly Positive Fragments for Logics with Bimodal Version of Confluence

In this section, we consider logic with bimodal versions of confluence $chr={\diamond }_1{\square }_{2}p\to {\square }_2{\diamond }_{1}p$. We start by considering this axiom on its own.

We define

$$\begin{array}{cc}\hfill chr{1}_n^{+}& ={\diamond }_{1}p\wedge {\diamond }_2^n\top \to {\diamond }_1(p\wedge {\diamond }_2^n\top ),\hfill \\ \hfill chr{2}_n^{+}& ={\diamond }_{2}p\wedge {\diamond }_1^n\top \to {\diamond }_2(p\wedge {\diamond }_1^n\top ),\hfill \\ \hfill {\Gamma }_1& =\left\{chr{1}_n^{+}|n\in \mathbb{N}\right\}\hfill \\ \hfill {\Gamma }_2& =\left\{chr{2}_n^{+}|n\in \mathbb{N}\right\}\hfill \end{array}$$

${\Gamma }_1$ and ${\Gamma }_2$ correspond to the TGDs:

$$\begin{array}{cc}\hfill PosChR1& =\{\forall x_1\dots \forall x_n\forall y_1(R_2(x_1,x_2)\wedge \cdots \wedge R_2(x_{n-1},x_n)\wedge R_1(x_1,y_1)\hfill \\ \hfill & \to \exists y_2\cdots \exists y_n{R}_2(y_1,y_2)\wedge \cdots \wedge R_2(y_{n-1},y_n))\mid n\in \mathbb{N}\},\hfill \\ \hfill PosChR2& =\{\forall x_1\dots \forall x_n\forall y_1(R_1(x_1,x_2)\wedge \cdots \wedge R_1(x_{n-1},x_n)\wedge R_2(x_1,y_1)\hfill \\ \hfill & \to \exists y_2\cdots \exists y_n{R}_1(y_1,y_2)\wedge \cdots \wedge R_1(y_{n-1},y_n))\mid n\in \mathbb{N}\}.\hfill \end{array}$$

The next part of the paper is dedicated to the proof of the following theorem:

Theorem 4.

$SPF({\mathbf{K}}_2+chr)=K_2^{+}+{\Gamma }_1+{\Gamma }_2$.

Lemma 4.

All formulas in ${\Gamma }_1$ and ${\Gamma }_2$ are theorems of ${\mathbf{K}}_2+chr$.

Proof. 

First take $chr{1}_n^{+}={\diamond }_{1}p\wedge {\diamond }_2^n\top \to {\diamond }_1(p\wedge {\diamond }_2^n\top )$ and note that

$$Chase(M_{{\diamond }_{1}p\wedge {\diamond }_2^n\top },ChRos),root\models {\diamond }_1(p\wedge {\diamond }_2^n\top )$$

(see Figure 2).

Figure 2. $Chase(M_{{\diamond }_{1}p\wedge {\diamond }_2^3\top },ChRos),root\models {\diamond }_1(p\wedge {\diamond }_2^3\top )$.

The argument for $chr{2}_n^{+}$ is similar. □

To illustrate the interplay between ${\Gamma }_1$ and ${\Gamma }_2$, consider the following inference:

$$\begin{array}{ccc}\left(1\right)& {\diamond }_1\top \wedge {\diamond }_{2}p\to {\diamond }_2(p\wedge {\diamond }_1\top )& \left[chr{2}_1^{+}\right]\\ \left(2\right)& {\diamond }_1\top \wedge {\diamond }_2\top \to {\diamond }_2{\diamond }_1\top & [substitutionp:=\top in(1\left)\right]\\ \left(3\right)& {\diamond }_1({\diamond }_1\top \wedge {\diamond }_2\top )\to {\diamond }_1{\diamond }_2{\diamond }_1\top & \left[introduce{\diamond }_{1}in\left(2\right)\right]\\ \left(4\right)& {\diamond }_{1}p\wedge {\diamond }_2\top \to {\diamond }_1(p\wedge {\diamond }_2\top )& \left[chr{1}_1^{+}\right]\\ \left(5\right)& {\diamond }_1{\diamond }_1\top \wedge {\diamond }_2\top \to {\diamond }_1({\diamond }_1\top \wedge {\diamond }_2\top )& [substitutionp:={\diamond }_1\top in\left(4\right)]\\ \left(6\right)& {\diamond }_1{\diamond }_1\top \wedge {\diamond }_2\top \to {\diamond }_1{\diamond }_2{\diamond }_1\top & \left[from\right(5\left)and\right(3\left)\right]\end{array}$$

This deduction exemplifies the following ‘completeness lemma’ for $s={\diamond }_1{\diamond }_1\top \wedge {\diamond }_2\top$ and $t={\diamond }_1{\diamond }_2{\diamond }_1\top$:

Lemma 5.

Suppose that s and t are sp-terms. Then if $M_t$ maps homomorphically into the model $Chase(M_s,PosChR1\cup PosChR2)$ (with preservation of roots), then the implication $s\to t$ is derivable in $K_2^{+}+{\Gamma }_1+{\Gamma }_2$.

To prove it, we need more verbose modifications of $chr{1}_n^{+}$ and $chr{2}_n^{+}$. We define, by recursion, the terms $u_n^i$ for $i=1,2$ and $n\ge 0$ by setting $u_0^1=u_0^2=p_0$, $u_n^1=p_n\wedge {\diamond }_2{u}_{n-1}^1$ and $u_n^2=p_n\wedge {\diamond }_1{u}_{n-1}^2$ for $n>0$. Now we set $chr{1}_n^{+}{}^{\prime }={\diamond }_{1}p\wedge u_n^1\to {\diamond }_1(p\wedge {\diamond }_2^n\top )\wedge u_n^1$ and $chr{2}_n^{+}{}^{\prime }={\diamond }_{2}p\wedge u_n^2\to {\diamond }_2(p\wedge {\diamond }_1^n\top )\wedge u_n^2.$ Since one can easily derive in $K^{+}$ implications $u_n^1\to {\diamond }_2^n\top$ and $u_n^2\to {\diamond }_1^n\top$ and then use admissible rule (3), we have

Lemma 6.

The formula $chr{1}_n^{+}{}^{\prime }$ is derivable in $K_2^{+}+chr{1}_n^{+}$ and the formula $chr{2}_n^{+}{}^{\prime }$ is derivable in $K_2^{+}+chr{2}_n^{+}$.

The proof of Lemma 5.

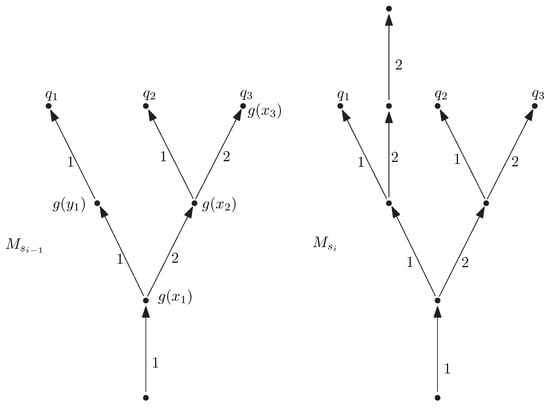
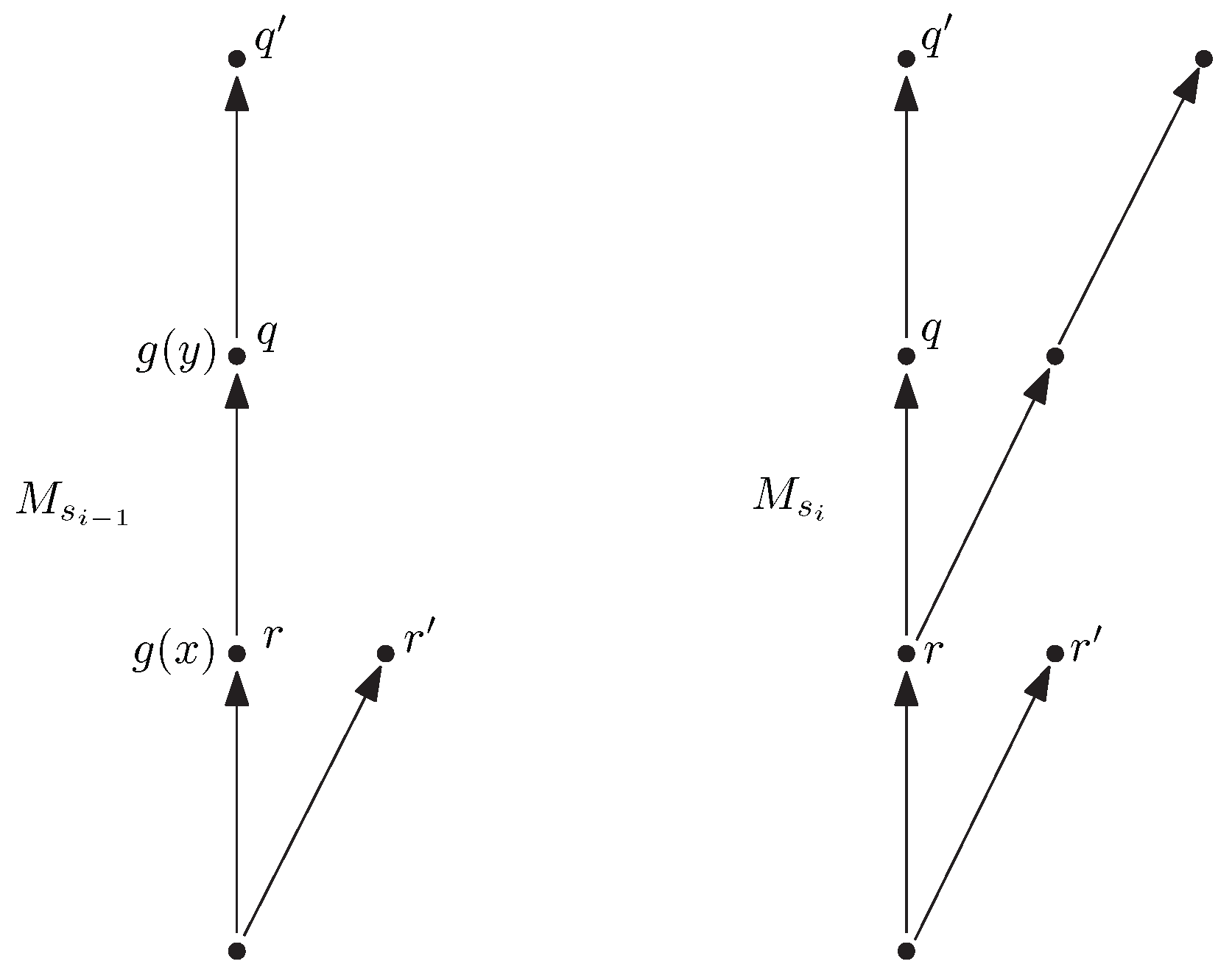
The proof is similar to the proof of Lemma 1. Recall that a chase is a sequence of applications of triggers. Further, note that if a model M is obtained by an application of a trigger for $PosChR1$ or $PosChR2$ to a model $M_{s^{\prime }}$ for an sp-term $s^{\prime }$, then there is an sp-term $s^{″}$ such that M is isomorphic to $M_{s^{″}}$. (This is due to the fact that applications of $PosChR1$ and $PosChR2$ preserve the ‘tree-shapedness’ of models.) Thus there is a sequence of terms $s_0=s,s_1,s_2,\cdots ,s_n$, such that $M_{s_i}$ is obtained from $M_{s_{i-1}}$ by an application of a trigger for $PosChR1$ or $PosChR2$ and a homomorphism from $M_t$ into $M_{s_n}$. We argue that implications $s_{i-1}\to s_i$ are deducible in $K_2^{+}+{\Gamma }_1+{\Gamma }_2$. Indeed, we start with an axiom $chr{1}_n^{+}{}^{\prime }$ or $chr{2}_n^{+}{}^{\prime }$ expressing the application of a trigger, and then apply substitutions and the rules

$$\frac{\sigma \to \tau \sigma \to \varrho }{\sigma \to \tau \wedge \varrho },\frac{\sigma \to \tau }{{\diamond }_j\sigma \to {\diamond }_j\tau }$$

for $j=1,2$ to infer full implication $s_{i-1}\to s_i$ (cf. (2) and (3)). This argument is explained in Figure 3. Additional variables $p_0,\dots ,p_n$ in $chr{1}_n^{+}{}^{\prime }$ and $chr{2}_n^{+}{}^{\prime }$ serve as substitution slots at object variables $x_i$ and $y_i$ in the body of TGDs. Implication $s_n\to t$ is deducible in $K_2^{+}$ by Proposition 2. Now it remains to apply $n+1$ times the rule

$$\frac{\sigma \to \tau \tau \to \varrho }{\sigma \to \varrho }.$$

 □

Figure 3. Suppose that $s_{i-1}={\diamond }_1({\diamond }_1{\diamond }_1{q}_1\wedge {\diamond }_2({\diamond }_1{q}_2\wedge {\diamond }_2{q}_3))$ and $s_i={\diamond }_1({\diamond }_1({\diamond }_1{q}_1\wedge {\diamond }_2{\diamond }_2\top )\wedge {\diamond }_2({\diamond }_1{q}_2\wedge {\diamond }_2{q}_3))$ with $M_{s_{i-1}}$, $M_{s_i}$ and trigger g as in the figure. To infer $s_{i-1}\to s_i$, we take $chr{1}_2^{+}{}^{\prime }={\diamond }_{1}p\wedge (p_2\wedge {\diamond }_2(p_1\wedge {\diamond }_2{p}_0))\to {\diamond }_1(p\wedge {\diamond }_2{\diamond }_2\top )\wedge (p_2\wedge {\diamond }_2(p_1\wedge {\diamond }_2{p}_0))$, substitute $p:={\diamond }_1{q}_1$, $p_2:=\top$, $p_1:={\diamond }_1{q}_2$, $p_0:=q_3$, obtain ${\diamond }_1{\diamond }_1{q}_1\wedge {\diamond }_2({\diamond }_1{q}_2\wedge {\diamond }_2{q}_3)\to {\diamond }_1({\diamond }_1{q}_1\wedge {\diamond }_2{\diamond }_2\top )\wedge {\diamond }_2({\diamond }_1{q}_2\wedge {\diamond }_2{q}_3)$ and apply $\frac{\sigma \to \tau }{{\diamond }_1\sigma \to {\diamond }_1\tau }$.

Let $F=(W,R_1,R_1)$ be a frame and $x\in W$. The i-depth of x is the maximum overall lengths of $R_i$-path starting in x if its finite and ∞ otherwise. Notation: ${\mathrm{depth}}_i(F,x)$. For example, for a reflexive point x, we have ${\mathrm{depth}}_i(F,x)=\infty$.

Lemma 7.

Let $F=(W,R_1,R_2)$ be an arbitrary frame satisfying $PosChR1$ and $PosChR2$. Then for each x and y in W we have

• if $(x,y)\in R_1$, then ${\mathrm{depth}}_2(F,x)\le {\mathrm{depth}}_2(F,y)$, and
• if $(x,y)\in R_2$, then ${\mathrm{depth}}_1(F,x)\le {\mathrm{depth}}_1(F,y)$.

To see this, note that the statements of Lemma 7 simply rephrase $PosChR1$ and $PosChR2$ using the notion of depth.

Given an sp-term t with operators ${\diamond }_1$ and ${\diamond }_2$, a root branch in $M_t$ is a finite sequence $b=b_1\dots b_m$ of 1 and 2 such that if we define, by recursion, the terms $u_n$ for $n\ge 0$ by setting $u_0=\top$ and $u_n={\diamond }_{b_n}{u}_{n-1}$ for $n>0$, there is a rooted homomorphism from $M_{u_m}$ into $M_t$. For a term t by ${\left|t\right|}_i$ we denote the largest number of i’s in any root branch in $M_t$ for $i\in \left\{1,2\right\}$. For example, for $t={\diamond }_1({\diamond }_{2}p\wedge {\diamond }_{1}q)$ ${\left|t\right|}_1=2$ and ${\left|t\right|}_2=1$.

Lemma 8.

Let $F=(W,R_1,R_2)$ be an arbitrary frame satisfying $PosChR1$ and $PosChR2$. Suppose that $x\in W$ and t is a variable-free term such that ${\left|t\right|}_1\le dept{h}_1\left(x\right)$ and ${\left|t\right|}_2\le dept{h}_2\left(x\right)$. Then there is a homomorphism from $M_t$ into F, sending the root of t to x.

Proof. 

The proof is by induction on the length of term t. The case when $t=\top$ is obvious.

If $t={\diamond }_{1}s$, then $dept{h}_1\left(x\right)\ge 1$, and there exists y with $x{R}_{1}y$ and

$${\left|s\right|}_1={\left|t\right|}_1-1\le dept{h}_1\left(x\right)-1=dept{h}_1\left(y\right).$$

Assuming $dept{h}_2\left(x\right)=k$, we use $PosChR1$ and deduce that $dept{h}_2\left(y\right)=k$. We apply the IH and conclude that there is a homomorphism from $M_s$ to F, sending the root of $M_s$ to y. This homomorphism can be easily extended to $M_t$ by sending the root of $M_t$ to x.

The case when $t={\diamond }_{2}s$ is similar. If $t=s_1\wedge s_2$, then IH can be applied to $s_1$ and $s_2$. The desired homomorphism is the union of homomorphisms from $M_{s_1}$ and from $M_{s_2}$. □

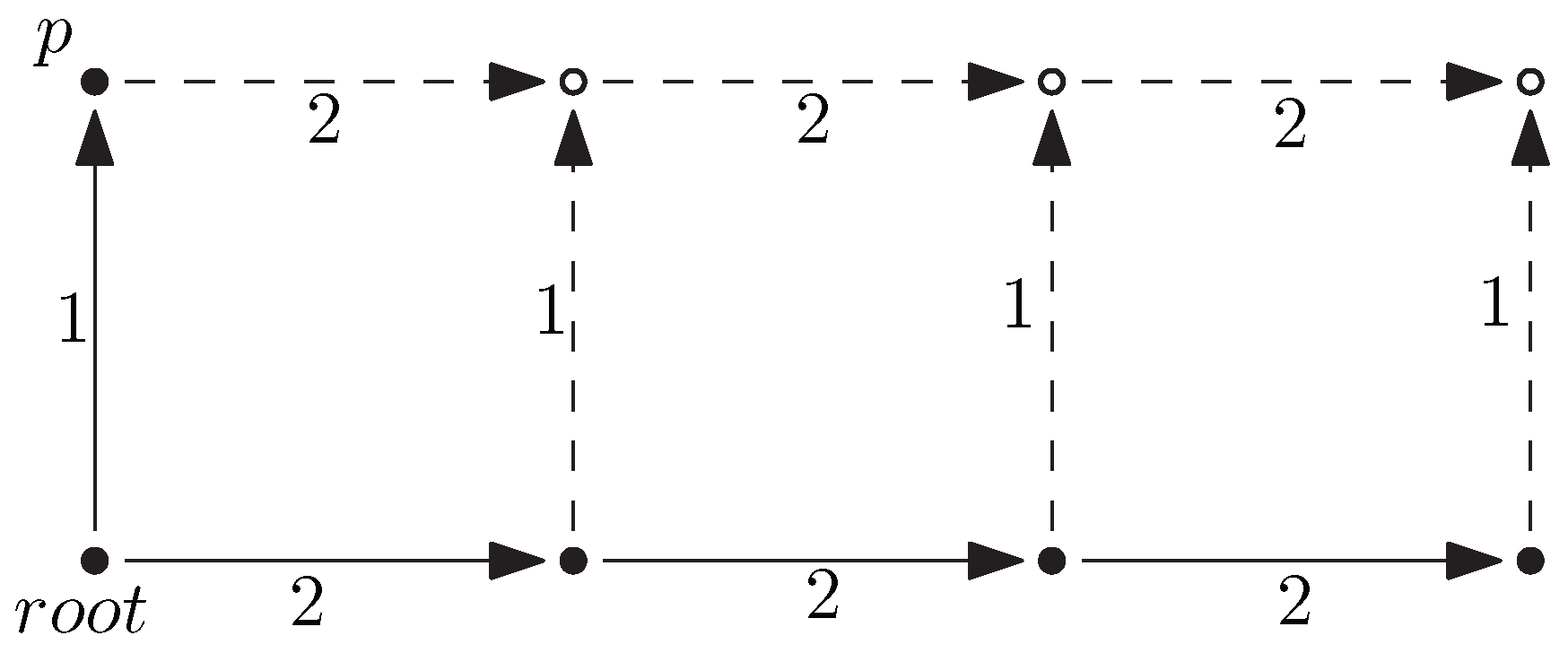
This argument is illustrated in Figure 4 for $t={\diamond }_1{\diamond }_2{\diamond }_2{\diamond }_1{\diamond }_2\top$.

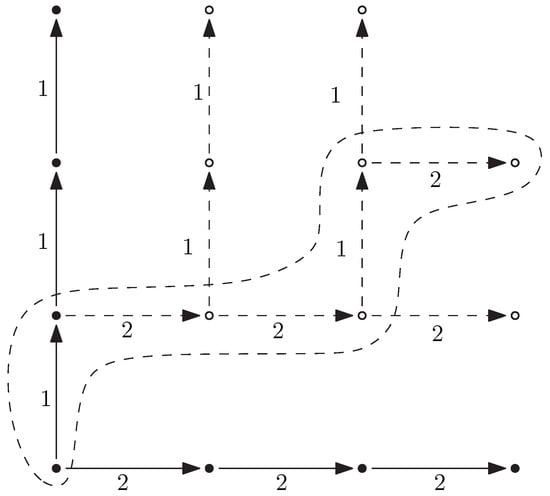
Figure 4. Proof of Lemma 8 for $t={\diamond }_1{\diamond }_2{\diamond }_2{\diamond }_1{\diamond }_2\top$.

The following lemma says that for any term s, the ‘anonymous part’ of $Chase(M_s,ChRos)$ is commutative in the strong following sense.

Lemma 9.

Fix a term s. Suppose that h is a trigger for $Com12$ into $Chase(M_s,ChRos)$ such that $h\left(z\right)$ is an anonymous point of rank $n\ge 1$. Then there is a point v in $Chase(M_s,ChRos)$ of rank $n-1$ such that $(h\left(x\right),v)\in Chase(M_s,ChRos).R_2$ and $(v,h\left(z\right))\in Chase(M_s,ChRos).R_1$. A similar claim holds for $Com21$.

To see this, focus on the moment when z is created by trigger $h^{\prime }$ for $ChRos$ and take $h^{\prime }\left(z\right)$ as v.

Suppose that t is an sp-term and x is a point in $M_t$ such that $x\notin V\left(p\right)$ for all propositional variables p. In this case, by $t_x$ we denote such a term that the submodel of $M_t$ generated by x is isomorphic to $M_{t_x}$.

The proof of Theorem 4.

(⊇) In Lemma 4, we prove that all formulas in ${\Gamma }_1$ and ${\Gamma }_2$ are theorems of ${\mathbf{K}}_2+chr$.

(⊆) Now take a strictly positive implication $s\to t$ such that $s\to t\in {\mathbf{K}}_2+chr$. By Proposition 3 it follows that $Chase(M_s,ChRos),root\models t$. Therefore, there exists a rooted homomorphism h from $M_t$ into $Chase(M_s,ChRos)$. Suppose that $R_1(x,y)$ holds in $M_t$, $h\left(x\right)$ is not anonymous, but $h\left(y\right)$ is anonymous. By the iterative application of Lemma 9 we obtain that $|t_y{|}_1\le {\mathrm{depth}}_1(M_s,x)-1$ and $|t_y{|}_2\le {\mathrm{depth}}_2(M_s,x)$. Therefore, by Lemma 8, there exists a homomorphism $h_{xy}$ from the subtree of $M_t$ generated at x in the direction of y into $Chase(M_s,PosChR1\cup PosChR2)$, sending x to $h\left(x\right)$. In a similar way, we define homomorphisms $h_{xy}$ for pairs $(x,y)$ of points of $M_t$ such that $R_2(x,y)$ holds in $M_t$, $h\left(x\right)$ is not anonymous, but $h\left(y\right)$ is anonymous. By applying this argument to all such pairs $(x,y)$ in $M_t$, we obtain a homomorphism $h^{\prime }$ from $M_t$ into $Chase(M_s,PosChR1\cup PosChR2)$. Again (P1) and (P2) are used to ensure that no points above an anonymous u in $M_t$ can be in $V\left(p\right)$ for any p. Finally, by Lemma 5, we conclude that $s\to t$ is derivable in $K_2^{+}+{\Gamma }_1+{\Gamma }_2$. □

Now let us turn to the product logic $\mathbf{K}\times \mathbf{K}$, which, in addition to $chr$, contains axioms $co{m}_{12}={\diamond }_1{\diamond }_{2}p\to {\diamond }_2{\diamond }_{1}p$ and $co{m}_{21}={\diamond }_2{\diamond }_{1}p\to {\diamond }_1{\diamond }_{2}p$. Let us define a set of TGDs

$$\begin{array}{cc}\hfill Com& =Com12\cup Com21.\hfill \end{array}$$

These axioms are already strictly positive and from a general result of [10] (Theorem 35). Therefore, it follows that $SPF(\mathbf{K}+co{m}_{\#})=K^{+}+co{m}_{\#}$ for $\#\in \{12,21\}$. Now we argue that indeed

Theorem 5.

$SPF(\mathbf{K}\times \mathbf{K})=K_2^{+}+co{m}_{12}+co{m}_{21}+{\Gamma }_1+{\Gamma }_2$.

Since TGDs $Com$ create points that do not satisfy (P2), we need a softer condition. Suppose that $\Pi =Com\cup ChRos$ and ${\Pi }^{+}=Com\cup PosChR1\cup PosChR2$. Take an sp-term s and consider $Chase(M_s,\Pi )$. All anonymous points in $Chase(M_s,\Pi )$ fall into two groups: introduced by $Com$ (type 1) and introduced by $ChRos$ (type 2). Relying on Lemma 9, we claim that

(P2’)

given an sp-term s, every generated submodel rooted at an anonymous point of $Chase(M_s,\Pi )$ of type 2 contains only anonymous points of type 2.

Like in Theorem 4, we first establish ‘completeness with respect to TGDs’ for $K_2^{+}+co{m}_{12}+co{m}_{21}+{\Gamma }_1+{\Gamma }_2$:

Lemma 10.

Suppose that s and t are sp-terms. Then if $M_t$ maps homomorphically into the model $Chase(M_s,PosChR1\cup PosChR2\cup Com)$ (with preservation of roots), then the implication $s\to t$ is derivable in $K_2^{+}+co{m}_{12}+co{m}_{21}+{\Gamma }_1+{\Gamma }_2$.

Proof. 

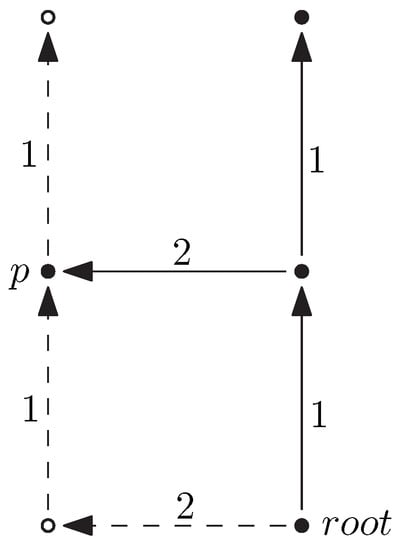
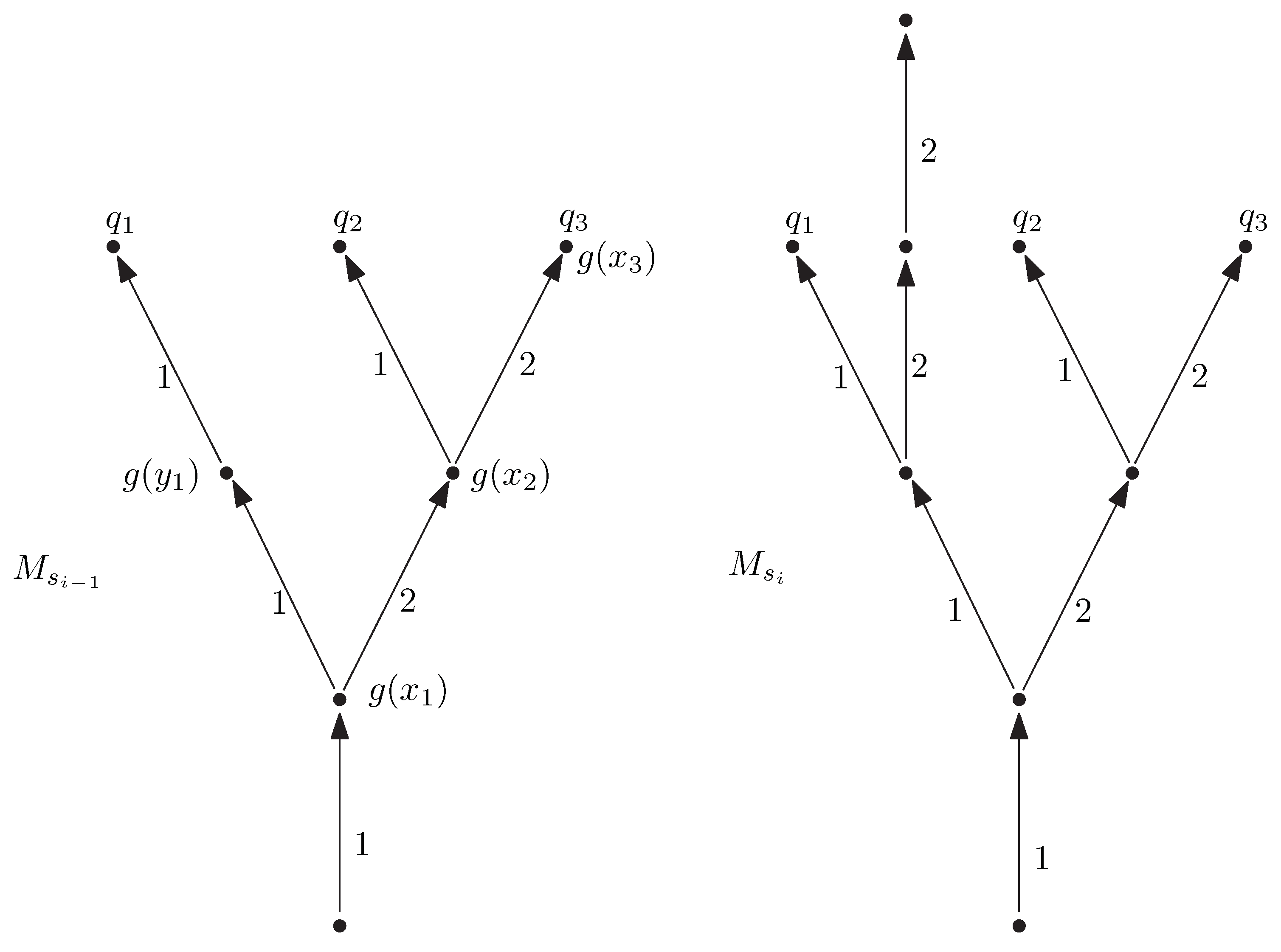
Suppose that h is a rooted homomorphism from $M_t$ into $Chase(M_s,PosChR1\cup PosChR2\cup Com)$. Suppose that $\beta$ is a point of $M_t$ such that $h\left(\beta \right)$ is an anonymous point of type 1 in $Chase(M_s,PosChR1\cup PosChR2\cup Com)$ introduced by $Com12$ by trigger g (defined on $\left\{x,y,z\right\}$). Suppose that $\alpha$ is the predecessor of $\beta$ in $M_t$ and ${\gamma }_1,\dots ,{\gamma }_m$ are successors of $\beta$ in $M_t$. Note that this can happen only in case $(\alpha ,\beta )\in M_t.R_2$, $(\beta ,{\gamma }_i)\in M_t.R_1$ for $1\le i\le m$, and all $h\left({\gamma }_i\right)$ are equal. We say that a homomorphism $h^{\prime }$ from $M_{t^{\prime }}$ into $Chase(M_s,PosChR1\cup PosChR2\cup Com)$ is obtained by $co{m}_{12}$-surgery of h at $\alpha$ if

• $M_{t^{\prime }}$ is obtained from $M_t$ by changing

  -

  $R_2$-arrow between $\alpha$ and $\beta$ into $R_1$-arrow

  -

  $R_1$-arrows between $\beta$ and ${\gamma }_i$ into $R_2$-arrows for $1\le i\le m$

  -

  terms ‘sitting’ at ${\gamma }_i$ in $M_t$ into their conjunction.

• $h^{\prime }$ coincides with h on all points except $\beta$
• $h^{\prime }\left(\beta \right)=g\left(y\right)$ (here g is the trigger, and y is a variable of $Com12$).

We argue that in this case, the implication $t^{\prime }\to t$ is derivable in $K_2^{+}+co{m}_{12}$. Indeed, we take the axiom ${\diamond }_1{\diamond }_{2}p\to {\diamond }_2{\diamond }_{1}p$, apply the substitution $p:=t_{\gamma }$, inclusion ${\diamond }_1{t}_{\gamma }\to {\diamond }_1{t}_{\gamma }\wedge \dots {\diamond }_1{t}_{\gamma }$ ‘weakening’ from $t_{\gamma }$ to $t_{{\gamma }_i}$, and then we ‘grow’ the common part of h and $h^{\prime }$ by the rules

$$\frac{\sigma \to \tau \sigma \to \varrho }{\sigma \to \tau \wedge \varrho },\frac{\sigma \to \tau }{\diamond \sigma \to \diamond \tau }.$$

We similarly define $co{m}_{21}$-surgeries and argue that by a sequence of surgeries, h may be reduced to a homomorphism $h^{*}$ from $t^{*}$ into $Chase(M_s,PosChR1\cup PosChR2\cup Com)$, which does not use any points of type 1. Thus we can apply Lemma 5 and derive the implication $s\to t^{*}$ as well as implications between the terms $t^{\prime }$ corresponding to the intermediate steps of the surgeries. Finally, we apply the rule a few times

$$\frac{\sigma \to \tau \tau \to \varrho }{\sigma \to \varrho }.$$

This argument is illustrated in Figure 5. □

Figure 5. To derive ${\diamond }_1({\diamond }_{2}p\wedge {\diamond }_1\top )\to {\diamond }_2{\diamond }_1(p\wedge {\diamond }_1\top )$ in $K_2^{+}+co{m}_{12}+co{m}_{21}+{\Gamma }_1+{\Gamma }_2$ we first derive ${\diamond }_1({\diamond }_{2}p\wedge {\diamond }_1\top )\to {\diamond }_1{\diamond }_2(p\wedge {\diamond }_1\top )$ and then ${\diamond }_1{\diamond }_2(p\wedge {\diamond }_1\top )\to {\diamond }_2{\diamond }_1(p\wedge {\diamond }_1\top )$.

Proof of Theorem 5.

Inclusion from right to left is proved in Lemma 4.

Now, take a strictly positive implication $s\to t$ such that $s\to t\in \mathbf{K}\times \mathbf{K}$. By Proposition 3, it follows that $Chase(M_s,ChRos\cup Com),root\models t$. Therefore, there exists a rooted homomorphism h from $M_t$ into $Chase(M_s,ChRos\cup Com)$. Now, we argue that there exists a homomorphism $h^{\prime }$ from $M_t$ into $Chase(M_s,PosChR1\cup PosChR2\cup Com)$. Suppose that $R_1(x,y)$ holds in $M_t$, $h\left(x\right)$ is not anonymous, but $h\left(y\right)$ is anonymous of type 2. By the iterative application of Lemma 9, we obtain that $|t_y{|}_1\le {\mathrm{depth}}_1(M_s,x)-1$ and $|t_y{|}_2\le {\mathrm{depth}}_2(M_s,x)$. Therefore, by Lemma 8 there exists a homomorphism $h_{xy}^{\prime }$ from the subtree of $M_t$ at x in the direction of y into $Chase(M_s,PosChR1\cup PosChR2\cup Com)$, sending x to $h\left(x\right)$. We similarly deal with points x and y such that $R_2(x,y)$ holds in $M_t$, $h\left(x\right)$ is not anonymous, but $h\left(y\right)$ is anonymous of type 2. By applying this argument to all such pairs $(x,y)$ of points of $M_t$, we obtain a homomorphism from $M_t$ into $Chase(M_s,PosChR1\cup PosChR2\cup Com)$. Finally, by Lemma 10, we conclude that $s\to t$ is derivable in $K_2^{+}+co{m}_{12}+co{m}_{21}+{\Gamma }_1+{\Gamma }_2$. □

Theorem 6.

There is no finite set of formulas Φ such tha $SPF(\mathbf{K}\times \mathbf{K})=K_2^{+}+\Phi$.

Proof. 

This follows from the fact that in

$$K_2^{+}+com+chr{1}_1^{+}+chr{2}_1^{+}+\dots +chr{1}_n^{+}+chr{2}_n^{+}$$

the formula $chr{2}_{n+1}^{+}$ is not derivable and a standard argument due to Tarski. □

Theorem 7.

For logics $L_1,L_2\in \left\{\mathbf{D},\mathbf{T},\mathbf{D}\mathbf{4},\mathbf{S}\mathbf{4}\right\}$

$$SPF(L_1\times L_2)=SPF\left(\left[L_1,L_2\right]\right)=K_2^{+}+com+L_1^{\prime }+L_2^{\prime }.$$

where $L_i^{\prime }$ is the set of all additional axioms in $L_i$ with all ⋄ replaced by ${\diamond }_i$.

Proof. 

The main remaining ingredient of the proof is ‘completeness of $K_2^{+}+com+L_1^{\prime }+L_2^{\prime }$ with respect to the corresponding set of TGDS ${\Pi }^{\prime }$’ (${\Pi }^{\prime }$ because $\Pi$ stands for ${\Pi }^{\prime }\cup \left\{ChRos\right\}$). It follows from Theorem 35 of [10], Proposition 3, and Kripke completeness of modal counterparts of logics in question. Indeed, if $h^{\prime }$ is a rooted homomorphism from $M_t$ into $Chase(M_s,{\Pi }^{\prime })$, then by Proposition 3 $s\to t$ is derivable in ${\mathbf{K}}_2+com+L_1^{\prime }+L_2^{\prime }$, and by Theorem 35 (see also the text at the beginning of Section 2 of this paper) of [10] any sp-implication in ${\mathbf{K}}_2+com+L_1^{\prime }+L_2^{\prime }$ is derivable in $K_2^{+}+com+L_1^{\prime }+L_2^{\prime }$.

Now we proceed as before. We assume that s and t are sp-terms such that there is a rooted homomophism h from $M_t$ into $Chase(M_s,\Pi )$. Then using (P2’) for $\Pi$ and the fact that there are no final points in $Chase(M_s,{\Pi }^{\prime })$, we transform h into a rooted homomorphism $h^{\prime }$ from $M_t$ into $Chase(M_s,{\Pi }^{\prime })$. Finally, we apply the corresponding ’completeness statement’ to conclude that $s\to t$ is derivable in $K_2^{+}+com+L_1^{\prime }+L_2^{\prime }$. □

6. Conclusions

In this paper, we develop a technique for axiomatising strictly positive fragments of normal modal logics with confluence axioms $\diamond \square p\to \square \diamond p$ and ${\diamond }_1{\square }_{2}p\to {\square }_2{\diamond }_{1}p$. We apply it to obtain strictly positive axiomatisation for strictly positive fragments of some two-dimensional products of modal logics. Possible directions of future research include axiomatising strictly positive fragments of $\ge 3$-dimensional modal logics and strictly positive fragments of restricted fragments of first-order logic that correspond to products of modal logics directly [18] or indirectly [19]. In the context of cylindrical correspondence [18], products of $\mathbf{S}\mathbf{5}$ (which are not covered in this paper) are particularly interesting because then modal operators are interpreted as quantifiers, and the confluence axiom turns into the principle $\exists x\forall y\varphi (x,y)\to \forall y\exists x\varphi (x,y)$, which plays a crucial role in the axiomatisation of these fragments.