Negativity of Green’s Functions to Focal and Two-Point Boundary Value Problems for Equations of Second Order with Delay and Impulses in Their Derivatives

Abstract

We consider the second-order impulsive differential equation with impulses in derivative and without the damping term. Sufficient conditions that a nontrivial solution of the homogeneous equation having a zero of its derivative does not have a zero itself are obtained. On the basis of the obtained results on differential inequalities, which can be considered as analogues of the Vallee–Poussin theorems, new sufficient conditions on the negativity of Green’s functions are obtained.

1. Introduction

Impulsive differential equations are used in mathematical models of many processes in economical sciences, medicine, physics and biology [1,2,3,4]. Various concepts which can be considered as the basis of our approach are presented in [5,6]. Their development for the positivity of Green’s function for the initial value and periodic problems for first-order functional differential equations can be found in [7] (see also [8] in this context) and for nonlocal problems in [9]. For second-order impulsive equations, results on the positivity of the solutions of one- and two-point boundary value problems can be found in [10,11,12,13,14,15,16,17].

In this paper, we consider the following delay differential equation

$$\left(\pounds x\right)\left(t\right)\equiv x^{″}\left(t\right)+\sum _{j=1}^m{p}_j\left(t\right)x_j\left(h_j\left(t\right)\right)=f\left(t\right),t\in [0,\omega ],$$

(1)

$$x\left(\xi \right)=0\mathrm{for}\xi <0,$$

(2)

with impulses of the first derivative at the points $t_i:0=t_0<t_1<t_2<,\dots ,<t_n<t_{n+1}=\omega$

$$x^{\prime }\left(t_i\right)={\delta }_i{x}^{\prime }(t_i-0),i=1,\dots ,n,$$

(3)

where f, $p_j$: $[0,\omega ]\to \mathbb{R}$ are from the space $L_{\infty }$ of essentially bounded functions and $h_j$:$[0,\omega ]\to (-\infty ,+\infty ),h_j\left(t\right)\le t$ is a measurable function for $j=1,2,\dots ,m$, m and n are natural numbers and ${\delta }_i$ is a real positive number for $i=1,2,\dots ,n$.

Let $D(t_1,t_2,\dots ,t_n)$ be a space of functions x: $[0,\omega ]\to \mathbb{R}$ such that their derivative $x^{\prime }\left(t\right)$ is absolutely continuous on every interval $t\in [t_i,t_{i+1})$, $i=0,1,\dots ,n$, $x^{″}\in L_{\infty }$; we also assume that there exist the finite limits $x^{\prime }(t_i-0)={lim}_{t\to t_i^{-}}{x}^{\prime }\left(t\right)$ and condition (3) is satisfied at points $t_i$$(i=0,1,\dots ,n)$. As a solution x, we understand a function $x\in D(t_1,t_2,\dots ,t_n)$ satisfying (1)–(3).

In this paper, we study the case of $p_j\left(t\right)\ge 0$ for $j=1,\dots ,m$ and ${\delta }_i>1$ for $i=1,\dots ,n,$ which naturally appears in the use of control in the process of a plane’s takeoff based on the feedback control of the height. The autopilot control can be of the form $u\left(t\right)=-$${\sum }_{j=1}^m{p}_j\left(t\right)x_j\left(h_j\left(t\right)\right)$. It is the so-called “slow” control. The direct (“fast”) control is implemented by a pilot, which can be modeled by impulses. It is important to have a sufficiently long length of time interval on which the solution, starting with the initial condition $x\left(0\right)=0$, is increasing, i.e., a semi-nonoscillation interval (focal interval in another terminology) of the homogeneous equation

$$\left(\pounds x\right)\left(t\right)\equiv x^{″}\left(t\right)+\sum _{j=1}^m{p}_j\left(t\right)x_j\left(h_j\left(t\right)\right)=0,t\in [0,\omega ],$$

(4)

$$x\left(\xi \right)=0\mathrm{for}\xi <0.$$

In this paper, estimates of the semi-nonoscillation interval are obtained. Our approach to study the negativity of Green’s functions is based on the nonoscillation properties of solutions. We define the so-called semi-nonoscillation interval in [12] as an interval where a nontrivial solution of the homogeneous equation having a zero of its derivative does not have a zero itself. It is clear that the semi-nonoscillation interval is a corresponding development of the known definition of the focal interval. It is important to estimate the solution $x\left(t\right)$ of problem (1)–(3) with the boundary conditions $x\left(0\right)=0,x^{\prime }\left(\omega \right)=0$ by corresponding test functions $v\left(t\right)$ and $w\left(t\right)$ satisfying the differential inequalities $\left(\pounds v\right)\left(t\right)\le f\left(t\right)\le \left(\pounds w\right)\left(t\right)$ for $t\in [0,\omega ].$ This is the problem of the negativity of Green’s function $G(t,s).$ The sign-constancy of the Green’s function of one-point and two-point boundary value problems for impulsive functional differential equations of the second order was studied in [7,9,10,11,12,18,19].

We study problems with two-point boundary value conditions. The results on the negativity of Green’s function for impulsive two-point problems for Equations (1)–(3) in the case of $p_j\left(t\right)\le 0$ and the case of $p_j\left(t\right)\ge 0$ for $t\in [0,\omega ],$$j=1,\dots ,m,$ were obtained in [11,18,20]. Those results assumed, in explicit or implicit forms, a corresponding smallness of the interval $[0,\omega ].$

As an example of such results, we can note the following (see Corollary $4.6$ in [20]):

If $0<{\delta }_i\le 1$ and

$$\sum _{j=1}^m{p}_j\left(t\right)(\frac{1}{4}+n)<\frac{2}{{\omega }^2}$$

(5)

then the Green’s function $G(t,s)$ of a two-point boundary value problem, i.e., for problem (1)–(3) with boundary condition (8) defined below, satisfies the inequality $G(t,s)<0$ for $t,s\in (0,\omega )$.

We see that in the case of Equation (1) without impulses in its derivatives (i.e., $n=0$ in (1)), we get the classical Vallee–Poussin inequality

$$\sum _{j=1}^m{p}_j\left(t\right)<\frac{8}{{\omega }^2}$$

(6)

for the unique solvability of the two-point problem and negativity of its Green’s function $G(t,s)$. It is known that inequality (6) cannot been improved in a general case. The appearance of impulses, i.e., the case of $n>0$, disproves this inequality.

Our development is in the study of the case of ${\delta }_i>1$. We demonstrate that the impulses in the derivative of this sort can improve the estimates. The estimates of nonoscillation and focal intervals can be essentially increased. For example, for a nonimpulsive ordinary differential equation

$$x^{″}\left(t\right)+px\left(t\right)=0,$$

(7)

where p is a positive constant, the function $sin\left(\sqrt{p}t\right)$ is a nontrivial solution which has focal interval $[0,\frac{\pi }{2\sqrt{p}}]$ and nonoscillation interval $[0,\frac{\pi }{\sqrt{p}}]$. In all sufficient conditions known to us, the impulses disprove the tests of nonoscillation, semi-nonoscillation and negativity of Green’s functions. In contrast with it, in the following, in the examples of Section 5, we see that impulses in the derivative (in the case when ${\delta }_i>1$) increase the focal and nonoscillation intervals of the solution to impulsive equations. Our approach first demonstrates that adding impulses of the derivative could “improve” the so-called non-oscillation properties of solutions and consequently to increase the distances between adjacent zeros of the derivative, adjacent zeros of the solution and the zones of Green’s function negativity. This allows us essentially to improve the exactness of the intervals, where the test functions $v\left(t\right)$ and $w\left(t\right)$ estimate the solution. It is important for building a control strategy in applications.

2. Preliminaries

For Equations (1)–(3), we consider the following variants of the boundary conditions:

$$x\left(0\right)=0,x\left(\omega \right)=0,$$

(8)

$$x\left(0\right)=0,x^{\prime }\left(\omega \right)=0,$$

(9)

A general solution of Equations (1)–(3) can be represented in the form [7]:

$$x\left(t\right)={\nu }_1\left(t\right)x\left(0\right)+C(t,0)x^{\prime }\left(0\right)+{\int }_0^{t}C(t,s)f\left(s\right)ds,$$

(10)

where

• ${\nu }_1\left(t\right)$ is a solution of the homogeneous Equation (4) with the initial conditions $x\left(0\right)=1$, $x^{\prime }\left(0\right)=0$.
• $C(t,s)$, called the Cauchy function of Equation (4), is the solution of the equation

  $$\left(L_{s}x\right)\left(t\right)\equiv x^{″}\left(t\right)+\sum _{j=1}^m{p}_j\left(t\right)x_j\left(h_j\left(t\right)\right)=0,t\in [s,\omega ],$$

  (11)

  $$\begin{array}{cc}& x^{\prime }\left(t_i\right)={\delta }_i{x}^{\prime }(t_i-0),i=k,\dots ,n,\hfill \\ & 0=t_0<t_1<t_2<,\dots ,<t_n<t_{n+1}=\omega ,\hfill \end{array}$$

  (12)

  for every fixed $s\ge 0$, where k is a number, such that $t_{k-1}<s\le t_k$,

  $$x\left(\zeta \right)=0,\zeta <s,$$

  (13)

  satisfying the initial conditions $C(s,s)=0$, $C_t^{\prime }(s,s)=1$ and $C(t,s)=0$ for $t<s$.

If the boundary value problem (1)–(3), with boundary conditions (8) or (9) respectively, is uniquely solvable, then its solution can be represented as

$$x\left(t\right)={\int }_0^{\omega }{G}_i(t,s)f\left(s\right)ds,i=1,2,$$

(14)

where $G_i(t,s)$ is the Green’s function of the problem (1)–(3), with boundary conditions (8) or (9) respectively [11].

Using the general representation of solution (10), the following formulas for Green’s functions can be obtained:

$$G_1(t,s)=C(t,s)-C(t,0)\frac{C(\omega ,s)}{C(\omega ,0)},$$

(15)

$$G_2(t,s)=C(t,s)-C(t,0)\frac{C_t^{\prime }(\omega ,s)}{C_t^{\prime }(\omega ,0)},$$

(16)

3. Formulation of Main Results

Consider the auxiliary problem

$$\left\{\begin{array}{c}{v}^{″}\left(t\right)=z\left(t\right),\hfill \\ v\left(0\right)=0,v^{\prime }\left(\omega \right)=0.\hfill \end{array}\right.$$

(17)

Let us define the operator $K:L_{\infty }[0,\omega ]\to L_{\infty }[0,\omega ]$, where $L_{\infty }$ is a space of essentially bounded functions $x:[0,\omega ]\to \mathbb{R}$, by the equality

$$\left(Kz\right)\left(t\right)=-\sum _{j=1}^m{p}_j\left(t\right)\left[{\int }_0^{\omega }{G}_0(h_j\left(t\right),s)z\left(s\right)ds\right],$$

(18)

where $G_0(t,s)$ is the Green’s function of problem (17). We assume that $G_0(h_j\left(t\right),s)=0$ for $h_j\left(t\right)<0$.

Theorem 1.

Let $p_j\left(t\right)\ge 0$ for $t\in [0,\omega ]$, $j=1,\dots ,m$. Then, the following assertions are equivalent:

(1) 

There exists a function $v\left(t\right)\in D(t_1,t_2,\dots ,t_n)$ such that

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left(\pounds v\right)\left(t\right)=\psi \left(t\right)\le -ϵ<0,v\left(t\right)>0,v^{\prime }\left(t\right)>0,v^{″}\left(t\right)<0,\\ \hfill t\in (0,t_1)\cup (t_1,t_2)\cup \dots \cup (t_{n-1},t_n)\cup (t_n,\omega ),\end{array}\end{array}$$

(19)

where the differential operator £ is defined by (1).

(2) 

The spectral radius $\rho \left(K\right)$ of the operator $K:L_{\infty }[0,\omega ]\to L_{\infty }[0,\omega ]$ is less than one.

(3) 

The problem (1)–(3) with boundary condition (9) is uniquely solvable and its Green’s function $G_2(t,s)$ satisfies the inequality $G_2(t,s)<0$ for $(t,s)\in (0,\omega )$×$(0,\omega )$.

Remark 1.

The following assertion can be also considered:

(4) 

Let ${\sum }_{j=1}^m{p}_j\left(t\right)\sigma (h_j\left(t\right),0)>0$ for $t\in [0,\omega ]$, $j=1,\dots ,m,$ and there exists a function $v\left(t\right)\in D(t_1,t_2,\dots ,t_n)$ such that

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left(\pounds v\right)\left(t\right)=\psi \left(t\right)\le 0,v\left(t\right)>0,v^{\prime }\left(t\right)>0,v^{″}\left(t\right)<0,\\ \hfill t\in (0,t_1)\cup (t_1,t_2)\cup \dots \cup (t_{n-1},t_n)\cup (t_n,\omega ),v\left(0\right)+v^{\prime }\left(\omega \right)>0,\end{array}\end{array}$$

(20)

where the differential operator £ is defined by (1).

If we compare assertions (1) and $\left(4\right)$, it is clear that we assume in $\left(4\right):v\left(0\right)+v^{\prime }\left(\omega \right)>0$ instead of the condition of strict negativity of $\psi \left(t\right)$.

It can be proven that assertions (2) and (3) follow from assertion (4).

It is clear now that the choice of the function $v\left(t\right)$ in the condition of Theorem 1 allows us to obtain tests of the negativity of the Green’s function $G(t,s)$ of the problem (1)–(3) with boundary condition (9).

Remark 2.

The assertion (1)=>(3) can be considered as an analog of the Vallee–Poussin theorem about the differential inequality for second-order impulsive equations.

Remark 3.

In a general case the process of construction of the test function $v\left(t\right)$ is complicated. The calculations made below, before the proof of Theorem 4, explain how the test function $v\left(t\right)$ can be constructed and how the explicit conditions guaranteeing the condition $\rho \left(K\right)<1$ can be obtained. Of course, these conditions are more complicated than condition (5) and include restrictions on the smallness of the distance between adjacent points of impulses.

We propose a new idea to choose $v\left(t\right)$, using a solution of the ordinary impulsive differential equation

$$\left(Mx\right)\left(t\right)\equiv x^{″}\left(t\right)+\left\{\sum _{j=1}^m{p}_j\left(t\right)\right\}x\left(t\right)=0,t\in [0,\omega ]$$

(21)

$$x\left(\xi \right)=0\mathrm{for}\xi <0,$$

(22)

$$x^{\prime }\left(t_i\right)={\delta }_i{x}^{\prime }(t_i-0),i=1,\dots ,n.$$

(23)

Let us define the function:

$$\sigma (t,s)=\left\{\begin{array}{c}1,t\ge s,\hfill \\ 0,t<s.\hfill \end{array}\right.$$

(24)

The influence of the fact that $[0,\omega ]$ is a semi-nonoscillation interval on the negativity of the Green’s function of problem (1)–(3) with boundary condition (9) can be explained by the next assertion.

Theorem 2.

If ${\sum }_{j=1}^m{p}_j\left(t\right)\sigma (h_j\left(t\right),0)>0$ for $t\in [0,\omega ]$, and $[0,\omega ]$ is a semi-nonoscillation interval of the solution of (21)–(23), (9), then the Green’s function of problem (1)–(3) with boundary condition (9) is negative for $t,s\in (0,\omega ).$

The clear relation between the negativity of Green’s function $G_1(t,s)$ and the negativity of the Green’s functions of problems with the boundary conditions $x\left(0\right)=0,x^{\prime }\left(a\right)=0$ for every $a:0<a<\omega$ can be done by the following assertion.

Theorem 3.

If the Green’s function of the problem consisting of Equations (1)–(3) and boundary conditions $x\left(0\right)=0,x^{\prime }\left(a\right)=0$ for every $a:0<a<\omega$ is negative for $t,s\in (0,a)$, and $[0,a]$ is a semi-nonoscillation interval of the solution of (21)–(23), then the Green’s function of problem (1)–(3), (8) is nonpositive for $t,s\in (0,\omega )$.

We propose the following test for the negativity of Green’s functions. Consider the equation

$$\left(\pounds x\right)\left(t\right)\equiv x^{″}\left(t\right)+px\left(h\left(t\right)\right)=0,h\left(t\right)\le t,t\in [0,\omega ],$$

(25)

where

$$x\left(\xi \right)=0for\xi <0,$$

and p is a positive constant.

Theorem 4.

Let p be positive and the distance $t_{i+1}-t_i$ between two adjacent points of impulses satisfy the inequalities

$$\begin{array}{c}{t}_{i+1}-t_i<\frac{\pi }{2\sqrt{p}}-\frac{1}{\sqrt{p}}arctan(\frac{1}{{\delta }_i}tan(\sqrt{p}(t_i-t_{i-1}-\frac{1}{\sqrt{p}}arctan(\frac{1}{{\delta }_{i-1}}tan\left(\sqrt{p}\right(t_{i-1}-t_{i-2}-\dots \hfill \\ \hfill -\frac{1}{\sqrt{p}}arctan(\frac{1}{{\delta }_1}tan(\sqrt{p}(t_1-{\alpha }_0)\dots ),i=0,1,2,\dots ,n,\end{array}$$

(26)

where $t_0=0,t_{n+1}=\omega .$

Then, $[0,\omega ]$ is a semi-nonoscillation interval of the solution of Equation (25) and the Green’s functions of the impulsive problems

$$\left(\pounds x\right)\left(t\right)=f\left(t\right),t\in [0,\omega ],x\left(0\right)=0,x^{\prime }\left(\omega \right)=0$$

(27)

and

$$\left(\pounds x\right)\left(t\right)=f\left(t\right),t\in [0,\omega ],x\left(0\right)=0,x\left(\omega \right)=0$$

(28)

with impulses defined by (3) are negative for $(t,s)\in (0,\omega )$×$(0,\omega )$.

4. Proofs

Proof of Theorem 1.

 

(1)=>(2)

In (1) we have the function $v\in D(t_1,t_2,\dots ,t_n)$ satisfying the inequality

$$\left(\pounds v\right)\left(t\right)=\psi \left(t\right)\le -ϵ<0.$$

(29)

The function $v\left(t\right)$ can be written in the form

$$v\left(t\right)={\int }_0^{\omega }{G}_0(t,s)z\left(s\right)ds+u\left(t\right),$$

(30)

where $G_0(t,s)$ is the Green’s function of (17) and $u\left(t\right)$ is a solution of

$$\left\{\begin{array}{c}{u}^{″}\left(t\right)=0,t\in [0,\omega ],\hfill \\ u\left(0\right)=v\left(0\right)\ge 0,u^{\prime }\left(\omega \right)=v^{\prime }\left(\omega \right)\ge 0.\hfill \end{array}\right.$$

(31)

It follows from (17) that the condition $v^{″}\left(t\right)<0$ implies that $z\left(t\right)<0$ for $t\in (0,\omega )$. Substituting the presentation of solution (30) into (29), we get

$$z\left(t\right)+\sum _{j=1}^m{p}_j\left(t\right)\left[{\int }_0^{\omega }{G}_0(h_j\left(t\right),s)z\left(s\right)ds\right]=\eta \left(t\right),t\in [0,\omega ],$$

(32)

where $\eta \left(t\right)=\psi \left(t\right)-{\sum }_{j=1}^m{p}_j\left(t\right)u\left(h_j\left(t\right)\right)$.

Let us denote

$$\tilde{z}\left(t\right)=-z\left(t\right),\tilde{\eta }\left(t\right)=-\eta \left(t\right),\tilde{\psi }\left(t\right)=-\psi \left(t\right)$$

(33)

and rewrite (32) in the form

$$\tilde{z}\left(t\right)-\sum _{j=1}^m{p}_j\left(t\right)[{\int }_0^{\omega }|G_0(h_j\left(t\right),s)\left|\tilde{z}\left(s\right)ds\right]=\tilde{\eta }\left(t\right),t\in [0,\omega ],$$

(34)

It is clear that $\tilde{\eta }\left(t\right)={\sum }_{j=1}^m{p}_j\left(t\right)u\left(h_j\left(t\right)\right)+\tilde{\psi }\left(t\right)>0$. Thus, from [21] (p. 86) we can conclude that the spectral radius $\rho \left(K\right)$ of the operator K is less than one.

(2)=>(3)

Consider the problem consisting of the equation

$$\left(\pounds x\right)\left(t\right)=f\left(t\right),t\in [0,\omega ]$$

(35)

with impulses (3) and boundary condition (9).

Assume that $f\in L_{\infty }[0,\omega ]$ is nonpositive for $t\in [0,\omega ]$.

After the substitution

$$x\left(t\right)={\int }_0^{\omega }{G}_0(t,s)z\left(s\right)ds,$$

(36)

we have

$$z\left(t\right)+\sum _{j=1}^m{p}_j\left(t\right)\left[{\int }_0^{\omega }{G}_0(t,s)z\left(s\right)ds\right]=f\left(t\right).$$

(37)

If the spectral radius $\rho \left(K\right)$ of the positive operator $K:L_{\infty }[0,\omega ]\to L_{\infty }[0,\omega ]$ is less than one, then there exists a bounded operator ${(I-K)}^{-1}=I+K+K^2+K^3+$… $:L_{\infty }[0,\omega ]\to L_{\infty }[0,\omega ]$ which is positive. This implies that $z\left(t\right)={(I-K)}^{-1}f$ is nonpositive for every nonpositive $f\left(t\right),t\in [0,\omega ]$.

According to representation (14), we have

$$x\left(t\right)={\int }_0^{\omega }{G}_2(t,s)f\left(s\right)ds,$$

(38)

and on the other hand,

$$x\left(t\right)={\int }_0^{\omega }{G}_0(t,s){(I-K)}^{-1}f\left(s\right)ds.$$

(39)

Thus,

$$\begin{array}{c}\hfill x\left(t\right)={\int }_0^{\omega }{G}_2(t,s)f\left(s\right)ds={\int }_0^{\omega }{G}_0(t,s){(I-K)}^{-1}f\left(s\right)ds={\int }_0^{\omega }{G}_0(t,s)[I+K+K^2+K^3+\dots ]f\left(s\right)ds\ge 0\end{array}$$

(40)

It is clear now that $G_2(t,s)<G_0(t,s)<0$ for $(t,s)\in (0,\omega )$×$(0,\omega )$.

(3)=>(1)

In order to prove this, we set ${\displaystyle v\left(t\right)=-{\int }_0^t{G}_2(t,s)ds}$ in the assertion (1).

This completes the proof of Theorem 1. □

The proof of the assertion in Remark 1 is obvious. It can be made by repeating the proof of the implication (1)=>(2). Note that $u\left(t\right)>0$ and ${\sum }_{j=1}^m{p}_j\left(t\right)u\left(h_j\left(t\right)\right)>0$ for $t\in (0,\omega ]$.

Proof of Theorem 2.

 

Let us take the solution $x\left(t\right)$ of Equations (1)–(3) satisfying the initial conditions $x\left(0\right)=0,x^{\prime }\left(0\right)=1$ as a function $v\left(t\right)$ in the assertion $1)$ of Theorem 1. This function $v\left(t\right)$ is positive and its derivative $v^{\prime }\left(t\right)$ is positive in every one of the intervals $(t_i,t_{i+1})$, since $[0,\omega ]$ is a semi-nonoscillation interval of the solution of Equations (1)–(3), and its second derivative $v^{″}\left(t\right)$ is negative since $v^{″}\left(t\right)=-{\sum }_{j=1}^m{p}_j\left(t\right)v\left(h_j\left(t\right)\right)<0.$ The reference to Remark 1 completes the proof. □

Proof of Theorem 3.

 

Let us assume, on the contrary, that the Green’s function $G_1(t,s)$ of problem (1)–(3) with boundary condition (8) changes its sign on the interval $(0,\omega )$. Then, for a corresponding $f\left(t\right)\ge 0$ the solution $x\left(t\right)$ of (1)–(3) with boundary condition (8) changes it sign at some point $b\in (0,\omega )$.

It follows from our assumption that there exists a point $a:0<b<a<\omega$ such that the solution $x\left(t\right)$ satisfies the boundary value problem consisting of Equations (1)–(3) and boundary conditions $x\left(0\right)=0,x^{\prime }\left(a\right)=0$. Its Green’s function is negative for $(t,s)\in (0,a)$×$(0,a)$.

This implies that $x\left(t\right)<0$ for $t\in (0,a]$, and we have a contradiction with the assumption about the change of sign of the solution $x\left(t\right)$. □

Consider the ordinary differential equation of second order with constant positive p and the impulses

$$x^{″}\left(t\right)+px\left(t\right)=0,t\in [0,\omega ],$$

(41)

$$x^{\prime }\left(t_i\right)={\delta }_i{x}^{\prime }(t_i-0),i=1,2,\dots ,n,$$

with the initial conditions

$$x\left(0\right)=0,x^{\prime }\left(0\right)=\sqrt{p}.$$

Let us construct its solution and this is the basis of the proof of Theorem 4 which is given below.

On the interval $[0,t_1)$, we have

$$x\left(t\right)=sin\left(\sqrt{p}(t-{\alpha }_0)\right),$$

(42)

$$x^{\prime }\left(t\right)=\sqrt{p}cos\left(\sqrt{p}(t-{\alpha }_0)\right),$$

(43)

where ${\alpha }_0=0$. Let us assume that $t_1<\frac{\pi }{2\sqrt{p}}$. On the next interval $[t_1,t_2)$, we search for a solution of the form

$$x\left(t\right)=A_{1}sin\left(\sqrt{p}(t_1-{\alpha }_1)\right).$$

(44)

Taking into account that $x\left(t\right)$ has to be continuous but $x^{\prime }\left(t\right)$ has an impulse at the point $t_1$, we come to the equalities

$$sin\left(\sqrt{p}(t_1-{\alpha }_0)\right)=A_{1}sin\left(\sqrt{p}(t_1-{\alpha }_1)\right),$$

(45)

$${\delta }_1\sqrt{p}cos\left(\sqrt{p}(t_1-{\alpha }_0)\right)=A_1\sqrt{p}cos\left(\sqrt{p}(t_1-{\alpha }_1)\right).$$

(46)

Using (45) and (46), we obtain

$$tan\left(\sqrt{p}(t_1-{\alpha }_1)\right)=\frac{1}{{\delta }_1}tan\left(\sqrt{p}(t_1-{\alpha }_0)\right)$$

(47)

and

$$t_1-{\alpha }_1=\frac{1}{\sqrt{p}}arctan(\frac{1}{{\delta }_1}tan\left(\sqrt{p}(t_1-{\alpha }_0)\right)).$$

(48)

Assuming

$${\alpha }_1+\frac{\pi }{2\sqrt{p}}>t_2,$$

(49)

one can derive that

$$t_2-t_1<\frac{\pi }{2\sqrt{p}}-\frac{1}{\sqrt{p}}arctan(\frac{1}{{\delta }_1}tan\left(\sqrt{p}(t_1-{\alpha }_0)\right)).$$

(50)

Thus, on the interval $[t_1,t_2)$ we have:

$$x\left(t\right)=sin\left(\sqrt{p}(t-{\alpha }_1)\right),$$

(51)

$$x^{\prime }\left(t\right)=\sqrt{p}cos\left(\sqrt{p}(t-{\alpha }_1)\right).$$

(52)

Then, we obtain at the point $t_2$

$$x\left(t_2\right)=sin\left(\sqrt{p}(t_2-{\alpha }_1)\right),$$

(53)

$$x^{\prime }\left(t_2\right)={\delta }_2\sqrt{p}cos\left(\sqrt{p}(t_2-{\alpha }_1)\right),$$

(54)

and consequently

$$sin\left(\sqrt{p}(t_2-{\alpha }_1)\right)=A_{1}sin\left(\sqrt{p}(t_2-{\alpha }_2)\right),$$

(55)

$${\delta }_2\sqrt{p}cos\left(\sqrt{p}(t_2-{\alpha }_1)\right)=A_1\sqrt{p}cos\left(\sqrt{p}(t_2-{\alpha }_2)\right).$$

(56)

Using (55) and (56), we obtain

$$tan\left(\sqrt{p}(t_2-{\alpha }_2)\right)=\frac{1}{{\delta }_2}tan\left(\sqrt{p}(t_2-{\alpha }_1)\right)$$

(57)

and

$$t_2-{\alpha }_2=\frac{1}{\sqrt{p}}arctan(\frac{1}{{\delta }_2}tan\left(\sqrt{p}(t_2-{\alpha }_1)\right)).$$

(58)

Assuming

$${\alpha }_2+\frac{\pi }{2\sqrt{p}}>t_3,$$

(59)

one can derive that

$$t_3-t_2<\frac{\pi }{2\sqrt{p}}-\frac{1}{\sqrt{p}}arctan(\frac{1}{{\delta }_2}tan\left(\sqrt{p}(t_2-t_1-\frac{1}{\sqrt{p}}arctan(\frac{1}{{\delta }_1}tan\left(\sqrt{p}(t_1-{\alpha }_0)\right)))\right)).$$

(60)

Eventually, such iterations lead us to the following inequality

$$\begin{array}{c}{t}_{i+1}-t_i<\frac{\pi }{2\sqrt{p}}-\frac{1}{\sqrt{p}}arctan(\frac{1}{{\delta }_i}tan(\sqrt{p}(t_i-t_{i-1}-\frac{1}{\sqrt{p}}arctan(\frac{1}{{\delta }_{i-1}}tan\left(\sqrt{p}\right(t_{i-1}-t_{i-2}-\dots \hfill \\ \hfill -\frac{1}{\sqrt{p}}arctan(\frac{1}{{\delta }_1}tan(\sqrt{p}(t_1-{\alpha }_0)\dots ),i=0,1,2,\dots ,n.\end{array}$$

(61)

Proof of Theorem 4.

 

Let us set the solution of ordinary Equation (41) constructed above instead of $v\left(t\right)$ in assertion (1) of Theorem 1. The function $v\left(t\right)$ increases and this allows us to write

$$\left(\pounds v\right)\left(t\right)\equiv v^{″}\left(t\right)+p\left(t\right)v\left(h\left(t\right)\right)\le v^{″}\left(t\right)+p\left(t\right)v\left(t\right)=0,t\in [0,\omega ],$$

(62)

since $h\left(t\right)\le t$.

It is clear now that this function $v\left(t\right)$ satisfies the assertion $1)$ of Theorem 1 from which all the assertions of Theorem 4 follow. □

5. Computation Results

In this section, we construct the function $v\left(t\right)$ in condition (1) of Theorem 1 as a solution of the ordinary impulsive differential equation

$$v^{″}\left(t\right)+pv\left(t\right)=0,t\in [0,\omega ],$$

(63)

$$v^{\prime }\left(t_i\right)={\delta }_i{v}^{\prime }(t_i-0),i=1,2,\dots ,n,$$

where p is a real positive constant, $v\left(0\right)=0,v^{\prime }\left(\omega \right)=0$ and $t_i$ are points at which the derivative $v^{\prime }\left(t\right)$ has impulses. If we assume that $\sqrt{p}(t-{\alpha }_i)<\frac{\pi }{2}$, then the solution of (63) on the interval $[t_i,t_{i+1})$ can be written in the form

$$v\left(t\right)=A_{i}sin\left(\sqrt{p}(t-{\alpha }_i)\right).$$

(64)

Let us assume, for simplicity, that the distances between impulses are equal to each other (i.e., $t_i=i\tau$, where $\tau$ is the distance between the points of impulses). The following equalities are fulfilled at the points $t_i$:

$$A_{i+1}sin\left(\sqrt{p}((i+1)\tau -{\alpha }_{i+1})\right)=A_{i}sin\left(\sqrt{p}((i+1)\tau -{\alpha }_i)\right),$$

(65)

$$A_{i+1}cos\left(\sqrt{p}((i+1)\tau -{\alpha }_{i+1})\right)={\delta }_i{A}_{i}cos\left(\sqrt{p}((i+1)\tau -{\alpha }_i)\right).$$

(66)

Denoting $a_i=sin\left(\sqrt{p}((i+1)\tau -{\alpha }_i)\right)$, $b_i={\delta }_{i}cos\left(\sqrt{p}((i+1)\tau -{\alpha }_i)\right)$, we obtain the formula for finding the amplitudes $A_i$:

$$A_{i+1}=A_i\sqrt{a_i^2+b_i^2},i=1,2,3,\dots ,n.$$

(67)

From (65) and (66), we obtain

$$sin\left(\sqrt{p}((i+1)\tau -{\alpha }_{i+1})\right)=\frac{A_{i}sin\left(\sqrt{p}((i+1)\tau -{\alpha }_i)\right)}{A_{i+1}}=\frac{a_i}{\sqrt{a_i^2+b_i^2}},$$

(68)

$$cos\left(\sqrt{p}((i+1)\tau -{\alpha }_{i+1})\right)=\frac{{\delta }_i{A}_{i}cos\left(\sqrt{p}((i+1)\tau -{\alpha }_i)\right)}{A_{i+1}}=\frac{b_i}{\sqrt{a_i^2+b_i^2}}.$$

(69)

Thus, using (68) we have

$${\alpha }_{i+1}=\left\{\begin{array}{c}(i+1)\tau -\frac{1}{\sqrt{p}}arcsin\frac{a_i}{\sqrt{a_i^2+b_i^2}},if{b}_{i}cos(arcsin\frac{a_i}{\sqrt{a_i^2+b_i^2}})\ge 0,\hfill \\ (i+1)\tau -\frac{1}{\sqrt{p}}(\pi -arcsin\frac{a_i}{\sqrt{a_i^2+b_i^2}}),otherwise.\hfill \end{array}\right.$$

(70)

The program based on this algorithm (we took $p=1$ and the maximal amplitude of $v\left(t\right)$ was $A_{max}=$10,500) gives the connection between impulse constant of the derivative ${\delta }_i=\delta$$(i=1,\dots ,n)$ and the maximal possible distance $\tau$ between every two adjacent points of impulses, which provides the required amplitude $A_{max}$. The maximal amplitude $A_{max}$ describes in the application the cruising altitude of the plane after completing the takeoff process (see Figure 1).

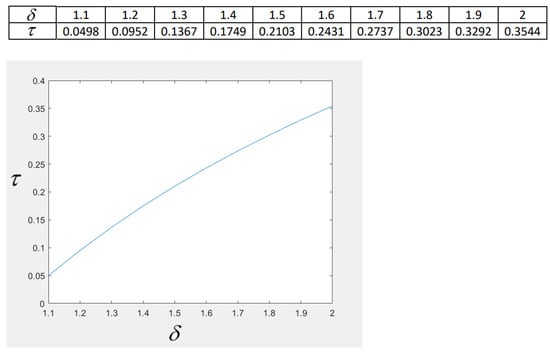
Figure 1. Connection between impulse of derivative $\delta$ and the maximal possible distance between points of impulses $\tau$.

We see that in the nonimpulsive case (Figure 2), the length of the interval where the function $x\left(t\right)$ stays positive and increasing is $\frac{\pi }{2}$, while in the impulsive case (Figure 3), the length of this interval is more than $9.8$ (≈3.12 $\pi$).

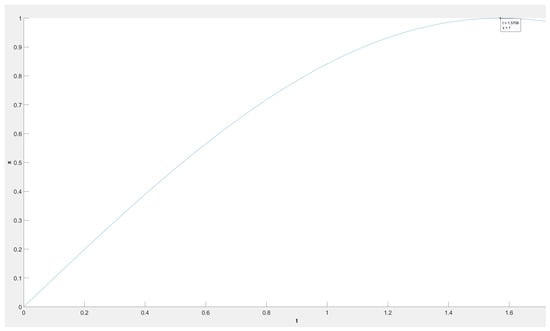
Figure 2. Solution without impulses of the derivative of $x\left(t\right)$.

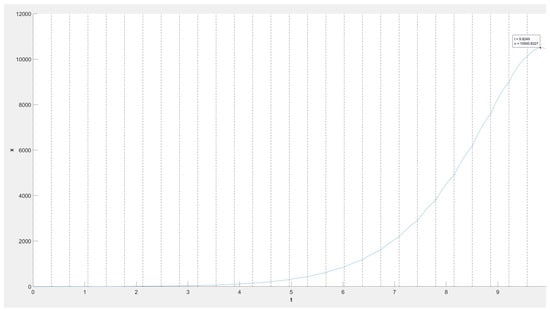
Figure 3. Solution with impulses of the derivative of $x\left(t\right)$ ($\delta =2,\tau =0.3544$).

Thus, it is possible to enlarge the interval where solution $x\left(t\right)$ is positive, using the impulses of the derivative $x^{\prime }\left(t\right)$. In the application of a plane’s takeoff, the cruising altitude $A_{max}$ and limited takeoff angle are given. Then, the problem of the enlargement of the interval, on which the solution $x\left(t\right)$ is increasing, becomes important. We proposed an approach to this enlargement using impulses in the derivative of $x\left(t\right)$.

6. Conclusions

In this paper, we obtained sufficient conditions of the semi-nonoscillation of the solution of the homogeneous Equation (4) with initial function defined by (2) and impulses of the first derivative at the points $t_i:0=t_0<t_1<t_2<,\dots ,<t_n<t_{n+1}=\omega$ defined by (3).

We demonstrated that adding impulses in the derivative could significantly enlarge the length of the interval where a positive solution increased. It should be stressed that our results are the first ones of this type. Using these results, we formulated theorems on differential inequalities and the sign-constancy of Green’s functions for two-point boundary value problems.

The future developments of these results could be in their generalization to systems of impulsive equations and to nonlinear impulsive equations. The negativity of Green’s functions presents the basis for these developments.