Abstract
With the rapid development of cloud computing and mobile networks, more and more application scenarios require a secret group key for secure communication. Group Key Exchange (GKE) protocol provides a secret group key for three or more members. Burmester and Desmedt presented an influential GKE protocol, which has a broadcast version and a cyclic version. In this paper, we investigate the security weaknesses of the Burmester-Desmedt protocol. We report that both the broadcast version and the cyclic version of the Burmester-Desmedt protocol suffer member tampering attacks if the two members that belong to both group A and group B are corrupted. That is, two corrupted members can add some unknowing members of group A to group B and trick the legal members of group B to believe that these unknowing members share the secret group key with them after a protocol run. Furthermore, to defeat the member tampering attack, we propose digital signature-based improvements on the broadcast version and the cyclic version of the Burmester-Desmedt protocol. We hope our research results will encourage the development of more robust and effective GKE protocols that stand rigorous security analysis.
Keywords:
group key exchange; member tampering attack; scalability; security protocol; security analysis MSC:
68M12
1. Introduction
Group Key Exchange (GKE) protocol makes an extension for the traditional two-member key establishment [1]. The function of the GKE protocol is to provide a shared secret group key for three or more members. With the rapid development of cloud computing and mobile networks, more and more application scenarios require group communication. Naturally, the security of group communication depends on the security of the group key [2,3]. We can summarize the general requirements of the GKE protocols as follows.
- (1)
- Members in various groups generate different shared secret group keys (also named group session keys).
- (2)
- The group session key is dynamic and can be updated as needed.
- (3)
- The protocol messages exchanged among the members are open and via the public channel.
- (4)
- Each member calculates his group session key independently.
To realize group key generation, an obvious method is to deploy a Trusted Third Party (TTP) recognized by all members in a group communication system. Moreover, each member shares a secret key with the TTP in advance. When the group session key needs to be established, the TTP randomly generates a group session key, determines the group of members and encrypts the group session key by using the shared secret key with each member. Upon receiving the ciphertext of the group session key, each member in the group can decrypt it using his shared key and obtain the group session key. The disadvantage of this method is that there must be a TTP to provide group key generation services for all members in real-time. That is, the online TTP means heavy computation and communication overhead and may become the technical bottleneck.
Another optional method that does not require a TTP is to choose a member of the group as the group controller. The group controller negotiates a secret Diffie-Hellman key [4] with each member of the group. Then, the group controller randomly generates a group session key, uses each Diffie-Hellman key to encrypt the group session key, and sends it to each member of the group. After receiving the ciphertext of the group session key, the members can respectively decrypt the group session key using its own Diffie-Hellman key. The disadvantage of this method is that the large overhead of computation and communication is a burden on the group controller, and the members of the group need to designate a group controller before the group key generation services.
In this paper, we investigate the GKE protocols based on generalizing Diffie-Hellman two-member key exchange [4], because such protocols can potentially avoid the TTP or the group controller. This is a desirable feature under decentralized computing environments such as ad hoc networks and Blockchain.
1.1. Basic Notion of Group Key Exchange
Let k be a security parameter and U1, U2, …, Un, n = poly(k) (a polynomial in the security parameter k), be members that are allowed to take part in a specified GKE protocol P to generate a group session key K. We can define the GKE protocol as follows.
Definition 1.
Protocol P is called a GKE if: when a group of any t members has honestly executed the protocol P as specified, then each member Ui in the group will finally compute his own session key Ki such that K = Ki, where 3 ≤ t ≤ n and i∊ {1,2, …, n}.
Assume that any GKE protocol P runs on public networks in which all members in a group can broadcast or send messages (bit strings) to other members in the presence of a (polynomially bounded) passive adversary E. Passive adversary E can eavesdrop on the transmitting messages and keep a log of the messages during past protocol runs. However, the passive adversary E does not modify the transmitting messages of protocol runs. A formal security definition as an example is presented to address the above passive adversary of the GKE protocol P [5] as follows.
Definition 2.
The GKE protocol P guarantees privacy if it is computationally infeasible for the passive adversary E to compute the group session key K. The GKE protocol P guarantees secrecy if the passive adversary E cannot distinguish the group session key K from a random bit string of the same length with probability better than 1/2 + ε, where ε is negligible (in the security parameter k).
1.2. Related Work
Some of the literature in the GKE domain mainly revolves around the exposition of new construction of the GKE protocols. An early investigation of GKE protocols by Ingemarsson, Tang, and Wong [6] described a number of so-called Diffie-Hellman generalizations based on the idea of symmetric functions. Steer et al. [7] gave other GKE protocols generalizing the Diffie-Hellman two-member key exchange. Their protocol is suitable for adding new group members; however, deleting members is relatively difficult. Latter, Steiner, Tsudik, and Waidner [8] presented three GKE protocols (named GDH.1, GDH.2, and GDH.3) to improve the communication and computation costs of the Ingemarsson-Tang-Wong GKE protocols. Kim, Perrig, and Tsudik [9], and Bresson and Manulis [10] considered tree-based Diffie-Hellman two-member key exchange and showed that their protocols are very suitable when the composition of the group is changed without restarting the whole protocol. Burmester and Desmedt [5] presented an influential GKE protocol by extending in a natural way of the Diffie-Hellman two-member key exchange. Harn and Lin [11], Harn and Hsu [12] proposed GKE protocols based on both the secret sharing scheme and the group Diffie-Hellman key exchange scheme. Moriya, Takashima, and Takagi [13] and Fan, Xu, and Li [14] proposed the GKE protocols based on Commutative Supersingular Isogeny Diffie-Hellman (CSIDH), which are the post-quantum Diffie-Hellman type key exchange protocols from commutative group action.
Some of the literature in the GKE domain research on the security analysis of the GKE protocols. Katz and Yung [15] presented a compiler that transforms the GKE protocol secure against a passive adversary and proved the Burmester-Desmedt protocol secure against the passive adversary. Emmanuel, Chevassut, and Pointcheval [16] provided a formal security model and several security definitions, which are adapted to many cryptographic scenarios for authenticated Diffie-Hellman key exchange in a group. To prevent stronger attacks against honest but open members, Bresson, Manulis, and Schwenk [17] gave examples where m uncorrupted members accept each other but have different session keys. Gorantla, Boyd, and Nieto [18] specifically analyzed the security of the GKE protocol under the key-compromise impersonation attacks. Baouch et al. [19] introduced an active attack on the Burmester-Desmedt protocol, that is, the adversary can obtain a copy of the shared key, which is created in a collaborative manner with the legal members in a group. Yang et al. [20] presented a security model for generic dynamic authenticated GKE to cover more active attacks (such as leakage of the ephemeral secret key) than previous similar models. As another line of security analysis work on GKE, Cohn-Gordon et al. [21] considered the post-compromise security of group messaging, that is, an adversary who compromises a single group member can indefinitely read and inject messages and built a formal security model on the ideas of multi-stage key exchange by Fischlin and Günther [22]. Alwen et al. [23] further analyzed the TreeKEM protocol [24], which is proposed by the Internet Engineering Task Force (IETF) working group and is the core of the secure group messaging protocols on message-layer security. Alwen et al. [25] also defined optimal security notions for GKE and considered two settings, i.e., the passive setting and the active setting. In addition, Hougaard and Miyaji [26] recently proposed a GKE compiler using any two-member key exchange for which the shared key space is the subset of a group and whose security reduces to the Decisional Diffie-Hellman (DDH) problem. Poettering et al. [27] classified characteristics of a large selection of game based GKE models, including those proposed for GKE with post-compromise security, and observed a range of shortcomings in some of the studied models.
1.3. Our Motivations and Contributions
When a GKE protocol is running, the adversary may illegally add some dummy members to the group. Although these dummy members do not belong to the group, the legal members believe that they are in the group and share a group session key with them. We call it the member tampering attack. To the best of our knowledge, the member tampering problem of the GKE protocol has not been studied yet. It is widely known that the Burmester-Desmedt protocol has advantages over other existing GKE protocols in terms of computation cost, communication cost, and the number of rounds. Moreover, since broadcasting messages can be expensive in some communications networks, the Burmester-Desmedt protocol [1,5] has not only a broadcast version but also a cyclic version. Therefore, we investigate the member tampering attack on the broadcast version and cyclic version of the Burmester-Desmedt protocol. We report that both the broadcast version and cyclic version suffer the member tampering attack when two members are corrupted. That is, two corrupted members, who belong to two groups A and B, can collude to include some unknowing members of group A into the group B and cheat other legal members of the group B to believe that these unknowing members exist in their group and share a group session key after the protocol run.
2. Review of the Burmester-Desmedt Group Key Exchange Protocol
Burmester and Desmedt [5] employed a certain structure of the cyclic group to design their GKE protocol. Without loss of generality, we can write it as follows. Let G be a cyclic group with prime order q and let g be a fixed generator of G. Let Zp = Z/pZ be the integers modulo p. The cyclic group requires choosing two primes p and q such that q|p−1 and a generator g ∊ Zp with the order q. Then, the cyclic group is formed by G = {gx mod p, x ∊ Z}.
Assume that U1, U2, …, Un are all legal members of the GKE system. Initially, a GKE center chooses the system parameters for the GKE protocol. That is, the GKE center determines a security parameter k and a constant c ≥ 1, randomly generates a prime p = Θ(2ck) and an element g ∊ Zp of order q = Θ(2k), where Θ denotes asymptotic tight bound, and publishes the parameters p, g, and q to build the cyclic group G. Let U1, U2, …, Ut ≤ n be a group of members who want to generate a group session key K. To enable a general description, we always allow any index i but Ui and Uj are the same members when satisfying i = j mod t.
2.1. Broadcast Version
The Burmester-Desmedt protocol is simplest to describe in the version that allows broadcast communications. Here, any message sent to more than one member means the broadcast.
- Protocol 1: Broadcast version
Round 1. Each member Ui (i = 1, 2, …, t) selects a random ri ∊ Zq and computes and broadcasts zi = gri mod p.
Round 2. Each member Ui (i = 1, 2, …, t) computes and broadcasts Xi = (zi+1/zi−1)ri mod p.
Key Computation. Each member Ui (i = 1, 2, …, t) computes his own session key:
Figure 1 shows the communication and computation of broadcast version. If each member Ui (i = 1, 2, …, t) honestly generates and broadcasts his zi and Xi, all members will secretly share the same group session key K = gr1rt+r1r2+ r2r3+…+rt−2rt−1+rt−1rt mod p. That is to say, for every member Ui (i = 1, 2, …, t), we have
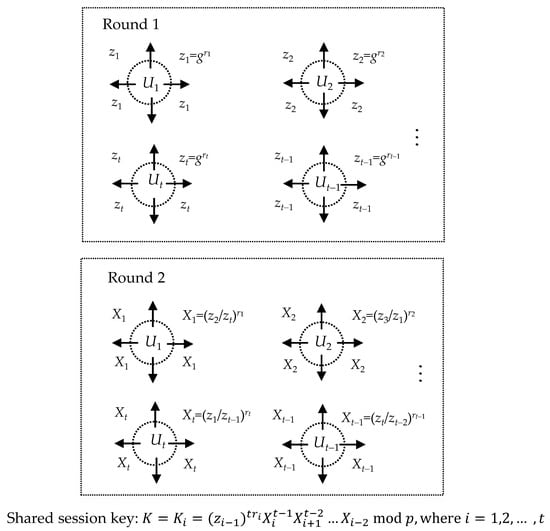
Figure 1.
Communication and computation of broadcast protocol.
2.2. Cyclic Version
In the broadcast version, the protocol messages always need to be sent to all of the members. In some communications environments such as wired communications, the broadcast of messages to all involved members may be more costly than sending them to a single member. Therefore, the cyclic version can maintain the same Diffie-Hellman generalization function as the broadcast version but implement the point-to-point message transmission among the members.
- Protocol 2: Cyclic version
Round 1. Each member Ui (i = 1, 2,…, t) selects a random ri ∊ Zq, and then computes and sends zi = gri mod p to the members Ui−1 and Ui−1.
Round 2. Each member Ui (i = 1, 2,…, t) computes Xi = (zi+1/zi−1)ri mod p. Let b0 = c0 = 1. For i = 1 to t, the member Ui computes bi = bi−1Xi mod p and ci= bi−1ci−1 mod p, and then sends bi and ci to the member Ui+1.
Round 3. Let d0 = ct and d = bt. For i = 1 to t − 1, the member Ui computes di = ddi−1Xi −t mod p, and then sends di and d to the member Ui+1.
Key Computation. Each member Ui (i = 1, 2,…, t) computes his own session key:
It is easily to see that cyclic version does not require the broadcast channel. We know that in Round 2, b0 = c0 = 1, b1 = b0X1 = X1 mod p, c1 = b0c0 = 1, b2 = b1X2 = X1X2 mod p, c2 = b1c1 = X1 mod p, b3 = b2X3 = X1X2X3 mod p, c3 = b2c2 = X12X2 mod p,…, bt = bt−1Xt = X1X2…Xt mod p, ct = bt−1ct−1 = X1X2…Xt−2Xt−1X1t−2X2t−3…Xt−2 = X1t−1X2t−2…Xt−22Xt−1 mod p. Since d0 = ct = X1t−1X2t−2…Xt−1 mod p and d = bt = X1X2…Xt mod p during Round 3, we get d1 = dd0X1−t = X1X2X3…Xt−1XtX1t−1X2t−2 X3t−3…Xt−1X1−t = X2t−1X3t−2…Xt−12Xt mod p, d2 = dd1X2−t = X1X2X3X4…XtX2t−1X3t−2X4t−3…XtX2−t = X3t−1X4t−2…Xt2X1 mod p,…, dt−1 = ddt−2Xt−1−t = X1X2…Xt−3Xt−2Xt−1XtXt−1t−1Xtt−2X1t−3 X2t−4…Xt−3Xt−1−t = Xtt−1X1t−2X2t−3…Xt−32Xt−2 mod p. We therefore know di−1 = Xit−1Xi+1t−2…Xi−2 mod p, where i = 1, 2,…, t. Thus, for all 1 ≤ i ≤ t, it follows that
Hence, we conclude that all members in cyclic version can finally share the same group session key as broadcast version. Figure 2 shows the communication and computation of cyclic version.

Figure 2.
Communication and computation of cyclic protocol.
2.3. Security Results
The security of the Burmester-Desmedt protocol depends on the Computational Diffie-Hellman (CDH) problem and the DDH problem. We describe the CDH problem and the DDH problem as follows.
Definition 3.
The CDH problem: given two primes p and g and two random numbers x = ga mod p, y =gb mod p, find gab mod p.
Definition 4.
The DDH problem: given two primes p and g and three random numbers x = ga mod p, y = gb mod p, and z = gc mod p, decide if ab = c.
The Burmester-Desmedt protocol achieves the following security properties [5].
Fact 1.
Protocol 1 and Protocol 2 guarantee the privacy as in Definition 2 if, and only if, the CDH problem is intractable. Protocol 1 and Protocol 2 guarantee the secrecy as in Definition 2 if, and only if, the DDH problem is intractable.
Fact 1 indicates that both Protocol 1 and Protocol 2 maintain a sound security promise when the CDH problem and the DDH problem are hard to solve.
3. Member Tampering Attacks on the Burmester-Desmedt Protocol
We know that any group U1, U2,…, Ut named as group A can execute a protocol run and negotiate a group session key K by using Equation (1) or Equation (3). We assume that members Ui′ and Ui″ are two malicious insiders in group A, that is, i′, i″∊ {1, 2,…, t} and i′ ≠ i″. Without loss of generality, let 0 < i’ < i″ < t+1. Moreover, both members Ui′ and Ui″ simultaneously initiate an abnormal protocol run with another group Ua1, Ua2, …, Uat′ named as the group B. Here, 0 < aj < n + 1 for 0 < j < t’ + 1.
3.1. Attacks on Broadcast Version
In the protocol run as shown in Figure 1, each member Ui (i = 1, 2,…, t) of group A should compute and broadcast zi = gri mod p and Xi = (zi+1/zi−1)ri mod p during Round 1 and Round 2 of Protocol 1. Finally, each member Ui (i = 1, 2,…, t) is able to compute and share the same group session key K = gr1rt+r1r2+ r2r3+…+rt−2rt−1+rt−1rt mod p by computing (zi−1)triXit−1Xi+1t−2…Xi−2 mod p. To realize the member tampering attack, two malicious insiders Ui′ and Ui″ of group A simultaneously start an abnormal protocol run with another group B. Let i″ − i′ > 1. We assume that each member Ui (i = i′ + 1, i′ + 2,…, i″ − 1) in the group A does not belong to the group B, that is, aj∉{i′+1, i′+2,…, i″ − 1} for all j ∊ {1, 2,…, t’}. After the abnormal protocol run of the group B, each member Uaj (j = 1, 2,…, t′) believes that not only members Uaj (j = 1, 2,…, t′) but also members Ui (i = i′, i′ + 1,…, i″) take part in negotiating a group session key. However, all members Ui (i = i′ + 1, i′ + 2,…, i″ − 1) in group A actually do not involve themselves in the abnormal protocol run of group B. In the following, we always write t′ + i″ − i′ as f to make the expression concise and easy to understand. We describe the abnormal protocol run as follows.
Round 1. Each member Uaj (j = 1, 2,…, t′) selects a random number r′j∊ Zq, and computes and broadcasts z′j= gr′j mod p. Each zi generated by the member Ui (i = i′, i′+1,…, i″) also is broadcasted to group B.
Round 2. The malicious insider Ui″ computes and broadcasts X′f+1 = (z′1/zi″−1)ri″ mod p and the member Ua1 computes and broadcasts X′1 = (z′2/zi″)r′1 mod p. Each member Uaj (j = 2,…, t′ − 1) computes and broadcasts X′j = (z′j+1/z′j−1)r′j mod p. The member Uat′ computes and broadcasts X′t′ = (zi′/z′t′−1)r′t′ mod p and the malicious insider Ui′ computes and broadcasts X′t′+1 = (zi′−1/z′t′)ri′ mod p. In addition, each Xi generated by the member Ui (i = i′ + 1,…, i″ − 1) is broadcasted to all members Uaj (j = 1, 2,…, t′).
Key Computation. Assume that r′i= ri+i′−t′−1 and z′i= zi+i′−t′−1, where i = t′ + 1, t′ + 2,…, t′ + i″ − i′ + 1 and X′i= Xi+i′−t′−1, where i = t′ + 2, t′ + 3,…, f. Each member Uaj (j = 1, 2,…, t′) computes the group session key:
where the indexes j in both z′j and X′j are performed modulo f + 1.
The member Ui′ can share the group session key by calculating
The member Ui″ also can obtain the group session key by calculating
According to Equation (5), we have
Since ri′ = r′t′+1 and ri″ = r′f+1, we know that Equations (6) and (7) satisfy Equation (5) when j = t′ + 1 and j = f + 1. Hence, all members Ui′, Uaj (j = 1, 2,…, t′), Ui″ should share the same group session key K′ = K′i′ = K′i″ = K′j = gr′1rt″+r′1r′2+ r′2r′3+…+ ri″−2ri″−1+ri″−1ri″ mod p. Moreover, all members Uaj (j = 1, 2,…, t′) believe that the members Ui (i = i′ + 1, i′ + 2,…, i″ − 1) also exist in their group. Figure 3 shows member tampering attacks, which exploits two parallel protocol runs of group A and group B. In fact, the malicious insiders Ui′ and Ui″ also can use above attack to add the unknowing members Ui (i = 1, 2,…, i′ − 1, i″ + 1, i″ + 2,…, t) of the group A into the group B.
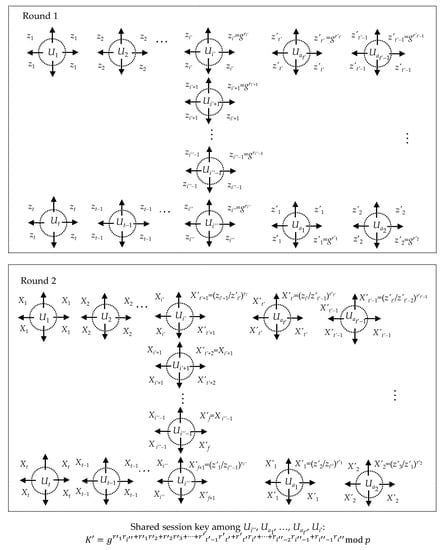
Figure 3.
Member tampering attack on the broadcast protocol.
3.2. Attack on Cyclic Version
Consider the protocol run of group A. As shown in Figure 2, each member Ui (i = 1, 2,…, t) computes zi = gri mod p and sends it to the members Ui−1 and Ui+1 during Round 1 of Protocol 2. Each member Ui (i = 1, 2,…, t) computes Xi = (zi+1/zi−1)ri mod p, bi = bi−1Xi mod p, ci = bi−1ci−1 mod p, where b0 = c0= 1, and then sends bi and ci to the member Ui+1 during Round 2 of Protocol 2. In Round 3 of Protocol 2, each member Ui (i = 1, 2,…, t − 1) computes di = ddi−1Xi−t mod p, where d = bt and d0 = ct, and then sends di and d to the next member Ui+1. Finally, each member Ui (i = 1, 2,…, t) computes and secretly shares the group session key K = Ki = (zi−1)tridi−1 mod p.
Meanwhile, the malicious insiders Ui′ and Ui″ of group A also simultaneously start another abnormal protocol run with the group Ua1, Ua2,…, Uat′, i.e., group B. Here, we assume that i″ − i′ < t − 1 and aj ∉ {1, 2,…, i′ − 1, i″+1, i″+2,…, t} for any j ∊ {1, 2,…, t′}. At the end of the abnormal protocol run of group B, each member Uaj (j = 1, 2,…, t′) mistakenly believes that the members Ui, where i = 1, 2,…, i′ − 1, i″ + 1, i″+ 2,…, t, also are in their group and share a group session key with them, although any of these members do not participate in in the abnormal protocol run. We assume that the malicious insider Ui″ eavesdrops on all bi, where i = 1, 2,…, i′ − 2, i″ + 1, i″ + 2,…, t. Since the malicious insider Ui″ knows b0 = 1, he can further compute all Xi = bi/bi−1 mod p, where i = 1, 2,…, i′ − 1, i″ + 1, i″ + 2,…, t. Figure 4 depicts the member tampering attack on the cyclic version. For simplicity, we write t + i′ + t′ − i″ as h in the following. We further describe the abnormal protocol run of group B as follows.
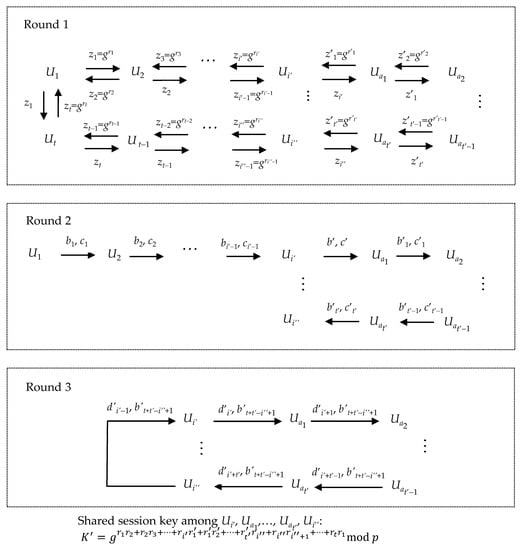
Figure 4.
Member tampering attack on the cyclic protocol.
Round 1. The member Ui′ sends zi′ to member Ua1. The member Ua1 selects a random number r′1 ∊ Zq, computes z′1 = gr′1 mod p and sends z′1 to the members Ui′ and Ua2. Each member Uaj (j = 2, 3,…, t′ − 1) selects a random number r′j ∈ Zq, computes z′j = gr′j mod p, and sends z′j to the members Uaj−1 and Uaj+1. The member Uat′ selects a random number r′t′ ∊ Zq and computes z′t′ = gr′t′ mod p, and then sends z′t′ to the members Uat′−1 and Ui″. The member Ui″ sends his zi″ to the member Uat′.
Round 2. The member Ui′ computes and updates his new X′h+1 = (z′1/zi′−1)ri′ mod p. The member Ui′ then computes b′ = bi′−1X′h+1 mod p and c′ = ci′ = bi′−1ci′−1 mod p, and further sends b′ and c′ to the member Ua1. The member Ua1 computes X′1 = (z′2/zi′)r′1 mod p. Moreover, member Ua1 computes b′1 = b′X′1 mod p and c′1 = b′c′ mod p, and then sends b′1 and c′1 to the next member Ua2. Each member Uaj (j = 2, 3,…, t’ − 1) computes X′j = (z′j+1/z′j−1)r′j mod p. For j = 2 to t′ − 1, the member Uaj computes b′j = b′j−1X′j mod p and c′j = b′j−1c′j−1 mod p, and then sends b′j and c′j to Uaj+1. Upon receiving the member Uat′−1’s b′t′−1 and c′t′−1, the member Uat’ computes X′t′ = (zi″/z′t′−1)r′t′ mod p, b′t′ = b′t′−1X′t′ mod p, c′t′ = b′t′−1c′t′−1 mod p, and then sends b′t′ and c′t′ to the member Ui″. Upon receiving the member Uat′’s b′t′ and c′t′, the member Ui″ calculates his X′t′+1 = (zi″−1/z′t′)ri″ mod p, b′t′+1 = b′t′X′t′+1 mod p, c′t′+1 = b′t′c′t′ mod p. For i = i″ + 1 to t, the member Ui″ further computes b′i+t′−i″+1 = b′i+t′−i″Xi mod p and c′i+t′−i″+1 = b′i+t′−i″c′i+t′−i″ mod p.
Round 3. Let d′0 = c′t+t′−i″+1. For i = 1 to i′ − 1, the member Ui″ computes d′i = b′t+t′−i″+1d′i−1Xi−(h+1) mod p. And then, the member Ui″ sends d′i′−1 and b′t+t′−i″+1 to the member Ui′. The member Ui′ computes d′i′ = b′t+t′−i″+1d′i′−1X′h+1−(h+1) mod p and sends d′i′ and b′t+t′−i″+1 to the member Ua1. For j = 1 to t′ − 1, the member Uaj computes d′j+i′ = b′t+t′−i″+1d′j+i′−1X′j−(h+1) mod p, and then sends dj+i′ and b′t+t′−i″+1 to the member Uaj+1. Upon receiving the member Uaj−1’s d′i′+t′−1 and b′t+t′−i″+1, the member Uat′ computes d′i′+t′ = b′t+t′−i″+1d′i′+t′−1X′t′−(h+1) mod p, and then sends d′i′+t and b′t+t′−i″+1 to the member Ui″.
Key Computation. Let z′0 = zi′. Each member Uaj (j = 1, 2,…, t′) computes the group session key:
The member Ui′ shares the group session key by calculating
The member Ui″ also obtains the group session key by computing
In the following, we analyze and confirm the group session key shared among the members Ui′, Uaj (j = 1, 2,…, t′), Ui″. During Round 1, the members Ui′ and Ui″ reuse their zi′ and zi″ generated in the protocol run of the group A and send zi′ to the member Ua1 and zi″ to the member Uat′. During Round 2, the member Ui′ computes his new X′h+1 = (z′1/zi′−1)ri′ mod p instead of the old X i′ = (z i′+1/zi′−1)ri′ mod p in the protocol run of the group A, and uses this X′h+1 to compute b′ = bi′−1X′h+1 mod p. Then, the member Ua1 computes X′1 = (z′2/zi′)r′1 mod p and b′1 = b′X′1 mod p and the member Uaj computes X′j = (z′j+1/z′j−1)r′j mod p and b′j = b′j−1X′j mod p for j = 2 to t′. After calculating X′t′+1 = (zi″−1/z′t′)ri″ mod p and b′t′+1 = b′t′X′t′+1 mod p, the member Ui″ can sequentially compute each member Ui′s b′i+t′−i″+1 = b′i+t′−i″Xi mod p, where i = i″ + 1, i″ + 2,…, t. The reason is that the member Ui″ had eavesdropped on all bi for i = i″ + 1, i″ + 2,…, t in the protocol run of the group A and can derive the member Ui′s Xi by computing bi/bi−1 mod p. Therefore, we know that
and
According to the analysis in Section 2.2, we have c′ = ci′ = bi′−1ci′−1 = X1X2…Xi′−2Xi′−1X1i′−2 X2i′−3…Xi′−2 = X1i′−1X2i′−2…Xi′−22Xi′−1 mod p. Since b′ = bi′−1X′h+1 mod p in Round 2 of the group B, c′1 = b′c′ = bi′−1X′h+1c′ = bi′−1X′h+1X1i′−1X2i′−2…Xi′−22Xi′−1 = X1X2…Xi′−2Xi′−1X′h+1X1i′−1X2i′−2…Xi′−22Xi′−1 = X1i′X2i′−1…Xi′−23Xi′−12X′ h+1 mod p. We further get c′j= b′j−1c′j−1 = b′j−1b′j−2 c′j−2 =…= b′j−1b′j−2…b′1c′1 mod p for j = 2 to t′. Therefore,
Since the member Ui″ in Round 2 of the group B computes b′t′+1 = b′t′X′t′+1 mod p and c′t′+1 = b′t′c′t′ mod p, and then calculates b′i+t′−i″+1 = b′i+t′−i″Xi mod p and c′i+t′−i″+1 = b′i+t′−i″c′i+t′−i″ mod p for i = i″ + 1 to t, we have
In Round 3 of the group B, we know d′0 = c′t+t′−i″+1 and d′i = b′t+t′−i″+1d′i−1Xi –(h+1) mod p or i = 1 to i′ − 1. That is, d′i′−1 = b′t+t′−i″+1d′i′−2Xi′−1−(h+1) = b′t+t′−i″+12d′i′−3Xi′−1−(h+1)Xi′−2−(h+1) =…= b′t+t′−i″+1i′−1Xi′−1−(h+1)Xi′−2−(h+1) … X1−(h+1)d′0 = b′t+t′−i″+1i′−1Xi′−1−(h+1)Xi′−2−(h+1)…X2−(h+1)X1−(h+1)c′t+t′−i″+1 mod p. Now we have
Owing to d′i′ = b′t+t′−i″+1d′i′−1X′h+1−(h+1) mod p, we get
Since d′j+i′ = b′t+t′−i″+1d′j+i′−1X′j–(h+1) mod p for j = 1 to t′ − 1 and d′t′+i′ = b′t+t′−i″+1d′t′+i′−1X′t–(h+1) mod p, we get
and
Let X′ l+t+t′−i″+1
= Xl mod p for l = 1 to i′ − 1 and X′ l+t′−i″+1 = Xl mod p
for l = i″ + 1 to t. Moreover, let n′ = h + 1 and any index j but X′i and X′j
are the same value when satisfying i = j mod n’. According
to Equations (11), (25), and (28), we have
for j = 1, 2,…, t′. We write z′h = zi′−1, r′h+1 = ri′, r′t′+1 = ri″. By Equations (23) and (30), and Equations (12) and (13) become
and
According to Equations (31)–(33), we know Equations (11)–(13) are strictly consistent with Equation (1). This means that h+1 members, i.e., the members Uaj (j = 1, 2,…, t’) and Ui (i = 1, 2,…, i′, i″, i″ + 1, …, t), run cyclic version of the protocol. Finally, we can concluded that each member Uaj (j = 1, 2,…, t’) believes the members Ui (i = 1, 2,…, i′, i″, i″ + 1, …, t) of group A are in their group and share the secret key, i.e., K′ =gr1r2+r2r3+…+ri′ r′1+ r′1r′2+…+ r′t′ri″ + ri″ ri″+1+…+ rt r1 mod p. However, the fact is that the members Ui (i = 1, 2,…, i′ − 1, i″ + 1, i″ + 2,…, t) do not take part in the abnormal protocol run with the group B. It needs to point out that the member Ui″ can select the part of the members Ui (i = i″ + 1, i″ + 2, …, t) to add in the group B or ignore them all. Assume that S ⊂ {i″ + 1, i″ + 2,…, t } and the member Ui″ wants to include the members Ui∈S into group B. The member Ui″ only modifies the computation of the b′i+t′−i″+1 and c′i+t′−i″+1 in Round 2. That is, for i = i″ + 1 to t, the member Ui″ computes b′i+t′−i″+1 = b′i+t′−i″Xi mod p and c′i+t′−i″+1 = b′i+t′−i″c′i+t′−i″ mod p, when i∈S.
Further comment. The member tampering attacks are possibly exploited to cheat the members of the group and threaten group communication security. One threat scenario is patient consultation in telemedicine. When the medical experts and the patient establish a group communication by using the Burmester-Desmedt protocol, two medical experts can add some experts who have not participated in the consultation to the group as needed. This behavior can improve the authority of the consultation. Another threat scenario is the online auction system. If the online auction system runs the Burmester-Desmedt protocol, two members in the auction group can include the auction notaries, who do not exist in the auction group.
4. Countermeasure and Open Problem
The reason why the Burmester-Desmedt protocol suffers is that the members have not explicitly verified the identity of other members in the group. Therefore, the malicious insiders in the group can reuse messages of another protocol run to cheat other members into believing the non-existent members. If each member can confirm the identity of other members in the group during the protocol run, it is difficult for malicious insiders to add those dummy members.
Let SignskUi() and VrfypkUi() (i = 1, 2, …, n) denote the member Ui’s signature function using private key skUi and verification function using public key pkUi. We require the signature scheme that is existentially unforgeable under an adaptive chosen-message attack. Here, the existentially unforgeable property and the game of adaptive chosen-message attack are the standard notions of security for digital signature schemes. Let UIi (i = 1, 2, …, n) be the member Ui’s recognizable identities (in lexicographic order) wishing to establish the group session key. Let ‖ be the concatenation operator. In the following, we provide the improvements on the Burmester-Desmedt protocol to defeat the member tampering attack.
In broadcast version as Figure 1, we require each member Ui (i = 1, 2, …, t) to receiving all zj and Xj during Round 1 and Round 2, where j = 1, 2, …, t and j ≠ i. More importantly, each member Ui simultaneously computes and broadcasts Si = SignskUi(z1 ‖ X1 ‖ UI1 ‖ z2 ‖ X2 ‖ UI2 ‖…‖ zt ‖ Xt ‖ UIt) in Round 2. Moreover, upon receiving all messages from other members, each member Ui also should verify all Sj by computing VrfypkUj(Sj), where j = 1, 2, …, t and j ≠ i. If any verification operation fails, the member Ui should terminate the protocol run. When an adversary wants to illegally include any member Uj into a certain group and cheat other members of the group, he must forge the member Uj′s signature Sj during the protocol run. This signature signs recognizable identities of all group members and the fresh random values generated by all group members. However, the security of the signature algorithm [28] prevents the possibility of forging the member Uj′s signature without his private key skUi.
In cyclic version as Figure 2, we assume that each member Ui (i = 1, 2, …, t) knows all other members Uj, where j = 1, 2, …, t and j ≠ i, potentially are in the group before the protocol run starts. Figure 5 shows our improvement of cyclic version. Our Round 1 and Round 2 are fully same as cyclic version described in Figure 2. During Round 3, we require each member Ui (i = 1, 2, …, t) simultaneously computes the signature SCi = SignskUi(Ki ‖ UI1 ‖ UI2 ‖…‖ UIt), and then each member Ui (i = 1, 2, …, t − 1) sends the signatures SC1, SC2, …, SCi to the next member Ui+1 and the member Ut sends the signatures SC2, SC3, …, SCt to the member U1. After Round 3, we additionally demand a new round named Round 4. In Round 4, each member Ui (i = 1, 2, …, t − 2) sends the signatures SCi+2, SCi+3, …, SCt to the member Ui+1. In Round 3 and Round 4, each member Ui (i = 1, 2, …, t) should verify all signatures SCj by computing VrfypkUj(SCj), where j = 1, 2, …, t and j ≠ i. If any verification operation fails, the member Ui should immediately terminate the protocol run. For reasons similar to the improved broadcast version, the improved cyclic version also can resist the member tampering attack under the malicious active insider or outsider, when the signature algorithm is secure.
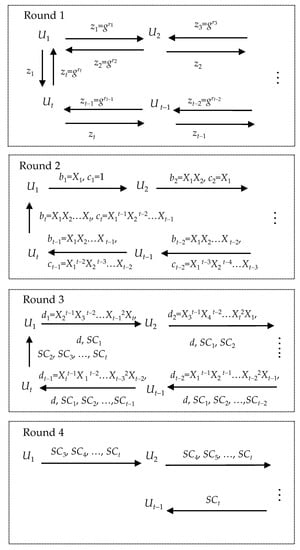
Figure 5.
Improvement on cyclic protocol.
However, we argue that the above signature-based improvements on the Burmester-Desmedt protocol have at least two disadvantages, though they can resist member tampering attacks. First, the signature mechanism means that the group system needs to be equipped with Public Key Infrastructure (PKI) and issue digital certificates to ensure the authenticity of the members’ public keys. In addition, the certificate chain may also increase the complexity of the group system. Second, the signature mechanism requires the members of the group to generate, verify, transmit, and receive a considerable number of signatures. For example, each member in the improved broadcast version needs to generate and broadcast 1 signature and receive and verify the t − 1 signature, if there are t members in the group. Moreover, the members of the group must run an extra round in an improved cyclic version. Obviously, these two disadvantages indicate a significant increase in the implementation overheads of the group system, when the Burmester-Desmedt protocol adopts the signature mechanism. Hence, the signature-based improvements on the Burmester-Desmedt protocol are not suitable for resource-constrained security environments, such as Bluetooth security [29,30]. The group systems based on Bluetooth low-energy devices are very popular in wireless personal area networks and Internet-of-Things (IoT). However, to maintain the low energy feature, Bluetooth security currently does not support the signature mechanism. Hence, an interesting open problem is whether one could enhance the Burmester-Desmedt protocol to prevent member tampering attacks without relying on resource-intensive public key algorithms, e.g., the signature and the public encryption. A related approach might be to rely on the cryptographic hash techniques to develop a more intricate hybrid structure for the Burmester-Desmedt protocol. This requires in-depth studies, including protocol design, efficiency evaluation, security analysis, etc. We leave it as future work.
5. Conclusions
One advantage of the Burmester-Desmedt protocol is scalability, that is, any t > 2 members can establish a group session key after the protocol run. The scalability is very fit to ad hoc networks, where the number of members is often changing. However, we have shown that two malicious insiders in both group A and the group B can exploit its scalability to add the unknowing members of group A into the group B and make other members of the group B mistakenly believe that their group session key is shared with those unknowing members. Hence, owing to our member tampering attacks, the number of members is a security parameter and needs to be protected in the appropriate way when the scalable GKE protocol is deployed.
We proposed the signature-based improvement on the Burmester-Desmedt protocols, which is secure against our member tampering attacks. We compared our improvement with Katz-Yung protocol [15], because they are all base on the Burmester-Desmedt protocol and employ the signature schemes. In the broadcast version, the Katz-Yung protocol requires signing the messages of Round 1 and Round 2, respectively. Therefore, each member in the Katz-Yung protocol demands double signature operations compared with our improvement on the broadcast version. To the best of our knowledge, no other signature-based improvement on the cyclic version is proposed. However, under resource-constrained environments, our signature-based improvement is still not practical in view of the implementation costs.
Author Contributions
Conceptualization, D.-Z.S.; methodology, D.-Z.S.; validation, D.-Z.S. and Y.T.; formal analysis, D.-Z.S.; investigation, D.-Z.S.; writing—original draft preparation, D.-Z.S. and Y.T.; writing—review and editing, D.-Z.S. and Y.T.; supervision, D.-Z.S.; funding acquisition, D.-Z.S. All authors have read and agreed to the published version of the manuscript.
Funding
The work of Da-Zhi Sun was supported in part by the National Natural Science Foundation of China under Grant No. 61872264. The APC was funded by the National Natural Science Foundation of China under Grant No. 61872264.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors would like to thank the editor and the reviewers for their valuable suggestions and comments.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Boyd, C.; Mathuria, A.; Stebila, D. Protocols for Authentication and Key Establishment, 2nd ed.; Springer: Berlin, Germany, 2020; pp. 389–440. [Google Scholar]
- Ramakrishna, O.; Churi, P. Systematic Survey on Cryptographic Methods Used for Key Management in Cloud Computing. In Proceedings of the International Conference on Innovative Computing and Communications (ICICC 2021), Delhi, India, 20–21 February 2021; Khanna, A., Gupta, D., Bhattacharyya, S., Hassanien, A.E., Anand, S., Jaiswal, A., Eds.; Advances in Intelligent Systems and Computing (AISC). Springer: Singapore, 2022; Volume 1388, pp. 445–460. [Google Scholar]
- Juric, R.; Lyth, A.; Larson, D. Group Key Management in Wireless Sensor Networks: Introducing Context for Managing the Re-Keying Process. In Proceedings of the 55th Hawaii International Conference on System Sciences (HICSS–55), Virtual Event, 15 June 2022; pp. 7434–7443. Available online: https://scholarspace.manoa.hawaii.edu/items/3f78810f-0fd2-41b7-bbe8-c2bacd9420de (accessed on 29 August 2022).
- Diffie, W.; Hellman, M.E. New directions in cryptography. IEEE Trans. Inf. Theory 1976, IT-22, 644–654. [Google Scholar] [CrossRef]
- Burmester, M.; Desmedt, Y. A secure and scalable group key exchange system. Inf. Process. Lett. 2005, 94, 137–143. [Google Scholar] [CrossRef]
- Ingemarsson, I.; Tang, D.T.; Wong, C.K. A conference key distribution system. IEEE Trans. Info. Theory 1982, IT-28, 714–720. [Google Scholar] [CrossRef]
- Steer, D.G.; Strawczynski, L.; Diffie, W.; Wiener, M. A Secure Audio Teleconference System. In Proceedings of the Conference on the Theory and Application of Cryptography: Advances in Cryptology (CRYPTO’88), Santa Barbara, CA, USA, 21–25 August 1988; Goldwasser, S., Ed.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 1990; Volume 403, pp. 520–528. [Google Scholar]
- Steiner, M.; Tsudik, G.; Waidner, M. Diffie-Hellman Key Distribution Extended to Group Communication. In Proceedings of the 3rd ACM Conference on Computer and Communications Security (CCS’96), New Delhi, India, 14–15 March 1996; Association for Computing Machinery: New York, NY, USA, 1996; pp. 31–37. [Google Scholar]
- Kim, Y.; Perrig, A.; Tsudik, G. Simple and Fault-Tolerant Key Agreement for Dynamic Collaborative Groups. In Proceedings of the 7th ACM Conference on Computer and Communications Security (CCS 2000), Athens, Greece, 1–4 November 2000; Samarati, P., Ed.; Association for Computing Machinery: New York, NY, USA, 2000; pp. 235–244. [Google Scholar]
- Bresson, E.; Manulis, M. Securing Group Key Exchange against Strong Corruptions. In Proceedings of the 2008 ACM Symposium on Information, Computer and Communications Security (ASIACCS 2008), Tokyo, Japan, 18–20 March 2008; Association for Computing Machinery: New York, NY, USA, 2008; pp. 249–260. [Google Scholar]
- Harn, L.; Lin, C.L. Efficient group Diffie–Hellman key agreement protocols. Comput. Electr. Eng. 2014, 40, 1972–1980. [Google Scholar] [CrossRef]
- Harn, L.; Hsu, C.F. A practical hybrid group key establishment for secure group communications. Comput. J. 2017, 60, 1582–1589. [Google Scholar] [CrossRef][Green Version]
- Moriya, T.; Takashima, K.; Takagi, T. Group Key Exchange from CSIDH and Its Application to Trusted Setup in Supersingular Isogeny Cryptosystems. In Proceedings of the International Conference on Information Security and Cryptology (Inscrypt 2019), Nanjing, China, 6–8 December 2019; Liu, Z., Yung, M., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2019; Volume 12020, pp. 86–98. [Google Scholar]
- Fan, X.J.; Xu, X.; Li, B. Group Key Exchange Protocols from Supersingular Isogenies. In Proceedings of the International Conference on Information Security and Cryptology (Inscrypt 2020), Guangzhou, China, 11–14 December 2020; Wu, Y.D., Yung, M., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2020; Volume 12612, pp. 157–173. [Google Scholar]
- Katz, J.; Yung, M. Scalable protocols for authenticated group key exchange. J. Cryptol. 2007, 20, 85–113. [Google Scholar] [CrossRef]
- Bresson, E.; Chevassut, O.; Pointcheval, D. Provably secure authenticated group Diffie-Hellman key exchange. ACM Trans. Inf. Syst. Secur. 2007, 10, 10. [Google Scholar] [CrossRef]
- Bresson, E.; Manulis, M.; Schwenk, J. On Security Models and Compilers for Group Key Exchange Protocols. In Proceedings of the Advances in Information and Computer Security, Second International Workshop on Security (IWSEC 2007), Nara, Japan, 29–31 October 2007; Miyaji, A., Kikuchi, H., Rannenberg, K., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2007; Volume 4752, pp. 292–307. [Google Scholar]
- Gorantla, M.C.; Boyd, C.; Nieto, J.M.G. Modeling Key Compromise Impersonation Attacks on Group Key Exchange Protocols. In Proceedings of the International Workshop on Public Key Cryptography (PKC 2009), Irvine, CA, USA, 18–20 March 2009; Jarecki, S., Tsudik, G., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2009; Volume 5443, pp. 105–123. [Google Scholar]
- Baouch, M.; López-Ramos, J.A.; Schnyder, R.; Torrecillas, B. An Active Attack on a Distributed Group Key Exchange System. arXiv 2016, arXiv:1603.09090. Available online: https://arxiv.org/abs/1603.09090 (accessed on 29 August 2022). [CrossRef]
- Yang, Z.; Khan, M.; Liu, W.P.; He, J. On Security Analysis of Generic Dynamic Authenticated Group Key Exchange. In Proceedings of the Secure IT Systems–23rd Nordic Conference (NordSec 2018), Oslo, Norway, 28–30 November 2018; Gruschka, N., Ed.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2018; Volume 11252, pp. 121–137. [Google Scholar]
- Cohn-Gordon, K.; Cremers, C.; Garratt, L.; Millican, J.; Milner, K. On Ends-to-Ends Encryption: Asynchronous Group Messaging with Strong Security Guarantees. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security (CCS 2018), Toronto, ON, Canada, 15–19 October 2018; Backes, M., Wang, X.F., Eds.; Association for Computing Machinery: New York, NY, USA, 2018; pp. 1802–1819. [Google Scholar]
- Fischlin, M.; Günther, F. Multi-Stage Key Exchange and the Case of Google’s QUIC Protocol. In Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security (CCS 2014), Scottsdale, AZ, USA, 3–7 November 2014; Yung, M., Li, N.H., Eds.; Association for Computing Machinery: New York, NY, USA, 2014; pp. 1193–1204. [Google Scholar]
- Alwen, J.; Coretti, S.; Dodis, Y.; Tselekounis, Y. Security Analysis and Improvements for the IETF MLS Standard for Group Messaging. In Proceedings of the 40th Annual International Cryptology Conference: Advances in Cryptology (CRYPTO 2020), Part I, Santa Barbara, CA, USA, 17–21 August 2020; Micciancio, D., Ristenpart, T., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2020; Volume 12170, pp. 248–277. [Google Scholar]
- Barnes, R.; Beurdouche, B.; Raphael, R.; Millican, J.; Omara, E.; Cohn-Gordon, K. The Messaging Layer Security (MLS) Protocol. Technical Report. 2020. Available online: https://datatracker.ietf.org/doc/draft-ietf-mls-protocol/ (accessed on 29 August 2022).
- Alwen, J.; Coretti, S.; Jost, D.; Mularczyk, M. Continuous Group Key Agreement with Active Security. In Proceedings of the 18th Theory of Cryptography Conference (TCC 2020), Part II, Durham, NC, USA, 16–19 November 2020; Pass, R., Pietrzak, K., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2020; Volume 12551, pp. 261–290. [Google Scholar]
- Hougaard, H.B.; Miyaji, A. Group Key Exchange Compilers from Generic Key Exchanges. In Proceedings of the 15th International Conference on Network and System Security (NSS 2021), Tianjin, China, 23 October 2021; Yang, M., Chen, C., Liu, Y., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2020; Volume 13041, pp. 162–184. [Google Scholar]
- Poettering, B.; Rösler, P.; Schwenk, J.; Stebila, D. SoK: Game-Based Security Models for Group Key Exchange. In Proceedings of the Cryptographers’ Track at the RSA Conference 2021: Topics in Cryptology (CT–RSA 2021), Virtual Event, 17–20 May 2021; Paterson, K.G., Ed.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2021; Volume 12704, pp. 148–176. [Google Scholar]
- Katz, J.; Lindell, Y. Introduction to Modern Cryptography: Principles and Protocols, 3rd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2020; pp. 463–495. [Google Scholar]
- Sun, D.Z.; Sun, L. On secure simple pairing in Bluetooth standard v5.0-part i: Authenticated link key security and its home automation and entertainment applications. Sensors 2019, 19, 1158. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.Z.; Sun, L.; Yang, Y. On secure simple pairing in Bluetooth standard v5.0-part ii: Privacy analysis and enhancement for low energy. Sensors 2019, 19, 3259. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).