Abstract
Graph-based molecular structure descriptors (often called “topological indices”) are useful for modeling the physical and chemical properties of molecules, designing pharmacologically active compounds, detecting environmentally hazardous substances, etc. The graph invariant , known under the name general reduced second Zagreb index, is defined as , where is the degree of the vertex v of the graph and is any real number. In this paper, among all trees of order n, and all unicyclic graphs of order n with girth g, we characterize the extremal graphs with respect to . Using the extremal unicyclic graphs, we obtain a lower bound on of graphs in terms of order n with k cut edges, and completely determine the corresponding extremal graphs. Moreover, we obtain several upper bounds on of different classes of graphs in terms of order n, size m, independence number , chromatic number k, etc. In particular, we present an upper bound on of connected triangle-free graph of order , edges with , and characterize the extremal graphs. Finally, we prove that the Turán graph gives the maximum among all graphs of order n with chromatic number k.
MSC:
05C07; 05C35
1. Introduction
Let be a simple graph with vertex set and edge set , where and . The degree of the vertex u of , denoted , is the number of vertices adjacent to the vertex u. For , denotes the set of vertices adjacent to v, that is, . Let be the maximum degree of graph . As usual, , and g denote, respectively, the chromatic number, the clique number, the independence number, and the girth. Let be the complete graph of order n, and also let be a complete k-partite graph of order n. The Turán graph is the complete k-partite graph on n vertices whose partite sets differ in size by at most 1. An edge is a cut edge if, and only if, it is not contained in any cycle. For , denotes the graph obtained from by removing the edges in F. Similarly, the graph obtained from by adding a set of edges F is denoted by . For , we write and . We skip the definitions of other standard graph-theoretical notions, these can be found in [1,2,3] and other textbooks.
The most famous and studied degree-based topological indices of a graph are the first Zagreb index and second Zagreb index of a graph , are defined as
respectively. The quantities and were found to occur within certain approximate expressions for the total -electron energy [4]. For more informations on the mathematical theory and chemical applications of the Zagreb indices, see [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44] and the references cited therein. The Zagreb indices has been studied independently in the mathematical literature under other names in [45,46,47,48,49,50].
Li et al. [51] studied on the extremal cacti of given parameters with respect to the difference of Zagreb indices. Furtula et al. [52] presented some results on and then showed that is closely related to the reduced second Zagreb index, which is defined as
The Wiener polarity index, denoted by , is defined as the number of unordered pairs of vertices that are at distance 3 in . When the graph is isomorphic to a tree, we have and it was examined in the recent papers [52,53,54]. An and Xiong [55] gave some bounds on in terms of vertex connectivity, independence number, and matching number, and also characterized the extremal graphs. In [56], the authors obtained the extremal graphs for in the class of cyclic graphs of order n with k cut edges. In [57], some upper bounds of were estimated and the extremal graphs with respect to among all unicyclic graphs of order n with girth g were characterized.
In [58], Horoldagva et. al studied a generalization of both the reduced second Zagreb index and the second Zagreb index, which is defined as
and named it general reduced second Zagreb index, where is any real number. They characterized some properties of and the extremal graphs of order n with k cut edges with maximum when .
The structure of the paper is as follows. We give a list of propositions and preliminaries in Section 2. Among all trees of order n, and all unicyclic graphs of order n with girth g, we characterize the extremal graphs with respect to in Section 3. Using the extremal unicyclic graphs, we determine the lower bound for the general reduced second Zagreb index of graphs of order n with k cut edges and completely determine the corresponding extremal graphs in Section 4. In Section 5, we obtain several upper bounds on of different class of graphs in terms of order n, size m, independence number , chromatic number k, etc. In particular, we present an upper bound on of connected triangle-free graph of order , edges with , and characterize the extremal graphs. Finally, we prove that the Turán graph gives the maximum among all graphs of order n with chromatic number k.
2. Preliminaries
Here, we list some previously known results and their direct consequences, which are used to prove our main results. The following propositions were proved in [58].
Proposition 1
([58]). Let Γ be a connected graph, and . Additionally, let . Consider the graph . Then
Denote by the set of connected graphs of order n with m edges.
Proposition 2
([58]). Let Γ be a graph in . Additionally, let be maximum.
- (i)
- If then all cut edges of Γ are pendant.
- (ii)
- If , and Γ is different from a double-star, then all cut edges of Γ are pendant.
In [59], the upper bounds in terms of order and size for the Zagreb indices of -free graphs were given. Two of these bounds are stated as the next proposition.
Proposition 3
([57,59]). Let Γ be a -free graph with n vertices and edges. Then
Moreover, both equalities hold if, and only if, Γ is isomorphic to a regular complete r-partite graph for , and a complete bipartite graph for .
In [57,60], it is proved that the Turán graph gives the maximum Zagreb indices and reduced second Zagreb index among all graphs of order n with chromatic number . From the proof of these results, we can formulate the following proposition. We denote .
Proposition 4.
Let such that for some integers with . Additionally, let . Then we have
3. Maximum and Minimum in Trees and Unicyclic Graphs
A star, denoted is a tree with only one vertex of degree greater than one. A double-star is a tree with diameter 3. Let be a double-star, where degrees of non-pendant vertices are a and b. Then we have
and
If then we can easily get
Since each edge in a tree is cut edge, one can easily obtain the following theorem using the above result with Proposition 2.
Theorem 1.
Let T be a tree of order n and . Then
with equality if, and only if,
- (i)
- T is isomorphic to star graph if ,
- (ii)
- T is isomorphic to star graph or double-star if .
Before determining the minimum value of for trees of order n, we introduce the following transformation:
Transformation D:
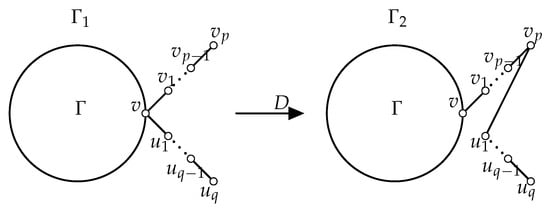
Let be a connected graph of order greater than one with . Let be the graph obtained from by attaching two new paths and of length p and q, respectively, at v, where and are distinct new vertices. A graph is obtained from by deleting and adding , as shown in Figure 1.

Figure 1.
Transformation D.
Now, we prove a lemma that shows that the general reduced second Zagreb index is decreasing by Transformation D when and it will play an important role in the proof of the next result.
Lemma 1.
Let and be the graphs in Figure 1.
- (i)
- Let . Then .
- (ii)
- Let and . Then if .
- (iii)
- Let and . Then .
Proof.
Repeating the Transformation D, any tree can be changed into a path. Thus, we can obtain the next theorem.
Theorem 2.
Let T be a tree of order n and . Then
with equality if, and only if, .
We now determine the extremal unicyclic graphs with respect to general reduced second Zagreb index. First, we give a sharp upper bound of of graphs from the class of connected unicyclic graphs of order n with girth g, denoted by when . Let be a unicyclic graph of order n with girth g and pendant vertices (see, Figure 2), where is the number of pendant vertices adjacent to i-th vertex of the cycle (the vertices in the cycle are numbered clockwise). Then, clearly and . We denote by and g are integers with the class of all unicyclic graphs (), such that and , and , such that .
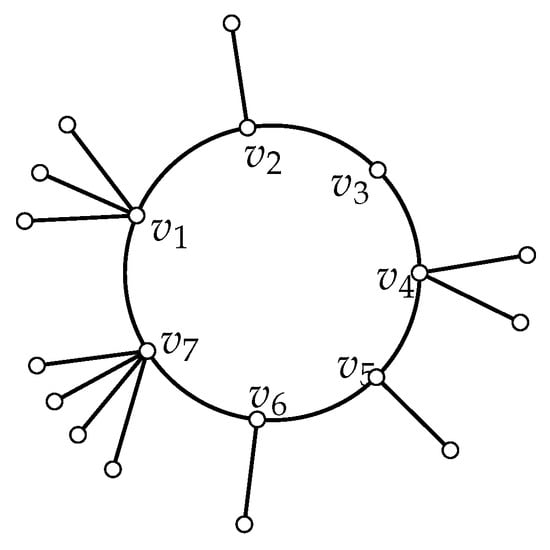
Figure 2.
The graph .
Lemma 2.
Let be an integer, α be a real number and , where are non-negative integers, such that . Then
Proof.
By the definition of , we have
This completes the proof of the lemma. □
Note that for the graph , depends only on n and g. We denote by the set of all unicyclic graphs , such that and , where n and g are integers with . Denote by the set of graphs of order n with clique number and all the remaining N vertices are pendant.
Theorem 3.
Let , and . Then
with equality if, and only if,
- (i)
- when ,
- (ii)
- when and ,
- (iii)
- when and .
Proof.
Let be a unicyclic graph of order n with girth g and maximum -value. Then we have
By Proposition 2, all cut edges of are pendant. Hence, there exist non-negative integers such that and . Let be the vertices of the graph whose degrees are greater than one. Then we have for . From (2), we obtain
where .
Case 1.
. From the equality in (5), we obtain , that is, as for . So we have . Additionally, by Lemma 2, one can easily check that
when . Hence, the equality holds if, and only if, .
Case 2.
and . From the equality in (5), we obtain
that is,
that is,
If , then for all (as for all ), that is, , that is, . Otherwise, . From (7), we obtain , that is, . From (6), we obtain
Therefore, or . Without loss of generality, we can assume that . Hence the equality holds if, and only if, , and . Hence .
Case 3.
Corollary 1.
Let Γ be a unicyclic graph of order n with . Then
with equality if, and only if,
- (i)
- when ,
- (ii)
- when .
Proof.
Denote by g the girth of the graph . Then, by Theorem 3 and , we have
with equality if and only if
- (i)
- when ,
- (ii)
- when .
By this, the proof is completed. □
Let be a unicyclic graph obtained from cycle by joining an edge between the vertex with a pendant vertex of a path of length , , that is, . The graph has thus vertices (see, Figure 3). By relabeling, we can assume that . Let be a class of unicyclic graphs of order n with girth g, is defined as
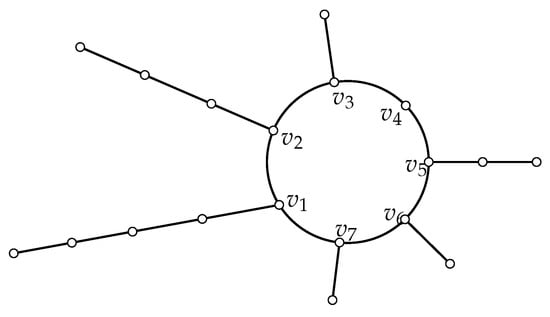
Figure 3.
The graph in .
Repeating Transformation D, any tree T attached to a graph can be changed into a path, as shown in Figure 4, and the general reduced second Zagreb index decreases when by Lemma 1. Thus, the next lemma follows immediately.
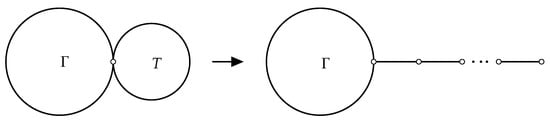
Figure 4.
Repeating Transformation D.
Lemma 3.
Let with minimum -value and . Then .
Theorem 4.
Let with minimum -value and . Then .
Proof.
By Lemma 3, we have . So there exist non-negative integers such that . If for , then we consider the graph . By definition of , we have
as for all . This is a contradiction that tells us . The proof of the theorem is completed. □
An elementary calculation yields
Corollary 2.
Let Γ be a unicyclic graph of order n with . Then
with equality if, and only if, .
4. Lower Bounds on
Denote by and the class of connected graphs of order n with at least k cut edges and the class of connected graphs of order n with exactly k cut edges. In [58], the extremal graphs with maximum from and were characterized. However, the extremal graphs with minimum from and were not characterized. In this section, we give the lower sharp bounds on for these two classes of graphs. Let be the class of connected graphs of order n with girth g. All trees of order n belong to the class . The next two results immediately follow from our results in the previous section.
Theorem 5.
Let Γ be a graph in and . Then
with equality if, and only if,
Proof.
Let be a set of non-cut edges in , such that is a tree. Then we have
by Proposition 1 and Theorem 2. Equality holding if, and only if, and
This completes the proof. □
Theorem 6.
Let Γ be a graph in and . Then
with equality if, and only if, .
Proof.
Let C be a cycle of length g in . Let be a graph in , obtained by deleting the edges (which do not lie on the cycle C) of . By Proposition 1, Theorem 4 and (8), we obtain
Equality holding if, and only if, and . □
We now consider cyclic graphs in . Thus we have , but there is no graph of order n with k cut edges if . Therefore, we assume that . Now, we characterize the extremal cyclic graphs from with minimum using Theorem 6. Let be the set of all unicyclic graphs , such that . Because the number of cut edges in the graph is at least k, we have the girth of is at most .
Theorem 7.
Let Γ be a cyclic graph from with minimum . Let be positive integers, such that and . Then
- (i)
- if .
- (ii)
- if .
- (iii)
- if .
Proof.
Let g be the girth of . Then, by Theorem 6, , and we have Equation (8). Additionally, we have as . Hence, we obtain, easily, the required result and this completes the proof. □
Note that if , then all graphs in belong to the set of cyclic graphs in and . Therefore, we can obtain the following theorem that determines the extremal graphs of order n with k cut edges having minimum when .
Theorem 8.
Let Γ be a cyclic graph in with minimum and , . Then, .
5. Upper Bounds on
In this section, we give some upper bounds on the general reduced second Zagreb index . Recall that a complete split graph is defined as the graph join , where is the complement of the complete graph on vertices.
Theorem 9.
Let Γ be a graph of order n with independence number γ and . Then
with equality if, and only if, .
Proof.
Let be a graph of order n with independence number and maximum . Additionally, let S be an independent set in such that . If then there exist non-adjacent vertices u and v so that . For the graph , the order is n and the independence number is . By Proposition 1, we have
and it is a contradiction to the fact that is maximum for the set of graphs of order n with independence number . Thus, we have and
One can easily check that
From this, the theorem is proved. □
Recall that is the set of graphs of order n with clique number , and all the remaining r vertices are pendant. Denote by the class of connected graphs of order n with r pendant vertices. Then, we have . For any graph in , there are some non-negative integers such that , and the graph is constructed by attaching pendent vertices to the i-th vertex of a complete graph , denoted (see Figure 5). Clearly, we have .

Figure 5.
All graphs in . For example, the fourth graph is denoted by .
Lemma 4.
Let Γ be a graph in and . If is maximum in then .
Proof.
If , then there exist two vertices u and v in , such that and . Denote by . Then, and by Proposition 1, we obtain , a contradiction as is maximum in . Hence . □
Theorem 10.
Let Γ be a graph with maximum in and . Then
- (i)
- , where for if .
- (ii)
- if .
- (iii)
- if .
Proof.
By Lemma 4, we have . Therefore, for some integers , such that and . By the definition of , we obtain
- (i)
- Let . Suppose that there are integers and such that . Then, we consider non-negative integers with , and for all . Then we getUsing this result in (9), we conclude that is not maximum as . This is a contradiction. Hence , where for .
- (ii)
- Let . ThenHence .
- (iii)
- Let . One can easily see that with equality holding if, and only if, and . Using this result in (9), we obtainwith equality if, and only if, and , that is, if, and only if, .
This completes the proof of the theorem. □
From Proposition 3, the following theorem is obtained.
Theorem 11.
Let Γ be a -free graph of order n with m edges. Additionally, let be positive integers and α be real number, such that and . Then
with equality if, and only if, Γ is isomorphic to a regular complete r-partite graph for and a complete bipartite graph for .
Proof.
From the definition of with Proposition 3, we obtain
as . Moreover, the equality holds in (10) if, and only if, is isomorphic to a complete bipartite graph for and a regular complete r-partite graph for . This completes the proof. □
Note that if or and then for all , Theorem 11 holds as . Moreover, for all , the following theorem, which is a generalization of Theorem 2.3 in [57] holds. Denote the graph of order 4 with size 1.
Theorem 12.
Let Γ be a -free graph with n vertices and edges. If and , then
with equality if, and only if, Γ is isomorphic to a regular complete r-partite graph.
Proof.
If , or and , then we obtain and by Theorem 11, the proof is finished. Hence, we have only the following two cases.
Case 1.
Case 2.

and . The right-hand side of (11) is equal to . For , we have . Let now . For , we obtain
as and . Let . Then clearly . For , is . If there is a graph H of order 4 such that is , then by the previous case, we have
as . For , is the fork graph. Of course, the strict inequality in (11) holds for the fork. Let . Then has at least one vertex of degree less than three by the handshaking lemma. Hence
as and .
Let now . If or , then is or . For , all - free graphs of order 5 with m edges and maximum degree 4 are displayed in Figure 6. One can easily check that the strict inequality in (11) holds for all of the graphs in Figure 6. □

Figure 6.
All - free graphs of order 5 with m () edges and .
Corollary 3.
Let Γ be a -free graph with n vertices and edges. If , then
with equality if, and only if, Γ is isomorphic to a regular complete r-partite graph.
We give now an upper bound on , which is a generalization of Theorem 2.5 in [57] for the class of triangle-free graphs.
Theorem 13.
Let Γ be a connected triangle-free graph of order with edges and . Then
with equality if, and only if, .
Proof.
Let be an edge in such that is maximum. Since is triangle free, we have , which means that . Therefore
Let us consider a function
One can easily see that
Since and , we have , that is,
Since is connected and , we have . Using these results in (14), we obtain
The first part of the proof is done.
Suppose now that equality holds in (12). Then, all inequalities in the above must be equalities. From the equality in (13), we have
From the equality in (14), we have
Moreover, we have . Thus, we have . From this we conclude that or . Let be any vertex in which is different from u and v. Then is adjacent to either u or v, because is triangle free and . Suppose that . Then, all neighbors of are adjacent to v as is triangle-free and . Hence . If is any vertex adjacent to , then . Similarly, we get . From (15), we have and . Hence .
Conversely, let . Then
□
Let be the set of graphs of order n with chromatic number k. In [57,60], the extremal graphs of order n with chromatic number k respect to and were characterized. We now generalize these results. From the definition of and Proposition 1, we obtain, easily, the following lemma.
Lemma 5.
Let be a graph with maximal and . Then .
Theorem 14.
Let and . If is maximum in , then .
Proof.
Let such that is maximum. From Lemma 5, . By contradiction we prove that . For this we assume that . Then, there are two parts of the partitions in whose sizes are and , such that for .
Consider the complete k-partite graph and by definition of , we have
From Proposition 4, we have
Additionally, by the definition of a complete k-partite graph, we have
Thus, we obtain
This is contradicts the fact that is maximum. Hence and the proof is completed. □
Author Contributions
Conceptualization, L.B., B.H. and K.C.D.; investigation, L.B., B.H. and K.C.D.; writing—original draft preparation, L.B., B.H. and K.C.D.; writing—review and editing, L.B., B.H. and K.C.D. All authors have read and agreed to the submitted version of the manuscript.
Funding
This work is supported by Mongolian Foundation for Science and Technology (Grant No. SHUTBIKHKHZG-2022/162). K. C. Das is supported by National Research Foundation funded by the Korean government (Grant No. 2021R1F1A1050646).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; MacMillan: New York, NY, USA, 1976. [Google Scholar]
- Harary, F. Graph Theory; Addison–Wesley: Reading, PA, USA, 1969. [Google Scholar]
- Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors; Wiley–VCH: Weinheim, Germany, 2000. [Google Scholar]
- Gutman, I.; Trinajstić, N. Graph theory and molecular orbitals. Total π-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 1971, 17, 535–538. [Google Scholar] [CrossRef]
- Abdo, H.; Dimitrov, D.; Gutman, I. On the Zagreb indices equality. Discret. Appl. Math. 2012, 160, 1–8. [Google Scholar] [CrossRef]
- Borovicanin, B.; Das, K.C.; Furtula, B.; Gutman, I. Bounds for Zagreb Indices. MATCH Commun. Math. Comput. Chem. 2017, 78, 17–100. [Google Scholar]
- Caporossi, G.; Hansen, P.; Vukičević, D. Comparing Zagreb indices of cyclic graphs. MATCH Commun. Math. Comput. Chem. 2010, 63, 441–451. [Google Scholar]
- Chen, S.; Zhou, H. Extremal Zagreb indices of unicyclic graphs. Ars Comb. 2010, 97, 241–248. [Google Scholar]
- Das, K.C.; Ali, A. On a Conjecture about the Second Zagreb Index. Discret. Math. Lett. 2019, 2, 38–43. [Google Scholar]
- Das, K.C.; Akgünes, N.; Togan, M.; Yurttas, A.; Cangül, I.N.; Cevik, A.S. On the first Zagreb index and multiplicative Zagreb coindices of graphs. Analele Stiintifice Ale Univ. Ovidius Constanta 2016, 24, 153–176. [Google Scholar] [CrossRef]
- Das, K.C.; Gutman, I.; Horoldagva, B. Comparison between Zagreb indices and Zagreb coindices of trees. MATCH Commun. Math. Comput. Chem. 2012, 68, 189–198. [Google Scholar]
- Das, K.C.; Xu, K.; Nam, J. Zagreb indices of graphs. Front. Math. China 2015, 10, 567–582. [Google Scholar] [CrossRef]
- Deng, H. A unified approach to the extremal Zagreb indices for trees, unicyclic graphs and bicyclic graphs. MATCH Commun. Math. Comput. Chem. 2007, 57, 597–616. [Google Scholar]
- Eliasi, M.; Ghalavand, A. Trees with the minimal second Zagreb index. Kragujev J. Math. 2018, 42, 325–333. [Google Scholar] [CrossRef]
- Elphick, C.; Reti, T. On the relations between the Zagreb indices, clique numbers and walks in graphs. MATCH Commun. Math. Comput. Chem. 2015, 74, 19–34. [Google Scholar]
- Farukh, E.; Muhammad, H.; Roslan, H. On topological aspects of bilayer germanium phosphide. J. Math. Comput. Sci. 2020, 22, 347–362. [Google Scholar]
- Gutman, I.; Das, K.C. The first Zagreb indices 30 years after. MATCH Commun. Math. Comput. Chem. 2004, 50, 83–92. [Google Scholar]
- Gutman, I.; Milovanović, E.; Milovanović, I. Beyond the Zagreb indices. AKCE Int. J. Graphs Comb. 2020, 17, 74–85. [Google Scholar] [CrossRef]
- Habibi, N.; Zadeh, T.D.; Ashrafi, A. Extremal tetracyclic graphs with respect to the first and second Zagreb indices. Trans. Comb. 2016, 5, 35–55. [Google Scholar]
- Hansen, P.; Vukićevixcx, D. Comparing the Zagreb indices. Croat. Chem. Acta 2007, 80, 165–168. [Google Scholar]
- Ali, A. Tetracyclic graphs with maximum second Zagreb index: A simple approach. Asian-Eur. J. Math. 2018, 2018, 1850064. [Google Scholar] [CrossRef]
- Horoldagva, B. Relations between the first and second Zagreb indices of graphs. In Bounds in Chemical Graph Theory-Mainstreams; Gutman, I., Furtula, B., Das, K.C., Milovanovic, E., Milovanovic, I., Eds.; Mathematical Chemistry Monographs; University of Kragujevac Rectorate: Kragujevac, Serbia, 2017; Volume 20, pp. 69–81. [Google Scholar]
- Horoldagva, B.; Das, K.C. On Zagreb Indices of Graphs. MATCH Commun. Math. Comput. Chem. 2021, 85, 295–301. [Google Scholar]
- Horoldagva, B.; Das, K.C. Sharp lower bounds for the Zagreb indices of unicyclic graphs. Turk. J. Math. 2015, 39, 595–603. [Google Scholar] [CrossRef]
- Jahanbani, A.; Sheikholeslami, S.M.; Khoeilar, R. General reduced second Zagreb index of graph operations. Asian-Eur. J. Math. 2021, 14, 2150082. [Google Scholar]
- Lang, R.; Deng, X.; Lu, H. Bipartite graphs with the maximal value of the second Zagreb index. Bull. Malays. Math. Sci. Soc. 2013, 36, 1–6. [Google Scholar]
- Li, S.; Zhao, Q. On acyclic and unicyclic conjugated graphs with maximum Zagreb indices. Util. Math. 2011, 86, 115–128. [Google Scholar]
- Li, S.; Zhou, H. On the maximum and minimum Zagreb indices of graphs with connectivity at most k. Appl. Math. Lett. 2010, 23, 128–132. [Google Scholar] [CrossRef]
- Liu, B.; Gutman, I. Upper bounds for Zagreb indices of connected graphs. MATCH Commun. Math. Comput. Chem. 2006, 55, 439–446. [Google Scholar]
- Liu, M.; Liu, B. The second zagreb indices and wiener polarity indices of trees with given degree sequences. MATCH Commun. Math. Comput. Chem. 2012, 67, 439–450. [Google Scholar]
- Liu, J.-B.; Wang, C.; Wang, S.; Wei, B. Zagreb indices and multiplicative Zagreb indices of eulerian graphs. Bull. Malays. Math. Sci. Soc. 2019, 42, 67–78. [Google Scholar] [CrossRef]
- Ma, X.; Bian, H.; Yu, H. Schultz and Zagreb indices in corona of two graphs. Ars Comb. 2013, 112, 55–64. [Google Scholar]
- Mingyao, Z.; Hanyuan, D. An open problem on the exponential of the second zagreb index. MATCH Commun. Math. Comput. Chem. 2021, 85, 367–373. [Google Scholar]
- Mojdeh, D.A.; Habibi, M.; Badakhshian, L.; Rao, Y. Zagreb indices of trees, unicyclic and bicyclic graphs with given (total) domination. IEEE Access 2019, 7, 1–7. [Google Scholar] [CrossRef]
- Nikolić, S.; Kovačević, G.; Milićević, A.; Trinajstić, N. The Zagreb indices 30 years after. Croat. Chem. Acta 2003, 76, 113–124. [Google Scholar]
- Réti, T. On the relationships between the first and second Zagreb indices. MATCH Commun. Math. Comput. 2012, 68, 169–188. [Google Scholar]
- Selenge, T.; Horoldagva, B.; Das, K.C. Direct comparison of the variable Zagreb indices of cyclic graphs. MATCH Commun. Math. Comput. 2017, 78, 351–360. [Google Scholar]
- Shafique, S.; Ali, A. On the reduced second Zagreb index of trees. Asian-Eur. J. Math. 2017, 10, 1750084. [Google Scholar] [CrossRef]
- Stevanovič, D.; Milanixcx, M. Improved inequality between Zagreb indices of trees. MATCH Commun. Math. Comput. Chem. 2012, 68, 147–156. [Google Scholar]
- Ali, A.; Das, K.C.; Akhter, S. On the extremal graphs for second Zagreb index with fixed number of vertices and cyclomatic number. Miskolc Math. Notes 2022, 23, 41–50. [Google Scholar] [CrossRef]
- Yiqiao, W.; Lina, Z. Computation on the difference of Zagreb indices of maximal planar graphs with diameter two. Appl. Math. Comput. 2020, 377, 125187. [Google Scholar]
- Shao, Z.; Siddiqui, M.K. Computing Zagreb indices and Zagreb polynomials for symmetrical nanotubes. Symmetry 2018, 10, 244. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, Q.; Chen, Y. New bounds on Zagreb indices. J. Math. Ineq. 2017, 11, 167–179. [Google Scholar] [CrossRef]
- Zhao, Q.; Li, S. On the maximum Zagreb indices of graphs with k cut vertices. Acta Appl. Math. 2010, 111, 93–106. [Google Scholar] [CrossRef]
- Cioabǎ, S.M. Sums of powers of the degrees of a graph. Discret. Math. 2006, 306, 1959–1964. [Google Scholar] [CrossRef]
- Peled, U.N.; Petreschi, R.; Sterbini, A. (n, e)-graphs with maximum sum of squares of degrees. J. Graph Theory 1999, 31, 283–295. [Google Scholar] [CrossRef]
- Das, K.C. Maximizing the sum of the squares of the degrees of a graph. Discret. Math. 2004, 285, 57–66. [Google Scholar] [CrossRef]
- Bollobás, B.; Erdos, P.; Sarkar, A. Extremal graphs for weights. Discret. Math. 1999, 200, 5–19. [Google Scholar] [CrossRef]
- Wang, H.; Yuan, S. On the sum of squares of degrees and products of adjacent degrees. Discret. Math. 2016, 339, 1212–1220. [Google Scholar] [CrossRef]
- de Caen, D. An upper bound on the sum of squares of degrees in a graph. Discret. Math. 1998, 85, 245–248. [Google Scholar] [CrossRef]
- Li, S.; Zhang, L.; Zhang, M. On the extremal cacti of given parameters with respect to the difference of Zagreb indices. J. Comb. Opt. 2019, 38, 421–442. [Google Scholar] [CrossRef]
- Furtula, B.; Gutman, I.; Ediz, S. On difference of Zagreb indices. Discret. Appl. Math. 2014, 178, 83–88. [Google Scholar] [CrossRef]
- Du, W.; Li, X.; Shi, Y. Algorithms and extremal problem on Wiener polarity index. MATCH Commun. Math. Comput. Chem. 2009, 62, 235–244. [Google Scholar]
- Horoldagva, B.; Das, K.C.; Selenge, T. Complete characterization of graphs for direct comparing Zagreb indices. Discret. Appl. Math. 2016, 215, 146–154. [Google Scholar] [CrossRef]
- An, M.; Xiong, L. Some results on the difference of the Zagreb indices of a graph. Bull. Aust. Math. Soc. 2015, 92, 177–186. [Google Scholar] [CrossRef]
- Horoldagva, B.; Buyantogtokh, L.; Dorjsembe, S. Difference of Zagreb indices and reduced second Zagreb index of cyclic graphs with cut edges. MATCH Commun. Math. Comput. Chem. 2017, 78, 337–350. [Google Scholar]
- Buyantogtokh, L.; Horoldagva, B.; Das, K.C. On reduced second Zagreb index. J. Comb. Opt. 2020, 39, 776–791. [Google Scholar] [CrossRef]
- Horoldagva, B.; Buyantogtokh, L.; Das, K.C.; Lee, S.-G. On general reduced second Zagreb index of graphs. Hacet. J. Math. Stat. 2019, 48, 1046–1056. [Google Scholar] [CrossRef]
- Zhou, B. Remarks on Zagreb indices. MATCH Commun. Math. Comput. Chem. 2007, 57, 591–596. [Google Scholar]
- Xu, K. The Zagreb indices of graphs with a given clique number. Appl. Math. Lett. 2011, 24, 1026–1030. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).