Abstract
The discovery of hybrid carbon nanotubes shows the tendency toward the improvement of heat transfer performance in comparison to various classical fluids. This paper expands the novelty in utilizing the hybrid carbon nanotubes over vertical stretching/shrinking cylinder in presence of hydromagnetic and thermal radiation. It is essential to analyze the hydromagnetic due to its high potential capability especially in drug and gene release, hyperthermia effects as well as cell separation and manipulation in bio-medical field. The investigation on thermal radiation effect is added in this current study as it enhances the rate of heat transfer. To initiate this problem, partial differential equations (PDE) for the hybrid nanofluid flow with relevant boundary conditions (BCs) is set up and transformed into an ordinary differential equation (ODE). Adopting the similarity solutions and numerically solved using bvp4c (MATLAB). Findings on the variation of local Nusselt number, skin friction coefficient, shear stress and local heat flux having the effects of magnetic, curvature, ϒ, thermal radiation, Nr, mixed convection parameter, as well as volume fraction of nanoparticles, are demonstrated and elaborated in detail. Moreover, the research reveals that duality of solutions occurs when the buoyance force is in opposing flow with respect to the fluid motion, , as well as shrinking area, . The occurrence of magnetic reduces the heat transfer as well as skin friction coefficient. In addition, the skin friction coefficient and local Nusselt number tend to improve as volume fraction of nanoparticles and curvature are increased. In contrast, the low of thermal radiation enhance the heat transfer. Indeed, the consequences of using hybrid carbon nanotubes help intensify the skin friction coefficient and Nusselt number compared to SWCNT nanofluid and MWCNT nanofluid. These crucial findings may benefit the scientists and academicians hence giving an add-on value to their expertise. A stability analysis must be performed since there exists a non-unique solution throughout the computation.
Keywords:
hybrid carbon nanotubes; vertical stretching/shrinking cylinder; thermal radiation; MHD; stability analysis MSC:
80A05; 80M20; 76D10
1. Introduction
Over the past few decades, a series of discussions regarding convection has been tackled by researchers. Initially, the process of convection ensues once the heat is transmitted, hence exchanging the heat from the hot to the cool position. Convection can occur in three different ways: forced, free (natural), and mixed. The most favorable problem is in mixed convection, which combines forced and natural convection, manifesting most prominently in the movement of air boundary layers, solar collectors, heat exchangers, electronic devices, as well as nuclear reactors. When buoyancy forces in forced convection or forced flow in free convection are significant, these processes occur. [1] pioneered researchers in exploring the problem towards a vertical surface. The author investigates the two-dimensional (2D) flow of a uniform stream past an impermeable vertical surface embedded in a saturated porous medium. Later, [2] extended the knowledge into 2D stagnation flows, taking into account both cases of arbitrary wall temperature as well as arbitrary surface heat flux variations. Furthermore, [3] took into account the effect of viscous dissipation, which affects both shear stress and heat transfer at the surface, in their research. Meanwhile, [4] portrayed the issue in sphere coordinates, which took into account viscoelastic nanofluid as its nanoparticles. The findings show that the velocity and shear stress is reduced when the elasticity parameter is prominent in the flow. [5] revealed their discovery of the problem of a semi-infinite upward flat plate for both opposing as well as assisting buoyancy-induced flow cases. The authors discovered that dual solutions occurred in the opposing flow case. More discussions can be found [6,7,8,9,10] regarding mixed convection problems that have been intensively enfolded by numerous researchers in various surfaces and effects.
Due to its numerous applications in engineering and science, and technology, stagnation point flow represents among the most significant problems in fluid dynamics. The early idea of formulation analytically 2D stagnation point flow originated by [11] and soon [12] considered the problem of steady flow near the surface of a cylinder in a stream. Additionally, researchers added the problem over cylinder geometry. The issue of axisymmetric stagnation flow over an infinite stationary circular cylinder’s precise solution was originally revealed by [13]. Compilation of study conducted by [14,15,16] highlighted the stagnation point flow on steady and unsteady flow over moving and circular cylinders. Later, [17] proceeded with his work and found out that lengthening the curvature’s surface helps in delaying the blow-up time. Furthermore, [18] examines the lower stagnation point flow over a horizontal circular cylinder of brinkman-viscoelastic fluid. [19] explore the use of homogeneous and heterogenous reaction over a permeable cylinder. The work on stagnation flow with the effect of slip continued to be investigated by [20]. Extended problems that were covered by other researchers by taking into account different effects and surfaces can be found in this literature [21,22,23,24,25] for more details.
Since the initial discovery of carbon nanotubes (CNTs) was made by the Russian researchers [26], followed by [27,28] in 1991 and 1993, respectively. Due to their remarkable structure and exceptional physical properties, they have garnered significant amount of interest from researchers over the past few decades. The theoretical study has been published by numerous researchers with regards to different surfaces and effects. Through the use of RSM, [29] investigate the marginal impact of thermal radiation on the enhancement of heat transfer associated with Darcy-Forchheimer (DF) flow in carbon nanotubes along a stretched rotating surface. [30] examined magnetic effect over a vertically moving rotating disc. Demonstration on long chain hydrocarbons flows through carbon nanotubes (CNTs) was covered by [31]. Meanwhile, [32] discourse the attractive aspects of suction/injection and heat generation/absorption effects in the flow. It is noted that the suction effect and heat-absorption parameters increase the range of the solution. In addition, the rate of heat transfer for hybrid carbon nanotube was higher when compared with carbon nanotube and ordinary fluid.
However, the use of carbon nanotubes in biomedical, biotechnology and bio-engineering field are not a new dawn to scientists and researchers. Instead, the carbon nanotubes have the potential to be used as therapeutically beneficial nanostructures due to their extremely large surface area, rich electronic polyaromatic structure, low weight but excellent mechanical strength, also exceptional chemical and thermal stability [33,34,35]. In some circumstances, the CNTs show a remarkable ability when we combined with external magnetic properties. They will be high functionalized in biomedical application especially as a targeted drug delivery agent [36,37]. Furthermore, another discernible advantage of using magnetic CNTs is to look similar to a needle shape, which allows easy penetration and movement through cell walls and bloods, respectively, since they have less resistance [38]. The outstanding reviews made by [39] covers on latest advance in the synthesis and application of magnetic carbon nanotubes.
Thermal radiation is a process by which energy is emitted directly from the radiated surface in the form of an electromagnetic wave in all direction. From the engineering and physical point of view, thermal radiation effect has a pivotal role in the flow of different liquid and heat transfer. Thermal radiation is found to be useful in engineering processes which require high operating temperature. These include the design of the nuclear plant, gas turbine, aircraft, space vehicle, reliable equipment, satellite etc. [40] pioneered the study on aircraft structure. Series of literature with regards on aircraft structure can be seen in [41,42,43]. However, the theoretical work on unsteady stagnation point nanofluid flow with convective boundary conditions was carried out by [44]. Later, [45] analyzed the mixed convection problem by taking into account the effect of Soret and Dufour. [46] studied simultaneous impact of thermal radiation and thermophoresis near an inclined porous plate.
Motivated by the above aforementioned works, this paper decomposes the novelty in (i) utilizing hybrid carbon nanotubes as an essential component in improving the heat transfer effectiveness [32], (ii) adding the hydromagnetic effect for this problem due to its high potential capability especially in drug and gene delivery, cell separation and manipulation in bio-medical field [47,48], (iii) analyzing the thermal radiation effect in this current study as it enhances the rate of heat transfer [49], (iv) performing the stability analysis in order to identify the stability of the solution since non-unique solution is expected to exist. This contribution may benefit the scientists and academicians and give add-on value to their expertise.
2. Mathematical Framework
A vertical stretching/shrinking cylinder is passed by a 2D stagnation point flow that is submerged in an SWCNT-MWCNT/water hybrid nanofluid. The following presumptions apply to the illustration shown in Figure 1:
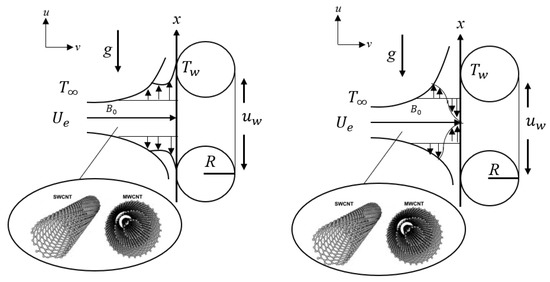
Figure 1.
Physical model and coordinate system representation for vertical stretching/shrinking cylinder.
- A uniform magnetic field is employed in the radial direction. Assuming that we have the low Reynold number, Rm, then the magnetic field formed by induction is trivial compared to the applied magnetic field.
- The fluid velocities are expressed by u and that are in axial coordinate, x and radial coordinate, r, accordingly.
- The surface temperature, is higher than the ambient temperature, .
- The cylinder with radius R is assumed to move in linear velocity, while the free stream velocity is in which L resembles the cylinder’s characteristic length.
- The flow is characterized by the Buoyancy parameter, in which Gr denotes Grashoff number, and Re denotes Reynolds number. Here, the mixed convection regime is generally expressed as the range of , in which and are the upper and lower bounds of the mixed convection flow regime.
In this present problem, we are using various volumes of solid fraction SWCNT dispersed in a constantly 0.01 volume fraction of MWCNT/water to produce SWCNT-MWCNT/ water. Table 1 lists the thermophysical characteristics of the hybrid nanofluid.

Table 1.
Base fluid and nanoparticles numerical values for thermophysical properties [50].
The related governing equation to model the fluid flow for our problem in presence of magnetic field and thermal radiation is as follows: [51,52]
with assumptions of boundary conditions (BCs) [53,54],
where u and denote the component of velocity for x and r axes, accordingly. Meanwhile, and T referring to radiative heat flux and temperature, respectively. Meanwhile, and are kinematic viscosity and magnetic field. Furthermore, the term in Equation (3) may be derived by means of the idea from Rosseland approximation for an optically thick layer [55] which leads to,
The denotes Stefan-Boltzmann constant while refers to the mean absorption coefficient. In an intense absorption flow, it is claimed that Equation (5) is effective at a position far from the boundary layer surface. Moreover, the term may be understood as a linear function of temperature T with the assumption of the temperature distinction within the flow is very minute. Employing Taylor’s expansion of around which denotes the ambient temperature while ignoring the higher order terms, we obtain,
Hence, the right-hand side of Equation (3) can be abridged as,
where, is thermal diffusivity and is radiation parameter [56]. Table 2 condenses all the thermophysical properties that correspond to these parameters.

Table 2.
Thermophysical properties with respect to hybrid nanofluid [57,58].
From Table 2, the description for hybrid nanofluids, nanofluids as well as fluids are denoted by hnf, nf and f, respectively. To present the two distinct nanoparticles’ solid volume fractions, is for SWCNT meanwhile, for MWCNT. Apart from that, s1 is for SWCNT, while s2 is for MWCNT nanoparticles in which S = s1 + s2.
The following similarity variables are added to the model in order to convert the governing equations above into ordinary differential equations [59,60],
where and which identically satisfied Equation (1). Hence, the new momentum and energy equations which similar to the become,
along the BCs,
where is the velocity ratio parameter. Moreover, for case > 0 (cylinder), corresponds to the shrinking flow case, and correlates to the stretching flow case, meanwhile for static flow. Moreover, the related parameter refers to curvature, denotes magnetic, resembles mixed convection in which < 0 for opposing flow, for assisting flow as well as for forced convection flow, whereas Pr denotes Prandtl number. These parameters may be written explicitly as,
where, and .
The physical quantities interest in this research are skin friction coefficient, and local Nusselt number, which are expressed as,
The reduction to ODE for Equation (13) are obtained by using the similarities solution in (8). Hence, the simplified expressions are;
3. Solutions on Stability Analysis
In dealing with the boundary layer flow problem, we might deal with possibility of having zero, unique, multiple, or even ghost solution(s) [61,62,63,64] under some boundary conditions. Commonly, the solution that initially satisfies the far field boundary condition is designated as the first solution for case of multiple solutions (non-unique). Numerous researchers [65,66,67,68] showed that the first solution is stable and reliable solution. However, [69] testified that in certain existence problems, second solution is stable. Due to this, a stability analysis is important to validate the reliability of the solutions. With respect to [70], a temporal stability analysis is discovered. Three vital steps are performed to identify the solutions’ stability. First, by inaugurating a new dimensionless parameter, with a new set of similarity variables in terms of and . Second, we implement the linear eigenvalues equations. Third, to attain the range of possible eigenvalues, the BCs need to be relaxed.
Introduce a new dimensionless time variable, and the similarity transformations with respect to are as follows [71]
In this context, the term t in the expression is the time since the disturbance may decay or grow with time.
By differentiating Equation (15), Equations (2) and (3) are reduced to,
subject to BCs,
According to [72], eigenvalues may be employed as a method of solving the ODEs. Given a set of eigenvalues equations;
in which as well as are set as the small relative with respect to and , accordingly. Meanwhile, refers to an unknown parameter of eigenvalue. The eigenvalues problem with respect to Equations (16) and (17) yields an infinite inequality given by This indicates any early decay or growth of disruptions To investigate the solution’s stability, a small perturbation also needs to be taken into consideration in which and . Moreover, upon differentiating Equation (19) and equating it to Equations (16) and (17) with yields the linearized equations given below:
together with;
The possible eigenvalues range may be obtained by relaxing one of the BCs, which is either or [73]. In this problem, the condition that we relax is and the linear eigenvalues problems (20)–(22) are unfold as . Here, numerical findings for stability were calculated by placing an algorithm in bvp4c MATLAB.
4. Numerical Computation
The set of linear ODEs Equations (9) and (10) together with the boundary conditions Equation (11) are computed using bvp4c (MATLAB). This solver is built in follow a finite difference formula that implements the formulation of three-stage Lobatto IIIa which furnish the 4th-order precision. Details on computation using bvp4c can be seen in [74]. Before initiate the computation, Equations (9) and (10) need to reduce to a set of first order. For instance,
For the BCs of Equation (11), we set:
Note that to implement an acceptable solution, the boundary layer thickness value, the governing parameters, and the initial guess should be specified and guessed accordingly. If there is no warning or error appeared while executing the coding, the numerical solution is said to be acceptable. During the computation, dual solutions are appeared in some array of parameters. The presence of the dual solution was captured by setting two sets of initial guesses for the first and second solutions. These sets of initial guesses will be executed in MATLAB for various trials until they satisfy the boundary conditions and the desired solutions are obtained. Hence, a stability analysis must be performed to confirm the solution’s stability. We have to reduce Equations (20) and (21) together with the relaxation boundary conditions Equation (22) that we have considered. Let us say,
together with Equation (22);
The smallest eigenvalues are attained by taking some values that approximate the critical values obtained from our numerical computation.
5. Analysis of Results
The intention of this section is to discuss on the comprehension of the highlighted parameters’ effect in the model, for instance, the SWCNT/MWCNT concentration volume (, thermal radiation (Nr), magnetic (M), curvature parameter, and mixed convection parameter, towards and our quantities interest of study; the local Nusselt number including the temperature, profiles and velocity, are ingrained in the form of graph from Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25 and Figure 26. Through our graphical computation, the interrelation between the effects with respect to the physical quantities is apparent. In addition, the parameters’ identification that affects the parting of the boundary layer flow may be observed via Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 as well as Figure 16. A comparison of the values of when with the previous studies are presented in Table 3. The data are clearly discernible to be in good agreement, despite the fact that the solutions provided in earlier works are solved in various approaches. As a result, we are confident that the method we picked is appropriate and that the model we developed, the numerical calculations, and the results below are accurate. It is important to note that this confirms the novelty and originality of the model and the findings presented in this research.
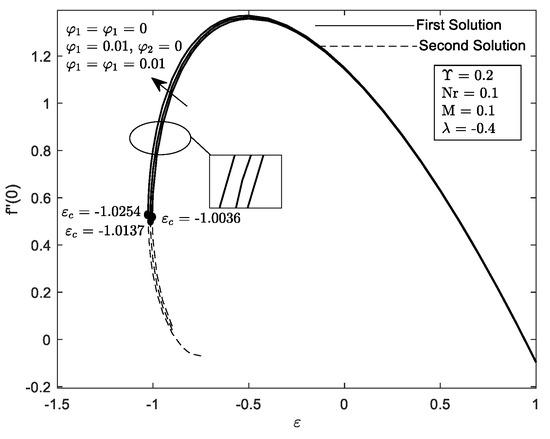
Figure 2.
Variation of with velocity parameter, for types of fluid.
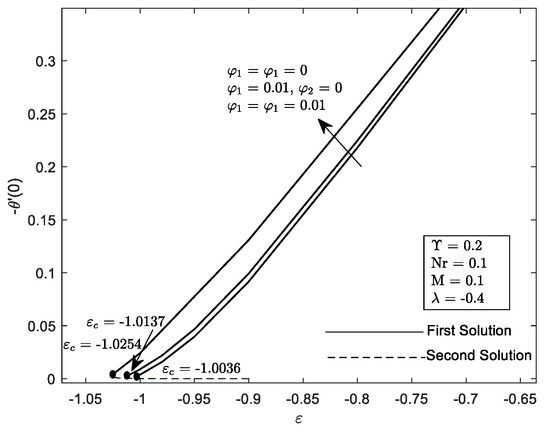
Figure 3.
Variation of with velocity parameter, for types of fluid.
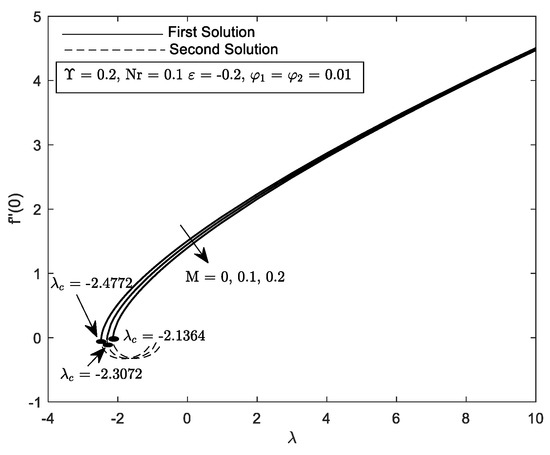
Figure 4.
Variation of with mixed convection parameter, for several values of M.
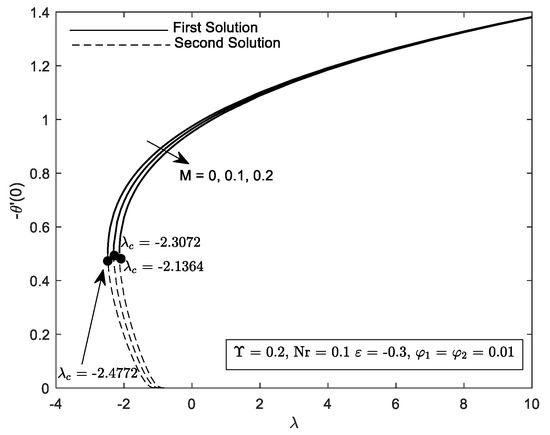
Figure 5.
Variation of with mixed convection parameter, for several values of M.
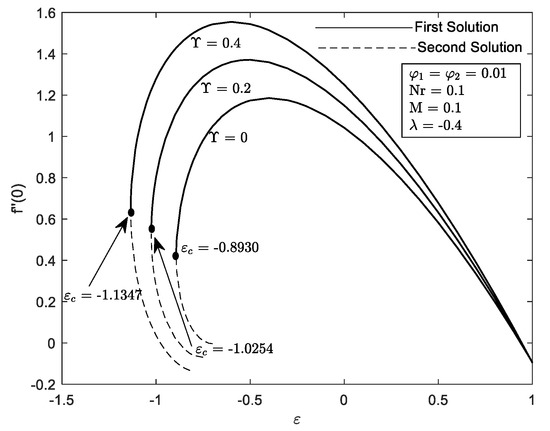
Figure 6.
Variation of with velocity parameter, for different
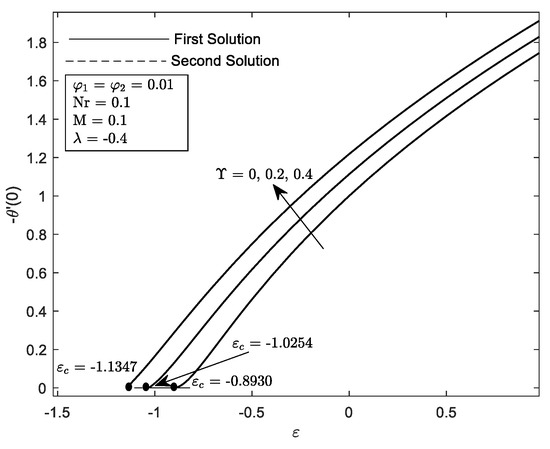
Figure 7.
Variation of with velocity parameter, for different .
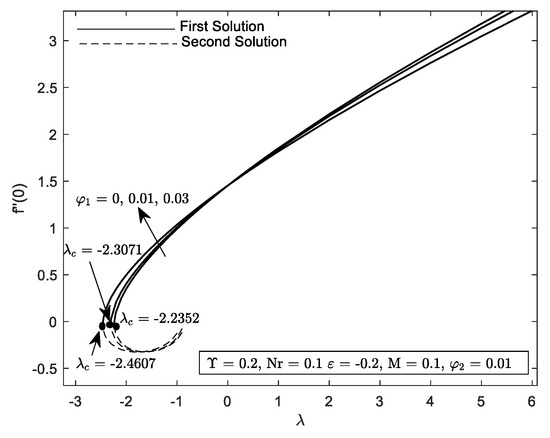
Figure 8.
Variation of with mixed convection parameter, for several values of .
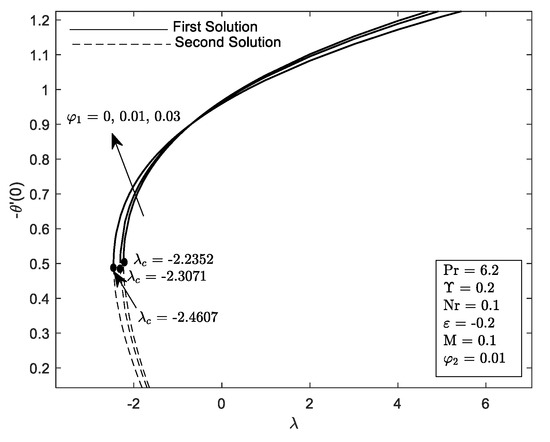
Figure 9.
Variation of with mixed convection parameter, for several values of .
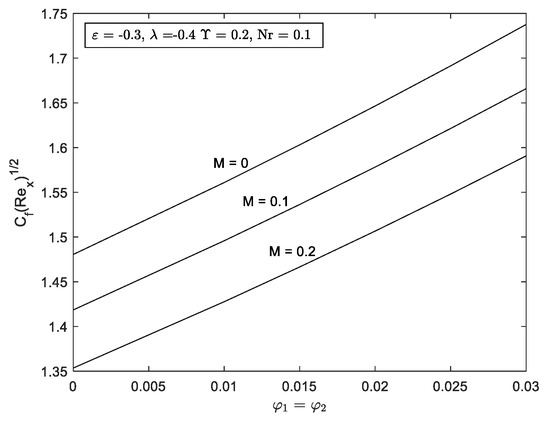
Figure 10.
for several M with
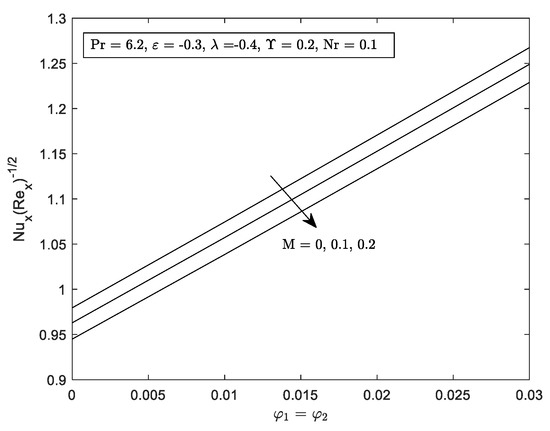
Figure 11.
for several M with
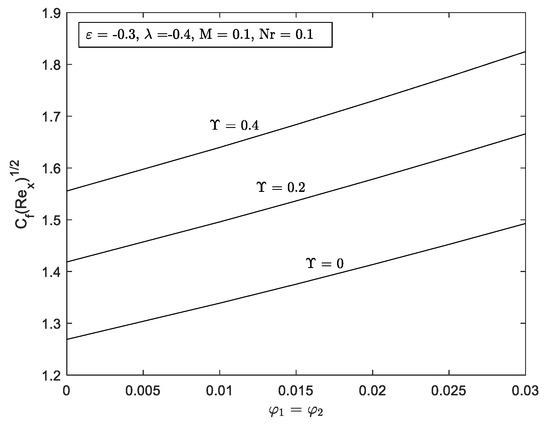
Figure 12.
for several with
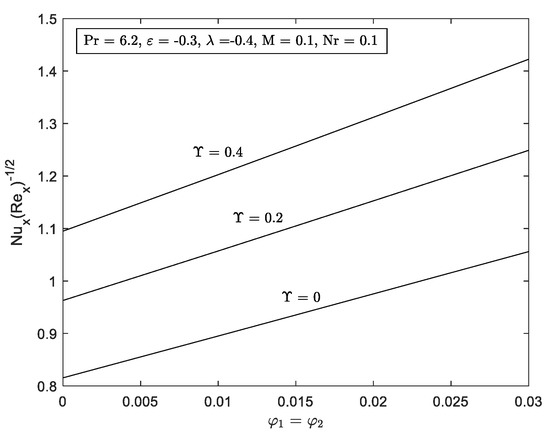
Figure 13.
for several with
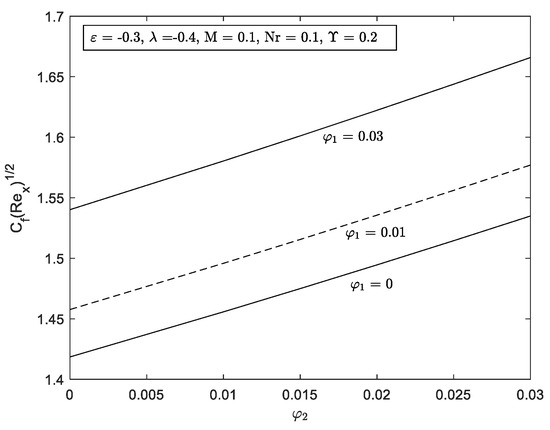
Figure 14.
for several with
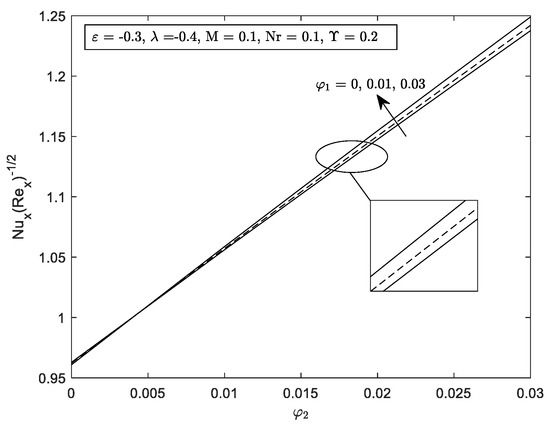
Figure 15.
for several with
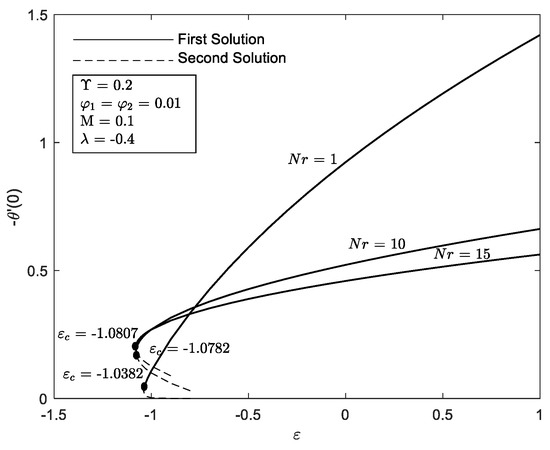
Figure 16.
Variation of with velocity parameter, for several values of
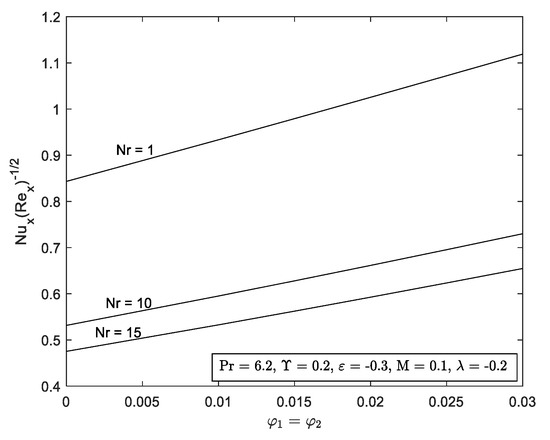
Figure 17.
for several Nr with
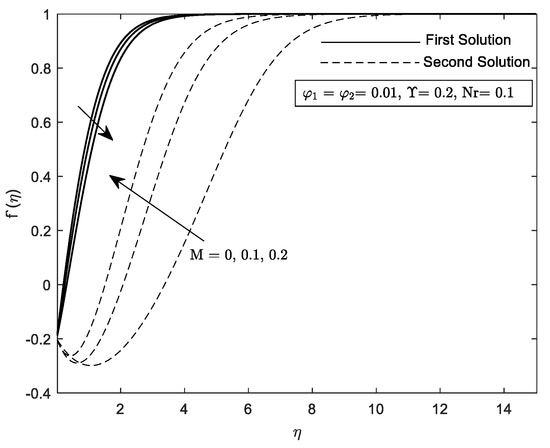
Figure 18.
on different .
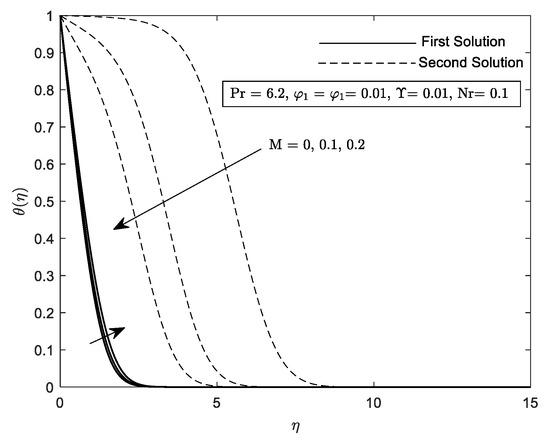
Figure 19.
on different .
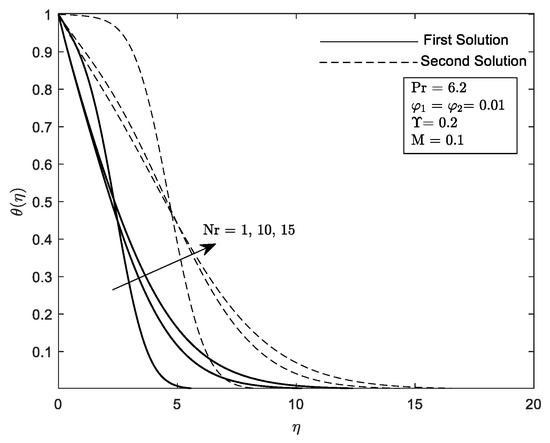
Figure 20.
on different .
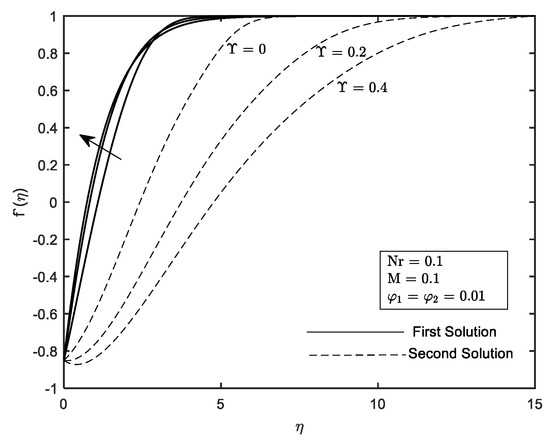
Figure 21.
on different .
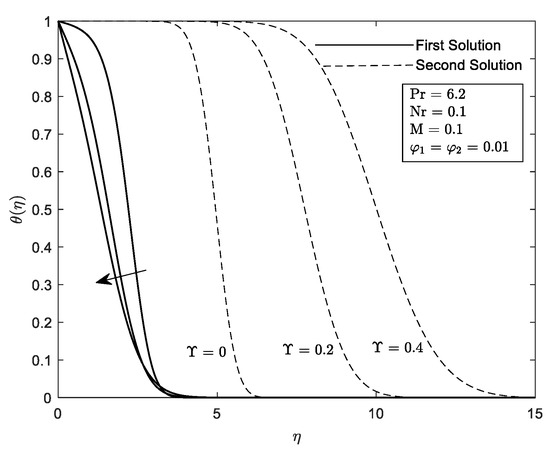
Figure 22.
on different .
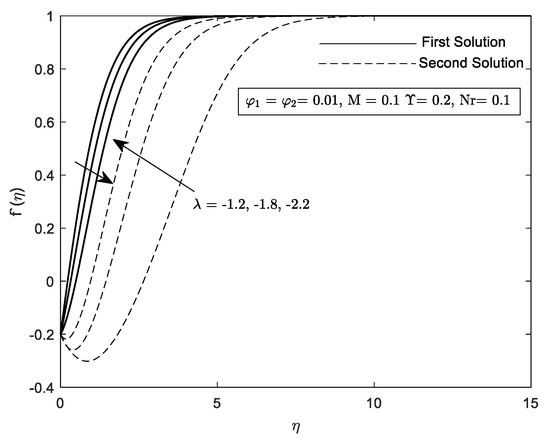
Figure 23.
on different .
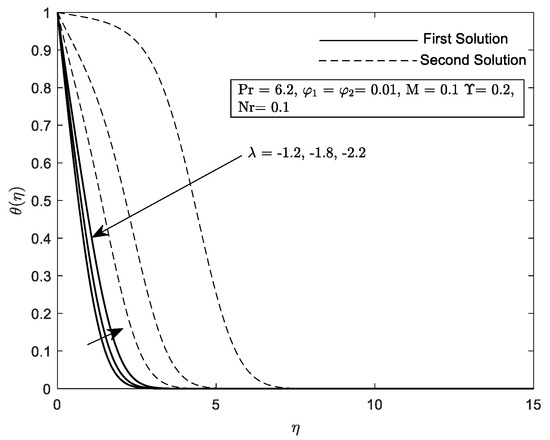
Figure 24.
on different .
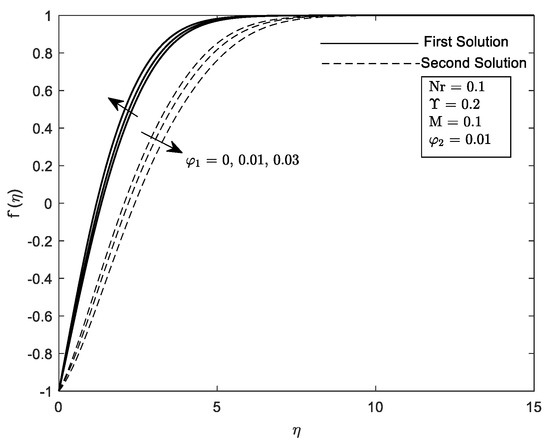
Figure 25.
on different nanoparticles .
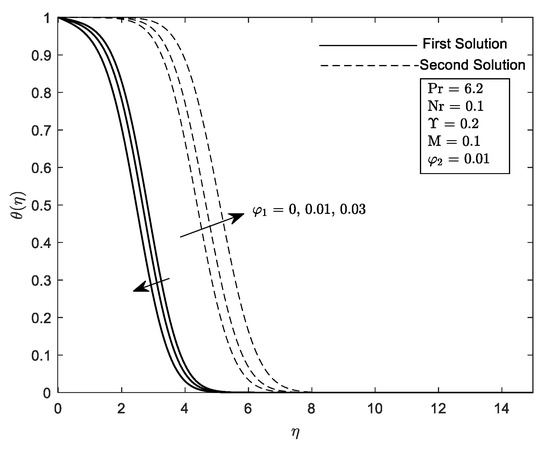
Figure 26.
on different nanoparticles .

Table 3.
Numerical computation for when with several values of and [75,76,77].
In this study, two parameters are set to be fixed, and . While the other governing parameters such as , , and vary for further computation. Graph for local skin friction, and local Nusselt number, are highlighted in Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 17. Profiles for velocity, and temperature, are pictorial in Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25 and Figure 26. Since the thermophysical properties equations relate with the different volume of nanoparticles, hence the range for the thermophysical properties values are: and .
Different concentration of and are selected to illustrate three behavior of the fluid, for instance, (viscous fluid), (SWCNT/water nanofluid) as well as (SWCNT-MWCNT/water hybrid nanofluid) are plotted in Figure 2 and Figure 3. The graphs clearly show that the range of solution widens as the volume concentration of nanoparticles is added. Moreover, the hybrid nanofluid assist in delaying the detachment of the first and second solutions for and , when by means that the opposite movement between the hybrid carbon nanotubes and the plate, respectively where , and .
Figure 4 and Figure 5 exhibit the and variation with respect to mixed convection parameter, for multiple values of M. It is noticed that the range of solution deteriorating as M is prominent in the flow for both graphs. The denotes the detachment between the first and second solution, which may be seemed in the opposing flow . Furthermore, the increment of M fastens the separation of boundary layer flow, i.e., and This figure was supported by Figure 10 and Figure 11, where the value of and were reduced as the strength of M increased. As a result of the increase of M, there will be more resistance and a drag force known as the Lorentz force. In turn, this force might lessen heat transfer and skin friction by opposing and slowing the hybrid nanofluid’s velocity. On top of that, it is important to note that the increment in concentration of hybrid nanofluid increased the value of and . Basically, the strong interaction between the hydromagnetic and the concentrated nanoparticles in the fluid led the fluid to be gradually dragged in the direction of the nanoparticle’s motion, consequently increasing both and .
Figure 6 and Figure 7 illustrate the influence of different values of with the velocity parameter ε. It can be seen that a dual solution occurs when the governing parameter is inserted. The dual solution appears when the region is shrunk . The hybrid nanofluid seems to accelerate the boundary layer’s separation at the flat plat quicker in comparison to when and . Moreover, the presence of causes the widening of the range solution and increasing of and . Additionally, the increment of curvature parameter by means decreasing the radius of the cylinder. Therefore, more particles can fit into the cylinder surface area offering greater resistance to the particles of the fluid. Thus, boost up the heat transfer. These results are supported by Figure 12 and Figure 13. Consequently, come to a consensus with the aforementioned [22] that the performance of heat transfer is enhanced provided that the value of increases.
Variation and with respect to for distinct values of is given in Figure 8 and Figure 9. The duality of the solution exists at the buoyancy opposing flow in which as well as and unique solution appears at buoyancy assisting flow, . The additional on nanoparticles help in dispensing the energy in the form of heat [58]. The collision between the hybrid fluid nanoparticles caused by the increase of volume fraction with respect to SWCNT also results in the increment of the thermophoretic force and heat conduction caused by shear; leading to increasing of and .
The impact of over and can be seen in Figure 12 and Figure 13. This control parameter indicates reliable support, as reported in Figure 6 and Figure 7, in which the findings increased when is prominent. Obviously, the larger causes the reduction of the radius of the cylinder and less resistive force between the fluid and surface. Furthermore, increasing the friction between the surface shear stress, causing the thickness of the boundary layer. Here, the drag friction produces energy in the form of heat, leading to an increase in .
Figure 14 and Figure 15 explain the improvement in for and . The and improved with the increment of in the flow. Note that the edge of the dotted line of , when represents the SWCNT-water. It shows that the value of which means lower than the value of MWCNT-water as increase. Surprisingly, and increased drastically when increase with the increase of . When the nanoparticles of SWCNT be more concentrated, the hybrid nanofluid’s velocity will be improved, raising the shear stress and therefore enhancing the skin friction coefficient. This phenomenon happens due to the attractive force called Van der Waals forces that occurred between the molecules, resulting in the changes in the thermophoretic force. As we can see the increase of nanoparticle volume fraction for is not giving much significant on the reduced Nusselt number. To the best author’s view, this is due to the influence of the Nr parameter in the local Nusselt number which explained the insignificant result that occurs when the volume of nanoparticles, increased.
The effect of several values of thermal radiation, Nr on are portrayed in Figure 16. Duality of the solution exists in the shrinking region, between the range a unique solution occurs at and no solution was discovered at . It may also be observed from the graph that the critical value, , such as , and . The large Nr impede the separation of the boundary layer. Thermal radiation is the process where heat is transferred by electromagnetic waves without the presence of any constituents. It is noticed from Figure 17 that the reduces with the increment in radiation parameter . The mark of in the flow district is to reduce the temperature substantially. The increment in implies the release of heat energy from the flow region and which improve the random movement of the nanoparticles. However, in this problem, the lowest value of is said enough to have a high ability in heat transfer.
Profiles on velocity, , temperature, and concentration, are given in Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25 and Figure 26 with respect to the essential controlled parameter aimed in this research which is Nr, as well as For the first and second solutions, the profiles show features that are opposing. Note that, we only present the result for the local temperature profile due to the fact that the parameter Nr only exist in Equation (10). Every profile published satisfies the BCs asymptotically (11). It is intriguing that the first solution reaches zero faster than the second solution. Practically, the boundary layer thickness of the second solution is thicker compared to the first solution.
The temporal stability analysis approach introduced by [73] is via solving the linearized eigenvalue problem in (19)–(22) with introductory of new BC, . To define the two solutions’ stability, the value is vital. Numerical values achieved are shown in Table 4 and Table 5. This table demonstrates that the second solution exhibits the positive values of , meanwhile the first solution illustrates the positive values with respect to . The smallest eigenvalues against were plotted in Figure 27. The results from the table above, where we saw stable solutions for both systems, were ultimately supported by this figure. As opposed to earlier literature, it is worth noting that some of the positive values of in the second solution for our problem are considered to be stable solution. When there are non-unique solutions, it is crucial to identify stable solutions in order to accurately anticipate the flow behaviour.

Table 4.
Least eigenvalues for selected with several values of M when and .

Table 5.
Least eigenvalues for selected with several values of M when and .
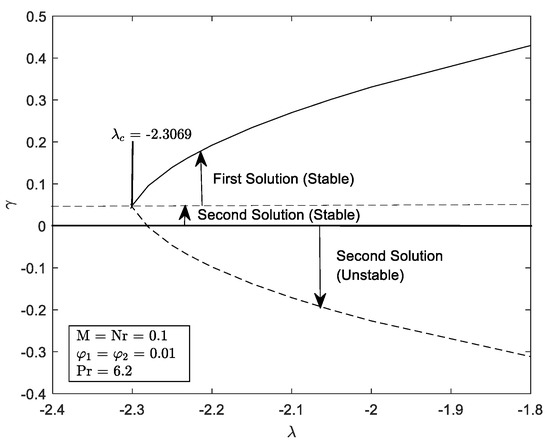
Figure 27.
Minimum eigenvalues for selected values of .
6. Conclusions
Stability analysis on mixed convection on stagnation point flow over SWCNT/MWCNT hybrid carbon nanotube has been formulated and analyzed numerically. The influence of parameter and have also been highlighted. Thus, some important conclusions can be outlined as follows:
- The double solutions presence is apparent at the shrinking sheet, and opposing flow, , whereas a unique solution is found at the stretching sheet, and assisting flow, .
- Throughout the stability analysis, it was determined that not only is the first solution stable, but also some of the positive values in the second solution.
- An increment of (SWCNT) hybrid nanofluid and in the flow proneness to improve the and . Meanwhile the opposite trend is noted when M is exists.
- The low Nr helps in enhance the heat transfer of the flow.
- The range of the solutions widen broadly with an augmentation in (SWCNT) and , therefore slowing down the boundary layer separation. Furthermore, the adding amount of M fastens the separation of boundary layer.
- In addition, the hybrid carbon nanotubes possess excellent result in skin friction and local Nusselt number compared to the SWCNT-water and MWCNT-water. This will give an insight to scientists or technologists in improving industrial and bio-medical production with regards to their expertise.
Author Contributions
Formal analysis, N.A.L.A.; Methodology, N.A.L.A.; Project administration, N.B.; Supervision, N.B., H.R., N.W., N.A.A.R. and N.M.A.; Writing—original draft, N.A.L.A.; Writing—review & editing, N.B. and N.M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
A high appreciation to Collaborative UPNM Research Grant (CRG/UPNM/2019/ST/04), study leave scholarship from Ministry of Higher Education, Malaysia and MATLAB software license from Universiti Pertahanan Nasional Malaysia (UPNM).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| ODE | Ordinary Differential Equation |
| Pr | Prandtl number |
| T | Temperature |
| U | Uniform free stream |
| qw | Plate heat flux |
| Nux | Local Nusselt number |
| Rex | Reynolds number |
| Cf | Skin friction coefficient |
| w | Condition on plate |
| ∞ | Ambient condition |
| hnf | Hybrid nanofluid |
| nf | Nanofluid |
| f | Fluid |
| α | Thermal diffusivity |
| μ | Dynamic viscosity |
| ρ | Density |
| ψ | Stream function |
| η | Similarity variables |
| θ | Dimensionless temperature |
| (ρCp)f | Specific heat for base fluid |
| Cp | Specific heat at constant pressure |
| τ | Dimensionless time |
| k | Thermal conductivity |
| Concentration of nanoparticles | |
| Eigenvalues | |
| υ | Kinematic viscosity |
| Mixed convection parameter | |
| Velocity ratio parameter | |
| ϒ | Curvature |
| Nr | Thermal radiation |
References
- Merkin, J.H. Mixed convection boundary layer flow on a vertical surface in a saturated porous medium. J. Eng. Math. 1980, 14, 301–313. [Google Scholar] [CrossRef]
- Ramachandran, N.; Chen, T.S.; Armaly, B.F. Mixed Convection in Stagnation Flows Adjacent to Vertical Surfaces. J. Heat Transf. 1988, 110, 373–377. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Mixed Convection Boundary Layer Flow over a Moving Vertical Flat Plate in an External Fluid Flow with Viscous Dissipation Effect. PLoS ONE 2013, 8, e60766. [Google Scholar] [CrossRef] [PubMed]
- Kejing, W.; Abdullahb, W.R.W. Solving Mixed Convection Boundary Layer Flow of Viscoelastic Nanofluid Past Over a Sphere Using MATLAB with BVP4C Solver. Proc. Sci. Math. 2021, 3, 192–202. [Google Scholar]
- Maji, S.; Sahu, A.K. Numerical investigation of mixed convection boundary layer flow for nanofluids under quasilinearization technique. SN Appl. Sci. 2021, 3, 1–13. [Google Scholar] [CrossRef]
- Maleque, K.A. Similarity Requirements for Mixed Convective Boundary Layer Flow over Vertical Curvilinear Porous Surfaces with Heat Generation/Absorption. Int. J. Aerosp. Eng. 2020, 2020, 7486971. [Google Scholar] [CrossRef]
- Mandal, S.K.; Deb, A.; Sen, D. Mixed Convective Heat Transfer with Surface Radiation in a Vertical Channel in Presence of Heat Spreader. In Advances in Applied Mechanical Engineering; Springer: Singapore, 2020; pp. 53–61. [Google Scholar] [CrossRef]
- Ali, M.; Alim, M.A. Mixed Convection Boundary Layer Flow with Heat Transfer over a Non-Linear Stretching Wedge-Shaped Surface with the Correlation Coefficient and Multiple Regressions Models. Int. J. Sci. Res. Math. Stat. Sci. 2021, 8, 6–22. [Google Scholar]
- Ahmad, U.; Ashraf, M.; Abbas, A.; Rashad, A.M.; Nabwey, H.A. Mixed convection flow along a curved surface in the presence of exothermic catalytic chemical reaction. Sci. Rep. 2021, 11, 1–10. [Google Scholar] [CrossRef]
- Meena, O.P.; Janapatla, P.; Srinivasacharya, D. Mixed Convection Flow across a Vertical Cone with Heat Source/Sink and Chemical Reaction Effects. Math. Model. Comput. Simul. 2022, 14, 532–546. [Google Scholar] [CrossRef]
- Hiemenz, K. Die Grenzschicht an einem in den gleichformigen Flussigkeitsstrom eingetauchten geraden Kreiszylinder. Dinglers Polytech. J. 1911, 326, 321–324. [Google Scholar]
- Howarth, L. On the Calculation of Steady Flow in the Boundary Layer Near the Surface of a Cylinder in a Stream (No. ARC-R/M-1632); Aeronautical Research Council London: London, UK, 1934. [Google Scholar]
- Wang, C. Free convection plume from the tip of a vertical needle. Mech. Res. Commun. 1989, 16, 95–101. [Google Scholar] [CrossRef]
- Gorla, R.S.R. Unsteady laminar axisymmetric stagnation flow over a circular cylinder. Dev. Mech. 1977, 9, 286–288. [Google Scholar]
- Gorla, R.S.R. Nonsimilar axisymmetric stagnation flow on a moving cylinder. Int. J. Eng. Sci. 1978, 16, 397–400. [Google Scholar] [CrossRef]
- Gorla, R.S.R. Transient response behavior of an axisymmetric stagnation flow on a circular cylinder due to time dependent free stream velocity. Int. J. Eng. Sci. 1978, 16, 493–502. [Google Scholar] [CrossRef]
- Sanz, M.S.; Blyth, M. Unsteady axisymmetric stagnation flow on a circular cylinder. Q. J. Mech. Appl. Math. 2007, 60, 125–138. [Google Scholar] [CrossRef]
- Kanafiah, S.F.H.M.; Kasim, A.R.M.; Zokri, S.M.; Arifin, N.S. Numerical Investigation at Lower Stagnation Point Flow Over a Horizontal Circular Cylinder of Brinkman-Viscoelastic Fluid. J. Adv. Res. Fluid Mech. Therm. Sci. 2021, 87, 56–65. [Google Scholar] [CrossRef]
- Nasir, S.; Shah, Z.; Khan, W.; Alrabaiah, H.; Islam, S.; Khan, S.N. MHD stagnation point flow of hybrid nanofluid over a permeable cylinder with homogeneous and heterogenous reaction. Phys. Scr. 2020, 96, 035201. [Google Scholar] [CrossRef]
- Som, A.N.M.; Adnan, N.S.M.; Arifin, N.; Bachok, N.; Ali, F.; Rahim, Y.F. A Stability Analysis of Boundary Layer Stagnation-Point Slip Flow and Heat Transfer towards a Shrinking/Stretching Cylinder over a Permeable Surface. CFD Lett. 2020, 12, 97–105. [Google Scholar] [CrossRef]
- Dey, D.; Borah, R.; Mahanta, B. Boundary Layer Flow and Its Dual Solutions Over a Stretching Cylinder: Stability Analysis. In Emerging Technologies in Data Mining and Information Security; Springer: Singapore, 2021; pp. 27–38. [Google Scholar] [CrossRef]
- Najib, N.; Bachok, N. Numerical Analysis of Boundary Layer Flow and Heat Transfer over a Shrinking Cylinder. CFD Lett. 2022, 14, 56–67. [Google Scholar] [CrossRef]
- Chamkha, A.J. Heat and Mass Transfer from MHD Flow over a Moving Permeable Cylinder with Heat Generation or Absorption and Chemical Reaction. Commun. Numer. Anal. 2011, 2011, 1–20. [Google Scholar] [CrossRef]
- Pandey, A.K.; Kumar, M. Boundary layer flow and heat transfer analysis on Cu-water nanofluid flow over a stretching cylinder with slip. Alex. Eng. J. 2017, 56, 671–677. [Google Scholar] [CrossRef]
- Ramsay, J.; Sellier, M.; Ho, W.H. Eliminating Boundary Layer Separation on a Cylinder with Nonuniform Suction. Int. J. Aerosp. Eng. 2020, 2020, 9137369. [Google Scholar] [CrossRef]
- Radushkevich, L.; Lukyanovich, V. O strukture ugleroda, obrazujucegosja pri termiceskom razlozenii okisi ugleroda na zeleznom kontakte. Zurn Fisic Chim. 1952, 26, 88–95. [Google Scholar]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Iijima, S.; Ichihashi, T. Single-shell carbon nanotubes of 1-nm diameter. Nature 1993, 363, 603–605. [Google Scholar] [CrossRef]
- Shafiq, A.; Sindhu, T.N.; Al-Mdallal, Q.M. A sensitivity study on carbon nanotubes significance in Darcy–Forchheimer flow towards a rotating disk by response surface methodology. Sci. Rep. 2021, 11, 1–26. [Google Scholar] [CrossRef]
- Manjunatha, P.; Gowda, R.P.; Kumar, R.N.; Suresha, S.; Sarwe, D.U. Numerical simulation of carbon nanotubes nanofluid flow over vertically moving disk with rotation. Partial Differ. Equations Appl. Math. 2021, 4, 100124. [Google Scholar] [CrossRef]
- Asai, P.; Panja, P.; Velasco, R.; Deo, M. Flow of long chain hydrocarbons through carbon nanotubes (CNTs). Sci. Rep. 2021, 11, 1–10. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Pop, I. Hybrid Carbon Nanotube Flow near the Stagnation Region over a Permeable Vertical Plate with Heat Generation/Absorption. Mathematics 2021, 9, 2925. [Google Scholar] [CrossRef]
- Kostarelos, K.; Bianco, A.; Prato, M. Promises, facts and challenges for carbon nanotubes in imaging and therapeutics. Nat. Nanotechnol. 2009, 4, 627–633. [Google Scholar] [CrossRef]
- Kaur, S.; Mehra, N.K.; Jain, K.; Jain, N.K. Development and evaluation of targeting ligand-anchored CNTs as prospective targeted drug delivery system. Artif. Cells Nanomed. Biotechnol. 2016, 45, 242–250. [Google Scholar] [CrossRef] [PubMed]
- Hong, G.; Diao, S.; Antaris, A.L.; Dai, H. Carbon Nanomaterials for Biological Imaging and Nanomedicinal Therapy. Chem. Rev. 2015, 115, 10816–10906. [Google Scholar] [CrossRef]
- Arruebo, M.; Fernández-Pacheco, R.; Ibarra, M.R.; Santamaría, J. Magnetic nanoparticles for drug delivery. Nano Today 2007, 2, 22–32. [Google Scholar] [CrossRef]
- Lee, N.; Yoo, D.; Ling, D.; Cho, M.H.; Hyeon, T.; Cheon, J. Iron Oxide Based Nanoparticles for Multimodal Imaging and Magnetoresponsive Therapy. Chem. Rev. 2015, 115, 10637–10689. [Google Scholar] [CrossRef] [PubMed]
- Cai, D.; Mataraza, J.M.; Qin, Z.-H.; Huang, Z.; Huang, J.; Chiles, T.C.; Carnahan, D.; Kempa, K.; Ren, Z. Highly efficient molecular delivery into mammalian cells using carbon nanotube spearing. Nat. Methods 2005, 2, 449–454. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Jiang, H.; Teng, Y.; Xiong, Y.; Chen, Z.; You, L.; Xiao, D. Recent advances in magnetic carbon nanotubes: Synthesis, challenges and highlighted applications. J. Mater. Chem. B 2021, 9, 9076–9099. [Google Scholar] [CrossRef] [PubMed]
- Loria, J.C.; Blackstock, W.J.; Mar, J.W. The Effects of Thermal Radiation on Aircraft Structures. Part I. The Mit Mark I Radiant Heating Structural Test Facility; Massachusetts Inst. of Tech. Cambridge Aeroelastic and Structures Research Lab: Cambridge, MA, USA, 1954. [Google Scholar]
- Schmit, L.A.; Williams, F.L. The Effects of Thermal Radiation on Aircraft Structures. Part II. The Response Of A Simple Structure To Radiant Heating; Massachusetts Inst. of Tech. Cambridge Aeroelastic and Structures Research Lab: Cambridge, MA, USA, 1955. [Google Scholar]
- Loria, J.C.; Engel, S.J.; Mar, J.E. The Effects of Thermal Radiation on Aircraft Structures. Part III. Structural Behavior of Box-Beams Under Combined Static and Thermal Loads; Massachusetts Inst. of Tech. Cambridge Aeroelastic and Structures Research Lab: Cambridge, MA, USA, 1957. [Google Scholar]
- Blackstock, W.J.; Loria, J.C. The Effects of Thermal Radiation on Aircraft Structures. Part IV. the Mit Mark II Radiant Heating Structural Test Facility; Massachusetts Inst. of Tech. Cambridge Aeroelastic and Structures Research Lab: Cambridge, MA, USA, 1957. [Google Scholar]
- Rasheed, H.U.; Islam, S.; Khan, Z.; Alharbi, S.O.; A Khan, W.; Khan, W.; Khan, I. Thermal Radiation Effects on Unsteady Stagnation Point Nanofluid Flow in View of Convective Boundary Conditions. Math. Probl. Eng. 2021, 2021, 5557708. [Google Scholar] [CrossRef]
- Dzulkifli, N.F.; Bachok, N.; Yacob, N.A.; Arifin, N.; Rosali, H.; Pop, I. Thermal radiation on mixed convection heat and mass transfer over a vertical permeable stretching/shrinking sheet with Soret and Dufour effects. J. Eng. Math. 2021, 132, 1–19. [Google Scholar] [CrossRef]
- Jha, B.K.; Samaila, G. The Combined Impact of Thermal Radiation and Thermophoresis on Buoyancy-Driven Flow Near An Inclined Porous Plate. J. Heat Transf. 2022, 144, 102602. [Google Scholar] [CrossRef]
- Zhang, M.; Yudasaka, M. Potential application of nanocarbons as a drug delivery system. Carbon 2014, 69, 642. [Google Scholar] [CrossRef]
- Sajid, M.I.; Jamshaid, U.; Jamshaid, T.; Zafar, N.; Fessi, H.; Elaissari, A. Carbon nanotubes from synthesis to in vivo biomedical applications. Int. J. Pharm. 2016, 501, 278–299. [Google Scholar] [CrossRef] [PubMed]
- Jha, B.K.; Samaila, G. The role of thermal radiation on the boundary layer past a stationary flat plate with constant surface boundary condition. J. Nat. 2021, 2, 7–11. [Google Scholar]
- Aman, S.; Khan, I.; Ismail, Z.; Salleh, M.Z.; Al-Mdallal, Q.M. Heat transfer enhancement in free convection flow of CNTs Maxwell nanofluids with four different types of molecular liquids. Sci. Rep. 2017, 7, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Loganathan, P.; Kannan, M.; Ganesan, P. Thermal radiation effects on MHD flow over a moving semi-infinite vertical cylinder. Int. J. Math. Anal. 2011, 5, 257–274. [Google Scholar]
- Wahid, N.S.; Arifin, N.M.; Khashi’ie, N.S.; Pop, I.; Bachok, N.; Hafidzuddin, M.E.H. MHD mixed convection flow of a hybrid nanofluid past a permeable vertical flat plate with thermal radiation effect. Alex. Eng. J. 2022, 61, 3323–3333. [Google Scholar] [CrossRef]
- Aladdin NA, L.; Bachok, N. Effects of hydromagnetic and chemical reaction over a stagnation point flow of horizontal stretching/shrinking cylinder in Ag-CuO/water hybrid nanofluid. Int. J. Numer. Methods Heat Fluid Flow 2021, 32, 660–683. [Google Scholar] [CrossRef]
- Kho, Y.B.; Jusoh, R.; Salleh, M.Z.; Mohamed MK, A.; Ismail, Z.; Hamid, R.A. Inclusion of Viscous Dissipation on the Boundary Layer Flow of Cu-TiO2 Hybrid Nanofluid over Stretching/Shrinking Sheet. J. Adv. Res. Fluid Mech. Therm. Sci. 2021, 88, 64–79. [Google Scholar]
- Sajid, M.; Hayat, T. Influence of thermal radiation on the boundary layer flow due to an exponentially stretching sheet. Int. Commun. Heat Mass Transf. 2008, 35, 347–356. [Google Scholar] [CrossRef]
- Ishak, A.; Yacob, N.A.M.; Bachok, N. Radiation effects on the thermal boundary layer flow over a moving plate with convective boundary condition. Meccanica 2010, 46, 795–801. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Devi, S.P.A.; Devi, S.S.U. Numerical investigation of hydromagnetic hybrid Cu-Al2O3/water nanofluid flow over a permeable stretching sheet with suction. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 249–257. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Hafidzuddin, E.H.; Arifin, N.M.; Wahi, N. Stagnation point flow of hybrid nanofluid over a permeable vertical stretching/shrinking cylinder with thermal stratification effect. CFD Lett. 2020, 12, 80–94. [Google Scholar]
- Aladdin, N.A.L.; Bachok, N. Duality Solutions in Hydromagnetic Flow of SWCNT-MWCNT/Water Hybrid Nanofluid over Vertical Moving Slender Needle. Mathematics 2021, 9, 2927. [Google Scholar] [CrossRef]
- Hataue, I. Ghost numerical solutions in upwind difference scheme and effects of linearization. In Proceedings of the 35th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–10 January 1997. [Google Scholar] [CrossRef]
- Angiulli, G.; Jannelli, A.; Morabito, F.C.; Versaci, M. Reconstructing the membrane detection of a 1D electrostatic-driven MEMS device by the shooting method: Convergence analysis and ghost solutions identification. Comput. Appl. Math. 2018, 37, 4484–4498. [Google Scholar] [CrossRef]
- Yensiri, S.; Skulkhu, R.J. An Investigation of Radial Basis Function-Finite Difference (RBF-FD) Method for Numerical Solution of Elliptic Partial Differential Equations. Mathematics 2017, 5, 54. [Google Scholar] [CrossRef]
- Bihs, H.; Kamath, A. A combined level set/ghost cell immersed boundary representation for floating body simulations. Int. J. Numer. Methods Fluids 2016, 83, 905–916. [Google Scholar] [CrossRef]
- Rehman, A.U.; Abbas, Z. Stability analysis of heat transfer in nanomaterial flow of boundary layer towards a shrinking surface: Hybrid nanofluid versus nanofluid. Alex. Eng. J. 2022, 61, 10757–10768. [Google Scholar] [CrossRef]
- Wu, Y.; Rist, U. Stability Analysis of Boundary Layer Flow with Rotating Cylindrical Surface Roughness Elements. In IUTAM Laminar-Turbulent Transition; Springer: Cham, Switzerland, 2021; pp. 815–824. [Google Scholar] [CrossRef]
- Khashi’Ie, N.S.; Arifin, N.M.; Pop, I. Magnetohydrodynamics (MHD) boundary layer flow of hybrid nanofluid over a moving plate with Joule heating. Alex. Eng. J. 2021, 61, 1938–1945. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Turkyilmazoglu, M.; Arifin, N.; Rosali, H. Analytical and stability analysis of MHD flow past a nonlinearly deforming vertical surface in Carbon Nanotubes. Alex. Eng. J. 2020, 59, 497–507. [Google Scholar] [CrossRef]
- Weidman, P.; Kubitschek, D.; Davis, A. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Pop, I. A Stability Analysis of Solutions in Boundary Layer Flow and Heat Transfer of Carbon Nanotubes over a Moving Plate with Slip Effect. Energies 2018, 11, 3243. [Google Scholar] [CrossRef]
- Weidman, P.D.; Davis, A.M.J.; Kubitschek, D.G. Crocco variable formulation for uniform shear flow over a stretching surface with transpiration: Multiple solutions and stability. Z. Angew. Math. Phys. 2006, 59, 313–332. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed Convection Boundary-Layer Flow Near the Stagnation Point on a Vertical Surface in a Porous Medium: Brinkman Model with Slip. Transp. Porous Media 2008, 77, 267–285. [Google Scholar] [CrossRef]
- Shampine, L.F.; Gladwell, I.; Shampine, L.; Thompson, S. Solving ODEs with Matlab; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Ishak, A.; Lok, Y.Y.; Pop, I. Stagnation-point flow over a shrinking sheet in a micropolar fluid. Chem. Eng. Commun. 2010, 197, 1417–1427. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Nandy, S.K. Slip effects on unsteady stagnation-point flow and heat transfer over a shrinking sheet. Meccanica 2013, 48, 1599–1606. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N. Double Solutions and Stability Analysis of Micropolar Hybrid Nanofluid with Thermal Radiation Impact on Unsteady Stagnation Point Flow. Mathematics 2021, 9, 276. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).