On the Signless Laplacian Spectral Radius of Graphs without Small Books and Intersecting Quadrangles

Abstract

In this paper, we determine the maximum signless Laplacian spectral radius of all graphs which do not contain small books as a subgraph and characterize all extremal graphs. In addition, we give an upper bound of the signless Laplacian spectral radius of all graphs which do not contain intersecting quadrangles as a subgraph.

1. Introduction

Let G be an undirected simple graph with vertex set $V\left(G\right)=\{v_1,\dots ,v_n\}$ and edge set $E\left(G\right)$. $e\left(G\right)$ denotes the number of edges in G, i.e., $e\left(G\right)=\left|E\right(G\left)\right|$. For $v\in V\left(G\right)$, the neighborhood of v is $N_G\left(v\right)=\{u:uv\in E\left(G\right)\}$ and the degree of v is $d_G\left(v\right)=\left|N_G\left(v\right)\right|$. We write $N\left(v\right)$ and $d\left(v\right)$ for $N_G\left(v\right)$ and $d_G\left(v\right)$ respectively if there is no ambiguity. $▵\left(G\right)$ denotes the maximum degree of G. For $A,B\subseteq V\left(G\right)$, $e\left(A\right)$ denotes the number of edges in G with both end vertices in A and $e(A,B)$ denotes the number of edges in G with one end vertex in A and the other in B. For two vertex disjoint graphs G and H, we denote by $G\cup H$ and $G\nabla H$ the union of G and H, and the join of G and H, respectively. $kG$ denotes the union of k disjoint copies of G; $\overline{G}$ denotes the complement graph of G. We say that a graph G is F-free if it does not contain a subgraph isomorphic to F, i.e., G contains no copy of F.

The adjacency matrix of G is the $n\times n$ matrix $A\left(G\right)=\left(a_{ij}\right)$, where $a_{ij}=1$ if $v_i$ is adjacent to $v_j$, and 0 otherwise. The signless Laplacian matrix of G is the $Q\left(G\right)=D\left(G\right)+A\left(G\right)$, where $D\left(G\right)$ is the degree diagonal matrix of G. The signless Laplacian spectral radius of G is the largest eigenvalue of $Q\left(G\right)$, denoted by $q\left(G\right)$. For graph notation and terminology undefined here, we refer readers to [1].

In the following, we give the signless Laplacian matrix and signless Laplacian spectral radius of $C_3$ as an example:

$$Q\left(C_3\right)=\left[\begin{array}{ccc}2& 0& 0\\ 0& 2& 0\\ 0& 0& 2\end{array}\right]+\left[\begin{array}{ccc}0& 1& 1\\ 1& 0& 1\\ 1& 1& 0\end{array}\right]=\left[\begin{array}{ccc}2& 1& 1\\ 1& 2& 1\\ 1& 1& 2\end{array}\right]\mathrm{and}q\left(C_3\right)=4.$$

In 2013, de Freitas, Nikiforov and Patuzzi [2] proposed the following problem.

Problem 1.

Given a graph F, what is the maximum signless Laplacian spectral radius of all F-free graphs on n vertices?

In recent years, this problem is intensively investigated in the literature for many classes of graphs, such as matchings [3], paths [4], complete graphs [5], odd cycles [6], even cycles [7], complete bipartite graphs [8], linear forests [9], friendship graphs [10], and so on. For the problems of the least signless Laplacian eigenvalue, readers are referred to [11,12].

We define some special graphs as follows, see Figure 1. For integers $k\ge 1$, $h\ge 2$, and $n>k+h$, let $F_{n,k}\left(H\right)=K_k\nabla (H\cup p{K}_2\cup K_s)$, where H is a connected graph on h vertices, $n-(k+h)=2p+s$ and $0\le s<2$. In particular, if $H=K_2$, then we write $F_{n,k}$ for $F_{n,k}\left(K_2\right)$. For an integer $k\ge 2$, let $B_k$ be the k-book, i.e., the graph on $k+2$ vertices consisting of k triangles which share one common edge. For an integer $k\ge 2$, let $H_k$ be a graph on $3k+1$ vertices consisting of k quadrangles which intersect in exactly a common vertex, which is called an intersecting quadrangle.

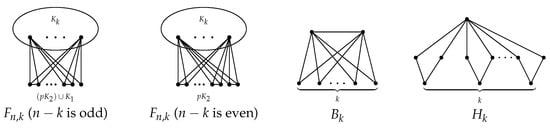
Figure 1. The graphs $F_{n,k},B_k$ and $H_k$.

We mention that de Freitas, Nikiforov, and Patuzzi [13] solved Problem 1 when $F=C_4$ and they also characterized all extremal graphs.

Theorem 1

([13]). If G is a $C_4$-free graph on $n\ge 4$ vertices, then $q\left(G\right)\le q\left(F_{n,1}\right)$ with equality if and only if $G=F_{n,1}$.

It is interesting to consider Problem 1 for the forbidden subgraph containing $C_4$ as a subgraph. Note that $H_k$ and $B_k$ are graphs containing $C_4$ as a subgraph. Inspired by the above results, in this paper, we investigate the maximum signless Laplacian spectral radius of all $B_2$-free graphs and characterize all extremal graphs attaining the maximum signless Laplacian spectral radius. In addition, we also obtain an upper bound of the signless Laplacian spectral radius of all $H_k$-free graphs.

Theorem 2.

If G is a $B_2$-free graph on $n\ge 4$ vertices, then $q\left(G\right)\le q\left(F_{n,1}\right)$ with equality if and only if $G=F_{n,1}$.

It is easy to see that Theorem 1 is a corollary of Theorem 2.

Theorem 3.

Let $k\ge 2$ and $n\ge 15k^2-5k$. If G is an $H_k$-free graph on n vertices, then $q\left(G\right)\le t(n,k)$, where

$$t(n,k)=\left\{\begin{array}{ccc}n+2+\frac{1}{n-2},\hfill & & k=2;\hfill \\ n+2k-2,\hfill & & k\ge 3.\hfill \end{array}\right.$$

The rest of this paper is organized as follows. In Section 2, some known lemmas are presented. In Section 3, we give the proof of Theorem 2. In Section 4, we give the proof of Theorem 3. In Section 5, we round up the general discussion and state three problems.

2. Some Lemmas

Suppose M is a symmetric real matrix whose rows and columns are indexed by $X=\{1,\dots ,n\}$. Let $\pi =\{X_1,\dots ,X_m\}$ be a partition of X. Let M be partitioned according to $\{X_1,\dots ,X_m\}$, i.e.,

$$\begin{array}{cc}\hfill M=& \left[\begin{array}{ccc}{M}_{11}& \dots & M_{1m}\\ ⋮& & ⋮\\ M_{m1}& \dots & M_{mm}\end{array}\right],\end{array}$$

where $M_{ij}$ denotes the block of M formed by rows in $X_i$ and the columns in $X_j$. Let $b_{ij}$ denote the average row sum of $M_{ij}$, i.e., $b_{ij}=\frac{{\mathbf{1}}^{\mathrm{T}}{M}_{ij}\mathbf{1}}{|X_i|}$, where $\mathbf{1}$ is a column vector with all the elements 1. Then the matrix $M/\pi ={\left(b_{ij}\right)}_{m\times m}$ is called the quotient matrix of M. If the row sum of each block $M_{ij}$ is a constant, then the partition is called equitable.

Lemma 1

([14]). Let G be a connected graph. If π is an equitable partition of $V\left(G\right)$ corresponding to $Q\left(G\right)$, then $q\left(G\right)$ is equal to the largest eigenvalue of $Q\left(G\right)/\pi$.

The graph $F_{n,k}$ plays an important role in our results. We present an upper bound of $q\left(F_{n,k}\right)$.

Lemma 2

([9]). Let $k\ge 2$ and $n\ge 2{(k+1)}^2$. Then $q\left(F_{n,k}\right)\le n+2k-2$.

Next we present two lemmas, one of which is related to the maximum number of edges of $k{P}_3$-free graphs and the other is the edge stability theorem of $k{P}_3$-free graphs.

Denote by $M_n=p{K}_2\cup K_s$, where $n=2p+s$ and $0\le s<2$. Denote by $N_6$ the graph of order 6 obtain from $K_3$ by adding a pendant edge to every vertex of $K_3$.

Lemma 3

([15]). Let G be a graph on n vertices. Then

$$q\left(G\right)\le \underset{v\in V\left(G\right)}{max}\left\{d\left(v\right)+\frac{1}{d\left(v\right)}\sum _{z\in N\left(v\right)}d\left(z\right)\right\},$$

and the equality holds if and only if G is either a regular graph or a semi-regular bipartite graph.

Lemma 4

([16,17,18]). Let G be a $k{P}_3$-free graph on n vertices. Then

$$e\left(G\right)\le \left\{\begin{array}{ccc}\left(\genfrac{}{}{0pt}{}{n}{2}\right),\hfill & & for n<3k;\hfill \\ \left(\genfrac{}{}{0pt}{}{3k-1}{2}\right)+⌊\frac{n-3k+1}{2}⌋,\hfill & & for 3k\le n<5k-1;\hfill \\ \left(\genfrac{}{}{0pt}{}{3k-1}{2}\right)+k,\hfill & & for n=5k-1;\hfill \\ \left(\genfrac{}{}{0pt}{}{k-1}{2}\right)+(n-k+1)(k-1)+⌊\frac{n-k+1}{2}⌋,\hfill & & for n>5k-1.\hfill \end{array}\right.$$

Moreover, (i) If $n<3k$, then the equality holds if and only if $G=K_n$;

(ii) If $3k\le n<5k-1$, then the equality holds if and only if $G=K_{3k-1}\cup M_{n-3k+1}$;

(iii) If $n=5k-1$, then the equality holds if and only if $G=K_{3k-1}\cup M_{2k}$ or $G=F_{5k-1,k-1}$;

(iv) If $n>5k-1$, then the equality holds if and only if $G=F_{n,k-1}$.

Lemma 5

([9]). Let $k\ge 2$ and G be a graph on $n\ge \frac{11}{2}{k}^2+2k-\frac{3}{2}$ vertices. If $e\left(G\right)>(k-\frac{3}{2})n$, then G contains $k{P}_3$ as a subgraph unless one of the following holds:

(i) $G\subseteq F_{n,k-1}$;

(ii) $G\subseteq F_{n,k-2}\left(K_t\right)$, where $4\le t\le 5$;

(iii) $G\subseteq F_{n,k-2}\left(N_6\right)$.

3. Proof of Theorem 2

We first prove the following lemma, which plays an important role in the proof of Theorem 2.

Lemma 6.

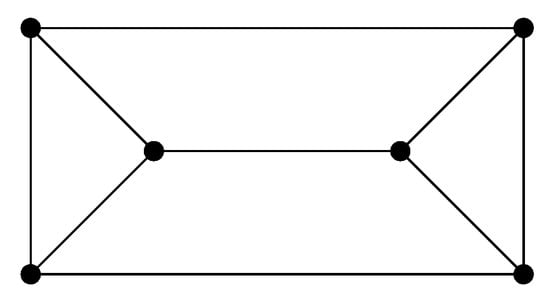
Let G be a $B_2$-free graph on $n\ge 4$ vertices. If $\Delta \left(G\right)\le n-3$, then $q\left(G\right)\le n$, and the equality holds if and only if G is a triangular prism (see Figure 2) or G is $K_{s,n-s}$ with $s\ge 3$ and $n-s\ge 3$.

Figure 2. The graph of triangular prism.

Proof. 

By Lemma 3, there exists a vertex $u\in V\left(G\right)$ such that

$$\begin{array}{c}\hfill q\left(G\right)\le \underset{v\in V\left(G\right)}{max}\left\{d\left(v\right)+\frac{1}{d\left(v\right)}\sum _{z\in N\left(v\right)}d\left(z\right)\right\}=d\left(u\right)+\frac{1}{d\left(u\right)}\sum _{z\in N\left(u\right)}d\left(z\right),\end{array}$$

(1)

and the equality holds if and only if G is either a regular graph or a semi-regular bipartite graph.

If $1\le d\left(u\right)\le 3$, then

$$\begin{array}{c}\hfill q\left(G\right)\le 3+\Delta \left(G\right)\le 3+(n-3)=n.\end{array}$$

(2)

By (1), the equality in (2) holds if and only if G is either a $B_2$-free regular graph or a $B_2$-free semi-regular bipartite graph with $d\left(u\right)=3$ and $\Delta \left(G\right)=n-3$. If G is a $B_2$-free regular graph with $d\left(u\right)=3$ and $\Delta \left(G\right)=n-3$, it is easy to see that $n=6$ and G is a triangular prism. If G is a $B_2$-free semi-regular bipartite graph with $d\left(u\right)=3$ and $\Delta \left(G\right)=n-3$, then G is $K_{3,n-3}$ with $n\ge 6$.

So next we suppose that $4\le d\left(u\right)\le n-3$. Let $A=N\left(u\right)$ and $B=V\left(G\right)\backslash \{A\cup \{u\left\}\right\}$. By (1), it can be seen that

$$\begin{array}{c}\hfill q\left(G\right)\le d\left(u\right)+\frac{1}{d\left(u\right)}\sum _{z\in N\left(u\right)}d\left(z\right)=\left|A\right|+1+\frac{2e\left(A\right)+e(A,B)}{\left|A\right|},\end{array}$$

(3)

and the equality holds if and only if G is either a regular graph or a semi-regular bipartite graph.

Since G is $B_2$-free, it follows that $G\left[A\right]$ consists of independent edges and isolated vertices. Further, for any $v\in B$, v is adjacent to at most one end vertex of any edge in $G\left[A\right]$, implying that

$$\begin{array}{c}\hfill \left|N\right(v)\cap A|\le \left|A\right|-e\left(A\right).\end{array}$$

(4)

It is easy to see that the equality in (4) holds if and only if v is adjacent to only one end vertex of every edge and all isolated vertices in $G\left[A\right]$. Therefore,

$$\begin{array}{c}\hfill e(A,B)=\sum _{v\in B}|N\left(v\right)\cap A|\le \left(\right|A|-e\left(A\right))\left|B\right|=\left|A\right|\left|B\right|-e\left(A\right)\left|B\right|.\end{array}$$

(5)

The equality in (5) holds if and only if any vertex $v\in B$ is adjacent to only one end vertex of every edge and all isolated vertices in $G\left[A\right]$. Now it follows from (3) and (5) that

$$\begin{array}{ccc}\hfill q\left(G\right)& \le & \left|A\right|+1+\frac{2e\left(A\right)+\left|A\right|\left|B\right|-e\left(A\right)\left|B\right|}{\left|A\right|}\hfill \\ & =& \left|A\right|+1+\left|B\right|-\frac{e\left(A\right)\left(\right|B|-2)}{\left|A\right|}=n-\frac{e\left(A\right)\left(\right|B|-2)}{\left|A\right|}\le n.\hfill \end{array}$$

(6)

The equality in (6) holds if and only if the equalities in (3) and (5) hold, and either $e\left(A\right)=0$ or $\left|B\right|=2$. In other words, if $e\left(A\right)=0$, then the equality in (6) holds if and only if G is a $B_2$-free semi-regular bipartite graph $K_{\left|A\right|,n-\left|A\right|}$ with $4\le \left|A\right|\le n-3$ as G is $B_2$-free. If $\left|B\right|=2$, then the equality in (6) holds if and only if G is a $B_2$-free semi-regular bipartite graph $K_{3,n-3}$ with $n\ge 7$ (in fact, G can not be a $B_2$-free regular graph with $d\left(u\right)=\left|A\right|=n-3\ge 4$). This completes the proof. □

Proof of Theorem 2.

Let G be the graph with the maximum signless Laplacian spectral radius among all $B_2$-free graphs on n vertices. We first claim that G is connected. Otherwise, let $G_1,G_2,\dots ,G_s(s\ge 2)$ be the components of G, and we add an edge between $G_i$ and $G_{i+1}$ for $i=1,\dots ,s-1$. It is clear that the resulting graph $G^{\prime }$ is a connected $B_2$-free graph and $q\left(G^{\prime }\right)>q\left(G\right)$, which contradicts our choice of G. Further, since $F_{n,1}$ is $B_2$-free, we see that $q\left(G\right)\ge q\left(F_{n,1}\right)>n$. By Lemma 6, we have $n-2\le \Delta \left(G\right)\le n-1$.

If $\Delta \left(G\right)=n-1$, then the induced subgraph of the neighborhood of the vertex with degree $n-1$ consists of independent edges and isolate vertices. Noting that adding an edge to a connected graph, the signless Laplacian spectral radius increases strictly. Hence, by the choice of G, we have $G=F_{n,1}$.

If $\Delta \left(G\right)=n-2$, then we let $u\in V\left(G\right)$ denote a vertex of degree $n-2$. Let $A=N\left(u\right)$ and $B=V\left(G\right)\backslash \{A\cup \{u\left\}\right\}=\left\{v\right\}$. Since G is $B_2$-free, it follows that $G\left[A\right]$ consists of independent edges and isolated vertices. If $G\left[A\right]$ is an empty graph, then by the choice of G, we have $G=K_{2,n-2}$, showing that $q\left(G\right)=q\left(K_{2,n-2}\right)=n$. This is a contradiction. So $G\left[A\right]$ contains at least one edge. Since G is $B_2$-free, it follows from the choice of G again that v is adjacent to only one end vertex of every edge and all isolated vertices in $G\left[A\right]$. Denote $t=\left|e\right(A\left)\right|$. It is clear that $1\le t\le \frac{n-2}{2}$. For convenience, now we use $G_{n,t}$ to denote G. Let $X_1$, $X_2$, $X_3$, $X_4$ and $X_5$ be the sets of vertices in $G_{n,t}$ with degree $n-2$, 3, 2, 2 and $n-t-2$, respectively, where the neighborhood of any vertex in $X_4$ is $\{u,v\}$. It is clear that $X_1=\left\{u\right\}$, $X_5=\left\{v\right\}$, and $V\left(G_{n,t}\right)={\bigcup }_{1\le i\le 5}{X}_i$. Let $\pi =\{X_1,X_2,X_3,X_4,X_5\}$. Then $\pi$ is an equitable partition of $V\left(G_{n,t}\right)$ with respect to $Q\left(G_{n,t}\right)$. From the definition of the quotient matrix, we see that

$$Q\left(G_{n,t}\right)/\pi =\left[\begin{array}{ccccc}n-2& t& t& n-2t-2& 0\\ 1& 3& 1& 0& 1\\ 1& 1& 2& 0& 0\\ 1& 0& 0& 2& 1\\ 0& t& 0& n-2t-2& n-2-t\end{array}\right].$$

Let $f\left(x\right)=det(x{I}_5-Q\left(G_{n,t}\right)/\pi )$, where $I_5$ is an identity matrix of order 5 and $det\left(A\right)$ represents the determinant of A, and $f^{\left(i\right)}\left(x\right)$ is the $i^{th}$ order derivative of $f\left(x\right)$. Using MATLAB, we get that

$$\begin{array}{ccc}\hfill f\left(x\right)& =& x^5+(t-3-2n)x^4+(n^2-nt+8n-4t-5)x^3\hfill \\ & & +(5nt-5n^2-4t+10)x^2+(5n^2-10n-4t^2)x+(16t+8t^2-8nt),\hfill \\ \hfill f^{\left(1\right)}\left(x\right)& =& 5x^4+4(t-3-2n)x^3+3(n^2-nt+8n-4t-5)x^2\hfill \\ & & +2(5nt-5n^2-4t+10)x+(5n^2-10n-4t^2),\hfill \\ \hfill f^{\left(2\right)}\left(x\right)& =& 20x^3+12(t-3-2n)x^2+6(n^2-nt+8n-4t-5)x\hfill \\ & & +2(5nt-5n^2-4t+10),\hfill \\ \hfill f^{\left(3\right)}\left(x\right)& =& 60x^2+24(t-3-2n)x+6(n^2-nt+8n-4t-5),\hfill \\ \hfill f^{\left(4\right)}\left(x\right)& =& 120x+24(t-3-2n),\hfill \\ \hfill f^{\left(5\right)}\left(x\right)& =& 120.\hfill \end{array}$$

For $n\ge 7$, by a direct calculation, it can be seen that

$$\begin{array}{ccc}\hfill f\left(n\right)& =& t{n}^3-4t{n}^2-(4t^2+8t)n+16t+8t^2\hfill \\ & \ge & n^3-4n^2-12n+16+8=n(n-6)(n+2)+24>0,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill f^{\left(1\right)}\left(n\right)& =& (t+2)n^3-(2t+10)n^2+(10-8t)n-4t^2\hfill \\ & \ge & 3n^3-12n^2+2n-4=3n^2(n-4)+2n-4>0,\hfill \\ \hfill f^{\left(2\right)}\left(n\right)& =& 2n^3+(6t+2)n^2-(14t+30)n-8t+20\ge 2n^3+8n^2-44n+12>0,\hfill \\ \hfill f^{\left(3\right)}\left(n\right)& =& 18n^2+(18t-24)n-24t-30\ge 18n^2-6n-54>0,\hfill \\ \hfill f^{\left(4\right)}\left(n\right)& =& 72n+24t-72>0,\hfill \\ \hfill f^{\left(5\right)}\left(n\right)& =& 120>0.\hfill \end{array}$$

Hence, for $n\ge 7$, by the Fourier-Budan theorem (Prasolov 2001), there is no root of the polynomial $f\left(x\right)$ in the interval $[n,+\infty )$, namely, the largest eigenvalue of $Q(G_{n,t}/\pi )$ is less than n. Further, by Lemma 1, $q\left(G\right)<n$, which is a contradiction. This implies that $n=5,6$ ($n=4$ is impossible as $t=1$ and $\Delta \left(G_{4,1}\right)=3$). Noting $1\le t\le \frac{n-2}{2}$, we see that $G\in \left\{G_{5,1},G_{6,1},G_{6,2}\right\}$. Using MATLAB, we have

$$\begin{array}{ccc}\hfill q\left(G_{5,1}\right)& =& 5.1149<5.5616=q\left(F_{5,1}\right),\hfill \\ \hfill q\left(G_{6,1}\right)& =& 5.2863<6<q\left(F_{6,1}\right),\hfill \\ \hfill q\left(G_{6,2}\right)& =& 5.9452<6<q\left(F_{6,2}\right).\hfill \end{array}$$

which is also a contradiction. This completes the proof.

Example 1.

Since $F_{n,1}$ contains $K_{1,n-1}$ as a proper subgraph, we have $q\left(F_{n,1}\right)>q\left(K_{1,n-1}\right)=n$. Since a cycle $C_n$ with $n\ge 4$ is $B_2$-free and 2-regular, we have $q\left(C_n\right)=4\le n<q\left(F_{n,1}\right)$.

Example 2.

Every bipartite graph G is $B_2$-free and it is a subgraph of some complete bipartite graph G’. So $q\left(G\right)\le q\left(G^{\prime }\right)=n<q\left(F_{n,1}\right)$.

4. Proof of Theorem 3

In order to prove Theorem 3, we first present the following technical lemma.

Lemma 7.

Let $k\ge 2$, $n\ge 15k^2-5k$ and G be an $H_k$-free graph of on n vertices. If $\Delta \left(G\right)\le n-2$, then $q\left(G\right)\le t_{n,k}$.

Proof. 

Assume for a contradiction that $q\left(G\right)>t_{n,k}\ge n+2k-2$. By Lemma 3, there exists a vertex $u\in V\left(G\right)$ such that

$$\begin{array}{c}\hfill q\left(G\right)\le \underset{v\in V\left(G\right)}{max}\left\{d\left(v\right)+\frac{1}{d\left(v\right)}\sum _{z\in N\left(v\right)}d\left(z\right)\right\}=d\left(u\right)+\frac{1}{d\left(u\right)}\sum _{z\in N\left(u\right)}d\left(z\right).\end{array}$$

(7)

If $d\left(u\right)\le 2k$, then it follows from (7) that $q\left(G\right)\le d\left(u\right)+\Delta \left(G\right)=2k+n-2=n+2k-2$, which is a contradiction. So $d\left(u\right)\ge 2k+1$. Let $A=N\left(u\right)$ and $B=V\left(G\right)\backslash \left(N\right(u)\cup \{u\left\}\right)$. It is clear that $\left|A\right|+\left|B\right|+1=n$ and

$$\begin{array}{c}\hfill n+2k-2<q\left(G\right)\le d\left(u\right)+\frac{1}{d\left(u\right)}\sum _{z\in N\left(u\right)}d\left(z\right)=\left|A\right|+1+\frac{2e\left(A\right)+e(A,B)}{\left|A\right|}.\end{array}$$

(8)

Next we consider the following two cases.

Case 1.$2k+1\le \left|A\right|\le 5k-2$. Let $B^{\prime }$ be the vertices in B that are adjacent to all vertices in A. We claim that $|B^{\prime }|\ge k$. In fact, if $|B^{\prime }|\le k-1$ then

$$\begin{array}{ccc}\hfill 2e\left(A\right)+e(A,B)& \le & 2\left(\genfrac{}{}{0pt}{}{\left|A\right|}{2}\right)+|B^{\prime }\left|\right|A|+(\left|B\right|-|B^{\prime }\left|\right)\left(\right|A|-1)\hfill \\ & =& {\left|A\right|}^2+\left|A\right|\left|B\right|+|B^{\prime }{|-n+1\le |A|}^2+\left|A\right|\left|B\right|-n+k.\hfill \end{array}$$

Combining with (8), we see that

$$n+2k-2<\left|A\right|+1+\frac{{\left|A\right|}^2+\left|A\right|\left|B\right|-n+k}{\left|A\right|}=n+\left|A\right|-\frac{n-k}{\left|A\right|}\le n+5k-2-\frac{n-k}{5k-2},$$

showing that $n<15k^2-5k$, which contradicts that $n\ge 15k^2-5k$. Since $|B^{\prime }|\ge k$, we obtain a copy of a $k{P}_3$ with all vertices of degree 2 in $B^{\prime }$ and all vertices of degree 1 in A. Noting that $A=N\left(u\right)$, it is seen that G contains a copy of $H_k$ with u as the common vertex of k quadrangles, which is a contradiction.

Case 2.$5k-1\le \left|A\right|\le n-2$. We first claim that all vertices in B have at most $3k-2$ neighbors in A. In fact, if there exists a vertex $v\in B$ with $3k-1$ neighbors in A, then $G\left[A\right]$ is $(k-1)P_3$-free. Otherwise, let $U=V\left((k-1)P_3\right)$ and there exists a path $P_3$ with v as the vertex of degree 2 and two vertices of degree 1 in $A\backslash U$, which implies that $H_k$ is a subgraph of G. This is a contradiction. By Lemma 4, we have

$$2e\left(A\right)+e(A,B)\le (2k-3)\left|A\right|-k^2+2k+\left|A\right|\left|B\right|.$$

Combining with (8), we have

$$\begin{array}{ccc}\hfill n+2k-2& <& q\left(G\right)\le \left|A\right|+1+\frac{(2k-3)\left|A\right|-k^2+2k+\left|A\right|\left|B\right|}{\left|A\right|}\hfill \\ & =& n+2k-3-\frac{k^2-2k}{\left|A\right|}\le n+2k-3,\hfill \end{array}$$

which is a contradiction. Therefore, all vertices in B have at most $3k-2$ neighbors in A. Noting that $G\left[A\right]$ is $k{P}_3$-free, it follows from Lemma 4 that

$$2e\left(A\right)\le (2k-1)\left|A\right|-k^2+1.$$

Combining with (8), we see that

$$\begin{array}{ccc}\hfill n+2k-2& <& q\left(G\right)\le \left|A\right|+1+\frac{(2k-1)\left|A\right|-k^2+1+(3k-2)\left|B\right|}{\left|A\right|}\hfill \\ & =& \left|A\right|-k+2+\frac{(3k-2)n-k^2-3k+3}{\left|A\right|}.\hfill \end{array}$$

Define a function $f\left(x\right)=x-k+2+\frac{(3k-2)n-k^2-3k+3}{x}$. By a direct calculation, we have

$$\begin{array}{ccc}\hfill f(5k-1)& =& 5k-1-k+2+\frac{(3k-2)n-k^2-3k+3}{5k-1}\hfill \\ & =& 4k+1+\frac{3k-2}{5k-1}n-\frac{k^2+3k-3}{5k-1}<t_{n,k}\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill f(n-2)& =& n-2-k+2+\frac{(3k-2)n-k^2-3k+3}{n-2}\hfill \\ & =& n+2k-2-\frac{k^2-3k+1}{n-2}\le t_{n,k}.\hfill \end{array}$$

So

$$t_{n,k}<q\left(G\right)\le max\{f(5k-1),f(n-2)\}\le t_{n,k},$$

which is a contradiction. This completes the proof. □

Now we are ready to prove Theorem 3.

Proof of Theorem 3.

Assume for a contradiction that $q\left(G\right)>t(n,k)\ge n+2k-2$. By Lemma 7, $\Delta \left(G\right)=n-1$. Let u be the vertex of maximum degree, i.e., $d\left(u\right)=\Delta \left(G\right)=n-1$. By [19], Theorem 3.1,

$$n+2k-2<q\left(G\right)\le \frac{2e\left(G\right)}{n-1}+n-2,$$

implying that

$$e\left(G\right)\ge kn-k+1.$$

It follows directly that

$$e(G-u)=e\left(G\right)-(n-1)\ge kn-k+1-(n-1)=(k-1)n-k+2>(k-\frac{3}{2})(n-1).$$

By Lemma 5, one of the following three cases holds: (i) $G-u$ is a subgraph of $F_{n-1,k-1}$, (ii) $G-u$ is a subgraph of $F_{n-1,k-2}\left(K_t\right)$ with $4\le t\le 5$, (iii) $G-u$ is a subgraph of $F_{n-1,k-2}\left(N_6\right)$. However, it is easy to calculate that $e\left(F_{n-1,k-2}\left(K_t\right)\right)<(k-1)n-k+2$, where $4\le t\le 5$, and $e\left(F_{n-1,k-2}\left(N_6\right)\right)<(k-1)n-k+2$. So (ii) and (iii) are impossible., i.e., only (i) occurs. Since $d\left(u\right)=n-1$, G is a subgraph of $F_{n,k}$. By Lemma 2, we have $q\left(G\right)\le q\left(F_{n,k}\right)\le n+2k-2$, which is a contradiction. This completes the proof.

Example 3.

For $k\ge 2$, every cycle $C_n$ is $H_k$-free. Since $C_n$ is 2-regular, we have $q\left(C_n\right)=4\le n<t_{n,k}$.

Example 4.

For $k\ge 2$, the graph $F_{n,k-1}$ is $H_k$-free. By Lemma 2, $q\left(F_{n,k-1}\right)\le n+2k-4<t_{n,k}$.

5. Concluding Remarks

We say that a graph F is edge-color-critical if F contains an edge e with $\chi (F-e)<\chi \left(F\right)$, where $\chi \left(F\right)$ is the chromatic number of F. $T_r\left(n\right)$ denotes the complete r-partite graph with as equal as possible partition sizes.

By a result of Simonovits [20] and a result of Nikiforov [21], for sufficiently large n, $T_r\left(n\right)$ is the only extremal graph attaining the maximum number of edges or the maximum spectral radius over all n-vertex graphs not containing an edge-color-critical graph F with $\chi \left(F\right)=r+1$ as a subgraph.

There are many edge-color-critical graphs, such as the complete graph $K_{r+1}$, the odd cycle $C_{2k+1}$, the k-book $B_k$, and the even wheel $W_{2k}=K_1\nabla C_{2k-1}$. In [5], He, Jin, and Zhang proved that $T_r\left(n\right)$ is the only extremal graph attaining the maximum signless Laplacian spectral radius over all n-vertex $K_{r+1}$-free graphs for $r\ge 3$. In [6], Yuan proved that $K_k\nabla {\overline{K}}_{n-k}$ is the only extremal graph attaining the maximum signless Laplacian spectral radius over all n-vertex $C_{2k+1}$-free graphs for $k\ge 3$ and $n\ge 110k^2$. Our Theorem 2 shows that $F_{n,1}$ is the only extremal graph attaining the maximum signless Laplacian spectral radius over all $B_2$-free graphs on $n\ge 4$ vertices.

It deserves to be mentioned that, dissimilar to the results of Simonovits [20] and Nikiforov [21], for different edge-color-critical graphs F, the types of extremal graphs attaining the maximum signless Laplacian spectral radius over all n-vertex F-free graphs are also different. So it is interesting to consider Problem 1 for all kinds of edge-color-critical graphs. Next we propose the following two problems.

Problem 2.

For $k\ge 3$, determine the maximum signless Laplacian spectral radius over all $B_k$-free graphs on n vertices and characterize all extremal graphs.

Problem 3.

For $k\ge 2$, determine the maximum signless Laplacian spectral radius over all n-vertex $W_{2k}$-free graphs and characterize all extremal graphs.

Noting that $K_k\nabla {\overline{K}}_{n-k}$ is $H_k$-free and $q(K_k\nabla {\overline{K}}_{n-k})>n+2k-2-\frac{2(k^2-k)}{n+2k-3}$ for $k\ge 2$ and $n\ge 7k^2$ [4]. The upper bound in Theorem 3 is asymptotically tight. Furthermore, noting that $F_{n,k}$ is $H_k$-free, we propose the following problem.

Problem 4.

Let $k\ge 2$. If G is an $H_k$-free graph on n vertices, then there exists an integer N such that for any $n\ge N$, $q\left(G\right)\le q\left(F_{n,k}\right)$ with equality if and only if $G=F_{n,k}$.