Abstract
In this work, the mixed convection flow of non-Newtonian Eyring–Powell fluid with the effects of temperature dependent viscosity (TDV) were studied together with the interaction of dust particles under the influence of Newtonian Heating (NH) boundary condition, which assume to move over a vertical stretching sheet. Alternatively, the dusty fluid model was categorized as a two-phase flow that consists of phases of fluid and dust. Through the use of similarity transformations, governing equations of fluid and dust phases are reduced into ordinary differential equations (ODE), then solved by efficient numerical Keller–box method. Numerical solution and asymptotic results for limiting cases will be presented to investigate how the flow develops at the leading edge and its end behaviour. Comparison with the published outputs in literature evidence verified the precision of the present results. Graphical diagrams presenting velocity and temperature profiles (fluid and dust) were conversed for different influential parameters. The effects of skin friction and heat transfer rate were also evaluated. The discovery indicates that the presence of the dust particles have an effect on the fluid motion, which led to a deceleration in the fluid transference. The present flow model can match to the single phase fluid cases if the fluid particle interaction parameter is ignored. The fluid velocity and temperature distributions are always higher than dust particles, besides, the opposite trend between both phases is noticed with . Meanwhile, both phases share the similar trend in conjunction with the rest factors. Almost all of the temperature profiles are not showing a significant change, since the viscosity of fluid is high, which can be perceived in the figures. Furthermore, the present study extends some theoretical knowledge of two-phase flow.
Keywords:
dusty Eyring–Powell fluid; Newtonian heating; temperature dependent viscosity; vertical stretching sheet MSC:
35Q30; 76D05; 35Q35; 34A45; 65Q10
1. Introduction
Research and studies in the area of heat and mass transport of fluids flow have discovered strategies for their development, as well as key problems. Nevertheless, it is important to choose the form of ideal fluid from the point of view of homogeneous or inhomogeneous, compressible or incompressible, Newtonian or non-Newtonian, and monophasic or polyphasic fluids, which have a significant role in determining suitable solutions for heat transfer and fluid flow enhancement. In the past few years, the new environment of accelerated technical progress has contributed to the emergence of creative approaches to analyse the suspension of fluid particles in a fluid flow that is also known as a two-phase flow model, which explains the actions of fluid dust characteristics. Industrial applications, such as petroleum transport, wastewater treatment, vehicle smoke emissions, power plant piping, and corrosive particulate matter in mining, generally involve fluid dust movement activities [1]. The movement of dust particles in a fluid leads to a two-phase cycle. Numerous pieces of research on the dynamics of solid particles in the fluid have been conducted as a result of recent advancements in the field of two-phase flow. The fluid and solid phases of this solid–liquid system are independently formulated using different continuum equations. This phenomenon includes micro-propulsion, aerosol filtration, powder transport, oil industry, and the flow of corpuscle in plasma (a liquid with suspended solids). Overall, it is very useful for modelling flow with a binary mixture of non-Newtonian fluid and solid particles linked to certain conditions. It can thus be suggested that this two-phase model could benefit in studying the dusty Eyring–Powell fluid that exhibits the binary characteristics of the Eyring–Powell fluid and spherical dust particles, such as undertaken here. Ref. [2] studied the process of radiative heat transfer in the flow of dusty liquid under the power generation aspects. The boundary layer flow of a dusty fluid with electrically conducting criteria in a porous medium has been studied by [3]. When the interaction of these phases is significant, the temperature of the fluid is always higher than that of the dust. In accordance with these applications, the literature includes a variety of works in corresponding flow for various contexts, such as multiple geometries, boundary conditions and fluid-based forms. The non-Newtonian Casson model with dust particles have been developed by [4,5]. In addition, [6,7] utilized the treating fluid–particle interaction with buoyancy forces on Jeffrey fluid with Newtonian heating indicates that the presence of the dust particles has an effect on the fluid motion, which led to decelerate the fluid transference. The natural convection flow caused by non-Newtonian fluid with dust nanoparticles has been addressed in [8,9]. Furthermore, [10] theoretically analysed along a vertical stretching sheet for magnetohydrodynamic (MHD) mixed convection of non-Newtonian tangent hyperbolic nanofluid flow with suspended dust particles. In [11], a detailed study has been done on a two-phase model implemented in the presence of hybrid nanoparticles on the dusty liquid flow through a stretching cylinder by employing the modified Fourier heat flux law. The study was conducted by considering the effect of viscous dissipation and non-linear thermal radiation, which demonstrated a two-phase dusty liquid movement across a permeable surface. Other contributions of flow models on dusty non-Newtonian fluid have drawn substantial interest among researchers under different conditions [12,13,14,15].
Consideration of the study on boundary layer phenomenon focussing on non-Newtonian heat-transported substances is essential for a deeper comprehension of engineering and industrial–technology issues, and the movement of these materials occurs extensively in various industrial processes, such as guided missiles, rain erosion, fluidisation, atmospheric failure, lunar ash fall, paint and aerosol spraying, as well as the cooling of nuclear reactors. Although the existence of such substances is greatly complicated and troublesome, a variety of constitutive models have been developed and studied to research the correct flow behaviour. Eyring–Powell fluid model is one of the subcategories of the non-Newtonian fluid model. It has a clear characteristic under other non-Newtonian models, conveniently derived from the kinetic theory of gases rather than empirical relations and comes baked from Newtonian behaviour for low and high shear rates. The rheological paradigm is known for its robustness and versatility in physical action. Ref. [12] addressed movement attributable to pulsatile pressure gradient of dusty non-Newtonian fluid with heat transfer in a channel. A preliminary analysis of the magnetohydrodynamic movement of the Eyring–Powell liquid under the suspension of nanoparticles and dust has been done by [13] in which this model has shown that the intensity of heat transfer in the aluminium oxide nanofluid was higher than that in the ferro oxide nanofluid with the current viscous variance parameter. In [14], by considering variable thermal conductivity and thermal radiation, analytical solutions of unstable flow Eyring–Powell and Carreau non-Newtonian fluids in the suspension of dust and nickel nanoparticles, a higher heat transfer rate was recorded in the nickel + Eyring–Powell mixture compared to the nickel + Carreau case. Ref. [15] attempted to examine the effects of heat and mass transfer in the presence of nonlinear convection and thermal radiation of MHD rheological Eyring–Powell fluid with dust and graphene nanoparticles in a mixture of ethylene glycol. In order to study the relationship between the fluid and dust phased, this analysis was conducted to further investigate the flow behaviour of dusty Powell–Eyring fluid in the vertical stretching sheet associated with temperature-dependent viscosity combined with NH as a thermal boundary conditions.
Over recent decades, the thermal boundary conditions have a great influence on the heat transfer in the laminar boundary layer flow problem. However, there is a situation in which the heat transfer rate is proportional to the local difference in temperature with ambient conditions or usually termed conjugate boundary conditions, which are driven by NH, should be considered as well. The case of NH has been mentioned by [16] during a study on the boundary layer flow over an upright plate. Ref. [17] made further headway during an investigation on free convection flow across horizontal surface. Ref. [18] proposed a series of solutions and numerical Eyring fluid flow with NH. Ref. [19] provided detailed nonlinear convective magneto nanofluid Eyring fluid with the effects of NH, while Ref. [20] included the effects of the thermal radiation Eyring fluid subjected to NH boundary condition. Meanwhile, Refs. [21,22] highlighted the effects of MHD and NH on Powell–Eyring fluid over a stretching cylinder and inclined permeable surface, respectively. Ref. [23] reviewed the problem of temperature-dependent viscosity on mixed convection flow of Eyring–Powell fluid studied together with NH. A mathematical model of forced convective flow on non-Newtonian Eyring–Powell fluid under temperature-dependent viscosity circumstance is formulated by [24]. The effects of non-Newtonian magnetohydrodynamic nanofluid over a stretched plate with NH effect have been investigated by [25]. Other studies associated with particular impact for fluid–solid flow considering different fluid models were established and reported in [26,27,28,29].
Motivated by the impactful research as scrutinised above, this present study is dedicated to examining the two-phase boundary layer flow of Eyring–Powell fluid together with the temperature-dependent viscosity from a vertical stretching sheet, the temperature of which is higher than that of the ambient fluid. The simulation of mixed convection influence with NH was also implanted in this investigation. The mathematical formulations of the problems are constructed as mentioned in the study scope, which involves the derivation of governing equations for the proposed problem. The similarity transformation is used to transform the non-linear governing equations into ordinary differential equations (ODE). Then, the numerical solutions of the transformed equations are solved using the Keller-box method.
The step size of time and space can be arbitrary, since this method is implicit with second order accuracy, which makes it suitable to solve the parabolic partial differential equations efficiently [30]. However, the computation could be time consuming if the small step size of time and space is inserted. The algorithm of the Keller-box method is computed in Matlab software to generate the results and the figures for various non-dimensional parameters on the velocity and temperature profile. The comparison with the previous published result were tabulated to verify the present results by fixing several parameters. The output from the investigation are useful for the scientist and experimentalist in studying the behaviour of fluids, which have interactions with dust particles.
2. Mathematical Formulation
Flow suspended with particles affected by TDV over a vertical stretching sheet was introduced for the steady incompressible mixed convection of non-Newtonian Eyring fluid under NH condition. The term, , is related to temperature of ambient fluid. The -axis was oriented to the vertical plane, and the -axis to the plane was perpendicular. The sheet is stretched with the velocity, where, is stretching rate. The flow was created by the stretching of the sheet due to the simultaneous application of two equal and opposite forces along the -axis, holding the origin fixed and finding the flow to be limited to the area, . The configuration of a physical model is displayed in Figure 1.
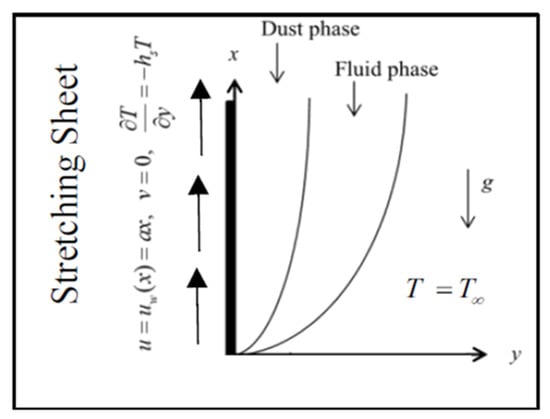
Figure 1.
Physical sketch and coordinate system.
The solid particles are presumed to be spherical in shape and uniform size, where their density remains constant and the inter-particle collision may be neglected, since they are considered to be diluted throughout the flow. In terms of heat transfer from one atom to another, all of these were ignored: the volume fraction of dust particles, coagulation, phase transition and deposition. The fluid and sediment particle motions were linked only through drag-and-heat flow across them, the stokes linear drag theory was used for modelling the drag force. Based on the preceding assumptions, the basic two-dimensional boundary layer equations involving continuity, momentum and energy for both the fluid and particle phases with usual ratings can be written as [31,32] shown below:
For fluid phase:
For dust phase:
Here, and represents the components of velocity in directions, temperature, density, specific heat at constant pressure and viscosity coefficient, respectively. Meanwhile, and denote the velocity components in directions, temperature, density, specific heat, velocity and thermal relaxation time for dust phase, respectively. The corresponding fluid and particle phase boundary conditions were given as.
In (7), the parameter was corresponded to the velocity of the stretching surface with being a positive constant of , thermal conductivity , heat transfer coefficient and ambient temperature . To obtain the set of similarity equations in the form of ordinary differential equations, the similarity transformations (8) were adopted and applied to the governing Equations (1)–(6).
The Reynolds exponential viscosity model was used to predict temperature-dependent variability in viscosity that gave a detailed approach as:
The Equations (1)–(6) are changeable from PDEs to ODEs, which can be represented as:
Subjected to boundary conditions:
In Equations (10)–(14), a notation prime corresponds to the differentiation with respect to Additionally, the dimensionless numbers and parameters are as follows where and are the fluid parameters, represents Prandtl number, represents viscosity parameter, conjugate parameter of heat transfer, is mixed convection parameter, specific heat ratio of mixture parameter, parameter of mass concentration of particle phase, fluid–particle interaction parameter and Reynolds number . A limiting case arising in this problem was without the presence of dust particles effect where the buoyancy force is negligible and can be obtained using the following expression [33]:
It is important to mention here that the comparison between the present results with the exact solution is necessary to claim the accuracy of the current model and its output. The primary physical quantity of importance is the dimensionless coefficient of skin friction and the local Nusselt number, which has been described by (16), where the shear stress and surface heat are compatible with those referred in [34].
where
The shear stress and surface heat transfer is calculated using the following definition:
3. Results and Discussion
Equations (10)–(13) were solved numerically, along with boundary conditions (14) using the Keller-box approach as computed in the Matlab program. The Keller-box method comprise of four steps which are:
Step 1: The nonlinear partial differential equation are first transformed to first order system;
Step 2: The first order system is then approximated using central difference;
Step 3: The Newton’s method is applied to linearize the system;
Step 4: The linearized system is solved by block elimination technique;
To initially integrate the procedure, the nonlinear structure of ordinary differential equations was converted into a structure of linear first-order equations. Our bulk calculations were viewed with and identified as appropriate for all values of the parameters, which were considered asymptotically to achieve the far-field boundary conditions as seen in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17. The interaction force among two phases is significant, where usually, both governing equations are coupled through the term of total fluid–particle interaction force per unit volume that is clearly different from single phase flow. Numerical computation are conducted for fluid parameters, namely and , Prandtl number , viscosity parameter , mixed convection parameter , conjugate parameter of heat transfer, a parameter of mass concentration of particle phase and fluid–particle interaction parameter .
The local Nusselt number is one of the important characteristics in the heat transfer field, which indicates the ratio of convective heat transfer to conductive heat transfer. Hence, in order to check the accuracy of the numerical method used, the comparison in Nusselt number for a fixed value of with the established results in [35,36,37] and it is revealed to be in strong agreement as displayed in Table 1. In addition, a direct comparative study was carried out with the exact Equation (15), as well as the existing study reported with the available published result by [38,39,40,41] shown in Table 2. From Table 1 and Table 2, an excellent agreement is achieved, which indicates that the current model and its findings are acceptable. It is worth declaring here, even in the limiting cases, the present model does not exactly give the same solution, but the difference is very small. It is logical since the present model is more complex with multiple parameters. Table 3 demonstrates the variance of the skin friction coefficient and the Nusselt numbers for various parameters of the present analysis.

Table 1.
Comparative study on value .

Table 2.
Comparative study on .

Table 3.
Numerical results of and for various values of and .
Figure 2, Figure 3, Figure 4 and Figure 5 was plotted to understand the velocity and temperature distribution of the fluid and particle phase under variance of and . It was revealed that the velocity were decreased for both fluid and particle phases as and increases. The similar trend was noticed in temperature distribution for both phases in increasing but contrary in the growing of . At far from the surface, it is remarked the profile asymptotically reached the boundary conditions, and, therefore, the authors are confident on the correctness of present results.
Figure 6, Figure 7, Figure 8 and Figure 9 display the distribution on velocity and temperature for multiple values of and . It was found that with higher elasticity parameter (presence Eyring fluid), the magnitude of velocity for both fluid and particle were enhanced. The change in the velocity contributed to boosting the heat of the fluid (for increasing ) but against the heating development (for increasing ).
Figure 10 and Figure 11 indicate that the amount of . Physically, the heat transfer rate with the was reduced; this reduced the temperature and resulting thickness of the boundary layer. During the event with large values of the heat transfer equation, which implies a strong heat transfer rate as it slowly declines, the fluid became a small heat transfer rate. Through mixed convection and the effects of the fluid–particle interaction parameters and , the velocity of all the phases and their associated boundary layer thicknesses increased. The response to the temperature profile was quite the opposite of the speed field with and , as seen in Figure 12, Figure 13, Figure 14 and Figure 15, further finding that the flow properties of the dusty fluid can be greatly regulated by changing the influence of the parameters of fluid–particle interaction .
Figure 16 and Figure 17 were plotted to evaluate all fluid and particle phase velocity and temperature components for the variance of . Within the boundary layer, temperature profiles reduced with improvement within . On the other hand, the velocity profile was improved by increasing the parameter . This was because the fluid tends to raise the intensity of drag between the phases with the mass content of dust particles rising. The fluid movement was thus slowed down, resulting in reduced surface-phase energy, since the surface layer was pulled together with the liquid. By continuing to increase the mass content of the dust particles, more fluid-phase energy was converted into a larger number of particles, but less energy from the fluid phase was supplied to the individual particles. Therefore, it can be inferred that varying will greatly affect the flow characteristics. Furthermore, the boundary momentum layer for ordinary Eyring fluid was observed thinner than that of the dusty Eyring fluid.
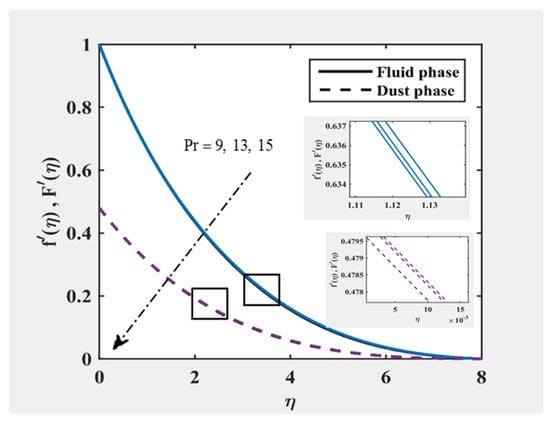
Figure 2.
and at , and for various values of .
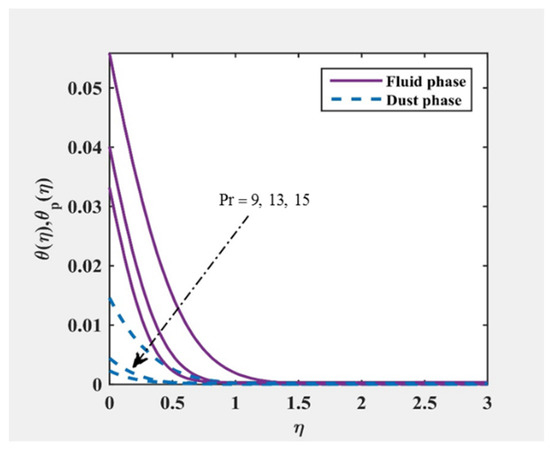
Figure 3.
and at , and for various values of .
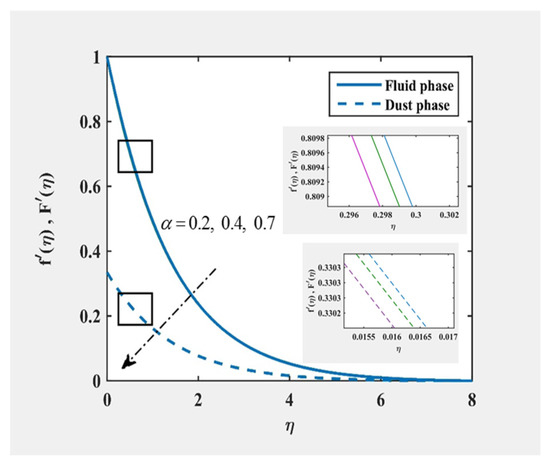
Figure 4.
and at , and for various values of .
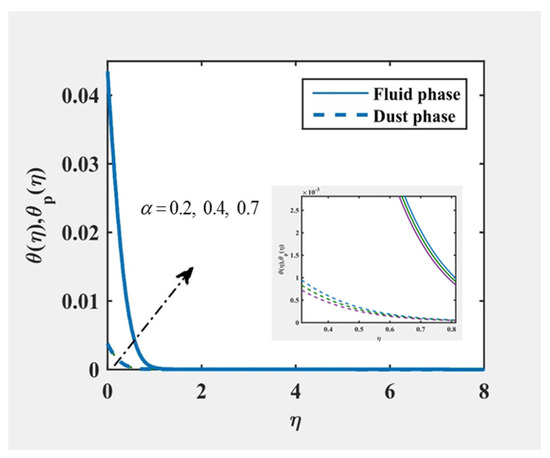
Figure 5.
and at , and for various values of .
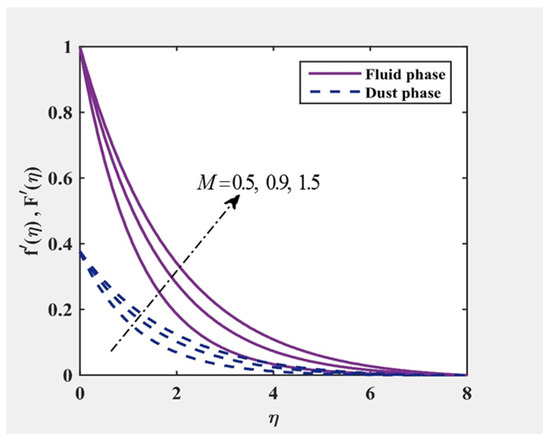
Figure 6.
and at , and for various values of .
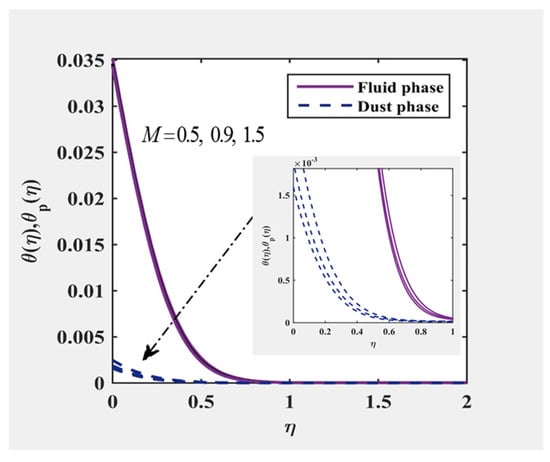
Figure 7.
and at , and for various values of .
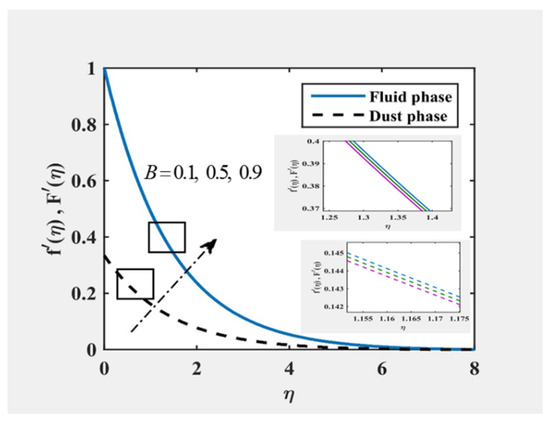
Figure 8.
and at , and for various values of .
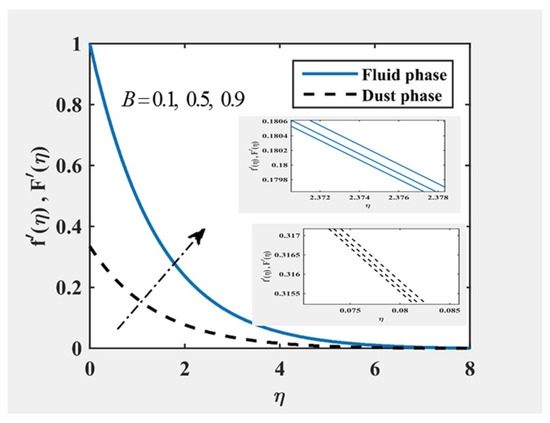
Figure 9.
and at , and for various values of .
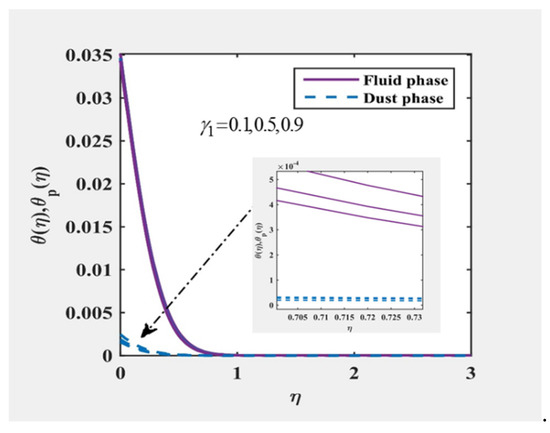
Figure 10.
and at , and for various values of .
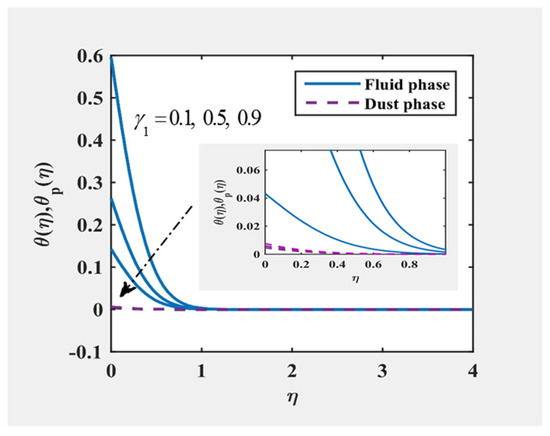
Figure 11.
and at , and for various values of .
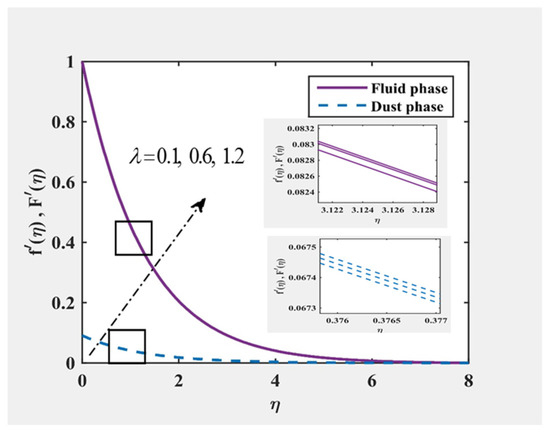
Figure 12.
and at , and for various values of .
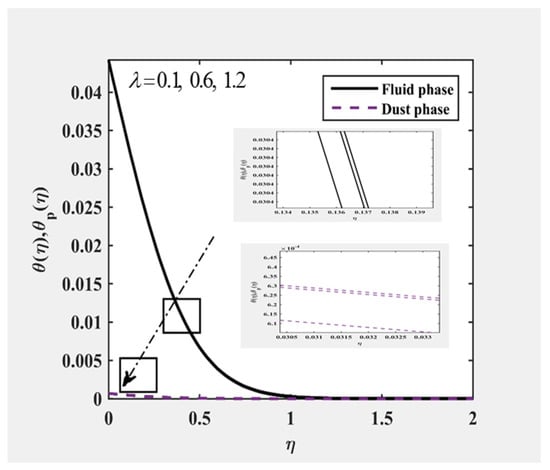
Figure 13.
and at , and for various values of .
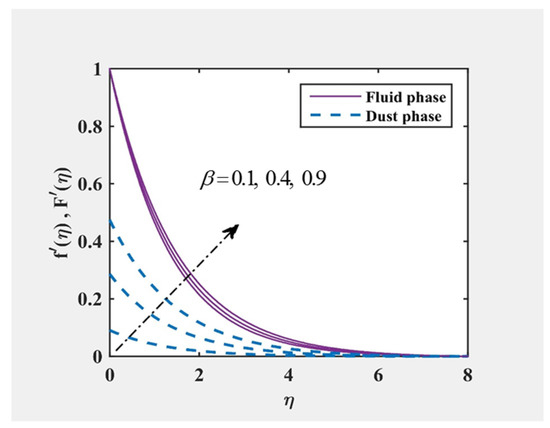
Figure 14.
and at , and for various values of .
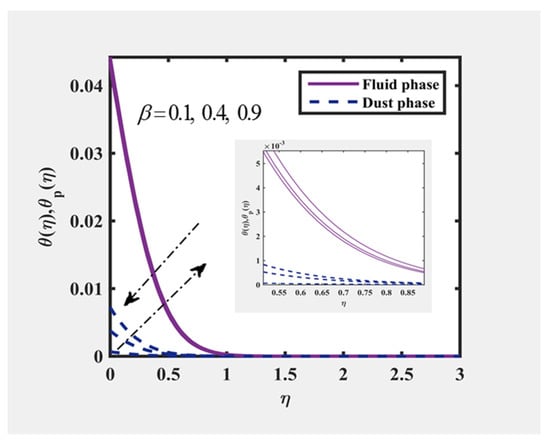
Figure 15.
and at , and for various values of .
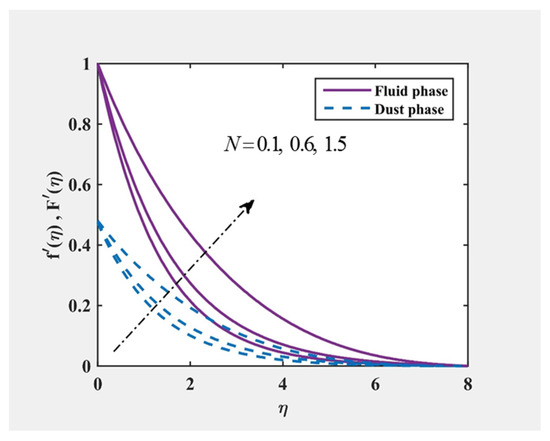
Figure 16.
and at , and for various values of .
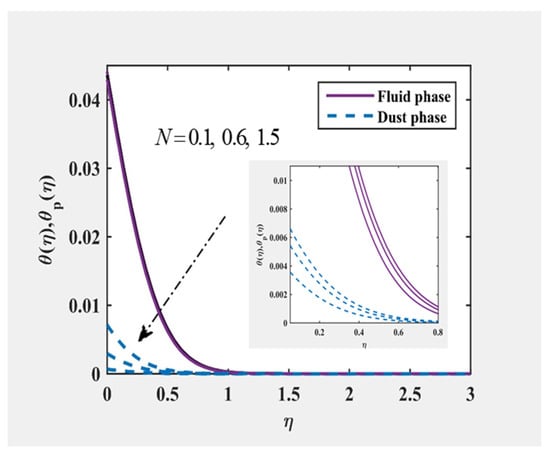
Figure 17.
and at , and for various values of .
4. Conclusions and Future Work
The results of temperature-dependent viscosity on the mixed convection flow of non-Newtonian Eyring–Powell fluid due to a vertical stretching surface interacting with dust particles under the control of NH boundary conditions have been numerically explained. Highly non-linear governing PDEs were first converted to ODEs, utilising similarity transformations and then numerically resolved using the Keller-box method. MATLAB program has been applied to conduct computational. Velocity and temperature profile for all fluid and particle phases were illustrated graphically. The value of sheer rate and heat transfer coefficient were calculated and have tabulated in table for various pertinent parameters. In addition, the current output was validated by comparative study with previously reported results and perceived a good agreement between them. In conjunction, a few important findings from the existing research are indicated as:
- For certain applications, the fluid’s flow and heat transfer can be regulated by embedding the particles of fine dust.
- The process velocity (temperature) of fluid and dust have the opposite effects for buoyancy force parameter variability.
- In the mixed convection regime, the local shear stress increases and the local rate of heat transfer decreases as the value of buoyancy parameter increases for all values of the Prandtl number and the viscosity variation parameter.
- The fluid–particle interaction parameter variability is favourable for the thickness of the dust boundary layer. However, for the thickness of boundary layer of momentum, it is unfavourable.
- The velocity distribution was suppressed with the Prandtl number compared to temperature distribution.
- The velocity profiles increase and the viscosity of the fluid decrease near the surface of the plate owing to increase in the value of the viscosity variation parameter. The temperature profiles of both phases are enhanced by rising .
- The quantity of skin friction decreases with greater values of fluid parameters, mixed convection, conjugate parameter of heat transfer, mass concentration of particle phase and fluid–particle interaction parameter.
- Increase in the value of the viscosity variation parameter leads to increase in the local shear stress and to decrease in the local rate of heat transfer. Its effect on the increase of the rate of heat transfer is less than that of the local shear stress.
Ultimately, it is worth concluding that the existence of dust particles has a substantial effect on the flow behaviour of Eyring fluid in the presence of TDV.
Author Contributions
Funding acquisition, A.R.M.K.; Investigation, A.A., N.A.N.A., I.W., N.S.K. and N.A.Z.; Methodology, A.A. and N.S.A.; Resources, A.R.M.K., N.S.A., N.A.N.A., D.L.C.C., I.W. and N.S.K.; Software, D.L.C.C. and N.A.Z.; Writing—original draft, A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Universiti Malaysia Pahang under RDU213206 and the APC was funded by Universiti Malaysia Pahang through RDU213206 and Universiti Teknologi Petronas through 015MCO–030.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors wish to thank Universiti Malaysia Pahang for the financial support through RDU213206 and Universiti Teknologi Petronas through 015MCO–030. Our heartfelt thanks also go to Universiti Teknologi MARA Cawangan Johor and Cawangan Pahang as well as Universiti Teknikal Melaka for their assistance and support.
Conflicts of Interest
The authors of this manuscript declare no conflict of interest.
References
- Ramesh, G.K.; Kumar, K.G.; Shehzad, S.; Gireesha, B. Enhancement of radiation on hydromagnetic Casson fluid flow towards a stretched cylinder with suspension of liquid-particles. Can. J. Phys. 2018, 96, 18–24. [Google Scholar] [CrossRef]
- Manjunatha, P.T.; Gireesha, B.J.; Prasannakumara, B. Effect of Radiation on Flow and Heat Transfer of MHD Dusty Fluid Over a Stretching Cylinder Embedded in a Porous Medium in Presence of Heat Source. Int. J. Appl. Comput. Math. 2015, 3, 293–310. [Google Scholar] [CrossRef]
- Kalpana, G.; Madhura, K.; Kudenatti, R.B. Impact of temperature-dependant viscosity and thermal conductivity on MHD boundary layer flow of two-phase dusty fluid through permeable medium. Eng. Sci. Technol. Int. J. 2018, 22, 416–427. [Google Scholar] [CrossRef]
- Arifin, N.S.; Zokri, S.M.; Kasim, A.R.M.; Salleh, M.Z.; Mohammad, N.F.; Yusoff, W.N.S.W. Aligned magnetic field on dusty Casson fluid over a stretching sheet with Newtonian heating. Malays. J. Fundam. Appl. Sci. 2017, 13, 245–248. [Google Scholar] [CrossRef]
- Kasim, A.R.M.; Arifin, N.S.; Zokri, S.M.; Salleh, M.Z.; Mohammad, N.F.; Ching, D.L.C.; Shafie, S.; Ariffin, N.A.N. Convective Transport of Fluid–Solid Interaction: A Study between Non-Newtonian Casson Model with Dust Particles. Crystals 2020, 10, 814. [Google Scholar] [CrossRef]
- Kasim, A.R.M.; Arifin, N.S.; Zokri, S.M.; Salleh, M.Z. Fluid-particle interaction with buoyancy forces on Jeffrey fluid with Newtonian heating. CFD Lett. 2019, 11, 1–16. [Google Scholar]
- Kasim, A.R.M.; Arifin, N.S.; Zokri, S.M.; Salleh, M.Z. The Investigation of a Fluid-Solid Interaction Mathematical Model under Combined Convective Jeffrey Flow and Radiation Effect Embedded Newtonian Heating as the Thermal Boundary Condition over a Vertical Stretching Sheet. In Defect and Diffusion Forum; Trans Tech Publications Ltd.: Kapellweg, Switzerland, 2020; Volume 399, pp. 65–75. [Google Scholar]
- Siddiqa, S.; Begum, N.; Hossain, A.; Gorla, R.S.R. Natural convection flow of a two-phase dusty non-Newtonian fluid along a vertical surface. Int. J. Heat Mass Transf. 2017, 113, 482–489. [Google Scholar] [CrossRef]
- Mohamed, R.A.; Hady, F.M.; Mahdy, A.; Abo-Zai, O.A. Laminar MHD natural convection flow due to non-Newtonian nanofluid with dust nanoparticles around an isothermal sphere: Non-similar solution. Phys. Scr. 2021, 96, 035215. [Google Scholar] [CrossRef]
- Mahdy, A.; Hoshoudy, G.A. Two-phase mixed convection nanofluid flow of a dusty tangent hyperbolic past a nonlinearly stretching sheet. J. Egypt. Math. Soc. 2019, 27, 1–16. [Google Scholar] [CrossRef]
- Kumar, R.S.V.; Gowda, R.J.P.; Radhika, M.; Prasannakumara, B.C. Two-phase flow of dusty fluid with suspended hybrid nanoparticles over a stretching cylinder with modified Fourier heat flux. SN Appl. Sci. 2021, 3, 1–9. [Google Scholar]
- Shawky, H.M. Pulsatile flow with heat transfer of dusty magnetohydrodynamic Ree-Eyring fluid through a channel. Heat Mass Transf. 2009, 45, 1261–1269. [Google Scholar] [CrossRef]
- Upadhya, S.M.; Mahesha; Raju, C.; Shehzad, S.; Abbasi, F. Flow of Eyring-Powell dusty fluid in a deferment of aluminum and ferrous oxide nanoparticles with Cattaneo-Christov heat flux. Powder Technol. 2018, 340, 68–76. [Google Scholar] [CrossRef]
- Upadhya, S.M.; Mahesha; Raju, C.S.K. Comparative study of Eyring and Carreau fluids in a suspension of dust and nickel nanoparticles with variable conductivity. Eur. Phys. J. Plus 2018, 133, 156. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Saleem, S.; Al-Qarni, M.M.; Upadhya, S.M. Unsteady nonlinear convection on Eyring–Powell radiated flow with suspended graphene and dust particles. Microsyst. Technol. 2018, 25, 1321–1331. [Google Scholar] [CrossRef]
- Merkin, J.H. Natural-convection boundary-layer flow on a vertical surface with Newtonian heating. Int. J. Heat Fluid Flow 1994, 15, 392–398. [Google Scholar] [CrossRef]
- Lesnic, D.; Ingham, D.B.; Pop, I.; Storr, C. Free convection boundary-layer flow above a nearly horizontal surface in a porous medium with newtonian heating. Heat Mass Transf. 2003, 40, 665–672. [Google Scholar] [CrossRef]
- Hayat, T.; Ali, S.; Farooq, M.A.; Alsaedi, A. On Comparison of Series and Numerical Solutions for Flow of Eyring-Powell Fluid with Newtonian Heating And Internal Heat Generation/Absorption. PLoS ONE 2015, 10, e0129613. [Google Scholar] [CrossRef]
- Qayyum, S.; Hayat, T.; Shehzad, S.A.; Alsaedi, A. Nonlinear convective flow of Powell-Erying magneto nanofluid with Newtonian heating. Results Phys. 2017, 7, 2933–2940. [Google Scholar] [CrossRef]
- Hayat, T.; Waqas, M.; Shehzad, S.A.; Alsaedi, A. Mixed convection stagnation-point flow of Powell-Eyring fluid with Newtonian heating, thermal radiation, and heat generation/absorption. J. Aerosp. Eng. 2017, 30, 04016077. [Google Scholar] [CrossRef]
- Hayat, T.; Hussain, Z.; Farooq, M.; Alsaedi, A. Magnetohydrodynamic flow of Powell-Eyring fluid by a stretching cylinder with Newtonian heating. Therm. Sci. 2018, 22, 371–382. [Google Scholar] [CrossRef]
- Parmar, A.; Jain, S. Unsteady convective flow for MHD Powell-Eyring fluid over inclined permeable surface. J. Comput. Appl. Res. Mech. Eng. 2019, 9, 297–312. [Google Scholar]
- Aljabali, A.; Kasim, A.R.M.; Arifin, N.S.; Isa, S.M. Mixed Convection of Non-Newtonian Erying Powell Fluid with Temperature-Dependent Viscosity over a Vertically Stretched Surface. Comput. Mater. Contin. 2020, 66, 421–435. [Google Scholar] [CrossRef]
- Aljabali, A.; Kasim, A.R.M.; Arifin, N.S.; Isa, S.M.; Ariffin, N.A.N. Analysis of Convective Transport of Temperature-Dependent Viscosity for Non-Newtonian Erying Powell Fluid: A Numerical Approach. Comput. Mater. Contin. 2020, 66, 675–689. [Google Scholar] [CrossRef]
- Gangadhar, K.; Kumar, D.V.; Rao, M.V.S.; Kannan, T.; Sakthivel, G. Effects of Newtonian heating on the boundary layer flow of non-Newtonian magnetohydrodynamic nanofluid over a stretched plate using spectral relaxation method. Int. J. Ambient Energy 2019, 43, 1248–1261. [Google Scholar] [CrossRef]
- Amin, W.N.Z.; Qasim, M.; Shafie, S. G-Jitter Induced Mixed Convection Flow between Two Parallel Plates with Newtonian Heating. Sci. Proc. Ser. 2019, 1, 107–110. [Google Scholar] [CrossRef]
- Mohamed, M.K.A.; Ismail, N.A.; Hashim, N.; Shah, N.; Salleh, M. MHD Slip Flow and Heat Transfer on Stagnation Point of a Magnetite (Fe3O4) Ferrofluid towards a Stretching Sheet with Newtonian Heating. CFD Lett. 2019, 11, 17–27. [Google Scholar]
- Ahmad, S.; Nadeem, S. Application of CNT-based micropolar hybrid nanofluid flow in the presence of Newtonian heating. Appl. Nanosci. 2020, 10, 5265–5277. [Google Scholar] [CrossRef]
- Hasan, M.; Samad, A.; Hossain, M. Effects of Hall Current and Ohmic Heating on Non-Newtonian Fluid Flow in a Channel due to Peristaltic Wave. Appl. Math. 2020, 11, 292–306. [Google Scholar] [CrossRef]
- Sarif, N.; Salleh, M.; Nazar, R. Numerical solution of flow and heat transfer over a stretching sheet with newtonian heating using the keller box method. Procedia Eng. 2013, 53, 542–544. [Google Scholar] [CrossRef]
- Siddiqa, S.; Hossain, M.A.; Saha, S.C. Two-phase natural convection flow of a dusty fluid. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 1542–1556. [Google Scholar] [CrossRef]
- Hayat, T.; Iqbal, Z.; Qasim, M.; Obaidat, S. Steady flow of an Eyring Powell fluid over a moving surface with convective boundary conditions. Int. J. Heat Mass Transf. 2012, 55, 1817–1822. [Google Scholar] [CrossRef]
- Imtiaz, M.; Hayat, T.; Hussain, M.; Shehzad, S.A.; Chen, G.Q.; Ahmad, B. Mixed convection flow of nanofluid with Newtonian heating. Eur. Phys. J. Plus 2014, 129, 97. [Google Scholar] [CrossRef]
- Javed, T.; Ali, N.; Abbas, Z.; Sajid, M. Flow of an Eyring-Powell non-Newtonian fluid over a stretching sheet. Chem. Eng. Commun. 2013, 200, 327–336. [Google Scholar] [CrossRef]
- Grubka, L.; Bobba, K. Heat transfer characteristics of a continuous, stretching surface with variable temperature. ASME J. Heat Transf. 1985, 107, 248–250. [Google Scholar] [CrossRef]
- El-Aziz, M.A. Unsteady mixed convection heat transfer along a vertical stretching surface with variable viscosity and viscous dissipation. J. Egypt. Math. Soc. 2014, 22, 529–537. [Google Scholar] [CrossRef]
- Mamatha, S.; Mahesha; Raju, C.S.; Makinde, O.D. Effect of Convective Boundary Condition on MHD Carreau Dusty Fluid over a Stretching Sheet with Heat Source. Defect Diffus. Forum 2017, 377, 233–241. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Boundary layer flow and heat transfer over an unsteady stretching vertical surface. Meccanica 2008, 44, 369–375. [Google Scholar] [CrossRef]
- Arnold, J.C.; Asir, A.A.; Somasundaram, S.; Christopher, T. Heat transfer in a viscoelastic boundary layer flow over a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 1112–1118. [Google Scholar] [CrossRef]
- Wahab, H.A.; Hussain, S.; Naeem, M. Mixed convection flow of Powell-Eyring fluid over a stretching cylinder with Newtonian heating. Kuwait J. Sci. 2016, 43, 1–13. [Google Scholar]
- Khan, I.; Malik, M.Y.; Salahuddin, T.; Khan, M.; Rehman, K.U. Homogenous–heterogeneous reactions in MHD flow of Powell–Eyring fluid over a stretching sheet with Newtonian heating. Neural Comput. Appl. 2017, 30, 3581–3588. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).