High-Order Multivariate Spectral Algorithms for High-Dimensional Nonlinear Weakly Singular Integral Equations with Delay

Abstract

One of the open problems in the numerical analysis of solutions to high-dimensional nonlinear integral equations with memory kernel and proportional delay is how to preserve the high-order accuracy for nonsmooth solutions. It is well-known that the solutions to these equations display a typical weak singularity at the initial time, which causes challenges in developing high-order and efficient numerical algorithms. The key idea of the proposed approach is to adopt a smoothing transformation for the multivariate spectral collocation method to circumvent the curse of singularity at the beginning of time. Therefore, the singularity of the approximate solution can be tailored to that of the exact one, resulting in high-order spectral collocation algorithms. Moreover, we provide a framework for studying the rate of convergence of the proposed algorithm. Finally, we give a numerical test example to show that the approach can preserve the nonsmooth solution to the underlying problems.

1. Introduction

In this paper, we consider the following nonlinear multi-dimensional Volterra–Fredholm integral equation with memory kernel and proportional delay:

$$\begin{array}{c}\psi \left(t_1,\dots ,t_m\right)=h\left(t_1,\dots ,t_m\right)\hfill \\ +{\int }_0^{t_1}\cdots {\int }_0^{t_m}{(t_1-z_1)}^{-u_1}\dots {(t_m-z_m)}^{-u_m}g(z_1,\dots ,z_m,\psi (z_1,\dots ,z_m),\psi (q{z}_1,\dots ,q{z}_m))d{z}_m\cdots d{z}_1\hfill \\ +{\int }_0^1\cdots {\int }_0^1{(1-z_1)}^{-u_1}\dots {(1-z_m)}^{-u_m}f(z_1,\dots ,z_m,\psi (z_1,\dots ,z_m),\psi (q{z}_1,\dots ,q{z}_m))d{z}_m\cdots d{z}_1,\hfill \end{array}$$

(1)

where $\psi \left(t_1,\dots ,t_m\right)\in C\left({[0,1]}^m\right)$, $0\le u_j\le 1$, $j=1,\dots ,m, f, g:D\to {\mathbb{R}}^m$ with $D:=\{\left(z_1,\dots ,z_m\right):0\le z_j\le t_j\le 1, j=1,2,\dots ,m\}$ are given functions and $q\in (0,1)$ is the proportional delay.

Non-linear integral equations with weakly singular kernels have recently attracted the attention of researchers due to their applications to the solution of some general problems of fluid mechanics. Such problems are converted to the solution of a non-linear integral equation with a memory kernel, linked to a large number of studies of an applied character; see ([1,2,3,4], Section 7.8). The Volterra integral equation with proportional delay is an important type of Volterra integral equation [5,6]. It arises frequently in the modelling of many applied science problems, including bioscience modeling, ecological competition systems, and population growth. The book [7], with various physical and engineering applications, is one of the most recent contributions to this area. The analysis of Volterra functional integral equations with proportional delays dates back to Volterra’s work ([8], pp. 92–101). Fox et al. [9] were the first to address the approximate solution to the so-called pantograph equations.

Because explicit solutions to even linear weakly singular Volterra–Fredholm integral equations are difficult to acquire, robust numerical methods are required in order to discretize the model equations [10,11,12,13,14,15]. A series of numerical methods for approximating the solutions of Volterra–Fredholm integral equations and other singular problems have been developed, including Runge–Kutta methods, Nyström methods, piecewise polynomial collocation methods, and the finite element method [16,17,18,19,20,21,22,23,24,25,26,27,28]. Some numerical approaches to Volterra–Fredholm integral equations with various delays have recently been developed. Brunner and his colleagues [29] have conducted a lot of ground-breaking work in this area. They mostly used geometric meshes to solve the Volterra–Fredholm integral equations with proportional delay. Xie et al. [30] analyzed the existence, uniqueness, and regularity aspects of solutions to general Volterra functional integral equations with vanishing delay. Wang and Sheng [31] proposed and analyzed a high-order multistep Gauss–Legendre spectral collocation approach for second-kind nonlinear Volterra integral equations with regular kernel and vanishing variable delays.

Near the boundary domain of integration, the solution to nonlinear Volterra–Fredholm integral equations with weakly singular kernels is often nonsmooth (its derivatives are unbounded). If one wants to achieve a high-order rate of convergence in a numerical approach for these equations, one should take into consideration, in some way, the nonsmooth behavior of the exact solution. Traditionally, the theory, application, and implementation of spectral approaches for the solution of nonlinear integral equations have been focused on problems with a certain amount of inherent regularity in the solutions. When the solutions are smooth, spectral methods provide exponential rates of convergence accuracy with a relatively small number of unknowns [32,33]. In contrast, finite element methods and finite difference methods provide only algebraic rates of convergence. However, spectral accuracy is not possible when the approximated solutions have lower regularities, as is the case when, for example, a weakly singular kernel exists in Volterra–Fredholm integral equations. There are relatively few papers on spectral methods for the nonsmooth solution to integral equations. Allaei et al. [11] developed a Jacobi spectral collocation method for weakly singular nonlinear Volterra integral equations with nonsmooth solutions. Zaky et al. [34,35,36,37,38] studied the convergence analysis of the collocation spectral method for general classes of nonlinear fractional differential and related integral equations with limited regular solutions. Zhang et al. [39] proposed a spectral element approach based on the shifted Muntz–Jacobi functions and shifted Legendre polynomials for the numerical solution to nonlinear weakly singular Volterra integral equations. Li et al. [40] considered the second kind of Volterra integral equations with weakly singular kernels and nonsmooth solutions and constructed a spectral approach based on Legendre and Chebyshev polynomial approximations. Wang et al. [41] developed and analyzed an $hp$-version discontinuous Galerkin time-stepping method for linear weakly singular Volterra integral equations. They demonstrated that utilizing geometrically refined time steps can achieve high-order rates of convergence for solutions with start-up singularities. Mokhtary et al. [42] constructed a well-conditioned Jacobi–Galerkin spectral technique for the numerical solution of weakly singular Volterra–Hammerstein integral equations with proportional delay. On the other hand, many authors constructed non-polynomial singular functions as basis functions of spectral techniques to approximate the nonsmooth solutions of many problems, which can accurately capture the singularities of the solutions [43,44,45,46,47,48,49,50,51].

One of the open problems in the numerical analysis of solutions to these equations is how to obtain high-order accuracy for nonsmooth solutions. It is well-known that the solutions to these problems exhibit singularities, which causes challenges in developing high-order and efficient spectral methods. Moreover, the spectral techniques of Galerkin or Petrov–Galerkin type formulations are inefficient in handling nonlinear problems. In contrast, the spectral techniques of the collocation type do not suffer from such limitations and are especially well suited for nonlinear fractional integral equations. The singular behavior of the exact solution can be properly considered in collocation methods by utilizing polynomial splines on specific nonuniform grids that are suitably graded to compensate for the general boundary singularities of the exact solution’s derivatives. However, in the application, the usage of strongly graded grids may cause serious technical challenges, since such grids can produce significant round-off errors in computations, resulting in unstable numerical outputs. To overcome the issues associated with the use of strongly graded grids, a variable change is frequently used to enhance the smoothness of the solutions, resulting in milder or disappearing singularities of the derivatives of the exact solution (see, for instance [52,53]). In the present work, we adopt a transformed spectral scheme to solve nonlinear high-dimensional weakly singular integral equations with proportional delay and nonsmooth solutions. The modified spectral approach is built on multivariate Jacobi polynomials and adopted smoothing transformations to circumvent the curse of singularity at the beginning of time. Furthermore, we investigate the convergence, existence, and uniqueness of approximation solutions.

The rest of the paper is structured as follows. In Section 2, we present the essential properties of multivariate Jacobi polynomials as well as several relevant lemmas for the convergence analysis. In Section 3, we develop the spectral collocation approach for the integral Equation (1). In Section 4, we study the convergence analysis of the spectral collocation method. In Section 5, we investigate the existence of the approximate solution. In Section 6, we present a numerical example to demonstrate the accuracy and the efficiency of the numerical scheme. Conclusions and remarks are considered in Section 7.

2. Multivariate Jacobi Polynomials

Throughout the paper, the notations $\mathbb{N}$ and $\mathbb{R}$ denote the set of all positive integers and real numbers, respectively, and ${\mathbb{N}}_0=\left\{0\right\}\cup \mathbb{N}$. Let $P_N$ be the space of all algebraic polynomials of degree at most N in $\Omega$.

For $m\in \mathbb{N}$, the lowercase boldface letters are used to denote vectors and m-dimensional multi-indexes, e.g., $\mathit{j}=(j_1,\dots ,j_m)\in {\mathbb{N}}_0^m$ and $\mathit{u}=(u_1,\dots ,u_m)\in {\mathbb{R}}^m$. In addition, let ${\mathit{e}}_k=(0,\dots ,1,\dots ,0)$ be the kth unit vector in ${\mathbb{R}}^m$ and $\mathbf{1}=(1,1,\dots ,1)\in {\mathbb{N}}^m$. We identify the following component-wise operations for a scalar $q\in \mathbb{R}$:

$$\mathit{v}+\mathit{b}=(v_1+b_1,\dots ,v_m+b_m), \mathit{v}+q:=\mathit{v}+q\mathbf{1}=(v_1+q,\dots ,v_m+q).$$

(2)

We also employ the following patterns:

$$\mathit{v}\ge \mathit{b}\iff {\forall }_{1\le s\le m} v_s\ge b_s; \mathit{v}\ge r\iff \mathit{v}\ge r\mathbf{1}\iff {\forall }_{1\le s\le m} v_s\ge r.$$

(3)

We denote

$$\begin{array}{c}{\left|\mathit{d}\right|}_1=\sum _{s=1}^m{d}_s, {\left|\mathit{d}\right|}_{\infty }=\underset{1\le s\le m}{max}{d}_s, \prod \mathit{x}{\mathit{y}}^{\mathit{q}}=\prod _{s=1}^m{x}_s{y}_s^{q_s},\hfill \\ {\int }_{\mathit{u}}^{\mathit{v}}· d\mathit{r}={\int }_{u_1}^{v_1}\cdots {\int }_{u_m}^{v_m}· d{r}_m\cdots d{r}_1.\hfill \end{array}$$

(4)

Let $\Omega :=(-1,1)$ and ${\Omega }^m:={(-1,1)}^m$. Given a multivariate function $\psi \left(\mathit{y}\right)$, the ${\left|\mathit{d}\right|}_1$-th partial (mixed) derivative is denoted by

$${\mathbf{\partial }}_{\mathit{y}}^{\mathit{d}}\psi =\frac{{\partial }^{{\left|\mathit{d}\right|}_1}\psi }{{\partial }_{y_1}^{d_1}\cdots {\partial }_{y_m}^{d_m}}={\partial }_{y_1}^{d_1}\cdots {\partial }_{y_m}^{d_m}\psi .$$

Now, let us start by recalling some properties of the Jacobi polynomials in one dimension (cf. [54]). Let ${\omega }^{u,v}\left(y\right)={(1-y)}^u{(1+y)}^v$ be the Jacobi weight function defined in $\Omega$. The set of Jacobi polynomials, denoted by $Q_n^{u,v}\left(y\right), (u, v>-1)$, forms a complete orthogonal system in $L_{{\omega }^{u,v}}^2(\Omega )$,

$${\int }_{\Omega }{Q}_n^{u,v}\left(y\right)Q_m^{u,v}\left(y\right){\omega }^{u,v}\left(y\right)dy=h_n^{u,v}{\delta }_{n,m},$$

(5)

where

$$h_n^{u,v}=\frac{2^{(u+v+1)}\mathsf{\Gamma }(u+n+1)\mathsf{\Gamma }(n+v+1)}{(u+v+2n+1)\mathsf{\Gamma }(n+1+u+v)n!},$$

(6)

and ${\delta }_{m,n}$ is Kronecker Delta symbol. The m-dimensional multivariate Jacobi polynomial and Jacobi weight function are defined, respectively, as

$${\mathit{Q}}_{\mathit{n}}^{\mathit{u},\mathit{v}}\left(\mathit{y}\right)=\prod _{i=1}^m{Q}_{n_i}^{u_i,v_i}\left(y_i\right),\hspace{1em}{\mathbf{\omega }}^{\mathit{u},\mathit{v}}\left(\mathit{y}\right)=\prod _{i=1}^m{\omega }^{u_i,v_i}\left(y_i\right)\hspace{1em}\forall \mathit{u},\mathit{v}>-1,\hspace{1em}\mathit{y}\in {\Omega }^m,$$

(7)

we also have

$${\int }_{{\Omega }^m}{\mathit{Q}}_{\mathit{n}}^{\mathit{u},\mathit{v}}\left(\mathit{y}\right){\mathit{Q}}_{\mathit{s}}^{\mathit{u},\mathit{v}}\left(\mathit{y}\right){\mathbf{\omega }}^{\mathit{u},\mathit{v}}\left(\mathit{y}\right)d\mathit{y}={\mathit{h}}_{\mathit{n}}^{\mathit{u},\mathit{v}}{\delta }_{\mathit{n},\mathit{s}}=\prod _{i=1}^m{h}_{n_i}^{u_i,v_i}{\delta }_{n_i,s_i},\hspace{1em}\mathit{n},\mathit{s}\ge 0, \mathit{u},\mathit{v}>-1.$$

(8)

Let ${\left\{{\zeta }_{j_k}^{u_k,v_k}\right\}}_{j_k=0}^N$ be the Jacobi–Gauss nodes, ${\left\{{\chi }_{j_k}^{u_k,v_k}\right\}}_{j_k=0}^N$, and their related weights in $\Omega$ for the one-dimensional case, and ${\mathcal{I}}_{y_k,N}^{u_k,v_k}$ be its associated interpolation operator in $y_k$ direction. The m-dimensional multivariate weights and nodes ${\left\{{\mathbf{\chi }}_{\mathit{j}}^{\mathit{u},\mathit{v}},{\mathbf{\zeta }}_{\mathit{j}}^{\mathit{u},\mathit{v}}\right\}}_{{\left|\mathit{j}\right|}_{\infty }\le N}$ in ${\Omega }^m$ are given by

$$\begin{array}{c}\hfill {\mathbf{\chi }}_{\mathit{j}}^{\mathit{u},\mathit{v}}=\left({\chi }_{j_1}^{u_1,v_1},\dots ,{\chi }_{j_m}^{u_m,v_m}\right),\hspace{1em}{\mathbf{\zeta }}_{\mathit{j}}=\left({\mathbf{\zeta }}_{j_1}^{u_1,v_1},\dots ,{\zeta }_{j_m}^{u_m,v_m}\right).\end{array}$$

The multidimensional Gauss–Jacobi quadrature formula satisfies

$${\int }_{{\Omega }^m}\varphi \left(\mathit{y}\right){\mathbf{\omega }}^{\mathit{u},\mathit{v}}\left(\mathit{y}\right)d\mathit{y}=\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}\varphi \left({\mathbf{\zeta }}_{\mathit{j}}\right){\mathbf{\chi }}_{\mathit{j}}^{\mathit{u},\mathit{v}},\hspace{1em}\forall \varphi \left(\mathit{y}\right)\in P_{2N+1}^m.$$

(9)

Hence

$$\sum _{{\left|\mathit{k}\right|}_{\infty }\le N}{\mathit{Q}}_{\mathit{n}}^{\mathit{u},\mathit{v}}\left({\mathbf{\zeta }}_{\mathit{k}}^{\mathit{u}.\mathit{v}}\right){\mathit{Q}}_{\mathit{s}}^{\mathit{u},\mathit{v}}\left({\mathbf{\zeta }}_{\mathit{k}}^{\mathit{u}.\mathit{v}}\right){\mathbf{\chi }}_{\mathit{k}}^{\mathit{u},\mathit{v}}={\mathit{h}}_{\mathit{n}}^{\mathit{u},\mathit{v}}{\mathbf{\delta }}_{\mathit{n},\mathit{s}},\hspace{1em}\forall 0\le \mathit{n}+\mathit{s}\le 2N+1.$$

(10)

For any $\psi \in C\left({\Omega }^m\right)$, the Gauss–Jacobi interpolation operator ${\mathcal{I}}_{\mathit{y},N}^{\mathit{u},\mathit{v}}:C\left({\Omega }^m\right)⟶P_N^m$ is determined uniquely by

$$\left({\mathcal{I}}_{\mathit{y},N}^{\mathit{u},\mathit{v}}\psi \right)\left({\mathbf{\zeta }}_{\mathit{j}}^{\mathit{u},\mathit{v}}\right)=\psi \left({\mathbf{\zeta }}_{\mathit{j}}^{\mathit{u},\mathit{v}}\right) \forall \hspace{1em}\mathit{j}\in {\mathbb{N}}^m, {\left|\mathit{j}\right|}_{\infty }\le N.$$

(11)

For the sake of technical notation, we assume that the collocation points in each direction are the same (i.e., $N+1$ points). Accordingly,

$${\mathcal{I}}_{\mathit{y},N}^{\mathit{u},\mathit{v}}={\mathcal{I}}_{y_1,N}^{u_1,v_1}\circ \dots \circ {\mathcal{I}}_{y_m,N}^{u_m,v_m}.$$

(12)

The interpolation condition (11) implies that ${\mathcal{I}}_{\mathit{y},N}^{\mathit{u},\mathit{v}}\psi =\psi$ for all $\psi \in P_N^m$ and as ${\mathcal{I}}_{\mathit{y},N}^{\mathit{u},\mathit{v}}\psi \in P_N^m$, we can write

$${\mathcal{I}}_{\mathit{y},N}^{\mathit{u},\mathit{v}}\psi \left(\mathit{y}\right)=\sum _{{\left|\mathit{n}\right|}_{\infty }\le N}{\widehat{\psi }}_{\mathit{n}}^{\mathit{u},\mathit{v}}{\mathit{Q}}_{\mathit{n}}^{(\mathit{u},\mathit{v})}\left(\mathit{y}\right),$$

(13)

where

$${\widehat{\psi }}_{\mathit{n}}^{\mathit{u},\mathit{v}}=\frac{1}{{\mathit{h}}_{\mathit{n}}^{\mathit{u},\mathit{v}}}\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}\psi \left({\mathbf{\zeta }}_{\mathit{j}}^{\mathit{u},\mathit{v}}\right){\mathit{Q}}_{\mathit{n}}^{\mathit{u},\mathit{v}}\left({\mathbf{\zeta }}_{\mathit{j}}^{\mathit{u},\mathit{v}}\right){\mathbf{\chi }}_{\mathit{j}}^{\mathit{u},\mathit{v}}.$$

For the sake of convergence analysis, we introduce the space ${\tilde{A}}_{\mathit{u},\mathit{v}}^q\left({\Omega }^m\right)$ for $q\ge m$ with the semi-norm and norm

$$\begin{array}{c}{\left|v\right|}_{{\tilde{A}}_{\mathit{u},\mathit{v}}^q\left({\Omega }^m\right)}={\left(\sum _{s=1}^m\sum _{\mathit{q}\in {\Lambda }_s}{∥{\mathbf{\partial }}_{\mathit{y}}^{\mathit{q}}v∥}_{{\mathbf{\omega }}^{\mathit{u}+q_s{\mathit{e}}_s,\mathit{v}+q_s{\mathit{e}}_s}}^2\right)}^{1/2},\hfill \\ {\parallel v\parallel }_{{\tilde{A}}_{\mathit{u},\mathit{v}}^q\left({\Omega }^m\right)}={\left({∥v∥}_{{\mathbf{\omega }}^{\mathit{u},\mathit{v}}}^2+{\left|v\right|}_{{\tilde{A}}_{\mathit{u},\mathit{v}}^q\left({\Omega }^m\right)}\right)}^{1/2},\hfill \end{array}$$

(14)

where for $1\le s\le m$, the index sets

$${\Lambda }_s=\left\{\mathit{q}\in {\mathbb{N}}_0^m : m\le q_s\le q; q_i\in \left\{0,1\right\}, i\ne s; \sum _{k=1}^m{q}_k=q\right\}.$$

Lemma 1

(see [55], Theorem 8.6). For $\mathit{u},\mathit{v}>-1$, and $f\in {\tilde{A}}_{\mathit{u},\mathit{v}}^q\left({\Omega }^m\right)$ with $d\le q\le N+1$,

$${∥{\mathcal{I}}_{\mathit{y},N}^{\mathit{u},\mathit{v}}f-f∥}_{{\mathbf{\omega }}^{\mathit{u},\mathit{v}}}\le c\sqrt{\frac{(N-q+1)!}{N!}}{(N+q)}^{-(q+1)/2}{\left|f\right|}_{{\tilde{A}}_{\mathit{u},\mathit{v}}^q\left({\Omega }^m\right)},$$

(15)

where c is a positive constant independent of $q, N$, and v.

3. Construction of the Scheme

Generally, the singularities of the kernel function in (1) may cause a nonsmooth solution. The goal of this section is to recover the low-regularity property of the solution by a smoothing transformation.

Using the change of variable $t_i\to {\phi }_i\left(y_i\right)={\left(\frac{y_i+1}{2}\right)}^{{\rho }_i}$ in Equation (1), where ${\rho }_i$ are suitable positive integers, and letting $z_i\to {\phi }_i\left({\sigma }_i\right)={\left(\frac{{\sigma }_i+1}{2}\right)}^{{\rho }_i}$, ${\sigma }_i\in \Omega$, we obtain the corresponding equation to (1) as follows

$$\begin{array}{c}\psi \left({\phi }_1\left(y_1\right)\dots ,{\phi }_m\left(y_m\right)\right)=h\left({\phi }_1\left(y_1\right)\dots ,{\phi }_d\left(y_m\right)\right)\hfill \\ {\int }_{-1}^{y_1}\cdots {\int }_{-1}^{y_m}g\left({\phi }_1\left({\sigma }_1\right),\dots ,{\phi }_m\left({\sigma }_m\right),\psi \left({\phi }_1\left({\sigma }_1\right),\dots ,{\phi }_m\left({\sigma }_m\right)\right),\psi \left(q {\phi }_1\left({\sigma }_1\right),\dots ,q {\phi }_m\left({\sigma }_m\right)\right)\right)\hfill \\ \hspace{1em}\times \prod _{i=1}^m{({\phi }_i\left(y_i\right)-{\phi }_i\left({\sigma }_i\right))}^{-u_i}{\phi }_i^{\prime }\left({\sigma }_i\right)d{\sigma }_m\cdots d{\sigma }_1\hfill \\ +{\int }_{-1}^1\cdots {\int }_{-1}^{1}f\left({\phi }_1\left({\sigma }_1\right),\dots ,{\phi }_m\left({\sigma }_m\right),\psi \left({\phi }_1\left({\sigma }_1\right),\dots ,{\phi }_m\left({\sigma }_m\right)\right),\psi \left(q {\phi }_1\left({\sigma }_1\right),\dots ,q {\phi }_m\left({\sigma }_m\right)\right)\right)\hfill \\ \hspace{1em}\times \prod _{i=1}^m{(1-{\phi }_i\left({\sigma }_i\right))}^{-u_i}{\phi }_i^{\prime }\left({\sigma }_i\right)d{\sigma }_m\cdots d{\sigma }_1.\hfill \end{array}$$

(16)

This equation still has a weakly singular kernel, but its solution is smooth. It can be rewritten as

$$\begin{array}{cc}\hfill \mathsf{\Psi }\left(\mathit{y}\right)=& \frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{\int }_{-\mathbf{1}}^{\mathit{y}}G\left(\mathit{y},\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }(q \mathbf{\sigma })\right)\prod {(\mathit{y}-\mathbf{\sigma })}^{-\mathit{u}}d\mathbf{\sigma }+H\left(\mathit{y}\right)\hfill \\ \hfill \hspace{1em}& +\frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{\int }_{-\mathbf{1}}^{\mathbf{1}}F\left(\mathit{y},\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }(q \mathbf{\sigma })\right)\prod {(1-\mathbf{\sigma })}^{-\mathit{u}}d\mathbf{\sigma },\hfill \end{array}$$

(17)

where

$$\begin{array}{c}\mathsf{\Psi }\left(\mathit{y}\right)=\mathsf{\Psi }\left(y_1\dots ,y_m\right)=\psi \left({\phi }_1\left(y_1\right)\dots ,{\phi }_m\left(y_m\right)\right)\hfill \\ H\left(\mathit{y}\right)=H\left(y_1\dots ,y_m\right)=h\left({\phi }_1\left(y_1\right)\dots ,{\phi }_m\left(y_m\right)\right),\hfill \\ G\left(\mathit{y},\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }(q \mathbf{\sigma })\right)=k_1\left(y_1,{\sigma }_1,\dots ,y_m,{\sigma }_m\right)\hfill \\ \hspace{1em}\times g\left({\phi }_1\left({\sigma }_1\right),\dots ,{\phi }_m\left({\sigma }_m\right),\psi \left({\phi }_1\left({\sigma }_1\right),\dots ,{\phi }_m\left({\sigma }_m\right)\right),\psi \left(q {\phi }_1\left({\sigma }_1\right),\dots ,q {\phi }_m\left({\sigma }_m\right)\right)\right),\hfill \\ k_1\left(y_1,{\sigma }_1,\dots ,y_m,{\sigma }_m\right)=\prod _{i=1}^m{\rho }_i{\left(\frac{{\sigma }_i+1}{2}\right)}^{{\rho }_i-1}{\left(\sum _{j=0}^{{\rho }_i-1}{\left(\frac{y_i+1}{2}\right)}^j{\left(\frac{{\sigma }_i+1}{2}\right)}^{{\rho }_i-j-1}\right)}^{-u_i},\hfill \\ F\left(\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }(q \mathbf{\sigma })\right)=k_2\left({\sigma }_1,\dots ,{\sigma }_m\right)\hfill \\ \hspace{1em}\times f\left({\phi }_1\left({\sigma }_1\right),\dots ,{\phi }_m\left({\sigma }_m\right),\psi \left({\phi }_1\left({\sigma }_1\right),\dots ,{\phi }_m\left({\sigma }_m\right)\right),\psi \left(q {\phi }_1\left({\sigma }_1\right),\dots ,q {\phi }_m\left({\sigma }_m\right)\right)\right),\hfill \\ k_2\left({\sigma }_1,\dots ,{\sigma }_m\right)=\prod _{i=1}^m{\rho }_i{\left(\frac{{\sigma }_i+1}{2}\right)}^{{\rho }_i-1}{\left(\sum _{j=0}^{{\rho }_i-1}{\left(\frac{{\sigma }_i+1}{2}\right)}^{{\rho }_i-j-1}\right)}^{-u_i}\hfill \end{array}$$

(18)

In order to compute the integral terms using the Gauss–Jacobi quadrature formula, Equation (17) can be reformulated as

$$\begin{array}{cc}\hfill \mathsf{\Psi }\left(\mathit{y}\right)=& H\left(\mathit{y}\right)+{\int }_{-\mathbf{1}}^{\mathbf{1}}G\left(\mathit{y},{\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }},\mathsf{\Psi }\left({\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }}\right),\mathsf{\Psi }\left(q {\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }}\right)\right)\prod {(1-\mathbf{\tau })}^{-\mathit{u}}{\left(\frac{\mathit{y}+1}{4}\right)}^{1-\mathit{u}}d\mathbf{\tau }\hfill \\ \hfill \hspace{1em}& +{\int }_{-\mathbf{1}}^{\mathbf{1}}F\left(\mathbf{\tau },\mathsf{\Psi }\left(\mathbf{\tau }\right),\mathsf{\Psi }\left(q \mathbf{\tau }\right)\right)\prod {(1-\mathbf{\tau })}^{-\mathit{u}}{\left(\frac{1}{2}\right)}^{1-\mathit{u}}d\mathbf{\tau },\hfill \end{array}$$

(19)

where

$$\begin{array}{c}{\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }}=\left({\sigma }_1(y_1,{\tau }_1),\dots ,{\sigma }_m(y_m,{\tau }_m)\right),\hfill \\ {\sigma }_i(y_i,{\tau }_i)=\frac{1+y_i}{2}{\tau }_i-\frac{1-y_i}{2}, y_i, {\tau }_i\in \Omega , i=1,\dots ,m.\hfill \end{array}$$

(20)

The starting point of the Jacobi collocation spectral method is to approximate the solution $\mathsf{\Psi }\left(\mathit{y}\right)$ (19) by a finite sum

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_N\left(\mathit{y}\right):=& {\psi }_N\left({\phi }_1\left(y_1\right)\dots ,{\phi }_m\left(y_m\right)\right)=\sum _{{\left|\mathit{i}\right|}_{\infty }⩽N}{\widehat{u}}_{\mathit{i}}{\mathit{Q}}_{\mathit{i}}^{-\mathit{u},\mathbf{0}}\left(\mathit{y}\right)\in P_N^m,\hfill \\ \hfill {\mathsf{\Psi }}_N\left(q\mathit{y}\right):=& {\psi }_N\left(q{\phi }_1\left(y_1\right)\dots ,q{\phi }_m\left(y_m\right)\right)=\sum _{{\left|\mathit{i}\right|}_{\infty }⩽N}{\widehat{u}}_{\mathit{i}}{\mathit{Q}}_{\mathit{i}}^{-\mathit{u},\mathbf{0}}(q^{\frac{1}{\sigma }}(\mathit{y}+1)-1)\in P_N^m.\hfill \end{array}$$

(21)

Hence, substituting (21) into (19) leads to the following

$$\begin{array}{c}{\mathsf{\Psi }}_N\left(\mathit{y}\right)={\mathcal{I}}_{\mathit{y},N}^{-\mathit{u},\mathbf{0}}H\left(\mathit{y}\right)\hfill \\ +{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u},\mathbf{0}}\left[{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {(1-\mathbf{\tau })}^{-\mathit{u}}{\left(\frac{1+\mathit{y}}{4}\right)}^{1-\mathit{u}}{\mathcal{I}}_{\mathbf{\tau },N}^{-\mathit{u},\mathbf{0}}G\left(\mathit{y},{\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }},{\mathsf{\Psi }}_N\left({\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }}\right),{\mathsf{\Psi }}_N\left(q {\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }}\right)\right)d\mathbf{\tau }\right]\hfill \\ +{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {(1-\mathbf{\tau })}^{-\mathit{u}}{\left(\frac{1}{2}\right)}^{1-\mathit{u}}{\mathcal{I}}_{\mathbf{\tau },N}^{-\mathit{u},\mathbf{0}}F\left(\mathbf{\tau },{\mathsf{\Psi }}_N\left(\mathbf{\tau }\right),{\mathsf{\Psi }}_N\left(q \mathbf{\tau }\right)\right)d\mathbf{\tau }.\hfill \end{array}$$

(22)

We now provide a detailed implementation procedure. Setting

$$\begin{array}{c}{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u},\mathbf{0}}{\mathcal{I}}_{\mathbf{\tau },N}^{-\mathit{u},\mathbf{0}}\left(G\left(\mathit{y},{\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }},{\mathsf{\Psi }}_N\left({\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }}\right),{\mathsf{\Psi }}_N\left(q {\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }}\right)\right)\prod {\left(\frac{1+\mathit{y}}{4}\right)}^{1-\mathit{u}}\right)\hfill \\ \hspace{1em}\hspace{1em}=\sum _{{\left|\mathit{i}\right|}_{\infty }\le N}\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\widehat{v}}_{\mathit{i},\mathit{j}}{\mathit{Q}}_{\mathit{i}}^{-\mathit{u},\mathbf{0}}\left(\mathit{y}\right){\mathit{Q}}_{\mathit{j}}^{-\mathit{u},\mathbf{0}}\left(\mathbf{\tau }\right),\hfill \end{array}$$

(23)

we obtain

$$\begin{array}{c}{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {(1-\mathbf{\tau })}^{-\mathit{u}}{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u},\mathbf{0}}{\mathcal{I}}_{\mathbf{\tau },N}^{-\mathit{u},\mathbf{0}}\left[G\left(\mathit{y},{\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }},{\mathsf{\Psi }}_N\left({\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }}\right),{\mathsf{\Psi }}_N\left(q {\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }}\right)\right)\prod {\left(\frac{1+\mathit{y}}{4}\right)}^{1-\mathit{u}}\right]d\mathbf{\tau }\hfill \\ =\sum _{{\left|\mathit{i}\right|}_{\infty }\le N}\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\widehat{v}}_{\mathit{i},\mathit{j}}{\mathit{Q}}_{\mathit{i}}^{-\mathit{u},\mathbf{0}}\left(\mathit{y}\right){\int }_{-\mathbf{1}}^{\mathbf{1}}{\mathit{Q}}_{\mathit{j}}^{-\mathit{u},\mathbf{0}}\left(\mathbf{\tau }\right)\prod {(1-\mathbf{\tau })}^{-\mathit{u}}d\mathbf{\tau }\hfill \\ =\sum _{{\left|\mathit{i}\right|}_{\infty }\le N}{\widehat{v}}_{\mathit{i},\mathbf{0}}{\mathit{Q}}_{\mathit{i}}^{-\mathit{u},\mathbf{0}}\left(\mathit{y}\right)\prod \left(\frac{2^{1-\mathit{u}}}{1-\mathit{u}}\right).\hfill \end{array}$$

(24)

Using (10) and (23) yields

$$\begin{array}{c}{\widehat{v}}_{\mathit{i},\mathbf{0}}=\prod \frac{(1-\mathit{u})(2 \mathit{i}+1-\mathit{u})}{4^{1-\mathit{u}}}\sum _{{\left|\mathit{r}\right|}_{\infty }\le N}\sum _{{\left|\mathit{s}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{r}}^{-\mathit{u},\mathbf{0}}{\mathbf{\chi }}_{\mathit{s}}^{-\mathit{u},\mathbf{0}}\prod {\left(\frac{{\mathit{y}}_{\mathit{r}}^{-\mathit{u},\mathbf{0}}+1}{4}\right)}^{1-\mathit{u}}\hfill \\ \times G\left({\mathit{y}}_{\mathit{r}}^{-\mathit{u},\mathbf{0}},{\mathbf{\sigma }}_{{\mathit{y}}_{\mathit{r}}^{-\mathit{u},\mathbf{0}},{\mathbf{\tau }}_{\mathit{s}}^{-\mathit{u},\mathbf{0}}},{\mathsf{\Psi }}_N\left({\sigma }_{{\mathit{y}}_{\mathit{r}}^{-\mathit{u},\mathbf{0}},{\mathbf{\tau }}_{\mathit{s}}^{-\mathit{u},\mathbf{0}}}\right),{\mathsf{\Psi }}_N\left(q {\mathbf{\sigma }}_{{\mathit{y}}_{\mathit{r}}^{-\mathit{u},\mathbf{0}},{\mathbf{\tau }}_{\mathit{s}}^{-\mathit{u},\mathbf{0}}}\right)\right){\mathit{Q}}_{\mathit{i}}^{-\mathit{u},\mathbf{0}}\left({\mathit{y}}_{\mathit{r}}^{-\mathit{u},\mathbf{0}}\right).\hfill \end{array}$$

(25)

Moreover

$$\begin{array}{c}{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {(1-\mathbf{\tau })}^{-\mathit{u}}{\mathcal{I}}_{\mathbf{\tau },N}^{-\mathit{u},\mathbf{0}}\left[F\left(\mathbf{\tau },{\mathsf{\Psi }}_N\left(\mathbf{\tau }\right),{\mathsf{\Psi }}_N\left(q \mathbf{\tau }\right)\right)\prod {\left(\frac{1}{2}\right)}^{1-\mathit{u}}\right]d\mathbf{\tau }\hfill \\ =\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\widehat{O}}_{\mathit{j}}{\int }_{-\mathbf{1}}^{\mathbf{1}}{\mathit{Q}}_{\mathit{j}}^{-\mathit{u},\mathbf{0}}\left(\mathbf{\tau }\right)\prod {(1-\mathbf{\tau })}^{-\mathit{u}}d\mathbf{\tau }\hfill \\ ={\widehat{O}}_{\mathbf{0}}\prod \left(\frac{2^{1-\mathit{u}}}{1-\mathit{u}}\right),\hfill \end{array}$$

(26)

where

$$\begin{array}{c}{\widehat{O}}_{\mathbf{0}}=\prod \frac{(1-\mathit{u})}{4^{1-\mathit{u}}}\sum _{{\left|\mathit{s}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{s}}^{-\mathit{u},\mathbf{0}}F({\mathbf{\tau }}_{\mathit{s}}^{-\mathit{u},\mathbf{0}},{\mathsf{\Psi }}_N({\mathbf{\tau }}_{\mathit{s}}^{-\mathit{u},\mathbf{0}}),{\mathsf{\Psi }}_N(q {\mathbf{\tau }}_{\mathit{s}}^{-\mathit{u},\mathbf{0}})).\hfill \end{array}$$

(27)

Making using of (21)–(25), we get

$$\begin{array}{c}\sum _{{\left|\mathit{s}\right|}_{\infty }⩽N}{\widehat{u}}_{\mathit{s}}{\mathit{Q}}_{\mathit{s}}^{-\mathit{u},\mathbf{0}}\left(\mathit{y}\right)=\hfill \\ \sum _{{\left|\mathit{s}\right|}_{\infty }\le N}{\widehat{v}}_{\mathit{s},\mathbf{0}}{\mathit{Q}}_{\mathit{s}}^{-\mathit{u},\mathbf{0}}\left(\mathit{y}\right)\prod \left(\frac{2^{1-\mathit{u}}}{1-\mathit{u}}\right)+\sum _{{\left|\mathit{s}\right|}_{\infty }\le N}{\widehat{\mathit{w}}}_{\mathit{s}}{\mathit{Q}}_{\mathit{s}}^{-\mathit{u},\mathbf{0}}\left(\mathit{y}\right)+{\widehat{O}}_{\mathbf{0}}\prod \left(\frac{2^{1-\mathit{u}}}{1-\mathit{u}}\right).\hfill \end{array}$$

(28)

where

$${\widehat{\mathit{w}}}_{\mathit{s}}=\prod \frac{(2 \mathit{s}+1-\mathit{u})}{2^{1-\mathit{u}}}\sum _{{\left|\mathit{r}\right|}_{\infty }\le N}G\left({\mathit{y}}_{\mathit{r}}^{-\mathit{u},\mathbf{0}}\right){\mathbf{\chi }}_{\mathit{r}}^{-\mathit{u},\mathbf{0}}{\mathit{Q}}_{\mathit{s}}^{-\mathit{u},\mathbf{0}}\left({\mathit{y}}_{\mathit{r}}^{-\mathit{u},\mathbf{0}}\right).$$

We obtain following system of algebraic equations by comparing the expansion coefficients of (28)

$$\begin{array}{c}\hfill {\widehat{u}}_{\mathit{i}}={\widehat{v}}_{\mathit{i},\mathbf{0}}\prod \left(\frac{2^{1-\mathit{u}}}{1-\mathit{u}}\right)+{\widehat{O}}_{\mathbf{0}}\prod \left(\frac{2^{1-\mathit{u}}{\delta }_{\mathit{i},\mathbf{0}}}{1-\mathit{u}}\right)+{\widehat{\mathit{w}}}_{\mathit{i}},\hspace{1em}\mathrm{for}\hspace{1em}0\le i\le N.\end{array}$$

(29)

This nonlinear system can be solved by an iterative process (e.g., the Newton–Raphson iteration method or the successive substitution method). The full system (29) is solved using the Mathematica built-in function FindRoot with zero initial approximation.

4. Convergence Analysis

In this section, we investigate the convergence of the scheme (22) in the function space $L_{{\mathbf{\omega }}^{-\mathit{u},0}}^2\left({\Omega }^m\right)$, which confirms the practicability of the algorithm theoretically. We will drop the superscript $\mathit{v}$ if $\mathit{v}=0$.

Let ${\tau }_{\mathit{i}}^{-\mathit{u}}$ be the Jacobi–Gauss nodes in ${\Omega }^m$ and ${\mathbf{\sigma }}_i^{-\mathit{u}}={\mathbf{\sigma }}_{\mathit{y},{\mathbf{\tau }}_{\mathit{i}}^{-\mathit{u}}}$. The mapped Jacobi–Gauss interpolation operator ${}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}:C^m(-\mathbf{1},\mathit{y})⟶P_N^m(-\mathbf{1},\mathit{y})$ is defined by

$${}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\psi \left({\mathbf{\sigma }}_{\mathit{i}}^{-\mathit{u}}\right)=\psi \left({\mathbf{\sigma }}_{\mathit{i}}^{-\mathit{u}}\right).$$

(30)

Hence,

$${}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\psi \left({\mathbf{\sigma }}_{\mathit{i}}^{-\mathit{u}}\right)=\psi \left({\mathbf{\sigma }}_{\mathit{i}}^{-\mathit{u}}\right)=\psi \left({\mathbf{\sigma }}_{\mathit{y},{\mathbf{\tau }}_{\mathit{i}}^{-\mathit{u}}}\right)={\mathcal{I}}_{\mathbf{\tau },N}^{-\mathit{u}}\psi \left({\mathbf{\sigma }}_{\mathit{y},{\mathbf{\tau }}_{\mathit{i}}^{-\mathit{u}}}\right),$$

(31)

and

$${}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\psi \left(\mathbf{\sigma }\right)={\left.{\mathcal{I}}_{\mathbf{\tau },N}^{-\mathit{u}}\psi \left({\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }}\right)\right|}_{\tau =\frac{2\mathbf{\sigma }}{\mathit{y}+1}+\frac{1-\mathit{y}}{1+\mathit{y}}}.$$

(32)

Accordingly, we can easily derive the following results

$$\begin{array}{cc}\hfill {\int }_{-\mathbf{1}}^{\mathit{y}}\prod {(\mathit{y}-\mathbf{\sigma })}^{-\mathit{u}}{}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\psi \left(\mathbf{\sigma }\right)d\mathbf{\sigma }& =\prod {\left(\frac{1+\mathit{y}}{2}\right)}^{1-\mathit{u}}{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {(1-\mathbf{\tau })}^{-\mathit{u}}{\mathcal{I}}_{\mathbf{\tau },N}^{-\mathit{u}}\psi \left({\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }}\right)d\mathbf{\tau }\hfill \\ \hfill \hspace{1em}& =\prod {\left(\frac{1+\mathit{y}}{2}\right)}^{1-\mathit{u}}\sum _{{\left|\mathit{i}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{i}}^{-\mathit{u}}\psi \left({\mathbf{\sigma }}_{\mathit{j}}^{-\mathit{u}}\right),\hfill \end{array}$$

(33)

$$\begin{array}{c}\hfill {\int }_{-\mathbf{1}}^{\mathit{y}}\prod {(\mathit{y}-\mathbf{\sigma })}^{-\mathit{u}}{\left({}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\psi \left(\mathbf{\sigma }\right)\right)}^{2}d\sigma =\prod {\left(\frac{1+\mathit{y}}{2}\right)}^{1-\mathit{u}}\sum _{{\left|\mathit{i}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{i}}^{-\mathit{u}}{u}^2\left({\mathbf{\sigma }}_{\mathit{i}}^{-\mathit{u}}\right).\end{array}$$

(34)

Let us denote the identity operator in m dimensions by $\mathcal{I}$. Then, for any $m\le r\le N+1$, we have

$$\begin{array}{cc}\hfill {\int }_{-\mathbf{1}}^{\mathit{y}}\prod {(\mathit{y}-\mathbf{\sigma })}^{-\mathit{u}}& {\left|\left(\mathcal{I}-{}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\right)\psi \left(\mathbf{\sigma }\right)\right|}^{2}d\mathbf{\sigma }\hfill \\ \hfill \hspace{1em}& =\prod {\left(\frac{1+\mathit{y}}{2}\right)}^{1-\mathit{u}}{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {(1-\mathbf{\tau })}^{-\mathit{u}}{\left|\left(\mathcal{I}-{\mathcal{I}}_{\mathbf{\tau },N}^{-\mathit{u}}\right)\psi \left({\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }}\right)\right|}^{2}d\mathbf{\tau }\hfill \\ \hfill \hspace{1em}& \le C\frac{\left(1+N-r\right)!}{N!}{\left(r+N\right)}^{-(1+r)}\prod {\left(\frac{1+\mathit{y}}{2}\right)}^{1-\mathit{u}}{\left|\psi \left({\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }}\right)\right|}_{{\tilde{A}}_{-\mathit{u}}^r}^2.\hfill \end{array}$$

(35)

For convenience, we denote ${\mathsf{{\rm Y}}}_N=\mathsf{\Psi }\left(\mathit{y}\right)-{\mathsf{\Psi }}_N\left(\mathit{y}\right)$. Clearly

$${∥{\mathsf{{\rm Y}}}_N∥}_{{\mathbf{\omega }}^{-\mathit{u}}}\le {∥\mathsf{\Psi }-{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}\mathsf{\Psi }∥}_{{\mathbf{\omega }}^{-\mathit{u}}}+{∥{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}\mathsf{\Psi }-{\mathsf{\Psi }}_N∥}_{{\mathbf{\omega }}^{-\mathit{u}}}.$$

(36)

Lemma 2.

The following inequality holds:

$$\begin{array}{c}\hfill {∥{\mathsf{{\rm Y}}}_N∥}_{{\mathbf{\omega }}^{-\mathit{u}}}\le \sum _{i=1}^5{∥{\mathsf{{\rm Y}}}_i∥}_{{\mathbf{\omega }}^{-\mathit{u}}},\end{array}$$

(37)

where

$$\begin{array}{cc}\hfill {\mathsf{{\rm Y}}}_1=& \mathsf{\Psi }\left(\mathit{y}\right)-{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}\mathsf{\Psi }\left(\mathit{y}\right),\hfill \\ \hfill {\mathsf{{\rm Y}}}_2=& \frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}{\int }_{-\mathbf{1}}^{\mathit{y}}\prod {\left(\mathit{y}-\mathbf{\sigma }\right)}^{-\mathit{u}}\left(\mathcal{I}-{}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\right)G\left(\mathit{y},\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }\left(q \mathbf{\sigma }\right)\right)d\mathbf{\sigma },\hfill \\ \hfill {\mathsf{{\rm Y}}}_3=& \frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}{\int }_{-\mathbf{1}}^{\mathit{y}}\prod {\left(\mathit{y}-\mathbf{\sigma }\right)}^{-\mathit{u}}{}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(G\left(\mathit{y},\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }\left(q \mathbf{\sigma }\right)\right)-G(\mathit{y},\mathbf{\sigma },{\mathsf{\Psi }}_N\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N(q \mathbf{\sigma }))\right)d\mathbf{\sigma },\hfill \\ \hfill {\mathsf{{\rm Y}}}_4=& \frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {\left(\mathbf{1}-\mathbf{\sigma }\right)}^{-\mathit{u}}\left(\mathcal{I}-{\mathcal{I}}_{\mathbf{\sigma },N}^{-\mathit{u}}\right)F\left(\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }\left(q \mathbf{\sigma }\right)\right)d\mathbf{\sigma },\hfill \\ \hfill {\mathsf{{\rm Y}}}_5=& \frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {\left(\mathbf{1}-\mathbf{\sigma }\right)}^{-\mathit{u}}{\mathcal{I}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(F\left(\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }\left(q \mathbf{\sigma }\right)\right)-F(\mathbf{\sigma },{\mathsf{\Psi }}_N\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N(q \mathbf{\sigma }))\right)d\mathbf{\sigma }.\hfill \end{array}$$

(38)

Proof. 

We obtain from (17) that

$$\begin{array}{cc}\hfill {\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}\mathsf{\Psi }\left(\mathit{y}\right)=& \frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}{\int }_{-\mathbf{1}}^{\mathit{y}}\prod {\left(\mathit{y}-\mathbf{\sigma }\right)}^{-\mathit{u}}G(\mathit{y},\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }(q \mathbf{\sigma }))d\mathbf{\sigma }+{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}H\left(\mathit{y}\right)\hfill \\ \hfill \hspace{1em}& +\frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {\left(\mathbf{1}-\mathbf{\sigma }\right)}^{-\mathit{u}}F(\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }(q \mathbf{\sigma }))d\mathbf{\sigma },\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_N\left(\mathit{y}\right)=& \frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}{\int }_{-\mathbf{1}}^{\mathit{y}}\prod {\left(\mathit{y}-\mathbf{\sigma }\right)}^{-\mathit{u}}{}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}G(\mathit{y},\mathbf{\sigma },{\mathsf{\Psi }}_N\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N(q \mathbf{\sigma }))d\mathbf{\sigma }+{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}H\left(\mathit{y}\right)\hfill \\ \hfill \hspace{1em}& +\frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {\left(\mathbf{1}-\mathbf{\sigma }\right)}^{-\mathit{u}}{\mathcal{I}}_{\mathbf{\sigma },N}^{-\mathit{u}}F(\mathbf{\sigma },{\mathsf{\Psi }}_N\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N(q \mathbf{\sigma }))d\mathbf{\sigma }.\hfill \end{array}$$

(40)

Subtracting (40) from (39) yields

$$\begin{array}{c}{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}\mathsf{\Psi }\left(\mathit{y}\right)-{\mathsf{\Psi }}_N\left(\mathit{y}\right)\hfill \\ =\frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}{\int }_{-\mathbf{1}}^{\mathit{y}}\prod {\left(\mathit{y}-\mathsf{\sigma }\right)}^{-\mathit{u}}\left(G(\mathit{y},\mathsf{\sigma },\mathsf{\Psi }\left(\mathsf{\sigma }\right),\mathsf{\Psi }(q \mathsf{\sigma }))-{}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathsf{\sigma },N}^{-\mathit{u}}G(\mathit{y},\mathsf{\sigma },{\mathsf{\Psi }}_N\left(\mathsf{\sigma }\right),{\mathsf{\Psi }}_N(q \mathsf{\sigma }))\right)d\mathsf{\sigma }\hfill \\ \hspace{1em}+\frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {\left(\mathbf{1}-\mathsf{\sigma }\right)}^{-\mathit{u}}\left(F(\mathsf{\sigma },\mathsf{\Psi }\left(\mathsf{\sigma }\right),\mathsf{\Psi }(q \mathsf{\sigma }))-{\mathcal{I}}_{\mathsf{\sigma },N}^{-\mathit{u}}F(\mathsf{\sigma },{\mathsf{\Psi }}_N\left(\mathsf{\sigma }\right),{\mathsf{\Psi }}_N(q \mathsf{\sigma }))\right)d\mathsf{\sigma }\hfill \\ =\frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}{\int }_{-\mathbf{1}}^{\mathit{y}}\prod {\left(\mathit{y}-\mathsf{\sigma }\right)}^{-\mathit{u}}\left(\mathcal{I}-{}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathsf{\sigma },N}^{-\mathit{u}}\right)G(\mathit{y},\mathsf{\sigma },\mathsf{\Psi }\left(\mathsf{\sigma }\right),\mathsf{\Psi }(q \mathsf{\sigma }))d\mathsf{\sigma }\hfill \\ \hspace{1em}+\frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}{\int }_{-\mathbf{1}}^{\mathit{y}}\prod {\left(\mathit{y}-\mathsf{\sigma }\right)}^{-\mathit{u}}{}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathsf{\sigma },N}^{-\mathit{u}}\left(G(\mathit{y},\mathsf{\sigma },\mathsf{\Psi }\left(\mathsf{\sigma }\right),\mathsf{\Psi }(q \mathsf{\sigma }))-G(\mathit{y},\mathsf{\sigma },{\mathsf{\Psi }}_N\left(\mathsf{\sigma }\right),{\mathsf{\Psi }}_N(q \mathsf{\sigma }))\right)d\mathsf{\sigma }\hfill \\ +\frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {\left(\mathbf{1}-\mathsf{\sigma }\right)}^{-\mathit{u}}\left(\mathcal{I}-{\mathcal{I}}_{\mathsf{\sigma },N}^{-\mathit{u}}\right)F(\mathsf{\sigma },\mathsf{\Psi }\left(\mathsf{\sigma }\right),\mathsf{\Psi }(q \mathsf{\sigma }))d\mathsf{\sigma }\hfill \\ \hspace{1em}+\frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {\left(\mathbf{1}-\mathsf{\sigma }\right)}^{-\mathit{u}}{\mathcal{I}}_{\mathsf{\sigma },N}^{-\mathit{u}}\left(F(\mathsf{\sigma },\mathsf{\Psi }\left(\mathsf{\sigma }\right),\mathsf{\Psi }(q \mathsf{\sigma }))-F(\mathsf{\sigma },{\mathsf{\Psi }}_N\left(\mathsf{\sigma }\right),{\mathsf{\Psi }}_N(q \mathsf{\sigma }))\right)d\mathsf{\sigma }.\hfill \end{array}$$

(41)

The desired result can be obtained directly from the above. □

Theorem 1.

Let $\mathsf{\Psi }$ be the exact solution of the Equation (19) and ${\mathsf{\Psi }}_N$ be its approximate solution. Assume that $\mathsf{\Psi }\in {\tilde{A}}_{-\mathit{u}}^r\left({\Omega }^m\right), m\le r\le N+1$, and F and G fulfill the Lipschitz condition w with the Lipschitz constant $L<\prod \frac{1-\mathit{u}}{2}$. Then, we have the estimate:

$$\begin{array}{cc}\hfill {∥{\mathsf{{\rm Y}}}_N∥}_{{\mathbf{\omega }}^{-\mathit{u},\mathbf{0}}}& \le c\sqrt{\frac{(1+N-r)!}{N!}}{(r+N)}^{-(1+r)/2}\left({\left|\mathsf{\Psi }\right|}_{{\tilde{A}}_{-\mathit{u}}^r\left({\Omega }^m\right)}+{\left|G(\mathbf{1},\mathbf{\sigma },\mathsf{\Psi }(\mathbf{\sigma }),\mathsf{\Psi }(q \mathbf{\sigma }\left)\right)\right|}_{{\tilde{A}}_{-\mathit{u}}^r\left({\Omega }^m\right)}\right.\hfill \\ \hfill \hspace{1em}& +\left.{\left|F(\mathbf{\sigma },\mathsf{\Psi }(\mathbf{\sigma }),\mathsf{\Psi }(q \mathbf{\sigma }\left)\right)\right|}_{{\tilde{A}}_{-\mathit{u}}^r\left({\Omega }^m\right)}\right).\hfill \end{array}$$

Proof. 

Making use of Lemma 1, we obtain

$${∥{\mathsf{{\rm Y}}}_1∥}_{{\mathbf{\omega }}^{-\mathit{u}}}={∥\mathsf{\Psi }-{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}\mathsf{\Psi }∥}_{{\mathbf{\omega }}^{-\mathit{u}}}\le c\sqrt{\frac{(1+N-r)!}{N!}}{(r+N)}^{-(1+r)/2}{\left|\mathsf{\Psi }\right|}_{{\tilde{A}}_{-\mathit{u}}^r\left({\Omega }^m\right)}.$$

(42)

We next estimate the term ${∥{\mathsf{{\rm Y}}}_2∥}_{{\mathbf{\omega }}^{-\mathit{u}}}$. Using the Jacobi–Gauss integration Formula (9), we have

$$\begin{array}{c}{∥{\mathsf{{\rm Y}}}_2∥}_{{\mathbf{\omega }}^{-\mathit{u}}}\hfill \\ =\frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{∥{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}{\int }_{-\mathbf{1}}^{\mathit{y}}\prod {\left(\mathit{y}-\mathbf{\sigma }\right)}^{-\mathit{u}}\left(\mathcal{I}-{}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\right)G(\mathit{y},\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }(q \mathbf{\sigma }))d\mathbf{\sigma }∥}_{{\omega }^{-\mathit{u}}}\hfill \\ =\frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}\left[\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{j}}^{-\mathit{u}}\left({\int }_{-\mathbf{1}}^{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}\prod {\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}-\mathbf{\sigma }\right)}^{-\mathit{u}}\right.\right.\hfill \\ {\left.{\left.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times \left(\mathcal{I}-{}_{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\right)G({\mathit{y}}_{\mathit{j}}^{-\mathit{u}},\mathbf{\sigma },\mathsf{\Psi }(\mathbf{\sigma }),\mathsf{\Psi }(q \mathbf{\sigma }))d\mathbf{\sigma }\right)}^2\right]}^{1/2}.\hfill \end{array}$$

(43)

Using the Cauchy–Schwarz inequality yields, we obtain that

$$\begin{array}{cc}\hfill {∥{\mathsf{{\rm Y}}}_2∥}_{{\omega }^{-\mathit{u}}}& \le \frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}\left[\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{j}}^{-\mathit{u}}{\int }_{-\mathbf{1}}^{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}\prod {\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}-\mathbf{\sigma }\right)}^{-\mathit{u}}d\mathbf{\sigma }\right.\hfill \\ & {\left.\hspace{1em}\times {\int }_{-\mathbf{1}}^{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}\prod {\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}-\mathbf{\sigma }\right)}^{-\mathit{u}}{\left|\left(\mathcal{I}-{}_{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\right)G({\mathit{y}}_{\mathit{j}}^{-\mathit{u}},\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }(q \mathbf{\sigma }))\right|}^{2}d\mathbf{\sigma }\right]}^{1/2}\hfill \\ \hfill \hspace{1em}& \le \left(\prod \frac{2^{\mathit{u}-\mathbf{1}}}{1-\mathit{u}}\right)\left[\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{j}}^{-\mathit{u}}\prod \left(1-\mathit{u}\right){\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}+1\right)}^{1-\mathit{u}}\right.\hfill \\ & {\left.\hspace{1em}\times {\int }_{-\mathbf{1}}^{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}\prod {\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}-\mathbf{\sigma }\right)}^{-\mathit{u}}{\left|\left(\mathcal{I}-{}_{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\right)G({\mathit{y}}_{\mathit{j}}^{-\mathit{u}},\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }(q \mathbf{\sigma }))\right|}^{2}d\mathbf{\sigma }\right]}^{1/2}\hfill \\ \hfill \hspace{1em}& \le \left(\prod \frac{2^{\mathit{u}-\mathbf{1}}}{1-\mathit{u}}\right){\left(\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{j}}^{-\mathit{u}}\prod \left(1-\mathit{u}\right){\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}+1\right)}^{1-\mathit{u}}\right)}^{1/2}\hfill \\ & \times \underset{{\left|\mathit{j}\right|}_{\infty }\le N}{max}{\left({\int }_{-\mathbf{1}}^{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}\prod {\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}-\mathbf{\sigma }\right)}^{-\mathit{u}}{\left|\left(\mathcal{I}-{}_{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\right)G({\mathit{y}}_{\mathit{j}}^{-\mathit{u}},\mathbf{\sigma },\mathsf{\Psi }(\mathbf{\sigma }),\mathsf{\Psi }(q \mathbf{\sigma }))\right|}^{2}d\mathbf{\sigma }\right)}^{1/2}.\hfill \end{array}$$

(44)

for any $y_{j_1}^{-u_1}\in {\Omega }^1$ and $u_1\in (0,1)$. Let $g\left(\rho \right)={(y_{j_1}^{-u_1}+1)}^{\rho }$. We note that $g(\rho )$ is a convex function of $\rho$. Accordingly, by using Jensen’s inequality for all $\rho \in [0,1]$

$$g\left(\rho \right)\le (1-\rho )g\left(0\right)+\rho g\left(1\right).$$

The previous inequality yields

$$\begin{array}{c}\sum _{j_1=0}^N{\chi }_{j_1}^{-u_1}\left(1-u_1\right){\left(y_{j_1}^{-u_1}+1\right)}^{1-u_1}\le \sum _{j_1=0}^N{\chi }_{j_1}^{-u_1}\left(1-u_1\right)\left[u_1+(1-u_1)\left(y_{j_1}^{-u_1}+1\right)\right]\hfill \\ =(1-u_1)\left[u_1{\int }_{{\Omega }^1}{(1-y)}^{-u_1}dy+(1-u_1){\int }_{{\Omega }^1}{(1-y)}^{-u_1}(y+1)dy\right]\hfill \\ =\frac{2^{1-u_1}(u_1^2-2)}{u_1-2}={\kappa }_1\le 2.\hfill \end{array}$$

(45)

Hence, for any ${\mathit{y}}_{\mathit{j}}^{-\mathit{u}}\in {\Omega }^m$ and $\mathit{u}\in {(0,1)}^m$, it is clear that

$$\begin{array}{c}\hfill \sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{j}}^{-\mathit{u}}\prod \left(1-\mathit{u}\right){\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}+1\right)}^{1-\mathit{u}}\le {\kappa }^m\le 2^m.\end{array}$$

(46)

Using (35) and (46) leads to

$$\begin{array}{c}{∥{\mathsf{{\rm Y}}}_2∥}_{{\mathbf{\omega }}^{-\mathit{u}}}\le c\sqrt{\frac{(1+N-r)!}{N!}}{(r+N)}^{-(1+r)/2}{\left|G(\mathbf{1},\mathbf{\sigma },\mathsf{\Psi }(\mathbf{\sigma }),\mathsf{\Psi }(q \mathbf{\sigma }\left)\right)\right|}_{{\tilde{A}}_{-\mathit{u}}^r\left({\Omega }^m\right)}.\end{array}$$

(47)

An estimate for the term ${∥{\mathsf{{\rm Y}}}_3∥}_{{\mathbf{\omega }}^{-\mathit{u}}}$ can be obtained by using the Jacobi–Gauss integration Formula (9) to give

$$\begin{array}{c}{∥{\mathsf{{\rm Y}}}_3∥}_{{\mathbf{\omega }}^{-\mathit{u}}}\hfill \\ =\frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{∥{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}{\int }_{-\mathbf{1}}^{\mathit{y}}\prod {\left(\mathit{y}-\mathbf{\sigma }\right)}^{-\mathit{u}}{}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(G\left(\mathit{y},\mathbf{\sigma },\mathsf{\sigma }\left(\mathbf{\sigma }\right),\mathsf{\sigma }\left(q \mathbf{\sigma }\right)\right)-G(\mathit{y},\mathbf{\sigma },{\mathsf{\sigma }}_N\left(\mathbf{\sigma }\right),{\mathsf{\sigma }}_N(q \mathbf{\sigma }))\right)d\mathbf{\sigma }∥}_{{\mathbf{\omega }}^{-\mathit{u}}}\hfill \\ ={\left[{\int }_{-\mathbf{1}}^{\mathbf{1}}{\mathbf{\omega }}^{-\mathit{u}}{\left({\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}{\int }_{-\mathbf{1}}^{\mathit{y}}\prod {\left(\mathit{y}-\mathbf{\sigma }\right)}^{-\mathit{u}}{}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(G(\mathit{y},\mathbf{\sigma },\mathsf{\sigma }\left(\mathbf{\sigma }\right),\mathsf{\sigma }(q \mathbf{\sigma }))-G(\mathit{y},\mathbf{\sigma },{\mathsf{\sigma }}_N\left(\mathbf{\sigma }\right),{\mathsf{\sigma }}_N(q \mathbf{\sigma }))\right)d\mathbf{\sigma }\right)}^{2}d\mathit{y}\right]}^{\frac{1}{2}}\hfill \\ =\frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}\left[\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\chi }_{\mathit{j}}^{-\mathit{u}}\left({\int }_{-\mathbf{1}}^{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}\prod {\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}-\mathbf{\sigma }\right)}^{-\mathit{u}}\right.\right.\hfill \\ {\left.{\left.\hspace{1em}\hspace{1em}\hspace{1em}\times {}_{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(G({\mathit{y}}_{\mathit{j}}^{-\mathit{u}},\mathbf{\sigma },\mathsf{\sigma }(\mathbf{\sigma }),\mathsf{\sigma }(q \mathbf{\sigma }))-G({\mathit{y}}_{\mathit{j}}^{-\mathit{u}},\mathbf{\sigma },{\mathsf{\sigma }}_N(\mathbf{\sigma }),{\mathsf{\sigma }}_N(q \mathbf{\sigma }))\right)d\mathbf{\sigma }\right)}^2\right]}^{1/2}.\hfill \end{array}$$

Using the Cauchy–Schwarz inequality and (33), we further obtain

$$\begin{array}{c}{∥{\mathsf{{\rm Y}}}_3∥}_{{\omega }^{-\mathit{u}}}\hfill \\ \le \frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}\left[\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{j}}^{-\mathit{u}}\prod \frac{{\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}+1\right)}^{1-\mathit{u}}}{1-\mathit{u}}\right.\hfill \\ {\left.\hspace{1em}\hspace{1em}\times {\int }_{-\mathbf{1}}^{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}\prod {\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}-\mathbf{\sigma }\right)}^{-\mathit{u}}{\left|{}_{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(G({\mathit{y}}_{\mathit{j}}^{-\mathit{u}},\mathbf{\sigma },\mathsf{\Psi }(\mathbf{\sigma }),\mathsf{\Psi }(q \mathbf{\sigma }))-G({\mathit{y}}_{\mathit{j}}^{-\mathit{u}},\mathbf{\sigma },{\mathsf{\Psi }}_N(\mathbf{\sigma }),{\mathsf{\Psi }}_N(q \mathbf{\sigma }))\right)\right|}^{2}d\mathbf{\sigma }\right]}^{1/2}\hfill \\ \le \frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}\left[\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{j}}^{-\mathit{u}}\prod \frac{{\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}+1\right)}^{2\left(1-\mathit{u}\right)}}{2^{1-\mathit{u}}\left(1-\mathit{u}\right)}\right.\hfill \\ {\left.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times \sum _{{\left|\mathit{q}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{q}}^{-\mathit{u}}{\left|G({\mathit{y}}_{\mathit{j}}^{-\mathit{u}},{\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}},\mathsf{\Psi }({\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}),\mathsf{\Psi }(q {\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}))-G({\mathit{y}}_{\mathit{j}}^{-\mathit{u}},{\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}},{\mathsf{\Psi }}_N({\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}),{\mathsf{\Psi }}_N(q {\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}))\right|}^2\right]}^{1/2}.\hfill \end{array}$$

Using the Lipschitz condition, we deduce that

$$\begin{array}{cc}\hfill \hspace{1em}& {∥{\mathsf{{\rm Y}}}_3∥}_{{\omega }^{-\mathit{u}}}\hfill \\ & \le \frac{L}{\prod 2^{\mathbf{1}-\mathit{u}}}{\left[\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{j}}^{-\mathit{u}}\prod \frac{{\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}+1\right)}^{2\left(1-\mathit{u}\right)}}{2^{1-\mathit{u}}\left(1-\mathit{u}\right)}\sum _{{\left|\mathit{q}\right|}_{\infty }\le N}{\left|\mathsf{\Psi }({\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}})-{\mathsf{\Psi }}_N({\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}})\right|}^2{\mathbf{\chi }}_{\mathit{q}}^{-\mathit{u}}\right]}^{1/2}\hfill \\ \hfill \hspace{1em}& \le \frac{L}{\prod 2^{1-\mathit{u}}}\left[\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{j}}^{-\mathit{u}}\prod \frac{{\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}+1\right)}^{1-\mathit{u}}}{1-\mathit{u}}\right.\hfill \\ & {\left.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times {\int }_{-\mathbf{1}}^{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}\prod {\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}-\mathbf{\sigma }\right)}^{-\mathit{u}}{\left|{}_{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(\mathsf{\Psi }\left(\mathbf{\sigma }\right)-{\mathsf{\Psi }}_N\left(\mathbf{\sigma }\right)\right)\right|}^{2}d\mathbf{\sigma }\right]}^{1/2}\hfill \\ \hfill \hspace{1em}& \le \frac{L}{\prod 2^{1-\mathit{u}}(1-\mathit{u})}{\left(\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{j}}^{-\mathit{u}}\prod \left(1-\mathit{u}\right){\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}+1\right)}^{1-\mathit{u}}\right)}^{1/2}\hfill \\ & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times \underset{{\left|\mathit{j}\right|}_{\infty }\le N}{max}{\left({\int }_{-\mathbf{1}}^{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}\prod {\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}-\mathbf{\sigma }\right)}^{-\mathit{u}}{\left|{}_{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(\mathsf{\Psi }\left(\mathbf{\sigma }\right)-{\mathsf{\Psi }}_N\left(\mathbf{\sigma }\right)\right)\right|}^{2}d\mathbf{\sigma }\right)}^{\frac{1}{2}}.\hfill \end{array}$$

Moreover, by using the triangle inequality, we obtain that

$$\begin{array}{cc}\hfill \hspace{1em}& {∥{\mathsf{{\rm Y}}}_3∥}_{{\omega }^{-\mathit{u}}}\le \frac{L}{\prod \mathbf{\kappa }(1-\mathit{u})2^{-\mathit{u}}}\underset{{\left|\mathit{j}\right|}_{\infty }\le N}{max}\left[{\left({\int }_{-\mathbf{1}}^{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}\prod {\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}-\mathbf{\sigma }\right)}^{-\mathit{u}}{\left|{}_{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\mathsf{\Psi }\left(\mathbf{\sigma }\right)-\mathsf{\Psi }\left(\mathbf{\sigma }\right)\right|}^{2}d\mathbf{\sigma }\right)}^{\frac{1}{2}}\right.\hfill \\ \hfill \hspace{1em}& \left.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\left({\int }_{-\mathbf{1}}^{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}\prod {\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}-\mathbf{\sigma }\right)}^{-\mathit{u}}{\left|\mathsf{\Psi }\left(\mathbf{\sigma }\right)-{\mathsf{\Psi }}_N\left(\mathbf{\sigma }\right)\right|}^{2}d\mathbf{\sigma }\right)}^{\frac{1}{2}}\right].\hfill \end{array}$$

We further obtain the following result from (35)

$$\begin{array}{cc}\hfill \hspace{1em}& {∥{\mathsf{{\rm Y}}}_3∥}_{{\omega }^{-\mathit{u}}}\le c\sqrt{\frac{(1+N-r)!}{N!}}{(r+N)}^{-(1+r)/2}{\left|\mathsf{\Psi }\right|}_{{\tilde{A}}_{-\mathit{u}}^r\left({\Omega }^m\right)}+\frac{L}{\prod (1-\mathit{u})2^{-\mathit{u}} \mathbf{\kappa }}{∥{\mathsf{{\rm Y}}}_N∥}_{{\omega }^{-\mathit{u}}}.\hfill \end{array}$$

(48)

We can estimate the following term using (35) and Theorem 1

$$\begin{array}{cc}\hfill {∥{\mathsf{{\rm Y}}}_4∥}_{{\omega }^{-\mathit{u}}}& =\frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{∥{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {\left(\mathbf{1}-\mathbf{\sigma }\right)}^{-\mathit{u}}\left(\mathcal{I}-{\mathcal{I}}_{\mathbf{\sigma },N}^{-\mathit{u}}\right)F\left(\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }\left(q \mathbf{\sigma }\right)\right)d\mathbf{\sigma }∥}_{{\omega }^{-\mathit{u}}}\hfill \\ \hfill \hspace{1em}& =\frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{\left[{\int }_{-1}^1\prod {(1-y)}^{-\mathit{u}}{\left|{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {\left(\mathbf{1}-\mathbf{\sigma }\right)}^{-\mathit{u}}\left(\mathcal{I}-{\mathcal{I}}_{\mathbf{\sigma },N}^{-\mathit{u}}\right)F\left(\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }\left(q \mathbf{\sigma }\right)\right)d\mathbf{\sigma }\right|}^{2}dy\right]}^{\frac{1}{2}}\hfill \\ \hfill \hspace{1em}& =\prod \frac{1}{\sqrt{2^{\mathbf{1}-\mathit{u}}(1-\mathit{u})}}\left|{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {\left(\mathbf{1}-\mathbf{\sigma }\right)}^{-\mathit{u}}\left(\mathcal{I}-{\mathcal{I}}_{\mathbf{\sigma },N}^{-\mathit{u}}\right)F\left(\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }\left(q \mathbf{\sigma }\right)\right)d\mathbf{\sigma }\right|\hfill \\ \hfill \hspace{1em}& \le c\sqrt{\frac{(1+N-r)!}{N!}}{(r+N)}^{-(1+r)/2}{\left|F(\mathbf{\sigma },\mathsf{\Psi }(\mathbf{\sigma }),\mathsf{\Psi }(q \mathbf{\sigma }\left)\right)\right|}_{{\tilde{A}}_{-\mathit{u}}^r\left({\Omega }^m\right)}.\hfill \end{array}$$

(49)

We now estimate the last term

$$\begin{array}{cc}\hfill {∥{\mathsf{{\rm Y}}}_5∥}_{{\omega }^{-\mathit{u}}}=& \frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{∥{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {\left(\mathbf{1}-\mathbf{\sigma }\right)}^{-\mathit{u}}{\mathcal{I}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(F\left(\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }\left(q \mathbf{\sigma }\right)\right)-F(\mathbf{\sigma },{\mathsf{\Psi }}_N\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N(q \mathbf{\sigma }))\right)d\mathbf{\sigma }∥}_{{\omega }^{-\mathit{u}}}\hfill \\ & =\frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{\left[{\int }_{-1}^1\prod {(1-y)}^{-\mathit{u}}{\left|{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {\left(\mathbf{1}-\mathbf{\sigma }\right)}^{-\mathit{u}}{\mathcal{I}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(F\left(\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }\left(q \mathbf{\sigma }\right)\right)-F(\mathbf{\sigma },{\mathsf{\Psi }}_N\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N(q \mathbf{\sigma }))\right)d\mathbf{\sigma }\right|}^{2}dy\right]}^{\frac{1}{2}}\hfill \\ & =\prod \frac{1}{\sqrt{2^{\mathbf{1}-\mathit{u}}(1-\mathit{u})}}\left|{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {\left(\mathbf{1}-\mathbf{\sigma }\right)}^{-\mathit{u}}{\mathcal{I}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(F\left(\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }\left(q \mathbf{\sigma }\right)\right)-F(\mathbf{\sigma },{\mathsf{\Psi }}_N\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N(q \mathbf{\sigma }))\right)d\mathbf{\sigma }\right|.\hfill \end{array}$$

(50)

By using the Cauchy–Schwarz inequality, we deduce that

$$\begin{array}{c}{∥{\mathsf{{\rm Y}}}_5∥}_{{\omega }^{-\mathit{u}}}\le \prod \frac{\mathbf{1}}{\mathbf{1}-\mathit{u}}{\left[{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {\left(\mathbf{1}-\mathbf{\sigma }\right)}^{-\mathit{u}}{\left|{\mathcal{I}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(F\left(\mathbf{\sigma },\mathsf{\Psi }\left(\mathbf{\sigma }\right),\mathsf{\Psi }\left(q \mathbf{\sigma }\right)\right)-F(\mathbf{\sigma },{\mathsf{\Psi }}_N\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N(q \mathbf{\sigma }))\right)\right|}^{2}d\mathbf{\sigma }\right]}^{\frac{1}{2}}\hfill \\ \le \prod \frac{\mathbf{1}}{\mathbf{1}-\mathit{u}}{\left[\sum _{{\left|\mathit{q}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{q}}^{-\mathit{u}}\prod {\left|\left(F\left({\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}},\mathsf{\Psi }\left({\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}\right),\mathsf{\Psi }\left(q {\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}\right)\right)-F({\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}},{\mathsf{\Psi }}_N\left({\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}\right),{\mathsf{\Psi }}_N(q {\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}))\right)\right|}^2\right]}^{\frac{1}{2}}.\hfill \end{array}$$

(51)

Using the Lipschitz condition, we deduce that

$$\begin{array}{cc}\hfill {∥{\mathsf{{\rm Y}}}_5∥}_{{\omega }^{-\mathit{u}}}& \le \prod \frac{\mathbf{L}}{\mathbf{1}-\mathit{u}}{\left[\sum _{{\left|\mathit{q}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{q}}^{-\mathit{u}}\prod {\left|\mathsf{\Psi }\left({\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}\right)-{\mathsf{\Psi }}_N\left({\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}\right)\right|}^2\right]}^{\frac{1}{2}},\hfill \\ \hfill \hspace{1em}& \le \prod \frac{\mathbf{L}}{\mathbf{1}-\mathit{u}}{\left[{\int }_{-1}^1\prod {(1-\mathbf{\sigma })}^{-\mathit{u}}{\left|{\mathcal{I}}_{\mathbf{\sigma },N}^{-\mathit{u}}\mathsf{\Psi }\left(\mathbf{\sigma }\right)-{\mathsf{\Psi }}_N\left(\mathbf{\sigma }\right)\right|}^2\right]}^{\frac{1}{2}}.\hfill \end{array}$$

(52)

Moreover, by using the triangle inequality, we obtain that

$$\begin{array}{cc}\hfill {∥{\mathsf{{\rm Y}}}_5∥}_{{\omega }^{-\mathit{u}}}& \le \prod \frac{\mathbf{L}}{\mathbf{1}-\mathit{u}}\left[{\left[{\int }_{-1}^1\prod {(1-\mathbf{\sigma })}^{-\mathit{u}}{\left|{\mathcal{I}}_{\mathbf{\sigma },N}^{-\mathit{u}}\mathsf{\Psi }\left(\mathbf{\sigma }\right)-\mathsf{\Psi }\left(\mathbf{\sigma }\right)\right|}^2\right]}^{\frac{1}{2}}+{\left[{\int }_{-1}^1\prod {(1-\mathbf{\sigma })}^{-\mathit{u}}{\left|\mathsf{\Psi }\left(\mathbf{\sigma }\right)-{\mathsf{\Psi }}_N\left(\mathbf{\sigma }\right)\right|}^2\right]}^{\frac{1}{2}}\right].\hfill \end{array}$$

(53)

We further obtain from Theorem 1 the following result

$$\begin{array}{c}{∥{\mathsf{{\rm Y}}}_5∥}_{{\omega }^{-\mathit{u}}}\le c\sqrt{\frac{(1+N-r)!}{N!}}{(r+N)}^{-(1+r)/2}{\left|\mathsf{\Psi }\right|}_{{\tilde{A}}_{-\mathit{u}}^r\left({\Omega }^m\right)}+\prod \frac{L}{\mathbf{1}-\mathit{u}}{∥{\mathsf{{\rm Y}}}_N∥}_{{\omega }^{-\mathit{u}}}.\hfill \end{array}$$

(54)

Hence, a combination of (42), (47), (49), and (54) leads to the desired conclusion of this theorem with

$$\prod \frac{L}{\mathbf{1}-\mathit{u}}+\frac{L}{\prod (1-\mathit{u})2^{-\mathit{u}} \mathbf{\kappa }}<1.$$

 □

5. Existence and Uniqueness of the Approximate Solution

Consider the following iteration process $(p=1,2,\dots )$:

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_N^p\left(\mathit{y}\right)=& {\mathcal{I}}_{\mathit{y},N}^{-\mathit{u},\mathbf{0}}\left[{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {(1-\mathbf{\tau })}^{-\mathit{u}}{\left(\frac{1+\mathit{y}}{4}\right)}^{1-\mathit{u}}{\mathcal{I}}_{\mathbf{\tau },N}^{-\mathit{u},\mathbf{0}}G\left(\mathit{y},{\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }},{\mathsf{\Psi }}_N^{p-1}\left({\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }}\right),{\mathsf{\Psi }}_N^{p-1}\left(q {\mathbf{\sigma }}_{\mathit{y},\mathbf{\tau }}\right)\right)d\mathbf{\tau }\right]\hfill \\ \hfill \hspace{1em}& +{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {(1-\mathbf{\tau })}^{-\mathit{u}}{\left(\frac{1}{2}\right)}^{1-\mathit{u}}{\mathcal{I}}_{\mathbf{\tau },N}^{-\mathit{u},\mathbf{0}}F\left(\mathbf{\tau },{\mathsf{\Psi }}_N\left(\mathbf{\tau }\right),{\mathsf{\Psi }}_N\left(q \mathbf{\tau }\right)\right)d\mathbf{\tau }+{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u},\mathbf{0}}H\left(\mathit{y}\right).\hfill \end{array}$$

(55)

Let ${\overrightarrow{\mathsf{\Psi }}}_N^p\left(\mathit{y}\right)={\mathsf{\Psi }}_N^p\left(\mathit{y}\right)-{\mathsf{\Psi }}_N^{p-1}\left(\mathit{y}\right)$. Then, we have

$$\begin{array}{c}{\overrightarrow{\mathsf{\Psi }}}_N^p\left(\mathit{y}\right)\hfill \\ =\prod 2^{\mathit{u}-1}{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u},\mathbf{0}}\left[{\int }_{-\mathbf{1}}^{\mathit{y}}\prod {(\mathit{y}-\mathbf{\sigma })}^{-\mathit{u}}{}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(G\left(\mathit{y},\mathbf{\sigma },{\mathsf{\Psi }}_N^{p-1}\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N^{p-1}\left(q \mathbf{\sigma }\right)\right)-G\left(\mathit{y},\mathbf{\sigma },{\mathsf{\Psi }}_N^{p-2}\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N^{p-2}\left(q \mathbf{\sigma }\right)\right)\right)d\mathbf{\sigma }\right]\hfill \\ +\prod 2^{\mathit{u}-1}\left[{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {(1-\mathbf{\tau })}^{-\mathit{u}}{\mathcal{I}}_{\mathbf{\tau },N}^{-\mathit{u},\mathbf{0}}\left(F\left(\mathbf{\tau },{\mathsf{\Psi }}_N^{p-1}\left(\mathbf{\tau }\right),{\mathsf{\Psi }}_N^{p-1}\left(q \mathbf{\tau }\right)\right)-F\left(\mathbf{\tau },{\mathsf{\Psi }}_N^{p-2}\left(\mathbf{\tau }\right),{\mathsf{\Psi }}_N^{p-2}\left(q \mathbf{\tau }\right)\right)\right)d\mathbf{\tau }\right]\hfill \\ :=T_1+T_2,\hfill \end{array}$$

(56)

where

$$\begin{array}{cc}\hfill T_1=& \prod 2^{\mathit{u}-1}{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u},\mathbf{0}}\left[{\int }_{-\mathbf{1}}^{\mathit{y}}\prod {(\mathit{y}-\mathbf{\sigma })}^{-\mathit{u}}{}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(G\left(\mathit{y},\mathbf{\sigma },{\mathsf{\Psi }}_N^{p-1}\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N^{p-1}\left(q \mathbf{\sigma }\right)\right)-G\left(\mathit{y},\mathbf{\sigma },{\mathsf{\Psi }}_N^{p-2}\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N^{p-2}\left(q \mathbf{\sigma }\right)\right)\right)d\mathbf{\sigma }\right],\hfill \\ \hfill T_2=& \prod 2^{\mathit{u}-1}\left[{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {(1-\mathbf{\tau })}^{-\mathit{u}}{\mathcal{I}}_{\mathbf{\tau },N}^{-\mathit{u},\mathbf{0}}\left(F\left(\mathbf{\tau },{\mathsf{\Psi }}_N^{p-1}\left(\mathbf{\tau }\right),{\mathsf{\Psi }}_N^{p-1}\left(q \mathbf{\tau }\right)\right)-F\left(\mathbf{\tau },{\mathsf{\Psi }}_N^{p-2}\left(\mathbf{\tau }\right),{\mathsf{\Psi }}_N^{p-2}\left(q \mathbf{\tau }\right)\right)\right)d\mathbf{\tau }\right].\hfill \end{array}$$

We now estimate the term ${∥T_1∥}_{{\omega }^{-\mathit{u}}}.$ By the Jacobi–Gauss integration Formula (9), we have

$$\begin{array}{c}{∥T_1∥}_{{\omega }^{-\mathit{u}}}\hfill \\ =\frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}{∥{\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}{\int }_{-\mathbf{1}}^{\mathit{y}}\prod {\left(\mathit{y}-\mathbf{\sigma }\right)}^{-\mathit{u}}{}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(G\left(\mathit{y},\mathbf{\sigma },{\mathsf{\Psi }}_N^{p-1}\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N^{p-1}\left(q \mathbf{\sigma }\right)\right)-G(\mathit{y},\mathbf{\sigma },{\mathsf{\Psi }}_N^{p-2}\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N^{p-2}(q \mathbf{\sigma }))\right)d\mathbf{\sigma }∥}_{{\omega }^{-\mathit{u}}}\hfill \\ ={\left[{\int }_{-\mathbf{1}}^{\mathbf{1}}{\omega }^{-\mathit{u}}{\left({\mathcal{I}}_{\mathit{y},N}^{-\mathit{u}}{\int }_{-\mathbf{1}}^{\mathit{y}}\prod {\left(\mathit{y}-\mathbf{\sigma }\right)}^{-\mathit{u}}{}_{\mathit{y}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(G(\mathit{y},\mathbf{\sigma },{\mathsf{\Psi }}_N^{p-1}\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N^{p-1}(q \mathbf{\sigma }))-G(\mathit{y},\mathbf{\sigma },{\mathsf{\Psi }}_N^{p-2}\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N^{p-2}(q \mathbf{\sigma }))\right)d\mathbf{\sigma }\right)}^{2}d\mathit{y}\right]}^{\frac{1}{2}}\hfill \\ =\frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}\left[\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{j}}^{-\mathit{u}}\left({\int }_{-\mathbf{1}}^{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}\prod {\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}-\mathbf{\sigma }\right)}^{-\mathit{u}}\right.\right.\hfill \\ {\left.{\left.\hspace{1em}\hspace{1em}\hspace{1em}\times {}_{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(G({\mathit{y}}_{\mathit{j}}^{-\mathit{u}},\mathbf{\sigma },{\mathsf{\Psi }}_N^{p-1}\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N^{p-1}(q \mathbf{\sigma }))-G({\mathit{y}}_{\mathit{j}}^{-\mathit{u}},\mathbf{\sigma },{\mathsf{\Psi }}_N^{p-2}\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N^{p-2}(q \mathbf{\sigma }))\right)d\mathbf{\sigma }\right)}^2\right]}^{1/2}.\hfill \end{array}$$

Using the Cauchy-Schwarz inequality and (33), we further obtain

$$\begin{array}{c}{∥T_1∥}_{{\mathbf{\omega }}^{-\mathit{u}}}\hfill \\ \le \frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}\left[\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{j}}^{-\mathit{u}}\prod \frac{{\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}+1\right)}^{1-\mathit{u}}}{1-\mathit{u}}\right.\hfill \\ {\left.\hspace{1em}\hspace{1em}\times {\int }_{-\mathbf{1}}^{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}\prod {\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}-\mathbf{\sigma }\right)}^{-\mathit{u}}{\left|{}_{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}{\widehat{\mathcal{I}}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(G({\mathit{y}}_{\mathit{j}}^{-\mathit{u}},\mathbf{\sigma },{\mathsf{\Psi }}_N^{p-1}\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N^{p-1}(q \mathbf{\sigma }))-G({\mathit{y}}_{\mathit{j}}^{-\mathit{u}},\mathbf{\sigma },{\mathsf{\Psi }}_N^{p-2}\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N^{p-2}(q \mathbf{\sigma }))\right)\right|}^{2}d\mathbf{\sigma }\right]}^{1/2}\hfill \\ \le \frac{1}{\prod 2^{\mathbf{1}-\mathit{u}}}\left[\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{j}}^{-\mathit{u}}\prod \frac{{\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}+1\right)}^{2\left(1-\mathit{u}\right)}}{2^{1-\mathit{u}}\left(1-\mathit{u}\right)}\right.\hfill \\ {\left.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times \sum _{{\left|\mathit{q}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{q}}^{-\mathit{u}}{\left|G({\mathit{y}}_{\mathit{j}}^{-\mathit{u}},{\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}},{\mathsf{\Psi }}_N^{p-1}\left({\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}\right),{\mathsf{\Psi }}_N^{p-1}(q {\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}))-G({\mathit{y}}_{\mathit{j}}^{-\mathit{u}},{\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}},{\mathsf{\Psi }}_N^{p-2}\left({\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}\right),{\mathsf{\Psi }}_N^{p-2}(q {\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}))\right|}^2\right]}^{1/2}.\hfill \end{array}$$

Using the Lipschitz condition, we deduce that

$$\begin{array}{c}{∥T_1∥}_{{\mathbf{\omega }}^{-\mathit{u}}}\le \frac{L}{\prod 2^{\mathbf{1}-\mathit{u}}}{\left[\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{j}}^{-\mathit{u}}\prod \frac{{\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}+1\right)}^{2\left(1-\mathit{u}\right)}}{2^{1-\mathit{u}}\left(1-\mathit{u}\right)}\sum _{{\left|\mathit{q}\right|}_{\infty }\le N}{\left|{\overrightarrow{\mathsf{\Psi }}}_N^{p-1}\left({\mathbf{\sigma }}_{\mathit{q}}\right)\right|}^2{\mathbf{\chi }}_{\mathit{q}}^{-\mathit{u}}\right]}^{1/2}\hfill \\ \le \frac{L}{\prod 2^{1-\mathit{u}}}{\left[\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{j}}^{-\mathit{u}}\prod \frac{{\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}+1\right)}^{1-\mathit{u}}}{1-\mathit{u}}{\int }_{-\mathbf{1}}^{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}\prod {\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}-\mathbf{\sigma }\right)}^{-\mathit{u}}{\left|{\overrightarrow{\mathsf{\Psi }}}_N^{p-1}\left(\mathbf{\sigma }\right)\right|}^{2}d\mathbf{\sigma }\right]}^{1/2}\hfill \\ \le \frac{L}{\prod 2^{1-\mathit{u}}(1-\mathit{u})}{\left(\sum _{{\left|\mathit{j}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{j}}^{-\mathit{u}}\prod \left(1-\mathit{u}\right){\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}+1\right)}^{1-\mathit{u}}\right)}^{1/2}\underset{{\left|\mathit{j}\right|}_{\infty }\le N}{max}{\left({\int }_{-\mathbf{1}}^{{\mathit{y}}_{\mathit{j}}^{-\mathit{u}}}\prod {\left({\mathit{y}}_{\mathit{j}}^{-\mathit{u}}-\mathbf{\sigma }\right)}^{-\mathit{u}}{\left|{\overrightarrow{\mathsf{\Psi }}}_N^{p-1}\left(\mathbf{\sigma }\right)\right|}^{2}d\mathbf{\sigma }\right)}^{\frac{1}{2}}\hfill \\ \le \frac{L}{\prod (1-\mathit{u})2^{-\mathit{u}} \mathbf{\kappa }}{∥{\overrightarrow{\mathsf{\Psi }}}_N^{p-1}\left(\mathbf{\sigma }\right)∥}_{{\mathbf{\omega }}^{-\mathit{u}}}.\hfill \end{array}$$

It remains to estimate the term ${∥T_2∥}_{{\mathbf{\omega }}^{-\mathit{u}}}$. By the Cauchy–Schwarz inequality, we have

$$\begin{array}{c}{∥T_2∥}_{{\mathbf{\omega }}^{-\mathit{u}}}\hfill \\ \le \prod \frac{\mathbf{1}}{\mathbf{1}-\mathit{u}}{\left[{\int }_{-\mathbf{1}}^{\mathbf{1}}\prod {\left(\mathbf{1}-\mathbf{\sigma }\right)}^{-\mathit{u}}{\left|{\mathcal{I}}_{\mathbf{\sigma },N}^{-\mathit{u}}\left(F\left(\mathbf{\sigma },{\mathsf{\Psi }}_N^{p-1}\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N^{p-1}\left(q \mathbf{\sigma }\right)\right)-F(\mathbf{\sigma },{\mathsf{\Psi }}_N^{p-2}\left(\mathbf{\sigma }\right),{\mathsf{\Psi }}_N^{p-2}(q \mathbf{\sigma }))\right)\right|}^{2}d\mathbf{\sigma }\right]}^{\frac{1}{2}}\hfill \\ \le \prod \frac{\mathbf{1}}{\mathbf{1}-\mathit{u}}{\left[\sum _{{\left|\mathit{q}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{q}}^{-\mathit{u}}\prod {\left|\left(F\left({\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}},{\mathsf{\Psi }}_N^{P-1}\left({\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}\right),{\mathsf{\Psi }}_N^{P-1}\left(q {\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}\right)\right)-F({\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}},{\mathsf{\Psi }}_N^{P-2}\left({\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}\right),{\mathsf{\Psi }}_N^{P-2}(q {\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}))\right)\right|}^2\right]}^{\frac{1}{2}}.\hfill \end{array}$$

(57)

Using the Lipschitz condition, we obtain that

$$\begin{array}{cc}\hfill {∥T_2∥}_{{\mathbf{\omega }}^{-\mathit{u}}}& \le \prod \frac{L}{\mathbf{1}-\mathit{u}}{\left[\sum _{{\left|\mathit{q}\right|}_{\infty }\le N}{\mathbf{\chi }}_{\mathit{q}}^{-\mathit{u}}\prod {\left|{\mathsf{\Psi }}_N^{P-1}\left({\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}\right)-{\mathsf{\Psi }}_N^{P-2}\left({\mathbf{\sigma }}_{\mathit{q}}^{-\mathit{u}}\right)\right|}^2\right]}^{\frac{1}{2}},\hfill \\ \hfill \hspace{1em}& \le \prod \frac{L}{\mathbf{1}-\mathit{u}}{\left[{\int }_{-1}^1\prod {(1-\mathbf{\sigma })}^{-\mathit{u}}{\left|{\overrightarrow{\mathsf{\Psi }}}_N^{p-1}\left(\mathbf{\sigma }\right)\right|}^{2}d\mathbf{\sigma }\right]}^{\frac{1}{2}}\hfill \\ \hfill \hspace{1em}& \le \prod \frac{L}{\mathbf{1}-\mathit{u}}{∥{\overrightarrow{\mathsf{\Psi }}}_N^{p-1}\left(\mathbf{\sigma }\right)∥}_{{\mathbf{\omega }}^{-\mathit{u}}},\hfill \end{array}$$

(58)

with

$$\prod \frac{L}{\mathbf{1}-\mathit{u}}+\frac{L}{\prod (1-\mathit{u})2^{-\mathit{u}} \mathbf{\kappa }}<1.$$

For $m\to \infty$, then $∥{\overrightarrow{\mathsf{\Psi }}}_N^{p-1}∥\to 0$. This implies the existence of solution of (22). It is easy to prove the uniqueness of the solution to (22).

6. Numerical Test Example

In this section, we test the proposed algorithm on a test problem and show the efficiency of the present method.

Consider the following Volterra–Fredholm nonlinear integral equation with proportional delay:

$$\begin{array}{cc}\hfill \psi (x,y)=h(x,y)& +{\int }_0^1{\int }_0^1{(1-r)}^{-u}{(1-s)}^{-v}{\psi }^2(q r,q s)dsdr\hfill \\ \hfill \hspace{1em}& +{\int }_0^x{\int }_0^y{(x-r)}^{-u}{(y-s)}^{-v}{\psi }^3(q r,q s)dsdr,\hfill \end{array}$$

(59)

where

$$\begin{array}{cc}\hfill h(x,y)=& x^{1-u}{y}^{1-v}-\frac{q^{-2(-2+u+v)}\mathsf{\Gamma }(3-2u)\mathsf{\Gamma }(1-u)\mathsf{\Gamma }(3-2v)\mathsf{\Gamma }(1-v)}{\mathsf{\Gamma }(4-3u)\mathsf{\Gamma }(4-3v)}\hfill \\ \hfill \hspace{1em}& -\frac{q^{-3(-2+u+v)}{x}^{4-4u}{y}^{4-4v}\mathsf{\Gamma }(4-3u)\mathsf{\Gamma }(1-u)\mathsf{\Gamma }(4-3v)\mathsf{\Gamma }(1-v)}{\mathsf{\Gamma }(5-4u)\mathsf{\Gamma }(5-4v)}.\hfill \end{array}$$

(60)

The analytical solution of (59) is $\psi (x,y)=x^{1-u}{y}^{1-v}$. In Figure 1 and Figure 2, the absolute errors are displayed for various choices of $u, v, {\rho }_1,$${\rho }_2$, and N in $L_{\omega }^2$. The weighted function $\omega$ is $\omega (x,y)={\omega }^{-u,0}\left({\phi }_1^{-1}\left(x\right)\right){\omega }^{-v,0}\left({\phi }_2^{-1}\left(y\right)\right){\partial }_x{\phi }_1^{-1}\left(x\right){\partial }_y{\phi }_2^{-1}\left(y\right)$.

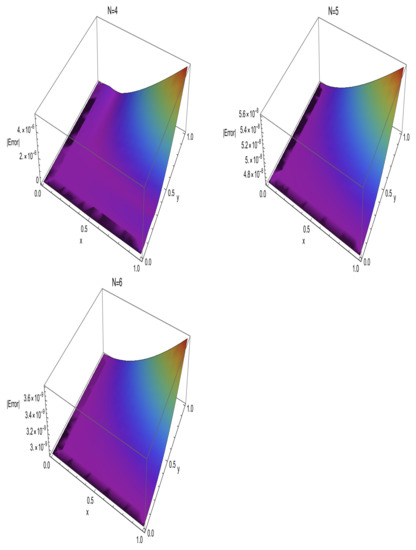
Figure 1. The absolute errors with $(u,v,{\rho }_1,{\rho }_2)=(2/5,1/4,5,4)$.

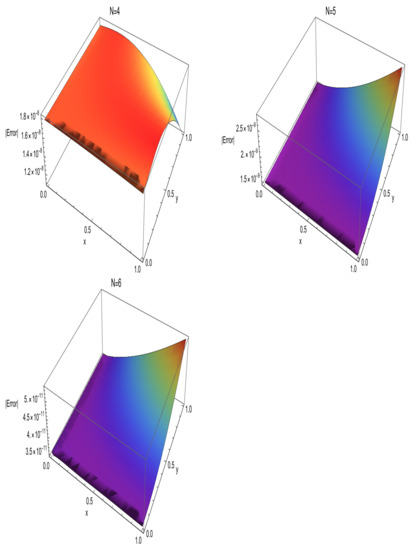
Figure 2. The absolute errors with $(u,v,{\rho }_1,{\rho }_2)=(1/2,1/3,2,3)$.

7. Concluding Remarks

We have adopted a regularized spectral scheme to solve nonlinear high-dimensional weakly singular integral equations with proportional delay and nonsmooth solutions. The transformed spectral method has been constructed based on multivariate Jacobi polynomials and some smoothing transformations, hence inheriting the advantages of the spectral collocation methods even for nonsmooth solutions. Furthermore, we studied the convergence, the existence, and the uniqueness of the approximate solutions. This scheme has various advantages, which are listed below:

• The numerical results shown in the figures demonstrate that the provided technique is accurate and efficient, producing acceptable results for nonsmooth solutions.
• With a modest number of points and base functions considered in the examples, our technique produced satisfactory results. With a minimal number of computations, this approach yields an accurate numerical result.

An extension of the work to different types of singular initial and boundary-value problems of integer or fractional orders [56,57,58,59] is of high concern in works in the near future.