Abstract
For a function p analytic in the open unit disc and satisfying , we prove certain subordination implications of the first order differential subordination , which provides sufficient conditions for a function to belong to various subclasses of Ma-Minda starlike functions. The pre-Schwarzian norm estimate and inclusion criteria for certain subclasses of analytic function are also obtained. Additionally, using Gronwall’s inequality we give a sufficient condition for a normalized function to belong to a class of functions with bounded arguments that extends the class of strongly -Bazilevič functions of order studied by Gao in 1996.
Keywords:
starlike; convex and close-to-convex functions; differential subordination; norm estimate; Schwarzian derivative; pre-Schwarzian derivative; Gronwall’s inequality MSC:
30C45; 30C50; 30C55
1. Introduction and Preliminaries
Let denote the class of analytic functions in the unit disc of the complex plane, with the usual normalization . The class consists of all normalized and univalent functions in .
A function belongs to the class of starlike functions, or to the class of convex functions, if f maps conformally the unit disc onto the domains that are starlike with respect to the origin, or convex, and the analytical characterization of these classes are given by and in , respectively.
If f and g are two analytic functions on , we say fis subordinated tog, written , if for some analytic function , with . If g is univalent in , then if, and only if, , and (cf. ([1] p. 90); see also [2]).
Let , and let h be univalent in . If p is analytic in and satisfies the differential subordination
then p is called a solution of the differential subordination. The univalent function q is called a dominant of the solutions of the differential subordination, or more simply a dominant, if for all p satisfying (1). A dominant that satisfies for all dominants q of (1) is said to be the best dominant (for details see [2]).
For a convex univalent function h defined on with , , , in 1985 Padmanabhan and Parvatham [3], and Shanmugam [4] in 1989, introduced and studied certain subclasses defined in terms of convolution and subordination as follows, respectively:
where , , and
where g is a fixed function. For and , the corresponding subclasses are denoted by and , respectively.
If h is a univalent function with positive real part, which maps onto a domain symmetric with respect to the real axis and starlike with respect to and , in 1992 Ma and Minda [5] studied growth, distortion, and coefficient estimates for functions belonging to the above mentioned classes, and . In recent years, many researchers have taken specific functions and studied numerous subordination implications that provide sufficient conditions for functions to belong to various subclasses of Ma-Minda starlike functions (see Table 1).

Table 1.
Ma-Minda starlike subclasses .
In 1996, Sokół and Stankiewicz [6] studied the radius of convexity of some subclasses of strongly starlike functions. Raina and Sokół in [7] have discussed certain geometric properties of the functions belonging to the class , while in [8] the authors have obtained sharp radii for functions belonging to the class . In [9,10,11], the authors used the method of differential subordination to obtain sufficient conditions for functions of the class to belong to Ma-Minda subclasses of starlike functions.
On the other hand, subordination implications and subclasses of analytic functions have been recently studied in literature, such as [16] and [17].
Motivated by their works, in the Section 2, we have used the subordination as a tool to obtain bounds on M for an analytic function p, with , such that implies the function p is subordinate to each of the following functions:
In the Section 3, in connection with [18,19], we determine the pre-Schwarzian norm estimates for function belonging to the classes
and
where , and is an analytic function in , with and for all ; also, . Moreover, norm estimates for various classes mentioned in the Table 1 are obtained.
In the Section 4, using the Gronwall’s inequality [20] we obtained a sufficient condition involving the Schwarzian derivative, such that a given function belongs to a certain class associated with .
2. Subordination Results for Some Special Dominants
To obtain bounds on M for an analytic function p, with , such that implies the function p is subordinate to each of the following functions mentioned in (2) the following lemma will be used to prove our main results.
Lemma 1.
([2]) Let q be univalent in and let ϕ and ν be analytic in a domain D containing , with when . Set and . Suppose that:
(i) either h is convex or Q is starlike univalent in ,
and
(ii) for .
Let p be analytic in with and . If p satisfies
then , and q is the best dominant of the above subordination.
Theorem 1.
Let p be an analytic function in , with , such that
Then, the following subordination results hold:
- (a)
- , for ;
- (b)
- , for ;
- (c)
- , for ;
- (d)
- , for ;
- (e)
- , for ;
- (f)
- , with , for ;
- (g)
- , for ;
- (h)
- , for ;
- (i)
- , for .
The bounds of M are the best possible.
Proof.
If we let the function defined by
then is a solution for the first order differential equation . If we take in Lemma 1, then we have
Since the function Q is starlike, and , , from Lemma 1 it follows that the subordination assumption implies .
Each of the conclusions in all the parts of this theorem are of the form , for appropriate choices of , whenever the subordination holds.
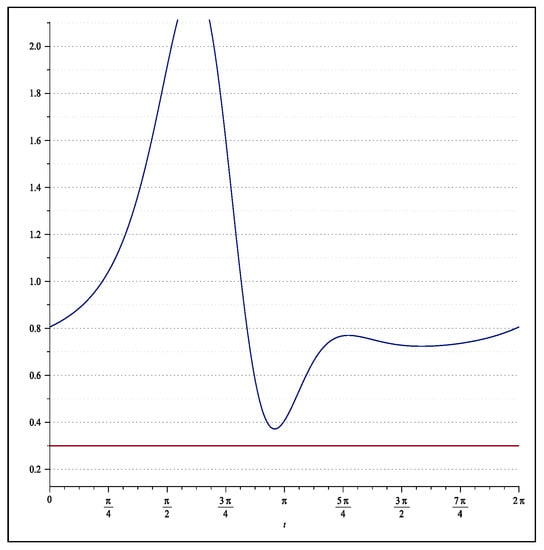
(a) Letting , then implies
A simple calculation yields that the above double inequality holds whenever . Therefore, according to the Figure 1a made by MAPLE™ software, we see that , and since , it follows that , hence the subordination is proved.

Figure 1.
Figures for the Theorem 1. (a) Boundary curve of and for . (b) Boundary curve of and for . (c) Boundary curve of and for . (d) Boundary curve of and for . (e) Boundary curve of and for . (f) Boundary curve of and for . (g) Boundary curve of and for . (h) Boundary curve of and for . (i) Boundary curve of and for .
(b) If , then implies
that holds whenever . From the Figure 1b made by MAPLE™ software, since we see that , and combining with , it follows that , thus the subordination is holds.
For proving the items (c)–(i) we proceed similarly and obtain the required results.
The bounds are the best possible in each cases because, such as in the cases (a) and (b) presented above, the left and right hand side inequalities are attained for the mentioned values of M, respectively. □
For , such that for , if we let in Theorem 1, we obtain the following special cases:
Corollary 1.
If and the function satisfies the subordination
then:
- (a)
- , for ;
- (b)
- , for ;
- (c)
- , for ;
- (d)
- , for ;
- (e)
- , with , for ;
- (f)
- , for ;
- (g)
- , for ;
- (h)
- , for .
The bounds of M are the best possible.
Taking in Corollary 1 we obtain the next sufficient condition for the function to belong to various Ma-Minda type subclasses:
Remark 1.
If the function satisfies the subordination
then:
The bounds of M are the best possible.
3. Norm Estimates for the Classes and
In this section, we derive pre-Schwarzian norm estimate for the classes and defined by (3) and (4), respectively, followed by certain applications of the main results. Additionally, inclusion criteria for various subclasses of analytic function are obtained using Gronwall’s inequality.
The pre-Schwarzian derivative of a locally univalent function f in the unit disc , i.e.,
and the Schwarzian derivative
and their respective norms
play a crucial role in the theory of Teichmüller spaces [21]. The Teichmüller space can be associated with the set of Schwarzian derivatives of univalent functions on with quasiconformal extensions to the Riemann sphere, . Moreover, for , if f extends to a k-quasiconformal mapping of , then , and, conversely, if , then f is a k-quasiconformal mapping of .
It is well known that for and that for , and, conversely, for , implies (the well-known Becker’s theorem).
Yamashita [22] showed that if (i.e., f is starlike of order alpha), then .
Let denote the class of analytic functions , , and for a given let . The Dieudonné Lemma ([1] p. 198) which plays a pivotal role in the proof of our next results states that for a fixed pair of points with , the value belongs the closed disc centered at with radius . Moreover, if lies on the boundary of this disc, then w has the form:
where with .
Kim and Sugawa [19] obtained the pre-Schwarzian norm estimate for some close-to-convex functions of specified type. Additionally,
and the sharp inequality for was obtained in [19].
The following two lemmas will be used to prove Theorem 2:
Lemma 2
([19] Proposition 2.4., (2.3) and (2.4)). For a continuous function F defined on the interval , the maximal function of F, denoted by , and defined by
where
satisfies
Lemma 3
([19] Corollary 2.5., (2.3) and (2.4)). For two functions , we have
Theorem 2.
For a function we have
Proof.
For a function , from the definition of the subordination we have
where the function w is analytic in , such that , , and . According to the definition of the class , since for all , it follows that f is locally univalent in .
By taking derivative on both sides of the last equation, a simple computation yields
which implies
Generally, for a function g analytic in let define , and be the maximal function of . Additionally, we denote
For a fixed point with , let . Therefore, from the well-known Schwarz lemma we have , hence . From the above inequality, using (6) it follows that
From here, using Lemma 2 and Lemma 3, we obtain
that is (7) holds for all . □
Remark 2.
The inequality (7) of Theorem 2 gives an estimation for the upper bound of the norm of the pre-Schwarzian derivative for the functions that belong to the class . Since this estimation is not the best possible, to find the sharp result remains still an open question.
Taking the function , , the parameter in Theorem 2 and using Lemma 4.2 of [19] we obtain the next result:
Corollary 2.
For , if , then
If we consider in Corollary 2, then with , and we obtain the following norm estimate for the class :
Example 1.
For , if , then
Letting in Theorem 2 the special case and , we will obtain the norm estimate for , as follows.
A simple computation shows that
and
where
and
We obtain that
and
hence ..., and next result holds:
Corollary 3.
If , then
Remark 3.
For and various specializations of the function ψ, we know that the class represents various Ma-Minda type starlike subclasses showed in the Table 1. Additionally, as given in the above corollary, we can obtain estimates for the pre-Schwarzian norm for the functions belonging to , , , , , , , and .
Theorem 3.
For a function we have
and the estimate is sharp if the inequality
hold for all , where with .
Proof.
If , then
hence
where the function w is analytic in , such that , , and . Therefore,
and denote
As in the proof of Theorem 2, let us define , and be the maximal function of .
For a fixed point with , let . Thus, from the well-known Schwarz lemma we have , hence . From the above inequality we have
btain
hence (9) holds for all . Since the remaining part of the proof concerning the sharpness is similar to that proved for the Theorem 2 it will be omitted. □
Example 2.
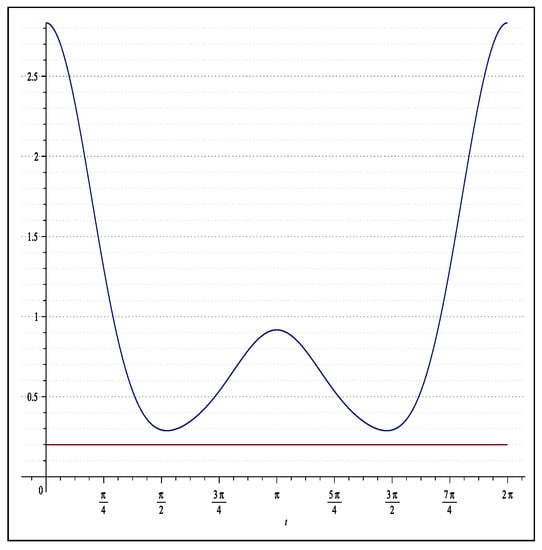
We will prove that the function
belongs to the class . Thus, denoting
like we could see in the Figure 2 we have

Figure 2.
The graphics of for , and .
The function P is analytic in , hence is a harmonic function in , and thus it attains its extremal values of the boundary of . Therefore, this inequality combined with leads to
hence . Since and φ is a univalent function in , we conclude that , that is .
Since for we have
and using the inequality (7) it follows that
Denoting
a simple computation shows that
hence .
4. An Application of the Gronwall Inequality
Suppose that and are two linearly independent solutions with initial conditions
of the second order differential equation
where , and is the Schwarzian derivative of the function , that is
Thus, the function f has the following representation (see also ([1] p. 259), [23,24])
hence
An important tool used in this section is the following Gronwall’s inequality.
Lemma 4
([20] p. 19). Suppose that P and q are non-negative continuous real functions for . If is a constant, then the inequality
implies
Using the integral representation of the fundamental solutions of (11) we have
and using the Gronwall’s inequality in [25] the author proved that if , whenever for all , where and , then
for all (for details see [24,25]).
Using the Gronwall’s inequality Chiang [25] investigated conditions involving the Schwarzian derivatives for a function to belong to the class of strongly starlike functions, and to the class of convex functions. In [24], the authors have obtained inclusion criteria for various subclasses of analytic functions.
The subclass which is of interest in the next study is defined as follows:
where , and .
Consequently, this class reduces to the class of starlike functions, and to the class of convex functions of order for specified values of and . For instance, if and we obtain the class of strongly -Bazilevič functions of order studied by Gao [26].
The next result represents a sufficient condition for a function to belong to the class .
Theorem 4.
Let and . For , let and satisfy the relation
If
and δ satisfies the inequality
then .
Proof.
First, the condition (17) assures the existence of a real number satisfying the inequality (18). This follows from the fact that, taking the assumption (17) shows that there exists a real number such that the inequality (18) holds for .
Representing the function f as in (12) in terms of the linearly independent solutions and of the differential equation (11), and using (13) we obtain
Additionally, for we have that implies . Using this implication combined with the inequalities (15) and (16), the above inequality leads to
Since
following the method of proof given in ([24] Theorem 3.3, p. 69) we obtain
hence
Taking in Theorem 4, the sufficient condition for a function to belong to the class , with , is given by the following corollary.
Corollary 4.
Let and . For , let and satisfy the relation
If
and δ satisfies the inequality
then .
Remark 4.(i) If we choose of , with , and in Theorem 4 we obtain the result of ([24] Theorem 3.2, p. 68).
(ii) For , if or we obtain the sufficient conditions for a function to be strongly starlike and strongly convex of order γ, with , respectively.
5. Conclusions
Concluding, by using the general subordination theory and the graphical representations, we obtained bounds on M for an analytic function p, with , such that implies the function p is subordinate to each of the functions given by (2).
Secondly, we determine the pre-Schwarzian norm estimates for function belonging to the classes given by (3) and (4), and we gave some simple applications of the main results given by Theorems 2 and 3.
The article ends with an application of the Gronwall’s inequalities, that represents a sufficient condition for an analytic and normalized function to belong a subclass of functions with bounded arguments and connected with the class of strongly -Bazilevič functions of order studied by Gao [26].
Author Contributions
Conceptualization, A.F.H., M.P.J., and T.B.; methodology, A.F.H., M.P.J., and T.B.; validation, A.F.H., M.P.J., and T.B.; formal analysis, A.F.H., M.P.J., and T.B.; investigation, A.F.H., M.P.J., and T.B.; resources, A.F.H., M.P.J., and T.B.; writing—original draft preparation, A.F.H., M.P.J., and T.B.; writing—review and editing, A.F.H., M.P.J., and T.B.; supervision, A.F.H., M.P.J., and T.B.; project administration, A.F.H., M.P.J., and T.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful to the reviewers for their valuable remarks, comments, and advices, that help us to remove some mistakes and to improve the quality of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Duren, P.L. Univalent Functions. In Grundlehren der Mathematischen Wissenschaften; Springer: New York, NY, USA, 1983; Volume 259. [Google Scholar]
- Miller, S.S.; Mocanu, P.T. Differential subordinations. Theory and applications. In Monographs and Textbooks in Pure and Applied Mathematics; Marcel Dekker, Inc.: New York, NY, USA, 2000; Volume 225. [Google Scholar]
- Padmanabhan, K.S.; Parvatham, R. Some applications of differential subordination. Bull. Aust. Math. Soc. 1985, 32, 321–330. [Google Scholar]
- Shanmugam, T.N. Convolution and differential subordination. Int. J. Math. Math. Sci. 1989, 12, 333–340. [Google Scholar]
- Ma, W.C.; Minda, D. A unified treatment of some special classes of univalent functions. In Proceedings of the Conference on Complex Analysis, Tianjin, China, 19–23 June 1992; Li, Z., Ren, F., Yang, L., Zhang, S., Eds.; International Press: Cambridge, MA, USA, 1994; pp. 157–169. [Google Scholar]
- Sokół, J.; Stankiewicz, J. Radius of convexity of some subclasses of strongly starlike functions. Zesz. Nauk. Politech. Rzesz. Mat. 1996, 19, 101–105. [Google Scholar]
- Raina, R.K.; Sokół, J. Some properties related to a certain class of starlike functions. C. R. Math. Acad. Sci. 2015, 353, 973–978. [Google Scholar]
- Khatter, K.; Ravichandran, V.; Sivaprasad Kumar, S. Starlike functions associated with exponential function and the lemniscate of Bernoulli. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 2019, 113, 233–253. [Google Scholar] [CrossRef]
- Sharma, K.; Jain, N.K.; Ravichandran, V. Starlike functions associated with a cardioid. Afr. Mat. 2016, 27, 923–939. [Google Scholar]
- Wani, L.A.; Swaminathan, A. Starlike and convex functions associated with a nephroid domain having cusps on the real axis. arXiv 2019, arXiv:1912.05767. [Google Scholar]
- Kumar, S.; Ravichandran, V. A subclass of starlike functions associated with a rational function. Southeast Asian Bull. Math. 2016, 40, 199–212. [Google Scholar]
- Cho, N.E.; Kumar, V.; Kumar, S.S.; Ravichandran, V. Radius problems for starlike functions associated with the sine function. Bull. Iran. Math. Soc. 2019, 45, 213–232. [Google Scholar] [CrossRef]
- Goel, P.; Sivaprasad Kumar, S. Certain class of starlike functions associated with modified sigmoid function. Bull. Malays. Math. Sci. Soc. 2020, 43, 957–991. [Google Scholar] [CrossRef]
- Yunus, Y.; Halim, S.A.; Akbarally, A.B. Subclass of starlike functions associated with a limacon. AIP Conf. Proc. 2018, 1974, 030023. [Google Scholar]
- Janowski, W. Some extremal problems for certain families of analytic functions I. Ann. Polon. Math. 1973, 28, 297–326. [Google Scholar] [CrossRef]
- Aouf, M.K.; Seoudy, T. Certain class of Bi-Bazilevič functions with bounded boundary rotation involving Sălăgean operator. Constr. Math. Anal. 2020, 3, 139–149. [Google Scholar] [CrossRef]
- Seoudy, T.; Aouf, M.K. Fekete-Szego Problem for certain subclass of analytic functions with complex order defined by q-analogue of Ruscheweyh operator. Constr. Math. Anal. 2020, 3, 36–44. [Google Scholar] [CrossRef]
- Dziok, J.; Raina, R.K.; Sokół, J. Applications of differential subordinations for norm estimates of an integral operator. Proc. R. Soc. Edinb. Sect. A 2018, 148, 281–291. [Google Scholar] [CrossRef]
- Kim, Y.C.; Sugawa, T. Norm estimates of the pre-Schwarzian derivatives for certain classes of univalent functions. Proc. Edinb. Math. Soc. 2006, 49, 131–143. [Google Scholar] [CrossRef]
- Hille, E. Lectures on Ordinary Differential Equations; Addison-Wesley Publ. Co.: Reading, MA, USA, 1969. [Google Scholar]
- Zhuravlev, I.V. A model of the universal Teichmüller space. Siberian Math. J. 1986, 27, 691–697. [Google Scholar] [CrossRef]
- Yamashita, S. Norm estimates for function starlike or convex of order alpha. Hokkaido Math. J. 1999, 28, 217–230. [Google Scholar] [CrossRef]
- Kim, J.A.; Sugawa, T. Geometric properties of functions with small Schwarzian derivatives. (preprint). Available online: http://www.cajpn.org/pp04/0403.pdf (accessed on 24 January 2021).
- Ali, R.M.; Nargesi, M.M.; Ravichandran, V.; Swaminathan, A. Inclusion criteria for subclasses of functions and Gronwall’s inequality. Tamsui Oxf. J. Inf. Math. Sci. 2013, 29, 61–75. [Google Scholar]
- Chiang, Y.M. Properties of analytic functions with small Schwarzian derivative. Complex Var. Theory Appl. 1994, 25, 107–118. [Google Scholar] [CrossRef]
- Gao, C. Fekete-Szego problem for strongly Bazilevič functions. Northeast Math. J. 1996, 12, 469–474. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).