Properties of Statistical Depth with Respect to Compact Convex Random Sets: The Tukey Depth

Abstract

We study a statistical data depth with respect to compact convex random sets, which is consistent with the multivariate Tukey depth and the Tukey depth for fuzzy sets. In addition, it provides a different perspective to the existing halfspace depth with respect to compact convex random sets. In studying this depth function, we provide a series of properties for the statistical data depth with respect to compact convex random sets. These properties are an adaptation of properties that constitute the axiomatic notions of multivariate, functional, and fuzzy depth-functions and other well-known properties of depth.

1. Introduction

In some real cases, statistical data appear in the form of sets, for instance, in the form of compact convex sets. Examples can be found in datasets related to health, such as the range of blood pressure over a day [1], or related to sport measures, such as the range of weights and heights of a soccer team [2]. Thanks to these phenomena having a convex compact set nature, it is possible to use some good properties of convex compact sets, for instance the existence of support functions. This type of statistical data is studied by the theory of random sets, which, from a statistical point of view, models observed phenomena that are sets rather than points in ${\mathbb{R}}^p$, as in multivariate statistics, or functions, as in functional data analysis. Thus, a random set is a generalization of a random variable: it is a set-valued random variable. A random set can also be understood as a simplification of a fuzzy random variable, as the $\alpha$-levels of a fuzzy set are nested compact sets. The literature about random sets contains well-established theoretical results [3], some of which are generalizations to random sets of classical statistical results, for instance, the strong law of large numbers [4]. Statistical methods are also part of the development of the area of compact convex random sets, such as proposing linear regression methods [5] or the median of a random interval [6]. Recent literature also includes theoretical results, such as results about the intersection of random sets [7], and applications, such as underwater sonar images [8].

Statistical depth functions have become a very useful tool in non-parametric statistics. Nowadays, depth functions are applied in different fields of statistics, such as clustering and classification [9] or real data analysis [10,11]. Given a distribution $\mathbb{P}$ in a space, a depth function, $D(·;\mathbb{P})$, orders the elements in the space with respect to $\mathbb{P}$. Roughly speaking, statistical depth functions measure how close an element is to a data cloud, in the sense that, if we move the element to the center of the cloud, its depth increases, and, if we move it out of the center, its depth decreases. Assuming it is unique, this center is the center of symmetry if the distribution is symmetric for a particular notion of symmetry. For multivariate spaces, there are notions of symmetry widely used in the literature: central, angular [12], and halfspace symmetry [13]. Notions of symmetry specific for functional [14] and fuzzy spaces [15] are, however, quite recent.

Formally, an axiomatic definition of the depth function for the multivariate case was proposed by Zuo and Serfling [13]. According to this definition, a depth function, $D(·;\mathbb{P})$, satisfies the following properties. To introduce them, let X be a random variable with distribution $\mathbb{P}$ on ${\mathbb{R}}^n,$ ${\mathcal{M}}_{n\times n}(\mathbb{R})$ be the space of $n\times n$ matrices with entries in $\mathbb{R}$, and $\parallel ·\parallel$ be the Euclidean norm. Abusing the notation, we indistinctly write $D(·;X)$ and $D(·;\mathbb{P}).$

M1.

Affine invariance. A depth function does not depend on the coordinate system, that is, for any non-singular $M\in {\mathcal{M}}_{n\times n}(\mathbb{R})$ and $b\in {\mathbb{R}}^n$, $D(x;X)=D(Mx+b;MX+b)$.

M2.

Maximality at center. If the distribution $\mathbb{P}$ has a uniquely defined center of symmetry, for a certain notion of symmetry $D(·;X)$ is maximized at it.

M3.

Monotonicity relative to the deepest point. Let $x_0\in {\mathbb{R}}^n$ be a point of maximal depth. Then, for any $x\in {\mathbb{R}}^n$, $D((1-\lambda )x_0+\lambda x;X)\ge D(x;X)$ for all $\lambda \in [0,1]$.

M4.

Vanishing at infinity. The limit of $D(x;X)$ goes to 0, as the limit of $\parallel x\parallel$ goes to infinity.

Formal axiomatic definitions of a depth function were later provided in the functional [16] and fuzzy settings [15,17].

The first instance of a depth function was proposed prior to the axiomatic definitions. It is the Tukey depth, an instance provided in 1975 by Tukey [18] for multivariate data, which is still the most well-known depth function. It is also known as halfspace depth, as it computes the infimum of the probabilities of closed halfspaces, which contain the point at which the depth function is evaluated. That is:

$$HD(x;\mathbb{P}):=inf\{\mathbb{P}(H):\mathrm{H}\mathrm{is}\mathrm{a}\mathrm{closed}\mathrm{halfspace}\mathrm{and}x\in H\}.$$

(1)

Zuo and Serfling [13] proved that $HD$ satisfies M1-M4, and, therefore, it is a statistical depth function. We emphasize the satisfaction of the axioms, because it is customary in the statistical depth community not to consider the axioms as cut-off, regarding a function as a depth function, even when all the axioms are not satisfied in their entirety.

Since Tukey coined the term in 1975, many other instances of depth functions have been proposed, and their use in statistics has grown considerably. Some commonly used depth functions are the simplicial depth, proposed by Liu [12]; the spatial depth, proposed by Serfling [19]; and the random Tukey depth, proposed by Cuesta-Albertos and Nieto-Reyes [20], which, being based on random projections, is a computationally effective approximation of the Tukey depth. The spatial and random Tukey depth functions can be applied in both multivariate and functional spaces [21,22]. However, the random Tukey depth does not satisfy the axiomatic definition of a functional depth [16], which only the metric depth [14] has yet been proven to satisfy. It is worth noting that the spatial and random Tukey depth functions were introduced before the functional axiomatic definition in [16]. Furthermore, while the Tukey depth has not yet being defined in functional spaces, it has being generalized to the fuzzy setting and proved to satisfy the axiomatic definitions in that setting [15,23].

The aim of this paper is to propose some desirable properties of depth with respect to compact convex random sets, which can be considered to be an axiomatic definition for this setting. Some of these properties are an adaptation for compact convex sets of those proposed in González-De La Fuente et al. [15] for fuzzy data. The properties are also largely inspired by the multivariate definition [13] and, in addition, by the functional one [16], because the set of compact convex sets can be considered to be a metric space by using the Hausdorff distance, for instance. In order to test the viability of those properties, with a generalization of halfspaces suitable for the space of compact convex sets, we present an adaptation of Tukey depth and show that almost all of them are satisfied. These definitions of halfspace and Tukey depth can be regarded as stemming naturally from their corresponding multivariate definitions and, in addition, are a particular case of their fuzzy analogs [15]. Furthermore, we show that the definition of Tukey depth with respect to compact convex random sets coincides with that derived recently in Cascos et al. [24], which does not make an explicit use of halfspaces in its definition. The advantage of using our proposal is that it helps in proving some desirable properties of the Tukey depth, for instance the monotonicity relative to the deepest point (see proof of Proposition 3). In addition, it is clear that our proposal is a natural generalization of the multivariate halfspace depth, because it generalizes the concept of halfspace to the set of subsets of ${\mathbb{R}}^p$. Moreover, we also show that the Tukey depth, with respect to compact convex random sets, can be rewritten in terms of the multivariate halfspace depth of the support function of compact convex sets.

The paper is organized as follows. The background about compact convex random sets is contained in Section 2. The definition of the Tukey depth with respect compact convex random sets is in Section 3, together with its relationships with and equivalences to other definitions. Section 4 presents and studies the properties of depth with respect to compact convex random sets and their satisfaction by the Tukey depth with respect to compact convex random sets. Section 5 includes a real-data analysis of compact convex sets in ${\mathbb{R}}^3.$ The paper concludes with some final remarks in Section 6.

2. Preliminaries on Compact Convex Random Sets

Let us denote using ${\mathcal{K}}_c({\mathbb{R}}^p)$ the set of non-empty compact convex sets of ${\mathbb{R}}^p$. In the case $p=1$, the elements of ${\mathcal{K}}_c(\mathbb{R})$ are intervals of the form $[a,b]$ with $a\le b$. For any $K\in {\mathcal{K}}_c({\mathbb{R}}^p),$ its support function $s_K:{\mathbb{S}}^{p-1}\to \mathbb{R}$ is defined by

$$s_K(u):=\underset{k\in K}{sup}⟨k,u⟩,$$

where $⟨·,·⟩$ denotes the usual dot product, ${\mathbb{S}}^{p-1}:=\{x\in {\mathbb{R}}^p:\parallel x\parallel =1\}$ is the unit sphere, and $\parallel ·\parallel$ is the Euclidean norm.

Let $(\Omega ,\mathcal{A},\mathbb{P})$ be a probability space. A map

$$\Gamma :\Omega \to {\mathcal{K}}_c({\mathbb{R}}^p)$$

is called a compact convex random set if

$$\{\omega \in \Omega :\Gamma (\omega )\cap K\ne \varnothing \}\in \mathcal{A}$$

for all $K\in {\mathcal{K}}_c({\mathbb{R}}^p)$ [25]. Himmelberg [26] proved the Fundamental Measurability Theorem, which is useful to prove that $s_{\Gamma }(u)$ is a real random variable for all $u\in {\mathbb{S}}^{p-1}$. As in the Euclidean space, in ${\mathcal{K}}_c({\mathbb{R}}^p)$ there exists a predominant distance, the Hausdorff metric. The Hausdorff distance between $K\in {\mathcal{K}}_c({\mathbb{R}}^p)$ and $L\in {\mathcal{K}}_c({\mathbb{R}}^p)$ is

$$d_{\mathcal{H}}(K,L):=max\{\underset{k\in K}{sup}\underset{l\in L}{inf}\parallel k-l\parallel ,\underset{l\in L}{sup}\underset{k\in K}{inf}\parallel k-l\parallel \},$$

which can be expressed in terms of their support function (e.g., [27]) as

$$d_{\mathcal{H}}(K,L)=\underset{u\in {\mathbb{S}}^{p-1}}{sup}|s_K(u)-s_L(u)|.$$

(2)

The Borel measurability with respect to $d_{\mathcal{H}}$ is equivalent to the above-mentioned definition of compact convex random sets.

Some properties of the support functions of the elements of ${\mathcal{K}}_c({\mathbb{R}}^p)$ can be deduced from the properties of the supremum function. For instance, let $K,L\in {\mathcal{K}}_c({\mathbb{R}}^p)$, taking into account that

$$K+L=\{k+l:k\in K,l\in L\}\in {\mathcal{K}}_c({\mathbb{R}}^p),$$

we can conclude that the support function of $K+L$ can be expressed as the sum of the support functions of K and L, that is,

$$s_{K+L}(u)=s_K(u)+s_L(u)$$

for all $u\in {\mathbb{S}}^{p-1}$. It is also possible to define the product of K by a scalar $\gamma \in {\mathbb{R}}^{+}$, as

$$\gamma ·K=\{\gamma k:k\in K\}.$$

Then, it is clear that

$$s_{\gamma ·K}(u)=\gamma ·s_K(u)$$

for all $u\in {\mathbb{S}}^{p-1}$.

3. Halfspaces and Halfspace Depth in ${\mathcal{K}}_{\mathit{c}}({\mathbb{R}}^{\mathit{p}})$

As is observable from (1), the Tukey depth of a multivariate point x is the infimum of the probability of halfspaces which contain x. However, ${\mathcal{K}}_c({\mathbb{R}}^p)$ is not a linear space. In this section, we define generalized halfspaces (simply called halfspaces in the sequel) for ${\mathcal{K}}_c({\mathbb{R}}^p)$ in a natural way from the multivariate case.

Let S be a halfspace of ${\mathbb{R}}^n$. Then, $v\in {\mathbb{R}}^n$ and $b\in \mathbb{R}$ exist, such that

$$S=\{y\in {\mathbb{R}}^n:v^{T}y\le b\}.$$

Taking $u=(1/\parallel v\parallel )v\in {\mathbb{S}}^{p-1}$ and $c=b/\parallel v\parallel$, it is clear that

$$S=\{y\in {\mathbb{R}}^n:u^{T}y\le c\}.$$

Thus, the halfspaces of ${\mathbb{R}}^n$ can be viewed as subsets $S_{u,c}\subseteq {\mathbb{R}}^n$, such that

$$S_{u,c}=\{y\in {\mathbb{R}}^n:u^{T}y\le c\}$$

with $u\in {\mathbb{S}}^{p-1}$ and $c\in \mathbb{R}$. This generalizes naturally to ${\mathcal{K}}_c({\mathbb{R}}^p)$ by using the support function of a set. Thus, we define halfspaces $S_{u,t}^{-},S_{u,t}^{+}\subseteq {\mathcal{K}}_c({\mathbb{R}}^p)$ as

$$S_{u,t}^{-}:=\{K\in {\mathcal{K}}_c({\mathbb{R}}^p):s_K(u)\le t\},$$

(3)

$$S_{u,t}^{+}:=\{K\in {\mathcal{K}}_c({\mathbb{R}}^p):s_K(u)\ge t\},$$

(4)

for all $u\in {\mathbb{S}}^{p-1}$ and $t\in \mathbb{R}$. We explicitly consider both halfspaces because

$$s_K(-u)=-\underset{k\in K}{inf}⟨u,k⟩\ne -s_K(u)$$

with

$$\begin{array}{cc}\hfill S_{u,t}^{+}& \subseteq S_{-u,-t}^{-},\hfill \\ \hfill S_{u,t}^{-}& \subseteq S_{-u,-t}^{+},\hfill \end{array}$$

for all $u\in {\mathbb{S}}^{p-1}$ and $t\in \mathbb{R}$.

Making use of both directions of the inequality that defines the halfspaces, the Tukey depth with respect to a compact convex random set can be defined. Let $\Gamma$ be a compact convex random set. The Tukey depth of$K\in {\mathcal{K}}_c({\mathbb{R}}^p)$ with respect to $\Gamma$ is defined by the function

$$D_{CT}(·;\Gamma ):{\mathcal{K}}_c({\mathbb{R}}^p)\to [0,1]$$

given by

$$D_{CT}(K;\Gamma ):=min\{\underset{\underset{K\in S_{u,t}^{-}}{u\in {\mathbb{S}}^{p-1},t\in \mathbb{R}:}}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-}),\underset{\underset{K\in S_{u,t}^{+}}{u\in {\mathbb{S}}^{p-1},t\in \mathbb{R}:}}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{+})\}.$$

(5)

We indistinctively refer to it as the Tukey depth for compact convex random sets or the Tukey depth with respect to compact convex random sets. It is worth noting that (5) is a particularization for compact convex sets of the Tukey depth for fuzzy sets proposed in [15]; (3) and (4) are of the fuzzy halfspaces proposed there.

In what follows, we operate on (5) to show it coincides with the definition of halfspace depth with respect to compact convex random sets provided in Cascos et al. [24], which does not explicitly use halfspaces. From (3), $K\in S_{u,t}^{-}$ means that $(u,t)$ is a pair such that $s_K(u)\le t$. Thus,

$$S_{u,s_K(u)}^{-}\subseteq S_{u,t}^{-}$$

and, consequently,

$$\mathbb{P}(\Gamma \in S_{u,s_K(u)}^{-})\le \mathbb{P}(\Gamma \in S_{u,t}^{-}).$$

Analogously, from (4),

$$\mathbb{P}(\Gamma \in S_{u,s_K(u)}^{+})\le \mathbb{P}(\Gamma \in S_{u,t}^{+}).$$

Taking the infimum in (5), we can express $D_{CT}$ as

$$D_{CT}(K;\Gamma )=min\{\underset{u\in {\mathbb{S}}^{p-1}}{inf}\mathbb{P}(\Gamma \in S_{u,s_K(u)}^{-}),\underset{u\in {\mathbb{S}}^{p-1}}{inf}\mathbb{P}(\Gamma \in S_{u,s_K(u)}^{+})\}.$$

Making use of the definition of the halfspaces in (3) and (4), we have

$$D_{CT}(K;\Gamma )=min\{\underset{u\in {\mathbb{S}}^{p-1}}{inf}\mathbb{P}(s_{\Gamma }(u)\le s_K(u)),\underset{u\in {\mathbb{S}}^{p-1}}{inf}\mathbb{P}(s_{\Gamma }(u)\ge s_K(u))\},$$

(6)

which coincides with the definition of the halfspace depth proposed by Cascos et al. [24].

Interchanging the minimum and infimum in (6),

$$D_{CT}(K;\Gamma )=\underset{u\in {\mathbb{S}}^{p-1}}{inf}min\{\mathbb{P}(s_{\Gamma }(u)\le s_K(u)),\mathbb{P}(s_{\Gamma }(u)\ge s_K(u))\}.$$

(7)

Then, taking into account (1), we can express the Tukey depth for compact convex random sets in terms of the multivariate halfspace depth in the following way

$$D_{CT}(K;\Gamma )=\underset{u\in {\mathbb{S}}^{p-1}}{inf}HD(s_K(u);s_{\Gamma }(u)).$$

(8)

Sample Halfspace Depth

We define the sample version $D_{CT,n}$ of the Tukey depth for compact convex sets. Let

$$\Gamma :\Omega \to {\mathcal{K}}_c({\mathbb{R}}^p)$$

be a compact convex random set associated with the probabilistic space $(\Omega ,\mathcal{A},\mathbb{P})$ and $X_1,\dots ,X_n$ independent random sets distributed as $\Gamma$. We define the sample version of the Tukey depth $D_{CT,n}$ as

$$D_{CT,n}(K;\Gamma ):=min\{\underset{u\in {\mathbb{S}}^{p-1}}{inf}{\mathbb{P}}_n^u((-\infty ,s_K(u)]),\underset{u\in {\mathbb{S}}^{p-1}}{inf}{\mathbb{P}}_n^u([s_K(u),\infty ))\},$$

(9)

for every $K\in {\mathcal{K}}_c({\mathbb{R}}^p)$, where

$$\begin{array}{cc}\hfill {\mathbb{P}}_n^u((-\infty ,x])& =\frac{1}{n}·\sum _{i=1}^n\mathrm{I}(s_{X_i}(u)\in (-\infty ,x]),\hfill \\ \hfill {\mathbb{P}}_n^u([x,\infty ))& =\frac{1}{n}·\sum _{i=1}^n\mathrm{I}(s_{X_i}(u)\in [x,\infty )),\hfill \end{array}$$

for all $u\in {\mathbb{S}}^{p-1}$ and $x\in \mathbb{R}$. The function $D_{CT,n}$ coincides with the sample version of the halfspace depth proposed by Cascos et al. [24]. Interchanging the minimum and infimum in (9), we also have that

$$D_{CT,n}(K;\Gamma ):=\underset{u\in {\mathbb{S}}^{p-1}}{inf}min\{{\mathbb{P}}_n^u((-\infty ,s_K(u)]),{\mathbb{P}}_n^u([s_K(u),\infty ))\}.$$

(10)

4. Properties of Depth for Compact Convex Sets

In this section, we propose some desirable properties for the depth for compact convex sets. They are mainly based on the properties that constitute the notion of the depth function for multivariate spaces [13], for functional (metric) spaces [16], and for the fuzzy setting [15]. Furthermore, we study whether $D_{CT}$ satisfies them.

Some of these properties parallel the ones considered in [15], and, in certain cases, they follow for a random set $\Gamma$ by applying the corresponding property in [15] to the indicator function $I_{\Gamma }$. However, this application is simplest for the properties whose direct proof is already very simple, which does not support the cost-effectiveness of doing so. In the longer proofs, additional arguments are needed, due, for instance, to the subtlety that the deepest point in the (larger) space of fuzzy sets might conceivably be deeper than the deepest non-fuzzy set. Therefore, the properties referring to deepest points are parallel in wording but might potentially have different content. It can be proved that this does not actually happen, but we also found that direct proofs make the paper more self-contained. Thus we opted for proofs which do not require the reader to be familiar with the specifics of fuzzy sets, by adapting the arguments in [15]. Still, some other properties in this section were not considered in [15].

4.1. Property 1: Affine Invariance

We focus on the M1. property of the multivariate case reported in the introduction. In the case of ${\mathcal{K}}_c({\mathbb{R}}^p)$, the product of $M\in {\mathcal{M}}_{n\times n}(\mathbb{R})$ times $K\in {\mathcal{K}}_c({\mathbb{R}}^p)$ is defined as the compact convex set

$$\begin{array}{c}\hfill M·K=\{M·k:k\in K\}.\end{array}$$

(11)

The affine invariance property that we propose is the following.

(P1.)

Let Γ be a compact convex random set, $D(·;\Gamma ):{\mathcal{K}}_c({\mathbb{R}}^p)\to [0,\infty )$ a function. Then,

$$D(M·K+L;M·\Gamma +L)=D(K;\Gamma ),$$

for all $M\in {\mathcal{M}}_{n\times n}(\mathbb{R})$ non-singular matrix and any $K,L\in {\mathcal{K}}_c({\mathbb{R}}^p)$.

Thus, this property is analogous to the multivariate case. The property in the fuzzy case is different only in that we need the Zadeh’s extension principle [28,29,30] to apply a matrix to a fuzzy set. The property for functional data also differs, since [16] demands isometry invariance. However, note that, in this context, affine invariance actually implies isometry invariance, since, as a result of Gruber and Lettl [31], all isometries of ${\mathcal{K}}_c({\mathbb{R}}^p)$ are of the form $K\mapsto M·K+L$ with M orthogonal.

Proposition 1.

The function $D_{CT}$ satisfies P1.

The following lemma (cf. [15], Proposition 8.2) is used to prove Proposition 1.

Lemma 1.

Let $K\in {\mathcal{K}}_c({\mathbb{R}}^p)$ and $M\in {\mathcal{M}}_{n\times n}(\mathbb{R})$ a non-singular matrix. Then,

$$s_{M·K}(u)=\parallel M^T·u\parallel ·s_K((1/(\parallel M^T·u\parallel ))·M^T·u)$$

for all $u\in {\mathbb{S}}^{p-1}$.

Proof. 

Taking into account (11), it is clear that

$$s_{M·K}(u)=\underset{v\in M·K}{sup}⟨u,v⟩=\underset{k\in K}{sup}⟨u,M·k⟩=\underset{k\in K}{sup}⟨M^T·u,k⟩,$$

for any $u\in {\mathbb{S}}^{p-1}$. In general, $M^T·u$ does not belong to ${\mathbb{S}}^{p-1}$. Thus, normalizing it, we have that

$$\begin{array}{cc}\hfill s_{M·K}(u)=& \underset{k\in K}{sup}⟨\parallel M^T·u\parallel ·\frac{1}{\parallel M^{T}u\parallel }·M^T·u,k⟩=\hfill \\ \hfill & \parallel M^T·u\parallel ·\underset{k\in K}{sup}⟨\frac{1}{\parallel M^T·u\parallel }·M^T·u,k⟩=\parallel M^T·u\parallel ·s_K(\frac{1}{\parallel M^T·u\parallel }·M^T·u).\hfill \end{array}$$

 □

It is clear that, if $M\in {\mathcal{M}}_{n\times n}(\mathbb{R})$ is a non-singular matrix, the map

$$f:{\mathbb{S}}^{p-1}\to {\mathbb{S}}^{p-1}$$

defined by

$$f(u)=(1/\parallel M^T·u\parallel )·M^T·u$$

is bijective. We make use of this to prove Proposition 1.

Proof of Proposition 1.

Using the properties of the support function and Lemma 1, we obtain

$$s_{M·K+L}(u)=\parallel M^T·u\parallel ·s_K(\frac{1}{\parallel M^T·u\parallel }·M^T·u)+s_L(u),$$

for all $u\in {\mathbb{S}}^{p-1}$. From (6), we have that

$$\begin{array}{cc}\hfill & \underset{u\in {\mathbb{S}}^{p-1}}{inf}\mathbb{P}(s_{M·\Gamma +L}(u)\le s_{M·K+L}(u))=\underset{u\in {\mathbb{S}}^{p-1}}{inf}\mathbb{P}(s_{M·\Gamma }(u)\le s_{M·K}(u))=\hfill \\ \hfill & \underset{u\in {\mathbb{S}}^{p-1}}{inf}\mathbb{P}(s_{\Gamma }(\frac{1}{\parallel M^T·u\parallel }·M^T·u)\le s_A(\frac{1}{\parallel M^T·u\parallel }·M^T·u))=\hfill \\ \hfill & \underset{u\in {\mathbb{S}}^{p-1}}{inf}\mathbb{P}(s_{\Gamma }(u)\le s_K(u))\hfill \end{array}$$

where the last equality follows from the fact that f is bijective. □

4.2. Property 2: Maximality at the Center of Symmetry

In this case, the property is the same for multivariate, functional, and fuzzy settings, but for the fact that the notion of symmetry applied has to be defined in the corresponding space. In the multivariate case, several notions of symmetry exist, for instance central, angular, and halfspace symmetry [12,13]. In the functional case, one proved to be topologically valid exists [10,14], while there have been two proposals in the fuzzy setting [15]. To propose a notion of symmetry in ${\mathcal{K}}_c({\mathbb{R}}^p),$ we make use of the central symmetry notion and of the support function of compact convex random sets. A random variable X on ${\mathbb{R}}^p$ is centrally symmetric (or C-symmetric) with respect to $x\in {\mathbb{R}}^p$ if $X-x$ and $x-X$ are equally distributed.

Definition 1.

Let Γ be a compact convex random set. We say that Γ is compact-symmetric with respect to K if $s_{\Gamma }(u)$ is C-symmetric with respect to $s_K(u)$ for all $u\in {\mathbb{S}}^{p-1}$.

We propose the following property.

(P2.)

Let Γ be a compact convex random set which is symmetric (for a certain notion of symmetry) with respect to $K\in {\mathcal{K}}_c({\mathbb{R}}^p)$. Let $D(·;\Gamma ):{\mathcal{K}}_c({\mathbb{R}}^p)\to [0,\infty )$ be a function. Then

$$D(K;\Gamma )=\underset{L\in {\mathcal{K}}_c({\mathbb{R}}^p)}{sup}D(L;\Gamma ).$$

Thus, this property is analogous in the multivariate, functional, and fuzzy cases. The only difference is the notion of symmetry defined for each case. Note that the above defined notion of symmetry for compact convex random sets, which makes use of C-symmetry, is also an adaptation of the F-symmetry [15] of the fuzzy case, based on support functions. It is possible to consider another notion of symmetry for random sets by identifying every set with its support function and considering central symmetry in the function space. However, our notion is more general, which makes it a natural choice.

With the above notion of compact-symmetry, we have the following result.

Proposition 2.

The function $D_{CT}$ satisfies P2.

Proof. 

By hypothesis, let us suppose that $\Gamma$ is compact-symmetric with respect to K. By definition, we have that the real random variable $s_{\Gamma }(u)$ is C-symmetric with respect to $s_K(u)$ for all $u\in {\mathbb{S}}^{p-1}$. This means that

$$s_K(u)\in \mathrm{Med}(s_{\Gamma }(u))$$

for all $u\in {\mathbb{S}}^{p-1}$, where $\mathrm{Med}(·)$ denotes the univariate median. It implies that

$$\mathbb{P}(s_{\Gamma }(u)\le s_K(u))\ge 1/2 \mathrm{and} \mathbb{P}(s_{\Gamma }(u)\ge s_K(u))\ge 1/2.$$

Using the expression of $D_{CT}$ in Equation (6), we have that $D_{CT}(·;\Gamma )$ is maximized in K. □

4.3. Property 3: Monotonicity with Respect to the Center

In the multivariate case [13], this property is understood in an algebraic way, as the convex combinations between the element of maximal depth and another point are considered. As the operations of sum and product by a scalar are defined in ${\mathcal{K}}_c({\mathbb{R}}^p)$, we can propose the same property.

(P3a.)

Let Γ be a compact convex random set and let $K\in {\mathcal{K}}_c({\mathbb{R}}^p)$ maximize $D(·;\Gamma )$. Then,

$$D((1-\lambda )·K+\lambda ·L;\Gamma )\ge D(L;\Gamma )$$

for all $\lambda \in [0,1]$ and $L\in {\mathcal{K}}_c({\mathbb{R}}^p)$.

Additionally, this property is analogous to property P3a. in the definition of semi-linear depth in the fuzzy setting [15].

In the functional (metric) case, a different property was proposed by (Nieto-Reyes and Battey [16], Property P-3.) which explicitly uses the metric in the space. We can see ${\mathcal{K}}_c({\mathbb{R}}^p)$ as a metric space with the Hausdorff metric $d_{\mathcal{H}}$. Thus, another possible property is the following.

(P3b.)

Let Γ be a compact convex random set, d be a metric in ${\mathcal{K}}_c({\mathbb{R}}^p)$, and $K,L,S\in {\mathcal{K}}_c({\mathbb{R}}^p)$ be three sets such that K maximizes $D(·;\Gamma )$ and $d(K,S)=d(K,L)+d(L,S)$. Then,

$$D(L;\Gamma )\ge D(S;\Gamma ).$$

This property is analogous to property P3b. in the definition of geometric depth in the fuzzy setting [15].

For these two possible translations of the multivariate property, we have the following two results.

Proposition 3.

The function $D_{CT}$ satisfies P3a.

Proof. 

Let $\Gamma$ be a compact convex random set, and let $K,L\in {\mathcal{K}}_c({\mathbb{R}}^p)$ be two sets such that K maximizes $D_{CT}(·;\Gamma )$. Using the properties of the support function of a set, we have that

$$s_{(1-\lambda )·K+\lambda ·L}(u)=(1-\lambda )s_K(u)+\lambda s_L(u)$$

for all $u\in {\mathbb{S}}^{p-1}$ and $\lambda \in [0,1]$.

We consider the set

$$\mathbb{K}=\{(u,t)\in {\mathbb{S}}^{p-1}\times \mathbb{R}:(1-\lambda )·K+\lambda ·L\in S_{u,t}^{-}\}.$$

It can be expressed as ${\mathbb{K}}_1\cup {\mathbb{K}}_2\cup {\mathbb{K}}_3$, where

$$\begin{array}{cc}\hfill {\mathbb{K}}_1& =\{(u,t)\in {\mathbb{S}}^{p-1}\times \mathbb{R}:K,L\in S_{u,t}^{-},L\in S_{u,t}^{-}\},\hfill \\ \hfill {\mathbb{K}}_2& =\{(u,t)\in {\mathbb{S}}^{p-1}\times \mathbb{R}:K\in S_{u,t}^{-},L\notin S_{u,t}^{-},(1-\lambda )·K+\lambda ·L\in S_{u,t}^{-}\},\hfill \\ \hfill {\mathbb{K}}_3& =\{(u,t)\in {\mathbb{S}}^{p-1}\times \mathbb{R}:K\notin S_{u,t}^{-},L\in S_{u,t}^{-},(1-\lambda )·K+\lambda ·L\in S_{u,t}^{-}\}.\hfill \end{array}$$

It is clear that they are disjoint sets. Thus, we have that

$$\begin{array}{cc}\hfill & \underset{\underset{(1-\lambda )·K+\lambda ·L\in S_{u,t}^{-}}{u\in {\mathbb{S}}^{p-1},t\in \mathbb{R}:}}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-})=\underset{(u,t)\in \mathbb{K}}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-})=\hfill \\ \hfill & min\{\underset{(u,t)\in {\mathbb{K}}_1}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-}),\underset{(u,t)\in {\mathbb{K}}_2}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-}),\underset{(u,t)\in {\mathbb{K}}_3}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-})\}.\hfill \end{array}$$

(12)

Taking into account that

$${\mathbb{K}}_1,{\mathbb{K}}_2\subseteq \{(u,t)\in {\mathbb{S}}^{p-1}\times \mathbb{R}:K\in S_{u,t}^{-}\}$$

and

$${\mathbb{K}}_3\subseteq \{(u,t)\in {\mathbb{S}}^{p-1}\times \mathbb{R}:L\in S_{u,t}^{-}\},$$

it is obtained that

$$\begin{array}{cc}\hfill \underset{(u,t)\in {\mathbb{K}}_1}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-})& \ge \underset{\underset{K\in S_{u,t}^{-}}{u\in {\mathbb{S}}^{p-1},t\in \mathbb{R}:}}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-})\ge D_{CT}(K;\Gamma ),\hfill \\ \hfill \underset{(u,t)\in {\mathbb{K}}_2}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-})& \ge \underset{\underset{K\in S_{u,t}^{-}}{u\in {\mathbb{S}}^{p-1},t\in \mathbb{R}:}}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-})\ge D_{CT}(K;\Gamma ),\hfill \\ \hfill \underset{(u,t)\in {\mathbb{K}}_3}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-})& \ge \underset{\underset{L\in S_{u,t}^{-}}{u\in {\mathbb{S}}^{p-1},t\in \mathbb{R}:}}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-})\ge D_{CT}(L;\Gamma ).\hfill \end{array}$$

(13)

Using (12) and (13) and taking into account that K maximizes $D_{CT}$, we have that

$$\underset{\underset{(1-\lambda )·K+\lambda ·L\in S_{u,t}^{-}}{u\in {\mathbb{S}}^{p-1},t\in \mathbb{R}:}}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-})\ge D_{CT}(L;\Gamma ).$$

Analogously, we obtain

$$\underset{\underset{(1-\lambda )·K+\lambda ·L\in S_{u,t}^{+}}{u\in {\mathbb{S}}^{p-1},t\in \mathbb{R}:}}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{+})\ge D_{CT}(L;\Gamma ).$$

Thus, $D_{CT}((1-\lambda )·K+\lambda L;\Gamma )\ge D_{CT}(L;\Gamma )$, and $D_{CT}$ satisfies property P3a. □

Proposition 4.

The function $D_{CT}$ does not satisfy P3b with respect to the distance $d_{\mathcal{H}}$.

Proof. 

The proof is by counterexample. Let $(\{{\omega }_1,{\omega }_2\},\mathcal{P}(\{{\omega }_1,{\omega }_2\}),\mathbb{P})$ be a probabilistic space such that

$$\mathbb{P}({\omega }_1)=3/4 \mathrm{and} \mathbb{P}({\omega }_2)=1/4.$$

We consider the compact convex random set $\Gamma :\Omega \to {\mathcal{K}}_c(\mathbb{R})$ defined by

$$\Gamma ({\omega }_1)=[1,2] \mathrm{and} \Gamma ({\omega }_2)=[2,7].$$

It is clear that

$$D_{CT}(\Gamma ({\omega }_1);\Gamma )=3/4,$$

and it is the set which maximizes $D_{CT}$. Let us consider $L=[3,5]$. We have that

$$5=d_{\mathcal{H}}(\Gamma ({\omega }_1),\Gamma ({\omega }_2))=d_{\mathcal{H}}(\Gamma ({\omega }_1),L)+d_{\mathcal{H}}(\Gamma ({\omega }_2),L)=3+2.$$

Moreover,

$$D_{CT}(\Gamma ({\omega }_2);\Gamma )=1/4 \mathrm{and} D_{CT}(L;\Gamma )=\mathbb{P}(s_{\Gamma }(-1)\le s_C(-1))=0.$$

Thus, $D_{CT}$ violates property P3b. □

Notice that the Tukey depth may satisfy Property P3b if the distances between the sets are not measured with the Hausdorff metric, e.g., in the $L^p$-type metrics introduced by Vitale [32].

4.4. Property 4: Vanishing at Infinity

The property in the multivariate case is understood in a geometrical way, considering a sequence ${\left\{x_n\right\}}_n$ such that $\parallel x_n\parallel \to \infty$ [13]. We can also consider a sequence ${\{a+nb\}}_n$ with $a,b\in {\mathbb{R}}^p$, such that $b\ne 0$, and suppose that the sequence of distances diverges. Thus, in this setting, we also propose two possible properties, the first one from an algebraic point of view and the second one taking into account that the set ${\mathcal{K}}_c({\mathbb{R}}^p)$ can be viewed as a metric space using the Hausdorff distance.

(P4a.)

Let Γ be a compact convex random set, and let $K,L\in {\mathcal{K}}_c({\mathbb{R}}^p)$ be two sets such that K maximizes $D(·;\Gamma )$ and $L\ne \left\{0\right\}$. Then,

$$\underset{n}{lim}D(K+n·L;\Gamma )=0.$$

(P4b.)

Let Γ be a compact convex random set, d a metric in ${\mathcal{K}}_c({\mathbb{R}}^p)$, $K\in {\mathcal{K}}_c({\mathbb{R}}^p)$ a set that maximizes $D(·;\Gamma )$ and ${\left\{K_n\right\}}_n$ a sequence of elements of ${\mathcal{K}}_c({\mathbb{R}}^p)$ such that ${lim}_{n}d(K,K_n)=\infty$. Then,

$$\underset{n}{lim}D(K_n;\Gamma )=0.$$

Property P4a. parallels the fourth property of the semi-linear depth for fuzzy sets, while P4b. parallels the fourth property of geometric depth for fuzzy sets.

Concerning those properties, we have the following results.

Proposition 5.

The function $D_{CT}$ satisfies P4a. and P4b. with respect to the distance $d_{\mathcal{H}}$.

The following proposition is used in the proof of Proposition 5 for property P4b.

Proposition 6.

Let ${\left\{K_n\right\}}_n$ be a sequence of elements of ${\mathcal{K}}_c({\mathbb{R}}^p)$ such that ${lim}_n{d}_{\mathcal{H}}(K_n;\left\{0\right\})=\infty$. Then, there exists $u\in {\mathbb{S}}^{p-1}$ such that

$$\underset{n}{lim}{s}_{K_n}(u)=\infty .$$

Proof. 

It is a basic property of the Hausdorff distance that

$$d_{\mathcal{H}}(K_n,\left\{0\right\})=sup\{\parallel x\parallel :x\in K_n\}$$

for all $n\in \mathbb{N}$. The function

$$f_n:K_n\to \mathbb{R}$$

defined by

$$f_n(x)=\parallel x\parallel$$

is a continuous function defined over a compact convex set, thus it attains its maximum on $K_n$, for all $n\in \mathbb{N}$. Let us denote by $x_n$ the point of $K_n$ where $f_n$ attains its maximum for every $n\in \mathbb{N}$. By hypothesis we have that

$$\underset{n}{lim}\parallel x_n\parallel =\infty .$$

It implies that there exists $u\in {\mathbb{S}}^{p-1}$ such that

$$\underset{n}{lim}⟨u,x_n⟩=\infty .$$

By definition of the support function of a compact convex set, we have that

$$⟨u,x_n⟩\le s_{K_n}(u).$$

Thus, ${lim}_n{s}_{K_n}(u)=\infty$. □

Proof of Proposition 5.

 

Property P4a. Let $L\ne \left\{0\right\}$. There exists $u_0\in {\mathbb{S}}^{p-1}$ such that

$$s_L(u_0)\ne 0.$$

Without loss of generality, we assume $s_L(u_0)>0$. Clearly, the sequence

$${\{s_K(u_0)+n·s_L(u_0)\}}_n$$

is such that

$$\underset{n}{lim}{s}_K(u_0)+n·s_L(u_0)=\infty .$$

We have that

$$D_{CT}(K+·L;\Gamma )\le \mathbb{P}(s_{\Gamma }(u_0)\ge s_K(u_0)+n·s_L(u_0)).$$

If we take limits on both sides

$$\underset{n\to \infty }{lim}{D}_{CT}(K+n·L;\Gamma )\le \underset{n\to \infty }{lim}\mathbb{P}(s_{\Gamma }(u_0)\ge s_K(u_0)+n·s_L(u_0))=0.$$

Using Sandwhich’s Rule, we have that ${lim}_n{D}_{CT}(K+n·L;\Gamma )=0$.

Property P4b. As the set K is fixed, the condition

$$\underset{n}{lim}{d}_{\mathcal{H}}(K,K_n)=\infty$$

is equivalent to

$$\underset{n}{lim}{d}_{\mathcal{H}}(K_n,\left\{0\right\})=\infty .$$

From Proposition 6, we have that there exists $u_0\in {\mathbb{S}}^{p-1}$ such that

$$\underset{n}{lim}{s}_{K_n}(u)=\infty .$$

The rest of the proof is analogous to that of Property P4a. □

4.5. Property 5: Upper Semi-Continuity

This property regards a depth as an upper semi-continuous function at every point of its domain. In the multivariate case it is not considered to be a canonical requirement, but continuity properties are studied in different papers, for instance in [13]. This property is considered in the definition of the depth function for functional (metric) spaces [16]. According to [16], a depth $D,$ of a metric space $(\mathbb{E},d)$ with respect to a distribution $\mathbb{P}$ in the space, is upper semi-continuous if, for all $x\in \mathbb{E}$ and for all $\epsilon >0$, there exists $\delta >0$ such that

$$\underset{y:d(x,y)<\delta }{sup}D(y;\mathbb{P})\le D(x;\mathbb{P}).$$

The property has not yet being considered in the fuzzy setting.

(P5.)

Let Γ be a compact convex random set, and d be a metric defined over ${\mathcal{K}}_c({\mathbb{R}}^p)$. The function $D(·;\Gamma )$ is upper semi-continuous with respect to the distance d in the sense that

$$lim\underset{n}{sup}D(K_n;\Gamma )\le D(K;\Gamma )$$

for every set $K\in {\mathcal{K}}_c({\mathbb{R}}^p)$ and every sequence of sets ${\left\{K_n\right\}}_n$ such that $li{m}_{n}d(K,K_n)=0.$

Notice that upper semi-continuity implies that the contours of the depth function are closed sets.

Proposition 7.

The function $D_{CT}$ satisfies P5. with respect to the distance $d_{\mathcal{H}}$.

Proof. 

Let $\Gamma$ be a compact convex random set and $K\in {\mathcal{K}}_c({\mathbb{R}}^p)$ be a set, and let ${\left\{K_n\right\}}_n$ be a sequence of compact convex sets such that

$$\underset{n\to \infty }{lim}{d}_{\mathcal{H}}(K,K_n)=0.$$

We need to prove

$$lim\underset{n}{sup}{D}_{CT}(K_n;\Gamma )\le D_{CT}(K;\Gamma ).$$

From (2),

$$d_{\mathcal{H}}(K,K_n)=\underset{u}{sup}|s_K(u)-s_{K_n}(u)|$$

and then

$$\underset{n\to \infty }{lim}|s_K(u)-s_{K_n}(u)|=0$$

for each $u\in {\mathbb{S}}^{p-1}$. Thus

$$\underset{n\to \infty }{lim}{s}_{K_n}(u)=s_K(u)$$

for every $u\in {\mathbb{S}}^{p-1}$. Without loss of generality (the other case is analogous), assume

$$D_{CT}(K;\Gamma )=\underset{u}{inf}\mathbb{P}(s_K(u)\le s_{\Gamma }(u)).$$

Now, we prove that, for all $u\in {\mathbb{S}}^{p-1}$,

$$U:=\{\omega \in \Omega :\forall k\in \mathbb{N},\exists n\ge k:\omega \in \{s_{K_n}(u)\le s_{\Gamma }(u)\}\}\subseteq \{\omega \in \Omega :s_K(u)\le s_{\Gamma (\omega )}(u)\}.$$

Let $\omega \in U$. There exists a sub-sequence ${\left\{K_{n^{\prime }}\right\}}_n$ of ${\left\{K_n\right\}}_n$ such that

$$s_{K_{n^{\prime }}}(u)\le s_{\Gamma (\omega )}(u)$$

for all $n^{\prime }$. Taking limits,

$$s_K(u)=\underset{n^{\prime }\to \infty }{lim}{s}_{K_{n^{\prime }}}(u)\le s_{\Gamma (\omega )}(u),$$

therefore

$$\omega \in \{\omega \in \Omega :s_K(u)\le s_{\Gamma }(u)\}.$$

By definition, $U={lim\; sup}_n\{s_{K_n}(u)\le s_{\Gamma }(u)\}$. Thus

$$\begin{array}{cc}\hfill D_{CT}(K;\Gamma )& =\mathbb{P}(s_K(u)\le s_{\Gamma }(u))\ge \mathbb{P}(\underset{n}{lim\; sup}\{s_{K_n}(u)\le s_{\Gamma }(u)\})\ge \hfill \\ \hfill & \ge \underset{n\to \infty }{lim\; sup}\mathbb{P}(s_{K_n}(u)\le s_{\Gamma }(u))\hfill \end{array}$$

(14)

where the second inequality is due to the Fatou’s lemma. Taking the infimum on both sides yields

$$\underset{u}{inf}\mathbb{P}(s_K(u)\le s_{\Gamma }(u))\ge \underset{u}{inf}lim\underset{n\to \infty }{sup}\mathbb{P}(s_{K_n}(u)\le s_{\Gamma }(u)).$$

(15)

Since

$$lim\underset{n}{sup}\mathbb{P}(s_{K_n}(u)\le s_{\Gamma }(u))=\underset{n}{inf}\underset{k\ge n}{sup}\mathbb{P}(s_{K_k}(u)\le s_{\Gamma }(u)),$$

it is clear that

$$\begin{array}{cc}\hfill & \underset{u}{inf}\underset{n}{inf}\underset{k\ge n}{sup}\mathbb{P}(s_{K_k}(u)\le s_{\Gamma }(u))\ge \underset{n}{inf}\underset{k\ge n}{sup}\underset{u}{inf}\mathbb{P}(s_{K_k}(u)\le s_{\Gamma }(u))=\hfill \\ \hfill & =lim\underset{n\to \infty }{sup}\underset{u}{inf}\mathbb{P}(s_K(u)\le s_{\Gamma }(u))\ge lim\underset{n\to \infty }{sup}{D}_{CT}(K_n;\Gamma ).\hfill \end{array}$$

(16)

From (14)–(16), $D_{CT}(·;\Gamma )$ is upper semi-continuous. □

4.6. Property 6: Consistency

Another desirable property for depth functions is that the sample version converges to the population counterpart (consistency). This property is a particular case of the weak continuity (as a function of the distribution P) property of the axiomatic functional (metric) notion of depth [16], but it is not part of the axiomatic notions of multivariate and fuzzy depth. However, it is generally studied when an instance of depth function is introduced. To the best of our knowledge, the first time that appeared in the literature for depth functions was in Liu [12].

We propose the following property.

(P6.)

Let Γ be a compact convex random set, $D(·;\Gamma ):{\mathcal{K}}_c({\mathbb{R}}^p)\to [0,\infty )$ a function, and $D_n(·;\Gamma ){\mathcal{K}}_c({\mathbb{R}}^p)\to [0,\infty )$ its sample version. Then, D and $D_n$ satsify

$$\underset{K\in {\mathcal{K}}_c({\mathbb{R}}^p)}{sup}|D(K;\Gamma )-D_n(K;\Gamma )|⟶0,a.s.\left[\mathbb{P}\right].$$

This is a uniform consistency requirement which is satisfied by the Tukey depth, but the uniformity may eventually have to be dropped for other depth functions.

Theorem 2.

The function $D_{CT},$ with $D_{CT,n}$ in (9), satisfies P6.

Proof. 

In terms of measurability, we have that $s_{X_1}(u),\cdots ,s_{X_n}(u)$ is a random sample of the random variable $s_{\Gamma }(u)$ for all $u\in {\mathbb{S}}^{p-1}$. Let us fix $K\in {\mathcal{K}}_c({\mathbb{R}}^p)$. To ease the notation, let us denote

$$F(s_K(u)):=\{\mathbb{P}(s_{\Gamma }(u)\le s_K(u)),\mathbb{P}(s_{\Gamma }(u)\ge s_K(u))\},$$

$$F_n(s_K(u)):=\{{\mathbb{P}}_n^u((-\infty ,s_K(u)]),{\mathbb{P}}_n^u([s_K(u),\infty ))\}.$$

From (7) and (10) and basic properties of the supremum and infimum functions, we have that

$$\begin{array}{cc}\hfill |D_{CT}(K;\Gamma )-D_{CT,n}(K;\Gamma )|& =|\underset{u\in {\mathbb{S}}^{p-1}}{inf}minF(s_K(u))-\underset{u\in {\mathbb{S}}^{p-1}}{inf}min{F}_n(s_K(u))|\hfill \\ \hfill & \le \underset{u\in {\mathbb{S}}^{p-1}}{sup}|minF(s_K(u))-min{F}_n(s_K(u))|.\hfill \end{array}$$

Step 1. Setting

$$\begin{array}{cc}\hfill F^{+}(t,u)& :=\mathbb{P}(s_{\Gamma }(u)\le t)\hfill \\ \hfill F^{-}(t,u)& :=\mathbb{P}(s_{\Gamma }(u)\ge t)\hfill \\ \hfill F_n^{+}(t,u)& :={\mathbb{P}}_n^u((-\infty ,t])\hfill \\ \hfill F_n^{-}(t,u)& :={\mathbb{P}}_n^u([t,\infty ))\hfill \end{array}$$

and applying these again basic properties, we obtain

$$\begin{array}{cc}\hfill |D_{CT}(K;\Gamma )-D_{CT,n}(K;\Gamma )|\le & \underset{u\in {\mathbb{S}}^{p-1}}{sup}max\{|F^{+}(s_K(u),u)-F_n^{+}(s_K(u),u)|,\hfill \\ \hfill & |F^{-}(s_K(u),u)-F_n^{-}(s_K(u),u)|\}.\hfill \end{array}$$

Then

$$\begin{array}{cc}\hfill \underset{K\in {\mathcal{K}}_c({\mathbb{R}}^p)}{sup}& |D_{CT}(K;\Gamma )-D_{CT,n}(K;\Gamma )|\le \hfill \\ \hfill & \le \underset{K\in {\mathcal{K}}_c({\mathbb{R}}^p)}{sup}\underset{u\in {\mathbb{S}}^{p-1}}{sup}max\{|F^{+}(s_K(u),u)-F_n^{+}(s_K(u),u)|,\hfill \\ \hfill & |F^{-}(s_K(u),u)-F_n^{-}(s_K(u),u)|\}\hfill \\ \hfill & \le \underset{u\in {\mathbb{S}}^{p-1}}{sup}\underset{t\in \mathbb{R}}{sup}max\{|F^{+}(t,u)-F_n^{+}(t,u)|,|F^{-}(t,u)-F_n^{-}(t,u)|\}.\hfill \end{array}$$

The Dvoretzky–Kiefer–Wolfowitz inequality ([33], Corollary 1) gives, for each $u\in {\mathbb{S}}^{p-1}$ and $\epsilon >0$,

$$P(\underset{t\in \mathbb{R}}{sup}|F^{+}(t,u)-F_n^{+}(t,u)|>\epsilon )\le 2exp\{-2{\epsilon }^{2}n\}$$

and there easily follows

$$P(\underset{t\in \mathbb{R}}{sup}|F^{-}(t,u)-F_n^{-}(t,u)|>\epsilon )\le 2exp\{-2{\epsilon }^{2}n\}.$$

Since the bound is independent of u, that implies

$$P(\underset{u\in {\mathbb{S}}^{p-1}}{sup}\underset{t\in \mathbb{R}}{sup}max\{|F^{+}(t,u)-F_n^{+}(t,u)|,|F^{-}(t,u)-F_n^{-}(t,u)|\}>\epsilon )\le 4exp\{-2{\epsilon }^{2}n\}$$

which, by the arbitrariness of $\epsilon$, establishes

$$\underset{u\in {\mathbb{S}}^{p-1}}{sup}\underset{t\in \mathbb{R}}{sup}max\{|F^{+}(t,u)-F_n^{+}(t,u)|,|F^{-}(t,u)-F_n^{-}(t,u)|\}\to 0$$

in probability.

Step 2. To prove almost sure convergence, we rewrite the supremum in terms of an empirical process. Taking

$$\mathcal{F}=\{{\varphi }_{t,u}^{+},{\varphi }_{t,u}^{-}\mid (t,u)\in \mathbb{R}\times {\mathbb{S}}^{p-1}\},$$

where ${\varphi }_{t,u}^{+},{\varphi }_{t,u}^{-}:\Omega \to \mathbb{R}$ are given by

$${\varphi }_{t,u}^{+}(\omega )=I_{(-\infty ,t](s_{\Gamma (\omega )})},{\varphi }_{t,u}^{-}(\omega )=I_{[t,\infty )(s_{\Gamma (\omega )})},$$

we have

$$\underset{u\in {\mathbb{S}}^{p-1}}{sup}\underset{t\in \mathbb{R}}{sup}max\{|F^{+}(t,u)-F_n^{+}(t,u)|,|F^{-}(t,u)-F_n^{-}(t,u)|\}=\underset{\varphi \in \mathcal{F}}{sup}|E_{P_n}(\varphi )-E_P(\varphi )|,$$

where $P_n$ is the empirical distribution. From ([34], Corollary 3.7.9), the above supremum converges to 0 almost surely because it does so in probability (which was proved in Step 1), and the family $\mathcal{F}$ has a P-integrable measurable envelope, which is obvious since all functions in $\mathcal{F}$ take on values in $[0,1]$. Accordingly, also

$$\underset{K\in {\mathcal{K}}_c({\mathbb{R}}^p)}{sup}|D_{CT}(K;\Gamma )-D_{CT,n}(K;\Gamma )|⟶0,\mathrm{a}.\mathrm{s}.\left[\mathbb{P}\right].$$

 □

4.7. Property 7: Convexity of the Contours

This property is not part of any of the existing axiomatic notions of statistical depth. However, it has been commonly studied in the literature since it first appeared in Donoho and Gasko [35]. In addition, Serfling [36], which focuses on multivariate properties, lists it as a desirable property.

The set ${\mathcal{K}}_c({\mathbb{R}}^p)$ is endowed with the operation’s sum and product by a scalar. Thus, given $U\subseteq {\mathcal{K}}_c({\mathbb{R}}^p)$, we can say that U is a convex set if

$$(1-\lambda )·K+\lambda ·L\in U$$

for every pair of sets $K,L\in U$ and for all $\lambda \in [0,1]$. We propose the following property.

(P7.)

Let Γ be a compact convex random set and $D(·;\Gamma ):{\mathcal{K}}_c({\mathbb{R}}^p)\to [0,\infty )$ a function. Then, the set

$$D_{\alpha }:=\{K\in {\mathcal{K}}_c({\mathbb{R}}^p):D(K;\Gamma )\ge \alpha \}\subseteq {\mathcal{K}}_c({\mathbb{R}}^p)$$

is convex for every $\alpha \in [0,1]$.

The next result states that the function $D_{CT}$ satisfies the above property, that is, the $\alpha$-contours of $D_{CT}$ are convex subsets of ${\mathcal{K}}_c({\mathbb{R}}^p)$.

Theorem 3.

The function $D_{CT}$ satisfies P7.

Proof. 

Let us fix $\alpha \in [0,1]$, $K,L\in D_{\alpha }$, and $\lambda \in [0,1]$. The aim is to prove

$$(1-\lambda )·K+\lambda ·L\in D_{\alpha }.$$

For that, we follow the same idea of the proof of Proposition 3. By the definition of Tukey depth,

$$D_{CT}((1-\lambda )·K+\lambda ·L;\Gamma )=min\{\underset{\underset{(1-\lambda )·K+\lambda ·L\in S_{u,t}^{-}}{u\in {\mathbb{S}}^{p-1},t\in \mathbb{R}:}}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-}),\underset{\underset{(1-\lambda )·K+\lambda ·L\in S_{u,t}^{+}}{u\in {\mathbb{S}}^{p-1},t\in \mathbb{R}:}}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{+})\}.$$

We now prove that

$$\underset{\underset{(1-\lambda )·K+\lambda ·L\in S_{u,t}^{-}}{u\in {\mathbb{S}}^{p-1},t\in \mathbb{R}:}}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-})\ge \alpha .$$

As in the proof of Proposition 3, we define the following sets

$$\begin{array}{cc}\hfill \mathbb{K}& :=\{(u,t)\in {\mathbb{S}}^{p-1}\times \mathbb{R}:(1-\lambda )·K+\lambda ·K\in S_{u,t}^{-}\},\hfill \\ \hfill {\mathbb{K}}_1& :=\{(u,t)\in {\mathbb{S}}^{p-1}\times \mathbb{R}:K,L\in S_{u,t}^{-},L\in S_{u,t}^{-}\},\hfill \\ \hfill {\mathbb{K}}_2& :=\{(u,t)\in {\mathbb{S}}^{p-1}\times \mathbb{R}:K\in S_{u,t}^{-},L\notin S_{u,t}^{-},(1-\lambda )·K+\lambda ·L\in S_{u,t}^{-}\},\hfill \\ \hfill {\mathbb{K}}_3& :=\{(u,t)\in {\mathbb{S}}^{p-1}\times \mathbb{R}:K\notin S_{u,t}^{-},L\in S_{u,t}^{-},(1-\lambda )·K+\lambda ·L\in S_{u,t}^{-}\}.\hfill \end{array}$$

It is clear that

$$\underset{(u,t)\in \mathbb{K}}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-})=min\{\underset{(u,t)\in {\mathbb{K}}_1}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-}),\underset{(u,t)\in {\mathbb{K}}_2}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-}),\underset{(u,t)\in {\mathbb{K}}_3}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-})\}.$$

Taking into account (13) and the fact that $D_{CT}(K;\Gamma ),D_{CT}(L;\Gamma )\ge \alpha$, we have that

$$\underset{(u,t)\in {\mathbb{K}}_i}{inf}\mathbb{P}(\Gamma \in S_{u,t}^{-})\ge \alpha$$

for every $i\in \{1,2,3\}$. The case with $S_{u,t}^{+}$ is conducted analogously. Thus,

$$D_{CT}((1-\lambda )·K+\lambda ·L;\Gamma )\ge \alpha$$

and $D_{CT}{(·;\Gamma )}_{\alpha }$ is a convex set. □

5. Real-Data Application

There are many examples of real interval-valued data. We comment here on some examples that are present in different fields of science where the elements of the dataset are in ${\mathcal{K}}_c({\mathbb{R}}^p)$ with $p>1.$ One of these examples is the Greek wines dataset [37], a real dataset with elements in the space ${\mathcal{K}}_c({\mathbb{R}}^{24})\times {\mathbb{R}}^7.$ There, measures of some properties of Greek wines are studied. They include interval-valued variables, such as the mineral ion concentration, the phenol concentrations, or the anthocyanin concentration, and numerical values, such as astringency, sweetness, or acidity.

Another example of compact and convex random sets is about measures related to some tree species [38]. In particular, the maximum and minimum values of the volume of the trunk and of the height of the tree species are measured. Thus, the resulting data are rectangles in ${\mathbb{R}}^2.$ A third dataset is of compact convex square data related to unemployment in Portugal [39]. It contains measurements of the unemployment period and the period of activity before unemployment for some patients.

The rest of this section is dedicated to computing the Tukey depth of a real dataset made of compact convex sets in ${\mathbb{R}}^3,$ studying the elements of minimum and maximum depth, and comparing this last one with the Aumann mean and the trimmed Aumann mean.

5.1. Dataset

The dataset studied in what follows is a cardiology dataset comprised of three-dimensional cuboids with the ranges over a day of pulse rate, systolic blood pressure, and diastolic blood pressure of 59 patients. It was collected in 1997 by the Nephrology Unit of the Hospital Valle del Nalón in Langreo, Spain, and it has been applied before in the literature, see, for instance, [40]. For the sake of illustration, the dataset is graphically represented in Figure 1, and part of it is included in Table 1.

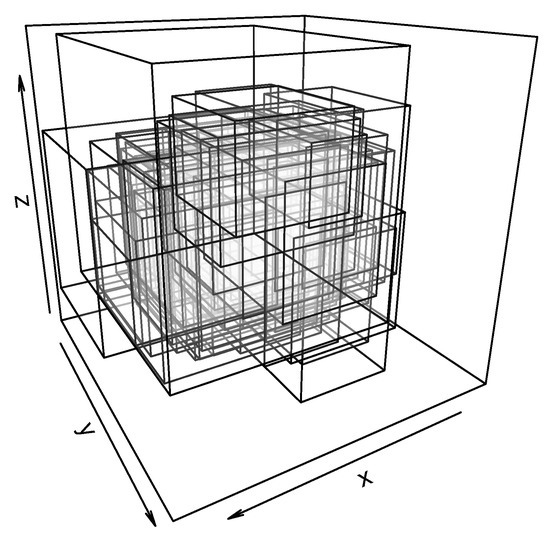
Figure 1. Representation of the cardiology three-dimensional cuboid dataset. The x-axes represent, for each patient, the range of the blood pulse over a same day, the y-axes the range of the systolic blood pressure over the same day, and the z-axes the range of the diastolic blood pressure over the same day. There are a total of 59 patients, with one cuboid per patient.

Table 1. Cardiology three-dimensional cuboid dataset for some patients. Columns 2 and 6, named Pulse, contain the range of blood pulse over a day for each patient, labelled by an identification number (ID) in columns 1 and 5. Columns 3 and 7, named Systolic, provide the range of systolic blood pressure over the same day per patient. Columns 4 and 8, named Diastolic, display the range of diastolic blood pressure over the same day per patient.

ID	Pulse	Systolic	Diastolic	ID	Pulse	Systolic	Diastolic
1	$58–90$	$118–173$	$63–102$	31	$52–78$	$119–212$	$47–93$
2	$47–68$	$104–161$	$71–118$	32	$55–84$	$122–178$	$73–105$
…	…	…	…	…	…	…	…
28	$71–121$	$113–176$	$57–95$	58	$56–97$	$92–173$	$45–107$
29	$68–91$	$114–186$	$46–103$	59	$37–86$	$83–140$	$45–91$
30	$62–100$	$145–210$	$100–136$

From Table 1 we can observe that the dataset consists of 59 rectangular cuboids, in ${\mathbb{R}}^3$; one per patient. We denote each cuboid by

$$C_i:=[m{P}_i,M{P}_i]\times [m{S}_i,M{S}_i]\times [m{D}_i,M{D}_i]$$

for $i=1,\dots ,59.$ There,

• $[m{P}_i,M{P}_i]$ denotes the range of blood pulse over a day of patient $i,$ with $m{P}_i$ being the minimal value and $M{P}_i$ the largest,
• $[m{S}_i,M{S}_i]$ the range of systolic blood pressure over the same day of patient i and
• $[m{D}_i,M{D}_i]$ the same but for diastolic blood pressure.

As observable from Table 1,

$$C_1=[58,90]\times [118,173]\times [63,102]$$

(17)

for instance. Each cuboid $C_i$ is also represented by its eight vertices, which are points in ${\mathbb{R}}^3.$ With the above notation, these vertices are

$$\begin{array}{cc}\hfill & (m{P}_i,m{S}_i,m{D}_i),(m{P}_i,m{S}_i,M{D}_i),(m{P}_i,M{S}_i,m{D}_i),(m{P}_i,M{S}_i,M{D}_i),\hfill \\ \\ \hfill & (M{P}_i,m{S}_i,m{D}_i),(M{P}_i,m{S}_i,M{D}_i),(M{P}_i,M{S}_i,m{D}_i)\mathrm{and}(M{P}_i,M{S}_i,M{D}_i).\hfill \end{array}$$

5.2. Tukey Depth Computation

Let us denote by $\mathcal{T}$ the compact convex random set corresponding to the empirical distribution of ${\left\{C_i\right\}}_{i=1}^{59}$; that is, each cuboid has the probability given by its relative frequency in the dataset, in our case $1/59$. Additionally, let us denote using

$${\mathcal{V}}_1,\dots ,{\mathcal{V}}_8$$

the multivariate random variables corresponding to the empirical distribution associated with

$$\begin{array}{cc}\hfill & {\left\{(m{P}_i,m{S}_i,m{D}_i)\right\}}_{i=1}^{59},{\left\{(m{P}_i,m{S}_i,M{D}_i)\right\}}_{i=1}^{59},{\left\{(m{P}_i,M{S}_i,m{D}_i)\right\}}_{i=1}^{59},\hfill \\ \\ \hfill & {\left\{(m{P}_i,M{S}_i,M{D}_i)\right\}}_{i=1}^{59},{\left\{(M{P}_i,m{S}_i,m{D}_i)\right\}}_{i=1}^{59},{\left\{(M{P}_i,m{S}_i,M{D}_i)\right\}}_{i=1}^{59},\hfill \\ \\ \hfill & {\left\{(M{P}_i,M{S}_i,m{D}_i)\right\}}_{i=1}^{59}\mathrm{and}{\left\{(M{P}_i,M{S}_i,M{D}_i)\right\}}_{i=1}^{59},\mathrm{respectively}.\hfill \end{array}$$

To compute the Tukey depth of each cuboid in the dataset, it suffices to calculate the minimum of the multivariate Tukey depth in ${\mathbb{R}}^3$ of each vertex of the cuboid. Thus, given a cuboid $C_i$, its Tukey depth with respect to $\mathcal{T}$ is

$$\begin{array}{cc}\hfill D_{CT}(C_i,\mathcal{T})=min\{& HD((m{P}_i,m{S}_i,m{D}_i);{\mathcal{V}}_1),HD((m{P}_i,m{S}_i,M{D}_i);{\mathcal{V}}_2),\hfill \\ \hfill \\ \hfill & HD((m{P}_i,M{S}_i,m{D}_i);{\mathcal{V}}_3),HD((m{P}_i,M{S}_i,M{D}_i);{\mathcal{V}}_4)\hfill \\ \\ \hfill & HD((M{P}_i,m{S}_i,m{D}_i);{\mathcal{V}}_5),HD((M{P}_i,m{S}_i,M{D}_i);{\mathcal{V}}_6)\hfill \\ \\ \hfill & HD((M{P}_i,M{S}_i,m{D}_i);{\mathcal{V}}_7),HD((M{P}_i,M{S}_i,M{D}_i);{\mathcal{V}}_8)\},\hfill \end{array}$$

where $HD(x;\mathcal{V})$ denotes the multivariate halfspace depth of $x\in {\mathbb{R}}^3$ with respect to $\mathcal{V}.$

Table 2 provides the obtained depth values for each element in the dataset, that is, the values ${\left\{D_{CT}(C_i;\mathcal{T})\right\}}_{i=1}^{59}$. Taking into account these values, we have that the element $C_1$ in (17) has the maximum depth, it is the deepest one, and the elements in the following set have minimum depths

$$\begin{array}{cc}\hfill \{& C_2,C_3,C_4,C_6,C_9,C_{10},C_{12},C_{13},C_{15},C_{17},C_{19},C_{20},C_{23},C_{24},C_{25},C_{27},C_{28},C_{29},\hfill \\ \\ & C_{30},C_{31},C_{34},C_{35},C_{38},C_{39},C_{40},C_{41},C_{42},C_{44},C_{49},C_{50},C_{51},C_{53},C_{55},C_{56},C_{58},C_{59}\}.\hfill \end{array}$$

(18)

Table 2. Tukey depth value of each element in the cardiology three-dimensional cuboid dataset.

ID	Depth Value	ID	Depth Value
1	0.15254	31	0.01694
2	0.01694	32	0.06779
3	0.01694	33	0.05084
4	0.01694	34	0.01694
5	0.03389	35	0.01694
6	0.01694	36	0.03389
7	0.08474	37	0.03389
8	0.03389	38	0.01694
9	0.01694	39	0.01694
10	0.01694	40	0.01694
11	0.05084	41	0.01694
12	0.01694	42	0.01694
13	0.01694	43	0.03389
14	0.13559	44	0.01694
15	0.01694	45	0.08474
16	0.03389	46	0.10169
17	0.01694	47	0.10169
18	0.03389	48	0.08474
19	0.01694	49	0.01694
20	0.01694	50	0.01694
21	0.03389	51	0.01694
22	0.03389	52	0.10169
23	0.01694	53	0.01694
24	0.01694	54	0.03389
25	0.01694	55	0.01694
26	0.10169	56	0.01694
27	0.01694	57	0.03389
28	0.01694	58	0.01694
29	0.01694	59	0.01694
30	0.01694

To display this information, Figure 2 represents the sets of maximum and minimum depth. In particular, the left panel of the Figure represents the five deeper cuboids, with the sets of maximum depth colored in red. Meanwhile, the right panel of the Figure represents the sets with minimum depth in color blue. That is, those in (18). In addition, the right panel of the figure also displays $C_1$, the cuboid with maximum depth, in red. This is completed in order to visualize that the ordering given by the Tukey depth is natural, and the element $C_1$ is the deepest set with respect to the cloud of cuboids.

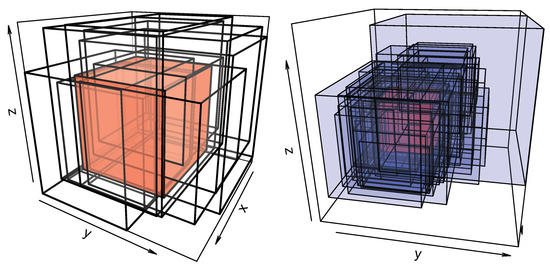
Figure 2. Representation of the sets with maximum and minimum depths. The left panel represents the five sets of maximum depth with the deepest one, $C_1,$ in red. The right panel represents the sets with minimum depth, in (18), and again the set $C_1$ in red.

One may think that it is possible to compute the Tukey depth of each cuboid by considering the variables Pulse, Systolic, and Diastolic separately. Let $\mathcal{P},\mathcal{S}$, and $\mathcal{D}$ denote the compact convex random sets corresponding to the empirical distribution associated with

$${\left\{[m{P}_i,M{P}_i]\right\}}_{i=1}^{59},{\left\{[m{S}_i,M{S}_i]\right\}}_{i=1}^{59}\mathrm{and}{\left\{[m{D}_i,M{D}_i]\right\}}_{i=1}^{59},$$

respectively. Additionally, let us denote by

$$mP,MP,mS,MS,mD\mathrm{and}MD$$

the real random variables corresponding to the empirical distribution associated with

$${\left\{m{P}_i\right\}}_{i=1}^{59},{\left\{M{P}_i\right\}}_{i=1}^{59},{\left\{m{S}_i\right\}}_{i=1}^{59},{\left\{M{S}_i\right\}}_{i=1}^{59},{\left\{m{D}_i\right\}}_{i=1}^{59},\mathrm{and}{\left\{M{D}_i\right\}}_{i=1}^{59},$$

respectively. Given an index $i\in \{1,\dots ,59\}$, the Tukey depth of the i-th interval element with respect to $\mathcal{P},\mathcal{S}$, and $\mathcal{D}$ are

$$\begin{array}{cc}\hfill & D_{CT}([m{P}_i,M{P}_i];\mathcal{P})=min\{HD(m{P}_i;mP),HD(M{P}_i;MP)\},\hfill \\ \hfill \\ \hfill & D_{CT}([m{S}_i,M{S}_i];\mathcal{S})=min\{HD(m{S}_i;mS),HD(M{S}_i;MS)\},\mathrm{and}\hfill \\ \hfill \\ \hfill & D_{CT}([m{D}_i,M{D}_i];\mathcal{D})=min\{HD(m{D}_i;mD),HD(M{D}_i;MD)\}.\hfill \end{array}$$

The element with the maximum depth with respect to $\mathcal{P}$ is the 48-th element, which has a depth value of $0.08474$ with respect to $\mathcal{T}$. The elements with maximum depths with respect to $\mathcal{S}$ and $\mathcal{D}$ are the 28-th and 19-th element, respectively, which have minimum depth values with respect to $\mathcal{T}$. Thus, it is clear that we must consider all three variables simultaneously.

The calculation of the Tukey depth breaks the dataset into an outer layer of 36 patients with depth $1/59$, which envelopes an inner core of 23 patients with higher depth. The depth value $1/59$ means that, taking the support function in a certain direction in ${\mathbb{R}}^3$, the point is separated from the remainder of the data. Since each direction represents a linear combination of all three variables, there is some combination of weights for the variables which distinguishes that patient from all others. That suggests that many different patterns of behavior between the three variables are within the ordinary.

5.3. Aumann Mean

We first compute the Aumann mean, ${\widehat{\mu }}_A$, for the complete dataset. The Aumann mean is a generalization of the real-valued mean that works for compact convex sets. We then compare it with the Aumann mean of the dataset after removing the cuboids with minimum depth, ${\widehat{\mu }}_{tA}.$ The Aumann mean of the complete dataset is

$$\begin{array}{cc}\hfill {\widehat{\mu }}_A=& \left[\frac{1}{59}\sum _{i=1}^{59}m{P}_i,\frac{1}{59}\sum _{i=1}^{59}M{P}_i\right]\times \left[\frac{1}{59}\sum _{i=1}^{59}m{S}_i,\frac{1}{59}\sum _{i=1}^{59}M{S}_i\right]\times \left[\frac{1}{59}\sum _{i=1}^{59}m{D}_i,\frac{1}{59}\sum _{i=1}^{59}M{D}_i\right]\hfill \\ \\ \hfill =& [53.97,95.07]\times [111.83,181.58]\times [58.64,108.25].\hfill \end{array}$$

When we consider the inner core of the dataset by removing the set of cuboids with minimal depth (set in Equation (18)), the Aumann mean becomes

$${\widehat{\mu }}_{tA}=[54.34783,91.47826]\times [112.2174,178.4348]\times [59.82609,107.4783].$$

This is conceptually similar to a trimmed mean (but trims more than half of the sample). The mean values are very similar, meaning that data in the outer layer have a similar average behavior to those in the inner core, and their outlier nature exerts little influence. In that situation, one would expect that the deepest point to be close to those means, and indeed the maximal depth in the sample is reached at $C_1=[58,90]\times [118,173]\times [63,102]$, which is also very similar albeit the intervals are a bit narrower.

We have that both means, ${\widehat{\mu }}_A$ and ${\widehat{\mu }}_{tA},$ have similar values in every variable. This can be explained by the fact that some linear combination between the elements with minimal depth exists that distinguishes them from the rest of the dataset, but this does not affect the mean. Note that the set with maximal depth, $C_1=[58,90]\times [118,173]\times [63,102]$, is also very similar to the above means.

6. Discussion

Considering the properties studied in the literature for depth functions, we propose nine different properties for depth functions with respect to compact convex random sets. They are:

• P1. Affine invariance,
• P2. Maximality at the center of symmetry,
• P3a. Monotonicity with respect to the center in an algebraic way,
• P3b. Monotonicity with respect to the center in relation to the associated distance (in a geometric way),
• P4a. Vanishing at infinity in an algebraic way,
• P4b. Vanishing at infinity in a geometric way,
• P5. Upper semi-continuity,
• P6. Consistency, and
• P7. Convexity of the contours.

It is clear that all of them are desirable properties for a depth function of compact convex sets. However, not all of them have to be part of an axiomatic definition. For instance, it seems appropriate to have either P3a. and P4a. or P3b. and P4b. At the same time, P7., although important, does not belong to any of the existing axiomatic definitions, and P5. and a general case of P6. only belong to the functional (metric) axiomatic definition of statistical depth.

Taking all of this into account, we propose to consider:

• the algebraic depth of compact convex sets, when properties P1., P2., P3a., and P4a. are satisfied;
• the restricted algebraic depth of compact convex sets, when properties P1., P2., P3a., P4a., P5., P6., and P7. are satisfied;
• the geometric depth of compact convex sets, when properties P1., P2., P3b., and P4b. are satisfied; and
• the restricted geometric depth of compact convex sets, when properties P1., P2., P3b., P4b., P5., P6., and P7. are satisfied.

Note that the algebraic depth can be considered to be an adaptation of the notions of multivariate depth and of semi-linear fuzzy depth. Meanwhile, the geometric depth can be seen as a conversion of the geometric fuzzy depth and the restricted geometric depth as a modification of the functional (metric) depth.

We have studied the satisfaction of the above properties for the Tukey depth of compact convex sets, which is an adaptation of this setting of the multivariate Tukey depth and a simplification of the Tukey for fuzzy sets. It happens that this depth function satisfies all of these properties but for P3b., for which we have provided a counterexample. Thus, the Tukey depth of compact convex sets is a restricted algebraic depth and, in particular, an algebraic depth. However, it is not a geometric depth, and, consequently, neither is it a restricted geometric depth.

Cascos et al. [24] proposed a notion of depth for random closed sets. They require properties P1, P5 (for the Fell topology instead of the Hausdorff metric), and the property that a degenerate random set should assign depth 1 to its only value and 0 to any other random set. Admitting unbounded sets as values leads to some defining properties of depth being hard to adapt; a situation they solve by opting for a minimal list of properties. It is worth mentioning that, in the case of compact convex values, convergence in the Fell topology and in the Hausdorff metric are equivalent ([41], Corollary 3A). Hence, both upper semi-continuity requirements are equivalent for the Tukey depth, and Proposition 7 provides a proof of upper semi-continuity with respect to the Fell topology. Such a proof is missing in [24] on the grounds of it being ‘easy’ (a direct proof without invoking extra facts does not seem to be that easy).