On Some Properties of Signed Cayley Graph S_n

Abstract

We define the signed Cayley graph on Cayley graph $X_n$ denoted by $S_n$, and study several properties such as balancing, clusterability and sign-compatibility of the signed Cayley graph $S_n$. Apart from it we also study the characterization of the canonical consistency of $S_n$, for some n.

1. Introduction

We refer to the standard books of Harary [1] and West [2] for graph theory and for the signed graphs we refer to Zaslavsky [3,4]. All the signed graphs considered in this paper are simple, finite and loopless.

A graph in which every edge receives charges (signs) ‘+’ or ‘−’ is called a signed graph denoted by S (see [5]). Removing all the signs from the edges of a signed graph provides us with its underlying graph, $S^u$, and we use notations $V\left(S^u\right)$ and $E\left(S^u\right)$ for the vertex set and edge set of $S^u$, respectively. Similarly, we employ $V\left(S\right)$ and $E\left(S\right)$ for the vertex set and edge set of S, respectively. For any vertex v in a signed graph S, $d^{+}\left(v\right)$ denotes the positive degree of the vertex v, and $d^{-}\left(v\right)$ denotes the negative degree of the vertex v, due to the positively (negatively) charged edges incident at the vertex v. The negation of a signed graph S is obtained by interchanging the sign of each edge. It is denoted by η(S)

The positive (negative) section of a signed graph S is a maximal edge induced positive (negative) connected subsigned graph of S.

Two signed graphs $S_1$ and $S_2$ are said to be isomorphic if there exists an edge preserving bijection between their underlying graphs $S_1^u$ and $S_1^u$, along with the signs of the corresponding edges.

A positive (negative) cycle is a cycle which contains an even (odd) number of negatively charged edges. A signed graph S is a balanced signed graph if every cycle in S is positive (see [5]).

The Harary’s partition criterion [5] to characterize the balancing property of a signed graph motivated Zaslavsky to give the following lemma;

Lemma 1

([6]). A signed graph in which every cordless cycle is positive is balanced.

The balancing of an algebraic structure has also been worked out in ([7]).

A signed graph S is clusterable if its vertex set can be partitioned into the subsets called clusters, such that the positively charged edge lies in the same subset and the negatively charged edge has its end vertices in different subsets.

Theorem 1

([8]). A signed graph S is clusterable, if and only if, S contains no cycle with exactly one negatively charged edge.

A marked signed graph is an ordered pair $S_{\mu }=(S,\mu )$ where $S=(S^u,\sigma )$; $\sigma :E\left(S^u\right)⟶\{+,-\}$ is a signed graph and $\mu :V\left(S\right)⟶\{+,-\}$ is a function from the vertex set $V\left(S\right)$ onto the set $\{+,-\}$, called marking of S.

A consistent cycle Z in a signed graph S has an even number of ‘-’ marked vertices. A signed graph is consistent if all its cycles are consistent [9].

Particularly, in a signed graph $S=(S^u,\sigma )$, $\sigma$ induces a unique marking ${\mu }_{\sigma }$ defined by

$${\mu }_{\sigma }\left(v\right)=\prod _{e_j\in E_v}\sigma \left(e_j\right),v\in V\left(S\right),$$

called the canonical marking ($\mathcal{C}$-marking) of S, where $E_v$ is the set of edges $e_j$ incident at $v\in V\left(S\right)$ (see [10]).

A cycle Z is $\mathcal{C}$-consistent if it is consistent with respect to $\mathcal{C}$-marking in a signed graph, and the signed graph itself is $\mathcal{C}$-consistent if all its cycles are $\mathcal{C}$-consistent.

Sinha and Acharya in [11] talked about S-consistency. Zaslavsky also independently worked out the consistency of the signed structure (see [12]).

A signed graph is called sign-compatible [10] if it is possible to mark the vertices of the signed graph in such a manner that for every negatively charged edge there are negatively marked vertices on its both ends and for any positively charged edge its ends are not assigned a negative sign-incompatible otherwise.

A signed structure called line signed graph (see [13]) is a derived signed graph where the vertices are the edges of S and two vertices are adjacent whenever they are adjacent edges in S and the sign of this edge is negative, if and only if, both the edges in S are negative and positive otherwise. It is denoted by $L\left(S\right)$ for a signed graph S. If $T\cong L\left(S\right)$ for some signed graphs T and S, then S is said to be the line signed root of T.

Gill [14] defined the structure ×-line signed graph $L_{\times }\left(S\right)$ with $L\left(S^u\right)$ as it’s underlying graph and the edge is negative, if and only if, the product of the charges of both the edges of S are negative. If $T\cong L_{\times }\left(S\right)$ for some signed graphs T and S, then S said to be ×-line signed root of T.

Next, in [15] work about the structure called common-edge signed graph $C_E\left(S\right)$ is pursued.

A unitary Cayley graph $X_n$, where $n\in I^{+}$, I⁺ is set of positive integers, is a graph in which the vertex set is a ring of integers modulo n, $Z_n$. Any two vertices $x_1$ and $x_2$ are adjacent in $X_n$, if and only if, $(x_1-x_2)\in U_n$, where $U_n$ denotes the unit set (see [16]).

The study of unitary Cayley graphs began for finding some insight into the graph representation problem (see [17]) and we can extend it to the signed graphs (see [18]).

Now, we introduce the definition of a signed Cayley graph $S_n$ as follows:

The signed Cayley graph $S_n=(X_n,\sigma )$, where $X_n$ is the Cayley graph, $n\in I^{+}$, is a graph in which the vertex set is a ring of integers modulo n, $Z_n$.

Any two vertices $x_1$ and $x_2$ are adjacent in $X_n$, if and only if, $x_1-x_2$ is in $U_n$, where $U_n$ is a unit set.

For any edge $ab$ in $S_n$,

$$\sigma \left(ab\right)=\left\{\begin{array}{cc}+\hfill & \mathrm{if}a,b\in U_n,\hfill \\ -\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Some examples of signed Cayley graphs $S_n$, $n\ge 2$, can be seen in Figure 1. Throughout the paper, $n\ge 2$.

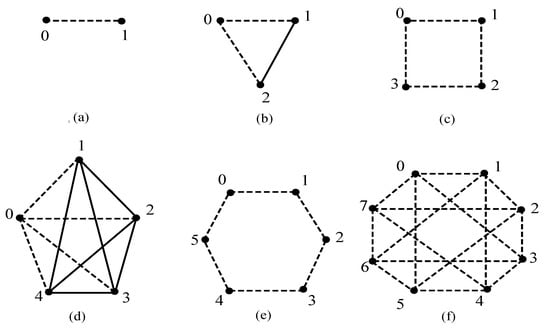
Figure 1. Examples of signed Cayley graphs $S_n$.

2. Some Properties of ${\mathit{S}}_{\mathit{n}}$

2.1. Balancing in $S_n$

The balancing of some derived signed Cayley graphs have been studied in the literature (see [19]). Here we find out the property of balancing for signed Cayley graphs $S_n$, for which the following result, can be used as a tool.

Theorem 2

([20]). The unitary Cayley graph $X_n$, $n\ge 2$, is bipartite, if and only if, n is even.

Sampathkumar [21] gave the following characterization to prove the balancing in a signed graph:

Theorem 3

(Marking Criterion [21]). A signed graph $S=(G,\sigma )$ is balanced, if and only if, there exists a marking μ of its vertices such that each edge $uv$ in S satisfies $\sigma \left(uv\right)=\mu \left(u\right)\mu \left(v\right)$.

Lemma 2.

For the signed Cayley graph $S_n=(X_n,\sigma )$, $S_n$ is a balanced signed graph if for any prime p, $n=p^a$.

Proof. 

Let the signed Cayley graph $S_n=(X_n,\sigma )$, where $n=p^a$ and p is a prime number. Now, let $\mu :V\left(S_n\right)⟶\left\{+,-\right\}$ be a marking such that $\mu \left(u\right)=-$, if $u\in U_n$ and $\mu \left(u\right)=+$, if $u\notin U_n$ for every u in $V\left(S_n\right)$.

Let $\sigma \left(ij\right)=+$, based on the definition of $S_n$, $i,j\in U_n$. Now, by the marking $\mu$, $\mu \left(i\right)=-$, $\mu \left(j\right)=-$ and $\mu \left(i\right)\mu \left(j\right)=+$. Thus,

$$\sigma \left(ij\right)=\mu \left(i\right)\mu \left(j\right)=+$$

Let $ij$ be a negatively charged edge in $S_n$, i.e., $\sigma \left(ij\right)=-$. This leads to three cases:

$\left(a\right)$

$i\notin U_n$ and $j\notin U_n$,

$\left(b\right)$

$i\notin U_n$ and $j\in U_n$,

$\left(c\right)$

$i\in U_n$ and $j\notin U_n$.

Therefore, the difference of i and j is again a multiple of p. Thus, $ij\notin E\left(S_n\right)$. As a result, $\left(a\right)$ is impossible.

Now, suppose $i\notin U_n$ and $j\in U_n$ or vice-versa. Then, by the marking $\mu$, we have $\mu \left(i\right)\mu \left(j\right)=-$, since $\mu \left(i\right)=-\mu \left(j\right)$. Thus,

$$\sigma \left(ij\right)=\mu \left(i\right)\mu \left(j\right)=-$$

The result is true for every edge of $S_n$, for $ij$ being an arbitrary edge of $S_n$. Thus $S_n$ is balanced by Theorem 3. □

Lemma 3.

For signed Cayley graph $S_n=(X_n,\sigma )$, is all-negative signed graph, if n is even.

Proof. 

In the signed Cayley graph $S_n$, where n is even, the elements of $U_n$ are odd numbers. Then for any positively charged edge $ij\in S_n$, $i,j\in U_n$ and i and j are both odd numbers. Since the difference of i and j is an even number, thus, $i-j\notin U_n$, and $ij$ is not an edge in $S_n$. This is a contradiction to the assumption. Hence $S_n$ is all-negative signed graph. □

Theorem 4.

Signed Cayley graph $S_n=(X_n,\sigma )$ is balanced, if and only if, either n is even or n can not be factorized into more than one distinct prime factor, then n is odd.

Proof. 

Necessity: Let signed Cayley graph $S_n=(X_n,\sigma )$ be balanced. If possible, let n be odd and it can be factorized into at least two distinct prime factors, that is, n is equal to $n=p_1^{a_1}{p}_2^{a_2}\dots p_m^{a_m}$, $p_1\ne 2$, $p_1,p_2,\dots ,p_m$ being distinct primes.

Now, $U_n$ contains all the numbers less than $p_1$. So, $p_1-1\in U_n$. Thus, $p_1$ is adjacent with 1 in $X_n$. Now, we claim that $p_1$ and $p_2$ are also adjacent in $X_n$. If possible, suppose $p_1$ and $p_2$ are not adjacent in $X_n$. This shows that $p_2-p_1\notin U_n$. Then, $p_2-p_1$ being multiple of any $p_i$ values, for $i=1,2,\cdots ,m$, let $p_2-p_1$ be a multiple of $p_1$ (say) that is, for some positive integer $\alpha$, we have

$$\begin{array}{cc}\hfill p_2-p_1& =\alpha p_1\hfill \\ \hfill p_2& =p_1+\alpha p_1\hfill \\ \hfill & =(1+\alpha )p_1\hfill \end{array}$$

which is not possible. Thus $p_2-p_1$ is not a multiple of $p_1$. Moreover, $p_2-p_1<p_2<p_3<\cdots <p_m$, i.e., $p_2-p_1$ is not a multiple of any $p_i$ values ∀$i=1,2,\cdots m$. Therefore, $p_1$ and $p_2$ are adjacent in $X_n$. Now, if $p_2$ is adjacent with 1 in $X_n$, there is therefore a cycle

$$Z=(p_1,p_2,1,p_1)$$

in $X_n$. Clearly $p_1$ and $p_2$ do not belong to $U_n$ and $1\in U_n$. Then, Z is all-negative cycle in $S_n$. Thus, Z has a negative sign, which implies that $S_n$ is not balanced. Next, let $p_2$ not be adjacent to 1 in $X_n$, i.e., $p_2-1\notin U_n$. Then, $p_2-1$ is a multiple of any $p_i$ values for $i=1,2,\cdots ,m$ (say $p_1$). Suppose,

$$p_2-1=\alpha p_1$$

(1)

for any positive integer $\alpha$.

Now, $n-p_2\notin U_n$. We claim $n-p_2$ is adjacent with 1, i.e., $n-p_2-1=n-(p_2+1)\in U_n$. If $p_2+1\in U_n$, then $n-(p_2+1)\in U_n$. Suppose $p_2+1\notin U_n$. Then, $p_2+1=\alpha p_i$, $\alpha \in I^{+}$, $i=1,2,\cdots ,m$. Hence, $p_2+1$ is a multiple of $p_1$. Suppose $p_2+1=\beta p_1$. However, from Equation (1), $p_2=\alpha p_1+1$. Thus,

$$\begin{array}{cc}\hfill p_2+1& =\beta p_1\hfill \\ \hfill \alpha p_1+1+1& =\beta p_1\hfill \\ \hfill \alpha p_1+2& =\beta p_1\hfill \\ \hfill \beta p_1-\alpha p_1& =2\hfill \\ \hfill (\beta -\alpha )p_1& =2\hfill \end{array}$$

which is not possible as $p_1$ is at least 3. Thus, $n-p_2-1$ is not a multiple of any $p_i$ values for $i=1,2,\cdots ,m$. Hence, $n-p_2-1\in U_n$, i.e., $n-p_2$ is adjacent with 1 in $X_n$. Now, $n-p_2-p_1=n-(p_2+p_1)$. Clearly, $p_2+p_1$ is not a multiple of any $p_i$ values for $i=1,2,\cdots ,m$. This shows that $p_2+p_1\in U_n$ and $n-(p_2+p_1)\in U_n$. This shows that $n-p_2$ is adjacent with $p_1$ in $X_n$. Thus, we have a cycle

$$Z^{\prime }=(p_1,n-p_2,1,p_1)$$

in $X_n$. Clearly, $p_1$ and $n-p_2$ are not in $U_n$ and $1\in U_n$. Then, by the definition of $S_n$, $Z^{\prime }$ has three negatively charged edges in $S_n$. Thus, this is a contradiction to the hypothesis and so by the contraposition, necessity holds.

Sufficiency: Let n be even. Then, by Lemma 3, $S_n$ is an all-negative signed graph. Moreover, by Theorem 2, $X_n$ is a bipartite graph. Hence, by Lemma 3 and Theorem 2, $S_n$ is balanced.

Next, suppose n is odd and does not have more than one distinct prime factor. Then, by Lemma 2, $S_n$ is balanced. Hence the theorem. □

2.2. Clusterability in $S_n$

Theorem 5.

The signed Cayley graph $S_n=(X_n,\sigma )$ is always clusterable.

Proof. 

Assume that $S_n=(X_n,\sigma )$ is a signed Cayley graph. Let v be a vertex of $S_n$. Now, we define a set $V^{*}\subseteq V\left(S_n\right)$ which contains v and all the vertices $u_i$ of $S_n$ such that $\sigma \left(v{u}_i\right)=+.$ By the definition of $S_n$, it is clear that $u_i$ values and v are in $U_n$. If some $u_i$ values are adjacent, then according to the definition of $S_n$, it is clear that those edges will be positive. Thus, $V^{*}$ contains all the vertices which are in $U_n$. Since $\left|U_n\right|=\varphi \left(n\right)$, remaining vertices are $n-\varphi \left(n\right)=k$ (say) and these vertices are not in $U_n$. There are only negatively charged edges incident on these vertices. Put all these vertices in k partition $V_1,V_2,\cdots ,V_k$. There are only one vertex in each partition. Now, it is clear that all the edges induced by $V^{*}$ are positive. There is no positively charged edge joining $V^{*}$ and any $V_i^{\prime }$s for $i=1,2,\cdots ,k$. Thus, there is no positively charged edge of type $uv$ such that $u\in V^{*}$ and $v\in V_i$ for $i=1,2,\cdots ,k$. Moreover, there is no negatively charged edge of type $xy$ such that $x,y\in V^{*}$. So the vertex set of $S_n$ can be partitioned into subsets such that every positively charged edge joins vertices within the same subset and every negatively charged edge joins the vertices in different subsets. Hence, $S_n$ is clusterable. □

2.3. Sign-Compatibility in $S_n$

Theorem 6

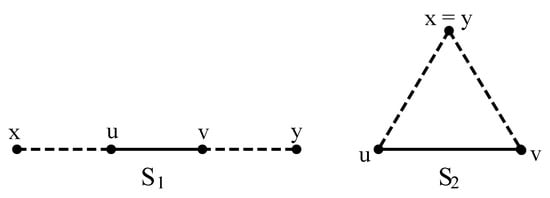
([22]). A signed graph S is sign-compatible, if and only if, S does not contain a sub-signed graph isomorphic to either of the two signed graphs, $S_1$, formed by taking the path $P_4=(x,u,v,y)$ with both the edges $xu$ and $vy$ negative and the edge $uv$ positive, and $S_2$, formed by taking $S_1$ and identifying the vertices x and y (Figure 2).

Figure 2. Two forbidden sub-signed graphs for a sign-compatible signed graph [10].

Theorem 7.

Signed Cayley graph $S_n$, is sign-compatible, if and only if, n is $0(mod2)$.

Proof. 

Suppose signed Cayley graph $S_n$ is sign-compatible. If possible, let n be odd. Since n is odd, $2\in U_n.$ Moreover, 0 is adjacent with 1 and 2 in $S_n$ as $1-0=1$ and $2-0=2$ are in $U_n.$ Additionally, 1 and 2 are adjacent in $S_n$ as $2-1=1$ is in $U_n.$ Consider a triangle $Z=(0,1,2,0)$ in $S_n$. By the definition of $S_n$, Z contains a positively charged edge 12 and two negatively charged edges 01 and 02. This shows that $S_n$ contains a sub-signed graph isomorphic to $S_2$ in Figure 2, a contradiction to sign-compatibility. Hence, n is $0(mod$).

Conversely, suppose n is even. Then, by Lemma 3, $S_n$ is all-negative, hence trivially sign-compatible. This completes the proof. □

Remark 1.

Every line-signed graph is sign-compatible [23].

Next, we discuss the value of n for which $S_n$ is a line-signed graph.

Theorem 8.

The underlying graph $X_n$ of $S_n$ is a line graph, if and only if, $n=4$, or 6, or a prime number.

Proof. 

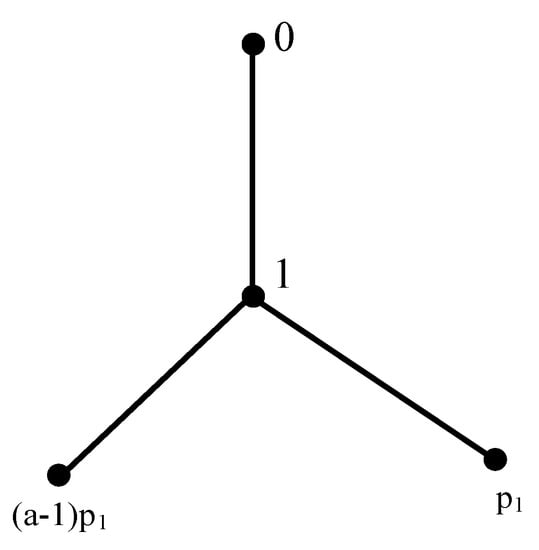
Let the underlying graph $X_n$ of a signed Cayley graph $S_n$ be a line graph. If possible, suppose $n\ne 4,6$ and a prime number. Then, 1 is adjacent with 0 and also with $p_1$, as $p_1-1\in U_n$; $p_1$ being the smallest multiple of n.

Suppose b is some number such that $b{p}_1=n.$ Now,

$$\begin{array}{cc}\hfill (b-1)p_1-1& =b{p}_1-p_1-1\hfill \\ \hfill & =n-p_1-1\hfill \\ \hfill & =n-(p_1+1).\hfill \end{array}$$

Since $p_1+1\in U_n,$ therefore $n-(p_1+1)\in U_n.$ Thus, 1 and $(b-1)p_1$ are adjacent in $X_n.$ Clearly, 0 is not adjacent with $p_1$ and $(b-1)p_1.$ Moreover, $p_1$ and $(b-1)p_1$ are not adjacent in $X_n$ as their subtraction is a multiple of $p_1.$ This shows that $X_n$, has an induced subgraph $K_{1,3}$ shown in Figure 3 which is a forbidden subgraph for a line graph. Thus, $X_n$ is not a line graph [1]. Hence, by contraposition, the condition is satisfied.

Figure 3. Showing $K_{1,3}$ as an induced subgraph of $X_n$, which is forbidden for $X_n$ to be a line graph.

Conversely, if $n=4$ or 6 or a prime number then $X_n$ is $C_4$ or $C_6$, respectively, which is a line graph of $C_4$ or $C_6$, respectively. If $n\ne 2$ is a prime number, then $X_n$ is a complete graph on n vertices which is a line graph of $K_{1,n}$. If $n=2$, then $X_n$ is $P_2$ which is a line graph of $P_3$ then $X_n$ is a line graph. Hence the result. □

Theorem 9.

Signed Cayley graph $S_n$ is a line-signed graph, if and only if, $n=2$ or 4 or 6.

Proof. 

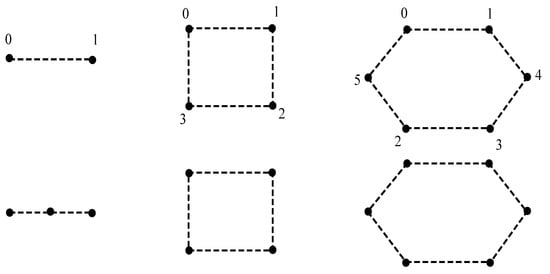
Suppose $S_n$ is a line-signed graph and $n\ne 2,4$ and 6. If n is not a prime number, then by Theorem 8, $X_n$ is not a line graph. Thus, we have a contradiction. So n must be a prime number. Yet, if n is a prime number, then by Theorem 7, $S_n$ is not sign-compatible and, by the Remark 1, is not a line graph. Hence by contraposition, the condition holds.

Conversely, suppose $n=2,4$ or 6. The corresponding signed graphs $S_2,S_4$ and $S_6$ and the signed graphs whose line-signed graphs are these signed graphs are shown in Figure 4. □

Figure 4. Showing $S_2$, $S_4$ and $S_6$ and the signed graphs whose line-signed graphs are these signed graphs.

Theorem 10.

$S_n$ is an ×-line signed graph, if and only if, $n=4$, or $n=6$ or a prime number.

Proof. 

Suppose $S_n$ is an ×-line-signed graph. We know that the underlying structure for line-signed graphs and product line-signed graphs are same. Thus the condition comes from Theorem 8.

Conversely, suppose $n=4,6$ or a prime number. By Theorem 4 it is clear that for these values of $n,$ the signed Cayley graph is balanced. Moreover, $L_{\times }\left(S\right)$ of any signed graph is always balanced and its underlying graph being a line graph (see [24]), the result follows from Theorems 4 and 8. □

2.4. $\mathcal{C}$-Consistency of $S_n$

Theorem 11

([25]). Let G be a marked graph and T be a spanning tree of G. Then, G is consistent, if and only if, G satisfies the following two conditions:

$\left(i\right)$

Each fundamental cycle relative to T is positive, and

$\left(ii\right)$

The two end vertices of any common path between each pair of fundamental cycles relative to T have the same mark.

Lemma 4.

For the signed Cayley graph $S_n=(X_n,\sigma )$, if n is even, then $S_n$ is canonically consistent.

Proof. 

Given a signed Cayley graph $S_n=(X_n,\sigma )$, where n is even. Then, by Lemma 3, $S_n$ is an all-negative signed graph. Moreover, $d\left(v\right)=\varphi \left(n\right)$ = even ∀$v\in V\left(S_n\right)$. Thus, all the vertices of $S_n$ are positively marked under the canonical marking. Hence, if n is even, then $S_n$ is canonically-consistent. □

Lemma 5.

For the signed Cayley graph $S_n=(X_n,\sigma )$, if $n=p^a$, p an odd prime; then $d^{-}\left(2\right)$ in $S_n$ is odd.

Proof. 

Given a signed Cayley graph $S_n=(X_n,\sigma )$, where $n=p^a$ and p is an odd prime. n being odd implies $2\in U_n$. By the definition of $S_n$, 2 is adjacent with the multiples of p with a negative sign only when 2 is adjacent with all the multiples of p. Now, all the multiples of p in n are in the form of $p^{a-1}$, as p is an odd prime, $d^{-}\left(2\right)=p^{a-1}=$ odd. □

Lemma 6.

For the signed Cayley graph $S_n=(X_n,\sigma )$, if $n=p_1^{a_1}{p}_2^{a_2}$, where $p_1\ne p_2$ and $p_2$ are odd primes, then $d^{-}\left(2\right)$ of $S_n$ is odd.

Proof. 

Given that $n=p_1^{a_1}{p}_2^{a_2}$ in $S_n$, where $p_1$ and $p_2$ are distinct odd primes. n being odd implies $2\in U_n$. By the definition of $S_n$, 2 is adjacent with the multiples of p with a negative sign when 2 is adjacent with all multiples of $p_1$ and $p_2$. Let $A_i$ be the set of multiples of $p_1$ and $p_2$. Then,

$$\begin{array}{c}\hfill \left|A_1\right|=p_1^{a_1-1}{p}_2^{a_2}\\ \hfill \left|A_2\right|=p_1^{a_1}{p}_2^{a_2-1}\end{array}$$

and

$$\begin{array}{c}\hfill \left|A_1\cap A_2\right|=p_1^{a_1-1}{p}_2^{a_2-1}\end{array}$$

Thus, using inclusion-exclusion principle

$$\begin{array}{c}\hfill \left|A_1\cup A_2\right|=p_1^{a_1-1}{p}_2^{a_2}+p_1^{a_1}{p}_2^{a_2-1}-p_1^{a_1-1}{p}_2^{a_2-1}\end{array}$$

Since some multiples of $p_1$($p_2$) whose difference with 2 may be a multiple of $p_2$($p_1$), then such multiples of $p_1$($p_2$) are not adjacent with 2 and such multiples of $p_1$($p_2$) are given by linear congruence:

$$\begin{array}{c}\hfill p_{1}x\equiv 2(mod{p}_2)\end{array}$$

(2)

and

$$\begin{array}{c}\hfill p_{2}y\equiv 2(mod{p}_1)\end{array}$$

(3)

There exists a unique incongruent solution, say $x_0$ of Equation (2) and all the solutions of (2), for which $p_{1}x-2<n$ are,

$$\begin{array}{c}\hfill x_0+0\left(p_2\right),x_0+1\left(p_2\right),x_0+2\left(p_2\right),\cdots ,x_0+(p_1^{a_1-1}{p}_2^{a_2-1}-1)\left(p_2\right)\end{array}$$

(4)

Thus, the total number of solutions for Equation (2) are $p_1^{a_1-1}{p}_2^{a_2-1}$. Similarly, the total solution of Equation (3) are $p_1^{a_1-1}{p}_2^{a_2-1}$. Hence, the total number of negatively charged edges incident at the vertex 2 are

$$\begin{array}{cc}\hfill d^{-}\left(2\right)& =p_1^{a_1-1}{p}_2^{a_2}+p_1^{a_1}{p}_2^{a_2-1}-p_1^{a_1-1}{p}_2^{a_2-1}-p_1^{a_1-1}{p}_2^{a_2-1}-p_1^{a_1-1}{p}_2^{a_2-1}\hfill \\ \hfill & =p_1^{a_1-1}{p}_2^{a_2-1}(p_1+p_2-3)\hfill \end{array}$$

Since $p_1$ and $p_2$ are odd primes, it follows that $d^{-}\left(2\right)$ is odd. □

Theorem 12.

For the signed Cayley graph $S_n=(X_n,\sigma )$, n having two distinct odd prime factors, is $\mathcal{C}$-consistent, if and only if,$n\equiv 0(mod2)$.

Proof. 

Given $S_n$, where n has at most two distinct odd prime factors. Suppose $S_n$ is $\mathcal{C}$-consistent. Let on contrary n be odd which implies $2\in U_n$. Then, by Lemmas 5 and 6, $d^{-}\left(2\right)$ = odd. Thus, by $\mathcal{C}$-marking ${\mu }_{\sigma }$, we have ${\mu }_{\sigma }\left(2\right)$ = −. Clearly, by the definition of $S_n$, $d\left(0\right)=d^{-}\left(0\right)=\varphi \left(n\right)=0\left(mod2\right)$. Now, by $\mathcal{C}$-marking we have ${\mu }_{\sigma }\left(0\right)=+$. Thus, we have ${\mu }_{\sigma }\left(0\right)=+$ and ${\mu }_{\sigma }\left(2\right)=-$. Next, considering two cycles. $Z^{\prime }$ and $Z^{\prime \prime }$. as $(0,1,2,0)$ and $(0,2,3,\cdots ,(n-1),0)$, respectively, in $S_n$, we see that both the cycles, $Z^{\prime }$ and $Z^{\prime \prime }$, shared the chord whose end vertices are 0 and 2. However, the end vertices 0 and 2 of the common chord are marked oppositely under the $\mathcal{C}$-marking implies $S_n$ is not $\mathcal{C}$-consistent (by Theorem 11). Thus, by contraposition =, if $S_n$ is $\mathcal{C}$-consistent, then $n\equiv 0(mod2)$.

Sufficiency: Suppose n is even. Then, by Lemma 4, $S_n$ is canonically consistent. □

3. Balance in Certain Derived Signed Graphs

Theorem 13.

$\eta \left(S_n\right)$ is balanced, if and only if, $n\equiv 0(mod2)$.

Proof. 

First, suppose $\eta \left(S_n\right)$ is balanced. Assume that conclusion is false. Suppose n is odd. Then, $2\in U_n$. Now, we consider a triangle $T:(0,1,2,0)$ in $S_n$. Since $1,2\in U_n$ and $0\notin U_n$, by the definition of $S_n$, we have a triangle with one positively charged edge 12 and two negatively charged edges 01 and 02. Then in $\eta \left(S_n\right)$ we have a triangle with one negatively charged edge and two positively charged edges. Thus, $\eta \left(S_n\right)$ is unbalanced. Hence, n is even.

Conversely, let $n\equiv 0(mod2)$. Now, by Lemma 3, $\eta \left(S_n\right)$ is all-positive and hence balanced. □

Theorem 14.

$L\left(S_n\right)$ is balanced, if and only if, $n=2$, or 4 or $6.$

Proof. 

Let $L\left(S_n\right)$ is balanced $n\ne 2,4$ and 6.

Case I:$n\ne 3$.

By the definition of $S_n$, $d\left(0\right)=d^{-}\left(0\right)=\varphi \left(n\right)=0$ (mod 2). However, in this case $\varphi \left(n\right)\ge 4$, which contradicts the condition $\left(ii\right)$ of Theorem 4 in [26] for $S_n$.

Case II:$n=3$.

It is easy to see that there is a positive section of length 2 in $S_n$ which contradicts the condition $\left(i\right)\left(b\right)$ of Theorem 4 in [26] for $S_n$.

Hence, by contradiction, the conditions follows.

Conversely, when $n=2,4$ or 6, then by Lemma 3, $S_n$ is all-negative and by Theorem 2, $X_n$ is bipartite. Thus $S_n$ is an all-negative signed graph with even cycle. So $L\left(S_n\right)$ is also an all-negative signed graph with even cycle and hence balanced. □

Theorem 15.

$C_E\left(S_n\right)$ is balanced, if and only if, $n=3,4$ or $6.$

Proof. 

Suppose $C_E\left(S_n\right)$ is balanced for the signed Cayley graph $S_n$. Let $n\ne 3,4$ and 6. Then, $d\left(0\right)=d^{-}\left(0\right)=\varphi \left(n\right)=0$(mod 2). However, in this case $\varphi \left(n\right)\ge 4$, which contradicts condition $\left(i\right)$ of Theorem 13 in [15] for $S_n$ and so n = 3, 4 or 6. Hence $C_E\left(S_n\right)$ is balanced.

Conversely, when $n=4$ or 6, then by Lemma 3, $S_n$ is all-negative and by Theorem 2, $X_n$ is bipartite. Thus $S_n$ is an all-negative signed graph with even cycle. So $C_E\left(S_n\right)$ is also an all-negative signed graph of even cycle and hence balanced.

Moreover, it is easy to see that $C_E\left(S_3\right)$ is balanced. Thus the result follows. □