Regularization Method for the Variational Inequality Problem over the Set of Solutions to the Generalized Equilibrium Problem

Abstract

The paper is devoted to bilevel problems: variational inequality problems over the set of solutions to the generalized equilibrium problems in a Hilbert space. To solve these problems, an iterative algorithm is proposed that combines the ideas of the Tseng’s extragradient method, the inertial idea and iterative regularization. The proposed method adopts a non-monotonic stepsize rule without any line search procedure. Under suitable conditions, the strong convergence of the resulting method is obtained. Several numerical experiments are also provided to illustrate the efficiency of the proposed method with respect to certain existing ones.

1. Introduction

Let $\mathcal{H}$ be a real Hilbert space, let $\mathcal{C}$ be a closed, convex and nonempty subset of $\mathcal{H}$, let $\mathcal{A}:\mathcal{C}\to \mathcal{H}$ be an operator, and let $f:\mathcal{C}\times \mathcal{C}\to \mathbb{R}$ be a bifunction. The generalized equilibrium problem ( GEP) is defined as: find a point $v^{*}\in \mathcal{H}$ such that

$$f(v^{*},v)+⟨\mathcal{A}{v}^{*},v-v^{*}⟩\ge 0,\forall v\in \mathcal{C}.$$

(1)

Denote by $\mathrm{GEP}(f,\mathcal{A})$ the set of solutions of the GEP. Next, we give two special cases of the GEP (1).

(I) If $\mathcal{A}=0$, then the GEP (1) becomes the equilibrium problem (EP): find a point $v^{*}\in \mathcal{C}$ such that

$$f(v^{*},v)\ge 0,\forall v\in \mathcal{C}.$$

The GEPs unifies in a simple form many mathematical models in applied sciences, such as variational inequalities [1], operator Equations [2,3], optimization problems [4], fixed point problems [5], saddle point problems [6], the Nash equilibrium problem [7] and so on. Due to its importance in applications, this problem has received attention from several authors.

(II) If $f(u,v)=0$ for all $u,vs.\in \mathcal{C},$ then the GEP (1) becomes the variational inequality problem (VIP): find a point $v^{*}\in \mathcal{C}$ such that

$$⟨\mathcal{A}{v}^{*},v-v^{*}⟩\ge 0,\forall v\in \mathcal{C},$$

(2)

where the solutions set is denoted by $\mathrm{VI}(\mathcal{C},\mathcal{A})$. The VIP theory was proposed independently by Fichera [8] and Stampacchia [9]. It provides a natural, convenient and unified framework for the study of many problems in engineering operation research, necessary optimality conditions and engineering mechanics. It covers, as special cases, well-known problems in mathematical programming, such as systems of optimization and control problems [6], traffic network problems [10], nonlinear Equations [11] and fixed point problems [12].

Recently, many authors introduced and studied various methods for solving the VIP. The simplest and oldest projection method is the gradient projection method:

$$x_{n+1}=P_{\mathcal{C}}(x_n-\eta \mathcal{A}{x}_n).$$

(3)

It is well known that the iterative process defined by (3) converges to an element of $\mathrm{VI}(\mathcal{C},\mathcal{A})$ when $\mathcal{A}$ is strongly monotone and L-Lipschitz continuous. In order to weaken such a strong hypothesis, Korpelevich [13] introduced the following extragradient method (EGM) for an L-Lipschitz continuous and monotone operator $\mathcal{A}$. This method is of the form:

$$\left\{\begin{array}{c}{x}_{n+1}=P_{\mathcal{C}}(x_n-\eta \mathcal{A}{y}_n),\hfill \\ y_n=P_{\mathcal{C}}(x_n-\eta \mathcal{A}{x}_n),\hfill \end{array}\right.$$

(4)

where $\eta \in (0,1/L)$. They proved that the sequence $\left\{x_n\right\}$ generated by the EGM converges to a solution of the VIP. Notice that the EGM is required to calculate the projection onto the feasible set $\mathcal{C}$ and evaluations of the cost operator $\mathcal{A}$ twice in each iteration. This, in general, may be computationally expensive if the feasible set $\mathcal{C}$ and the operator $\mathcal{A}$ have a complicated structure. Thus, it might affect the efficiency of the method (see, e.g., [14,15,16,17]). In order to overcome the drawback, the Tseng’s extragradient method (TEGM) [18] has been suggested. This method is described as follows (Algorithm 1):

Algorithm 1: The Tseng’s extragradient method (TEGM).

Initialization: Given $x_0\in \mathcal{H}$ as arbitrary, take $\eta >0$. Step 1. Calculate $$y_n=P_{\mathcal{C}}(x_n-\eta \mathcal{A}{x}_n).$$ Step 2. Calculate the next iterate $$x_{n+1}=y_n-\eta (\mathcal{A}{y}_n-\mathcal{A}{x}_n).$$

A major improvement on the TEGM is that it requires computing only one projection onto $\mathcal{C}$ in each iteration. Furthermore, the main shortcoming of the TEGM is the choice of stepsize. It should be noted that the stepsize takes a significant part in the convergence analysis. We should also notice that the stepsizes are defined to be dependent on the Lipschitz constant of the monotone operator in the TEGM.

Recently, Yang et al. [19] introduced a new self-adaptive subgradient extragradient method (STEGM) for solving the VIPs. In the following Algorithm 2, the mapping g is a contraction on $\mathcal{H}$. It should be noted that Algorithm 2 has strong convergence theorems established in real Hilbert spaces. However, the stepsize used in Algorithm 2 is monotonically decreasing, which may also affect the execution efficiency of such a method. Following the ideas of the EGM, the TEGM and the STEGM, Tan and Qin [20] proposed the following inertial extragradient methods with non-monotonic stepsizes (SVTEGM) for solving the VIPs in Hilbert spaces.

Algorithm 2: Self-adaptive Tseng’s extragradient method (STEGM).

Initialization: Given $x_0\in \mathcal{H}$ as arbitrary, take $\left\{{\alpha }_n\right\}\subset (0,+\infty )$, ${\eta }_0>0$ and $\upsilon \in (0,1)$. Step 1. Calculate $$y_n=P_{\mathcal{C}}\left(x_n-{\eta }_n\mathcal{A}{x}_n\right),$$ and $$z_n=y_n-{\eta }_n(\mathcal{A}{y}_n-\mathcal{A}{x}_n).$$ If $x_n=y_n$, then stop: $x_n$ is a solution. Otherwise: Step 2. Compute $$x_{n+1}={\alpha }_{n}g\left(x_n\right)+(1-{\alpha }_n)z_n,$$ where $\left\{{\eta }_n\right\}$ is updated by $${\eta }_{n+1}=\left\{\begin{array}{cc}min\{\frac{\upsilon ∥x_n-y_n∥}{∥\mathcal{A}{x}_n-\mathcal{A}{y}_n∥},{\eta }_n\},\hfill & \hfill \mathrm{if}\mathcal{A}{x}_n-\mathcal{A}{y}_n\ne 0;\\ {\eta }_n,\hfill & \hfill \mathrm{otherwise}.\end{array}\right.$$ Step 3. Set $n:=n+1$ and return to Step 1.

They proved that the iterative process $\left\{x_n\right\}$ constructed by Algorithm 3 converges to a solution of the VIP (2) under certain appropriate conditions.

Algorithm 3: The self-adaptive viscosity-type inertial Tseng extragradient algorithm (SVTEGM).

Initialization: Given $x_0,x_1\in \mathcal{H}$ as arbitrary, take $\left\{{\xi }_n\right\}\subset (0,+\infty )$, $\left\{{\alpha }_n\right\}\subset (0,+\infty )$, $\rho >0$, ${\eta }_0>0$, and $\upsilon \in (0,1)$. Step 1. Calculate $$u_n=x_n+{\mu }_n(x_n-x_{n-1}),$$ where $${\mu }_n=\left\{\begin{array}{cc}min\{\frac{{\xi }_n}{∥x_n-x_{n-1}∥},\rho \},\hfill & \mathrm{if}{x}_n\ne x_{n-1};\hfill \\ \rho ,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$ (5) Step 2. Compute $$y_n=P_{\mathcal{C}}\left(u_n-{\eta }_n\mathcal{A}{u}_n\right),$$ and $$z_n=y_n-{\eta }_n(\mathcal{A}{y}_n-\mathcal{A}{x}_n),$$ where $\left\{{\eta }_n\right\}$ is updated by $${\eta }_{n+1}=\left\{\begin{array}{c}min\{\frac{\upsilon ∥u_n-y_n∥}{∥\mathcal{A}{u}_n-\mathcal{A}{y}_n∥},{\eta }_n+{ϵ}_n\},\mathrm{if}\mathcal{A}{u}_n-\mathcal{A}{y}_n\ne 0;\hfill \\ {\eta }_n+{ϵ}_n,\mathrm{otherwise}.\hfill \end{array}\right.$$ (6) Step 3. Compute $$x_{n+1}={\alpha }_{n}g\left(x_n\right)+(1-{\alpha }_n)z_n.$$ Step 5. Set $n:=n+1$ and return to Step 1.

In recent years, the bilevel variational inequality problem (BVIP), has spurred the interest of many authors; see, e.g., [21]. The BVIP in $\mathcal{H}$ is presented as follows: find $v^{*}\in \mathrm{VI}(\mathcal{C},\mathcal{A})$ such that

$$⟨\mathcal{F}{v}^{*},v-v^{*}⟩\ge 0,\forall v\in \mathrm{VI}(\mathcal{C},\mathcal{A}),$$

(7)

where $\mathcal{A}:\mathcal{C}\to \mathcal{H}$ and $\mathcal{F}:\mathcal{H}\to \mathcal{H}$ are operators. This class is interesting because it includes a couple of classes of mathematical programs with variational inequality problems, equilibrium constraints, linear complementarity problems, bilevel optimization problems and bilevel linear programs.

In the present work, we consider a more general bilevel problem: a variational inequality over the set of solutions to the generalized equilibrium problem (VIOGE). Furthermore, this problem is described as follows: find $v^{*}\in \mathrm{GEP}(f,\mathcal{A})$ such that

$$⟨\mathcal{F}{v}^{*},v-v^{*}⟩\ge 0,\forall v\in \mathrm{GEP}(f,\mathcal{A}),$$

(8)

where f is a bifunction, $\mathcal{F}$ is strongly monotone and $\mathcal{A}$ is monotone.

It is easy to see that the VIOGE is a special class of bilevel equilibrium problems. The bilevel equilibrium problems have interested many authors, and particularly, the bilevel equilibrium problem has been widely and intensively studied after the appearance of the monograph books [22]. It is worth noting that the VIOGE contains some classes of mathematical programs with equilibrium constraints [23], minimum-norm problems of the solution set of variational inequalities [24], variational inequalities [25], bilevel convex programming models [26], bilevel minimization problems [27] and bilevel linear programming [28]. For these reasons, we find that it is necessary to study and propose new iterative methods with better efficiency for solving the VIOGE.

Inspired by Korpelevich [13], Tseng [18] and Tan and Qin [20], we research the VIOGE (8) and introduce a new iterative method for finding a solution of the VIOGE (8) in Hilbert spaces. The proposed method is constructed around the TEGM, the inertial idea, and the regularization technique and uses a non-monotonic stepsize rule without any line search procedure. Strong convergence theorems are established under appropriate conditions. Several numerical experiments are also provided to show the effectiveness and the fast convergence of the new method over certain known methods.

2. Preliminaries

In this section, we assume that $\mathcal{C}$ is a closed, convex and nonempty subset of a Hilbert space $\mathcal{H}$. The set of real numbers is denoted by $\mathbb{R}$. The symbols “→”and “⇀” denote the strong and weak convergence, respectively. For a given sequence $\left\{x_n\right\}\subset \mathcal{H}$, $\omega \left(x_n\right):=\{x:x_{n_j}\rightharpoonup x\}$ denotes a set of weak limits of $\left\{x_n\right\}$. The set of fixed points of a mapping $S:\mathcal{C}\to \mathcal{H}$ is denoted by $\mathrm{Fix}\left(S\right)$.

Definition 1

([7]). An operator $\mathcal{S}:\mathcal{C}\to \mathcal{H}$ is called:

(i) 

monotone, if

$$⟨\mathcal{S}x-\mathcal{S}y,x-y⟩\ge 0,\forall x,y\in \mathcal{C};$$

(ii) 

α-strongly monotone, if there exists a number $\alpha >0$ such that

$$⟨\mathcal{S}x-\mathcal{S}y,x-y⟩\ge \alpha {∥x-y∥}^2,\forall x,y\in \mathcal{C};$$

(iii) 

r-contractive, if there exists a positive number $r<1$ such that

$$∥\mathcal{S}x-\mathcal{S}y∥\le r∥x-y∥,\forall x,y\in \mathcal{C};$$

(iv) 

k-Lipschitz continuous, if there exists $k>0$ such that

$$∥\mathcal{S}x-\mathcal{S}y∥\le k∥x-y∥,\forall x,y\in \mathcal{C};$$

(v) 

nonexpansive, if

$$∥\mathcal{S}x-\mathcal{S}y∥\le ∥x-y∥,\forall x,y\in \mathcal{C}.$$

Definition 2

([29]). A single-valued operator $\mathcal{S}:\mathcal{C}\to \mathcal{H}$ is called hemicontinuous if the real function

$$t\mapsto ⟨S\left(\right(1-t)x+ty),z⟩$$

is continuous on $[0,1]$ for all $x,y,z\in \mathcal{C}$.

Definition 3

([30]). The mapping $P_{\mathcal{C}}:\mathcal{H}\to \mathcal{C}$ which assigns to each point $x\in \mathcal{H}$ the unique point $w\in \mathcal{C}$ such that

$$∥x-P_{\mathcal{C}}x∥=\underset{y\in \mathcal{C}}{inf}∥x-y∥.$$

is called the metric (or nearest point) projection of $\mathcal{H}$ onto $\mathcal{C}$.

Proposition 1

([31]). The metric projection $P_{\mathcal{C}}$ satisfies

$${∥P_{\mathcal{C}}x-P_{\mathcal{C}}y∥}^2\le ⟨P_{\mathcal{C}}x-P_{\mathcal{C}}y,x-y⟩,\forall x,y\in \mathcal{C}.$$

Given $x\in \mathcal{H}$ and $y\in \mathcal{C},$ then $y=P_{\mathcal{C}}x$ if there holds

$$0\le ⟨x-y,y-z⟩,\forall z\in \mathcal{C}.$$

Assumption 1.

Assume $\mathcal{C}$ is a closed, nonempty, and convex subset of a Hilbert space $\mathcal{H}$. Let $f:\mathcal{C}\times \mathcal{C}\to \mathbb{R}$ be a bifunction satisfying the following restrictions:

(A1) 

$f(x,x)=0$ , $\forall x\in \mathcal{C}$;

(A2) 

f is monotone, i.e., for all $x,y\in \mathcal{C},$ $f(x,y)+f(y,x)\le 0;$

(A3) 

for all $x\in \mathcal{C},f(x,·)$ is convex and lower semicontinuous; and

(A4) 

for all $x,y,z\in \mathcal{C},$ ${\displaystyle \underset{t\to 0^{+}}{lim\; sup}f(tz+(1-t)x,y)\le f(x,y).}$

Lemma 1

([1]). Let $f:\mathcal{C}\times \mathcal{C}\to \mathbb{R}$ be a bifunction satisfying Assumption 1 (A1)–(A4). For $x\in \mathcal{H}$ and $r>0$, define a mapping $T_r^f:\mathcal{H}\to \mathcal{C}$ by:

$$T_r^{f}x=\{z\in \mathcal{C}:f(z,y)+\frac{1}{r}⟨y-z,z-x⟩\ge 0,\forall y\in \mathcal{C}\}.$$

Then, it holds that:

(i) 

$T_r^f$ is nonempty and single-valued;

(ii) 

$T_r^f$ is a firmly nonexpansive mapping, that is, ${∥T_r^{f}x-T_r^{f}y∥}^2\le ⟨T_r^{f}x-T_r^{f}y,x-y⟩$ for all $x,y\in \mathcal{H};$

(iii) 

$\mathrm{Fix}\left(T_r^f\right)=\mathrm{EP}\left(f\right);$ and

(iv) 

$\mathrm{EP}\left(f\right)$ is convex and closed.

Remark 1.

Assume $\mathcal{A}:\mathcal{C}\to \mathcal{H}$ is Lipschitz continuous and monotone, $f:\mathcal{C}\times \mathcal{C}\to \mathbb{R}$ is a bifunction satisfying Assumption 1 (A1)–(A4). We find that the mapping $\widehat{F}(x,y):=f(x,y)+⟨\mathcal{A}x,y-x⟩$ also satisfies Assumption 1. Thus, we deduce, by Lemma 1, that

(i) 

$T_r^{\widehat{F}}$ is nonempty and single-valued;

(ii) 

$T_r^{\widehat{F}}$ is a firmly nonexpansive mapping;

(iii) 

$\mathrm{Fix}(T_r^{\widehat{F}})=\mathrm{Fix}\left(T_r^f(I-r\mathcal{A})\right)=\mathrm{EP}(\widehat{F})=\mathrm{GEP}(f,\mathcal{A});$ and

(iv) 

$\mathrm{GEP}(f,\mathcal{A})$ is closed and convex.

Lemma 2.

Assume $f:\mathcal{C}\times \mathcal{C}\to \mathbb{R}$ is a bifunction satisfying Assumption 1 (A1)–(A4), $\mathcal{A}:\mathcal{C}\to \mathcal{H}$ is monotone and L-Lipschitz continuous, $\mathcal{F}:\mathcal{C}\to \mathcal{H}$ is τ-strongly monotone and k-Lipschitz continuous. Then, $T_r^f(I-r(A+\alpha \mathcal{F}))$ is a contraction on $\mathcal{C}$ provided $r\in \left(0,\frac{2\alpha \tau }{{(L+\alpha k)}^2}\right).$

Proof. 

For $x,y\in C$, we have, from Lemma 1(ii), that

$$\begin{array}{ccc}\hfill & & {∥T_r^f(I-r(\mathcal{A}+\alpha \mathcal{F}))x-T_r^f(I-r(\mathcal{A}+\alpha \mathcal{F}))y∥}^2\hfill \\ & \le & {∥(I-r(\mathcal{A}+\alpha \mathcal{F}\left)\right)x-(I-r(\mathcal{A}+\alpha \mathcal{F}\left)\right)y∥}^2\hfill \\ & \le & {∥x-y∥}^2-2r⟨x-y,(\mathcal{A}+\alpha \mathcal{F})x-(\mathcal{A}+\alpha \mathcal{F})y⟩+r^2{∥(\mathcal{A}+\alpha \mathcal{F})x-(\mathcal{A}+\alpha \mathcal{F})y∥}^2\hfill \\ & \le & {∥x-y∥}^2-2r\alpha ⟨x-y,\mathcal{F}x-\mathcal{F}y⟩+r^2{(L+\alpha k)}^2{∥x-y∥}^2\hfill \\ & \le & \left(1-r(2\alpha \tau -r{(L+\alpha k)}^2)\right){∥x-y∥}^2.\hfill \end{array}$$

(9)

Since $\mathcal{F}:\mathcal{C}\to \mathcal{H}$ is $\tau$-strongly monotone and k-Lipschitz continuous, then one finds $\tau \le k$. Notice that

$$\begin{array}{ccc}\hfill 1-r(2\alpha \tau -r{(L+\alpha k)}^2)& =& 1-2r\alpha \tau +r^2{(L+\alpha k)}^2\hfill \\ & >& 1-2r\alpha \tau +r^2{\alpha }^2{k}^2\hfill \\ & \ge & 1-2r\alpha \tau +r^2{\alpha }^2{\tau }^2\hfill \\ & =& {(1-r\alpha \tau )}^2.\hfill \end{array}$$

Then, we deduce that $1-r(2\alpha \tau -r{(L+\alpha k)}^2)\ge 0$ for all $r>0$. By using the assumption that $r\in \left(0,\frac{2\alpha \tau }{{(L+\alpha k)}^2}\right),$ we derive $1-r(2\alpha \tau -r{(L+\alpha k)}^2)<1$. Thus, $0\le 1-r(2\alpha \tau -r{(L+\alpha k)}^2)<1$ for each $r\in \left(0,\frac{2\alpha \tau }{{(L+\alpha k)}^2}\right).$ Furthermore, $T_r^f(I-r(A+\alpha \mathcal{F}))$ is a contraction on $\mathcal{C}$ provided $r\in \left(0,\frac{2\alpha \tau }{{(L+\alpha k)}^2}\right).$ This completes the proof.  □

Lemma 3.

Assume $\mathcal{A}:\mathcal{C}\to \mathcal{H}$ is monotone and hemicontinuous, and $f:\mathcal{C}\times \mathcal{C}\to \mathbb{R}$ is a bifunction satisfying Assumption 1 (A1)–(A4). Then, $v^{*}$ is a solution to the GEP (1) if $v^{*}$ is a solution to the problem: find a point $v^{*}\in \mathcal{C}$ such that

$$-f(v,v^{*})+⟨\mathcal{A}v,v-v^{*}⟩\ge 0,\forall v\in \mathcal{C}.$$

(10)

Proof. 

Let $v^{*}\in \mathcal{C}$ be a solution of the GEP (1). From (A2) and the monotonicity of $\mathcal{A}$, one finds, for all $v\in \mathcal{C}$, that

$$\begin{array}{c}\hfill -f(v,v^{*})+⟨\mathcal{A}v,v-v^{*}⟩\ge f(v^{*},v)+⟨\mathcal{A}{v}^{*},v-v^{*}⟩\ge 0.\end{array}$$

(11)

Thus, $v^{*}\in \mathcal{C}$ is a solution of the problem (10).

Conversely, let $v^{*}\in \mathcal{C}$ be a solution of the problem (10). For all $v\in \mathcal{C}$, let $v_t=(1-t)v^{*}+tv,$ and then $v_t\in \mathcal{C}$. Since $v^{*}\in \mathcal{C}$ is a solution of the problem (10), it follows that

$$-f(v_t,v^{*})+⟨\mathcal{A}{v}_t,v_t-v^{*}⟩\ge 0.$$

(12)

From Assumption 1 (A1) and (A3), we have

$$\begin{array}{ccc}\hfill 0& =& f(v_t,v_t)\hfill \\ & =& f(v_t,(1-t)v^{*}+tv)\hfill \\ & \le & (1-t)f(v_t,v^{*})+tf(v_t,v)\hfill \\ & =& (1-t)\left(f(v_t,v^{*})-⟨\mathcal{A}{v}_t,v_t-v^{*}⟩\right)+(1-t)⟨\mathcal{A}{v}_t,v_t-v^{*}⟩+tf(v_t,v)\hfill \\ & =& (1-t)\left(f(v_t,v^{*})-⟨\mathcal{A}{v}_t,v_t-v^{*}⟩\right)+(1-t)t⟨\mathcal{A}{v}_t,v-v^{*}⟩+tf(v_t,v).\hfill \end{array}$$

This, together with (12), implies

$$\begin{array}{c}\hfill 0\le (1-t)t⟨\mathcal{A}{v}_t,v-v^{*}⟩+tf(v_t,v),\end{array}$$

which implies

$$\begin{array}{ccc}\hfill 0& \le & (1-t)⟨\mathcal{A}{v}_t,v-v^{*}⟩+f(v_t,v).\hfill \end{array}$$

Letting $t\to 0$ and noticing (A4) and the fact that $\mathcal{A}$ is hemicontinuous, we obtain

$$\begin{array}{ccc}\hfill 0& \le & f(v^{*},v)+⟨\mathcal{A}{v}^{*},v-v^{*}⟩.\hfill \end{array}$$

Therefore, $v^{*}$ is a solution of the GEP (1). This completes the proof.  □

Applying Lemma 2, we obtain the following results immediately.

Corollary 1

([32]). Suppose $\mathcal{A}:\mathcal{C}\to \mathcal{H}$ is a monotone and hemicontinuous mapping, and then $v^{*}$ is a solution to the VIP (2) if $v^{*}$ is a solution to the problem: find $v^{*}\in \mathcal{C}$ such that

$$⟨\mathcal{A}v,v-v^{*}⟩\ge 0,\forall v\in \mathcal{C}.$$

Lemma 4

([33]). Assume $\left\{v_n\right\}$ is a sequence in $\mathcal{H}$. If $v_n\rightharpoonup v$ and $∥v_n∥\rightharpoonup ∥v∥$, then $v_n\to v$.

Lemma 5

([34]). Assume $\left\{x_n\right\}$ is a sequence of nonnegative real numbers. Suppose that

$$x_{n+1}\le (1-a_n)x_n+b_n,n\in \mathbb{N},$$

where $\left\{a_n\right\},\left\{b_n\right\}$ satisfy the conditions

(i) 

${\displaystyle \sum _{n=1}^{\infty }{a}_n=\infty ,\underset{n\to \infty }{lim}{a}_n=0}$,

(ii) 

${\displaystyle \underset{n\to \infty }{lim\; sup}\frac{b_n}{a_n}\le 0}$.

Then, ${\displaystyle \underset{n\to \infty }{lim}{x}_n=0}$.

3. Main Results

In this section, we focus on the strong convergence analysis for the VIOGE by using the Tseng’s extragradient method, the inertial idea and regularization technique. In what follows, suppose that $f:\mathcal{H}\times \mathcal{H}\to \mathbb{R}$ is a bifunction satisfying (A1)–(A4), $\mathcal{A}:\mathcal{H}\to \mathcal{H}$ is L-Lipschitz continuous and monotone, $\mathcal{F}:\mathcal{H}\to \mathcal{H}$ is $\tau$-strongly monotone and k-Lipschitz continuous. Additionally, we also assume that $\mathrm{GEP}(f,\mathcal{A})$ is nonempty. One finds from Remark 1(iv) that $\mathrm{GEP}(f,\mathcal{A})$ is closed and convex. This, by the strong monotonicity and continuity of $\mathcal{F}$, ensures the uniqueness of solutions $x^{†}$ to the VIOGE (8). Together with the GEP (1), we consider the following regularized generalized equilibrium problem (RGEP) for each $\alpha >0$: we find a point $x\in \mathcal{C}$ such that

$$f(x,y)+⟨\mathcal{A}x+\alpha \mathcal{F}x,y-x⟩\ge 0,\forall y\in \mathcal{C}.$$

(13)

Remark 2.

Under above assumptions, one deduces that RGEP (13) has a unique solution. Indeed, the solutions set of RGEP (13) is $\mathrm{GEP}(f,\mathcal{A}+\alpha \mathcal{F})$. It is also not hard to see from Remark 1 (iii) that $\mathrm{Fix}\left(T_r^f(I-r(\mathcal{A}+\alpha \mathcal{F}))\right)=\mathrm{GEP}(f,\mathcal{A}+\alpha \mathcal{F})$ for each $r>0$. In particular, for each $r\in \left(0,\frac{2\alpha \tau }{{(L+\alpha k)}^2}\right),$ by Lemma 2, the mapping $T_r^f(I-r(\mathcal{A}+\alpha \mathcal{F}))$ is contractive. Then, this mapping has a unique fixed point by the Banach contraction principle. Hence, RGEP (13) has a unique solution, which is denoted by $x_{\alpha }$ , for each $\alpha >0.$

Now, we study some properties of the solution $x_{\alpha }$.

Lemma 6.

It holds that

(i) 

$∥x_{\alpha }∥\le ∥x^{†}∥+\frac{∥\mathcal{F}{x}^{†}∥}{\tau },\forall \alpha >0$;

(ii) 

${\displaystyle \underset{\alpha \to 0^{+}}{lim}∥x_{\alpha }-x^{†}∥=0}$, $\forall \alpha >0$;

(iii) 

$∥x_a-x_b∥\le \frac{\left|b-a\right|}{a}M$, $\forall a,b>0$, where M is a positive constant.

Proof. 

(i) Taking an arbitrary $w\in \mathrm{GEP}(f,\mathcal{A})$, one has $f(w,y)+⟨\mathcal{A}w,y-w⟩\ge 0$ for all $y\in \mathcal{C}$, which with $y=x_{\alpha }\in \mathcal{C}$, implies that

$$f(w,x_{\alpha })+⟨\mathcal{A}w,x_{\alpha }-w⟩\ge 0.$$

(14)

Since $x_{\alpha }$ is the solution of the RGEP, one then finds

$$f(x_{\alpha },y)+⟨\mathcal{A}{x}_{\alpha }+\alpha \mathcal{F}{x}_{\alpha },y-x_{\alpha }⟩\ge 0,\forall y\in \mathcal{C}.$$

(15)

Substituting $y=w\in \mathcal{C}$ into (15), one obtains

$$f(x_{\alpha },w)+⟨\mathcal{A}{x}_{\alpha }+\alpha \mathcal{F}{x}_{\alpha },w-x_{\alpha }⟩\ge 0.$$

Then, by combining this inequality with (14), one finds

$$f(w,x_{\alpha })+f(x_{\alpha },w)+⟨\mathcal{A}{x}_{\alpha }-\mathcal{A}w,w-x_{\alpha }⟩+\alpha ⟨\mathcal{F}{x}_{\alpha },w-x_{\alpha }⟩\ge 0.$$

(16)

Observe that

$$\begin{array}{c}\hfill ⟨\mathcal{F}{x}_{\alpha },w-x_{\alpha }⟩=⟨\mathcal{F}{x}_{\alpha }-\mathcal{F}w,w-x_{\alpha }⟩+⟨\mathcal{F}w,w-x_{\alpha }⟩.\end{array}$$

(17)

It follows from the $\tau$-strong monotonicity of $\mathcal{F}$ and (17) that

$$\begin{array}{c}\hfill ⟨\mathcal{F}{x}_{\alpha },w-x_{\alpha }⟩\le -\tau {∥x_{\alpha }-w∥}^2+⟨\mathcal{F}w,w-x_{\alpha }⟩.\end{array}$$

(18)

Substituting (18) into (16), one obtains

$$f(w,x_{\alpha })+f(x_{\alpha },w)+⟨\mathcal{A}{x}_{\alpha }-\mathcal{A}w,w-x_{\alpha }⟩-\alpha \tau {∥x_{\alpha }-w∥}^2+\alpha ⟨\mathcal{F}w,w-x_{\alpha }⟩\ge 0.$$

(19)

Utilizing (A2) and the monotonicity of $\mathcal{A}$ , one deduces

$$\begin{array}{c}\hfill \tau {∥x_{\alpha }-w∥}^2\le ⟨\mathcal{F}w,w-x_{\alpha }⟩.\end{array}$$

(20)

Notice that

$$\begin{array}{c}\hfill ⟨\mathcal{F}w,w-x_{\alpha }⟩\le ∥\mathcal{F}w∥∥w-x_{\alpha }∥,\end{array}$$

which, by (20), implies

$$\begin{array}{c}\hfill ∥x_{\alpha }∥\le ∥w∥+\frac{∥\mathcal{F}w∥}{\tau },\forall w\in \mathrm{GEP}(f,\mathcal{A}).\end{array}$$

This, together with the fact that $x^{†}\in \mathrm{GEP}(f,\mathcal{A})$, leads to

$$\begin{array}{c}\hfill ∥x_{\alpha }∥\le ∥x^{†}∥+\frac{∥\mathcal{F}{x}^{†}∥}{\tau }.\end{array}$$

(21)

Thus, one deduces that $\left\{x_{\alpha }\right\}$ is bounded.

(ii) Since $\mathcal{C}$ is closed and convex, then $\mathcal{C}$ is weakly closed. Therefore, there is a subsequence $\left\{x_{{\alpha }_j}\right\}$ of $\left\{x_{\alpha }\right\}$ and some element $x^{*}\in \mathcal{C}$ such that $x_{{\alpha }_j}\rightharpoonup x^{*}.$ In view of (A2) and the monotone property of $\mathcal{A}$, we deduce, for all $v\in \mathcal{C}$, that

$$\begin{array}{ccc}\hfill & & (-f(y,x_{{\alpha }_j})+⟨\mathcal{A}y,y-x_{{\alpha }_j}⟩)-(f(x_{{\alpha }_j},y)+⟨\mathcal{A}{x}_{{\alpha }_j}+{\alpha }_j\mathcal{F}{x}_{{\alpha }_j},y-x_{{\alpha }_j}⟩)\hfill \\ & =& (-f(y,x_{{\alpha }_j})-f(x_{{\alpha }_j},y))+⟨\mathcal{A}y-\mathcal{A}{x}_{{\alpha }_j},y-x_{{\alpha }_j}⟩-{\alpha }_j⟨\mathcal{F}{x}_{{\alpha }_j},y-x_{{\alpha }_j}⟩\hfill \\ & \ge & -{\alpha }_j⟨\mathcal{F}{x}_{{\alpha }_j},y-x_{{\alpha }_j}⟩.\hfill \end{array}$$

(22)

Considering the fact that $f(x_{{\alpha }_j},y)+⟨\mathcal{A}{x}_{{\alpha }_j}+{\alpha }_j\mathcal{F}{x}_{{\alpha }_j},y-x_{{\alpha }_j}⟩\ge 0$ and noticing (22), one infers that

$$\begin{array}{c}\hfill -f(y,x_{{\alpha }_j})+⟨\mathcal{A}y,y-x_{{\alpha }_j}⟩\ge -{\alpha }_j⟨\mathcal{F}{x}_{{\alpha }_j},y-x_{{\alpha }_j}⟩,\forall y\in \mathcal{C}.\end{array}$$

As $y\mapsto f(x,y)$ is convex and lower semicontinuous, then it is also weakly lower semicontinuous. Taking $j\to \infty$, noticing (A3) and the boundedness of $\left\{x_{\alpha }\right\}$ (see, Lemma 6(i)), one concludes that

$$\begin{array}{c}\hfill -f(y,x^{*})+⟨\mathcal{A}y,y-x^{*}⟩\ge 0,\forall y\in \mathcal{C},\end{array}$$

which, by Lemma 2, immediately yields

$$\begin{array}{c}\hfill x^{*}\in \mathrm{GEP}(f,\mathcal{A}).\end{array}$$

(23)

It follows from (20) that

$$\begin{array}{c}\hfill 0\le ⟨\mathcal{F}w,w-x_{{\alpha }_j}⟩,\forall w\in \mathrm{GEP}(f,\mathcal{A}).\end{array}$$

(24)

Passing to the limit in (24) as $j\to \infty$ and noticing the fact $x_{{\alpha }_j}\rightharpoonup x^{*}(\mathrm{as}j\to \infty ),$ one infers that

$$\begin{array}{c}\hfill 0\le ⟨\mathcal{F}w,w-x^{*}⟩,\forall w\in \mathrm{GEP}(f,\mathcal{A}),\end{array}$$

which implies, by Corollary 1, that

$$\begin{array}{c}\hfill 0\le ⟨\mathcal{F}{x}^{*},w-x^{*}⟩,\forall w\in \mathrm{GEP}(f,\mathcal{A}).\end{array}$$

Hence, $x^{*}$ is the solution of the VIOGE (8). Since the solution $x^{†}$ of the VIOGE (8) is unique, one deduces that $x^{*}=x^{†}.$ Therefore, the set $\omega \left(x_{\alpha }\right)$ only has one element $x^{†}$—that is, $\omega \left(x_{\alpha }\right)=\left\{x^{†}\right\}.$ Thus, one finds $x_{\alpha }\rightharpoonup x^{†}$. Further, utilizing (20), one finds

$$\begin{array}{c}\hfill \tau {∥x_{\alpha }-x^{†}∥}^2\le ⟨\mathcal{F}{x}^{†},x^{†}-x_{\alpha }⟩.\end{array}$$

Passing to the limit in the above inequality as $\alpha \to 0^{+}$ and noticing the fact that $x_{\alpha }\rightharpoonup x^{†}$, one deduces ${\displaystyle \underset{\alpha \to 0^{+}}{lim}∥x_{\alpha }-x^{†}∥=0}$. This is the desired result (ii).

(iii) Assume that $x_a$, $x_b$ are the solutions of the RGEP. Then, one has

$$f(x_a,x_b)+⟨\mathcal{A}{x}_a+a\mathcal{F}{x}_a,x_b-x_a⟩\ge 0$$

and

$$f(x_b,x_a)+⟨\mathcal{A}{x}_b+b\mathcal{F}{x}_b,x_a-x_b⟩\ge 0.$$

Summing up the above two inequalities, one finds

$$\begin{array}{ccc}& & f(x_a,x_b)+f(x_b,x_a)+⟨\mathcal{A}{x}_a-\mathcal{A}{x}_b,x_b-x_a⟩+a⟨\mathcal{F}{x}_a-\mathcal{F}{x}_b,x_b-x_a⟩\hfill \\ & & +(a-b)⟨\mathcal{F}{x}_b,x_b-x_a⟩\ge 0.\hfill \end{array}$$

Noting the monotonic property of $\mathcal{A}$ and (A2), one finds

$$\begin{array}{c}\hfill a⟨\mathcal{F}{x}_a-\mathcal{F}{x}_b,x_b-x_a⟩+(a-b)⟨\mathcal{F}{x}_b,x_b-x_a⟩\ge 0,\end{array}$$

or, equivalently,

$$\begin{array}{c}\hfill (b-a)⟨\mathcal{F}{x}_b,x_a-x_b⟩\ge a⟨\mathcal{F}{x}_a-\mathcal{F}{x}_b,x_a-x_b⟩.\end{array}$$

It follows from the $\tau$-strong monotonicity of $\mathcal{F}$ that

$$\begin{array}{c}\hfill (b-a)⟨\mathcal{F}{x}_b,x_a-x_b⟩\ge a\tau {∥x_a-x_b∥}^2,\end{array}$$

which leads to

$$\left|b-a\right|∥\mathcal{F}{x}_b∥∥x_a-x_b∥\ge a\tau {∥x_a-x_b∥}^2.$$

Thus, one concludes that

$$∥x_a-x_b∥\le \frac{\left|b-a\right|}{a}\frac{∥\mathcal{F}{x}_b∥}{\tau }.$$

(25)

Since the operator $\mathcal{F}$ is Lipschitz continuous, noting (21), we then deduce that $\left\{∥\mathcal{F}{x}_a∥\right\}$ is also bounded. Thus, by (25), there exists $M>0$ such that $∥x_a-x_b∥\le \frac{\left|b-a\right|}{a}M$. This completes the proof.  □

In the following, combining with the Tseng’s extragradient method, the inertial idea and the regularization method, we propose a new numerical algorithm for solving the VIOGE (8).

Lemma 7

([20]). The sequence $\left\{{\eta }_n\right\}$ generated by (27) is well-defined and ${\displaystyle \underset{n\to \infty }{lim}{\eta }_n=\eta }$ and $\eta \in [min\{\frac{\upsilon }{L},{\eta }_0\},{\eta }_0+\zeta ]$, where ${\displaystyle \zeta =\sum _{i=1}^{\infty }{ϵ}_n.}$

Assumption 2.

(C1) 

$\underset{n\to \infty }{lim}{\alpha }_n=0$ and ${\displaystyle \sum _{n=0}^{\infty }{\alpha }_n=\infty }$;

(C2) 

${\displaystyle \underset{n\to \infty }{lim}\frac{{\alpha }_n-{\alpha }_{n+1}}{{\alpha }_n^2}=0}$;

(C3) 

${\displaystyle \underset{n\to \infty }{lim}\frac{{\xi }_n}{{\alpha }_n}=0}$; and

(C4) 

$\mathrm{GEP}(f,\mathcal{A})\ne \varnothing .$

Theorem 1.

Assume $\mathcal{C}$ is a nonempty convex closed subsets of real Hilbert space $\mathcal{H}$, $f:\mathcal{H}\times \mathcal{H}\to \mathbb{R}$ is a bifunction satisfying (A1)–(A4), $\mathcal{A}:\mathcal{H}\to \mathcal{H}$ is L-Lipschitz continuous and monotone. Then, the sequence $\left\{x_n\right\}$ constructed by Algorithm 4 converges strongly to the unique solution $x^{†}$ of the $\mathrm{VIOGE}$ (8) under Assumption 2 (C1)–(C4).

Algorithm 4: The Tseng’s extragradient method with regularization (TEGMR).

Initialization: Take $\left\{{\xi }_n\right\}\subset (0,+\infty )$, $\left\{{\alpha }_n\right\}\subset (0,+\infty )$, $\rho >0$, ${\eta }_0>0$, $\upsilon \in (0,1)$. Choose a nonnegative real sequence $\left\{{ϵ}_n\right\}$ such that ${\displaystyle \sum _{n=0}^{\infty }{ϵ}_n<\infty }$. Let $x_0,x_1\in \mathcal{H}$ is arbitrary. Step 1.Compute $$u_n=x_n+{\mu }_n(x_n-x_{n-1}),$$ where $${\mu }_n=\left\{\begin{array}{c}min\{\frac{{\xi }_n}{∥x_n-x_{n-1}∥},\rho \},\mathrm{if}{x}_n\ne x_{n-1};\hfill \\ \rho ,\mathit{otherwise}.\hfill \end{array}\right.$$ (26) Step 2.  Given $x_n(n\ge 0)$, compute $$y_n=T_{{\eta }_n}^f\left(u_n-{\eta }_n(\mathcal{A}{u}_n+{\alpha }_n\mathcal{F}{u}_n)\right),$$ where $\left\{{\eta }_n\right\}$ is updated by $${\eta }_{n+1}=\left\{\begin{array}{c}min\{\frac{\upsilon ∥u_n-y_n∥}{∥\mathcal{A}{u}_n-\mathcal{A}{y}_n∥},{\eta }_n+{ϵ}_n\},\mathrm{if}\mathcal{A}{u}_n-\mathcal{A}{y}_n\ne 0;\hfill \\ {\eta }_n+{ϵ}_n,\mathit{otherwise}.\hfill \end{array}\right.$$ (27) Step 3.  Compute $$x_{n+1}=y_n-{\eta }_n(\mathcal{A}{y}_n-\mathcal{A}{u}_n).$$ Step 4.  Set $n:=n+1$ and return to  Step 1.

Proof. 

In view of Lemma 6(ii) and (C1), one obtains $x_{{\alpha }_n}\to x^{†}$ as $n\to \infty$. Therefore, it is sufficient to show that

$$\begin{array}{c}\hfill {\displaystyle \underset{n\to \infty }{lim}∥x_n-x_{{\alpha }_n}∥=0.}\end{array}$$

Observe that

$$\begin{array}{ccc}\hfill {∥x_{n+1}-x_{{\alpha }_n}∥}^2& =& {∥y_n-{\eta }_n(\mathcal{A}{y}_n-\mathcal{A}{u}_n)-x_{{\alpha }_n}∥}^2\hfill \\ & =& {∥y_n-x_{{\alpha }_n}∥}^2+{\eta }_n^2{∥\mathcal{A}{y}_n-\mathcal{A}{u}_n∥}^2-2{\eta }_n⟨y_n-x_{{\alpha }_n},\mathcal{A}{y}_n-\mathcal{A}{u}_n⟩.\hfill \end{array}$$

(28)

We also notice that

$$\begin{array}{c}\hfill {∥y_n-x_{{\alpha }_n}∥}^2={∥y_n-u_n∥}^2+{∥u_n-x_{{\alpha }_n}∥}^2+2⟨y_n-u_n,u_n-x_{{\alpha }_n}⟩\end{array}$$

(29)

and

$$\begin{array}{ccc}\hfill 2⟨y_n-u_n,u_n-x_{{\alpha }_n}⟩& =& 2⟨y_n-u_n,u_n-y_n⟩+2⟨y_n-u_n,y_n-x_{{\alpha }_n}⟩\hfill \\ & =& -2{∥y_n-u_n∥}^2+2⟨y_n-u_n,y_n-x_{{\alpha }_n}⟩.\hfill \end{array}$$

(30)

Substituting (29) and (30) into (31), one finds

$$\begin{array}{ccc}\hfill & & {∥x_{n+1}-x_{{\alpha }_n}∥}^2\hfill \\ & =& {∥u_n-x_{{\alpha }_n}∥}^2-{∥y_n-u_n∥}^2+2⟨y_n-u_n,y_n-x_{{\alpha }_n}⟩+{\eta }_n^2{∥\mathcal{A}{y}_n-\mathcal{A}{u}_n∥}^2\hfill \\ & & -2{\eta }_n⟨y_n-x_{{\alpha }_n},\mathcal{A}{y}_n-\mathcal{A}{u}_n⟩.\hfill \end{array}$$

(31)

Since $x_{\alpha }$ is a solution of RGEP (13) for each $\alpha >0$, we obtain, by Remark 2, that

$$\begin{array}{c}\hfill x_{{\alpha }_n}=T_{{\eta }_n}^f(x_{{\alpha }_n}-{\eta }_n(\mathcal{A}{x}_{{\alpha }_n}+{\alpha }_n\mathcal{F}{x}_{{\alpha }_n})).\end{array}$$

(32)

In view of Lemma 1(ii), one finds that

$$\begin{array}{ccc}& & {∥y_n-x_{{\alpha }_n}∥}^2\hfill \\ & =& {∥T_{{\eta }_n}^f\left(u_n-{\eta }_n(\mathcal{A}{u}_n+{\alpha }_n\mathcal{F}{u}_n)\right)-T_{{\eta }_n}^f(x_{{\alpha }_n}-{\eta }_n(\mathcal{A}{x}_{{\alpha }_n}+{\alpha }_n\mathcal{F}{x}_{{\alpha }_n}))∥}^2\hfill \\ & \le & ⟨T_{{\eta }_n}^f\left(u_n-{\eta }_n(\mathcal{A}{u}_n+{\alpha }_n\mathcal{F}{u}_n)\right)-T_{{\eta }_n}^f(x_{{\alpha }_n}-{\eta }_n(\mathcal{A}{x}_{{\alpha }_n}+{\alpha }_n\mathcal{F}{x}_{{\alpha }_n})),\hfill \\ & & \left(u_n-{\eta }_n(\mathcal{A}{u}_n+{\alpha }_n\mathcal{F}{u}_n)\right)-(x_{{\alpha }_n}-{\eta }_n(\mathcal{A}{x}_{{\alpha }_n}+{\alpha }_n\mathcal{F}{x}_{{\alpha }_n}))⟩\hfill \\ & =& ⟨y_n-x_{{\alpha }_n},\left(u_n-{\eta }_n(\mathcal{A}{u}_n+{\alpha }_n\mathcal{F}{u}_n)\right)-(x_{{\alpha }_n}-{\eta }_n(\mathcal{A}{x}_{{\alpha }_n}+{\alpha }_n\mathcal{F}{x}_{{\alpha }_n}))⟩,\hfill \end{array}$$

which implies

$$\begin{array}{c}\hfill ⟨y_n-x_{{\alpha }_n},\left(u_n-{\eta }_n(\mathcal{A}{u}_n+{\alpha }_n\mathcal{F}{u}_n)\right)-(x_{{\alpha }_n}-{\eta }_n(\mathcal{A}{x}_{{\alpha }_n}+{\alpha }_n\mathcal{F}{x}_{{\alpha }_n}))⟩-{∥y_n-x_{{\alpha }_n}∥}^2\ge 0.\end{array}$$

That is,

$$\begin{array}{c}\hfill ⟨y_n-x_{{\alpha }_n},u_n-y_n-{\eta }_n(\mathcal{A}{u}_n+{\alpha }_n\mathcal{F}{u}_n)+{\eta }_n(\mathcal{A}{x}_{{\alpha }_n}+{\alpha }_n\mathcal{F}{x}_{{\alpha }_n})⟩\ge 0,\end{array}$$

or equivalently

$$\begin{array}{c}\hfill ⟨y_n-x_{{\alpha }_n},u_n-y_n⟩\ge {\eta }_n⟨y_n-x_{{\alpha }_n},(\mathcal{A}{u}_n+{\alpha }_n\mathcal{F}{u}_n)-(\mathcal{A}{x}_{{\alpha }_n}+{\alpha }_n\mathcal{F}{x}_{{\alpha }_n})⟩.\end{array}$$

(33)

Substituting (33) into (31), noting (27) and the monotonicity of $\mathcal{A}$, one obtains

$$\begin{array}{ccc}\hfill & & {∥x_{n+1}-x_{{\alpha }_n}∥}^2\hfill \\ & \le & {∥u_n-x_{{\alpha }_n}∥}^2-{∥y_n-u_n∥}^2-2{\eta }_n⟨y_n-x_{{\alpha }_n},(\mathcal{A}{u}_n+{\alpha }_n\mathcal{F}{u}_n)-(\mathcal{A}{x}_{{\alpha }_n}+{\alpha }_n\mathcal{F}{x}_{{\alpha }_n})⟩\hfill \\ & & +{\eta }_n^2{∥\mathcal{A}{y}_n-\mathcal{A}{u}_n∥}^2-2{\eta }_n⟨y_n-x_{{\alpha }_n},\mathcal{A}{y}_n-\mathcal{A}{u}_n⟩\hfill \\ & =& {∥u_n-x_{{\alpha }_n}∥}^2-{∥y_n-u_n∥}^2+{\eta }_n^2{∥\mathcal{A}{y}_n-\mathcal{A}{u}_n∥}^2\hfill \\ & & -2{\eta }_n⟨y_n-x_{{\alpha }_n},\mathcal{A}{y}_n-\mathcal{A}{x}_{{\alpha }_n}⟩-2{\alpha }_n{\eta }_n⟨y_n-x_{{\alpha }_n},\mathcal{F}{u}_n-\mathcal{F}{x}_{{\alpha }_n}⟩\hfill \\ & \le & {∥u_n-x_{{\alpha }_n}∥}^2-{∥y_n-u_n∥}^2+{\eta }_n^2{∥\mathcal{A}{y}_n-\mathcal{A}{u}_n∥}^2+2{\alpha }_n{\eta }_n⟨y_n-x_{{\alpha }_n},\mathcal{F}{x}_{{\alpha }_n}-\mathcal{F}{u}_n⟩\hfill \\ & \le & {∥u_n-x_{{\alpha }_n}∥}^2-{∥y_n-u_n∥}^2+{\eta }_n^2\frac{{\upsilon }^2}{{\eta }_{n+1}^2}{∥y_n-u_n∥}^2+2{\alpha }_n{\eta }_n⟨y_n-x_{{\alpha }_n},\mathcal{F}{x}_{{\alpha }_n}-\mathcal{F}{u}_n⟩\hfill \\ & \le & {∥u_n-x_{{\alpha }_n}∥}^2-\left(1-\frac{{\upsilon }^2{\eta }_n^2}{{\eta }_{n+1}^2}\right){∥y_n-u_n∥}^2+2{\alpha }_n{\eta }_n⟨y_n-x_{{\alpha }_n},\mathcal{F}{x}_{{\alpha }_n}-\mathcal{F}{u}_n⟩.\hfill \end{array}$$

(34)

Now, select three positive numbers ${\sigma }_1,{\sigma }_2,{\sigma }_3\in (0,1)$ such that

$$2\tau -{\sigma }_{1}k-{\sigma }_2-{\sigma }_3>0.$$

(35)

We estimate the last term in (34) as follows

$$\begin{array}{ccc}\hfill & & 2⟨y_n-x_{{\alpha }_n},\mathcal{F}{x}_{{\alpha }_n}-\mathcal{F}{u}_n⟩\hfill \\ & =& 2⟨y_n-u_n,\mathcal{F}{x}_{{\alpha }_n}-\mathcal{F}{u}_n⟩+2⟨u_n-x_{{\alpha }_n},\mathcal{F}{x}_{{\alpha }_n}-\mathcal{F}{u}_n⟩\hfill \\ & \le & 2k∥y_n-u_n∥∥x_{{\alpha }_n}-u_n∥-2\tau {∥u_n-x_{{\alpha }_n}∥}^2\hfill \\ & \le & k\frac{1}{{\sigma }_1}{∥y_n-u_n∥}^2+k{\sigma }_1{∥x_{{\alpha }_n}-u_n∥}^2-2\tau {∥u_n-x_{{\alpha }_n}∥}^2,\hfill \end{array}$$

which, together with (34), yields

$$\begin{array}{ccc}\hfill & & {∥x_{n+1}-x_{{\alpha }_n}∥}^2\hfill \\ & \le & {∥u_n-x_{{\alpha }_n}∥}^2-\left(1-\frac{{\upsilon }^2{\eta }_n^2}{{\eta }_{n+1}^2}\right){∥y_n-u_n∥}^2\hfill \\ & & +{\alpha }_n{\eta }_n\left(k\frac{1}{{\sigma }_1}{∥y_n-u_n∥}^2+k{\sigma }_1{∥x_{{\alpha }_n}-u_n∥}^2-2\tau {∥u_n-x_{{\alpha }_n}∥}^2\right)\hfill \\ & =& (1-(2\tau -{\sigma }_{1}k){\alpha }_n{\eta }_n){∥u_n-x_{{\alpha }_n}∥}^2-\left(1-\frac{{\upsilon }^2{\eta }_n^2}{{\eta }_{n+1}^2}-\frac{k{\alpha }_n{\eta }_n}{{\sigma }_1}\right){∥y_n-u_n∥}^2.\hfill \end{array}$$

(36)

Utilizing assumptions $\upsilon \in (0,1)$, ${\alpha }_n\to 0$ and applying Lemma 7 and Assumption 2 (C3), it follows that there exists $n_0\ge 1$ such that

$$1-\frac{{\upsilon }^2{\eta }_n^2}{{\eta }_{n+1}^2}-\frac{k{\alpha }_n{\eta }_n}{{\sigma }_1}>0,{\xi }_n<1\mathrm{and}{\xi }_n\le {\sigma }_2{\alpha }_n{\eta }_n,\forall n\ge n_0.$$

(37)

Consequently, from (36) and (37), we find that

$$\begin{array}{c}\hfill {∥x_{n+1}-x_{{\alpha }_n}∥}^2\le (1-(2\tau -{\sigma }_{1}k){\alpha }_n{\eta }_n){∥u_n-x_{{\alpha }_n}∥}^2.\end{array}$$

(38)

From (37), we find ${\xi }_n<1,\forall n\ge n_0$. Then, we deduce that ${\xi }_n^2<{\xi }_n,\forall n\ge n_0$. Utilizing (26) and (37), one deduces that

$$\begin{array}{ccc}\hfill {∥u_n-x_{{\alpha }_n}∥}^2& =& {∥x_n+{\mu }_n(x_n-x_{n-1})-x_{{\alpha }_n}∥}^2\hfill \\ & \le & {(∥x_n-x_{{\alpha }_n}∥+{\mu }_n∥x_n-x_{n-1}∥)}^2\hfill \\ & \le & {∥x_n-x_{{\alpha }_n}∥}^2+{\mu }_n^2{∥x_n-x_{n-1}∥}^2+2∥x_n-x_{{\alpha }_n}∥{\mu }_n∥x_n-x_{n-1}∥\hfill \\ & \le & {∥x_n-x_{{\alpha }_n}∥}^2+{\xi }_n^2+2∥x_n-x_{{\alpha }_n}∥{\xi }_n\hfill \\ & \le & {∥x_n-x_{{\alpha }_n}∥}^2+{\xi }_n^2+{∥x_n-x_{{\alpha }_n}∥}^2{\xi }_n+{\xi }_n\hfill \\ & \le & (1+{\xi }_n){∥x_n-x_{{\alpha }_n}∥}^2+2{\xi }_n\hfill \\ & \le & (1+{\sigma }_2{\alpha }_n{\eta }_n){∥x_n-x_{{\alpha }_n}∥}^2+2{\xi }_n.\hfill \end{array}$$

(39)

On the other hand, in terms of the Cauchy–Schwartz inequality, one concludes that

$$2∥x_{{\alpha }_{n+1}}-x_{n+1}∥∥x_{{\alpha }_{n+1}}-x_{{\alpha }_n}∥\le \frac{1}{{\sigma }_3{\alpha }_n{\eta }_n}{∥x_{{\alpha }_{n+1}}-x_{{\alpha }_n}∥}^2+{\sigma }_3{\alpha }_n{\eta }_n{∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2.$$

(40)

Thus, for each $n\ge n_0$, one obtains from (40) and Lemma 6(iii) that

$$\begin{array}{ccc}& & {∥x_{{\alpha }_n}-x_{n+1}∥}^2\hfill \\ & =& {∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2+{∥x_{{\alpha }_{n+1}}-x_{{\alpha }_n}∥}^2-2⟨x_{{\alpha }_{n+1}}-x_{n+1},x_{{\alpha }_{n+1}}-x_{{\alpha }_n}⟩\hfill \\ & \ge & {∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2+{∥x_{{\alpha }_{n+1}}-x_{{\alpha }_n}∥}^2-2∥x_{{\alpha }_{n+1}}-x_{n+1}∥∥x_{{\alpha }_{n+1}}-x_{{\alpha }_n}∥\hfill \\ & \ge & {∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2+{∥x_{{\alpha }_{n+1}}-x_{{\alpha }_n}∥}^2-\frac{1}{{\sigma }_3{\alpha }_n{\eta }_n}{∥x_{{\alpha }_{n+1}}-x_{{\alpha }_n}∥}^2-{\sigma }_3{\alpha }_n{\eta }_n{∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2\hfill \\ & \ge & (1-{\sigma }_3{\alpha }_n{\eta }_n){∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2-\frac{1-{\sigma }_3{\alpha }_n{\eta }_n}{{\sigma }_3{\alpha }_n{\eta }_n}{∥x_{{\alpha }_{n+1}}-x_{{\alpha }_n}∥}^2\hfill \\ & \ge & (1-{\sigma }_3{\alpha }_n{\eta }_n){∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2-\frac{1-{\sigma }_3{\alpha }_n{\eta }_n}{{\sigma }_3{\alpha }_n{\eta }_n}{\left(\frac{{\alpha }_{n+1}-{\alpha }_n}{{\alpha }_n}\right)}^2{M}^2\hfill \\ & =& (1-{\sigma }_3{\alpha }_n{\eta }_n){∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2-\frac{(1-{\sigma }_3{\alpha }_n{\eta }_n){({\alpha }_{n+1}-{\alpha }_n)}^2}{{\sigma }_3{\alpha }_n^3{\eta }_n}{M}^2,\hfill \end{array}$$

which yields

$${∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2\le \frac{1}{1-{\sigma }_3{\alpha }_n{\eta }_n}{∥x_{n+1}-x_{{\alpha }_n}∥}^2+\frac{{({\alpha }_{n+1}-{\alpha }_n)}^2}{{\sigma }_3{\alpha }_n^3{\eta }_n}{M}^2.$$

(41)

By relation (35), (38), (39) and (41), one finds

$$\begin{array}{ccc}\hfill & & {∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2\hfill \\ & \le & \frac{1-(2\tau -{\sigma }_{1}k){\alpha }_n{\eta }_n}{1-{\sigma }_3{\alpha }_n{\eta }_n}{∥u_n-x_{{\alpha }_n}∥}^2+\frac{{({\alpha }_{n+1}-{\alpha }_n)}^2}{{\sigma }_3{\alpha }_n{\eta }_n^3}{M}^2\hfill \\ & \le & \frac{(1-(2\tau -{\sigma }_{1}k){\alpha }_n{\eta }_n)(1+{\sigma }_2{\alpha }_n{\eta }_n)}{1-{\sigma }_3{\alpha }_n{\eta }_n}{∥x_n-x_{{\alpha }_n}∥}^2+\frac{1-(2\tau -{\sigma }_{1}k){\alpha }_n{\eta }_n}{1-{\sigma }_3{\alpha }_n{\eta }_n}2{\xi }_n\hfill \\ & & +\frac{{({\alpha }_{n+1}-{\alpha }_n)}^2}{{\sigma }_3{\alpha }_n^3{\eta }_n}{M}^2\hfill \\ & \le & \frac{1-(2\tau -{\sigma }_{1}k-{\sigma }_2){\alpha }_n{\eta }_n}{1-{\sigma }_3{\alpha }_n{\eta }_n}{∥x_n-x_{{\alpha }_n}∥}^2-\frac{(2\tau -{\sigma }_{1}k){\sigma }_2{\eta }_n^2{\alpha }_n^2}{1-{\sigma }_3{\alpha }_n{\eta }_n}{∥x_n-x_{{\alpha }_n}∥}^2\hfill \\ & & +\frac{1-(2\tau -{\sigma }_{1}k){\alpha }_n{\eta }_n}{1-{\sigma }_3{\alpha }_n{\eta }_n}2{\xi }_n+\frac{{({\alpha }_{n+1}-{\alpha }_n)}^2}{{\sigma }_3{\alpha }_n^3{\eta }_n}{M}^2\hfill \\ & \le & \frac{1-(2\tau -{\sigma }_{1}k-{\sigma }_2){\alpha }_n{\eta }_n}{1-{\sigma }_3{\alpha }_n{\eta }_n}{∥x_n-x_{{\alpha }_n}∥}^2+4{\xi }_n+\frac{{({\alpha }_{n+1}-{\alpha }_n)}^2}{{\sigma }_3{\alpha }_n^3{\eta }_n}{M}^2\hfill \\ & =& (1-a_n){∥x_n-x_{{\alpha }_n}∥}^2+b_n,\hfill \end{array}$$

(42)

where $a_n=\frac{(2\tau -{\sigma }_{1}k-{\sigma }_2-{\sigma }_3){\alpha }_n{\eta }_n}{1-{\sigma }_3{\alpha }_n{\eta }_n}$ and $b_n=4{\xi }_n+\frac{{({\alpha }_{n+1}-{\alpha }_n)}^2}{{\sigma }_3{\alpha }_n^3{\eta }_n}{M}^2.$ By condition (C1), one obtains that $a_n\to 0$ and ${\displaystyle \sum _{n=1}^{\infty }{a}_n=+\infty }$. Furthermore, one derives from condition (C2) and (C3) that

$$\frac{b_n}{a_n}=\left(\frac{4{\xi }_n}{{\alpha }_n}+\frac{{({\alpha }_{n+1}-{\alpha }_n)}^2}{{\sigma }_3{\alpha }_n^4{\eta }_n}{M}^2\right)\left(\frac{1-{\sigma }_3{\alpha }_n{\eta }_n}{(2\tau -{\sigma }_{1}k-{\sigma }_2-{\sigma }_3){\eta }_n}\right)\to 0.$$

Applying Lemma 5 to (42), one infers ${\displaystyle \underset{n\to \infty }{lim}∥x_n-x_{{\alpha }_n}∥=0}$. Thus, one finds ${\displaystyle \underset{n\to \infty }{lim}∥x_n-x^{†}∥=0}$.  □

4. Application to the BVIP

Assume $\mathcal{C}$ be a closed convex and nonempty subset of $\mathbb{R}$. Further assume $f(x,y)\equiv 0$ , $\forall x,y\in \mathcal{C}$. Noticing Proposition 1, one obtains $T_{{\eta }_n}^f=P_{\mathcal{C}}.$ Furthermore, the VIOGE becomes the BVIP. Next, by Theorem 1, we give the following result for the BVIP.

Theorem 2.

Assume that $\mathcal{C}$ is a closed convex and nonempty subset of Hilbert space $\mathcal{H}$, $\mathcal{A}:\mathcal{C}\to \mathcal{H}$ is L-Lipschitz continuous and monotone. Further, assume $\mathrm{VI}(\mathcal{C},\mathcal{A})\ne \varnothing .$ Then, the sequence $\left\{x_n\right\}$ constructed by Algorithm 5 converges strongly to the unique solution $x^{†}$ to the BVIP (7) under Assumption 2 (C1)–(C4).

Algorithm 5: Tseng’s extragradient method with regularization for the BVIP.

Initialization: Take $\left\{{\xi }_n\right\}\subset (0,+\infty )$, $\left\{{\alpha }_n\right\}\subset (0,+\infty )$, $\rho >0$, ${\eta }_0>0$, $\upsilon \in (0,1)$. Choose a nonnegative real sequence $\left\{{ϵ}_n\right\}$ such that ${\displaystyle \sum _{n=0}^{\infty }{ϵ}_n<\infty }$. Let $x_0,x_1\in \mathcal{H}$ be arbitrary. Step 1.Compute $$u_n=x_n+{\mu }_n(x_n-x_{n-1}),$$ where $${\mu }_n=\left\{\begin{array}{c}min\{\frac{{\xi }_n}{∥x_n-x_{n-1}∥},\rho \},\mathrm{if}{x}_n\ne x_{n-1};\hfill \\ \rho ,\mathit{otherwise}.\hfill \end{array}\right.$$ Step 2.Given $x_n(n\ge 0)$, compute $$y_n=P_{\mathcal{C}}\left(u_n-{\eta }_n(\mathcal{A}{u}_n+{\alpha }_n\mathcal{F}{u}_n)\right).$$ Step 3.Compute $$x_{n+1}=y_n-{\eta }_n(\mathcal{A}{y}_n-\mathcal{A}{u}_n).$$ where $\left\{{\eta }_n\right\}$ is updated by $${\eta }_{n+1}=\left\{\begin{array}{c}min\{\frac{\upsilon ∥u_n-y_n∥}{∥\mathcal{A}{u}_n-\mathcal{A}{y}_n∥},{\eta }_n+{ϵ}_n\},\mathrm{if}\mathcal{A}{u}_n-\mathcal{A}{y}_n\ne 0;\hfill \\ {\eta }_n+{ϵ}_n,\mathit{otherwise}.\hfill \end{array}\right.$$ Step 4.Set $n:=n+1$ and go back toStep 1.

5. Numerical Examples

In this subsection, several numerical examples are supported to show the behavior and performance of our Algorithm 4 (TEGMR) as well as comparing it with Algorithm 1 (TEGM of Tseng [18]), Algorithm 2 (STEGM of Yang et al. [19]) and Algorithm 3 (SVTEGM of Tan and Qin [20]).

Example 3.

Let $\mathcal{H}=l_2\left(\mathbb{R}\right)$ be the linear spaces whose elements are all 2-summable sequences of scalars in $\mathbb{R}$—namely,

$${\displaystyle l_2\left(\mathbb{R}\right):=\{x=(x_1,x_2,\cdots ,x_j,\cdots ),x_j\in \mathbb{R}\mathit{and}\sum _{j=1}^{\infty }|x_j{|}^2<\infty \}}$$

with inner product $⟨·,·⟩:\mathcal{H}\times \mathcal{H}\to \mathbb{R}$ and ${∥·∥}_{l_2}:\mathcal{H}\to \mathbb{R}$ defined by ${\displaystyle ⟨x,y⟩:=\sum _{j=1}^{\infty }{x}_j{y}_j}$ and ${∥·∥}_{l_2}:={\left({\displaystyle \sum _{j=1}^{\infty }{\left|x_j\right|}^2}\right)}^{1/2}$, respectively, where ${\left\{x_j\right\}}_{j=1}^{\infty }$, ${\left\{y_i\right\}}_{i=1}^{\infty }$. Let $\mathcal{F}:\mathcal{H}\to \mathcal{H}$ be defined by $\mathcal{F}x=\frac{x}{6}$, $\mathcal{A}:\mathcal{H}\to \mathcal{H}$ be defined by $\mathcal{A}x=\frac{x}{4}$, $\forall x={\left\{x_j\right\}}_{j=1}^{\infty }\in \mathcal{H}.$ Then, ${\mathcal{A}}^{*}x=\frac{x}{4}$, $\forall x={\left\{x_j\right\}}_{j=1}^{\infty }\in \mathcal{H}.$ Define the set $\mathcal{C}:=\{x\in \mathcal{H}:∥x∥<1\}$. Let the bifunctions $f:\mathcal{H}\times \mathcal{H}\to \mathbb{R}$ be given by $f(x,y)=2y^2+3xy-5x^2$ for all $x,y\in \mathcal{H}$. We find that $T_{\eta }^f=\frac{x}{1+7\eta }$, and 0 is a unique solution to VIOGE (8). Choose ${\alpha }_n={(n+1)}^{-0.9}$, ${\xi }_n={(n+1)}^{-0.8}$, $\rho =0.4$, ${\eta }_0=\nu =0.6$. The stopping criterion used for our computation is $∥x_{n+1}-x_n∥<{10}^{-3}.$ We test our Algorithm 4 for different values of $x_0$ and $x_1$ as follows:

Case I: $x_0=\left(\frac{2}{3},\frac{1}{9},\frac{2}{5},0,\dots ,0,\dots \right)$ and $x_1=\left(\frac{7}{6},\frac{10}{11},\frac{1}{9},0,\dots ,0,\dots \right)$;

Case II: $x_0=\left(\frac{4}{3},\frac{5}{3},\frac{2}{3},0,\dots ,0,\dots \right)$ and $x_1=\left(\frac{5}{7},\frac{4}{5},\frac{6}{5},0,\dots ,0,\dots \right)$;

Case III: $x_0=\left(3,3,\frac{19}{6},0,\dots ,0,\dots \right)$ and $x_1=\left(\frac{5}{3},\frac{11}{4},\frac{7}{5},0,\dots ,0,\dots \right)$; and

Case IV: $x_0=\left(\frac{50}{9},\frac{73}{11},6,0,\dots ,0,\dots \right)$ and $x_1=\left(\frac{76}{9},6,\frac{11}{2},0,\dots ,0,\dots \right)$.

Example 4.

Let $\mathcal{H}=L^2\left([0,1]\right)$ with norm ${∥x∥}_{L^2}={\left({\int }_0^1{\left|x\left(t\right)\right|}^{2}dt\right)}^{\frac{1}{2}}$ and inner product $⟨x,y⟩={\int }_0^{1}x\left(t\right)y\left(t\right)dt$, $x,y\in L^2\left([0,1]\right)$. The feasible set $\mathcal{C}$ is given by $\mathcal{C}=\{x\in L^2\left([0,1]\right):∥x∥\le 1\}.$ We choose ${\alpha }_n={(n+1)}^{-0.9},$ $\nu ={\lambda }_0=\frac{1}{2},{\xi }_n={(n+1)}^{-0.8},$ $\rho =\frac{3}{10},r_n=\frac{3}{5},{\beta }_n=\frac{1}{8}.$ Let $f:\mathcal{H}\times \mathcal{H}\to \mathbb{R}$ be given by $f(x,y)=y^2-x^2$, $\mathcal{A}:\mathcal{H}\to \mathcal{H}$ be given by $\mathcal{A}x=\frac{x}{4}$, $\mathcal{F}:\mathcal{H}\to \mathcal{H}$ be given by $fx=\frac{x}{6}$ for all $x\in \mathcal{H}$. We find that A is monotone and $\frac{1}{4}$-Lipschitz continuous. It is easy to check that $T_{\eta }^f=\frac{x}{1+7\eta }$ and 0 is unique solution to VIOGE (8). Let us ${\alpha }_n={(n+1)}^{-0.9}$, ${\xi }_n={(n+1)}^{-0.8}$, $\rho =0.4$, ${\eta }_0=\nu =0.6$. Using $∥x_{n+1}-x_n∥<{10}^{-3}$ as our stopping criterion, we test our Algorithm 4 for different values of $x_0$ and $x_1$ as follows:

Case I: $x_0=2t^3$ and $x_1=t+1$;

Case II: $x_0=2t^4+t^2-6$ and $x_1=3t$;

Case III: $x_0=cost$ and $x_1=sint$; and

Case IV: $x_0=3e^t$ and $x_1=e^t$.

Example 5.

Let $\mathcal{H}={\mathbb{R}}^m$ with inner product $⟨·,·⟩:\mathcal{H}\times \mathcal{H}\to \mathbb{R}$ defined by ${\displaystyle ⟨x,y⟩:=\sum _{j=1}^m{x}_j{y}_j}$. Let $\mathcal{A}=N^{T}Nx+p$, where q is a vector in ${\mathbb{R}}^m$ and N is a $m\times m$ matrix. Let $\mathcal{F}\left(x\right)=Qx+q$ where Q is a symmetric and positive-definite matrix of size $m\times m$, and q is a vector in ${\mathbb{R}}^m$. It is easy to check that $\mathcal{A}$ is monotone and Lipschitz continuous with the constant $L={∥N∥}^2$, and $\mathcal{F}$ is Lipschitz continuous and strongly monotone. Define the set $\mathcal{C}:=\{x\in \mathcal{H}:∥x∥<1\}$. Let the bifunctions $f:\mathcal{H}\times \mathcal{H}\to \mathbb{R}$ be given by $f(x,y)=2y^2+3xy-5x^2$ for all $x,y\in \mathcal{H}$. We deduce that $T_{\eta }^f=\frac{x}{1+7\eta }$. Furthermore, 0 is unique solution to VIOGE (8). Choose ${\alpha }_n={(n+1)}^{-0.9}$, ${\xi }_n={(n+1)}^{-0.8}$, $\rho =0.4$, ${\eta }_0=\nu =0.6$. The maximum number of iterations is 300 as the stopping criterion and the initial values $x_0$ are randomly generated by rand $(0,1)$ in MATLAB. We test Algorithm 4 with different values m as follows.

According to Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, one finds that the TEGMR performs better than TEGM, STEGM and SVTEGM in terms of the CPU-time taken for computation.

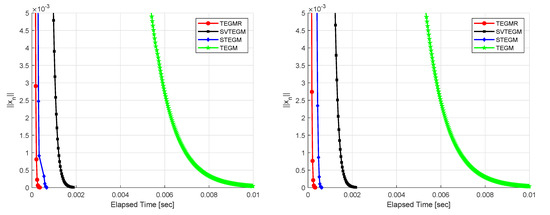
Figure 1. Example 3, (left): Case I and (right): Case II.

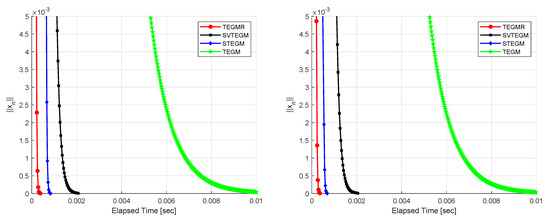
Figure 2. Example 3, (left): Case III and (right): Case IV.

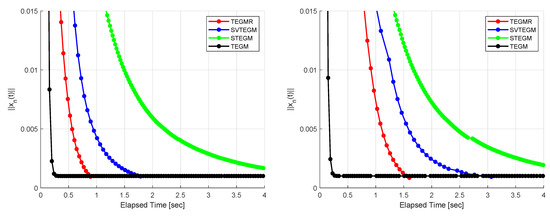
Figure 3. Example 4, (left): Case I and (right): Case II.

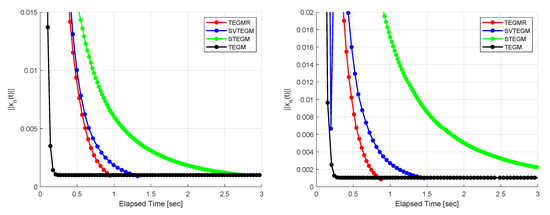
Figure 4. Example 4, (left): Case III and (right): Case IV.

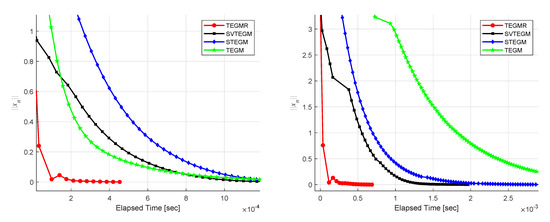
Figure 5. Example 5, (left): m = 5 and (right): m = 10.

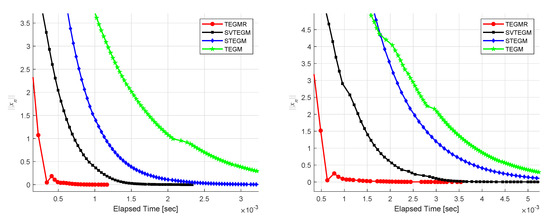
Figure 6. Example 5, (left): m = 100 and (right): m = 200.

6. Conclusions

In the paper, we considered a more general bilevel problem: a variational inequality over the set of solutions of the generalized equilibrium problem in a Hilbert space. The new proposed problem covers many well-known problems, such as the bilevel variational inequality problem, generalized equilibrium problem and bilevel optimization problems. We also introduced a new iterative method for solving the proposed bilevel problem in real Hilbert spaces.

The introduced method was constructed around the TEGM, the inertial idea and the regularization technique, and we used a non-monotonic stepsize rule without any line search procedure. Under some suitable conditions, strong convergence of the sequences generated by the proposed method was obtained. Several numerical experiments were also provided to demonstrate the effectiveness and the fast convergence of the new method over certain known methods.