Abstract
Geosynchronous orbit (GEO) is a very important strategic resource. In order to maximize the utilization of the GEO resources, the use of all-electric propulsion GEO platforms can greatly extend the service life of satellites. Therefore, this paper proposes a control scheme of the north/south station keeping (NSSK) by using electric propulsion with a manipulator. First, on the basis of the traditional calculation method of the semi-diurnal period of the orbital inclination, the calculation method of the semi-monthly period and the semi-annual period of the orbital inclination are proposed. The new method can reduce the fuel consumption and reduce the control amount and control frequency of the station keeping (SK). Secondly, a fuel-optimized NSSK algorithm by using electric propulsion with a manipulator is proposed. The algorithm can not only be applied to a large initial orbital inclination but also can unload the large angular momentum of the asymmetric satellites while keeping the north/south station, thereby avoiding the loss of control of the satellite’s attitude. The research results of this paper provide a new idea for the SK control of the GEO satellites and have great engineering application value.
MSC:
85-10
1. Introduction
Geosynchronous orbit (GEO) satellites [,] rotate in the same direction as the earth’s rotation. Its orbital period is equal to the earth’s rotation period, the orbital plane coincides with the earth’s equatorial plane, and the orbital semi-major axis is also a constant (about 42,165.7 km). Therefore, the ideal GEO satellite is stationary relative to any point on the earth, and the continuous and uninterrupted communication can be achieved by using a fixed-point antenna at a fixed point on the ground. At the same time, due to the high orbital altitude of the GEO satellites and a wide range of ground coverage, a GEO satellite can perform long-term repeated observations on about one-third of the world’s mid- and low-latitude regions. Due to these characteristics, GEO satellites can be widely used in communication, navigation and meteorological observation and other fields. Therefore, the GEO is actually a very important strategic resource.
However, under the action of various natural perturbations, satellites in GEO will gradually drift away from the original orbit, which will not only reduce the work efficiency of satellites but may also cause satellites in GEO to collide. Therefore, orbital control of the GEO satellite is required on a regular basis to keep the GEO satellite near the designed orbital position. Similarly, under the action of various natural perturbation torques, the angular momentum of the GEO satellite will gradually accumulate and may exceed the capacity of the on-board angular momentum storage device (here, the on-board angular momentum storage device generally refers to the flywheel or the control moment gyro). At the limit, it will cause the satellite’s attitude to be out of control and unable to work, and it may even cause the satellite to be scrapped early and become space junk because it cannot obtain enough solar energy. Therefore, it is necessary to unload the angular momentum of the GEO satellite regularly, so that the angular momentum of the on-board angular momentum storage device is always within the limit range, and it can always have sufficient control capability of the attitude to maintain the stability of the satellite’s attitude and ensure the safety of the energy of the GEO satellite.
In order to maximize the utilization of the GEO resources, large-scale high-carrying ratio and long-life satellite platforms are the future development trend []. Conventional station keeping (SK) of the GEO satellite uses chemical thrusters. Zhang [] used dual tangential thrust control to realize the EWSK and NWSK. It adopts the iterative shooting method to obtain the optimal orbital control interval that meets the requirements of positional accuracy. Simulation shows that this method can achieve an SK accuracy of 0.005°. Li [,] combined engineering practice to introduce several kinds of strategies of the SK of the GEO satellite based on pulse thrust in detail, and they analyzed the advantages, disadvantages and uses of various SK strategies. Park [], Li [], Shi [], etc. gave the co-location isolation strategy, the co-location strategy of multiple satellites and the design method of the corresponding nominal orbit based on the eccentricity vector and orbital inclination vector. Shi [] discussed the relationship between the orbital control period and the EWSK fuel consumption and gave an EWSK control strategy based on the pulse method. Li et al. [,,] introduced the EWSK method based on chemical thruster in detail, and they successfully applied it on the Fengyun-2 satellite. No [] designed the mean longitude keeping strategy based on dead zone control and the mean eccentricity keeping strategy based on the orbital eccentricity control by predicting the change of the mean eccentricity vector, and they realized the EWSK of the satellite. Yang [] adopted the LQG (Linear Quadratic Gaussian) method to achieve an accuracy of the EWSK of 0.05° and an accuracy of the NWSK of 0.02°. Yang [] draws on the idea of a “Deep Space One” intelligent autonomous control system structure and tries to design a GEO satellite SK strategy with strong autonomy. Vinod [] designed an EWSK strategy based on perigee pointing to the sun, which can effectively reduce the EWSK velocity increment. Chang [] adopted the method of equally spaced pulses to divide the jet volume required for one EWSK into several smaller jets, which reduced the interference of a single jet on the satellite attitude and improved the control accuracy of the mean longitude. The control amount needs to be calculated and bet on the ground.
However, the specific impulse of chemical propellants is low, and a greater amount of propellant is consumed for the velocity increments, which makes it difficult to ensure the long life requirement of the GEO satellite. The specific impulse of electric propulsion (EP) is 5–10 times that of chemical propulsion, and the propellant consumed to generate the same velocity increment is only about 10% of that of chemical propulsion. Configuring an all-EP system can not only increase the life of the GEO satellite but also reduce the weight of the satellite, which can meet the requirement of the high load-carrying ratio and long life of the GEO satellite.
In recent years, scholars have conducted a series of studies on the SK of the GEO satellite. Weiss [] introduced a Model Predictive Control (MPC)-based online real-time control algorithm for GEO satellite SK. Weiss developed a feedback control algorithm in the form of a linear quadratic constraint model over-policy control strategy, and through co-simulation with commercial software high-precision orbital dynamics, the satellite’s angular momentum management was realized, and the accuracy of the east/west station keeping or north/south station keeping reached 0.01°, which verifies the feasibility of real-time closed-loop high-precision SK. However, he assumed that electric thrusters were installed on all six surfaces of the satellite, leaving no layout space for solar panels and payload antennas. He assumed that the electric thrusters were variable thrust, which was inconsistent with the general switch-controlled constant small thrust model. In addition, his controller uses a 15-dimensional dynamic equation, which requires high computing power. Frederik [] used a convex optimization algorithm to study the problem of the high-precision SK of the GEO satellite based on pulse and small thrust. Gazzino [,] et al. decompose the SK problem into three steps to solve: the first step adopts the pulse method, and the optimal control sequence is obtained by the indirect method; the second step is to convert the pulse into a small thrust; the third step is to further optimize the moment of the low-thrust switch. Gazzino [,] considered the SK period and the orbital determination period as a whole, transformed the small thrust SK problem of the GEO satellite into a linear integer programming problem, and realized the sub-optimal fuel GEO SK. However, this strategy is computationally complex and can only be used on the ground. A.A. Sukhanov [] et al. introduced a small-thrust SK optimization algorithm, based on which the SK of the GEO satellite was achieved. Roth [] improved the optimization algorithm by taking the solar light pressure dynamics with earth shadow as one of the constraints of the global optimization of fuel for the nonlinear optimization problem of the small thrust SK of the GEO satellite.
The above-mentioned low-thrust position-keeping algorithm has a high dimension and a large amount of calculation; it needs to use a complex optimization algorithm []. Furthermore, some GEO satellites use asymmetric configurations (such as single-wing solar panels) due to the needs of payload work, which may cause the accumulation of the satellite’s daily angular momentum to reach 100 Nms []. Therefore, the angular momentum unloading must be performed every day; otherwise, the satellite will be affected by the actuator (flywheel or control moment gyroscope) exceeding its control limit and losing attitude control ability []. This paper proposes a control method of the north/south station keeping (NSSK) by using the electric propulsion (EP) with the manipulator. By placing the electric thruster at the end of the manipulator, the active adjustment of the position and direction of the manipulator end can be used to realize the unloading of the satellite’s angular momentum while keeping the north/south station.
The novel contributions of this paper are as follows:
- (1)
- The method proposed in this paper has great advantages in control accuracy and fuel consumption.
- (2)
- The method proposed in this paper can solve the problem that the angular momentum cannot be unloaded in the traditional NWSK method, and it prevents the satellite’s attitude from running out of control.
The structure of this paper is as follows: In Section 2, the basic concepts of the vernal equinox orbital elements is introduced. The calculation method of the mean orbital inclination for semi-monthly and semi-annual periods is proposed to be suitable for satellites with different control precision or fuel requirements. The NSSK accuracy and the required velocity increments for SK corresponding to different periods of the mean orbital inclination are analyzed. Section 3 proposes a strategy of using the EP with a manipulator to unload the large-scale angular momentum while in NSSK, and it proposes a zone control method based on the angular momentum unloading requirements The correctness of the method proposed in this paper is verified through mathematical simulation in Section 4; the full text is summarized in Section 5.
2. Calculation of the Mean Orbital Inclination under Different NSSK Accuracy
2.1. The Vernal Equinox Orbital Elements
For an ideal GEO, when , , the values of and are uncertain; they are only singular values in the mathematical sense. In order to avoid singular values in orbital calculation, this paper adopts the following vernal equinox orbital elements [] (pp. 61–64):
where
- is the orbital semi-major axis, the unit is m.
- is the mean orbital longitude, the unit is rad;
- is the Y-component of the orbital eccentricity vector, dimensionless;
- is the X-component of the orbital eccentricity vector, dimensionless;
- is the Y-component of the orbital inclination vector, the unit is rad;
- is the X-component of the orbital inclination vector, the unit is rad.
The expressions in formula (1) are expanded into:
where
- is the argument of perigee of the satellite in the J2000.0 coordinate system, in rad;
- M is the mean anomaly of the satellite in the J2000.0 coordinate system, in rad;
- Ω is the right ascending of ascension node of the satellite in the J2000.0 coordinate system, in rad;
- is the orbital inclination of the satellite in the J2000.0 coordinate system, in rad;
- is the rotational angular velocity of the earth, the unit is rad/s;
- is the Greenwich sidereal hour angle at the current moment, the unit is rad;
- is the Greenwich sidereal hour angle at the time of J2000.0, the value is 4.899787426069032 rad.
2.2. Calculation of the Mean Orbital Inclination
Generally speaking, the more period terms are eliminated by the mean orbital inclination vector of the GEO satellite, the lower the fuel required to keep the orbital inclination, and the lower the required accuracy of the orbital inclination keeping. Therefore, when calculating the mean orbital inclination vector, it is not enough to only deduct the semi-diurnal period term. Generally, it is necessary to select the corresponding algorithm of the mean orbital inclination vector according to the mission requirements.
The orbital inclination of the GEO satellite is mainly affected by the three-body gravitational force, and the three-body motion is approximated as follows []:
where
- , , and are the position of the third body (sun or moon) in the J2000 coordinate system, the units are m;
- is the longitude of the third body (moon or sun) in the J2000 coordinate system, in rad;
- , is the right ascending of the ascension node of the third body (moon or sun) in the J2000 coordinate system, in rad;
- is the orbital inclination of the ascension node of the third body (moon or sun) in the J2000 coordinate system, in rad.
The effect of three-body gravity on the orbital inclination vector is []:
where is the orbital angular velocity of the third body (sun or moon), the unit is rad/s. Combining Equations (3) and (4), ignoring the short period (semi-diurnal) term, the influence of the three-body gravity on the semi-monthly period, semi-annual period and nutation period of the orbital inclination vector is obtained as follows:
where subscript “long” means long-term drift caused by the semi-monthly period term and semi-annual period term; subscript “D” means drift caused by the nutation period term.
2.2.1. Nutation Period Term Perturbation
In formula (5), the perturbation equation including the nutation period term is:
In Equation (6), considering the variation law of the ephemeris of the sun and the moon, superimposing the perturbation forces of the sun and the moon on the GEO orbital inclination, and deducting the semi-diurnal, semi-monthly and semi-annual period terms, the perturbation equation of the mean orbit inclination vector under the perturbation effect of the nutation period term can be obtained as follows [] (p. 137):
where is the angle between the vernal equinox and the intersection of the lunar orbital plane and the ecliptic plane, in rad, and its expression is []
where is the Julian century number corresponding to the current moment.
It can be seen from Formula (8) that the ecliptic period of the ascending node of the lunar orbit is 18.6 years, which is a nutation period of the earth.
The drift angle of the mean orbital inclination vector is defined as the projection of the angle from the inertial system axis to the orbital mean inclination vector on the instantaneous equatorial plane of the earth. According to the definition, it can be seen from Equation (7) that the drift angle of the mean inclination vector under the nutation period term perturbation is:
It can be seen from Equation (9) that under the influence of the nutation period perturbation, the drift angle of the mean orbital inclination vector is around 90°. Equation (7) shows that the mean orbital inclination of GEO moves in an ellipse under the influence of the nutation period perturbation, and the major semi-axis of the ellipse can represent the oscillation amplitude of the mean orbital inclination under the influence of the nutation period perturbation, which is:
2.2.2. Semi-Annual and Semi-Monthly Period Term Perturbation
In Equation (5), retaining the semi-annual and semi-monthly period terms, the perturbation equation of the mean orbital inclination vector under the influence of the semi-annual and semi-monthly period terms of the sun-moon gravity can be obtained:
The semi-annual oscillation of the mean orbital inclination vector of the GEO satellite caused by the gravity of the sun is:
Substitute Equation (11) into (12), and let the solar orbital parameter , be a constant; then, the semi-annual oscillation of the mean orbital inclination vector of the GEO satellite caused by the solar gravity can be calculated as:
By formula (13), it can be seen that the semi-annual period fluctuation of the orbital inclination of the GEO satellite under the influence of the sun’s gravity is about:
Similarly, the semi-monthly periodic oscillation of the orbital inclination vector of the GEO satellite under the influence of the moon’s gravity is:
Substitute Equation (11) into (15), and let the solar orbit parameter
be a constant; then, the semi-monthly oscillation of the mean orbital inclination vector of the GEO satellite caused by the moon’s gravity can be calculated as:
In Formula (16), , approximately, let , ; then, the semi-monthly periodic oscillation amplitude of the mean orbital inclination of the GEO satellite under the influence of lunar gravity is about:
2.2.3. Semi-Diurnal Period Term Perturbation
The semi-diurnal periodic oscillation of the mean orbital inclination vector of the GEO satellite under the influence of the three-body gravitational perturbation is:
Retaining only the semi-diurnal term in Equation (4), and substituting it into Equation (18), the short-period oscillation of the mean orbital inclination vector of the GEO satellite under the influence of three-body gravitational perturbation can be obtained as:
According to Equation (19), the semi-diurnal oscillation amplitudes of the orbital inclination of the GEO satellite under the influence of the sun’s gravitational and lunar gravitational perturbations are:
To sum up, the period term of the orbital inclination vector of the satellites is mainly affected by the three-body gravitational perturbation, which includes the semi-annual period term, semi-monthly period term, and semi-diurnal period term. Among them, the semi-annual period fluctuation of the orbital inclination of the GEO satellite under the influence of the sun’s gravity is about 0.03°; the semi-monthly period oscillation amplitude of the mean orbital inclination of the GEO satellites under the influence of lunar gravity is about 0.003°; the semi-diurnal oscillation amplitudes of the orbital inclination of the GEO satellite under the influence of the sun’s gravitational and lunar gravitational perturbations is about 0.0008°.
Therefore, we can draw the following conclusions:
- (1)
- For a GEO satellite whose north/south keeping accuracy is required to be about 0.1°, it is recommended to use the calculation method of the mean orbital inclination after deducting the semi-diurnal period term, semi-monthly period term and semi-annual period term; that is, the item needed to be deducted is
The remaining term is the mean orbital inclination vector under the influence of the nutation period term, as shown in Figure 1.
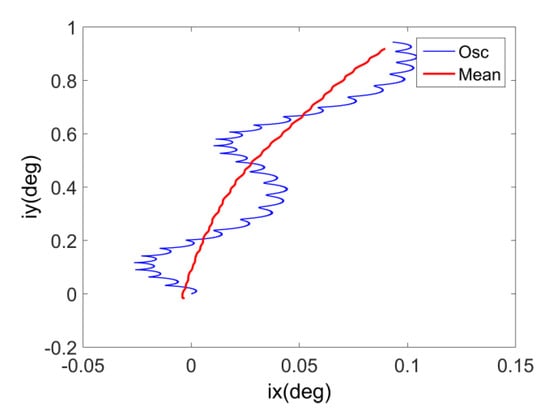
Figure 1.
Mean orbital inclination vector under the influence of the nutation period term.
- (2)
- For a GEO satellite whose north/south keeping accuracy is required to be about 0.01°, it is recommended to use the calculation method of the mean inclination after deducting the semi-monthly periodic term and semi-diurnal period term; that is, the item needed to be deducted is
The remaining term is the mean orbital inclination vector under the influence of the semi-annual period term, as shown in Figure 2.
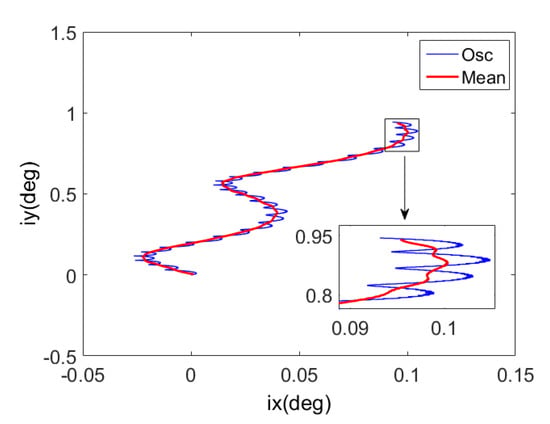
Figure 2.
Mean orbital inclination vector under the influence of the semi-annual period term.
- (3)
- For GEO satellites whose NSSK accuracy is required to be about 0.005°, it is recommended to use the calculation method of the mean orbital inclination after deducting the semi-diurnal period term; that is, the item needed to be deducted is
The remaining term is the mean orbital inclination vector under the influence of the semi-monthly period term, as shown in Figure 3.
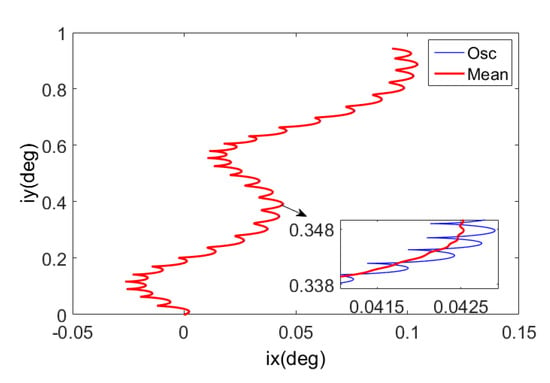
Figure 3.
Mean orbital inclination vector under the influence of the semi-monthly period term.
3. North/South Station Keeping Control by Electric Propulsion with Manipulator
3.1. Basic Concepts
The SK of the GEO satellite is divided into north/south station keeping (NSSK) and east/west station keeping (EWSK). The NSSK is also called orbital inclination keeping, which is the out-of-plane control; the EWSK includes the mean longitude keeping and the eccentricity vector keeping, which is the orbital in-plane control. The required velocity increment of the satellite’s orbital semi-major axis keeping is no more than 2 m/s per year; the required velocity increment of satellite’s orbital eccentricity vector keeping is no more than 2 m/s per year; the required velocity increment of the satellite’s orbital inclination vector keeping is no more than 51 m/s per year. Therefore, the NSSK accounts for more than 92% of the velocity increment required for the SK of the GEO satellite, and it occupies a large portion in the SK of the GEO satellite.
At this stage, chemical thrusters are used to keep the north/south station, which has low control accuracy and large fuel consumption. This paper proposes a scheme of a four-degree-of-freedom manipulator with the EP system. As shown in Figure 4, the EP points to the Y-direction of the satellite. The manipulator includes a shoulder joint, an elbow joint, a wrist joint and a double-degree-of-freedom wrist joint. Because there is no need to offset the influence of eccentricity, the electric thrust only needs to work once in an orbital period. By deflecting the thrust position and direction by the manipulator, the angular momentum can be unloaded while keeping the north/south station.
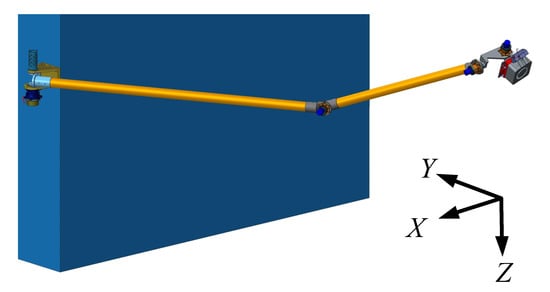
Figure 4.
Four-degree-of-freedom manipulator with EP solution.
3.2. Range for North/South Station Keeping Zone
The process of the NSSK is essentially to offset the influence of the environmental perturbation force on the orbital inclination vector through the velocity increment generated by the EP. The NSSK can be regarded as keeping the orbital inclination of the satellite relative to the target orbital inclination near zero. In order to facilitate the description of the target orbit, the target orbit generally adopts constant orbital parameters. The mean orbital inclination after deducting the period term mentioned in Section 2.2 of the satellite is also used.
NSSK can be achieved by providing a negative normal velocity increment near the relative orbital ascending node, or it can provide a positive normal velocity increment near the relative orbital descending node. The magnitude of the control vector of the SK is equal to the magnitude of the mean orbital inclination vector under the influence of natural perturbation, and the direction of the control vector of the SK is opposed to the direction of the mean orbital inclination vector under the influence of natural perturbation. Because the natural drift direction of the mean orbital inclination vector is generally near the Y-axis of the inertial system, in the steady-state control, the relative orbital ascending node is generally near the inertial system Y-axis, and the relative orbital descending node is generally near the inertial system Y-axis. Figure 5 shows the drift range of the mean orbital inclination vector and the range of the SK zone.
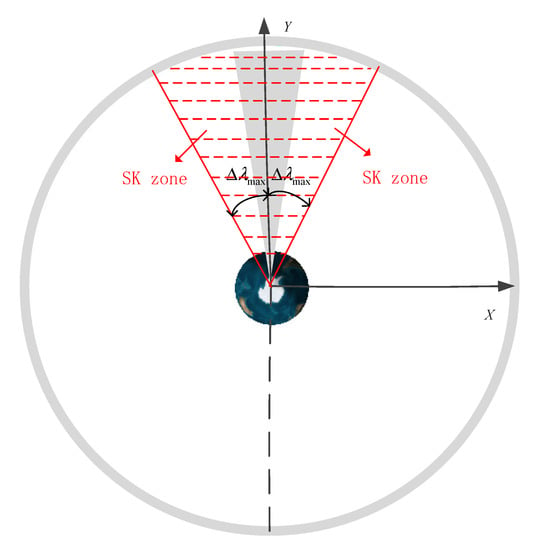
Figure 5.
The range for NSSK zone of the GEO satellite.
In Figure 5, the gray zone is the envelope of the mean orbital inclination vector direction. The zone enclosed by the red dotted line is the “normal SK zone”. Because the EP points to the Y-direction of the satellite, the electric thrust points to the south, producing a northward thrust. The range of the mean right ascension covered by each SK zone is . During the SK, the larger is, the larger interval of the optional SK point is, and the stronger the orbital control adjustment ability, but the consistency of the station between the initial position capture and steady SK may be poor. On the contrary, the smaller is, the smaller interval of the optional SK point is, and the weaker the orbital control adjustment ability, but the consistency of the station between the initial station capture and steady SK may be better. Obviously, in order for the satellite to have sufficient SK ability, needs to be large enough, but in order to make the SK point more consistent, should be designed to be as small as possible.
According to Figure 5, the NSSK capability of the GEO satellite needs to cover the drift range of the mean orbit inclination vector under the influence of the natural perturbation, that is:
where, is the maximum value of the drift angle of the mean orbital inclination vector, the unit is rad; is the minimum value of the drift angle of the mean orbital inclination vector, the unit is rad.
According to the definition of the SK zone, there are:
where is the velocity increment required to control the inclination vector in the X-direction of the inertial frame, in m/s; is the velocity increment required to control the inclination vector in the Y-direction of the inertial frame, in m /s; its calculation formula is:
where
- is the mean orbital inclination used for control, and it is also the orbital inclination of the satellite’s orbit relative to the target orbit, in rad;
- is the initial orbital semi-major axis;
- is the orbital angular velocity.
In order to achieve the lowest fuel consumption, the velocity increment generated by control needs to be opposite to the velocity increment generated by environmental perturbation. The minimum velocity increment must meet the following conditions:
Then, when the electric thruster is used for SK, the calculation formula of the orbital argument corresponding to the center point of the ignition arc segment is:
3.3. Duration of the North/South Station Keeping
After entering the stable maintenance state, the control duration of each SK theoretically corresponds to the change rate of the mean orbital inclination, and it changes continuously. However, due to the initial orbital error, orbital control target switching (co-location configuration switching, fixed-point position switching) and other requirements, the control time of the orbit may be too long or too short. If the orbital control time is too long, the entire satellite consumes too much energy, making it difficult to achieve energy balance, and the orbital arc loss effect is obvious, reducing the efficiency of the orbital control. If the orbit control time is too short, not only the daily angular momentum cannot be fully unloaded, causing the attitude to be out of control, but also the ability to keep mean longitude may be insufficient, resulting in a decrease in the accuracy of the EWSK or an increase in the motion envelope of the manipulator. Therefore, before entering a stable maintenance state, it is hoped that the daily orbital control duration should be as uniform as possible; that is, the difference between the maximum duration designed for the SK each time and the shortest duration for the SK each time is minimized so as to ensure the energy consumption of the whole satellite is smooth and the angular momentum unloading capability varies smoothly.
Obviously, if we need to ensure that there is sufficient NSSK capability throughout the whole process, it needs to meet:
where is the longest orbital control time required to offset the daily drift of the mean orbital inclination vector; is the shortest orbital control time required to offset the daily drift of the mean orbital inclination vector.
and can be calculated as follows:
The linear velocity of the GEO satellite is
The maximum value of the velocity increment required for daily NSSK is
where
- is the maximum daily drift of the mean orbital inclination vector, in rad;
- is the initial velocity of the satellite.
When arc loss is not considered, the duration of the SK is
where
- is the mass of the satellite;
- is the magnitude of the thrust acting on the satellite.
When considering the arc loss, the orbital control efficiency of the thruster is
where is the orbital control arc (true anomaly) of the satellite under the action of the thrust. is calculated as
In order to offset the effect of arc loss, it is necessary to extend the original orbital control arc to
Combined with Equations (35) and (36), we can obtain
Therefore, the longest orbital control time required to offset the daily drift of the mean orbital inclination vector is:
Similarly, the shortest orbital control time required to offset the daily drift of the mean orbital inclination vector
where
- is the maximum daily drift of the mean orbital inclination vector, in rad;
- is the minimum daily drift of the mean orbital inclination vector, in rad;
However, it is also necessary to consider that during the SK, the thrust direction and the thrust position are slightly offset by the manipulator to achieve unloading of the three-axis angular momentum, so the daily SK time cannot be too short. Therefore, it must meet:
where is the daily minimum time required for angular momentum unloading.
Depending on the choice of the mean orbital inclination vector, Equations (30) and (40) may conflict. Among them, Equation (40) must be satisfied, while Equation (30) does not need to be satisfied. When Equation (30) is satisfied, it means that there is sufficient control capability of the mean orbital inclination vector in the whole SK process. It is worth noting that and are theoretical analysis values, the errors such as mean/osculating orbital inclination conversions error and orbital control error have not been considered. Therefore, margins need to be considered when designing the algorithm. When Equation (30) is not satisfied, it means that when the natural drift of the orbital inclination vector is small, and the change of the orbital inclination vector caused by the minimum orbital control amount is relatively large, the orbital inclination vector will continue to be controlled to the moving direction (mainly the inertial frame-Y direction) under the control action, and the mean orbital inclination vector cannot be normally kept near zero during this period. However, once the natural drift of the orbital inclination vector is greater than the change of the orbital inclination vector caused by the minimum orbital control amount, the orbital inclination vector will gradually approach zero under the control and return to the normal SK state.
3.4. The Control Amount of the North/South Station Keeping
The NSSK needs to meet the following five functional requirements and design constraints: (1) In order to facilitate the design of the entire satellite mission sequence and the on-board autonomous SK sequence, the initial station capture and the steady-state SK need to have a good consistency; (2) In order to have enough time to use EP for daily angular momentum management, the single SK time must be large enough; (3) In order to ensure optimal fuel during station capture and keeping, in the direction of the inclination vector, the control amount must only be used for to overcome the orbital perturbation; (4) It needs to have the ability to capture any orbital inclination angle vector within 0.1° of the initial deviation; (5) There is no constraint on the duration of capturing the target.
When the SK is in a steady state, the orbital control amount and the environmental perturbation amount cancel each other out, which can naturally meet the above functional requirements. When the initial orbital deviation is too large or the station capture is performed again, the overall design needs to be combined with the law of the environmental perturbation force and the above functional requirements.
3.4.1. Zone Control Method
For the convenience of illustration, the SK zone where the control position of the orbital is the same as the drift direction of the current mean orbital inclination vector is selected for illustration. The shaded part of the blue solid line in Figure 6 is the SK zone. The orbital inclination control is used to adjust the orbital surface. When pulse control is used, it can be understood as instantaneous control, that is, it is considered that the orbital inclination will be adjusted in the decreasing direction under the action of orbital control at the next moment. Therefore, the input of the orbital inclination control is the orbital inclination deviation during orbital control, and it is not necessary to pay attention to the orbital inclination change rate. Figure 6 shows the NSSK strategy.
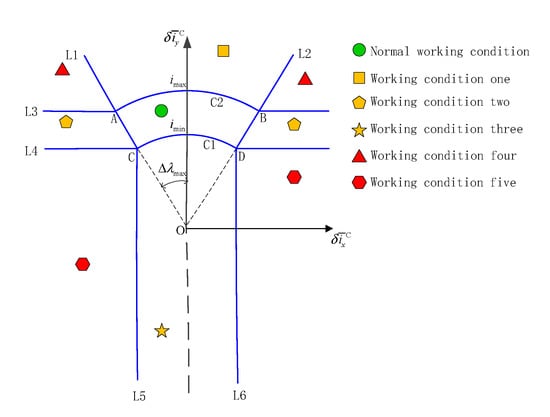
Figure 6.
The NSSK strategy.
The coordinate system in Figure 6 is the inertial system, and the object described is the mean orbital inclination vector for control. is the orbital inclination of the GEO satellite changed by the time of the EP working time , and is the orbital inclination of the GEO satellite changed by the EP working time .The radius of the small circle C1 is , and the radius of the large circle C2 is . The straight line L1 is the boundary of the SK zone, which is greater than 90°. The straight line L2 is the boundary of the SK zone, which is less than 90°. Point A is the intersection of L1 and the circle C2, point B is the intersection of L2 and the circle C2, point C is the intersection of L1 and the circle C1, and point D is the intersection of L2 and the circle C1. L3 is a straight line passing through point A and parallel to X, L4 is a straight line passing through point C and parallel to X, L5 is a straight line passing through point C and parallel to Y, and L6 is a straight line passing through point D and parallel to Y.
L1~L6, C1 and C2 divide XOY into nine zones, corresponding to six different working conditions, namely:
- (1)
- Normal working condition: closed zone enclosed by ABCD;
- (2)
- Working condition one: It is a half-zone closed zone surrounded by L1, L2 and AB arcs, and the modulus of the mean orbital inclination vector corresponding to the target to the current orbit in this zone is greater than ;
- (3)
- Working condition two: It consists of two half-zone enclosed zones; one is enclosed by L1, L3 and L4, and the other is enclosed by L2, L3 and L4, and they are all outside the allowed SK zone;
- (4)
- Working condition three: It is a half-zone closed zone surrounded by L5, L6 and CD arcs, and the component in the Y-direction of this zone is less than ;
- (5)
- Working condition four: It consists of two half-zone enclosed zones; one is enclosed by L1 and L3, the other is enclosed by L2 and L3, and both are outside the range of the allowable SK zone;
- (6)
- Working condition five: It includes two half-zone closed zones; one is enclosed by L4 and L5, the other is enclosed by L4 and L6, and the absolute value of the components in X-direction of the two zones is greater than .
The nine zones in Figure 6 can be divided into three categories: stable (the zone where the green geometry is located), semi-stable (the zone where the yellow geometry is located) and unstable (the zone where the red geometry is located).
- (1)
- It contains a stable zone, namely the normal working condition. Under the normal working condition, the orbital inclination vector from the target orbit to the current orbit will continue to maintain the normal working condition, that is, the steady-state SK;
- (2)
- It contains four semi-stable zones, including two zones of working condition two, as well as working condition one and working condition three. These zones, in the shape of pipelines, are connected to the intermediate normal working conditions, and their orbital inclination vectors in the X-axis or Y-axis are in a closed-loop stable state, so they will not leave the steady-state pipeline and will eventually enter the normal working conditions along the pipeline. The semi-stable zone is further divided into X-axis stability (condition two) and Y-axis stability (condition one and condition three). In the semi-stable zone where the X-axis is stable, the center position of the NSSK is unchanged, and the duration of the orbital control changes in real time with the orbital inclination. In the semi-stable zone where the Y-axis is stable, the duration of NSSK control is unchanged (the longest or the shortest duration), but the center of the SK will change in real time with the orbital inclination.
- (3)
- It contains four unstable zones, including two zones in working condition four and two zones in working condition five. These zones are in the form of sectors. In these zones, the orbital inclination vector will move under the combined action of orbital control and natural perturbation. It will enter the semi-stable zone adjacent to it, and then reaches the stable zone through the semi-stable zone.
Since the control force acting on the orbital inclination vector covers the drifting of the orbital inclination vector caused by orbital perturbation, the switching between zones is theoretically irreversible. Even if the reversible zone switching occurs due to environmental perturbation changes, since the control law calculated at the junction of two adjacent zones is the same, there will be no “jitter” of the control law caused by frequent switching between two zones. In the unstable zone (working condition four and working condition five), the point and the amount of the SK are both constant, and the control strategy remains unchanged.
In the semi-stable zone (working condition one, working condition two and working condition three) and stable zone (normal working condition), the orbital control amount and orbital control position will fluctuate slightly with the motion of the mean orbital inclination vector under the influence of perturbation. It can also be seen from Figure 6 that under all orbital control strategies, the orbital control amount in the Y-axis direction of the inertial system is negative, that is to say, all the y-direction velocity increments are used to overcome the natural drift of the mean orbital inclination vector under the influence of perturbation. Therefore, the strategy of NSSK proposed in this paper is also the SK strategy with the least fuel consumption.
In Figure 6, the SK point of working condition four is located at point A (B), which means that the time of the single orbital control is the longest. The Y-axis component of the orbital inclination vector in this zone is large, so it is not only necessary to perform orbital adjustment in the X-axis direction but also to ensure that the Y-axis direction continues to decrease. In working condition one, at point A (B), the control ability in the Y-axis direction is the weakest. In order to make the Y-axis still overcome the natural drift of the orbital inclination and converge to zero, it is necessary to satisfy:
Therefore, the maximum duration of the single SK should satisfy:
In Figure 6, for working condition three, it is necessary to use the environmental perturbation force to realize the movement of the X-axis of the component of the orbital inclination vector to zero. Therefore, the maximum point in the X-axis direction (the midpoint of the CD arc) should be less than the minimum daily drift of the orbital inclination vector; then, we have
Combined with Equations (42) and (43), in the subsequent design and simulation of this paper, we may make:
The detailed control amount of the SK for each working condition is described as follows.
(1) Normal working condition
The normal working condition is the stable zone (complete coverage of the natural drift range of the orbital inclination vector). The mean orbital inclination vector is moderate in the inertial system, and the control amount of the NSSK and the drifting amount of the mean orbital inclination vector are equal in magnitude and opposite in direction. The position of the orbital control is within the allowable orbital control range. The NSSK in normal working condition is shown in Figure 7.
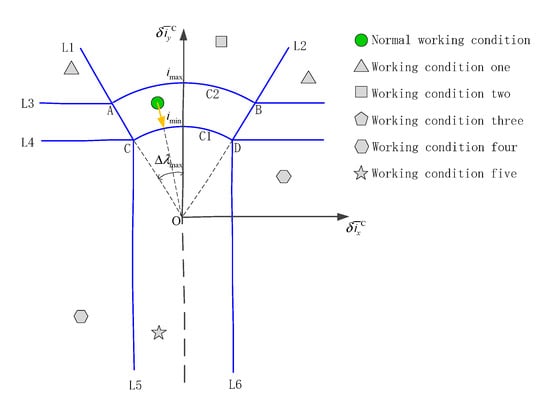
Figure 7.
The NSSK in normal working condition.
In Figure 7 the direction of the straight arrow represents the change direction of the orbital inclination vector under the action of orbital control. The starting point of the straight arrow represents the control amount, and the starting point of the straight arrow is located in the center of the normal working condition, indicating that the orbital control duration is between the shortest and longest duration. The straight arrow is yellow, indicating that the amount of orbital control is moderate. Under normal working conditions, under the combined effect of the perturbation and control force, the orbital inclination vector from the target to the current will continue to remain within the normal working conditions.
To meet the normal working conditions, the following conditions must be met at the same time:
Considering the arc loss, under normal working condition, the mean orbital right ascension and the north/south ignition duration corresponding to the midpoint of the EP arc are:
(2) Working condition one
Working condition one is a semi-stable zone, and the orbital inclination vector is in a positive bias state. The mean orbital inclination vector has a larger absolute value in the Y-axis direction of the inertial system and a smaller absolute value in the X-axis direction of the inertial system. Therefore, it is necessary to use the maximum orbital control capability to overcome the drift of the orbital inclination vector under the perturbation, and finally make the orbital inclination vector approach the target orbital inclination. In this condition, the ignition duration of the control is longest, and the ignition position fluctuates a small amount with the current orbital inclination vector within the range of the SK zone. The NSSK in working condition one is shown in Figure 8.
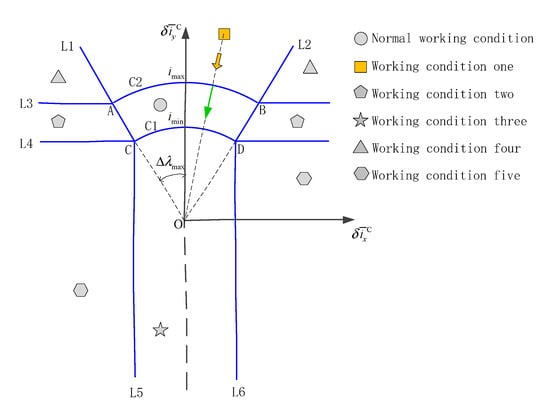
Figure 8.
The NSSK in working condition one.
In Figure 8, the starting point of the straight line arrow is located on the AB arc on the C2 circle, indicating that the orbital control time is the longest and remains unchanged, which is most conducive to the management of angular momentum. The direction of the straight line arrow points to the center of the circle, indicating that the SK point is in the SK zone and needs to be adjusted in real time according to the actual orbital inclination vector. The 45° arrow describes the approximate direction of the motion of the orbital inclination vector under the combined action of the perturbation force and the control force. Because the control force on the orbital inclination vector in two directions is greater than the perturbation force on it, the working condition one will only enter the normal working condition in one direction.
To meet the working conditions one, the following conditions must be met at the same time:
Considering the arc loss, under working condition one, the mean orbital right ascension
and the north/south ignition duration corresponding to the midpoint of the EP arc are:
(3) Working condition two
Working condition two is in the semi-stable zone, and the absolute value of the mean orbital inclination vector is small in the Y-axis direction of the inertial system, which can keep stable control. The mean orbital inclination vector has a large absolute value in the X-axis direction, and it is necessary to provide the control capability in the X-axis direction as much as possible while ensuring the Y-axis control. The orbital inclination vector approaches the normal working condition along the X-axis under control. During the above process, the orbital control position of the orbital inclination does not change, and the orbital control duration is between the longest and the shortest. The orbital control position fluctuates slightly with the drift rate of the Y-axis orbital inclination. The NSSK in working condition two is shown in Figure 9.
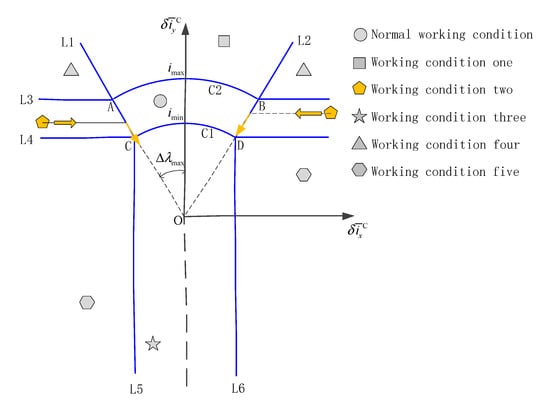
Figure 9.
The NSSK in working condition two.
In Figure 9, the starting point of the straight line arrow is located on the straight line AC or BD between the C2 circle and the C1 circle, indicating that the SK duration is between the shortest and longest duration. The straight-line arrows point in the AC direction, indicating that the SK control points remain unchanged in the inertial space. The 45° arrow points to the normal zone, indicating that working condition two will enter the normal working condition in one direction.
To meet the working conditions two, the following conditions must be met at the same time:
Considering the arc loss, under working condition two, the mean orbital right ascension and the north/south ignition duration corresponding to the midpoint of the EP arc are:
(4) Working condition three
Working condition three is a semi-stable zone, and the orbital inclination vector is in a negative bias state. It is necessary to take advantage of the natural perturbation force to make the current orbital inclination vector approach the target orbital inclination. Under this working condition, it is necessary to provide as little orbital control capability as possible, so that the orbital inclination vector can drift to the normal working condition as soon as possible under the action of natural perturbation. At the same time, the orbital control adjustment capability is used to make the X-axis component of the orbit inclination vector drift toward zero as much as possible. Under this condition, the orbital control duration is the shortest, and the ignition position fluctuates a little within the SK zone along with the current orbital inclination vector. The NSSK in working condition three is shown in Figure 10.
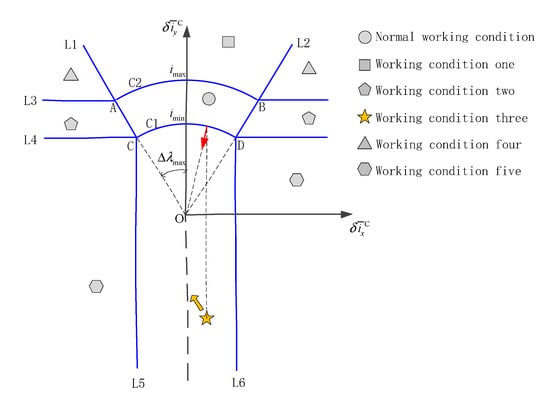
Figure 10.
The NSSK in working condition three.
In Figure 10, the starting point of the straight arrow is located between the CD arc segments on the C1 circle, indicating that the duration of the SK is shortest. The control point of the SK is dynamically adjusted with the fluctuation of the current mean orbital inclination vector. The 45° arrow points to the normal zone, indicating that working condition three will enter the normal working condition in one direction. Working condition three cannot be easily described with simple mathematical expressions. However, since all six working conditions, including normal working conditions, cover all zones of a two-dimensional plane, the exclusion method can be used to complete the conditions of working condition three.
Considering the arc loss, under working condition three, the mean orbital right ascension and the north/south ignition duration corresponding to the midpoint of the EP arc are:
(5) Working condition four
Working condition four is an unstable zone, and the absolute value of the mean orbital inclination vector in the X-axis and Y-axis directions of the inertial system is large, and it is positive in the Y-direction. In this case, it is necessary to have the orbital control capability on both the X and Y axes, the position of orbital control is at the boundary of the allowable orbital control range, and the orbital control time is the longest. The NSSK in working condition four is shown in Figure 11.
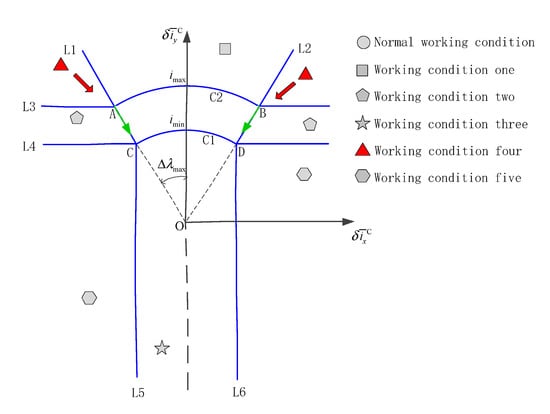
Figure 11.
The NSSK in working condition four.
In Figure 11, the starting point of the straight line arrow is located at A or B on the C2 circle, indicating that the duration of the orbital control is longest. The straight arrow points in the direction of AC or BD, indicating that the orbital position is constant in the inertial frame. The 45° arrow describes the approximate movement direction of the orbital inclination vector under the combined action of the perturbation force and the control force of the SK. Since the orbital control duration remains constant, if the rate of change of the mean orbital inclination vector caused by the environmental perturbation force is also regarded as a constant value, then under the action of the orbital control force and the natural perturbation force, the mean orbital inclination vector will move in a fixed direction. Because the control force of the inclination vector in both directions is greater than the natural perturbation force, the working condition four will theoretically enter into two adjacent semi-stable zones along one direction (working condition one or working condition two, which is related to the initial stage).
To meet the working condition four, the following conditions must be met at the same time:
Considering the arc loss, under working condition two, the mean orbital right ascension and the north/south ignition duration corresponding to the midpoint of the EP arc are:
(5) Working condition five
Working condition five is an unstable zone, and the absolute value of the mean orbital inclination vector in the X-axis and Y-axis directions of the inertial system is large, and it is negative in the Y-direction. In this case, it is necessary to have orbital control capability on both the X and Y axes at the same time. The position of the orbital control is at the boundary of the allowable orbital control range, and the orbital control time is the shortest. The NSSK in working condition five is shown in Figure 11.
In Figure 12, the starting point of the head of the straight arrow is located at C or D on the C1 circle, which means that the orbital control time is the shortest. Straight arrows point in the AC or BD direction, indicating that the position of the orbit is constant in the inertial frame. The 45° arrow describes the approximate movement direction of the orbital inclination vector under the combined action of the perturbation force and the control force of the SK.
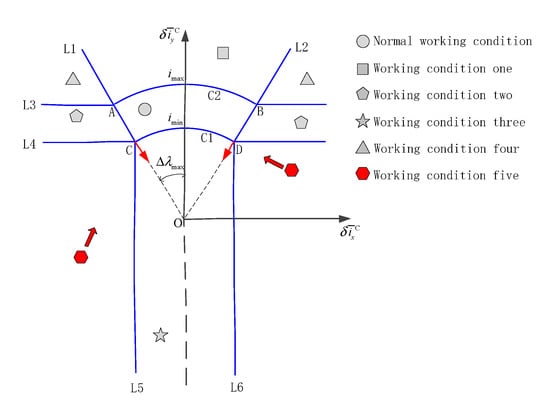
Figure 12.
The NSSK in working condition five.
Since the duration of the orbital control remains constant, if the rate of change of the mean orbital inclination vector caused by the environmental perturbation force is also regarded as a constant value, then under the action of the orbit control force and the natural perturbation force, the mean orbital inclination vector will move in a fixed direction. Because the control force of the inclination vector in the two directions is greater than the natural perturbation force, working condition five will theoretically enter into two adjacent semi-stable zones along one direction (working condition two or working condition three, which is related to the initial stage).
To meet working condition five, the following conditions must be met at the same time:
Considering the arc loss, under working condition two, the mean orbital right ascension and the north/south ignition duration corresponding to the midpoint of the EP arc are:
The five working conditions are summarized in Table 1.

Table 1.
Summary of five working conditions.
3.4.2. Analysis of Fuel Consumption
In the stable stage of the NSSK, the control position of the north/south station is kept at the ascending node or the descending node, which is the most ideal point of the SK. At this time, the velocity increment generated by EP is due south or due north, and the direction of the velocity increment is also optimal. Therefore, it can be considered that the velocity increment generated by EP is equal to the velocity increment generated by environmental perturbation (three-body gravitational force), and the direction is opposite, which is the optimal NSSK scheme for fuel.
In the initial state, for any initial orbital inclination vector within the allowable range, the direction of the velocity increments generated by EP is opposite to the velocity increments generated by the environmental perturbation force; that is, the velocity increments generated by EP are only used to overcome the environmental perturbation force. The change of the orbital inclination vector caused by the environmental perturbation force is mainly along the Y-axis direction, so the initial orbital inclination vector deviation in the X-direction needs to be offset by the velocity increment generated by the EP. When the initial orbital inclination vector in the Y-direction is greater than zero, it is necessary to use additional electric thrust control force to eliminate the deviation on the basis of the normal NSSK. At this time, the fuel consumption is slightly more than the fuel consumption required by the SK in a steady state. When the initial orbital inclination vector in the Y-direction is less than zero, the current orbital inclination vector can be made closer to the target orbital inclination vector by using the environmental perturbation force. At this time, the fuel consumption for the SK is slightly less than that required for the SK in a steady state.
3.5. Orbital Inclination Vector for Control
The NSSK of the satellite can be regarded as the SK of the orbital inclination of the deputy satellite relative to the chief satellite. The error between the current orbital inclination and the target orbital inclination for control should be clarified. The determination of the orbital inclination of the target orbit for control includes two aspects: first, there is the determination of the orbital inclination vector of the chief satellites. When multi-satellite formation or multi-satellite co-location is kept, the orbital inclination vector of the chief satellite is set by the ground and can be changed as required. For the SK of satellites generally located in GEO, the orbital inclination vector of the chief satellite can be regarded as (0, 0). Second, on the basis of the first point, to improve the accuracy of the keeping control of the orbital inclination, it is necessary to make the orbital inclination vector properly negatively biased on the basis of predicting the change law of the orbital inclination. The orbital inclination vector is ultimately kept within the minimum envelope radius centered on the orbital inclination vector of the chief satellite.
The orbital inclination vector for control is shown in Figure 13.
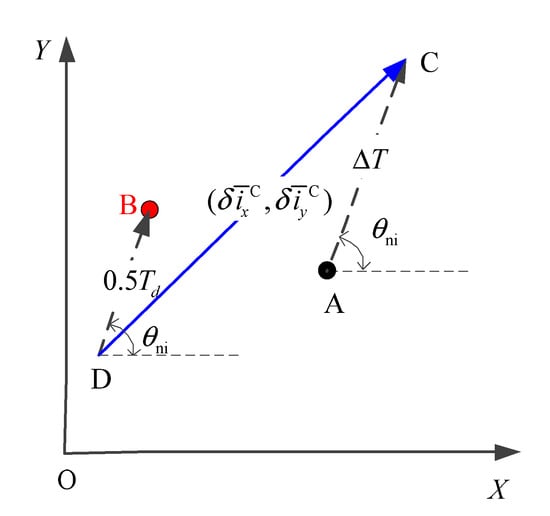
Figure 13.
The orbital inclination vector for control.
In Figure 13, point A represents the coordinates of the current mean orbital inclination vector. Point C represents the coordinates of the mean orbital inclination vector under the action of the natural perturbation force at the central moment of SK. Point B represents the coordinates of the target mean orbital inclination vector. Point D represents the target of the SK. AC and DB represent the drifting direction of the mean orbital inclination vector caused by the natural perturbation force. After the orbit is controlled to point D, the mean orbital inclination vector will pass through point B under the action of natural perturbation force, and the natural drift trajectory of the orbital inclination vector will be evenly distributed at both ends of point B. Therefore, taking D point as the target of the SK can improve the keeping accuracy of the mean orbital inclination vector as much as possible. DC is the orbital inclination vector for control.
The formula for calculating the mean orbital inclination vector for control is:
where
- is the current mean orbital inclination vector of the satellite, in rad;
- is the target mean orbital inclination vector of the satellite, in rad;
- is the daily drift of the orbital inclination vector, in rad;
- is the orbital period, which is 86,400.091s.
- is the time of the current position to the center of the target position.
The calculation formula of is:
4. Simulation and Analysis
Let be the minimum time required per day for angular momentum unloading. The correctness of the SK control law under each working condition is verified based on mathematical simulation. The design principles of the example include:
- (1)
- The control law covers all working conditions;
- (2)
- The result of the SK of the mean orbital inclination vector under the influence of different period term perturbations is verified;
- (3)
- The feasibility of parameter adaptation is verified.
Table 2 shows the examples used in the simulation.

Table 2.
The examples used in the simulation.
The results of the five working conditions are shown in Table 3.

Table 3.
Summary of Simulation.
4.1. Example One
The simulation conditions are shown in Table 2, the simulation time is 360 days, and the results are shown in Figure 14.
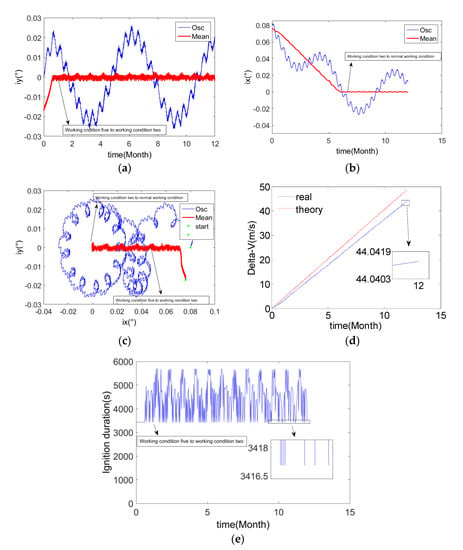
Figure 14.
The results of example one. (a) Y-axis component of orbital inclination vector; (b) X-axis component of orbital inclination vector; (c) Orbital inclination vector; (d) Velocity increment for SK; (e) Duration of SK.
It can be seen from Figure 14a,b that under the control action, the orbital inclination vector converges and remains near zero. The keeping accuracy of the mean inclination vector is better than 0.005°.
It can be seen from Figure 14c that the initial value of the mean inclination is located in working condition five (unstable zone). Under the action of the control law of working condition five, it enters working condition two (semi-stable zone) with a certain slope, and it finally enters and stays in normal working condition (stable zone) through working condition two.
It can be seen from Figure 14d that the actual annual velocity increment used for the NSSK is about 43 m/s, which is less than the theoretical velocity increment. There are two main reasons: first, the total velocity increment calculated by the theoretical formula is slightly larger; second, the initial orbital inclination vector in the Y- direction is less than zero. According to Section 3.4.2, when the initial orbital inclination vector in the Y-direction is less than 0, the fuel consumption for the SK is slightly less than that required for the SK in a steady state.
It can be seen from Figure 14e that the duration of the orbital control of the condition five is the shortest, which is consistent with the strategy of condition five, and the shortest control duration is about 3417 s, which is consistent with the calculated value of 3426 s in formula (36). In working condition two and normal working condition, the duration of the orbital control varies between the longest and shortest according to different orbital parameters. It is worth noting that when this strategy is used to calculate the duration of the orbital control, error factors such as the semi-major axis and the eccentricity of the orbit are ignored. Therefore, the duration of the orbital control calculated by the actual control strategy will have a small error with the theoretical longest and shortest durations.
It can also be seen from Figure 14e that although the duration of the orbital control is frequently abrupt within the allowed longest and shortest durations, the result of the NSSK is good. Due to the existence of the orbital control error, the mean/osculating orbital inclination conversions error and the target position prediction error, the single orbital control amount will be too large or too small; thus, it breaks the allowable range. However, the above error can be regarded as a high-frequency error compared with the orbital control frequency, and the daily drift of the orbital inclination vector under the influence of the perturbation of the nutation period term is close to a constant value. Therefore, the limiting effect of the orbital control duration is equivalent to filtering the high-frequency error part of the constant physical quantity, thereby realizing the high-precision SK of the mean orbital inclination.
It can be seen from Figure 14a that the mean orbital inclination vector fluctuates slightly in the Y-direction about 12 times a year. The peak of the fluctuation corresponds to the longest orbital control duration in Figure 14e, indicating that there is still some residual error when calculating the perturbation of the semi-monthly period term, which causes the mean orbital inclination vector to drift and periodically exceeds the orbital control capability. Nevertheless, the control error is still small, and it can be seen from Figure 14c that the error hardly affects the accuracy of the final NSSK.
The algorithm of NSSK in this paper has the advantages of optimal fuel, fixed SK points, and wide application range. The disadvantage is that small initial errors will cause long orbital adjustment times. It can be seen from Figure 14a–c that the error of the initial orbital inclination vector is 0.08°, and it takes about six months to complete the final inclination capture and keeping.
4.2. Example Two
The initial conditions of the simulation are shown in Table 2. In order to simulate from working condition five to working condition three, the ascending node right ascension in example two is rotated 90 degrees clockwise, and the other conditions are the same as those in example one. The results are shown in Figure 15.
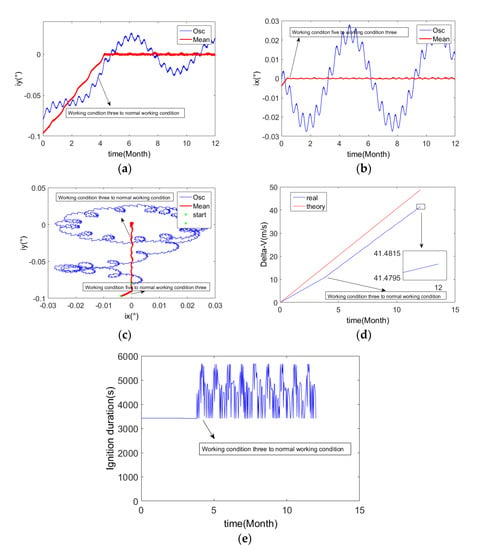
Figure 15.
The results of example two. (a) Y-axis component of orbital inclination vector; (b) X-axis component of orbital inclination vector; (c) Orbital inclination vector; (d) Velocity increment for SK; (e) Duration of SK.
It can be seen from Figure 15a–c that under the control action, the orbital inclination vector converges and remains near zero. It can be seen from Figure 15c that the initial value of the mean orbital inclination is located in working condition five (unstable zone). Under the action of the control law of working condition five, it enters working condition three (semi-stable zone) with a certain slope, and it enters and stays in normal working condition (stable zone) through working condition three.
In Figure 15d, the actual velocity increment is significantly lower than the theoretical velocity increment, which is mainly because the Y-component of the initial inclination vector has a large negative offset in this example. The greater the negative offset of the initial orbital inclination, the more fuel is saved in NSSK. Therefore, using the NSSK algorithm proposed in this paper can reduce a lot of velocity increment requirements.
4.3. Example Three
The initial conditions of the simulation are shown in Table 2. In order to simulate from working condition four to working condition one, the right ascending of the ascension node in example two is rotated 60 degrees clockwise, and the other conditions are the same as those in example one. The results are shown in Figure 16.
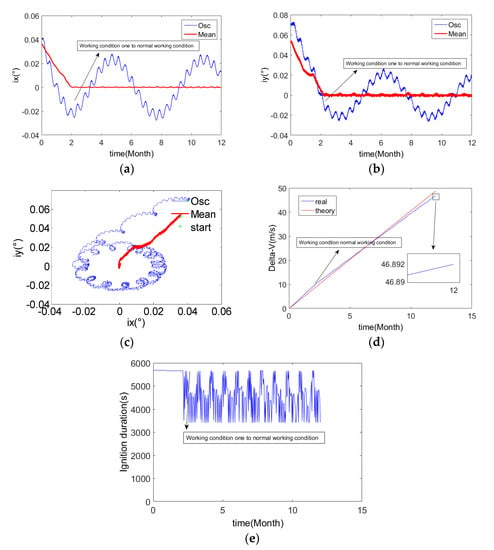
Figure 16.
The results of example three. (a) Y-axis component of orbital inclination vector; (b) X-axis component of orbital inclination vector; (c) Orbital inclination vector; (d) Velocity increment for SK; (e) Duration of SK.
It can be seen from Figure 16a–c that under the control action, the orbital inclination vector converges and remains near zero. It can be seen from Figure 16a,c that since the control laws in working condition four and working condition one are relatively close, the ignition time is the longest, so it is not easy to clearly distinguish the switching point from working condition four to working condition one.
It can be seen from Figure 16d that in working condition four and working condition one, the daily duration of orbital control is the longest. Therefore, the increase in the actual velocity increment is faster than the theoretical velocity increment, and this part of the extra velocity increment is caused by the positive bias of the mean orbital inclination vector in the y-direction at the initial moment.
4.4. Example Four
The initial conditions of the simulation are shown in Table 2. The minimum orbital control duration calculated by Equation (30) is 2157 s, which contradicts the orbital control duration of 3207 s required by Equation (32), so the shortest orbital control duration is finally taken as 3207 s. Other conditions are the same as in example three. The results are shown in Figure 17.
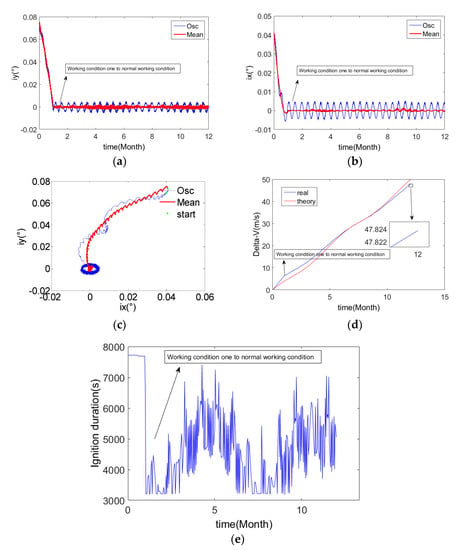
Figure 17.
The results of the example four. (a) Y-axis component of orbital inclination vector; (b) X-axis component of orbital inclination vector; (c) Orbital inclination vector; (d) Velocity increment for SK; (e) Duration of SK.
It can be seen from Figure 17a,b that under the control action, the orbital inclination vector converges and remains near zero. It can be seen from Figure 17c that the precision of the mean orbital inclination vector is about 0.002°, and the osculating accuracy of the orbital inclination vector is about 0.005°.
It can also be seen from Figure 17b that the mean orbital inclination vector fluctuates significantly twice a year in the X-direction. This is because the mean orbital inclination vector under the influence of the semi-annual period term perturbation presents the form of semi-annual periodic fluctuation, and the orbital control capability lags behind the controlled target, resulting in the error of the system of the orbital control.
After entering the normal working condition, the fluctuation range of the duration of the SK in Figure 17e is larger than that in Figure 16e. Although the initial orbital parameters are the same as those of example three, the longest orbital control time allowed in example three is longer after using the calculation method of the mean orbital inclination vector under the influence of the semi-annual term perturbation. Therefore, in this example, the duration from working condition four to the normal working condition is shorter than that of example three. Although the fluctuation range of the SK duration in Figure 17e is larger than that of Figure 16e, the design should consider global convergence; that is, the longest time of the orbital control allowed by the design should also be larger. Therefore, the duration of the SK does not always reach the maximum allowed duration. During the stable state of the NSSK, although the minimum duration of the orbital control often touches the lower boundary of the allowed duration of the orbital control, this does not affect the stable keeping of the orbital inclination, which is consistent with the analysis in Section 3.4.
4.5. Example Five
The initial conditions of the simulation are shown in Table 2. The minimum duration of the orbital control calculated by Equation (30) is 1112 s, which contradicts the orbital control duration of 3207 s required by Equation (32), so the shortest orbital control duration is finally taken as 3207 s. According to the above analysis, in this example, it is theoretically impossible to realize the controllability of any global point. Therefore, in order to achieve the NSSK simulation, it is necessary to sacrifice the controllability of some areas and focus on the overall controllability. In this simulation, let , and the other conditions are the same as those in example three. The results are shown in Figure 18.
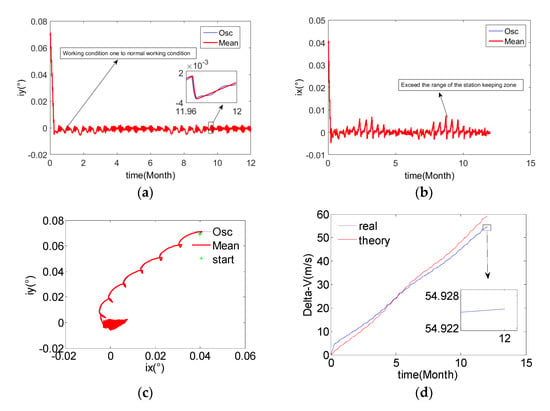
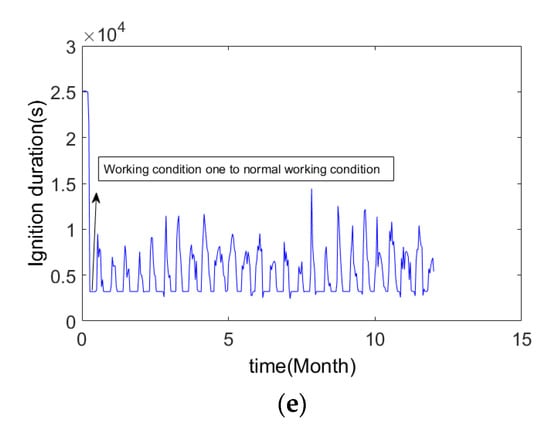
Figure 18.
The results of the example five. (a) Y-axis component of orbital inclination vector; (b) X-axis component of orbital inclination vector; (c) Orbital inclination vector; (d) Velocity increment for SK; (e) Duration of SK.
It can be seen from Figure 18a,b that under the control action, the orbital inclination vector converges and remains near zero. It can be seen from Figure 18c that the precision of the mean orbital inclination vector is about 0.008°. It can also be seen from Figure 18b that the mean orbital inclination vector fluctuates significantly twenty-six times a year in the X-direction. This is because the mean orbital inclination vector under the influence of the semi-annual period term perturbation presents the form of semi-annual periodic fluctuation, and the orbital control capability lags behind the controlled target (flat orbital inclination), resulting in the error of the system of the orbital control.
After entering the normal working condition, the fluctuation range of the duration of the SK in Figure 18e is larger than that in Figure 17e. Although the initial orbital parameters are the same as those of example four and example three, the longest orbital control time allowed in example five is the longest after using the calculation method of the mean orbital inclination vector under the influence of the semi-monthly term perturbation. Therefore, in this example, the duration from working condition four to the normal working condition is shorter than that of example three and example three. It can also be seen from Figure 18e that the maximum SK time per day is about 14,400s, while the longest allowed orbital control duration is 24,970s, which does not trigger the limiting effect of the longest allowed orbital control duration. This is because in order to ensure that the calculation method of the mean orbital inclination vector can still achieve the convergence of the global orbital inclination under the influence of the semi-monthly period term perturbation, the boundary relationship of each zone needs to be seamlessly connected. Therefore, the conditions of Equations (26), (35) and (36) need to be satisfied at the same time, and finally, the longest and shortest allowable durations of the orbital control are obtained according to Equation (36). This longest duration of the orbital control is mainly used in the capture phase of the initial inclination, and it will not be used in the stable keeping of the orbital inclination.
In addition, the variation of the duration of daily SK in Figure 18e is more continuous than that in Figure 16e and Figure 17e. Because the fluctuation of the mean orbital inclination vector is the most severe under the influence of the semi-monthly period perturbation, using the same method of the orbital control, the error in this example is the smallest. That is to say, the orbital control amount that overcomes the influence of the natural perturbation of the orbital inclination plays a more dominant role, so the daily time length of the SK is relatively continuous.
5. Conclusions
Aiming at the characteristics of low fuel utilization and weak angular momentum unloading ability of traditional all-electric satellites, semi-monthly and semi-annual inclination calculation methods for mean orbital inclination are proposed, and a low fuel consumption NSSK method based on zone control strategy is proposed. The method in this paper has the following characteristics:
- (1)
- The longer the period of the drifting of the mean orbit inclination under the influence of perturbation, the smaller the fluctuation of the center of the SK, the shorter required duration for orbital control, and the smaller the velocity increment required for the SK, but the accuracy of the NSSK is lower;
- (2)
- The velocity increment required for the NSSK of the mean orbital inclination for a semi-monthly period is about 45.5 m/s, and the accuracy of the NSSK is about 0.004°, which is suitable for a high-precision NSSK. The velocity increment required for the NSSK of the mean orbital inclination for the semi-annual period is about 45.5 m/s, and the accuracy of the NSSK is about 0.03°, which is suitable for the NSSK with medium precision and low fuel consumption;
- (3)
- The zone control method of the NSSK has strong adaptability to the initial large orbital inclination;
- (4)
- When the initial orbital inclination has a negative bias, the velocity increment required for the NSSK is less. When the initial orbital inclination has a positive bias, the velocity increment requirements for the NSSK is large;
- (5)
- The manipulator can also be used as a despinning platform for the satellite to achieve the NSSK and angular momentum unloading during the attitude maneuver. The angular momentum unloading scheme of manipulator with an electric thruster is worthy of further study;
- (6)
- The EWSK scheme of the manipulator with EP is worthy of further in-depth study.
The NSSK method proposed in this paper is applicable to any electric thrust and specific impulse. However, from the perspective of optimal fuel, theoretically, the larger the thrust, the better the specific impulse. From the perspective of engineering maturity, the recommended electric propulsion is 80 mN, and the specific impulse is 3000 s.
For the NWSK by EP with manipulator, further research can be conducted in the following aspects in the future:
- (1)
- Carrying out EWSK at the same time in NWKS;
- (2)
- Unloading angular momentum of a large number of stages (such as 50 Nms each time) while in SK;
- (3)
- Online solution for inverse motion of manipulator.
Author Contributions
Methodology, L.Y., F.L. and H.B.; software, L.Y.; writing—original draft preparation, L.Y. and C.L.; funding acquisition, W.Z.; data curation, H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Basic Research and Development (973) Program, grant number 2016YFB0501003.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Chao, C.C. Applied Orbit Perturbation and Maintenance; The Aerospace Press: Reston, VA, USA, 2005. [Google Scholar]
- Wang, Z.C.; Xing, G.H.; Zhang, H.W. Handbook of Geostationary Orbits; National Defense Industry Press: Beijing, China, 1999. [Google Scholar]
- Hu, Z.; Wang, M.; Yuan, J.G. Development and enlightenment of foreign all-EP satellite platforms. Spacecr. Environ. Eng. 2015, 32, 566–570. [Google Scholar]
- Zhang, N. High-Precision Positioning Technology for Geostationary Orbit Satellites. Ph.D. Thesis, Tsinghua University, Beijing, China, 2017. [Google Scholar]
- Li, H.N. Geostationary Satellite Orbit and Co-Location Control Technology, 1st ed.; National Defense Industry Press: Beijing, China, 2010; pp. 61–64. [Google Scholar]
- Li, H.N.; Gao, Y.J.; Yu, P.J. Research on GEO Co-location Control Strategy. Chin. J. Astronaut. 2009, 30, 967–973. [Google Scholar]
- Park, B.K.; Tahk, M.J.; Bang, H.C.; Choi, S.B. Station Collocation Design algorithm for Multiple Geostationary Satellites Operation. J. Spacecr. Rockers 2003, 40, 889–893. [Google Scholar]
- Li, J.C.; An, J.W. Co-location isolation strategy based on orbital eccentricity and orbital inclination vector square root. Spacecr. Eng. 2009, 18, 20–24. [Google Scholar]
- Shi, S.B.; Dong, G.L.; Luo, Q. Orbit maintenance strategy for GEO co-located satellites based on isolation in the tangent plane. Shanghai Aerosp. 2009, 3, 47–55. [Google Scholar]
- Shi, S.B.; Han, Q.L.; Lv, B.T. Optimal control of east-west orbit maintenance for GEO co-located satellites. Shanghai Aerosp. 2011, 2, 43–49. [Google Scholar]
- Li, Y.H. Principles and Implementation Strategies of Orbit Maintenance for Geostationary Communication Satellites. J. Aircr. Meas. Control. 2003, 22, 53–61. [Google Scholar]
- Li, Y.H.; Wei, W.; Yi, K.C. Calculation and Engineering Implementation of Orbit Control Parameters of On-orbit Geostationary Satellites. Acta Space Sci. 2007, 27, 72–76. [Google Scholar]
- Chen, Z.J.; Li, Y.H. Optimization method of east-west position keeping strategy for bias momentum satellites. Shanghai Aerosp. 2011, 28, 37–41. [Google Scholar]
- No, T.S. Simple Approach to East-West Station Keeping of Geosynchronous spacecraft. J. Guid. Control Dyn. 1999, 22, 734–736. [Google Scholar] [CrossRef]
- Yang, W.B.; Li, S.Y.; Li, N. Station-Keeping Control Method for GEO Satellite based on Relative Orbit Dynamics. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014. [Google Scholar]
- Yang, W.B.; Li, S.Y.; Li, N. Station-Keeping Control Method for High Orbit Spacecraft Based on Autonomous Control Architecture. In Proceedings of the 32nd Chinese Control Conference, Xi’an, China, 26–28 July 2013. [Google Scholar]
- Vinod, K.; Hari, B.H. Autonomous Formation Keeping of Geostationary Satellites with Regional Navigation Satellites and Dynamics. J. Guid. Control Dyn. 2017, 40, 53–57. [Google Scholar]
- Chang, J.S.; Li, Q.J.; Yuan, Y. East-west position keeping strategy of continuous equally spaced pulse thrust for geostationary satellites. Space Control. Technol. Appl. 2013, 39, 24–32. [Google Scholar]
- Weiss, A.; Cairano, D. Station Keeping and Momentum Management of Low-thrust Satellites Using MPC. Aerosp. Sci. Technol. 2019, 76, 229–241. [Google Scholar] [CrossRef]
- Frederik, J.; Bruijn, D. Geostationary Satellite Station-Keeping Using Convex Optimization. J. Guid. Control Dyn. 2015, 39, 605–616. [Google Scholar] [CrossRef] [Green Version]
- Gazzino, C.; Arzelier, D.; Cerri, L.; Losa, D.; Louembet, C.; Pittet, C. A Three-step Decomposition Method for Solving the Minimum-fuel Geostationary SK of Satellites Equipped with EP. Acta Astronaut. 2019, 158, 12–22. [Google Scholar] [CrossRef] [Green Version]
- Gazzino, C.; Arzelier, D.; Losa, D.; Louembet, C.; Pittet, C.; Cerri, L. Optimal Control for Minimum-fuel Geostationary SK of Satellites Equipped with EP. IFAC Pap. Online 2016, 49, 379–384. [Google Scholar] [CrossRef]
- Gazzino, C.; Louembet, C.; Arzelier, D.; Jozefowiez, N.; Losa, D.; Pittet, C.; Cerri, L. Interger Programming for Optimal Control of Geostationary SK of Low-thrust Satellites. IFAC-Pap. OnLine 2017, 50, 8169–8174. [Google Scholar] [CrossRef]
- Gazzino, C.; Arzelier, D.; Louembet, C.; Cerri, L.; Pittet, C.; Losa, D. Long-Term Electric-Propulsion Geostationary Station-Keeping via Integer Programming. J. Guid. Control Dyn. 2019, 42, 976–991. [Google Scholar] [CrossRef]
- Sukhanov, A.A.; Prado, A.F. On one Approach to the Optimization of Low-thrust SK Manoeuvres. Adv. Space Res. 2012, 50, 1478–1488. [Google Scholar] [CrossRef]
- Roth, M. Strategies for Geostationary Spacecraft Orbit SK Using Electrical Propulsion Only. Ph.D. Thesis, Czech Technical University, Prague, Czech Republic, 2020. [Google Scholar]
- Ogawa, N.; Terui, F.; Mimasu, Y.; Yoshikawa, K.; Ono, G.; Yasuda, S.; Matsushima, K.; Masuda, T.; Hihara, H.; Sano, J.; et al. Image-based autonomous navigation of Hayabusa2 using artificial landmarks: The design and brief in-flight results of the first landing on asteroid Ryugu. Astrodynamics 2020, 4, 89–103. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, S. Non-equatorial equilibrium points around an asteroid with gravitational orbit-attitude coupling perturbation. Astrodynamics 2020, 4, 1–16. [Google Scholar] [CrossRef]
- Zhang, T.-J.; Wolz, D.; Shen, H.-X.; Luo, Y.-Z. Spanning tree trajectory optimization in the galaxy space. Astrodynamics 2021, 5, 27–37. [Google Scholar] [CrossRef]
- Kuai, Z. Research on GEO Satellite Orbit Maintenance and Orbit Transfer Strategy under Pulse and EP. Ph.D. Thesis, University of Science and Technology of China, Hefei, China, 2017. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).