Non-Separable Meyer-like Wavelet Frames

Abstract

In the theory of wavelet frames, the known Daubechies wavelet bases have been generalized to compactly supported (Daubechies-like) wavelet frames, while the known bandlimited Meyer wavelet bases have not been generalized to date. In this study, we will generalize known Meyer wavelet basis into non-separable Meyer-like wavelet frames. By using a characteristic function to mask the Fourier transform of the one-dimensional Meyer scaling function with a width parameter, we can produce a family of Meyer-like frame scaling functions and associated Meyer-like wavelet frames. After that, by inserting a real-valued function into the width parameter of a one-dimensional Meyer-like frame scaling function, we propose a novel approach to construct non-separable Meyer-like frame scaling functions with unique circular symmetry. Finally, we construct the corresponding non-separable Meyer-like wavelet frames.

1. Introduction

Wavelet analysis has become a common tool for data compression, feature extraction and denoising [1,2]. An orthonormal basis for $L^2\left({\mathbb{R}}^d\right)$, which is generated by dyadic dilations and integer translates of one or several functions, is called a wavelet basis for $L^2\left({\mathbb{R}}^d\right)$ [3,4]. The decomposition of data by using wavelet bases can reveal the increment in information from a coarser approximation to a higher resolution approximation. Inspired by it, Mallat [1] proposed the concept of multiresolution analysis.

Let ${\left\{V_m\right\}}_{m\in \mathbb{Z}}$ be a sequence of subspaces of $L^2\left({\mathbb{R}}^d\right)$ such that

(i)

$V_m\subset V_{m+1}(m\in \mathbb{Z}),{{\displaystyle \overline{\bigcup }}}_{m\in \mathbb{Z}}{V}_m=L^2\left({\mathbb{R}}^d\right),{\bigcap }_m{V}_m=\left\{0\right\}$;

(ii)

$f\left(\mathbf{t}\right)\in V_m$ if and only if $f\left(2\mathbf{t}\right)\in V_{m+1}(m\in \mathbb{Z})$;

(iii)

there exists a $\phi \left(\mathbf{t}\right)\in V_0$ such that ${\left\{\phi \left(\mathbf{t}-\mathbf{n}\right)\right\}}_{\mathbf{n}\in {\mathbb{Z}}^d}$ is an orthonormal basis for $V_0$.

Then $\left\{V_m\right\}$ is called a multiresolution analysis (MRA), and $\phi$ is called a scaling function.

The Meyer wavelet is among the first wavelets in the history of wavelet theory [3]. Its construction is based on the Meyer scaling function $\phi \left(t\right)$ whose Fourier transform is

$$\widehat{\phi }\left(\mathit{\omega }\right)=\left\{\begin{array}{ccc}cos\left(\frac{\pi }{2}\nu (\frac{\left|\mathit{\omega }\right|}{\frac{2\pi }{3}}-1)\right),\hfill & \mathit{\omega }\in [-\frac{4\pi }{3},\frac{4\pi }{3}],\hfill & \\ \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

where

$${\displaystyle \begin{array}{c}{\displaystyle \nu \left(\tau \right)=\left\{\begin{array}{ccc}0,\hfill & \tau \le 0,\hfill & \\ 1,\hfill & \tau \ge 1,\hfill \end{array}\right.}\hfill \\ \\ 0<\nu \left(\tau \right)<1(0<\tau <1),\nu \left(\tau \right)+\nu (1-\tau )=1(\tau \in \mathbb{R}).\hfill \end{array}}$$

The corresponding Meyer wavelet $\psi \left(t\right)$ is defined by its Fourier transform:

$${\displaystyle \widehat{\psi }\left(\mathit{\omega }\right)=\left\{\begin{array}{ccc}{e}^{-\frac{i\mathit{\omega }}{2}}sin\left(\frac{\pi }{2}\nu \left(\frac{\left|\mathit{\omega }\right|-\frac{2\pi }{3}}{\frac{2\pi }{3}}\right)\right),\hfill & \frac{2\pi }{3}\le \left|\mathit{\omega }\right|\le \frac{4\pi }{3},\hfill & \\ \\ e^{-\frac{i\mathit{\omega }}{2}}cos\left(\frac{\pi }{2}\nu \left(\frac{\left|\mathit{\omega }\right|-\frac{4\pi }{3}}{\frac{4\pi }{3}}\right)\right),\hfill & \frac{4\pi }{3}\le \left|\mathit{\omega }\right|\le \frac{8\pi }{3},\hfill & \\ \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.}$$

The dyadic dilations and integer translates of the Meyer wavelet can form a wavelet basis for $L^2\left(\mathbb{R}\right)$. In the high dimension, the tensor product of the Meyer scaling function and Meyer wavelet can generate a separable Meyer wavelet basis for $L^2\left({\mathbb{R}}^d\right)$ [5].

Frames are an overcomplete version of bases [5,6]. Let ${\left\{h_n\right\}}_1^{\infty }$ be a sequence in $L^2\left({\mathbb{R}}^d\right)$. If there exists $A,B>0$ such that

$$A∥f∥l^2\le \sum _{n=1}^{\infty }{\left|(f,h_n)\right|}^2\le B{∥f∥}^2\forall f\in L^2\left({\mathbb{R}}^d\right),$$

where $(·,·)$ and $∥·∥$ are the inner product and the norm, respectively, then ${\left\{h_n\right\}}_1^{\infty }$ is called a frame for $L^2\left({\mathbb{R}}^d\right)$ with bounds A and B [1,6].

Wavelet frames are a generalization of both wavelet bases and frames [6]. Let ${\psi }_1,{\psi }_2,\dots ,{\psi }_r\in L^2\left({\mathbb{R}}^d\right)$ be such that their dyadic dilations and integer translates

$${\psi }_{\mathit{\mu },m,\mathbf{n}}\left(\mathbf{t}\right)=2^{\frac{md}{2}}{\psi }_{\mathit{\mu }}(2^m\mathbf{t}-\mathbf{n}),\mathit{\mu }=1,2,\dots ,r,m\in \mathbb{Z},\mathbf{n}\in {\mathbb{Z}}^d$$

consists of a frame for $L^2\left({\mathbb{R}}^d\right)$. Then such a frame is called a wavelet frame, and the family ${\psi }_1,{\psi }_2,\dots ,{\psi }_r$ is called a wavelet frame generator [6,7,8]. Compared with wavelet bases, wavelet frames can provide redundant representations of data, leading to better performances in time-frequency analysis, feature extraction, data compression and compressed sensing [7].

Until now, the known Daubechies wavelet bases have been generalized to compactly supported (Daubechies-like) wavelet frames [9,10,11], while the known bandlimited Meyer wavelet bases have not been generalized to date. In this study, we will generalize known Meyer wavelet bases into non-separable Meyer-like wavelet frames.

2. Construction of Wavelet Frames

In order to construct wavelet frames, the classic MRA is extended to the frame MRA [8,12] when the condition (iii) in MRA is replaced by

$$\sum _{\mathbf{k}\in {\mathbb{Z}}^{\mathbf{d}}}{\left|\widehat{\phi }(\mathit{\omega }+2\mathbf{k}\pi )\right|}^2={\chi }_Q.$$

where ${\chi }_Q$ is the characteristic function on Q. In this case, $\left\{V_m\right\}$ is called a frame MRA for $L^2\left({\mathbb{R}}^d\right)$, $\phi$ is called a frame scaling function, and Q is called the spectrum of frame scaling function. When $Q={\mathbb{R}}^d$, the frame scaling function in frame MRA is just a scaling function in MRA [8,12].

By the bi-scale equation of frame MRA, there exists a $2\pi$-periodic function $H_0$ such that

$$\widehat{\phi }\left(2\mathit{\omega }\right)=H_0\left(\mathit{\omega }\right)\widehat{\phi }\left(\mathit{\omega }\right)(\mathit{\omega }\in {\mathbb{R}}^d).$$

$H_0$ is called the filter of frame MRA [8,12]. Conversely, we have

Proposition 1

([6,13,14]). If a function φ satisfies

(i) 

$\widehat{\phi }\left(\mathbf{0}\right)=0$ and $\widehat{\phi }\left(\mathit{\omega }\right)$ is continuous at $\mathit{\omega }=\mathbf{0}$;

(ii) 

${\displaystyle \sum _{\mathbf{k}\in {\mathbb{Z}}^{\mathbf{d}}}}{\left|\widehat{\phi }(\mathit{\omega }+2\mathbf{k}\pi )\right|}^2=0or1$;

(iii) 

there exists a $2\pi$-periodic function $H_0$ such that $\widehat{\phi }\left(2\mathit{\omega }\right)=H_0\left(\mathit{\omega }\right)\widehat{\phi }\left(\mathit{\omega }\right)$,

then φ is a frame scaling function for $L^2\left({\mathbb{R}}^d\right)$.

The following unitary extension principle [9] can be used to construct wavelet frames from frame MRAs.

Proposition 2

([9]). For a given frame MRA with filter $H_0$ and spectrum Q. Let $H_1,\dots ,H_r$ be $2\pi$-periodic bounded functions and define the matrix

$$H={\left(H_{\mathit{\mu }}(\mathit{\omega }+\nu \pi ){\chi }_Q(\mathit{\omega }+\nu \pi )\right)}_{\mathit{\mu }=0,1,\dots r,\nu \in {\{0,1\}}^d},$$

where the set ${\{0,1\}}^d$ consists of the vertices of the cube ${[0,1]}^d$. Let ${\left\{{\psi }_{\mathit{\mu }}\right\}}_{\mathit{\mu }=1,\dots ,r}$ be such that

$${\widehat{\psi }}_{\mathit{\mu }}\left(2\mathit{\omega }\right)=H_{\mathit{\mu }}\left(\mathit{\omega }\right)\widehat{\phi }\left(\mathit{\omega }\right)(\mathit{\mu }=1,\dots ,r).$$

If $H^{*}H=diag{\left\{{\chi }_Q(\mathit{\omega }+\nu \pi )\right\}}_{\nu \in {\{0,1\}}^d}$, then $\{{\psi }_1,\dots ,{\psi }_r\}$ is a wavelet frame generator for $L^2\left({\mathbb{R}}^d\right)$.

3. One-Dimensional Meyer-like Wavelet Frames

For $\alpha \in [\pi ,\frac{4\pi }{3}]$, we take a point set E satisfying $E\subset [-\alpha ,-\pi ]$ and then define a point set F as follows (Figure 1)

$$F=E\bigcup \frac{E}{2}\bigcup (E+2\pi )\bigcup (\frac{E}{2}+\pi ).$$

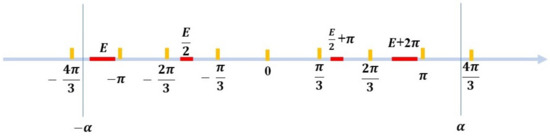
Figure 1. The point set F.

Let ${\phi }_F(t,\alpha )$ be a function whose Fourier transform is

$${\displaystyle {\widehat{\phi }}_F(\mathit{\omega },\alpha )=\left\{\begin{array}{ccc}cos\left(\frac{\pi }{2}\zeta (\frac{\left|\mathit{\omega }\right|}{2\pi -\alpha }-1,\alpha )\right),\hfill & \mathit{\omega }\in [-\alpha ,\alpha ]\backslash F,\hfill & \\ \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.}$$

(1)

where

$${\displaystyle \begin{array}{c}{\displaystyle \zeta (\tau ,\alpha )=\left\{\begin{array}{ccc}0,\hfill & \tau \le 0,\hfill & \\ 1,\hfill & \tau \ge \frac{2\alpha -2\pi }{2\pi -\alpha },\hfill \end{array}\right.}\hfill \\ \\ 0<\zeta (\tau ,\alpha )<1(0<\tau <\frac{2\alpha -2\pi }{2\pi -\alpha }),\zeta (\tau ,\alpha )+\zeta (\frac{2\alpha -2\pi }{2\pi -\alpha }-\tau ,\alpha )=1(\tau \in \mathbb{R}).\hfill \end{array}}$$

(2)

Then we have

Theorem 1.

For $\alpha \in [\pi ,\frac{4\pi }{3}]$, ${\phi }_F(t,\alpha )$ is a frame scaling function in $L^2\left(\mathbb{R}\right)$.

Proof. 

For $\mathit{\omega }\in [\alpha -2\pi ,2\pi -\alpha ]$, By Equations (1) and (2), we have

$${\displaystyle {\widehat{\phi }}_F(\mathit{\omega },\alpha )=\left\{\begin{array}{ccc}1,\hfill & \mathit{\omega }\in [\alpha -2\pi ,2\pi -\alpha ]\backslash \left(\frac{E}{2}\bigcup (\frac{E}{2}+\pi )\right),\hfill & \\ \\ 0,\hfill & \mathit{\omega }\in \frac{E}{2}\bigcup (\frac{E}{2}+\pi ).\hfill \end{array}\right.}$$

(3)

When $\mathit{\omega }\in [\alpha -2\pi ,2\pi -\alpha ]$, we have $\mathit{\omega }+2k\pi \ge \alpha (k\ge 1)$ and $\mathit{\omega }+2k\pi \le -\alpha (k\le -1)$. Again by Equation (3), we obtain

$${\displaystyle \sum _k|{\widehat{\phi }}_F{(\mathit{\omega }+2k\pi ,\alpha )|}^2={\left|{\widehat{\phi }}_F(\mathit{\omega },\alpha )\right|}^2=\left\{\begin{array}{ccc}1,\hfill & \mathit{\omega }\in [\alpha -2\pi ,2\pi -\alpha ]\backslash \left(\frac{E}{2}\bigcup (\frac{E}{2}+\pi )\right),\hfill & \\ \\ 0,\hfill & \mathit{\omega }\in \frac{E}{2}\bigcup (\frac{E}{2}+\pi ).\hfill \end{array}\right.}$$

(4)

For $\mathit{\omega }\in [-\alpha ,\alpha -2\pi ]\backslash E$, we have $\mathit{\omega }+2\pi =2\pi -\left|\mathit{\omega }\right|$. Again, by $\zeta (\tau ,\alpha )+\zeta (\frac{2\alpha -2\pi }{2\pi -\alpha }-\tau ,\alpha )=1$, we deduce

$${\displaystyle \begin{array}{ccc}{\widehat{\phi }}_F(\mathit{\omega }+2\pi ,\alpha )\hfill & =\hfill & {\widehat{\phi }}_F(2\pi -|\mathit{\omega }|,\alpha )=cos\left(\frac{\pi }{2}\zeta (\frac{2\pi -\left|\mathit{\omega }\right|}{2\pi -\alpha }-1,\alpha )\right)\hfill \\ \\ & =\hfill & cos\left(\frac{\pi }{2}(1-\zeta (\frac{\left|\mathit{\omega }\right|}{2\pi -\alpha }-1,\alpha ))\right)=sin\left(\frac{\pi }{2}\zeta (\frac{\left|\mathit{\omega }\right|}{2\pi -\alpha }-1,\alpha )\right).\hfill \end{array}}$$

Again, by Equation (1), when $\mathit{\omega }\in E$, we have ${\widehat{\phi }}_F(\mathit{\omega },\alpha )={\widehat{\phi }}_F(\mathit{\omega }+2\pi ,\alpha )=0$. Furthermore

$${\displaystyle |{\widehat{\phi }}_F{(\mathit{\omega },\alpha )|}^2+{\left|{\widehat{\phi }}_F(\mathit{\omega }+2\pi ,\alpha )\right|}^2=\left\{\begin{array}{ccc}1,\hfill & \mathit{\omega }\in [-\alpha ,\alpha -2\pi ]\backslash E,\hfill & \\ \\ 0,\hfill & \mathit{\omega }\in E.\hfill \end{array}\right.}$$

For $\mathit{\omega }\in [-\alpha ,\alpha -2\pi ]$, we have $\mathit{\omega }+2k\pi \ge \mathit{\omega }+4\pi >\alpha (k\ge 2)$ and $\mathit{\omega }+2k\pi <-\alpha (k\le -1)$. Noticing that $\mathrm{supp}{\widehat{\phi }}_F=[-\alpha ,\alpha ]$, we can deduce that

$${\displaystyle \sum _k|{\widehat{\phi }}_F{(\mathit{\omega }+2k\pi ,\alpha )|}^2=|{\widehat{\phi }}_F{(\mathit{\omega },\alpha )|}^2+{\left|{\widehat{\phi }}_F(\mathit{\omega }+2\pi ,\alpha )\right|}^2=\left\{\begin{array}{ccc}1,\hfill & \mathit{\omega }\in [-\alpha ,\alpha -2\pi ]\backslash E,\hfill & \\ \\ 0,\hfill & \mathit{\omega }\in E.\hfill \end{array}\right.}$$

(5)

Since the length of the interval $[-\alpha ,2\pi -\alpha ]$ is $2\pi$ and ${\sum }_k{\left|{\widehat{\phi }}_F(\mathit{\omega }+2k\pi )\right|}^2$ is $2\pi$-periodic, by Equations (4) and (5), we have

$$\sum _k{\left|{\widehat{\phi }}_F(\mathit{\omega }+2k\pi ,\alpha )\right|}^2={\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right)(\mathit{\omega }\in \mathbb{R}),$$

(6)

where ${\chi }_{\mathbb{R}\backslash F^{*}}$ is the characteristic function of $\mathbb{R}\backslash F^{*}$ and $F^{*}={\bigcup }_k(F+2k\pi )$. Furthermore,

$${\displaystyle {\widehat{\phi }}_F(\mathit{\omega },\alpha )=\left\{\begin{array}{ccc}1\hfill & for\mathit{\omega }\in [\alpha -2\pi ,2\pi -\alpha ]\backslash F,\hfill & \\ \\ 0\hfill & for\mathit{\omega }\in [\alpha -2\pi ,2\pi -\alpha ]\bigcap F.\hfill \end{array}\right.}$$

(7)

Define

$${\displaystyle H_F(\mathit{\omega },\alpha )=\left\{\begin{array}{ccc}{\widehat{\phi }}_F(2\mathit{\omega },\alpha ),\hfill & \mathit{\omega }\in [-\frac{\alpha }{2},\frac{\alpha }{2}],\hfill & \\ \\ 0,\hfill & \mathit{\omega }\in [\frac{\alpha }{2},-\frac{\alpha }{2}+2\pi ],\hfill \end{array}\right.}$$

(8)

and then we extend $H_F(\mathit{\omega },\alpha )$ into a $2\pi$-periodic function on $\mathbb{R}$.

Now we will prove that

$${\widehat{\phi }}_F(2\mathit{\omega },\alpha )=H_F(\mathit{\omega },\alpha ){\widehat{\phi }}_F(\mathit{\omega },\alpha ).$$

(9)

When $\mathit{\omega }\notin [-\alpha ,\alpha ]$, we have ${\widehat{\phi }}_F(\mathit{\omega },\alpha )=0$ and $2\mathit{\omega }\notin [-2\alpha ,2\alpha ]$, and so ${\widehat{\phi }}_F(2\mathit{\omega },\alpha )=0$. From this, we know that when $\mathit{\omega }\notin [-\alpha ,\alpha ]$, Equation (9) holds.

When $\mathit{\omega }\in (-\alpha ,-\frac{\alpha }{2})\bigcup (\frac{\alpha }{2},\alpha )$, we have $2\mathit{\omega }\in (-2\alpha ,-\alpha )\bigcup (\alpha ,2\alpha )$, and so ${\widehat{\phi }}_F(2\mathit{\omega },\alpha )=0$. Moreover, by Equation (7) and $\alpha \le \frac{4\pi }{3}$, it follows that $H_F(\mathit{\omega },\alpha )=0$. Therefore, when $\mathit{\omega }\in (-\alpha ,-\frac{\alpha }{2})\bigcup (\frac{\alpha }{2},\alpha )$, Equation (9) holds.

When $\mathit{\omega }\in [-\frac{\alpha }{2},\frac{\alpha }{2}]\backslash (\frac{E}{2}\bigcup (\frac{E}{2}+\pi ))$, we have $H_F(\mathit{\omega },\alpha )={\widehat{\phi }}_F(2\mathit{\omega },\alpha )$. By Equation (3) and noticing that $\frac{\alpha }{2}\le 2\pi -\alpha$, $-\frac{\alpha }{2}\ge \alpha -2\pi$, we obtain ${\widehat{\phi }}_F(\mathit{\omega },\alpha )=1$ for $\mathit{\omega }\in [-\frac{\alpha }{2},\frac{\alpha }{2}]\backslash (\frac{E}{2}\bigcup (\frac{E}{2}+\pi ))$. Therefore, when $\mathit{\omega }\in [-\frac{\alpha }{2},\frac{\alpha }{2}]\backslash (\frac{E}{2}\bigcup (\frac{E}{2}+\pi ))$, Equation (9) holds.

When $\mathit{\omega }\in \frac{E}{2}\bigcup (\frac{E}{2}+\pi )$, we have $2\mathit{\omega }\in E\bigcup (E+2\pi )$. From this and Equation (1), ${\widehat{\phi }}_F(\mathit{\omega },\alpha )={\widehat{\phi }}_F(2\mathit{\omega },\alpha )=0$. Therefore, when $\mathit{\omega }\in \frac{E}{2}\bigcup (\frac{E}{2}+\pi )$, Equation (9) holds.

By Equation (9), we deduce that

$${\widehat{\phi }}_F(2\mathit{\omega },\alpha )=H_F(\mathit{\omega },\alpha ){\widehat{\phi }}_F(\mathit{\omega },\alpha )(\mathit{\omega }\in \mathbb{R}),$$

(10)

where $H_F(\mathit{\omega },\alpha )$ is stated as in Equation (8)

By Equations (6) and (10), noticing that ${\widehat{\phi }}_F(\mathit{\omega },\alpha )=1$ and ${\widehat{\phi }}_F$ is continuous at $\mathit{\omega }=0$, using Proposition 1, we know that ${\phi }_F(t,\alpha )$ is a frame scaling function in $L^2\left(\mathbb{R}\right)$. □

Below we begin to construct wavelet frame generators associated with the frame scaling function ${\phi }_F$. By Equation (8), it follows that

$$|H_F{(\mathit{\omega },\alpha )|}^2=\sum _k>|{\widehat{\phi }}_F{(2\mathit{\omega }+4k\pi ,\alpha )|}^2,|H_F{(\mathit{\omega }+\pi ,\alpha )|}^2=\sum _k{\left|{\widehat{\phi }}_F(2\mathit{\omega }+4k\pi +2\pi ,\alpha )\right|}^2$$

Furthermore, we have

$$\sum _k|{\widehat{\phi }}_F{(2\mathit{\omega }+2k\pi ,\alpha )|}^2=|H_F{(\mathit{\omega },\alpha )|}^2+{\left|H_F(\mathit{\omega }+\pi ,\alpha )\right|}^2(\mathit{\omega }\in \mathbb{R}),$$

By Equation (6), it follows that

$${\chi }_{\mathbb{R}\backslash F^{*}}\left(2\mathit{\omega }\right)=|H_F{(\mathit{\omega },\alpha )|}^2|+|H_F{(\mathit{\omega }+\pi ,\alpha )|}^2,$$

and then

$${\chi }_{\mathbb{R}\backslash F^{*}}\left(2\mathit{\omega }\right){\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right)=|H_F{(\mathit{\omega },\alpha )|}^2|{\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right)+{\left|H_F(\mathit{\omega }+\pi ,\alpha )\right|}^2{\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right)(\mathit{\omega }\in \mathbb{R}).$$

(11)

Therefore, the matrix

$${\displaystyle {\mathsf{\Omega }}_s\left(\mathit{\omega }\right)=\left(\begin{array}{cc}{H}_F(\mathit{\omega },\alpha ){\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right)& H_F(\mathit{\omega }+\pi ,\alpha ){\chi }_{\mathbb{R}\backslash F^{*}}(\mathit{\omega }+\pi )\\ \\ e^{-i\mathit{\omega }}{H}_F(\mathit{\omega }+\pi ,\alpha ){\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right)& -e^{-i\mathit{\omega }}{H}_F(\mathit{\omega },\alpha ){\chi }_{\mathbb{R}\backslash F^{*}}(\mathit{\omega }+\pi )\end{array}\right)}$$

satisfies

$${\displaystyle {\mathsf{\Omega }}_s^{*}\left(\mathit{\omega }\right){\mathsf{\Omega }}_s\left(\mathit{\omega }\right)=\left(\begin{array}{cc}{\chi }_{\mathbb{R}\backslash F^{*}}\left(2\mathit{\omega }\right){\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right)& 0\\ \\ 0& {\chi }_{\mathbb{R}\backslash F^{*}}\left(2(\mathit{\omega }+\pi )\right){\chi }_{\mathbb{R}\backslash F^{*}}(\mathit{\omega }+\pi )\end{array}\right).}$$

(12)

Let

$$M=\mathrm{supp}\{{\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right)-{\chi }_{\mathbb{R}\backslash F^{*}}\left(2\mathit{\omega }\right){\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right)\}.$$

(13)

It is clear that M is a $2\pi$-periodic point set, i.e., $M+2\pi =M$. We divide M into two $2\pi$-periodic point sets as follows

$$M_1=M\bigcap ([-\pi ,0]+2\pi \mathbb{Z}),M_2=M\bigcap ([0,\pi ]+2\pi \mathbb{Z}),$$

(14)

By Equations (11), (13) and (14), we have

$${\displaystyle \begin{array}{c}{\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right)=|H_F{(\mathit{\omega },\alpha )|}^2|{\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right)+{\left|e^{-i\mathit{\omega }}{H}_F(\mathit{\omega }+\pi ,\alpha )\right|}^2{\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right)\hfill \\ \\ +|{\chi }_{M_1}{(\mathit{\omega },\alpha )|}^2{\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right)+{\left|{\chi }_{M_2}(\mathit{\omega },\alpha )\right|}^2{\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right).\hfill \end{array}}$$

(15)

Define ${\psi }_F^{\left(1\right)}$, ${\psi }_F^{\left(2\right)}$ and ${\psi }_F^{\left(3\right)}$ as

$${\displaystyle \begin{array}{ccc}{\widehat{\psi }}_F^{\left(1\right)}(\mathit{\omega },\alpha )\hfill & =\hfill & e^{-i\frac{\mathit{\omega }}{2}}{H}_F\left(\frac{\mathit{\omega }}{2}+\pi ,\alpha \right){\widehat{\phi }}_F\left(\frac{\mathit{\omega }}{2},\alpha \right),\hfill \\ \\ {\widehat{\psi }}_F^{\left(2\right)}(\mathit{\omega },\alpha )\hfill & =\hfill & {\chi }_{M_1}\left(\frac{\mathit{\omega }}{2}\right){\widehat{\phi }}_F\left(\frac{\mathit{\omega }}{2},\alpha \right),\hfill \\ \\ {\widehat{\psi }}_F^{\left(3\right)}(\mathit{\omega },\alpha )\hfill & =\hfill & {\chi }_{M_2}\left(\frac{\mathit{\omega }}{2}\right){\widehat{\phi }}_F\left(\frac{\mathit{\omega }}{2},\alpha \right).\hfill \end{array}}$$

(16)

Now we compute ${\psi }_F^{\left(1\right)}$:

$${\widehat{\psi }}_F^{\left(1\right)}(\mathit{\omega },\alpha )=e^{-i\frac{\mathit{\omega }}{2}}{H}_F\left(\frac{\mathit{\omega }}{2}+\pi ,\alpha \right){\widehat{\phi }}_F\left(\frac{\mathit{\omega }}{2},\alpha \right)=e^{-i\frac{\mathit{\omega }}{2}}\left(\sum _k{\widehat{\phi }}_F(\mathit{\omega }+(4k+2)\pi ,\alpha )\right){\widehat{\phi }}_F\left(\frac{\mathit{\omega }}{2},\alpha \right),$$

For $k\ne 0,-1$,

$$\mathrm{supp}{\widehat{\phi }}_F(\mathit{\omega }+(4k+2)\pi ,\alpha )\bigcap \mathrm{supp}{\widehat{\phi }}_F\left(\frac{\mathit{\omega }}{2},\alpha \right)=\varnothing .$$

It means that

$${\widehat{\psi }}_F^{\left(1\right)}(\mathit{\omega },\alpha )=e^{-i\frac{\mathit{\omega }}{2}}({\widehat{\phi }}_F(\mathit{\omega }+2\pi ,\alpha )+{\widehat{\phi }}_F(\mathit{\omega }-2\pi ,\alpha )){\widehat{\phi }}_F\left(\frac{\mathit{\omega }}{2},\alpha \right).$$

(17)

and

$$\mathrm{supp}{\widehat{\psi }}_F^{\left(1\right)}(\mathit{\omega },\alpha )=\left([-2\alpha ,\alpha -2\pi ]\bigcup [2\pi -\alpha ,2\alpha ]\right)\backslash R_E,$$

where

$$R_E=2E\bigcup E\bigcup (\frac{E}{2}-2\pi )\bigcup (\frac{E}{2}-\pi )\bigcup (E+2\pi )\bigcup (\frac{E}{2}+2\pi )\bigcup (\frac{E}{2}+3\pi )\bigcup (2E+4\pi )$$

When $2\pi -\alpha \le \mathit{\omega }\le \alpha$ and $\mathit{\omega }\notin E+2\pi$, we have ${\widehat{\phi }}_F(\mathit{\omega }+2\pi ,\alpha )=0$. By Equation (7),

$${\widehat{\phi }}_F(\frac{\mathit{\omega }}{2},\alpha )=1\mathrm{for}\mathit{\omega }\in [2\alpha -4\pi ,4\pi -2\alpha ]\backslash 2F.$$

we deduce that

$$e^{i\frac{\mathit{\omega }}{2}}{\widehat{\psi }}_F^{\left(1\right)}(\mathit{\omega },\alpha )={\widehat{\phi }}_F(\mathit{\omega }-2\pi ,\alpha )=cos\left(\frac{\pi }{2}\zeta \left(\frac{2\pi -\mathit{\omega }}{2\pi -\alpha }-1,\alpha \right)\right)=sin\left(\frac{\pi }{2}\zeta \left(\frac{\mathit{\omega }}{2\pi -\alpha }-1,\alpha \right)\right).$$

When $-\alpha \le \mathit{\omega }\le \alpha -2\pi$ and $\alpha \notin E$, we have ${\widehat{\phi }}_F(\mathit{\omega }-2\pi ,\alpha )=0$. Again by Equation (13), we deduce that

$$e^{i\frac{\mathit{\omega }}{2}}{\widehat{\psi }}_F^{\left(1\right)}(\mathit{\omega },\alpha )={\widehat{\phi }}_F(2\pi +\mathit{\omega },\alpha )=cos\left(\frac{\pi }{2}\zeta \left(\frac{2\pi +\mathit{\omega }}{2\pi -\alpha }-1,\alpha \right)\right)=sin\left(\frac{\pi }{2}\zeta \left(\frac{-\mathit{\omega }}{2\pi -\alpha }-1,\alpha \right)\right).$$

When $\alpha <\mathit{\omega }<2\alpha$ and $\mathit{\omega }\notin (\frac{E}{2}+2\pi )\bigcup (\frac{E}{2}+3\pi )\bigcup (2E+4\pi )$, we have ${\widehat{\phi }}_F(\mathit{\omega }+2\pi ,\alpha )=0$ and ${\widehat{\phi }}_F(\mathit{\omega }-2\pi )=1$. From this and Equations (1) and (17), we obtain

$$e^{i\frac{\mathit{\omega }}{2}}{\widehat{\psi }}_F^{\left(1\right)}(\mathit{\omega },\alpha )={\widehat{\phi }}_F\left(\frac{\mathit{\omega }}{2},\alpha \right)=cos\left(\frac{\pi }{2}\zeta \left(\frac{\mathit{\omega }}{4\pi -2\alpha }-1,\alpha \right)\right).$$

When $-2\alpha <\mathit{\omega }<-\alpha$ and $\mathit{\omega }\notin 2E\bigcup (\frac{E}{2}-\pi )\bigcup (\frac{E}{2}-2\pi )$, we have ${\widehat{\phi }}_F(\mathit{\omega }+2\pi ,\alpha )=1$ and ${\widehat{\phi }}_F(\mathit{\omega }-2\pi )=0$. From this and Equations (1) and (17), we obtain

$$e^{i\frac{\mathit{\omega }}{2}}{\widehat{\psi }}_F^{\left(1\right)}(\mathit{\omega },\alpha )={\widehat{\phi }}_F\left(\frac{\mathit{\omega }}{2},\alpha \right)=cos\left(\frac{\pi }{2}\zeta \left(\frac{-\mathit{\omega }}{4\pi -2\alpha }-1,\alpha \right)\right).$$

Summarizing the above results, we have

$${\displaystyle {\widehat{\psi }}_F^{\left(1\right)}(\mathit{\omega },\alpha )=\left\{\begin{array}{ccc}{e}^{-i\frac{\mathit{\omega }}{2}}cos\left(\frac{\pi }{2}\zeta \left(\frac{-\mathit{\omega }}{4\pi -2\alpha }-1,\alpha \right)\right),\hfill & -2\alpha \le \mathit{\omega }\le -\alpha \mathrm{and}\mathit{\omega }\notin 2E\bigcup (\frac{E}{2}-\pi )\bigcup (\frac{E}{2}-2\pi )\hfill & \\ \\ e^{-i\frac{\mathit{\omega }}{2}}sin\left(\frac{\pi }{2}\zeta \left(\frac{-\mathit{\omega }}{2\pi -\alpha }-1,\alpha \right)\right),\hfill & -\alpha \le \mathit{\omega }\le \alpha -2\pi \mathrm{and}\mathit{\omega }\notin E\hfill & \\ \\ e^{-i\frac{\mathit{\omega }}{2}}sin\left(\frac{\pi }{2}\zeta \left(\frac{\mathit{\omega }}{2\pi -\alpha }-1,\alpha \right)\right),\hfill & 2\pi -\alpha \le \mathit{\omega }\le \alpha \mathrm{and}\mathit{\omega }\notin E+2\pi \hfill & \\ \\ e^{-i\frac{\mathit{\omega }}{2}}cos\left(\frac{\pi }{2}\zeta \left(\frac{\mathit{\omega }}{4\pi -2\alpha }-1,\alpha \right)\right),\hfill & \alpha \le \mathit{\omega }\le 2\alpha \mathrm{and}\mathit{\omega }\notin (\frac{E}{2}+2\pi )\bigcup (\frac{E}{2}+3\pi )\bigcup (2E+4\pi )\hfill & \\ \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.}$$

(18)

Similarly, by Equations (6) and (16), for ${\psi }_F^{\left(2\right)}$, we have

$${\displaystyle {\widehat{\psi }}_F^{\left(2\right)}(\mathit{\omega },\alpha )=\left\{\begin{array}{ccc}cos\left(\frac{\pi }{2}\zeta (\frac{-\mathit{\omega }}{4\pi -2\alpha }-1,\alpha )\right),\hfill & \mathit{\omega }\in 2M_1\bigcap \left(([-2\pi ,0]\backslash E)\right),\hfill & \\ \\ cos\left(\frac{\pi }{2}\zeta (\frac{\mathit{\omega }}{4\pi -2\alpha }-1,\alpha )\right),\hfill & \mathit{\omega }\in 2M_1\bigcap ([2\pi ,4\pi ]\backslash (2E+4\pi )),\hfill & \\ \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.}$$

(19)

For ${\psi }_F^{\left(3\right)}$, we have

$${\displaystyle {\widehat{\psi }}_F^{\left(3\right)}(\mathit{\omega },\alpha )=\left\{\begin{array}{ccc}cos\left(\frac{\pi }{2}\zeta (\frac{-\mathit{\omega }}{4\pi -2\alpha }-1,\alpha )\right),\hfill & \mathit{\omega }\in 2M_2\bigcap ([-4\pi ,-2\pi ]\backslash (2E\bigcup (E-2\pi ))),\hfill & \\ \\ cos\left(\frac{\pi }{2}\zeta (\frac{\mathit{\omega }}{4\pi -2\alpha }-1,\alpha )\right),\hfill & \mathit{\omega }\in 2M_2\bigcap ([0,2\pi ]\backslash (E+2\pi )\bigcup (2E+4\pi )),\hfill & \\ \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.}$$

(20)

By Equations (12), (14) and (15), the matrix

$${\displaystyle \mathsf{\Omega }\left(\mathit{\omega }\right)=\left(\begin{array}{cc}{H}_F(\mathit{\omega },\alpha ){\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right)& H_F(\mathit{\omega }+\pi ,\alpha ){\chi }_{\mathbb{R}\backslash F^{*}}(\mathit{\omega }+\pi )\\ \\ e^{-i\mathit{\omega }}{H}_F(\mathit{\omega }+\pi ,\alpha ){\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right)& -e^{-i\mathit{\omega }}{H}_F(\mathit{\omega },\alpha ){\chi }_{\mathbb{R}\backslash F^{*}}(\mathit{\omega }+\pi )\\ \\ {\chi }_{M_1}\left(\mathit{\omega }\right){\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right)& {\chi }_{M_1}(\mathit{\omega }+\pi ){\chi }_{\mathbb{R}\backslash F^{*}}(\mathit{\omega }+\pi )\\ \\ {\chi }_{M_2}\left(\mathit{\omega }\right){\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right)& {\chi }_{M_2}(\mathit{\omega }+\pi ){\chi }_{\mathbb{R}\backslash F^{*}}(\mathit{\omega }+\pi )\end{array}\right)}$$

satisfies

$${\displaystyle {\mathsf{\Omega }}^{*}\left(\mathit{\omega }\right)\mathsf{\Omega }\left(\mathit{\omega }\right)=\left(\begin{array}{cc}{\chi }_{\mathbb{R}\backslash F^{*}}\left(\mathit{\omega }\right)& 0\\ \\ 0& {\chi }_{\mathbb{R}\backslash F^{*}}(\mathit{\omega }+\pi ).\end{array}\right)}$$

Again by Equation (16) and Proposition 2, we have

Theorem 2.

For $\alpha \in [\pi ,\frac{4\pi }{3}]$, the system $\{{\psi }_F^{\left(1\right)},{\psi }_F^{\left(2\right)},{\psi }_F^{\left(3\right)}\}$ is a wavelet frame generator in $L^2\left(\mathbb{R}\right)$, where ${\psi }_F^{\left(1\right)}$, ${\psi }_F^{\left(2\right)}$, and ${\psi }_F^{\left(3\right)}$ are stated in Equations (18)–(20).

Remark 1.

Since ${\widehat{\psi }}_F^{\left(1\right)}$ is just the known Meyer wavelet masked by some characteristic function, and ${\widehat{\psi }}_F^{\left(2\right)}$ and ${\psi }_F^{\left(3\right)}$ are just the Meyer scaling function masked by some characteristic function, the system $\{{\psi }_F^{\left(1\right)},{\psi }_F^{\left(2\right)},{\psi }_F^{\left(3\right)}\}$ is called a Meyer-like wavelet frame generator.

4. Non-Separable Meyer-like Frame Scaling Functions

Let $\gamma$ be a real-valued function satisfying the conditions:

$$\pi <b\le \gamma \left(\eta \right)\le \frac{4\pi }{3}\left(\right|\eta |<\frac{2\pi }{3})\mathrm{and}\gamma \left(\eta \right)=b,(\left|\eta \right|\ge \frac{2\pi }{3}),$$

(21)

where b is a constant. In this section, we always take $E\subset [-b,-\pi ]$ and $F=E\bigcup \frac{E}{2}\bigcup (E+2\pi )\bigcup (\frac{E}{2}+\pi )$. Based on ${\phi }_F(t,\alpha )$ as stated in (1), we define a bivariate function ${\phi }^{\left(0\right)}\left(\mathbf{t}\right)$ such that its Fourier transform satisfies

$${\widehat{\phi }}^{\left(0\right)}\left(\mathit{\omega }\right)={\widehat{\phi }}_F({\mathit{\omega }}_1,\gamma \left({\mathit{\omega }}_2\right)){\widehat{\phi }}_F({\mathit{\omega }}_2,\gamma \left({\mathit{\omega }}_1\right))(\mathit{\omega }=({\mathit{\omega }}_1,{\mathit{\omega }}_2)\in {\mathbb{R}}^2).$$

(22)

Define two curvilinear quadrangles G and $G_0$ as

$${\displaystyle \begin{array}{c}G=\{\mathit{\omega }=({\mathit{\omega }}_1,{\mathit{\omega }}_2):|{\mathit{\omega }}_1|\le \gamma \left({\mathit{\omega }}_2\right),|{\mathit{\omega }}_2|\le \gamma \left({\mathit{\omega }}_1\right)\},\hfill \\ \\ G_0=\{\mathit{\omega }=({\mathit{\omega }}_1,{\mathit{\omega }}_2):|{\mathit{\omega }}_1|\le 2\pi -\gamma \left({\mathit{\omega }}_2\right),|{\mathit{\omega }}_2|\le 2\pi -\gamma \left({\mathit{\omega }}_1\right)\}\hfill \end{array}}$$

and define $F_0=\{\mathit{\omega }=({\mathit{\omega }}_1,{\mathit{\omega }}_2):{\mathit{\omega }}_1\in F\mathrm{or}{\mathit{\omega }}_2\in F\}$.

Theorem 3. 

(i) ${\phi }^{\left(0\right)}$ is a non-separable frame scaling function in $L^2\left({\mathbb{R}}^2\right)$

(ii) ${\phi }^{\left(0\right)}$ is circularly symmetric and $supp{\widehat{\phi }}^{\left(0\right)}=G\backslash F_0$.

Remark 2.

In Theorem 3, by inserting a real-valued function into the width parameter of the one-dimensional Meyer-like frame scaling function, we give a novel approach to construct non-separable Meyer-like frame scaling functions in the two-dimensional case. At present, only separable frame scaling functions are circularly symmetric, the Meyer-like frame scaling function in Theorem 3 is the first non-separable frame scaling function with circular symmetry.

Proof. 

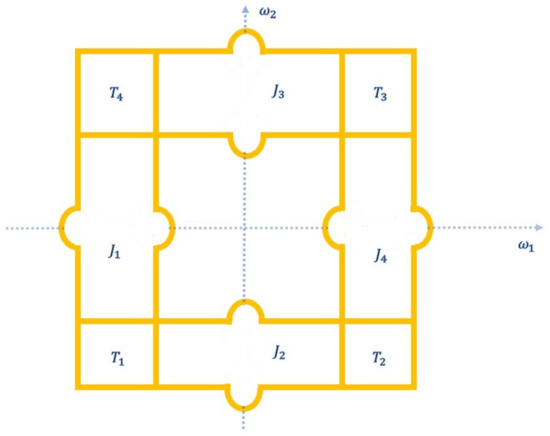
By Equation (22), it is clear that ${\phi }^{\left(0\right)}$ is non-separable and circularly symmetric (i.e., ${\widehat{\phi }}^{\left(0\right)}({\mathit{\omega }}_1,{\mathit{\omega }}_2)={\widehat{\phi }}^{\left(0\right)}({\mathit{\omega }}_2,{\mathit{\omega }}_1)$). Since $\mathrm{supp}{\widehat{\phi }}_F(·,\gamma \left(\alpha \right))=[-\gamma \left(\alpha \right),\gamma \left(\alpha \right)]\backslash F$, it follows that $\mathrm{supp}{\widehat{\phi }}^{\left(0\right)}\left(\mathit{\omega }\right)\subset G\backslash F_0$.

Now, we will prove that

$$R\left(\mathit{\omega }\right)=\sum _{\mathbf{k}\in {\mathbb{Z}}^2}{\left|{\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+2\mathbf{k}\pi )\right|}^2=1\mathrm{or}0(\mathit{\omega }\in {\mathbb{R}}^2).$$

(23)

Since $G\supset {[-\pi ,\pi ]}^2$ and $R\left(\mathit{\omega }\right)$ is $2\pi {\mathbb{Z}}^2-$periodic, we only need to prove that $R\left(\mathit{\omega }\right)=1\mathrm{or}0(\mathit{\omega }\in G)$.

Since $G_0$ is a region bounded by four curves in the ${\mathit{\omega }}_1{\mathit{\omega }}_2$-plane:

$$\left(\mathrm{i}\right){\mathit{\omega }}_1=2\pi -\gamma \left({\mathit{\omega }}_2\right),\left(\mathrm{i}\mathrm{i}\right){\mathit{\omega }}_1=-2\pi +\gamma \left({\mathit{\omega }}_2\right),$$

$$\left(\mathrm{i}\mathrm{i}\mathrm{i}\right){\mathit{\omega }}_2=2\pi -\gamma \left({\mathit{\omega }}_1\right),\left(\mathrm{i}\mathrm{v}\right){\mathit{\omega }}_2=-2\pi +\gamma \left({\mathit{\omega }}_1\right),$$

we can divide $G\backslash G_0$ into eight domains (Figure 2):

$${\displaystyle \begin{array}{c}{J}_1:=\{\mathit{\omega }=({\mathit{\omega }}_1,{\mathit{\omega }}_2):-\gamma \left({\mathit{\omega }}_2\right)\le {\mathit{\omega }}_1\le \gamma \left({\mathit{\omega }}_2\right)-2\pi ,|{\mathit{\omega }}_2|\le 2\pi -b\},\hfill \\ \\ J_2:=\{\mathit{\omega }=({\mathit{\omega }}_1,{\mathit{\omega }}_2):-\gamma \left({\mathit{\omega }}_1\right)\le {\mathit{\omega }}_2\le \gamma \left({\mathit{\omega }}_1\right)-2\pi ,|{\mathit{\omega }}_1|\le 2\pi -b\},\hfill \\ \\ J_3:=\{\mathit{\omega }=(-{\mathit{\omega }}_1,{\mathit{\omega }}_2):({\mathit{\omega }}_1,{\mathit{\omega }}_2)\in J_1\},\hfill \\ \\ J_4:=\{\mathit{\omega }=({\mathit{\omega }}_1,-{\mathit{\omega }}_2):({\mathit{\omega }}_1,{\mathit{\omega }}_2)\in J_2\},\hfill \\ \\ T_1:=[-b,b-2\pi ]\times [-b,b-2\pi ],\hfill \\ \\ T_2:=T_1+2\pi (1,0),\hfill \\ \\ T_3=-T_1,\hfill \\ \\ T_4=-T_2.\hfill \end{array}}$$

(24)

Figure 2. Divide $G\backslash G_0$ into eight domains: $J_1,J_2,J_3,J_4$ and $T_1,T_2,T_3,T_4$.

For $\mathbf{k}=(k_1,k_2)\in {\mathbb{Z}}^2$, we have

$${\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+2\mathbf{k}\pi )={\widehat{\phi }}_F({\mathit{\omega }}_1+2k_1\pi ,\gamma ({\mathit{\omega }}_2+2k_2\pi )){\widehat{\phi }}_F({\mathit{\omega }}_2+2k_2\pi ,\gamma ({\mathit{\omega }}_1+2k_1\pi )).$$

(a) Let $\mathit{\omega }\in G_0$. Then $|{\mathit{\omega }}_1|\le 2\pi -\gamma \left({\mathit{\omega }}_2\right)$ and $|{\mathit{\omega }}_2|\le 2\pi -\gamma \left({\mathit{\omega }}_1\right)$, and so

$$|{\mathit{\omega }}_1+2k_1\pi |\ge 2|k_1|\pi -|{\mathit{\omega }}_1|\ge 2|k_1|\pi -2\pi +\gamma \left({\mathit{\omega }}_2\right)\ge \gamma \left({\mathit{\omega }}_2\right)(k_1\ne 0).$$

Similarly, we have $|{\mathit{\omega }}_2+2k_2\pi |\ge \gamma \left({\mathit{\omega }}_1\right)(k_2\ne 0)$. By $\mathrm{supp}{\widehat{\phi }}^{\left(0\right)}\subset G$, we have ${\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+2\mathbf{k}\pi )=0(\mathbf{k}\ne \mathbf{0})$. Again by Equation (7), we have

$$R\left(\mathit{\omega }\right)=\sum _{\mathbf{k}\in {\mathbb{Z}}^2}|{\widehat{\phi }}^{\left(0\right)}{(\mathit{\omega }+2\mathbf{k}\pi )|}^2={\left|{\widehat{\phi }}^{\left(0\right)}\left(\mathit{\omega }\right)\right|}^2=1\mathrm{or}0(\mathit{\omega }\in G_0).$$

(b) Let $\mathit{\omega }\in {\bigcup }_{i=1}^4{J}_i$.

For $\mathit{\omega }\in J_1$, when $\mathit{\omega }+2\mathbf{k}\pi \notin G(k_1\ne 0,1\mathrm{or}{k}_2\ne 0)$, we have ${\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+2\mathbf{k}\pi )=0$. This implies that

$$R\left(\mathit{\omega }\right)={\left|{\widehat{\phi }}_F({\mathit{\omega }}_1,\gamma \left({\mathit{\omega }}_2\right)){\widehat{\phi }}_F({\mathit{\omega }}_2,\gamma \left({\mathit{\omega }}_1\right))\right|}^2+{\left|{\widehat{\phi }}_F({\mathit{\omega }}_1+2\pi ,\gamma \left({\mathit{\omega }}_2\right)){\widehat{\phi }}_F({\mathit{\omega }}_2,\gamma ({\mathit{\omega }}_1+2\pi ))\right|}^2.$$

Since $\mathit{\omega }\in J_1$, we have ${\mathit{\omega }}_1\le -\frac{2\pi }{3}$ and ${\mathit{\omega }}_1+2\pi \ge \frac{2\pi }{3}$, and then $\gamma \left({\mathit{\omega }}_1\right)=\gamma ({\mathit{\omega }}_1+2\pi )=b$. Hence,

$$R\left(\mathit{\omega }\right)={\left|{\widehat{\phi }}_F({\mathit{\omega }}_2,b)\right|}^2\left(|{\widehat{\phi }}_F({\mathit{\omega }}_1,\gamma \left({\mathit{\omega }}_2\right)){|}^2+{\left|{\widehat{\phi }}_F({\mathit{\omega }}_1+2\pi ,\gamma \left({\mathit{\omega }}_2\right))\right|}^2\right).$$

(25)

From $\mathit{\omega }\in J_1$, we know that $-\gamma \left({\mathit{\omega }}_2\right)\le {\mathit{\omega }}_1\le \gamma \left({\mathit{\omega }}_2\right)-2\pi$. By (3.5), we know that

$$R\left(\mathit{\omega }\right)=1\mathrm{or}0(\mathit{\omega }\in J_1).$$

Similarly, we have $R\left(\mathit{\omega }\right)=1\mathrm{or}0(\mathit{\omega }\in J_i(i=2,3,4))$.

(c) Let $\mathit{\omega }\in {\bigcup }_{i=1}^4{T}_i$.

For $\mathit{\omega }\in T_1$, we have ${\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+2\mathbf{k}\pi )=0(\mathbf{k}\notin \{(0,0),(0,1),(1,0),(1,1)\})$. Furthermore,

$$R\left(\mathit{\omega }\right)=\sum _{k_1=0}^1\sum _{k_2=0}^1{\left|{\widehat{\phi }}_F({\mathit{\omega }}_1+2k_1\pi ,\gamma ({\mathit{\omega }}_2+2k_2\pi ))\right|}^2{\left|{\widehat{\phi }}_F({\mathit{\omega }}_2+2k_2\pi ,\gamma ({\mathit{\omega }}_1+2k_1\pi ))\right|}^2.$$

From $\mathit{\omega }=({\mathit{\omega }}_1,{\mathit{\omega }}_2)\in T_1$, we have ${\mathit{\omega }}_2+2\pi \ge 2\pi -b\ge \frac{2\pi }{3}$. Again by Equation (21), we have $\gamma ({\mathit{\omega }}_2+2k_2\pi )=b$$(k_2=0,1)$. Similarly, we have $\gamma ({\mathit{\omega }}_1+2k_1\pi )=b(k_1=0,1)$. Therefore,

$$R\left(\mathit{\omega }\right)=\left(\sum _{k_1=0}^1{\left|{\widehat{\phi }}_F({\mathit{\omega }}_1+2k_1\pi ,b)\right|}^2\right)\left(\sum _{k_2=0}^1{\left|{\widehat{\phi }}_F({\mathit{\omega }}_2+2k_2\pi ,b)\right|}^2\right).$$

By Equation (5), we have $R\left(\mathit{\omega }\right)=1\mathrm{or}0(\mathit{\omega }\in T_1)$. Similarly, we have $R\left(\mathit{\omega }\right)=1\mathrm{or}0(\mathit{\omega }\in T_i(i=2,3,4))$.

Combining (a)–(c) and Equation (24), we obtain $R\left(\mathit{\omega }\right)=1\mathrm{or}0(\mathit{\omega }\in G)$. Since $G\supset {[-\pi ,\pi ]}^2$ and $R\left(\mathit{\omega }\right)$ is $2\pi {\mathbb{Z}}^2-$periodic, it follows that

$$R\left(\mathit{\omega }\right)=\sum _{\mathbf{k}}{\left|{\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+2\mathbf{k}\pi )\right|}^2=1\mathrm{or}0(\mathit{\omega }\in {\mathbb{R}}^2).$$

(26)

By Equation (7), we have ${\widehat{\phi }}_F({\mathit{\omega }}_1,{\gamma }_1\left({\mathit{\omega }}_2\right))=1$ for $\mathit{\omega }\in [{\gamma }_1\left({\mathit{\omega }}_2\right)-2\pi ,2\pi -\gamma \left({\mathit{\omega }}_2\right)]\backslash F$. Furthermore,

$${\widehat{\phi }}^{\left(0\right)}({\mathit{\omega }}_1,{\mathit{\omega }}_2)=1,\mathrm{for}({\mathit{\omega }}_1,{\mathit{\omega }}_2)\in G_0\backslash F_0=G_0\backslash E_0,$$

(27)

where

$$E_0=\left\{\mathit{\omega }=({\mathit{\omega }}_1,{\mathit{\omega }}_2):{\mathit{\omega }}_1\in \frac{E}{2}\bigcup \left(\frac{E}{2}+\pi \right)\mathrm{or}{\mathit{\omega }}_2\in \frac{E}{2}\bigcup \left(\frac{E}{2}+\pi \right)\right\}.$$

By $\pi <\gamma \left(\eta \right)\le \frac{4\pi }{3}$, we have $\frac{G}{2}\subset G_0$. Noticing that

$$\mathrm{supp}{\widehat{\phi }}^{\left(0\right)}(2{\mathit{\omega }}_1,2{\mathit{\omega }}_2)=\mathrm{supp}{\widehat{\phi }}^{\left(0\right)}({\mathit{\omega }}_1,{\mathit{\omega }}_2)=0\mathrm{for}({\mathit{\omega }}_1,{\mathit{\omega }}_2)\in E_0,$$

by Equation (27) and $\frac{G}{2}\subset G_0$, we have

$${\widehat{\phi }}^{\left(0\right)}\left(\mathbf{2}\mathit{\omega }\right)={\widehat{\phi }}^{\left(0\right)}\left(\mathbf{2}\mathit{\omega }\right){\widehat{\phi }}^{\left(0\right)}\left(\mathit{\omega }\right)(\mathit{\omega }\in {\mathbb{R}}^2).$$

Since $\mathrm{supp}{\widehat{\phi }}^{\left(0\right)}\subset {[-\frac{4\pi }{3},\frac{4\pi }{3}]}^2$, we have

$$\mathrm{supp}{\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+4\mathbf{k}\pi )\bigcap \mathrm{supp}{\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+4{\mathbf{k}}^{\prime }\pi )=0(\mathbf{k}\ne {\mathbf{k}}^{\prime }).$$

(28)

Furthermore,

$$\left(\sum _{\mathbf{k}\in {\mathbb{Z}}^2}{\widehat{\phi }}^{\left(0\right)}(\mathbf{2}\mathit{\omega }+4\mathbf{k}\pi )\right){\widehat{\phi }}^{\left(0\right)}\left(\mathit{\omega }\right)={\widehat{\phi }}^{\left(0\right)}\left(2\mathit{\omega }\right)(\mathit{\omega }\in {\mathbb{R}}^2).$$

Let

$$H^{(0,0)}\left(\mathit{\omega }\right)=\sum _{\mathbf{k}\in {\mathbb{Z}}^2}{\widehat{\phi }}^{\left(0\right)}(2\mathit{\omega }+4\mathbf{k}\pi ).$$

(29)

Then

$${\widehat{\phi }}^{\left(0\right)}\left(\mathit{\omega }\right)=H^{(0,0)}\left(\frac{\mathit{\omega }}{2}\right){\widehat{\phi }}^{\left(0\right)}\left(\frac{\mathit{\omega }}{2}\right)(\mathit{\omega }\in {\mathbb{R}}^2).$$

(30)

From this and Equation (26), noticing that ${\widehat{\phi }}^{\left(0\right)}(0,0)=1$ and ${\widehat{\phi }}^{\left(0\right)}$ is continuous at $\mathit{\omega }=(0,0)$, by Proposition 1, we that ${\phi }^{\left(0\right)}$ is a frame scaling function of $L^2\left({\mathbb{R}}^2\right)$. □

5. Non-Separable Meyer-like Wavelet Frames

In this section, we construct the wavelet frame corresponding to the frame scaling function ${\phi }^{\left(0\right)}$. Define

$${\displaystyle \begin{array}{c}{H}^{(0,1)}\left(\mathit{\omega }\right)=e^{i{\mathit{\omega }}_2}{H}^{(0,0)}(\mathit{\omega }+\pi (0,1)),\hfill \\ \\ H^{(1,0)}\left(\mathit{\omega }\right)=e^{i({\mathit{\omega }}_1+{\mathit{\omega }}_2)}{H}^{(0,0)}(\mathit{\omega }+\pi (1,0)),\hfill \\ \\ H^{(1,1)}\left(\mathit{\omega }\right)=e^{i{\mathit{\omega }}_1}{H}^{(0,0)}(\mathit{\omega }+\pi (1,1)).\hfill \end{array}}$$

(31)

By Equations (28) and (29), we have

$${\displaystyle \begin{array}{ccc}|H^{(0,0)}{\left(\mathit{\omega }\right)|}^2\hfill & =\hfill & {\displaystyle \sum _{\mathbf{k}\in {\mathbb{Z}}^2}}{\left|{\widehat{\phi }}^{\left(0\right)}(2\mathit{\omega }+4\mathbf{k}\pi )\right|}^2,\hfill \\ \\ |H^{(0,1)}{\left(\mathit{\omega }\right)|}^2\hfill & =\hfill & {\displaystyle \sum _{\mathbf{k}\in {\mathbb{Z}}^2}}{\left|{\widehat{\phi }}^{\left(0\right)}(2\mathit{\omega }+4\mathbf{k}\pi +2\pi (0,1))\right|}^2,\hfill \\ \\ |H^{(1,0)}{\left(\mathit{\omega }\right)|}^2\hfill & =\hfill & {\displaystyle \sum _{\mathbf{k}\in {\mathbb{Z}}^2}}{\left|{\widehat{\phi }}^{\left(0\right)}(2\mathit{\omega }+4\mathbf{k}\pi +2\pi (1,0))\right|}^2,\hfill \\ \\ |H^{(1,1)}{\left(\mathit{\omega }\right)|}^2\hfill & =\hfill & {\displaystyle \sum _{\mathbf{k}\in {\mathbb{Z}}^2}}{\left|{\widehat{\phi }}^{\left(0\right)}(2\mathit{\omega }+4\mathbf{k}\pi +2\pi (1,1))\right|}^2.\hfill \end{array}}$$

Adding the above four formulas together, we have

$$|H^{(0,0)}{\left(\mathit{\omega }\right)|}^2+|H^{(0,1)}{\left(\mathit{\omega }\right)|}^2+|H^{(1,0)}{\left(\mathit{\omega }\right)|}^2+|H^{(1,1)}{\left(\mathit{\omega }\right)|}^2=\sum _{\mathbf{k}\in {\mathbb{Z}}^2}{\left|{\widehat{\phi }}^{\left(0\right)}(2\mathit{\omega }+2\mathbf{k}\pi )\right|}^2.$$

(32)

Define $G^{*}=(G\backslash F_0)+2\pi {\mathbb{Z}}^2$. By Theorem 3(ii) and Equation (26), we have

$$\sum _{\mathbf{k}}{\left|{\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+2\mathbf{k}\pi )\right|}^2={\chi }_{G^{*}}\left(\mathit{\omega }\right),$$

where ${\chi }_{G^{*}}$ is the characteristic function of $G^{*}$. Again by Equation (32), we have

$$|H^{(0,0)}{\left(\mathit{\omega }\right)|}^2{\chi }_{G^{*}}\left(\mathit{\omega }\right)+|H^{(0,1)}{\left(\mathit{\omega }\right)|}^2{\chi }_{G^{*}}\left(\mathit{\omega }\right)+|H^{(1,0)}{\left(\mathit{\omega }\right)|}^2{\chi }_{G^{*}}\left(\mathit{\omega }\right)+{\left|H^{(1,1)}\left(\mathit{\omega }\right)\right|}^2{\chi }_{G^{*}}\left(\mathit{\omega }\right)={\chi }_{G^{*}}\left(\mathit{\omega }\right){\chi }_{G^{*}}\left(2\mathit{\omega }\right).$$

(33)

Define a matrix

$$H_s={\left(H^{\left(\mathit{\mu }\right)}(\mathit{\omega }+\nu \pi ){\chi }_{G^{*}}(\mathit{\omega }+\nu \pi )\right)}_{\mathit{\mu },\nu \in {\{0,1\}}^2},$$

where ${\{0,1\}}^2=\{(0,0),(0,1),(1,0),(1,1)\}$. By Equation (31), we have

$${\displaystyle \begin{array}{c}{\displaystyle \sum _{\mathit{\mu }}}{H}^{\left(\mathit{\mu }\right)}\left(\mathit{\omega }\right){\chi }_{G^{*}}\left(\mathit{\omega }\right)\overline{H^{\left(\mathit{\mu }\right)}(\mathit{\omega }+\pi (0,1)){\chi }_{G^{*}}(\mathit{\omega }+\pi (0,1))}\hfill \\ \\ =H^{(0,0)}\left(\mathit{\omega }\right){\chi }_{G^{*}}\left(\mathit{\omega }\right)H^{(0,0)}(\mathit{\omega }+\pi (0,1)){\chi }_{G^{*}}(\mathit{\omega }+\pi (0,1))\hfill \\ \\ +e^{i{\mathit{\omega }}_2}{H}^{(0,0)}(\mathit{\omega }+\pi (0,1)){\chi }_{G^{*}}\left(\mathit{\omega }\right)(-e^{-i{\mathit{\omega }}_2})H^{(0,0)}\left(\mathit{\omega }\right){\chi }_{G^{*}}(\mathit{\omega }+\pi (0,1))\hfill \\ \\ +e^{i({\mathit{\omega }}_1+{\mathit{\omega }}_2)}{H}^{(0,0)}(\mathit{\omega }+\pi (1,0)){\chi }_{G^{*}}\left(\mathit{\omega }\right)(-e^{-i({\mathit{\omega }}_1+{\mathit{\omega }}_2)})H^{(0,0)}(\mathit{\omega }+\pi (1,1)){\chi }_{G^{*}}(\mathit{\omega }+\pi (0,1))\hfill \\ \\ +e^{i{\mathit{\omega }}_1}{H}^{(0,0)}(\mathit{\omega }+\pi (1,1)){\chi }_{G^{*}}\left(\mathit{\omega }\right)e^{-i{\mathit{\omega }}_1}{H}^{(0,0)}(\mathit{\omega }+\pi (1,0)){\chi }_{G^{*}}(\mathit{\omega }+\pi (0,1))\hfill \\ \\ =0.\hfill \end{array}}$$

It means that the inner product of first and second columns of the matrix $H_s$ are orthogonal. Similarly, all columns of $H_s$ are mutually orthogonal. Again by Equation (33), we have

$${\displaystyle H_s^{*}{H}_s=\left(\begin{array}{cccc}L\left(\mathit{\omega }\right)& 0& 0& 0\\ \\ 0& L(\mathit{\omega }+\pi (0,1\left)\right)& 0& 0\\ \\ 0& 0& L(\mathit{\omega }+\pi (1,0\left)\right)& 0\\ \\ 0& 0& 0& L(\mathit{\omega }+\pi (1,1\left)\right)\end{array}\right)}$$

(34)

where $L\left(\mathit{\omega }\right)={\chi }_{G^{*}}\left(\mathit{\omega }\right){\chi }_{G^{*}}\left(2\mathit{\omega }\right)$

Let

$$K=\mathrm{supp}\{{\chi }_{G^{*}}\left(\mathit{\omega }\right)-{\chi }_{G^{*}}\left(2\mathit{\omega }\right){\chi }_{G^{*}}\left(\mathit{\omega }\right)\}.$$

(35)

It is clear that K is a $2\pi$-periodic point set. We divide K into four $2\pi$-periodic point sets as follows

$${\displaystyle \begin{array}{ccc}{K}^{(0,0)}\hfill & =\hfill & K\bigcap ({[-\pi ,0]}^2+2\pi {\mathbb{Z}}^2),\hfill \\ \\ K^{(0,1)}\hfill & =\hfill & K^{(0,0)}+\pi (0,1),\hfill \\ \\ K^{(1,0)}\hfill & =\hfill & K^{(0,0)}+\pi (1,0),\hfill \\ \\ K^{(1,1)}\hfill & =\hfill & K^{(0,0)}+\pi (1,1).\hfill \end{array}}$$

(36)

Define a matrix

$${\displaystyle H=\left(\begin{array}{c}{H}_s\\ K_s\end{array}\right)}$$

where $K_s={\left({\chi }_{K^{\left(\mathit{\mu }\right)}}(\mathit{\omega }+\nu \pi ){\chi }_{G^{*}}(\mathit{\omega }+\nu \pi )\right)}_{\mathit{\mu },\nu \in {\{0,1\}}^2}$. Therefore, by Equations (34)–(36), we have

$${\displaystyle H^{*}H=\left(\begin{array}{cccc}{\chi }_{G^{*}}\left(\mathit{\omega }\right)& 0& 0& 0\\ \\ 0& {\chi }_{G^{*}}(\mathit{\omega }+\pi (0,1))& 0& 0\\ \\ 0& 0& {\chi }_{G^{*}}(\mathit{\omega }+\pi (1,0))& 0\\ \\ 0& 0& 0& {\chi }_{G^{*}}(\mathit{\omega }+\pi (1,1))\end{array}\right)}$$

For $\mathit{\mu }\in ({\{0,1\}}^2\backslash (0,0))$, we define ${\psi }_{\mathit{\mu }}$ as

$${\widehat{\psi }}_{\mathit{\mu }}\left(2\mathit{\omega }\right)=H_{\mathit{\mu }}\left(\mathit{\omega }\right){\widehat{\phi }}^{\left(0\right)}\left(\mathit{\omega }\right),{\widehat{g}}_{\mathit{\mu }}\left(2\mathit{\omega }\right)={\chi }_{K^{\left(\mathit{\mu }\right)}}\left(\mathit{\omega }\right){\widehat{\phi }}^{\left(0\right)}\left(\mathit{\omega }\right)(\mathit{\omega }\in {\mathbb{R}}^2).$$

(37)

By Proposition 2, we have the following theorem:

Theorem 4.

The system ${\left\{{\psi }_{\mathit{\mu }}\right\}}_{\mathit{\mu }\in {\{0,1\}}^2\backslash (0,0)}\bigcup {\left\{g_{\mathit{\mu }}\right\}}_{\mathit{\mu }\in {\{0,1\}}^2}$ is a non-separable wavelet frame generator for $L^2\left({\mathbb{R}}^2\right)$.

Finally, we give the representation of the frame generator in Theorem 4. By Equation (29), we have

$${\widehat{\psi }}_{(0,1)}\left(\mathit{\omega }\right)=e^{i\frac{{\mathit{\omega }}_2}{2}}{H}_{(0,0)}\left(\frac{\mathit{\omega }}{2}+\pi (0,1)\right){\widehat{\phi }}^{\left(0\right)}\left(\frac{\mathit{\omega }}{2}\right)=e^{i\frac{{\mathit{\omega }}_2}{2}}\sum _{\mathbf{k}\in {\mathbb{Z}}^2}{\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+4\mathbf{k}\pi +2\pi (0,1)){\widehat{\phi }}^{\left(0\right)}\left(\frac{\mathit{\omega }}{2}\right).$$

Again, noticing that $supp{\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+2\pi (0,1)+4\mathbf{k}\pi )\bigcap supp\widehat{\phi }\left(\frac{\mathit{\omega }}{2}\right)=\varnothing (\mathbf{k}\ne (0,0),(0,-1))$, we

$${\widehat{\psi }}_{(0,1)}\left(\mathit{\omega }\right)=e^{i\frac{{\mathit{\omega }}_2}{2}}\left({\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+2\pi (0,1))+{\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+2\pi (0,-1))\right){\widehat{\phi }}^{\left(0\right)}\left(\frac{\mathit{\omega }}{2}\right).$$

Similarly, we have

$${\displaystyle \begin{array}{c}{\widehat{\psi }}_{(1,0)}\left(\mathit{\omega }\right)=e^{i\frac{{\mathit{\omega }}_1+{\mathit{\omega }}_2}{2}}\left({\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+2\pi (1,0))+{\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+2\pi (-1,0))\right){\widehat{\phi }}^{\left(0\right)}\left(\frac{\mathit{\omega }}{2}\right),\hfill \\ \\ {\widehat{\psi }}_{(1,1)}\left(\mathit{\omega }\right)=e^{i\frac{{\mathit{\omega }}_1}{2}}\left({\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+2\pi (1,1))+{\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+2\pi (-1,1))\right){\widehat{\phi }}^{\left(0\right)}\left(\frac{\mathit{\omega }}{2}\right)\hfill \\ \\ +e^{i\frac{{\mathit{\omega }}_1}{2}}\left({\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+2\pi (1,-1))+{\widehat{\phi }}^{\left(0\right)}(\mathit{\omega }+2\pi (-1,-1))\right){\widehat{\phi }}^{\left(0\right)}\left(\frac{\mathit{\omega }}{2}\right).\hfill \end{array}}$$

By Equation (37), we have

$${\widehat{g}}_{(0,0)}\left(\mathit{\omega }\right)={\chi }_{K^{(0,0)}}\left(\frac{\mathit{\omega }}{2}\right){\widehat{\phi }}^{\left(0\right)}\left(\frac{\mathit{\omega }}{2}\right),{\widehat{g}}_{(0,1)}\left(\mathit{\omega }\right)={\chi }_{K^{(0,1)}}\left(\frac{\mathit{\omega }}{2}\right){\widehat{\phi }}^{\left(0\right)}\left(\frac{\mathit{\omega }}{2}\right)$$

$${\widehat{g}}_{(1,0)}\left(\mathit{\omega }\right)={\chi }_{K^{(1,0)}}\left(\frac{\mathit{\omega }}{2}\right){\widehat{\phi }}^{\left(0\right)}\left(\frac{\mathit{\omega }}{2}\right),{\widehat{g}}_{(1,1)}\left(\mathit{\omega }\right)={\chi }_{K^{(1,1)}}\left(\frac{\mathit{\omega }}{2}\right){\widehat{\phi }}^{\left(0\right)}\left(\frac{\mathit{\omega }}{2}\right)$$

where

$$K^{(0,0)}=K\bigcap ({[-\pi ,0]}^2+2\pi {\mathbb{Z}}^2),K^{(0,1)}=K^{(0,0)}+\pi (0,1),$$

$$K^{(1,0)}=K^{(0,0)}+\pi (1,0),K^{(1,1)}=K^{(0,0)}+\pi (1,1),$$

and $K=supp\{{\chi }_{G^{*}}\left(\mathit{\omega }\right)-{\chi }_{G^{*}}\left(2\mathit{\omega }\right){\chi }_{G^{*}}\left(\mathit{\omega }\right)\}$.

Example 1.

Let $N_4\left(\eta \right)$ be the cubic spline:

$$N_4\left(\eta \right)={\chi }_{[0,1]}*{\chi }_{[0,1]}*{\chi }_{[0,1]}*{\chi }_{[0,1]}\left(\eta \right),$$

It is well-known that $0\le N_4\left(\eta \right)\le 1(\eta \in \mathbb{R})$ and $supp{N}_4=[0,4]$. Let

$$\gamma \left(\eta \right)=\frac{13\pi }{12}+\frac{\pi }{5}{N}_4\left(\frac{6}{\pi }\left|\eta \right|\right)(\eta \in \mathbb{R}).$$

Then γ satisfy Equation (21) and $b=\frac{13\pi }{12}$. Now we take

$$E=[-\frac{19\pi }{18},-\frac{37\pi }{36}]\subset [-\frac{13\pi }{12},-\pi ]$$

and

$$F=[-\frac{19\pi }{18},-\frac{37\pi }{36}]\bigcup [-\frac{19\pi }{36},-\frac{37\pi }{72}]\bigcup [\frac{17\pi }{18},\frac{35\pi }{36}]\bigcup [\frac{17\pi }{36},\frac{35\pi }{72}].$$

By Equation (1), we define a bivariate function ${\phi }^{\left(0\right)}\left(\mathbf{t}\right)$ such that its Fourier transform satisfies

$$\widehat{\phi }\left(\mathit{\omega }\right)={\widehat{\phi }}_F({\mathit{\omega }}_1,\gamma \left({\mathit{\omega }}_2\right)){\widehat{\phi }}_F({\mathit{\omega }}_2,\gamma \left({\mathit{\omega }}_1\right))(\mathit{\omega }=({\mathit{\omega }}_1,{\mathit{\omega }}_2)\in {\mathbb{R}}^2).$$

By Theorem 3, we know that φ is a non-separable frame scaling function. Again by Equation (37) and Theorem 4, it is clear that the system ${\left\{{\psi }_{\mathit{\mu }}\right\}}_{\mathit{\mu }\in {\{0,1\}}^2\backslash (0,0)}\bigcup {\left\{g_{\mathit{\mu }}\right\}}_{\mathit{\mu }\in {\{0,1\}}^2}$ is a non-separable wavelet frame generator for $L^2\left({\mathbb{R}}^2\right)$.

6. Conclusions

In this study, we generalized the known Meyer wavelet basis into non-separable Meyer-like wavelet frames. By using a characteristic function to mask the Fourier transform of the one-dimensional Meyer scaling function with width parameter, we can produce a family of Meyer-like frame scaling functions. Compared with the Meyer scaling function, the Meyer-like frame scaling function’s spectrum is not $\mathbb{R}$. After that, we construct the corresponding Meyer-like wavelet frame generator, which consists of three functions: The Fourier transform of the first function is just that of the known Meyer wavelet masked by some characteristic function; the Fourier transform of the second and third functions are just that of the Meyer scaling function masked by some characteristic function.

Separable Meyer-like wavelet frames can be constructed directly through the tensor product of one-dimensional Meyer-like wavelet frames. For the non-separable case, by inserting a real-valued function into the width parameter of the one-dimensional Meyer-like frame scaling function, we propose a novel approach to construct non-separable Meyer-like frame scaling functions. At present, only separable frame scaling functions are circularly symmetric, and our Meyer-like frame scaling function is the first non-separable frame scaling function with circular symmetry. Moreover, we construct the corresponding non-separable Meyer-like wavelet frame generator, which consists of seven functions.