On the Fuzzy Solution of Linear-Nonlinear Partial Differential Equations

Abstract

In this article, we present the fuzzy Adomian decomposition method (ADM) and fuzzy modified Laplace decomposition method (MLDM) to obtain the solutions of fuzzy fractional Navier–Stokes equations in a tube under fuzzy fractional derivatives. We have looked at the turbulent flow of a viscous fluid in a tube, where the velocity field is a function of only one spatial coordinate, in addition to time being one of the dependent variables. Furthermore, we investigate the fuzzy Elzaki transform, and the fuzzy Elzaki decomposition method (EDM) applied to solving fuzzy linear-nonlinear Schrodinger differential equations. The proposed method worked perfectly without any need for linearization or discretization. Finally, we compared the fuzzy reduced differential transform method (RDTM) and fuzzy homotopy perturbation method (HPM) to solving fuzzy heat-like and wave-like equations with variable coefficients. The RDTM and HPM solutions are simpler than other already existing methods. Several examples are provided to illustrate the methods that have been offered. The results obtained using the scheme presented here agree well with the analytical solutions and the numerical results presented elsewhere. These studies are important in the context of the development of the theory of fuzzy partial differential equations.

1. Introduction

The fuzzy differential equations, often known as FDEs, are an important tool for expanding the number of system models used in physics, engineering, biology, and other scientific fields; see [1,2,3,4,5]. The concept of FDEs was first presented by Kandel and Byatt [6] in 1978. The fuzzy FDEs and fuzzy Cauchy problems have been extensively investigated by Seikkala [7], Kaleva [8,9], Kloeden [10], Ouyang and Wu [11], and other researchers; Jowers et al. [12], Bede et al. [13], Chen et al. [14], Ding et al. [15], and Song and Wu [16,17]. Bede et al. [18] presented and investigated the notion of strongly generalized differentiability of fuzzy-valued functions, which broadened the class of differentiable fuzzy-valued functions [19].

Fractional calculus and fractional differential equations naturally arise in a number of fields, such as diffusion processes, viscoelasticity, electrochemistry, rheology, etc. Fractional calculus is usually used to replace the time derivative in a given evolution equation with a fractional derivative. For a general overview and applications of fractional differential equations in signal processing, as well as in the complex dynamic in biological tissues, the readers are referred to [20,21,22,23,24,25,26,27,28] and the references therein.

The ADM [29,30,31] generates a quick convergent series which may approach the exact solution. Recently, Wazwaz [32,33], Yan [34], and Zhu [35,36] demonstrated the ADM’s efficacy in solving various nonlinear equations via solitary construction. Furthermore, see [37,38,39,40,41].

The Laplace ADM is an efficient analytical techniques for solving linear-nonlinear equations [42,43,44,45]. This method is devoid of any small or large parameters and has advantages over other approximation techniques such as perturbation [46,47,48].

Elzaki invented the Elzaki transform (ET) from the classical Fourier integral in [49,50], and it is used to facilitate the solution of ordinary and partial differential equations (PDEs) in the time domain. Elzaki Transform is a mathematical method for solving differential equations, similar to Fourier Transform, Laplace Transform, and Sumudu Transform. Lately, this method has been considered by various researchers; see [51,52,53,54].

In electric circuit analysis, Zhou [55] developed DTM and solved engineering models principally. It is an iterative procedure that generates an analytic way out in the form of a polynomial using Taylor series expansions. This approach is addressed thoroughly in [56,57,58].

Keskin et al. devised the reduced DTM [59,60] and fractional reduced DTM (FRDTM) [61] to overcome the complex calculation flaw of DTM. These approaches have proven to be trustworthy semi-analytical methods, and have been used to estimate numerical solutions to PDEs and fractional order PDEs. RDTM and FRDTM have significant applications [40,57,62].

The HPM was developed by He [63] and used the homotopy in topology for nonlinear problems [64]. Various other authors have discussed the HPM. Altaie et al. [65] used the HPM to develop an approximate analytical solution for the fuzzy PDEs. Ates et al. [66] studied the application of the HPM to two-point boundary-value problems with a fractional-order derivative of the Caputo type. Sakar et al. [67] discussed the HPM applied to solve fractional PDEs with proportional delays. Jameel et al. [68] presented the application of HPM to solving one-dimensional heat-like and wave-like equations in a fuzzy environment. Osman et al. [40] investigated the comparison of fuzzy HPM and other methods to get the solutions of a fuzzy $(1+n)$-dimensional Burgers’ equation.

In this paper, we establish the comparison of fuzzy ADM and fuzzy modified LDM to get the solutions of fuzzy time-fractional Navier–Stokes equations in a tube. The nonlinear fuzzy time-fractional Navier–Stokes equations have no general solutions. Relatively, few circumstances can solve the problem exactly, assuming/given a simple fluid condition and flow pattern. We consider the unsteady flow of a viscous fluid in a tube where the velocity field is a function of just one space coordinate. Moreover, we studied the fuzzy EDM to give the exact solution for the fuzzy linear and nonlinear Schrodinger differential equations. The Schrodinger equations are often used in several more areas of physics and engineering science, such as optics, plasma physics, quantum mechanics, and others. Finally, we study the fuzzy RDTM and fuzzy HPM to solve fuzzy heat-like and wave-like equations with variable coefficients. These techniques are flexible and can solve the underlined problems without having to calculate complicated Adomian polynomials or make unrealistic assumptions about nonlinear behavior.

This work is organized as follows: In Section 2, we review some fundamental definitions, and the theorems that will be used are presented. In Section 3, we propose fuzzy fractional Navier–Stokes equations utilizing fuzzy ADM and modified LDM. In Section 4, we investigate the fuzzy EDM for solving the fuzzy linear-nonlinear Schrodinger differential equation. In Section 5, we apply the fuzzy RDTM and HPM to deduce the solutions of fuzzy heat-like and wave-like equations. Finally, conclusions are given in Section 6.

2. Basic Concepts

In this section, the most fundamental notations utilized in this article are presented as follows:

The set of all real numbers is denoted by the letter $\mathbb{R}$, and the set of all fuzzy numbers that are contained within $\mathbb{R}$ is denoted by the letter ${\mathbb{E}}^1.$ A fuzzy number is a mapping $\tilde{\omega }:\mathbb{R}\to [0,1]$ that possesses the following qualities [18]:

1.

$\tilde{w}$ is normal, i.e., there exists ${\psi }_0\in \mathbb{R}$ with $\tilde{w}\left({\psi }_0\right)=1;$

2.

$\tilde{w}$ stands for a convex fuzzy set (i.e., $\tilde{w}(\alpha \psi +(1-\alpha )\varphi )\ge min\{\tilde{w}(\psi ),\tilde{w}(\varphi )\},\mathrm{for}\mathrm{all}\alpha \in [0,1],\psi ,\varphi \in \mathbb{R});$

3.

$\tilde{w}$ is semicontinuous on $\mathbb{R}$;

4.

$supp\tilde{w}=\{\psi \in \mathbb{R}|\tilde{w}(\psi )>0\}$ is the support of the $\tilde{w};$ in addition, its closure cl$(supp\tilde{w})$ is compact.

The $\sigma$-level set of a fuzzy number $\tilde{w}(\psi )\in {\mathbb{E}}^1$ denoted by ${\left[\tilde{w}(\psi )\right]}_{\sigma }$ is given as:

$${\left[\tilde{w}(\psi )\right]}_{\sigma }=\left\{\begin{array}{cc}\{\psi \in \mathbb{R}|\tilde{w}(\psi )\ge \sigma \}\hfill & \sigma \in (0,1],\hfill \\ cl(supp\tilde{w}(\psi ))\hfill & \sigma =0.\hfill \end{array}\right.$$

(1)

Definition 1

([69]). For arbitrary fuzzy numbers $\tilde{w},\tilde{\tau }\in {\mathbb{E}}^1,\tilde{w}=[{\underline{w}}_{\sigma },{\overline{w}}_{\sigma }],\tilde{\tau }=[{\underline{\tau }}_{\sigma },{\overline{\tau }}_{\sigma }]$, the quantity $\mathbb{D}(\tilde{w},\tilde{\tau })={sup}_{\sigma \in [0,1]}max\left\{\right|{\underline{w}}_{\sigma }-{\underline{\tau }}_{\sigma }|,|{\overline{w}}_{\sigma }-{\overline{\tau }}_{\sigma }\left|\right\}$ is the distance between $\tilde{w}$ and $\tilde{\tau }$, and the following properties also hold:

1.

$({\mathbb{E}}^1,\mathbb{D})$ is a complete metric space,

2.

$\mathbb{D}(\tilde{w}\oplus \tilde{q},\tilde{\tau }\oplus \tilde{q})=\mathbb{D}(\tilde{w},\tilde{\tau }),\forall \tilde{w},\tilde{\tau },\tilde{q}\in {\mathbb{E}}^1,$

3.

$\mathbb{D}(\tilde{w}\oplus \tilde{\tau },\tilde{q}\oplus \tilde{e})\le \mathbb{D}(\tilde{w},\tilde{q})+\mathbb{D}(\tilde{\tau },\tilde{e}),\forall \tilde{w},\tilde{\tau },\tilde{q},\tilde{e}\in {\mathbb{E}}^1$,

4.

$\mathbb{D}(\tilde{w}\oplus \tilde{\tau },\tilde{0})\le \mathbb{D}(\tilde{w},\tilde{0})+\mathbb{D}(\tilde{\tau },\tilde{0}),\forall \tilde{w},\tilde{\tau }\in {\mathbb{E}}^1,$

5.

$\mathbb{D}(\ell \odot \tilde{w},\ell \odot \tilde{\tau })=|\ell |D(\tilde{w},\tilde{\tau }),\forall \tilde{w},\tilde{\tau }\in {\mathbb{E}}^1,\ell \in \mathbb{R},$

6.

$\mathbb{D}({\ell }_1\odot \tilde{w},{\ell }_2\odot \tilde{w})=|{\ell }_1-{\ell }_2|\mathbb{D}(\tilde{w},\tilde{0}),\forall \tilde{w}\in {\mathbb{E}}^1,\mathrm{and}{\ell }_1,{\ell }_2\in \mathbb{R},$ with ${\ell }_1·{\ell }_2\ge 0$.

Now, we state the definition of the Hukuhara difference from [20]. Let $\tilde{w}\mathrm{and}\tilde{\tau }\in {\mathbb{E}}^1$. A Hukuhara difference is defined by the set $\tilde{\hslash }$ such that $\tilde{w}{\ominus }_H\tilde{\tau }=\tilde{\hslash }\iff \tilde{w}=\tilde{\tau }\oplus \tilde{\hslash }$. The H-difference is unique, but it does not always exist (a necessary condition for $\tilde{w}{\ominus }_H\tilde{\tau }$ to exist is that $\tilde{w}$ contains a translate $\left\{c\right\}\oplus \tilde{\tau }of\tilde{\tau }$).

Definition 2

([20]). The gH-difference between two fuzzy numbers $\tilde{w}\mathrm{and}\tilde{\tau }\in {\mathbb{E}}^1$ is defined by the following setting:

$$\tilde{w}{\ominus }_{gH}\tilde{\tau }=\tilde{\hslash }\iff \left\{\begin{array}{cc}\hfill & \left(i\right)\tilde{w}=\tilde{\tau }\oplus \tilde{\hslash },\hfill \\ \hfill & or\left(ii\right)\tilde{\tau }=\tilde{w}\oplus (-\tilde{\hslash }).\hfill \end{array}\right.$$

(2)

In terms of the $\sigma$-level, we get ${\left[\tilde{w}{\ominus }_{gH}\tilde{\tau }\right]}_{{}_{\sigma }}=[min\{{\underline{w}}_{\sigma }-{\underline{\tau }}_{\sigma },{\overline{w}}_{\sigma }-{\overline{\tau }}_{\sigma }\},max\{{\underline{w}}_{\sigma }-{\underline{\tau }}_{\sigma },{\overline{w}}_{\sigma }-{\overline{\tau }}_{\sigma }\}]$ and, if the H-difference exists, then $\tilde{w}\ominus \tilde{\tau }=\tilde{w}{\ominus }_{gH}\tilde{\tau }$; the conditions for the existence of $\tilde{\hslash }=\tilde{w}{\ominus }_{gH}\tilde{\tau }\in {\mathbb{E}}^1$ are

$$\begin{array}{cc}\hfill Case\left(i\right)& \left\{\begin{array}{cc}\hfill & {\underline{\hslash }}_{\sigma }={\underline{w}}_{\sigma }-{\underline{\tau }}_{\sigma }and{\overline{\hslash }}_{\sigma }={\overline{w}}_{\sigma }-{\overline{\tau }}_{\sigma },\forall \sigma \in [0,1],\hfill \\ \hfill & with{\underline{\hslash }}_{\sigma }increasing,{\overline{\hslash }}_{\sigma }decreasing,{\underline{\hslash }}_{\sigma }\le {\overline{\hslash }}_{\sigma }.\hfill \end{array}\right.\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill Case\left(ii\right)& \left\{\begin{array}{cc}\hfill & {\underline{\hslash }}_{\sigma }={\overline{w}}_{\sigma }-{\overline{\tau }}_{\sigma }and{\overline{\hslash }}_{\sigma }={\underline{w}}_{\sigma }-{\underline{\tau }}_{\sigma },\forall \sigma \in [0,1],\hfill \\ \hfill & with{\underline{\hslash }}_{\sigma }increasing,{\overline{\hslash }}_{\sigma }decreasing,{\underline{\hslash }}_{\sigma }\le {\overline{\hslash }}_{\sigma }.\hfill \end{array}\right.\hfill \end{array}$$

(4)

It is simple to demonstrate that both (i) and (ii) are true if and only if $\tilde{\hslash }$ is a crisp number. It is probable that the gH-difference between two fuzzy numbers does not exist. To remedy this flaw, a new distinction between fuzzy numbers is developed [20].

Definition 3

([18]). Let $\tilde{w}(\psi ,t):\mathbb{D}\to {\mathbb{E}}^1$ and $({\psi }_0,t)\in \mathbb{D}$. We say that $\tilde{w}$ is a strongly generalized Hukuhara differentiability (or GH-differentiability for short) on $({\psi }_0,t)$, if there exists an element $\frac{\partial \tilde{w}}{\partial \psi }{|}_{({\psi }_0,t)}\in {\mathbb{E}}^1$ such that

(i)

for all $h>0$ sufficiently small, $\exists \tilde{w}({\psi }_0+h,t){\ominus }_H\tilde{w}({\psi }_0,t),\tilde{w}({\psi }_0,t){\ominus }_H\tilde{w}({\psi }_0-h,t)$ and the limits (in the metric D)

$$\underset{h\to 0+}{lim}\frac{\tilde{w}({\psi }_0+h,t){\ominus }_H\tilde{w}({\psi }_0,t)}{h}=\underset{h\to 0+}{lim}\frac{\tilde{w}({\psi }_0,t){\ominus }_H\tilde{w}({\psi }_0-h,t)}{h}=\frac{\partial \tilde{w}}{\partial \psi }{|}_{({\psi }_0,t)},$$

or

(ii)

for all $h>0$ sufficiently small, $\exists \tilde{w}({\psi }_0,t){\ominus }_H\tilde{w}({\psi }_0+h,t),\tilde{w}({\psi }_0-h,t){\ominus }_H\tilde{w}({\psi }_0,t)$ and the limits

$$\underset{h\to 0+}{lim}\frac{\tilde{w}({\psi }_0,t){\ominus }_H\tilde{w}({\psi }_0+h,t)}{-h}=\underset{h\to 0+}{lim}\frac{\tilde{w}({\psi }_0-h,t){\ominus }_H\tilde{w}({\psi }_0,t)}{-h}=\frac{\partial \tilde{w}}{\partial \psi }{|}_{({\psi }_0,t)},$$

or

(iii)

for all $h>0$ sufficiently small, $\exists \tilde{w}({\psi }_0+h,t){\ominus }_H\tilde{w}({\psi }_0,t),\tilde{w}({\psi }_0-h,t){\ominus }_H\tilde{w}({\psi }_0,t)$ and the limits

$$\underset{h\to 0+}{lim}\frac{\tilde{w}({\psi }_0+h,t){\ominus }_H\tilde{w}({\psi }_0,t)}{h}=\underset{h\to 0+}{lim}\frac{\tilde{w}({\psi }_0-h,t){\ominus }_H\tilde{w}({\psi }_0,t)}{-h}=\frac{\partial \tilde{w}}{\partial \psi }{|}_{({\psi }_0,t)},$$

or

(iv)

for all $h>0$ sufficiently small, $\exists \tilde{w}({\psi }_0,t){\ominus }_H\tilde{w}({\psi }_0+h,t),\tilde{w}({\psi }_0,t){\ominus }_H\tilde{w}({\psi }_0-h,t)$ and the limits

$$\underset{h\to 0+}{lim}\frac{\tilde{w}({\psi }_0,t){\ominus }_H\tilde{w}({\psi }_0+h,t)}{-h}=\underset{h\to 0+}{lim}\frac{\tilde{w}({\psi }_0,t){\ominus }_H\tilde{w}({\psi }_0-h,t)}{h}=\frac{\partial \tilde{w}}{\partial \psi }{|}_{({\psi }_0,t)}.$$

Definition 4

([20]). Let us assume that $\tilde{w}(\psi ,t):\mathbb{D}\to {\mathbb{E}}^1$ is a function and that $\tilde{w}(\psi ,t;\sigma )=[(\underline{w}(\psi ,t;\sigma ),\overline{w}(\psi ,t;\sigma )]$ for each $\sigma \in [0,1]$. Then,

(1) If $\tilde{w}$ is gH-differentiable in the first form (i), then $[\underline{w}(\psi ,t;\sigma )$ and $\overline{w}(\psi ,t;\sigma )]$ are differentiable functions and

$${\left[\frac{\partial \tilde{w}}{\partial \psi }\right]}_{\sigma }=\left[\frac{\partial \underline{w}(\psi ,t;\sigma )}{\partial \psi },\frac{\partial \overline{w}(\psi ,t;\sigma )}{\partial \psi }\right],$$

(5)

(2) If $\tilde{w}$ is gH-differentiable in the second form (ii), then $[\overline{w}(\psi ,t;\sigma )$ and $\underline{w}(\psi ,t;\sigma )]$ are differentiable functions and

$${\left[\frac{\partial \tilde{w}}{\partial \psi }\right]}_{\sigma }=\left[\frac{\partial \overline{w}(\psi ,t;\sigma )}{\partial \psi },\frac{\partial \underline{w}(\psi ,t;\sigma )}{\partial \psi }\right].$$

(6)

Definition 5

([70]). A fuzzy-valued function $\tilde{w}$ of two variables is a rule that assigns to every ordered pair of real numbers, $(\psi ,t)$, in a set $\mathbb{D}$, a unique fuzzy number denoted by $\tilde{w}(\psi ,t)$. The set $\mathbb{D}$ is the domain of $\tilde{w}$ and its range is the set of values that $\tilde{w}$ takes on that is $\left\{\tilde{w}(\psi ,t)\right|(\psi ,t)\in \mathbb{D}\}$. The parametric representation of the fuzzy-valued function $\tilde{w}:\mathbb{D}\to {\mathbb{E}}^1$ is expressed by $\tilde{w}(\psi ,t;\sigma )=[\underline{w}(\psi ,t;\sigma ),\overline{w}(\psi ,t;\sigma )]$, for any $(\psi ,t)\in \mathbb{D}$ and $\sigma \in [0,1]$.

Theorem 1

([71]). Suppose that $\tilde{w}$ is a fuzzy-valued function on $[a,\infty )$ represented by σ-level set $[\underline{w}(\psi ;\sigma ),\overline{w}(\psi ;\sigma )]$. For any fixed $\sigma \in [0,1]$, assume $\underline{w}(\psi ;\sigma ),$ and $\overline{w}(\psi ;\sigma )$ are Riemann integrable on $[a,b]$ for every $b\ge a$, and assume there are two positive functions $\underline{\mathcal{N}}(\sigma )$ and $\overline{\mathcal{N}}(\sigma )$ such that ${\int }_a^b\left|\underline{w}(\psi ;\sigma )\right|d\psi \le \underline{\mathcal{N}}(\sigma )$ and ${\int }_a^b\left|\overline{w}(\psi ;\sigma )\right|d\psi \le \overline{\mathcal{N}}(\sigma )$ for every $b\ge a$. Then, $\tilde{w}(\psi )$ is improper fuzzy Riemann integrable on $[a,\infty )$ and the improper fuuzy Riemann integral is a fuzzy number. Furthermore, we obtain

$${\int }_a^{\infty }\tilde{w}(\psi ;\sigma )d\psi =\left[{\int }_a^{\infty }\underline{w}(\psi ;\sigma )d\psi ,{\int }_a^{\infty }\overline{w}(\psi ;\sigma )d\psi \right].$$

Fuzzy Fractional Calculus

We denote ${\mathcal{C}}^{\mathcal{F}}[a,b]$ as a space of all fuzzy-valued functions which are continuous on $[a,b]$. In addition, we denote the space of all Lebesgue integrable fuzzy-valued functions on the bounded interval $[a,b]\subset \mathbb{R}$ by ${\mathcal{L}}^{\mathcal{F}}[a,b]$, refs. [71].

Definition 6

([71]). Let $\tilde{f}(\psi )\in {\mathcal{C}}^{\mathcal{F}}[a,b]\cap {\mathcal{L}}^{\mathcal{F}}[a,b]$. The fuzzy Riemann–Liouville integral of fuzzy-valued function f is defined as:

$$\left(I_{a+}^{\Im }\tilde{f}\right)(\psi )=\frac{1}{\Gamma (\Im )}{\int }_a^{\psi }\frac{\tilde{f}\left(t\right)dt}{{(\psi -t)}^{1-\Im }},\psi >a,0<\Im ⩽1.$$

Suppose that the σ-level representation of fuzzy-valued function f as $f(\psi ;\sigma )=[\underline{f}(\psi ;\sigma ),\overline{f}(\psi ;\sigma )]$, for $0,⩽\sigma ⩽1$, then we can indicate the fuzzy Riemann–Liouville integral of fuzzy-valued function f based on the lower and upper functions as follows:

Definition 7

([71]). Suppose that $\tilde{f}(\psi )\in {\mathcal{C}}^{\mathcal{F}}[a,b]\cap {\mathcal{L}}^{\mathcal{F}}[a,b]$, and the fuzzy Riemann–Liouville integral of fuzzy-valued function f is defined as:

$$\left({\mathcal{I}}_{a+}^{\Im }\tilde{f}\right)(\psi ;\sigma )=[\left({\mathcal{I}}_{a+}^{\Im }\underline{f}\right)(\psi ;\sigma ),\left({\mathcal{I}}_{a+}^{\Im }\overline{f}\right)(\psi ;\sigma )],$$

where $0\le \sigma \le 1$ and

$$\begin{array}{cc}\hfill \left({\mathcal{I}}_{a+}^{\Im }\underline{f}\right)(\psi ;\sigma )& =\frac{1}{\Gamma (\Im )}{\int }_a^{\psi }\frac{\underline{f}(t;\sigma )\mathrm{d}t}{{(\psi -t)}^{1-\Im }},0\le \sigma \le 1,\hfill \\ \hfill \left({\mathcal{I}}_{a+}^{\Im }\overline{f}\right)(\psi ;\sigma )& =\frac{1}{\Gamma (\Im )}{\int }_a^{\psi }\frac{\overline{f}(t;\sigma )\mathrm{d}t}{{(\psi -t)}^{1-\Im }},0\le \sigma \le 1.\hfill \end{array}$$

Definition 8.

The Mittag–Leffler function $E_{\Im }\left(t\right)$ with $\Im >0$ is expressed as follows:

$$E_{\Im }\left(t\right)=\sum _{n=0}^{\infty }\frac{t^n}{\Gamma (\Im n+1)},\Im >0.$$

Definition 9

([71,72]). Let $\tilde{f}\in C^{\mathcal{F}}[a,b]\cap L^{\mathcal{F}}[a,b]$ be a fuzzy-valued function and $0<\Im \le 1$. Then, $\tilde{f}$ is said to be Caputo’s gH-differentiable at ψ when

$${}^{\mathcal{C}}{D}_a^{\Im }\tilde{f}(\psi ;\sigma )=\frac{1}{\Gamma (1-\Im )}{\int }_{{\psi }_0}^{\psi }{(\psi -t)}^{-\Im }{\tilde{f}}^{\prime }(t;\sigma )dt.$$

Note that later we indicate ${}^{\mathcal{C}}{D}_0^{\Im }\tilde{f}(t;\sigma )$ using ${}^{\mathcal{C}}{D}^{\Im }\tilde{f}(t;\sigma ).$

Theorem 2

([72]). Suppose that $\tilde{f}\in C^{\mathcal{F}}[a,b]\cap L^{\mathcal{F}}[a,b],{\psi }_0\in (a,b)$ and $0<\Im \le 1.$ Then,

(i)

if $\tilde{f}$ is (i)-differentiable fuzzy-valued function, then

$$\left({}_i^{\mathcal{C}}{D}_{{\psi }_0}^{\Im }\right)\tilde{f}(\psi ;\sigma )=\left[\left({}^{\mathcal{C}}{D}_{{\psi }_0}^{\Im }\right)\underline{f}(\psi ;\sigma ),\left({}^{\mathcal{C}}{D}_{{\psi }_0}^{\Im }\right)\overline{f}(\psi ;\sigma )\right],0\le \sigma \le 1,$$

(ii)

if $\tilde{f}$ is (ii)-differentiable fuzzy-valued function, then

$$\left({}_{ii}^{\mathcal{C}}{D}_{{\psi }_0}^{\Im }\right)\tilde{f}(\psi ;\sigma )=\left[\left({}^{\mathcal{C}}{D}_{{\psi }_0}^{\Im }\right)\overline{f}(\psi ;\sigma ),\left({}^{\mathcal{C}}{D}_{{\psi }_0}^{\Im }\right)\underline{f}(\psi ;\sigma )\right],0\le \sigma \le 1.$$

3. Analytical Solution of Fuzzy Fractional Navier–Stokes Equation

In this section, we analyze fuzzy time-fractional Navier–Stokes equations via fuzzy ADM and fuzzy modified LDM as follows:

$$\begin{array}{c}\hfill \frac{{\partial }^{\Im }\tilde{w}(\wp ,t)}{\partial t^{\Im }}=\mathcal{P}\oplus \tau \left(\frac{{\partial }^2\tilde{w}(\wp ,t)}{\partial {\wp }^2}\oplus \frac{1}{\wp }\odot \frac{\partial \tilde{w}(\wp ,t)}{\partial \wp }\right),0<\Im \le 1,\end{array}$$

(7)

with the initial condition

$$\begin{array}{c}\hfill \tilde{w}(\wp ,0)=\tilde{g}(\wp ),\end{array}$$

(8)

where $\mathcal{P}=-\frac{\partial p}{{}_{\rho }\partial z},\Im$ is a parameter describing the order of the time fractional derivative.

3.1. Fuzzy Adomian Decomposition Method

We consider the following parametric of fuzzy fractional Navier–Stokes Equation (7) of the form:

$$\begin{array}{cc}\hfill \frac{\partial \underline{w}(\wp ,t;\sigma )}{\partial t}& =-\frac{\partial p}{{}_{\rho }\partial \varphi }+\tau \left(\frac{{\partial }^2\underline{w}(\wp ,t;\sigma )}{\partial {\wp }^2}+\frac{1}{\wp }\frac{\partial \underline{w}(\wp ,t;\sigma )}{\partial \wp }\right),\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \frac{\partial \overline{w}(\wp ,t;\sigma )}{\partial t}& =-\frac{\partial p}{{}_{\rho }\partial \varphi }+\tau \left(\frac{{\partial }^2\overline{w}(\wp ,t;\sigma )}{\partial {\wp }^2}+\frac{1}{\wp }\frac{\partial \overline{w}(\wp ,t;\sigma )}{\partial \wp }\right).\hfill \end{array}$$

(10)

The time derivative term (9) and (10) takes the fractional derivative form

$$\begin{array}{cc}\hfill \frac{{\partial }^{\Im }\underline{w}(\wp ,t;\sigma )}{\partial t^{\Im }}& =\mathcal{P}+\tau \left(\frac{{\partial }^2\underline{w}(\wp ,t;\sigma )}{\partial {\wp }^2}+\frac{1}{\wp }\frac{\partial \underline{w}(\wp ,t;\sigma )}{\partial \wp }\right),0<\Im \le 1,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill \frac{{\partial }^{\Im }\overline{w}(\wp ,t;\sigma )}{\partial t^{\Im }}& =\mathcal{P}+\tau \left(\frac{{\partial }^2\overline{w}(\wp ,t;\sigma )}{\partial {\wp }^2}+\frac{1}{\wp }\frac{\partial \overline{w}(\wp ,t;\sigma )}{\partial \wp }\right),0<\Im \le 1.\hfill \end{array}$$

(12)

Employing the process of decomposition, we define (11) and (12) in an operator from

$$\begin{array}{cc}\hfill {\mathcal{D}}_t^{\Im }\underline{w}(\wp ,t;\sigma )& =\mathcal{P}+\tau \left({\mathcal{L}}_{\wp \wp }\underline{w}(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }\underline{w}(\wp ,t;\sigma )\right),\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\mathcal{D}}_t^{\Im }\overline{w}(\wp ,t;\sigma )& =\mathcal{P}+\tau \left({\mathcal{L}}_{\wp \wp }\overline{w}(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }\overline{w}(\wp ,t;\sigma )\right),\hfill \end{array}$$

(14)

where ${\mathcal{D}}_t^{{}^{\Im }},{\mathcal{L}}_{\wp },and{\mathcal{L}}_{\wp \wp }$ symbolize $\frac{{\partial }^{\Im }}{\partial t^{\Im }},\frac{\partial }{\partial \wp }$ and $\frac{{\partial }^2}{\partial {\wp }^2},$ respectively.

The procedure is determined by using the operator $J^{\Im }$, which is the inverse of ${\mathcal{D}}_t^{{}^{\Im }}$, for both sides of (13) and (14), we get

$$\begin{array}{cc}\hfill \underline{w}(\wp ,t;\sigma )& =\sum _{l=0}^{m-1}\frac{{\partial }^l\underline{w}}{\partial t^l}(\wp ,0^{+})(\sigma )\frac{t^l}{l!}+J^{\Im }\mathcal{P}+\tau J^{\Im }\left({\mathcal{L}}_{\wp \wp }\underline{w}(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }\underline{w}(\wp ,t;\sigma )\right),\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill \overline{w}(\wp ,t;\sigma )& =\sum _{l=0}^{m-1}\frac{{\partial }^l\overline{w}}{\partial t^l}(\wp ,0^{+})(\sigma )\frac{t^l}{l!}+J^{\Im }\mathcal{P}+\tau J^{\Im }\left({\mathcal{L}}_{\wp \wp }\overline{w}(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }\overline{w}(\wp ,t;\sigma )\right).\hfill \end{array}$$

(16)

Presupposing the existence of a series solution for $\tilde{w}(\wp ,t;\sigma )=[\underline{w}(\wp ,t;\sigma ),\overline{w}(\wp ,t;\sigma )],$ expressed as

$$\begin{array}{cc}\hfill \underline{w}(\wp ,t;\sigma )& =\sum _{n=0}^{\infty }{\underline{w}}_n(\wp ,t;\sigma ),\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill \overline{w}(\wp ,t;\sigma )& =\sum _{n=0}^{\infty }{\overline{w}}_n(\wp ,t;\sigma ),\hfill \end{array}$$

(18)

where ${\tilde{w}}_n(\wp ,t;\sigma )=[{\underline{w}}_n(\wp ,t;\sigma ),{\overline{w}}_n(\wp ,t;\sigma )]$ is obtained recursively. (18) into (15) gives

$$\begin{array}{cc}\hfill \sum _{n=0}^{\infty }{\underline{w}}_n(\wp ,t;\sigma )& =\sum _{l=0}^{\infty }\frac{{\partial }^l\underline{w}}{\partial t^l}(\wp ,0^{+})(\sigma )\frac{t^l}{l!}+J^{\Im }\mathcal{P}+\tau J^{\Im }\left({\mathcal{L}}_{\wp \wp }\sum _{n=0}^{\infty }{\underline{w}}_n(\wp ,t;\sigma )\right.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \left.+\frac{1}{\wp }{\mathcal{L}}_{\wp }\sum _{n=0}^{\infty }{\underline{w}}_n(\wp ,t;\sigma )\right),\hfill \\ \hfill \sum _{n=0}^{\infty }{\overline{w}}_n(\wp ,t;\sigma )& =\sum _{l=0}^{\infty }\frac{{\partial }^l\overline{w}}{\partial t^l}(\wp ,0^{+})(\sigma )\frac{t^l}{l!}+J^{\Im }\mathcal{P}+\tau J^{\Im }\left({\mathcal{L}}_{\wp \wp }\sum _{n=0}^{\infty }{\overline{w}}_n(\wp ,t;\sigma )\right.\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & \left.+\frac{1}{\wp }{\mathcal{L}}_{\wp }\sum _{n=0}^{\infty }{\overline{w}}_n(\wp ,t;\sigma )\right),\hfill \end{array}$$

(20)

and we use the recursive relations as

$$\begin{array}{cc}\hfill {\underline{w}}_0(\wp ,t;\sigma )& =\sum _{l=0}^{m-1}\frac{{\partial }^l\underline{w}}{\partial t^l}(\wp ,0^{+})(\sigma )\frac{t^l}{l!}+J^{\Im }\mathcal{P},\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill {\underline{w}}_{n+1}(\wp ,t;\sigma )& =\tau J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\underline{w}}_n(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\underline{w}}_n(\wp ,t;\sigma )\right),n\ge 0,\hfill \end{array}$$

(22)

and

$$\begin{array}{cc}\hfill {\overline{w}}_0(\wp ,t;\sigma )& =\sum _{l=0}^{m-1}\frac{{\partial }^l\overline{w}}{\partial t^l}(\wp ,0^{+})(\sigma )\frac{t^l}{l!}+J^{\Im }\mathcal{P},\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill {\overline{w}}_{n+1}(\wp ,t;\sigma )& =\tau J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\overline{w}}_n(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\overline{w}}_n(\wp ,t;\sigma )\right),n\ge 0.\hfill \end{array}$$

(24)

The components ${\tilde{w}}_n(\wp ,t;\sigma ),n\ge 1$ can be entirely identified such that each term is obtained by the prior term. As ${\tilde{w}}_0(\wp ,t;\sigma )$ is given

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{w}}_1(\wp ,t;\sigma )& =\tau J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\underline{w}}_0(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\underline{w}}_0(\wp ,t;\sigma )\right),\hfill \\ \hfill {\underline{w}}_2(\wp ,t;\sigma )& =\tau J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\underline{w}}_1(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\underline{w}}_1(\wp ,t;\sigma )\right),\hfill \\ \hfill {\underline{w}}_3(\wp ,t;\sigma )& =\tau J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\underline{w}}_2(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\underline{w}}_2(\wp ,t;\sigma )\right),\hfill \\ \hfill ⋮\\ \hfill {\underline{w}}_n(\wp ,t;\sigma )& =\tau J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\underline{w}}_{n-1}(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\underline{w}}_{n-1}(\wp ,t;\sigma )\right),\hfill \end{array}\right.\end{array}$$

(25)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\overline{w}}_1(\wp ,t;\sigma )& =\tau J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\overline{w}}_0(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\overline{w}}_0(\wp ,t;\sigma )\right),\hfill \\ \hfill {\overline{w}}_2(\wp ,t;\sigma )& =\tau J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\overline{w}}_1(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\overline{w}}_1(\wp ,t;\sigma )\right),\hfill \\ \hfill {\overline{w}}_3(\wp ,t;\sigma )& =\tau J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\overline{w}}_2(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\overline{w}}_2(\wp ,t;\sigma )\right),\hfill \\ \hfill ⋮\\ \hfill {\overline{w}}_n(\wp ,t;\sigma )& =\tau J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\overline{w}}_{n-1}(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\overline{w}}_{n-1}(\wp ,t;\sigma )\right).\hfill \end{array}\right.\end{array}$$

(26)

The series solution is defined by

$$\begin{array}{cc}\hfill \underline{w}(\wp ,t;\sigma )& ={\underline{w}}_0(\wp ,t;\sigma )+\sum _{n=1}^{\infty }\tau J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\underline{w}}_n(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\underline{w}}_n(\wp ,t;\sigma )\right),\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill \overline{w}(\wp ,t;\sigma )& ={\overline{w}}_0(\wp ,t;\sigma )+\sum _{n=1}^{\infty }\tau J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\overline{w}}_n(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\overline{w}}_n(\wp ,t;\sigma )\right).\hfill \end{array}$$

(28)

3.2. Convergence Analysis

We analyze fuzzy ADM convergence for the general fuzzy operator equation

$$\mathcal{L}\left(\tilde{w}(\wp ,t;\sigma )\right)+\mathcal{R}\left(\tilde{w}(\wp ,t;\sigma )\right)+\mathcal{N}\left(\tilde{w}(\wp ,t;\sigma )\right)=\tilde{g}(\wp ,t;\sigma ),0\le \sigma \le 1,$$

(29)

where $\tilde{g}(\wp ,t;\sigma )$ is given in ${\mathbb{H}}^{\prime }.$ Suppose that $\mathbb{T}$ an operator defined by $\mathbb{T}\tilde{w}(\wp ,t;\sigma )=-\mathbb{R}\tilde{w}(\wp ,t;\sigma )-\mathcal{N}\tilde{w}(\wp ,t;\sigma ).$ We consider the Hilbert space $\mathbb{H}={\mathbb{L}}^2\left((\alpha ,\beta )\times [0,\mathbb{T}]\right)$ defined by

$$\tilde{w}(\wp ,t;\sigma ):(\alpha ,\beta )\times [0,\mathbb{T}]⟶\mathbb{R},$$

with

$${\int }_{(\alpha ,\beta )\times [0,\mathbb{T}]}\tilde{w}(\wp ,t;\sigma )d\wp dt<+\infty ,$$

(30)

where $\tilde{w}(\wp ,t;\sigma )=\left[\underline{w}(\wp ,t;\sigma ),\overline{w}(\wp ,t;\sigma )\right].$

Theorem 3.

Let $\mathbb{T}\tilde{w}(\wp ,t;\sigma )=-\mathbb{R}\tilde{w}(\wp ,t;\sigma )-\mathcal{N}\tilde{w}(\wp ,t;\sigma )$ be a semicontinuous (i.e., the restriction of $(-\mathbb{R}-\mathcal{N})$ to the segments of $\mathbb{H}$ is continuous, in ${\mathbb{H}}^{\prime }$ weak) and satisfies the hypotheses ${\mathbb{H}}_1,{\mathbb{H}}_2$ as:

• $\left[{\mathbb{H}}_1\right]:\left(\mathbb{T}\tilde{w}(\wp ,t;\sigma )-\mathbb{T}\tilde{\tau }(\wp ,t;\sigma ),\tilde{w}(\wp ,t;\sigma )-\tilde{\tau }(\wp ,t;\sigma )\right)\ge K{\parallel \tilde{w}(\wp ,t;\sigma )-\tilde{\tau }(\wp ,t;\sigma )\parallel }^2,$
  $K>0,\forall \tilde{w},\tilde{\tau }\in \mathbb{H}.$
• $\left[{\mathbb{H}}_2\right]:\forall M>0,\exists D\left(M\right)>0sothatfor\parallel \tilde{w}\parallel \le M,\parallel \tilde{\tau }\parallel \le M,\tilde{w},\tilde{\tau }\in \mathbb{H},wehave$
  $\Rightarrow \left(\mathbb{T}\tilde{w}(\wp ,t;\sigma )-\tilde{\tau }(\wp ,t;\sigma ),\tilde{f}(\wp ,t;\sigma )\right)\le D\left(M\right)\parallel \tilde{w}(\wp ,t;\sigma )-\tilde{\tau }(\wp ,t;\sigma )\parallel \parallel \tilde{f}(\wp ,t;\sigma )\parallel ,$
  $\forall \tilde{f}\in \mathbb{H}.$

For any $\tilde{g}(\wp ,t;\sigma )\in {\mathbb{H}}^{\prime },$ the fuzzy nonlinear functional Equation (29) admits a unique solution $\tilde{w}(\wp ,t;\sigma )\in \mathcal{H}.$ Moreover, if the solution $\tilde{w}(\wp ,t;\sigma )$, it can be assimilated as:

$$\tilde{w}(\wp ,t;\sigma )=\sum _{n=0}^{\infty }{\tilde{w}}_n(\wp ,t;\sigma ){\hslash }^n,$$

Consequently, the fuzzy ADM diagram corresponding to the functional equation under study converges strongly to $\tilde{w}(\wp ,t;\sigma )\in \mathbb{H},$ which is the unique solution to the functional equation.

The proof of this theorem is similar to the proof of Theorem 3.3 in [40].

3.3. Fuzzy Modified Laplace Decomposition Method

We consider the fuzzy nonlinear fractional PDEs as follows:

$$\begin{array}{c}\hfill {\mathcal{D}}_t^{n\Im }\tilde{w}(\wp ,t)\oplus \mathcal{R}[\wp ]\tilde{w}(\wp ,t)\oplus \mathcal{N}[\wp ]\tilde{w}(\wp ,t)=\tilde{g}(\wp ,t),t>0,\end{array}$$

(31)

where $\wp \in \mathcal{R},n-1<n\Im \le n,{\mathcal{D}}_t^{n\Im }=\frac{{\partial }^{n\Im }}{\partial t^{n\Im }},$ and $\mathcal{R}[\wp ],\mathcal{N}[\wp ]$ denotes the linear and nonlinear terms in ℘, respectively, and $\tilde{g}(\wp ,t;\sigma )=[\underline{g}(\wp ,t;\sigma ),\overline{g}(\wp ,t;\sigma )]$ denotes continuous fuzzy-valued functions. Therefore, through firstly using the Laplace transform for (31), we obtain

$$\begin{array}{cc}\hfill \mathcal{L}\left[{\mathcal{D}}_t^{n\Im }\underline{w}(\wp ,t;\sigma )\right]+\mathcal{L}\left[\mathcal{R}[\wp ]\underline{w}(\wp ,t;\sigma )+\mathcal{N}[\wp ]\underline{w}(\wp ,t;\sigma )\right]& =\mathcal{L}\left[\underline{g}(\wp ,t;\sigma )\right],t>0,\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill \mathcal{L}\left[{\mathcal{D}}_t^{n\Im }\overline{w}(\wp ,t;\sigma )\right]+\mathcal{L}\left[\mathcal{R}[\wp ]\overline{w}(\wp ,t;\sigma )+\mathcal{N}[\wp ]\overline{w}(\wp ,t;\sigma )\right]& =\mathcal{L}\left[\overline{g}(\wp ,t;\sigma )\right],t>0.\hfill \end{array}$$

(33)

In order to compute the fractional derivative, the differential property of the Laplace transform must be used

$$\begin{array}{cc}\hfill s^{n\Im }\mathcal{L}\left[\underline{w}(\wp ,t;\sigma )\right]-\sum _{l=0}^{n-1}{s}^{(n\Im -l-1)}{\underline{w}}^l(\wp ,0)(\sigma )+\mathcal{L}\left[\mathcal{R}[\wp ]\underline{w}(\wp ,t;\sigma )+\mathcal{N}[\wp ]\underline{w}(\wp ,t;\sigma )\right]& =\mathcal{L}\left[\underline{g}(\wp ,t;\sigma )\right],\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill s^{n\Im }\mathcal{L}\left[\overline{w}(\wp ,t;\sigma )\right]-\sum _{l=0}^{n-1}{s}^{(n\Im -l-1)}{\overline{w}}^l(\wp ,0)(\sigma )+\mathcal{L}\left[\mathcal{R}[\wp ]\overline{w}(\wp ,t;\sigma )+\mathcal{N}[\wp ]\overline{w}(\wp ,t;\sigma )\right]& =\mathcal{L}\left[\overline{g}(\wp ,t;\sigma )\right].\hfill \end{array}$$

(35)

To simplify,

$$\begin{array}{cc}\hfill \mathcal{L}\left[\underline{w}(\wp ,t;\sigma )\right]& =s^{-n\Im }\sum _{l=0}^{n-1}{s}^{(n\Im -l-1)}{\underline{w}}^l(\wp ,0)(\sigma )+s^{-n\Im }\mathcal{L}\left[\underline{g}(\wp ,t;\sigma )\right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill & -s^{-n\Im }\mathcal{L}\left[\mathcal{R}[\wp ]\underline{w}(\wp ,t;\sigma )+\mathcal{N}[\wp ]\underline{w}(\wp ,t;\sigma )\right],\hfill \\ \hfill \mathcal{L}\left[\overline{w}(\wp ,t;\sigma )\right]& =s^{-n\Im }\sum _{l=0}^{n-1}{s}^{(n\Im -l-1)}{\overline{w}}^l(\wp ,0)(\sigma )+s^{-n\Im }\mathcal{L}\left[\overline{g}(\wp ,t;\sigma )\right]\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill & -s^{-n\Im }\mathcal{L}\left[\mathcal{R}[\wp ]\overline{w}(\wp ,t;\sigma )+\mathcal{N}[\wp ]\overline{w}(\wp ,t;\sigma )\right].\hfill \end{array}$$

(37)

From (36) and (37), we obtain

$$\begin{array}{c}\hfill \underline{w}(\wp ,t;\sigma )=\underline{\mathcal{G}}(\wp ,t;\sigma )-{\mathcal{L}}^{-1}\left(s^{-n\Im }L[\mathcal{R}[\wp ]\underline{w}(\wp ,t;\sigma )+\mathcal{N}[\wp ]\underline{w}(\wp ,t;\sigma )]\right),\end{array}$$

(38)

$$\begin{array}{c}\hfill \overline{w}(\wp ,t;\sigma )=\overline{\mathcal{G}}(\wp ,t;\sigma )-{\mathcal{L}}^{-1}\left(s^{-n\Im }L[\mathcal{R}[\wp ]\overline{w}(\wp ,t;\sigma )+\mathcal{N}[\wp ]\overline{w}(\wp ,t;\sigma )]\right),\end{array}$$

(39)

in which $\tilde{\mathcal{G}}(\wp ,t;\sigma )=[\underline{\mathcal{G}}(\wp ,t;\sigma ),\overline{\mathcal{G}}(\wp ,t;\sigma )]$ denotes the term resulting from the source term and the specified initial conditions. The fuzzy LDM allows for the existence of a solution of the form

$$\begin{array}{cc}\hfill \underline{w}(\wp ,t;\sigma )& =\sum _{\mu =0}^{\infty }{\underline{w}}_{\mu }(\wp ,t;\sigma ),\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill \overline{w}(\wp ,t;\sigma )& =\sum _{\mu =0}^{\infty }{\overline{w}}_{\mu }(\wp ,t;\sigma ).\hfill \end{array}$$

(41)

$\mathcal{N}\tilde{w}(\wp ,t;\sigma )=[\mathcal{N}\underline{w}(\wp ,t;\sigma ),\mathcal{N}\overline{w}(\wp ,t;\sigma )]$ is a nonlinear term that can be decomposed as

$$\begin{array}{cc}\hfill \mathcal{N}\underline{w}(\wp ,t;\sigma )& =\sum _{\mu =0}^{\infty }{\underline{\mathcal{A}}}_{\mu }(\sigma ),\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill \mathcal{N}\overline{w}(\wp ,t;\sigma )& =\sum _{\mu =0}^{\infty }{\overline{\mathcal{A}}}_{\mu }(\sigma ),\hfill \end{array}$$

(43)

where ${\tilde{\mathcal{A}}}_{\mu }(\sigma )=\left[{\underline{\mathcal{A}}}_{\mu }(\sigma ),{\overline{\mathcal{A}}}_{\mu }(\sigma )\right]$ denotes Adomian polynomials with coefficients ${\tilde{w}}_0,{\tilde{w}}_1,{\tilde{w}}_2,$ $\cdots {\tilde{w}}_n$, and it can be determined using the following formula:

$$\begin{array}{cc}\hfill {\underline{\mathcal{A}}}_{\mu }(\sigma )& =\frac{1}{\mu !}\frac{d^{\mu }}{d{t}^{\mu }}{\left.\left[\left(\mathcal{N}\sum _{i=0}^{\infty }{\sigma }^{*i}{\underline{w}}_{\mu }(\wp ,t;\sigma )\right)\right]\right|}_{{\sigma }^{*}=0},\mu =0,1,2,3,\cdots \hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill {\overline{\mathcal{A}}}_{\mu }(\sigma )& =\frac{1}{\mu !}\frac{d^{\mu }}{d{t}^{\mu }}{\left.\left[\left(\mathcal{N}\sum _{i=0}^{\infty }{\sigma }^{*i}{\overline{w}}_{\mu }(\wp ,t;\sigma )\right)\right]\right|}_{{\sigma }^{*}=0},\mu =0,1,2,3,\cdots \hfill \end{array}$$

(45)

Taking (43) into (38), we obtain

$$\begin{array}{cc}\hfill \sum _{i=0}^{\infty }{\underline{w}}_{\mu }(\wp ,t;\sigma )& =\underline{\mathcal{G}}(\wp ,t;\sigma )-{\mathcal{L}}^{-1}\left(s^{-n\Im }\mathcal{L}\left[\mathcal{R}[\wp ]\left(\sum _{i=0}^{\infty }{\underline{w}}_{\mu }(\wp ,t;\sigma )\right)\right.\right.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \left.\left.+\left(\sum _{i=0}^{\infty }{\underline{\mathcal{A}}}_{\mu }(\sigma )\right)\right]\right),\hfill \\ \hfill \sum _{i=0}^{\infty }{\overline{w}}_{\mu }(\wp ,t;\sigma )& =\overline{\mathcal{G}}(\wp ,t;\sigma )-{\mathcal{L}}^{-1}\left(s^{-n\Im }\mathcal{L}\left[\mathcal{R}[\wp ]\left(\sum _{i=0}^{\infty }{\overline{w}}_{\mu }(\wp ,t;\sigma )\right)\right.\right.\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill & \left.\left.+\left(\sum _{i=0}^{\infty }{\overline{\mathcal{A}}}_{\mu }(\sigma )\right)\right]\right).\hfill \end{array}$$

(47)

We obtain the following relationship by equating the terms (46) and (47)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\underline{w}}_0(\wp ,t;\sigma )=\underline{\mathcal{G}}(\wp ,t;\sigma ),\hfill \\ \hfill & {\underline{w}}_{\mu +1}(\wp ,t;\sigma )={\mathcal{L}}^{-1}\left(s^{-n\Im }\mathcal{L}[\mathcal{R}[\wp ]{\underline{w}}_{\mu }(\wp ,t;\sigma )+A_{\mu }(\sigma )]\right),\mu \ge 0,\hfill \end{array}\end{array}$$

(48)

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\overline{w}}_0(\wp ,t;\sigma )=\overline{\mathcal{G}}(\wp ,t;\sigma ),\hfill \\ \hfill & {\overline{w}}_{\mu +1}(\wp ,t;\sigma )={\mathcal{L}}^{-1}\left(s^{-n\Im }\mathcal{L}[\mathcal{R}[\wp ]{\overline{w}}_{\mu }(\wp ,t;\sigma )+A_{\mu }(\sigma )]\right),\mu \ge 0.\hfill \end{array}\end{array}$$

(49)

According to the modified LDM, the fuzzy-valued function $\tilde{\mathcal{G}}(\wp ,t;\sigma )$ stated above should be divided into two pieces, ${\tilde{\mathcal{G}}}_0(\wp ,t;\sigma )$ and ${\tilde{\mathcal{G}}}_1(\wp ,t;\sigma )$

$$\begin{array}{cc}\hfill \underline{\mathcal{G}}(\wp ,t;\sigma )& ={\underline{\mathcal{G}}}_0(\wp ,t;\sigma )+{\underline{\mathcal{G}}}_1(\wp ,t;\sigma ),\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill \overline{\mathcal{G}}(\wp ,t;\sigma )& ={\overline{\mathcal{G}}}_0(\wp ,t;\sigma )+{\overline{\mathcal{G}}}_1(\wp ,t;\sigma ).\hfill \end{array}$$

(51)

However, we consider the variations below

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & {\underline{w}}_0(\wp ,t;\sigma )={\underline{\mathcal{G}}}_0(\wp ,t;\sigma ),\hfill \\ \hfill & {\underline{w}}_1(\wp ,t;\sigma )={\underline{\mathcal{G}}}_1(\wp ,t;\sigma )+{\mathcal{L}}^{-1}\left(s^{-n\Im }\mathcal{L}[\mathcal{R}[\wp ]{\underline{w}}_0(\sigma )+{\underline{A}}_0(\sigma )]\right),\hfill \\ \hfill & {\underline{w}}_2(\wp ,t;\sigma )={\mathcal{L}}^{-1}\left(s^{-n\Im }\mathcal{L}[\mathcal{R}[\wp ]{\underline{w}}_1(\sigma )+{\underline{A}}_1(\sigma )]\right),\hfill \\ \hfill ⋮\\ \hfill & {\underline{w}}_{\mu +1}(\wp ,t;\sigma )={\mathcal{L}}^{-1}\left(s^{-n\Im }\mathcal{L}[\mathcal{R}[\wp ]{\underline{w}}_{\mu }(\sigma )+{\underline{A}}_{\mu }(\sigma )]\right),\hfill \end{array}\right.\end{array}$$

(52)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & {\overline{w}}_0(\wp ,t;\sigma )={\overline{\mathcal{G}}}_0(\wp ,t;\sigma ),\hfill \\ \hfill & {\overline{w}}_1(\wp ,t;\sigma )={\overline{\mathcal{G}}}_1(\wp ,t;\sigma )+{\mathcal{L}}^{-1}\left(s^{-n\Im }\mathcal{L}[\mathcal{R}[\wp ]{\overline{w}}_0(\sigma )+{\overline{A}}_0(\sigma )]\right),\hfill \\ \hfill & {\overline{w}}_2(\wp ,t;\sigma )={\mathcal{L}}^{-1}\left(s^{-n\Im }\mathcal{L}[\mathcal{R}[\wp ]{\overline{w}}_1(\sigma )+{\overline{A}}_1(\sigma )]\right),\hfill \\ \hfill ⋮\\ \hfill & {\overline{w}}_{\mu +1}(\wp ,t;\sigma )={\mathcal{L}}^{-1}\left(s^{-n\Im }\mathcal{L}[\mathcal{R}[\wp ]{\overline{w}}_{\mu }(\sigma )+{\overline{A}}_{\mu }(\sigma )]\right).\hfill \end{array}\right.\end{array}$$

(53)

Convergence Analysis

The series expressed from fuzzy ADM in (40) and (41) rapidly and uniformly converge to the exact solution of the system. The series of solutions represented by using fuzzy ADM (40) and (41) is as follows:

$$\begin{array}{cc}\hfill {\tilde{w}}_n(\wp ,t;\sigma )& =T{\tilde{w}}_{n-1}(\wp ,t;\sigma ),{\tilde{w}}_{n-1}(\wp ,t;\sigma )=\sum _{\varsigma =1}^n{\tilde{w}}_{\varsigma }(\wp ,t;\sigma ),\hfill \end{array}$$

(54)

where $n=1,2,3,\dots .$

State the convergence conditions of $\left\{{\tilde{w}}_n(\wp ,t;\sigma )\right\}$ in the following theorem.

Theorem 4.

LetΨ be a Banach space and $T:\Psi \to \Psi$ a contraction map and $h\in (0,1)$ be a contractive; then, T has a unique point $\tilde{w}(\wp ,t;\sigma )$ such that $T(\tilde{w}(\wp ,t;\sigma )=\tilde{w}(\wp ,t;\sigma ))$ where $\tilde{w}(\wp ,t;\sigma )=(S,I,R).$ Suppose that ${\tilde{w}}_0(\wp ,t;\sigma )\in F_{\theta }\tilde{w}(\wp ,t;\sigma ),$ where $F_{\theta }\tilde{w}(\wp ,t;\sigma )=\{{\tilde{w}}^{\prime }(\wp ,t;\sigma )\in \Psi :\parallel {\tilde{w}}^{\prime }(\wp ,t;\sigma )-\tilde{w}(\wp ,t;\sigma )\parallel <\theta \},$ then

(i) 

${\tilde{w}}_n(\wp ,t;\sigma )\in F_{\theta }\left(\tilde{w}(\wp ,t;\sigma )\right),$

(ii) 

${lim}_{n\to \infty }{\tilde{w}}_n(\wp ,t;\sigma )=\tilde{w}(\wp ,t;\sigma ).$

Proof. 

(i) Taking the mathematical induction for $n=1,$ we obtain

$$\begin{array}{cc}\hfill \parallel {\tilde{w}}_0(\wp ,t;\sigma )-\tilde{w}(\wp ,t;\sigma )\parallel & =\parallel T\left({\tilde{w}}_0(\wp ,t;\sigma )\right)-T\left(\tilde{w}(\wp ,t;\sigma )\right)\parallel \le h\parallel {\tilde{w}}_0(\wp ,t;\sigma )-\tilde{w}(\wp ,t;\sigma )\parallel .\hfill \end{array}$$

Supposing that a result is true for $n-1$, then

$$\begin{array}{cc}\hfill \parallel {\tilde{w}}_{n-1}(\wp ,t;\sigma )-\tilde{w}(\wp ,t;\sigma )\parallel & \le h^{n-1}\parallel {\tilde{w}}_0(\wp ,t;\sigma )-\tilde{w}(\wp ,t;\sigma )\parallel ,\hfill \end{array}$$

we obtain

$$\begin{array}{cc}\hfill \parallel {\tilde{w}}_n(\wp ,t;\sigma )-\tilde{w}(\wp ,t;\sigma )\parallel & =\parallel T\left({\tilde{w}}_{n-1}(\wp ,t;\sigma )\right)-T\left(\tilde{w}(\wp ,t;\sigma )\right)\parallel \le h\parallel {\tilde{w}}_{n-1}(\wp ,t;\sigma )-\tilde{w}(\wp ,t;\sigma )\parallel ,\hfill \\ \hfill & \le h^n\parallel {\tilde{w}}_0(\wp ,t;\sigma )-\tilde{w}(\wp ,t;\sigma )\parallel .\hfill \end{array}$$

Furthermore,

$$\begin{array}{cc}\hfill {\tilde{w}}_0(\wp ,t;\sigma )& \in F_{\theta }\left(\tilde{w}(\wp ,t;\sigma )\right),\hfill \end{array}$$

thus $\parallel {\tilde{w}}_0(\wp ,t;\sigma )-\tilde{w}(\wp ,t;\sigma )\parallel <\theta ,$ we have

$$\begin{array}{cc}\hfill \parallel {\tilde{w}}_n(\wp ,t;\sigma )-\tilde{w}(\wp ,t;\sigma )\parallel & \le h^n\parallel {\tilde{w}}_0(\wp ,t;\sigma )-\tilde{w}(\wp ,t;\sigma )\parallel \le h^n\theta <\theta .\hfill \end{array}$$

This implies that

$$\begin{array}{cc}\hfill {\tilde{w}}_n(\wp ,t;\sigma )& \in F_{\theta }\left(\tilde{w}(\wp ,t;\sigma )\right).\hfill \end{array}$$

(ii) Since $\parallel {\tilde{w}}_n(\wp ,t;\sigma )-\tilde{w}(\wp ,t;\sigma )\parallel \le h^n\parallel {\tilde{w}}_0(\wp ,t;\sigma )-\tilde{w}(\wp ,t;\sigma )\parallel ,$ and ${lim}_{n\to \infty }{h}^n=\tilde{0},$ we obtain

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}\parallel {\tilde{w}}_n(\wp ,t;\sigma )-\tilde{w}(\wp ,t;\sigma )\parallel & =\tilde{0},\hfill \end{array}$$

then

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}{\tilde{w}}_n(\wp ,t;\sigma )& =\tilde{w}(\wp ,t;\sigma ),\hfill \end{array}$$

which completes the proof. □

3.4. Examples

In this part, we applied the methods for solving fuzzy fractional Navier–Stokes equation. In the ending, two examples are proposed.

Example 1.

Consider the fuzzy time-fractional Navier–Stokes equation below:

$$\frac{{\partial }^{\Im }\tilde{w}(\wp ,t)}{\partial t^{\Im }}=\mathcal{P}\oplus \frac{{\partial }^2\tilde{w}(\wp ,t)}{\partial {\wp }^2}\oplus \frac{1}{\wp }\odot \frac{\partial \tilde{w}(\wp ,t)}{\partial \wp },0<\Im \le 1,$$

(55)

with the initial condition

$$\tilde{w}(\wp ,0)=[{(1+2\sigma )}^n,{(5-2\sigma )}^n]\oplus (1-{\wp }^2),$$

(56)

where $(n=1,2,3,\cdots ).$

Case [A]. Fuzzy Adomian decomposition method

Using the FADM, we simply substitute the initial condition (56) into (48), we obtain

$$\begin{array}{cc}\hfill & {\underline{w}}_0(\wp ,t;\sigma )={(1+2\sigma )}^n\left[1-{\wp }^2+J^{\Im }\mathcal{P}\right],\hfill \end{array}$$

(57)

$$\begin{array}{cc}\hfill & {\underline{w}}_{\mu +1}(\wp ,t;\sigma )=J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\underline{w}}_{\mu }(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\underline{w}}_{\mu }(\wp ,t;\sigma )\right),\mu \ge 0,\hfill \end{array}$$

(58)

and

$$\begin{array}{cc}\hfill & {\overline{w}}_0(\wp ,t;\sigma )={(5-2\sigma )}^n\left[1-{\wp }^2+J^{\Im }\mathcal{P}\right],\hfill \end{array}$$

(59)

$$\begin{array}{cc}\hfill & {\overline{w}}_{\mu +1}(\wp ,t;\sigma )=J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\overline{w}}_{\mu }(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\overline{w}}_{\mu }(\wp ,t;\sigma )\right),\mu \ge 0.\hfill \end{array}$$

(60)

The first few terms of the decomposition series are defined by

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{w}}_0(\wp ,t;\sigma )& ={(1+2\sigma )}^n+\left[1-{\wp }^2+\frac{\mathcal{P}}{\Gamma (\Im +1)}{t}^{\Im }\right],\hfill \\ \hfill {\underline{w}}_1(\wp ,t;\sigma )& =\left[J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\underline{w}}_0(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\underline{w}}_0(\wp ,t;\sigma )\right)\right]\hfill \\ \hfill & ={(1+2\sigma )}^n+\left[-\frac{4}{\Gamma (\Im +1)}{t}^{\Im }\right],\hfill \\ \hfill {\underline{w}}_2(\wp ,t;\sigma )& =\left[J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\underline{w}}_1(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\underline{w}}_1(\wp ,t;\sigma )\right)\right]=\tilde{0},\hfill \\ \hfill ⋮\\ \hfill {\underline{w}}_{\mu }(\wp ,t;\sigma )& =\left[J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\underline{w}}_{\mu }(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\underline{w}}_{\mu }(\wp ,t;\sigma )\right)\right]=\tilde{0},\hfill \end{array}\right.\end{array}$$

(61)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\overline{w}}_0(\wp ,t;\sigma )& ={(5-2\sigma )}^n+\left[1-{\wp }^2+\frac{\mathcal{P}}{\Gamma (\Im +1)}{t}^{\Im }\right],\hfill \\ \hfill {\overline{w}}_1(\wp ,t;\sigma )& =\left[J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\overline{w}}_0(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\overline{w}}_0(\wp ,t;\sigma )\right)\right]\hfill \\ \hfill & ={(5-2\sigma )}^n+\left[-\frac{4}{\Gamma (\Im +1)}{t}^{\Im }\right],\hfill \\ \hfill {\overline{w}}_2(\wp ,t;\sigma )& =\left[J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\overline{w}}_1(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\overline{w}}_1(\wp ,t;\sigma )\right)\right]=\tilde{0},\hfill \\ \hfill ⋮\\ \hfill {\overline{w}}_{\mu }(\wp ,t;\sigma )& =\left[J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\overline{w}}_{\mu }(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\overline{w}}_{\mu }(\wp ,t;\sigma )\right)\right]=\tilde{0},\hfill \end{array}\right.\end{array}$$

(62)

where $\mu =0,1,2,3,\cdots .$

Thus, we can obtain the solution as follows:

$$\begin{array}{c}\hfill \tilde{w}(\wp ,t;\sigma )=[{(1+2\sigma )}^n,{(5-2\sigma )}^n]\oplus \left(1-{\wp }^2+\frac{(\mathcal{P}-4)t^{\Im }}{\Gamma (\Im +1)}\right),0\le \sigma \le 1.\end{array}$$

Case [B]. Fuzzy modified Laplace decomposition method

Using the fuzzy Laplace transform in (55) yields

$$\begin{array}{c}\hfill \mathcal{L}\left[\underline{w}(\wp ,t;\sigma )\right]={(1+2\sigma )}^n+\left[\frac{1-{\wp }^2}{s}\right]+\frac{\mathcal{P}}{s^{\Im +1}}+\frac{1}{s^{\Im }}\mathcal{L}\left[{\underline{w}}_{\wp \wp }(\wp ,t;\sigma )+\frac{1}{\wp }{\underline{w}}_{\wp }(\wp ,t;\sigma )\right],\end{array}$$

(63)

$$\begin{array}{c}\hfill \mathcal{L}\left[\overline{w}(\wp ,t;\sigma )\right]={(5-2\sigma )}^n+\left[\frac{1-{\wp }^2}{s}\right]+\frac{\mathcal{P}}{s^{\Im +1}}+\frac{1}{s^{\Im }}\mathcal{L}\left[{\overline{w}}_{\wp \wp }(\wp ,t;\sigma )+\frac{1}{\wp }{\overline{w}}_{\wp }(\wp ,t;\sigma )\right].\end{array}$$

(64)

Taking the fuzzy inverse Laplace transform (63) and (64), it follows that

$$\begin{array}{cc}\hfill \underline{w}(\wp ,t;\sigma )& ={(1+2\sigma )}^n+(1-{\wp }^2)+\frac{\mathcal{P}{t}^{\Im }}{\Gamma (\Im +1)}+{\mathcal{L}}^{-1}\left(s^{-\Im }\mathcal{L}\left[{\underline{w}}_{\wp \wp }(\wp ,t;\sigma )+\frac{1}{\wp }{\underline{w}}_{\wp }(\wp ,t;\sigma )\right]\right),\hfill \end{array}$$

(65)

$$\begin{array}{cc}\hfill \overline{w}(\wp ,t;\sigma )& ={(5-2\sigma )}^n+(1-{\wp }^2)+\frac{\mathcal{P}{t}^{\Im }}{\Gamma (\Im +1)}+{\mathcal{L}}^{-1}\left(s^{-\Im }\mathcal{L}\left[{\overline{w}}_{\wp \wp }(\wp ,t;\sigma )+\frac{1}{\wp }{\overline{w}}_{\wp }(\wp ,t;\sigma )\right]\right).\hfill \end{array}$$

(66)

Allowing an infinite series solution of the type (40) and (41), and using the technique above, we obtain

$$\begin{array}{cc}\hfill \sum _{\mu =0}^{\infty }{\underline{w}}_{\mu }(\wp ,t;\sigma )& ={(1+2\sigma )}^n+(1-{\wp }^2)+\frac{\mathcal{P}{t}^{\Im }}{\Gamma (\Im +1)}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +{\mathcal{L}}^{-1}\left(s^{-\Im }\mathcal{L}\left[{\left(\sum _{\mu =0}^{\infty }{\underline{w}}_{\mu }(\wp ,t;\sigma )\right)}_{\wp }\wp +\frac{1}{\wp }{\left(\sum _{\mu =0}^{\infty }{\underline{w}}_{\mu }(\wp ,t;\sigma )\right)}_{\wp }\right]\right),\hfill \\ \hfill \sum _{\mu =0}^{\infty }{\overline{w}}_{\mu }(\wp ,t;\sigma )& ={(5-2\sigma )}^n+(1-{\wp }^2)+\frac{\mathcal{P}{t}^{\Im }}{\Gamma (\Im +1)}\hfill \end{array}$$

(67)

$$\begin{array}{cc}\hfill & +{\mathcal{L}}^{-1}\left(s^{-\Im }\mathcal{L}\left[{\left(\sum _{\mu =0}^{\infty }{\overline{w}}_{\mu }(\wp ,t;\sigma )\right)}_{\wp }\wp +\frac{1}{\wp }{\left(\sum _{\mu =0}^{\infty }{\overline{w}}_{\mu }(\wp ,t;\sigma )\right)}_{\wp }\right]\right).\hfill \end{array}$$

(68)

Using the fuzzy fractional LDM, we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{w}}_0(\wp ,t;\sigma )& ={(1+2\sigma )}^n+\left(1-{\wp }^2\right),\hfill \\ \hfill {\underline{w}}_1(\wp ,t;\sigma )& =\frac{\mathcal{P}{t}^{\Im }}{\Gamma (\Im +1)}+{\mathcal{L}}^{-1}\left[s^{-\Im }\mathcal{L}\left({\underline{w}}_{0\wp \wp }(\wp ,t;\sigma )+\frac{1}{\wp }{\underline{w}}_{0\wp }(\wp ,t;\sigma )\right)\right]\hfill \\ \hfill & ={(1+2\sigma )}^n+\frac{(\mathcal{P}-4)t^{\Im }}{\Gamma (\Im +1)},\hfill \\ \hfill {\underline{w}}_2(\wp ,t;\sigma )& =\frac{\mathcal{P}{t}^{\Im }}{\Gamma (\Im +1)}+{\mathcal{L}}^{-1}\left[s^{-\Im }\mathcal{L}\left({\underline{w}}_{1\wp \wp }(\wp ,t;\sigma )+\frac{1}{\wp }{\underline{w}}_{1\wp }(\wp ,t;\sigma )\right)\right]=\tilde{0},\hfill \\ \hfill ⋮\\ \hfill {\underline{w}}_{\mu }(\wp ,t;\sigma )& =\frac{\mathcal{P}{t}^{\Im }}{\Gamma (\Im +1)}+{\mathcal{L}}^{-1}\left[s^{-\Im }\mathcal{L}\left({\underline{w}}_{\mu \wp \wp }(\wp ,t;\sigma )+\frac{1}{\wp }{\underline{w}}_{\mu \wp }(\wp ,t;\sigma )\right)\right]=\tilde{0},\hfill \\ \hfill & \forall \mu \ge 2,\hfill \end{array}\right.\end{array}$$

(69)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\overline{w}}_0(\wp ,t;\sigma )& ={(5-2\sigma )}^n+\left(1-{\wp }^2\right),\hfill \\ \hfill {\overline{w}}_1(\wp ,t;\sigma )& =\frac{\mathcal{P}{t}^{\Im }}{\Gamma (\Im +1)}+{\mathcal{L}}^{-1}\left[s^{-\Im }\mathcal{L}\left({\overline{w}}_{0\wp \wp }(\wp ,t;\sigma )+\frac{1}{\wp }{\overline{w}}_{0\wp }(\wp ,t;\sigma )\right)\right],\hfill \\ \hfill & ={(5-2\sigma )}^n+\frac{(\mathcal{P}-4)t^{\Im }}{\Gamma (\Im +1)}\hfill \\ \hfill {\overline{w}}_2(\wp ,t;\sigma )& =\frac{\mathcal{P}{t}^{\Im }}{\Gamma (\Im +1)}+{\mathcal{L}}^{-1}\left[s^{-\Im }\mathcal{L}\left({\overline{w}}_{1\wp \wp }(\wp ,t;\sigma )+\frac{1}{\wp }{\overline{w}}_{1\wp }(\wp ,t;\sigma )\right)\right]=\tilde{0},\hfill \\ \hfill ⋮\\ \hfill {\overline{w}}_{\mu }(\wp ,t;\sigma )& =\frac{\mathcal{P}{t}^{\Im }}{\Gamma (\Im +1)}+{\mathcal{L}}^{-1}\left[s^{-\Im }\mathcal{L}\left({\overline{w}}_{\mu \wp \wp }(\wp ,t;\sigma )+\frac{1}{\wp }{\overline{w}}_{\mu \wp }(\wp ,t;\sigma )\right)\right]=\tilde{0},\hfill \\ \hfill & \forall \mu \ge 2,\hfill \end{array}\right.\end{array}$$

(70)

we can obtain the solution as follows:

$$\begin{array}{c}\hfill \tilde{w}(\wp ,t;\sigma )=[{(1+2\sigma )}^n,{(5-2\sigma )}^n]\oplus \left(1-{\wp }^2+\frac{(\mathcal{P}-4)t^{\Im }}{\Gamma (\Im +1)}\right),0\le \sigma \le 1.\end{array}$$

Example 2.

We consider the following fuzzy time-fractional Navier–Stokes equation

$$\frac{{\partial }^{\Im }\tilde{w}(\wp ,t)}{\partial t^{\Im }}=\frac{{\partial }^2\tilde{w}(\wp ,t)}{\partial {\wp }^2}\oplus \frac{1}{\wp }\odot \frac{\partial \tilde{w}(\wp ,t)}{\partial \wp },0<\Im \le 1,$$

(71)

with the initial condition

$$\tilde{w}(\wp ,0)=[{(1.5\sigma -0.5)}^n,{(1.5-0.5\sigma )}^n]\odot \wp ,$$

(72)

where $(n=1,2,3,\cdots ).$

Case [A]. Fuzzy Adomian decomposition method

The decomposition series’ first few terms are provided as

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{w}}_0(\wp ,t;\sigma )& ={(1.5\sigma -0.5)}^n\wp ,\hfill \\ \hfill {\underline{w}}_1(\wp ,t;\sigma )& =J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\underline{w}}_0(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\underline{w}}_0(\wp ,t;\sigma )\right)\hfill \\ \hfill & ={(1.5\sigma -0.5)}^n\left[\frac{1}{\wp }\frac{t^{\Im }}{\Gamma (\Im +1)}\right],\hfill \\ \hfill {\underline{w}}_2(\wp ,t;\sigma )& =\left[J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\underline{w}}_1(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\underline{w}}_1(\wp ,t;\sigma )\right)\right]\hfill \\ \hfill & ={(1.5\sigma -0.5)}^n\left[\frac{1}{{\wp }^3}\frac{t^{2\Im }}{\Gamma (2\Im +1)}\right],\hfill \\ \hfill ⋮\\ \hfill {\underline{w}}_{\mu }(\wp ,t;\sigma )& =\left[J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\underline{w}}_{\mu -1}(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\underline{w}}_{\mu -1}(\wp ,t;\sigma )\right)\right]\hfill \\ \hfill & ={(1.5\sigma -0.5)}^n\left[\frac{1^2\times 3^2\times \cdots \times {(2n-3)}^2}{{\wp }^{2n-1}}\frac{t^{\mu \Im }}{\Gamma (\mu \Im +1)}\right],\hfill \end{array}\right.\end{array}$$

(73)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\overline{w}}_0(\wp ,t;\sigma )& ={(1.5-0.5\sigma )}^n\wp ,\hfill \\ \hfill {\overline{w}}_1(\wp ,t;\sigma )& =J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\overline{w}}_0(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\overline{w}}_0(\wp ,t;\sigma )\right)\hfill \\ \hfill & ={(1.5-0.5\sigma )}^n\left[\frac{1}{\wp }\frac{t^{\Im }}{\Gamma (\Im +1)}\right],\hfill \\ \hfill {\overline{w}}_2(\wp ,t;\sigma )& =\left[J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\overline{w}}_1(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\overline{w}}_1(\wp ,t;\sigma )\right)\right]\hfill \\ \hfill & ={(1.5-0.5\sigma )}^n\left[\frac{1}{{\wp }^3}\frac{t^{2\Im }}{\Gamma (2\Im +1)}\right],\hfill \\ \hfill ⋮\\ \hfill {\overline{w}}_{\mu }(\wp ,t;\sigma )& =\left[J^{\Im }\left({\mathcal{L}}_{\wp \wp }{\overline{w}}_{\mu -1}(\wp ,t;\sigma )+\frac{1}{\wp }{\mathcal{L}}_{\wp }{\overline{w}}_{\mu -1}(\wp ,t;\sigma )\right)\right]\hfill \\ \hfill & ={(1.5-0.5\sigma )}^n\left[\frac{1^2\times 3^2\times \cdots \times {(2n-3)}^2}{{\wp }^{2n-1}}\frac{t^{\mu \Im }}{\Gamma (\mu \Im +1)}\right].\hfill \end{array}\right.\end{array}$$

(74)

Hence, the solution as

$$\begin{array}{c}\hfill \underline{w}(\wp ,t;\sigma )={(1.5\sigma -0.5)}^n\left[\wp +\sum _{\mu =1}^{\infty }\frac{1^2\times 3^2\times \cdots \times {(2\mu -3)}^2}{{\wp }^{2\mu -1}}\frac{t^{\mu \Im }}{\Gamma (\mu \Im +1)}\right],\\ \hfill \overline{w}(\wp ,t;\sigma )={(1.5-0.5\sigma )}^n\left[\wp +\sum _{\mu =1}^{\infty }\frac{1^2\times 3^2\times \cdots \times {(2\mu -3)}^2}{{\wp }^{2\mu -1}}\frac{t^{\mu \Im }}{\Gamma (\mu \Im +1)}\right],\end{array}$$

when $\Im =1$, so

$$\begin{array}{c}\hfill \tilde{w}(\wp ,t;\sigma )=[{(1.5\sigma -0.5)}^n,{(1.5-0.5\sigma )}^n]\odot \left(\wp +\sum _{\mu =1}^{\infty }\frac{1^2\times 3^2\times \cdots \times {(2\mu -3)}^2}{{\wp }^{2\mu -1}}\frac{t^{\mu }}{\mu !}\right),0\le \sigma \le 1.\end{array}$$

Case [B]. Fuzzy modified Laplace decomposition method

Using the same approach as in the preceding example, we obtain

$$\begin{array}{cc}\hfill \sum _{\mu =0}^{\infty }{\underline{w}}_{\mu }(\wp ,t;\sigma )& ={(1.5\sigma -0.5)}^n\wp \hfill \\ \hfill & +{\mathcal{L}}^{-1}\left(s^{-\Im }\mathcal{L}\left[{\left(\sum _{\mu =0}^{\infty }{\underline{w}}_{\mu }(\wp ,t;\sigma )\right)}_{\wp \wp }+\frac{1}{\wp }{\left(\sum _{\mu =0}^{\infty }{\underline{w}}_{\mu }(\wp ,t;\sigma )\right)}_{\wp }\right]\right),\hfill \end{array}$$

(75)

$$\begin{array}{cc}\hfill \sum _{\mu =0}^{\infty }{\overline{w}}_{\mu }(\wp ,t;\sigma )& ={(1.5-0.5\sigma )}^n\wp \hfill \\ \hfill & +{\mathcal{L}}^{-1}\left(s^{-\Im }\mathcal{L}\left[{\left(\sum _{\mu =0}^{\infty }{\overline{w}}_{\mu }(\wp ,t;\sigma )\right)}_{\wp \wp }+\frac{1}{\wp }{\left(\sum _{\mu =0}^{\infty }{\overline{w}}_{\mu }(\wp ,t;\sigma )\right)}_{\wp }\right]\right),\hfill \end{array}$$

(76)

the decomposition series’ starting terms are obtained from

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{w}}_0(\wp ,t;\sigma )& ={(1.5\sigma -0.5)}^n\wp ,\hfill \\ \hfill {\underline{w}}_1(\wp ,t;\sigma )& ={\mathcal{L}}^{-1}\left(s^{-\Im }\mathcal{L}\left[{\underline{w}}_{0\wp \wp }(\wp ,t;\sigma )+\frac{1}{\wp }{\underline{w}}_{0\wp }(\wp ,t;\sigma )\right]\right)\hfill \\ \hfill & ={(1.5\sigma -0.5)}^n\left[\frac{1}{\wp }\frac{t^{\Im }}{\Gamma (\Im +1)}\right],\hfill \\ \hfill {\underline{w}}_2(\wp ,t;\sigma )& ={\mathcal{L}}^{-1}\left(s^{-\Im }\mathcal{L}\left[{\underline{w}}_{1\wp \wp }(\wp ,t;\sigma )+\frac{1}{\wp }{\underline{w}}_{1\wp }(\wp ,t;\sigma )\right]\right)\hfill \\ \hfill & ={(1.5\sigma -0.5)}^n\left[\frac{1^2}{{\wp }^3}\frac{t^{2\Im }}{\Gamma (2\Im +1)}\right],\hfill \\ \hfill ⋮\\ \hfill {\underline{w}}_{\mu }(\wp ,t;\sigma )& ={\mathcal{L}}^{-1}\left(s^{-\Im }\mathcal{L}\left[{\underline{w}}_{(\mu -1)\wp \wp }(\wp ,t;\sigma )+\frac{1}{\wp }{\underline{w}}_{(\mu -1)\wp }(\wp ,t;\sigma )\right]\right),\hfill \\ \hfill & ={(1.5\sigma -0.5)}^n\left[\frac{1^2\times 3^2\times \cdots \times {(2\mu -3)}^2}{{\wp }^{2\mu -1}}\frac{t^{\mu \Im }}{\Gamma (\mu \Im +1)}\right],\hfill \end{array}\right.\end{array}$$

(77)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\overline{w}}_0(\wp ,t;\sigma )& ={(1.5-0.5\sigma )}^n\wp ,\hfill \\ \hfill {\overline{w}}_1(\wp ,t;\sigma )& ={\mathcal{L}}^{-1}\left(s^{-\Im }\mathcal{L}\left[{\overline{w}}_{0\wp \wp }(\wp ,t;\sigma )+\frac{1}{\wp }{\overline{w}}_{0\wp }(\wp ,t;\sigma )\right]\right)\hfill \\ \hfill & ={(1.5-0.5\sigma )}^n\left[\frac{1}{\wp }\frac{t^{\Im }}{\Gamma (\Im +1)}\right],\hfill \\ \hfill {\overline{w}}_2(\wp ,t;\sigma )& ={\mathcal{L}}^{-1}\left(s^{-\Im }\mathcal{L}\left[{\overline{w}}_{1\wp \wp }(\wp ,t;\sigma )+\frac{1}{\wp }{\overline{w}}_{1\wp }(\wp ,t;\sigma )\right]\right)\hfill \\ \hfill & ={(1.5-0.5\sigma )}^n\left[\frac{1^2}{{\wp }^3}\frac{t^{2\Im }}{\Gamma (2\Im +1)}\right],\hfill \\ \hfill ⋮\\ \hfill {\overline{w}}_{\mu }(\wp ,t;\sigma )& ={\mathcal{L}}^{-1}\left(s^{-\Im }\mathcal{L}\left[{\overline{w}}_{(\mu -1)\wp \wp }(\wp ,t;\sigma )+\frac{1}{\wp }{\overline{w}}_{(\mu -1)\wp }(\wp ,t;\sigma )\right]\right)\hfill \\ \hfill & ={(1.5-0.5\sigma )}^n\left[\frac{1^2\times 3^2\times \cdots \times {(2\mu -3)}^2}{{\wp }^{2\mu -1}}\frac{t^{\mu \Im }}{\Gamma (\mu \Im +1)}\right].\hfill \end{array}\right.\end{array}$$

(78)

Thus, the solution of the standard fuzzy Navier–Stokes equation, when $\Im =1$ as:

$$\begin{array}{c}\hfill \tilde{w}(\wp ,t;\sigma )=[{(1.5\sigma -0.5)}^n,{(1.5-0.5\sigma )}^n]\odot \left(\wp +\sum _{\mu =1}^{\infty }\frac{1^2\times 3^2\times \cdots \times {(2\mu -3)}^2}{{\wp }^{2\mu -1}}\frac{t^{\mu }}{\mu !}\right),0\le \sigma \le 1.\end{array}$$

4. Fuzzy Linear and Nonlinear Schrodinger Equations

In this section, we propose some theorems of fuzzy Elzaki transform and fuzzy EDM for solving linear-nonlinear Schrodinger differential equations.

• Consider the following fuzzy linear Schrodinger equation:

  $$\begin{array}{c}\hfill i{\tilde{w}}_t(\psi ;t)\oplus {\tilde{w}}_{\psi \psi }(\psi ;t)=\tilde{0},\end{array}$$

  (79)

  with the initial condition

  $$\begin{array}{c}\hfill \tilde{w}(\psi ;0)=f(\psi ),i=\sqrt{-1}.\end{array}$$

  (80)
• Consider the fuzzy nonlinear Schrodinger equation as:

  $$\begin{array}{c}\hfill i{\tilde{w}}_t(\psi ;t)\oplus {\tilde{w}}_{\psi \psi }(\psi ;t)\oplus \zeta {\left|\tilde{w}(\psi ;t)\right|}^{2\wp }\tilde{w}(\psi ;t)=\tilde{0},\wp \ge 1,\end{array}$$

  (81)

  with the initial condition

  $$\begin{array}{c}\hfill \tilde{w}(\psi ;0)=\tilde{f}(\psi ),\end{array}$$

  (82)

  and

  $$\begin{array}{c}\hfill i{\tilde{w}}_t(\psi ;t)\oplus {\tilde{w}}_{\psi \psi }(\psi ;t)\oplus \zeta {\left|\tilde{w}(\psi ;t)\right|}^2\tilde{w}(\psi ;t)=\tilde{0},\end{array}$$

  (83)

  with the initial condition

  $$\begin{array}{c}\hfill \tilde{w}(\psi ;0)=\tilde{f}(\psi ),\end{array}$$

  (84)

where $\zeta$ is a constant and $\tilde{w}(\psi ;t)$ is a complex fuzzy-valued function. Equation (79) discusses the time evolution of a free particle.

4.1. Elzaki Transform

We present the fuzzy Elzaki transform of the fuzzy-valued functions belonging to a class $\mathcal{A}$, where $\mathcal{A}=\left\{\tilde{w}\left(t\right):\exists M,{\ell }_1,{\ell }_2>0sothat\left|u\left(t\right)\right|<M{e}^{\mid t\mid /{\ell }_j},ift\in {(-1)}^j\times [0,\infty )\right\}$, where $\tilde{w}\left(t\right)$ is denoted by $\mathfrak{E}\left[\tilde{w}\left(t\right)\right]=W(\tau )$ and defined by the setting:

$$\begin{array}{c}\hfill \mathfrak{E}\left[\tilde{w}\left(t\right)\right]=\tau \odot {\int }_0^{\infty }\tilde{w}\left(t\right)\odot e^{-\frac{t}{\tau }}dt=W(\tau ),\tau \in ({\ell }_1,{\ell }_2).\end{array}$$

(85)

Here are some Elzaki transform properties:

• $\mathfrak{E}\left\{t^n\right\}=n!{\tau }^{n+2},n\ge 0,$
• $\mathfrak{E}\left\{e^{-at}\right\}=\frac{{\tau }^2}{1+a\tau },$
• $\mathfrak{E}\left\{sinat\right\}=\frac{a{\tau }^3}{1+a^2{\tau }^2},$
• $\mathfrak{E}\{w\left(t\right\}=\frac{W(\tau )}{\tau }{\ominus }_{gH}\tau w\left(0\right),$
• $\mathfrak{E}\left\{w^n\left(t\right)\right\}=\frac{W(\tau )}{{\tau }^n}{\ominus }_{gH}{\sum }_{\ell =0}^{n-1}{\tau }^{2-n+\ell }{w}^{\ell }\left(0\right).$

4.2. Fuzzy Elzaki Adomian Decomposition Method

The nonlinear Schrodinger differential equation is represented by the fuzzy complex valued function $\tilde{w}(\psi ,t;\sigma )=[\underline{w}(\psi ,t;\sigma ),\overline{w}(\psi ,t;\sigma )]$ of the form

$$\begin{array}{c}\hfill i{\tilde{w}}_t(\psi ;t)\oplus {\tilde{w}}_{\psi \psi }(\psi ;t)\oplus \zeta {\left|\tilde{w}(\psi ;t)\right|}^{2\wp }\tilde{w}(\psi ;t)=\tilde{0},\wp \ge 1,i=\sqrt{-1},\end{array}$$

(86)

with the initial condition

$$\begin{array}{c}\hfill \tilde{w}(\psi ;0)=\tilde{f}(\psi ),\end{array}$$

(87)

and boundary condition

$$\begin{array}{c}\hfill \tilde{w}(0,t)=\tilde{g}(\psi ),{\tilde{w}}_{\psi }(0,t)=\tilde{h}(\psi ).\end{array}$$

(88)

When $\zeta =0$ in (86), we obtain

$$\begin{array}{cc}\hfill i{\underline{w}}_t(\psi ,t;\sigma )+{\underline{w}}_{\psi \psi }(\psi ,t;\sigma )& =\tilde{0},\hfill \end{array}$$

(89)

$$\begin{array}{cc}\hfill i{\overline{w}}_t(\psi ,t;\sigma )+{\overline{w}}_{\psi \psi }(\psi ,t;\sigma )& =\tilde{0}.\hfill \end{array}$$

(90)

The more general Schrodinger Equation (86), we can define as

$$\begin{array}{cc}\hfill {\underline{w}}_t(\psi ,t;\sigma )& =i{\underline{w}}_{\psi \psi }(\psi ,t;\sigma )+i\zeta {\left|\underline{w}(\psi ,t;\sigma )\right|}^{2\wp }\underline{w}(\psi ,t;\sigma ),\hfill \end{array}$$

(91)

$$\begin{array}{cc}\hfill {\overline{w}}_t(\psi ,t;\sigma )& =i{\overline{w}}_{\psi \psi }(\psi ,t;\sigma )+i\zeta {\left|\overline{w}(\psi ,t;\sigma )\right|}^{2\wp }\overline{w}(\psi ,t;\sigma ).\hfill \end{array}$$

(92)

Hence, for both sides of (91) and (92), we apply the fuzzy Elzaki transform given in (85):

$$\begin{array}{cc}\hfill \mathfrak{E}\left[{\underline{w}}_t(\psi ,t;\sigma )\right]& =\mathfrak{E}\left[i{\underline{w}}_{\psi \psi }(\psi ,t;\sigma )\right]+\mathfrak{E}\left[i\zeta |\underline{w}{(\psi ,t;\sigma )|}^{2\wp }\underline{w}(\psi ,t;\sigma )\right],\hfill \end{array}$$

(93)

$$\begin{array}{cc}\hfill \mathfrak{E}\left[{\overline{w}}_t(\psi ,t;\sigma )\right]& =\mathfrak{E}\left[i{\overline{w}}_{\psi \psi }(\psi ,t;\sigma )\right]+\mathfrak{E}\left[i\zeta |\overline{w}{(\psi ,t;\sigma )|}^{2\wp }\overline{w}(\psi ,t;\sigma )\right].\hfill \end{array}$$

(94)

We obtain by combining the differentiation property of the fuzzy Elzaki transform with the initial condition

$$\begin{array}{cc}\hfill & \frac{1}{\tau }\mathfrak{E}\left[\underline{w}(\psi ,t;\sigma )\right]-\tau \underline{f}(\psi ;\sigma )=i\mathfrak{E}\left[{\underline{w}}_{\psi \psi }(\psi ,t;\sigma )\right]+i\zeta \mathfrak{E}\left[|\underline{w}{(\psi ,t;\sigma )|}^{2\wp }\underline{w}(\psi ,t;\sigma )\right],\hfill \end{array}$$

(95)

$$\begin{array}{cc}\hfill & \mathfrak{E}\left[\underline{w}(\psi ,t;\sigma )\right]={\tau }^2\underline{f}(\psi ;\sigma )+i\tau \mathfrak{E}\left[{\underline{w}}_{\psi \psi }(\psi ,t;\sigma )\right]+i\zeta \tau \mathfrak{E}\left[|\underline{w}{(\psi ,t;\sigma )|}^{2\wp }\underline{w}(\psi ,t;\sigma )\right],\hfill \end{array}$$

(96)

and

$$\begin{array}{cc}\hfill & \frac{1}{\tau }\mathfrak{E}\left[\overline{w}(\psi ,t;\sigma )\right]-\tau \overline{f}(\psi ;\sigma )=i\mathfrak{E}\left[{\overline{w}}_{\psi \psi }(\psi ,t;\sigma )\right]+i\zeta \mathfrak{E}\left[|\overline{w}{(\psi ,t;\sigma )|}^{2\wp }\overline{w}(\psi ,t;\sigma )\right],\hfill \end{array}$$

(97)

$$\begin{array}{cc}\hfill & \mathfrak{E}\left[\overline{w}(\psi ,t;\sigma )\right]={\tau }^2\overline{f}(\psi ;\sigma )+i\tau \mathfrak{E}\left[{\overline{w}}_{\psi \psi }(\psi ,t;\sigma )\right]+i\zeta \tau \mathfrak{E}\left[|\overline{w}{(\psi ,t;\sigma )|}^{2\wp }\overline{w}(\psi ,t;\sigma )\right].\hfill \end{array}$$

(98)

The following step is to substitute an infinite series for the arbitrary fuzzy-valued function $\tilde{w}(\psi ,t;\sigma )$.

$$\begin{array}{cc}\hfill \underline{w}(\psi ,t;\sigma )& =\sum _{\mu =0}^{\infty }{\underline{w}}_{\mu }(\psi ,t;\sigma ),\hfill \end{array}$$

(99)

$$\begin{array}{cc}\hfill \overline{w}(\psi ,t;\sigma )& =\sum _{\mu =0}^{\infty }{\overline{w}}_{\mu }(\psi ,t;\sigma ),\hfill \end{array}$$

(100)

and substitute $\mathcal{N}\tilde{w}(\psi ,t;\sigma )={\left|\tilde{w}(\psi ,t;\sigma )\right|}^{2\wp }\tilde{w}(\psi ,t;\sigma )$ by the series

$$\begin{array}{cc}\hfill \mathcal{N}\underline{w}(\psi ,t;\sigma )& =\sum _{\mu =0}^{\infty }{\underline{A}}_{\mu }({\underline{w}}_0,{\underline{w}}_1,{\underline{w}}_3,\cdots )(\sigma ),\hfill \end{array}$$

(101)

$$\begin{array}{cc}\hfill \mathcal{N}\overline{w}(\psi ,t;\sigma )& =\sum _{\mu =0}^{\infty }{\overline{A}}_{\mu }({\overline{w}}_0,{\overline{w}}_1,{\overline{w}}_3,\cdots )(\sigma ).\hfill \end{array}$$

(102)

The Adomian polynomials ${\tilde{\mathcal{A}}}_{\mu }{({\tilde{w}}_0,{\tilde{w}}_1,{\tilde{w}}_2,\cdots )}^{\prime }$ are determined by the following formula:

$$\begin{array}{cc}\hfill {\underline{\mathcal{A}}}_{\mu }(\sigma )& =\frac{1}{n!}\frac{d^n}{d{\zeta }^n}{\left[\mathcal{N}\left(\sum _{i=0}^n{\zeta }^i{\underline{w}}_i(\psi ,t;\sigma )\right)\right]}_{\zeta =0},n=0,1,2,\cdots ,\hfill \end{array}$$

(103)

$$\begin{array}{cc}\hfill {\overline{\mathcal{A}}}_{\mu }(\sigma )& =\frac{1}{n!}\frac{d^n}{d{\zeta }^n}{\left[\mathcal{N}\left(\sum _{i=0}^n{\zeta }^i{\overline{w}}_i(\psi ,t;\sigma )\right)\right]}_{\zeta =0},n=0,1,2,\cdots .\hfill \end{array}$$

(104)

Substituting (104) into (99), we obtain

$$\begin{array}{cc}\hfill \mathfrak{E}\left[\sum _{\mu =0}^{\infty }{\underline{w}}_{\mu }(\psi ,t;\sigma )\right]& ={\tau }^2\underline{f}(\psi ;\sigma )+i\tau \mathfrak{E}\left[\sum _{\mu =0}^{\infty }{\underline{w}}_{{\mu }_{\psi \psi }}(\psi ,t;\sigma )\right]+i\zeta \tau \mathfrak{E}\left[\sum _{\mu =0}^{\infty }{\underline{\mathcal{A}}}_{\mu }(\sigma )\right],\hfill \end{array}$$

(105)

$$\begin{array}{cc}\hfill \mathfrak{E}\left[\sum _{\mu =0}^{\infty }{\overline{w}}_{\mu }(\psi ,t;\sigma )\right]& ={\tau }^2\overline{f}(\psi ;\sigma )+i\tau \mathfrak{E}\left[\sum _{\mu =0}^{\infty }{\overline{w}}_{{\mu }_{\psi \psi }}(\psi ,t;\sigma )\right]+i\zeta \tau \mathfrak{E}\left[\sum _{\mu =0}^{\infty }{\overline{\mathcal{A}}}_{\mu }(\sigma )\right],\hfill \end{array}$$

(106)

we obtain

$$\begin{array}{cc}\hfill \sum _{\mu =0}^{\infty }\mathfrak{E}\left[{\underline{w}}_{\mu }(\psi ,t;\sigma )\right]& ={\tau }^2\underline{f}(\psi ;\sigma )+i\tau \mathfrak{E}\left[\sum _{\mu =0}^{\infty }{\underline{w}}_{{\mu }_{\psi \psi }}(\psi ,t;\sigma )\right]+i\zeta \tau \mathfrak{E}\left[\sum _{\mu =0}^{\infty }{\underline{\mathcal{A}}}_{\mu }(\sigma )\right],\hfill \end{array}$$

(107)

$$\begin{array}{cc}\hfill \sum _{\mu =0}^{\infty }\mathfrak{E}\left[{\overline{w}}_{\mu }(\psi ,t;\sigma )\right]& ={\tau }^2\overline{f}(\psi ;\sigma )+i\tau \mathfrak{E}\left[\sum _{\mu =0}^{\infty }{\overline{w}}_{{\mu }_{\psi \psi }}(\psi ,t;\sigma )\right]+i\zeta \tau \mathfrak{E}\left[\sum _{\mu =0}^{\infty }{\overline{\mathcal{A}}}_{\mu }(\sigma )\right].\hfill \end{array}$$

(108)

Applying the general solution of (86), we compare both sides of (107) and (108) and take the inverse Elzaki transform

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{w}}_0(\psi ,t;\sigma )& =\underline{f}(\psi ;\sigma ),\hfill \\ \hfill {\underline{w}}_1(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{w}}_{0_{\psi \psi }}(\psi ,t;\sigma )\right]\right]+i\zeta {\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{\mathcal{A}}}_0(\sigma )\right]\right],\hfill \\ \hfill {\underline{w}}_2(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{w}}_{1_{\psi \psi }}(\psi ,t;\sigma )\right]\right]+i\zeta {\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{\mathcal{A}}}_1(\sigma )\right]\right],\hfill \\ \hfill {\underline{w}}_3(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{w}}_{2_{\psi \psi }}(\psi ,t;\sigma )\right]\right]+i\zeta {\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{\mathcal{A}}}_2(\sigma )\right]\right],\hfill \\ \hfill ⋮\\ \hfill {\underline{w}}_n(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{w}}_{n_{\psi \psi }}(\psi ,t;\sigma )\right]\right]+i\zeta {\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{\mathcal{A}}}_n(\sigma )\right]\right],n\ge 0,\hfill \end{array}\right.\end{array}$$

(109)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\overline{w}}_0(\psi ,t;\sigma )& =\overline{f}(\psi ;\sigma ),\hfill \\ \hfill {\overline{w}}_1(\psi ,t;\sigma )& ={\mathfrak{iE}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{w}}_{0_{\psi \psi }}(\psi ,t;\sigma )\right]\right]+i\zeta {\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{\mathcal{A}}}_0(\sigma )\right]\right],\hfill \\ \hfill {\overline{w}}_2(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{w}}_{1_{\psi \psi }}(\psi ,t;\sigma )\right]\right]+i\zeta {\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}{\overline{[\mathcal{A}}}_1(\sigma )]\right],\hfill \\ \hfill {\overline{w}}_3(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{w}}_{2_{\psi \psi }}(\psi ,t;\sigma )\right]\right]+i\zeta {\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}{\overline{[\mathcal{A}}}_2(\sigma )]\right],\hfill \\ \hfill ⋮\\ \hfill {\overline{w}}_n(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{w}}_{n_{\psi \psi }}(\psi ,t;\sigma )\right]\right]+i\zeta {\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{\mathcal{A}}}_n(\sigma )\right]\right],n\ge 0,\hfill \end{array}\right.\end{array}$$

(110)

where $\tilde{f}(\psi ;\sigma )=[\underline{f}(\psi ;\sigma ),\overline{f}(\psi ;\sigma )]$ is the prescribed initial condition, and ${\tilde{\mathcal{A}}}_n(\sigma )=[{\underline{\mathcal{A}}}_n(\sigma ),$

${\overline{\mathcal{A}}}_n(\sigma )]$ are the Adomian polynomials. The solution is

$$\begin{array}{c}\hfill \tilde{w}(\psi ,t,\sigma )=\sum _{n=0}^{\infty }{\tilde{w}}_n(\psi ,t,\sigma ).\end{array}$$

(111)

4.3. Convergence Analysis

We consider the following fuzzy convergence analysis of fuzzy EADM for the general fuzzy nonlinear partial differential equations given by

$$\begin{array}{c}\hfill \mathcal{L}\tilde{w}(\psi ,t)+\mathcal{R}\tilde{w}(\psi ,t)+\mathcal{N}\tilde{w}(\psi ,t)=\tilde{g}(\psi ,t).\end{array}$$

(112)

The 2nd order operator is shown by $\mathcal{L}=\frac{{\partial }^2}{\partial t}$, the linear operator of order less than $\mathcal{L}$ is denoted by $\mathcal{R}$, the nonlinear operator is $\mathcal{N}$, and the source term is denoted by $\tilde{g}(\psi ,t).$

Theorem 5.

Assume $\mathcal{N}:\mathcal{H}\to \mathcal{H}$ a nonlinear operator. $\mathcal{H}$ denotes Hilbert space and suppose $\tilde{w}(\psi ,t,\sigma ),$ an exact solution to (112). ${\sum }_{i=0}^{\infty }{\tilde{w}}_i(\psi ,t;\sigma ),$ which is obtained by Equation (111) converges to $\tilde{w}(\psi ,t;\sigma ),$ if $\exists \gamma ,0\le \gamma <1,$ such that

$$\begin{array}{c}\hfill \parallel {\tilde{w}}_{\ell +1}(\psi ,t;\sigma )\parallel \le \gamma \parallel {\tilde{w}}_{\ell }(\psi ,t;\sigma )\parallel ,\mathrm{for}\mathrm{all}\ell \in \mathcal{N}\cup \left\{0\right\}.\end{array}$$

Proof. 

Define the sequence ${\left\{{\tilde{S}}_n(\psi ,t;\sigma )\right\}}_{n=0}^{\infty }$, where $\sigma \in [0,1],$ we have

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\tilde{S}}_0(\psi ,t;\sigma )& =0,\hfill \\ \hfill {\tilde{S}}_1(\psi ,t;\sigma )& ={\tilde{w}}_1(\psi ,t;\sigma ),\hfill \\ \hfill {\tilde{S}}_2(\psi ,t;\sigma )& ={\tilde{w}}_1(\psi ,t;\sigma )+{\tilde{w}}_2(\psi ,t;\sigma ),\hfill \\ \hfill & ⋮\hfill \\ \hfill {\tilde{S}}_n(\psi ,t;\sigma )& ={\tilde{w}}_1(\psi ,t;\sigma )+{\tilde{w}}_2(\psi ,t;\sigma )+\cdots +{\tilde{w}}_n(\psi ,t;\sigma ),\hfill \end{array}\right.\end{array}$$

(113)

and we prove that ${\left\{{\tilde{S}}_n(\psi ,t;\sigma )\right\}}_{n=0}^{\infty }$ is the Cauchy sequence in the Hilbert space, then

$$\begin{array}{c}\hfill ∥{\tilde{S}}_{n+1}(\psi ,t;\sigma )-{\tilde{S}}_n(\psi ,t;\sigma )∥=\parallel {\tilde{w}}_{n+1}(\psi ,t;\sigma )\parallel \le \gamma \parallel {\tilde{w}}_n(\psi ,t;\sigma )\parallel \le {\gamma }^2\parallel {\tilde{w}}_{n-1}(\psi ,t;\sigma )\parallel \le \cdots \le {\gamma }^{n+1}\parallel {\tilde{w}}_0(\psi ,t;\sigma )\parallel .\end{array}$$

On the other hand, for $\forall n,\mu \in \mathcal{N},n\ge \mu ,$ we obtain

$$\begin{array}{cc}\hfill ∥{\tilde{S}}_n(\psi ,t;\sigma )-{\tilde{S}}_{\mu }(\psi ,t;\sigma )∥& =∥\left({\tilde{S}}_n(\psi ,t;\sigma )-{\tilde{S}}_{n-1}(\psi ,t;\sigma )\right)+\left({\tilde{S}}_{n-1}(\psi ,t;\sigma )-{\tilde{S}}_{n-2}(\psi ,t;\sigma )\right)\hfill \\ \hfill & +\cdots +\left({\tilde{S}}_{\mu +1}(\psi ,t;\sigma )-{\tilde{S}}_{\mu }(\psi ,t;\sigma )\right)∥\hfill \\ \hfill & \le ∥\left({\tilde{S}}_n(\psi ,t;\sigma )-{\tilde{S}}_{n-1}(\psi ,t;\sigma )\right)+\left({\tilde{S}}_{n-1}(\psi ,t;\sigma )-{\tilde{S}}_{n-2}(\psi ,t;\sigma )\right)\hfill \\ \hfill & +\cdots +\left({\tilde{S}}_{\mu +1}(\psi ,t;\sigma )-{\tilde{S}}_{\mu }(\psi ,t;\sigma )\right)∥\hfill \\ \hfill & \le {\gamma }^n\parallel {\tilde{w}}_0(\psi ,t;\sigma )\parallel +{\gamma }^{n-1}{\tilde{w}}_0(\psi ,t;\sigma )+\cdots +{\gamma }^{\mu +1}\parallel {\tilde{w}}_0(\psi ,t;\sigma )\parallel \hfill \\ \hfill & \le \left({\gamma }^{\mu +1}+{\gamma }^{\mu +2}+\cdots +{\gamma }^{\mu +m}\right)\parallel {\tilde{w}}_0(\psi ,t;\sigma )\parallel \hfill \\ \hfill & =\frac{{\gamma }^{\mu +1}}{1-\gamma }\parallel {\tilde{w}}_0(\psi ,t;\sigma )\parallel .\hfill \end{array}$$

Hence,

$$\begin{array}{c}\hfill \underset{n,m\to \infty }{lim}∥{\tilde{S}}_n(\psi ,t;\sigma )-{\tilde{S}}_{\mu }(\psi ,t;\sigma )∥=0,0\le \sigma \le 1,\end{array}$$

and i.e., ${\left\{{\tilde{S}}_n(\psi ,t;\sigma )\right\}}_{n=0}^{\infty }$ is a Cauchy sequence in a Hilbert space, for $S\in \mathcal{H}$, the proof complies. □

Corollary 1.

${\sum }_{n=0}^{\infty }{\tilde{w}}_n(\psi ,t;\sigma )$ converges to the exact solution $\tilde{w}(\psi ,t;\sigma )$, if $0⩽{\gamma }_n<1,n=$$1,2,3\dots$

4.4. Examples

In this part, we investigate the fuzzy EDM for solving the fuzzy linear-nonlinear Schrodinger differential equation.

4.4.1. The Fuzzy Linear Schrodinger Equation

Here are two examples of the fuzzy linear Schrodinger differential equation.

Example 3.

We take into account the fuzzy linear Schrodinger differential equation with $\zeta =0$

$$\begin{array}{c}\hfill i{\tilde{w}}_t(\psi ,t)\oplus {\tilde{w}}_{\psi \psi }(\psi ,t)=\tilde{0},\end{array}$$

(114)

with the initial condition

$$\begin{array}{c}\hfill \tilde{w}(\psi ;0)=[{(0.4+0.1\sigma )}^n,{(0.6-0.1\sigma )}^n]\odot \rho exp(i\ell \psi ),\end{array}$$

(115)

where $\rho ,\ell$ are constants, for $(n=1,2,3,\dots ).$

Taking the fuzzy Elzaki transform to (114), we obtain

$$\begin{array}{cc}\hfill \frac{1}{\tau }\mathfrak{E}\left[\underline{w}(\psi ,t;\sigma )\right]-\tau \underline{w}(\psi ,0)(\sigma )& =i\mathfrak{E}\left[{\underline{w}}_{\psi \psi }(\psi ,t;\sigma )\right],\hfill \end{array}$$

(116)

$$\begin{array}{cc}\hfill \frac{1}{\tau }\mathfrak{E}\left[\overline{w}(\psi ,t;\sigma )\right]-\tau \overline{w}(\psi ,0)(\sigma )& =i\mathfrak{E}\left[{\overline{w}}_{\psi \psi }(\psi ,t;\sigma )\right],\hfill \end{array}$$

(117)

and

$$\begin{array}{cc}\hfill \mathfrak{E}\left[\underline{w}(\psi ,t;\sigma )\right]& ={\tau }^2\underline{w}(\psi ,0)(\sigma )+i\tau \mathfrak{E}\left[{\underline{w}}_{\psi \psi }(\psi ,t;\sigma )\right],\hfill \end{array}$$

(118)

$$\begin{array}{cc}\hfill \mathfrak{E}\left[\overline{w}(\psi ,t;\sigma )\right]& ={\tau }^2\overline{w}(\psi ,0)(\sigma )+i\tau \mathfrak{E}\left[{\overline{w}}_{\psi \psi }(\psi ,t;\sigma )\right].\hfill \end{array}$$

(119)

From the initial condition (115), we obtain

$$\begin{array}{cc}\hfill \mathfrak{E}\left[\underline{w}(\psi ,t;\sigma )\right]& ={(0.4+0.1\sigma )}^n{\tau }^2\rho exp(i\ell \psi )+i\tau \mathfrak{E}\left[{\underline{w}}_{\psi \psi }(\psi ,t;\sigma )\right],\hfill \end{array}$$

(120)

$$\begin{array}{cc}\hfill \mathfrak{E}\left[\overline{w}(\psi ,t;\sigma )\right]& ={(0.6-0.1\sigma )}^n{\tau }^2\rho exp(i\ell \psi )+i\tau \mathfrak{E}\left[{\overline{w}}_{\psi \psi }(\psi ,t;\sigma )\right].\hfill \end{array}$$

(121)

According to the inverse Elzaki transform (120) and (121), we obtain

$$\begin{array}{cc}\hfill \underline{w}(\psi ,t;\sigma )& ={(0.4+0.1\sigma )}^n\rho exp(i\ell \psi )+{\mathfrak{E}}^{-1}\left[i\tau \mathfrak{E}\left[{\underline{w}}_{\psi \psi }(\psi ,t;\sigma )\right]\right],\hfill \end{array}$$

(122)

$$\begin{array}{cc}\hfill \overline{w}(\psi ,t;\sigma )& ={(0.6-0.1\sigma )}^n\rho exp(i\ell \psi )+{\mathfrak{E}}^{-1}\left[i\tau \mathfrak{E}\left[{\overline{w}}_{\psi \psi }(\psi ,t;\sigma )\right]\right].\hfill \end{array}$$

(123)

Adopting the infinite series solution of the unknown fuzzy-valued function $\tilde{w}(\psi ,t;\sigma )$ and comparing both sides of (122) and (123) in the manner indicated above, we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\underline{w}}_0(\psi ,t;\sigma )={(0.4+0.1\sigma )}^n\rho exp(i\ell \psi )\hfill \\ {\underline{w}}_{n+1}(\psi ,t;\sigma )=i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{w}}_{n_{\psi \psi }}(\psi ,t;\sigma )\right]\right],n\ge 0,\hfill \end{array}\right.\end{array}$$

(124)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\overline{w}}_0(\psi ,t;\sigma )={(0.6-0.1\sigma )}^n\rho exp(i\ell \psi )\hfill \\ {\overline{w}}_{n+1}(\psi ,t;\sigma )=i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{w}}_{n_{\psi \psi }}(\psi ,t;\sigma )\right]\right],n\ge 0,\hfill \end{array}\right.\end{array}$$

(125)

$\tilde{w}(\psi ,t;\sigma )$ components are provided by

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{w}}_0(\psi ,t;\sigma )& ={(0.4+0.1\sigma )}^n\rho exp(i\ell \psi ),\hfill \\ \hfill {\underline{w}}_1(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{w}}_{0_{\psi \psi }}(\psi ,t;\sigma )\right]\right],\hfill \\ \hfill & =i{\mathfrak{E}}^{-1}\left[-{(0.4+0.1\sigma )}^n\mu {\ell }^2{\tau }^{3}exp(i\ell \psi )\right]\hfill \\ \hfill & =-{(0.4+0.1\sigma )}^n\mu i{\ell }^{2}texp(i\ell \psi ),\hfill \\ \hfill {\underline{w}}_2(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{w}}_{1_{\psi \psi }}(\psi ,t;\sigma )\right]\right],\hfill \\ \hfill & =i{\mathfrak{E}}^{-1}\left[-{(0.4+0.1\sigma )}^n\rho {\ell }^4{\tau }^{4}exp(i\ell \psi )\right]\hfill \\ \hfill & ={(0.4+0.1\sigma )}^n\frac{-\rho {\ell }^4{t}^{2}exp(i\ell \psi )}{2!},\hfill \\ \hfill ⋮\\ \hfill {\underline{w}}_{n+1}(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{w}}_{n_{\psi \psi }}(\psi ,t;\sigma )\right]\right],\hfill \\ \hfill & =i{\mathfrak{E}}^{-1}\left[-{(0.4+0.1\sigma )}^n\rho {\ell }^{n+2}{\tau }^{n+1}exp(i\ell \psi )\right]\hfill \\ \hfill & ={(0.4+0.1\sigma )}^n\frac{-\rho {\ell }^{n+2}{t}^{n+1}exp(i\ell \psi )}{n!},\hfill \end{array}\right.\end{array}$$

(126)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\overline{w}}_0(\psi ,t;\sigma )& ={(0.6-0.1\sigma )}^n\rho exp(i\ell \psi ),\hfill \\ \hfill {\overline{w}}_1(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{w}}_{0_{\psi \psi }}(\psi ,t;\sigma )\right]\right],\hfill \\ \hfill & =i{\mathfrak{E}}^{-1}\left[-{(0.6-0.1\sigma )}^n\mu {\ell }^2{\tau }^{3}exp(i\ell \psi )\right]\hfill \\ \hfill & =-{(0.6-0.1\sigma )}^n\rho i{\ell }^{2}texp(i\ell \psi ),\hfill \\ \hfill {\overline{w}}_2(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{w}}_{1_{\psi \psi }}(\psi ,t;\sigma )\right]\right],\hfill \\ \hfill & =i{\mathfrak{E}}^{-1}\left[-{(0.6-0.1\sigma )}^n\mu {\ell }^4{\tau }^{4}exp(i\ell \psi )\right]\hfill \\ \hfill & =\frac{-{(0.6-0.1\sigma )}^n\mu {\ell }^4{t}^{2}exp(i\ell \psi )}{2!},\hfill \\ \hfill ⋮\\ \hfill {\overline{w}}_{n+1}(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{w}}_{n_{\psi \psi }}(\psi ,t;\sigma )\right]\right],\hfill \\ \hfill & =i{\mathfrak{E}}^{-1}\left[-{(0.6-0.1\sigma )}^n\mu {\ell }^{n+2}{\tau }^{n+1}exp(i\ell \psi )\right]\hfill \\ \hfill & =\frac{-{(0.6-0.1\sigma )}^n\mu {\ell }^{n+2}{t}^{n+1}exp(i\ell \psi )}{n!}.\hfill \end{array}\right.\end{array}$$

(127)

Thus, we can obtain the exact solution as:

$$\begin{array}{c}\hfill \tilde{w}(\psi ,t;\sigma )=[{(0.4+0.1\sigma )}^n,{(0.6-0.1\sigma )}^n]\odot \rho exp(i\ell (\psi -\ell t)),0\le \sigma \le 1.\end{array}$$

Example 4.

We take into account the fuzzy linear Schrodinger differential equation with $\zeta =0$

$$\begin{array}{c}\hfill i{\tilde{w}}_t(\psi ,t)\oplus {\tilde{w}}_{\psi \psi }(\psi ,t)=\tilde{0},\end{array}$$

(128)

with the initial condition

$$\begin{array}{c}\hfill \tilde{w}(\psi ,0)=[{(0.1+0.1\sigma )}^n,{(0.3-0.1\sigma )}^n]\odot cosh(3\psi ),\end{array}$$

(129)

where $(n=1,2,3,\dots ).$

According to (128) with the initial condition (129), we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\underline{w}}_0(\psi ,t;\sigma )={(0.1+0.1\sigma )}^{n}cosh(3\psi )\hfill \\ {\underline{w}}_{n+1}(\psi ,t;\sigma )=i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{w}}_{n_{\psi \psi }}(\psi ,t;\sigma )\right]\right],n\ge 0,\hfill \end{array}\right.\end{array}$$

(130)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\overline{w}}_0(\psi ,t;\sigma )={(0.6-0.1\sigma )}^{n}cosh(3\psi )\hfill \\ {\overline{w}}_{n+1}(\psi ,t;\sigma )=i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{w}}_{n_{\psi \psi }}(\psi ,t;\sigma )\right]\right],n\ge 0.\hfill \end{array}\right.\end{array}$$

(131)

The first few components of $\tilde{w}(\psi ,t;\sigma )=\left[\underline{w}(\psi ,t;\sigma ),\overline{w}(\psi ,t;\sigma )\right]$ are

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{w}}_0(\psi ,t;\sigma )& ={(0.1+0.1\sigma )}^{n}cosh(3\psi )\hfill \\ \hfill {\underline{w}}_1(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{w}}_{0_{\psi \psi }}(\psi ,t;\sigma )\right]\right],\hfill \\ \hfill & ={(0.1+0.1\sigma )}^n\left[i{\mathfrak{E}}^{-1}\left[9{\tau }^{3}cosh(3\psi )\right]\right]\hfill \\ \hfill & ={(0.4+0.1\sigma )}^n\left[9icosh(3\psi )\right]\hfill \\ \hfill {\underline{w}}_2(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{w}}_{1_{\psi \psi }}(\psi ,t;\sigma )\right]\right],\hfill \\ \hfill & ={(0.1+0.1\sigma )}^n\left[i{\mathfrak{E}}^{-1}\left[81i{\tau }^{4}cosh(3\psi )\right]\right]\hfill \\ \hfill & ={(0.1+0.1\sigma )}^n\left[-\frac{81}{2!}{t}^{2}cosh(3\psi )\right]\hfill \\ \hfill ⋮,\end{array}\right.\end{array}$$

(132)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\overline{w}}_0(\psi ,t;\sigma )& ={(0.3-0.1\sigma )}^{n}cosh(3\psi )\hfill \\ \hfill {\overline{w}}_1(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{w}}_{0_{\psi \psi }}(\psi ,t;\sigma )\right]\right],\hfill \\ \hfill & ={(0.3-0.1\sigma )}^n\left[i{\mathfrak{E}}^{-1}\left[9{\tau }^{3}cosh(3\psi )\right]\right]\hfill \\ \hfill & ={(0.3-0.1\sigma )}^n\left[9icosh(3\psi )\right]\hfill \\ \hfill {\overline{w}}_2(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{w}}_{1_{\psi \psi }}(\psi ,t;\sigma )\right]\right],\hfill \\ \hfill & ={(0.3-0.1\sigma )}^n\left[i{\mathfrak{E}}^{-1}\left[81i{\tau }^{4}cosh(3\psi )\right]\right]\hfill \\ \hfill & ={(0.3-0.1\sigma )}^n\left[-\frac{81}{2!}{t}^{2}cosh(3\psi )\right]\hfill \\ \hfill ⋮.\end{array}\right.\end{array}$$

(133)

Thus, when using the above iterations, we can obtain the exact solution as:

$$\begin{array}{c}\hfill \tilde{w}(\psi ,t;\sigma )=[{(0.1+0.1\sigma )}^n,{(0.3-0.1\sigma )}^n]\odot cosh(3\psi )exp\left(9it\right),0\le \sigma \le 1.\end{array}$$

4.4.2. The Fuzzy Nonlinear Schrodinger Equation

In this part, we show two examples of the fuzzy nonlinear Schrodinger differential equation.

Example 5.

We take into account the fuzzy nonlinear Schrodinger differential equation with $\zeta =-2$ and $\wp =1$ as:

$$\begin{array}{c}\hfill i{\tilde{w}}_t(\psi ,t)\oplus {\tilde{w}}_{\psi \psi }(\psi ,t){\ominus }_{gH}2\odot {\left|\tilde{w}(\psi ,t)\right|}^2\odot \tilde{w}(\psi ,t)=\tilde{0},\end{array}$$

(134)

with the initial condition

$$\begin{array}{c}\hfill \tilde{w}(\psi ,0)=[{(1+2\sigma )}^n,{(5-2\sigma )}^n]\oplus exp(i\psi ),\end{array}$$

(135)

where $(n=1,2,3,\dots ).$

Applying the fuzzy Elzaki transform to (134) with the initial condition (135), we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\underline{w}}_0(\psi ,t;\sigma )={(1+2\sigma )}^n+exp(i\psi ),\hfill \\ {\underline{w}}_{n+1}(\psi ,t;\sigma )=i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{w}}_{n_{\psi \psi }}(\psi ,t;\sigma )\right]\right]-2i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{\mathcal{A}}}_n(\sigma )\right]\right],n\ge 0,\hfill \end{array}\right.\end{array}$$

(136)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\overline{w}}_0(\psi ,t;\sigma )={(5-2\sigma )}^n+exp(i\psi ),\hfill \\ {\overline{w}}_{n+1}(\psi ,t;\sigma )=i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{w}}_{n_{\psi \psi }}(\psi ,t;\sigma )\right]\right]-2i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{\mathcal{A}}}_n(\sigma )\right]\right],n\ge 0,\hfill \end{array}\right.\end{array}$$

(137)

where ${\underline{\mathcal{A}}}_n(\sigma )$ and ${\overline{\mathcal{A}}}_n(\sigma )$ are the Adomian polynomials to be determined from the nonlinear term

$$\begin{array}{cc}\hfill \mathcal{N}\underline{w}(\psi ,t;\sigma )& =|\underline{w}{(\psi ,t;\sigma )|}^2\underline{w}(\psi ,t;\sigma )=\underline{w}{(\psi ,t;\sigma )}^2\underline{\overline{w}}(\psi ,t;\sigma ),\hfill \end{array}$$

(138)

$$\begin{array}{cc}\hfill \mathcal{N}\overline{w}(\psi ,t;\sigma )& =|\overline{w}{(\psi ,t;\sigma )|}^2\overline{w}(\psi ,t;\sigma )=\overline{w}{(\psi ,t;\sigma )}^2\overline{\overline{w}}(\psi ,t;\sigma ),\hfill \end{array}$$

(139)

where $\overline{\underline{w}}(\psi ,t;\sigma )$ and $\overline{\overline{w}}(\psi ,t;\sigma )$ are the conjugate of $\tilde{w}(\psi ,t;\sigma )$, and few terms using the formulas in (103) and (104), we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{\mathcal{A}}}_0(\sigma )& ={\underline{w}}_0^2(\psi ,t;\sigma ){\overline{\underline{w}}}_0(\psi ,t;\sigma ),\hfill \\ \hfill {\underline{\mathcal{A}}}_1(\sigma )& =2{\underline{w}}_0(\psi ,t;\sigma ){\underline{w}}_1(\psi ,t;\sigma ){\overline{\underline{w}}}_0(\psi ,t;\sigma )+{\underline{w}}_0^2(\psi ,t;\sigma ){\overline{\underline{w}}}_1(\psi ,t;\sigma ),\hfill \\ \hfill {\underline{\mathcal{A}}}_2(\sigma )& =2{\underline{w}}_0(\psi ,t;\sigma ){\underline{w}}_2(\psi ,t;\sigma ){\overline{\underline{w}}}_0(\psi ,t;\sigma )+{\underline{w}}_1^2(\psi ,t;\sigma ){\overline{\underline{w}}}_0(\psi ,t;\sigma ),\hfill \\ \hfill & +2{\underline{w}}_0(\psi ,t;\sigma ){\underline{w}}_1(\psi ,t;\sigma ){\overline{\underline{w}}}_1(\psi ,t;\sigma )+{\underline{w}}_0^2(\psi ,t;\sigma ){\overline{\underline{w}}}_2(\psi ,t;\sigma ),\hfill \\ \hfill ⋮,\end{array}\right.\end{array}$$

(140)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\overline{\mathcal{A}}}_0(\sigma )& ={\overline{w}}_0^2(\psi ,t;\sigma ){\overline{\overline{w}}}_0(\psi ,t;\sigma ),\hfill \\ \hfill {\overline{\mathcal{A}}}_1(\sigma )& =2{\overline{w}}_0(\psi ,t;\sigma ){\overline{w}}_1(\psi ,t;\sigma ){\overline{\overline{w}}}_0(\psi ,t;\sigma )+{\overline{w}}_0^2(\psi ,t;\sigma ){\overline{\overline{w}}}_1(\psi ,t;\sigma ),\hfill \\ \hfill {\overline{\mathcal{A}}}_2(\sigma )& =2{\overline{w}}_0(\psi ,t;\sigma ){\overline{w}}_2(\psi ,t;\sigma ){\overline{\overline{w}}}_0(\psi ,t;\sigma )+{\overline{w}}_1^2(\psi ,t;\sigma ){\overline{\overline{w}}}_0(\psi ,t;\sigma ),\hfill \\ \hfill & +2{\overline{w}}_0(\psi ,t;\sigma ){\overline{w}}_1(\psi ,t;\sigma ){\overline{\overline{w}}}_1(\psi ,t;\sigma )+{\overline{w}}_0^2(\psi ,t;\sigma ){\overline{\overline{w}}}_2(\psi ,t;\sigma ),\hfill \\ \hfill ⋮.\end{array}\right.\end{array}$$

(141)

The few components are

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{w}}_0(\psi ,t;\sigma )& ={(1+2\sigma )}^n+exp(i\psi )\hfill \\ \hfill {\underline{w}}_1(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{w}}_{0_{\psi \psi }}(\psi ,t;\sigma )\right]\right]-2i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{\mathcal{A}}}_0(\sigma )\right]\right],\hfill \\ \hfill & ={(1+2\sigma )}^n+\left[i{\mathfrak{E}}^{-1}[i^2{\tau }^{3}exp(i\psi )]\right.\hfill \\ \hfill & \left.-2i{\mathfrak{E}}^{-1}[{\tau }^{3}exp(i\psi )]\right]\hfill \\ \hfill & =-{(1+2\sigma )}^n-3itexp(i\psi ),\hfill \\ \hfill {\underline{w}}_2(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{w}}_{1_{\psi \psi }}(\psi ,t;\sigma )\right]\right]-2i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{\mathcal{A}}}_1(\sigma )\right]\right],\hfill \\ \hfill & ={(1+2\sigma )}^n+\left[i{\mathfrak{E}}^{-1}\left[3i{\tau }^{4}exp(i\psi )\right]\right.\hfill \\ \hfill & \left.-2i{\mathfrak{E}}^{-1}\left[-3i{\tau }^{4}exp(i\psi )\right]\right]\hfill \\ \hfill & =-{(1+2\sigma )}^n-\left[\frac{9t^{2}exp(i\psi )}{2!}\right],\hfill \\ \hfill ⋮,\end{array}\right.\end{array}$$

(142)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\overline{w}}_0(\psi ,t;\sigma )& ={(5-2\sigma )}^n+exp(i\psi )\hfill \\ \hfill {\overline{w}}_1(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{w}}_{0_{\psi \psi }}(\psi ,t;\sigma )\right]\right]-2i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{\mathcal{A}}}_0(\sigma )\right]\right],\hfill \\ \hfill & ={(5-2\sigma )}^n+\left[i{\mathfrak{E}}^{-1}\left[[i^2{\tau }^{3}exp(i\psi )]\right]\right.\hfill \\ \hfill & \left.-2i{\mathfrak{E}}^{-1}[{\tau }^{3}exp(i\psi )]\right]\hfill \\ \hfill & ={(5-2\sigma )}^n-3itexp(i\psi ),\hfill \\ \hfill {\overline{w}}_2(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{w}}_{1_{\psi \psi }}(\psi ,t;\sigma )\right]\right]-2i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{\mathcal{A}}}_1(\sigma )\right]\right],\hfill \\ \hfill & ={(5-2\sigma )}^n+\left[i{\mathfrak{E}}^{-1}[3i{\tau }^{4}exp(i\psi )]\right.\hfill \\ \hfill & \left.-2i{\mathfrak{E}}^{-1}[-3i{\tau }^{4}exp(i\psi )]\right]\hfill \\ \hfill & ={(5-2\sigma )}^n-\left[\frac{9t^{2}exp(i\psi )}{2!}\right],\hfill \\ \hfill ⋮.\end{array}\right.\end{array}$$

(143)

Thus, we can obtain the exact solution as:

$$\begin{array}{c}\hfill \tilde{w}(\psi ,t;\sigma )=[{(1+2\sigma )}^n,{(5-2\sigma )}^n]\oplus exp\left(i(\psi -3t)\right),0\le \sigma \le 1.\end{array}$$

Example 6.

Consider the fuzzy nonlinear Schrodinger differential equation with $\zeta =2$ and $\wp =1$

$$\begin{array}{c}\hfill i{\tilde{w}}_t(\psi ,t)\oplus {\tilde{w}}_{\psi \psi }(\psi ,t)\oplus 2\odot {\left|\tilde{w}(\psi ,t)\right|}^2\odot \tilde{w}(\psi ,t)=\tilde{0},\end{array}$$

(144)

with the initial condition

$$\begin{array}{c}\hfill \tilde{w}(\psi ,0)=[{(1+2\sigma )}^n,{(5-2\sigma )}^n]\oplus exp(i\psi ),\end{array}$$

(145)

where $(n=1,2,3,\dots ).$

According to (144) and the initial condition, (145) yields

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\underline{w}}_0(\psi ,t;\sigma )={(1+2\sigma )}^n+exp(i\psi ),\hfill \\ {\underline{w}}_{n+1}(\psi ,t;\sigma )=i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{w}}_{n_{\psi \psi }}(\psi ,t;\sigma )\right]\right]+2i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{\mathcal{A}}}_n(\sigma )\right]\right],n\ge 0,\hfill \end{array}\right.\end{array}$$

(146)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\overline{w}}_0(\psi ,t;\sigma )={(5-2\sigma )}^n+exp(i\psi ),\hfill \\ {\overline{w}}_{n+1}(\psi ,t;\sigma )=i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{w}}_{n_{\psi \psi }}(\psi ,t;\sigma )\right]\right]+2i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{\mathcal{A}}}_n(\sigma )\right]\right],n\ge 0,\hfill \end{array}\right.\end{array}$$

(147)

where ${\underline{\mathcal{A}}}_n(\sigma )$ and ${\overline{\mathcal{A}}}_n(\sigma )$ are the Adomian polynomials to be determined from the nonlinear term given in Equations (140) and (141). Consequently, we express the few components as:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{w}}_0(\psi ,t;\sigma )& ={(1+2\sigma )}^n+exp(i\psi )\hfill \\ \hfill {\underline{w}}_1(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{w}}_{0_{\psi \psi }}(\psi ,t;\sigma )\right]\right]+2i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{\mathcal{A}}}_0(\sigma )\right]\right],\hfill \\ \hfill & ={(1+2\sigma )}^n+\left[i{\mathfrak{E}}^{-1}[i^2{\tau }^{3}exp(i\psi )]+2i{\mathfrak{E}}^{-1}[{\tau }^{3}exp(i\psi )]\right]\hfill \\ \hfill & ={(1+2\sigma )}^n+itexp(i\psi ),\hfill \\ \hfill {\underline{w}}_2(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{w}}_{1_{\psi \psi }}(\psi ,t;\sigma )\right]\right]+2i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\underline{\mathcal{A}}}_1(\sigma )\right]\right],\hfill \\ \hfill & ={(1+2\sigma )}^n+\left[i{\mathfrak{E}}^{-1}[i^3{\tau }^{4}exp(i\psi )]\right.\hfill \\ \hfill & \left.+2i{\mathfrak{E}}^{-1}[i{\tau }^{4}exp(i\psi )]\right]\hfill \\ \hfill & ={(1+2\sigma )}^n-\left[\frac{t^{2}exp(i\psi )}{2!}\right],\hfill \\ \hfill ⋮,\end{array}\right.\end{array}$$

(148)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\overline{w}}_0(\psi ,t;\sigma )& ={(5-2\sigma )}^n+exp(i\psi )\hfill \\ \hfill {\overline{w}}_1(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{w}}_{0_{\psi \psi }}(\psi ,t;\sigma )\right]\right]+2i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{\mathcal{A}}}_0(\sigma )\right]\right],\hfill \\ \hfill & ={(5-2\sigma )}^n+\left[i{\mathfrak{E}}^{-1}[i^2{\tau }^{3}exp(i\psi )]+2i{\mathfrak{E}}^{-1}[{\tau }^{3}exp(i\psi )]\right]\hfill \\ \hfill & ={(5-2\sigma )}^n+itexp(i\psi ),\hfill \\ \hfill {\overline{w}}_2(\psi ,t;\sigma )& =i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{w}}_{1_{\psi \psi }}(\psi ,t;\sigma )\right]\right]+2i{\mathfrak{E}}^{-1}\left[\tau \mathfrak{E}\left[{\overline{\mathcal{A}}}_1(\sigma )\right]\right],\hfill \\ \hfill & ={(5-2\sigma )}^n+\left[i{\mathfrak{E}}^{-1}[i^3{\tau }^{4}exp(i\psi )]\right.\hfill \\ \hfill & \left.+2i{\mathfrak{E}}^{-1}[i{\tau }^{4}exp(i\psi )]\right]\hfill \\ \hfill & ={(5-2\sigma )}^n-\left[\frac{t^{2}exp(i\psi )}{2!}\right],\hfill \\ \hfill ⋮.\end{array}\right.\end{array}$$

(149)

Thus, we can obtain the exact solution as follows:

$$\begin{array}{c}\hfill \tilde{w}(\psi ,t;\sigma )=[{(1+2\sigma )}^n,{(5-2\sigma )}^n]\oplus exp\left(i(\psi +t)\right),0\le \sigma \le 1.\end{array}$$

In the preceding instances, Figure 1 demonstrates that the left-hand functions of the $\sigma$-level set of $\tilde{w}$ (w lower) are always increasing functions of $\sigma$ and the right-hand functions of the $\sigma$-level set of $\tilde{w}$ (w upper) are always decreasing functions of $\sigma$.

Figure 1. $\left(\mathbf{a}\right)$ Ex (4.1) $\psi =3,\rho =1,\ell =2,t=4,n=2;$$\left(\mathbf{b}\right)$ Ex (4.2) $\psi =30,t=0.0001,n=3;$$\left(\mathbf{c}\right)$ Ex (4.3) $\psi =0.0002,t=0.01,n=4;$$\left(\mathbf{d}\right)$ Ex (4.4) $\psi =0.0002,t=0.01,n=5$.

5. Fuzzy Heat-Like and Wave-like Equations with Variable Coefficients

In this section, we apply the fuzzy RDTM and HPM to obtain the fuzzy solutions of heat-like and wave-like equations with variable coefficients as follows:

• Consider the fuzzy heat-like equation of the form

  $$\begin{array}{cc}\hfill {\tilde{w}}_t\oplus {\phi }_1(\psi ,\varphi ,\varphi )\odot & {\tilde{w}}_{\psi \psi }\oplus {\phi }_2(\psi ,\varphi ,\varphi )\odot {\tilde{w}}_{\varphi \varphi }\oplus {\phi }_3(\psi ,\varphi ,\varphi )\odot {\tilde{w}}_{\varphi \varphi }=0,{\phi }_1(\psi ,\varphi ,\varphi )\ge 0,\hfill \\ \hfill & {\phi }_2(\psi ,\varphi ,\varphi )\ge 0,{\phi }_3(\psi ,\varphi ,\varphi )\ge 0,\hfill \end{array}$$

  (150)

  with the initial condition

  $$\tilde{w}(\psi ,\varphi ,\varphi ,0)={\tilde{\phi }}_4(\psi ,\varphi ,\varphi ).$$

  (151)
• Consider the fuzzy wave-like equation of the form

  $$\begin{array}{cc}\hfill {\tilde{w}}_{tt}\oplus {\vartheta }_1(\psi ,\varphi ,\varphi )\odot & {\tilde{w}}_{\psi \psi }\oplus {\vartheta }_2(\psi ,\varphi ,\varphi )\odot {\tilde{w}}_{\varphi \varphi }\oplus {\vartheta }_3(\psi ,\varphi ,\varphi )\odot {\tilde{w}}_{\varphi \varphi }=0,{\vartheta }_1(\psi ,\varphi ,\varphi )\ge 0,\hfill \\ \hfill & {\vartheta }_2(\psi ,\varphi ,\varphi )\ge 0,{\vartheta }_3(\psi ,\varphi ,\varphi )\ge 0,\hfill \end{array}$$

  (152)

  with the initial condition

  $$\tilde{w}(\psi ,\varphi ,\varphi ,0)={\tilde{\vartheta }}_4(\psi ,\varphi ,\varphi ),{\tilde{w}}_t(\psi ,\varphi ,\varphi ,0)={\tilde{\vartheta }}_5(\psi ,\varphi ,\varphi ).$$

  (153)

5.1. The Fuzzy Reduced Differential Transform Method

We consider the fuzzy-valued function of two variables $\tilde{w}(\psi ,t)$. Based on the properties theory of one-dimensional DTM, the fuzzy-valued function $\tilde{w}(\psi ,t;\sigma )=[\underline{w}(\psi ,t;\sigma ),\overline{w}(\psi ,t;\sigma )]$ can be represented as:

$$\begin{array}{cc}\hfill \underline{w}(\psi ,t;\sigma )& =\sum _{j=0}^{\infty }{\underline{W}}_j(\psi ;\sigma )t^j,\hfill \end{array}$$

(154)

$$\begin{array}{cc}\hfill \overline{w}(\psi ,t;\sigma )& =\sum _{j=0}^{\infty }{\overline{W}}_j(\psi ;\sigma )t^j,\hfill \end{array}$$

(155)

where ${\tilde{W}}_j(\psi ;\sigma )=[{\underline{W}}_j(\psi ;\sigma ),{\overline{W}}_j(\psi ;\sigma )]$ is called t-dimensional spectrum fuzzy-valued function of $\tilde{w}(\psi ,t;\sigma ).$

Definition 10.

If a fuzzy-valued function $\tilde{w}(\psi ,t;\sigma )$ is analytic and differentiated continuously with respect to time t and space ψ in the domain of interest, then let

$$\begin{array}{cc}\hfill {\underline{W}}_j(\psi ;\sigma )& =\frac{1}{j!}{\left[\frac{{\partial }^j}{\partial t^j}\underline{w}(\psi ,t,\sigma )\right]}_{t=0},\hfill \end{array}$$

(156)

$$\begin{array}{cc}\hfill {\overline{W}}_j(\psi ;\sigma )& =\frac{1}{j!}{\left[\frac{{\partial }^j}{\partial t^j}\overline{w}(\psi ,t,\sigma )\right]}_{t=0},\hfill \end{array}$$

(157)

where the t-dimensional spectrum fuzzy-valued function ${\tilde{w}}_j(\psi ;\sigma )$ is the transformed function.

Definition 11.

The fuzzy differential inverse transform of ${\tilde{w}}_j(\psi ;\sigma )$ is defined as:

$$\begin{array}{cc}\hfill \underline{w}(\psi ,t;\sigma )& =\sum _{j=0}^{\infty }{\underline{W}}_j(\psi ;\sigma )t^j,\hfill \end{array}$$

(158)

$$\begin{array}{cc}\hfill \overline{w}(\psi ,t;\sigma )& =\sum _{j=0}^{\infty }{\overline{W}}_j(\psi ;\sigma )t^j.\hfill \end{array}$$

(159)

Subsequently, combining Equations (159) into (156), we obtain

$$\begin{array}{cc}\hfill \underline{w}(\psi ,t;\sigma )& =\sum _{j=0}^{\infty }\frac{1}{j!}{\left[\frac{{\partial }^j}{\partial t^j}\underline{w}(\psi ,t;\sigma )\right]}_{t=0}{t}^j,\hfill \end{array}$$

(160)

$$\begin{array}{cc}\hfill \overline{w}(\psi ,t;\sigma )& =\sum _{j=0}^{\infty }\frac{1}{j!}{\left[\frac{{\partial }^j}{\partial t^j}\overline{w}(\psi ,t;\sigma )\right]}_{t=0}{t}^j.\hfill \end{array}$$

(161)

Next, using the aforementioned definitions, we can find that the concept of fuzzy RDTM is derived from the expansion of the power series. To illustrate the basic concepts of fuzzy RDTM, we consider the following fuzzy nonlinear PDE written in the operator form

$$\mathcal{L}\tilde{w}(\psi ,t)\oplus \mathcal{R}\tilde{w}(\psi ,t)\oplus \mathcal{N}\tilde{w}(\psi ,t)=\tilde{g}(\psi ,t),$$

(162)

with the initial condition

$$\tilde{w}(\psi ,0)=\tilde{f}(\psi ),$$

(163)

where $\mathcal{L}=\frac{\partial }{\partial t},\mathcal{R}$ is a linear operator which has fuzzy partial derivatives, $\mathcal{N}\tilde{w}(\psi ,t;\sigma )=[\mathcal{N}\underline{w}(\psi ,t;\sigma ),\mathcal{N}\overline{w}(\psi ,t;\sigma )]$ is a fuzzy nonlinear operator and $\tilde{g}(\psi ,t;\sigma )=[\underline{g}(\psi ,t;\sigma ),\overline{g}(\psi ,t;\sigma )]$ is an fuzzy inhomogeneous term. Applying the fuzzy RDTM, we obtain

$$\begin{array}{cc}\hfill (j+1){\underline{W}}_{j+1}(\psi ;\sigma )& ={\underline{G}}_j(\psi ;\sigma )-\mathcal{R}{\underline{W}}_j(\psi ;\sigma )-\mathcal{N}{\underline{W}}_j(\psi ;\sigma ),\hfill \end{array}$$

(164)

$$\begin{array}{cc}\hfill (j+1){\overline{W}}_{j+1}(\psi ;\sigma )& ={\overline{G}}_j(\psi ;\sigma )-\mathcal{R}{\overline{W}}_j(\psi ;\sigma )-\mathcal{N}{\overline{W}}_j(\psi ;\sigma ),\hfill \end{array}$$

(165)

where ${\tilde{w}}_j(\psi ;\sigma ),\mathcal{R}{\tilde{w}}_j(\psi ;\sigma ),\mathcal{N}{\tilde{w}}_j(\psi ;\sigma )$, and ${\tilde{G}}_j(\psi ;\sigma )$ are the fuzzy transformations of the fuzzy-valued functions $\mathcal{L}\tilde{w}(\psi ,t),$ $\mathcal{R}\tilde{w}(\psi ,t),\mathcal{N}\tilde{w}(\psi ,t)$ and $\tilde{g}(\psi ,t)$, respectively. According to the initial condition (163), we obtain

$$\begin{array}{cc}\hfill {\underline{W}}_0(\psi ;\sigma )& =\underline{f}(\psi ;\sigma ),\hfill \end{array}$$

(166)

$$\begin{array}{cc}\hfill {\overline{W}}_0(\psi ;\sigma )& =\overline{f}(\psi ;\sigma ).\hfill \end{array}$$

(167)

From (167) into (164) and by straightforward iterative calculation, we obtain the following ${\underline{W}}_j(\psi ;\sigma ),{\overline{W}}_j(\psi ;\sigma )$ values. Moreover, the fuzzy inverse transformation of the set of values ${\left[{\tilde{w}}_j(\psi ;\sigma )\right]}_{j=0}^n$ gives the n-terms approximation solution as:

$$\begin{array}{cc}\hfill {\underline{w}}_n(\psi ,t;\sigma )& =\sum _{j=0}^n{\underline{W}}_j(\psi ;\sigma )t^j,\hfill \end{array}$$

(168)

$$\begin{array}{cc}\hfill {\overline{w}}_n(\psi ,t;\sigma )& =\sum _{j=0}^n{\overline{W}}_j(\psi ;\sigma )t^j.\hfill \end{array}$$

(169)

Thus, the exact solution of the problem is given by

$$\begin{array}{cc}\hfill \underline{w}(\psi ,t;\sigma )& =\underset{n\to \infty }{lim}{\underline{w}}_n(\psi ,t;\sigma ),\hfill \end{array}$$

(170)

$$\begin{array}{cc}\hfill \overline{w}(\psi ,t;\sigma )& =\underset{n\to \infty }{lim}{\overline{w}}_n(\psi ,t;\sigma ).\hfill \end{array}$$

(171)

Next, the basic mathematical operations performed by RDTM proposed in [60,61] as follows:

1.

If $w(\psi ,t)$, then $W_j(\psi )=\frac{1}{j!}{\left[\frac{{\partial }^j}{\partial t^j}w(\psi ,t)\right]}_{t=0}.$

2.

If $f(\psi ,t)=w(\psi ,t)\pm \tau (\psi ,t)$, then $F_j(\psi )=W_j(\psi )\pm {\mathcal{T}}_j(\psi ).$

3.

If $f(\psi ,t)=\sigma w(\psi ,t)$, then $F_j(\psi )=\sigma W_j(\psi )$, where $\sigma$ is a constant.

4.

If $f(\psi ,t)={\psi }^{\mu }{t}^n$, then $F_j(\psi )={\psi }^{\mu }\delta (j-n),$ $\delta \left(j\right)=\left\{\begin{array}{cc}& 1,j=0,\hfill \\ & 0,j\ne 0.\hfill \end{array}\right.$

5.

If $f(\psi ,t)={\psi }^{\mu }{t}^{n}w(\psi ,t)$, then $F_j(\psi )={\psi }^{\mu }{W}_{j-n}(\psi ).$

6.

If $f(\psi ,t)=w(\psi ,t)\tau (\psi ,t)$, then $F_j(\psi )={\sum }_{r=0}^j{W}_r(\psi ){\mathcal{T}}_{j-r}(\psi )={\sum }_{r=0}^j{W}_r(\psi ){\mathcal{T}}_{j-r}(\psi ).$

7.

If $f(\psi ,t)=\frac{{\partial }^r}{\partial t^r}w(\psi ,t)$, then $F_j(\psi )=(j+1)···(j+r)W_{j+r}(\psi )=\frac{(j+r)!}{j!}{W}_{j+r}(\psi ).$

8.

If $f(\psi ,t)=\frac{\partial }{\partial \psi }w(\psi ,t)$, then $F_j(\psi )=\frac{\partial }{\partial \psi }{W}_j(\psi ).$

5.2. The Fuzzy Homotopy Perturbation Method

Consider the fuzzy nonlinear differential equation as:

$$\begin{array}{c}\hfill \tilde{\mathcal{A}}\left(\tilde{w}\right)=\tilde{f}(\wp ),\wp \in \Psi ,\end{array}$$

(172)

where $\tilde{f}(\wp ,\sigma )=[\underline{f}(\wp ,\sigma ),\overline{f}(\wp ,\sigma )]\in E^1$, we define:

1.

$\tilde{\mathcal{A}}\left(\tilde{w}\right)$ a fuzzy differential operator, which means $\underline{\mathcal{A}\left(\tilde{w}\right)}$ and $\overline{\mathcal{A}\left(\tilde{w}\right)}$ are differential operator,

2.

$\underline{\tilde{\mathcal{A}}\left(\tilde{w}\right)}(\sigma )=\underline{f}(\wp ,\sigma )$ and $\overline{\tilde{\mathcal{A}}\left(\tilde{w}\right)}(\sigma )=\overline{f}(\wp ,\sigma )$, for any $\sigma \in [0,1],$

under the boundary condition

$$\begin{array}{c}\hfill \mathcal{B}\left(\tilde{w},\frac{\partial \tilde{w}}{\partial \wp }\right)=0,\wp \in \partial \Psi ,\end{array}$$

(173)

where $\mathcal{B}$ stand for boundary operator and $\partial \Psi$ stand for boundary of the domain $\Psi$. The fuzzy operator $\tilde{\mathcal{A}}$ can be divided into two parts $\mathcal{L}$ and $\mathcal{N}$, where $\mathcal{L}$ is a linear operator while $\mathcal{N}$ is a nonlinear operator. Moreover, Equation (172) can be rewritten as follows:

$$\begin{array}{cc}\hfill \mathcal{L}\left(\underline{w}\right)+\mathcal{N}\left(\underline{w}\right)-\underline{f}(\wp ;\sigma )& =\tilde{0},\hfill \end{array}$$

(174)

$$\begin{array}{cc}\hfill \mathcal{L}\left(\overline{w}\right)+\mathcal{N}\left(\overline{w}\right)-\overline{f}(\wp ;\sigma )& =\tilde{0}.\hfill \end{array}$$

(175)

By the fuzzy homotopy technique, we construct a homotopy:

$$\tilde{\tau }(\wp ,p;\sigma ):\Psi \times [0,1]\to \mathbb{R},whichsatisfies$$

$$\left.\begin{array}{c}\mathcal{H}(\underline{\tau }(\sigma ),p)=(1-p)\left[\mathcal{L}\left(\underline{\tau }(\sigma )\right)-\mathcal{L}\left({\underline{w}}_0(\sigma \right))\right]+p[\mathcal{A}\left(\underline{\tau }(\sigma )\right)-\underline{f}(\wp ,\sigma )],\hfill \\ or\hfill \\ \mathcal{H}(\underline{\tau }(\sigma ),p)=\mathcal{L}\left(\underline{\tau }(\sigma )\right)-\mathcal{L}\left({\underline{w}}_0(\sigma \right))+p\mathcal{L}\left({\underline{w}}_0(\sigma \right))+p[\mathcal{N}\left(\underline{\tau }(\sigma )\right)-\underline{f}(\wp ,\sigma )],\hfill \end{array}\right\}$$

(176)

and

$$\left.\begin{array}{c}\mathcal{H}(\overline{\tau }(\sigma ),p)=(1-p)\left[\mathcal{L}\left(\overline{\tau }(\sigma )\right)-\mathcal{L}\left({\overline{w}}_0(\sigma \right))\right]+p[\mathcal{A}\left(\overline{\tau }(\sigma )\right)-\overline{f}(\wp ,\sigma )],\hfill \\ or\hfill \\ \mathcal{H}(\overline{\tau }(\sigma ),p)=L\left(\overline{\tau }(\sigma )\right)-\mathcal{L}\left({\overline{w}}_0(\sigma \right))+p\mathcal{L}\left({\overline{w}}_0(\sigma \right))+p[\mathcal{N}\left(\overline{\tau }(\sigma )\right)-\overline{f}(\wp ,\sigma )],\hfill \end{array}\right\}$$

(177)

where $\wp \in \Psi ,$ and $p\in [0,1]$ is an embedding parameter, ${\tilde{w}}_0(\sigma )=[{\underline{w}}_0(\sigma ),{\overline{w}}_0(\sigma )]$ is the initial approximation to (172), which satisfies the boundary conditions. According to (176) and (177), we have

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \mathcal{H}(\underline{\tau }(\sigma ),0)& =[\mathcal{L}\left(\underline{\tau }(\sigma )\right)-\mathcal{L}\left({\underline{w}}_0(\sigma )\right)]=\tilde{0},\hfill \\ \hfill \mathcal{H}(\underline{\tau }(\sigma ),1)& =[\mathcal{A}\left(\underline{\tau }(\sigma )\right)-\underline{f}(\wp ,\sigma )]=\tilde{0},\hfill \end{array}\right.\end{array}$$

(178)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \mathcal{H}(\overline{\tau }(\sigma ),0)& =[\mathcal{L}\left(\overline{\tau }(\sigma )\right)-\mathcal{L}\left({\overline{w}}_0(\sigma )\right)]=\tilde{0},\hfill \\ \hfill \mathcal{H}(\overline{\tau }(\sigma ),1)& =[\mathcal{A}\left(\overline{\tau }(\sigma )\right)-\overline{f}(\wp ,\sigma )]=\tilde{0},\hfill \end{array}\right.\end{array}$$

(179)

and the changing process of p from zero to unity is just that $\tilde{\tau }(\wp ,p;\sigma )=[\underline{\tau }(\wp ,p;\sigma ),\overline{\tau }(\wp ,p,\sigma )]$ from ${\tilde{w}}_0(\wp ,\sigma )=[{\underline{w}}_0(\wp ,\sigma ),{\overline{w}}_0(\wp ,\sigma )]$ to $\tilde{w}(\wp ,\sigma )=[\underline{w}(\wp ,\sigma ),\overline{w}(\wp ,\sigma )]$. In topology, this is called deformation, $\mathcal{L}\left(\tilde{\tau }\right)(\sigma )$ and $\mathcal{A}\underline{\tau }(\sigma )-\underline{f}(\wp ,\sigma ),\mathcal{A}\overline{\tau }(\sigma )-\overline{f}(\wp ,\sigma ),$ are called Homotopy. The Homotopy parameter p is used as an expanding parameter by the fuzzy HPM to obtain

$$\begin{array}{cc}\hfill \underline{\tau }(\sigma )& =\sum _{\mu =0}^{\infty }{p}^{\mu }{\underline{\tau }}_{\mu }(\sigma ),\hfill \end{array}$$

(180)

$$\begin{array}{cc}\hfill \overline{\tau }(\sigma )& =\sum _{\mu =0}^{\infty }{p}^{\mu }{\overline{\tau }}_{\mu }(\sigma ).\hfill \end{array}$$

(181)

Finally, on setting p = 1, this results in the formal solution

$$\begin{array}{cc}\hfill \underline{w}(\sigma )=\underset{p\to 1}{lim}\underline{\tau }(\sigma )& =\sum _{\mu =0}^{\infty }{\underline{\tau }}_{\mu }(\sigma ),\hfill \end{array}$$

(182)

$$\begin{array}{cc}\hfill \overline{w}(\sigma )=\underset{p\to 1}{lim}\overline{\tau }(\sigma )& =\sum _{\mu =0}^{\infty }{\overline{\tau }}_{\mu }(\sigma ).\hfill \end{array}$$

(183)

5.2.1. Fuzzy Heat-like Equations

We take into consideration the parametric fuzzy heat-like Equation (150) with the form

$$\begin{array}{cc}\hfill {\underline{w}}_t+{\phi }_1(\psi ,\varphi ,\varphi ){\underline{w}}_{\psi \psi }+{\phi }_2(\psi ,\varphi ,\varphi ){\underline{w}}_{\varphi \varphi }+{\phi }_3(\psi ,\varphi ,\varphi ){\underline{w}}_{\varphi \varphi }& =\tilde{0},\hfill \end{array}$$

(184)

$$\begin{array}{cc}\hfill {\overline{w}}_t+{\phi }_1(\psi ,\varphi ,\varphi ){\overline{w}}_{\psi \psi }+{\phi }_2(\psi ,\varphi ,\varphi ){\overline{w}}_{\varphi \varphi }+{\phi }_3(\psi ,\varphi ,\varphi ){\overline{w}}_{\varphi \varphi }& =\tilde{0}.\hfill \end{array}$$

(185)

Using the fuzzy HPM, construct the homotopy $\Psi \times [0,1]\to \mathbb{R}$ which satisfies

$$\begin{array}{cc}\hfill & {\underline{w}}_t(\sigma )-{\underline{\Xi }}_{0t}(\psi ,\varphi ,\varphi ;\sigma )+p{\underline{\Xi }}_{0t}(\psi ,\varphi ,\varphi ;\sigma )+p\left({\phi }_1(\psi ,\varphi ,\varphi ){\underline{w}}_{\psi \psi }\right.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \left.+{\phi }_2(\psi ,\varphi ,\varphi ){\underline{w}}_{\varphi \varphi }+{\phi }_3(\psi ,\varphi ,\varphi ){\underline{w}}_{\varphi \varphi }\right)=\tilde{0},\hfill \\ \hfill & {\overline{w}}_t(\sigma )-{\overline{\Xi }}_{0t}(\psi ,\varphi ,\varphi ;\sigma )+p{\overline{\Xi }}_{0t}(\psi ,\varphi ,\varphi ;\sigma )+p\left({\phi }_1(\psi ,\varphi ,\varphi ){\overline{w}}_{\psi \psi }\right.\hfill \end{array}$$

(186)

$$\begin{array}{cc}\hfill & \left.+{\phi }_2(\psi ,\varphi ,\varphi ){\overline{w}}_{\varphi \varphi }+{\phi }_3(\psi ,\varphi ,\varphi ){\overline{w}}_{\varphi \varphi }\right)=\tilde{0},\hfill \end{array}$$

(187)

and the initial approximation ${\tilde{\Xi }}_0(\psi ,\varphi ,\varphi ;\sigma )=\tilde{w}(\psi ,\varphi ,\varphi ,0)(\sigma )={\tilde{\phi }}_4(\psi ,\varphi ,\varphi ;\sigma ).$ Suppose that the solution to (184) and (185) can be represented as:

$$\begin{array}{cc}\hfill \underline{w}(\sigma )& ={\underline{w}}_0(\sigma )+p{\underline{w}}_1(\sigma )+p^2{\underline{w}}_2(\sigma )+\dots ,\hfill \end{array}$$

(188)

$$\begin{array}{cc}\hfill \overline{w}(\sigma )& ={\overline{w}}_0(\sigma )+p{\overline{w}}_1(\sigma )+p^2{\overline{w}}_2(\sigma )+\dots .\hfill \end{array}$$

(189)

Substituting (189) into (186), and equating the terms of the same power of p, we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}^0:{\underline{w}}_{0t}(\sigma )-{\underline{\Xi }}_{0t}(\psi ,\varphi ,\varphi ;\sigma )=0,{\underline{\Xi }}_0(\psi ,\varphi ,\varphi ;\sigma )={\underline{\phi }}_4(\psi ,\varphi ,\varphi ;\sigma ),\hfill \\ p^1:{\underline{w}}_{1t}(\sigma )+{\phi }_1(\psi ,\varphi ,\varphi ){\underline{w}}_{0\psi \psi }(\sigma )+{\phi }_2(\psi ,\varphi ,\varphi ){\underline{w}}_{0\varphi \varphi }(\sigma )+{\phi }_3(\psi ,\varphi ,\varphi ){\underline{w}}_{0\varphi \varphi }(\sigma )\hfill \\ +{\underline{\Xi }}_{0t}(\psi ,\varphi ,\varphi ;\sigma )=0,{\underline{w}}_1(\psi ,\varphi ,\varphi ,0)(\sigma )=0,\hfill \\ p^2:{\underline{w}}_{2t}(\sigma )+{\phi }_1(\psi ,\varphi ,\varphi ){\underline{w}}_{1\psi \psi }(\sigma )+{\phi }_2(\psi ,\varphi ,\varphi ){\underline{w}}_{1\varphi \varphi }(\sigma )+{\phi }_3(\psi ,\varphi ,\varphi ){\underline{w}}_{1\varphi \varphi }(\sigma )=0,\hfill \\ {\underline{w}}_2(\psi ,\varphi ,\varphi ;\sigma )=0,\hfill \\ ⋮,\hfill \end{array}\right.\end{array}$$

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}^0:{\overline{w}}_{0t}(\sigma )-{\overline{\Xi }}_{0t}(\psi ,\varphi ,\varphi ;\sigma )=0,{\overline{\Xi }}_0(\psi ,\varphi ,\varphi ;\sigma )={\overline{\phi }}_4(\psi ,\varphi ,\varphi ;\sigma ),\hfill \\ p^1:{\overline{w}}_{1t}(\sigma )+{\phi }_1(\psi ,\varphi ,\varphi ){\overline{w}}_{0\psi \psi }(\sigma )+{\phi }_2(\psi ,\varphi ,\varphi ){\overline{w}}_{0\varphi \varphi }(\sigma )+{\phi }_3(\psi ,\varphi ,\varphi ;\sigma ){\overline{w}}_{0\varphi \varphi }(\sigma )\hfill \\ +{\overline{\Xi }}_{0t}(\psi ,\varphi ,\varphi ;\sigma )=0,{\overline{w}}_1(\psi ,\varphi ,\varphi ;\sigma )=0,\hfill \\ p^2:{\overline{w}}_{2t}(\sigma )+{\phi }_1(\psi ,\varphi ,\varphi ){\overline{w}}_{1\psi \psi }(\sigma )+{\phi }_2(\psi ,\varphi ,\varphi ){\overline{w}}_{1\varphi \varphi }(\sigma )+{\phi }_3(\psi ,\varphi ,\varphi ){\overline{w}}_{1\varphi \varphi }(\sigma )=0,\hfill \\ {\overline{w}}_2(\psi ,\varphi ,\varphi ;\sigma )=0,\hfill \\ ⋮.\hfill \end{array}\right.\end{array}$$

Assume ${\tilde{w}}_0(\psi ,\varphi ,\varphi ;\sigma )={\tilde{\Xi }}_0(\psi ,\varphi ,\varphi ;\sigma )$, and solving the above equations results in the approximate solution

$$\begin{array}{cc}\hfill \underline{w}(\sigma )& =\underset{n\to \infty }{lim}\left({\underline{w}}_0+{\underline{w}}_1+{\underline{w}}_2+···\right)(\sigma ),\hfill \end{array}$$

(190)

$$\begin{array}{cc}\hfill \overline{w}(\sigma )& =\underset{n\to \infty }{lim}\left({\overline{w}}_0+{\overline{w}}_1+{\overline{w}}_2+···\right)(\sigma ).\hfill \end{array}$$

(191)

5.2.2. Inhomogeneous Fuzzy Heat-like Equations

Here, the parametric form of the inhomogeneous fuzzy heat-like equation is investigated:

$$\begin{array}{cc}\hfill & {\tilde{w}}_t\oplus \widetilde{{\rm Y}}(\psi ,\varphi ,\varphi )\oplus {\phi }_1(\psi ,\varphi ,\varphi )\odot {\tilde{w}}_{\psi \psi }\oplus {\phi }_2(\psi ,\varphi ,\varphi )\odot {\tilde{w}}_{\varphi \varphi }\oplus {\phi }_3(\psi ,\varphi ,\varphi )\odot {\tilde{w}}_{\varphi \varphi }=0,\hfill \\ \hfill & {\phi }_1(\psi ,\varphi ,\varphi )\ge 0,{\phi }_2(\psi ,\varphi ,\varphi )\ge 0,{\phi }_3(\psi ,\varphi ,\varphi )\ge 0.\hfill \end{array}$$

(192)

The parametric form of (192) is

$$\begin{array}{cc}\hfill {\underline{w}}_{tt}(\sigma )+\underline{{\rm Y}}(\psi ,\varphi ,\varphi ;\sigma )+{\phi }_1(\psi ,\varphi ,\varphi ){\underline{w}}_{\psi \psi }(\sigma )+{\phi }_2(\psi ,\varphi ,\varphi ){\underline{w}}_{\varphi \varphi }(\sigma )+{\phi }_3(\psi ,\varphi ,\varphi ){\underline{w}}_{\varphi \varphi }(\sigma )& =0,\hfill \end{array}$$

(193)

$$\begin{array}{cc}\hfill {\overline{w}}_{tt}(\sigma )+\overline{{\rm Y}}(\psi ,\varphi ,\varphi ;\sigma )+{\phi }_1(\psi ,\varphi ,\varphi ){\overline{w}}_{\psi \psi }(\sigma )+{\phi }_2(\psi ,\varphi ,\varphi ){\overline{w}}_{\varphi \varphi }(\sigma )+{\phi }_3(\psi ,\varphi ,\varphi ){\overline{w}}_{\varphi \varphi }(\sigma )& =0.\hfill \end{array}$$

(194)

Applying the fuzzy HPM, we construct the homotopy $\Psi \times [0,1]\to \mathbb{R}$ which satisfies

$$\begin{array}{cc}\hfill {\underline{w}}_t(\sigma )-{\underline{\Xi }}_{0t}(\psi ,\varphi ,\varphi ;\sigma )& +p{\underline{\Xi }}_{0t}(\psi ,\varphi ,\varphi ;\sigma )+\underline{{\rm Y}}(\psi ,\varphi ,\varphi ;\sigma )+p\left({\phi }_1(\psi ,\varphi ,\varphi ){\underline{w}}_{\psi \psi }(\sigma )\right.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \left.+{\phi }_2(\psi ,\varphi ,\varphi ){\underline{w}}_{\varphi \varphi }(\sigma )+{\phi }_3(\psi ,\varphi ,\varphi ){\underline{w}}_{\varphi \varphi }(\sigma )\right)=0,\hfill \\ \hfill {\overline{w}}_t(\sigma )-{\overline{\Xi }}_{0t}(\psi ,\varphi ,\varphi ;\sigma )& +p{\overline{\Xi }}_{0t}(\psi ,\varphi ,\varphi ;\sigma )+\overline{{\rm Y}}(\psi ,\varphi ,\varphi ;\sigma )+p\left({\phi }_1(\psi ,\varphi ,\varphi ){\overline{w}}_{\psi \psi }(\sigma )\right.\hfill \end{array}$$

(195)

$$\begin{array}{cc}\hfill & \left.+{\phi }_2(\psi ,\varphi ,\varphi ){\overline{w}}_{\varphi \varphi }(\sigma )+{\phi }_3(\psi ,\varphi ,\varphi ){\overline{w}}_{\varphi \varphi }(\sigma )\right)=0,\hfill \end{array}$$

(196)

and the initial approximation ${\tilde{\Xi }}_0(\psi ,\varphi ,\varphi ;\sigma )=\tilde{w}(\psi ,\varphi ,\varphi ,0)(\sigma )={\phi }_4(\psi ,\varphi ,\varphi ;\sigma ).$

Suppose the solution to (192) as

$$\begin{array}{cc}\hfill \underline{w}(\sigma )& ={\underline{w}}_0(\sigma )+p{\underline{w}}_1(\sigma )+p^2{\underline{w}}_2(\sigma )+\dots ,\hfill \end{array}$$

(197)

$$\begin{array}{cc}\hfill \overline{w}(\sigma )& ={\overline{w}}_0(\sigma )+p{\overline{w}}_1(\sigma )+p^2{\overline{w}}_2(\sigma )+\dots .\hfill \end{array}$$

(198)

Substituting (198) into (195), and equating the terms of the same power of p, we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}^0:{\underline{w}}_{0t}(\sigma )-{\underline{\Xi }}_{0t}(\psi ,\varphi ,\varphi ;\sigma )=\tilde{0},{\underline{\Xi }}_0(\psi ,\varphi ,\varphi ;\sigma )={\underline{\phi }}_4(\psi ,\varphi ,\varphi ;\sigma )+\underline{{\rm Y}}(\psi ,\varphi ,\varphi ;\sigma ),\hfill \\ p^1:{\underline{w}}_{1t}(\psi ,\varphi ,\varphi ;\sigma )+\underline{{\rm Y}}(\psi ,\varphi ,\varphi ;\sigma )+{\phi }_1(\psi ,\varphi ,\varphi ){\underline{w}}_{0\psi \psi }(\sigma )+{\phi }_2(\psi ,\varphi ,\varphi ){\underline{w}}_{0\varphi \varphi }(\sigma )\hfill \\ +{\phi }_3(\psi ,\varphi ,\varphi ){\underline{w}}_{0\varphi \varphi }(\sigma )+{\underline{\Xi }}_{0t}(\psi ,\varphi ,\varphi ;\sigma )=\tilde{0},\hfill \\ {\underline{w}}_1(\psi ,\varphi ,\varphi ,0)(\sigma )=\tilde{0},\hfill \\ p^2:{\underline{w}}_{2t}(\psi ,\varphi ,\varphi ;\sigma )+\underline{{\rm Y}}(\psi ,\varphi ,\varphi ;\sigma )+{\phi }_1(\psi ,\varphi ,\varphi ){\underline{w}}_{1\psi \psi }(\sigma )+{\phi }_2(\psi ,\varphi ,\varphi ){\underline{w}}_{1\varphi \varphi }(\sigma )\hfill \\ +{\phi }_3(\psi ,\varphi ,\varphi ){\underline{w}}_{1\varphi \varphi }(\sigma )=\tilde{0},\hfill \\ {\underline{w}}_2(\psi ,\varphi ,\varphi ;\sigma )=\tilde{0},\hfill \\ ⋮,\hfill \end{array}\right.\end{array}$$

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}^0:{\overline{w}}_{0t}(\sigma )-{\overline{\Xi }}_{0t}(\psi ,\varphi ,\varphi ;\sigma )=\tilde{0},{\overline{\Xi }}_0(\psi ,\varphi ,\varphi ;\sigma )={\overline{\phi }}_4(\psi ,\varphi ,\varphi ;\sigma )+\overline{{\rm Y}}(\psi ,\varphi ,\varphi ;\sigma ),\hfill \\ p^1:{\overline{w}}_{1t}(\psi ,\varphi ,\varphi ;\sigma )+\overline{{\rm Y}}(\psi ,\varphi ,\varphi ;\sigma )+{\phi }_1(\psi ,\varphi ,\varphi ){\overline{w}}_{0\psi \psi }(\sigma )+{\phi }_2(\psi ,\varphi ,\varphi ){\overline{w}}_{0\varphi \varphi }(\sigma )\hfill \\ +{\phi }_3(\psi ,\varphi ,\varphi ){\overline{w}}_{0\varphi \varphi }(\sigma )+{\overline{\Xi }}_{0t}(\psi ,\varphi ,\varphi ;\sigma )=\tilde{0},\hfill \\ {\overline{w}}_1(\psi ,\varphi ,\varphi ,0)(\sigma )=\tilde{0},\hfill \\ p^2:{\overline{w}}_{2t}(\psi ,\varphi ,\varphi ;\sigma )+\overline{{\rm Y}}(\psi ,\varphi ,\varphi ;\sigma )+{\phi }_1(\psi ,\varphi ,\varphi ){\overline{w}}_{1\psi \psi }(\sigma )+{\phi }_2(\psi ,\varphi ,\varphi ){\overline{w}}_{1\varphi \varphi }(\sigma )\hfill \\ +{\phi }_3(\psi ,\varphi ,\varphi ){\overline{w}}_{1\varphi \varphi }(\sigma )=\tilde{0},\hfill \\ {\overline{w}}_2(\psi ,\varphi ,\varphi ;\sigma )=\tilde{0},\hfill \\ ⋮.\hfill \end{array}\right.\end{array}$$

5.2.3. Fuzzy Wave-like Equations

The parametric fuzzy wave-like Equation (152), can be written as follows:

$$\begin{array}{cc}\hfill {\underline{w}}_{tt}(\sigma )+{\vartheta }_1(\psi ,\varphi ,\varphi ){\underline{w}}_{\psi \psi }(\sigma )+{\vartheta }_2(\psi ,\varphi ,\varphi ){\underline{w}}_{\varphi \varphi }(\sigma )+{\vartheta }_3(\psi ,\varphi ,\varphi ){\underline{w}}_{\varphi \varphi }(\sigma )& =\tilde{0},\hfill \end{array}$$

(199)

$$\begin{array}{cc}\hfill {\overline{w}}_{tt}(\sigma )+{\vartheta }_1(\psi ,\varphi ,\varphi ){\overline{w}}_{\psi \psi }(\sigma )+{\vartheta }_2(\psi ,\varphi ,\varphi ){\overline{w}}_{\varphi \varphi }(\sigma )+{\vartheta }_3(\psi ,\varphi ,\varphi ){\overline{w}}_{\varphi \varphi }(\sigma )& =\tilde{0}.\hfill \end{array}$$

(200)

Applying the fuzzy HPM, we construct the homotopy $\Psi \times [0,1]\to \mathbb{R}$, which satisfies

$$\begin{array}{cc}\hfill & {\underline{w}}_{tt}(\sigma )-{\underline{\Xi }}_{0tt}(\psi ,\varphi ,\varphi ,t;\sigma )+p{\underline{\Xi }}_{0tt}(\psi ,\varphi ,\varphi ,t;\sigma )+p({\vartheta }_1(\psi ,\varphi ,\varphi ){\underline{w}}_{\psi \psi }(\sigma )\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +{\vartheta }_2(\psi ,\varphi ,\varphi ){\underline{w}}_{\varphi \varphi }(\sigma )+{\vartheta }_3(\psi ,\varphi ,\varphi ){\underline{w}}_{\varphi \varphi })(\sigma )=\tilde{0},\hfill \\ \hfill & {\overline{w}}_{tt}(\sigma )-{\overline{\Xi }}_{0tt}(\psi ,\varphi ,\varphi ,t;\sigma )+p{\overline{\Xi }}_{0tt}(\psi ,\varphi ,\varphi ,t;\sigma )+p({\vartheta }_1(\psi ,\varphi ,\varphi ){\overline{w}}_{\psi \psi }(\sigma )\hfill \end{array}$$

(201)

$$\begin{array}{cc}\hfill & +{\vartheta }_2(\psi ,\varphi ,\varphi ){\overline{w}}_{\varphi \varphi }(\sigma )+{\vartheta }_3(\psi ,\varphi ,\varphi ){\overline{w}}_{\varphi \varphi })(\sigma )=\tilde{0},\hfill \end{array}$$

(202)

and the initial approximation ${\tilde{\Xi }}_0(\psi ,\varphi ,\varphi ;\sigma )={\vartheta }_4(\psi ,\varphi ,\varphi ;\sigma )+t{\vartheta }_5(\psi ,\varphi ,\varphi ;\sigma )$. Assume that the solution to (199) and (200) as

$$\begin{array}{cc}\hfill \underline{w}(\sigma )& ={\underline{w}}_0(\sigma )+p{\underline{w}}_1(\sigma )+p^2{\underline{w}}_2(\sigma )+\dots ,\hfill \end{array}$$

(203)

$$\begin{array}{cc}\hfill \overline{w}(\sigma )& ={\overline{w}}_0(\sigma )+p{\overline{w}}_1(\sigma )+p^2{\overline{w}}_2(\sigma )+\dots .\hfill \end{array}$$

(204)

Substituting (204) into (201), and equating the terms of the same power of p, we have

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}^0:{\underline{w}}_{0tt}(\sigma )-{\underline{\Xi }}_{0tt}(\psi ,\varphi ,\varphi ;\sigma )=\tilde{0},{\underline{\Xi }}_0(\psi ,\varphi ,\varphi ,t;\sigma )={\underline{\vartheta }}_4(\psi ,\varphi ,\varphi ;\sigma )+t{\underline{\vartheta }}_5(\psi ,\varphi ,\varphi ;\sigma ),\hfill \\ p^1:{\underline{w}}_{1tt}(\sigma )+{\vartheta }_1(\psi ,\varphi ,\varphi ){\underline{w}}_{0\psi \psi }(\sigma )+{\vartheta }_2(\psi ,\varphi ,\varphi ){\underline{w}}_{0\varphi \varphi }(\sigma )+{\vartheta }_3(\psi ,\varphi ,\varphi ){\underline{w}}_{0\varphi \varphi }(\sigma )\hfill \\ +{\underline{\Xi }}_{0tt}(\psi ,\varphi ,\varphi ,t;\sigma )=\tilde{0},{\underline{w}}_1(\psi ,\varphi ,\varphi ,0)(\sigma )=\tilde{0},\hfill \\ p^2:{\underline{w}}_{2tt}(\sigma )+{\vartheta }_1(\psi ,\varphi ,\varphi ){\underline{w}}_{1\psi \psi }(\sigma )+{\vartheta }_2(\psi ,\varphi ,\varphi ){\underline{w}}_{1\varphi \varphi }(\sigma )+{\vartheta }_3(\psi ,\varphi ,\varphi ){\underline{w}}_{1\varphi \varphi }(\sigma )=\tilde{0},\hfill \\ {\underline{w}}_2(\psi ,\varphi ,\varphi ;\sigma )=\tilde{0},\hfill \\ ⋮,\hfill \end{array}\right.\end{array}$$

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}^0:{\overline{w}}_{0tt}(\sigma )-{\overline{\Xi }}_{0tt}(\psi ,\varphi ,\varphi ;\sigma )=\tilde{0},{\overline{\Xi }}_0(\psi ,\varphi ,\varphi ,t;\sigma )={\overline{\vartheta }}_4(\psi ,\varphi ,\varphi ;\sigma )+t{\overline{\vartheta }}_5(\psi ,\varphi ,\varphi ;\sigma ),\hfill \\ p^1:{\overline{w}}_{1tt}(\sigma )+{\vartheta }_1(\psi ,\varphi ,\varphi ){\overline{w}}_{0\psi \psi }(\sigma )+{\vartheta }_2(\psi ,\varphi ,\varphi ){\overline{w}}_{0\varphi \varphi }(\sigma )+{\vartheta }_3(\psi ,\varphi ,\varphi ){\overline{w}}_{0\varphi \varphi }(\sigma )\hfill \\ +{\underline{\Xi }}_{0tt}(\psi ,\varphi ,\varphi ,t;\sigma )=\tilde{0},{\overline{w}}_1(\psi ,\varphi ,\varphi ,0)(\sigma )=\tilde{0},\hfill \\ p^2:{\overline{w}}_{2tt}(\sigma )+{\vartheta }_1(\psi ,\varphi ,\varphi ){\overline{w}}_{1\psi \psi }(\sigma )+{\vartheta }_2(\psi ,\varphi ,\varphi ){\overline{w}}_{1\varphi \varphi }(\sigma )+{\vartheta }_3(\psi ,\varphi ,\varphi ){\overline{w}}_{1\varphi \varphi }(\sigma )=\tilde{0},\hfill \\ {\overline{w}}_2(\psi ,\varphi ,\varphi ;\sigma )=\tilde{0},\hfill \\ ⋮.\hfill \end{array}\right.\end{array}$$

Assume ${\tilde{w}}_0(\psi ,\varphi ,\varphi ;\sigma )={\tilde{\Xi }}_0(\psi ,\varphi ,\varphi ;\sigma )$,

$$\begin{array}{cc}\hfill \underline{w}(\sigma )& =\underset{n\to \infty }{lim}\left({\underline{w}}_0+{\underline{w}}_1+{\underline{w}}_2+···\right)(\sigma ),\hfill \end{array}$$

(205)

$$\begin{array}{cc}\hfill \overline{w}(\sigma )& =\underset{n\to \infty }{lim}\left({\overline{w}}_0+{\overline{w}}_1+{\overline{w}}_2+···\right)(\sigma ).\hfill \end{array}$$

(206)

The convergence analysis theory of the fuzzy HPM; see (Osman et al. [40]).

5.3. Examples

In this part, we present the exact solutions to the fuzzy heat-like and wave-like equations with variable coefficients discussed by Osman et al. [39] to assess the efficiency of the fuzzy RDTM and HPM.

Example 7.

Consider the following one-dimensional fuzzy heat-like equation with variable coefficients in the form [39]

$${\tilde{w}}_t(\psi ,t){\ominus }_{gH}\frac{{\psi }^2}{2}\odot {\tilde{w}}_{\psi \psi }(\psi ,t)=0,$$

(207)

subject to the initial condition

$$\tilde{w}(\psi ,0)={\tilde{k}}^n\odot {\psi }^2.$$

(208)

Above ${\tilde{k}}^n\in {\mathbb{E}}^1$, $n=1,2,3,\dots ,$ fuzzy number is defined by

$$\tilde{k}\left(s\right)=\left\{\begin{array}{c}\frac{1}{3}(2s+1),s\in [-0.5,1],\hfill \\ 3-2ss\in (1,1.5],\hfill \\ 0s\notin [-0.5,1.5],\hfill \end{array}\right.$$

(209)

and $\left[\underline{{\tilde{k}}^n}\right](\sigma )={(-0.5+1.5\sigma )}^n,\left[\overline{{\tilde{k}}^n}\right](\sigma )={(1.5-0.5\sigma )}^n.$

Case [A]. Fuzzy reduced differential transform method

Using the fuzzy RDTM to (207) yields

$$\begin{array}{cc}\hfill (j+1){\underline{W}}_{j+1}(\psi ;\sigma )& =\frac{{\psi }^2}{2}\frac{{\partial }^2}{\partial {\psi }^2}{\underline{W}}_j(\psi ;\sigma ),\hfill \end{array}$$

(210)

$$\begin{array}{cc}\hfill (j+1){\overline{W}}_{j+1}(\psi ;\sigma )& =\frac{{\psi }^2}{2}\frac{{\partial }^2}{\partial {\psi }^2}{\overline{W}}_j(\psi ;\sigma ).\hfill \end{array}$$

(211)

From the initial condition (208), we obtain

$$\begin{array}{cc}\hfill {\underline{W}}_0(\psi ;\sigma )& ={(1.5\sigma -0.5)}^n{\psi }^2,\hfill \end{array}$$

(212)

$$\begin{array}{cc}\hfill {\overline{W}}_0(\psi ;\sigma )& ={(1.5-0.5\sigma )}^n{\psi }^2.\hfill \end{array}$$

(213)

Substituting (213) into (210), we obtain

$$\begin{array}{cc}\hfill {\underline{W}}_1(\psi ;\sigma )& ={(1.5\sigma -0.5)}^n{\psi }^2,{\underline{W}}_2(\psi ;\sigma )=\frac{{(1.5\sigma -0.5)}^n}{2!}{\psi }^2,\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\underline{W}}_3(\psi ;\sigma )& =\frac{{(1.5\sigma -0.5)}^n}{3!}{\psi }^2,\cdots \hfill \\ \hfill {\overline{W}}_1(\psi ;\sigma )& ={(1.5-0.5\sigma )}^n{\psi }^2,{\overline{W}}_2(\psi ;\sigma )=\frac{{(1.5-0.5\sigma )}^n}{2!}{\psi }^2,\hfill \end{array}$$

(214)

$$\begin{array}{cc}\hfill {\overline{W}}_3(\psi ;\sigma )& =\frac{{(1.5-0.5\sigma )}^n}{3!}{\psi }^2,\cdots \hfill \end{array}$$

(215)

Applying the fuzzy inverse transformation of the set of values ${\left[{\tilde{w}}_j(\psi ;\sigma )\right]}_{j=0}^n$ gives n-terms approximation solutions as

$$\begin{array}{cc}\hfill {\underline{w}}_n(\psi ,t;\sigma )& =\sum _{j=0}^{\infty }{\underline{W}}_j(\psi ,\sigma )t^j\hfill \\ \hfill & =\left[{\underline{W}}_0(\psi ;\sigma )+{\underline{W}}_1(\psi ,\sigma )t+{\underline{W}}_2(\psi ;\sigma )t^2+{\underline{W}}_3(\psi ;\sigma )t^3+···\right],\hfill \\ \hfill & ={(1.5\sigma -0.5)}^n\left[\left(1+t+\frac{t^2}{2!}+\frac{t^3}{3!}+···\right){\psi }^2\right],\hfill \\ \hfill {\overline{w}}_n(\psi ,t;\sigma )& =\sum _{j=0}^{\infty }{\overline{W}}_j(\psi ,\sigma )t^j\hfill \\ \hfill & =\left[{\overline{W}}_0(\psi ;\sigma )+{\overline{W}}_1(\psi ,\sigma )t+{\overline{W}}_2(\psi ,\sigma )t^2+{\overline{W}}_3(\psi ,\sigma )t^3+···\right],\hfill \\ \hfill & ={(1.5-0.5\sigma )}^n\left[\left(1+t+\frac{t^2}{2!}+\frac{t^3}{3!}+···\right){\psi }^2\right].\hfill \end{array}$$

Thus, we can obtain the exact solution as:

$$\tilde{w}(\psi ,t;\sigma )=[{(1.5\sigma -0.5)}^n,{(1.5-0.5\sigma )}^n]\odot \left(exp\left(t\right){\psi }^2\right),0\le \sigma \le 1.$$

Case [B]. Fuzzy Homotopy perturbation method

Using the fuzzy HPM, we can construct the homotopy $\Psi \times [0,1]\to \mathbb{R}$ which satisfies

$$\begin{array}{cc}\hfill {\underline{w}}_t(\psi ,t;\sigma )-{\underline{\Xi }}_{0t}+p{\underline{\Xi }}_{0t}-p\left(\frac{{\psi }^2}{2}{\underline{w}}_{\psi \psi }(\psi ,t;\sigma )\right)& =\tilde{0},\hfill \end{array}$$

(216)

$$\begin{array}{cc}\hfill {\overline{w}}_t(\psi ,t;\sigma )-{\overline{\Xi }}_{0t}+p{\overline{\Xi }}_{0t}-p\left(\frac{{\psi }^2}{2}{\overline{w}}_{\psi \psi }(\psi ,t;\sigma )\right)& =\tilde{0},\hfill \end{array}$$

(217)

and the initial approximation ${\tilde{\Xi }}_0(\psi ,t;\sigma )=\tilde{w}(\psi ;\sigma )(\sigma )=[{(1.5\sigma -0.5)}^n,{(1.5-0.5\sigma )}^n]\odot {\psi }^2,$ where (n = 1,2,3,…). Let the solution of (207) be represented as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \underline{w}(\sigma )& =\left({\underline{w}}_0+{\underline{w}}_{1}p+{\underline{w}}_2{p}^2+···\right)(\sigma ),\hfill \\ \hfill \overline{w}(\sigma )& =\left({\overline{w}}_0+{\overline{w}}_{1}p+{\overline{w}}_2{p}^2+···\right)(\sigma ).\hfill \end{array}\right.\end{array}$$

(218)

Substituting (218) into (216), and equations the terms of the same power of p

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}^0:{\underline{w}}_{0t}(\psi ,t;\sigma )-{\underline{\Xi }}_{0t}(\sigma )=\tilde{0},{\underline{\Xi }}_0(\psi ,t;\sigma )={(1.5\sigma -0.5)}^n{\psi }^2,\hfill \\ p^1:{\underline{w}}_{1t}(\psi ,t;\sigma )-\frac{{\psi }^2}{2}{\underline{w}}_{0\psi \psi }(\psi ,t;\sigma )-{\Xi }_{0t}(\sigma )=\tilde{0},{\underline{w}}_1(\psi ,t;\sigma )=\tilde{0},\hfill \\ p^2:{\underline{w}}_{2t}(\psi ,t;\sigma )-\frac{{\psi }^2}{2}{\underline{w}}_{1\psi \psi }(\psi ,t;\sigma )=\tilde{0},{\underline{w}}_2(\psi ,t;\sigma )=\tilde{0}\hfill \\ ⋮,\hfill \end{array}\right.\end{array}$$

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}^0:{\overline{w}}_{0t}(\psi ,t;\sigma )-{\overline{\Xi }}_{0t}(\sigma )=\tilde{0},{\overline{\Xi }}_0(\psi ,t;\sigma )={(1.5-0.5\sigma )}^n{\psi }^2,\hfill \\ p^1:{\overline{w}}_{1t}(\psi ,t;\sigma )-\frac{{\psi }^2}{2}{\overline{w}}_{0\psi \psi }(\psi ,t;\sigma )-{\overline{\Xi }}_{0t}(\sigma )=\tilde{0},{\overline{w}}_1(\psi ,t;\sigma )=\tilde{0},\hfill \\ p^2:{\overline{w}}_{2t}(\psi ,t;\sigma )-\frac{{\psi }^2}{2}{\overline{w}}_{1\psi \psi }(\psi ,t;\sigma )=\tilde{0},{\overline{w}}_2(\psi ,t;\sigma )=\tilde{0}\hfill \\ ⋮.\hfill \end{array}\right.\end{array}$$

By choosing ${\tilde{w}}_0(\psi ,t;\sigma )={\tilde{\Xi }}_0(\psi ,t;\sigma ),$ and the solving the mentioned equations, we get power of p as

$$\begin{array}{cc}\hfill {\underline{w}}_1(\psi ,t;\sigma )& ={(1.5\sigma -0.5)}^{n}t{\psi }^2,{\underline{w}}_2(\psi ,t;\sigma )={(1.5\sigma -0.5)}^n\left(\frac{t^2}{2!}{\psi }^2\right),\dots \hfill \\ \hfill {\overline{w}}_1(\psi ,t;\sigma )& ={(1.5-0.5\sigma )}^{n}t{\psi }^2,{\overline{w}}_2(\psi ,t;\sigma )={(1.5-0.5\sigma )}^n\left(\frac{t^2}{2!}{\psi }^2\right),\dots \hfill \end{array}$$

Therefore, the exact solution of (207) is obtained as:

$$\tilde{w}(\psi ,t;\sigma )=[{(1.5\sigma -0.5)}^n,{(1.5-0.5\sigma )}^n]\odot \left(exp\left(t\right){\psi }^2\right),0\le \sigma \le 1.$$

Example 8.

Consider the two-dimensional fuzzy heat-like equation with variable coefficients in the form [39]

$${\tilde{w}}_t(\psi ,\varphi ,t){\ominus }_{gH}\frac{1}{2}({\varphi }^2\odot {\tilde{w}}_{\psi \psi }\oplus {\psi }^2\odot {\tilde{w}}_{\varphi \varphi })=0,$$

(219)

with the initial condition

$$\tilde{w}(\psi ,\varphi ,0)=\left[{(1+2\sigma )}^n,{(5-2\sigma )}^n\right]{\ominus }_{gH}{\varphi }^2,$$

(220)

where $n=1,2,3,\dots$

Case [A]. Fuzzy reduced differential transform method

Taking the fuzzy RDTM to (219) yields

$$\begin{array}{cc}\hfill (j+1){\underline{W}}_{j+1}(\psi ,\varphi ;\sigma )& =\frac{1}{2}\left[{\varphi }^2\frac{{\partial }^2}{\partial {\psi }^2}+{\psi }^2\frac{{\partial }^2}{\partial {\varphi }^2}\right]{\underline{W}}_j(\psi ,\varphi ;\sigma ),\hfill \end{array}$$

(221)

$$\begin{array}{cc}\hfill (j+1){\overline{W}}_{j+1}(\psi ,\varphi ;\sigma )& =\frac{1}{2}\left[{\varphi }^2\frac{{\partial }^2}{\partial {\psi }^2}+{\psi }^2\frac{{\partial }^2}{\partial {\varphi }^2}\right]{\overline{W}}_j(\psi ,\varphi ;\sigma ),\hfill \end{array}$$

(222)

Taking the initial conditions (220), we have

$$\begin{array}{cc}\hfill {\underline{W}}_0(\psi ,\varphi ;\sigma )& ={(1+2\sigma )}^n-{\varphi }^2,\hfill \end{array}$$

(223)

$$\begin{array}{cc}\hfill {\overline{W}}_0(\psi ,\varphi ;\sigma )& ={(5-2\sigma )}^n-{\varphi }^2.\hfill \end{array}$$

(224)

Substituting (224) into (221), we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{W}}_1(\psi ,\varphi ;\sigma )& ={(1+2\sigma )}^n-{\psi }^2,{\underline{W}}_2(\psi ,\varphi ;\sigma )={(1+2\sigma )}^n-\frac{1}{2!}{\varphi }^2,\hfill \\ \hfill {\underline{W}}_3(\psi ,\varphi ;\sigma )& ={(1+2\sigma )}^n-\frac{1}{3!}{\psi }^2,{\underline{W}}_4(\psi ,\varphi ;\sigma )={(1+2\sigma )}^n-\frac{1}{4!}{\varphi }^2,\cdots \hfill \end{array}\right.\end{array}$$

(225)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\overline{W}}_1(\psi ,\varphi ;\sigma )& ={(5-2\sigma )}^n-{\psi }^2,{\overline{W}}_2(\psi ,\varphi ,\sigma )={(5-2\sigma )}^n-\frac{1}{2!}{\varphi }^2,\hfill \\ \hfill {\overline{W}}_3(\psi ,\varphi ;\sigma )& ={(5-2\sigma )}^n-\frac{1}{3!}{\psi }^2,{\overline{W}}_4(\psi ,\varphi ;\sigma )={(5-2\sigma )}^n-\frac{1}{4!}{\varphi }^2,\cdots \hfill \end{array}\right.\end{array}$$

(226)

According to the fuzzy inverse transformation of the set of values, ${\left[{\tilde{w}}_j(\psi ,\varphi ;\sigma )\right]}_{j=0}^n$ gives n-terms approximation solutions as:

$$\begin{array}{cc}\hfill {\underline{w}}_n(\psi ,\varphi ,t;\sigma )& ={(1+2\sigma )}^n-\left[\left(t+\frac{t^3}{3!}+···\right){\psi }^2+\left(1+\frac{t^2}{2!}+···\right){\varphi }^2\right],\hfill \\ \hfill {\overline{w}}_n(\psi ,\varphi ,t;\sigma )& ={(5-2\sigma )}^n-\left[\left(t+\frac{t^3}{3!}+···\right){\psi }^2+\left(1+\frac{t^2}{2!}+···\right){\varphi }^2\right].\hfill \end{array}$$

Thus, the exact solution can be obtained as:

$$\begin{array}{cc}\hfill \tilde{w}(\psi ,\varphi ,t;\sigma )& =[{(1+2\sigma )}^n,{(5-2\sigma )}^n]{\ominus }_{gH}\left({\psi }^{2}sinht+{\varphi }^{2}cosht\right),0\le \sigma \le 1.\hfill \end{array}$$

Case [B]. Fuzzy Homotopy perturbation method

Similarly, using the fuzzy HPM to (219) yields

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}^0:{\underline{w}}_{0t}(\psi ,\varphi ,t;\sigma )-{\underline{\Xi }}_{0t}(\sigma )=\tilde{0},{\underline{\Xi }}_0(\psi ,\varphi ,t;\sigma )={(1+2\sigma )}^n-{\varphi }^2,\hfill \\ p^1:\left({\underline{w}}_{1t}(\psi ,\varphi ,t;\sigma )-\frac{{\varphi }^2}{2}{\underline{w}}_{0\psi \psi }(\psi ,\varphi ,t;\sigma )-\frac{{\psi }^2}{2}{\underline{w}}_{0\varphi \varphi }(\psi ,\varphi ,t;\sigma )+{\underline{\Xi }}_{0t}(\sigma )\right)=\tilde{0},\hfill \\ {\underline{w}}_1(\psi ,\varphi ,0)(\sigma )=\tilde{0},\hfill \\ p^2:\left({\underline{w}}_{2t}(\psi ,\varphi ,t;\sigma )-\frac{{\varphi }^2}{2}{\underline{w}}_{1\psi \psi }(\psi ,\varphi ,t;\sigma )-\frac{{\psi }^2}{2}{\underline{w}}_{1\varphi \varphi }(\psi ,\varphi ,t;\sigma )\right)=\tilde{0},\hfill \\ {\underline{w}}_2(\psi ,\varphi ,0)(\sigma )=\tilde{0},\hfill \\ ⋮,\hfill \end{array}\right.\end{array}$$

(227)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}^0:{\overline{w}}_{0t}(\psi ,\varphi ,t;\sigma )-{\overline{\Xi }}_{0t}(\sigma )=\tilde{0},{\overline{\Xi }}_0(\psi ,\varphi ,t;\sigma )={(5-2\sigma )}^n-{\varphi }^2,\hfill \\ p^1:\left({\overline{w}}_{1t}(\psi ,\varphi ,t;\sigma )-\frac{{\varphi }^2}{2}{\overline{w}}_{0\psi \psi }(\psi ,\varphi ,t;\sigma )-\frac{{\psi }^2}{2}{\overline{w}}_{0\varphi \varphi }(\psi ,\varphi ,t;\sigma )+{\overline{\Xi }}_{0t}(\sigma )\right)=\tilde{0},\hfill \\ {\overline{w}}_1(\psi ,\varphi ,0)(\sigma )=\tilde{0},\hfill \\ p^2:\left({\overline{w}}_{2t}(\psi ,\varphi ,t;\sigma )-\frac{{\varphi }^2}{2}{\overline{w}}_{1\psi \psi }(\psi ,\varphi ,t;\sigma )-\frac{{\psi }^2}{2}{\overline{w}}_{1\varphi \varphi }(\psi ,\varphi ,t;\sigma )\right)=\tilde{0},\hfill \\ {\overline{w}}_2(\psi ,\varphi ,0)(\sigma )=\tilde{0},\hfill \\ ⋮.\hfill \end{array}\right.\end{array}$$

(228)

According to (227) and (228) with the initial approximation ${\tilde{w}}_0(\psi ,\varphi ,t;\sigma )={\tilde{\Xi }}_0(\psi ,\varphi ,t;\sigma ),$ we have

$$\begin{array}{cc}\hfill {\underline{w}}_1(\psi ,\varphi ,t;\sigma )& ={(1+2\sigma )}^n-t{\psi }^2,{\underline{w}}_2(\psi ,\varphi ,t;\sigma )={(1+2\sigma )}^n-\frac{t^2}{2!}{\varphi }^2,\hfill \\ \hfill {\underline{w}}_3(\psi ,\varphi ,t;\sigma )& ={(1+2\sigma )}^n-\frac{t^3}{3!}{\psi }^2\dots .,\hfill \\ \hfill {\overline{w}}_1(\psi ,\varphi ,t;\sigma )& ={(5-2\sigma )}^n-t{\psi }^2,{\overline{w}}_2(\psi ,\varphi ,t;\sigma )={(5-2\sigma )}^n-\frac{t^2}{2!}{\varphi }^2,\hfill \\ \hfill {\overline{w}}_3(\psi ,\varphi ,t;\sigma )& ={(5-2\sigma )}^n-\frac{t^3}{3!}{\psi }^2\dots .\hfill \end{array}$$

Therefore, the exact solution can be represented as:

$$\tilde{w}(\psi ,\varphi ,t;\sigma )=[{(1+2\sigma )}^n,{(5-2\sigma )}^n]{\ominus }_{gH}\left({\psi }^{2}sinht+{\varphi }^{2}cosht\right),0\le \sigma \le 1.$$

Example 9.

Consider the three-dimensional inhomogeneous fuzzy heat-like equation with variable coefficients [39]

$${\tilde{w}}_t(\psi ,\varphi ,t){\ominus }_{gH}\widetilde{{\rm Y}}(\psi ,\varphi ,z){\ominus }_{gH}\frac{1}{36}({\psi }^2\odot {\tilde{w}}_{\psi \psi }\oplus {\varphi }^2\odot {\tilde{w}}_{\varphi \varphi }\oplus {\varphi }^2\odot {\tilde{w}}_{\varphi \varphi })=\tilde{0},$$

(229)

with the initial condition

$$\tilde{w}(\psi ,\varphi ,0)=\tilde{0},$$

(230)

where

$$\begin{array}{cc}\hfill \widetilde{{\rm Y}}(\psi ,\varphi ,\varphi ;\sigma )& ={(-1,0,1)}^n\odot {(\psi \varphi \varphi )}^4\hfill \\ \hfill & =[{(\sigma -1)}^n,{(1-\sigma )}^n]\odot {(\psi \varphi \varphi )}^4,n=1,2,3,\dots ,\tilde{0}\in E^1,0\le \sigma \le 1.\hfill \end{array}$$

Case [A]. Fuzzy reduced differential transform method

Using the fuzzy RDTM to (229) yields

$$\begin{array}{cc}\hfill (j+1){\underline{W}}_{j+1}(\psi ,\varphi ,\varphi ;\sigma )& =\frac{1}{36}\left[{\psi }^2\frac{{\partial }^2}{\partial {\psi }^2}+{\varphi }^2\frac{{\partial }^2}{\partial {\varphi }^2}+{\varphi }^2\frac{{\partial }^2}{\partial {\varphi }^2}\right]{\underline{W}}_j(\psi ,\varphi ,\varphi ;\sigma )\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +\mathcal{N}\left({\underline{W}}_j(\psi ,\varphi ,\varphi ;\sigma )\right),\hfill \\ \hfill (j+1){\overline{W}}_{j+1}(\psi ,\varphi ,\varphi ;\sigma )& =\frac{1}{36}\left[{\psi }^2\frac{{\partial }^2}{\partial {\psi }^2}+{\varphi }^2\frac{{\partial }^2}{\partial {\varphi }^2}+{\varphi }^2\frac{{\partial }^2}{\partial {\varphi }^2}\right]{\overline{W}}_j(\psi ,\varphi ,\varphi ;\sigma )\hfill \end{array}$$

(231)

$$\begin{array}{cc}\hfill & +\mathcal{N}\left({\overline{W}}_j(\psi ,\varphi ,\varphi ;\sigma )\right),\hfill \end{array}$$

(232)

where $\mathcal{N}\left({\tilde{w}}_j(\psi ,\varphi ,\varphi ;\sigma )\right)$ is the transformed form of the nonlinear terms.

Taking the initial condition (230), we have

$$\begin{array}{cc}\hfill {\underline{W}}_0(\psi ,\varphi ,\varphi ;\sigma )& =\tilde{0},\hfill \end{array}$$

(233)

$$\begin{array}{cc}\hfill {\overline{W}}_0(\psi ,\varphi ,\varphi ;\sigma )& =\tilde{0}.\hfill \end{array}$$

(234)

Substituting (234) into (231), we obtain

$$\begin{array}{cc}\hfill {\underline{W}}_1(\psi ,\varphi ,\varphi ;\sigma )& ={(\sigma -1)}^n{(\psi \varphi \varphi )}^4,{\underline{W}}_2(\psi ,\varphi ,\varphi ;\sigma )={(\sigma -1)}^n\frac{{(\psi \varphi \varphi )}^4}{2!},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\underline{W}}_3(\psi ,\varphi ,\varphi ;\sigma )& ={(\sigma -1)}^n\frac{{(\psi \varphi \varphi )}^4}{3!},\cdots \hfill \\ \hfill {\overline{W}}_1(\psi ,\varphi ,\varphi ;\sigma )& ={(1-\sigma )}^n{(\psi \varphi \varphi )}^4,{\overline{W}}_2(\psi ,\varphi ,\varphi ;\sigma )={(1-\sigma )}^n\frac{{(\psi \varphi \varphi )}^4}{2!},\hfill \end{array}$$

(235)

$$\begin{array}{cc}\hfill {\overline{W}}_3(\psi ,\varphi ,\varphi ;\sigma )& ={(1-\sigma )}^n\frac{{(\psi \varphi \varphi )}^4}{3!},\cdots \hfill \end{array}$$

(236)

According to the fuzzy inverse transformation of the set of values, ${\left[{\tilde{w}}_j(\psi ,\varphi ,\varphi ;\sigma )\right]}_{j=0}^n$ gives n-terms approximation solutions as:

$$\begin{array}{cc}\hfill {\underline{w}}_n(\psi ,\varphi ,\varphi ,t;\sigma )& ={(\sigma -1)}^n\left[t+\frac{t^2}{2!}+\frac{t^3}{3!}+···\right]{(\psi \varphi \varphi )}^4,\hfill \end{array}$$

(237)

$$\begin{array}{cc}\hfill {\overline{w}}_n(\psi ,\varphi ,\varphi ,t;\sigma )& ={(1-\sigma )}^n\left[t+\frac{t^2}{2!}+\frac{t^3}{3!}+···\right]{(\psi \varphi \varphi )}^4.\hfill \end{array}$$

(238)

The exact solution can be obtained as:

$$\begin{array}{cc}\hfill \tilde{w}(\psi ,\varphi ,\varphi ,t;\sigma )& =[{(\sigma -1)}^n,{(1-\sigma )}^n]\odot \left((exp\left(t\right)-1){(\psi \varphi \varphi )}^4\right),0\le \sigma \le 1.\hfill \end{array}$$

Case [B]. Fuzzy Homotopy perturbation method

Using the fuzzy HPM to (229), we obtain

$$\begin{array}{cc}\hfill {\underline{w}}_t(\psi ,\varphi ,t;\sigma )-{(\sigma -1)}^n{(\psi \varphi \varphi )}^4-{\underline{\Xi }}_{0t}+p{\underline{\Xi }}_{0t}+p\left(\frac{1}{36}({\psi }^2{\underline{w}}_{\psi \psi }+{\varphi }^2{\underline{w}}_{\varphi \varphi }+{\varphi }^2{\underline{w}}_{\varphi \varphi })\right)& =\tilde{0},\hfill \end{array}$$

(239)

$$\begin{array}{cc}\hfill {\overline{w}}_t(\psi ,\varphi ,t;\sigma )-{(1-\sigma )}^n{(\psi \varphi \varphi )}^4-{\overline{\Xi }}_{0t}+p{\overline{\Xi }}_{0t}+p\left(\frac{1}{36}({\psi }^2{\overline{w}}_{\psi \psi }+{\varphi }^2{\overline{w}}_{\varphi \varphi }+{\varphi }^2{\overline{w}}_{\varphi \varphi })\right)& =\tilde{0},\hfill \end{array}$$

(240)

with the initial approximation $\tilde{w}(\psi ,\varphi ,0)(\sigma )=\tilde{0}$ where (n = 1,2,3,…), and $\tilde{0}\in E^1$.

Substituting (218), (240) and (239), with equating the terms of the same power of p, it follows that

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill p^0:& {\underline{w}}_{0t}(\psi ,\varphi ,\varphi ,t;\sigma )-{\underline{\Xi }}_{0t}(\sigma )=0,{\underline{\Xi }}_0(\psi ,\varphi ,\varphi ,t;\sigma )=\tilde{0},\hfill \\ \hfill p^1:& {\underline{w}}_{1t}(\psi ,\varphi ,\varphi ,t;\sigma )-{(\sigma -1)}^n{(\psi \varphi \varphi )}^4-\frac{1}{36}\left({\psi }^2{\underline{w}}_{0\psi \psi }(\psi ,\varphi ,\varphi ,t;\sigma )+{\varphi }^2{\underline{w}}_{0\varphi \varphi }(\psi ,\varphi ,\varphi ,t;\sigma )\right.\hfill \\ \hfill & \left.+{\varphi }^2{\underline{w}}_{0\varphi \varphi }(\psi ,\varphi ,\varphi ,t;\sigma )\right)+{\underline{\Xi }}_{0t}(\sigma )=\tilde{0},{\underline{w}}_1(\psi ,\varphi ,\varphi ;\sigma )=\tilde{0},\hfill \\ \hfill p^2:& {\underline{w}}_{2t}(\psi ,\varphi ,\varphi ,t;\sigma )-{(\sigma -1)}^n{(\psi \varphi \varphi )}^4-\frac{1}{36}\left({\psi }^2{\underline{w}}_{1\psi \psi }(\psi ,\varphi ,\varphi ,t;\sigma )+{\varphi }^2{\underline{w}}_{1\varphi \varphi }(\psi ,\varphi ,\varphi ,t;\sigma )\right.\hfill \\ \hfill & \left.+{\varphi }^2{\underline{w}}_{1\varphi \varphi }(\psi ,\varphi ,\varphi ,t;\sigma )\right)=\tilde{0},{\underline{w}}_2(\psi ,\varphi ,\varphi ;\sigma )=\tilde{0},\hfill \\ \hfill & ⋮,\hfill \end{array}\right.\end{array}$$

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill p^0:& {\overline{w}}_{0t}(\psi ,\varphi ,\varphi ,t;\sigma )-{\overline{\Xi }}_{0t}(\sigma )=0,{\overline{\Xi }}_0(\psi ,\varphi ,\varphi ,t;\sigma )=\tilde{0},\hfill \\ \hfill p^1:& {\overline{w}}_{1t}(\psi ,\varphi ,\varphi ,t;\sigma )-{(1-\sigma )}^n{(\psi \varphi \varphi )}^4-\frac{1}{36}\left({\psi }^2{\overline{w}}_{0\psi \psi }(\psi ,\varphi ,\varphi ,t;\sigma )+{\varphi }^2{\overline{w}}_{0\varphi \varphi }(\psi ,\varphi ,\varphi ,t;\sigma )\right.\hfill \\ \hfill & \left.+{\varphi }^2{\overline{w}}_{0\varphi \varphi }(\psi ,\varphi ,\varphi ,t;\sigma )\right)+{\overline{\Xi }}_{0t}(\sigma )=\tilde{0},{\overline{w}}_1(\psi ,\varphi ,\varphi ;\sigma )=\tilde{0},\hfill \\ \hfill p^2:& {\overline{w}}_{2t}(\psi ,\varphi ,\varphi ,t;\sigma )-{(1-\sigma )}^n{(\psi \varphi \varphi )}^4-\frac{1}{36}\left({\psi }^2{\overline{w}}_{1\psi \psi }(\psi ,\varphi ,\varphi ,t;\sigma )+{\varphi }^2{\overline{w}}_{1\varphi \varphi }(\psi ,\varphi ,\varphi ,t;\sigma )\right.\hfill \\ \hfill & \left.+{\varphi }^2{\overline{w}}_{1\varphi \varphi }(\psi ,\varphi ,\varphi ,t;\sigma )\right)=\tilde{0},{\overline{w}}_2(\psi ,\varphi ,\varphi ;\sigma )=\tilde{0},\hfill \\ \hfill & ⋮.\hfill \end{array}\right.\end{array}$$

Therefore, the exact solution is given as:

$$\tilde{w}(\psi ,\varphi ,\varphi ,t;\sigma )=[{(\sigma -1)}^n,{(1-\sigma )}^n]\odot \left((exp\left(t\right)-1){(\psi \varphi \varphi )}^4\right),0\le \sigma \le 1.$$

Example 10.

Consider the one-dimensional fuzzy wave-like equation with variable coefficients as [39]

$${\tilde{w}}_{tt}(\psi ,t){\ominus }_{gH}\frac{{\psi }^2}{2}\odot {\tilde{w}}_{\psi \psi }(\psi ,t)=\tilde{0},$$

(241)

subject to the initial conditions

$$\tilde{w}(\psi ,0)=\left[{\sigma }^n,{(2-\sigma )}^n\right]\odot \psi ,{\tilde{w}}_t(\psi ,0)=\left[{\sigma }^n,{(2-\sigma )}^n\right]\odot {\psi }^2,$$

(242)

where n = 1,2,3,…

Case [A]. Fuzzy reduced differential transform method

Using the fuzzy RDTM to (241) yields

$$\begin{array}{cc}\hfill (j+1)(j+2){\underline{W}}_{j+2}(\psi ;\sigma )& =\frac{{\psi }^2}{2}\frac{{\partial }^2}{\partial {\psi }^2}{\underline{W}}_j(\psi ;\sigma ),\hfill \end{array}$$

(243)

$$\begin{array}{cc}\hfill (j+1)(j+2){\overline{W}}_{j+2}(\psi ;\sigma )& =\frac{{\psi }^2}{2}\frac{{\partial }^2}{\partial {\psi }^2}{\overline{W}}_j(\psi ;\sigma ).\hfill \end{array}$$

(244)

From the initial conditions (242), we obtain

$$\begin{array}{cc}\hfill {\underline{W}}_0(\psi ;\sigma )& ={\sigma }^n\psi ,{\underline{W}}_1(\psi ;\sigma )={\sigma }^n{\psi }^2,\hfill \end{array}$$

(245)

$$\begin{array}{cc}\hfill {\overline{W}}_0(\psi ;\sigma )& ={(2-\sigma )}^n\psi ,{\overline{W}}_1(\psi ;\sigma )={(2-\sigma )}^n{\psi }^2.\hfill \end{array}$$

(246)

Substituting (246) into (243), we obtain

$$\begin{array}{cc}\hfill {\underline{W}}_2(\psi ;\sigma )& =\tilde{0},{\underline{W}}_3(\psi ;\sigma )=\frac{{\sigma }^n}{3!}{\psi }^2,{\underline{W}}_4(\psi ;\sigma )=\tilde{0},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\underline{W}}_5(\psi ;\sigma )& =\frac{{\sigma }^n}{5!}{\psi }^2,\cdots ,\hfill \\ \hfill {\overline{W}}_2(\psi ;\sigma )& =\tilde{0},{\overline{W}}_3(\psi ;\sigma )=\frac{{(2-\sigma )}^n}{3!}{\psi }^2,{\overline{W}}_4(\psi ;\sigma )=\tilde{0},\hfill \end{array}$$

(247)

$$\begin{array}{cc}\hfill {\overline{W}}_5(\psi ;\sigma )& =\frac{{(2-\sigma )}^n}{5!}{\psi }^2,\cdots .\hfill \end{array}$$

(248)

Applying the fuzzy inverse transformation of the set of values ${\left\{{\tilde{w}}_j(\psi ;\sigma )\right\}}_{j=0}^n$ gives n-terms approximation solutions as:

$$\begin{array}{cc}\hfill {\underline{w}}_n(\psi ;\sigma )& ={\sigma }^n\left[\psi +\left(t+\frac{t^3}{3!}+\frac{t^5}{5!}+···\right){\psi }^2\right],\hfill \\ \hfill {\overline{w}}_n(\psi ;\sigma )& ={(2-\sigma )}^n\left[\psi +\left(t+\frac{t^3}{3!}+\frac{t^5}{5!}+···\right){\psi }^2\right].\hfill \end{array}$$

The exact solution is given as:

$$\begin{array}{cc}\hfill \tilde{w}(\psi ,t;\sigma )& =[{\sigma }^n,{(2-\sigma )}^n]\odot \left(\psi +{\psi }^{2}sinht\right),0\le \sigma \le 1.\hfill \end{array}$$

Case [B]. Fuzzy Homotopy perturbation method

Applying the fuzzy HPM to (241) yields

$$\begin{array}{cc}\hfill {\underline{w}}_{tt}(\psi ,t;\sigma )-{\underline{\Xi }}_{0tt}(\sigma )+p{\underline{\Xi }}_{0tt}(\sigma )-p\left(\frac{{\psi }^2}{2}{\underline{w}}_{\psi \psi }(\psi ,t;\sigma )\right)& =\tilde{0},\hfill \end{array}$$

(249)

$$\begin{array}{cc}\hfill {\overline{w}}_{tt}(\psi ,t;\sigma )-{\overline{\Xi }}_{0tt}(\sigma )+p{\overline{\Xi }}_{0tt}(\sigma )-p\left(\frac{{\psi }^2}{2}{\overline{w}}_{\psi \psi }(\psi ,t;\sigma )\right)& =\tilde{0},\hfill \end{array}$$

(250)

with the initial approximation $\tilde{w}(\psi ;\sigma )(\sigma )=[{\sigma }^n,{(2-\sigma )}^n]\odot (\psi +t{\psi }^2),$ where (n = 1, 2, 3,…).

Suppose the solution of (241) can be represented as:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \underline{w}(\sigma )& =\left({\underline{w}}_0+{\underline{w}}_{1}p+{\underline{w}}_2{p}^2+···+{\underline{w}}_n\right)(\sigma ),\hfill \\ \hfill \overline{w}(\sigma )& =\left({\overline{w}}_0+{\overline{w}}_{1}p+{\overline{w}}_2{p}^2+···+{\overline{w}}_n\right)(\sigma ).\hfill \end{array}\right.\end{array}$$

(251)

Substituting (251) into (249), we have

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}^0:{\underline{w}}_{0tt}(\psi ,t;\sigma )-{\underline{\Xi }}_{0tt}(\sigma )=\tilde{0},{\underline{\Xi }}_0(\psi ,t;\sigma )={\sigma }^n(\psi +t{\psi }^2),\hfill \\ p^1:{\underline{w}}_{1tt}(\psi ,t;\sigma )-\frac{{\psi }^2}{2}{\underline{w}}_{0\psi \psi }(\psi ,t;\sigma )+{\underline{\Xi }}_{0tt}(\sigma )=\tilde{0},{\underline{w}}_1(\psi ,t;\sigma )=\tilde{0},\hfill \\ p^2:{\underline{w}}_{2tt}(\psi ,t;\sigma )-\frac{{\psi }^2}{2}{\underline{w}}_{1\psi \psi }(\psi ,t;\sigma )=\tilde{0},{\underline{w}}_2(\psi ;\sigma )(\sigma )=\tilde{0},\hfill \\ ⋮,\hfill \end{array}\right.\end{array}$$

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}^0:{\overline{w}}_{0tt}(\psi ,t;\sigma )-{\overline{\Xi }}_{0tt}(\sigma )=\tilde{0},{\overline{\Xi }}_0(\psi ,t;\sigma )={(2-\sigma )}^n(\psi +t{\psi }^2),\hfill \\ p^1:{\overline{w}}_{1tt}(\psi ,t;\sigma )-\frac{{\varphi }^2}{2}{\overline{w}}_{0\psi \psi }(\psi ,t;\sigma )+{\overline{\Xi }}_{0tt}(\sigma )=\tilde{0},{\overline{w}}_1(\psi ,t;\sigma )=\tilde{0},\hfill \\ p^2:{\overline{w}}_{2tt}(\psi ,t;\sigma )-\frac{{\psi }^2}{2}{\overline{w}}_{1\psi \psi }(\psi ,t;\sigma )=\tilde{0},{\overline{w}}_2(\psi ;\sigma )(\sigma )=\tilde{0},\hfill \\ ⋮,\hfill \end{array}\right.\end{array}$$

and the initial approximation ${\tilde{w}}_0(\psi ,t;\sigma )={\tilde{\Xi }}_0(\psi ,t;\sigma ),$ we obtain

$$\begin{array}{cc}\hfill {\underline{w}}_1(\psi ,t;\sigma )& =\frac{t^3{\sigma }^n}{3!}{\psi }^2,{\underline{w}}_2(\psi ,t;\sigma )=\frac{t^5{\sigma }^n}{5!}{\psi }^2,\cdots ,\hfill \\ \hfill {\overline{w}}_1(\psi ,t;\sigma )& =\frac{t^3{(2-\sigma )}^n}{3!}{\psi }^2,{\overline{w}}_2(\psi ,t;\sigma )=\frac{t^5{(2-\sigma )}^n}{5!}{\psi }^2,\cdots .\hfill \end{array}$$

Thus, the exact solution can be obtained as:

$$\begin{array}{cc}\hfill \tilde{w}(\psi ,t;\sigma )& =[{\sigma }^n,{(2-\sigma )}^n]\odot \left(\psi +{\psi }^{2}sinht\right),0\le \sigma \le 1.\hfill \end{array}$$

Example 11.

Consider the two-dimensional fuzzy wave-like equation with variable coefficients as [39]

$${\tilde{w}}_{tt}(\psi ,\varphi ,t){\ominus }_{gH}\frac{1}{12}({\psi }^2\odot {\tilde{w}}_{\psi \psi }\oplus {\varphi }^2\odot {\tilde{w}}_{\varphi \varphi })=\tilde{0},$$

(252)

with the initial conditions

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \tilde{w}(\psi ,\varphi ,0)=\left[{(0.2+0.2\sigma )}^n,{(0.6-0.2\sigma )}^n\right]\odot {\psi }^4,\hfill \\ \hfill & {\tilde{w}}_t(\psi ,\varphi ,0)=\left[{(0.2+0.2\sigma )}^n,{(0.6-0.2\sigma )}^n\right]\odot {\varphi }^4,\hfill \end{array}\end{array}$$

(253)

where $n=1,2,3,\dots$

Case [A]. Fuzzy reduced differential transform method

Applying the fuzzy RDTM to (252) yields

$$\begin{array}{cc}\hfill (j+1)(j+2){\underline{W}}_{j+2}(\psi ,\varphi ,t;\sigma )& =\frac{1}{12}\left[{\psi }^2\frac{{\partial }^2}{\partial {\psi }^2}+{\varphi }^2\frac{{\partial }^2}{\partial {\varphi }^2}\right]{\underline{W}}_j(\psi ,\varphi ,t;\sigma ),\hfill \end{array}$$

(254)

$$\begin{array}{cc}\hfill (j+1)(j+2){\overline{W}}_{j+2}(\psi ,\varphi ,t;\sigma )& =\frac{1}{12}\left[{\psi }^2\frac{{\partial }^2}{\partial {\psi }^2}+{\varphi }^2\frac{{\partial }^2}{\partial {\varphi }^2}\right]{\overline{W}}_j(\psi ,\varphi ,t;\sigma ).\hfill \end{array}$$

(255)

From the initial conditions (253), we obtain

$$\begin{array}{cc}\hfill {\underline{W}}_0(\psi ,\varphi ,t;\sigma )& ={(0.2+0.2\sigma )}^n{\psi }^4,{\underline{W}}_1(\psi ,\varphi ,t;\sigma )={(0.2+0.2\sigma )}^n{\varphi }^4,\hfill \end{array}$$

(256)

$$\begin{array}{cc}\hfill {\overline{W}}_0(\psi ,\varphi ,t;\sigma )& ={(0.6-0.2\sigma )}^n{\psi }^4,{\overline{W}}_1(\psi ,\varphi ,t;\sigma )={(0.6-0.2\sigma )}^n{\varphi }^4.\hfill \end{array}$$

(257)

Substituting (257) into (254), we obtain

$$\begin{array}{cc}\hfill {\underline{W}}_2(\psi ,\varphi ,t;\sigma )& =\frac{{(0.2+0.2\sigma )}^n{\psi }^4}{2!},{\underline{W}}_3(\psi ,\varphi ,t;\sigma )=\frac{{(0.2+0.2\sigma )}^n{\varphi }^4}{3!},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\underline{W}}_4(\psi ,\varphi ,t;\sigma )& =\frac{{(0.2+0.2\sigma )}^n{\psi }^4}{4!},\cdots ,\hfill \\ \hfill {\overline{W}}_2(\psi ,\varphi ,t;\sigma )& =\frac{{(0.6-0.2\sigma )}^n{\psi }^4}{2!},{\overline{W}}_3(\psi ,\varphi ,t;\sigma )=\frac{{(0.6-0.2\sigma )}^n{\varphi }^4}{3!},\hfill \end{array}$$

(258)

$$\begin{array}{cc}\hfill {\overline{W}}_4(\psi ,\varphi ,t;\sigma )& =\frac{{(0.6-0.2\sigma )}^n{\psi }^4}{4!},\cdots .\hfill \end{array}$$

(259)

Applying the fuzzy inverse transformation of the set of values ${\left\{{\tilde{w}}_j(\psi ,\varphi ;\sigma )\right\}}_{j=0}^n$ gives n-terms approximation solutions as:

$$\begin{array}{cc}\hfill {\underline{w}}_n(\psi ,\varphi ,t;\sigma )& ={(0.2+0.2\sigma )}^n\left[\left(1+\frac{t^2}{2!}+···\right){\psi }^4+\left(t+\frac{t^3}{3!}+···\right){\varphi }^4\right],\hfill \\ \hfill {\overline{w}}_n(\psi ,\varphi ,t;\sigma )& ={(0.6-0.2\sigma )}^n\left[\left(1+\frac{t^2}{2!}+···\right){\psi }^4+\left(t+\frac{t^3}{3!}+···\right){\varphi }^4\right].\hfill \end{array}$$

The exact solution can be represented as:

$$\begin{array}{cc}\hfill \tilde{w}(\psi ,\varphi ,t;\sigma )& =[{(0.2+0.2\sigma )}^n,{(0.6-0.2\sigma )}^n]\odot \left({\psi }^{4}cosht+{\varphi }^{4}sinht\right),0\le \sigma \le 1.\hfill \end{array}$$

Case [B]. Fuzzy Homotopy perturbation method

Similarly, using the fuzzy HPM to (252) yields

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}^0:{\underline{w}}_{0tt}(\psi ,\varphi ,t;\sigma )-{\underline{\Xi }}_{0tt}(\sigma )=\tilde{0},{\underline{\Xi }}_0(\psi ,\varphi ,t;\sigma )={(0.2+0.2\sigma )}^n({\psi }^4+t{\varphi }^4),\hfill \\ p^1:{\underline{w}}_{1tt}(\psi ,\varphi ,t;\sigma )-\frac{{\psi }^2}{12}{\underline{w}}_{0\psi \psi }(\psi ,\varphi ,t;\sigma )-\frac{{\varphi }^2}{12}{\underline{w}}_{0\varphi \varphi }(\psi ,\varphi ,t;\sigma )+{\underline{\Xi }}_{0tt}(\sigma )=\tilde{0},\hfill \\ {\underline{w}}_1(\psi ,\varphi ,t;\sigma )=\tilde{0},\hfill \\ p^2:{\underline{w}}_{2tt}(\psi ,\varphi ,t;\sigma )-\frac{{\psi }^2}{12}{\underline{w}}_{1\psi \psi }(\psi ,\varphi ,t;\sigma )-\frac{{\varphi }^2}{12}{\underline{w}}_{1\varphi \varphi }(\psi ,\varphi ,t;\sigma )=\tilde{0},\hfill \\ {\underline{w}}_2(\psi ,\varphi ,t;\sigma )=\tilde{0},\hfill \\ ⋮,\hfill \end{array}\right.\end{array}$$

(260)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}^0:{\overline{w}}_{0tt}(\psi ,\varphi ,t;\sigma )-{\overline{\Xi }}_{0tt}(\sigma )=\tilde{0},{\overline{\Xi }}_0(\psi ,\varphi ,t;\sigma )={(0.6-0.2\sigma )}^n({\psi }^4+t{\varphi }^4),\hfill \\ p^1:{\overline{w}}_{1tt}(\psi ,\varphi ,t;\sigma )-\frac{{\psi }^2}{12}{\overline{w}}_{0\psi \psi }(\psi ,\varphi ,t;\sigma )-\frac{{\varphi }^2}{12}{\overline{w}}_{0\varphi \varphi }(\psi ,\varphi ,t;\sigma )+{\overline{\Xi }}_{0tt}(\sigma )=\tilde{0},\hfill \\ {\overline{w}}_1(\psi ,\varphi ,t;\sigma )=\tilde{0},\hfill \\ p^2:{\overline{w}}_{2tt}(\psi ,\varphi ,t;\sigma )-\frac{{\psi }^2}{12}{\overline{w}}_{1\psi \psi }(\psi ,\varphi ,t;\sigma )-\frac{{\varphi }^2}{12}{\overline{w}}_{1\varphi \varphi }(\psi ,\varphi ,t;\sigma )=\tilde{0},\hfill \\ {\overline{w}}_2(\psi ,\varphi ,t;\sigma )=\tilde{0},\hfill \\ ⋮.\hfill \end{array}\right.\end{array}$$

(261)

According to (260) and (261) with the initial approximation ${\tilde{w}}_0(\psi ,\varphi ,t;\sigma )={\tilde{\Xi }}_0(\psi ,\varphi ,t;\sigma )$

$=[{(0.2+0.2\sigma )}^n,{(0.6-0.2\sigma )}^n]\odot ({\psi }^4+t{\varphi }^4),$ we have

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\underline{w}}_1(\psi ,\varphi ,t;\sigma )=\frac{t^2{(0.2+0.2\sigma )}^n}{2!}{\psi }^4+\frac{t^3{(0.2+0.2\sigma )}^n}{3!}{\varphi }^4\hfill \\ {\underline{w}}_2(\psi ,\varphi ,t;\sigma )=\frac{t^4{(0.2+0.2\sigma )}^n}{4!}{\psi }^4+\frac{t^5{(0.2+0.2\sigma )}^n}{5!}{\varphi }^4\hfill \\ ⋮,\hfill \end{array}\right.\end{array}$$

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\overline{w}}_1(\psi ,\varphi ,t;\sigma )=\frac{t^2{(0.6-0.2\sigma )}^n}{2!}{\psi }^4+\frac{t^3{(0.6-0.2\sigma )}^n}{3!}{\varphi }^4\hfill \\ {\overline{w}}_2(\psi ,\varphi ,t;\sigma )=\frac{t^4{(0.6-0.2\sigma )}^n}{4!}{\psi }^4+\frac{t^5{(0.6-0.2\sigma )}^n}{5!}{\varphi }^4,\hfill \\ ⋮.\hfill \end{array}\right.\end{array}$$

Hence, the exact solution of (252) is given as:

$$\begin{array}{cc}\hfill \tilde{w}(\psi ,\varphi ,t;\sigma )& =[{(0.2+0.2\sigma )}^n,{(0.6-0.2\sigma )}^n]\odot \left({\psi }^{4}cosht+{\varphi }^{4}sinht\right),0\le \sigma \le 1.\hfill \end{array}$$

Example 12.

Consider the three-dimensional fuzzy wave-like equation with variable coefficients in the form [39]

$${\tilde{w}}_{tt}{\ominus }_{gH}({\psi }^2+{\varphi }^2+{\varphi }^2){\ominus }_{gH}\frac{1}{2}({\psi }^2\odot {\tilde{w}}_{\psi \psi }\oplus {\varphi }^2\odot {\tilde{w}}_{\varphi \varphi }\oplus {\varphi }^2\odot {\tilde{w}}_{\varphi \varphi })=0,$$

(262)

subject to the initial conditions

$$\tilde{w}(\psi ,\varphi ,\varphi ,0)=\left[{(0.5\sigma )}^n,{(1-0.5\sigma )}^n\right],{\tilde{w}}_t(\psi ,\varphi ,\varphi ,0)=\left[{(0.5\sigma )}^n,{(1-0.5\sigma )}^n\right]\oplus ({\psi }^2+{\varphi }^2-{\varphi }^2),$$

(263)

where $n=1,2,3,\dots$

Case [A]. Fuzzy reduced differential transform method

Taking the fuzzy RDTM to (262) yields

$$\begin{array}{cc}\hfill (j+1)(j+2){\underline{W}}_{j+2}(\psi ,\varphi ,\varphi ;\sigma )& =\frac{1}{2}\left[{\psi }^2\frac{{\partial }^2}{\partial {\psi }^2}+{\varphi }^2\frac{{\partial }^2}{\partial {\varphi }^2}+{\varphi }^2\frac{{\partial }^2}{\partial {\varphi }^2}\right]{\underline{W}}_j(\psi ,\varphi ,\varphi ;\sigma )\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +\mathcal{N}\left({\underline{W}}_j(\psi ,\varphi ,\varphi ;\sigma )\right),\hfill \\ \hfill (j+1)(j+2){\overline{W}}_{j+2}(\psi ,\varphi ,\varphi ;\sigma )& =\frac{1}{2}\left[{\psi }^2\frac{{\partial }^2}{\partial {\psi }^2}+{\varphi }^2\frac{{\partial }^2}{\partial {\varphi }^2}+{\varphi }^2\frac{{\partial }^2}{\partial {\varphi }^2}\right]{\overline{W}}_j(\psi ,\varphi ,\varphi ;\sigma )\hfill \end{array}$$

(264)

$$\begin{array}{cc}\hfill & +\mathcal{N}\left({\overline{W}}_j(\psi ,\varphi ,\varphi ;\sigma )\right).\hfill \end{array}$$

(265)

From the initial conditions (263), we obtain

$$\begin{array}{cc}\hfill {\underline{W}}_0(\psi ,\varphi ,\varphi ;\sigma )& ={(0.5\sigma )}^n,{\underline{W}}_1(\psi ,\varphi ,\varphi ;\sigma )={(0.5\sigma )}^n+({\psi }^2+{\varphi }^2-{\varphi }^2),\hfill \end{array}$$

(266)

$$\begin{array}{cc}\hfill {\overline{W}}_0(\psi ,\varphi ,\varphi ;\sigma )& ={(1-0.5\sigma )}^n,{\overline{W}}_1(\psi ,\varphi ,\varphi ;\sigma )={(1-0.5\sigma )}^n+({\psi }^2+{\varphi }^2-{\varphi }^2).\hfill \end{array}$$

(267)

Substituting (267) into (264), we have

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{W}}_2(\psi ,\varphi ,\varphi ;\sigma )& ={(0.5\sigma )}^n+\left(\frac{1}{2!}({\psi }^2+{\varphi }^2+{\varphi }^2)\right),\hfill \\ \hfill {\underline{W}}_3(\psi ,\varphi ,\varphi ;\sigma )& ={(0.5\sigma )}^n+\left(\frac{1}{3!}({\psi }^2+{\varphi }^2-{\varphi }^2)\right),\hfill \\ \hfill {\underline{W}}_4(\psi ,\varphi ,\varphi ;\sigma )& ={(0.5\sigma )}^n+\left(\frac{1}{4!}({\psi }^2+{\varphi }^2+{\varphi }^2)\right),\hfill \\ \hfill ⋮,\end{array}\right.\end{array}$$

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\overline{W}}_2(\psi ,\varphi ,\varphi ;\sigma )& ={(1-0.5\sigma )}^n+\left(\frac{1}{2!}({\psi }^2+{\varphi }^2+{\varphi }^2)\right),\hfill \\ \hfill {\overline{W}}_3(\psi ,\varphi ,\varphi ;\sigma )& ={(1-0.5\sigma )}^n+\left(\frac{1}{3!}({\psi }^2+{\varphi }^2-{\varphi }^2)\right),\hfill \\ \hfill {\overline{W}}_4(\psi ,\varphi ,\varphi ;\sigma )& ={(1-0.5\sigma )}^n+\left(\frac{1}{4!}({\psi }^2+{\varphi }^2+{\varphi }^2)\right),\hfill \\ \hfill ⋮.\end{array}\right.\end{array}$$

Using the fuzzy inverse transformation of the set of values ${\left\{{\tilde{w}}_j(\psi ,\varphi ,\varphi ;\sigma )\right\}}_{j=0}^n$ gives n-terms approximation solutions as:

$$\begin{array}{cc}\hfill {\underline{w}}_n(\psi ,\varphi ,\varphi ,t;\sigma )& ={(0.5\sigma )}^n+\left[\left(t+\frac{t^2}{2!}+\frac{t^3}{3!}+···\right)({\psi }^2+{\varphi }^2)+\left(-t+\frac{t^2}{2!}-\frac{t^3}{3!}+···\right){\varphi }^2\right],\hfill \\ \hfill {\overline{w}}_n(\psi ,\varphi ,\varphi ,t;\sigma )& ={(1-0.5\sigma )}^n+\left[\left(t+\frac{t^2}{2!}+\frac{t^3}{3!}+···\right)({\psi }^2+{\varphi }^2)+\left(-t+\frac{t^2}{2!}-\frac{t^3}{3!}+···\right){\varphi }^2\right].\hfill \end{array}$$

The exact solution can be obtained as:

$$\begin{array}{cc}\hfill \tilde{w}(\psi ,\varphi ,\varphi ,t;\sigma )& =[{(0.5\sigma )}^n,{(1-0.5\sigma )}^n]\oplus \left(({\psi }^2+{\varphi }^2)e^t+{\varphi }^2{e}^{-t}-({\psi }^2+{\varphi }^2+{\varphi }^2)\right),0\le \sigma \le 1.\hfill \end{array}$$

Case [B]. Fuzzy Homotopy perturbation method

Similarly, using the fuzzy HPM to (262) yields

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill p^0:& {\underline{w}}_{0tt}(\psi ,\varphi ,\varphi ,t;\sigma )-{\underline{\Xi }}_{0tt}(\sigma )=\tilde{0},{\underline{\Xi }}_0(\sigma )={(0.5\sigma )}^n+t\left({\psi }^2+{\varphi }^2-{\varphi }^2\right),\hfill \\ \hfill p^1:& ({\underline{w}}_{1tt}(\psi ,\varphi ,\varphi ,t;\sigma )-({\psi }^2+{\varphi }^2-{\varphi }^2)+{(0.5\sigma )}^n-\frac{1}{2}\left({\psi }^2{\underline{w}}_{0\psi \psi }(\psi ,\varphi ,\varphi ,t;\sigma )\right.\hfill \\ \hfill & \left.+{\varphi }^2{\underline{w}}_{0\varphi \varphi }(\psi ,\varphi ,\varphi ,t;\sigma )+{\varphi }^2{\underline{w}}_{0\varphi \varphi }(\psi ,\varphi ,\varphi ,t;\sigma )\right)=\tilde{0},{\underline{w}}_1(\psi ,\varphi ,\varphi ,t;\sigma )=\tilde{0},\hfill \\ \hfill p^2:& ({\underline{w}}_{2tt}(\psi ,\varphi ,\varphi ,t;\sigma )-({\psi }^2+{\varphi }^2-{\varphi }^2)+{(0.5\sigma )}^n-\frac{1}{2}\left({\psi }^2{\underline{w}}_{1\psi \psi }(\psi ,\varphi ,\varphi ,t;\sigma )\right.\hfill \\ \hfill & \left.+{\varphi }^2{\underline{w}}_{1\varphi \varphi }(\psi ,\varphi ,\varphi ,t;\sigma )+{\varphi }^2{\underline{w}}_{1\varphi \varphi }(\psi ,\varphi ,\varphi ,t;\sigma )\right)=\tilde{0},{\underline{w}}_1(\psi ,\varphi ,t;\sigma )=\tilde{0},\hfill \\ \hfill & ⋮,\hfill \end{array}\right.\end{array}$$

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill p^0:& {\overline{w}}_{0tt}(\psi ,\varphi ,\varphi ,t;\sigma )-{\overline{\Xi }}_{0tt}(\sigma )=\tilde{0},{\overline{\Xi }}_0(\psi ,t;\sigma )={(1-0.5\sigma )}^n+t\left({\psi }^2+{\varphi }^2-{\varphi }^2\right),\hfill \\ \hfill p^1:& ({\overline{w}}_{1tt}(\psi ,\varphi ,\varphi ,t;\sigma )-({\psi }^2+{\varphi }^2-{\varphi }^2)+{(1-0.5\sigma )}^n-\frac{1}{2}\left({\psi }^2{\overline{w}}_{0\psi \psi }(\psi ,\varphi ,\varphi ,t;\sigma )\right.\hfill \\ \hfill & \left.+{\varphi }^2{\overline{w}}_{0\varphi \varphi }(\psi ,\varphi ,\varphi ,t;\sigma )+{\varphi }^2{\overline{w}}_{0\varphi \varphi }(\psi ,\varphi ,\varphi ,t;\sigma )\right)=\tilde{0},{\overline{w}}_1(\psi ,\varphi ,t;\sigma )=\tilde{0},\hfill \\ \hfill p^2:& ({\overline{w}}_{2tt}(\psi ,\varphi ,\varphi ,t;\sigma )-({\psi }^2+{\varphi }^2-{\varphi }^2)+{(1-0.5\sigma )}^n-\frac{1}{2}\left({\psi }^2{\overline{w}}_{1\psi \psi }(\psi ,\varphi ,\varphi ,t;\sigma )\right.\hfill \\ \hfill & \left.+{\varphi }^2{\overline{w}}_{1\varphi \varphi }(\psi ,\varphi ,\varphi ,t;\sigma )+{\varphi }^2{\overline{w}}_{1\varphi \varphi }(\psi ,\varphi ,\varphi ,t;\sigma )\right)=\tilde{0},{\overline{w}}_1(\psi ,\varphi ,t;\sigma )=\tilde{0},\hfill \\ \hfill & ⋮.\hfill \end{array}\right.\end{array}$$

Using the above equations and the initial approximation ${\tilde{w}}_0(\psi ,\varphi ,t;\sigma )={\tilde{\Xi }}_0(\psi ,\varphi ,t;\sigma )=[{(0.5\sigma )}^n,{(1-0.5\sigma )}^n]\oplus t({\psi }^2+{\varphi }^2-{\varphi }^2),$ we have

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\underline{w}}_1(\psi ,\varphi ,\varphi ,t;\sigma )={(0.5\sigma )}^n+\left[\frac{t^2({\psi }^2+{\varphi }^2+{\varphi }^2)}{2!}+\frac{t^3({\psi }^2+{\varphi }^2-{\varphi }^2)}{3!}\right],\hfill \\ {\underline{w}}_2(\psi ,\varphi ,\varphi ,t;\sigma )={(0.5\sigma )}^n+\left[\frac{t^4({\psi }^2+{\varphi }^2+{\varphi }^2)}{4!}+\frac{t^5({\psi }^2+{\varphi }^2-{\varphi }^2)}{5!}\right],\hfill \\ ⋮,\hfill \end{array}\right.\end{array}$$

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\overline{w}}_1(\psi ,\varphi ,\varphi ,t;\sigma )={(1-0.5\sigma )}^n+\left[\frac{t^2({\psi }^2+{\varphi }^2+{\varphi }^2)}{2!}+\frac{t^3({\psi }^2+{\varphi }^2-{\varphi }^2)}{3!}\right],\hfill \\ {\overline{w}}_2(\psi ,\varphi ,\varphi ,t;\sigma )={(1-0.5\sigma )}^n+\left[\frac{t^4({\psi }^2+{\varphi }^2+{\varphi }^2)}{4!}+\frac{t^5({\psi }^2+{\varphi }^2-{\varphi }^2)}{5!}\right],\hfill \\ ⋮.\hfill \end{array}\right.\end{array}$$

Thus, we can obtain the exact solution as follows:

$$\begin{array}{cc}\hfill \tilde{w}(\psi ,\varphi ,\varphi ,t;\sigma )& =[{(0.5\sigma )}^n,{(1-0.5\sigma )}^n]\oplus \left(({\psi }^2+{\varphi }^2)e^t+{\varphi }^2{e}^{-t}-({\psi }^2+{\varphi }^2+{\varphi }^2)\right),0\le \sigma \le 1.\hfill \end{array}$$

This section figures are the same as Figure 1 and 2 in Osman et al. [39]; we proposed these to clarify the solutions.

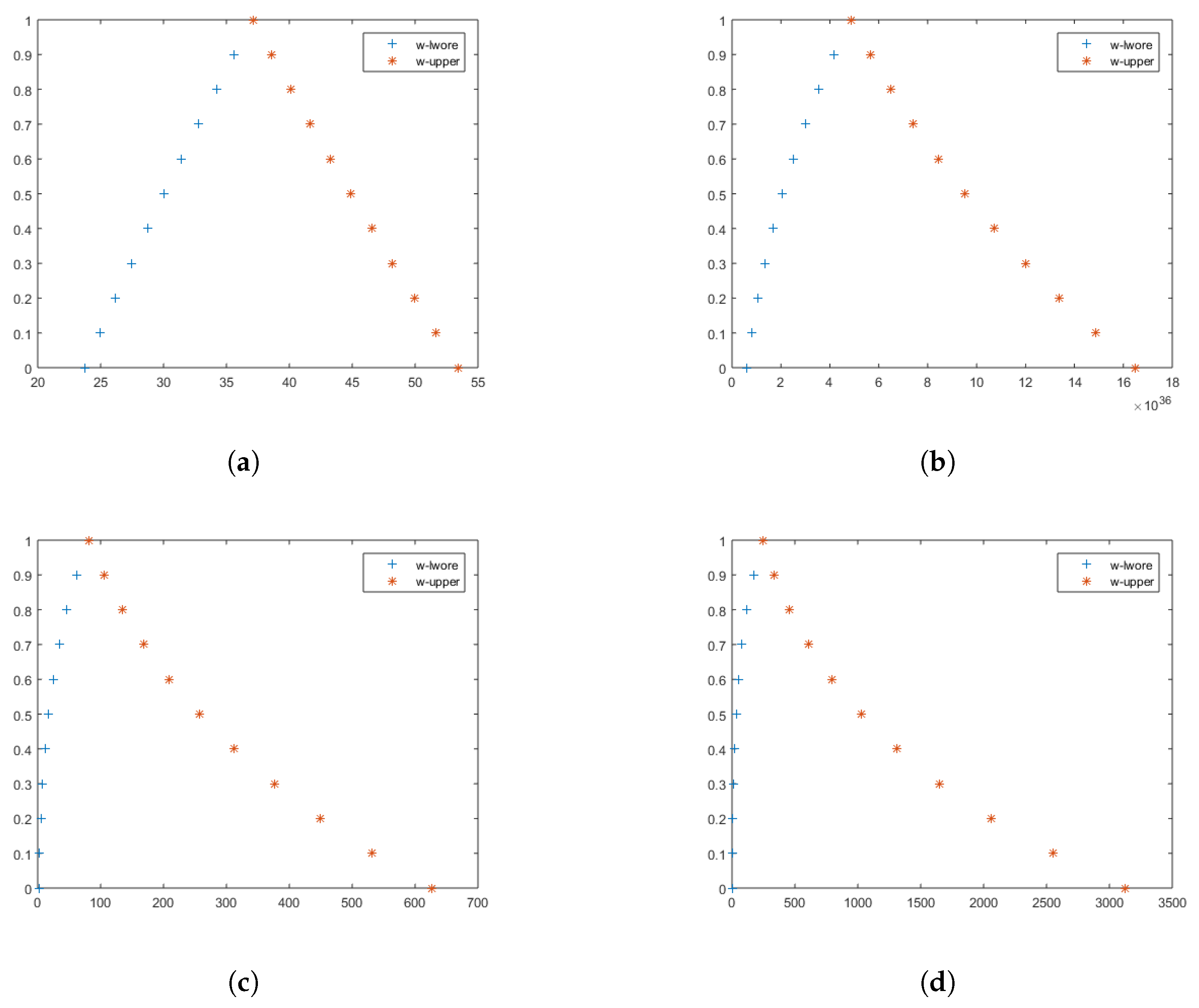
5.4. Discussion

The comparison between fuzzy RDTM and HPM with the fuzzy ADM, and VIM in [39] shows that, although the results of these methods when applied to the fuzzy heat-like and wave-like equations are the same, fuzzy RDTM, like fuzzy HPM, does not require specific algorithms and complex calculations such as fuzzy ADM or construction of correction functionals using general Lagrange multipliers in the fuzzy variational iteration method. Therefore, the fuzzy RDTM and HPM are more readily implemented and promising approaches to solving fuzzy partial differential equations with variable coefficients.

6. Conclusions

In this article, we successfully compared the fuzzy Adomian decomposition method (ADM) and fuzzy modified Laplace decomposition method (LDM) to obtain fuzzy fractional Navier–Stokes equations in a tube under fuzzy fractional derivative. The analytical results were expressed as a power series with easily calculated terms. Furthermore, we investigated the fuzzy Elzaki decomposition method (EDM) applied to solving fuzzy linear-nonlinear Schrodinger differential equations. For all four numerical problems investigated, the technique works wonderfully since the solutions found yield outstanding exact solutions. Finally, we proposed the comparison of the fuzzy reduced differential transform method (RDTM) and fuzzy homotopy perturbation method (HPM) to solving fuzzy heat-like and wave-like equations with variable coefficients. The results demonstrate that the methods are efficient and reliable, and a comparison of the approaches to other analytical methods accessible in the literature reveals that, while the results are similar, RDTM and HPM are more convenient and efficient. All these results demonstrate that the methods are powerful mathematical tools for solving fuzzy linear and nonlinear partial differential equations.