On Dihedralized Gyrogroups and Their Cayley Graphs

Abstract

The method of constructing the generalized dihedral group as a semidirect product of an abelian group and the group ${\mathbb{Z}}_2$ of integers modulo 2 is extended to the case of gyrogroups. This leads to the study of a new class of gyrogroups, which includes generalized dihedral groups and dihedral groups as a special case. In this article, we show that any dihedralizable gyrogroup can be enlarged to a dihedralized gyrogroup. Then, we establish algebraic properties of dihedralized gyrogroups as well as combinatorial properties of their Cayley graphs.

1. Introduction

It is a recurring theme in mathematics that theoretical results are sometimes motivated by concrete examples—the more examples are known, the more knowledge on the structure under consideration is gained. In view of Cayley’s theorem for groups, permutation groups are prominent examples of this process. Recall that if groups $\Gamma$ and $\Pi$, together with a homomorphism $\phi$ from $\Pi$ to the automorphism group $\mathrm{Aut}(\Gamma )$, are given, then one can construct a new group, called the (external) semidirect product of $\Gamma$ and $\Pi$ with respect to $\phi$, denoted by $\Gamma {⋊}_{\phi }\Pi$. The resulting group contains isomorphic copies of the initial groups $\Gamma$ and $\Pi$, and one of which is a normal subgroup. It turns out that direct products are simply a special case of this method (by letting $\phi$ be the trivial homomorphism) and that many groups arise as semidirect products of smaller groups. In particular, a generalized dihedral group is obtained as a semidirect product of an abelian group and a cyclic group of order two. The generalized dihedral group constructed from a cyclic group of order n with $n\ge 3$ is indeed the dihedral group of order $2n$.

In this article, we establish that the process of dihedralizing an abelian group can be extended to the case of a certain gyrocommutative gyrogroup, which is a nonassociative structure sharing common properties with abelian groups. Historically, the notion of a gyrogroup originated from the study of the parametrization of the Lorentz transformation group by Ungar [1]. The formation of a gyrogroup is intensively described in [2] and references therein. It turns out that gyrogroups may be regarded as a suitable generalization of groups, and several classical results continue to hold for gyrogroups, see, for instance, [3,4,5,6,7,8,9,10,11,12,13,14]. The main goal of this article is to introduce and to study a new class of gyrogroups that are constructed from smaller gyrogroups via the notion of semidirect products, called dihedralized gyrogroups. This results in a new non-gyrocommutative gyrogroup of order 16, as a concrete example. Then, we study algebraic properties of dihedralized gyrogroups and explore combinatorial properties of their Cayley graphs. For the sake of convenience, we summarize a few main results of this article below.

We show that, under a certain condition, a gyrogroup can be decomposed into a gyrosum of two subgyrogroups, one of which is a normal subgyrogroup.

Theorem 1

(See Theorem 8 for the proof). Let G be a gyrogroup, let H be a subgyrogroup of G, and let K be a normal subgyrogroup of G. Then, the following statements are equivalent:

1. 

$G=H\oplus K$ and $H\cap K=\left\{e\right\}$;

2. 

For each $a\in G$, there is a unique pair $(h,k)\in H\times K$ such that $a=h\oplus k$.

3. 

For each $a\in G$, there is a unique pair $(h,k)\in H\times K$ such that $a=k\oplus h$.

4. 

If $\iota :H\to G$ is the inclusion map and $\pi :G\to G/K$ is the canonical projection, then $\pi \circ \iota$ is a gyrogroup isomorphism from H to $G/K$.

5. 

There exists a gyrogroup homomorphism $\phi :G\to H$ with kernel K such that $\phi \left(h\right)=h$ for all $h\in H$; that is, the following is a split short exact sequence:

$$\left\{e\right\}\stackrel{}{⟶}K\stackrel{\iota }{⟶}G\stackrel{\phi }{⟶}H\stackrel{}{⟶}\left\{e\right\}.$$

Then, we show that, with a gyrocommutative gyrogroup satisfying the skew left loop property in hand, a new gyrogroup can be constructed.

Theorem 2

(See Theorem 10 for the proof). Suppose that G is a gyrocommutative gyrogroup and has the skew left loop property. Then, $G\times {\mathbb{Z}}_2$ is a gyrogroup under the operation defined by

$$(a,m){\oplus }_{\phi }(b,n)=(a\oplus \phi \left(m\right)\left(b\right),m+n)$$

and in this case the gyroautomorphisms are defined by

$$\mathrm{gyr}\left[(a,m),(b,n)\right](c,k)=(\mathrm{gyr}\left[a,\phi \left(m\right)\left(b\right)\right]\left(c\right),k)$$

for all $a,b,c\in G,m,n,k\in {\mathbb{Z}}_2$, where φ sends 0 to the identity automorphism of G and sends 1 to the inversion map of G.

Next, we describe how a Cayley graph of a dihedralized gyrogroup looks compared to that of the original gyrogroup.

Theorem 3

(See Theorem 12 for the proof). Let G be a finite dihedralizable gyrogroup with a right generating set S and let $\tilde{S}=(S\times \left\{0\right\})\cup \left\{(e,1)\right\}$. In $\mathrm{RCay}(\mathrm{Dih}\left(G\right),\tilde{S})$, the subgraph $C_0$ induced by $G\times \left\{0\right\}$ is isomorphic to $\mathrm{RCay}(G,S)$ and the subgraph $C_1$ induced by $G\times \left\{1\right\}$ is isomorphic to $\mathrm{RCay}(G,\ominus S)$. Furthermore, $C_0$ and $C_1$ are isomorphic.

Lastly, we give an explicit Hamiltonian path in a specific type of dihedralized gyro-groups.

Theorem 4

(See Theorem 14 for the proof). Let G be a finite gyrogroup that is an internal semi-direct product $K⋊H$, where $K=⟨r⟩\cong {\mathbb{Z}}_n$ and $H=⟨s⟩\cong {\mathbb{Z}}_2$. Let $S=\{r,s\}$. If $\mathrm{gyr}\left[r,g\right]\left(r\right)=r$ for all $g\in G$, then the walk $e\left[{\left[r\right]}^{n-1}\left[s\right]{\left[r\right]}^{n-1}\right]$ is a Hamiltonian path in $\mathrm{RCay}(G,S)$. In addition, if G is dihedralizable, then the walk

$$(e,0)\left[{\left[(r,0)\right]}^{n-1}\left[(s,0)\right]{\left[(r,0)\right]}^{n-1}\left[(0,1)\right]{\left[(r,0)\right]}^{n-1}\left[(s,0)\right]{\left[(r,0)\right]}^{n-1}\right]$$

is a Hamiltonian path in $\mathrm{RCay}(\mathrm{Dih}\left(G\right),\tilde{S})$, where $\tilde{S}=\{(r,0),(s,0),(e,1)\}$.

2. Preliminaries

In this section, we summarize some basic definitions and properties of gyrogroups for easy reference. See [2,15] for more details. In the case when ⊕ is a binary operation on a non-empty set G, let $\mathrm{Aut}\left(G\right)$ be the set of all automorphisms of $(G,\oplus )$.

Definition 1.

A non-empty set G, together with a binary operation ⊕ on G, is called a gyrogroup if it satisfies the following axioms:

(G1) 

There exists an element $e\in G$ such that $e\oplus a=a$ for all $a\in G$.

(G2) 

For each $a\in G$, there exists an element $b\in G$ such that $b\oplus a=e$.

(G3) 

For all a, $b\in G$, there is an automorphism $\mathrm{gyr}\left[a,b\right]\in \mathrm{Aut}\left(G\right)$ such that

$$a\oplus (b\oplus c)=(a\oplus b)\oplus \mathrm{gyr}\left[a,b\right]\left(c\right) (\mathrm{left} \mathrm{gyroassociative} \mathrm{law})$$

for all $c\in G$.

(G4) 

For all a, $b\in G$, $\mathrm{gyr}\left[a\oplus b,b\right]=\mathrm{gyr}\left[a,b\right]$.                              (left loop property)

Let G be a gyrogroup. The element e in (G1) is indeed a unique two-sided identity of G, called the identity element. The element b in (G2) is indeed a unique two-sided inverse of a in G, denoted by $\ominus a$. The automorphism $\mathrm{gyr}\left[a,b\right]$ in (G3) is called the gyroautomorphism generated by a and b. The map defined by $\gamma :(a,b)\mapsto \mathrm{gyr}\left[a,b\right]$ for all $a,b\in G$ is referred to as the gyrator map of G. The cooperation of G, denoted by ⊞, is defined by the equation $a⊞b=a\oplus \mathrm{gyr}\left[a,\ominus b\right]\left(b\right)$ for all $a,b\in G$. In addition, define $a\ominus b=a\oplus (\ominus b)$ and $a\boxminus b=a⊞(\ominus b)$. We say that a gyrogroup is degenerate if its gyroautomorphisms are all trivial, and in this case G is a group. A nondegenerate gyrogroup is a gyrogroup that is not degenerate.

Theorem 5

(See [2]). Let G be a gyrogroup. Then, the following properties hold for all $a,b,c\in G$:

1. 

$a\oplus b=a\oplus c$ implies $b=c$.                                   (left cancellation law I)

2. 

$\ominus a\oplus (a\oplus b)=b$.                                         (left cancellation law II)

3. 

$(b⊞a)\ominus a=b$.                                        (right cancellation law I)

4. 

$(b\ominus a)⊞a=b$.                                          (right cancellation law II)

5. 

$b\oplus a=c\oplus a$ implies $b=c$.                                   (right cancellation law III)

6. 

$(a\oplus b)\oplus c=a\oplus (b\oplus \mathrm{gyr}\left[b,a\right]\left(c\right))$.                             (right gyroassociative law)

Let G be a gyrogroup. A subset H of G is a subgyrogroup of G, denoted by $H\le G$, if H forms a gyrogroup under the operation inherited from G and $\mathrm{gyr}\left[a,b\right]\left(H\right)=H$ for all $a,b\in H$. An associative subgyrogroup of G is called a subgroup of G. A subgyrogroup H of G is called an L-subgyrogroup whenever $\mathrm{gyr}\left[a,h\right]\left(H\right)=H$ for all $a\in G,h\in H$. If H and K are subgyrogroups of G, define $H\oplus K=\{h\oplus k:h\in H,k\in K\}$.

Proposition 1

(The Subgyrogroup Criterion, Proposition 21 of [15]). A non-empty subset H of a gyrogroup G is a subgyrogroup if and only if $a\in H$ implies $\ominus a\in H$ and $a,b\in H$ implies $a\oplus b\in H$.

Let G and H be gyrogroups. A map $\phi$ from G to H is called a gyrogroup homomorphism if $\phi (a\oplus b)=\phi \left(a\right)\oplus \phi \left(b\right)$ for all $a,b\in G$. In this case, the kernel of $\phi$ is defined as $ker\phi =\{a\in G:\phi \left(a\right)=e\}$. A bijective gyrogroup homomorphism is called a gyrogroup isomorphism. If there is a gyrogroup isomorphism from G to H, we say that G is isomorphic to H, denoted by $G\cong H$. A subgyrogroup N of G is normal, denoted by $N⊴G$, if there exists a gyrogroup homomorphism $\phi$ from G to a gyrogroup such that $N=ker\phi$.

Theorem 6

(The second isomorphism theorem, Theorem 33 of [15]). Let G be a gyrogroup and let $A,B⩽G$. If $B⊴G$, then $A\cap B⊴A$ and $(A\oplus B)/B\cong A/(A\cap B)$ as gyrogroups.

Let G and H be gyrogroups. The direct product of G and H, denoted by $G\times H$, is a gyrogroup with underlying set $\{(g,h):g\in G,h\in H\}$ whose operation is defined componentwise by

$$(a,b)\oplus (c,d)=(a\oplus c,b\oplus d)$$

(1)

for all $a,c\in G,b,d\in H$ (cf. Section 2.1 of [16]).

Recall that a gyrogroup G is gyrocommutative if $a\oplus b=\mathrm{gyr}\left[a,b\right](b\oplus a)$ for all $a,b\in G$. Recall also that a gyrogroup G has the automorphic inverse property if $\ominus (a\oplus b)=(\ominus a)\oplus (\ominus b)$ for all $a,b\in G$. It is clear that a gyrogroup G has the automorphic inverse property if and only if the inversion map $\mathfrak{i}$, defined by $\mathfrak{i}\left(a\right)=\ominus a$, $a\in G$, is an automorphism of G. By Theorem 3.2 of [2], a gyrogroup G is gyrocommutative if and only if it has the automorphic inverse property. A gyrogroup G (finite or infinite) is said to be of exponent at most two if $a\oplus a=e$ for all $a\in G$. It is clear that G is of exponent at most two if and only if $a=\ominus a$ for all $a\in G$. An element a in a gyrogroup is of order two if $a\ne e$ and $a\oplus a=e$.

Let A be a subset of a gyrogroup G. We say that A is symmetric if either $A=\varnothing$ or $\ominus a\in A$ for all $a\in A$. The subgyrogroup of G generated by A, denoted by $⟨A⟩$, is defined as $⟨A⟩=\bigcap \{H\le G,A\subseteq H\}$. It is the smallest subgyrogroup of G containing A ordered by inclusion (cf. Proposition 26 of [15]). A subset S of G is a generating set for G if $⟨S⟩=G$. In this case, we say that G is generated by S or S generates G. A non-empty subset S of a gyrogroup G is called a left generating set for G if for each element $g\in G$, there are elements $s_1,s_2,\dots ,s_n\in S$ such that $g=s_n\oplus (s_{n-1}\oplus (\cdots \oplus (s_2\oplus s_1)\cdots ))$. In this case, we write $(S⟩=G$ (cf. p. 30 of [5]). It is called a right generating set for G if, for each element $g\in G$, there are elements $s_1,s_2,\dots ,s_n\in S$ such that $g=((\cdots (s_1\oplus s_2)\oplus \cdots )\oplus s_{n-1})\oplus s_n$. In this case, we write $⟨S)=G$. By the closure property, any left or right generating set for G is a generating set for G. We say that G is strongly generated by S if S is a generating set for G such that $\mathrm{gyr}\left[a,b\right]\left(S\right)=S$ for all $a,b\in G$ (cf. Definition 18 of [17]).

Proposition 2.

Let G and H be gyrogroups and let $\varphi :G\to H$ be a surjective gyrogroup homomorphism. If S is a (respectively, left, right) generating set for G, then $\varphi \left(S\right)$ is a (respectively, left, right) generating set for H.

Proof. 

Suppose that $⟨S⟩=G$. We show that $H=⟨\varphi \left(S\right)⟩=\bigcap \{K\le H,\varphi (S)\subseteq K\}$. Let $h\in H$. Suppose that $K\le H$ and $\varphi \left(S\right)\subseteq K$. Since $\varphi$ is surjective, $h=\varphi \left(g\right)$ for some $g\in G$. Since $\varphi$ is a homomorphism, ${\varphi }^{-1}\left(K\right)\le G$ (cf. Proposition 34 of [15]) and $S\subseteq {\varphi }^{-1}\left(K\right)$. Since S generates G, we obtain $g\in {\varphi }^{-1}\left(K\right)$. Hence, $h=\varphi \left(g\right)\in K$. This proves that $H\subseteq \bigcap \{K\le H,\varphi (S)\subseteq K\}$ and so equality holds. The proof of the remaining statements is straightforward, using the fact that $\varphi$ is surjective and preserves the gyrogroup operations. □

Next, let us mention two concrete examples of finite gyrogroups, which will be primary examples in the sequel.

Example 1.

In the gyrogroup $G_8=\{0,1,2,3,4,5,6,7\}$ (cf. p. 404 of [15]), the non-trivial gyroautomorphism of $G_8$ is given in cycle decomposition by

$$A=\left(46\right)\left(57\right).$$

(2)

The gyroaddition and gyration tables for $G_8$ are given in Tables 4 and 5 of [15], respectively.

Example 2.

In the gyrogroup $G_{15}=\{0,1,2,3,4,5,6,7,8,9,10,11,12,13,14\}$ (cf. p. 432 of [15]), the non-trivial gyroautomorphisms of $G_{15}$ are given in cycle decomposition by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill A& =\left(175106\right)\left(2381114\right),\hfill \\ \hfill B& =\left(161057\right)\left(2141183\right),\hfill \\ \hfill C& =\left(110765\right)\left(2113148\right),\hfill \\ \hfill D& =\left(156710\right)\left(2814311\right).\hfill \end{array}\end{array}$$

(3)

The gyroaddition and gyration tables for $G_{15}$ are given in Tables 6 and 7 of [15], respectively.

Standard terminology and notation in graph theory used throughout the article are defined as usual. A directed graph or digraph is an ordered pair $\overrightarrow{D}=(V,\overrightarrow{E})$, where V is a set of vertices and $\overrightarrow{E}\subseteq \{(u,v):u,v\in V\mathrm{and}u\ne v\}$ is a set of edges. In this article, we will write $u\to v$ instead of $(u,v)$ to emphasize the direction. For simplicity, we use the term “graph” instead of “digraph” from now on. We will refer to a walk in a graph by specifying its vertices as $v_1\to v_2\to \cdots \to v_n$, or by specifying its edge labelling as $[s_1,s_2,\cdots ,s_n]$. However, in the case of edge labelling, a walk is not unique unless the initial vertex is given. In this case, we write $v_1[s_1,s_2,\cdots ,s_n]$ to indicate that the initial vertex is $v_1$. We also write ${[s_1,s_2,\cdots ,s_n]}^i$ for a walk that repeats edge labelling $[s_1,s_2,\cdots ,s_n]$i times.

Definition 2

(Definition 2.8 of [11]). Let G be a gyrogroup and let S be a subset of G not containing the gyrogroup identity. The (color) right Cayley graph of G with respect to S, denoted by $\mathrm{RCay}(G,S)$, is a digraph whose vertices are the gyrogroup elements, and for any two vertices u and v, there is an edge $u\to v$ with color s if $v=u\oplus s$ for some $s\in S$.

The left Cayley graphs can be defined in the same way as in Definition 2 by adding s to the left-hand side instead.

Theorem 7

(Theorem 4.5 of [11]). Let G be a finite gyrogroup and let S be a symmetric subset of G not containing e such that $\mathrm{gyr}\left[a,b\right]\left(S\right)=S$ for all $a,b\in G$. Then, $\mathrm{RCay}(G,S)$ is transitive.

3. Construction of Gyrogroups

The method of constructing a group as a semidirect product of two groups is well-known in the literature. The main goal of this section is to extend this method to the case of gyrogroups. This leads to a new class of gyrogroups, which includes generalized dihedral groups and dihedral groups as a special case. As an application of this result, we obtain a new gyrogroup of order 16, as shown in Example 5. We begin by introducing the notion of an internal semidirect product for gyrogroups and then formulate the notion of an external semidirect product for a particular class of gyrogroups.

3.1. Internal and External Semidirect Products

We begin with the following lemma, which indicates the uniqueness of expression of a gyrosum under a certain condition.

Lemma 1.

Let G be a gyrogroup. If H and K are subgyrogroups of G such that $\mathrm{gyr}\left[a,b\right]\left(K\right)\subseteq K$ for all $a,b\in H$ and $H\cap K=\left\{e\right\}$, then $h_1\oplus k_1=h_2\oplus k_2$, where $h_1,h_2\in H,k_1,k_2\in K$, implies $h_1=h_2$ and $k_1=k_2$.

Proof. 

Let $h_1,h_2\in H$, let $k_1,k_2\in K$, and suppose that $h_1\oplus k_1=h_2\oplus k_2$. Using left cancellation law II, we obtain $k_1=\ominus h_1\oplus (h_2\oplus k_2)$. By the left gyroassociative law, $k_1=(\ominus h_1\oplus h_2)\oplus \mathrm{gyr}\left[\ominus h_1,h_2\right]\left(k_2\right)$. Set $k_3=\ominus \mathrm{gyr}\left[\ominus h_1,h_2\right]\left(k_2\right)$. By assumption, $k_3\in K$. Note that $k_1=(\ominus h_1\oplus h_2)\ominus k_3$. By right cancellation law II, $k_1⊞k_3=\ominus h_1\oplus h_2$. Note that $k_1⊞k_3=k_1\oplus \mathrm{gyr}\left[k_1,\ominus k_3\right]\left(k_3\right)\in K$ and that $\ominus h_1\oplus h_2\in H$. Hence, $\ominus h_1\oplus h_2\in H\cap K$ and so $\ominus h_1\oplus h_2=e$ by assumption. By the left cancellation law II, $h_1=h_2$. This in turn implies $k_1=k_2$ by the left cancellation law I. □

We are now in a position to prove the main theorem of this subsection. This enables us to decompose a gyrogroup into a gyrosum of two subgyrogroups, one of which is a normal subgyrogroup, under a certain condition.

Theorem 8.

Let G be a gyrogroup, let H be a subgyrogroup of G, and let K be a normal sub-gyrogroup of G. Then, the following statements are equivalent:

1. 

$G=H\oplus K$ and $H\cap K=\left\{e\right\}$;

2. 

For each $a\in G$, there is a unique pair $(h,k)\in H\times K$ such that $a=h\oplus k$.

3. 

For each $a\in G$, there is a unique pair $(h,k)\in H\times K$ such that $a=k\oplus h$.

4. 

If $\iota :H\to G$ is the inclusion map and $\pi :G\to G/K$ is the canonical projection, then $\pi \circ \iota$ is a gyrogroup isomorphism from H to $G/K$.

5. 

There exists a gyrogroup homomorphism $\phi :G\to H$ with kernel K such that $\phi \left(h\right)=h$ for all $h\in H$; that is, the following is a split short exact sequence:

$$\left\{e\right\}\stackrel{}{⟶}K\stackrel{\iota }{⟶}G\stackrel{\phi }{⟶}H\stackrel{}{⟶}\left\{e\right\}.$$

(4)

Proof. 

(1) ⇒ (2) Let $a\in G$. Since $G=H\oplus K$, we obtain $a=h\oplus k$ for some $h\in H,k\in K$. Hence, there is a pair $(h,k)\in H\times K$ such that $a=h\oplus k$. Let $(h^{\prime },k^{\prime })\in H\times K$ and suppose that $a=h^{\prime }\oplus k^{\prime }$. Then, $h\oplus k=h^{\prime }\oplus k^{\prime }$. By Lemma 1, $h=h^{\prime }$ and $k=k^{\prime }$. This shows that the pair $(h,k)$ is unique.

(2) ⇒ (3) Let $a\in G$. By assumption, $a=h\oplus k$ for some $h\in H,k\in K$. Since $K⊴G$, we have $h\oplus K=K\oplus h$ and so $h\oplus k=k^{\prime }\oplus h$ for some $k^{\prime }\in K$. Thus, $a=k^{\prime }\oplus h$. Let $h_1,h_2\in H$ and let $k_1,k_2\in K$. Suppose that $k_1\oplus h_1=k_2\oplus h_2$. Since $K\oplus h_1=h_1\oplus K$, we have $k_1\oplus h_1=h_1\oplus k_1^{\prime }$. Similarly, $k_2\oplus h_2=h_2\oplus k_2^{\prime }$ for some $k_2^{\prime }\in K$. Hence, $h_1\oplus k_1^{\prime }=h_2\oplus k_2^{\prime }$. By assumption, $h_1=h_2$. Applying right cancellation law I, we obtain $k_1=k_2$. This proves the uniqueness part.

(3) ⇒ (4) Note that $\pi$ and $\iota$ are gyrogroup homomorphisms. Hence, $\pi \circ \iota$ is a gyrogroup homomorphism from H to $G/K$. Let $h_1,h_2\in H$. Suppose that $\pi \circ \iota \left(h_1\right)=\pi \circ \iota \left(h_2\right)$. Then, $h_1\oplus K=h_2\oplus K$. Since $K⊴G$, we have $h_1\oplus K=K\oplus h_1$ and $h_2\oplus K=K\oplus h_2$. Thus, $K\oplus h_1=K\oplus h_2$. Since $h_1\in K\oplus h_1$, it follows that $e\oplus h_1=h_1=k\oplus h_2$ for some $k\in K$. By assumption, $h_1=h_2$. This proves that $\pi \circ \iota$ is injective. Let $X\in G/K$. Then, $X=a\oplus K$ for some $a\in G$. By assumption, $a=k^{\prime }\oplus h$ for some $k^{\prime }\in K,h\in H$. Since $K\oplus h=h\oplus K$, we have $k^{\prime }\oplus h=h\oplus k$ for some $k\in K$. It follows that

$$h\oplus K=(h\oplus K)\oplus (e\oplus K)=(h\oplus K)\oplus (k\oplus K)=(h\oplus k)\oplus K=a\oplus K.$$

Hence, $\pi \circ \iota \left(h\right)=h\oplus K=X$. This proves that $\pi \circ \iota$ is surjective.

(4) ⇒ (5) Set $\varphi =\pi \circ \iota$. By assumption, $\varphi$ is a gyrogroup isomorphism from H to $G/K$. Hence, ${\varphi }^{-1}$ exists and is a gyrogroup isomorphism from $G/K$ to H. Define $\phi ={\varphi }^{-1}\circ \pi$. Then, $\phi$ is a gyrogroup homomorphism from G to H. Let $k\in K$. Then, $\phi \left(k\right)={\varphi }^{-1}\left(\pi \left(k\right)\right)={\varphi }^{-1}(k\oplus K)={\varphi }^{-1}(e\oplus K)=e$. Hence, $k\in ker\phi$. This proves $K\subseteq ker\phi$. To prove the reverse inclusion, let $k\in ker\phi$. Then, ${\varphi }^{-1}(e\oplus K)=e=\phi \left(k\right)={\varphi }^{-1}\left(\pi \left(k\right)\right)={\varphi }^{-1}(k\oplus K)$. Since ${\varphi }^{-1}$ is injective, $e\oplus K=k\oplus K$. Hence, $k\in K$. This proves $K=ker\phi$. Let $h\in H$. By definition, $\phi \left(h\right)={\varphi }^{-1}(h\oplus K)=h$ since $\varphi \left(h\right)=\pi \circ \iota \left(h\right)=h\oplus K$.

(5) ⇒ (1) Let $a\in G$. By left cancellation law II, $a=\phi \left(a\right)\oplus (\ominus \phi (a)\oplus a)$. By assumption, $\phi \left(a\right)\in H$ and so $\phi \left(\phi \right(a\left)\right)=\phi \left(a\right)$. Since $\phi$ preserves the gyrogroup operations, $\phi (\ominus \phi (a)\oplus a)=\ominus \phi \left(\phi \right(a\left)\right)\oplus \phi \left(a\right)=\ominus \phi \left(a\right)\oplus \phi \left(a\right)=e$. This implies $\ominus \phi \left(a\right)\oplus a\in ker\phi =K$. This proves $G=H\oplus K$. Clearly, $e\in H\cap K$. Let $x\in H\cap K$. Since $x\in K$, we obtain $\phi \left(x\right)=e$. Since $x\in H$, we obtain $\phi \left(x\right)=x$. Hence, $x=e$. This proves $H\cap K=\left\{e\right\}$. □

Definition 3.

Let G be a gyrogroup, let H be a subgyrogroup of G, and let K be a normal subgyrogroup of G. If one of the (equivalent) conditions in Theorem 8 is true, then we say that G splits over K or that G is the internal semidirect product of K and H, denoted by $G=K⋊H$ or by $G=H⋉K$.

In the case when the gyrogroup G in Theorem 8 is degenerate (that is, G is a group), we recover the group-theoretic internal semidirect product. The notation in Definition 3 is chosen to emphasize that $K⊴K⋊H$. If G is the internal semidirect product of K and H, then the operation in G can be parametrized by

$$(h_1\oplus k_1)\oplus (h_2\oplus k_2)=(h_1\oplus h_2)\oplus \mathrm{gyr}\left[h_1,h_2\right](\ominus h_2\oplus (k_1\oplus \mathrm{gyr}\left[k_1,h_1\right](h_2\oplus k_2)))$$

(5)

for all $h_1,h_2\in H,k_1,k_2\in K$. The next proposition gives a sufficient condition for a finite gyrogroup to be an internal semidirect product of its subgyrogroups.

Proposition 3.

Let G be a finite gyrogroup, let H be a subgyrogroup of G, and let K be a normal subgyrogroup of G. If $H\cap K=\left\{e\right\}$ and $\left|G\right|=\left|H\right|\left|K\right|$, then $G=K⋊H$.

Proof. 

In view of Theorem 8, we need only prove that $G=H\oplus K$. By the second isomorphism theorem for gyrogroups, $(H\oplus K)/K\cong H/(H\cap K)$. This implies that ${\displaystyle \frac{\left|H\oplus K\right|}{\left|K\right|}}={\displaystyle \frac{\left|H\right|}{\left|H\cap K\right|}}$ and so $\left|H\oplus K\right|=\left|H\right|\left|K\right|=\left|G\right|$. Since G is finite, we obtain $G=H\oplus K$, as required. □

As an application of Proposition 3, we obtain the following two examples. This shows that $G_8$ and $G_{15}$ can be, in some senses, constructed from cyclic groups.

Example 3.

In the gyrogroup $G_8$, let $H=\{0,7\}$ and let $K=\{0,1,2,3\}$. Then, H and K are subgyrogroups of $G_8$ such that $H\cap K=\left\{0\right\}$. Furthermore, direct computation shows that $K⊴G_8$. By Proposition 3, $G_8=K⋊H$.

Example 4.

In the gyrogroup $G_{15}$, let $H=\{0,1,2\}$ and let $K=\{0,4,9,12,13\}$. Then, H and K are subgyrogroups of $G_{15}$ such that $H\cap K=\left\{0\right\}$. Furthermore, direct computation shows that $K⊴G_{15}$. By Proposition 3, $G_{15}=K⋊H$.

Proposition 4.

Let G be a gyrogroup. Suppose that G is the internal semidirect product of K and H, $G=K⋊H$, where $H\cong {\mathbb{Z}}_2$ is generated by s and R is a right (respectively, left) generating set for K. Then, $R\cup \left\{s\right\}$ is a right (respectively, left) generating set for G.

Proof. 

In view of Theorem 8, every element of G can be written as $g,g\oplus s$, or s for some $g\in K$. Expressing g in a right-generated manner of elements in R, we conclude that $R\cup \left\{s\right\}$ is a right generating set for G. The left counterpart can be proven in a similar fashion by noting that $G=H⋉K$. □

Following the construction of group-theoretic (external) semidirect products, we attempt to define an external semidirect product for gyrogroups. Let G be a gyrogroup, let $\Gamma$ be a group, and let $\phi :\Gamma \to \mathrm{Aut}\left(G\right)$ be a group homomorphism, where the operation on $\mathrm{Aut}\left(G\right)$ is composition of maps denoted by ∘. For $(a,g),(b,h)\in G\times \Gamma$, define ${\oplus }_{\phi }$ by

$$(a,g){\oplus }_{\phi }(b,h)=(a\oplus \phi \left(g\right)\left(b\right),gh).$$

(6)

In addition, define a map $\gamma$ by the formula

$$\gamma ((a,g),(b,h))(c,k)=(c^{\prime },k)\mathrm{for}\mathrm{all}c\in G,k\in \Gamma ,$$

(7)

where $c^{\prime }$ is defined by

$$c^{\prime }=\phi {\left(gh\right)}^{-1}\circ \mathrm{gyr}\left[a,\phi \left(g\right)\left(b\right)\right]\circ \phi \left(gh\right)\left(c\right).$$

(8)

In general, $(G\times \Gamma ,{\oplus }_{\phi })$ together with $\gamma$ may not be a gyrogroup. However, whenever $(G\times \Gamma ,{\oplus }_{\phi })$ is a gyrogroup with $\gamma$ as the gyrator map, this gyrogroup will be called the external semidirect product of G and $\Gamma$ with respect to $\phi$, denoted by $G{⋊}_{\phi }\Gamma$. It is clear that if G is degenerate, then Equation (8) reduces to $c^{\prime }=c$ and Equation (6) does define the usual operation on the group-theoretic semidirect product of G and $\Gamma$. The following theorem justifies the use of the term “external semidirect product”.

Theorem 9.

Let G be a gyrogroup, let Γ be a group with identity $1_{\Gamma }$, and let $\phi :\Gamma \to \mathrm{Aut}\left(G\right)$ be a group homomorphism. Suppose that $(G\times \Gamma ,{\oplus }_{\phi })$ is a gyrogroup with γ as the gyrator map, where ${\oplus }_{\phi }$ is defined by Equation (6) and γ is defined by Equations (7) and (8). Then, $G{⋊}_{\phi }\Gamma$ is the internal semidirect product of $\widehat{G}$ and $\widehat{\Gamma }$, where

$$\widehat{G}=\{(a,1_{\Gamma }):a\in G\}\mathrm{and}\widehat{\Gamma }=\{(e,g):g\in \Gamma \}.$$

(9)

Proof. 

Note that $(e,1_{\Gamma })$ must be the identity of $G{⋊}_{\phi }\Gamma$ by the uniqueness of the gyrogroup identity. Furthermore, the inverse of an element $(b,h)$ in $G{⋊}_{\phi }\Gamma$ must be $(\phi \left(h^{-1}\right)(\ominus b),h^{-1})$ by the uniqueness of a gyrogroup inverse. Let $g,h\in \Gamma$. By definition, $(e,g){\oplus }_{\phi }(e,h)=(e,gh)$ and $\ominus (e,g)=(e,g^{-1})$. By the subgyrogroup criterion (see Proposition 1), $\widehat{\Gamma }$ is a subgyrogroup of $G{⋊}_{\phi }\Gamma$. This also implies that $(e,g){\oplus }_{\phi }\left((e,h){\oplus }_{\phi }(e,k)\right)=(e,ghk)=\left((e,g){\oplus }_{\phi }(e,h)\right){\oplus }_{\phi }(e,k)$ for all $g,h,k\in \Gamma$. Hence, $\widehat{\Gamma }$ is a subgroup of $G{⋊}_{\phi }\Gamma$.

Next, we show that $\widehat{G}$ is a normal subgyrogroup of $G{⋊}_{\phi }\Gamma$. Define a map $\pi$ by $\pi (a,g)=(e,g)$ for all $a\in G,g\in \Gamma$. Then, $\pi$ is a gyrogroup homomorphism from $G{⋊}_{\phi }\Gamma$ to $\widehat{\Gamma }$. Furthermore, $ker\pi =\widehat{G}$, which implies that $\widehat{G}⊴G{⋊}_{\phi }\Gamma$. By normality, $\widehat{G}{\oplus }_{\phi }\widehat{\Gamma }=\widehat{\Gamma }{\oplus }_{\phi }\widehat{G}$ since $(a,g){\oplus }_{\phi }\widehat{G}=\widehat{G}{\oplus }_{\phi }(a,g)$ for all $a\in G,g\in \Gamma$ (cf. Proposition 39 of [15]).

Since $(a,g)=(a,1_{\Gamma }){\oplus }_{\phi }(e,g)$ for all $a\in G,g\in \Gamma$, we obtain $G\times \Gamma =\widehat{G}{\oplus }_{\phi }\widehat{\Gamma }$. Clearly, $\widehat{G}\cap \widehat{\Gamma }=\left\{(e,1_{\Gamma })\right\}$. Applying Theorem 8 with $H=\widehat{\Gamma }$ and $K=\widehat{G}$, we obtain that $G{⋊}_{\phi }\Gamma$ is the internal semidirect product of $\widehat{G}$ and $\widehat{\Gamma }$. □

In the next subsection, we give a sufficient condition for $(G\times \Gamma ,{\oplus }_{\phi })$ to be a gyrogroup with $\gamma$ as the gyrator map, where ${\oplus }_{\phi }$ is defined by Equation (6), $\gamma$ is defined by Equations (7) and (8), G is a certain gyrocommutative gyrogroup, and $\Gamma$ is a cyclic group of order two. This method allows us to construct a non-gyrocommutative gyrogroup from a gyrocommutative gyrogroup and an abelian group.

3.2. Dihedralized Gyrogroups

Recall that if A is an abelian group, then the generalized dihedral group associated with A is the semidirect product of A and the cyclic group ${\mathbb{Z}}_2=\{0,1\}$ with respect to the homomorphism sending 0 to the identity map of A and 1 to the inversion map of A. If A is chosen to be the group ${\mathbb{Z}}_n$ of integers modulo n with $n\ge 3$, then $A⋊{\mathbb{Z}}_2$ is isomorphic to the dihedral group $D_{2n}$. If A is chosen to be the additive group $\mathbb{Z}$ of integers, then $A⋊{\mathbb{Z}}_2$ is isomorphic to the infinite dihedral group $D_{\infty }$. In this section, we extend this method to the case of gyrocommutative gyrogroups. It turns out that some gyrocommutative gyrogroups give rise to non-gyrocommutative gyrogroups. We begin with the following definition, which will be crucial in the sequel.

Definition 4.

A gyrogroup G is said to have the skew left loop property if

$$\mathrm{gyr}\left[a\oplus b,\ominus b\right]=\mathrm{gyr}\left[a,b\right]$$

(10)

for all $a,b\in G$.

From now on, Identity (10) is referred to as the skew left loop property. It is clear that every group has the skew left loop property. Direct computation shows that the gyrogroup $G_8$ has the skew left loop property. Moreover, the gyrogroup $G_{15}$ is finite and gyrocommutative but does not have the skew left loop property since $\mathrm{gyr}\left[1\oplus 3,\ominus 3\right]=\mathrm{gyr}\left[4,7\right]=B$, whereas $\mathrm{gyr}\left[1,3\right]=A$. Next, we exhibit a class of gyrocommutative gyrogroups having the skew left loop property.

Proposition 5.

Every gyrogroup of exponent at most two is gyrocommutative and has the skew left loop property.

Proof. 

Suppose that G is a gyrogroup of exponent at most two. As noted earlier, $\ominus x=x$ for all $x\in G$. Let $a,b\in G$. Note that $\ominus (a\oplus b)=a\oplus b=(\ominus a)\oplus (\ominus b)$, which shows that G has the automorphic inverse property. We also obtain that $\mathrm{gyr}\left[a\oplus b,\ominus b\right]=\mathrm{gyr}\left[a\oplus b,b\right]=\mathrm{gyr}\left[a,b\right]$, where the latter equality follows by the left loop property. □

For instance, the gyrogroup in Example 3.2 of [5] is of exponent at most two, and so it is gyrocommutative and has the skew left loop property. From now on, let ${\mathbb{Z}}_2=\{0,1\}$ be the group of integers modulo 2, which is a cyclic group of order two. Furthermore, $G\times {\mathbb{Z}}_2$ is recognized as the set-theoretic cartesian product of G and ${\mathbb{Z}}_2$ unless otherwise stated. The next lemma shows that the group ${\mathbb{Z}}_2$ acts on any gyrocommutative gyrogroup by inverting elements.

Lemma 2.

Let G be a gyrocommutative gyrogroup. Define a map φ on ${\mathbb{Z}}_2$ by

$$\phi \left(0\right)={\mathrm{I}}_{G}and\phi \left(1\right)=\mathfrak{i},$$

(11)

where ${\mathrm{I}}_G$ is the identity map of G and $\mathfrak{i}$ is the inversion map of G. Then, the following properties hold:

1. 

φ is a group homomorphism from ${\mathbb{Z}}_2$ to $\mathrm{Aut}\left(G\right)$.

2. 

$\phi \left(m\right)\circ \mathrm{gyr}\left[a,b\right]=\mathrm{gyr}\left[a,b\right]\circ \phi \left(m\right)$ for all $m\in {\mathbb{Z}}_2,a,b\in G$.

Proof. 

Since G is gyrocommutative, the inversion map $\mathfrak{i}$ is an automorphism of G. Hence, $\phi$ sends ${\mathbb{Z}}_2$ to $\mathrm{Aut}\left(G\right)$. It is not difficult to see that $\phi$ preserves the group operations, which yields Part 1. It is clear that ${\mathrm{I}}_G\circ \mathrm{gyr}\left[a,b\right]=\mathrm{gyr}\left[a,b\right]\circ {\mathrm{I}}_G$. Since $\mathrm{gyr}\left[a,b\right]$ preserves the gyrogroup operations, we obtain

$$\mathfrak{i}\circ \mathrm{gyr}\left[a,b\right]\left(c\right)=\ominus \mathrm{gyr}\left[a,b\right]\left(c\right)=\mathrm{gyr}\left[a,b\right](\ominus c)=\mathrm{gyr}\left[a,b\right]\circ \mathfrak{i}\left(c\right)$$

for all $c\in G$. This shows that $\mathfrak{i}\circ \mathrm{gyr}\left[a,b\right]=\mathrm{gyr}\left[a,b\right]\circ \mathfrak{i}$, which proves Part 2. □

We are now in a position to prove the main theorem of this subsection, which shows that any gyrocommutative gyrogroup having the skew left loop property can be enlarged to a new gyrogroup.

Theorem 10.

Suppose that G is a gyrocommutative gyrogroup and has the skew left loop property. Then, $G\times {\mathbb{Z}}_2$ is a gyrogroup under the operation defined by

$$(a,m){\oplus }_{\phi }(b,n)=(a\oplus \phi \left(m\right)\left(b\right),m+n)$$

(12)

and in this case the gyroautomorphisms are defined by

$$\mathrm{gyr}\left[(a,m),(b,n)\right](c,k)=(\mathrm{gyr}\left[a,\phi \left(m\right)\left(b\right)\right]\left(c\right),k)$$

(13)

for all $a,b,c\in G,m,n,k\in {\mathbb{Z}}_2$. Here, φ is defined by Equation (11).

Proof. 

By Part 1 of Lemma 2, $\phi$ is a group homomorphism from ${\mathbb{Z}}_2$ to $\mathrm{Aut}\left(G\right)$. Since $\phi \left(0\right)={\mathrm{I}}_G$, it follows that $(e,0)$ acts as a left identity of $(G\times {\mathbb{Z}}_2,{\oplus }_{\phi })$. Let $(a,m)\in G\times {\mathbb{Z}}_2$. Since $\phi (-m)\in \mathrm{Aut}\left(G\right)$, it follows that $\left(\phi \right(-m\left)\right(\ominus a),-m)$ acts as a left inverse of $(a,m)$ in $G\times {\mathbb{Z}}_2$ with respect to $(e,0)$. Thus, $(G\times {\mathbb{Z}}_2,{\oplus }_{\phi })$ satisfies (G1) and (G2) of Definition 1.

Let $a,b,c\in G$ and let $m,n,k\in {\mathbb{Z}}_2$. Define $\gamma ((a,m),(b,n))(c,k)=(c^{\prime },k)$, where $c^{\prime }$ is defined by $c^{\prime }=\phi {(m+n)}^{-1}\circ \mathrm{gyr}\left[a,\phi \left(m\right)\left(b\right)\right]\circ \phi (m+n)\left(c\right)$. By Lemma 2, $\gamma$ is given by $\gamma \left(\right(a,m),(b,n\left)\right)(c,k)=(\mathrm{gyr}\left[a,\phi \left(m\right)\left(b\right)\right]\left(c\right),k)$. It is not difficult to check that $\gamma \left(\right(a,m),(b,n\left)\right)$ is an automorphism of $(G\times {\mathbb{Z}}_2,{\oplus }_{\phi })$ satisfying $(a,m){\oplus }_{\phi }\left((b,n){\oplus }_{\phi }(c,k)\right)=\left((a,m){\oplus }_{\phi }(b,n)\right){\oplus }_{\phi }\gamma ((a,m),(b,n))(c,k)$, which shows that $(G\times {\mathbb{Z}}_2,{\oplus }_{\phi })$ satisfies (G3) of Definition 1. To complete the proof, we calculate Table 1:

Table 1. Gyration forms in the proof of Theorem 10.

$(\mathit{m},\mathit{n})$	$\mathbf{gyr}\left[\mathit{a}\oplus \mathit{\phi }\left(\mathit{m}\right)\left(\mathit{b}\right),\mathit{\phi }(\mathit{m}+\mathit{n})\left(\mathit{b}\right)\right]$	$\mathbf{gyr}\left[\mathit{a},\mathit{\phi }\left(\mathit{m}\right)\left(\mathit{b}\right)\right]$
$(0,0)$	$\mathrm{gyr}\left[a\oplus b,b\right]$	$\mathrm{gyr}\left[a,b\right]$
$(0,1)$	$\mathrm{gyr}\left[a\oplus b,\ominus b\right]$	$\mathrm{gyr}\left[a,b\right]$
$(1,0)$	$\mathrm{gyr}\left[a\ominus b,\ominus b\right]$	$\mathrm{gyr}\left[a,\ominus b\right]$
$(1,1)$	$\mathrm{gyr}\left[a\ominus b,b\right]$	$\mathrm{gyr}\left[a,\ominus b\right]$

Since G has the left loop property as well as the skew left loop property, it follows that $(G\times {\mathbb{Z}}_2,{\oplus }_{\phi })$ satisfies (G4) of Definition 1. □

By Theorem 10, if G is a gyrocommutative gyrogroup and has the skew left loop property, then the external semidirect product of G and ${\mathbb{Z}}_2$ with respect to $\phi$ defined by Equation (11) exists, which will be denoted by $G⋊{\mathbb{Z}}_2$ for simplicity. By definition, the operation on $G⋊{\mathbb{Z}}_2$, written by ${\oplus }_{⋊}$, is given by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill (a,0){\oplus }_{⋊}(b,0)& =(a\oplus b,0),\hfill \\ \hfill (a,0){\oplus }_{⋊}(b,1)& =(a\oplus b,1),\hfill \\ \hfill (a,1){\oplus }_{⋊}(b,0)& =(a\ominus b,1),\hfill \\ \hfill (a,1){\oplus }_{⋊}(b,1)& =(a\ominus b,0)\hfill \end{array}\end{array}$$

(14)

for all $a,b\in G$. Furthermore, $\ominus (a,0)=(\ominus a,0)$ and $\ominus (a,1)=(a,1)$ for all $a\in G$. The gyroautomorphisms of $G⋊{\mathbb{Z}}_2$ are given by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathrm{gyr}\left[(a,0),(b,0)\right](c,k)& =(\mathrm{gyr}\left[a,b\right]\left(c\right),k),\hfill \\ \hfill \mathrm{gyr}\left[(a,0),(b,1)\right](c,k)& =(\mathrm{gyr}\left[a,b\right]\left(c\right),k),\hfill \\ \hfill \mathrm{gyr}\left[(a,1),(b,0)\right](c,k)& =(\mathrm{gyr}\left[a,\ominus b\right]\left(c\right),k),\hfill \\ \hfill \mathrm{gyr}\left[(a,1),(b,1)\right](c,k)& =(\mathrm{gyr}\left[a,\ominus b\right]\left(c\right),k)\hfill \end{array}\end{array}$$

(15)

for all $a,b,c\in G,k\in {\mathbb{Z}}_2$.

Henceforth, if G is a gyrocommutative gyrogroup having the skew left loop property, then the gyrogroup $G⋊{\mathbb{Z}}_2$ is called the dihedralized gyrogroup associated with G and denoted by $\mathrm{Dih}\left(G\right)$ for simplicity. In fact, in the case when G is an arbitrary abelian group, $\mathrm{Dih}\left(G\right)$ is the familiar generalized dihedral group. In the case when G is ${\mathbb{Z}}_n$ with $n\ge 3$, $\mathrm{Dih}\left(G\right)$ is the usual dihedral group of order $2n$. This justifies the use of the term “dihedralized gyrogroup”. By Theorem 9, $\mathrm{Dih}\left(G\right)$ is indeed the internal semidirect product of $\widehat{G}$ and $\widehat{{\mathbb{Z}}_2}$. Clearly, $\widehat{G}$ and G are isomorphic as gyrogroups, and $\widehat{{\mathbb{Z}}_2}$ and ${\mathbb{Z}}_2$ are isomorphic as groups.

As suggested by the proof of Theorem 10, if G is a gyrocommutative gyrogroup, then the left loop property holds in $(G\times {\mathbb{Z}}_2,{\oplus }_{\phi })$ if and only if G has the skew left loop property. Therefore, we introduce the following definition.

Definition 5.

A gyrogroup G is dihedralizable if it is gyrocommutative and has the skew left loop property.

In the next theorem, we give a necessary and sufficient condition for a dihedralized gyrogroup to be gyrocommutative.

Theorem 11.

Suppose that G is a dihedralizable gyrogroup. Then, the following statements are equivalent:

1. 

$\mathrm{Dih}\left(G\right)$ is gyrocommutative.

2. 

G is of exponent at most two.

3. 

$\mathrm{Dih}\left(G\right)$ and $G\times {\mathbb{Z}}_2$ are identical, where $G\times {\mathbb{Z}}_2$ is the direct product of G and ${\mathbb{Z}}_2$.

Proof. 

Suppose that $\mathrm{Dih}\left(G\right)$ is gyrocommutative. Let $b\in G$. By assumption,

$$(\ominus b,1)=(e,1){\oplus }_{⋊}(b,0)=\mathrm{gyr}\left[(e,1),(b,0)\right]\left(\right(b,0)\oplus (e,1\left)\right)=(b,1).$$

Hence, $\ominus b=b$, which shows that G is of exponent at most two. This proves the implication (1) ⇒ (2). Suppose that G is of exponent at most two. By assumption, $\ominus b=b$ for all $b\in G$. It follows by Equation (14) that the operations on $\mathrm{Dih}\left(G\right)$ and $G\times {\mathbb{Z}}_2$ are identical. Hence, the implication (2) ⇒ (1) is obtained by Proposition 5.

Suppose that $a\oplus a=e$ for all $a\in G$. Hence, $\ominus a=a$ for all $a\in G$. This implies $\phi \left(m\right)\left(a\right)=a$ for all $m\in {\mathbb{Z}}_2,a\in G$. Thus, if $(a,m),(b,n)\in \mathrm{Dih}\left(G\right)$, then

$$(a,m){\oplus }_{⋊}(b,n)=(a\oplus \phi \left(m\right)\left(b\right),m+n)=(a\oplus b,m+n)=(a,m)\oplus (b,n).$$

Hence, the operations on $\mathrm{Dih}\left(G\right)$ and $G\times {\mathbb{Z}}_2$ are identical. This proves the implication (2) ⇒ (3). Suppose that $\mathrm{Dih}\left(G\right)=G\times {\mathbb{Z}}_2$ and let $b\in G$. Note that $(e,1){\oplus }_{⋊}(b,0)=(e\ominus b,1)=(\ominus b,1)$ in $\mathrm{Dih}\left(G\right)$ and that $(e,1)\oplus (b,0)=(b,1)$ in $G\times {\mathbb{Z}}_2$. By assumption, $\ominus b=b$, which implies that $b\oplus b=e$. This proves the implication (3) ⇒ (2). □

The remainder of this section is devoted to the study of algebraic properties of dihedralizable gyrogroups and their dihedralized gyrogroups. These properties will prove useful in studying the Cayley graphs of dihedralized gyrogroups in the next section.

Proposition 6.

Any subgyrogroup of a dihedralizable gyrogroup is dihedralizable.

Proof. 

This follows from the fact that if H is a subgyrogroup of a gyrogroup G, then the operation on H is the restriction of the operation on G to H and the gyroautomorphism generated by a and b in H is the restriction of the gyroautomorphism of G generated by a and b to H. □

According to Proposition 6, if G is a dihedralizable gyrogroup and H is a subgyrogroup of G, then H is dihedralizable and $\mathrm{Dih}\left(H\right)$ exists. In fact, we have the following proposition.

Proposition 7.

Let G be a dihedralizable gyrogroup. If H is a subgyrogroup of G, then $\mathrm{Dih}\left(H\right)$ and $H\times \left\{0\right\}$ are subgyrogroups of $\mathrm{Dih}\left(G\right)$.

Proof. 

The proposition follows by Equation (14) and the subgyrogroup criterion. □

Corollary 1.

Let G be a dihedralizable gyrogroup. Then, $\mathrm{Dih}\left(G\right)$ contains an isomorphic copy of the dihedral group $D_{2n}$ for all $n\in \{\left|a\right|:a\in G,\left|a\right|<\infty \}$ with $n\ge 3$. If G has an element of infinite order, then $\mathrm{Dih}\left(G\right)$ contains an isomorphic copy of the infinite dihedral group $D_{\infty }$.

Proof. 

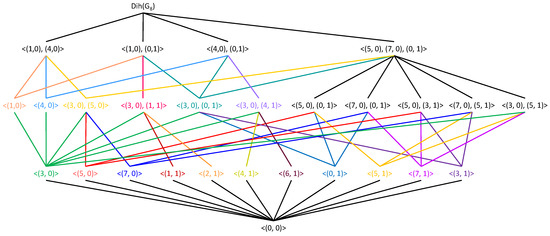
Let $a\in G$. In the case when $3\le n=\left|a\right|<\infty$, we know that $⟨a⟩$ is a subgyrogroup of G that forms a cyclic group of order n (cf. Corollaries 9 and 11 of [15]). Hence, $\mathrm{Dih}(⟨a⟩)$ is a subgyrogroup of $\mathrm{Dih}\left(G\right)$ and is isomorphic to $D_{2n}$. In the case when $\left|a\right|=\infty$, we know that $⟨a⟩$ is an infinite cyclic group. Hence, $\mathrm{Dih}(⟨a⟩)$ is isomorphic to $D_{\infty }$. □

Proposition 8.

Let G be a dihedralizable gyrogroup. If H is an L-subgyrogroup of G, then $\mathrm{Dih}\left(H\right)$ and $H\times \left\{0\right\}$ are L-subgyrogroups of $\mathrm{Dih}\left(G\right)$.

Proof. 

Suppose that H is an L-subgyrogroup of G. By Proposition 7, $\mathrm{Dih}\left(H\right)$ and $H\times \left\{0\right\}$ are subgyrogroups of $\mathrm{Dih}\left(G\right)$. Let $a\in G$ and let $h\in H$. From Equation (15), together with the fact that $\mathrm{gyr}\left[a,h\right]\left(H\right)=H$ and $\mathrm{gyr}\left[a,\ominus h\right]\left(H\right)=H$, we obtain

$$\mathrm{gyr}\left[(a,m),(h,n)\right]\left(\mathrm{Dih}\left(H\right)\right)=\mathrm{Dih}\left(H\right)\mathrm{and}\mathrm{gyr}\left[(a,m),(h,0)\right](H\times \{0\left\}\right)=H\times \left\{0\right\}.$$

This shows that $\mathrm{Dih}\left(H\right)$ and $H\times \left\{0\right\}$ are L-subgyrogroups of $\mathrm{Dih}\left(G\right)$. □

A partial converse of Proposition 7 holds, in the following sense.

Proposition 9.

Let G be a dihedralizable gyrogroup. If D is a subgyrogroup of $\mathrm{Dih}\left(G\right)$, then either $D=H\times \left\{0\right\}$ for some subgyrogroup H of G or there are an element b in G and a subgyrogroup K of G such that $\left\{\right(b,1\left)\right\}\subseteq D\subseteq \mathrm{Dih}\left(K\right)$.

Proof. 

Suppose that D is a subgyrogroup of $\mathrm{Dih}\left(G\right)$. Define

$$H_0\left(D\right)=\{a\in G:(a,0)\in D\}\mathrm{and}{H}_1\left(D\right)=\{a\in G:(a,1)\in D\}.$$

Note that $D=(H_0\left(D\right)\times \left\{0\right\})\cup (H_1\left(D\right)\times \left\{1\right\})$. First, we prove that $H_0\left(D\right)$ is always a subgyrogroup of G. Since $(e,0)\in D$, we obtain $e\in H_0\left(D\right)$. Let $a,b\in H_0\left(D\right)$. Then, $(a,0),(b,0)\in D$. Hence, $(\ominus a,0)=\ominus (a,0)\in D$, and so $(a\oplus b,0)=(a,0){\oplus }_{⋊}(b,0)\in D$. This implies $\ominus a\in H_0\left(D\right)$ and $a\oplus b\in H_0\left(D\right)$. Note that either $H_1\left(D\right)=\varnothing$ or $H_1\left(D\right)\ne \varnothing$. In the former case, we let $H=H_0\left(D\right)$ so that $D=H\times \left\{0\right\}$. In the latter case, we pick $b\in H_1\left(D\right)$. Hence, $(b,1)\in D$. Let K be the subgyrogroup of G generated by $H_0\left(D\right)\cup H_1\left(D\right)$. We show that $D\subseteq K\times {\mathbb{Z}}_2$. Let $(a,m)\in D$. If $m=0$, then $a\in H_0\left(D\right)\subseteq K$ and so $(a,m)\in K\times {\mathbb{Z}}_2$. If $m=1$, then $a\in H_1\left(D\right)\subseteq K$ and so $(a,m)\in K\times {\mathbb{Z}}_2$. This completes the proof. □

Proposition 10.

Let G be a dihedralizable gyrogroup and suppose that H is a subgyrogroup of G. If $H\times \left\{0\right\}$ is an L-subgyrogroup of $\mathrm{Dih}\left(G\right)$, then H is an L-subgyrogroup of G.

Proof. 

Let $a\in G$ and let $h\in H$. By assumption, $\mathrm{gyr}\left[(a,0),(h,0)\right]\left(\right(b,0\left)\right)=(\mathrm{gyr}\left[a,h\right]\left(b\right),0)$ belongs to $H\times \left\{0\right\}$ for all $b\in H$. This implies that $\mathrm{gyr}\left[a,h\right]\left(H\right)=H$. □

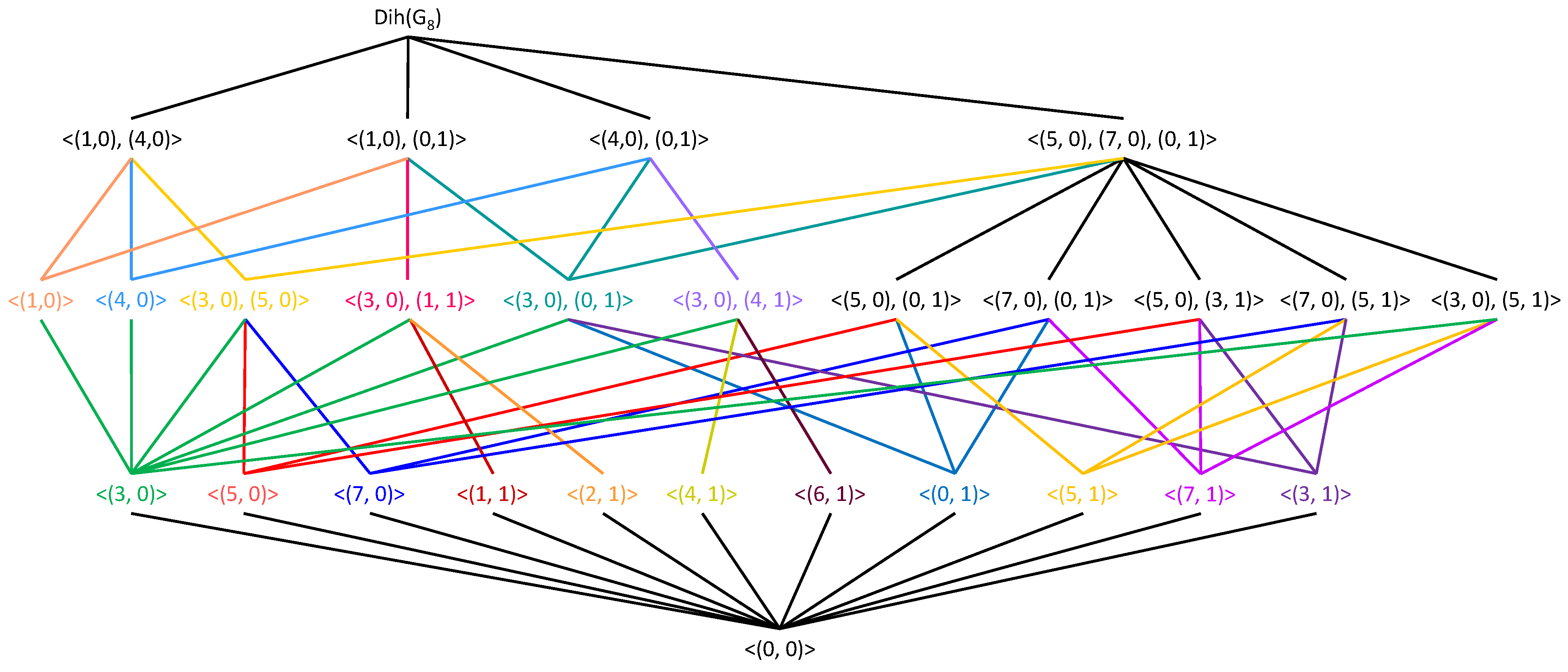
Propositions 7–10, together with Corollary 1, clarify some aspects of subgyrogroup lattices of dihedralized gyrogroups. For instance, any subgyrogroup of $\mathrm{Dih}\left(G\right)$ must be $H\times \left\{0\right\}$ or a subgyrogroup of $\mathrm{Dih}\left(H\right)$, where H is a subgyrogroup of G. The next lemma allows us to count the number of elements of order two in a dihedralized gyrogroup.

Lemma 3.

Let G be a dihedralizable gyrogroup.

1. 

Every element of the form $(a,1)$ in $\mathrm{Dih}\left(G\right)$ is of order two.

2. 

Any non-identity element of the form $(a,0)$ in $\mathrm{Dih}\left(G\right)$ is of order two if and only if a is of order two in G.

Proof. 

For each element $(a,1)\in \mathrm{Dih}\left(G\right)$, we obtain $(a,1){\oplus }_{⋊}(a,1)=(a\ominus a,0)=(e,0)$, where as $(a,1)\ne (e,0)$. This proves Part 1. Part 2 follows from the fact that $(e,0)=(a,0){\oplus }_{⋊}(a,0)=(a\oplus a,0)$ if and only if $a\oplus a=e$. □

From Lemma 3, we obtain the number of elements of order two in $\mathrm{Dih}\left(G\right)$ as follows.

Proposition 11.

Let G be a dihedralizable gyrogroup. The number of elements of order two in $\mathrm{Dih}\left(G\right)$ is $\left|G\right|+|G_2|-1$, where $G_2=\{a\in G:a\oplus a=e\}$.

Proof. 

Part 1 of Lemma 3 gives $\left|G\right|$ involutions, and Part 2 of Lemma 3 gives $|G_2|-1$ involutions. The involutions from the two parts are distinct and are all of the involutions in $\mathrm{Dih}\left(G\right)$, which completes the proof. □

Next, we show that a (respectively, strong, left, right, symmetric) generating set for a dihedralizable gyrogroup gives rise to a (respectively, strong, left, right, symmetric) generating set for the corresponding dihedralized gyrogroup.

Proposition 12.

Let G be a dihedralizable gyrogroup with a generating set S. Then, $(S\times \{0\left\}\right)\cup \left\{\right(e,1\left)\right\}$ is a generating set for $\mathrm{Dih}\left(G\right)$.

Proof. 

Define $T=(S\times \{0\left\}\right)\cup \left\{\right(e,1\left)\right\}$. We claim that $\mathrm{Dih}\left(G\right)=\bigcap \{D\le \mathrm{Dih}\left(G\right),T\subseteq D\}$. Note that by Proposition 2, $S\times \left\{0\right\}$ is a generating set of $\widehat{G}=\{(a,0):a\in G\}$ since G and $\widehat{G}$ are isomorphic via the isomorphism $a\mapsto (a,0)$. Let $a\in G$ and let $m\in {\mathbb{Z}}_2$. Suppose that $D\le \mathrm{Dih}\left(G\right)$ and $T\subseteq D$. First, we show that $(a,0)\in D$. Set $H_0\left(D\right)=\{a\in G:(a,0)\in D\}$. As in the proof of Proposition 9, $H_0\left(D\right)\le G$. By Proposition 7, $H_0\left(D\right)\times \left\{0\right\}\le \mathrm{Dih}\left(G\right)$ and so $H_0\left(D\right)\times \left\{0\right\}\le \widehat{G}$. Since $T\subseteq D$, we obtain $S\times \left\{0\right\}\subseteq H_0\left(D\right)\times \left\{0\right\}$. Hence, $(a,0)\in H_0\left(D\right)\times \left\{0\right\}$. This implies $a\in H_0\left(D\right)$, which, in turn, implies $(a,0)\in D$. This, in particular, shows that $\widehat{G}\subseteq D$. In the case when $m=0$, we obtain $(a,m)=(a,0)\in D$. In the case when $m=1$, we obtain $(a,m)=(a,1)=(a,0){\oplus }_{⋊}(e,1)\in D$ since both $(a,0)$ and $(e,1)$ belong to D. This shows that $\mathrm{Dih}\left(G\right)\subseteq \bigcap \{D\le \mathrm{Dih}\left(G\right),T\subseteq D\}$ and so equality holds. □

Proposition 13.

If a dihedralizable gyrogroup G is strongly generated by S, then $\mathrm{Dih}\left(G\right)$ is strongly generated by $(S\times \{0\left\}\right)\cup \left\{\right(e,1\left)\right\}$.

Proof. 

Suppose that S generates G and that $\mathrm{gyr}\left[a,b\right]\left(S\right)=S$ for all $a,b\in G$. By Proposition 12, $(S\times \{0\left\}\right)\cup \left\{\right(e,1\left)\right\}$ generates $\mathrm{Dih}\left(G\right)$. In view of Equation (15),

$$\mathrm{gyr}\left[(a,m),(b,n)\right]\left(\right(S\times \left\{0\right\})\cup \{(e,1)\left\}\right)=(S\times \{0\left\}\right)\cup \left\{\right(e,1\left)\right\}$$

for all $a,b\in G,m,n\in {\mathbb{Z}}_2$, which completes the proof. □

Proposition 14.

Let G be a dihedralizable gyrogroup. If S is a left (respectively, right) generating set of G, then $(S\times \{0\left\}\right)\cup \left\{\right(e,1\left)\right\}$ is a left (respectively, right) generating set of $\mathrm{Dih}\left(G\right)$.

Proof. 

Suppose that S is a left generating set for G. Let $(a,m)\in G\times {\mathbb{Z}}_2$. By assumption, $a=s_n\oplus (s_{n-1}\oplus (\cdots \oplus (s_2\oplus s_1)\cdots ))$ for some $s_1,s_2,\dots ,s_n\in S$. Moreover, $\ominus a=t_k\oplus (t_{k-1}\oplus (\cdots \oplus (t_2\oplus t_1)\cdots ))$ for some $t_1,t_2,\dots ,t_k\in S$. In the case when $m=0$, we obtain from Equation (14) that

$$\begin{array}{cc}\hfill (a,m)& =(a,0)\hfill \\ \hfill & =(s_n\oplus (s_{n-1}\oplus (\cdots \oplus (s_2\oplus s_1)\cdots )),0)\hfill \\ \hfill & =(s_n,0){\oplus }_{⋊}\left((s_{n-1},0){\oplus }_{⋊}(\cdots {\oplus }_{⋊}\left((s_2,0){\oplus }_{⋊}(s_1,0)\right)\cdots )\right).\hfill \end{array}$$

In the case when $m=1$, we obtain that

$$\begin{array}{cc}\hfill (a,m)& =(a,1)\hfill \\ \hfill & =(e,1){\oplus }_{⋊}(\ominus a,0)\hfill \\ \hfill & =(e,1){\oplus }_{⋊}\left((t_k,0){\oplus }_{⋊}\left((t_{k-1},0){\oplus }_{⋊}(\cdots {\oplus }_{⋊}\left((t_2,0){\oplus }_{⋊}(t_1,0)\right)\cdots )\right)\right).\hfill \end{array}$$

This shows that $(S\times \{0\left\}\right)\cup \left\{\right(e,1\left)\right\}$ is a left generating set of $\mathrm{Dih}\left(G\right)$. Using the fact that $(b,1)=(b,0){\oplus }_{⋊}(e,1)$ for all $b\in G$, one can prove in a similar fashion that if S is a right generating set for G, then $(S\times \{0\left\}\right)\cup \left\{\right(e,1\left)\right\}$ is a right generating set for $\mathrm{Dih}\left(G\right)$. □

Proposition 15.

Let G be a dihedralizable gyrogroup and let $S\subseteq G$. If S is symmetric, then $(S\times \{0\left\}\right)\cup \left\{\right(e,1\left)\right\}$ is symmetric.

Proof. 

This is because $\ominus (s,0)=(\ominus s,0)$ for all $s\in S$ and $\ominus (e,1)=(e,1)$. □

We complete this section by recording a new non-gyrocommutative gyrogroup of order 16, constructed by Theorem 10.

Example 5.

By inspection, $G_8$ is dihedralizable. Its dihedralized gyrogroup, $\mathrm{Dih}\left(G_8\right)$, is a gyro-group of order 16 whose gyroaddition and gyration tables are given in Table 2 and Table 3, respectively. The non-trivial gyroautomorphism $\tilde{A}$ of $\mathrm{Dih}\left(G_8\right)$ is given in cycle decomposition by

$$\tilde{A}=\left((4,0)(6,0)\right)\left((5,0)(7,0)\right)\left((4,1)(6,1)\right)\left((5,1)(7,1)\right).$$

(16)

In view of Propositions 7–10, together with Corollary 1, we draw the subgyrogroup lattice of the gyrogroup $\mathrm{Dih}\left(G_8\right)$, as shown in Figure 1.

Table 2. The gyroaddition table of the gyrogroup $\mathrm{Dih}\left(G_8\right)$.

${\oplus }_{⋊}$	(0,0)	(1,0)	(2,0)	(3,0)	(4,0)	(5,0)	(6,0)	(7,0)	(0,1)	(1,1)	(2,1)	(3,1)	(4,1)	(5,1)	(6,1)	(7,1)
(0,0)	(0,0)	(1,0)	(2,0)	(3,0)	(4,0)	(5,0)	(6,0)	(7,0)	(0,1)	(1,1)	(2,1)	(3,1)	(4,1)	(5,1)	(6,1)	(7,1)
(1,0)	(1,0)	(3,0)	(0,0)	(2,0)	(7,0)	(4,0)	(5,0)	(6,0)	(1,1)	(3,1)	(0,1)	(2,1)	(7,1)	(4,1)	(5,1)	(6,1)
(2,0)	(2,0)	(0,0)	(3,0)	(1,0)	(5,0)	(6,0)	(7,0)	(4,0)	(2,1)	(0,1)	(3,1)	(1,1)	(5,1)	(6,1)	(7,1)	(4,1)
(3,0)	(3,0)	(2,0)	(1,0)	(0,0)	(6,0)	(7,0)	(4,0)	(5,0)	(3,1)	(2,1)	(1,1)	(0,1)	(6,1)	(7,1)	(4,1)	(5,1)
(4,0)	(4,0)	(5,0)	(7,0)	(6,0)	(3,0)	(2,0)	(0,0)	(1,0)	(4,1)	(5,1)	(7,1)	(6,1)	(3,1)	(2,1)	(0,1)	(1,1)
(5,0)	(5,0)	(6,0)	(4,0)	(7,0)	(2,0)	(0,0)	(1,0)	(3,0)	(5,1)	(6,1)	(4,1)	(7,1)	(2,1)	(0,1)	(1,1)	(3,1)
(6,0)	(6,0)	(7,0)	(5,0)	(4,0)	(0,0)	(1,0)	(3,0)	(2,0)	(6,1)	(7,1)	(5,1)	(4,1)	(0,1)	(1,1)	(3,1)	(2,1)
(7,0)	(7,0)	(4,0)	(6,0)	(5,0)	(1,0)	(3,0)	(2,0)	(0,0)	(7,1)	(4,1)	(6,1)	(5,1)	(1,1)	(3,1)	(2,1)	(0,1)
(0,1)	(0,1)	(2,1)	(1,1)	(3,1)	(6,1)	(5,1)	(4,1)	(7,1)	(0,0)	(2,0)	(1,0)	(3,0)	(6,0)	(5,0)	(4,0)	(7,0)
(1,1)	(1,1)	(0,1)	(3,1)	(2,1)	(5,1)	(4,1)	(7,1)	(6,1)	(1,0)	(0,0)	(3,0)	(2,0)	(5,0)	(4,0)	(7,0)	(6,0)
(2,1)	(2,1)	(3,1)	(0,1)	(1,1)	(7,1)	(6,1)	(5,1)	(4,1)	(2,0)	(3,0)	(0,0)	(1,0)	(7,0)	(6,0)	(5,0)	(4,0)
(3,1)	(3,1)	(1,1)	(2,1)	(0,1)	(4,1)	(7,1)	(6,1)	(5,1)	(3,0)	(1,0)	(2,0)	(0,0)	(4,0)	(7,0)	(6,0)	(5,0)
(4,1)	(4,1)	(7,1)	(5,1)	(6,1)	(0,1)	(2,1)	(3,1)	(1,1)	(4,0)	(7,0)	(5,0)	(6,0)	(0,0)	(2,0)	(3,0)	(1,0)
(5,1)	(5,1)	(4,1)	(6,1)	(7,1)	(1,1)	(0,1)	(2,1)	(3,1)	(5,0)	(4,0)	(6,0)	(7,0)	(1,0)	(0,0)	(2,0)	(3,0)
(6,1)	(6,1)	(5,1)	(7,1)	(4,1)	(3,1)	(1,1)	(0,1)	(2,1)	(6,0)	(5,0)	(7,0)	(4,0)	(3,0)	(1,0)	(0,0)	(2,0)
(7,1)	(7,1)	(6,1)	(4,1)	(5,1)	(2,1)	(3,1)	(1,1)	(0,1)	(7,0)	(6,0)	(4,0)	(5,0)	(2,0)	(3,0)	(1,0)	(0,0)

Table 3. The gyration table of the gyrogroup $\mathrm{Dih}\left(G_8\right)$. Here, I is the identity automorphism of $\mathrm{Dih}\left(G_8\right)$ and $\tilde{A}$ is given by Equation (16).

gyr	(0,0)	(1,0)	(2,0)	(3,0)	(4,0)	(5,0)	(6,0)	(7,0)	(0,1)	(1,1)	(2,1)	(3,1)	(4,1)	(5,1)	(6,1)	(7,1)
(0,0)	I	I	I	I	I	I	I	I	I	I	I	I	I	I	I	I
(1,0)	I	I	I	I	$\tilde{A}$	$\tilde{A}$	$\tilde{A}$	$\tilde{A}$	I	I	I	I	$\tilde{A}$	$\tilde{A}$	$\tilde{A}$	$\tilde{A}$
(2,0)	I	I	I	I	$\tilde{A}$	$\tilde{A}$	$\tilde{A}$	$\tilde{A}$	I	I	I	I	$\tilde{A}$	$\tilde{A}$	$\tilde{A}$	$\tilde{A}$
(3,0)	I	I	I	I	I	I	I	I	I	I	I	I	I	I	I	I
(4,0)	I	$\tilde{A}$	$\tilde{A}$	I	I	$\tilde{A}$	I	$\tilde{A}$	I	$\tilde{A}$	$\tilde{A}$	I	I	$\tilde{A}$	I	$\tilde{A}$
(5,0)	I	$\tilde{A}$	$\tilde{A}$	I	$\tilde{A}$	I	$\tilde{A}$	I	I	$\tilde{A}$	$\tilde{A}$	I	$\tilde{A}$	I	$\tilde{A}$	I
(6,0)	I	$\tilde{A}$	$\tilde{A}$	I	I	$\tilde{A}$	I	$\tilde{A}$	I	$\tilde{A}$	$\tilde{A}$	I	I	$\tilde{A}$	I	$\tilde{A}$
(7,0)	I	$\tilde{A}$	$\tilde{A}$	I	$\tilde{A}$	I	$\tilde{A}$	I	I	$\tilde{A}$	$\tilde{A}$	I	$\tilde{A}$	I	$\tilde{A}$	I
(0,1)	I	I	I	I	I	I	I	I	I	I	I	I	I	I	I	I
(1,1)	I	I	I	I	$\tilde{A}$	$\tilde{A}$	$\tilde{A}$	$\tilde{A}$	I	I	I	I	$\tilde{A}$	$\tilde{A}$	$\tilde{A}$	$\tilde{A}$
(2,1)	I	I	I	I	$\tilde{A}$	$\tilde{A}$	$\tilde{A}$	$\tilde{A}$	I	I	I	I	$\tilde{A}$	$\tilde{A}$	$\tilde{A}$	$\tilde{A}$
(3,1)	I	I	I	I	I	I	I	I	I	I	I	I	I	I	I	I
(4,1)	I	$\tilde{A}$	$\tilde{A}$	I	I	$\tilde{A}$	I	$\tilde{A}$	I	$\tilde{A}$	$\tilde{A}$	I	I	$\tilde{A}$	I	$\tilde{A}$
(5,1)	I	$\tilde{A}$	$\tilde{A}$	I	$\tilde{A}$	I	$\tilde{A}$	I	I	$\tilde{A}$	$\tilde{A}$	I	$\tilde{A}$	I	$\tilde{A}$	I
(6,1)	I	$\tilde{A}$	$\tilde{A}$	I	I	$\tilde{A}$	I	$\tilde{A}$	I	$\tilde{A}$	$\tilde{A}$	I	I	$\tilde{A}$	I	$\tilde{A}$
(7,1)	I	$\tilde{A}$	$\tilde{A}$	I	$\tilde{A}$	I	$\tilde{A}$	I	I	$\tilde{A}$	$\tilde{A}$	I	$\tilde{A}$	I	$\tilde{A}$	I

Figure 1. The subgyrogroup lattice of the gyrogroup $\mathrm{Dih}\left(G_8\right)$.

Since $G_8$ is not of exponent at most two (for example, $1\oplus 1\ne 0$ in $G_8$), it follows by Theorem 11 that $\mathrm{Dih}\left(G_8\right)$ is not gyrocommutative. This indicates that our construction is not the same as the construction of Mahdavi et al. in [18]. This is because, when the initial gyrogroup in their construction is gyrocommutative, the resulting gyrogroup is also gyrocommutative (see Corollary 2.3 of [18]). Moreover, our construction is not the same as the construction presented in [19] since the so-called dihedral gyrogroup $G\left(n\right)$ has the property that all proper subgyrogroups of $G\left(n\right)$ are either cyclic or dihedral groups, whereas $\mathrm{Dih}\left(G\right)$ contains a proper non-degenerate subgyrogroup whenever G is a non-degenerate dihedralizable gyrogroup. Finally, $\mathrm{Dih}\left(G_8\right)$ is not isomorphic to the gyrogroup $K_{16}$ exhibited in p. 41 of [20], since their right nuclei are not isomorphic (see Section 3 of [16]).

4. Cayley Graphs of Dihedralized Gyrogroups

In this section, we inspect the right Cayley graphs of dihedralized gyrogroups and point out some differences between them and those of generalized dihedral groups. Let A be an abelian group (written multiplicatively) with a generating set S, let $\mathrm{Dih}\left(A\right)$ be the generalized dihedral group afforded by A, and let $\tilde{S}=(S\times \left\{0\right\})\cup \left\{(e,1)\right\}$. Then, the right Cayley graph $\mathrm{RCay}(\mathrm{Dih}\left(G\right),\tilde{S})$ is a graph composed of two main induced subgraphs, one consisting of the vertices of the form $(g,0)$ and the other consisting of the vertices of the form $(g,1)$. We denote the former by $C_0$ and the latter by $C_1$. Both $C_0$ and $C_1$ have the same underlying undirected graphs, isomorphic to $\mathrm{RCay}(G,S)$. While $C_0$ preserves the edge direction of $\mathrm{RCay}(G,S)$, $C_1$ reverses the edge direction. In this Cayley graph, the two induced subgraphs are connected to one another by every pair $(g,0)$ and $(g,1)$ (every pair $(g,0)$ and $(g^{-1},1)$ for the left Cayley graph) via the bi-directional edge $(e,1)$. This scenario is true regardless of whether we consider the left or right Cayley graphs. However, it is not necessarily true in the case of gyrogroups, as we will see in Example 7.

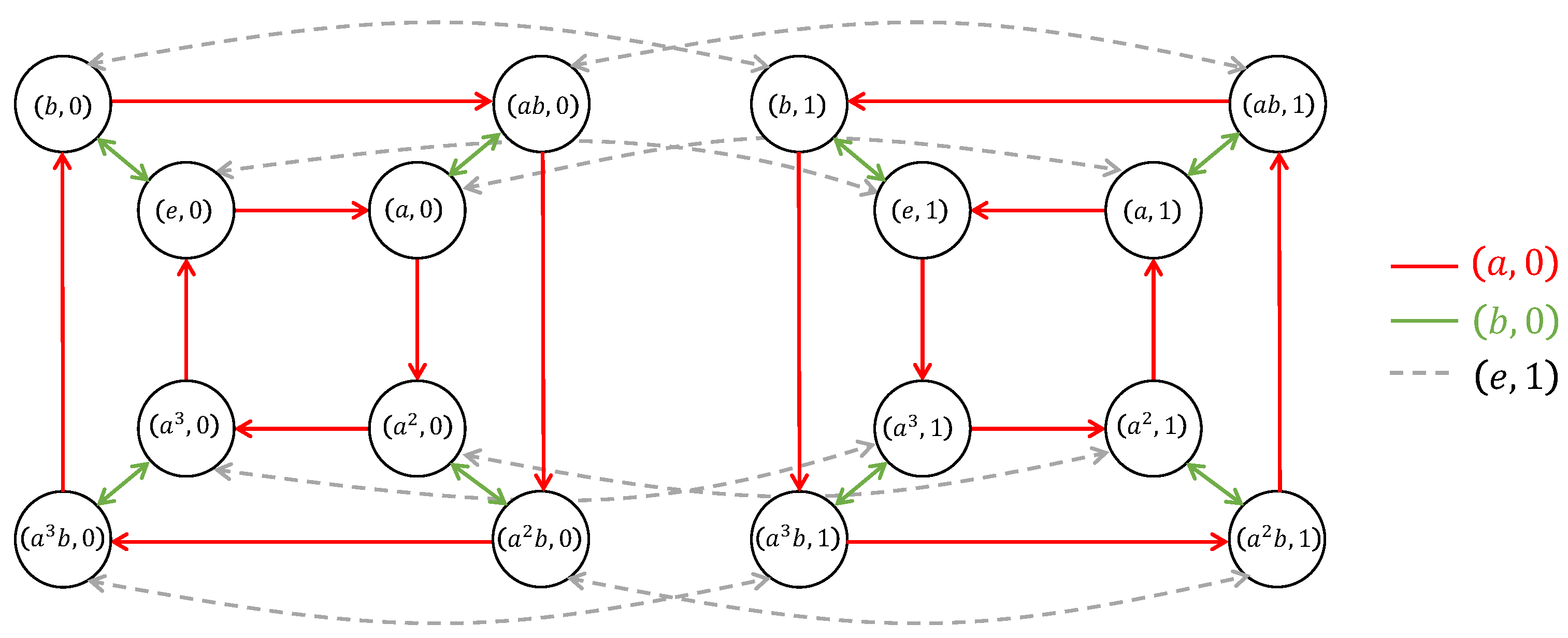
Example 6.

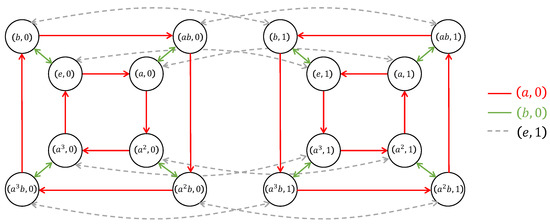
Consider the group $G=⟨a,b:a^4=b^2=e,ab=ba⟩$, isomorphic to ${\mathbb{Z}}_4\times {\mathbb{Z}}_2$. The right Cayley graph $\mathrm{RCay}(\mathrm{Dih}\left(G\right),\{(a,0),(b,0),(e,1)\left\}\right)$ is depicted in Figure 2, illustrating the discussion above. The subgraph $C_0$ induced by the vertices of the form $(g,0)$ is the left cube and the subgraph $C_1$ induced by the vertices of the form $(g,1)$ is the right cube.

Figure 2. The right Cayley graph $\mathrm{RCay}(\mathrm{Dih}\left(G\right),\tilde{S})$, where G is the group with presentation $⟨a,b:a^4=b^2=e,ab=ba⟩$ and $\tilde{S}=\{(a,0),(b,0),(e,1)\}$.

Next, we describe some combinatorial properties of $\mathrm{RCay}(\mathrm{Dih}\left(G\right),\tilde{S})$, where G is a finite dihedralizable gyrogroup, S is a right generating set for G, and $\tilde{S}=(S\times \left\{0\right\})\cup \left\{(e,1)\right\}$. As in the discussion at the beginning of this section, let $C_0$ and $C_1$ be the subgraphs of $\mathrm{RCay}(\mathrm{Dih}\left(G\right),\tilde{S})$ induced by $G\times \left\{0\right\}$ and $G\times \left\{1\right\}$, respectively. By definition, the edges in $C_1$ (and also $C_0$) must be generated by elements of the form $(s,0)$ with $s\in S$.

Proposition 16.

Let G be a finite dihedralizable gyrogroup with a right generating set S and let $\tilde{S}=(S\times \left\{0\right\})\cup \left\{(e,1)\right\}$. Then, $\mathrm{RCay}(\mathrm{Dih}\left(G\right),\tilde{S})$ is connected.

Proof. 

This proposition follows as a consequence of Proposition 14. □

Theorem 12.

Let G be a finite dihedralizable gyrogroup with a right generating set S and let $\tilde{S}=(S\times \left\{0\right\})\cup \left\{(e,1)\right\}$. In $\mathrm{RCay}(\mathrm{Dih}\left(G\right),\tilde{S})$, the subgraph $C_0$ induced by $G\times \left\{0\right\}$ is isomorphic to $\mathrm{RCay}(G,S)$ and the subgraph $C_1$ induced by $G\times \left\{1\right\}$ is isomorphic to $\mathrm{RCay}(G,\ominus S)$. Furthermore, $C_0$ and $C_1$ are isomorphic.

Proof. 

The subgraphs $C_0$ and $C_1$ are isomorphic to $\mathrm{RCay}(G,S)$ and $\mathrm{RCay}(G,\ominus S)$ via the maps $g\mapsto (g,0)$ and $g\mapsto (g,1)$, $g\in G$, respectively. To see that $C_0$ and $C_1$ are isomorphic, we use the bijective map $L_{(0,1)}:G\times \left\{0\right\}\to G\times \left\{1\right\}$ defined by $L_{(0,1)}\left((a,0)\right)=(\ominus a,1)$, $a\in G$. Suppose that there is an edge $(a,0)\to (b,0)$ in $C_0$. Hence, $b=a\oplus s$ for some $s\in S$. Then, $(\ominus a,1){\oplus }_{⋊}(s,0)=(\ominus a\ominus s,1)=(\ominus (a\oplus s),1)=(\ominus b,1)$ by its gyrocommutativity, which means that there is an edge $(\ominus a,1)\to (\ominus b,1)$ in $C_1$. Similarly, we obtain that an edge $(\ominus a,1)\to (\ominus b,1)$ exists in $C_1$ implies an edge $(a,0)\to (b,0)$ exists in $C_0$. Thus, $L_{(0,1)}$ defines a graph isomorphism. □

Theorem 13.

Let G be a finite dihedralizable gyrogroup, let S be a right generating set of G, and let $\tilde{S}=(S\times \left\{0\right\})\cup \left\{(e,1)\right\}$. Suppose that there is an edge $(a,0)\to (b,0)$ in $\mathrm{RCay}(\mathrm{Dih}\left(G\right),\tilde{S})$; that is, $(b,0)=(a,0)\oplus (s,0)$ for some $s\in S$. Then,

1. 

there is an edge $(a,1)\to (b,1)$ if and only if $\ominus s\in S$, and

2. 

there is an edge $(b,1)\to (a,1)$ if and only if $\mathrm{gyr}\left[b,s\right]\left(s\right)\in S$.

Proof. 

Suppose that there is an edge $(a,1)\to (b,1)$. Then, there exists an element $(s^{\prime },0)\in \tilde{S}$ such that $(b,1)=(a,1){\oplus }_{⋊}(s^{\prime },0)=(a\ominus s^{\prime },1)$. Hence, $b=a\ominus s^{\prime }$. By assumption, $b=a\oplus s$. Applying the left cancellation law I to $a\ominus s^{\prime }=a\oplus s$, we obtain $s=\ominus s^{\prime }$, which implies $\ominus s=s^{\prime }\in S$. Conversely, suppose that $\ominus s\in S$. Then, $(\ominus s,0)\in \tilde{S}$, and so $(a,1){\oplus }_{⋊}(\ominus s,0)=(a\oplus s,1)=(b,1)$, which shows that there is an edge $(a,1)\to (b,1)$. This proves Part 1.

Suppose that there is an edge $(b,1)\to (a,1)$. Then, there is an element $s^{\prime }\in S$ such that $(a,1)=(b,1){\oplus }_{⋊}(s^{\prime },0)=(b\ominus s^{\prime },1)$. Hence, $a=b\ominus s^{\prime }$. By assumption, $b=a\oplus s$ and by the right cancellation law II, $b\boxminus s=a$. Recall that $b\boxminus s=b\oplus \mathrm{gyr}\left[b,s\right](\ominus s)$. Applying the left cancellation law I and then using the fact that any gyroautomorphism preserves inverses, we conclude that $\mathrm{gyr}\left[b,s\right]\left(s\right)=s^{\prime }\in S$. Conversely, suppose that $\mathrm{gyr}\left[b,s\right]\left(s\right)\in S$. Then, $(b,1){\oplus }_{⋊}(\mathrm{gyr}\left[b,s\right]\left(s\right),0)=(b\ominus \mathrm{gyr}\left[b,s\right]\left(s\right),1)=(b\boxminus s,1)=(a,1)$, which implies that there is an edge $(b,1)\to (a,1)$. This proves Part 2. □

Next, we give a sufficient condition to specify a Hamiltonian path in the right Cayley graph of a certain gyrogroup, which can be decomposed as an internal semidirect product of some cyclic groups.

Theorem 14.

Let G be a finite gyrogroup that is an internal semidirect product $K⋊H$, where $K=⟨r⟩\cong {\mathbb{Z}}_n$ and $H=⟨s⟩\cong {\mathbb{Z}}_2$. Let $S=\{r,s\}$. If $\mathrm{gyr}\left[r,g\right]\left(r\right)=r$ for all $g\in G$, then the walk $e\left[{\left[r\right]}^{n-1}\left[s\right]{\left[r\right]}^{n-1}\right]$ is a Hamiltonian path in $\mathrm{RCay}(G,S)$. In addition, if G is dihedralizable, then the walk $(e,0)\left[{\left[(r,0)\right]}^{n-1}\left[(s,0)\right]{\left[(r,0)\right]}^{n-1}\left[(0,1)\right]{\left[(r,0)\right]}^{n-1}\left[(s,0)\right]{\left[(r,0)\right]}^{n-1}\right]$ is a Hamiltonian path in $\mathrm{RCay}(\mathrm{Dih}\left(G\right),\tilde{S})$, where $\tilde{S}=\{(r,0),(s,0),(e,1)\}$.

Proof. 

Note that G and $\mathrm{Dih}\left(G\right)$ are right generated by S and $\tilde{S}$, respectively, by Propositions 4 and 14. We will show that each walk is a path and exhaust the vertices in the respective Cayley graphs. First, consider $\mathrm{RCay}(G,S)$ and the walk $e\left[{\left[r\right]}^{n-1}\left[s\right]{\left[r\right]}^{n-1}\right]$. Starting with e and ending with $(n-1)r$, the subwalk $e\left[r^{n-1}\right]$ is clearly a path and consists of all elements in K. It is left to show that the rest of the walk consists of all elements in $K\oplus s$. The vertices in the rest of the walk are $(n-1)r\oplus s$, $((n-1)r\oplus s)\oplus r_1$,⋯, $(\cdots (((n-1)r\oplus s)\oplus r_1)\cdots )\oplus r_{n-1}$, where $r_i=r$ for all i. Any of these vertices is not in K. Otherwise, we would have $(\cdots (((n-1)r\oplus s)\oplus r_1)\cdots )\oplus r_k=mr$ for some $k\in \{0,1,\cdots ,n-1\}$ and some $m\in \mathbb{Z}$, leading to $s=m^{\prime }r\in K$ for some $m^{\prime }\in \mathbb{Z}$ after performing appropriate right and left cancellation laws, which is a contradiction. The assumption that $\mathrm{gyr}\left[r,g\right]\left(r\right)=r$ for all $g\in G$, together with the right gyroassociative law, allows us to move parentheses so that an element of the form $(\cdots ((x\oplus s)\oplus r_1)\oplus \cdots )\oplus r_k$ can be written as $(x\oplus s)\oplus kr$, where $r_i=r$ for all i. Given two non-negative integers i and j, where $0\le i<j\le n-1$, the two vertices $(x\oplus s)\oplus (r_1\oplus \cdots \oplus r_i)$ and $(x\oplus s)\oplus (r_1\oplus \cdots \oplus r_j)$ are not the same, since otherwise we would have $(j-i)r=e$, contrary to the order of r. We conclude that the second half of the walk exhausts all vertices in $K\oplus s$. Hence, the result follows.

The proof for $\mathrm{RCay}(\mathrm{Dih}\left(G\right),\tilde{S})$ follows by a similar reasoning. Consider the walk $(e,0)\left[{\left[(r,0)\right]}^{n-1}\left[(s,0)\right]{\left[(r,0)\right]}^{n-1}\left[(0,1)\right]{\left[(r,0)\right]}^{n-1}\left[(s,0)\right]{\left[(r,0)\right]}^{n-1}\right]$. As in the first part, the subwalk $(e,0)\left[{\left[(r,0)\right]}^{n-1}\left[(s,0)\right]{\left[(r,0)\right]}^{n-1}\right]$ visits all vertices in $G\times \left\{0\right\}$ and ends with the vertex $\left(\right((n-1)r\oplus s)\oplus (n-1)r,0)$. From this vertex, following the edge label $(0,1)$, we visit the vertex $\left(\right((n-1)r\oplus s)\oplus (n-1)r,1)$. Then, following the edge label $(r,0)$ and noting that $\mathrm{gyr}\left[(r,0),(g,m)\right]\left(\right(r,0\left)\right)=(\mathrm{gyr}\left[r,g\right]\left(r\right),0)=(r,0)$, we reach the vertex

$$\left(\right(\left(\right(n-1)r\oplus s)\oplus (n-1)r)\ominus r,1)=\left(\right((n-1)r\oplus s)\oplus (n-2)r,1).$$

Thus, the subwalk $(e,0)\left[{\left[(r,0)\right]}^{n-1}\left[(s,0)\right]{\left[(r,0)\right]}^{n-1}\left[(0,1)\right]{\left[(r,0)\right]}^{n-1}\right]$ ends with the vertex $\left(\right(n-1)r\oplus s,1)$ and exhausts all vertices in $G\times \left\{0\right\}$ and $(K\oplus s)\times \left\{1\right\}$. Following the edge label $(s,0)$, we visit the vertex $\left(\right((n-1)r\oplus s)\oplus s,1)$, which must be a vertex in $K\times \left\{1\right\}$. Otherwise, we would have $\left(\right(n-1)r\oplus s)\oplus s=mr\oplus s$ for some $m\in \mathbb{Z}$, leading to $s=m^{\prime }r\in K$ for some $m^{\prime }\in \mathbb{Z}$. Since we are visiting a vertex in $K\times \left\{1\right\}$ and $K=⟨r⟩\cong {\mathbb{Z}}_n$, following the subwalk $\left[{\left[(r,0)\right]}^{n-1}\right]$ is equivalent to adding to the first coordinate of the vertices by $\ominus r$. Hence, we visit all the vertices in $K\times \left\{1\right\}$. □

The following example shows that combinatorial properties of Cayley graphs of gyrogroups depend heavily on their gyrations and illustrates what we have discussed so far.

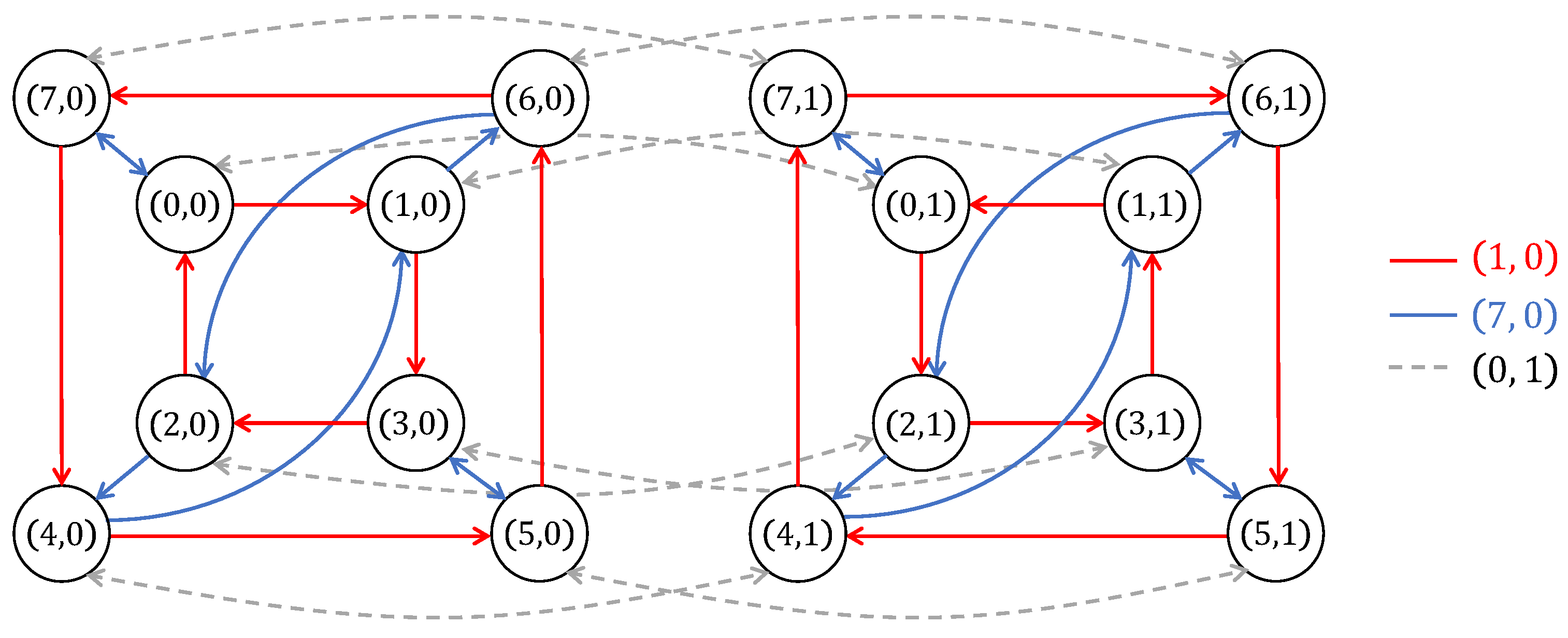
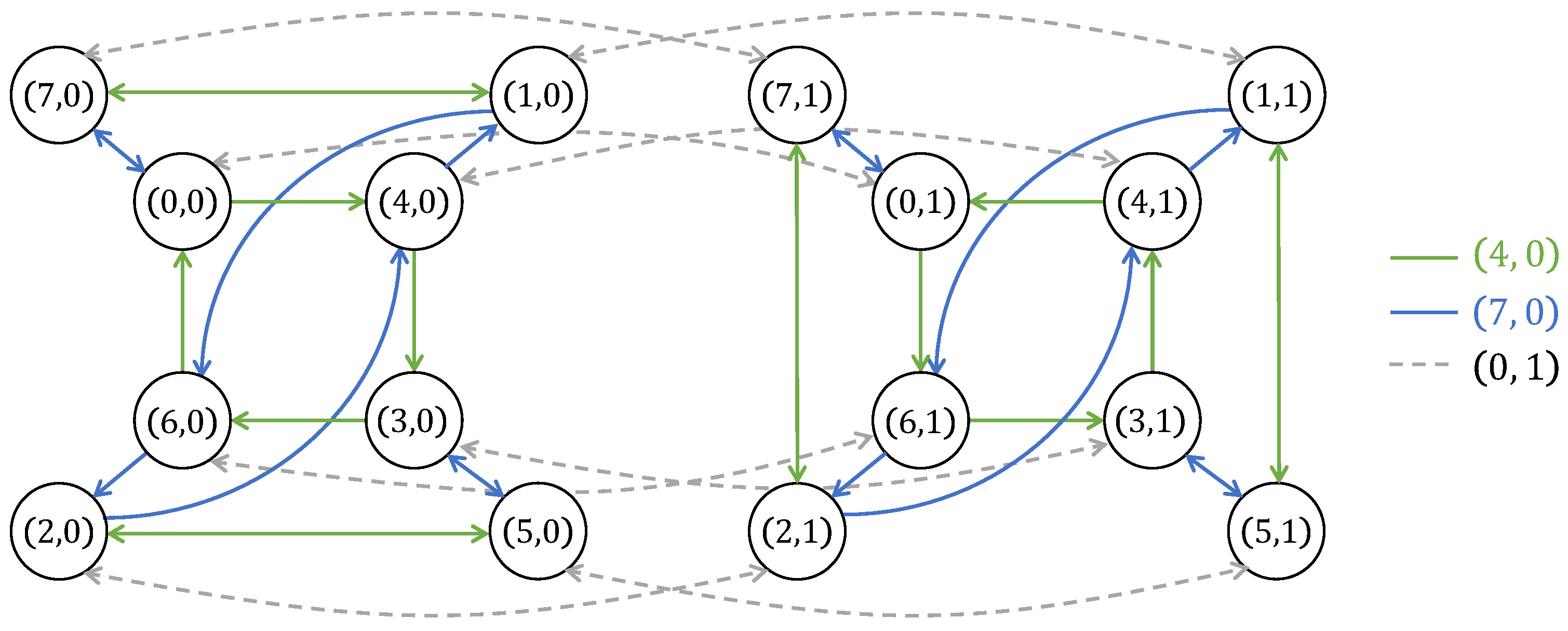
Example 7.

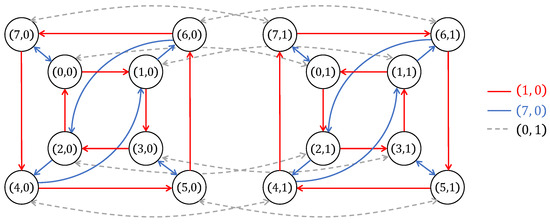
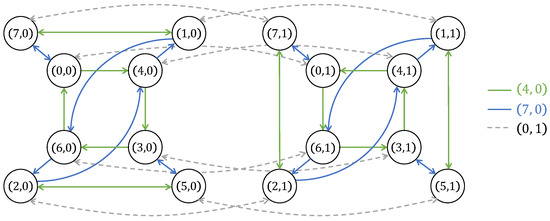
In this example, we exhibit two right Cayley graphs of $\mathrm{Dih}\left(G_8\right)$, where $G_8$ is given in Example 1, and make some observations on them:

$$\begin{array}{cc}\hfill {\mathcal{C}}_1=\mathrm{RCay}(\mathrm{Dih}\left(G_8\right),\widetilde{S_1}),& where{S}_1=\{1,7\},\hfill \\ \hfill {\mathcal{C}}_2=\mathrm{RCay}(\mathrm{Dih}\left(G_8\right),\widetilde{S_2}),& where{S}_2=\{4,7\}.\hfill \end{array}$$

Note that $⟨1⟩=\{0,1,2,3\}\cong {\mathbb{Z}}_4$, $⟨4⟩=\{0,3,4,6\}\cong {\mathbb{Z}}_4$, and $⟨7⟩=\{0,7\}\cong {\mathbb{Z}}_2$. The corresponding graphical representations are depicted in Figure 3 and Figure 4, respectively. The following are some observations we make for these Cayley graphs.

Figure 3. The right Cayley graph ${\mathcal{C}}_1=\mathrm{RCay}(\mathrm{Dih}\left(G_8\right),\widetilde{S_1}),\mathrm{where}{S}_1=\{1,7\}$, in Example 7.

Figure 4. The right Cayley graph ${\mathcal{C}}_2=\mathrm{RCay}(\mathrm{Dih}\left(G_8\right),\widetilde{S_2}),\mathrm{where}{S}_2=\{4,7\}$, in Example 7.

1. 

Since $⟨1⟩$ and $⟨4⟩$ are isomorphic to ${\mathbb{Z}}_4$, we obtain from Corollary 1 that $\mathrm{Dih}(⟨1⟩)$ and $\mathrm{Dih}(⟨4⟩)$ are indeed the dihedral group $D_8$ and subgyrogroups of $\mathrm{Dih}\left(G_8\right)$. Their Cayley graphs are the cubic subgraphs of ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$ induced by $⟨1⟩$ and $⟨4⟩$, respectively. Each is the cubic subgraph formed by two small squares in the corresponding Cayley graphs.

2. 

Observe that, in each Cayley graph, the subgraphs $C_0$ and $C_1$ are isomorphic as stated in Theorem 12.

3. 

Since $\mathrm{gyr}\left[a,b\right]\left(1\right)=1$ for all $a,b\in G_8$, we obtain from Theorem 13 that whenever we see an edge $(a,0)\to (b,0)$ with color $(1,0)$, we will see an edge $(b,1)\to (a,1)$ with the same color (see the figure of ${\mathcal{C}}_1$). This is not true for the edge label $(4,0)$ since 4 is not fixed by some gyroautomorphisms (see the figure of ${\mathcal{C}}_2$ and compare with ${\mathcal{C}}_1$).

4. 

Since 7 is its own inverse in $G_8$, we obtain from Theorem 13 that whenever we see an edge $(a,0)\to (b,0)$ with color $(7,0)$, we will see an edge $(a,1)\to (b,1)$ with the same color (see the figures of ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$).

5. 

In Example 3, $\mathrm{Dih}\left(G_8\right)=⟨1⟩⋊⟨7⟩$ and 1 is fixed by all of gyroautomorphisms of $G_8$. By Theorem 14, the walk

$$(0,0)\left[{\left[(1,0)\right]}^3\left[(7,0)\right]{\left[(1,0)\right]}^3\left[(0,1)\right]{\left[(1,0)\right]}^3\left[(7,0)\right]{\left[(1,0)\right]}^3\right]$$

is a Hamiltonian path in ${\mathcal{C}}_1$. In contrast, the walk

$$(0,0)\left[{\left[(4,0)\right]}^3\left[(7,0)\right]{\left[(4,0)\right]}^3\left[(0,1)\right]{\left[(4,0)\right]}^3\left[(7,0)\right]{\left[(4,0)\right]}^3\right]$$

is not even a path in ${\mathcal{C}}_2$. This is because 4 does not satisfy the gyration condition of Theorem 14, although $\mathrm{Dih}\left(G_8\right)=⟨1⟩⋊⟨4⟩$.

Proposition 17.

Suppose that G is a finite dihedralizable gyrogroup and let S be a symmetric subset of G not containing e such that $\mathrm{gyr}\left[a,b\right]\left(S\right)=S$ for all $a,b\in G$. Then, $\mathrm{RCay}(\mathrm{Dih}\left(G\right),\tilde{S})$ is transitive, where $\tilde{S}=(S\times \left\{0\right\})\cup \left\{(e,1)\right\}$.

Proof. 

By Proposition 15, $\tilde{S}$ is symmetric. As in the proof of Proposition 13, $\mathrm{gyr}\left[a,b\right]\left(\tilde{S}\right)=\tilde{S}$ for all $a,b\in G$. Hence, $\mathrm{RCay}(\mathrm{Dih}\left(G\right),\tilde{S})$ is transitive by Theorem 7. □