Parameterization of a Novel Nonlinear Estimator for Uncertain SISO Systems with Noise Scenario

Abstract

Dynamic observers are commonly used in feedback loops to estimate the system’s states from available control inputs and measured outputs. The presence of measurement noise degrades the performance of the observer and consequently degrades the performance of the controlled system. This paper presents a novel nonlinear higher-order extended state observer (NHOESO) for efficient state and disturbance estimation in presence of measurement noise for nonlinear single-input–single-output systems. The proposed nonlinear function allows a fast reconstruction of the system’s states and is robust against uncertainties and measurement noise. An analytical parameterization technique is proposed to parameterize the coefficients of the proposed nonlinear higher-order extended state observer in the case of measurement noise in the output signal. Several scenarios are simulated to demonstrate the effectiveness of the proposed observer.

1. Introduction

The presence of noise in engineering environments is inevitable and may reduce considerably the performance of the controlled system that uses, in the feedback loop, noisy outputs, directly or through state observers. The impact of noise may be attenuated by applying suited filters on the system outputs that are injected in the observer. However, it is difficult to overcome the differences in amplitude and phase between the filtered signals and the actual system outputs. These differences may also degrade the performance of the controlled system. However, in some nonlinear systems the noise is beneficial for enhancing weak signals of interest and signal estimation such as [1].

1.1. Related Work

An attenuation technique of measurement noise is applied to a state observer in [2] to decouple the effect of noise from the observed states. To manage noisy estimations, the extended state observer (ESO) structure is expanded with another fictional state variable which is the integral of the output signal. This noise attenuation method, which depends on augmenting the plant model with an extra integral state variable, permits designers to select higher values of observer gains to give quicker estimation convergence, without the risk of making the system less energy powerful because of noise intensification.

A Novel Augmented Extended State Observer (NAESO) was developed in [3] using a singular perturbation technique which offers adequate noise rejection and easier parameter selection. The Adaptive ESO (AESO) designed in [4] presented even better design flexibility and estimation capabilities than Linear ESO (LESO), and a capacity for more complex parameter refinement as the AESO order extends. Filtering of high-frequency noise measurement may also be addressed with a first-order low-pass filter, as presented in [5], which offers an additional alternative with which a modified active disturbance rejection control (ADRC) could provide satisfactory noise measurement. Unfortunately, this low-pass filter introduced a time delay. An amended ESO, which included a nonlinear function to improve the accuracy of estimations in the attenuation of measurement noises in system outputs, was proposed in [6]. Moreover, the work in [7] examined the construction of a Nonlinear ESO (NLESO) using piecewise, smooth, linear, and fractional power functions, the properties of which included improved robustness of measurement noise and reduced peaking values in the transient behaviour. In [8], the observer-based output feedback control (OBOFC) problem was focused on a class of discrete-time strict-feedback nonlinear systems (DTSFNS) with both multiplicative process noise and additive measurement noise. In [9], a nonlinear observer was designed to estimate the inertial pose and the velocity of a free-floating non-cooperative satellite using only relative pose measurements. In [10], a nonlinear high-gain observer is proposed to overcome the effect of measurement noise that is amplified in a traditional high-gain observer. In [11], a time-averaged Lyapunov function was used to show that the sensor noise can be effectively reduced, and to calculate explicitly a rate of convergence to the sliding surface of a noisy sliding mode observer. The paper provided necessary and sufficient conditions for observer design that would allow the proposed observer to be significantly less conservative than linear gain observers and H_∞ observers. In [12], a new observer, called High Gain (HG)/Linear Matrix Inequality (LMI) observer, was obtained by combining the standard high-gain methodology with the LMI-based observer design technique. Through analytical developments, the work showed how the new observer provided lower gains, how it applies to systems with nonlinear functions, and analysis performance in the presence of measurement noise and/or delayed output measurements. Observer design using fuzzy filtering is studied in [13,14,15,16].

1.2. Paper Motivation and Contribution

This paper introduces a new analytical technique to parameterize a novel NHOESO in the presence of measurement noise. Instead of adopting a trade-off between a fast estimation of system states and measurement noise, the new NHOESO with the proposed parameterization method aims to provide simultaneously fast estimation of systems states and robustness to uncertainties and measurement noise. The proposed method is robust to noise, which seems to create chaos in nonlinear systems [17].

The contribution of this paper is summarized as follows. The standard ESO is modified by adding an additional state to its state–space model and by introducing a smooth saturation-like nonlinear error function, which leads to a Nonlinear Higher Order ESO (NHOESO). This design enables accurate estimation of generalized disturbance with high-order derivatives. The parameters of the proposed NHOESO are designed by employing a novel analytical method based on the Lyapunov method, which confers a higher immunity against measurement noise.

1.3. Symbol Definitions

The symbols used in this paper are explained in Table 1.

Table 1. Symbol definitions.

Symbol	Definition
$ℝ$	Set of real numbers
$t$	Time (s)
$t_0$	Initial time
$u$	System input signal
$y$	Measured output signal
$f(·)$	Unknown system function
$w$	Uncertain exogenous disturbance
$b$	Input gain
$f_0(·)$	Nonlinear function of internal dynamics
$\mathrm{C}$	Class of Differentiable functions
$b_0$	Nominal input gain
$V(·)$	Lyapunov function
$\rho$	Relative degree
$\eta$	Internal state vector
$\xi$	External state vector
$L$	Generalized disturbance
$\Delta$	Derivative of the generalized disturbance
$M$	Upper bound of the derivative of the generalized disturbance
${\omega }_0$	Observer bandwidth
$u_0$	Nominal control signal
$r$	Reference input signal
$fal(·)$	ADRC nonlinear function
$\mathcal{N}$	Measurement noise
$P$	Symmetric positive definite matrix
${\Delta }_h$	Second derivative of the generalized disturbance
$M_h$	Upper bound of the second derivative of the generalized disturbance
$𝓰(·)$	Proposed nonlinear function
$O(·)$	Limiting behavior of a function, namely, “Big O” notation
${\lambda }_{max}$	Maximum Eigenvalue
${\lambda }_{min}$	Minimum Eigenvalue

1.4. Paper Structure

The rest of this paper is outlined as follows. The problem statement is introduced in Section 2. In Section 3, the theoretical background of the Linear ESO (LESO) and the tuning of its parameters are recalled. The proposed NHOESO with measurement noise is presented in Section 4. The parameterization of the NHOESO to reduce noise influence is introduced in Section 5. Section 6 presents numerical simulations of the proposed NHOESO with different measurement noise scenarios which illustrate the validity and performance of the proposed observer. Finally, a conclusion is given in Section 7.

2. Problem Statement

Consider an nth order uncertain nonlinear SISO system with relative degree $\rho$ where $\left(\rho \le n\right)$

$$\{\begin{array}{l}{\xi }^{\left(\rho \right)}=f\left(\xi ,\dots ,{\xi }^{\left(\rho -1\right)},\eta ,w,t\right)+b\left(t\right)u,\\ \begin{array}{c}y=\xi +\mathcal{N}, \\ \dot{\eta }=f_0\left(\eta ,\xi ,\dots ,{\xi }^{\left(\rho -1\right)}\right),\end{array} \end{array}$$

(1)

where ${\xi }_i, i\in \left\{1,2,\dots ,\rho \right\}$ are system states, $\eta$ is the state of internal dynamics, $u\left(t\right)\in \mathrm{C}\left(ℝ, ℝ\right)$ is the control signal, $y\left(t\right)\in \mathrm{C}\left(ℝ, ℝ\right)$ is the measured output, $w\left(t\right)\in \mathrm{C}\left(ℝ, ℝ\right)$ is the uncertain exogenous disturbance, $b\in \mathrm{C}\left(ℝ, ℝ\right)$ is the input gain, $f_0\in \mathrm{C}\left({ℝ}^n,{ℝ}^{n-\rho }\right)$ is the nonlinear function of internal dynamics, $\mathcal{N}\in ℝ$ is a Gaussian measurement noise, and $f\in \mathrm{C}\left({ℝ}^n\times ℝ\times ℝ, ℝ\right)$ is uncertain dynamics that are a part of the generalized disturbance and may involve exogenous disturbances $w$, parameter uncertainties, and unmodeled dynamics. The system (1) is not written as a “pure chain of integrators”. Assuming ${\xi }_1=y, {\xi }_2=\dot{y}.\dots ,{\xi }_{\rho }={\xi }^{\left(\rho -1\right)}$, one gets

$$\{\begin{array}{l}{\xi }_i={\xi }_{i+1} i\in \left\{1,2.\dots ,\rho -1\right\}\\ {\dot{\xi }}_{\rho }=f\left({\xi }_1,{\xi }_2,\dots ,{\xi }_{\rho },w,t\right)+\left(b\left(t\right)-b_0\right)u+b_{0}u\end{array}$$

(2)

Extending the system with an additional state,

$${\xi }_{\rho +1}=f+\left(b\left(t\right)-b_0\right)u=L$$

in which $L=f+\left(b\left(t\right)-b_0\right)u$ is called the generalized disturbance [18,19,20], it includes all of the unidentified internal dynamics, uncertainties, and exogenous disturbances. There are two methods with which to select the value of the coefficient $b_0\in ℝ\backslash \left\{0\right\}$:

(i)

The parameter $b_0$ is a rough estimate of $b\left(t\right)$ in the system within a ±50% range [7].

(ii)

The parameter $b_0$ is typically selected plainly by the designer as a design coefficient [21].

The second method will be adopted in this work. It is required to observe the system states $\xi$ and the generalized disturbance of (1) in the presence of measurement noise $\mathcal{N}$ using the proposed NHOESO. Incorporating the ESO as part of the feedback control system will ensure that (1) will be converted into a chain of integrators up to $\rho$. The estimated states $\xi$ will be used to realize feedback, whilst removing the generalized disturbance from (1) in the ADRC structure.

3. Theoretical Background

The aim of an observer is to provide accurate estimation of the states of the system from its known inputs and outputs. Luenberger [22] first proposed observer schemes for linear dynamical systems, and various subsequent versions of state observers have followed, such as high-gain observers [23] and sliding-mode observers [24]. The ESO was pioneering in its autonomy of being independent on the mathematical model of the plant. It was established for active disturbance rejection control (ADRC) to estimate in real-time the individual elements of the generalized disturbance, which are model uncertainties, exogenous disturbances, or unmodelled dynamics of the nonlinear system.

As in [25], the following three assumptions are considered for system (1):

Assumption 1.

$\mathrm{L}$is a continuously differentiable function.

Assumption 2.

There exists$M_h\in {ℝ}^{+}$such that$su{p}_{t\in \left[0,\infty \right)}\left|{\Delta }_h\left(t\right)\right|=M_h$.

Assumption 3.

$V:{ℝ}^{\rho +2}\to {ℝ}^{+}$and$W:{ℝ}^{\rho +2}\to {ℝ}^{+}$are functions that are continuously differentiable, with:

$${\lambda }_1\left|\right|\eta |{|}^2\le V\left(\eta \right)\le {\lambda }_2|\left|\eta \right|{|}^2, W\left(\eta \right)=\left|\right|\eta |{|}^2,$$

(3)

$${\displaystyle \sum }_{i=1}^{\rho +1}\frac{\partial V\left(\eta \right)}{{\eta }_i}\left({\eta }_{i+1}-a_{i}k\left(\frac{{\eta }_1}{{\omega }_0{}^{\rho }}\right)·{\eta }_1\right)-\frac{\partial V\left(\eta \right)}{\partial y_{\rho +2}}{a}_{\rho +2}k\left(\frac{{\eta }_1}{{\omega }_0{}^{\rho }}\right){\eta }_1\le -W\left(\eta \right)$$

(4)

where ${\lambda }_1$ and ${\lambda }_2$ are positive constants, and where $\eta$ is the scaled estimation error which will be described later in (16)–(18). Based on Assumptions 1, 2, and 3, a ${\left(\rho +1\right)}^{th}$ order ESO can be designed to estimate generalized disturbance. An ESO is either linear (LESO) or nonlinear (NLESO) depending on the estimation error function that is used. As an extension of the Luenberger observer [22], the LESO equation includes only linear correcting terms. These terms act on the error between the estimated states and the actual system states such that the error tends to zero. In the NLESO, the error-correcting terms benefit from the inclusion of a nonlinear function of estimation error, which enables a faster and smoother convergence to zero.

The system states given in Equation (1) with the generalized disturbance $L$ will be observed by the following LESO (2), as presented in [4]:

$$\{\begin{array}{l}{\dot{\widehat{\xi }}}_i={\widehat{\xi }}_{i+1}+{\beta }_i\left(y-{\widehat{\xi }}_1\right), i\in \left\{1,2,\dots ,\rho -1\right\}\\ {\dot{\widehat{\xi }}}_{\rho }={\widehat{\xi }}_{\rho +1}+{\beta }_{\rho }\left(y-{\widehat{\xi }}_1\right)+b_{0}u\\ {\dot{\widehat{\xi }}}_{\rho +1}={\beta }_{\rho +1}\left(y-{\widehat{\xi }}_1\right)\end{array}$$

(5)

where ${\beta }_i$ is the ESO gain parameter to be tuned, $i=1,2,\dots ,\rho +1$.

The pole-placement technique [26] and the bandwidth-based method [27] are the conventional ways to tune an LESO. If the objective is to limit the number of parameters, they may be defined in terms of the LESO bandwidth. The observer gains, selected as in [28], are given by

$$\left(\begin{array}{c}{\beta }_1\\ {\beta }_2\\ \begin{array}{c}⋮\\ {\beta }_{\rho +1}\end{array}\end{array}\right)=\left(\begin{array}{c}{a}_1{\omega }_0\\ a_2{\omega }_0^2\\ \begin{array}{c}⋮\\ a_{\rho +1}{\omega }_0^{\rho +1}\end{array}\end{array}\right)$$

(6)

where ${\omega }_0$ is the ESO bandwidth, $a_i, i=1, 2,\dots ,\rho +1$ are carefully chosen in such a way that the characteristic polynomial $s^{\rho +1}+a_1{s}^{\rho }+\dots +a_{\rho }s+a_{\rho +1}$ is Hurwitz. That is, all the roots of the characteristic polynomial are in the open left-half complex plane. For the sake of simplicity, let $s^{\rho +1}+a_1{s}^{\rho }+\dots +a_{\rho }s+a_{\rho +1}={\left(s+1\right)}^{\rho +1}$ where the binomial coefficients $a_i,i=1, 2,\dots ,\rho +1$ are defined as [29]:

$$a_i=\frac{\left(\rho +1\right)!}{i!\left(\rho +1-i\right)!}, 1\le i\le \rho +1$$

(7)

The characteristic polynomial of Equation (2) has the following form:

$$s^{\rho +1}+{\beta }_1{s}^{\rho }+\dots +{\beta }_{\rho }s+{\beta }_{\rho +1}={\left(s+{\omega }_0\right)}^{\rho +1}$$

(8)

Observer bandwidth ${\omega }_0$ is the lone adjusting observer parameter, which makes the adjustment of the LESO easier. By manipulating a single parameter ${\omega }_0$, one can quickly find the optimum balance between the speed at which the observer tracks the states and its sensitivity to disturbances. The chosen bandwidth should be adequately larger than the frequency of the disturbance while smaller than the unmodelled dynamics frequency [30]. LESO performance will worsen if the bandwidth takes an unacceptably high or low value [31]. Optimum values for the controller and LESO bandwidth will provide an effective elimination of exogenic disturbances and tracking performance [32,33,34,35,36,37,38,39]. The side effects of approving large bandwidth values can be summarized as measurement noise potentially degrading output tracking, deterioration of the transient response of the LESO, and the possibility of some unmodelled high-frequency dynamics being activated beyond a certain frequency.

The two most common causes of bandwidth constriction are noise and sampling rates. Consequently, it is essential to select an appropriate bandwidth that can elevate noise tolerance and tracking performance. Hence, a new parameterization method is needed to handle these issues without increasing the bandwidth.

4. The Proposed NHOESO with Measurement Noise

Measurement noise badly affects the performance and accuracy of controllers. Since the ESO is the key element of the ADRC, this unit is highly affected by the presence of such noise. This noise will cause a degradation in the performance of the system. Sometimes, it might destabilize the system if the high-gain observers (e.g., LESO) are used to estimate the states ${\xi }_i, i\in \left\{1, 2,\dots ,\rho \right\}$ and the generalized disturbance ${\xi }_{\rho +1}=L$ [4]. In this case, the generated control signal $u$ based on the estimated states ${\xi }_i i\in \left\{1, 2,\dots ,\rho \right\}$ and the generalized disturbance ${\xi }_{\rho +1}$ will include a high frequency that has many drawbacks. The first of these is large control activity, which introduces a large energy, delivered to the controlled plant. A reduction in tracking accuracy is another consequence due to the existence of noise.

The proposed NHOESO is described as,

$$\left\{\begin{array}{c}{\dot{\widehat{\xi }}}_i={\widehat{\xi }}_{i+1}+{\beta }_i𝓰\left(y-{\widehat{\xi }}_1\right),i\in \{1,2.\dots ,\rho -1\}\hfill \\ {\dot{\widehat{\xi }}}_{\rho }={\widehat{\xi }}_{\rho +1}+{\beta }_{\rho }𝓰\left(y-{\widehat{\xi }}_1\right)+b_{0}u\hfill \\ {\widehat{\xi }}_{\rho +1}={\widehat{\xi }}_{\rho +2}+{\beta }_{\rho +1}𝓰\left(y-{\widehat{\xi }}_1\right)\hfill \\ {\dot{\widehat{\xi }}}_{\rho +2}={\beta }_{\rho +2}𝓰\left(y-{\widehat{\xi }}_1\right)\hfill \end{array}\right.$$

(9)

where ${\beta }_i$, $i=\left\{1, 2,\dots ,\rho +2\right\},$ is observer gains to be tuned. Let ${\beta }_i=a_i{\omega }_0{}^i$, where $a_i$, $i\in \left\{1, 2.\dots ,\rho +2\right\}$ is the associated tuning coefficient with each ${\omega }_0{}^i$, and ${\omega }_0$ is the selected NHOESO bandwidth. The nonlinear function $𝓰:ℝ\to ℝ$ is designed as,

$$𝓰\left(e\right)=K_{\alpha }{\left|e\right|}^{\alpha }sign\left(e\right)+K_{\beta }{\left|e\right|}^{\beta }e$$

(10)

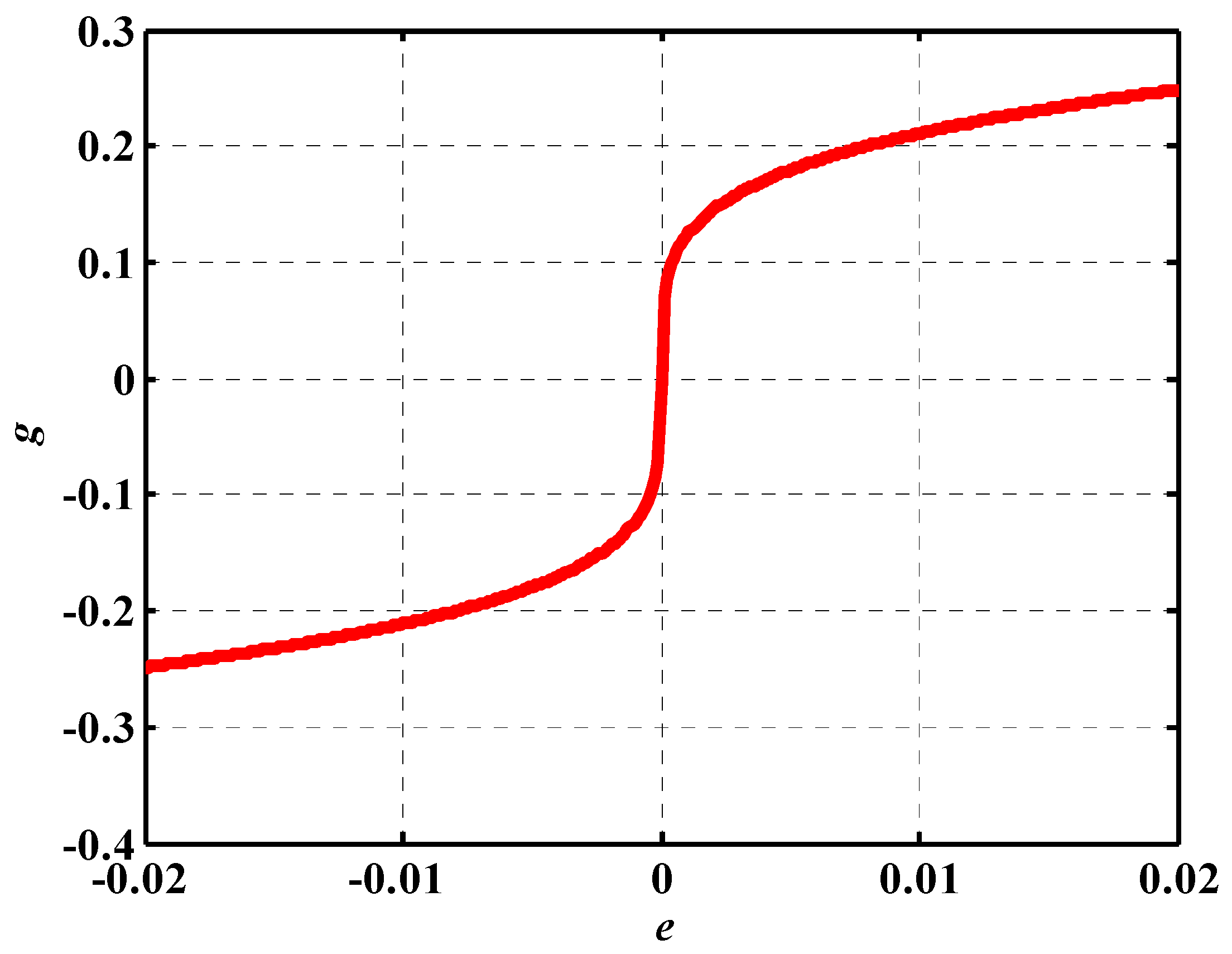
where $e=y-{\widehat{\xi }}_1$ is the estimation error, and $K_{\alpha },K_{\beta },\alpha \mathrm{and} \beta$ are positive tuning coefficients, see Figure 1. The proposed nonlinear function of (10) can be rewritten as,

$$𝓰\left(e\right)=\left(K_{\alpha }\frac{{\left|e\right|}^{\alpha }}{e}sign\left(e\right)+K_{\beta }{\left|e\right|}^{\beta }\right)e$$

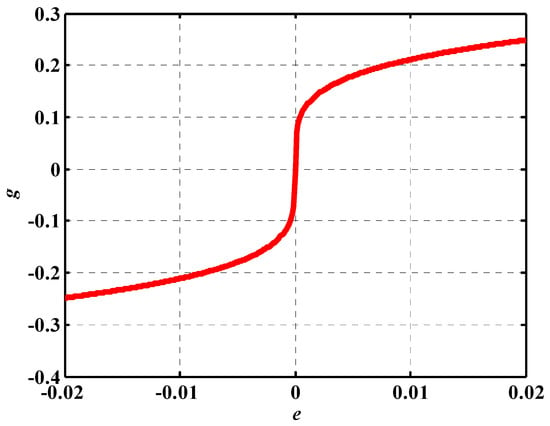
Figure 1. The $𝓰$ function with parameters $\alpha =0.233, \beta =0.334, k_{\alpha }=0.617 \mathrm{and} k_{\beta }=0.143$.

Since sign($e$) = $e$/|$e$| for $\left|e\right|\ne 0$, then

$$𝓰\left(e\right)=\{\begin{array}{c}\begin{array}{cc}0 & e=0\end{array}\\ \begin{array}{cc}k\left(e\right)e & e\ne 0\end{array}\end{array}$$

The function $k:ℝ/\left\{0\right\}\to {ℝ}^{+}$ is a nonlinear even-gain function with

$$k\left(e\right)=K_{\alpha }{\left|e\right|}^{\alpha -1}+K_{\beta }{\left|e\right|}^{\beta }$$

An analytical method is proposed in this paper to parameterize the coefficients of the proposed nonlinear function $𝓰(·)$ used in the NHOESO.

Authors should discuss the results and how they can be interpreted from the perspective of previous studies and of the working hypotheses. The findings and their implications should be discussed in the broadest context possible. Future research directions may also be highlighted.

5. Parameterization of NHOESO to Reduce Noise Influence

Consider a class of nonlinear affine single-input–single-output (SISO) systems with measurement noise, uncertainties, and exogenous disturbances which can be represented as follows:

$$\{\begin{array}{l}{\xi }_i={\xi }_{i+1}, i\in \left\{1,2,\dots ,\rho -1\right\}\\ \begin{array}{l}{\dot{\xi }}_{\rho }=f\left(\xi ,w,t\right)+b\left(t\right)u\\ y={\xi }_1+\mathcal{N}\end{array}\end{array}$$

(11)

where $u\in \mathrm{C}\left(ℝ, ℝ\right)$ is the control input, $y\in \mathrm{C}\left(ℝ,ℝ\right)$ is the measured output, $f\in \mathrm{C}\left({ℝ}^{\rho }\times ℝ\times ℝ,ℝ\right)$ is an unknown system function, $\xi ={\left({\xi }_1,{\xi }_2,\dots ,{\xi }_{\rho }\right)}^T\in {ℝ}^{\rho }$ is system states, $w\left(t\right)\in \mathrm{C}\left(ℝ,ℝ\right)$ is the uncertain exogenous disturbance, $b\in \mathrm{C}\left(ℝ,ℝ\right)$ is the input gain, and $\mathcal{N}\in \left[-\delta ,\delta \right]$ is the bounded measurement noise where $\delta$ is a positive small real number.

By adding an extended state ${\xi }_{\rho +1}=f+\left(\beta -b_0\right)u=L$, ${\xi }_{\rho +2}=\dot{L}$, the system given in Equation (11) can be written as

$$\left\{\begin{array}{c}{\dot{\xi }}_1={\xi }_2\hfill \\ {\dot{\xi }}_2={\xi }_3\hfill \\ ⋮\hfill \\ {\dot{\xi }}_n={\xi }_{n+1}+b_{0}u\hfill \\ {\dot{\xi }}_{n+1}={\xi }_{n+2}\hfill \\ {\dot{\xi }}_{n+2}={\Delta }_h\hfill \\ y={\xi }_1+\mathcal{N}\hfill \end{array}\right.$$

(12)

where ${\Delta }_h=\ddot{L}$.

Assumption 4.

$V:{ℝ}^{\rho +2}\to {ℝ}^{+}$and$W:{ℝ}^{\rho +2}\to {ℝ}^{+}$are functions that are continuously differentiable with:

$${\lambda }_1\left|\right|\eta |{|}^2\le V\left(\eta \right)\le {\lambda }_2|\left|\eta \right|{|}^2, W\left(\eta \right)=\left|\right|\eta |{|}^2$$

(13)

$$\begin{array}{l}{\displaystyle {\displaystyle \sum }_{i=1}^{\rho +1}}\frac{\partial V\left(\eta \right)}{{\eta }_i}\left({\eta }_{i+1}-a_{i}k\left(\frac{{\eta }_1}{{\omega }_0{}^{\rho }}+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right){\eta }_1\right)-\frac{\partial V\left(\eta \right)}{\partial {\eta }_{\rho +2}}{a}_{\rho +2}k\left(\frac{{\eta }_1}{{\omega }_0{}^{\rho }}+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right){\eta }_1\\ \le -W\left(\eta \right)\end{array}$$

(14)

where ${\lambda }_1$ and ${\lambda }_2$ are positive constants.

Theorem 1.

Given the system (12) and the NHOESO (9), under Assumptions 1, 2, 3, and 4 and$\underset{i\in \left\{1,2,\dots ,\rho +2\right\}}{max}\left(a_i\right)\le B$, where$B\in {ℝ}^{+}$for any initial values, it is proven that$\underset{\begin{array}{c}t\to \infty \\ {\omega }_0\to \infty \end{array}}{lim}\left|{\xi }_i\left(t\right)-{\widehat{\xi }}_i\left(t\right)\right|=0,$for specific values of the parameters of the nonlinear function$𝓰(·)$, where${\xi }_i$and${\widehat{\xi }}_i$($i\in \left\{1, 2,\dots ,\rho +2\right\}$) denote respectively the solutions of (12) and (9).

Proof of Theorem 1.

$$e_i={\xi }_i-{\widehat{\xi }}_i, i\in \left\{1,2,\dots ,\rho +2\right\}$$

(15)

$${\eta }_i\left(t\right)={\omega }_0{}^{\rho +1-i}{e}_i(\frac{t}{{\omega }_0}), i\in \left\{1,2,\dots ,\rho +2\right\}$$

(16)

$$e_i\left(\frac{t}{{\omega }_0}\right)=\frac{1}{{\omega }_0{}^{\rho +1-i}}{\eta }_i\left(t\right)$$

(17)

The time-scaled estimation error dynamics is:

$$\left\{\begin{array}{c}\frac{d{\eta }_1}{dt}={\eta }_2-a_{1}k\left(\frac{{\eta }_1}{{\omega }_0\rho }+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)\left({\eta }_1+{\omega }_0{}^{\rho }\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)\hfill \\ \frac{d{\eta }_2}{dt}={\eta }_3-a_{2}k\left(\frac{{\eta }_1}{{\omega }_0\rho }+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)\left({\eta }_1+{\omega }_0{}^{\rho }\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)\hfill \\ \hfill ⋮\hfill \\ \frac{d{\eta }_{\rho }}{dt}={\eta }_{\rho +1}-a_{\rho }k\left(\frac{{\eta }_1}{{\omega }_0\rho }+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)\left({\eta }_1+{{\omega }_0}^{\rho }\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)\hfill \\ \frac{d{\eta }_{\rho +1}}{dt}={\eta }_{\rho +2}-a_{\rho +1}k\left(\frac{{\eta }_1}{{\omega }_0\rho }+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)·\left({\eta }_1+{\omega }_0{}^{\rho }\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)\hfill \\ \frac{d{\eta }_{\rho +2}}{dt}=\frac{{\Delta }_h}{{\omega }_0{}^2}-a_{\rho +2}k\left(\frac{{\eta }_1}{{\omega }_0\rho }+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)·\left({\eta }_1+{\omega }_0{}^{\rho }\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)\hfill \end{array}\right.$$

(18)

Finding the derivative of $V\left(\eta \right)$ with respect to $t$ along the solution $\eta$ of Equation (18), one gets

$$\begin{array}{cc}\hfill {\left.\dot{V}\left(\eta \right)\right|}_{\mathrm{along}\left(18\right)}=& \sum _{i=1}^{\rho +1}\frac{\partial V\left(\eta \right)}{{\eta }_i}\left({\eta }_{i+1}\left(t\right)-a_{i}k\left(\frac{{\eta }_1\left(t\right)}{{\omega }_0\rho }+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)·{\eta }_1\right)-\frac{\partial V\left(\eta \right)}{{\eta }_{\rho +2}}{a}_{\rho +2}k\left(\frac{{\eta }_1\left(t\right)}{{\omega }_0^{\rho }}+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)·{\eta }_1\hfill \\ \hfill & +\sum _{i=1}^{\rho +2}\frac{\partial V\left(\eta \right)}{{\eta }_i}\left(-a_{i}k\left(\frac{{\eta }_1}{{\omega }_0\rho }+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)·{\omega }_0^{\rho }\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)+\frac{\partial V\left(\eta \right)}{{\eta }_{\rho +2}}\left(\frac{{\Delta }_h}{{\omega }_0^2}\right)\hfill \end{array}$$

(19)

Consider Equation (14) given in Assumption 4:

$${\dot{V}\left(\eta \right)|}_{along \left(18\right)}\le -W\left(\eta \right)+{\displaystyle \sum }_{i=1}^{\rho +2}\frac{\partial V\left(\eta \right)}{{\eta }_i}\left(-a_{i}k\left(\frac{{\eta }_1\left(t\right)}{{\omega }_0{}^{\rho }}+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)·{\omega }_0{}^{\rho }\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)+\frac{\partial V\left(\eta \right)}{{\eta }_{\rho +2}}\left(\frac{{\Delta }_h}{{\omega }_0{}^2}\right)$$

(20)

Given Assumption 4, consider the candidate Lyapunov functions $V,W:{ℝ}^{n+1}\to {ℝ}^{+}$ defined by $V\left(\eta \right)=⟨P\eta ,\eta ⟩$, where $\eta \in {ℝ}^{\rho +2}$ and $P$ is a symmetric positive definite matrix. Suppose (3) in Assumption 3 with ${\lambda }_1={\lambda }_{min}\left(P\right)$ and ${\lambda }_2={\lambda }_{max}\left(P\right)$. Thus, when $\left(\eta \right)\le {\lambda }_{max}\left(P\right)\left|\right|\eta |{|}^2$ and $\left|\frac{\partial V}{\partial {\eta }_{\rho +2}}\right|\le \left|\right|\frac{\partial V\left(\eta \right)}{\partial \eta }\left|\right|$, then $\left|\frac{\partial V}{\partial {\eta }_{\rho +2}}\right|\le 2{\lambda }_{max}\left(P\right)||\eta ||$. Moreover, $V\left(\eta \right)\le {\lambda }_{max}\left(P\right)\left|\right|\eta |{|}^2={\lambda }_{max}\left(P\right)W\left(\eta \right)$. Thus, $-W\left(\eta \right)\le -\frac{V\left(\eta \right)}{{\lambda }_{max}\left( P\right)}$. Finally, because ${\lambda }_{min}\left(P\right)\left|\right|\eta |{|}^2\le V\left(\eta \right)$, this leads to $||\eta ||\le \sqrt{\frac{V\left(\eta \right)}{{\lambda }_{min}\left(P\right)}}$. As a result,

$${\dot{V}\left(\eta \right)|}_{along \left(14\right)}\le \frac{-V\left(\eta \right)}{{\lambda }_{max}\left(P\right)}+2\left(\rho +2\right){\omega }_0{}^{\rho }\delta B{\lambda }_{max}\left(P\right)\sqrt{\frac{V\left(\eta \right)}{{\lambda }_{min}\left(P\right)}}k\left(\frac{{\eta }_1\left(t\right)}{{\omega }_0{}^{\rho }}+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)+2{\lambda }_{max}\left(P\right)\sqrt{\frac{V\left(\eta \right)}{{\lambda }_{min}\left(P\right)}}\left(\frac{M_h}{{\omega }_0{}^2}\right)$$

(21)

This is because $\frac{d}{dt}\sqrt{V\left(\eta \right)}=\frac{1}{2}\frac{1}{\sqrt{V\left(\eta \right)}}\dot{V}\left(\eta \right)$. Thus

$$\frac{d}{dt}\sqrt{V\left(\eta \right)}\le \frac{1}{2}\frac{1}{\sqrt{V\left(\eta \right)}}\left(\frac{-V\left(\eta \right)}{{\lambda }_{max}\left(P\right)}+2\left(\rho +2\right){\omega }_0{}^{\rho }\delta B{\lambda }_{max}\left(P\right)\sqrt{\frac{V\left(\eta \right)}{{\lambda }_{min}\left(P\right)}}k\left(\frac{{\eta }_1\left(t\right)}{{\omega }_0{}^{\rho }}+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)+2{\lambda }_{max}\left(P\right)\sqrt{\frac{V\left(\eta \right)}{{\lambda }_{min}\left(P\right)}}\left(\frac{M_h}{{\omega }_0{}^2}\right)\right)$$

(22)

$$\frac{d}{dt}\sqrt{V\left(\eta \right)}\le \frac{-\sqrt{V\left(\eta \right)}}{2{\lambda }_{max}\left(P\right)}+\left(\rho +2\right){\omega }_0{}^{\rho }\delta B{\lambda }_{max}\left(P\right)\sqrt{\frac{1}{{\lambda }_{min}\left(P\right)}}k\left(\frac{{\eta }_1\left(t\right)}{{\omega }_0{}^{\rho }}+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)+{\lambda }_{max}\left(P\right)\sqrt{\frac{1}{{\lambda }_{min}\left(P\right)}}\left(\frac{M_h}{{\omega }_0{}^2}\right)$$

(23)

To reduce the effect of noise on the NHOESO, the following constraint is considered:

$${\lambda }_{max}\left(P\right)\sqrt{\frac{1}{{\lambda }_{min}\left(P\right)}}\left(\frac{M_h}{{\omega }_0{}^2}\right)\gg \left(\rho +2\right){\omega }_0{}^{\rho }\delta B{\lambda }_{max}\left(P\right)\sqrt{\frac{1}{{\lambda }_{min}\left(P\right)}}k\left(\frac{{\eta }_1\left(t\right)}{{\omega }_0{}^{\rho }}+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)$$

(24)

which leads to $\left(\frac{M_h}{{\omega }_0{}^2}\right)\gg \left(\rho +2\right){\omega }_0{}^{\rho }\delta Bk\left(\frac{{\eta }_1\left(t\right)}{{\omega }_0{}^{\rho }}+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)$. After rearranging, one obtains $k\left(\frac{{\eta }_1}{{\omega }_0{}^{\rho }}+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right)\ll \frac{M}{\left(\rho +2\right)\delta B{\omega }_0{}^{\rho +2}}$.

Since $k\left(e\right)=K_{\alpha }{\left|e\right|}^{\alpha -1}+K_{\beta }{\left|e\right|}^{\beta }$, and by letting $e=\frac{{\eta }_1}{{\omega }_0{}^{\rho }}+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)$ in $k\left(e\right)$, the following is obtained:

$$K_{\alpha }{\left|\frac{{\eta }_1\left(t\right)}{{\omega }_0{}^{\rho }}+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right|}^{\alpha -1}+K_{\beta }{\left|\frac{{\eta }_1\left(t\right)}{{\omega }_0{}^{\rho }}+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right|}^{\beta }\ll \frac{M_h}{\left(\rho +2\right)\delta B{\omega }_0{}^{\rho +2}}$$

(25)

Firstly, letting $K_{\alpha }\to 0, and \alpha \to 1$, Equation (25) is then reduced to $K_{\beta }{\left|\frac{{\eta }_1}{{\omega }_0{}^{\rho }}+\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right|}^{\beta }\ll \frac{M_h}{\left(\rho +2\right)\delta B{\omega }_0{}^{\rho +2}}$, which leads to:

$$K_{\beta }{\left|{\eta }_1+{\omega }_0{}^{\rho }\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right|}^{\beta }\ll \frac{M_h}{\left(\rho +2\right)\delta B{\omega }_0{}^{\rho +2-\rho \beta }}$$

(26)

To cancel the term ${\omega }_0{}^{\rho +2-\rho \beta }$, $\rho +2-\rho \beta =0⟹\beta =\left(1+\frac{2}{\rho }\right)$ is considered. Subsequently, Equation (26) is reduced to a simpler form which is expressed as

$$K_{\beta }{\left|{\eta }_1+{\omega }_0{}^n\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right|}^{\beta }\ll \frac{M_h}{\left(n+2\right)\delta B{\omega }_0{}^{n+2-n\beta }}$$

(27)

Consequently,

$$K_{\beta }\ll \frac{M_h}{\left(\rho +2\right)\delta B{\left|{\eta }_1\left(t\right)+{\omega }_0{}^{\rho }\mathcal{N}\left(\frac{t}{{\omega }_0}\right)\right|}^{\beta }}$$

(28)

A very large value of ${\omega }_0$ leads to a very small value of $K_{\beta }$. The result of the parameterization step is given as

$$K_{\alpha }\ll 1, \alpha \to 1,K_{\beta }\ll 1,and \beta \to \left(1+\frac{2}{\rho }\right)$$

(29)

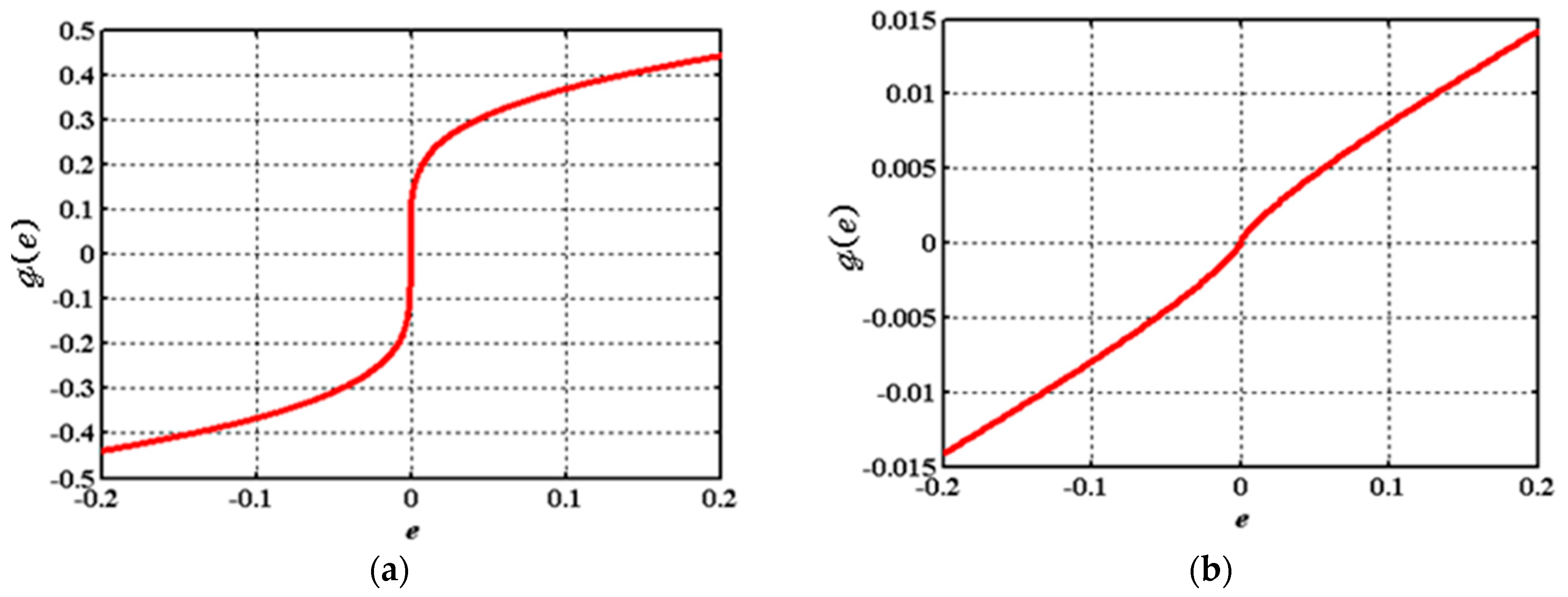
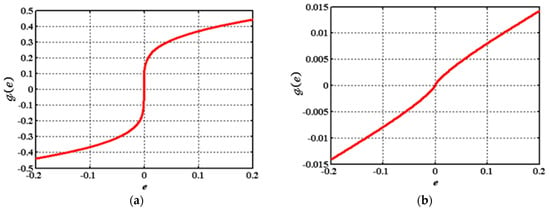
Figure 2 shows function (10) according to the parameters in (29), which is called ${𝓰}_{new}(·)$ and leads to

$$\frac{d}{dt}\sqrt{V\left(\eta \right)}\le \frac{-\sqrt{V\left(\eta \right)}}{2{\lambda }_{max}\left(P\right)}+{\lambda }_{max}\left(P\right)\sqrt{\frac{1}{{\lambda }_{min}\left(P\right)}}\left(\frac{M_h}{{\omega }_0{}^2}\right)$$

(30)

Figure 2. The curve of the nonlinear error function: (a) $𝓰(·)$ with $\alpha =0.233, \beta =0.334, k_{\alpha }=0.617, \mathrm{and} k_{\beta }=0.143$; (b) ${𝓰}_{new}(·) \mathrm{with} \alpha =$ 0.8$, \beta =2, k_{\alpha }=$ 0.05, $\mathrm{and} k_{\beta }=$ 0.05.

Solving the ordinary differential Equation (30) gives

$$\sqrt{V\left(\eta \right)}\le \frac{2M_h{\lambda }^2{}_{max}\left(P\right)}{{\omega }_0{}^2\sqrt{{\lambda }_{min}\left(P\right)}}\left(1-e^{-\frac{t}{2{\lambda }_{max}\left(P\right)}}\right)+\sqrt{V\left(\eta \left(0\right)\right)}{e}^{-\frac{t}{2{\lambda }_{max}\left(P\right)}}$$

(31)

Based on Assumption 4 and the foregoing analysis, then

$$||\eta ||\le \frac{2M_h{\lambda }^2{}_{max}\left(P\right)}{{\omega }_0{}^2{\lambda }_{min}\left(P\right)}\left(1-e^{-\frac{t}{2{\lambda }_{max}\left(P\right)}}\right)+\sqrt{\frac{V\left(\eta \left(0\right)\right)}{{\lambda }_{min}\left(P\right)}}{e}^{-\frac{t}{2{\lambda }_{max}\left(P\right)}}$$

(32)

It follows from Equation (17) that

$$\left|{\xi }_i-{\widehat{\xi }}_i\right|=\frac{1}{{\omega }_0{}^{\rho +1-i}}\left|{\eta }_i\left({\omega }_{0}t\right)\right|\Rightarrow \left|{\xi }_i-{\widehat{\xi }}_i\right|\le \frac{1}{{\omega }_0{}^{\rho +1-i}}\eta \left({\omega }_{0}t\right)$$

(33)

Thus, using Equation (32) gives

$$\left|{\xi }_i-{\widehat{\xi }}_i\right|\le \frac{1}{{\omega }_0{}^{\rho +1-i}}\left(\frac{2M_h{\lambda }^2{}_{max}\left(P\right)}{{\omega }_0{}^2{\lambda }_{min}\left(P\right)}\left(1-e^{-\frac{{\omega }_{0}t}{2{\lambda }_{max}\left(P\right)}}\right)+\sqrt{\frac{V\left(\eta \left(0\right)\right)}{{\lambda }_{min}\left(P\right)}}{e}^{-\frac{{\omega }_{0}t}{2{\lambda }_{max}\left(P\right)}}\right)$$

(34)

$$\underset{t\to \infty }{\lim }\left|{\xi }_i-{\widehat{\xi }}_i\right|=\frac{1}{{\omega }_0{}^{\rho +3-i}}\frac{2M_h{\lambda }^2{}_{max}\left(P\right)}{{\lambda }_{min}\left(P\right)}=O\left(\frac{1}{{\omega }_0{}^{n+3-i}}\right)$$

(35)

Finally,

$$\underset{\begin{array}{c}t\to \infty \\ {\omega }_0\to \infty \end{array}}{\lim }\left|{\xi }_i-{\widehat{\xi }}_i\right|=0$$

(36)

□

Comparing Figure 2a with Figure 2b, the slope in Figure 2b is lower than that of Figure 2a, which brings the benefits of reducing the gain multiplied by the measurement noise $\mathcal{N}$ to a lower gain value. To illustrate the above discussion with numerical values, consider the parameters of the LESO with the following values ${\omega }_0=50, a_1=4, a_2=6, a_3=4, \mathrm{and} a_4=1$.

The parameters of the nonlinear error function $𝓰(·)$ in the NHOESO are selected as $\alpha =0.233, \beta =0.334, k_{\alpha }=0.617, \mathrm{and} k_{\beta }=0.143$. The nonlinear error function ${𝓰}_{new}(·)$ is selected with the following parameters: $\alpha =0.8, \beta =2, k_{\alpha }=0.05 \mathrm{and} k_{\beta }=0.05$. Table 2 shows the value of the error-correcting term for $e_1=0.1$.

Table 2. The values of the error-correcting term.

$\mathit{i}$	${\mathit{a}}_{\mathit{i}}{\mathit{\omega }}_0^{\mathit{i}} {\mathit{e}}_1$	${\mathit{a}}_{\mathit{i}}{\mathit{\omega }}_0^{\mathit{i}} \mathit{𝓰}\left({\mathit{e}}_1\right)$	${\mathit{a}}_{\mathit{i}}{\mathit{\omega }}_0^{\mathit{i}} {\mathit{𝓰}}_{\mathit{n}\mathit{e}\mathit{w}}\left({\mathit{e}}_1\right)$
1	20	7 4	1.6
2	1500	5507.9	119.6
3	50,000	18,359 6	3987.2

The LESO with gain ${\beta }_i={\alpha }_i{\omega }^i$ for a large bandwidth leads to a high gain which is multiplied by the measurement noise $\mathcal{N}$. Therefore, the LESO shows a weaker level of performance.

6. Numerical Simulations

To evaluate the performance of the proposed NHOESO where measurement noise is present, a hypothetical nonlinear SISO system is used, with the dynamics given as

$$\{\begin{array}{l}{\dot{\xi }}_1={\xi }_2 \hfill \\ \begin{array}{c}{\dot{\xi }}_2=f\left({\xi }_1, {\xi }_2\right)+w\left(t\right)+\left(1+a_{3}sin\left(t\right)\right)u\hfill \\ y={\xi }_1\hfill \end{array}\end{array}$$

(37)

where $f\left({\xi }_1,{\xi }_2\right)=a_1{\xi }_1+a_{2}sin\left({\xi }_2\right)$, with $a_1=0.2$, $a_2=a_3=0.1$, and $w\left(t\right)=\exp \left(-t\right)cos\left(t\right)$. The reference input $r\left(t\right)$ is chosen as a periodic signal and is expressed as $cos\left(0.5t\right)$ applied at t = 0 sec. A noise of Gaussian type was applied to the output with variance σ² equal to 10⁻⁴ and the mean μ = 0.

The system (34) is used to evaluate the performance of the proposed parameterized NHOESO. The fal-based control law is chosen as

$$u=fal\left({\tilde{e}}_1,{\alpha }_1,{\delta }_1\right)+fal\left({\tilde{e}}_2,{\alpha }_2,{\delta }_2\right)-{\widehat{\xi }}_3$$

(38)

where $fal\left(e,\alpha ,\delta \right)$ is expressed as

$$fal\left(e,\alpha ,\delta \right)=\{\begin{array}{c}\begin{array}{cc}\frac{e}{{\delta }^{1-\alpha }} & \left|e\right|\le \delta \end{array}\\ \begin{array}{cc}{\left|e\right|}^{\alpha }sgn\left(e\right)& \left|e\right|>\delta \end{array}\end{array}$$

(39)

The tracking error which is driving the control signal is given by ${\left({\tilde{e}}_1, {\tilde{e}}_2\right)}^T={\left(r_1, r_2\right)}^T-{\left({\widehat{\xi }}_1, {\widehat{\xi }}_2\right)}^T$. The desired transient profile vector ${\left(r_1, r_2\right)}^T$ is obtained using the conventional TD given as in [1],

$$\{\begin{array}{c}{\dot{r}}_1=r_2, \hfill \\ {\dot{r}}_2=-Rsign\left(r_1-r+\frac{r_2\left|r_2\right|}{2R}\right)\hfill \end{array}$$

(40)

The simulation scenarios are explained below.

Scenario 1: The LESO is optimized for minimum Integral Time-weighted Absolute Error (ITAE) and integration of the square of the control signal (ISU) without measurement noise and tested in a noisy environment, where ITAE = ${{\displaystyle \int }}_0^{ t_f}t\left|e\right| dt$ and $\mathrm{ISU}={{\displaystyle \int }}_0^{t_f}{u}^2 dt$.

Scenario 2: The NHOESO is optimized for minimum ITAE and ISU without measurement noise and tested in a noisy environment.

Scenario 3: The NHOESO is tested in a noisy environment. The parameters are selected based on the values found in Theorem 1.

It should be noted that the difference between Scenario 3 and the other scenarios is that in Scenario 1 and 2 the NHOESO is tuned without taking into consideration the effect of measurement noise. While for Scenario 3, the noise is taken into account during the tuning while adopting Theorem 1 for the selection of the NHOESO parameters.

Both the LESO given in Equation (2) and the NHOESO of Equation (5) are used in these simulations to find the estimated states ${\left({\widehat{\xi }}_1,{\widehat{\xi }}_2\right)}^T$ and the estimated generalized disturbance ${\widehat{\xi }}_3$. The response curves of these scenarios are shown in Figure 3, Figure 4 and Figure 5, respectively.

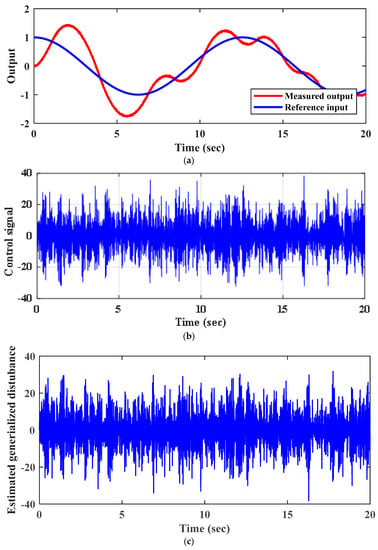
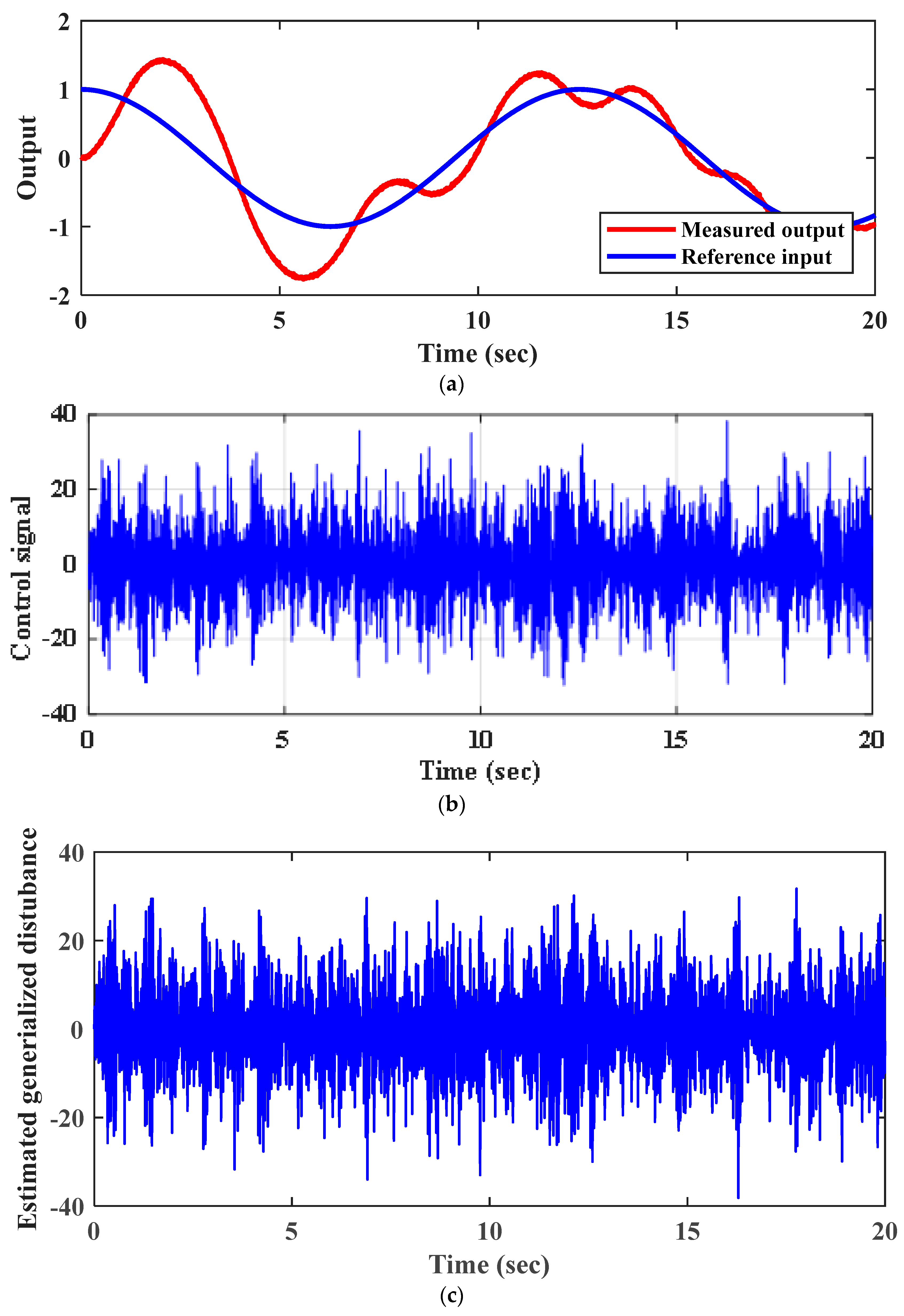
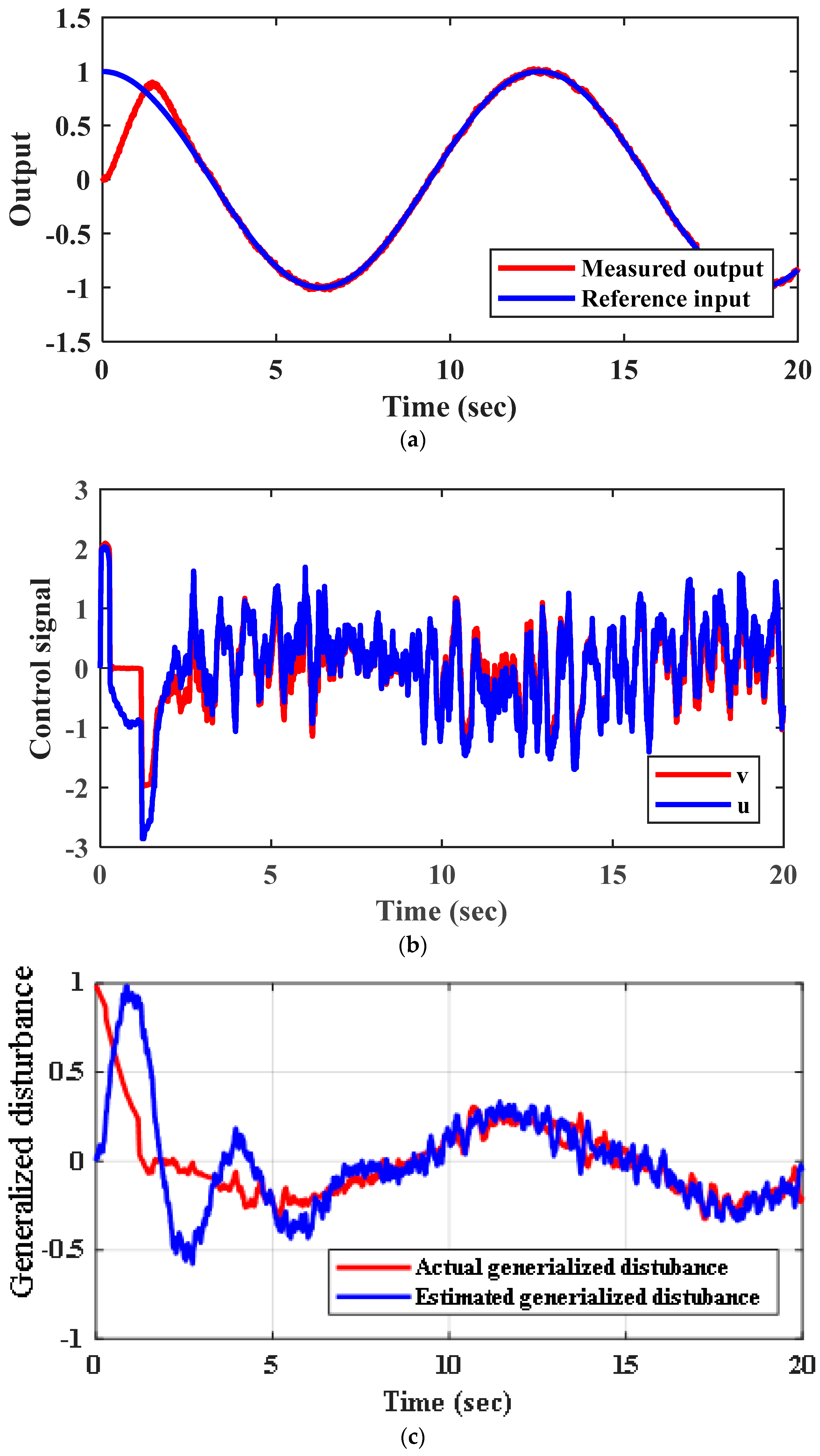
Figure 3. Results of the numerical simulation for Scenario 1: (a) tracking response $y$ of the reference input $r$; (b) control action $u$; (c) estimation of the generalized disturbance ${\widehat{\xi }}_3$.

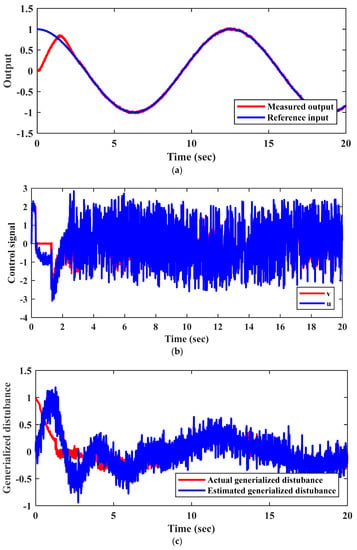
Figure 4. Results of the numerical simulation for Scenario 2, (a) tracking response $y$ of the reference input $r$; (b) control action $u$; (c) estimation of the generalized disturbance ${\widehat{\xi }}_3$.

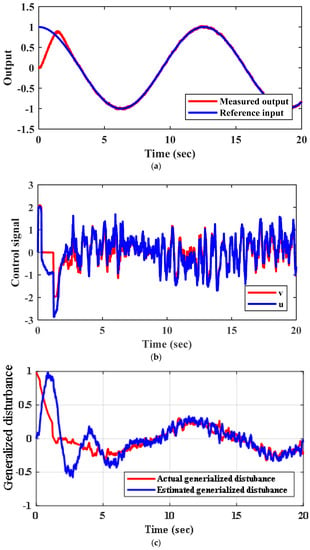
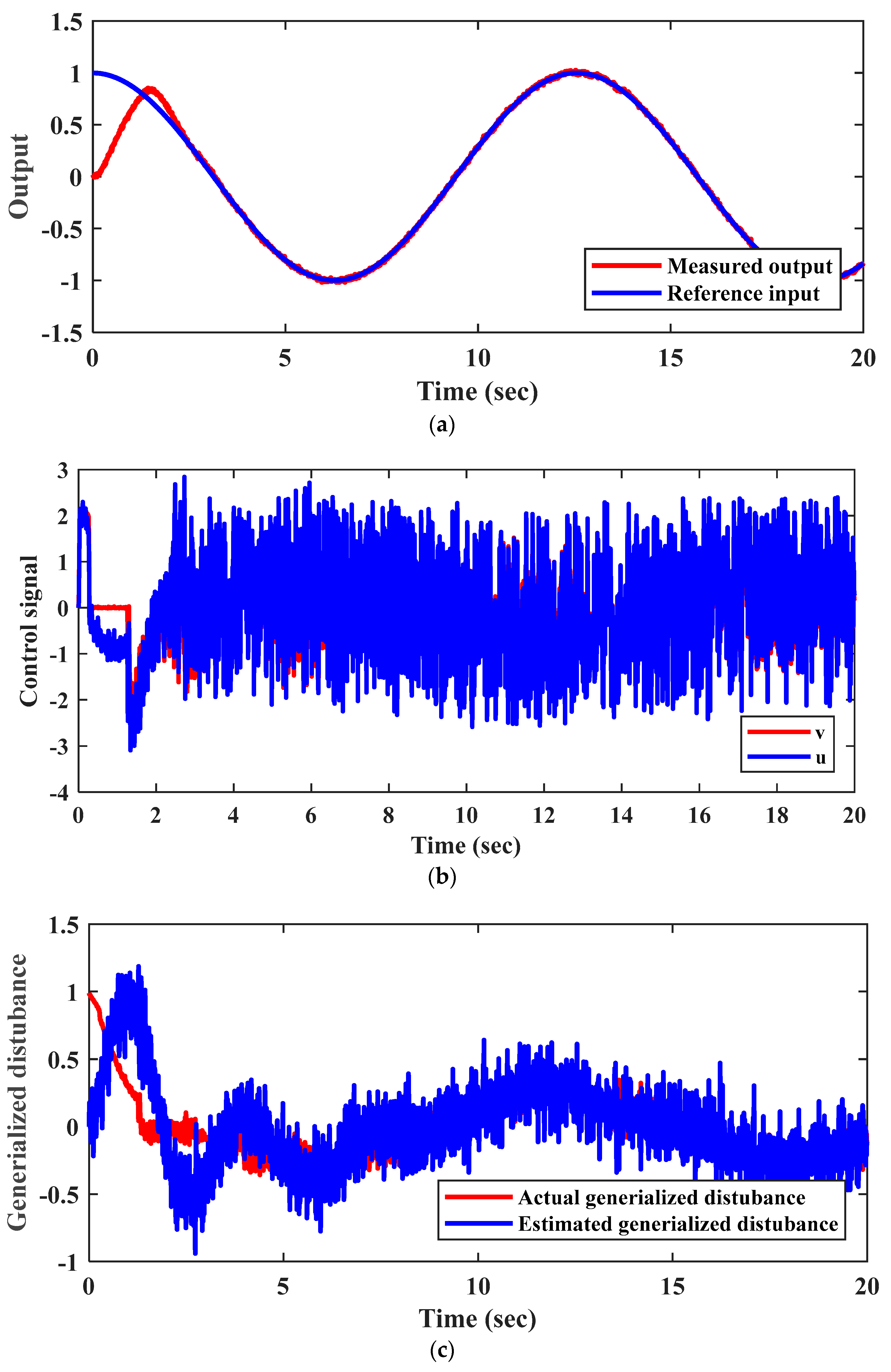
Figure 5. Numerical simulation results for Scenario 3: (a) tracking response $y$ of the reference input $r$; (b) control action $u$; (c) estimation of the generalized disturbance ${\widehat{\xi }}_3$.

Figure 3a illustrates the worst tracking response, where the LESO exhibits a bad response to noise. To alleviate the effect of the noise, several solutions are considered. Firstly, the NHOESO is tuned under no measurement noise. Next, the NHOESO with its tuned parameters is tested for the case of measurement noise. Figure 4 shows a better tracking response and a big reduction in chattering in the control signal and the estimated generalized disturbance.

Selecting the parameters of the NHOESO based on the method proposed in Equation (29) of Theorem 1 has a considerable effect on both the accuracy of the transient response and the energy of the controller. As can be seen from Figure 5, a greater reduction in chattering is obtained in both the control signal and the estimated generalized disturbance. This is very apparent, in contrast to the previous two scenarios. Applying the adaptive techniques leads to substantial improvement in the output response of the system.

Furthermore, in the presence of measurement noise $\mathcal{N}$, the NHOESO is the most practical ESO with moderated delivered energy. Using the NHOESO with an analytical approach (i.e., fixed parameters) shows a big reduction in control energy because the parameters are selected analytically to diminish the noise terms in the estimated error dynamics ${\beta }_i𝓰\left(y-{\widehat{\xi }}_1\right), i\in \left\{1, \dots ,\rho +2\right\}$. The performance of the NHOESO is improved because it leads to a better state estimation and minimum estimation errors under measurement noise $\mathcal{N}$. This has a direct effect on the generation of the appropriate control law $u$, which is a nonlinear combination of the feedback estimated states and reference signals.

The numerical results of the three scenarios in terms of both ITAE and ISU are listed in Table 3.

Table 3. Values of the performance indices of the three scenarios.

Scenario	ITAE	ISU
Scenario 1	41.347519	2782.555268
Scenario 2	1.321808	28.825156
Scenario 3	1.586651	11.719821

As illustrated in Table 3, large values of both the ITAE and ISU reflect the impact of measurement noise on the LESO, with a big reduction in performance indices for the second scenario concerning the indices of Scenario 1. Additionally, the NHOESO (Scenario 3), when the parameters are applied as indicated in (26), shows a reduction of 59.3% of the ISU.

7. Conclusions

To provide the controller with necessary information about the environment, it is required to use sensors. However, measurement noise is largely associated with these sensors, which badly affects the performance and accuracy of the control systems. The ESO is highly affected by the presence of measurement noise. In this case, control signals generated based on the estimated state and the generalized disturbance will include a high frequency that has many drawbacks. Firstly, a large control activity, which introduces large energy, is delivered to the controlled plant. Secondly, tracking accuracy is reduced. In this work, the proposed nonlinear function introduced in the NHOESO acts as a filter without introducing a delay in the estimation error. The proposed analytical parameterization technique of the proposed nonlinear observer error function has many advantages. It leads to a large reduction in the delivered control signal energy and a significant reduction in the chattering phenomena, which reduces wear on the mechanical parts. With the proposed parameterization technique of the NHOESO, measurement noise has a negligible effect on system performance, which is illustrated in simulations.