Abstract
The incorporation of high precision vehicle positioning systems has been demanded by the autonomous electric vehicle (AEV) industry. For this reason, research on visual odometry (VO) and Artificial Intelligence (AI) to reduce positioning errors automatically has become essential in this field. In this work, a new method to reduce the error in the absolute location of AEV using fuzzy logic (FL) is presented. The cooperative data fusion of GPS, odometer, and stereo camera signals is then performed to improve the estimation of AEV localization. Although the most important challenge of this work focuses on the reduction in the odometry error in the vehicle, the defiance of synchrony and the information fusion of sources of different nature is solved. This research is integrated by three phases: data acquisition, data fusion, and statistical evaluation. The first one is data acquisition by using an odometer, a GPS, and a ZED camera in AVE’s trajectories. The second one is the data analysis and fuzzy fusion design using the MatLab 2019® fuzzy logic toolbox. The last is the statistical evaluation of the positioning error of the different sensors. According to the obtained results, the proposed model with the lowest error is that which uses all sensors as input (stereo camera, odometer, and GPS). It can be highlighted that the best proposed model manages to reduce the positioning mean absolute error (MAE) up to 25% with respect to the state of the art.
Keywords:
autonomous electric vehicle (AEV); visual odometry (VO); fuzzy logic (FL); GPS; odometer; ZED camera MSC:
26E50
1. Introduction
A fundamental module of autonomous land vehicle navigation systems is absolute location, which in several works consists of a combination of data from different sensors including the GPS sensor [1]. It should be noted that high precision is required in the positioning of the vehicle to provide optimal security service. Recently, high precision positioning systems with an error of a few centimeters have been developed using cameras, inertial measurement unit (IMU), and light detection and ranging (LiDAR), among other methods [2,3,4,5,6]. The fundamental goal of data fusion is to obtain a lower probability of estimation error and greater reliability by using data from multiple sources. They are defined as complementary when the information provided by the input sources represents different parts of the scene and therefore could be used to obtain more complete global information. There is also redundant data fusion, which is used when two or more input sources provide information about the same objective and that information can be used to increase confidence, as well as a cooperative one when the information provided is combined with new information that is usually more complex than the original information [7,8]. In this sense, stereo visual odometry (SVO) sensors have become crucial for their ability to estimate camera movement based on images. SVO uses a relative scale to estimate the position and orientation of an agent using the images of one or more cameras attached to it. The SVO technique has been applied in the development of different vehicles such as autonomous vehicles, unmanned aerial vehicles, and submarines. Indeed, SVO was used to supplement the odometry of the wheel in the first exploration missions to Mars [9,10]. However, measurement noise and miscalibration induce an error (drift) in the estimated position, causing the heading reconstruction to deviate from the actual vehicle path. Slipping of the vehicle’s wheels in the sand caused the wheel odometry to malfunction, requiring a more accurate way to measure movement. For instance, estimating the relative displacement of the observed environment between images provides much more accurate results. Several works focused on various areas that are relevant in the image aspect. Such is the case of the topic of movement [9,11,12,13], in which the movement between two images of an environmental region is estimated by analyzing the relative displacements of the camera and the correspondences of characteristics present in the environment using various methods. On the other hand, there are studies focused on techniques for estimating depth from image [14,15,16,17,18,19,20], ranging from medical applications to applications of convolutional neural networks for robots. Several studies of embedded navigation systems are documented in the literature, showing how fuzzy systems can achieve this interaction by reducing error. For example, in [21], a study on an adaptive Kalman filter design based on fuzzy innovation is presented for the improvement of vehicle positioning performance in a dense urban environment. A fuzzy system is proposed to adaptively apply the covariance of the position precision, dilution measurement noise (DMN), the number of satellites that can be received, and the difference between the predicted position and the measurement position. In addition, the heading is checked and the covariance of the measurement noise of the inertial measurement unit and the on-board diagnostics (OBD) is applied based on the driving state of the vehicle. The proposed method corrects the MEMS-IMU yaw rate with the steering angle value obtained from the sensor on the vehicle and replaces the estimated MEMS-IMU speed by using the speed calculated from the 4-wheel revolutions per minute (RPM). This reduces the estimation error in the position, speed, and attitude of the MEMS-IMU.
The fuzzy inference has proven its power to compensate for sensor measurements and deliver a reference consistent output that helps to describe the measurement error. In [22], through intelligent fuzzy implications, an adaptive integration scheme is developed for the inertial navigation system (INS) with the global positioning system (GPS). Using knowledge-based fuzzy Mamdani-type inference, the inertial measurements comprising the outputs of the gyroscopes and accelerometers are examined to detect the level of vehicle maneuvering. Consequently, appropriate weighting coefficients are obtained to combine the INS/GPS and the attitude-heading reference system. In [23], a predictor-corrector guide method based on fuzzy logic is developed. The correction system is based on two fuzzy controllers, which correct longitudinal movement and lateral movement synergistically. The flight range error is eliminated by correcting the magnitude of the bank angle. The altitude error is eliminated by correcting the angle of attack. The lateral error is eliminated by regulating the inversion time of the bank angle. Compared to the traditional corrector based on Newton–Raphson iteration, the developed method only needs a single path prediction in a correction cycle, which is favorable for calculations. Furthermore, longitudinal movement and lateral movement are synergistically corrected in the predictor-corrector, which results in a robust and flexible method. Another important work is [24]. In this work they propose a simple method and the corresponding algorithm to build fuzzy logic systems to linearize sensors with a specified error in each interval of the measured parameter. The method has the advantage of requiring the same amount of memory as the piecewise linear approximation while the error decreases. Finding the FLS approximation is computationally only slightly more intensive than finding the optimal approximation piecemeal. The method is suboptimal in the sense that there are better solutions in terms of FLS for linearization but determining and effectively calculating these functions is computationally more intensive. In [25], the capacities of a routine, based on fuzzy logic, to elaborate a set of data from a CMM (Coordinate Measurement Machine) are analyzed. They show how to obtain, during hole measurement, the best measurement, so that the approximation error is minimized. In [26], a method based on fuzzy systems is considered for the correction of errors in Coriolis mass flowmeters through a two-phase fluid. The primary error-correcting capability of this technique is specified by testing through online experimental data. One more benefit of the suggested method is its small cost relative to other methods that require different hardware for error correction. In [22], a nonlinear correction algorithm for 2D-PSD based on a fuzzy neural network was investigated and implemented to reduce non-linear errors for two-dimensional position-sensitive detectors. Using this fuzzy neural network-based nonlinear correction algorithm, non-linear errors are reduced from ±0.4 mm to ±0.15 mm.
In this work, fuzzy fusion system data are designed, evaluated, and compared. This merges the data from three sensors: an odometer, a ZED camera, and a GPS module. Using the Takagi-Sugeno type fuzzy inference systems, which have been widely used in various industrial processes for a long time, this research takes advantage of the grand development in this technology. In recent years, due to the appearance of new electronic technologies, it has been decided to merge the information from different modern sensors. The deeper challenges of merging multiple sources lie in the nature of the information and its synchrony. This leads to highlighting some important aspects, such as the characteristics of the information, the representation of the information provided by the sources, and the formulation of the instructions on how to merge the information provided. We investigate the use of ANFIS to train a Takagi-Sugeno type fuzzy system with different membership functions at the inputs. Furthermore, in the method, we explain the architecture that reduces the error with respect to the actual literature [20,23].
In the following sections, the way in which the aforementioned research was developed is explained in detail. The article is organized as follows: Section 2 presents the Materials and Methods that include the general structure of fuzzy tracking system, the signals acquisition, fuzzy fusion, and the fuzzy system stages (fuzzification, inference, and defuzzification). In Section 3, the results of three different fuzzy fusion architectures are shown. Subsequently, in Section 4 of the discussion, the results are analyzed and compared to finally show the conclusions in Section 5.
2. Materials and Methods
The experimentation platform is an AEV developed in the TecNM autotronics laboratory in Celaya. Figure 1 shows the AEV and its sensors used in this experimental work: the odometer, GPS, and the stereo camera. The first is the FC-51 sensor, which is placed on the motor’s shaft to measure displacement from the number of revolutions (pulses) made by the engine and interpreted by a Raspberry Pi 3 mini computer. The second one is the GlobalTop FGPMMOPA6H, which uses the MediaTeK GPS chipset MT3339, and it can send position data over UART. The third is a ZED (StereoLabs, Orsay, France) camera, which allows one to perform stereoscopic visual odometry through the software included in it.

Figure 1.
Electric vehicle used for data collecting.
The measurement data were divided into two sets; these are the training and validation sets. The first used 70% of the measurements and the rest are for validation. To know the severity of the problem to be solved a priori, its particular deviations were calculated. The mean square error (MSE) of the odometer, GPS, and ZED are 448.56, 327.25, and 249.84, respectively. Figure 2 shows the route that was used to take the displacement data measured by the sensors of the electric vehicle shown in Figure 1.

Figure 2.
Route traveled (in white color). Source: https://www.google.com.mx/maps/@20.5515315,-100.7763127,176m/data=!3m1!1e3 (accessed on 28 January 2022). Map data © 2022 Google.
The path was traveled in a closed circuit in a residential area. The total distance was 477.44 m. Distance traveled data were acquired with three sensors; these were odometer, GPS, and a ZED camera. Moreover, the trajectory was measured every meter with a tape measure.
2.1. General Structure of Fuzzy Tracking System
In Figure 3, the proposed method to estimate the position of the AEV is shown. The upper part of the diagram shows the three proposed sensors: the GPS, the infrared odometer, and the ZED camera. It also shows the nature of the data provided by the sensors; the GPS provides the latitude and longitude of the absolute position of the vehicle on the earth (in degrees), the infrared odometer provides the progress that the rear wheels of the AEV traveled (in meters), and the ZED stereoscopic camera provides an estimate of the AEV’s progress (in meters). The second step consists of the fusion of signals; here, it was important to analyze the data of different natures and synchronize the information at different sampling frequencies, as well as design the TS fuzzy system with different membership functions to the inputs to find the best option to reduce the estimation error with respect to the reference. This was automated using the Python programming language on a Raspberry Pi 3 (with a Broadcom BCM2837 64-bit 1.2 GHz processor and 1 GB of RAM). The design of the fuzzy system was developed with the support of ANFIS-Matlab 2019.
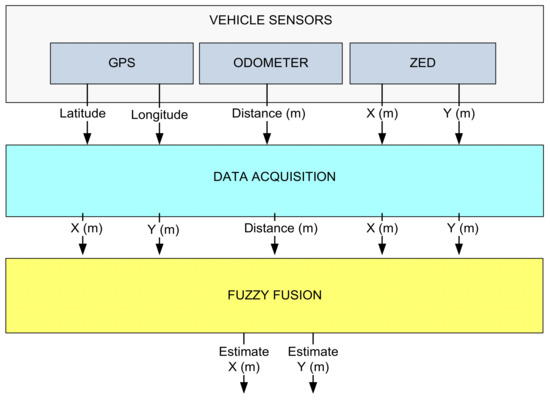
Figure 3.
Methodology’s flow diagram.
2.2. Signals Acquisition
The odometer system is an electronic optical sensor attached to the vehicle’s motor shaft. One revolution of the rotor corresponds to 0.67 m of forward advance. The optical sensor sends a signal for each turn to a Raspberry Pi 3. This information is stored in a count accumulator which corresponds to the displacement traveled. On the other hand, the latitude and longitude data are acquired by the GPS module and sent by using UART to a Raspberry Pi 3. The ZED stereoscopic camera is used to acquire images from the environment, and it estimates the translational and rotational movements of the terrestrial vehicle. Its estimation is also sent via USB communication to the Raspberry Pi 3. This camera is manufactured by the StereoLabs Company and uses the software tools provided by the manufacturer on their website. The camera can be operated with different resolutions and acquisition speed. In this work, the specifications were: 1280 × 720 resolution at 60 fps, the depth range that the camera has (0.3–25 m), and a viewing range: 90° (H) × 60° (V) × 100°, which was considered (D) max. The information generated by the three sensors is recorded in Raspberry Pi 3.
Once the measurements were obtained, the data from the three sensors was plotted and compared. Figure 4 shows the measurements made by each of the sensors. The odometer was not plotted because it only measures the forward or backward displacement relative to the AEV rear axle. It can be shown that there are differences in route reconstruction when using only the GPS or ZED camera compared to the actual route. It can also be noted that they both have a major error. The reference was drawn using QGIS software and it gives us the possibility to know the GPS coordinates of routes on real maps.
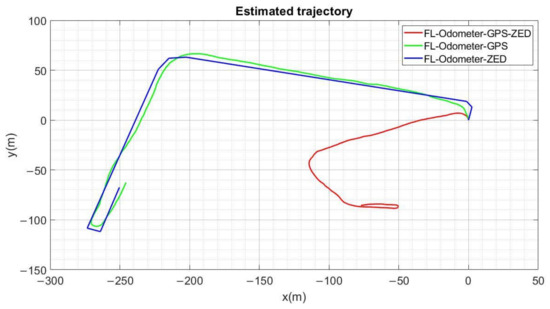
Figure 4.
Measurements of the sensors through the route traveled.
2.3. Fuzzy Fusion
Fuzzy logic is a discipline of Artificial Intelligence (AI) that is a generalization of classical logic. This has the advantage of using multiple degrees of membership between 0 and 1. Fuzzy inference systems (FIS) are used to reduce the uncertainty in position measurements. These have two fundamental parts, which are fuzzification and inference. The first aims to convert a numeric variable to linguistic variables. The second is made up of several linguistic rules that relate the input and output variables of the system. The Takagi-Sugeno fuzzy model is characterized by using linear functions of the inputs. Figure 5 shows the FIS proposed for the estimation of the ANFISedit position with MatLab 2019 [27,28,29].
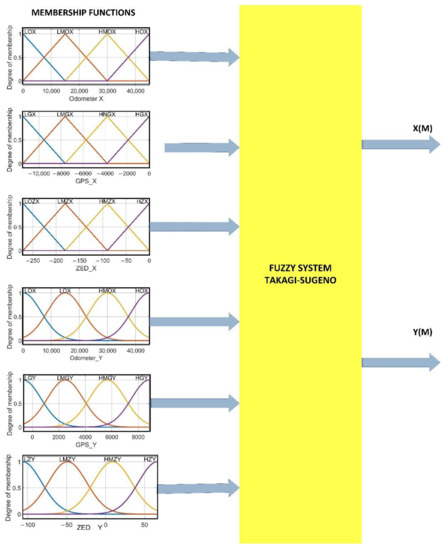
Figure 5.
Fuzzy system.
In Table 1, several FIS (5 epochs training) proposed models for determining the distance traveled by the vehicle are shown. All models were trained with 70% of the measurements, with the MatLab ANFISedit module. The outputs of the fuzzy systems were the measurements made with a tape measure on the path traveled. Model 1 used the odometer, GPS, and ZED measurements as input, and its training error was 0.0335. For Model 2, it was the odometer and ZED measurements, and its training error was 0.1042. Model 3 used the odometer and GPS measurements as input, its training error was 0.1382. Model 4 used as input the positions of the GPS and ZED. Models 2 to 4 used 6, 6, and 8 membership functions, respectively, and in the case of model 1 there were 10; it can be noted that the smallest error is obtained by including the three sensor measurements in the fuzzy system.

Table 1.
Fuzzy models proposed to estimate the distance.
2.4. Fuzzification
The fuzzification process consists of converting a real variable into a degree of belonging that quantifies the degree of possession toward its corresponding linguistic variable. To find and decide which ones, and the membership functions they would use, a search process supported by ANFIS was carried out. Different architectures were tested while their respective failures were recorded, which are shown in the following Table 2. As can be seen, the architecture with the least error for latitude is the triangular type. In the case of longitude, the option with the smallest error is that which uses Gaussian type functions.

Table 2.
Proposed architecture errors.
According to the research carried out, summarized in Table 2, it was found that the best option for this problem is to use four triangular membership functions for latitude and four Gaussian membership functions for longitude with their respective linguistic variables (low, medium low, medium high, and high) shown in Table 3 and Table 4. The parameters for the triangular functions are the left vertex, center, and right vertex, assuming that the left and right vertices output zero whereas the center vertices have the unit as output (Table 3). On the other hand, the Gaussian parameters are the mean and the standard deviation, which are also listed in the following Table 4.

Table 3.
Triangular membership functions’ parameters.

Table 4.
Gaussian membership functions’ parameters.
The membership functions used for latitude are of the triangular type and for longitude they are of the Gaussian type, as shown in Figure 6a–f. In these subfigures it is possible to appreciate the shape, the parameters, and the number of membership functions for each input.
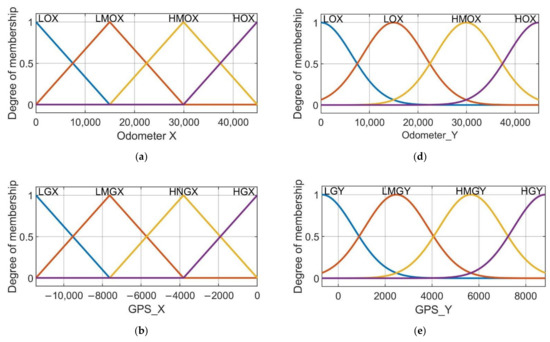
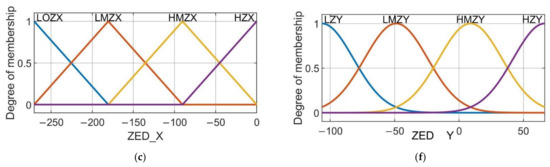
Figure 6.
Membership functions used in the proposed model. (a) Membership functions for odometer data of latitude fuzzy system. (b) Membership functions for odometer data of longitude fuzzy system. (c) Membership functions for GPS data of latitude fuzzy system. (d) Membership functions for GPS data of longitude fuzzy system. (e) Membership functions for ZED camera data of latitude fuzzy system. (f) Membership functions for ZED camera data of longitude fuzzy system.
2.5. Inference
The set of rules are of the if-else type with the AND operator; this was implemented with the scalar product between arguments. The result was delivered to each output variable corresponding to the respective output weights, and . Two rules of the 64 inference rules for each of the two fuzzy systems FLX and FLY are shown below. In Appendix A, all the rules and their respective weights are listed.
- if (odometer is LOX) and (GPSX is LGX) and (ZEDX is LOZX) then (Wx1)
- if (odometer is LOX) and (GPSY is LGY) and (ZEDY is LZY) then (Wy1)
2.6. Defuzzification
Defuzzification was carried out using Equations (1) and (2), which used 128 inference rules. Figure 7 shows the Takagi-Sugeno fuzzy model, where Zi represents the weight of the output fuzzy rule, Wi is the weight of the membership function, and N the number of fuzzy rules [26,27].
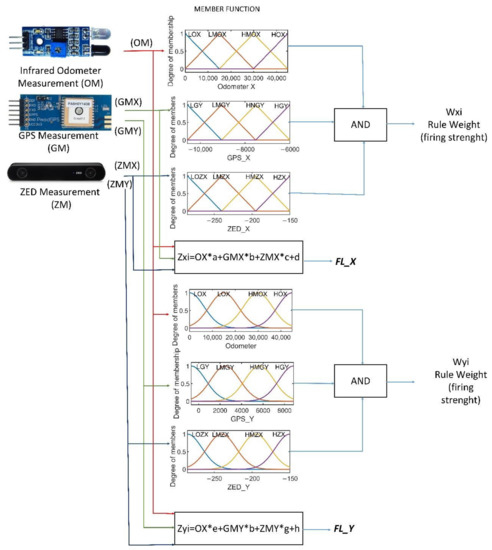
Figure 7.
Takagi-Sugeno defuzzification.
In order to observe the response of the fuzzy fusion system with five inputs and two outputs, the graphs between two inputs and one output were constructed and thus show the response of the complete system as illustrated in Figure 8. This gives us information on the work that the fuzzy system does to merge the information from the sensors and deliver the requested results.
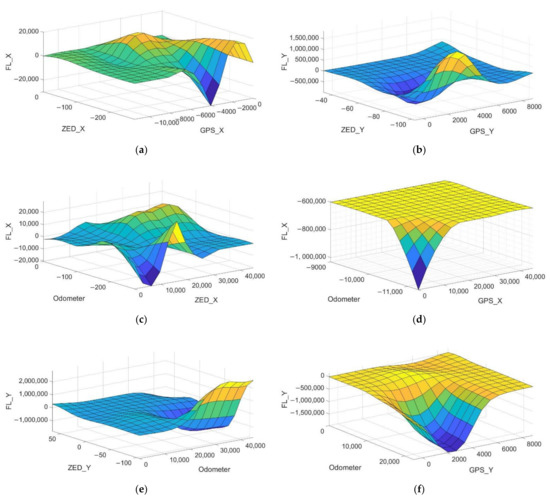
Figure 8.
Set of input-output graphs (a–f) in groups of two inputs-one output to observe the response of the fuzzy fusion system of five inputs two outputs. (a) Resulting surface from the causality of the ZED and GPS latitude inputs in the FL system. (b) Resulting surface from the causality of the GPS and ZED longitude inputs in the FL system. (c) Resulting surface from the causality of the GPS latitude and odometer inputs in the fuzzy logic system. (d) Resulting surface from the causality of the ZED camera latitude and the odometer inputs in the fuzzy logic system. (e) Resulting surface from the causality of the ZED camera latitude and odometer inputs in the fuzzy logic system. (f) Resulting surface from the causality of the ZED camera latitude and odometer inputs in the fuzzy logic system.
3. Results
In Figure 9, the positioning responses of the three proposed fuzzy logic (FL) systems are shown. The result of fashioning the data by using the GPS sensor and the ZED stereo camera is shown in blue. In green is the trajectory obtained using an FL with the odometer and the GPS as inputs. The FL system which fuses the odometer, the ZED camera, and the GPS information is plotted in red. Finally, the ground truth or reference was drawn in black using the QGIS software. It can be observed qualitatively in the zoom of Figure 9 that the approximation in red color (Odometer-GPS-ZED) is closer to the reference, especially in rotations or direction changes. From a global point of view, the difference between the three fuzzy fusion systems is almost imperceptible. A fine analysis of these differences was, however, performed by calculating the error for each output. Figure 10 shows the results of that analysis for the best fuzzy fusion system.
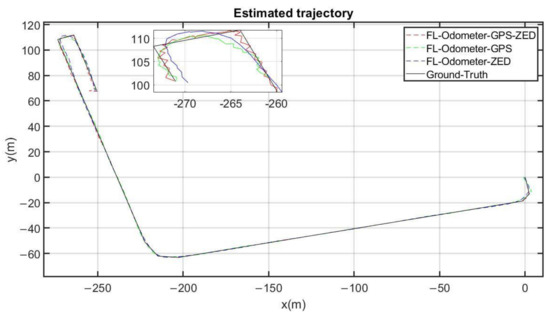
Figure 9.
The different three fuzzy system outputs on the same graph. In red, the Odometer-GPS-ZED FL system output is plotted; in green, the Odometer-GPS FL system output is drawn; in blue, the Odometer-ZED FL system output is illustrated, and the ground truth can be seen in black.
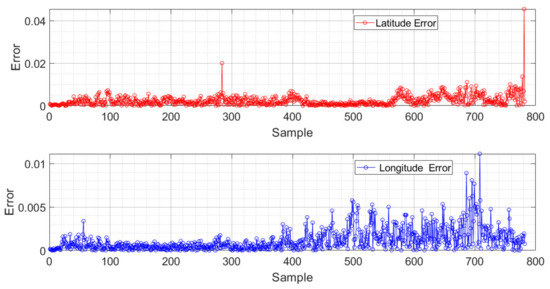
Figure 10.
Absolute error of Odometer-GPS-ZED fuzzy fusion systems outputs.
Statistical Evaluation
The statistical evaluation was performed using the mean absolute error (MAE) metric. This has the advantage of identifying the outliers predicted by the system. Figure 10 shows the momentary absolute errors of the fuzzy system during the test run. Error peaks of 3.5 m can be observed, although their (MAE) is 0.128 m. This error is caused by predicting an atypical trajectory. This allows us to see the trend in both errors simultaneously. In both cases it is a small error, but the latitude response is affected to a greater extent in rotations (Sample 282) and in drastic speed changes (in Sample 800 of the graph).
4. Discussion
Our method showed a lower error rate than actual methods in the literature in trajectory reconstruction by using the data fusion from the GPS, odometer, and ZED camera. The use of fuzzy systems allows linearizing the combined sensor response; this coincides with the results reported by [23]. The errors obtained by the fuzzy systems were less than the 0.48 m and 15 m reported in [20,23], respectively. In Table 5, the average errors of the three systems are shown. Our proposed system has a smaller average error than the one reported in [20,23]. We can highlight that the responses of the fuzzy system are close to the reference trajectory.

Table 5.
Comparative of models to estimate the distance.
The limitation shown by this configuration is the fact that the ZED camera becomes confused when facing the sun, whereas the GPS sends a greater error when there are obstacles between the sensor and the sky. Furthermore, the odometer in the configuration does not provide information about the laps.
The research carried out shows valuable information. The relative sensors, such as the odometer and the ZED camera, have a greater error in vehicle turns and a good precision in the straight course, whereas the global sensor (GPS) has a higher error in fast movements but a very good description at a global level. Each estimation of the position is complemented when a reasoning system adequately interprets the information.
5. Conclusions
In this work, a new fuzzy system was developed to merge the data from three sensors: an odometer, a ZED camera, and a GPS module. It allows for the estimation of the location with low error and competitive features with respect to other works of the state of the art. According to the results obtained, it can be concluded that the best proposed model presented the lowest MAE (0.1265 m). This is because the use of the fuzzy logic system complements the three different signals from the sensors used by the AEV location system. This architecture has the advantage of low cost and high precision. The proposed method can be extended for use in positioning systems of other types of autonomous vehicles, such as drones. Future work includes incorporating new sensors to improve the positioning of the AEV in different conditions and traffic paths.
Another adjunct challenge of this work at a technical level was the synchronization of the sensing time in the three sensors. This was solved by adding a mark to the file where the data of each source was saved. Among the most important limitations of this work is the speed of movement of the system, because the vehicle that was used reaches a maximum speed of 40 km/h.
We observe two directions in future research; the first is adding more sensors into the data fusion, such as: IMU, Electronic Compass, Lidar, among others. The second direction is to improve accuracy with fewer sensors for faster decision processing.
Author Contributions
Conceptualization, M.J.V.-A., J.E.P.-L. and A.I.B.-G.; methodology, J.A.P.-M.; software, D.L.-M.; validation, C.E.G.-A.; formal analysis, F.J.P.-P.; investigation, J.A.V.-L.; data curation, J.A.P.-M.; writing—original draft preparation, J.E.P.-L. and M.J.V.-A.; writing—review and editing, A.I.B.-G.; and supervision, A.I.B.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by CONACyT and Tecnológico Nacional de Mexico (Beca 703202).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The authors greatly appreciate the support of TecNM, UPGTO, CONACyT, and PRODEP.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Listed below are the 64 inference rules and weights for each of the two fuzzy systems
FLX and FLY:
1. if (Odometer is LOX) and (GPSX is LGX) and (ZEDX is LOZX) then (Wx1)
2. if (Odometer is LOX) and (GPSX is LGX) and (ZEDX is LMZX) then (Wx2)
3. if (Odometer is LOX) and (GPSX is LGX) and (ZEDX is HMZX) then (Wx3)
4. if (Odometer is LOX) and (GPSX is LGX) and (ZEDX is HZX) then (Wx4)
5. if (Odometer is LOX) and (GPSX is LMGX) and (ZEDX is LOZX) then (Wx5)
6. if (Odometer is LOX) and (GPSX is LMGX) and (ZEDX is LMZX) then (Wx6)
7. if (Odometer is LOX) and (GPSX is LMGX) and (ZEDX is HMZX) then (Wx7)
8. if (Odometer is LOX) and (GPSX is LMGX) and (ZEDX is HZX) then (Wx8)
9. if (Odometer is LOX) and (GPSX is HMGX) and (ZEDX is LOZX) then (Wx9)
10. if (Odometer is LOX) and (GPSX is HMGX) and (ZEDX is LMZX) then (Wx10)
11. if (Odometer is LOX) and (GPSX is HMGX) and (ZEDX is HMZX) then (Wx11)
12. if (Odometer is LOX) and (GPSX is HMGX) and (ZEDX is HZX) then (Wx12)
13. if (Odometer is LOX) and (GPSX is HGX) and (ZEDX is LOZX) then (Wx13)
14. if (Odometer is LOX) and (GPSX is HGX) and (ZEDX is LMZX) then (Wx14)
15. if (Odometer is LOX) and (GPSX is HGX) and (ZEDX is HMZX) then (Wx15)
16. if (Odometer is LOX) and (GPSX is HGX) and (ZEDX is HZX) then (Wx16)
17. if (Odometer is LMOX) and (GPSX is LGX) and (ZEDX is LOZX) then (Wx17)
18. if (Odometer is LMOX) and (GPSX is LGX) and (ZEDX is LMZX) then (Wx18)
19. if (Odometer is LMOX) and (GPSX is LGX) and (ZEDX is HMZX) then (Wx19)
20. if (Odometer is LMOX) and (GPSX is LGX) and (ZEDX is HZX) then (Wx20)
21. if (Odometer is LMOX) and (GPSX is LMGX) and (ZEDX is LOZX) then (Wx21)
22. if (Odometer is LMOX) and (GPSX is LMGX) and (ZEDX is LMZX) then (Wx22)
23. if (Odometer is LMOX) and (GPSX is LMGX) and (ZEDX is HMZX) then (Wx23)
24. if (Odometer is LMOX) and (GPSX is LMGX) and (ZEDX is HZX) then (Wx24)
25. if (Odometer is LMOX) and (GPSX is HMGX) and (ZEDX is LOZX) then (Wx25)
26. if (Odometer is LMOX) and (GPSX is HMGX) and (ZEDX is LMZX) then (Wx26)
27. if (Odometer is LMOX) and (GPSX is HMGX) and (ZEDX is HMZX) then (Wx27)
28. if (Odometer is LMOX) and (GPSX is HMGX) and (ZEDX is HZX) then (Wx28)
29. if (Odometer is LMOX) and (GPSX is HGX) and (ZEDX is LOZX) then (Wx29)
30. if (Odometer is LMOX) and (GPSX is HGX) and (ZEDX is LMZX) then (Wx30)
31. if (Odometer is LMOX) and (GPSX is HGX) and (ZEDX is HMZX) then (Wx31)
32. if (Odometer is LMOX) and (GPSX is HGX) and (ZEDX is HZX) then (Wx32)
33. if (Odometer is HMOX) and (GPSX is LGX) and (ZEDX is LOZX) then (Wx33)
34. if (Odometer is HMOX) and (GPSX is LGX) and (ZEDX is LMZX) then (Wx34)
35. if (Odometer is HMOX) and (GPSX is LGX) and (ZEDX is HMZX) then (Wx35)
36. if (Odometer is HMOX) and (GPSX is LGX) and (ZEDX is HZX) then (Wx36)
37. if (Odometer is HMOX) and (GPSX is LMGX) and (ZEDX is LOZX) then (Wx37)
38. if (Odometer is HMOX) and (GPSX is LMGX) and (ZEDX is LMZX) then (Wx38)
39. if (Odometer is HMOX) and (GPSX is LMGX) and (ZEDX is HMZX) then (Wx39)
40. if (Odometer is HMOX) and (GPSX is LMGX) and (ZEDX is HZX) then (Wx40)
41. if (Odometer is HMOX) and (GPSX is HMGX) and (ZEDX is LOZX) then (Wx41)
42. if (Odometer is HMOX) and (GPSX is HMGX) and (ZEDX is LMZX) then (Wx42)
43. if (Odometer is HMOX) and (GPSX is HMGX) and (ZEDX is HMZX) then (Wx43)
44. if (Odometer is HMOX) and (GPSX is HMGX) and (ZEDX is HZX) then (Wx44)
45. if (Odometer is HMOX) and (GPSX is HGX) and (ZEDX is LOZX) then (Wx45)
46. if (Odometer is HMOX) and (GPSX is HGX) and (ZEDX is LMZX) then (Wx46)
47. if (Odometer is HMOX) and (GPSX is HGX) and (ZEDX is HMZX) then (Wx47)
48. if (Odometer is HMOX) and (GPSX is HGX) and (ZEDX is HZX) then (Wx48)
49. if (Odometer is HOX) and (GPSX is LGX) and (ZEDX is LOZX) then (Wx49)
50. if (Odometer is HOX) and (GPSX is LGX) and (ZEDX is LMZX) then (Wx50)
51. if (Odometer is HOX) and (GPSX is LGX) and (ZEDX is HMZX) then (Wx51)
52. if (Odometer is HOX) and (GPSX is LGX) and (ZEDX is HZX) then (Wx52)
53. if (Odometer is HOX) and (GPSX is LMGX) and (ZEDX is LOZX) then (Wx53)
54. if (Odometer is HOX) and (GPSX is LMGX) and (ZEDX is LMZX) then (Wx54)
55. if (Odometer is HOX) and (GPSX is LMGX) and (ZEDX is HMZX) then (Wx55)
56. if (Odometer is HOX) and (GPSX is LMGX) and (ZEDX is HZX) then (Wx56)
57. if (Odometer is HOX) and (GPSX is HMGX) and (ZEDX is LOZX) then (Wx57)
58. if (Odometer is HOX) and (GPSX is HMGX) and (ZEDX is LMZX) then (Wx58)
59. if (Odometer is HOX) and (GPSX is HMGX) and (ZEDX is HMZX) then (Wx59)
60. if (Odometer is HOX) and (GPSX is HMGX) and (ZEDX is HZX) then (Wx60)
61. if (Odometer is HOX) and (GPSX is HGX) and (ZEDX is LOZX) then (Wx61)
62. if (Odometer is HOX) and (GPSX is HGX) and (ZEDX is LMZX) then (Wx62)
63. if (Odometer is HOX) and (GPSX is HGX) and (ZEDX is HMZX) then (Wx63)
64. if (Odometer is HOX) and (GPSX is HGX) and (ZEDX is HZX) then (Wx64)
65. if (Odometer is LOX) and (GPSY is LGY) and (ZEDY is LZY) then (Wy1)
66. if (Odometer is LOX) and (GPSY is WY) and (ZEDY is LMZY) then (Wy2)
67. if (Odometer is LOX) and (GPSY is LGY) and (ZEDY is HMZY) then (Wy3)
68. if (Odometer is LOX) and (GPSY is LGY) and (ZEDY is HZY) then (Wy4)
69. if (Odometer is LOX) and (GPSY is LMGY) and (ZEDY is LZY) then (Wy5)
70. if (Odometer is LOX) and (GPSY is LMGY) and (ZEDY is LMZY) then (Wy6)
71. if (Odometer is LOX) and (GPSY is LMGY) and (ZEDY is HMZY) then (Wy7)
72. if (Odometer is LOX) and (GPSY is LMGY) and (ZEDY is HZY) then (Wy8)
73. if (Odometer is LOX) and (GPSY is HMGY) and (ZEDY is LZY) then (Wy9)
74. if (Odometer is LOX) and (GPSY is HMGY) and (ZEDY is LMZY) then (Wy10)
75. if (Odometer is LOX) and (GPSY is HMGY) and (ZEDY is HMZY) then (Wy11)
76. if (Odometer is LOX) and (GPSY is HMGY) and (ZEDY is HZY) then (Wy12)
77. if (Odometer is LOX) and (GPSY is HGY) and (ZEDY is LZY) then (Wy13)
78. if (Odometer is LOX) and (GPSY is HGY) and (ZEDY is LMZY) then (Wy14)
79. if (Odometer is LOX) and (GPSY is HGY) and (ZEDY is HMZY) then (Wy15)
80. if (Odometer is LOX) and (GPSY is HGY) and (ZEDY is HZY) then (Wy16)
81. if (Odometer is LMOX) and (GPSY is LGY) and (ZEDY is LZY) then (Wy17)
82. if (Odometer is LMOX) and (GPSY is LGY) and (ZEDY is LMZY) then (Wy18)
83. if (Odometer is LMOX) and (GPSY is LGY) and (ZEDY is HMZY) then (Wy19)
84. if (Odometer is LMOX) and (GPSY is LGY) and (ZEDY is HZY) then (Wy20)
85. if (Odometer is LMOX) and (GPSY is LMGY) and (ZEDY is LZY) then (Wy21)
86. if (Odometer is LMOX) and (GPSY is LMGY) and (ZEDY is LMZY) then (Wy22)
87. if (Odometer is LMOX) and (GPSY is LMGY) and (ZEDY is HMZY) then (Wy23)
88. if (Odometer is LMOX) and (GPSY is LMGY) and (ZEDY is HZY) then (Wy24)
89. if (Odometer is LMOX) and (GPSY is HMGY) and (ZEDY is LZY) then (Wy25)
90. if (Odometer is LMOX) and (GPSY is HMGY) and (ZEDY is LMZY) then (Wy26)
91. if (Odometer is LMOX) and (GPSY is HMGY) and (ZEDY is HMZY) then (Wy27)
92. if (Odometer is LMOX) and (GPSY is HMGY) and (ZEDY is HZY) then (Wy28)
93. if (Odometer is LMOX) and (GPSY is HGY) and (ZEDY is LZY) then (Wy29)
94. if (Odometer is LMOX) and (GPSY is HGY) and (ZEDY is LMZY) then (Wy30)
95. if (Odometer is LMOX) and (GPSY is HGY) and (ZEDY is HMZY) then (Wy31)
96. if (Odometer is LMOX) and (GPSY is HGY) and (ZEDY is HZY) then (Wy32)
97. if (Odometer is HMOX) and (GPSY is LGY) and (ZEDY is LZY) then (Wy33)
98. if (Odometer is HMOX) and (GPSY is LGY) and (ZEDY is LMZY) then (Wy34)
99. if (Odometer is HMOX) and (GPSY is LGY) and (ZEDY is HMZY) then (Wy35)
100. if (Odometer is HMOX) and (GPSY is LGY) and (ZEDY is HZY) then (Wy36)
101. if (Odometer is HMOX) and (GPSY is LMGY) and (ZEDY is LZY) then (Wy37)
102. if (Odometer is HMOX) and (GPSY is LMGY) and (ZEDY is LMZY) then (Wy38)
103. if (Odometer is HMOX) and (GPSY is LMGY) and (ZEDY is HMZY) then (Wy39)
104. if (Odometer is HMOX) and (GPSY is LMGY) and (ZEDY is HZY) then (Wy40)
105. if (Odometer is HMOX) and (GPSY is HMGY) and (ZEDY is LZY) then (Wy41)
106. if (Odometer is HMOX) and (GPSY is HMGY) and (ZEDY is LMZY) then (Wy42)
107. if (Odometer is HMOX) and (GPSY is HMGY) and (ZEDY is HMZY) then (Wy43)
108. if (Odometer is HMOX) and (GPSY is HMGY) and (ZEDY is HZY) then (Wy44)
109. if (Odometer is HMOX) and (GPSY is HGY) and (ZEDY is LZY) then (Wy45)
110. if (Odometer is HMOX) and (GPSY is HGY) and (ZEDY is LMZY) then (Wy46)
111. if (Odometer is HMOX) and (GPSY is HGY) and (ZEDY is HMZY) then (Wy47)
112. if (Odometer is HMOX) and (GPSY is HGY) and (ZEDY is HZY) then (Wy48)
113. if (Odometer is HOX) and (GPSY is LGY) and (ZEDY is LZY) then (Wy49)
114. if (Odometer is HOX) and (GPSY is LGY) and (ZEDY is LMZY) then (Wy50)
115. if (Odometer is HOX) and (GPSY is LGY) and (ZEDY is HMZY) then (Wy51)
116. if (Odometer is HOX) and (GPSY is LGY) and (ZEDY is HZY) then (Wy52)
117. if (Odometer is HOX) and (GPSY is LMGY) and (ZEDY is LZY) then (Wy53)
118. if (Odometer is HOX) and (GPSY is LMGY) and (ZEDY is LMZY) then (Wy54)
119. if (Odometer is HOX) and (GPSY is LMGY) and (ZEDY is HMZY) then (Wy55)
120. if (Odometer is HOX) and (GPSY is LMGY) and (ZEDY is HZY) then (Wy56)
121. if (Odometer is HOX) and (GPSY is HMGY) and (ZEDY is LZY) then (Wy57)
122. if (Odometer is HOX) and (GPSY is HMGY) and (ZEDY is LMZY) then (Wy58)
123. if (Odometer is HOX) and (GPSY is HMGY) and (ZEDY is HMZY) then (Wy59)
124. if (Odometer is HOX) and (GPSY is HMGY) and (ZEDY is HZY) then (Wy60)
125. if (Odometer is HOX) and (GPSY is HGY) and (ZEDY is LZY) then (Wy61)
126. if (Odometer is HOX) and (GPSY is HGY) and (ZEDY is LMZY) then (Wy62)
127. if (Odometer is HOX) and (GPSY is HGY) and (ZEDY is HMZY) then (Wy63)
128. if (Odometer is HOX) and (GPSY is HGY and (ZEDY is HZY then (Wy64)
The coefficients obtained by the corresponding ANFIS optimizer are the following. For the FLX fuzzy system:
Zx1= [0 0 0 0]
Zx2= [82.6709540591307 140.57141931609 49.9089792698489 −0.405738805462074]
Zx3= [36.6599347407412 46.3590220490601 72.2216956159385 −0.542136329380006]
Zx4 = [0 0 0 0]
Zx5 = [0 0 0 0]
Zx6 = [6.14756428891982 −0.975154468190298 42.385604965837 12.7571431590778]
Zx7 = [7.84913466505093 −0.856339744729866 36.3938356735832 −25.0410741688257]
Zx8 = [−2.18201882409264 0.508544186984445 −119.854032662302 144.174393304261]
Zx9 = [0 0 0 0]
Zx10 = [1.88776650050903 1.77557553888513 −205.844752014103 −24.3326450130557]
Zx11 = [3.869306211076 0.632859583708402 −23.7782531853404 51.6955205183708]
Zx12 = [−0.91455852068420 0.260060774920087 −47.1610255910924 −288.3516597748]
Zx13 = [0 0 0 0]
Zx14 = [0 0 0 0]
Zx15 = [−0.1457012093679 0.12555249515918 −10.2776504984038 0.1675277449342]
Zx16 = [0.00301248558204 −0.070905722646 −4.838165794538 −0.0797474250354048]
Zx17 = [29.880783889326 37.748342718747 53.4443730643342 46.1709684098716]
Zx18 = [8.97875330514079 10.7679607033321 62.1327632680629 −119.80755376225]
Zx19 = [13.1687822854955 17.6800559607029 34.5118612240997 101.755928381209]
Zx20 = [0 0 0 0]
Zx21 = [19.765577678925 37.8051323069975 20.8815938440997 −69.2669294706063]
Zx22 = [5.91668383777419 10.8734137683193 31.4986360555686 179.726116914051]
Zx23 = [8.18520078495055 15.5633998028767 40.170978037927 −152.609936486828]
Zx24 = [−0.45826918596628 −1.3378725123247 63.572985992587 −0.00017657981574]
Zx25 = [2.542626080508 11.3094260862981 −22.4564614511257 0.0002963071395798]
Zx26 = [2.54262608050 11.30942608629 −22.4564614511257 0.000296307139579]
Zx27 = [3.52734175437 15.01570395938 −34.1666863960227 0.0004946975089971]
Zx28 = [−0.5717067357076 −3.75406955003 56.5689979184027 −9.94079419206818 × 10−5]
Zx29 = [0 0 0 0]
Zx30 = [0 0 0 0]
Zx31 = [−0.2978785761983 15.38423355074 −49.78464545773 −2.96670111896722 × 10−5]
Zx32 = [−0.0319350336605 −3.85107664314039 49.7872533833 −1.934162532747 × 10−6]
Zx33 = [29.9406465936505 78.1501364252389 7.80112961990164 −38.5887125725771]
Zx34 = [9.00870839945059 23.3672785382552 12.4440424356964 83.3922378417652]
Zx35 = [11.5927144714591 29.7705251055216 69.2575988987817 −50.8758875776323]
Zx36 = [0 0 0 0]
Zx37 = [19.89413295430 78.1482682446005 −0.736357284453164 58.0195161700337]
Zx38 = [5.84274870237134 23.4309496731088 −17.3847614703793 −125.305325272695]
Zx39 = [6.81793127917989 28.3188223037439 76.9078823196504 76.3062101507039]
Zx40 = [0 0 0 0]
Zx41 = [9.9957705018255 78.1613533613785 4.71041556075994 −0.266783823278485]
Zx42 = [2.86636379845013 23.32661384854 −9.28151201762766 0.425452955508286]
Zx43 = [0 0 0 0]
Zx44 = [0 0 0 0]
Zx45 = [0 0 0 0]
Zx46 = [0 0 0 0]
Zx47 = [0 0 0 0]
Zx48 = [0 0 0 0]
Zx49 = [29.5673693511635 117.574369827578 −43.687068927803 10.3370020581945]
Zx50 = [9.7984255934188 35.5438081559817 71.1259149835798 −15.6567821195735]
Zx51 = [0 0 0 0]
Zx52 = [0 0 0 0]
Zx53 = [19.8438428487293 116.981761901251 −3.40312313174215 −15.5896940129783]
Zx54 = [6.02374373908428 36.6747011458722 −40.8833222953607 23.6287179611743]
Zx55 = [0 0 0 0]
Zx56 = [0 0 0 0]
Zx57 = [10.0159047701173 116.945397117141 14.0876825724604 0.17830196325045]
Zx58 = [3.032066839646 36.726184658901 −11.19839706376 −0.283503790159247]
Zx59 = [0 0 0 0]
Zx60 = [0 0 0 0]
Zx61 = [0 0 0 0]
Zx62 = [0 0 0 0]
Zx63 = [0 0 0 0]
Zx64 = [0 0 0 0]
For the FLY diffuse system:
Zy1 = [−61.6394296511 10.0519667105192 −0.0352637308421657 0.00318141673894]
Zy2 = [0.30955235919 0.0804772616958248 −41.5073578615944 16.615318627553]
Zy3 = [−0.008575307946098 −0.0338140035266843 −4.39563844681077 −7.8506119094]
Zy4 = [0.3879358735691 −1.25381736099946 −64.2017404360238 −5.57225999113734]
Zy5 = [3.1130773730253 0.3454062208848 −0.0527066429116474 0.002753091180551]
Zy6 = [−0.72618055417945 −5.64872549329672 15.1140216850406 1.8361925054297]
Zy7 = [−0.0946981998549818 −0.882217798617659 49.476569775266 22.927398162131]
Zy8 = [−1.88451509304862 6.32959291217903 132.033968833885 3.33260271733161]
Zy9 = [0.1741481288795 0.05550891776454 −0.0001984482006563 8.7416960463 × 10−6]
Zy10 = [138.9030599198 40.0765769777781 0.0101057887695076 0.00877420322102]
Zy11 = [−16.7670056810461 37.3616106751062 1.31533516250802 −0.01726702887862]
Zy12 = [28.41030027985 −156.4672914282 −0.548841609177903 −0.0409322289827]
Zy13 = [1.465587067028 0.43612635399 −0.00034909096657 5.29414524257 × 10−5]
Zy14 = [97.55421064231 32.0345548645 −0.1485405218259 0.00346435998997]
Zy15 = [544.4427187349 145.548916904062 −0.150507440690915 0.020304588883]
Zy16 = [103.2631593618 25.33117809797 0.11007087517528 0.0042795005929314]
Zy17 = [−12.78472635974 3.5597306606321 0.01707461158129 −0.00270249229063387]
Zy18 = [3.49902368299109 2.88715349457969 53.0197226324676 1.10279177456225]
Zy19 = [−0.0520464393409 0.896772263014222 10.124248848648 11.1296970229]
Zy20 = [−0.564636034384 1.49719382580716 122.557596876111 −5.71354800624711]
Zy21 = [−0.16859627871 0.1270217183451 −0.006695201086519 0.0002147229565563]
Zy22 = [−17.6645703949 152.267040410836 −1.8504142401162 0.0511091559147964]
Zy23 = [0.05907736601478 −1.12041393290336 70.837682640622 −4.41206273798338]
Zy24 = [0.011417732467 −0.2644795038377 −3.79181000388194 −0.225392068358471]
Zy25 = [28.94303318865 14.7260738089 −0.185831011585323 0.00192154554629274]
Zy26 = [90.9171193213084 −336.459443404778 160.96742595133 1.11273403228666]
Zy27 = [9.36230471045555 −33.2955773709928 −206.168554338846 2.10020948010133]
Zy28 = [3.811160685055 −16.1798591737201 −215.471216876522 −2.37358956225612]
Zy29 = [−0.4920104101652 16.660869383524 0.1970818047509 −0.00626037501750486]
Zy30 = [−12.9033290656624 41.5791868777242 −464.335927992444 1.20082051675558]
Zy31 = [−43.1542550142609 157.185132012117 351.852157951199 4.22786520560589]
Zy32 = [−178.404083362914 686.600108381913 35.860161092854 0.293820711059665]
Zy33 = [−0.006434784293 0.002358161190 1.191507702212 × 10−5 −2.502334914 × 10−6]
Zy34 = [−16.181734571 −0.4683349828096 −0.006188301980001 −0.001920013063506]
Zy35 = [7.9104664012135 −135.734954338398 −1.24300296934534 0.018568624131907]
Zy36 = [0.1880752222292 −11.01249896981 155.960223538224 0.460053328945252]
Zy37 = [293.602420995 57.9209013039017 −1.452776030699 0.00770609645447751]
Zy38 = [−194.245466831 71.203138303312 6.825769166559 0.04314877334170]
Zy39 = [4.00153041567606 −45.1014404840967 508.35576829183 5.50976726819268]
Zy40 = [−0.14632147218 −2.14008344207651 80.6442197233144 −1.3512149763495]
Zy41 = [4.04334918503 −20.7770738518254 −122.57545871125 0.275980440502305]
Zy42 = [−2.063191712287 7.9241733896872 −48.6423550437377 −8.9846596844341]
Zy43 = [−3.483061482018 15.0005523757358 −157.623293929859 15.6670303306955]
Zy44 = [−2.36322272572 12.3912445228976 105.737524163892 8.80102718549545]
Zy45 = [0.3063272704709 −0.9291207779792 17.1847412956494 3.63891454559102]
Zy46 = [0.1012476756133 −0.270342723252411 17.053454802958 2.48550211537964]
Zy47 = [2.66610227141 −9.49056029977172 −122.058965554121 −38.6914973781024]
Zy48 = [27.0423694113738 −115.906775892189 19.07251219638 −0.476634857892608]
Zy49 = [−0.002886483 −0.0004546682089 −1.65867760827 × 10−6 −6.052004542214 × 10−8]
Zy50 = [−0.0184379618 −0.002289711811 −6.806256830362 × 10−5 −9.061796983004 × 10−7]
Zy51 = [4.29190353926 1.1352585186756 0.0248069611314 0.000114039264158]
Zy52 = [320.207438601191 33.8230806865483 1.38272019728003 0.0136394232237]
Zy53 = [−225.87093701977 −32.7680509254542 −1.06348175119 −0.0045493266524]
Zy54 = [481.1213219034 63.6879370144733 −1.880162021878 0.0062517234811]
Zy55 = [313.280717032275 382.276161411212 −8.80960840212665 −0.0291015397747]
Zy56 = [−5.3635353703504 216.450215812879 1.96938898397508 0.0212535627278]
Zy57 = [1.51092967578936 −7.05794566719034 64.797929263403 −0.399931649901]
Zy58 = [−2.40065251786272 9.39600987764601 −111.380685200674 2.0671755008108]
Zy59 = [59.1408404552257 −268.231865544057 −409.291161320353 −1.80963531067]
Zy60 = [−74.8515164879032 292.80972119823 −75.5703694328042 −0.204262545958]
Zy61 = [0.024314772135 −0.173078147362 −5.95046547435 9.28603038]
Zy62 = [0.125495529198 −0.316486559383 23.7574746816 −15.5300823122]
Zy63 = [−2.37294721751 6.71849603935 44.0009541499 16.0841390136]
Zy64 = [165.15434417 −320.4728280 10.8868146427 0.00872501083937]
References
- Kenney, J.B. Dedicated short-range communications (DSRC) standards in the United States. Proc. IEEE 2011, 99, 1162–1182. [Google Scholar] [CrossRef]
- Dobrev, Y.; Christmann, M.; Bilous, I.; Gulden, P. Steady delivery: Wireless local positioning systems for tracking and autonomous navigation of transport vehicles and mobile robots. IEEE Microw. Mag. 2017, 18, 26–37. [Google Scholar] [CrossRef]
- Tomita, H.; Iotake, Y.; Sugawara, S.; Nomura, T.; Kudo, H. High-precision Satellite Positioning Technique and Service for Next-generation Mobility. Hitachi Rev. 2019, 68, 1–8. [Google Scholar]
- Ho, V.; Rauf, K.; Passchier, I.; Rijks, F.; Witsenboer, T. Accuracy assessment of RTK GNSS based positioning systems for automated driving. In Proceedings of the 2018 15th Workshop on Positioning, Navigation and Communications (WPNC), Bremen, Germany, 25–26 October 2018. [Google Scholar]
- Ordóñez-Hurtado, R.H.; Crisostomi, E.; Shorten, R.N. An assessment on the use of stationary vehicles to support cooperative positioning systems. Int. J. Control 2018, 91, 608–621. [Google Scholar] [CrossRef]
- Somogyi, H.; Soumelidis, A. Comparison of High-Precision GNSS systems for development of an autonomous localization system. In Proceedings of the 2020 23rd International Symposium on Measurement and Control in Robotics (ISMCR), Budapest, Hungary, 15–17 October 2020. [Google Scholar]
- Crowley, J.L.; Demazeau, Y. Principles and techniques for sensor data fusion. Signal Process. 1993, 32, 5–27. [Google Scholar] [CrossRef] [Green Version]
- Rosique, F.; Navarro, P.J.; Padilla, A. A systematic review of perception system and simulators for autonomous vehicles research. Sensors 2019, 19, 648. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, R.; Yang, N.; Stückler, J.; Cremers, D. DirectShape: Direct Photometric Alignment of Shape Priors for Visual Vehicle Pose and Shape Estimation. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar]
- Esfahani, M.A.; Wang, H.; Wu, K.; Yuan, S. AbolDeepIO: A novel deep inertial odometry network for autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1941–1950. [Google Scholar] [CrossRef]
- Nguyen, T.; Mann, G.K.; Vardy, A.; Gosine, R.G. Developing computationally efficient nonlinear cubature Kalman filtering for visual inertial odometry. J. Dyn. Syst. Meas. Control 2019, 141, 081012. [Google Scholar] [CrossRef]
- Forster, F.; Pizzoli, P.; Scaramuzza, D. SVO: Fast semi-direct monocular visual odometry. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014. [Google Scholar]
- Zhang, Y.; Liu, Z.; Liu, T.; Peng, B.; Li, X. An efficient generation network for 3D object reconstruction from a single image. IEEE Access 2019, 7, 57539–57549. [Google Scholar] [CrossRef]
- Riegler, G.; Liao, Y.; Donne, S.; Koltun, V.; Geiger, G. Connecting the Dots: Learning Representations for Active Monocular Depth Estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Rau, A.; Edwards, P.J.; Ahmad, O.F.; Riordan, P.; Janatka, M.; Lovat, L.B.; Stoyanov, D. Implicit domain adaptation with conditional generative adversarial networks for depth prediction in endoscopy. Int. J. Comput. Assist. Radiol. Surg. 2019, 14, 1167–1176. [Google Scholar] [CrossRef] [Green Version]
- Ran, L.; Zhang, Y.; Zhang, Z.; Yang, T. Convolutional neural network-based robot navigation using uncalibrated spherical images. Sensors 2017, 17, 1341. [Google Scholar] [CrossRef] [PubMed]
- Shokry, K.; Alhawary, M. MonoSLAM: A Single Camera SLAM. Univ. Twente Stud. J. Biom. Comput. Vis. 2017, 1, 1–8. [Google Scholar]
- Zhou, K.; Wang, X.; Wang, Z.; Wei, H.; Yin, L. Complete initial solutions for iterative pose estimation from planar objects. IEEE Access 2018, 6, 22257–22266. [Google Scholar] [CrossRef]
- Nilwong, S.; Hossain, D.; Kaneko, S.; Capi, G. Deep learning-based landmark detection for mobile robot outdoor localization. Machines 2019, 7, 25. [Google Scholar] [CrossRef] [Green Version]
- Woo, R.; Yang, E.-J.; Seo, D.-W. DA fuzzy-innovation-based adaptive kalman filter for enhanced Vehicle positioning in dense urban environments. Sensors 2019, 19, 1142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nourmohammadi, H.; Keighobadi, J. Fuzzy adaptive integration scheme for low-cost SINS/GPS navigation system. MSSP 2018, 99, 434–449. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, H.; Tang, G. Predictor-corrector guidance for entry vehicle based on fuzzy logic. Proc. Inst. Mech. Eng. G. 2019, 233, 472–482. [Google Scholar] [CrossRef]
- Teodorescu, H.-N.L. Fuzzy logic system linearization for sensors. In Proceedings of the 2017 International Symposium on Signals, Iasi, Romania, 13–14 July 2017. [Google Scholar]
- Cappetti, N.; Naddeo, A.; Villecco, F. Fuzzy approach to measures correction on Coordinate Measuring Machines: The case of hole-diameter verification. Measurement 2019, 93, 41–47. [Google Scholar] [CrossRef]
- Chaudhary, D.R.; Chaudhari, D.F. Study on Coriolis Mass Flow Meter for Error Correction through Two-phase Fluid Using Fuzzy Logic. In Proceedings of the International Conference on Innovative Advancement in Engineering and Technology (IAET-2020), Jaipur, India, 21–22 February 2020. [Google Scholar]
- Villaseñor-Aguilar, M.J.; Botello-Álvarez, J.E.; Pérez-Pinal, F.J.; Cano-Lara, M.; León-Galván, M.F.; Bravo-Sánchez, M.G.; Bravo- Sánchez, M.G.; Barranco-Gutiérrez, A.I. Fuzzy Classification of the Maturity of the Tomato Using a Vision System. J. Sens. 2019, 2019, 3175848. [Google Scholar] [CrossRef]
- Villaseñor-Aguilar, M.J.; Bravo-Sánchez, M.G.; Padilla-Medina, J.A.; Vázquez-Vera, J.L.; Guevara-González, R.G.; García- Rodríguez, F.J.; Barranco-Gutiérrez, A.I. A maturity estimation of bell pepper (Capsicum annuum L.) by artificial vision system for quality control. J. Sens. 2020, 10, 5097. [Google Scholar] [CrossRef]
- Pena-Aguirre, J.C.; Barranco-Gutierrez, A.I.; Padilla-Medina, J.A.; Espinosa-Calderon, A.; Perez-Pinal, F.J. Fuzzy Logic Power Management Strategy for a Residential DC-Microgrid. IEEE Access 2020, 8, 116733–116743. [Google Scholar] [CrossRef]
- Wang, X. A driverless vehicle vision path planning algorithm for sensor fusion. In Proceedings of the 2019 IEEE 2nd International Conference on Automation, Electronics and Electrical Engineering (AUTEEE), Shenyang, China, 22–24 November 2019. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).