Odd-Graceful Total Colorings for Constructing Graphic Lattice

Abstract

The security of passwords generated by the graphic lattices is based on the difficulty of the graph isomorphism, graceful tree conjecture, and total coloring conjecture. A graphic lattice is generated by a graphic base and graphical operations, where a graphic base is a group of disjointed, connected graphs holding linearly independent properties. We study the existence of graphic bases with odd-graceful total colorings and show graphic lattices by vertex-overlapping and edge-joining operations; we prove that these graphic lattices are closed to the odd-graceful total coloring.

1. Introduction and Preliminary

1.1. Introduction

Considering current text passwords, once the password file is leaked, most of the plaintext passwords can be quickly deciphered using current cracking techniques, and personal privacy and property will face serious losses. Topological authentication is a new technique based on topological coding, a mixed branch of discrete mathematics, number theory, algebraic group, graph theory, and so on. This technology is more and more widely used in real life; for example, the user identity authentication of the smart-phone adopts a graphic password [1,2]. Johnson et al. proposed a picture signature password to determine access to computing devices or services [3]. Wang et al. [4] designed a topological code consisting of a topological structure and graph colorings. According to the order of vertex-edge-vertex, Yao et al. [5] arranged the labels or colors of each edge and two end-vertices of a graph G, with p vertices, and q edges in a topological matrix of order $3\times q$; that is

$$T_{code}={\left(\begin{array}{cccc}f\left(u_1\right)& f\left(u_2\right)& \cdots & f\left(u_q\right)\\ f\left(e_1\right)& f\left(e_2\right)& \cdots & f\left(e_q\right)\\ f\left(v_1\right)& f\left(v_2\right)& \cdots & f\left(v_q\right)\end{array}\right)}_{3\times q}$$

(1)

where f represents a function to obtain the colors of the vertices and edges. The topological matrix of G can derive $\left(3q\right)!$ number strings that can be used as digital-based passwords, and the preset coloring f can be needed during authentication, called topological authentication. It is feasible to generate passwords by topological coding, because its deciphering process involves NP-hard problems, for instance, the graph isomorphism problem and the graceful tree conjecture. Tian et al. [6] proved that the passwords generated by the labeling of a graph can resist brute force attacks, dictionary attacks, guessing attacks, reproduction attack, and denial of service attacks.

The lattice-based cryptosystem is based on NP-Hard or NP-C problems [7,8], which makes lattice-based cryptosystem a core research field in cryptosystems against quantum attacks. A lattice $\mathbf{L}\left(\mathbf{B}\right)$ is defined as the set of all integer combinations

$$\mathbf{L}\left(\mathbf{B}\right)=\left\{\sum _{i=1}^n{x}_i{\mathbf{b}}_i:x_i\in Z,1\le i\le n\right\}$$

(2)

of n linearly independent vectors ${\mathbf{b}}_1,{\mathbf{b}}_2,\cdots ,{\mathbf{b}}_n$ in $R^m$ with $n\le m$, where Z is the integer set, m is the dimension, and n is the rank of the lattice, and the vector group ${\mathbf{b}}_1,{\mathbf{b}}_2,\cdots ,{\mathbf{b}}_n$ is called a lattice base. Lattice theory involves the Shortest Vector Problem [9], Shortest Independent Vector Problem, Successive Minimum Problem [10], Closet Vector Problem, and other difficult problems. The security of the lattice-based cryptology depends on the difficulty of the difficult problems in classical number theory and computational complexity theory [11], many difficult problems in the lattice have been proven to be NP-hard, so this mechanism is generally considered to be resistant to the attacks from quantum computers when it is used in cryptanalysis and design.

Inspired by the ability of lattice-based cryptology to resist supercomputers and quantum computers, we propose graphic lattices for the encryption of network models or complex systems. According to the method of topological coding, large-scale graphs are more reliable than small-scale graphs. Therefore, it is necessary to generate large-scale graphs from existing small-scale graphs for identification. The graphic lattice combines operations and topological coding of the graphic base to generate the topological coding of a large-scale graph [12,13]. In this paper, we extend the theoretical tool of topological coding from graph labeling to graph coloring and define a new type of coloring for building graphic lattices and providing topological coding based on new coloring.

1.2. Preliminary

The graphs described in this paper are graphs that do not contain double edges. The labeling of a graph G refers to $f:V\left(G\right)\to [a,b]$, there is always $f\left(x\right)\ne f\left(y\right)$ for any pair of vertices $x,y\in V\left(G\right)$. The coloring of the graph G means that a function $g:V\left(G\right)\to [a,b]$, such that $g\left(u\right)=g\left(v\right)$ for some two vertices $u,v\in V\left(G\right)$ [14]. The degree of a vertex u of a $(p,q)$-graph G is denoted as $\left|N\right(u\left)\right|$, where $N\left(u\right)$ represents the neighbor set of the vertex u, and a vertex having degree one is called a leaf. For simplicity of description, we write $f\left(P\right)=\left\{f\right(w):w\in P\}$, where $f:P\subset V\left(G\right)\cup E\left(G\right)\to [1,M]$, $M>1$ is a positive integer.

A graph G admits a proper total coloring $f:V\left(G\right)\cup E\left(G\right)\to [1,M]$ if it satisfies the following conditions [15,16]. For $u,v,w\in V\left(G\right)$, then

(1) $f\left(u\right)\ne f\left(v\right)$ for each edge $uv\in E\left(G\right)$;

(2) $f\left(uv\right)\ne f\left(uw\right)$ for $v,w\in N\left(u\right)$;

(3) $f\left(uv\right)\ne f\left(u\right)$ for $v\in N\left(u\right)$.

The symbols used in this paper are shown in Table 1, and the other notations and terminologies not mentioned here can be found in [15,17].

Table 1. Abbreviations.

Symbol	Meaning
$(p,q)$-graph	A undirected graph with p vertices and q edges
$[a,b]$	A set $\{x\in Z:a\le x\le b\}$ with $a,b\in N$, $a<b$
${[m,n]}^o$	An odd integer set $\{m,m+2,\cdots ,n\}$ for two odd integers $1\le m<n$
$\left|X\right|$	The number of elements of a set X
$\left|N\right(u\left)\right|$	The degree of a vertex u
$f\left(P\right)$	The label/color set $f\left(P\right)=\left\{f\right(w):w\in P\}$, $P\subset V\left(G\right)\cup E\left(G\right)$
	for the labeling or coloring of a graph G

Definition 1.

A $(p,q)$-graph G admits a total coloring $f:V\left(G\right)\cup E\left(G\right)\to [1,M]$, if it satisfies

(1) Each edge $uv\in E\left(G\right)$ is colored as $f\left(uv\right)=\left|f\right(u)-f(v\left)\right|$;

(2) The edge color set is $f\left(E\left(G\right)\right)={[1,2q-1]}^o$;

(3) The vertex color set is $f\left(V\right(G\left)\right)\subseteq [1,2q]$.

Then f is called a quasi-odd-graceful total coloring if (1) and (2) hold, and f is called an odd-graceful total coloring if the above three conditions are met. Furthermore, if the vertex set of the $(p,q)$-graph G can be divided into $V\left(G\right)=X\cup Y$ with $X\cap Y=\varnothing$, so that each edge $uv\in E\left(G\right)$ satisfies $u\in X$ and $v\in Y$, besides, $maxf\left(X\right)<minf\left(Y\right)$ is true, then we call f a set-ordered odd-graceful total coloring.

Several examples are shown in Figure 1 for understanding Definition 1. Similar to the definition of a lattice, we give the definition of a graphic lattice.

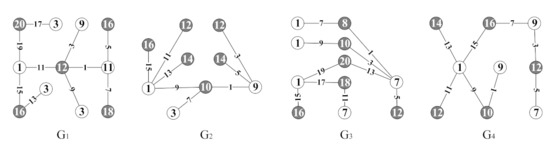
Figure 1. Four graphs $G_1$, $G_2$, $G_3$, $G_4$ admit set-ordered odd-graceful total colorings.

Definition 2.

Let $\mathrm{G}=(G_1,G_2,\cdots ,G_n)={\left(G_i\right)}_1^n$ be a graphic base composed of n linearly independent graphic vectors under a graphical operation “◊”, where each $G_i$ is a colored/uncolored graph, and $F_{p,q}$ is a set of colored/uncolored graphs of λ vertices and μ edges with respect to $\lambda \le p$, $\mu \le q$ and $2n-2\le p$. We write the resulting graph obtained by performing a graphical operation ◊ on a graph H and the graphic base $\mathit{G}$ with $a_i\in Z^0$, denoted as $\mathit{G}◊H=H{◊}_{i=1}^n{a}_i{G}_i$. In general, the graph set

$$\mathit{L}(\mathit{G}◊F_{p,q})=\{H{◊}_{i=1}^n{a}_i{G}_i:a_i\in Z^0,H\in F_{p,q}\}$$

(3)

with ${\sum }_{i=1}^n{a}_i\ge 1$ is called a graphic lattice, $\mathit{G}$ a graphic lattice base, p is the dimension and n is the rank of $\mathit{L}(\mathit{G}◊F_{p,q})$. Moreover, $\mathit{L}(\mathit{G}◊F_{p,q})$ is called a linear graphic lattice if every $H\in F_{p,q}$, each $G_i$ of base $\mathit{G}$ and $H{◊}_{i=1}^n{a}_i{G}_i$ are forests or trees. A colored tree-graph lattice is full-rank $p=n$ in Equation (3).

Based on the following two graphical operations, some large-scale graphs containing odd-graceful total colorings can be obtained, which increases the cryptographic space.

Definition 3.

For two graphs, $M_1$ and $M_2$, the two types of graphical operations related to the vertices and edges are as follows.

(1) Vertex-overlapping operation refers to overlapping a vertex u in graph $M_1$ with a vertex v in graph $M_2$ to form a new vertex w, then the neighbors of w are the union of the neighbors of u and the neighbors of v; the operation is denoted as $u\odot v$.

(2) Edge-joining operation means adding a new edge between a vertex u in the graph $M_1$ and a vertex v in the graph $M_2$, the operation is expressed as $u\oplus v$.

2. Graphic Lattices with Odd-Graceful Total Colorings

Lemma 1.

Each tree admits a quasi-odd-graceful total coloring.

Proof. 

Let $\left|E\right(T\left)\right|=q$ be the number of edges of a tree T, we proceed with the proof by induction on the number of edges of tree T. When $q=1$, T has one edge $e=uv$, there is a quasi-odd graceful total coloring $f^{\prime }$ defined as: $f^{\prime }\left(uv\right)=1$, $f^{\prime }\left(u\right)=2$ and $f^{\prime }\left(v\right)=3$. Suppose that this lemma is true for the tree with $q-1$ edges, then, when $\left|E\right(T\left)\right|=q$, we suppose that the vertex u is a leaf of tree T and its neighbor is vertex v. Because the tree $T-u$ admits a quasi-odd-graceful total coloring $f^{\prime }$ so that the edge color set of tree $T-u$ is $f^{\prime }\left(E(T-u)\right)={[1,2(q-1)-1]}^o$, based on this fact, we define a coloring f of tree T as follows: $f\left(w\right)=f^{\prime }\left(w\right)$ for $w\in V\left(T\right)\cup E\left(T\right)\setminus \{u,uv\}$, $f\left(u\right)=f^{\prime }\left(v\right)+2q-1$ and $f\left(uv\right)=2q-1$, obviously, $f\left(u\right)-f\left(v\right)=f\left(uv\right)$. Therefore, the edge color set of tree T is just ${[1,2q-1]}^o$, which means that f is a quasi-odd-graceful total coloring of tree T. The lemma follows induction. □

2.1. Results Based on the Vertex-Overlapping Operation

Given a graphic base $\mathrm{G}={\left(G_i\right)}_1^n$ with disjoint graphs $G_1,G_2,\cdots ,G_n$, and a connected graph H with n vertices, we overlap a vertex u of graph H with a vertex $v_i$ of graph $G_i$ into a new vertex for $i\in [1,n]$, the resulting connected graph is called a, H-graph, denoted as $H{\odot }_{i=1}^n{G}_i$.

Theorem 1.

Each $G_i$ of a graphic base $\mathrm{G}={\left(G_i\right)}_1^n$ and another connected bipartite graph H with n vertices admits a set-ordered odd-graceful total coloring for $i\in [1,n]$, then the H-graph is a connected bipartite graph and admits a set-ordered odd-graceful total coloring.

Proof. 

The numbers of vertices and edges of the connected bipartite graph $G_i$ in the graphic base $\mathrm{G}$ are $p_i$ and $q_i$. Suppose that $(X_i,Y_i)$ is the bipartition of vertex set of $G_i$, where $X_i=\{x_{i,1},x_{i,2},\cdots ,x_{i,a_i}\}$, $Y_i=\{y_{i,1},y_{i,2},\cdots ,y_{i,b_i}\}$ and $a_i+b_i=\left|V\left(G_i\right)\right|=p_i$. According to the assumption in the theorem, each connected bipartite graph $G_i$ admits a set-ordered odd-graceful total coloring $f_i$, so $max{f}_i\left(X_i\right)<min{f}_i\left(Y_i\right)$ holds true, without a loss of generality, we have $f_i\left(x_{i,k}\right)\le f_i\left(x_{i,k+1}\right)$ for $k\in [1,a_i-1]$, $f_i\left(x_{i,a_i}\right)<f_i\left(y_{i,1}\right)$ and $f_i\left(y_{i,l}\right)\le f_i\left(y_{i,l+1}\right)$ for $l\in [1,b_i-1]$.

Let $w_1,w_2,\cdots ,w_n$ be the vertices of the connected bipartite graph H, $\left|V\right(H\left)\right|=p\left(H\right)$ and $\left|E\right(H\left)\right|=q\left(H\right)$, the vertex bipartition of the graph H is denoted as $(X,Y)$, where $X=\{w_1,w_2,\cdots ,w_s\}$ and $Y=\{w_{s+1},w_{s+2},\cdots ,w_n\}$. Because H admits a set-ordered odd-graceful total coloring $\alpha$, we can get $max\alpha \left(X\right)<min\alpha \left(Y\right)$, $\alpha \left(w_n\right)-\alpha \left(w_1\right)=2q\left(H\right)-1$ and $\alpha \left(w_{s+1}\right)-\alpha \left(w_s\right)=1$.

We overlap a vertex of graph H with a vertex of each graph $G_i$ into a new vertex to obtain a connected H-graph, and let $A\left(n\right)={\sum }_{k=1}^n{q}_k$, $A^{*}(m,n)={\sum }_{k=m}^n{q}_k$ for $m\le n$, $B\left(k\right)={\sum }_{j=1}^k{q}_{s+j}$. We first define another total coloring g of the graph H as: $g\left(w_i\right)=\alpha \left(w_i\right)$ for $i\in [1,s]$, $g\left(w_j\right)=\alpha \left(w_j\right)+2A\left(n\right)$ for $j\in [s+1,n]$, then each edge $w_i{w}_j$ is colored as

$$g\left(w_i{w}_j\right)=g\left(w_j\right)-g\left(w_i\right)=\alpha \left(w_j\right)+2A\left(n\right)-\alpha \left(w_i\right)=2A\left(n\right)+\alpha \left(w_i{w}_j\right).$$

(4)

So the edge color set of graph H is $g\left(E\left(H\right)\right)={[2A\left(n\right)+1,2A\left(n\right)+2q\left(H\right)-1]}^o$. Next, we give each graph $G_i$ of the base $\mathrm{G}$ a new total coloring.

Overlap the vertex $y_{s+1,b_{s+1}}$ of graph $G_{s+1}$ and the vertex $w_{s+1}$ of graph H into a vertex $y_{s+1,b_{s+1}}\odot w_{s+1}$, and the vertex $y_{s+1,b_{s+1}}$ is recolored as

$$\begin{array}{cc}\hfill g\left(y_{s+1,b_{s+1}}\right)& =g\left(w_{s+1}\right)=\alpha \left(w_{s+1}\right)+2A\left(n\right)\hfill \\ \hfill & =f_{s+1}\left(y_{s+1,b_{s+1}}\right)+\alpha \left(w_{s+1}\right)+2A\left(n\right)-2q_{s+1}.\hfill \end{array}$$

(5)

The other vertices of graph $G_{s+1}$ can be colored as

$$g\left(x_{s+1,k}\right)=f_{s+1}\left(x_{s+1,k}\right)+\alpha \left(w_{s+1}\right)+2A\left(n\right)-2q_{s+1},k\in [1,a_{s+1}];$$

(6)

$$g\left(y_{s+1,l}\right)=f_{s+1}\left(y_{s+1,l}\right)+\alpha \left(w_{s+1}\right)+2A\left(n\right)-2q_{s+1},l\in [1,b_{s+1}].$$

(7)

Thereby, the edge color set of graph $G_{s+1}$ is just $g\left(E\left(G_{s+1}\right)\right)={[1,2q_{s+1}-1]}^o$.

For graph $G_{s+2}$, overlapping the vertex $y_{s+2,b_{s+2}}$ of $G_{s+2}$ and the vertex $w_{s+2}$ of graph H into a vertex $y_{s+2,b_{s+2}}\odot w_{s+2}$, the new color of vertex $y_{s+2,b_{s+2}}$ is

$$\begin{array}{cc}\hfill g\left(y_{s+2,b_{s+2}}\right)& =g\left(w_{s+2}\right)=\alpha \left(w_{s+2}\right)+2A\left(n\right)\hfill \\ \hfill & =f_{s+2}\left(y_{s+2,b_{s+2}}\right)+\alpha \left(w_{s+2}\right)+2A\left(n\right)-2q_{s+2},\hfill \end{array}$$

(8)

we also have

$$g\left(x_{s+2,k}\right)=f_{s+2}\left(x_{s+2,k}\right)+\alpha \left(w_{s+2}\right)+2A\left(n\right)-2(q_{s+2}+q_{s+1}),k\in [1,a_{s+2}];$$

(9)

$$g\left(y_{s+2,l}\right)=f_{s+2}\left(y_{s+2,l}\right)+\alpha \left(w_{s+2}\right)+2A\left(n\right)-2q_{s+2},l\in [1,b_{s+2}];$$

(10)

hence, the edge $x_{s+2,k}{y}_{s+2,l}$ can be colored as

$$g\left(x_{s+2,k}{y}_{s+2,l}\right)=g\left(y_{s+2,l}\right)-g\left(x_{s+2,k}\right)=f_{s+2}\left(x_{s+2,k}{y}_{s+2,l}\right)+2q_{s+1}.$$

(11)

We get the edge color set of the graph $G_{s+2}$ as $g\left(E\left(G_{s+2}\right)\right)={[2q_{s+1}+1,2(q_{s+1}+q_{s+2})-1]}^o$. Generally, we overlap the vertex $y_{s+r,b_{s+r}}$ of graph T and the vertex $w_{s+r}$ of graph H into a vertex $y_{s+r,b_{s+r}}\odot w_{s+r}$, and recolor the vertices and edges of connected bipartite graph $G_{s+r}$ for $r\in [3,t]$, where $s+t=n$, we have

$$\begin{array}{cc}\hfill g\left(y_{s+r,b_{s+r}}\right)& =g\left(w_{s+r}\right)=\alpha \left(w_{s+r}\right)+2A\left(n\right)\hfill \\ \hfill & =f_{s+r}\left(y_{s+r,b_{s+r}}\right)+\alpha \left(w_{s+r}\right)+2A\left(n\right)-2q_{s+r};\hfill \end{array}$$

(12)

the other vertices in the graph $G_{s+r}$ can be colored as

$$g\left(x_{s+r,k}\right)=f_{s+r}\left(x_{s+r,k}\right)+\alpha \left(w_{s+r}\right)+2A\left(n\right)-2B\left(r\right),k\in [1,a_{s+r}];$$

(13)

$$g\left(y_{s+r,l}\right)=f_{s+r}\left(y_{s+r,l}\right)+\alpha \left(w_{s+r}\right)+2A\left(n\right)-2q_{s+r},l\in [1,b_{s+r}];$$

(14)

so the coloring of edge $x_{s+r,k}{y}_{s+r,l}$ is

$$g\left(x_{s+r,k}{y}_{s+r,l}\right)=g\left(y_{s+r,l}\right)-g\left(x_{s+r,k}\right)=f_{s+r}\left(x_{s+r,k}{y}_{s+r,l}\right)+2B(r-1).$$

(15)

Thereby, we get the set $G_{s+r}$ as $g\left(E\left(G_{s+r}\right)\right)={\left[2B(r-1)+1,2B\left(r\right)-1\right]}^o$ for $r\in [3,t]$. Based on the above coloring process, we also get an edge color set $g\left({\bigcup }_{r=1}^{t}E\left(G_{s+r}\right)\right)={[1,2{\sum }_{r=1}^t{q}_{s+r}-1]}^o$, the maximum value of colors used is

$$\begin{array}{c}\hfill max\left\{g\left(v\right):v\in \bigcup _{r=1}^{t}V\left(G_{s+r}\right)\right\}=\alpha \left(w_{s+t}\right)+2A\left(n\right)=2A\left(n\right)+2q\left(H\right).\end{array}$$

(16)

The above part has given the new total colorings of graphs $G_{s+1}$, $G_{s+2}$, ⋯, $G_n$. Further, we recolor the graphs $G_1,G_2,\cdots ,G_s$ in the following. For each graph $G_i$ with $i\in [1,s]$, we perform the vertex-overlapping operation on the vertex $x_{i,1}$ of $G_i$ and the vertex $w_i$ of H, then we determine a new total coloring of $G_i$, $i=1,2,\cdots ,s$.

Recolor vertex $x_{s,1}$ as

$$g\left(x_{s,1}\right)=g\left(w_s\right)=\alpha \left(w_s\right)=f_s\left(x_{s,1}\right)+\alpha \left(w_s\right)-1,$$

(17)

and other vertices of graph $G_s$ as

$$g\left(x_{s,k}\right)=f_s\left(x_{s,k}\right)+\alpha \left(w_s\right)-1,k\in [1,a_s],$$

(18)

$$g\left(y_{s,l}\right)=f_s\left(y_{s,1}\right)+2[A(s-1)+A^{*}(s+1,n)]+\alpha \left(w_s\right)-1,l\in [1,b_s].$$

(19)

Each edge $x_{s,k}{y}_{s,l}$ of the graph $G_s$ is recolored as

$$g\left(x_{s,k}{y}_{s,l}\right)=g\left(y_{s,l}\right)-g\left(x_{s,k}\right)=f_s\left(x_{s,k}{y}_{s,l}\right)+2[A(s-1)+A^{*}(s+1,n)].$$

(20)

Therefore, the edge color set is

$$g\left(E\left(G_s\right)\right)={\left[2A(s-1)+2A^{*}(s+1,n)+1,2A(s-1)+2A^{*}(s+1,n)+2q_s-1\right]}^o.$$

We recolor the vertex $x_{s-1,1}$ as

$$g\left(x_{s-1,1}\right)=g\left(w_{s-1}\right)=h\left(w_{s-1}\right)=f_{s-1}\left(x_{s-1,1}\right)+\alpha \left(w_{s-1}\right)-1,$$

(21)

and recolor other vertices in the graph $G_{s-1}$ as

$$g\left(x_{s-1,k}\right)=f_{s-1}\left(x_{s-1,k}\right)+\alpha \left(w_{s-1}\right)-1,k\in [1,a_{s-1}];$$

(22)

$$g\left(y_{s-1,l}\right)=f_{s-1}\left(y_{s-1,l}\right)+2[A\left(n\right)-q_{s-1}-q_s]+\alpha \left(w_{s-1}\right)-1,l\in [1,b_{s-1}].$$

(23)

$$g\left(x_{s-1,k}{y}_{s-1,l}\right)=f_{s-1}\left(x_{s-1,k}{y}_{s-1,l}\right)-2(q_{s-1}+q_s)+2A\left(n\right).$$

(24)

Obviously, we get the edge color set $g\left(E\left(G_{s-1}\right)\right)={[2A\left(n\right)-2q_{s-1}-2q_s+1,2A\left(n\right)-2q_s-1]}^o$. In general, for $d\in [2,s-1]$, we have

$$g\left(x_{s-d,1}\right)=g\left(w_{s-d}\right)=\alpha \left(w_{s-d}\right)=f_{s-d}\left(x_{s-d,1}\right)+\alpha \left(w_{s-d}\right)-1,$$

(25)

$$g\left(x_{s-d,k}\right)=f_{s-d}\left(x_{s-d,k}\right)+\alpha \left(w_{s-d}\right)-1,k\in [1,a_{s-d}];$$

(26)

$$g\left(y_{s-d,l}\right)=f_{s-d}\left(y_{s-d,l}\right)+2[A\left(n\right)-A^{*}(s-d,s)]+\alpha \left(w_{s-d}\right)-1,l\in [1,b_{s-d}].$$

(27)

We color each edge $x_{s-d,k}{y}_{s-d,l}$ of graph $G_{s-d}$ as

$$\begin{array}{cc}\hfill g\left(x_{s-d,k}{y}_{s-d,l}\right)& =g\left(y_{s-d,l}\right)-g\left(x_{s-d,k}\right)\hfill \\ \hfill & =f_{s-d}\left(x_{s-d,k}{y}_{s-d,l}\right)+2\left[A\left(n\right)-A^{*}(s-d,s)\right].\hfill \end{array}$$

(28)

thus, we get the edge color set of the graph $G_{s-d}$,

$g\left(E\left(G_{s-d}\right)\right)={\left[2A\left(n\right)-2A^{*}(s-d,s)+1,2A\left(n\right)-2A^{*}(s-d,s)+2q_{s-d}-1\right]}^o$.

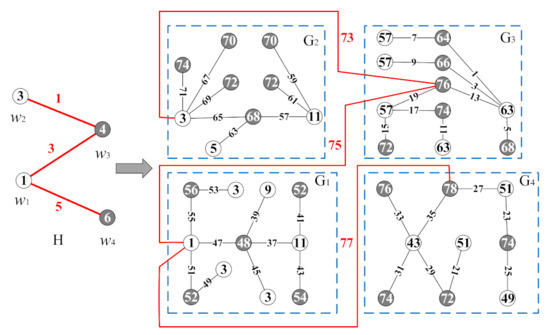
By recoloring the graph H and the graphs $G_i$ in the graphic base $\mathrm{G}$, we obtain the vertex color set of H-graph $H{\odot }_{i=1}^n{G}_i$ to be $g\left(V\left(H{\odot }_{i=1}^n{G}_i\right)\right)\subseteq [1,2A\left(n\right)+2q\left(H\right)]$, the edge color set of the H-graph to be $g\left(E\left(H{\odot }_{i=1}^n{G}_i\right)\right))={[1,2A\left(n\right)+2q\left(H\right)-1]}^o$. Thereby, we claim that g is a set-ordered odd-graceful total coloring of graph $H{\odot }_{i=1}^n{G}_i$. An example of the proof process of Theorem 1 is shown in Figure 2.

Figure 2. An example for illustrating the proof of Theorem 2.

□

2.2. Results Based on the Edge-Joining Operation

We divide the graphs obtained by edge operation into two categories according to the number of newly added edges between the graphs $G_i$ and $G_j$ in the graphic base $\mathrm{G}$, where $i,j\in [1,n]$ and $i\ne j$.

2.2.1. Single-Series Graphs

A single-series graph is obtained by connecting a vertex of the graph $G_i$ and a vertex of the graph $G_{i+1}$ with a new edge for $i\in [1,n-1]$, abbreviated as $E_s{\oplus }_{i=1}^n{G}_i$, $E_s$ contains all of the newly added edges.

Theorem 2.

Each $G_i$ in a graphic base $\mathrm{G}$ is a connected bipartite graph and admits a set-ordered odd-graceful total coloring; then a single-series graph admits a set-ordered odd-graceful total coloring.

Proof. 

Suppose that $(X_i,Y_i)$ is the bipartition of vertex set of connected bipartite graph $G_i$ in the graphic base $\mathrm{G}$, where $X_i=\{x_{i,1},x_{i,2},\cdots ,x_{i,s_i}\}$, $Y_i=\{y_{i,1},y_{i,2},\cdots ,y_{i,t_i}\}$ and $s_i+t_i=\left|V\left(G_i\right)\right|=p_i$, $|E\left(G_i\right)|=q_i$. Since graph $G_i$ admits a set-ordered odd-graceful total coloring $f_i$, the colors of all of the vertices can be arranged as $f_i\left(x_{i,1}\right)\le f_i\left(x_{i,2}\right)\le \cdots \le f_i\left(x_{i,s_i}\right)<f_i\left(y_{i,1}\right)\le f_i\left(y_{i,2}\right)\le \cdots \le f_i\left(y_{i,t_i}\right)$. The edge color set of graph $G_i$ under coloring $f_i$ is

$$\begin{array}{cc}\hfill f_i\left(E\left(G_i\right)\right)& =\{f_i\left(x_{i,k}{y}_{i,l}\right)=|f_i\left(y_{i,l}\right)-f_i\left(x_{i,k}\right)|:x_{i,k}{y}_{i,l}\in E\left(G_i\right)\}\hfill \\ \hfill & ={[1,2q_i-1]}^o,i\in [1,n].\hfill \end{array}$$

(29)

Let $F\left(r\right)={\sum }_{j=1}^r{f}_j\left(x_{j,s_j}\right)$ and $M\left(r\right)={\sum }_{j=1}^r{q}_{n-j+1}$, we define another total coloring g of graph $G_i$ as follows: $g\left(x_{1,k}\right)=f_1\left(x_{1,k}\right)$ for $x_{1,k}\in X_1$, $g\left(x_{2,k}\right)=f_2\left(x_{2,k}\right)+f_1\left(x_{1,s_1}\right)+1$ for $x_{2,k}\in X_2$. Generally, when $3\le i\le n$, we have $g\left(x_{i,k}\right)=f_i\left(x_{i,k}\right)+F(i-1)+i-1$ for $x_{i,k}\in X_i$.

Recolor vertex $y_{n,l}$ in the graph $G_n$ as

$$g\left(y_{n,l}\right)=f_n\left(y_{n,l}\right)+F(n-1)+n-1,$$

(30)

then the color of edge $x_{n,k}{y}_{n,l}\in E\left(G_n\right)$ is

$$\begin{array}{cc}\hfill g\left(x_{n,k}{y}_{n,l}\right)& =g\left(y_{n,l}\right)-g\left(x_{n,k}\right)\hfill \\ \hfill & =f_n\left(y_{n,l}\right)+F(n-1)+n-1-f_n\left(x_{n,k}\right)-F(n-1)-n+1\hfill \\ \hfill & =f_n\left(x_{n,k}{y}_{n,l}\right),\hfill \end{array}$$

(31)

the edge color set of graph $G_n$ is $g\left(G_n\right)={[1,2q_n-1]}^o$. Then, we recolor vertex $y_{n-1,l}\in Y_{n-1}$ in the graph $G_{n-1}$ as

$$g\left(y_{n-1,l}\right)=f_{n-1}\left(y_{n-1,l}\right)+F(n-2)+n+2q_n,$$

(32)

then the coloring of edge $x_{n-1,k}{y}_{n-1,l}$ in the graph $G_{n-1}$ can be expressed as

$$\begin{array}{cc}\hfill g\left(x_{n-1,k}{y}_{n-1,l}\right)=& g\left(y_{n-1,l}\right)-g\left(x_{n-1,k}\right)\hfill \\ \hfill =& f_{n-1}\left(y_{n-1,l}\right)+F(n-2)+n+2q_n-\left[f_{n-1}\left(x_{n-1,k}\right)+F(n-2)+n-2\right]\hfill \\ \hfill =& f_{n-1}\left(x_{n-1,k}{y}_{n-1,l}\right)+2q_n+2,\hfill \end{array}$$

(33)

hence the edge color set of graph $G_{n-1}$ is $g\left(E\left(G_{n-1}\right)\right)={[2q_n+3,2(q_n+q_{n-1})+1]}^o$.

When $2\le m\le n-1$, we recolor the vertex $y_{n-m,l}\in Y_{n-m}$ as

$$g\left(y_{n-m,l}\right)=f_{n-m}\left(y_{n-m,l}\right)+F(n-m-1)+2M\left(m\right)+n+m-1,$$

(34)

and color the edge $x_{n-m,k}{y}_{n-m,l}$ by

$$\begin{array}{cc}\hfill g\left(x_{n-m,k}{y}_{n-m,l}\right)=& g\left(y_{n-m,l}\right)-g\left(x_{n-m,k}\right)\hfill \\ \hfill =& f_{n-m}\left(y_{n-m,l}\right)+F(n-m-1)+2M\left(m\right)+n+m-1\hfill \\ \hfill & -[f_{n-m}\left(x_{n-m,k}\right)+F(n-m-1)+n-m-1]\hfill \\ \hfill =& 2M\left(m\right)+2m+f_{n-m}\left(x_{n-m,k}{y}_{n-m,l}\right).\hfill \end{array}$$

(35)

We can calculate that the edge color set of each graph $G_{n-m}$ for $m\in [2,n-1]$ as

$$g\left(E\left(G_{n-m}\right)\right)={[2M\left(m\right)+2m+1,2M(m+1)+2m-1]}^o.$$

Combining the following two equations

$$g\left(x_{n-m,1}\right)=f_{n-m}\left(x_{n-m,1}\right)+F(n-m-1)+n-m-1,$$

(36)

$$g\left(y_{n-m-1,1}\right)=f_{n-m-1}\left(y_{n-m-1,1}\right)+F(n-m-2)+n+2M(m+1)+m,$$

(37)

we can get $f_{n-m-1}\left(y_{n-m-1,1}\right)-f_{n-m}\left(x_{n-m,1}\right)=f_{n-m-1}\left(x_{n-m-1,s_{n-m-1}}\right)$, and the condition $f_{n-m}\left(x_{n-m,1}\right)=1$, then we have

$$\begin{array}{cc}\hfill g\left(x_{n-m,1}{y}_{n-m-1,1}\right)=& g\left(y_{n-m-1,1}\right)-g\left(x_{n-m,1}\right)\hfill \\ \hfill =& f_{n-m-1}\left(y_{n-m-1,1}\right)+F(n-m-2)+n+2M(m+1)\hfill \\ \hfill & +m-[f_{n-m}\left(x_{n-m,1}\right)+F(n-m-1)+n-m-1]\hfill \\ \hfill =& 2M(m+1)+f_{n-m-1}\left(y_{n-m-1,1}\right)-f_{n-m}\left(x_{n-m,1}\right)\hfill \\ \hfill & -f_{n-m-1}\left(x_{n-m-1,s_{n-m-1}}\right)+2m+1\hfill \\ \hfill =& 2M(m+1)+2m+1.\hfill \end{array}$$

(38)

For $d\in [0,n-2]$, we connect two vertices $x_{n-d,1}$ and $y_{n-d-1,1}$ with a new edge $x_{n-d,1}{y}_{n-d-1,1}$ to obtain a connected single-series graph $E_s{\oplus }_{i=1}^n{G}_i$, the set $E_s$ means $E_s=\{x_{n-d,1}{y}_{n-d-1,1}:d\in [0,n-2]\}$. We can obtain the following color set under total coloring g,

$$g\left(E_s\right)=\{2[M\left(1\right)+1]-1,2[M\left(2\right)+2]-1,2[M\left(3\right)+3]-1,\cdots ,2[M(n-1)+n-1]-1\}.$$

By the above deduction, the color set of the single-series graph $E_s{\oplus }_{i=1}^n{G}_i$ is

$$g\left(E\left(E_s{\oplus }_{i=1}^n{G}_i\right)\right)=g\left(E_s\right)\cup \left(\bigcup _{i=1}^{n}g\left(E\left(G_i\right)\right)\right)={\left[1,2A\left(n\right)+2n-3\right]}^o,$$

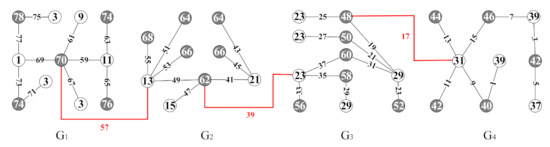
where $A\left(n\right)={\sum }_{j=1}^n{q}_j$. We let $X=X_1\cup X_2\cup \cdots \cup X_n$ and $Y=Y_1\cup Y_2\cup \cdots \cup Y_n$, then $(X,Y)$ is the vertex set bipartition of $E_s{\oplus }_{i=1}^n{G}_i$, in conclusion, g is a set-ordered odd-graceful total coloring of the single-series graph $E_s{\oplus }_{i=1}^n{G}_i$. An example of the proof process of Theorem 2 is shown in Figure 3.

Figure 3. A single-series graph, made by the four graphs shown in Figure 1, admits a set-ordered odd-graceful total coloring.

□

2.2.2. Multiple-Series Graphs

There is only one edge between two adjacent graphs $G_{i-1}$ and $G_i$ in the single-series graph for $i\in [2,n]$. However, when the number of new edges between two graphs $G_i$ and $G_j$$(i\ne j)$ is not equal to 1, but $t\ge 1$ new edges, the resulting graph $E_c{\oplus }_{i=1}^n{G}_i$ is called a multiple-series graph, $E_c$ represents the edge set of between $G_i$ and $G_j$ in graphic base $\mathrm{G}$.

Theorem 3.

Each $G_i$ in a graphic base $\mathit{G}$ admits a set-ordered odd-graceful total coloring, then the multiple-series graph admits a set-ordered odd-graceful total coloring.

Proof. 

According to the assumptions in the theorem, the connected bipartite graph $G_i$ admits a set-ordered odd-graceful total coloring $f_i$, we suppose that $(X_i,Y_i)$ is the bipartition of the vertex set of the connected bipartite graph $G_i$, where $X_i=\{x_{i,1},x_{i,2},\cdots ,x_{i,s_i}\}$, $Y_i=\{y_{i,1},y_{i,2},\cdots ,y_{i,t_i}\}$ and $s_i+t_i=p_i$, $|E\left(G_i\right)|=q_i$. Arrange the colors of all vertices as follows

$$f_i\left(x_{i,1}\right)\le f_i\left(x_{i,2}\right)\le \cdots \le f_i\left(x_{i,s_i}\right)<f_i\left(y_{i,1}\right)\le f_i\left(y_{i,2}\right)\le \cdots \le f_i\left(y_{i,t_i}\right),$$

(39)

then the edge color set of graph $G_i$ is

$$\begin{array}{cc}\hfill f_i\left(E\left(G_i\right)\right)& =\{f_i\left(x_{i,k}{y}_{i,l}\right)=|f_i\left(y_{i,l}\right)-f_i\left(x_{i,k}\right)|:x_{i,k}{y}_{i,l}\in E\left(G_i\right)\}\hfill \\ \hfill & ={[1,2q_i-1]}^o,i\in [1,n].\hfill \end{array}$$

(40)

The multiple-series graph $E_c{\oplus }_{i=1}^n{G}_i$ is generated by iterations. First of all, we define another total coloring $g_1$ for the two graphs $G_1$ and $G_2$ in graphic base $\mathrm{G}$. Let $t_1$ represents the number of new edges added between $G_1$ and $G_2$. We have $g_1\left(x_{1,k}\right)=f_1\left(x_{1,k}\right)$ for $x_{1,k}\in X_1$, $g_1\left(x_{2,k}\right)=f_2\left(x_{2,k}\right)+f_1\left(x_{1,s_1}\right)+1$ and $g_1\left(y_{2,l}\right)=f_2\left(y_{2,l}\right)+f_1\left(x_{1,s_1}\right)+1$ for $x_{2,k}\in X_2,y_{2,l}\in Y_2$, also $g_1\left(y_{1,l}\right)=f_1\left(y_{1,l}\right)+2(q_2+t_1)$ for $y_{1,l}\in Y_1$, and $g_1\left(x_{2,k}{y}_{2,l}\right)=f_2\left(x_{2,k}{y}_{2,l}\right)$ for $x_{2,k}{y}_{2,l}\in E\left(G_2\right)$; therefore, the edge color set in the connected graph $G_2$ is $g_1\left(E\left(G_2\right)\right)={[1,2q_2-1]}^o$, the coloring of the edge $x_{1,k}{y}_{1,l}\in E\left(G_1\right)$ can be further calculated as $g_1\left(x_{1,k}{y}_{1,l}\right)=f_1\left(x_{1,k}{y}_{1,l}\right)+2(q_2+t_1)$, then $g_1\left(E\left(G_1\right)\right)={[2(q_2+t_1)+1,2(q_1+q_2+t_1)-1]}^o$, we can get $g_1\left(E\left(G_1\right)\right)\cup g_1\left(E\left(G_2\right)\right)={[1,2q_2-1]}^o\cup {[2(q_2+t_1)+1,2(q_1+q_2+t_1)-1]}^o.$ Moreover, we have

$$g_1\left(x_{1,k}{y}_{2,l}\right)=g_1\left(y_{2,l}\right)-g_1\left(x_{1,k}\right)=f_2\left(y_{2,l}\right)+f_1\left(x_{1,s_1}\right)+1-f_1\left(x_{1,k}\right),$$

(41)

and $f_2\left(y_{2,t_2}\right)=2q_2$. In addition,

$$g_1\left(y_{1,l}{x}_{2,k}\right)=g_1\left(y_{1,l}\right)-g_1\left(x_{2,k}\right)=f_1\left(y_{1,l}\right)+2(q_2+t_1)-f_2\left(x_{2,k}\right)-f_1\left(x_{1,s_1}\right)-1.$$

(42)

For $w\in [1,t_1]$, we get the following inequality from the above derivation,

$$g_1\left(x_{1,k}{y}_{2,l}\right)\ge 2q_2-1+w,$$

(43)

$$g_1\left(y_{1,l}{x}_{2,k}\right)\ge 2q_2-1+w.$$

(44)

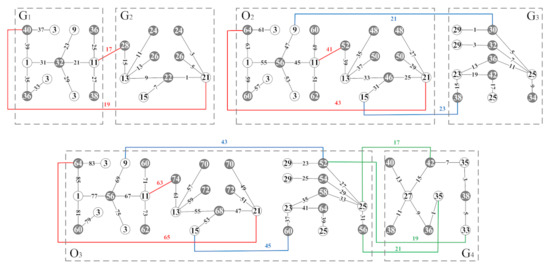
Obviously, $(X,Y)$ is the vertex bipartition of the connected graph $E_{c1}\oplus (G_1\cup G_2)$, where $X=X_1\cup X_2$ and $Y=Y_1\cup Y_2$. The edge $x_{1,k}{y}_{2,l}$ or $y_{1,l}{x}_{2,k}$ satisfies the above inequality conditions form a set $E_{c1}$, so that $|E_{c1}|=t_1$, we claim that $g_1$ is a set-ordered odd-graceful total coloring of $E_{c1}\oplus (G_1\cup G_2)$. Next, let $O_2=E_{c1}\oplus (G_1\cup G_2)$, then consider the total coloring of connected graph $O_2$ and graph $G_3$. According to the above method, the edge set $E_{c2}$ can be obtained, which is the set of all edges between $O_2$ and $G_3$; thereby, we can obtain a set-ordered odd-graceful total coloring $g_2$ of $O_3=E_{c2}\oplus (O_2\cup G_3)$, in this way, the theorem is proven. An example of the proof process of Theorem 3 is shown in Figure 4.

Figure 4. An example for illustrating the proof of Theorem 3.

□

3. Conclusions

This paper studies the existence of graphic bases with odd-graceful total colorings and shows graphic lattices by vertex-overlapping operations and edge-joining operations; further, we prove that these graphic lattices are closed to the odd-graceful total coloring. If the password generated by the graphic lattices is used to encrypt important information, then the problem of determining the graph isomorphism and some coloring conjectures will be involved in the process of decryption, so it is not easy to crack it, in addition, it has the characteristics of diverse and simple generation methods.

The theoretical research of graphic lattice and its corresponding key design has great practical significance, the topological authentication generated by combining the topological structure of graph with labeling or a coloring can be used to obtain honeywords [6], and can be used in fields, such as cryptographic design [18], topological coding [19] and network information security [20,21]. Our future work will further promote the concept of the graphic lattices, not limited to odd-graceful total coloring, but combines the topological structure of the graph with different new colorings or new labelings, and uses the graphic lattices to generate more authentication passwords.