Abstract
The integration of computational thinking (CT) in mathematics education is increasingly important due to its intersections with mathematical thinking and its role in the 21st century. Recent years have seen a growing interest in the use of innovative tools to enhance mathematics education, including the exploration of gamification techniques to improve student engagement. While previous research suggests that the inclusion of CT activities at an early age can positively impact students’ motivation and CT skills, the potential benefits of incorporating gamification techniques into CT instruction remain unexplored. In this study, we investigated the impact of shallow and deep gamification techniques on the CT skills and the intrinsic and extrinsic motivation of second-grade students in a blended teaching sequence that combined both unplugged and plugged CT activities. A quasi-experimental design was used with a control group and an experimental group. The findings suggest that both shallow and deep gamification techniques can be effective in improving CT skills in young students, but deep gamification may have a stronger impact on motivation. These results contribute to the growing body of literature on the integration of gamification techniques in CT instruction.
1. Introduction
1.1. Computational Thinking
The development of technology has brought significant changes in our daily lives, which has led to computational thinking (CT) becoming an essential skill for individuals in the 21st century [1]. This has led to increased attention to the integration of CT in education from the academic literature, which has recognized CT as a key component of digital literacy and considers it a critical skill for success in the modern workforce [2,3]. In response to this, many countries have developed policies and initiatives to promote CT education at all levels with different approaches: as a cross-curricular theme, as part of a separate subject (e.g., informatics) or within other subjects (e.g., Maths) [4].
Mathematics education has traditionally focused on developing students’ ability to perform calculations and solve problems [5]. However, the growing importance of technology in all areas of life has highlighted the need for a new set of skills in mathematics education, including CT skills [6,7,8]. CT has been defined as a set of problem-solving skills that primarily include decomposition, pattern recognition, abstraction and algorithmic thinking [9,10,11], which are essential for developing and implementing efficient and effective solutions to complex problems via thinking like a computer scientist [12], and whose solutions can be transferable to other contexts [13]. Several studies have acknowledged the potential of CT to enhance students’ mathematical thinking and improve their efficiency in learning mathematics [6,14], a relationship that seems to be reciprocal, as mathematical thinking also helps students solve problems in CT [15].
When it comes to learning CT ideas, the unplugged approach has emerged as an effective teaching strategy for cementing the understanding of CT fundamental principles [16]. This approach, which does not require the use of computing devices, has gained popularity, particularly among younger learners who may have limited experience with coding [11]. However, the potential of CT cannot be fully understood using only unplugged approaches, so they should be complemented with plugged approaches to transfer the CT principles and concepts to real situations and authentic problem solving [16]. This combined approach of unplugged and plugged activities has proven to be particularly effective with younger learners [17] and has been advocated to give students the opportunity to fully understand what computers are capable of as tools and prepare them to succeed in today’s society [16].
Technology plays a crucial role in shaping how students learn and interact with mathematical concepts too [18]. The inclusion of technology and innovative tools and approaches has great potential to enhance students’ math learning experience, including both their learning achievement as well as their motivation and attitudes [19,20,21]. Furthermore, the integration of ICT-rich learning environments in mathematics education can take many forms, ranging from the use of digital textbooks and online resources to the use of intelligent tutoring systems and gamified learning environments [22,23]. Therefore, given the rapid advancements in technology, it is imperative for educators to actively explore the potential of these tools and incorporate them into their teaching practices.
1.2. Gamification
Gamification is one of the innovative tools with potential to enhance the learning experience in different educational contexts [24]. Briefly and broadly defined, gamification is “the use of game design elements in non-game contexts” ([25], p. 10), with the purpose of engaging people, motivating action or promoting learning [26]. Although the term should not be limited to digital technology, the overwhelming majority of examples of gamification are digital [25]. Gamification techniques have been proven to have the potential to enhance a range of different educational activities, including learning [27,28,29], assessment, feedback and interaction [24,27].
Werbach and Hunter [30] proposed a classification of gamification elements, with components, mechanics and dynamics forming the building blocks of gamified systems. Components, such as achievements, badges, points and leaderboards, form the base of the system and are the tangible elements that users interact with. Mechanics, such as feedback, competition, cooperation and rewards, shape the gameplay experience and drive user engagement. Dynamics, at the top of the pyramid, define the broader context and structure of the game, encompassing aspects such as narrative, constraints and progression. Components, mechanics and dynamics work together to create an immersive and engaging experience for users in gamified systems.
The main reason for efforts to use gamification in education has been its theoretical ability to leverage motivational benefits that can enhance learning [31]. The most common theory associated with gamification’s fundamental purpose, motivation, is self-determination theory (SDT) [32]. This psychological theory developed by Deci and Ryan in the 1980s [33] provides a framework for understanding human motivation and behavior, suggesting that individuals have basic psychological needs for autonomy, competence and relatedness, which need to be satisfied for intrinsic motivation to flourish. Intrinsic motivation refers to the internal drive to engage in an activity simply for the pleasure and satisfaction derived from the activity itself. On the other hand, extrinsic motivation refers to engaging in an activity for external rewards or to avoid punishment.
In the context of gamification, “deep gamification” is designed to promote intrinsic motivation [34] through addressing users’ psychological needs for autonomy, competence and relatedness [35]. It involves incorporating game elements that are meaningful, challenging and enjoyable to the user and that provide a sense of autonomy and control over the experience [36]. Deep gamification aims to create a more memorable and engaging experience for users through leveraging game mechanics that are more immersive and motivating. Examples of deep gamification could include creating a narrative structure, offering purposeful choices or providing opportunities for exploration and discovery [37].
In contrast, “shallow gamification” is typically more extrinsic in nature, relying on incentives and rewards such as points, badges or leaderboards (PBL) to motivate users [34]. PBL, one of the most widely used implementations of gamification [27], can be seen as a “thin layer” of gamification added to the top of the system [38]. Its primary focus is often placed on achieving specific goals or objectives such as earning points or climbing the leaderboard [27]. While these extrinsic rewards can provide initial motivation, they are not as effective in promoting sustained engagement and may even lead to a decrease in intrinsic motivation over time, as users become overly focused on the rewards rather than the task itself [39]. Examples of shallow gamification include social media platforms that reward users with a system of likes or educational apps that offer badges for completing lessons. In essence, a key determinant in differentiating between deep and shallow gamification lies in the alignment of shallow gamification with extrinsic motivation, while deep gamification is associated with fostering intrinsic motivation [34].
The implementation of gamification techniques in CT contexts has been sparsely investigated in the literature, especially in primary education [32]. In [40], a web-based game was designed for learning CT with visual programming. In the game, players were asked to program virtual robots and were rewarded with “stars” depending on the tasks completed. The findings revealed that the majority of participants (20 undergraduate students studying computer science) expressed satisfaction with the game design and user interface, and that the game promoted CT learning and collaborative learning. Similarly, in another study [41], an online adaptively gamified course called Computational Thinking Quest was presented to 107 first-year undergraduate engineering and information and communication technology students. The results demonstrated that the completion of the gamified course led to improved CT assessment scores. Furthermore, a study by [42] investigated how a game-based teaching sequence based on the fundamentals of computer science could promote engagement in mathematical activities among 28 primary school children aged 10 to 12 years. The teaching sequence was structured into eight levels, with each activity being assigned points based on the execution and the ranking being determined by the team’s performance. The study found that after participating in ludic activities involving CT, the test group demonstrated a significant improvement in mathematical performance.
Despite the limited examples mentioned above, there remains a significant gap in the literature regarding the use of gamification in CT interventions in elementary education [43], which is particularly surprising given the potential benefits of enhancing motivation through gamification in STEM disciplines [31]. Therefore, the purpose of this study is to investigate the impact of gamification techniques on CT learning and motivation among second-grade primary school students. Specifically, this research will compare the effects of shallow gamification (control group) and deep gamification (experimental group) techniques applied to a CT sequence that comprises both unplugged and plugged activities. Through this investigation, the study aims to provide valuable insights into the effective utilization of gamification in CT education for young learners. The research questions that will guide this study are presented below.
RQ1. What is the impact of applying shallow and deep gamification techniques to a CT teaching sequence on the development of CT skills in second-grade primary school students?
RQ2. How does the application of shallow and deep gamification techniques to a CT teaching sequence influence the intrinsic and extrinsic motivation of second-grade primary school students?
2. Materials and Methods
2.1. Design
The study utilized a quasi-experimental design with two groups: a control group and an experimental group. Both groups received CT instruction with different gamification techniques. The control group received CT instruction with shallow gamification, while the experimental group received CT instruction with deep gamification.
The CT instruction in both groups was composed of a series of sessions that included unplugged and plugged CT activities. Specifically, each group participated in three 60 min sessions of unplugged CT activities and two 60 min sessions of plugged CT activities. The unplugged CT instruction involved hands-on and offline problem-solving tasks, while the plugged CT instruction involved visual programming tasks on an online platform using tablets.
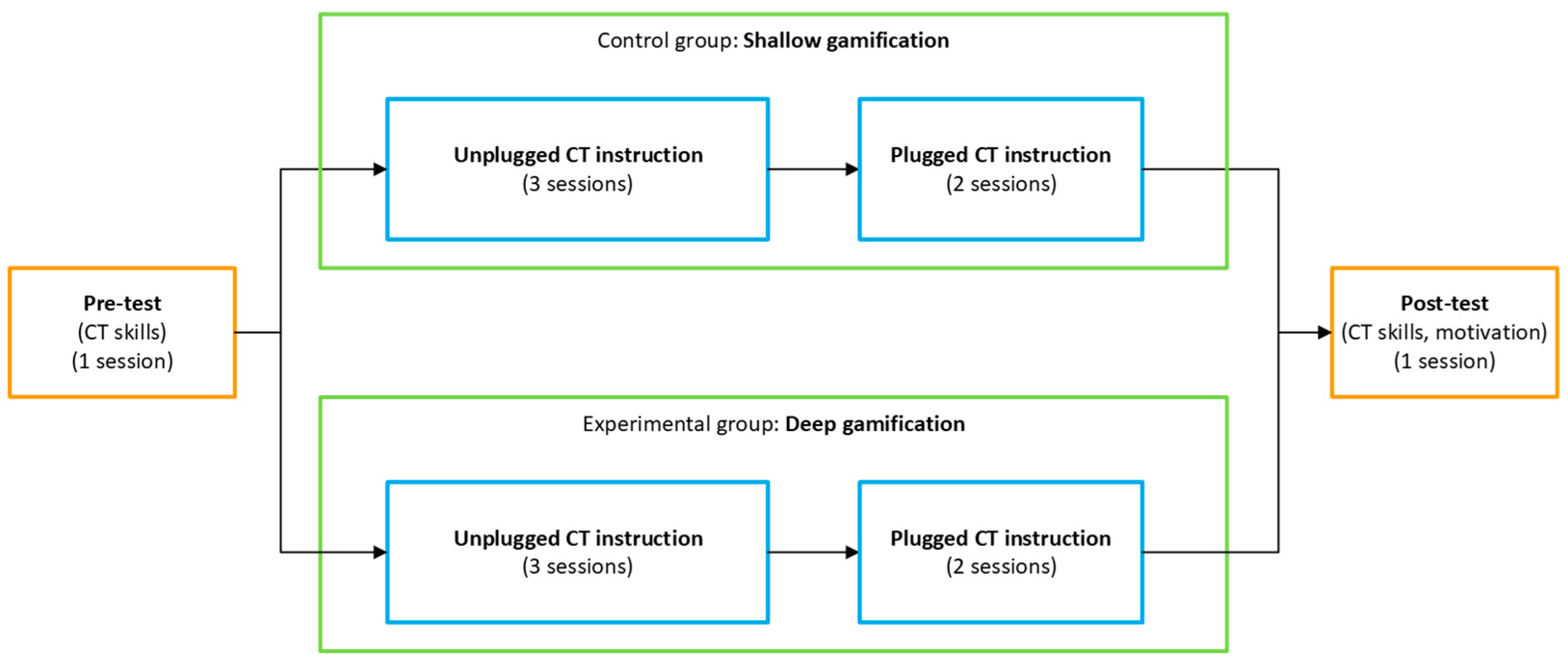
The timeline of the sessions followed a predetermined schedule (see Figure 1) that included pre- and post-assessment sessions as well as the instructional CT activity sessions, making a total of 7 sessions conducted during 7 weeks. The pre-assessment was conducted at the beginning of the intervention period to establish baseline levels of CT skills. The instructional CT activity sessions were then conducted over five sessions, following which the post-assessment was administered to measure the outcomes after the intervention in terms of CT skills and motivation.
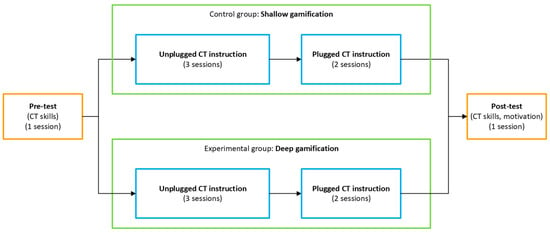
Figure 1.
Timeline of the sessions.
2.2. Context and Participants
The study was conducted in a public elementary school located in a city in the southeast region of *BLINDED FOR REVIEW PURPOSES*. Due to the restrictions and limitations imposed by the COVID-19 pandemic on student interactions, the groups were formed quasi-experimentally, naturally based on the existing composition of classrooms. Classrooms had been carefully distributed by the school’s management team to ensure comparability in terms of academic performance, gender and number of students. The selection of participants after this distribution process helped to mitigate potential sampling bias [44]. The participants belonged to four different classroom groups, with two groups randomly assigned to the control condition and two groups randomly assigned to the experimental condition.
The classrooms were equipped with modern technological tools, including tablets and interactive whiteboards, which allowed for seamless integration of the CT teaching sequence and gamification techniques. The two researchers involved in the participating classrooms had backgrounds in CT and were familiar with the use of technology in education.
A total of 82 students participated in the study, with 44 students in the control condition and 38 students in the experimental condition. The participants were in the 2nd grade, with an age range of 7 to 8 years old. The school had a diverse student population representing diverse socioeconomic backgrounds. The study was conducted in a regular classroom setting, where students received their typical curriculum-based instruction. The students’ daily routines remained largely unchanged, with the exception of the activities introduced during the intervention period. Each intervention session lasted 45 min, fitting within the school’s regular schedule and allowing the students to participate in the study without disrupting their typical educational experiences. Ethical guidelines and institutional protocols were adhered to ensure the protection of the rights and welfare of the participants.
2.3. Instruments and Assessment
This section provides a comprehensive overview of the two instruments utilized in the study, which encompassed both pre- and post-tests to measure the participants’ CT skills, as well as a post-test to assess their intrinsic and extrinsic motivation.
2.3.1. CT Skills Test
As of now, there is no unified definition of CT that has emerged; however, there is a growing consensus on the constituent CT skills, including abstraction, decomposition, algorithmic thinking and debugging, as noted in [45]. Notwithstanding, other authors also include abilities such as generalization and patterns or evaluation and logic [46]. Due to the diverse nature of CT and its applications in various contexts, there is no universal approach to assessing the concepts and practices that constitute CT [45]. In the literature, CT assessment tools can be categorized into different types, as identified in [4].
The classification of CT assessment tools proposed in [47] is based on the evaluative approach. It includes, among other categories, CT diagnostic tools, such as the Computational Thinking test (CTt), which aim to measure the level of CT and are typically applied as post-tests (i.e., after an educational intervention) to assess eventual improvements in CT ability. This classification also encompasses autonomous assessment approaches, such as the Bebras contest [48], which serves as a tool for assessing skill transfer. Bebras tasks are widely recognized for their efficacy in evaluating problem-solving and CT abilities [4] and have been used in several studies as an assessment tool for CT skills, with the objective of evaluating students’ ability to transfer their CT skills to different types of problems, contexts and situations, including real-life problems [49].
The categorization of CT assessments presented in [47] is not exhaustive but it provides a valuable map of the state of the art in this area. It is worth noting that the categories are not always independent, as a given CT tool can be used as another CT tool of a different category under certain conditions [46]. Indeed, positive correlations have been found between the CTt and Bebras tasks, indicating that higher performance in the CTt is associated with higher performance in Bebras tasks [47]. To address the lack of common ground in CT assessment approaches, a proposal is to consider knowledge transfer as an essential criterion, with a specific focus on students’ ability to apply their knowledge and thinking processes to diverse contexts [46].
Taking the above into consideration, Bebras tasks were chosen to measure participants’ CT skills in the current study. The UK Bebras Challenges are categorized by age, including Kits (ages 6–8), Castors (ages 8–10), Juniors (ages 10–12), Intermediate (ages 12–14), Seniors (ages 14–16), and Elite (ages 16–18), with tasks further classified by difficulty (A—easy, B—medium, C—difficult). Our CT skills tests, administered as both pre- and post-tests, were specifically designed for this study and incorporated carefully selected tasks that were aligned with the research questions and objectives of the study. Thus, these tests were appropriately adapted to suit the age and grade level of the participants and involved abstraction, algorithmic thinking, decomposition and evaluation skills. These four CT skills are briefly described as follows [12]:
- Abstraction: This is the process of simplifying complex problems through identifying the crucial aspects and ignoring the unimportant details. It helps students concentrate on the main elements of a problem, making it more understandable and approachable.
- Algorithmic thinking: This skill involves creating clear, step-by-step procedures or algorithms to solve problems in a systematic manner. Students learn how to break tasks into smaller steps, arrange these steps logically and carry them out in the correct order.
- Decomposition: This skill entails dividing complex problems into smaller, more manageable parts. Through breaking a problem down into its individual components, students can tackle each part separately, ultimately making the overall problem easier to solve.
- Evaluation: This skill involves examining and assessing possible solutions to determine how effective and efficient they are in addressing a given problem. Students can use this skill to identify the best solution or improve existing solutions, ultimately enhancing their problem-solving abilities.
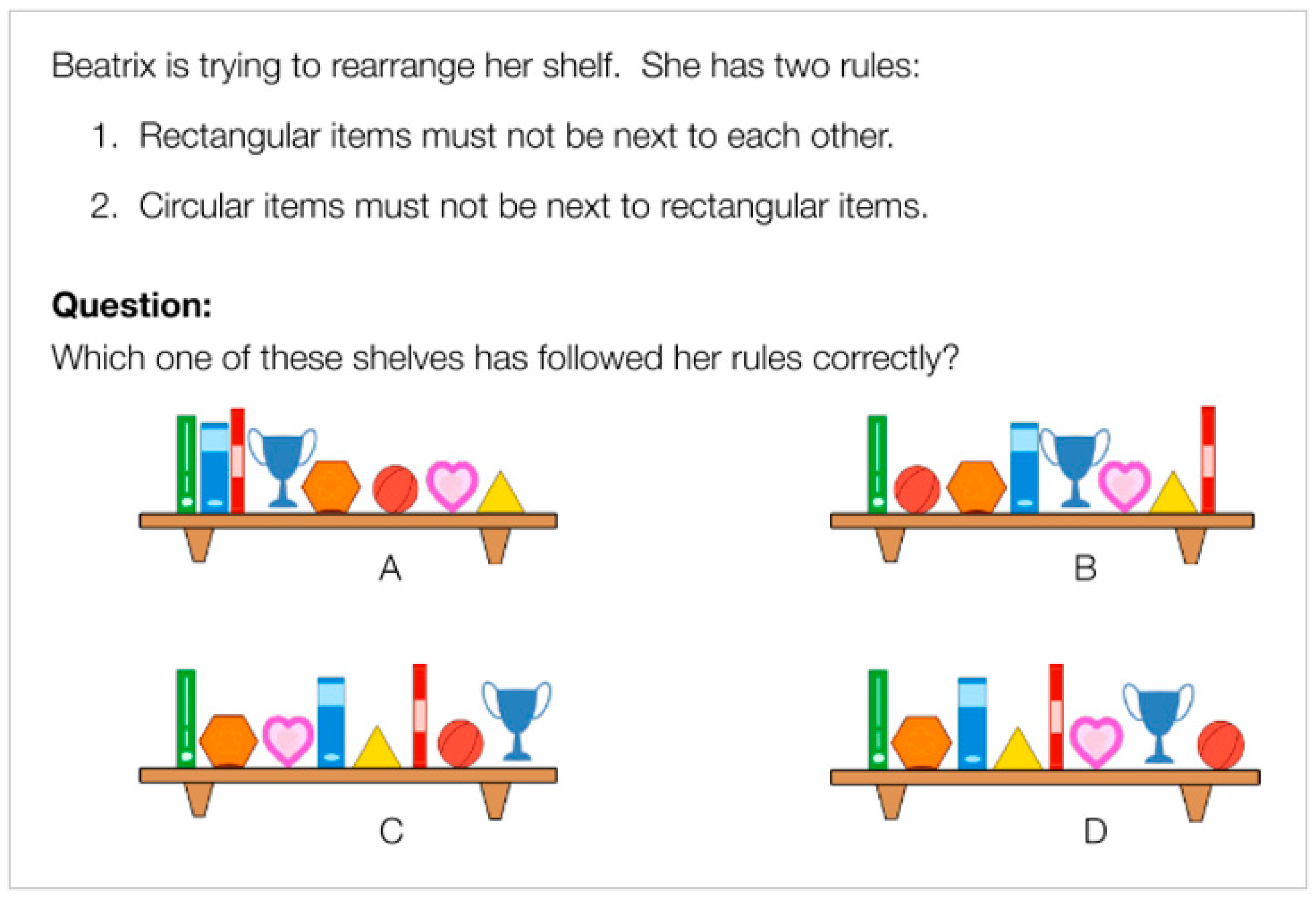
As in the case of [17], the final instrument used to respond to RQ1 of the present study consisted of 10 items sequenced by difficulty level (‘A’- and ‘B’-difficulty tasks) and chosen from the ‘Kits’ category of the 2016 and 2017 Editions of the International Bebras Contest [50,51]. Different versions with isomorphic items were created for the pre- and post-tests to measure the same skills. Each item in the test presented a problem with multiple-choice answers. Higher scores indicated higher levels of CT skills, since for each item, a score of 1 was given for correct answers and 0 for incorrect answers, based on predetermined criteria. As an example, Figure 2 shows one of the test items that measured algorithmic thinking, decomposition and evaluation skills.
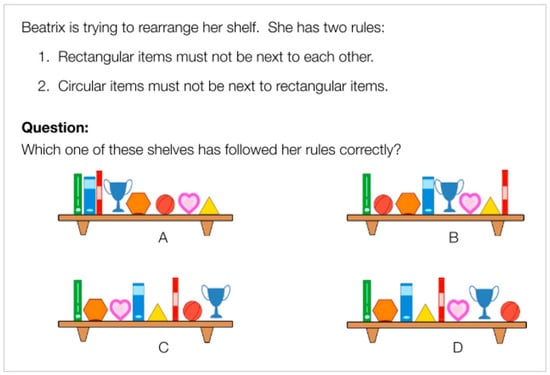
Figure 2.
Item 6 of the computational thinking (CT) skills test [50].
2.3.2. Motivation Test
The instrument used in this study to respond to RQ2 is based on the Elementary School Motivation Scale (ESMS) [52], which aims to measure children’s intrinsic and extrinsic motivation in educational settings. The ESMS comprises a total of 36 items and is adapted from two different questionnaires. Specifically, 27 items are adapted from the elementary school version of the Academic Motivation Scale [53], with three items each to assess intrinsic motivation, identified regulation and controlled regulation for each school subject (i.e., reading, writing and math). Additionally, 9 items are adapted from the Academic Self-Description Questionnaire [54] to assess academic self-concept in math, reading and writing, with three items for each subject. The scale uses a 5-point Likert-type response format, and higher scores indicate higher levels of motivation.
In the current study, the scale was adapted from the original ESMS, which measures motivation in the subjects of reading, writing and math (with 12 items each), but for this study, it was modified to align with the context of coding. Thus, the test utilized in the present study includes a total of 12 items that specifically assess motivation towards coding. Out of these 12 items, 3 items each are designed to measure 4 dimensions: intrinsic motivation, identified regulation, controlled regulation and academic self-concept related to coding. The items and dimensions of the motivation test can be consulted in Table 1.

Table 1.
Motivation test items and dimensions.
At this point, it is important to analyze the four dimensions measured with the instrument. According to [52,55,56], intrinsic motivation arises from intrinsic regulations rooted in the pleasure and interest experienced during an activity. Identified regulation represents a self-determined form of extrinsic motivation, evident when individuals personally identify with the reasons for engaging in a behavior or consider it important. Controlled regulation is a form of extrinsic motivation that encompasses external regulation, where behavior is driven by the pursuit of rewards or avoidance of punishment, as well as introjected regulation, which involves behavior carried out in response to internal pressures such as obligation or guilt. Finally, academic self-concept is a motivational construct that is positively associated with intrinsic motivation, as students who perceive themselves as competent tend to display higher levels of intrinsic motivation.
Therefore, this instrument allows for the assessment of motivation in the unique context of coding, providing insights into how intrinsic and extrinsic motivation, as well as academic self-concept, may be related to coding-related tasks and activities. Through using this adapted scale, the study aims to investigate the motivational factors that may influence coding engagement and performance among the participants in the study, shedding light on the role of motivation in visual programming education and practice.
The test was administered as a post-test after the CT skills post-test and participants were asked to rate their level of agreement with each item on a Likert scale ranging from 1 (Strongly disagree) to 5 (Strongly agree), with emoticons provided to facilitate their response.
2.4. Procedure
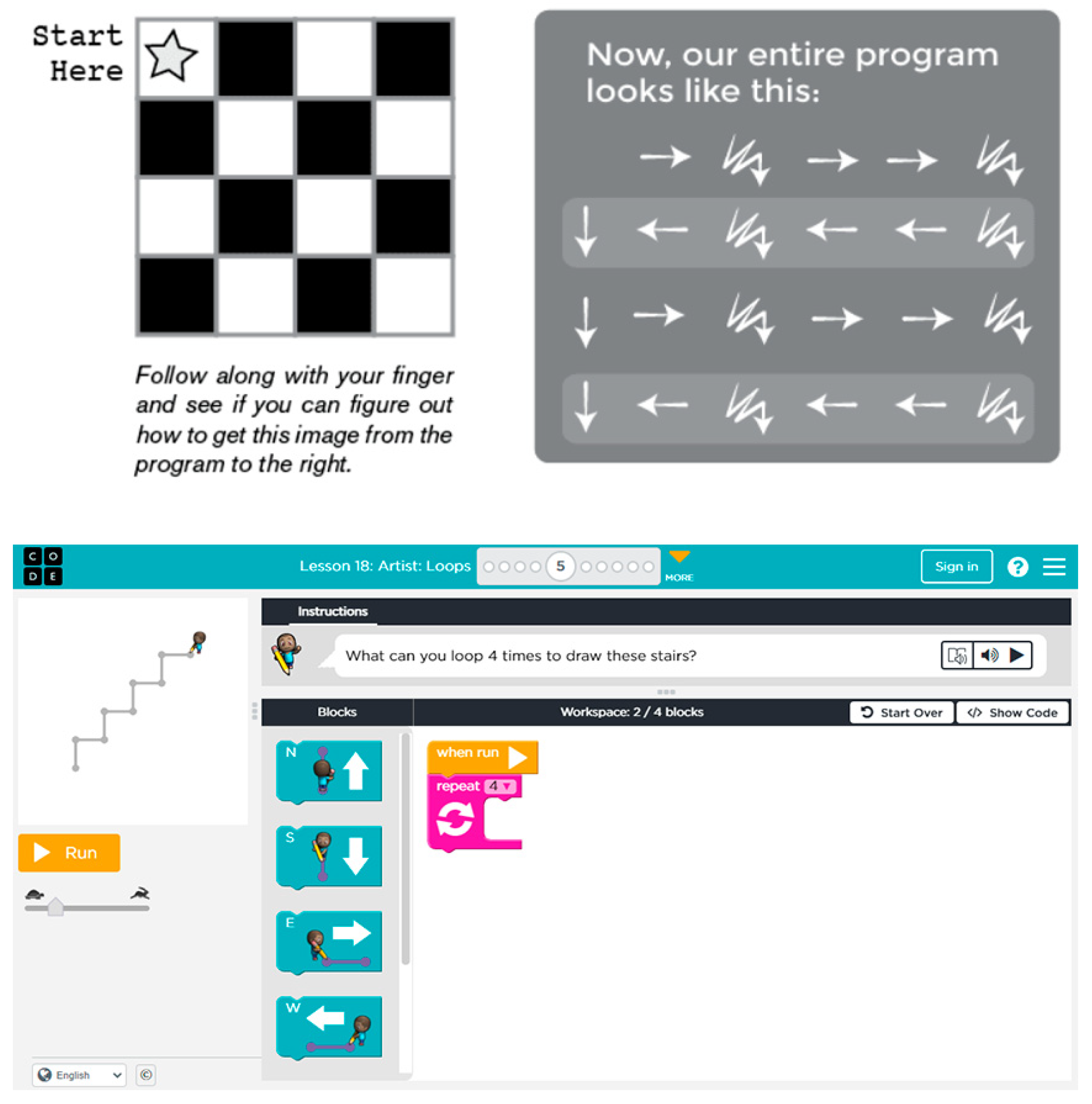
In this section, we will describe the procedure used for both the CT instruction and the gamification of the instructional sequence. For the CT instruction, the procedure was based on courses 1, 2 and B from the Code.org website [57], which are specifically designed for early readers and those with little or no prior computer science experience. The instructional design followed a blended approach, incorporating both unplugged and plugged CT sessions, with three unplugged and two plugged sessions (an example of each of them can be seen in Figure 3). This sequence of instruction has been successfully implemented in previous studies, as documented in references [17,58], and further details of the activities can be consulted therein.
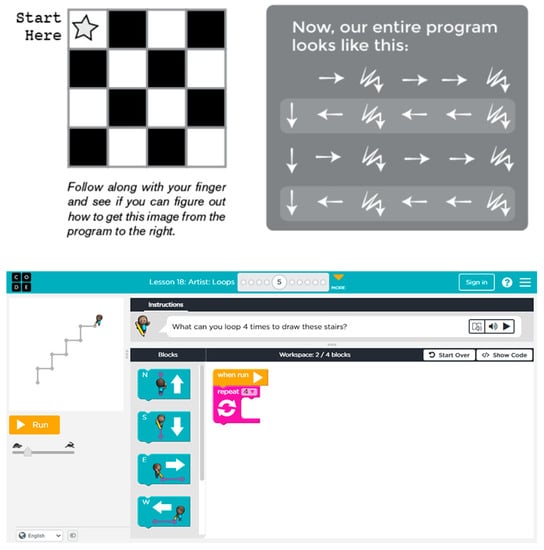
Figure 3.
Example of unplugged (top) and plugged (bottom) activities. Source: Code.org [57].
What sets this research apart from the aforementioned studies is the application of different gamification techniques to the blended CT instructional sequence. As explained in the design section, the control group received CT instruction with shallow gamification, while the experimental group received CT instruction with a deeper level of gamification. First, we will outline the common aspects for both groups, followed by an explanation of the shallow gamification techniques and, finally, the deep gamification techniques employed.
The first common point in both experimental conditions is the utilization of the @MyClassGame [59] as a platform to gamify the CT instruction sequence. @MyClassGame is a web-based, open-source platform designed to help teachers incorporate gamification strategies into their instruction. The platform offers various game mechanics and components, such as experience points, health points, badges, virtual coins and random events, which can be customized by teachers to suit their own needs. Teachers can also create a narrative and dynamics and define a “learning adventure” with missions and tasks that can be assessed using rubrics. The platform also includes configuration options for each student and team of students, allowing teachers to track progress and provide rewards. Overall, the platform is designed to motivate students and empower them to actively engage in the learning process.
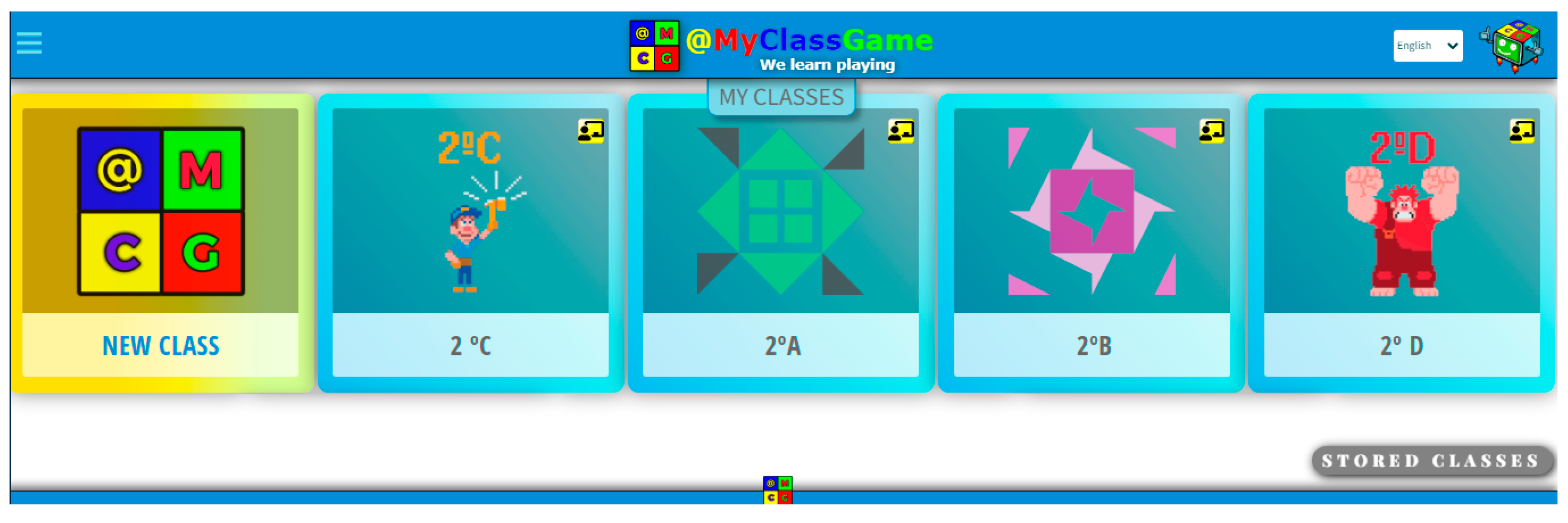
In the present study, the platform was introduced to all participants prior to the first instructional session, and the students’ progress in the platform was reviewed with them at the beginning of each of the subsequent sessions. An overview of the four class groups created within the platform can be seen in Figure 4.
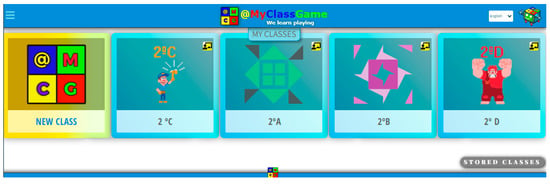
Figure 4.
Class groups created into the gamification platform @MyClassGame.
In the control group, only shallow gamification techniques were applied, primarily utilizing points, badges and leaderboards (PBL). Before the first session, avatars in the form of little monsters of different colors and shapes were randomly assigned on the platform to the students. After each session, the students’ productions from the activities were assessed and points were uploaded to each student profile in @MyClassGame when the student had successfully completed the activities. Badges with the inscription “Genius at work” were utilized as a form of recognition for good progress and behavior by each student. A physical “Genius at work” badge was assigned to each student at the beginning of each session but could be removed by the researchers if the student’s progress or behavior did not meet expectations. If the student maintained the physical badge at the end of the session, it was transferred to the virtual platform. Finally, leaderboards were automatically integrated into the platform, displaying the rankings of students based on their accumulated points, so they could see their progress compared to their peers on the leaderboard.
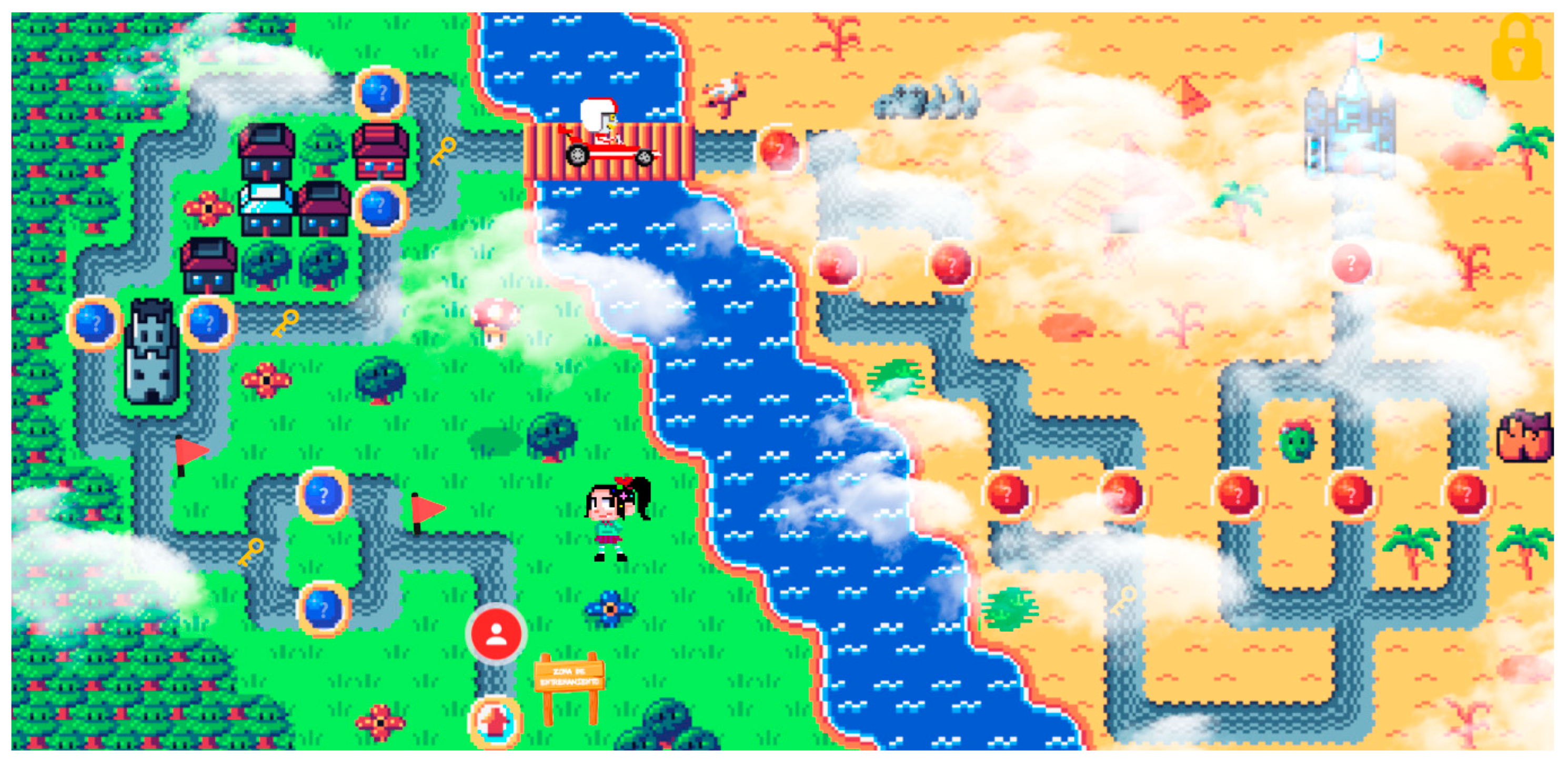
In the experimental group, PBL were also applied, but additional gamification techniques were included to deepen the level of gamification. These techniques involved incorporating game mechanics and dynamics beyond the basic level of points, badges and leaderboards. [31]. To begin with, before the first session, participants created personalized avatars from a paper template that were subsequently scanned and included in the virtual platform. Then, a narrative structure based on the Wreck-It Ralph franchise was devised, offering a coherent and continuous storyline. The narrative began from the very first moment of the initial instructional session, through a presentation video created using the web application Genially (genial.ly), which informed participants that they had to save the world of video games. This storyline allowed the participants to experience a sense of progression and development, as the unplugged activities were framed as a training zone that they had to start by going through together. Then followed the second zone, consisting of plugged activities, as the real challenge of “fixing” video games. Both zones can be distinguished in Figure 5, which shows an interactive map created with the World Map Builder web application (worldmapbuilder.com accessed on 1 April 2023) and subsequently integrated into Genially. This interactive map was managed by the researchers at the beginning and end of each session to situate the participants in the storyline and to show them their progress.
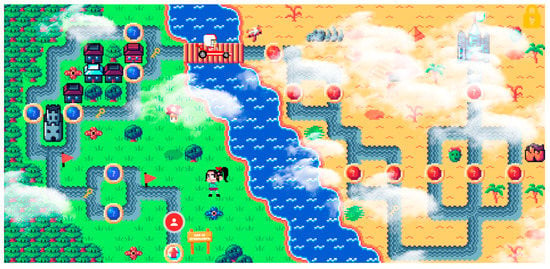
Figure 5.
World map created for the narrative using World Map Builder and Genially.
In addition, a trial narrative was proposed [60], i.e., participants were offered the opportunity to choose between equivalent activities at various points along the proposed itinerary, thus putting the power in their hands [37]. Upon successfully completing the proposed activities, participants would receive a valuable item in the form of a key at the end of each session, which would allow them to reach the common goal at the end of the adventure. These deep gamification elements were designed to enhance the engagement, motivation, and learning outcomes of the students in the experimental group. Through incorporating more complex mechanics and dynamics, the aim was to create a more immersive and meaningful gamified experience that went beyond simple point systems and leaderboards, and provided students with a deeper level of interaction, challenge and narrative context.
2.5. Data Analysis
The collected data were coded and analyzed using quantitative methods to derive meaningful insights and answer the research questions. Concerning the coding of data, each item in both the pre- and post-tests was scored 1 if correct or 0 if wrong according to the established criteria. The CT dimension and test scores were calculated as the average score of the responses, resulting in a score between 0 and 1 for each participant on each dimension and the overall test score. Similarly, regarding motivation, each student was assigned an average score in the four dimensions (motivation, identified regulation, controlled regulation and academic self-concept) and the total. Data analysis was conducted using R to process and analyze the data [61]. Missing data were handled appropriately, such as through exclusion of cases with missing values, as applicable.
Descriptive statistics, such as means and standard deviations, were calculated to summarize the data. Inferential statistics were also employed. In relation to RQ1, an analysis of covariance was conducted on the post-test scores, using the pre-test scores as a covariate. In pre–post designs, a covariance design is typically the most suitable for controlling the impact of pre-test results. Concerning RQ2, the Mann–Whitney U test was utilized as a non-parametric alternative to the independent-samples t-test. This was done to address non-normality in the data and to ensure valid inferences about group differences. The significance level (α = 0.05) was used to determine statistical significance, and the effect size measures were calculated to assess the practical significance of the findings.
3. Results
The analysis of the data collected for this study focused on examining the levels of CT skills (measured using Bebras tasks) and intrinsic and extrinsic motivation (measured using the ESMS) in both experimental conditions.
3.1. CT Skills
Table 2 presents the results broken down by group and overall CT skills level. Furthermore, we will evaluate whether the instruction was effective, for which we have included a pre–post comparison in the last column.

Table 2.
CT tests average results and average difference.
The results of the analysis of covariance reveal that there are no statistically significant differences between groups in the final level of CT after adjusting the starting level (F(1, 79) = 2.1, p = 0.15, = 0.03). That said, it should be noted that the effect size is not negligible and can be seen as small–medium-sized in favor of the control group. Regarding whether the instruction was effective, the descriptive statistics of the pre–post comparison suggest an improvement in both groups, which is also statistically significant (deep gamification, t(37) = 4.10, p < 0.0001; shallow gamification, t(43) = 9.23, p < 0.0001), although the effect size is higher in the shallow gamification group (r = 1.39) than in the deep gamification group (r = 0.67).
Secondly, Table 3 presents the results broken down by group and by each of the four CT dimensions (abstraction, algorithmic thinking, decomposition and evaluation). Both tables show the average score of the tests, and the standard deviation of each measure is also included in parentheses.

Table 3.
CT tests’ average results by dimension.
Concerning the abstraction dimension, the comparison of post-test scores after adjusting pre-test scores revealed statistically significant differences in favor of shallow gamification (F(1, 79) = 6.33, p = 0.0138, = 0.07). The effect size could be classified as medium-sized. The comparison between pre-test and post-scores in each condition showed a significant improvement for the shallow gamification group, but not for the deep gamification group (deep gamification, t(37) = 1.99, p = 0.0543; shallow gamification, t(43) = 7.64, p < 0.0001). In the same vein, in the shallow gamification group, the effect size is large (r = 1.15), while in the deep gamification group, it is small (r = 0.32).
For the case of the algorithmic thinking dimension, there are no differences between groups when comparing adjusted post-test scores (F(1, 79) = 2.73, p = 0.1023, = 0.03), although the effect size is not negligible (moderate–medium), again in favor of shallow gamification. The pre–post comparison points to an improvement in both groups, suggesting that the instruction was effective (deep gamification, t(37) = 4.02, p = 0.0003; shallow gamification, t(43) = 9.68, p < 0.0001). In the shallow gamification group, the effect size is large (r = 1.46), while in the deep gamification group, it is small (r = 0.65).
In the case of the decomposition dimension, there are no differences between groups, since the results are very similar between the two with a negligible effect size (F(1, 79) = 0.10, p = 0.7572, = 0.001). The pre–post comparison points to a significant improvement in both groups (deep gamification, t(37) = 2.34, p = 0.0246; shallow gamification, t(43) = 3.91, p = 0.0003), indicating that the instruction was effective in this dimension. The effect size in the shallow gamification group (r = 0.59) is slightly larger than in the deep gamification group (r = 0.38).
Finally, in the case of the evaluation dimension, there are no statistically significant differences between groups, but the effect size is medium in favor of shallow gamification (F(1, 79) = 3.81, p = 0.0545, = 0.05). Again, the pre–post comparison points to an improvement in both groups for this dimension (deep gamification, t(37) = 3.63, p = 0.0008; shallow gamification, t(43) = 9.18, p < 0.0001). However, the effect size is much higher in the shallow gamification group (r = 1.38) compared to the deep gamification group (r = 0.59).
3.2. Motivation
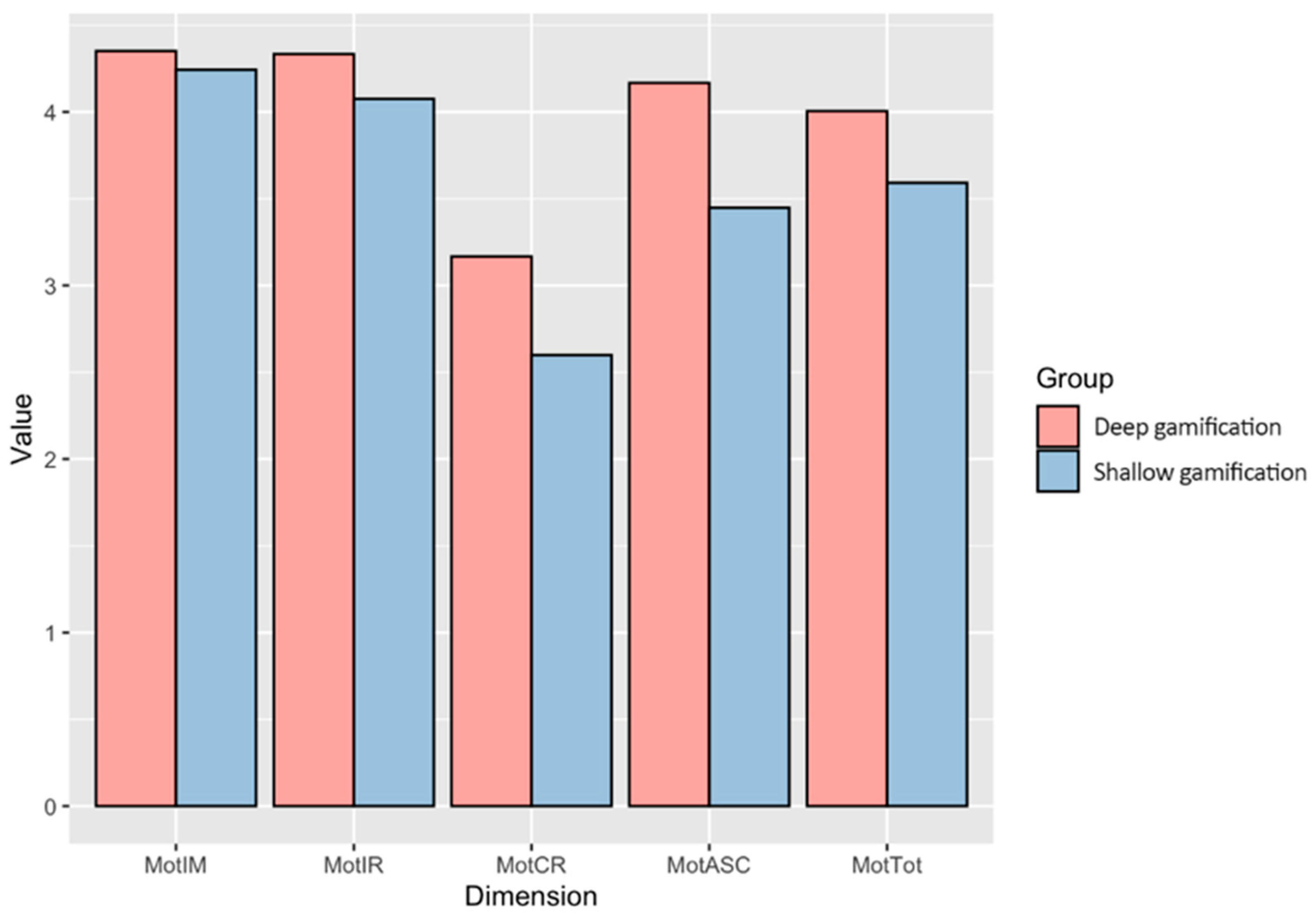
Firstly, Table 4 shows the results by group, broken down by dimensions (intrinsic motivation, identified regulation, controlled regulation, academic self-concept) and totals. The standard deviation of each measure is also included within parentheses. Figure 6 shows the differences between groups graphically.

Table 4.
Motivation tests average results by dimension.
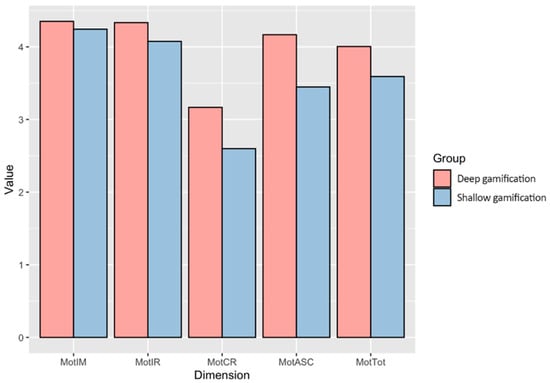
Figure 6.
Differences between groups in terms of motivation.
For the study of differences between groups, Table 4 also shows a comparison of means. Statistically significant differences appear in favor of the deep gamification group in the academic self-concept dimension (U = 1202, p = 0.0005, r = 0.38) and in the overall score (U = 1144, p = 0.0041, r = 0.32). In the case of controlled regulation (U = 1044, p = 0.0520, r = 0.22), identified regulation (U = 967, p = 0.21, r = 0.14) and intrinsic motivation, (U = 869, p = 0.7540, r = 0.04) no statistically significant differences were observed. However, with the exception of the intrinsic motivation dimension, the effect sizes are not negligible and point to higher motivational results in the deep gamification group.
4. Discussion and Conclusions
Regarding RQ1, “What is the impact of applying shallow and deep gamification techniques to a CT teaching sequence on the development of CT skills in second-grade primary school students?”, the analysis of the CT skills test results showed an overall improvement in the level of both groups in the overall scores, with no significant differences between the groups. This is consistent with the results of previous work where the same CT instruction was implemented [17]. However, differences in favor of shallow gamification were observed in some dimensions.
In future research, incorporating a third group without any gamification could provide valuable insights into the effectiveness of gamification techniques compared to traditional CT instruction. The inclusion of such a group would allow for a more comprehensive understanding of the impact of gamification on CT skills development, as it would enable researchers to differentiate between the effects attributable to gamification and those attributable to the CT teaching sequence itself. Furthermore, this additional comparison could potentially identify any unintended consequences or benefits of using gamification in CT education, leading to more informed pedagogical decisions and better instructional design.
Regarding RQ2, “How does the application of shallow and deep gamification techniques to a CT teaching sequence influence the intrinsic and extrinsic motivation of 2nd grade primary school students?”, the analysis of motivation results showed overall high levels, also similar to the findings of [17], although in the present study, a different instrument was used to measure motivation. In the present study, despite the short intervention time (five instructional sessions), higher motivation scores were observed for the deep gamification group both in the overall analysis and in the analysis of each of the dimensions, especially in the academic self-concept dimension.
One possible explanation for the lower results in CT skills for the deep gamification group is that they had to spend more time during the sessions on the processes involving deep gamification, taking time away from CT activities. In addition to the possible time constraint issue, it is worth considering that the level of complexity and engagement involved in deep gamification may have impacted the development of CT skills differently than shallow gamification. The creation of avatars, revision of storylines, and other elements of deep gamification may have required more cognitive load and attention, potentially diverting students’ focus from the CT skills being taught. On the other hand, the higher motivation levels observed in the deep gamification group could indicate that the engaging and immersive nature of deep gamification has a positive impact on students’ motivation, which may have contributed to their higher motivation scores. This leads us to hypothesize that, considering that intrinsic motivation is longer lasting [34], the application of deep gamification may require more time to have an effect on CT skill levels. Therefore, it would be interesting to conduct future research examining the long-term effects of the application of deep gamification techniques in CT sequences, as this could make it possible to leverage the time invested. The time investment required for deep gamification may need to be carefully considered in future implementations to ensure that it does not detract from the development of CT skills. Further research is warranted to explore the long-term effects of applying deep gamification techniques in CT teaching sequences and to investigate the underlying mechanisms through which gamification impacts motivation and CT skill development in young students.
Author Contributions
Conceptualization, J.d.O.-M., A.B.-B., J.A.G.-C. and R.C.-G.; methodology, J.d.O.-M., A.B.-B., J.A.G.-C. and R.C.-G.; software, J.d.O.-M., A.B.-B., J.A.G.-C. and R.C.-G.; validation, J.d.O.-M., A.B.-B., J.A.G.-C. and R.C.-G.; formal analysis, J.d.O.-M. and J.A.G.-C.; investigation, J.d.O.-M. and A.B.-B.; resources, J.d.O.-M., A.B.-B., J.A.G.-C. and R.C.-G.; data curation, J.d.O.-M., A.B.-B., J.A.G.-C. and R.C.-G.; writing—original draft preparation, J.d.O.-M., A.B.-B., J.A.G.-C. and R.C.-G.; writing—review and editing, J.d.O.-M., A.B.-B., J.A.G.-C. and R.C.-G.; visualization, J.d.O.-M., A.B.-B., J.A.G.-C. and R.C.-G.; supervision, J.d.O.-M.; project administration, J.A.G.-C. and R.C.-G.; funding acquisition, J.d.O.-M., J.A.G.-C. and R.C.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported by project 2022-GRIN-34039, funded by the University of Castilla-La Mancha and the European Regional Development Funds; project TED2021-131557B-I00, funded by MCIN/AEI/10.13039/501100011033 and European Union NextGenerationEU/PRTR; and grant FPU19/03857, funded by the Spanish Ministry of Universities.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and ethical review and approval were waived as the project involved a collaborative effort among researchers, teachers, students and school management.
Informed Consent Statement
Informed consent was obtained from all individuals who participated in the study.
Data Availability Statement
Data available upon reasonable request.
Acknowledgments
We would like to thank all of the teachers and students who participated in this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Barr, D.; Harrison, J.; Conery, L. Computational thinking: A digital age skill for everyone. Learn. Lead. Technol. 2011, 38, 20–23. [Google Scholar]
- Angeli, C.; Giannakos, M. Computational thinking education: Issues and challenges. Comput. Hum. Behav. 2020, 105, 106185. [Google Scholar] [CrossRef]
- Barr, V.; Stephenson, C. Bringing computational thinking to K-12. ACM Inroads 2011, 2, 48–54. [Google Scholar] [CrossRef]
- Bocconi, S.; Chioccariello, A.; Kampylis, P.; Dagiené, V.; Wastiau, P.; Engelhardt, K.; Earp, J.; Horvath, M.A.; Jasutė, E.; Malagoli, C.; et al. Reviewing Computational Thinking in Compulsory Education; Inamorato Dos Santos, A., Cachia, R., Giannoutsou, N., Punie, Y., Eds.; Publications Office of the European Union: Luxembourg, 2022. [Google Scholar]
- Gravemeijer, K.; Stephan, M.; Julie, C.; Lin, F.-L.; Ohtani, M. What Mathematics Education May Prepare Students for the Society of the Future? Int. J. Sci. Math. Educ. 2017, 15, 105–123. [Google Scholar] [CrossRef]
- Barcelos, T.S.; Munoz, R.; Villarroel, R.; Merino, E.; Silveira, I.F. Mathematics Learning through Computational Thinking Activities: A Systematic Literature Review. J. Univers. Comput. Sci. 2018, 24, 815–845. [Google Scholar]
- Weintrop, D.; Beheshti, E.; Horn, M.; Orton, K.; Jona, K.; Trouille, L.; Wilensky, U. Defining Computational Thinking for Mathematics and Science Classrooms. J. Sci. Educ. Technol. 2016, 25, 127–147. [Google Scholar] [CrossRef]
- Diago, P.D.; del Olmo-Muñoz, J.; González-Calero, J.A.; Arnau, D. Entornos tecnológicos para el desarrollo del pensamiento computacional y de la competencia en resolución de problemas. In Aportaciones al Desarrollo del Currículo Desde la Investigación en Educación Matemática; Blanco Nieto, L.J., Climent Rodríguez, N., González Astudillo, M.T., Moreno Verdejo, A., Sánchez-Matamoros García, G., de Castro Hernández, C., Gestal, C.J., Eds.; Editorial Universidad de Granada: Granada, Spain, 2022; pp. 399–424. Available online: https://editorial.ugr.es/libro/aportaciones-al-desarrollo-del-curriculo-desde-la-investigacion-en-educacion-matematica_139289/ (accessed on 1 April 2023).
- Brennan, K.; Resnick, M. New frameworks for studying and assessing the development of computational thinking. In Proceedings of the Annual American Educational Research Association Meeting, Vancouver, BC, Canada, 13–17 April 2012; pp. 1–25. [Google Scholar]
- Zhang, L.; Nouri, J. A systematic review of learning computational thinking through Scratch in K-9. Comput. Educ. 2019, 141, 103607. [Google Scholar] [CrossRef]
- Yadav, A.; Zhou, N.; Mayfield, C.; Hambrusch, S.; Korb, J.T. Introducing computational thinking in education courses. In Proceedings of the 42nd ACM Technical Symposium on Computer Science Education, Dallas, TX, USA, 9–12 March 2011; Yadav, A., Berthelsen, U.D., Eds.; ACM: New York, NY, USA, 2011; pp. 465–470. [Google Scholar] [CrossRef]
- Grover, S.; Pea, R. Computational Thinking: A Competency Whose Time Has Come. In Computer Science Education; Bloomsbury Academic: London, UK, 2018; Available online: http://www.bloomsburycollections.com/book/computer-science-education-perspectives-on-teaching-and-learning-in-school/ch3-computational-thinking-a-competency-whose-time-has-come (accessed on 1 April 2023).
- Shute, V.J.; Sun, C.; Asbell-Clarke, J. Demystifying computational thinking. Educ. Res. Rev. 2017, 22, 142–158. [Google Scholar] [CrossRef]
- Nordby, S.K.; Bjerke, A.H.; Mifsud, L. Computational Thinking in the Primary Mathematics Classroom: A Systematic Review. Digit. Exp. Math. Educ. 2022, 8, 27–49. [Google Scholar] [CrossRef]
- Wu, W.-R.; Yang, K.-L. The relationships between computational and mathematical thinking: A review study on tasks. Cogent Educ. 2022, 9, 2098929. [Google Scholar] [CrossRef]
- Caeli, E.N.; Yadav, A. Unplugged Approaches to Computational Thinking: A Historical Perspective. TechTrends 2020, 64, 29–36. [Google Scholar] [CrossRef]
- Del Olmo-Muñoz, J.; Cózar-Gutiérrez, R.; González-Calero, J.A. Computational thinking through unplugged activities in early years of Primary Education. Comput. Educ. 2020, 150, 103832. Available online: https://linkinghub.elsevier.com/retrieve/pii/S0360131520300348 (accessed on 1 April 2023). [CrossRef]
- National Council of Teachers of Mathematics (NCTM). Principles and Standards for School Mathematics; National Council of Teachers of Mathematics: Reston, VA, USA, 2000. [Google Scholar]
- Higgins, K.; Huscroft-D’Angelo, J.; Crawford, L. Effects of Technology in Mathematics on Achievement, Motivation, and Attitude: A Meta-Analysis. J. Educ. Comput. Res. 2019, 57, 283–319. [Google Scholar] [CrossRef]
- Verbruggen, S.; Depaepe, F.; Torbeyns, J. Effectiveness of educational technology in early mathematics education: A systematic literature review. Int. J. Child-Comput. Interact. 2021, 27, 100220. [Google Scholar] [CrossRef]
- Savelsbergh, E.R.; Prins, G.T.; Rietbergen, C.; Fechner, S.; Vaessen, B.E.; Draijer, J.M.; Bakker, A. Effects of innovative science and mathematics teaching on student attitudes and achievement: A meta-analytic study. Educ. Res. Rev. 2016, 19, 158–172. [Google Scholar] [CrossRef]
- Del Olmo-Muñoz, J.; González-Calero, J.A.; Diago, P.D.; Arnau, D.; Arevalillo-Herráez, M. Intelligent tutoring systems for word problem solving in COVID-19 days: Could they have been (part of) the solution? ZDM Math. Educ. 2023, 55, 35–48. [Google Scholar] [CrossRef]
- Hillmayr, D.; Ziernwald, L.; Reinhold, F.; Hofer, S.I.; Reiss, K.M. The potential of digital tools to enhance mathematics and science learning in secondary schools: A context-specific meta-analysis. Comput. Educ. 2020, 153, 103897. [Google Scholar] [CrossRef]
- Sailer, M.; Homner, L. The Gamification of Learning: A Meta-analysis. Educ. Psychol. Rev. 2020, 32, 77–112. [Google Scholar] [CrossRef]
- Deterding, S.; Dixon, D.; Khaled, R.; Nacke, L. From Game Design Elements to Gamefulness: Defining “Gamification”. In Proceedings of the 15th International Academic MindTrek Conference: Envisioning Future Media Environments, Tampere, Finland, 28–30 September 2011; ACM: New York, NY, USA, 2011; pp. 9–15. [Google Scholar] [CrossRef]
- Kapp, K.M. The Gamification of Learning and Instruction: Game-Based Methods and Strategies for Training and Education; Pfeiffer: San Francisco, CA, USA, 2011. [Google Scholar]
- Zainuddin, Z.; Chu, S.K.W.; Shujahat, M.; Perera, C.J. The impact of gamification on learning and instruction: A systematic review of empirical evidence. Educ. Res. Rev. 2020, 30, 100326. [Google Scholar] [CrossRef]
- Bai, S.; Hew, K.F.; Huang, B. Does gamification improve student learning outcome? Evidence from a meta-analysis and synthesis of qualitative data in educational contexts. Educ. Res. Rev. 2020, 30, 100322. [Google Scholar] [CrossRef]
- Huang, R.; Ritzhaupt, A.D.; Sommer, M.; Zhu, J.; Stephen, A.; Valle, N.; Hampton, J.; Li, J. The impact of gamification in educational settings on student learning outcomes: A meta-analysis. Educ. Technol. Res. Dev. 2020, 68, 1875–1901. [Google Scholar] [CrossRef]
- Werbach, K.; Hunter, D. The Gamification Toolkit: Dynamics, Mechanics, and Components for the Win; Wharton School Press: Philadelphia, PA, USA, 2015. [Google Scholar]
- Dichev, C.; Dicheva, D. Gamifying education: What is known, what is believed and what remains uncertain: A critical review. Int. J. Educ. Technol. High. Educ. 2017, 14, 9. [Google Scholar] [CrossRef]
- Kalogiannakis, M.; Papadakis, S.; Zourmpakis, A.-I. Gamification in Science Education. A Systematic Review of the Literature. Educ. Sci. 2021, 11, 22. [Google Scholar] [CrossRef]
- Deci, E.L.; Ryan, R.M. Conceptualizations of Intrinsic Motivation and Self-Determination. In Intrinsic Motivation and Self-Determination in Human Behavior; Springer: Boston, MA, USA, 1985; pp. 11–40. Available online: https://link.springer.com/chapter/10.1007/978-1-4899-2271-7_2 (accessed on 1 April 2023).
- Mozelius, P. Deep and Shallow Gamification in Higher Education, what is the difference? In Proceedings of the 15th International Technology, Education and Development Conference, Online, 8–9 March 2021; Gómez Chova, L., López Martínez, A., Candel Torres, I., Eds.; IATED Academy: Valencia, Spain, 2021; pp. 3150–3156. [Google Scholar]
- Niemiec, C.P.; Ryan, R.M. Autonomy, competence, and relatedness in the classroom. Theory Res. Educ. 2009, 7, 133–144. [Google Scholar] [CrossRef]
- Mekler, E.D.; Brühlmann, F.; Tuch, A.N.; Opwis, K. Towards understanding the effects of individual gamification elements on intrinsic motivation and performance. Comput. Hum. Behav. 2017, 71, 525–534. [Google Scholar] [CrossRef]
- Nicholson, S. A RECIPE for Meaningful Gamification. In Gamification in Education and Business; Springer International Publishing: Cham, Switzerland, 2015; pp. 1–20. Available online: http://www.zamzee.com (accessed on 1 April 2023).
- Marczewski, A. Thin Layer vs. Deep Level Gamification. Gamified, U.K. 2013. Available online: https://www.gamified.uk/2013/12/23/thin-layer-vs-deep-level-gamification/ (accessed on 1 April 2023).
- Seaborn, K.; Fels, D.I. Gamification in theory and action: A survey. Int. J. Hum. Comput. Stud. 2015, 74, 14–31. [Google Scholar] [CrossRef]
- Lee, L.-K.; Cheung, T.-K.; Ho, L.-T.; Yiu, W.-H.; Wu, N.-I. Learning Computational Thinking through Gamification and Collaborative Learning. In Blended Learning: Educational Innovation for Personalized Learning; Springer: Berlin/Heidelberg, Germany, 2019; pp. 339–349. Available online: http://link.springer.com/10.1007/978-3-030-21562-0_28 (accessed on 1 April 2023).
- Ng, A.K.; Atmosukarto, I.; Cheow, W.S.; Avnit, K.; Yong, M.H. Development and Implementation of an Online Adaptive Gamification Platform for Learning Computational Thinking. In Proceedings of the 2021 IEEE Frontiers in Education Conference (FIE), Lincoln, NE, USA, 13–16 October 2021; pp. 1–6. Available online: https://ieeexplore.ieee.org/document/9637467/ (accessed on 1 April 2023).
- Pires, F.; Maquine Lima, F.M.; Melo, R.; Serique Bernardo, J.R.; de Freitas, R. Gamification and Engagement: Development of Computational Thinking and the Implications in Mathematical Learning. In Proceedings of the 2019 IEEE 19th International Conference on Advanced Learning Technologies (ICALT), Maceio, Brazil, 15–18 July 2019; pp. 362–366. Available online: https://ieeexplore.ieee.org/document/8820891/ (accessed on 1 April 2023).
- Cheng, L.; Wang, X.; Ritzhaupt, A.D. The Effects of Computational Thinking Integration in STEM on Students’ Learning Performance in K-12 Education: A Meta-analysis. J. Educ. Comput. Res. 2022, 61, 073563312211141. [Google Scholar] [CrossRef]
- Bryman, A. Social Research Methods; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Weintrop, D.; Rutstein, D.; Bienkowski, M.; McGee, S. Assessment of Computational Thinking. In Computational Thinking in Education; Yadav, A., Berthelsen, U., Eds.; Routledge: New York, NY, USA, 2021; pp. 90–111. Available online: https://www.taylorfrancis.com/books/9781003102991/chapters/10.4324/9781003102991-6 (accessed on 1 April 2023).
- Poulakis, E.; Politis, P. Computational Thinking Assessment: Literature Review. In Research on E-Learning and ICT in Education; Springer International Publishing: Cham, Switzerland, 2021; pp. 111–128. Available online: https://link.springer.com/chapter/10.1007/978-3-030-64363-8_7 (accessed on 1 April 2023).
- Román-González, M.; Moreno-León, J.; Robles, G. Combining Assessment Tools for a Comprehensive Evaluation of Computational Thinking Interventions. In Computational Thinking Education; Kong, S.-C., Abelson, H., Eds.; Springer: Singapore, 2019; pp. 79–98. [Google Scholar] [CrossRef]
- Dagienė, V.; Sentence, S.; Sentance, S.; Sentence, S. It’s Computational Thinking! Bebras Tasks in the Curriculum. In Proceedings of the International Conference on Informatics in Schools: Situation, Evolution, and Perspectives, Münster, Germany, 13–15 October 2016; Springer: Cham, Switzerland, 2016; pp. 28–39. Available online: https://link.springer.com/chapter/10.1007/978-3-319-46747-4_3 (accessed on 1 April 2023).
- Dagiene, V.; Dolgopolovas, V. Short Tasks for Scaffolding Computational Thinking by the Global Bebras Challenge. Mathematics 2022, 10, 3194. [Google Scholar] [CrossRef]
- Blokhuis, D.; Millican, P.; Roffey, C.; Schrijvers, E.; Sentance, S. UK Bebras Computational Challenge 2016 Answers. 2016. Available online: http://www.bebras.uk/uploads/2/1/8/6/21861082/uk-bebras-2016-answers.pdf (accessed on 1 April 2023).
- Blokhuis, D.; Csizmadia, A.; Millican, P.; Roffey, C.; Schrijvers, E.; Sentance, S. UK Bebras Computational Challenge 2017 Answers. 2017. Available online: http://www.bebras.uk/uploads/2/1/8/6/21861082/uk-bebras-2017-answers.pdf (accessed on 1 April 2023).
- Guay, F.; Chanal, J.; Ratelle, C.F.; Marsh, H.W.; Larose, S.; Boivin, M. Intrinsic, identified, and controlled types of motivation for school subjects in young elementary school children. Br. J. Educ. Psychol. 2010, 80, 711–735. [Google Scholar] [CrossRef]
- Vallerand, R.J.; Blais, M.R.; Brière, N.M.; Pelletier, L.G. Construction et validation de l’échelle de motivation en éducation (EME). Can. J. Behav. Sci. Rev. Can. Sci. Comport. 1989, 21, 323–349. [Google Scholar] [CrossRef]
- Marsh, H.W. The structure of academic self-concept: The Marsh/Shavelson model. J. Educ. Psychol. 1990, 82, 623–636. [Google Scholar] [CrossRef]
- van Roy, R.; Zaman, B. Why Gamification Fails in Education and How to Make It Successful: Introducing Nine Gamification Heuristics Based on Self-Determination Theory. In Serious Games and Edutainment Applications; Springer International Publishing: Cham, Switzerland, 2017; pp. 485–509. Available online: http://link.springer.com/10.1007/978-3-319-51645-5_22 (accessed on 1 April 2023).
- Deci, E.L.; Ryan, R.M. Handbook of Self-Determination Research; University Rochester Press: Rochester, NY, USA, 2004. [Google Scholar]
- Code.org. Learn Computer Science. 2023. Available online: https://code.org/ (accessed on 1 April 2023).
- Del Olmo-Muñoz, J.; Cózar-Gutiérrez, R.; González-Calero, J.A. Promoting second graders’ attitudes towards technology through computational thinking instruction. Int. J. Technol. Des. Educ. 2022, 32, 2019–2037. [Google Scholar] [CrossRef]
- Torres Mancheño, J. @MyClassGame: We Learn Playing. 2023. Available online: https://www.myclassgame.es/ (accessed on 1 April 2023).
- Van De Meer, A. Structures of Choice in Narratives in Gamification and Games. UX Collective. 2019. Available online: https://uxdesign.cc/structures-of-choice-in-narratives-in-gamification-and-games-16da920a0b9a (accessed on 1 April 2023).
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2020. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).