Nonlinear Covariance Analysis-Based Robust Rendezvous Trajectory Design by Improved Differential Evolution Method

Abstract

This paper presents a robust trajectory design method for approaching and rendezvous with a space target considering multi-source uncertainties. A nonlinear covariance analysis method based on the state transition tensor is presented to formulate the propagation of uncertainties including environment parameter uncertainty, actuator error, sensor noise, navigation error and initial state dispersion of the closed-loop GN&C system. Then, the robust trajectory design problem is defined based on the quantified effect of the uncertainties, and an improved self-adaptive differential evolution algorithm is presented to solve the robust trajectory design problem with uncertainties. Finally, four groups of numerical simulations are carried out to show that the designed robust trajectories can satisfy the final state dispersion constraint under multi-source uncertainties.

1. Introduction

Rendezvous and proximity operation (RPO) with a space target is an essential precondition for the subsequent capture and on-orbit service [1]. The performance of RPO (rendezvous time, energy consumption, etc.) relies heavily on the RPO trajectory, and as a result, trajectory design has been an appealing area for decades. Trajectory design can provide impulse maneuvers needed by chaser spacecraft to approach target spacecraft and achieve goals such as flying by, capture or docking with the target. Lu et al. presented a new methodology for a spacecraft to autonomously rendezvous with a target spacecraft in an arbitrary orbit [2]. The N-impulse rendezvous problem was formalized by Zhou et al. and an improved particle swarm optimization method was proposed to solve the problem [3]. The minimum-fuel trajectory design problem was constructed by Zhao et al. and solved by the indirect optimization method [4]. A novel hierarchical optimization algorithm was proposed in Ref. [5] to speed up the optimization process of spacecraft trajectory design. An artificial emotion memory optimization method has been proposed in Ref. [6] for the trajectory design problem to avoid the local minimum solution. The trajectory design problem was addressed for Hayabusa2 rendezvousing with Ryugu [7] by minimizing the total fuel consumption. Considering the collision problem, Liu et al. proposed a trajectory design method based on the convex optimization algorithm [8]. Taking energy as the performance index, Sandberg et al. presented an autonomous trajectory design algorithm based on Pontryagin’s method [9]. Yang and Li proposed a fuel-optimal trajectory design method based on a novel irregular gravitational Lambert solver [10]. It is noteworthy that most of the RPO trajectory design methods do not take the uncertainties into consideration, but the designed trajectory will be applied in the scenario and spacecraft with uncertainties. The performance of the trajectory may be significantly degraded when considering the multi-source uncertainties.

There are multi-source uncertainties including errors in navigation, guidance and control during the RPO mission, and the uncertainties affect the actual trajectories significantly. Extra energies are needed when tracking the designed trajectories based on the ideal orbit dynamic models. Though the trajectory can be accurately tracked by the advanced tracking control methods [11,12,13,14,15], the whole performance of the GN&C system is not optimal. To solve this issue, researchers have carried out many works on the propagation of uncertainties. A comprehensive overview of the linear and nonlinear uncertainty propagation methods and related applications was provided in Ref. [16], including the Monte Carlo simulation, local linearization, polynomial chaos expansion, state transition tensors (STT), differential algebra, etc. Jones et al. employed the polynomial chaos expansion to give a solution to an uncertain differential equation considering orbit state uncertainty propagation [17]. Valli et al. used differential algebra for the nonlinear propagation of uncertainty, which can realize high-precision estimation with low computational complexity [18]. Uncertain maneuvers of the spacecraft were estimated by Zhai et al. in Ref. [19]. Yang et al. presented a modified uncertainty propagation method on the basis of the STT method [20]. Within the uncertainty propagation methods, the STT-based method is free with random samplings of the multi-source uncertainties, and thus provides an efficient scheme for uncertainty propagation in complex nonlinear dynamic systems.

Based on the uncertainty propagation methods, the uncertainty effect has been considered in the trajectory optimization. Li et al. investigated a multi-objective rendezvous optimization problem under uncertainty and defined a novel objective function containing the final state error [21]. Luo et al. proposed a robust rendezvous trajectory design method based on a novel non-dominated sorting genetic algorithm [22]. Louembet et al. developed a robust guidance algorithm considering the navigation, guidance and control uncertainties [23]. For the entry trajectory design problem, a novel robust trajectory design method was proposed in Ref. [24] by the quantification of both the dynamics of parametric uncertainty and initial state uncertainty. The Mars entry trajectory of Tianwen-1 was designed based on the estimation of uncertain aerodynamic states [25]. The uncertainties of the RPO process have been analyzed and quantized in the open-loop system, and the effect of the uncertainties was evaluated. However, the uncertainties of the closed-loop rendezvous system are rarely analyzed.

Motivated by the foregoing discussions, this work proposes a novel robust rendezvous trajectory design method for the closed-loop RPO system based on the STT method and improved differential evolution algorithm. The contributions of this work are summarized as follows:

• Uncertainties, including environment parameter uncertainty, actuator error, sensor noise, navigation error and initial state dispersion, of the RPO GN&C closed-loop system are modeled and the propagation, update and correction equations of the uncertainties are formalized based on the STT method.
• The effect of the uncertainties is rapidly analyzed and predicted quantitatively, and a robust trajectory design problem is constructed considering the uncertainties’ effect.
• An improved differential evolution algorithm is proposed to solve the robust trajectory design problem for the space rendezvous mission.

The remainder of this paper is organized as follows. Section 2 provides the rendezvous problem models including the dynamics model, environment model, actuator model, sensor model and navigation algorithm model. In Section 3, the effect of the multi-source uncertainties is quantified based on the STT method and the robust performance of the closed-loop GN&C system is evaluated. In Section 4, the robust trajectory design problem is formulated and finally solved by an improved differential evolution algorithm. The simulation results of the robust trajectory design method compared to the traditional optimal trajectory design method and nonlinear Monte Carlo method are presented in Section 5. Conclusions are drawn in Section 6.

2. Rendezvous Dynamic Modeling under Multi-Source Uncertainties

In this section, the rendezvous dynamic models between the service spacecraft (denoted as server for brevity) and the space target are constructed. The constructed models include the orbit dynamic model, environment model, sensor model, actuator model and the navigation algorithm model.

2.1. Orbit Dynamic Model

In the reference inertial frame, the position and velocity vectors of the server are denoted as ${\mathit{r}}_c^i\in {\mathbb{R}}^3$ and ${\mathit{v}}_c^i\in {\mathbb{R}}^3$, and the position and velocity vectors of the considered space target are denoted as ${\mathit{r}}_t^i\in {\mathbb{R}}^3$ and ${\mathit{v}}_t^i\in {\mathbb{R}}^3$, wherein the superscript i indicates the inertial frame, and the subscripts c and t indicate the parameters are associated with the server and the space target, respectively. Then, the orbit dynamic models of the server and target are given as

$$\left\{\begin{array}{ccc}\hfill {\dot{\mathit{r}}}_c^i& =& {\mathit{v}}_c^i\hfill \\ \hfill {\dot{\mathit{v}}}_c^i& =& -\frac{\mu }{{∥{\mathit{r}}_c^i∥}^3}{\mathit{r}}_c^i+{\mathit{a}}_c\left({\mathit{r}}_c^i,{\mathit{v}}_c^i,{\mathit{p}}_{env}\right)+{\mathit{u}}^i\left({\mathit{p}}_{\mathrm{\Delta }v}\right)\hfill \end{array}\right.$$

(1)

$$\left\{\begin{array}{ccc}\hfill {\dot{\mathit{r}}}_t^i& =& {\mathit{v}}_t^i\hfill \\ \hfill {\dot{\mathit{v}}}_t^i& =& -\frac{\mu }{{∥{\mathit{r}}_t^i∥}^3}{\mathit{r}}_t^i+{\mathit{a}}_t\left({\mathit{r}}_t^i,{\mathit{v}}_t^i,{\mathit{p}}_{env}\right)\hfill \end{array}\right.$$

(2)

where $\mu$ is the gravitational coefficient, $\mathit{u}$ denotes the thrust acceleration, and $\mathit{a}\in {\mathbb{R}}^3$ is the acceleration due to Earth’s oblateness. ${\mathit{p}}_{env}$ and ${\mathit{p}}_{\mathrm{\Delta }v}$ are the uncertainty parameters relevant to the environment model and actuator model, respectively, and will be defined later.

2.2. Environment Model

In the rendezvous process, the uncertainty of the Earth’s oblateness is considered in the environment model and defined as ${\mathit{p}}_{env}={\left[{\mathit{\eta }}_{J_2}^T,{\mathit{b}}_{J_2}^T\right]}^T\in {\mathbb{R}}^6$, where ${\mathit{\eta }}_{J_2}\in {\mathbb{R}}^3$ and ${\mathit{b}}_{J_2}\in {\mathbb{R}}^3$ are the scale-factor uncertainty and bias uncertainty, respectively. Then, the acceleration $\mathit{a}$ caused by the Earth’s oblateness is modeled as

$$\mathit{a}=\left[{\mathit{I}}_{3\times 3}+\mathrm{diag}\left({\mathit{\eta }}_{J_2}\right)\right]\widehat{\mathit{a}}+{\mathit{b}}_{J_2}$$

(3)

where $\widehat{\mathit{a}}\in {\mathbb{R}}^3$ is the theoretical value of the acceleration caused by the Earth’s oblateness.

2.3. Actuator Model

In the rendezvous process, all maneuvers are assumed to be impulsive, and the actuator uncertainty parameters are defined as ${\mathit{p}}_{\mathrm{\Delta }v}={\left[{\mathit{\eta }}_{\mathrm{\Delta }v}^T,{\mathit{ϵ}}_{\mathrm{\Delta }v}^T,{\mathit{b}}_{\mathrm{\Delta }v}^T\right]}^T\in {\mathbb{R}}^9$, where ${\mathit{\eta }}_{\mathrm{\Delta }v}\in {\mathbb{R}}^3$, ${\mathit{ϵ}}_{\mathrm{\Delta }v}\in {\mathbb{R}}^3$ and ${\mathit{b}}_{\mathrm{\Delta }v}\in {\mathbb{R}}^3$ are the scale-factor uncertainty, misalignment uncertainty and bias uncertainty, respectively. For the j-th impulsive maneuver $\mathrm{\Delta }{\mathit{v}}_j$, the actuator model is constructed as

$$\mathrm{\Delta }{\mathit{v}}_j=\delta T\left({\mathit{ϵ}}_{\mathrm{\Delta }v}\right)\left\{\left[{\mathit{I}}_{3\times 3}+\mathrm{diag}\left({\mathit{\eta }}_{\mathrm{\Delta }v}\right)\right]\mathrm{\Delta }{\widehat{\mathit{v}}}_j+{\mathit{b}}_{\mathrm{\Delta }v}+{\mathit{w}}_{\mathrm{\Delta }v}\right\}$$

(4)

where $\mathrm{\Delta }{\widehat{\mathit{v}}}_j\in {\mathbb{R}}^3$ is the calculated control instruction given by the guidance algorithm; ${\mathit{w}}_{\mathrm{\Delta }v}\in {\mathbb{R}}^3$ is a zero mean Gaussian white noise with a constant variance and satisfies

$$E\left[{\mathit{w}}_{\mathrm{\Delta }v}\left(t_{j_1}\right){\mathit{w}}_{\mathrm{\Delta }v}^T\left(t_{j_2}\right)\right]={\mathit{Q}}_{w_j}\delta \left(t_{j_1}-t_{j_2}\right)$$

(5)

where $t_{j_1}$ and $t_{j_2}$ are the maneuver time of $j_1$-th and $j_2$-th maneuvers; ${\mathit{Q}}_{w_j}\delta \left(t_{j_1}-t_{j_2}\right)$ is the standard Kronecker delta function.

2.4. Sensor Model

During the rendezvous process, the state vectors ${\mathit{x}}_c={\left[{{\mathit{r}}_c^i}^T,{{\mathit{v}}_c^i}^T\right]}^T$ and ${\mathit{x}}_t={\left[{{\mathit{r}}_t^i}^T,{{\mathit{v}}_t^i}^T\right]}^T$ cannot be accurately obtained. Sensors such as the ranging radar and GPS sensors are requisite and the uncertainties of the sensors should be considered and modeled. The sensor uncertainty parameters are defined as ${\mathit{p}}_{sen}={\left[{\mathit{\eta }}_{sen}^T,{\mathit{ϵ}}_{sen}^T,{\mathit{b}}_{sen}^T\right]}^T\in {\mathbb{R}}^{18}$, where ${\mathit{\eta }}_{sen}\in {\mathbb{R}}^6$, ${\mathit{ϵ}}_{sen}\in {\mathbb{R}}^6$ and ${\mathit{b}}_{sen}\in {\mathbb{R}}^6$ are the scale-factor uncertainty, misalignment uncertainty and bias uncertainty, respectively. For a state vector $\mathit{x}\left(t\right)$ at time $t_k$, the measurement model of the sensors is constructed as

$${\tilde{\mathit{x}}}_k=\delta T\left({\mathit{ϵ}}_{sen}\right)\left[{\mathit{I}}_{6\times 6}+\mathrm{diag}\left({\mathit{\eta }}_{sen}\right)\right]\mathit{x}\left(t_k\right)+{\mathit{b}}_{sen}+{\mathit{w}}_{sen}$$

(6)

where ${\tilde{\mathit{x}}}_k\in {\mathbb{R}}^6$ is the discrete measurement value of $\mathit{x}\left(t\right)$ at time $t_k$, and ${\mathit{w}}_{sen}\in {\mathbb{R}}^6$ is the zero-mean measurement noise, which satisfies

$$E\left[{\mathit{w}}_{sen}\left(t_k\right){\mathit{w}}_{sen}^T\left(t_k^{\prime }\right)\right]={\mathit{Q}}_{sen}\delta \left(t_k-t_k^{\prime }\right)$$

(7)

2.5. True Dynamic Model

With the constructed models in Section 2.1, Section 2.2, Section 2.3 and Section 2.4, the uncertainty parameters ${\mathit{p}}_{env}$, ${\mathit{p}}_{\mathrm{\Delta }v}$ and ${\mathit{p}}_{sen}$ are integrated as $\mathit{p}={\left[{\mathit{p}}_{env}^T,{\mathit{p}}_{\mathrm{\Delta }v}^T,{\mathit{p}}_{sen}^T\right]}^T={\left[p_1,p_2,\cdots ,p_{n_p}\right]}^T\in {\mathbb{R}}^{n_p}$. Without loss of generality, uncertainty parameter $p_l$ ($l=1,\cdots ,n_p$) is modeled as the first-order Markov process given as

$${\dot{p}}_l=-\frac{p_l}{{\tau }_l}+{\omega }_{p_l},l=1,\cdots ,n_p$$

(8)

where ${\tau }_l$ is the known time constant and ${\omega }_{p_l}$ satisfies

$$E\left[{\omega }_{p_l}\left(t\right){\omega }_{p_l}\left(t^{\prime }\right)\right]={\sigma }_{p_l}^2\delta (t-t^{\prime })$$

(9)

To simplify the presentation, the general expression for the true dynamic model can be reorganized as

$$\dot{\mathit{x}}=\mathit{f}\left(\mathit{x},\mathit{u},t\right)$$

(10)

where $\mathit{x}:={\left[{\mathit{x}}_c^T,{\mathit{x}}_t^T,{\mathit{p}}^T\right]}^T\in {\mathbb{R}}^{n_p+12}$ is the state vector of the true dynamic model.

2.6. Navigation Algorithm Model

After acquiring the measurement values of the system states by the sensors, a navigation algorithm is always needed. Without loss of generality, the most frequently used Kalman algorithm is employed to obtain the navigation states. The navigation state $\widehat{\mathit{x}}\in {\mathbb{R}}^{\widehat{n}}$ ($\widehat{n}=n_p+12$) of the true state $\mathit{x}$ is defined as

$$\widehat{\mathit{x}}={\left[{\widehat{\mathit{x}}}_c^T,{\widehat{\mathit{x}}}_t^T,{\widehat{\mathit{p}}}^T\right]}^T$$

(11)

which consists of six chaser states, six target states, and $n_p$ parameter states $\widehat{\mathit{p}}$ and given as

$$\widehat{\mathit{p}}={\left[{\widehat{\mathit{p}}}_{env}^T,{\widehat{\mathit{p}}}_{lidar}^T,{\widehat{\mathit{p}}}_{\mathrm{\Delta }v}^T\right]}^T$$

(12)

The propagation equations of the navigation state are presented as

$$\left\{\begin{array}{ccc}\hfill {\dot{\widehat{\mathit{r}}}}_c^i& =& {\widehat{\mathit{v}}}_c^i\hfill \\ \hfill {\dot{\widehat{\mathit{v}}}}_c^i& =& -\frac{\mu }{{∥{\widehat{\mathit{r}}}_c^i∥}^3}{\widehat{\mathit{r}}}_c^i+{\mathit{a}}_c\left({\widehat{\mathit{r}}}_c^i,{\widehat{\mathit{v}}}_c^i,{\widehat{\mathit{p}}}_{env}\right)+{\mathit{u}}^i\left({\widehat{\mathit{p}}}_{\mathrm{\Delta }v}\right)\hfill \end{array}\right.$$

(13)

$$\left\{\begin{array}{ccc}\hfill {\dot{\widehat{\mathit{r}}}}_t^i& =& {\widehat{\mathit{v}}}_t^i\hfill \\ \hfill {\dot{\widehat{\mathit{v}}}}_t^i& =& -\frac{\mu }{{∥{\widehat{\mathit{r}}}_t^i∥}^3}{\widehat{\mathit{r}}}_t^i+{\mathit{a}}_t\left({\widehat{\mathit{r}}}_t^i,{\widehat{\mathit{v}}}_t^i,{\widehat{\mathit{p}}}_{env}\right)\hfill \end{array}\right.$$

(14)

$${\dot{\widehat{p}}}_l=-\frac{{\widehat{p}}_l}{{\tau }_l},l=1,2,3,\dots ,n_p$$

(15)

To simplify the presentation, propagation equations of the navigation state $\widehat{\mathit{x}}$ in Equations (13)–(15) are integrated as

$$\dot{\widehat{\mathit{x}}}=\widehat{\mathit{f}}\left(\widehat{\mathit{x}},\mathit{u},t\right)$$

(16)

Based on Equation (16), the propagation equation of the navigation state covariance can be given as

$$\dot{\widehat{\mathit{P}}}={\widehat{\mathit{F}}}_{\widehat{\mathit{x}}}\widehat{\mathit{P}}+{\widehat{\mathit{P}}}^T{\widehat{\mathit{F}}}_{\widehat{\mathit{x}}}^T+{\widehat{\mathit{S}}}_{\omega }$$

(17)

where $\widehat{\mathit{P}}$ is the navigation state of the covariance matrix, ${\widehat{\mathit{F}}}_{\widehat{\mathit{x}}}$ is the state-transition matrix of system (16), and ${\widehat{\mathit{S}}}_{\omega }$ is the uncertainty parameter vector.

After acquiring new sensor states, the navigation state and covariance matrix are updated based on

$${\widehat{\mathit{x}}}_k^{+}={\widehat{\mathit{x}}}_k^{-}+{\widehat{\mathit{K}}}_k[{\tilde{\mathit{z}}}_k-{\widehat{\tilde{\mathit{z}}}}_k]$$

(18)

$${\widehat{\mathit{P}}}_k^{+}=({\mathit{I}}_{\widehat{n}\times \widehat{n}}-{\widehat{\mathit{K}}}_k{\widehat{\mathit{H}}}_k){\widehat{\mathit{P}}}_k^{-}{({\mathit{I}}_{\widehat{n}\times \widehat{n}}-{\widehat{\mathit{K}}}_k{\widehat{\mathit{H}}}_k)}^T+{\widehat{\mathit{K}}}_k{\widehat{\mathit{R}}}_{\nu }{\widehat{\mathit{K}}}_k^T$$

(19)

wherein the symbols + and − represent the navigation state and covariance matrix after and before this update, ${\widehat{\tilde{\mathit{z}}}}_k$ is the measurement value of the sensors, ${\widehat{\mathit{H}}}_k$ is the measurement sensitivity matrix, and ${\widehat{\mathit{K}}}_k$ is the Kalman filter gain and is presented as

$${\widehat{\mathit{K}}}_k={\widehat{\mathit{P}}}_k^{-}{\widehat{\mathit{H}}}_k^T{({\widehat{\mathit{H}}}_k{\widehat{\mathit{P}}}_k^{-}{\widehat{\mathit{H}}}_k^T+{\widehat{\mathit{R}}}_{\nu })}^{-1}$$

(20)

where ${\widehat{\mathit{R}}}_{\mathit{v}}$ is the measurement noise covariance.

When the j-th maneuver occurs, the navigation state and covariance matrix will be corrected. The navigation state ${\widehat{\mathit{x}}}_j$ is corrected according to

$${\widehat{\mathit{x}}}_j^{+c}={\widehat{\mathit{x}}}_j^{-c}+\widehat{\mathit{d}}({\widehat{\mathit{x}}}_j^{-c},\mathrm{\Delta }{\widehat{\mathit{v}}}_j)$$

(21)

where the symbols $+c$ and $-c$ represent the state after and before the correction, and $\widehat{\mathit{d}}({\widehat{\mathit{x}}}_j^{-c},\mathrm{\Delta }{\widehat{\mathit{v}}}_j)$ is given as

$$\widehat{\mathit{d}}({\widehat{\mathit{x}}}_j^{-c},\mathrm{\Delta }{\widehat{\mathit{v}}}_j)=\delta \widehat{T}\left({\mathit{ϵ}}_{\mathrm{\Delta }v}\right)\left[{\mathit{I}}_{3\times 3}+\mathrm{diag}\left({\widehat{\mathit{\eta }}}_{\mathrm{\Delta }v}\right)\right]\mathrm{\Delta }{\widehat{\mathit{v}}}_j+{\widehat{\mathit{b}}}_{\mathrm{\Delta }v}$$

(22)

The covariance matrix is corrected according to

$${\widehat{\mathit{P}}}_j^{+c}=[\mathit{I}+{\widehat{\mathit{D}}}_{\widehat{x}}]{\widehat{\mathit{P}}}_j^{-c}{[\mathit{I}+{\widehat{\mathit{D}}}_{\widehat{x}}]}^T+{\widehat{\mathit{S}}}_{{\omega }_j}$$

(23)

where ${\widehat{\mathit{D}}}_{\widehat{x}}$ is the Jacobian matrix of $\widehat{\mathit{d}}({\widehat{\mathit{x}}}_j^{-c},\mathrm{\Delta }{\widehat{\mathit{v}}}_j)$ with respect to $\widehat{\mathit{x}}$.

3. Uncertainty Effect Prediction and Robustness Evaluation of GN&C System

On the basis of the rendezvous orbit dynamic models formalized in Section 2, the prediction of the uncertainties’ effect is quantified based on the STT method. Then, the robust performance of the GN&C system against the uncertainties is evaluated quantitatively.

3.1. Uncertainty Effect Prediction Based on STT Method

The models for propagating the true state $\mathit{x}$ as well as the navigation state $\widehat{\mathit{x}}$ can be reorganized based on Equations (10) and (16) as

$$\mathit{x}\left(t\right)=\mathsf{\Phi }(t;{\mathit{x}}_j^{+c},t_j)$$

(24)

$$\widehat{\mathit{x}}\left(t\right)=\widehat{\mathsf{\Phi }}(t;{\widehat{\mathit{x}}}_j^{+c},t_j)$$

(25)

where $\mathsf{\Phi }$ and $\widehat{\mathsf{\Phi }}$ are functions satisfying the conditions

$$\frac{\mathrm{d}\mathsf{\Phi }}{\mathrm{d}t}=\mathit{f}(t,\mathsf{\Phi }(t;{\mathit{x}}_j^{+c},t_j))$$

(26)

$$\frac{\mathrm{d}\widehat{\mathsf{\Phi }}}{\mathrm{d}t}=\mathit{f}(t,\widehat{\mathsf{\Phi }}(t;{\widehat{\mathit{x}}}_j^{+c},t_j))$$

(27)

In order to analyze the true state $\mathit{x}$ and navigation state $\widehat{\mathit{x}}$ simultaneously, an augmented state vector $\mathit{X}$ is defined as $\mathit{X}={\left[{\mathit{x}}^T,{\widehat{\mathit{x}}}^T\right]}^T$, and then the effect of the uncertainties is defined as

$$\delta \mathit{X}=\left[\begin{array}{c}\delta \mathit{x}\\ \delta \widehat{\mathit{x}}\end{array}\right]=\left[\begin{array}{c}\mathit{x}-\overline{\mathit{x}}\\ \widehat{\mathit{x}}-\overline{\widehat{\mathit{x}}}\end{array}\right]$$

(28)

where $\overline{\mathit{x}}=E\left(\mathit{x}\right)$, $\overline{\widehat{\mathit{x}}}=E\left(\widehat{\mathit{x}}\right)$. Apparently, $\delta \mathit{X}$ contains the dispersions of the true state and navigation state, which are caused by the uncertainties. Therefore, the property of $\delta \mathit{X}$ can be used to analyze the effect of uncertainties.

This work employs the STT method [20] to obtain an analytical and nonlinear approximation to the solution of $\delta \mathit{X}$. The states’ deviation along the reference states $\overline{\mathit{x}}$ and $\overline{\widehat{\mathit{x}}}$ are presented based on Einstein’s summation notation as

$$\delta {\mathit{x}}_j\left(t\right)=\sum _{p=1}^m\frac{1}{p!}{\mathrm{\Phi }}_{j,k_1\cdots k_p}\left(t\right)\delta {\mathit{x}}_{k_1}\left(t_j^{+c}\right)\dots \delta {\mathit{x}}_{k_p}\left(t_j^{+c}\right)$$

(29)

$$\delta {\widehat{\mathit{x}}}_j\left(t\right)=\sum _{p=1}^m\frac{1}{p!}{\widehat{\mathrm{\Phi }}}_{j,k_1\cdots k_p}\left(t\right)\delta {\widehat{\mathit{x}}}_{k_1}\left(t_j^{+c}\right)\dots \delta {\widehat{\mathit{x}}}_{k_p}\left(t_j^{+c}\right)$$

(30)

where the subscript k is the component of each tensor, m is the order of the expansion, and the $\mathrm{\Phi }$ is the STT of the order p, which can be calculated by

$${\dot{\mathrm{\Phi }}}_{j,k_1\cdots k_p}=\mathit{h}\left({\mathit{A}}_{j,k_1},\cdots ,{\mathit{A}}_{j,k_1\cdots k_p};{\mathsf{\Phi }}_{j,k_1},\cdots ,{\mathsf{\Phi }}_{j,k_1\cdots k_p}\right)$$

(31)

where

$${\mathit{A}}_{j,k_1\cdots k_p}={\left.\frac{{\partial }^p{\mathit{f}}_j}{\partial {\mathit{x}}_{k_1}\cdots {\mathit{x}}_{k_p}}\right|}_{-}$$

(32)

and − indicates that ${\mathit{A}}_{i,k_1\cdots k_p}$ is evaluated over the reference trajectory.

Then, the propagation, update and correction equations of $\delta \mathit{X}$ can be written in compact form as

$${\delta \mathit{X}}_j\left(t\right)=\sum _{p=1}^m\frac{1}{p!}{\mathsf{\Phi }}_{j,k_1\cdots k_p}^a\left(t\right)\delta {\mathit{X}}_{k_1}\left(t_j^{+c}\right)\dots \delta {\mathit{X}}_{k_p}\left(t_j^{+c}\right)$$

(33)

$${\delta \mathit{X}}_k^{+}={\mathcal{A}}_k{\delta \mathit{X}}_k^{-}+{\mathcal{B}}_k{\mathit{\upsilon }}_k$$

(34)

$${\delta \mathit{X}}_j^{+c}={\mathcal{D}}_j{\delta \mathit{X}}_j^{-c}+{\mathcal{N}}_j{\mathit{w}}_j$$

(35)

where

$${\mathsf{\Phi }}_{j,k_1\cdots k_p}^a\left(t\right)=\left[\begin{array}{cc}{\mathsf{\Phi }}_{j,k_1\cdots k_p}\left(t\right)& {\mathbf{0}}_{6\times 6}\\ {\mathbf{0}}_{6\times 6}& {\widehat{\mathsf{\Phi }}}_{j,k_1\cdots k_p}\left(t\right)\end{array}\right]$$

(36)

$${\mathcal{A}}_k=\left[\begin{array}{cc}{\mathit{I}}_{6\times 6}& {\mathbf{0}}_{6\times 6}\\ {\mathit{K}}_k{\mathit{H}}_k,& {\mathit{I}}_{6\times 6}-{\mathit{K}}_k{\mathit{H}}_k\end{array}\right],{\mathcal{B}}_k=\left[\begin{array}{c}{\mathbf{0}}_{6\times 6}\\ {\mathit{K}}_k\end{array}\right]$$

(37)

$${\mathcal{D}}_j=\left[\begin{array}{cc}\hfill {\mathit{I}}_{6\times 6},& \hfill \mathit{BM}\\ \hfill {\mathbf{0}}_{6\times 6},& \hfill {\mathit{I}}_{6\times 6}+\mathit{BM}\end{array}\right],{\mathcal{N}}_j=\left[\begin{array}{c}\mathit{B}\\ {\mathbf{0}}_{6\times 3}\end{array}\right]$$

(38)

with $\mathit{B}={\left[{\mathbf{0}}_{3\times 3},{\mathit{I}}_{3\times 3}\right]}^T$.

Define the covariance ${\mathit{C}}_A$ of $\delta \mathit{X}$ as ${\mathit{C}}_A=E\left[\delta \mathit{X}\delta {\mathit{X}}^T\right]$. As $E\left(\delta {\mathit{X}}^T\right)=\mathbf{0}$; then, the propagation, update and correction equations of ${\mathit{C}}_A$ are obtained as

$$\begin{array}{cc}\hfill {\mathit{C}}_{A_{ij}}\left(t\right)=& \sum _{p=1}^m\sum _{q=1}^m\frac{1}{p!q!}{\mathsf{\Phi }}_{i,k_1\cdots k_p}^a\left(t\right){\mathsf{\Phi }}_{j,s_1\cdots s_q}^a\left(t\right)\hfill \\ \hfill & ·E[\delta {\mathit{X}}_{k_1}\left(t_j^{+c}\right)\dots \delta {\mathit{X}}_{k_p}\left(t_j^{+c}\right)\delta {\mathit{X}}_{s_1}\left(t_j^{+c}\right)\dots \delta {\mathit{X}}_{s_q}\left(t_j^{+c}\right)]\hfill \\ \hfill & -{\mathit{m}}_i\left(t\right){\mathit{m}}_j\left(t\right)\hfill \end{array}$$

(39)

$${\mathit{C}}_A\left(t_k^{+}\right)={\mathcal{A}}_k{\mathit{C}}_A\left(t_k^{-}\right){\mathcal{A}}_k^T+{\mathcal{B}}_k{\mathit{R}}_{\upsilon }{\mathcal{B}}_k^T$$

(40)

$${\mathit{C}}_A\left(t_j^{+c}\right)={\mathcal{D}}_j{\mathit{C}}_A\left(t_j^{-c}\right){\mathcal{D}}_j^T+{\mathcal{N}}_j{\mathit{Q}}_{w_j}{\mathcal{N}}_j^T$$

(41)

where the mean ${\mathit{m}}_i\left(t\right)$ can be given as

$${\mathit{m}}_i\left(t\right)=\sum _{p=1}^m\frac{1}{p!}{\mathsf{\Phi }}_{i,k_1\cdots k_p}^a\left(t\right)E[\delta {\mathit{X}}_{k_1}\left(t_j^{+c}\right)\dots \delta {\mathit{X}}_{k_p}\left(t_j^{+c}\right)]$$

(42)

3.2. Robustness Evaluation

The robustness of the GN&C system against multi-source uncertainties can be evaluated by analyzing the covariance matrix of the final true state dispersion. The covariance matrix is obtained by the augmented state covariance matrix as

$${\mathit{D}}_{true}=E\left[\delta \mathit{x}\left(t\right)\delta {\mathit{x}}^T\left(t\right)\right]=\left[{\mathit{I}}_{6\times 6}{\mathbf{0}}_{6\times 6}\right]{\mathit{C}}_A{\left[{\mathit{I}}_{6\times 6}{\mathbf{0}}_{6\times 6}\right]}^T$$

(43)

The covariance of the final true state dispersion is caused by the multi-source uncertainties such as the actuator errors and navigation errors. The covariance matrix of the navigation state dispersion $\delta \widehat{\mathit{x}}\left(t\right)$ can also be obtained as

$${\mathit{D}}_{nav}=E\left[\delta \widehat{\mathit{x}}\left(t\right)\delta {\widehat{\mathit{x}}}^T\left(t\right)\right]=\left[{\mathbf{0}}_{6\times 6}{\mathit{I}}_{6\times 6}\right]{\mathit{C}}_A{\left[{\mathbf{0}}_{6\times 6}{\mathit{I}}_{6\times 6}\right]}^T$$

(44)

As the desired control values are calculated by the navigation states, which contain dispersions, extra control is needed to correct the errors and this can be evaluated by the control covariance matrix ${\mathit{D}}_{co{m}_j}$ as

$${\mathit{D}}_{co{m}_j}=E\left[\delta {\mathit{u}}_j\delta {\mathit{u}}_j^T\right]={\widehat{\mathit{G}}}_j{\mathit{D}}_{nav}{\widehat{\mathit{G}}}_j^T$$

(45)

4. Robust Rendezvous Trajectory Design

In order to take the uncertainties’ effect into consideration in the RPO problem, a robust rendezvous trajectory design method is presented in this section. The objective of the robust rendezvous trajectory design is to propose the optimal maneuver plan that not only considers the total maneuver consumption (quantified by the sum of all the expected maneuvers ${∥\mathrm{\Delta }\mathit{v}\left(t_j\right)∥}_2$), but also the trajectory robustness against the multi-source uncertainties (quantified by the 3-${\sigma }_{\mathrm{\Delta }v}$ dispersion and final 3-$\sigma$ position dispersion).

4.1. Problem Formulation

The robust trajectory design problem is stated as follows:

$$min\sum _{j=1}^n({∥\mathrm{\Delta }\mathit{v}\left(t_j\right)∥}_2+3{\sigma }_{\mathrm{\Delta }v\left(t_j\right)})$$

(46)

$$s.t.\dot{\mathit{x}}=\mathit{f}\left(\mathit{x},\mathrm{\Delta }\mathit{v},t\right)$$

(47)

$$\mathit{x}\left(t_0\right)={\mathit{x}}_0$$

(48)

$$\mathit{x}\left(t_f\right)={\mathit{x}}_d$$

(49)

$${\sigma }_r\left(t_f\right)\le {\sigma }_r^{req}$$

(50)

where

$${\sigma }_{\mathrm{\Delta }v\left(t_j\right)}=\sqrt{trace\left({\mathit{D}}_{co{m}_j}\right)}$$

(51)

$${\sigma }_r\left(t_f\right)=\sqrt{trace\left({\mathit{M}}_r{\mathit{D}}_{true}^{t_f}{\mathit{M}}_r\right)}$$

(52)

and ${\mathit{D}}_{true}$ and ${\mathit{D}}_{co{m}_j}$ are given in Equations (43) and (45), ${\sigma }_{v\left(t_j\right)}$ is the dispersion of the j-th maneuver, ${\sigma }_r\left(t_f\right)$ is the position dispersion at the final time, ${\mathit{M}}_r$ is the mapping matrices from the true state to the position states, and ${\sigma }_r^{req}$ is the requirement of final state dispersion.

Remark 1.

In the traditional RPO studies, the rendezvous trajectory is usually optimized without considering the effect of uncertainties. In this work, the effect of multi-source uncertainties is considered by ${\sigma }_{\mathrm{\Delta }v\left(t_j\right)}$ and ${\sigma }_{\mathrm{\Delta }v\left(t_j\right)}$, which are both calculated based on the STT method. If the trajectory optimization problem in Equations (46)–(50) is solved, then the designed trajectory not only has good performance in fuel consumption, but also has strong robustness against the multi-source uncertainties.

4.2. Improved Self-Adaptive Differential Evolution Algorithm

To solve the stochastic optimization problem, an improved self-adaptive differential evolution algorithm for robust trajectory design is presented.

In the differential evolution algorithm, the evolution scaling factor F has an important impact on the optimization searching process. F is always set as a random value between 0 and 1 in the traditional differential evolution algorithm, which leads to the same search range and low efficiency. The robust trajectory design is a complex optimization problem; a self-adaptive search range can improve the search efficiency. To make the algorithm more efficient, a self-adaptive evolution scaling factor is designed and given as

$$F_{i,j}=F_{i,j}\left(Q_{(g-1)}^{best}\right)\times F_{i,j}\left(g\right)\times rand(0,1)$$

(53)

where i, j and g represent the sequence numbers of variables, individuals and generations; $F_{i,j}\left(Q_{(g-1)}^{best}\right)$ is relevant to the best fitness function of the last generation. To ensure that the factors $F_{i,j}\left(Q_{(g-1)}^{best}\right)$ change from C (C is related with $Q_{(g-1)}^{best}$) to 0.1 with the fitness function of the last generation decrease, $F_{i,j}\left(Q_{(g-1)}^{best}\right)$ is designed as

$$F_{i,j}\left(Q_{(g-1)}^{best}\right)=lg(Q_{(g-1)}^{best}+{10}^{0.1})\to F_{i,j}\left(g\right)\in (0.1,C)$$

(54)

where $F_{i,j}\left(g\right)$ is an adaptive function related to the generations. To guarantee that the factors $F_{i,j}\left(g\right)$ vary from 1 to 0.1 with the number of generations increasing, $F_{i,j}\left(g\right)$ is designed in this work as

$$F_{i,j}(g)=(cos(\frac{g}{K}\times \pi )+\frac{11}{9})\times \frac{9}{20}\to F_{i,j}\left(g\right)\in (0.1,1)$$

(55)

The proposed self-adaptive evolution scaling factor in Equation (55) can ensure that the search range is the whole solution set at the beginning and converges to a smaller set around the best solution, which can obviously improve the search efficiency.

Moreover, the search process of the traditional differential evolution algorithm is sometimes trapped in a local optimal solution. To solve this problem, a random mutant $U_{i,n}\left(g\right)$ is introduced to enhance its ability to jump out of the local optimal solution. When the search process is trapped in a local optimal solution, the mutant will try to find an individual with better performance, and then restart a new evolution process around this mutant. The random mutant is given as  

$$U_{i,n}\left(g\right)=B_i^L+ran{d}_j(0,1)\times (B_i^U-B_i^L),g=1,\dots ,K$$

(56)

where $B_i^L$ and $B_i^U$ are lower and upper bounds of the i-th variables.

The proposed improved self-adaptive differential evolution algorithm for robust trajectory design is summarized in Algorithm 1.    

Algorithm 1: Improved self-adaptive differential evolution algorithm for robust trajectory design

Remark 2.

It can be obtained from Step 4 in Algorithm 1 that the self-adaptive differential evolution algorithm is not actually applied when the final 3-σ position dispersion constraint in Equation (50) is satisfied under the uncertainties. This means that even applying $\mathrm{\Delta }\mathit{v}\left(t_j\right)$ of the deterministic trajectory calculated without uncertainties, the final states of the system with uncertainties satisfy the final 3-σ position dispersion constraint. There is no need to start the optimization algorithm as the current maneuver plan is sufficient to meet the needs of the RPO mission.

5. Simulation Results

Numerical simulations are carried out to verify the effectiveness of the novel robust rendezvous trajectory design method based on the STT method and improved differential evolution method.

5.1. Simulation Conditions

The proposed robust rendezvous trajectory design method is verified by a concrete orbit transfer problem. The measured initial relative states are given as ${\mathit{x}}_0={\left[0\mathrm{m},-10,000\mathrm{m},200\mathrm{m},0\mathrm{m}/\mathrm{s},0\mathrm{m}/\mathrm{s},0\mathrm{m}/\mathrm{s}\right]}^T$, and the expected final relative states are set as ${\mathit{x}}_f={\left[0\mathrm{m},-200\mathrm{m},0\mathrm{m},0\mathrm{m}/\mathrm{s},0\mathrm{m}/\mathrm{s},0\mathrm{m}/\mathrm{s}\right]}^T$. Different desired transfer times are set as $t_f=$ 2000 s, 6000 s, 12,000 s and free-time to produce different simulation examples. The deterministic optimal solutions to this scenario without uncertainties for $t_f$ = 2000 s, 6000 s and 12,000 s, respectively, are optimized and listed in Table 1.

Table 1. Deterministic maneuver data.

${\mathit{t}}_{\mathit{f}}$ (s)	Total $\mathrm{\Delta }\mathit{v}$ (m/s)	Number of Maneuvers	Maneuver Times (s)	$\mathrm{\Delta }\mathit{v}$ (m/s)	Maneuver Positions $\left[\begin{array}{ccc}\mathit{x}& \mathit{y}& \mathit{z}\end{array}\right]$ (km)
2000	9.480	2	$\left[\begin{array}{c}0\\ 2000\end{array}\right]$	$\left[\begin{array}{c}4.737\\ 4.743\end{array}\right]$	[0 −10 0.2] [0 0 0]
6000	1.267	4	$\left[\begin{array}{c}0\\ 1127\\ 4735\\ 6000\end{array}\right]$	$\left[\begin{array}{c}0.414\\ 0.221\\ 0.160\\ 0.472\end{array}\right]$	[0 −10 0.2] [−0.545 −9.950 0.012] [−0.744 −0.410 0.075] [0 0 0]
12,000	0.665	4	$\left[\begin{array}{c}0\\ 1359\\ \mathrm{10,183}\\ \mathrm{12,000}\end{array}\right]$	$\left[\begin{array}{c}0.133\\ 0.202\\ 0.071\\ 0.259\end{array}\right]$	[0 −10 0.2] [−0.227 −9.918 −0.020] [−0.639 −0.815 0.073] [0 0 0]

Different uncertainties are considered in this section. In order to clearly present the uncertainties’ effect on different levels, three typical GN&C systems are defined in Table 2 and denoted as a high-cost system, nominal-cost system and low-cost system, respectively. Here, “high/nominal/low cost” means that the system is equipped with expensive/nominal/cheap sensors and actuators, so the uncertainty levels are different. Different levels of uncertainties (3-$\sigma$) are also given in Table 2, including the initial state dispersions, measurement errors, actuator execution errors and final dispersion requirements. The initial position dispersion ranges from 10 m to 1 km, and the initial velocity dispersion ranges from 0.01 m/s to 1 m/s. The measurement errors range from 0.1 m to 10 m. The actuator execution errors range from 1 mm/s to 100 mm/s. The final position dispersion requirement ranges from 3 m to 30 m.

Table 2. Different levels of uncertainties (3-$\sigma$) for high-, nominal- and low-cost systems.

Uncertainty	Value (3-$\mathit{\sigma }$)			Unit
	High Cost	Nominal Cost	Low Cost
Initial State Dispersion
Position	10	100	1000	m
Velocity	0.01	0.1	1	m/s
Measurement Error
Noise	0.1	1	10	m
Misalignment	0.1	1	10	mrad
Scale factor	100	500	1000	ppm
Bias	0.01	0.03	0.05	m
Actuator Execution Error
Noise	0.001	0.01	0.1	m/s
Misalignment	0.1	1	5	mrad
Scale factor	100	500	1000	ppm
Bias	0.1	1	5	mm/s
Final Dispersion Requirement
Position	3	15	30	m

5.2. Robust Trajectory Design Results

In the proposed self-adaptive evolution algorithm, the maximum number of iterations is set as $100\times$ number of variables, population size is 1000, and the stopping criterion is that the change in the fitness function is smaller than ${10}^{-6}$.

Figure 1 shows the optimal fitness function with respect to the number of maneuvers when $t_f$ = 2000 s. Though only two maneuvers are needed in the optimal deterministic trajectory, it can be seen from the figure that three maneuvers are needed in the robust optimal trajectory for the high-cost system and four maneuvers are needed in the robust optimal trajectories for the nominal-cost and low-cost systems.

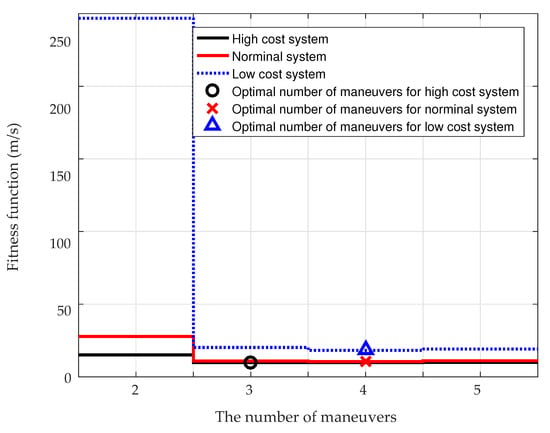
Figure 1. Optimal fitness function with respect to the number of maneuvers when $t_f$ = 2000 s.

Table 3 presents the simulation results when $t_f=$ 2000 s. For the total $\mathrm{\Delta }v$ representing the fuel consumption, it is obtained that more $\mathrm{\Delta }v$ is required to satisfy the constraint of final position dispersion when there are stronger uncertainties. This is because extra actuator execution errors are injected into the system due to extra maneuvers. For the optimal maneuver times, it is seen that the high-cost system requires only one mid-course correction at 576 s, the nominal-cost system requires two mid-course corrections—one early at 423 s and one late at 1504 s—and the low-cost system requires two very late mid-course corrections at 1406 s and 1880 s. The late maneuvers for the low-cost system are not surprising since injecting large maneuver execution errors earlier in the trajectory creates a larger final position dispersion.

Table 3. Optimal trajectory results when $t_f=$ 2000 s.

Case 1, ${\mathit{t}}_{\mathit{f}}=$ 2000 s
System	Deterministic	High Cost	Nominal	Low Cost
Fitness (m/s)	NA	9.537	10.009	14.181
$\mathrm{\Delta }v$ (m/s)	9.480	9.481	9.488	10.053
3-${\sigma }_{\mathrm{\Delta }v}$ (m/s)	NA	0.057	0.520	4.128
3-${\sigma }_r$ (m)	NA	2.999	14.968	20.246
Opt. no. of maneuvers	2	3	4	4
Maneuver times (s)	$\left[\begin{array}{c}0\\ 2000\end{array}\right]$	$\left[\begin{array}{c}0\\ 576\\ 2000\end{array}\right]$	$\left[\begin{array}{c}0\\ 423\\ 1504\\ 2000\end{array}\right]$	$\left[\begin{array}{c}80\\ 1406\\ 1888\\ 2000\end{array}\right]$

Figure 2 and Figure 3 show the in-plane and out-of-plane optimal trajectories (notation cvx indicates the optimal trajectory solved by convex optimization without uncertainties) and the associated maneuver locations (denoted as M1, M2, etc.) when $t_f$ = 2000 s. It can be seen from the two figures that the designed robust optimal trajectories are basically the same as the deterministic optimal trajectory, which means that the main objective of the robust trajectory optimization algorithm is to correct the trajectory against the uncertainties rather than replan a new trajectory.

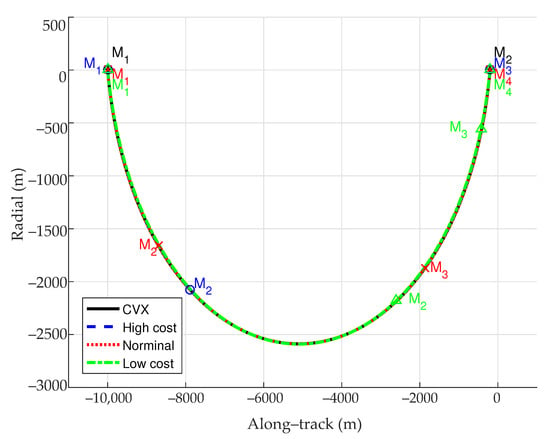
Figure 2. Optimal trajectories (in-plane) when $t_f$ = 2000 s.

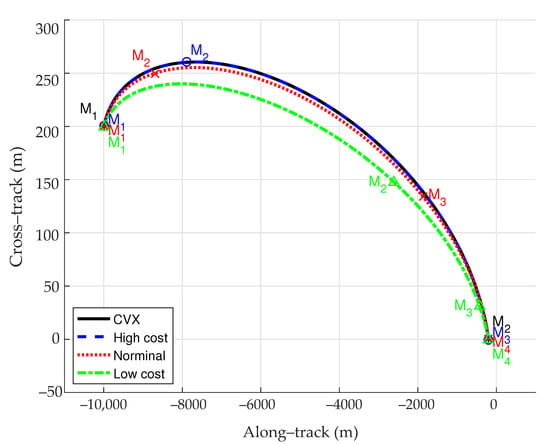
Figure 3. Optimal trajectories (out-of-plane) when $t_f$ = 2000 s.

Figure 4 presents the Monte Carlo analysis for the low-cost system when $t_f=$ 2000 s. A total of 1000 independent Monte Carlo simulations were carried out with the stochastic uncertainties and are shown in the figure with blue and solid lines. The uncertainty effect on the 3-$\sigma$ position dispersion is also analyzed by the proposed STT-based method and the result is shown in the figure with red and dashed line. Meanwhile, the yellow and dotted line in the figure denotes the mission constraint of the final position dispersion. It is verified that the proposed STT-based uncertainty effect evaluation method can provide the accurate upper bound of the Monte Carlo results. Moreover, all Monte Carlo trajectories satisfy the final position dispersion constraint, which indicates that the proposed robust trajectory design method is effective when considering strong uncertainties.

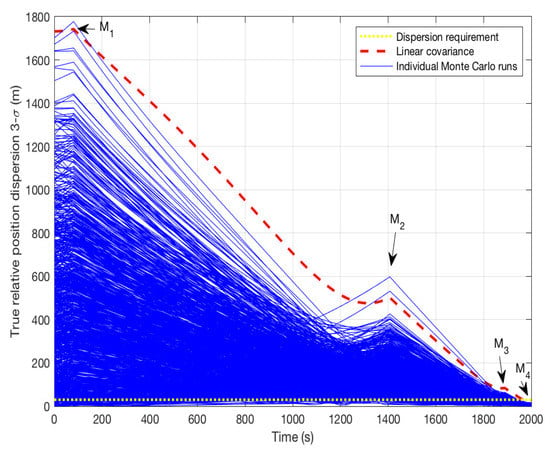
Figure 4. Monte Carlo analysis for low-cost system when $t_f$ = 2000 s.

Figure 5 shows the optimal fitness function with respect to the number of maneuvers when $t_f$ = 6000 s. Four maneuvers are needed in the robust optimal trajectories for both the high- and nominal-cost systems, while five maneuvers are needed in the robust optimal trajectories for the low-cost system.

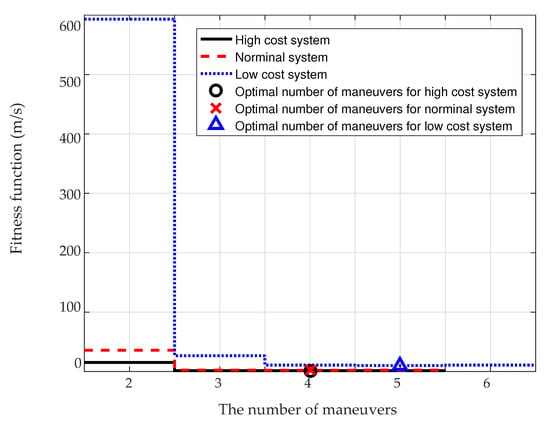
Figure 5. Optimal fitness function with respect to the number of maneuvers when $t_f$ = 6000 s.

Table 4 presents the simulation results when $t_f=$ 6000 s. For the optimal maneuver times, it is seen that the high-cost system requires two mid-course corrections at 1127 s and 4735 s, the nominal cost system requires two mid-course corrections—one at 3868 s and one late at 5162 s—and the low-cost system requires three mid-course corrections at 1377 s, 4741 s and 5829 s. It is noteworthy that the designed maneuvers are completely the same in the deterministic trajectory and the high-cost system trajectory. This is because even applying $\mathrm{\Delta }\mathit{v}\left(t_j\right)$ of the deterministic trajectory into the high-cost system, the final 3-$\sigma$ position dispersion constraint is still satisfied and, as a result, the self-adaptive differential evolution algorithm is not run to avoid unnecessary calculations. A detailed explanation can be found in Algorithm 1 and Remark 2.

Table 4. Optimal trajectory results when $t_f=$ 6000 s.

Case 2, ${\mathit{t}}_{\mathit{f}}=$ 6000 s
	Deterministic	High Cost	Nominal	Low Cost
Fitness (m/s)	NA	1.332	1.820	5.892
$\mathrm{\Delta }v$ (m/s)	1.267	1.267	1.416	1.354
3-${\sigma }_{\mathrm{\Delta }v}$ (m/s)	NA	0.065	0.404	4.538
3-${\sigma }_r$ (m)	NA	2.902	14.999	29.939
Opt. no. of maneuvers	4	4	4	5
Maneuver times (s)	$\left[\begin{array}{c}0\\ 1127\\ 4735\\ 6000\end{array}\right]$	$\left[\begin{array}{c}0\\ 1127\\ 4735\\ 6000\end{array}\right]$	$\left[\begin{array}{c}180\\ 3868\\ 5162\\ 6000\end{array}\right]$	$\left[\begin{array}{c}62\\ 1377\\ 4741\\ 5829\\ 6000\end{array}\right]$

Figure 6 and Figure 7 show the in-plane and out-of-plane optimal trajectories when $t_f$ = 6000 s, as well as the maneuver locations. It can be seen from the figures that the designed robust optimal trajectory of the high-cost system is basically the same as the deterministic optimal trajectory due to the same maneuvers, while the designed robust optimal trajectories of the nominal and low-cost systems are different from the deterministic optimal trajectory. A conclusion is drawn that the proposed method is capable of replanning a new trajectory when the uncertainty effect is great to the rendezvous system.

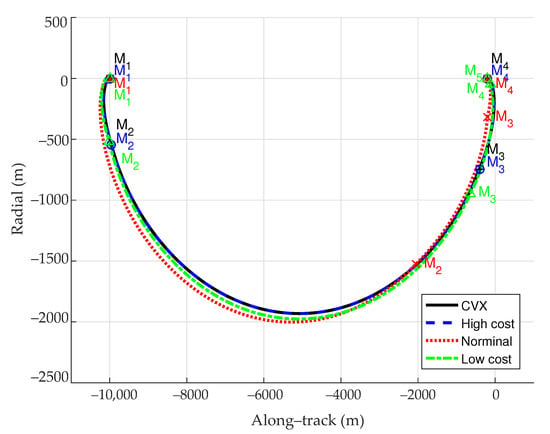
Figure 6. Optimal trajectories (in-plane) when $t_f$ = 6000 s.

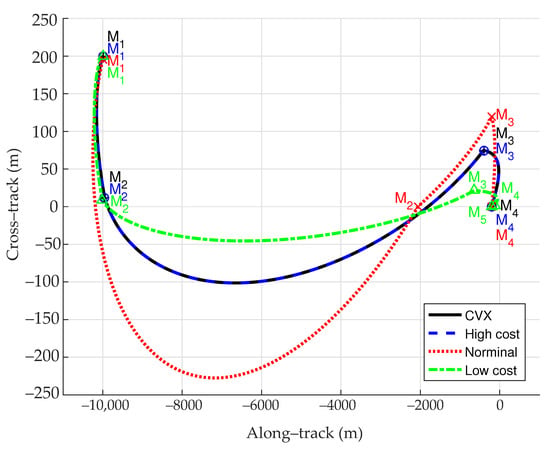
Figure 7. Optimal trajectories (out-of-plane) when $t_f$ = 6000 s.

Figure 8 presents the Monte Carlo analysis for the high-cost system when $t_f=$ 6000 s. It is verified that the proposed STT-based uncertainty effect evaluation method can provide the accurate upper bound of the Monte Carlo results. Moreover, all Monte Carlo trajectories satisfy the final position dispersion constraint.

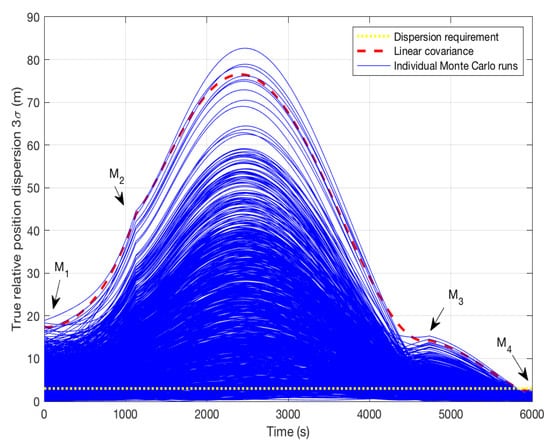
Figure 8. Monte Carlo analysis for high-cost system when $t_f$ = 6000 s.

Figure 9 shows the optimal fitness function with respect to the number of maneuvers when $t_f$ = 12,000 s. Four maneuvers are needed in the robust optimal trajectories for both the high- and nominal-cost systems, while five maneuvers are needed in the robust optimal trajectories for the low-cost system.

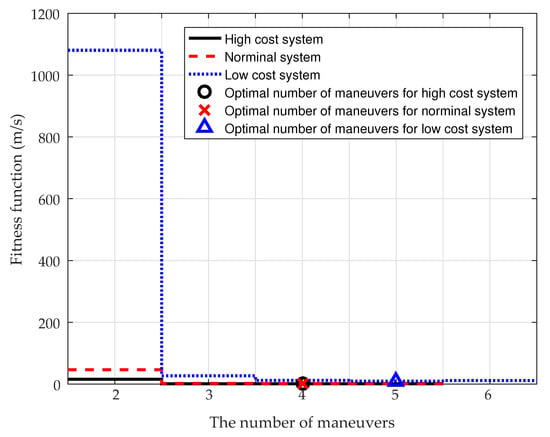
Figure 9. Optimal fitness function with respect to the number of maneuvers when $t_f$ = 12,000 s.

Table 5 presents the simulation results when $t_f=$ 12,000 s. For the optimal maneuver times, it is interesting to note that the time of the first maneuver is not 0 in all stochastic cases. This is because there are initial position and velocity dispersions at $t=0$ s. For a long transfer time, rather than using a poor measured state with large dispersion to compute the maneuver, it would be better to wait until the navigation algorithm has run for some time and the measured states are more accurate.

Table 5. Optimal trajectory results when $t_f=$ 12,000 s.

Case 3, ${\mathit{t}}_{\mathit{f}}=$ 12,000 s
	Deterministic	High Cost	Nominal	Low Cost
Fitness (m/s)	NA	0.796	1.258	5.437
$\mathrm{\Delta }v$ (m/s)	0.665	0.727	0.785	0.918
3-${\sigma }_{\mathrm{\Delta }v}$ (m/s)	NA	0.069	0.473	4.519
3-${\sigma }_r$ (m)	NA	2.994	14.986	29.959
Opt. no. of maneuvers	4	4	4	5
Maneuver times (s)	$\left[\begin{array}{c}0\\ 1359\\ \mathrm{10,183}\\ \mathrm{12,000}\end{array}\right]$	$\left[\begin{array}{c}858\\ 7343\\ \mathrm{10,572}\\ \mathrm{12,000}\end{array}\right]$	$\left[\begin{array}{c}171\\ 7021\\ \mathrm{11,162}\\ \mathrm{12,000}\end{array}\right]$	$\left[\begin{array}{c}161\\ 4222\\ \mathrm{10,527}\\ \mathrm{11,828}\\ \mathrm{12,000}\end{array}\right]$

Figure 10 and Figure 11 show the in-plane and out-of-plane optimal trajectories when $t_f$ = 12,000 s, as well as the optimal maneuver locations. In this case, the optimal maneuvers change the desired optimal trajectory.

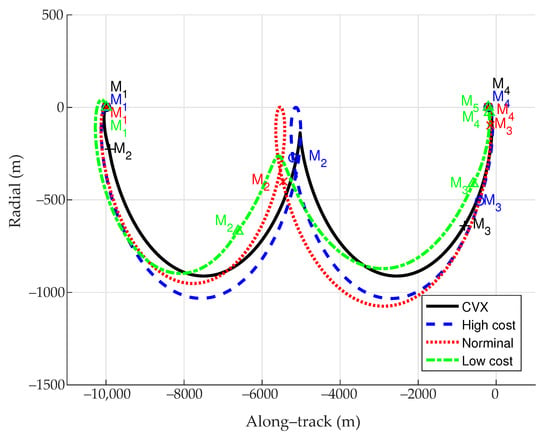
Figure 10. Optimal trajectories(in-plane) when $t_f$ = 12,000 s.

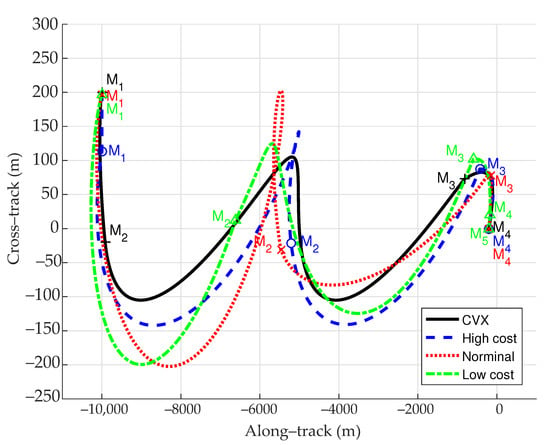
Figure 11. Optimal trajectories (out-of-plane) when $t_f$ = 12,000 s.

Figure 12 presents the Monte Carlo analysis for the high-cost system when $t_f=$ 12,000 s. It is verified that the proposed STT-based uncertainty effect evaluation method can provide the accurate upper bound of the Monte Carlo results. Moreover, all Monte Carlo trajectories satisfy the final position dispersion constraint.

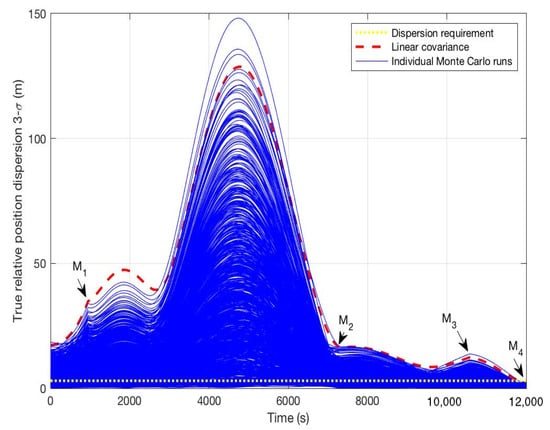
Figure 12. Monte Carlo analysis for high-cost system when $t_f$ = 12,000 s.

Table 6 presents the simulation results when the final time is free. Four maneuvers are needed in the robust optimal trajectories for both the high- and nominal-cost systems, while five maneuvers are needed in the robust optimal trajectories for the low-cost system. As expected, the optimal fitness functions in all systems are smaller than the fixed final time case $t_f$ = 12,000 s. Theoretically, when the system is free with uncertainties, $\mathrm{\Delta }v$ should approach zero when the final time is free, and the final time should approach infinity. When uncertainties are considered, however, an excessively long final time will lead to a large final state dispersion. It can be observed that the optimized final time is shorter when the uncertainties are stronger, which provides clear evidence of the uncertainty effect on the rendezvous system.

Table 6. Stochastic optimal performance results, $t_f=$ free.

Case 4, ${\mathit{t}}_{\mathit{f}}=$ free
System	High Cost	Nominal	Low Cost
Final time (s)	17,043	16,964	10,086
Fitness (m/s)	0.651	1.073	5.424
$\mathrm{\Delta }v$ (m/s)	0.602	0.609	1.018
3-${\sigma }_{\mathrm{\Delta }v}$ (m/s)	0.049	0.464	4.407
3-${\sigma }_r$ (m)	2.994	14.967	29.987
Opt. no. of maneuvers	4	4	5
Maneuver times (s)	$\left[\begin{array}{c}590\\ \mathrm{11,009}\\ \mathrm{15,615}\\ \mathrm{17,043}\end{array}\right]$	$\left[\begin{array}{c}179\\ \mathrm{12,629}\\ \mathrm{16,132}\\ \mathrm{16,964}\end{array}\right]$	$\left[\begin{array}{c}110\\ 4214\\ 8752\\ 9914\\ \mathrm{10,086}\end{array}\right]$

Figure 13 and Figure 14 show the in-plane and out-of-plane trajectories when $t_f$ = free, as well as the optimal maneuver locations.

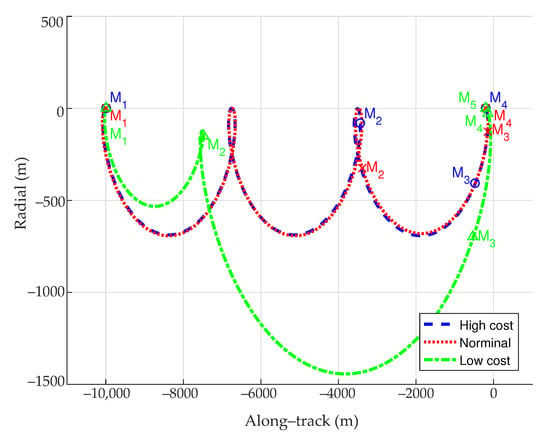
Figure 13. Optimal trajectories (in-plane) when $t_f=$ free.

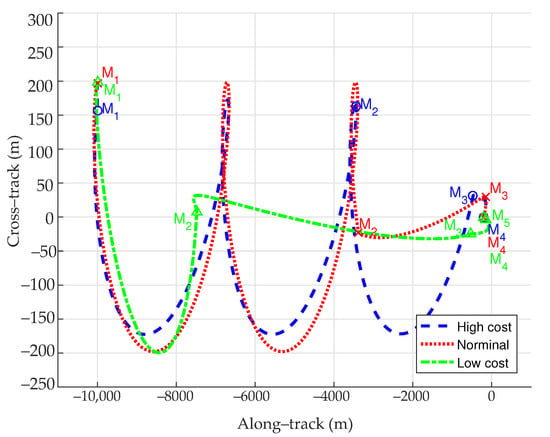
Figure 14. Optimal trajectories (out-of-plane) when $t_f=$ free.

6. Conclusions

A novel robust trajectory design method has been proposed in this work for the rendezvous and proximity operations mission in Earth orbit. Optimal maneuver plans have been provided that not only satisfy the final state dispersion constraints but minimize the effect of multi-source uncertainties. The main contributions and advantages are twofold: on the one hand, multi-source uncertainties are modeled of the closed-loop rendezvous system and the effect of the uncertainties is quantized and evaluated based on the state transition tensor method. On the other hand, the effect of the uncertainties is considered in the robust rendezvous trajectory design problem, which is effectively solved by an improved differential evolution algorithm. Numerical simulations clearly show that the multi-source uncertainties, including environment parameter uncertainty, actuator error, sensor noise, navigation error and initial state dispersion, may have significant effects on the designed trajectory. By employing the proposed method, the effect of uncertainties is effectively considered and the optimized robust rendezvous trajectory satisfies the mission requirements and has strong robustness against uncertainties. In future work, complex constraints including a no-fly zone constraint, collision avoidance constraint and docking axis constraint will be considered in the proposed robust trajectory design framework.